Local Density Correlations in Liquids

The structure and dynamics of liquids and glasses are usually discussed in terms of the short-range atomic structure and the nature of atomic bonds. However, many properties of liquids are rather similar and only weakly dependent on chemistry. Here we suggest that these properties are controlled not so much by the short-range atomic correlations but mainly by the medium-range density correlations which are similar among various liquids and supersede chemical details of the system. Taking metallic alloy liquids as examples we discuss the origin of the medium-range density correlations and argue they are only weakly dependent on the detailed nature of the atomic bond. We also discuss some consequences of the medium-range correlations on atomic transport. By extrapolating the coherence of density correlation to infinity we can define an ideal glass state which is very diverse in the local atomic structure but is characterized by long-range density correlations. This ideal state is very different from those previously proposed based on the coherence in the atomic structure.

Introduction

The atomic structure of liquid and glass appears random, but unlike gas they are condensed matters held together by cohesive force. The density of a liquid is comparable, or even higher as in the case of water, than that of a solid of the same composition. Therefore, atoms are strongly correlated in position and momentum, and the structure and dynamics of liquid should be described by not where the atoms are (structure), but in terms of the correlations. Actually the “structure of liquid” is an oxymoron, because liquid is intrinsically dynamic. In solids, the time-scales of the structure, diffusion and phonon are all very different, so that they can be characterized by different scattering methods; diffraction (elastic scattering) for structure, inelastic scattering for phonon and quasielastic scattering for diffusion. However, in liquids the time-scales for them are all in the same order of magnitude, about a pico-second (ps). Consequently liquid shows no elastic scattering [1], and phonons are overdamped and often localized. Thus, not only the method of characterization needs to be reconsidered, but also the terminology needs to be readdressed; structure, diffusion and phonon are all mixed up and are deeply entangled. We need a new experimental approach and a new description to characterize such mixed dynamics. The same difficulty is found for a large family of soft-matter including colloids and biological matters. Actually to call them soft-matter is missing the point, because softness is relative, and is not the most important characteristic of their nature. They may be more adeptly called dynamic aperiodic matter (DAM), rather than soft-matter.

A powerful approach to describe the dynamics of DAM is the time-dependent pair-distribution function (PDF) called the Van Hove function (VHF) [2]. The VHF is often spelled the van Hove function, but he is not Dutch but Belgian; we follow the original spelling. The VHF has been known for a long time, but only recently it became possible to determine it by inelastic scattering experiments as shown in Figure 1 [3]. At the same time the behavior of the VHF was examined by molecular dynamics (MD) simulation, which gave a new insight on the interpretation of the VHF [4]. In particular, it became clear that the dynamics of the medium-range correlations beyond the first nearest neighbors is quite distinct from that of the short-range structure represented by the first neighbor shell. Whereas, the short-range structure reflects the local chemistry, the medium-range part of the VHF describes collective density fluctuations which are more universal and less dependent on chemistry.

FIGURE 1

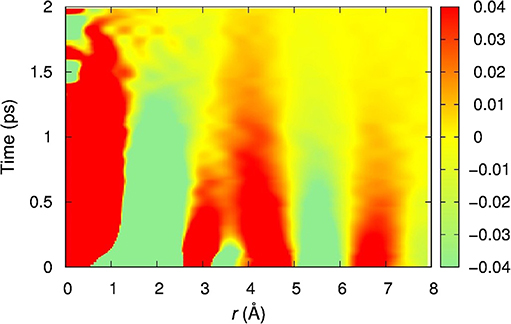
Figure 1. The Van Hove function of water at room temperature determined by inelastic x-ray scattering [3]. The cut at t = 0 corresponds to the snapshot PDF. As time proceeds the nearest neighbors move away, while the second neighbors move in, showing dynamic correlations.

Van Hove Function

The structure of liquid and glass is usually described by the atomic pair-distribution function (PDF),

$\begin{array}{ll}g(r)=\frac{1}{4\pi r^2{\rho }_{0}N}{\displaystyle \sum _{i,j}}\langle \delta (r-|{\text{r}}_{\text{i}}-{\text{r}}_{\text{j}}|)\rangle & (1)\end{array}$

where r_i is the position of the i-th atom at time t, ρ₀ is the atomic density of N atoms, and <…> denotes thermal average. However, for liquid this is misleading because r_i varies with time. The PDF is merely the same-time (snapshot) correlation function. The time-dependent, or time-delayed, correlation is described by the VHF,

$\begin{array}{ll}G(r,t)=\frac{1}{4\pi r^2{\rho }_{0}N}{\displaystyle \sum _{i,j}}\langle \delta (r-|{\text{r}}_{\text{i}}(0)-{\text{r}}_{\text{j}}(t)|)\rangle ,& (2)\end{array}$

where r_i(t) is the position of the i-th atom at time t. At t = 0, G(r, 0), is just the g(r). The VHF describes how g(r) decays with time, and is obtained from the dynamic structure factor measured by inelastic scattering, S(Q, ω) [5],

$\begin{array}{ll}S(\text{Q},\omega )=\frac{1}{2\pi N}{\displaystyle \sum _{i,j}}{\displaystyle \int }\langle exp(i\text{Q}[{\text{r}}_{\text{i}}(0)-{\text{r}}_{\text{j}}(t)])\rangle exp(-i\omega t)dt,& (3)\end{array}$

through the double Fourier-transformation,

$\begin{array}{ll}G(r,t)-1=\frac{1}{2{\pi }^2{\rho }_{0}r}{\displaystyle \int }S(Q,\omega )sin(Qr)exp(i\omega t)QdQd\omega ,& (4)\end{array}$

where Q = |Q|. Sometimes S(Q, ω) is Fourier-transformed to the time domain by

$\begin{array}{ll}F(Q,t)={\displaystyle \int }S(Q,\omega )exp(i\omega t)d\omega & (5)\end{array}$

which is called the intermediate scattering function and is widely used for the study of relaxation phenomena [5]. The VHF is obtained by the Fourier-transformation of F(Q, t) to real space. We should also note that the energy integral of S(Q, ω),

$\begin{array}{ll}S(\text{Q})={\displaystyle \int }S(\text{Q},\omega )d\omega ,& (6)\end{array}$

yields the snapshot PDF, g(r), upon Fourier-transformation. Therefore, the regular x-ray diffraction measurement with low energy resolution produces the snapshot PDF. For a long time this has been the only way to assess the structural nature of liquid. That is why g(r) is called the “structure of liquid.” Now that the VHF is experimentally accessible, we should focus on the VHF. To perform the double Fourier-transformation by Equation (4) requires the knowledge of S(Q, ω) over a wide Q-ω space, which has been difficult for a long time. But recent progress in the source and instrumentation [6, 7] made it possible to determine the VHF in a reasonable time.

Medium-range Density Correlation

At first it was assumed that the VHF decays uniformly for all distances, controlled by diffusion [8]. Then the decay rate of F(Q, t) should vary as 1/Q² as expected for diffusion. However, De Gennes showed that the decay rate of F(Q, t) depends non-monotonically on Q [9]. In particular, the quasi-elastic width, Δω, of S(Q, ω) shows strong narrowing at the first peak of S(Q), now known as the De Gennes narrowing. This effect is generally considered to be the evidence of collective excitations, but our recent results have shown otherwise. As shown in Figure 2 the decay time of the VHF increases linearly with distance, with the rate related to the Maxwell relaxation time [4]. In general the r-dependent decay time depends on r as,

$\begin{array}{ll}\tau (r)=\tau (0)+{\tau }_r{\left(\frac{r}{a}\right)}^{\chi },& (7)\end{array}$

where a is the nearest neighbor distance. The power exponent χ depends on the spatial dimension, D, as $\chi =\frac{(D-1)}{2}$. The argument for this dimensional dependence is as follows. The number of atoms in the shell from r to r + dr, Ndr, is proportional to r^D−1. Then the rate of fluctuation is proportional to $\sqrt{N}$, thus to r^(D−1)/2. The De Gennes narrowing occurs as a natural consequence of this r-dependence, and is not necessarily indicative of collective excitation. Whereas, the first peak of the VHF describes the dynamics of the nearest neighbors, the higher order peaks describe the dynamics of many atoms. The number of atoms involved in the first peak is the coordination number, N_C, which is 12–14 for close-packed systems. Then the number of atoms in the n-th shell is of the order of n²N_C, quite a large number as n increases. The width of the peaks of g(r) beyond the first peak is of the order of a/2, whereas the uncertainty in the atomic position, for instance the phonon amplitude, is smaller by an order of magnitude. That is why at large distances the PDF peaks do not reflect detailed atomic positions, but a coarse-grained density correlations.

FIGURE 2

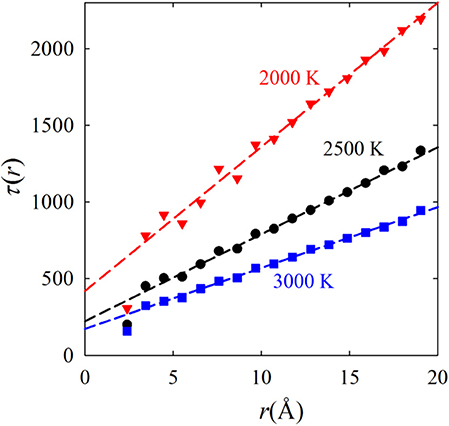
Figure 2. Linear dependence of the decay time of the Van Hove function on distance, simulated for liquid Fe [4].

At temperatures above the viscosity crossover temperature, T_A [10], which is about twice the glass transition temperature for metallic liquids [11], the phonon propagation length, λ_p = v_tτ_M, where v_t is the transverse sound velocity, becomes smaller than the interatomic distance [12]. In other words the structural relaxation time, τ_M, becomes shorter than the time-scale of phonon, ${\tau }_D=\frac{2\pi }{{\omega }_D}$, where ω_D is the Debye frequency. Then atoms separated by a distance beyond the range of the interatomic potential cannot communicate, and should show no correlation. The reason why the PDF shows oscillation beyond the first peak even at high temperatures is that these peaks represent not the detailed structural correlations of atoms, but coarse-grained medium-range density correlations. These density correlations interact via long wave longitudinal waves which survive well above T_A [13] and modulate only the local density, not the detailed structure. For this reason the medium-range correlations represent the coarse-grained density rather than the atomic structure.

More than a century ago Ornstein and Zernike published a paper with a remarkable insight [14]. They pointed out that g(r) has two components,

$\begin{array}{ll}g(\text{r})=1+c(\text{r})+m(\text{r}),& (8)\end{array}$

where c(r) describes short-range correlation, and m(r) medium-range correlation. The c(r) is directly influenced by the interatomic potential, whereas m(r) is a medium-range consequence of c(r), and as discussed above reflects coarse-grained density correlations. Then, they proposed a mean-field closure equation,

$\begin{array}{ll}h\left(r\right)=c\left(r\right)+{\rho }_0{\displaystyle \int c}\left(\left|r-r^{\prime }\right|\right)h\left(r^{\prime }\right)d{r}^{\prime }& (9)\end{array}$

where h(r) = c(r) + m(r). Then, as a result of integration the medium-range part of h(r) reflects the effect of the interatomic potential only indirectly, usually weakly. We now move to Q space by the Fourier-transformation. Equation (9) becomes [15],

$\begin{array}{ll}h(\text{Q})=c(\text{Q})+{\rho }_{0}c(\text{Q})h(\text{Q}),h(\text{Q})=\frac{c(\text{Q})}{1-{\rho }_{0}c(\text{Q})}.& (10)\end{array}$

c(r) has a relatively sharp peak at the interatomic distance, a, represented by

$\begin{array}{ll}c(\text{r})={\displaystyle \int }f(r-r^{\prime })\delta (r^{{}^{\prime }}-a)d{r}^{\prime }.& (11)\end{array}$

where f (r) is the peak shape function. Then,

$\begin{array}{ll}c(Q)=F(Q)\frac{sin(Qa)}{Qa},& (12)\end{array}$

where F(Q) is the Fourier-transform of f (r). Thus c(Q) has the first peak at Q = Q₁ ~ 5π/2a. The medium-range part of h(r), m(r), is determined primarily by the first peak of S(Q) [16], so that only the first peak of c(Q) at Q₁ is of interest for m(r). Note that the effects of the interatomic potential and composition are included solely in f (r), thus in F(Q), which is a slowly varying function of Q. Consequently the first peak of c(Q) is nearly universal, only weakly dependent on composition and the nature of bonding. As a result the behavior of m(r) is remarkably general. This makes sense because m(r) represents medium-range density correlations which are almost independent of atomic details. For oxide and polymeric glasses if we use the first sharp diffraction peak (FSDP) [17], similar results should be obtained.

We expand the first peak of c(Q) around Q₁

$\begin{array}{ll}c(Q)=c(Q_1)\left[1-\frac{{(Q-Q_1)}^2}{2{\sigma }_Q^2}+\dots \right]& (13)\end{array}$

Because c(r) has a relatively sharp peak F(Q) is a slowly varying function. Then,

$\begin{array}{llll}\frac{d^{2}c(Q)}{d{Q}^2}& \approx & -F(Q_1)\frac{a}{Q_1}=-c(Q_1)a^2,\frac{1}{{\sigma }_Q^2}\approx a^2.& (14)\end{array}$

$\begin{array}{llll}1& -& {\rho }_{0}c(Q)=1-{\rho }_{0}c(Q_1)\left[1-\frac{a^2}{2}{(Q-Q_1)}^2+\dots \right],& (15)\end{array}$

$\begin{array}{llll}h(Q)& \approx & \frac{\frac{c(Q_1)}{(1-{\rho }_{0}c(Q_1))}}{1+{\xi }_s^2{(Q-Q_1)}^2}=\frac{\frac{2{\xi }_s^2}{a^2{\rho }_0}}{1+{\xi }_s^2{(Q-Q_1)}^2},& (16)\end{array}$

where

$\begin{array}{ll}{\xi }_s^2=\frac{a^2}{2}\frac{{\rho }_{0}c(Q_1)}{1-{\rho }_{0}c(Q_1)}.& (17)\end{array}$

Thus, the medium-range coherence depends on both the physical density and the strength of the nearest neighbor correlation, c(Q₁). Now the first peak of S(Q) should be Lorentzian by Equation (16). Indeed it is Lorentzian for simple liquids [18]. For some liquids it is more Gaussian, and S(Q₁) is relatively small, as discussed elsewhere (Ryu et al., unpublished). The Fourier-transform of the Lorentzian is the screened Coulomb (or Yukawa) potential,

$\begin{array}{ll}h(r)\approx \frac{exp\left(-\frac{r}{{\xi }_s}\right)}{r}sin(Q_{1}r).& (18)\end{array}$

As shown in Figure 3 G(r) = 4πrρ₀[g(r) – 1] ~ 4πrh(r) shows an exponential decay with sin(Q₁r) oscillation. This form is widely found, even when the shape of the first peak of S(Q) is more Gaussian.

FIGURE 3

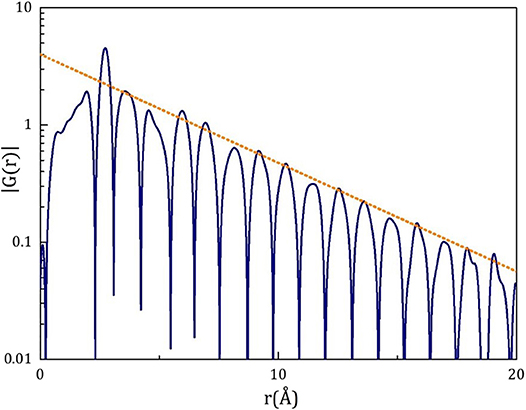
Figure 3. Exponential decay of |G(r)|, where G(r) = 4πrρ₀[g(r) – 1], for Pd_42.5Ni_7.5Cu₃₀P₂₀ liquid at 600 K (T_g = 573K) [18].

The coherence length, ξ_s, varies with temperature, through the temperature dependence of c(Q₁) by Equation (17). At temperatures above T_A τ_M is shorter than the phonon time-scale, ${\tau }_D=\frac{2\pi }{{\omega }_D}$. Thus atoms cannot communicate through phonons, and the transport is controlled by action of cutting the bond, anankeons [12, 19]. Then, the atomic transport is controlled by the nearest neighbors alone, and medium-range order has no direct relevance. The snapshot structure represented by S(Q) has little or no bearing to the transport properties. However, at temperatures well below T_A the dynamics is more cooperative, and is controlled by the density correlations represented by ξ_s(T). Also the time-scale of structural change is much slower than phonons. In this case the snapshot structure plays the usual role of the structure in determining the dynamic properties such as transport and mechanical deformation. The activation energy for viscosity, E_a(T),

$\begin{array}{ll}\eta (T)={\eta }_{\infty }exp\left(\frac{E_a(T)}{k_{B}T}\right).& (19)\end{array}$

Near the glass transition E_a(T) for Pd_42.5Ni_7.5Cu₃₀P₂₀ liquid depends on the coherence volume as,

$\begin{array}{ll}{E}_a(T)=E_0{\left(\frac{{\xi }_s(T)}{a}\right)}^3,& (20)\end{array}$

as shown in Figure 4. The coherence volume normalized by the atomic volume indicates the number of atoms involved in the coherent volume. Equation (20) means that the activation energy for viscosity depends linearly on the number of atoms involved in the local shear deformation event [20]. Through this relationship the temperature variation of ξ_s is related to liquid fragility [18]. Similar arguments were advanced for the height of the first peak of S(Q) for metallic liquids [21, 22] and the width of the FSDP of complex liquids [17].

FIGURE 4

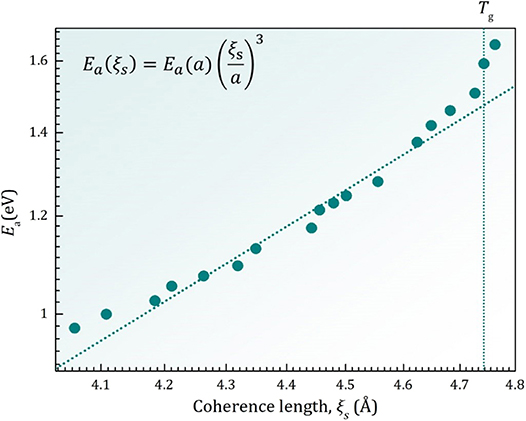
Figure 4. Dependence of the activation energy for viscosity, E_a(T), on the coherence length, ξ_s(T), of density correlation [18].

Various theories, notably the mode-coupling theory [23], use the first peak of S(Q) as a parameter to represent the atomic structure. Ironically their success originates from the fact that the first peak of S(Q) does not describe the detailed atomic structure but represent the coarse grained density fluctuations which are more general and do not depend on detailed chemistry. Conversely they indeed catch the universal aspects of the behavior of liquid and glass.

Ideal Glass State

The Equation (17) is quite enlightening. If

$\begin{array}{ll}Z={\rho }_{0}c(Q_1)\ll 1,& (21)\end{array}$

ξ_s is negligibly small, and the liquid structure has no correlation. When Z = 2/3, ξ_s = a. As Z approaches unity the coherence length ξ_s quickly increases, and diverges when Z = 1. Then h(Q) has a Bragg peak at Q₁. In other words,

$\begin{array}{ll}c(Q_1)=\frac{1}{{\rho }_0}=V_a=\frac{V}{N},& (22)\end{array}$

is the critical condition for the coherence length, ξ_s, to diverge, attaining the ideal glass state. By taking the limit of ξ_s → ∞ with Equation (18), its medium-range order is given by

$\begin{array}{ll}{h}_{IG}(r)\approx \frac{sin(Q_{1}r)}{r}.& (23)\end{array}$

Then, G₀(r) = 4πrρ₀[g₀(r) – 1] has long-range oscillation. This ideal glass state has long-range density correlation without positional order. Quasicrystal [24] was the first example of a state with long-range order without positional order. It is a crystal in six-dimensions, characterized by six order vectors. The ideal glass is a crystal in the infinite dimensions. Therefore the magnitude of the coherence length at the glass transition is a good measure of how close the structure is to the ideal glass state (Ryu et al., unpublished).

The S(Q) of the ideal glass state has a Bragg sphere with the radius of Q₁. The single atom density is given by

$\begin{array}{ll}\rho (\text{r})={\displaystyle \int }{\rho }_{Q}exp({\text{Q}}_1·\text{r}+\delta (\Omega ))d\Omega ,& (24)\end{array}$

where Ω is the solid angle of the vector Q₁, and the phase factor δ(Ω) varies randomly with Ω to avoid pile-up of atomic density at the same place. Each density wave has the same wavelength, λ₁ = 2π/Q₁ = (4/5)a, thus it is fairly coarse-grained. In order to specify the atomic position with higher precision higher order Bragg peaks are needed, just as in crystalline solids. For this reason the density correlation established in the ideal glass does not represent the order in the atomic structure, such as the icosahedral order. Indeed the model of ideal glass obtained by the reverse Monte-Carlo simulation to fit to G₀(r) has very diverse local structures. The local topology by Voronoi polyhedral analysis [18] shows there is no dominant topology with a wide distribution of local structures. For instance icosahedra, which dominate the simple liquid [25, 26], has the population of only 0.7% in this model of ideal glass. A liquid is stabilized by configurational entropy. This diversity in the local structure is an excellent signature of such a high entropy state. The high entropy state is achieved either by increasing temperature (usual way), or mixing a large number of elements. The discovery of bulk metallic glasses with many elements [27, 28] is consistent with the second approach. On the other hand the structure dominated by a single local structural motif, such as an icosahedron, has a low entropy and is far from ideal. It easily forms an ordered state including the crystalline state.

The idea that the growth of icosahedral clusters which are incompatible with periodicity is the origin of glass formation has been widely discussed [29–31]. The current discussion on the ideal glass assumes it is a low enthalpy [32], low entropy state dominated by one or two local structures [33]. In contrast, the ideal glass proposed here is characterized by the diversity in the local structure and high configurational entropy, which is the hallmark of the liquid state. The dominance by a particular structural motif, such as icosahedron, is seen in a single component system which is a poor glass former, or in glasses with particular compositions [34]. In our view it is a sign of nano-crystallization rather than glass formation.

Conclusions

Usually the structure of liquid is described in terms of the same-time two body correlation function, the snapshot pair-distribution function (PDF). However, liquid does not have a structure in the usual sense because it is inherently dynamic. It is much preferred to characterize the liquid dynamics through the dynamic two-body correlation function, the Van Hove function (VHF). The recent studies of the VHF by experiment and simulation revealed the fundamental difference in nature between the short-range order and the medium-range order. Whereas, the short-range order, represented by the first peak of the PDF, describes the atomic environment of an atom and reflects the nature of the atomic bond and some details of the interatomic potential, the medium-range order, represented by the PDF peaks beyond the first peak, describes more coarse-grained density correlations which supersedes local chemistry. Thus, various liquids with different bonding and chemistry share very similar medium-range order, characterized by the Ornstein-Zernike form and the coherence in density correlation. This density correlation is coarse-grained and does not represent detailed atom-atom correlation. Therefore, it is nearly independent of the details of local structure. The ideal glass state obtained by extrapolation has long-range correlations in density, but its local structure is very diverse and it has no structural coherence at the atomic level. In our view many properties of liquids, such as viscosity just above the glass transition, depend on such density correlations rather than atomic structural correlations. This explains why many properties of liquids depend only weakly upon chemistry, and are largely common for liquids with varying nature of atomic bonds. The efforts to seek the origin of these properties directly to local atomic structure may be misguided.

Data Availability Statement

The datasets for this study can be obtained from the author (ZWdhbWkmI3gwMDA0MDt1dGsuZWR1).

Author Contributions

This work was conceived, executed, and authored by TE.

Funding

This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Egelstaff PA. An Introduction to the Liquid State. 2nd ed.Oxford: Oxford University Press (1991).

Google Scholar

2. Van Hove L. Correlation in space and time and Born approximation scattering in systems of interacting particles. Phys Rev. (1954) 95:249–62. doi: 10.1103/PhysRev.95.249

CrossRef Full Text | Google Scholar

3. Iwashita T, Wu B, Chen W-R, Tsutsui S, Baron AQR, Egami T. Seeing real-space dynamics of liquid water through inelastic x-ray scattering. Sci. Adv. (2017) 3:e1603079. doi: 10.1126/sciadv.1603079

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wu B, Iwashita T, Egami T. Atomic dynamics in simple liquid: De Gennes narrowing revisited. Phys. Rev Lett. (2018) 120:135502. doi: 10.1103/PhysRevLett.120.135502

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Lovesay SW. Theory of Neutron Scattering from Condensed Matter. Vol. 1. Oxford: Oxford University Press (1984).

Google Scholar

6. Mason TE, Abernathy D, Anderson I, Ankner J, Egami T, Ehlers G, et al. The spallation neutron source in Oak Ridge: a powerful tool for materials research. Phys B. (2006) 385–86:955–60. doi: 10.1016/j.physb.2006.05.281

CrossRef Full Text | Google Scholar

7. Baron AQR. High-resolution inelastic X-ray scattering I: Context, spectrometers, samples, and superconductors. In: Jaeschke E, Khan S, Schneider J, Hastings J, editors. Synchrotron Light Sources and Free-Electron Lasers. Cham: Springer International Publishing (2015). p. 1–68. doi: 10.1007/978-3-319-04507-8_41-1

CrossRef Full Text

8. Vineyard GH. Scattering of slow neutrons by a liquid. Phys. Rev. (1958) 110:999–1010. doi: 10.1103/PhysRev.110.999

CrossRef Full Text | Google Scholar

9. De Gennes PG. Liquid dynamics and inelastic scattering of neutrons. Physica. (1959) 25:825–39. doi: 10.1016/0031-8914(59)90006-0

CrossRef Full Text | Google Scholar

10. Kivelson D, Kivelson SA, Zhao X, Nussinov Z, Tarjus G. A thermodynamic theory of supercooled liquids. Physica A. (1995) 219:27–38. doi: 10.1016/0378-4371(95)00140-3

CrossRef Full Text | Google Scholar

11. Blodgett ME, Egami T, Nussinov Z, Kelton KF. Proposal for universality in the viscosity of metallic liquids. Sci. Rep. (2015) 5:13837. doi: 10.1038/srep13837

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Iwashita T, Nicholson DM, Egami T. Elementary excitations and crossover phenomenon in liquids. Phys Rev Lett. (2013) 110:205504. doi: 10.1103/PhysRevLett.110.205504

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Levashov VA, Morris JR, Egami T. The origin of viscosity as seen through atomic level stress correlation function. J Chem Phys. (2013) 138:044507. doi: 10.1063/1.4789306

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ornstein LS, Zernike F. Accidental deviations of density and opalescence at the critical point of a single substance. Roy Netherlands Acad Arts Sci. (1914) 17:793–806.

Google Scholar

15. Hansen J-P, McDonald IR. Theory of Simple Liquids. New York, NY: Academic Press (2006).

Google Scholar

16. Cargill GS III. Structure of metallic alloy glasses. Solid State Phys. (1975) 30, 227–20. doi: 10.1016/S0081-1947(08)60337-9

CrossRef Full Text | Google Scholar

17. Voylov DN, Griffin PJ, Mercado B, Keum JK, Nakanishi M, Novikov VN, et al. Correlation between temperature variations of static and dynamic properties in glass-forming liquids. Phys Rev E. (2016) 94:060603. doi: 10.1103/PhysRevE.94.060603

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Ryu CW, Dmowski W, Kelton KF, Lee GW, Park ES, Morris JR, et al. Curie-Weiss behavior of liquid structure and ideal glass state. Sci Rep. (2019) 9:18579. doi: 10.1038/s41598-019-54758-y

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Egami T. Elementary excitation and energy landscape in simple liquids. Mod Phys Lett B. (2014) 28:1430006. doi: 10.1142/S0217984914300063

CrossRef Full Text | Google Scholar

20. Fan Y, Iwashita T, Egami T. How thermally activated deformation starts in metallic glass. Nature Commun. (2014) 5:5083. doi: 10.1038/ncomms6083

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Zhao Y, Bian X, Qin X, Qin J, Hou X. Liquid structure: Is it directly correlative to glass-forming ability? Phys Lett A. (2007) 367:364–8. doi: 10.1016/j.physleta.2007.03.023

CrossRef Full Text | Google Scholar

22. Mauro NA, Blodgett M, Johnson ML, Vogt AJ, Kelton KF. A structural signature of liquid fragility. Nat Commun. (2014) 5:4616. doi: 10.1038/ncomms5616

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Götze W. Complex Dynamics of Glass-Forming Liquids. Oxford: Oxford University Press (2009). doi: 10.1093/acprof:oso/9780199235346.001.0001

CrossRef Full Text | Google Scholar

24. Shectman D, Blech I, Gratias D, Cahn JW. Metallic phase with long-range orientational order and no translational symmetry. Phys Rev Lett. (1984) 53:1951–4. doi: 10.1103/PhysRevLett.53.1951

CrossRef Full Text | Google Scholar

25. Bernal JD. A geometrical approach to the structure of liquids. Nature. (1959) 183:141–7. doi: 10.1038/183141a0

CrossRef Full Text | Google Scholar

26. Finney J. Random packing and the structure of simple liquids. I. The geometry of random close packing. Proc Roy Soc Lond A. (1970) 319:479–93. doi: 10.1098/rspa.1970.0189

CrossRef Full Text | Google Scholar

27. Inoue A, Kita K, Zhang T, Masumoto T. An amorphous La₅₅Al₂₅Ni₂₀ alloy prepared by water quenching. Mater Trans JIM. (1989) 30:722–5. doi: 10.2320/matertrans1989.30.722

CrossRef Full Text | Google Scholar

28. Peker A, Johnson WL. A highly processable metallic glass: Zr_41.2Ti_13.8Cu_12.5Ni_10.0Be_22.5. Appl Phys Lett. (1993) 63:2342–4. doi: 10.1063/1.110520

CrossRef Full Text | Google Scholar

29. Sadoc JF. Use of regular polytopes for the mathematical description of the order in amorphous structures. J Non Cryst Solids. (1981) 44:1–16. doi: 10.1016/0022-3093(81)90128-9

CrossRef Full Text | Google Scholar

30. Steinhardt PJ, Nelson DR, Ronchetti M. Icosahedral bond order in supercooled liquids. Phys Rev Lett. (1981) 47:1297–300. doi: 10.1103/PhysRevLett.47.1297

CrossRef Full Text

31. Nelson DR. Order, frustration, and defects in liquids and glasses. Phys Rev B. (1983) 28:5515–35. doi: 10.1103/PhysRevB.28.5515

CrossRef Full Text | Google Scholar

32. Swallen SF, Kearns KL, Mapes MK, Kim YS, McMahon RJ, Ediger MD, et al. Organic glasses with exceptional thermodynamic and kinetic stability. Science. (2007) 315:353–56. doi: 10.1126/science.1135795

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Tanaka H, Kawasaki T, Shintani H, Watanabe K. Critical-like behaviour of glass-forming liquids. Nat Mater. (2020) 9:324–31. doi: 10.1038/nmat2634

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Cheng YQ, Ma E. Atomic-level structure and structure–property relationship in metallic glasses. Prog Mater Sci. (2011) 56:379–473. doi: 10.1016/j.pmatsci.2010.12.002

CrossRef Full Text | Google Scholar