- Laboratory of Applied Mathematics, Department of Civil, Environmental and Mechanical Engineering, University of Trento, Trento, Italy
In this paper we first review the development of high order ADER finite volume and ADER discontinuous Galerkin schemes on fixed and moving meshes, since their introduction in 1999 by Toro et al. We show the modern variant of ADER based on a space-time predictor-corrector formulation in the context of ADER discontinuous Galerkin schemes with a posteriori subcell finite volume limiter on fixed and moving grids, as well as on space-time adaptive Cartesian AMR meshes. We then present and discuss the unified symmetric hyperbolic and thermodynamically compatible (SHTC) formulation of continuum mechanics developed by Godunov, Peshkov, and Romenski (GPR model), which allows to describe fluid and solid mechanics in one single and unified first order hyperbolic system. In order to deal with free surface and moving boundary problems, a simple diffuse interface approach is employed, which is compatible with Eulerian schemes on fixed grids as well as direct Arbitrary-Lagrangian-Eulerian methods on moving meshes. We show some examples of moving boundary problems in fluid and solid mechanics.
1. Introduction and Review of the ADER Approach
The development of high order numerical schemes for hyperbolic conservation laws has been one of the major challenges of numerical analysis for the last decades. Godunov [1] proved that for the linear advection equation no monotone linear schemes of second or higher order of accuracy can be constructed. Therefore, even if physical viscosity is considered, a linear high order scheme will present spurious oscillations near discontinuities, as it can be seen, for instance for the Lax-Wendroff scheme, Lax and Wendroff [2]. A first idea to circumvent this theorem has been proposed in Kolgan [3], where limited slopes are employed to produce a non-linear scheme of second order of accuracy in space. Since then, many high order numerical methods have been developed like the Total Variation Disminishing methods (TVD) and Flux limiter methods (see, for instance, [4–9]). Despite these methodologies being already well-established at the end of the last century, their major drawback was that they just provided global second order of accuracy and reduced locally to first order in the vicinity of smooth extrema.
More advanced non-linear methods for advection dominated problems involve the family of ENO and WENO schemes, see Harten and Osher [10], Harten et al. [11], and Shu [12]. In particular, the method of Harten et al. [11] is a fully discrete high order scheme that can be re-interpreted in terms of the solution of a generalized Riemann problem (GRP), see Castro and Toro [13]. Moreover, it can be seen as a generalization of the MUSCL-Hancock method of van Leer, see van Leer [8], Toro [9], and Berthon [14].
Following the idea of solving a generalized Riemann problem (GRP), see also Ben-Artzi and Falcovitz [15], LeFloch and Tatsien [16], Ben-Artzi et al. [17], and Han et al. [18], the ADER approach (Arbitrary high order DErivative Riemann problem) has been first put forward for the linear advection equation with constant coefficients by Millington et al. [19] and Toro et al. [20]. The first step of the methodology involves piece-wise polynomial data reconstruction, where a non-linear ENO reconstruction is applied in order to avoid spurious oscillations of the numerical solution. Then, a GRP is defined at each cell interface. Classically, the initial condition for the GRP was given as piece-wise linear polynomials and second order schemes could be obtained by constructing a space-time integral of the solution in an appropriate control volume [21, 22], or following a MUSCL approach, van Leer [23] and Colella [24]. An alternative methodology proposed in Ben-Artzi and Falcovitz [25] consists in expressing the solution of the GRP as a Taylor series expansion in time. The ADER approach obtains the high order time derivatives of the GRP solution at the cell interface via the Cauchy-Kovalevskaya procedure, which replaces time derivatives by spatial derivatives using repeated differentiation of the differential form of the PDE. The spatial derivatives, which may also jump at the interface, are defined via the solution of linearized Riemann problems for the derivatives, where linearization is carried out about the Godunov state obtained from the classical Riemann problem between the boundary extrapolated values at the interface. In Figure 1, the classical piece-wise constant polynomials are plotted against a high order reconstruction and the similarity solutions for both cases are sketched. Finally, these similarity solutions are used to construct the numerical flux. The resulting schemes are arbitrary high order accurate in both space and time, in the sense that they have no theoretical accuracy barrier.
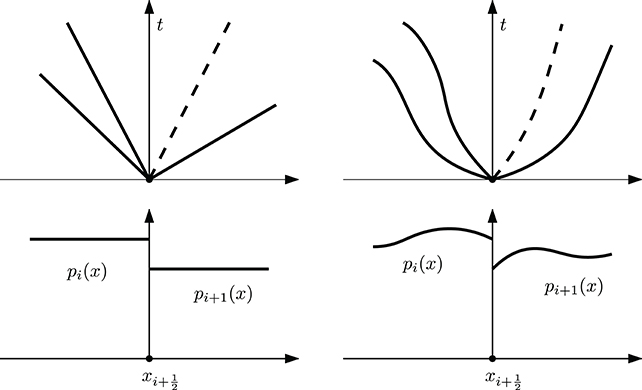
Figure 1. Classical piece-wise reconstruction polynomials used in the ADER approach, pi(x) and pi+1(x), and the structure of the Riemann problem solution at the intercell boundary . (Left) classical piece-wise constant data. (Right) piece-wise smooth reconstruction.
Since their introduction in Toro et al. [20] and Millington et al. [19], many extensions of the ADER methodology have been proposed. Regarding 2D linear PDEs, one may refer to Schwartzkopff et al. [26] and their simplification for the particular case of structured grids in Schwartzkopff et al. [27]. Moreover, non-linear systems have been initially addressed in Toro and Titarev [28] and Titarev and Toro [29]. Further applications of ADER on non-Cartesian meshes have been presented in Käser [30], Käser and Iske [31], Dumbser et al. [32], and Castro and Toro [13]. One should also mention the development of ADER schemes in the framework of discontinuous Galerkin (DG) finite element methods, see Qiu et al. [33], Dumbser and Munz [34] and Gassner et al. [35]. One of the main advantages of using DG is that the reconstruction step of classical ADER finite volume (ADER-FV) schemes can be skipped, since the discrete solution is already given by high order piecewise polynomials that can be directly evolved during each time step. Furthermore, ADER-DG schemes avoid the use of classical Runge-Kutta time stepping and thus provide efficient communication-avoiding schemes for parallel computing, see Fambri et al. [36] and allow for simple and natural time-accurate local time stepping (LTS), see Dumbser et al. [37].
An important step forward in the development of more general ADER schemes was achieved in Dumbser et al. [38], where a new class of ADER-FV methods has been introduced. The main contribution of this paper consists in the introduction of a new element-local space-time DG predictor, which allows at the same time the treatment of stiff source terms, as well as the replacement of the cumbersome Cauchy-Kovalevskaya procedure. First, a high order WENO method is employed to compute a polynomial reconstruction of the data inside each spatial element; then, an element-local weak formulation of the conservation law is considered in space-time and the predictor is applied to construct the time evolution of the WENO polynomials within each cell. Note that, in this step, the integration by parts is performed only in time, which differs from global space-time DG schemes [39, 40], which are globally implicit. Finally, the cell averages are updated with an explicit fully discrete one-step scheme, considering the integral form of the equations. As a result, the proposed methodology maintains arbitrary high order of accuracy, while avoiding the issues related to the use of a Taylor series expansion in time. As already mentioned above, it naturally provides an approach for the treatment of stiff source terms [for further details on this topic, see [41] and references therein].
The above methodology can also be applied in the discontiuous Galerkin framework as presented in Dumbser et al. [42], where, a unified PNPM framework for arbitrary high order one-step finite volume and DG schemes has been introduced. For other reconstruction-based DG schemes, see e.g., Luo et al. [43, 44]. Afterwards, the methodology has been extended to solve a wide variety of different PDE systems, such as the resistive relativistic MHD equations, Dumbser and Zanotti [45]; non-conservative hyperbolic systems found in geophysical flows, Dumbser et al. [46] in which a well-balanced and path-conservative version of the scheme has been developed; compressible multi-phase flows Dumbser et al. [47], the compressible Navier-Stokes equations, Dumbser [48]; the compressible Euler equations and divergence-free schemes for MHD, Balsara et al. [49], and Balsara and Dumbser [50], where ADER schemes were used in combination with genuinely multidimensional Riemann solvers. The last extensions concern the special and general relativistic MHD equations, see Zanotti et al. [51], and Fambri et al. [36], as well as the Einstein field equations of general relativity [52, 53].
Later, ADER schemes have been extended to adaptive mesh refinement on Cartesian grids (AMR), in combination with time accurate local time stepping (LTS). This technique has initially been introduced in Dumbser et al. [54, 55] for conservative and non-conservative hyperbolic systems, respectively. Moreover, the schemes of the ADER family were the first high order methods to be applied for the numerical solution of the unified first order hyperbolic formulation of continuum mechanics by Godunov, Peshkov and Romenski [56–58], see Dumbser et al. [59–61]. In the rest of this paper, we will refer to the Godunov-Peshkov-Romenski model of continuum mechanics as GPR model.
The ADER approach has also been extended to the direct Arbitrary-Lagrangian-Eulerian framework (ALE), where the mesh moves with an arbitrary velocity, taken as close as possible to the local fluid velocity. Initially developed for one space dimension, it has been soon extended to the case of the two and three dimensional Euler equations on unstructured meshes, Boscheri and Dumbser [62, 63], including the discretization of non-conservative products. Further works in this area involve the use of local timestepping techniques, [64, 65]; coupling with multidimensional HLL Riemann solvers, Boscheri et al. [66]; solution of magnetohydrodynamics problems (MHD), [67, 68]; development of a quadrature-free approach to increase the computational efficiency of the overall method, Boscheri and Dumbser [69]; use of curvilinear unstructured meshes, Boscheri and Dumbser [70]; or extension to solve the GPR model, Boscheri et al. [71] and Peshkov et al. [72]. Furthermore, in Gaburro et al. [73] a novel algorithm to deal with moving non-conforming polygonal grids has been presented. The methodology reduces the typical mesh distortion arising in shear flows and provides high quality elements even for long-time simulations. An exactly well-balanced path-conservative version of this approach for the Euler equations with gravity can be found in Gaburro et al. [74]. Still in the ALE framework, within this article, we will present new results for the family of ADER-FV and ADER-DG schemes on moving unstructured Voronoi meshes [75], as recently introduced in Gaburro [76] and Gaburro et al. [77].
It is well-known that when dealing with high order schemes special care must be paid to the limiting methodology employed. In most of the previous referenced papers classical a priori limiters have been used, such as WENO reconstruction. Nevertheless, some alternative contributions to this topic can be found in the series of papers [51, 77–85], where a novel a posteriori sub-cell FV limiter of high order DG schemes, based on the MOOD paradigm of Clain et al. [86] and Diot et al. [87, 88], has been employed.
Besides the references given above, which focus on the development of the ADER methodology with a local space-time Galerkin predictor, many recent papers have been devoted to the development of other families of ADER schemes, like the classical ADER finite volume methods. Without pretending to be exhaustive, we may refer to Castro et al. [89], Toro and Hidalgo [90], Taube et al. [91], Toro [9], Montecinos et al. [92], Montecinos and Toro [93], Toro and Montecinos [94, 95], Toro et al. [96], Busto [97], Montecinos et al. [98], Busto et al. [99], Contarino et al. [100], Busto et al. [101], and Dematté et al. [102] and references therein.
In this paper, as a promising application of the family of ADER schemes, we solve a diffuse interface formulation of the GPR model of continuum mechanics. In comparison with existing continuum mechanics models, the novel feature of the GPR model is in that it incorporates the two main branches of continuum mechanics, fluid and solid mechanics, in one single unified PDE system. Recall that traditionally fluid and solid mechanics are described by PDE systems of different types, i.e., parabolic (viscous fluids) and hyperbolic (linear elasticity and hyperelasticity), which imposes many theoretical and technical difficulties if one wishes to model natural and industrial processes involving co-existence of the fluid and solid states such as in fluid-structure interaction (FSI) problems, modeling of general solid-fluid transition such as in melting and solidification processes, e.g., additive manufacturing, see for example Francois et al. [103], flows of granular media [104], viscoplastic flows, e.g., debris flows, avalanches, mantle convection, flows of many industrial Bingham-type fluids, see Balmforth et al. [105]. Due to the unified treatment of fluids and solids, the GPR model thus has a great potential for simplifying the modeling process and code development for solving the aforementioned problems. Yet, before to be applied to practical problems, the GPR model may require a coupling with an interface tracking/capturing technique for the modeling of moving material boundaries such as in free surface flows or solid body motion. In particular, in this paper, we couple the GPR model with a simple diffuse interface approach, see Tavelli et al. [85], Dumbser [106], Gaburro et al. [107], Kemm et al. [108]. For example, very interesting computational results with similar diffuse interface approaches and level set techniques for compressible multi-material flows have been obtained for example in Gavrilyuk et al. [109], Favrie et al. [110], Favrie and Gavrilyuk [111], Ndanou et al. [112], de Brauer et al. [113], Michael and Nikiforakis [114], Jackson and Nikiforakis [115], and Barton [116]. Finally, we demonstrate that the ADER family of schemes is capable to resolve the GPR model in both solid and fluid regimes.
The paper is organized as follows. In section 2 we present the family of ADER finite volume and ADER discontinuous Galerkin finite element schemes on fixed Cartesian and moving polygonal meshes in two space dimensions. Next, in section 3 we introduce the diffuse interface formulation of the GPR model. In section 4 we show some computational results obtained with different kinds of ADER schemes (ADER-FV and ADER-DG) on different mesh topologies, including moving unstructured Voronoi meshes, as well as fixed and adaptive Cartesian grids. The paper is rounded off by some concluding remarks and an outlook to future work in section 5.
2. ADER Finite Volume and Discontinuous Galerkin Schemes
The numerical method adopted in this paper is the variant of the arbitrary high-order accurate ADER approach based on the space-time predictor-corrector formalism, which we have briefly reviewed in the previous section 1. It easily applies to the context of finite volume (FV) and discontinous Galerkin (DG) methods, using either space-time adaptive Cartesian grids (AMR), see Bungartz et al. [117],Weinzierl and Mehl [118], Dumbser et al. [54], Zanotti et al. [80], Fambri et al. [36, 84] and references therein, or unstructured meshes, and both on fixed Eulerian domains or in a moving Arbitrary-Lagrangian-Eulerian (ALE) framework, see Boscheri et al. [65, 68], Boscheri and Dumbser [62, 63, 119], Boscheri [82], Gaburro [120], Gaburro et al. [77], and references therein.
Here, we briefly describe the key features of our numerical scheme, keeping the notation as general as possible, and referring to the literature for further details. We start by introducing the general form of our governing PDE system and a moving unstructured discretization of two-dimensional domains (sections 2.1 and 2.2); next, in section 2.3 we describe the data representation of the discrete solution. Then, we explain how to obtain high order of accuracy in space: this is available by construction in the DG case, and obtained via some variants of the well-known WENO procedure [32, 121–125] for the FV approach. Finally, we focus on the predictor-corrector version of the ADER scheme that allows to achieve arbitrary high order of accuracy in space and time. Since it is out of the scope of this paper to recall all the details, a general overview is given in sections 2.5 and 2.7, and an inedited proof of the convergence of the predictor for a non-linear conservation law is presented in section 2.6.
We would like to emphasize that, besides this novel convergence proof, other progress has been introduced within this work. Indeed, up to our knowledge, it is the first time that: (i) the ADER approach is used to solve a diffuse interface formulation of the GPR model that addresses the free surface problem in both solid and fluid mechanics context (previously, a similar formulation was used only in the solid dynamics context [112, 126, 127]); (ii) non-conservative products are taken into account in the high order direct ALE scheme of Gaburro et al. [77], where they have to be integrated also on degenerate space–time control volumes (see section 2.5.2).
2.1. Governing PDE System
In this paper we consider high order fully-discrete schemes for non-linear systems of hyperbolic PDE with non-conservative products and algebraic source terms of the form
where is the state vector, is the time, x ∈ Ω ⊂ ℝd is the spatial coordinate, d is the number of space dimensions, ΩQ is the so-called state space or phase space, F(Q) is the non-linear flux tensor, B(Q)·∇Q is a non-conservative product and S(Q) is a purely algebraic source term. Introducing the system matrix A(Q) = ∂F/∂Q + B(Q) the above system can also be written in quasi-linear form as
The system is said to be hyperbolic if for all n ≠ 0 and for all Q ∈ ΩQ the matrix A(Q)·n has m real eigenvalues and a full set of m linearly independent right eigenvectors. The system (1) needs to be provided with an initial condition Q(x, 0) = Q0(x) and appropriate boundary conditions on ∂ Ω.
In this paper we focus on a particular, but very general, example of a first-order system (1) describing elastic and visco-plastic heat-conducting media; it will be discussed in section 3.
2.2. Domain Discretization
In the general ALE case, we consider a moving two-dimensional (d = 2) domain Ω(t) and we cover it using an unstructured mesh made of NP non-overlapping polygons Pi, i = 1, …NP. The mesh is first built at time t = 0 and then it is rearranged at each time step tn: elements and nodes are moved following the local fluid velocity and when necessary, in order to prevent mesh distortion, also the mesh topology (i.e., the shape of the elements and their connectivities) is changed.
Given a polygon we denote by the set of its Voronoi neighbors (the neighbors that share with at least a vertex), and by the set of its edges, and by the set of its vertexes, consistently ordered counterclockwise. Finally, the barycenter of is noted as . When necessary, by connecting with each vertex of we can subdivide a polygon in subtriangles denoted as .
The coordinates of each node at time tn are denoted by , and represents the velocity at which it is supposed to move, so that its new coordinates at time tn+1 are given from the following relation
More details on how to obtain can be found in Boscheri et al. [68], Boscheri and Dumbser [63, 119] for what concerns classical direct ALE schemes on conforming unstructured grids, in Gaburro et al. [73, 74] for non-conforming unstructured grids, in Boscheri and Dumbser [70] for curvilinear meshes, and we refer in particular to section 2.4 and 2.5 of Gaburro et al. [77] for what concerns moving unstructured polygonal grids allowing for topology changes, which indeed is the ALE case considered in this paper (see case B below). Moreover, working in the ALE framework, we are allowed to take , i.e., we can also work in a fixed Eulerian system where the initial mesh is never modified.
In particular, in this paper we will consider the following two situations for our domain discretization:
A. A fixed Cartesian mesh made of NP quadrilaterals elements, which is not moved during the simulation, but which can be successively refined, with a general space-tree-type data structure that allows element-by-element refinement with a general refinement factor 𝔯 ≥ 2, in order to increase the resolution in the areas of interest, as can be seen in Figure 2 (for the details on the refinement procedure we refer to Dumbser et al. [54] and Fambri et al. [36]). To ease the description of the numerical method, we will associate to each quadrilateral element , a set of indices that refer to its Cartesian coordinates, {j, k}, such that , , .
B. A moving polygonal grid as the one described in Gaburro et al. [77] that (i) moves with the fluid flow in order to reduce the numerical dissipation associated with transport terms and (ii) also allows for topology changes at any time step in order to maintain always a high quality of the moving mesh; in this case we remark that our method is also able to deal with degenerate space time control volumes at arbitrary high order of accuracy.
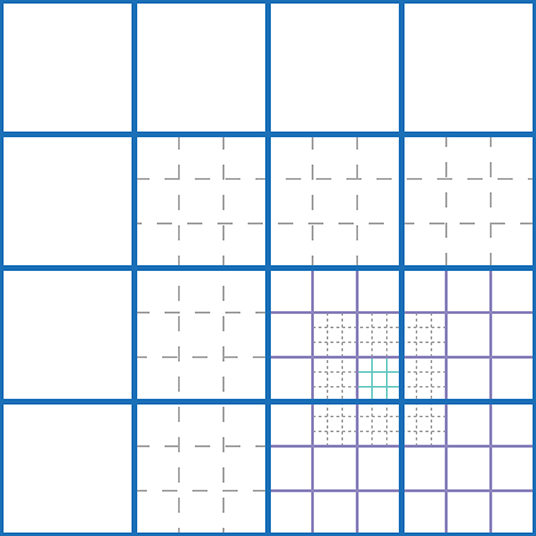
Figure 2. Sketch of the mesh refinement structure of three AMR levels with refinement factor 𝔯 = 3. Solid lines indicate active cells, whereas the dashed ones are the virtual cells allowing interpolation between the coarse and the refined mesh, needed in the case of high order WENO reconstruction.
2.2.1. Space-Time Connectivity
To better understand the context of moving meshes we refer the reader to Figure 3: note that the tessellation at time tn has been evolved resulting in a slightly different tessellation at time tn+1; for each element the new vertex coordinates , , are connected to the old coordinates via straight line segments, yielding the multidimensional space-time control volume , that involves space-time sub-surfaces. Specifically, the space-time volume is bounded on the bottom and on the top by the element configuration at the current time level and at the new time level , respectively, while it is closed with a total number of lateral space–time surfaces that are given by the evolution of each edge of element within the time step Δt = tn+1 − tn. A priori, are not parallel to the time direction: thus to be treated numerically they can be mapped to a reference square by using a set of of bilinear basis functions (see Boscheri and Dumbser [62]). To resume, the space-time volume is bounded by its surface which is given by
Note that in the fixed Cartesian case, reduces to a right parallelepiped with four lateral space–time surfaces parallel to the time-direction, so many simplifications are possible.
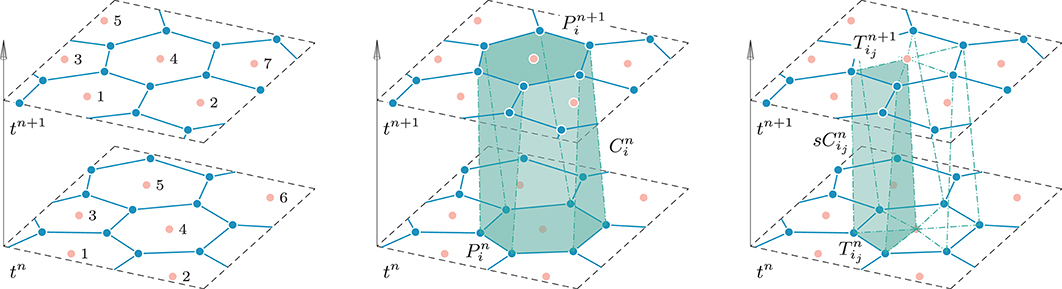
Figure 3. Space time connectivity. (Left) The tessellation at time tn and time tn+1. (Middle) is connected with to construct the space–time control volume . (Right) The sub-triangle is connected with to construct the sub–space–time control volume .
We close this part by emphasizing that the family of direct ALE schemes proposed in this work, based on the ADER predictor-corrector approach, is based on the integration of the governing Equation (1) in space and in time directly over these space–time control volumes, see section 2.7. Note that this procedure, which is more evident when is an oblique prism, is also hidden when is just a right parallelepiped.
2.3. Data Representation
The conserved variables Q in (1) are discretized in each polygon at the current time tn via piecewise polynomials of arbitrary high order N, denoted by and defined as
where in the last equality we have employed the classical tensor index notation based on the Einstein summation convention, which implies summation over two equal indices. The functions can be either:
i. Nodal spatial basis functions given by a set of Lagrange interpolation polynomials of maximum degree N with the property
where are the set of the Gauss-Legendre (GL) quadrature points on (see Stroud [128] for the multidimensional case). In particular, when employing these basis functions on a Cartesian grid, each quadrilateral is easily mapped to a reference square, we only need the tensor product of the GL quadrature points in the unit interval [0, 1], and the φℓ are simply generated by multiplying one-dimensional nodal basis functions, i.e.,
with φℓi satisfying (6) with d = 1, and , being the set of reference coordinates related to . In this case, the total number of GL quadrature points per polygon, as well as the total number of basis functions {φℓ} and expansion coefficients , the so-called degrees of freedom (DOF), is . These basis functions are used on Cartesian grids, i.e., for Case A.
ii. Modal spatial basis functions written through a Taylor series of degree N in the variables x = (x, y) directly defined on the physical element , expanded about its current barycenter and normalized by its current characteristic length hi
hi being the radius of the circumcircle of . In this case the total number of DOF is We employ this kind of basis functions in the moving unstructured polygonal Case B.
The discontinuous finite element data representation (5) leads naturally to discontinuous Galerkin (DG) schemes if N > 0, but also to finite volume (FV) schemes in the case N = 0. This indeed means that for N = 0 we have φℓ(x) = 1, with ℓ = 0 and (5) reduces to the classical piecewise constant data that are typical of finite volume methods. In the case N > 0 (DG) the form given by (5) already provides a spatially high order accurate data representation with accuracy N + 1, where instead for the case N = 0 (FV), if we are interested in increasing the spatial order of accuracy, up to M + 1 for examle, we need to perform a spatial reconstruction. With this notation, our method falls within the more general class of PNPM schemes introduced in Dumbser et al. [42] for fixed unstructured meshes.
2.4. Data Reconstruction
In this section we focus on the reconstruction procedure needed in the finite volume context (N = 0, M > 0) in order to obtain order of accuracy M + 1 in space starting from the piecewise constant values of in and its neighbors, i.e., in order to obtain a high order polynomial of degree M representing our solution in each
where the ψℓ functions simply coincide with the φℓ basis functions of (5). Our reconstruction procedures are based on the WENO algorithm in its polynomial formulation as presented in Dumbser et al. [38], Dumbser and Käser [32, 123], Titarev et al. [129], Tsoutsanis et al. [130], Levy et al. [131], Dumbser et al. [132], and Semplice et al. [133], and not based on the original version of WENO proposed in Jiang and Shu [121], Balsara and Shu [122], Hu and Shu [134], and Zhang and Shu [124] which provides only point values. For each , the basic idea consists in (i) selecting a central stencil of elements with a total number of
elements, containing the cell itself, its first layer of Voronoi neighbors and filled by recursively adding neighbors of those elements that have been already included in the stencil, and in (ii) using the cell-average values of the elements of to reconstruct a polynomial of degree M by imposing the integral conservation criterion, i.e., by requiring that its average on each cell match the known cell average. If f > 1 (which occurs in the unstructured case, where we take f = 1.5), this of course leads to an overdetermined linear system, which is solved using a constrained least-squares technique (CLSQ) [123], i.e., the reconstructed polynomial has exactly the cell average on the polygon and matches all the other cell averages of the remaining stencil elements in the least-square sense.
However, as well-known thanks to the Godunov theorem [1], the use of only one central stencil (which is indeed a linear procedure) would introduce oscillations in the presence of shock waves or other discontinuities. So, in order to make the reconstruction procedure non-linear, we will compute the final reconstruction polynomial as a non-linear combination or more than only one reconstruction polynomial, each one defined on a different reconstruction stencil .
We refer to the cited literature for further details, and here we just highlight the main characteristics of the two reconstruction procedures adopted in this work.
2.4.1. Case A: Cartesian Mesh
In Case A, of a fixed Cartesian mesh, we employ the polynomial WENO procedure given in Dumbser et al. [54], which is implemented in a dimension by dimension fashion. For each cell, we define its related sets of one-dimensional reconstruction stencils as
where L = {M, s} and R = {M, s} denote the order and stencil dependent spatial extension of the stencil to the left and to the right. For odd order schemes we consider three stencils, one central, one fully left–sided, and one fully right–sided stencil in each space dimension (see Figure 4 for a graphical interpretation for M = 2), while for even order schemes we have four stencils, two of which are central, while the remaining two are again given by the fully left–sided and fully right–sided in each space dimension. In both cases the total amount of elements in each stencil is always ne = M + 1, the order of the scheme.
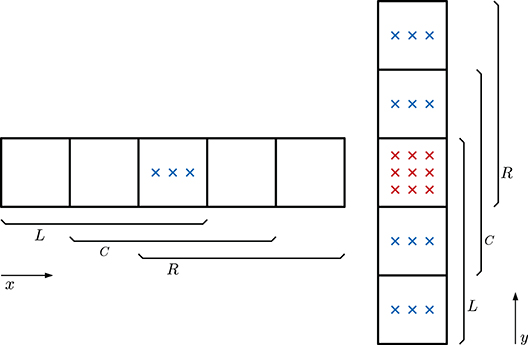
Figure 4. Reconstruction stencils for a fixed Cartesian mesh with M = 2, where L, C, and R denote the left–sided, central and right–sided stencils, respectively. (Left) Reconstruction on x direction. (Right) Reconstruction on y direction.
Focusing on the reconstruction procedure on the x direction, given a element , we start by expressing the first coordinate of the reconstruction polynomial at each stencil in terms of one dimensional basis functions,
Then, we integrate on the stencil elements obtaining an algebraic system on the polynomial coefficients:
with the average value obtained by integrating the solution at the previous time step on the cell Pmk. Once the coefficients, and thus the polynomials, related to all the stencils are obtained, we compute a reconstruction polynomial in the x direction as the data-dependent non-linear combination of these,
where ns is the number of stencils, ns = 3 if and ns = 4 otherwise; and ωs denote the non-linear weights (see Dumbser et al. [54] for further details).
To complete the reconstruction polynomial, we now repeat the above procedure in the y direction for each degree of freedom . First, we write the reconstruction polynomial in terms of the basis functions,
Then, we solve the algebraic system
and calculate
Finally, we get the WENO reconstruction polynomial
In order to enforce bounds on the WENO reconstruction polynomial, such as the condition 0 ≤ α ≤ 1 on the volume fraction function of for example (56a), we rescale the reconstruction coefficients around the cell average as follows:
where the scaling factor φjk is computed via the Barth and Jespersen limiter (see Barth and Jespersen [135]) applied to the volume fraction function α in all Gauss-Legendre and Gauss-Lobatto quadrature nodes, i.e., φjk = min(φjk, p) is the global minimum in each element, with the nodal limiter values given by
Here αmax = 1 − ε ≤ 1 is the upper bound of the volume fraction function and αmin = ε ≥ 0 is its lower bound; denotes the cell average of α and αp denotes the node value of α in the quadrature point xp under consideration. As already mentioned above, this strategy is inspired from the Barth and Jespersen limiter [135], but also from the new bound-preserving polynomial approximation introduced in Després [136] and Campos-Pinto et al. [137]. Since the physical solution of α must satisfy 0 ≤ α ≤ 1, the above bound preserving limiter does not reduce the formal order of accuracy of the reconstruction, as proven in Després [136].
2.4.2. Case B: Moving Polygonal Mesh
In Case B of our moving and topology changing polygonal mesh we adopt a CWENO reconstruction algorithm, first introduced in Levy et al. [138–140] and Semplice et al. [133], and which can be cast in the general framework described in Cravero et al. [141]. We closely follow the work outlined in Dumbser et al. [132] and Boscheri et al. [142] for unstructured triangular and tetrahedral meshes, and extended it to moving polygonal grids in Gaburro et al. [77].
We emphasize that the main advantages of such a procedure is that only one stencil (the central one) is required to contain the total amount of elements stated in (10) and only this one is used to construct a polynomial of degree M; the other ones are used to compute polynomials of lower degree. In particular, we consider stencils , each of them containing exactly cells, i.e., the central cell and two consecutive neighbors belonging to . Refer to Figure 5 for a graphical description of the stencils. For each stencil we compute a linear polynomial by solving a simple reconstruction system which is not overdetermined. According to the above mentioned literature, the reconstructed polynomial obtained via a non-linear combination of the polynomial of degree M, computed over , and of the linear polynomials, computed over , maintains the order of convergence of the method and avoids unwanted spurious oscillations. In particular, in the case of moving meshes with topology changes, where the set of neighbors may change at any time step, the use of smaller so-called sectorial stencils significantly speeds up computations.
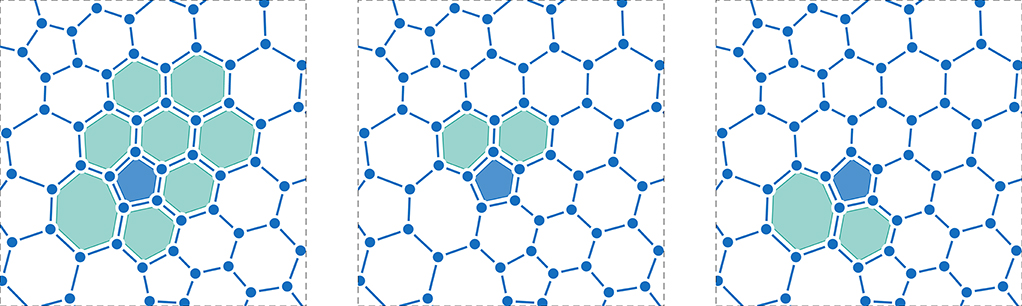
Figure 5. Stencils for the CWENO reconstruction of order three (M = 2) with f = 1.5 for a pentagonal element . Left: central stencil made of the element itself (in violet) and ne − 1 = 8 of its neighbors (in blue). In the other panels we report two of the sectorial stencils containing the element itself and two consecutive neighbors belonging to .
For the sake of uniform notation, in the DG case, i.e., when N > 0 and M = N, we trivially impose that the reconstruction polynomial is given by the DG polynomial, i.e., , which automatically implies that in the case N = M the reconstruction operator is simply the identity.
2.5. Space-Time Predictor Step
In this section we focus on the key feature, the element-local space-time predictor step, of our ADER FV-DG schemes: this part of the algorithm (the predictor) produces a high order approximation in both space and time of Q in all . This allows to obtain a fully discrete one-step scheme that is uniformly high order accurate in both space and time.
The predictor step consists in a completely local procedure which solves the governing PDE (1) in the small, see Harten et al. [11], inside each space-time element , and it only considers the geometry of volume , the initial data on and the governing Equations (1), without taking into account any interaction between and its neighbors. Because of this absence of communications, we refer to it as local. The procedure finally provides, for each , a space-time polynomial data representation , which serves as a predictor solution, only valid inside , to be used for evaluating the numerical fluxes, the non-conservative products and the algebraic source terms when integrating the PDE in the final corrector step (see section 2.7) of the ADER scheme.
The predictor is a polynomial of degree M, which takes the following form
where θℓ(x, t) can be either
i. For fixed and adaptive Cartesian grids (Case A), nodal space-time basis functions of degree M given by the product of one-dimensional nodal basis functions verifying (6) (with d = 1 ),
two of them mapped to the unit interval [0, 1] as in (7) and with the time coordinate mapped to the reference time τ ∈ [0, 1] via t = tn + τΔt. In this case, the total number of GL quadrature points per cell, as well as the total number of DOF is , see also Figure 6.
ii. For our moving polygonal meshes (Case B), modal space time basis functions of degree M in d + 1 dimensions (d space dimensions plus time) are used, which read
with the total number of DOF , see also Figure 7.
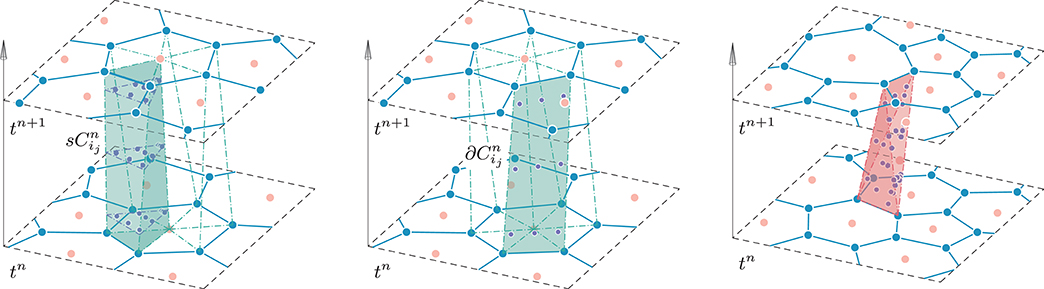
Figure 7. Space–time quadrature points for third order methods, i.e., M = 2, on a moving polygonal mesh with topology changes. (Left) Quadrature points for the volume integrals and the space–time predictor. (Middle) quadrature points for the surface integrals, i.e., for flux computation. (Right) Quadrature points for the volume integrals and the space–time predictor of a sliver element.
Now, multiplying our PDE system (1) with a test function θk and integrating over the space-time control volume (see section 2.2.1), we obtain the following weak form of the governing PDE, where both the test and the basis functions are time dependent
Since we are only interested in an element local predictor solution, i.e., we do not need to consider the interactions with the neighbors, we do not yet take into account the jumps of across the space–time lateral surfaces, because this will be done in the final corrector step (section 2.7).
Instead, we insert the known discrete solution at time tn in order to introduce a weak initial condition for solving our PDE; note that uses information coming from the past only (following an upwinding approach) in such a way that the causality principle is correctly respected. To this purpose, the first term is integrated by parts in time. This leads to
Equation (25) results in an element-local non-linear system for the unknown degrees of freedom of the space-time polynomials . The solution of (25) can be found via a simple and fast converging fixed point iteration (a discrete Picard iteration) as detailed e.g., in Dumbser et al. [42] and Hidalgo and Dumbser [41]. For linear homogeneous systems, the discrete Picard iteration converges in a finite number of at most N + 1 steps, since the involved iteration matrix is nilpotent, see Jackson [143]. Moreover a proof of the convergence of this procedure in the case of a non-linear homogeneous conservation law in 1D is given in next section 2.6.
2.5.1. Simplification in the Case of a Fixed Cartesian Mesh
The space-time predictor step formerly presented can be simplified in the case of a Cartesian mesh with nodal basis functions resulting in a more efficient algorithm. Under these assumptions the governing PDE (1), can be rewritten as
with
Next, we multiply each term by a test function θk and we integrate over the reference space-time control volume
Now, by substituting the discrete space-time predictor solution with its expansion on the nodal basis and after integrating by parts in time, we obtain
To recover the value of the unknown degrees of freedom , it is sufficient to solve the above equation locally for each element. One important advantage of using the nodal Gauss-Legendre basis is that the terms in (29) can be evaluated in a dimension-by-dimension fashion.
2.5.2. Space-Time Predictor for Sliver Space–Time Elements
When a topology change occurs, some space–time sliver elements, as those shown on the right side of Figure 8, are originated (see Gaburro et al. [77]), and the predictor procedure over them needs particular care. The problem connected with sliver elements is the fact that their bottom face, which consists only in a line segment, is degenerate, hence the spatial integral over vanishes, i.e., there is no possibility to introduce an initial condition for the local Cauchy problem at time tn into their predictor. Thus, in order to couple however (24) with some known data from the past, we will end up with a formula different from (25). We underline that we first carry out the space–time predictor for all standard elements using, which can be computed independently of each other, and only subsequently we process the remaining space–time sliver elements. Then, when considering a sliver, we use the upwinding in time approach on the entire space–time surface that closes a sliver control volume, and again respecting the causality principle, we take the information to feed the predictor only from the past, i.e., only from those space–time neighbors whose common surface exhibit a negative time component of the outward pointing space–time normal vector (). In this way, we can introduce information from the past into the space–time sliver elements.
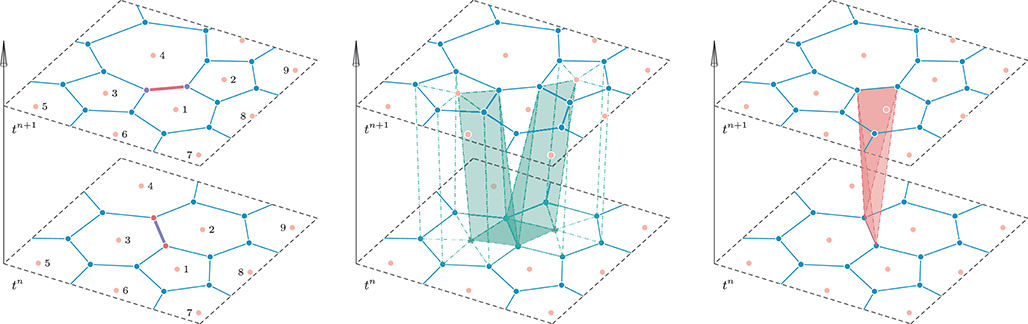
Figure 8. Space time connectivity with topology changes and sliver element. Left: at time tn the polygons and are neighbors and share the highlighted edge, instead at time tn+1 they do not touch each other; the opposite situation occurs for polygons and . This change of topology causes the appearance of degenerate elements of different types (refer to Gaburro et al. [77] for all the details). In particular, so-called space–time sliver elements (right) need to be taken into account when considering the space–time framework, so the predictor and the corrector step have to be a adapted to their special features. Sliver elements (right) are indeed completely new control volumes which do neither exist at time tn, nor at time tn+1, since they coincide with an edge of the tessellation and, as such, have zero areas in space. However, they have a non-negligible volume in space–time. The difficulties associated to this kind of element are due to the fact that wh is not clearly defined for it at time tn (thus the predictor has to be modified) and that contributions across it should not be lost at time tn+1 in order to guarantee conservation (thus the corrector has to be modified).
As a consequence, the predictor solution is again obtained by means of (24), but by treating the entire with the upwind in time approach, i.e., by considering also the jump terms between the still unknown predictor of the slivers (call it ) and the already known predictors of its neighbors (call them ),
where is the part of the space-time boundary that has a negative time component of the space-time normal vector. Note that here we have taken into account also the jump of the non-conservative terms, and that these contributions have been added entirely [i.e., not only half of them, as in (49)]. Indeed, in (49) half of the jump contribution goes to one element, while the other half goes to the neighboring element; here instead, since the interaction between neighbors is only computed from the side of the sliver element, the entire jump contributes to the predictor in the sliver element.
2.6. Convergence Proof of the Predictor Step for a Non-linear Conservation Law
In this section, the convergence proof of the predictor for a non-linear conservation law is given. The proof is provided, for simplicity, in the case of a fixed mesh in one space dimension, following the nomenclature already employed in section 2.5.1, but it still holds in higher dimensions. Let us consider a general hyperbolic system of conservation laws of the form
Then, the corresponding space-time DG predictor used in the ADER-DG framework reads
For convenience, all derivatives and integrals in (32) have been transformed to the reference space-time element [0, 1]2. Moreover, the discrete solution is given by , and the flux is expanded in the same basis as . When using a nodal basis, we can compute the degrees of freedom for the flux interpolant fh simply as . We also recall that the initial condition given by the DG scheme at time tn reads . Then, integration of the first term in (32) by parts in time yields
and insertion of the definitions of the discrete solution leads to
The iterative scheme employed to find the solution for the space-time degrees of freedom , at any Picard iteration r, can therefore be rewritten in compact matrix-vector notation as
with
where we have dropped the indices to ease the notation. After inverting K1 (this matrix is built using the linearly independent basis functions so that it is invertible), we obtain the explicit iteration formula
To prove that the former iterative formula will converge, we introduce the operator
and the induced matrix norm
Furthermore, we assume the flux to be Lipschitz continuous with Lipschitz constant L > 0 so that
We now need to show that the operator φ is a contraction:
The operator is therefore a contraction under the CFL-type condition on the time step Δt
which connects the Lipschitz constant L with the mesh spacing Δx and the matrix norm of . Since the operator is contractive under the above assumptions, the Banach fixed point theorem, Banach [144], guarantees convergence of the iterative method.
In the previous reasoning, we have assumed that the inequality in the right hand side of (43) be strict. Thus, to conclude the proof, let us assume that the equality holds, this is true if and only if . By taking into account the definition of the induced matrix norm (40), it implies for any x in the metric space. Thus, . Direct substitution in (38) gives
so that no iterative procedure is done.
Note: The matrix has been proven to be nilpotent and thus all its eigenvalues are zero, see Jackson [143], which guarantees convergence to the exact solution in a finite number of steps for linear homogeneous PDE.
2.7. Corrector Step
The corrector step is the last step of our path-conservative ADER FV-DG scheme, where the update of the solution from time tn up to time tn+1 can take place in a single step procedure thanks to the use of the predictor .
The update formula is recovered starting from the space–time divergence form of the PDE
which is multiplied by a set of space–time test functions and integrated over each space–time control volume
Note that the employed test functions coincide with the θk of (22) for the Cartesian Case A. Instead, for the moving polygonal Case B, they need to be tied to the motion of the barycenter xbi(t) and must be moved together with Pi(t) in such a way that at time t = tn they refer to the current barycenter and at time t = tn+1 they refer to the new barycenter , thus they are defined as follows
These moving modal basis functions are essential to the moving approach presented in Gaburro et al. [77] and used in this paper. They naturally allow for topology changes, without the need of any remapping steps, which we want to avoid in a direct ALE formulation.
Now, (46) by applying the Gauss theorem to the flux-divergence term and by splitting the non-conservative products into their volume and surface contribution, becomes
where Q on is represented by the unknown , on is taken to be the current representation of the conserved variables , in the interior of is given by the predictor and on the space–time lateral surfaces is given by and which are the so-called boundary-extrapolated data, i.e., the values assumed respectively by the predictors of the two neighbor elements and on the shared space–time lateral surface . Furthermore, we have employed a two-point path-conservative numerical flux function of Rusanov-type
where smax is the maximum eigenvalue of the ALE Jacobian matrices and being
and the path is a straight-line segment path
connecting and which allow to treat the jump of the non-conservative products following the theory introduced in Dal Maso et al. [145], Parés [146], and Castro et al. [147], and extended to ADER FV-DG schemes of arbitrary high order in Dumbser et al. [46] and Dumbser and Toro [148]. Despite in this paper we only consider the Rusanov flux, the above methodology can be extended to different flux functions, adapting to the new flux splitting techniques like the ones presented in Toro and Vázquez-Cendón [149]. Finally, the time step size Δt is given by
where hmin is the minimum characteristic mesh-size, ℓij is the length of the edge j of and |λmax| is the spectral radius of the Jacobian of the flux F. Stability on unstructured meshes is guaranteed by the satisfaction of the inequality , see Dumbser et al. [42].
We close this section by remarking that the integration of the governing PDE over closed space-time volumes automatically satisfies the geometric conservation law (GCL) for all test functions . This simply follows from the Gauss theorem and we refer to Boscheri and Dumbser [63] for a complete proof.
2.8. A Posteriori Subcell Finite Volume Limiter
Up to now, we have presented a family of FV and DG type schemes which achieves arbitrary high order of accuracy in space and time; the main difference between the FV and the DG approach lies in the fact that FV schemes, thanks to the WENO-type non-linear reconstruction procedure, are robust in the presence of shocks and discontinuities, while the DG formulation as presented so far, being linear in the sense of Godunov, is subject to the appearance of spurious oscillations. Thus, in order to employ a DG scheme in the context of solving hyperbolic partial differential equations, where usually discontinuities are developed, a technique that is able to limit spurious oscillations (called limiter) should be introduced. Several attempts in that direction can be found in the literature. For example, we could recall the artificial viscosity technique used in Hartmann and Houston [150],Persson and Peraire [151], and Cesenek et al. [152] which consists in adding a small parabolic term in the equation in order to smooth out the discontinuities.
Here, instead, we follow a different approach based on exploiting the respective strengths of FV and DG schemes, i.e., the resolution of DG in smooth regions and the robustness of FV across discontinuities. Thus, we first evolve the solution everywhere by using our DG scheme; then, we check a posteriori, at the end of each time step, if the obtained DG solution in each cell respects or not some criteria [as density and pressure positivity, a relaxed discrete maximum principle, specific physical bounds, or more elaborate choices as those of Guermond et al. [153]], and we mark as troubled those cells where the obtained DG solution is marked as not acceptable. Only for these troubled cells we repeat the time step using, instead of the DG scheme, a second order TVD FV method, which always assures a robust solution.
This idea is founded on works as those of Cockburn and Shu [154], Qiu and Shu [155, 156], Balsara et al. [157], Luo et al. [158], Krivodonova [159], Zhu et al. [160], Zhu and Qiu [161], Clain et al. [86], Diot et al. [87, 88], Loubére et al. [79], Boscheri et al. [162],and Boscheri and Loubére [83]; but in particular, here, we adopt a so-called subcell approach aimed at not losing the resolution of the DG scheme when switching to the FV method, as forwarded in Sonntag and Munz [163], Dumbser et al. [78], Zanotti et al. [80], Dumbser and Loubére [81], Boscheriand Dumbser [119], Fambri et al. [84], Rannabauer et al. [164], de la Rosa and Munz [165], and Boscheri et al. [142]. Indeed, at the beginning of the time step we project the DG solution of a troubled cell on a subdivision of it in sub-cells obtaining a value for the cell averages on at time tn
We evolve the cell averages up to time tn+1 using a classical TVD FV scheme, obtaining . Finally, we recover a DG polynomial representation of the solution at time tn+1 over using the values on the sub-grid level and by applying a reconstruction operator as
where the reconstruction is imposed to be conservative on the main cell yielding the additional linear constraint
Thus, the limited solution on a troubled cell is robust thanks to the use of a TVD scheme and accurate thanks to the subcell resolution.
For all the details of the a posteriori subcell FV limiter used in this work, we refer to Dumbser et al. [78] and Fambri et al. [36] for the fixed Cartesian Case A and to Gaburro et al. [77] for the moving polygonal Case B.
3. A Unified First Order Hyperbolic Model of Continuum Mechanics
3.1. Governing PDE System
A simplified diffuse interface formulation of the unified continuum fluid and solid mechanics model [57, 59, 60, 166], which can be used for modeling moving boundary problems of fluids and solids of arbitrary geometry, is given by the following PDE system (throughout this paper we make use of the Einstein summation convention over repeated indices)
Here, (56a) is the evolution equation for the color function α that is needed in the diffuse interface approach as introduced in Tavelli et al. [85] for the description of linear elastic solids of arbitrary geometry and as used in Dumbser [106] and Gaburro et al. [107] for a simple diffuse interface method for the simulation of non-hydrostatic free surface flows. We assume that the color function α equals to 1 in the regions of the computational domain occupied by the material and 0 outside these regions. In the computational code, α = 1 − ε inside of the material and α = ε outside the material. Here, ε is a small parameter ε ≪ 1, see section 4. Then, inside of the diffuse interface, α may take any values between 0 and 1 (between ε and 1 − ε in the computational code). Equation (56b) is the mass conservation law and ρ is the material density; (56c) is the momentum conservation law, where vi is the velocity field and gi is the gravity vector; (56d) is the evolution equation for distortion field Aik (non-holonomic basis triad, see Peshkov et al. [167]); (56e) is the evolution equation for the specific thermal impulse Jk constituting the heat conduction in the matter via a hyperbolic (non-Fourier–type) model. Finally, (56f) is the entropy balance equation and (56g) is the energy conservation law. Other thermodynamic parameters are defined via the total energy potential E = E(α, ρ, S, v, A, J): Σik = pδik − σik is the total stress tensor (δik is the Kronecker delta); is the thermodynamic pressure; σik = − ρAjkEAji is the non-isotropic part of the stress tensor, T = ES is the temperature, and the notations such as Eρ, EAik, etc. stand for the partial derivatives of the energy potential, e.g., , , etc.
The dissipation in the medium includes two relaxation processes: the shear stress relaxation characterized by the scalar function θ1(τ1) > 0 depending on the relaxation time τ1 and thermal impulse relaxation characterized by θ2(τ2) > 0 depending on the relaxation time τ2. Both these relaxation processes then contribute to the entropy production term [the source on the right hand-side of (56f)] which is positive because it is quadratic in EAik and EJk.
From the mathematical standpoint, the unification of the model (56) consists in the use of only first-order hyperbolic equations for both dissipative and non-dissipative processes in contrast to the classical continuum mechanics relying on the mixed hyperbolic-parabolic formulations such as the famous Navier-Stokes-Fourier equations, for example. From the physical standpoint, the unification of Equations (56) consists in treating solid and fluid states of matter from the solid-dynamics viewpoint. Indeed, as discussed in Peshkov and Romenski [57] and Dumbser et al. [59, 166], similarly to standard continuum solid-dynamics, the distortion field introduces additional degrees of freedom (in comparison to the classical continuum fluid mechanics) which characterizes deformation and rotational degrees of freedom of the continuum particles, represented not as scaleless mathematical points but characterized by a finite length scale, or equivalently, time scale τ1, e.g., see Dumbser et al. [166]. In such a formulation, solid-type behavior corresponds to relaxation times τ1 such that , while the fluid-type behavior corresponds to , where Tproblem is the characteristic time scale of the problem under consideration.
In order to close system (56), that is, in order to define pressure , stresses σik = − ρAjkEAji, temperature T = ES, and the dissipative source terms, one needs to provide the energy potential E. In this paper, we rely on a rather simple choice of E, which is, however, enough to deal with Newtonian fluids and simple hyperelastic solids. Thus, we assume that the specific total energy can be written as a sum of three contributions as
with the specific internal energy given by the ideal gas equation of state
in the case of gases, and given by either the so-called stiffened gas equation of state
or the well-known Mie-Grüneisen equation of state
in the case of solids and liquids. Here, cv is the specific heat capacity at constant volume, γ is the ratio of the specific heats, p0 is the reference (atmospheric) pressure, ρ0 is the reference material density, and Γ0, and s are some material parameters. The specific energy stored in material deformations and in the thermal impulse is
where is the trace-free part of the metric tensor Gij = AkiAkj, which is induced by the mapping from Eulerian coordinates to the current stress-free reference configuration. The coefficients and in (61) are the characteristic velocities for propagation of shear and thermal perturbations accordingly. In the present diffuse interface model, we choose the following simple linear mixture rule for the computation of the shear sound speed and of the heat wave propagation as a function of the volume fraction α
where cs and ch are the material parameters inside the continuum and and are free parameters that can be chosen for the region outside the continuum. The specific kinetic energy is contained in the third contribution to the total energy and reads .
With the equation of state chosen above, we get the following expressions for the stress tensor, the heat flux and the dissipative sources EAik and EJk present in the relaxation source terms:
The functions θ1 and θ2 are chosen in such a way that a constant viscosity and heat conduction coefficient are obtained in the stiff relaxation limit, see Dumbser et al. [59] for a formal asymptotic analysis,
Thus, following the procedure detailed in Dumbser et al. [59], one can show via formal asymptotic expansion that in the stiff relaxation limit τ1 → 0, τ2 → 0, the stress tensor and the heat flux reduce to
and
that is the effective shear viscosity and effective heat conductivity of model (56) are
with ρ0 and T0 are reference density and temperature, see Dumbser et al. [59], where also an explanation has been provided of how the relaxation times τ could be obtained experimentally via ultrasound measurements.
3.2. Symmetric Godunov Form of the Model
It is important to note an interesting structural feature of Equations (56) that may affect future developments of the ADER schemes in an attempt to respect such structural properties at the discrete level that may help to improve physical consistency of the numerical solution. Thus, as many PDE systems studied in some other of our papers [59, 60, 168, 169], system (56) belongs to the class of so-called Symmetric Hyperbolic Thermodynamically Compatible (SHTC) PDE systems originally studied by Godunov [170, 171] and later by Godunov and Romenski [172], Godunov et al. [173], Romenski [168] and Romensky [174].
Indeed, by simply rescaling the quantities , , and and replacing the non-conservative Equation (56a) by an equivalent (on smooth solutions) conservative form (69a), system (56) can be written as
where we have omitted the energy equation. Now, this system looks exactly as the system studied in Dumbser et al. [59], apart from the additional Equation (69a) which has the same structure as (69b) and does not change the essence. Then, after denoting and introducing new variables P = (ϱ1, ϱ2, vi, αik, Θi, σ)
which are thermodynamically conjugate to the conservative variables , and a new thermodynamic potential , system (69) can be written in a symmetric form
In this PDE system, the first two terms in each equation form the canonical Godunov form introduced in Godunov [170] which can be immediately written as a quasilinear symmetric form, e.g., see Peshkov et al. [169], Romenski [168], and Romensky [174]. The other (non-conservative) terms obviously form a symmetric matrix. Therefore, the entire system (71) can be written in a symmetric quasi-linear form and hence, it is a symmetric hyperbolic system if the thermodynamic potential L is convex.
We note that the understanding of the structural properties of the continuous equations might be beneficial for developing of so-called structure-preserving numerical integrators (e.g., symplectic integrators). Thus, the energy conservation law (56g) is in fact a consequence of the other Equations (56) or (71), e.g., see Dumbser et al. [59] and Peshkov et al. [169], and can be viewed as a constraint of the system (71). Its non-violation at the discrete level cannot be guaranteed by the general purpose ADER family of schemes studied in this paper and hence, usually, as well as in our implementation, it is included into the set of discretized PDEs instead of the entropy equation. In principle, a structure-preserving scheme which satisfies all SHTC properties [169] of the continuous equations at the discrete level should guarantee the automatic satisfaction of the energy conservation law, without its explicit discretization. We hope to cover this topic in future work.
4. Numerical Results
In this section, we present some numerical results in order to illustrate the capabilities and potential applicability of the proposed numerical approach in non-linear continuum mechanics. The first three test problems are carried out without making explicit use of the diffuse interface approach, i.e., setting α = 1 everywhere in the entire computational domain. The last three test problems illustrate the full potential of the diffuse interface extension of the GPR model in the context of moving free boundary problems. Gravity effects are neglected in all test cases, apart from the dambreak problem shown in subsection 4.6. Whenever values for ν = μ/ρ0 and cs are provided, the corresponding relaxation time τ1 is computed according to (68).
4.1. Numerical Convergence Studies in the Stiff Relaxation Limit
In order to verify the high order property of our ADER schemes in both space and time in the stiff relaxation limit, we first represent the numerical convergence study that was already carried out in Dumbser et al. [59] on a smooth unsteady flow, for which an exact analytical solution is known for the compressible Euler equations, i.e., in the stiff relaxation limit τ1 → 0 and τ2 → 0 of the GPR model. The problem setup is the one of the classical isentropic vortex, see Hu and Shu [175]. The initial condition consists in a stationary isentropic vortex, whose exact solution can easily be found by solving the compressible Euler equations in cylindrical coordinates. Due to the Galilean invariance of the Euler equations and of the GPR model, one can then simply superimpose a constant velocity field to this stationary vortex solution in order to get an unsteady version of the test problem. The vortex strength is chosen as ε = 5 and the perturbation of entropy is assumed to be zero. For details of the setup, see Hu and Shu [175] and Dumbser et al. [59]. In this test we set the distortion field initially to , while the heat flux vector is initialized with J = 0. As computational domain we choose Ω = [0;10] × [0;10] with periodic boundary conditions. The reference solution for the GPR model in the stiff relaxation limit is given by the exact solution of the compressible Euler equatons, which is the time–shifted initial condition Qe(x, t) = Q(x − vct, 0), where the convective mean velocity is vc = (1, 1). We run this benchmark on a mesh sequence until the final time t = 1.0. The physical parameters of the GPR model are chosen as γ = 1.4, cv = 2.5, ρ0 = 1, cs = 0.5, and ch = 1. The volume fraction function is set to α = 1 in the entire computational domain. The resulting numerical convergence rates obtained with ADER-DG schemes using polynomial approximation degrees from N = M = 2 to N = M = 5 are listed in Table 1, together with the chosen values for the effective viscosity μ and the effective heat conductivity coefficient κ. From Table 1 one can observe that high order of convergence of the numerical method is achieved also in the stiff limit of the governing PDE system.
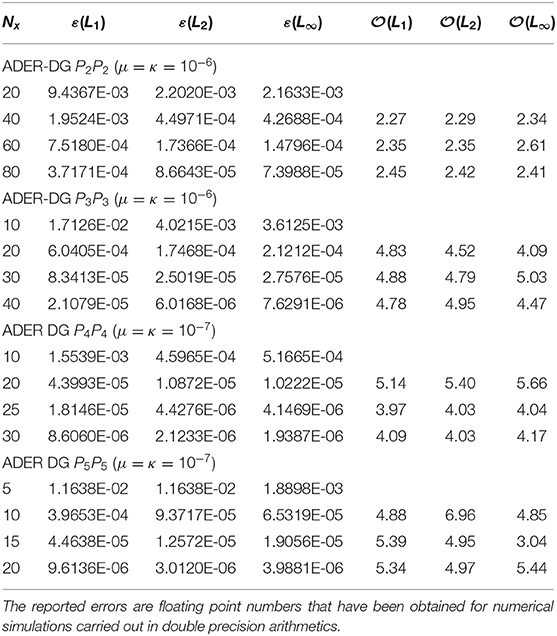
Table 1. Experimental errors and order of accuracy at time t = 1 for the density ρ for ADER-DG schemes applied to the GPR model (cs = 0.5, α = 1) in the stiff relaxation limit (μ ≪ 1, κ ≪ 1).
4.2. Circular Explosion Problem in a Solid
In this Section, we simulate a circular explosion problem in an ideal elastic solid. We compare the results obtained with a third order ADER-WENO finite volume scheme on moving unstructured Voronoi meshes with possible topology changes, Gaburro et al. [77], with those obtained with a fourth order ADER discontinuous Galerkin finite element scheme on a very fine uniform Cartesian mesh composed of 512 × 512 elements, which will be taken as the reference solution for this benchmark. The computational domain is Ω = [−1, 1] × [−1, 1] and the final simulation time is t = 0.25. We set α = 1, v = 0, A = I and J = 0 in the entire domain. For the initial density and the initial pressure are set to ρ = 1 and p = 1, while in the rest of the domain we set ρ = 0.1 and p = 10−3. The parameters of the GPR model are chosen as follows: cs = 0.2, ch = 0, τ1 → ∞ (in order to model an elastic solid). We use the stiffened gas equation of state with γ = 2 and p0 = 0. For the simulation on the moving Voronoi mesh, we employ a mesh with 82919 control volumes. The computational results obtained with the unstructured ADER-WENO ALE scheme and those obtained with the high order Eulerian ADER-DG scheme are presented and compared with each other in Figure 9. We can note a very good agreement between the two results. The high quality of the ADER-WENO finite volume scheme on coarse grids is mainly due to the natural mesh refinement around the shock, which is typical for Lagrangian schemes. Furthermore, Lagrangian schemes are well-known to capture material interfaces and contact discontinuities very well, since the mesh is moving with the fluid and thus numerical dissipation at linear degenerate fields moving with the fluid velocity is significantly lower than with classical Eulerian schemes.
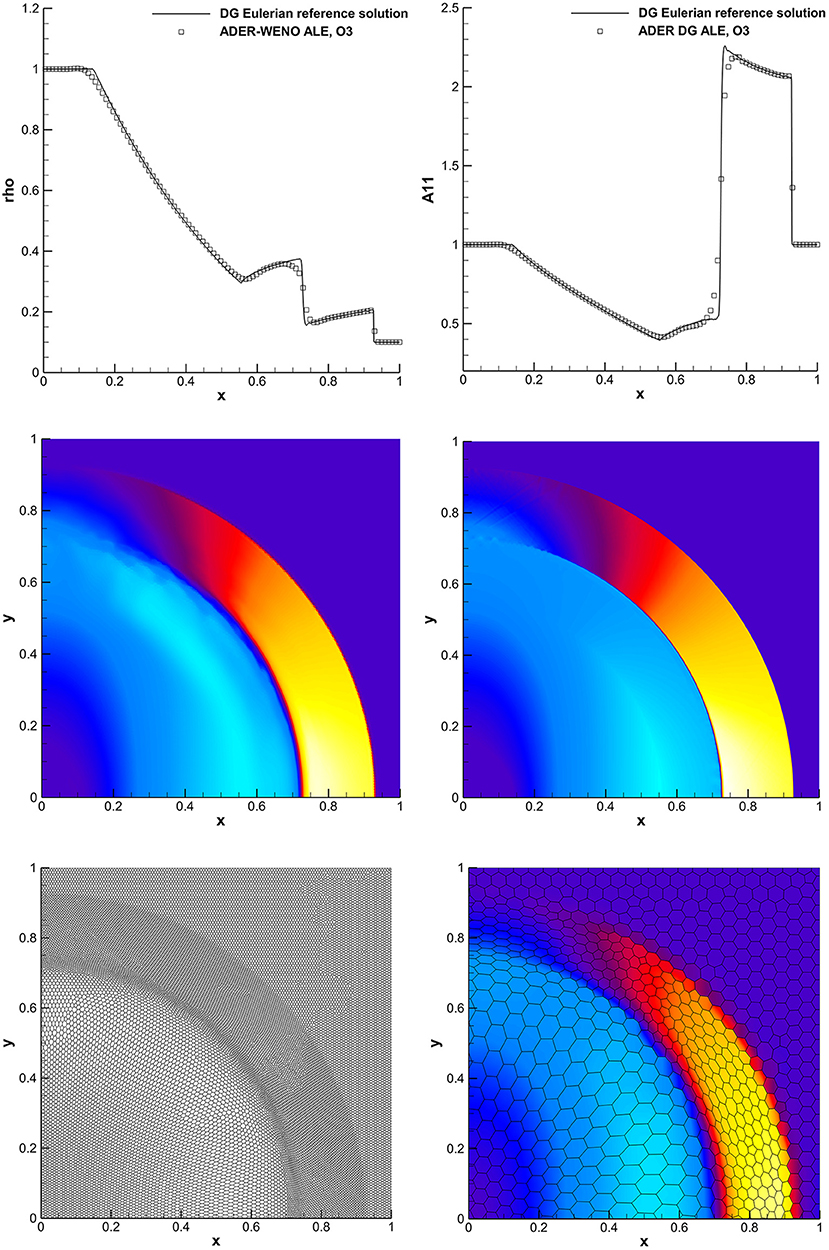
Figure 9. Simulation results for the explosion problem obtained with a third order ADER-WENO ALE finite volume scheme on a moving Voronoi grid composed of 82919 cells and with a fourth order ADER-DG scheme on a Cartesian grid of size 5122 = 262144 (4.2 × 106 DOF). In the top row, two cuts of the solution along the x-axis are shown; in the middle row, from the left, the solution for A11 obtained with the ADER-WENO ALE scheme and with the ADER-DG Eulerian scheme; in the bottom row, the Voronoi grid at the final simulation time and the results from the ADER-WENO ALE scheme on a coarser grid of 2727 elements.
4.3. Rotor Test Problem
A second solid mechanics benchmark consists in the simulation of a plate on which a rotational impulse is initially impressed, in a circular region centered with respect to the computational domain. This rotor will initially move according to the rotational impulse, while emitting elastic waves which ultimately determine the formation of a set of concentric rings with alternating direction of rotation. The test is analogous to the rotor problem shown in Peshkov et al. [72], but with a weakened material in order to show stronger motion of the Voronoi grid.
The results of the third order ADER-WENO finite volume method on a moving Voronoi grid with variable connectivity, composed of 150561 cells, are compared against a reference solution obtained with a fourth order ADER discontinuos Galerkin scheme on a very fine uniform Cartesian mesh counting 512 × 512 elements, for a total of over four million spatial degrees of freedom.
The computational domain is the square Ω = [−1, 1] × [−1, 1] and the final simulation time is set to t = 0.5. With exception made for the velocity field, all variables are initially constant throughout the domain. Specifically we set α = 1, ρ = 1, p = 1, A = I, J = 0, while the velocity field is v = [−y/R, x/R, 0] if , and v = 0 otherwise, that is, outside of the circle of radius R = 0.2; this way, the initial tangential velocity at r = R is one. The solid is taken to be elastic (τ1 → ∞), heat wave propagation is neglected (ch = 0), and the characteristic speed of shear waves is cs = 0.25. The constitutive law is chosen to be the stiffened-gas EOS with γ = 1.4 and p0 = 0. We can see in Figure 10 that, although some of the finer features are lost (specifically the small central counterclockwise-rotating ring) due to the lower resolution of the finite volume method on a coarser grid, the shear waves travel outwards with the correct velocity and the moving Voronoi finite volume simulation can be said to be in agreement with the high resolution discontinuous Galerkin results. Also in Figure 10, it is shown that the central region of the computational grid has undergone significant motion but thanks to the absence of constraints on the connectivity between elements, the Voronoi control volumes have not been stretched excessively as would instead happen for a similar moving unstructured grid, but with fixed connectivity.
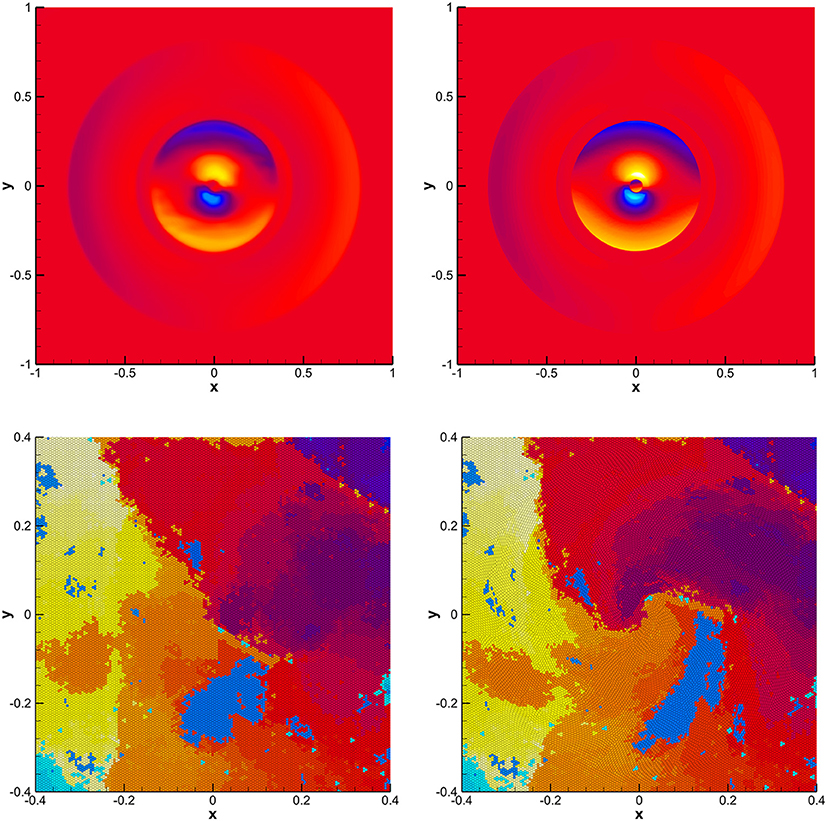
Figure 10. Simulation results for the solid rotor problem obtained from a third order ADER-WENO ALE finite volume scheme on a moving Voronoi grid composed of 150561 cells and with a fourth order ADER-DG scheme on a cartesian grid of size 5122 = 262144 (4.2 × 106 DOF). In the top row, the solutions for the u component of the velocity field are shown, on the left those obtained with the unstructured ADER-WENO ALE scheme on moving Voronoi meshes and on the right those of the ADER-DG scheme on a fixed Cartesian grid; in the bottom panels the cells are colored according to their mesh numbering to show the mesh motion between the beginning of the ALE simulation and the final time.
4.4. Elastic Vibrations of a Beryllium Plate
The first benchmark for our new diffuse interface version of the GPR model consists in the purely elastic vibrations of a beryllium plate, subject to an initial velocity distribution, see for example Sambasivan et al. [176], Maire et al. [177], Burton et al. [178], Boscheri et al. [71], and Peshkov et al. [72] for a setup of the same test problem in the framework of Lagrangian and ALE schemes.
Unlike in the Lagrangian simulations, the computational domain considered here is larger and is set to Ω = [−5;5] × [−2.5;2.5]. The computational grid consists of 512 × 256 uniform Cartesian cells with a characteristic mesh size of about h = 0.02. We use a third order ADER-WENO finite volume scheme in the entire domain. The initial geometry of the beryllium bar is now simply defined by setting α(x, 0) = 1−ε inside the subdomain Ωb = [−3, 3] × [−0.5, 0.5], while the solid volume fraction function α is set to α(x, 0) = ε elsewhere, with ε = 5·10−3. The initial velocity field inside Ωb is imposed according to Burton et al. [178], Boscheri et al. [71], and Peshkov et al. [72] as
with Ω = 0.7883401241, ω = 0.2359739922, A = 0.004336850425, S1 = 57.64552048, and C1 = 56.53585154, while we simply set v = 0 outside Ωb. For this test case we set ε = 5·10−3. The distortion field is initially set to A = I. The material properties of Beryllium in the Mie-Grüneisen equation of state are taken as follows: ρ0 = 1.845, c0 = 1.287, cs = 0.905, Γ = 1.11, and s0 = 1.124. We furthermore neglect heat conduction and set ch = 0 and J = 0.
Unlike in Lagrangian schemes, no boundary conditions need to be imposed on the surface of the bar. We simply use transmissive boundaries on ∂Ω. The entire computational domain is initialized with the reference density for beryllium as ρ(x, 0) = ρ0, while the pressure is set to p(x, 0) = 0. The distortion field is initialized with A = I. According to Burton et al. [178], the final time is set to tf = 53.25 so that it corresponds approximately to two complete flexural periods. The simulations are carried out with a third order ADER-WENO scheme on two uniform Cartesian meshes composed of 256 × 128 and 512 × 256 elements, respectively.
For the fine grid simulation in Figure 11, we present the temporal evolution of the color contour map of the volume fraction function α, which represents the moving geometry of the bar. Here, dark gray color is used to indicate the regions with α > 0.5 and white color is used for the regions of α < 0.5. In the same figure, we also depict the pressure field in the region α > 0.5 at times t = 5, t = 14, t = 23, and t = 28. These time instants cover approximately one flexural period. The time evolution of the vertical velocity component v(0, 0, t) in the origin is depicted in Figure 12. For comparison, in the same figure we also show the results obtained on the coarse mesh for the same test problem with a fourth order ADER-DG scheme with second order TVD subcell finite volume limiter (red line).
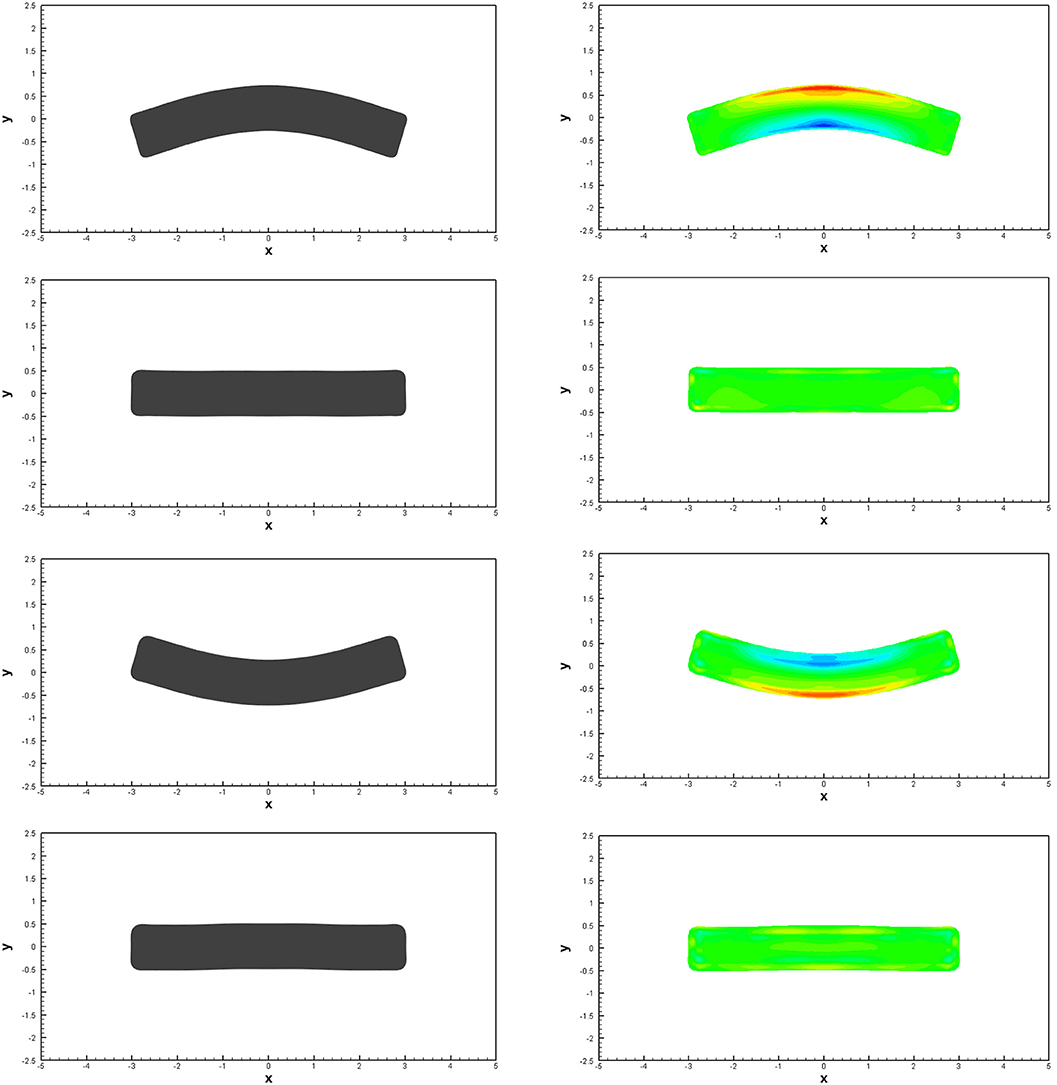
Figure 11. Vibration of an elastic beryllium plate. Temporal evolution of the volume fraction function α (left) and of the pressure field (right) at times t = 5, t = 14, t = 23, and t = 28, from top to bottom.
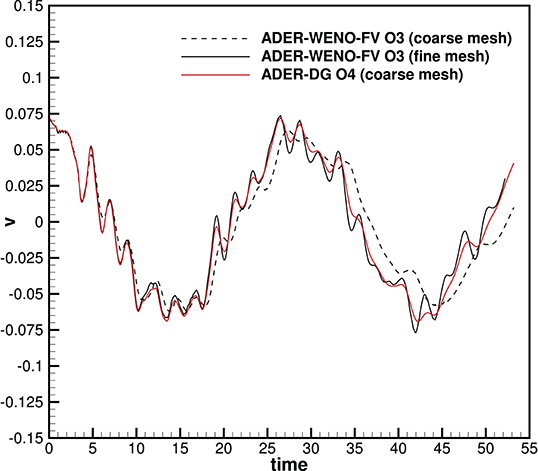
Figure 12. Temporal evolution of the vertical velocity component v(0, 0, t) obtained with a third order ADER-WENO scheme applied to the diffuse interface GPR model using two different mesh resolutions of 256 × 128 elements (coarse mesh) and 512 × 256 grid cells (fine mesh). For comparison, also a fourth order ADER-DG simulation on the coarse mesh is shown (red line).
Our computational results compare visually well against available reference solutions in the literature, see Sambasivan et al. [176], Maire et al. [177], Burton et al. [178], Boscheri et al. [71], and Peshkov et al. [72], which were all carried out with pure Lagrangian or Arbitrary-Lagrangian-Eulerian schemes on moving meshes, while here we use a diffuse interface approach on a fixed Cartesian grid.
4.5. Taylor Bar Impact Problem
So far, we have only considered ideal elastic material, i.e., the limit case τ1 → ∞. In this section we consider also non-linear elasto-plastic material behavior. Following Barton et al. [179, 180], Boscheri et al. [71], and Peshkov et al. [72] we choose the relaxation time τ1 as a non-linear function of an invariant of the stress tensor as follows:
where τ0 is a constant characteristic relaxation time, σ0 is the yield stress of the material and the von Mises stress σ is given by
In the formula (74) above, is the stress deviator, i.e., the trace-free part of the stress tensor. The non-linear relaxation time (73) tends to zero for σ ≫ σ0, while it tends to infinity for σ ≪ σ0.
The Taylor bar impact problem is a classical benchmark for an elasto-plastic aluminium projectile that hits a rigid solid wall, see Sambasivan et al. [176], Maire et al. [177], Dobrev et al. [181], and Boscheri et al. [71]. In this work the computational domain under consideration is Ω = [0, 600] × [−150, +150]. The aluminium bar is initially located in the region Ωb = [0, 500] × [−50, +50], where we set α = 1−ε, while in the rest of the computational domain we set α = ε, with ε = 1·10−2.
The aluminium bar is described by the Mie-Grüneisen equation of state with parameters ρ0 = 2.785, c0 = 0.533, cs = 0.305, Γ = 2, and s = 1.338. The yield stress of aluminium is set to σ0 = 0.003.
The projectile is initially moving with velocity v = (−0.015, 0) toward a wall located at x = 0. This velocity field is imposed within the subregion Ωb, while in the rest of the domain we set v = 0. The remaining initial conditions are chosen as ρ = ρ0, p = p0, A = I, J = 0 and with the parameters τ0 = 1 and m = 20 for the computation of the relaxation time (73). Unlike in Lagrangian schemes, we do not need to set any boundary conditions on the free surface of the moving bar. We only apply reflective slip wall boundary conditions on the wall in x = 0. According to Maire et al. [177], Dobrev et al. [181], and Boscheri et al. [71] the final time of the simulation is t = 5, 000. The computational domain is discretized on a regular Cartesian grid composed of 512 × 256 elements using a third order ADER-WENO finite volume scheme. As in Boscheri et al. [71] we employ a classical source splitting for the treatment of the stiff sources that arise in the regions of plastic deformations, i.e., when σ ≫ σ0. In Figure 13, we show the computational results at t = 1000 and at the final time t = 5, 000. The obtained solution is in agreement with the results presented in Maire et al. [177], Boscheri et al. [71], and Peshkov et al. [72]. At time t = 5, 000, we measure a final length of the projectile of Lf = 456, which fits the results achieved in Maire et al. [177] and Boscheri et al. [71] up to 2%.
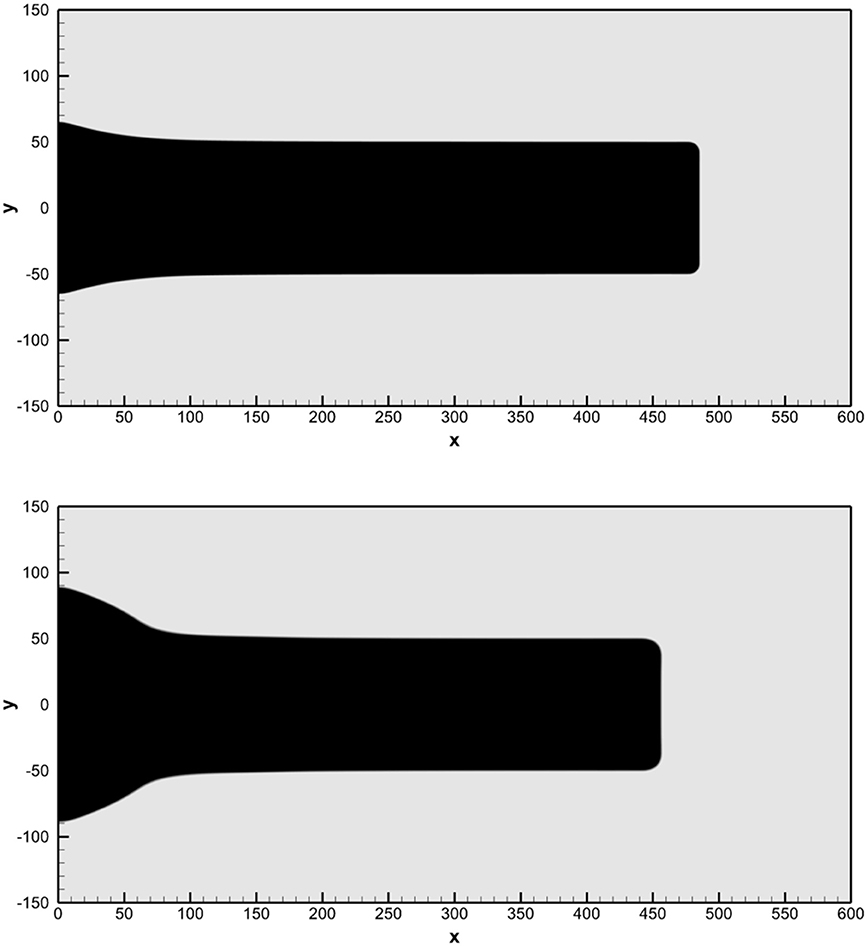
Figure 13. Geometry of the Taylor bar at time t = 1, 000 (top) and at the final time t = 5, 000 (bottom) obtained with a third order ADER-WENO finite volume scheme applied to the diffuse interface GPR model. We plot the contour colors of the volume fraction function α, where black regions denote α > 0.5 and white regions α < 0.5.
4.6. Dambreak Problem
In this last section on numerical test problems, we solve a two-dimensional dambreak problem with different relaxation times in order to show the entire range of potential applications of the GPR model. For this purpose, we also activate the gravity source term, setting the gravity vector to g = (0, −g) with g = 9.81. The computational domain is chosen as Ω = [0, 4] × [0, 2] and is discretized with a fourth order ADER discontinuous Galerkin finite element scheme with polynomial approximation degree N = 3 and a posteriori subcell TVD finite volume limiter. Computations are run on a uniform Cartesian mesh composed of 128 × 64 elements until the final time t = 0.5. The initial condition is chosen as follows: we set ρ = ρ0, v = 0, A = I and J = 0 in the entire computational domain. We impose the slip boundary condition on the bottom. In the subdomain Ωd = [0, 2] × [0, 1], we set α = 1 − ε, and p = ρ0g(y − 1), while in the rest of the domain we set α = ε and p = 0. In this test problem we set ε = 10−2 and use a stiffened gas equation of state with parameters ρ0 = 1, 000, , γ = 2, ch = 0 and a shear sound speed cs = 6. Simulations are run in three different regimes, only characterized by a different choice of the strain relaxation time τ1. In the first simulation, we set τ1 so that a kinematic viscosity is reached in the stiff relaxation limit, i.e., the GPR model in this case describes an almost inviscid fluid. In the second simulation we choose τ1 so that ν = 0.1, i.e., a high viscosity Newtonian fluid behavior is reached. In the last simulation we set τ1 → ∞, i.e., the strain relaxation term is switched off so that an ideal elastic solid with low shear resistance is described, similar to a jelly-type medium. In all cases, we apply solid slip wall boundary conditions on the left and on the right of the computational domain, while on the right and upper boundary, transmissive boundary conditions are set. The temporal evolution of the volume fraction function α, together with the coarse mesh used in this simulation, are depicted in Figure 14. The results for the almost inviscid fluid agree qualitatively well with those shown in Ferrari et al. [182], Dumbser et al. [106], and Gaburro et al. [107] for non-hydrostatic dambreak problems. In order to corroborate this statement quantitatively, we now repeat the simulation with ν = 10−3 using a fourth order ADER-DG scheme on a coarse AMR grid composed of only 32 × 16 elements on the level zero grid. We then apply two levels of AMR refinement with refinement factor 𝔯 = 3, i.e., we employ a general space-tree, rather than a simple quad-tree. We note that the simulations on the AMR grid are run in combination with time-accurate local time stepping (LTS), which is trivial to implement in high order ADER-DG and ADER-FV schemes, due to their fully-discrete one-step nature. For details on LTS, see Dumbser et al. [37, 54],Dumbser [64] and Gaburro et al. [65]. As a reference solution of this almost inviscid flow problem, we solve the reduced barotropic and inviscid Baer-Nunziato model introduced in Dumbser [106] and Gaburro et al. [107], using a third order ADER-WENO finite volume scheme on a very fine uniform Cartesian grid composed of 1024 × 512 elements. The direct comparison of the two simulations at time t = 0.4 is shown in Figure 15. Overall we can indeed note an excellent agreement between the behavior of the diffuse interface GPR model in the stiff relaxation limit and the weakly compressible inviscid non-hydrostatic free surface flow model of Dumbser [106] and Gaburro et al. [107].
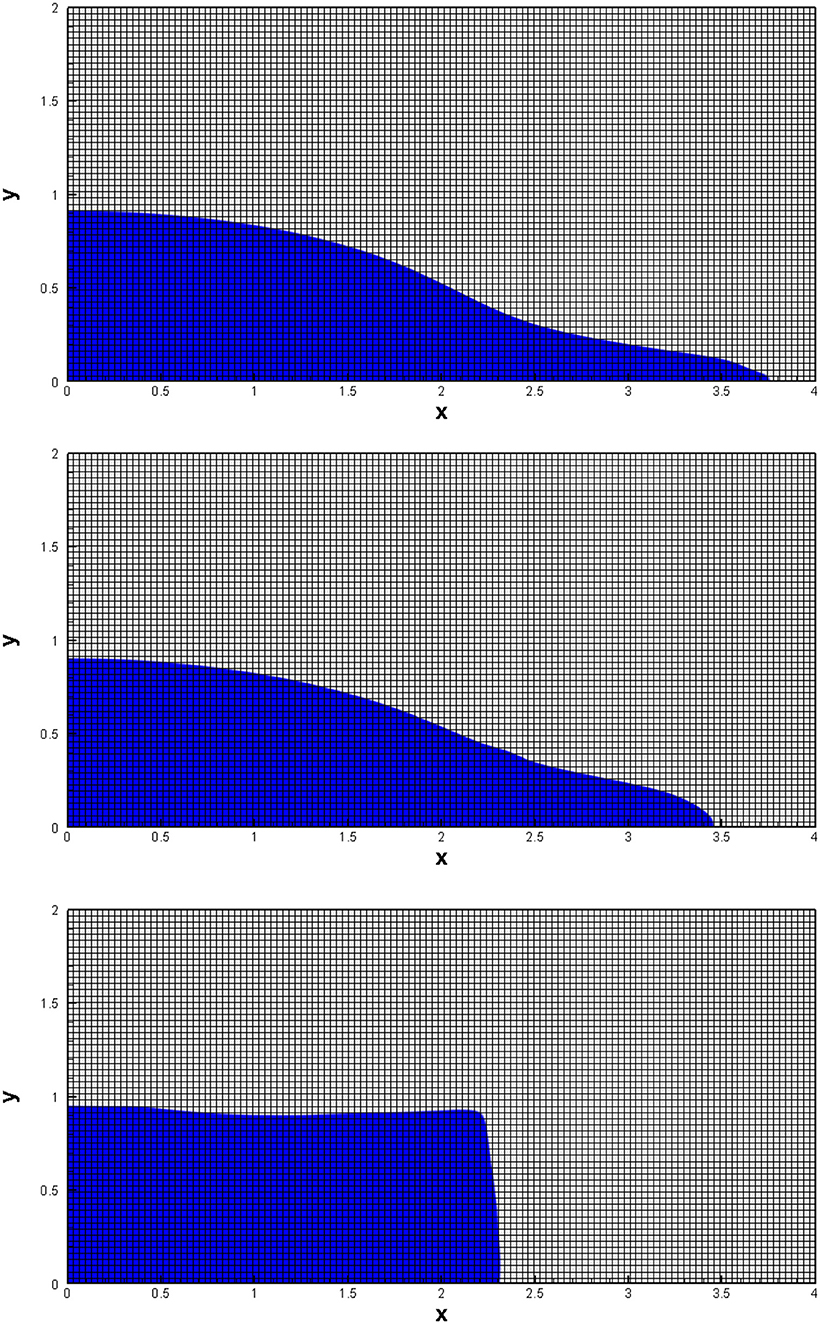
Figure 14. Dambreak problem at t = 0.5, simulated with a fourth order ADER-DG scheme using different relaxation times. (Top) Low viscosity fluid (stiff relaxation limit) with ν = 10− 3. (Center) High viscosity fluid with ν = 10−1. (Bottom) Ideal elastic solid (τ1 → ∞) with low shear resistance.
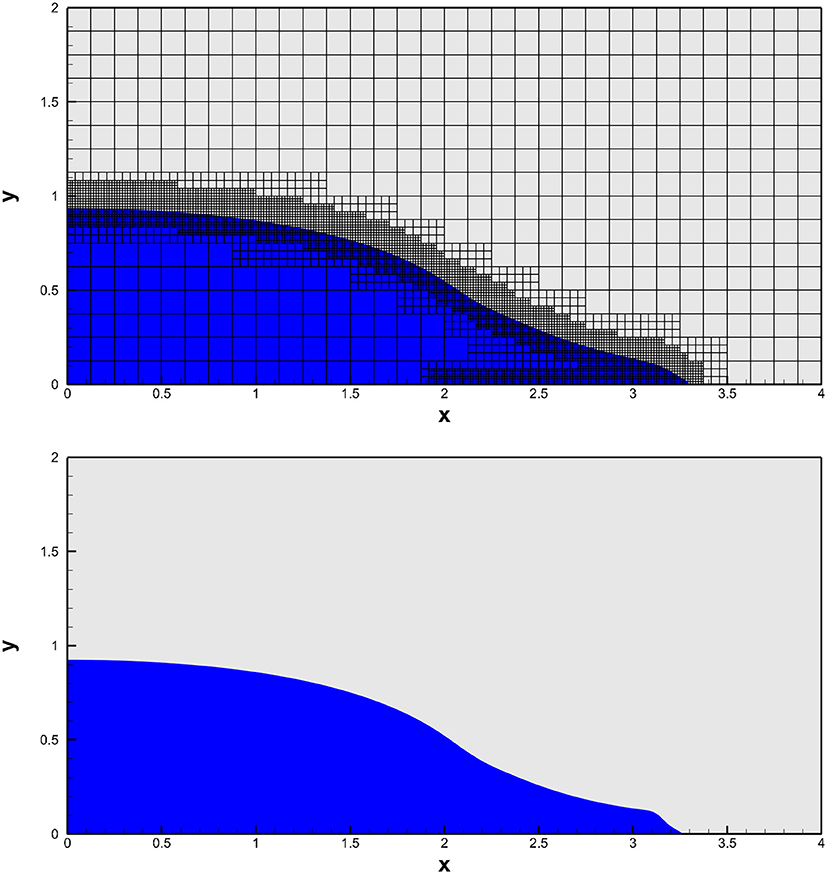
Figure 15. Dambreak problem at t = 0.4, simulated with a fourth order ADER-DG scheme using a space-time adaptive Cartesian AMR mesh applied to the GPR model with with ν = 10−3 (Top), and reference solution, computed with a third order ADER-WENO finite volume scheme on a very fine uniform Cartesian grid, solving the inviscid and barotropic reduced Baer-Nunziato approach presented in [106, 107] (Bottom).
5. Conclusions and Outlook
In the first part of this paper we have provided a review of the ADER approach, whose development started about 20 years ago with the seminal works of Toro et al. [20] Millington et al. [19], Titarev and Toro [29], and Toro and Titarev [28] in the context of approximate solvers for the generalized Riemann problem (GPR). The ADER method provides fully discrete explicit one-step schemes that are in principle arbitrary high order accurate in both space and time. The most recent developments include ADER schemes for stiff source terms, as well as ADER finite volume and discontinuous Galerkin finite element schemes on fixed and moving meshes, which are all based on a space-time predictor-corrector approach. The fact that ADER schemes are fully discrete makes the implementation of time accurate local time stepping (LTS) particularly simple, both on adaptive Cartesian AMR meshes [54], as well as in the context of Lagrangian schemes on moving grids [64, 65]. The fully discrete space-time formulation also allows the treatment of topology changes during one time step in a very natural way [77]. In the second part of the paper we have then shown several applications of high order ADER finite volume and discontinuous Galerkin finite element schemes to the novel unified hyperbolic model of continuum mechanics (GPR model) proposed by Godunov, Peshkov and Romenski [56, 57, 59]. The presented test problems cover the entire range of continuum mechanics, from ideal elastic solids over plastic solids to viscous fluids. The use of a diffuse interface approach allows also to simulate moving boundary problems on fixed Cartesian meshes. Future developments will concern the extension of the mathematical model to non-Newtonian fluids [183] and to free surface flows with surface tension, see Schmidmayer et al. [184] and Chiocchetti et al. [185], as well as to the conservative multi-phase model of Romenski et al. [186, 187]. In future work we will also consider the use of novel all speed schemes [188] and semi-implicit space-time discontinuous Galerkin finite element schemes [189–191] for the diffuse interface version of the GPR model used in this paper.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
The governing PDE system was developed by IP. The numerical method and the computer codes were developed by MD, EG, and SC. The test problems were computed by MD, EG, and SC. The analysis of the method was performed by SB. All authors discussed the results and contributed to the final manuscript.
Funding
The research presented in this paper has been financed by the European Union's Horizon 2020 Research and Innovation Programme under the project ExaHyPE, grant agreement number no. 671698 (call FET-HPC-1-2014). SB has also received funding by INdAM (Istituto Nazionale di Alta Matematica, Italy) under a Post-doctoral grant of the research project Progetto premiale FOE 2014-SIES. SC acknowledges the financial support received by the Deutsche Forschungsgemeinschaft (DFG) under the project Droplet Interaction Technologies (DROPIT), grant no. GRK 2160/1. MD also acknowledges the financial support received from the Italian Ministry of Education, University and Research (MIUR) in the frame of the Departments of Excellence Initiative 2018–2022 attributed to DICAM of the University of Trento (grant L. 232/2016) and in the frame of the PRIN 2017 project. MD has also received funding from the University of Trento via the Strategic Initiative Modeling and Simulation. EG has also been financed by a national mobility grant for young researchers in Italy, funded by GNCS-INdAM and acknowledges the support given by the University of Trento through the UniTN Starting Grant initiative.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Godunov SK. Finite difference methods for the computation of discontinuous solutions of the equations of fluid dynamics. Math USSR. (1959) 47:271–306.
2. Lax P, Wendroff B. Systems of conservation laws. Commun Pure Appl Math. (1960) 13:217–37. doi: 10.1002/cpa.3160130205
3. Kolgan VP. Application of the minimum-derivative principle in the construction of finite-difference schemes for numerical analysis of discontinuous solutions in gas dynamics. Trans Central Aerohydrodyn Inst. (1972) 3:68–77.
4. Harten A. High resolution schemes for hyperbolic conservation laws. J Comput Phys. (1983) 49:357–93. doi: 10.1016/0021-9991(83)90136-5
6. Gottlieb S, Shu C. Total variation diminishing Runge-Kutta schemes. Math Comput. (1998) 67:73–85. doi: 10.1090/S0025-5718-98-00913-2
7. van Leer B. Towards the ultimate conservative difference scheme V: a second order sequel to Godunov's Method. J Comput Phys. (1979) 32:101–36. doi: 10.1016/0021-9991(79)90145-1
8. van Leer B. On the relationship between the upwind-differencing schemes of Godunov, Engquist-Osher and Roe. SIAM J Sci Stat Comput. (1985) 5:1–20. doi: 10.1137/0905001
9. Toro E. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Berlin; Heidelberg: Springer-Verlag (2009).
10. Harten A, Osher S. Uniformly high-order accurate nonoscillatory schemes I. SIAM J Num Anal. (1987) 24:279–309. doi: 10.1137/0724022
11. Harten A, Engquist B, Osher S, Chakravarthy S. Uniformly high order accurate essentially non-oscillatory schemes III. J Comput Phys. (1987) 71:231–303. doi: 10.1016/0021-9991(87)90031-3
12. Shu C. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws. NASA/CR-97-206253 ICASE Report No97-65. (1997).
13. Castro CC, Toro EF. Solvers for the high-order Riemann problem for hyperbolic balance laws. J Comput Phys. (2008) 227:2481–513. doi: 10.1016/j.jcp.2007.11.013
14. Berthon C. Why the MUSCL-Hancock scheme is L1-stable. Numer Math. (2006) 104:27–46. doi: 10.1007/s00211-006-0007-4
15. Ben-Artzi M, Falcovitz J. A second-order Godunov-type scheme for compressible fluid dynamics. J Comput Phys. (1984) 55:1–32. doi: 10.1016/0021-9991(84)90013-5
16. LeFloch P, Tatsien L. A global asymptotic expansion for the solution of the generalized Riemann problem. Ann Inst Henri Poincaré (C) Analyse Non Linéaire. (1991) 3:321–40. doi: 10.3233/ASY-1991-3404
17. Ben-Artzi M, Li J, Warnecke G. A direct Eulerian GRP scheme for Compressible Fluid Flows. J Comput Phys. (2006) 218:19–43. doi: 10.1016/j.jcp.2006.01.044
18. Han E, Li J, Tang H. An adaptive GRP scheme for compressible fluid flows. J Comput Phys. (2010) 229:1448–66. doi: 10.1016/j.jcp.2009.10.038
19. Millington R, Toro E, Nejad L. Arbitrary High Order Methods for Conservation Laws I: The One Dimensional Scalar Case. Manchester Metropolitan University; Department of Computing and Mathematics (1999).
20. Toro E, Millington R, Nejad L. Towards very high order Godunov schemes. In: Toro E, , editor. Godunov Methods. Theory and Applications. Boston, MA: Springer (2001). p. 905–38.
21. Toro EF. A weighted average flux method for hyperbolic conservation laws. Proc R Soc Lond A Math Phys Eng Sci. (1989) 423:401–18. doi: 10.1098/rspa.1989.0062
22. Billett S, Toro E. On the accuracy and stability of explicit Schemes for Multidimensional linear homogeneous Advection Equations. J Comput Phys. (1997) 131:247–50. doi: 10.1006/jcph.1996.5610
23. van Leer B. Towards the Ultimate Conservative Difference Scheme II: monotonicity and conservation combined in a second order scheme. J Comput Phys. (1974) 14:361–70. doi: 10.1016/0021-9991(74)90019-9
24. Colella P. A direct Eulerian MUSCL scheme for gas dynamics. SIAM J Sci Stat Comput. (1985) 6:104–17. doi: 10.1137/0906009
25. Ben-Artzi M, Falcovitz J. Generalized Riemann Problems in Computational Fluid Dynamics. No. 11 in Cambridge Monographs on Applied and Computational Mathematics. Cambridge: Cambridge University Press (2003).
26. Schwartzkopff T, Munz C, Toro E. ADER: a high order approach for linear hyperbolic systems in 2D. J Sci Comput. (2002) 17:231–40. doi: 10.1023/A:1015160900410
27. Schwartzkopff T, Dumbser M, Munz C. Fast high order ADER schemes for linear hyperbolic equations. J Comput Phys. (2004) 197:532–9. doi: 10.1016/j.jcp.2003.12.007
28. Toro E, Titarev V. Solution of the generalized Riemann problem for advection-reaction equations. Proc R Soc Lond. (2002) 458:271–81. doi: 10.1098/rspa.2001.0926
29. Titarev V, Toro E. ADER: arbitrary high order Godunov approach. J Sci Comput. (2002) 17:609–18. doi: 10.1023/A:1015126814947
30. Käser MA. Adaptive Methods for the Numerical Simulation of Transport Processes. Technische Universität München (2003).
31. Käser M, Iske A. Adaptive ADER schemes for the solution of scalar non-linear hyperbolic problems. J Comput Phys. (2005) 205:489–508. doi: 10.1016/j.jcp.2004.11.015
32. Dumbser M, Käser M, Titarev VA, Toro EF. Quadrature-free non-oscillatory finite volume schemes on unstructured meshes for nonlinear hyperbolic systems. J Comput Phys. (2007) 226:204–43. doi: 10.1016/j.jcp.2007.04.004
33. Qiu J, Dumbser M, Shu C. The discontinuous Galerkin Method with Lax-Wendroff type time discretizations. Comput Methods Appl Mech Eng. (2005) 194:4528–43. doi: 10.1016/j.cma.2004.11.007
34. Dumbser M, Munz C. Building blocks for arbitrary high order discontinuous Galerkin schemes. J Sci Comput. (2006) 27:215–30. doi: 10.1007/s10915-005-9025-0
35. Gassner G, Dumbser M, Hindenlang F, Munz CD. Explicit one–step time discretizations for discontinuous Galerkin and finite volume schemes based on local predictors. J Comput Phys. (2011) 230:4232–47. doi: 10.1016/j.jcp.2010.10.024
36. Fambri F, Dumbser M, Köppel S, Rezzolla L, Zanotti O. ADER discontinuous Galerkin schemes for general-relativistic ideal magnetohydrodynamics. Mon Notices R Astron Soc. (2018) 477:4543–64. doi: 10.1093/mnras/sty734
37. Dumbser M, Käser M, Toro EF. An arbitrary high order discontinuous Galerkin method for elastic waves on unstructured meshes V: local time stepping and p-adaptivity. Geophys J Int. (2007) 171:695–717. doi: 10.1111/j.1365-246X.2007.03427.x
38. Dumbser M, Enaux C, Toro EF. Finite volume schemes of very high order of accuracy for stiff hyperbolic balance laws. J Comput Phys. (2008) 227:3971–4001. doi: 10.1016/j.jcp.2007.12.005
39. van der Vegt JJW, van der Ven H. Space–time discontinuous Galerkin finite element method with dynamic grid motion for inviscid compressible flows I. General formulation. J Comput Phys. (2002) 182:546–85. doi: 10.1006/jcph.2002.7185
40. van der Ven H, van der Vegt JJW. Space–time discontinuous Galerkin finite element method with dynamic grid motion for inviscid compressible flows II. Efficient flux quadrature. Comput Methods Appl Mech Eng. (2002) 191:4747–80. doi: 10.1016/S0045-7825(02)00403-6
41. Hidalgo A, Dumbser M. ADER schemes for nonlinear systems of stiff advection-diffusion-reaction equations. J Sci Comput. (2011) 48:173–89. doi: 10.1007/s10915-010-9426-6
42. Dumbser M, Balsara D, Toro EF, Munz CD. A unified framework for the construction of one-step finite–volume and discontinuous Galerkin schemes. J Comput Phys. (2008) 227:8209–53. doi: 10.1016/j.jcp.2008.05.025
43. Luo H, Luo L, Nourgaliev R, Mousseau VA, Dinh N. A reconstructed discontinuous Galerkin method for the compressible Navier-Stokes equations on arbitrary grids. J Comput Phys. (2010) 229:6961–78. doi: 10.1016/j.jcp.2010.05.033
44. Luo H, Xia Y, Spiegel S, Nourgaliev R, Jiang Z. A reconstructed discontinuous Galerkin method based on a Hierarchical WENO reconstruction for compressible flows on tetrahedral grids . J Comput Phys. (2013) 236:477–92. doi: 10.1016/j.jcp.2012.11.026
45. Dumbser M, Zanotti O. Very high order PNPM schemes on unstructured meshes for the resistive relativistic MHD equations. J Comput Phys. (2009) 228:6991–7006. doi: 10.1016/j.jcp.2009.06.009
46. Dumbser M, Castro M, Parés C, Toro EF. ADER schemes on unstructured meshes for non-conservative hyperbolic systems: applications to geophysical flows. Comput Fluids. (2009) 38:1731–48. doi: 10.1016/j.compfluid.2009.03.008
47. Dumbser M, Hidalgo A, Castro M, Parés C, Toro EF. FORCE schemes on unstructured meshes II: non-conservative hyperbolic systems. Comput Methods Appl Mech Eng. (2010) 199:625–47. doi: 10.1016/j.cma.2009.10.016
48. Dumbser M. Arbitrary high order PNPM schemes on unstructured meshes for the compressible Navier–Stokes equations. Comput Fluids. (2010) 39:60–76. doi: 10.1016/j.compfluid.2009.07.003
49. Balsara DS, Dumbser M, Abgrall R. Multidimensional HLLC riemann solver for unstructured meshes - With application to Euler and MHD flows. J Comput Phys. (2014) 261:172–208. doi: 10.1016/j.jcp.2013.12.029
50. Balsara DS, Dumbser M. Divergence-free MHD on unstructured meshes using high order finite volume schemes based on multidimensional Riemann solvers. J Comput Phys. (2015) 299:687–715. doi: 10.1016/j.jcp.2015.07.012
51. Zanotti O, Fambri F, Dumbser M. Solving the relativistic magnetohydrodynamics equations with ADER discontinuous Galerkin methods, a posteriori subcell limiting and adaptive mesh refinement. Mon Not R Astron Soc. (2015) 452:3010–29. doi: 10.1093/mnras/stv1510
52. Dumbser M, Guercilena F, Köppel S, Rezzolla L, Zanotti O. Conformal and covariant Z4 formulation of the Einstein equations: strongly hyperbolic first–order reduction and solution with discontinuous Galerkin schemes. Phys Rev D. (2018) 97:084053. doi: 10.1103/PhysRevD.97.084053
53. Dumbser M, Fambri F, Gaburro E, Reinarz A. On GLM curl cleaning for a first order reduction of the CCZ4 formulation of the Einstein field equations. J Comput Phys. (2020) 404:109088. doi: 10.1016/j.jcp.2019.109088
54. Dumbser M, Zanotti O, Hidalgo A, Balsara DS. ADER-WENO finite volume schemes with space-time adaptive mesh refinement. J Comput Phys. (2013) 248:257–86. doi: 10.1016/j.jcp.2013.04.017
55. Dumbser M, Hidalgo A, Zanotti O. High order space-time adaptive ADER-WENO finite volume schemes for non-conservative hyperbolic systems. Comput Methods Appl Mech Eng. (2014) 268:359–87. doi: 10.1016/j.cma.2013.09.022
56. Godunov SK, Romenskii EI. Nonstationary equations of nonlinear elasticity theory in eulerian coordinates. J Appl Mech Tech Phys. (1972) 13:868–84. doi: 10.1007/BF01200547
57. Peshkov I, Romenski E. A hyperbolic model for viscous Newtonian flows. Continuum Mech Thermodyn. (2016) 28:85–104. doi: 10.1007/s00161-014-0401-6
58. Godunov SK, Romenski EI. Elements of Continuum Mechanics and Conservation Laws. Boston, MA: Kluwer Academic/Plenum Publishers (2003).
59. Dumbser M, Peshkov I, Romenski E, Zanotti O. High order ADER schemes for a unified first order hyperbolic formulation of continuum mechanics: viscous heat-conducting fluids and elastic solids. J Comput Phys. (2016) 314:824–62. doi: 10.1016/j.jcp.2016.02.015
60. Dumbser M, Peshkov I, Romenski E, Zanotti O. High order ADER schemes for a unified first order hyperbolic formulation of Newtonian continuum mechanics coupled with electro-dynamics. J Comput Phys. (2017) 348:298–342. doi: 10.1016/j.jcp.2017.07.020
61. Dumbser M, Fambri F, Tavelli M, Bader M, Weinzierl T. Efficient implementation of ADER discontinuous Galerkin schemes for a scalable hyperbolic PDE engine. Axioms. (2018) 7:63. doi: 10.3390/axioms7030063
62. Boscheri W, Dumbser M. Arbitrary–Lagrangian–Eulerian One–step WENO finite volume schemes on unstructured triangular meshes. Commun Comput Phys. (2013) 14:1174–206. doi: 10.4208/cicp.181012.010313a
63. Boscheri W, Dumbser M. A direct Arbitrary-Lagrangian-Eulerian ADER-WENO finite volume scheme on unstructured tetrahedral meshes for conservative and non-conservative hyperbolic systems in 3D. J Comput Phys. (2014) 275:484–523. doi: 10.1016/j.jcp.2014.06.059
64. Dumbser M. Arbitrary-Lagrangian-Eulerian ADER-WENO finite volume schemes with time-accurate local time stepping for hyperbolic conservation laws. Comput Methods Appl Mech Eng. (2014) 280:57–83. doi: 10.1016/j.cma.2014.07.019
65. Boscheri W, Dumbser M, Zanotti O. High order cell-centered Lagrangian-type finite volume schemes with time-accurate local time stepping on unstructured triangular meshes. J Comput Phys. (2014) 291:120–50. doi: 10.1016/j.jcp.2015.02.052
66. Boscheri W, Balsara DS, Dumbser M. Lagrangian ADER-WENO finite volume schemes on unstructured triangular meshes based On Genuinely Multidimensional HLL Riemann Solvers. J Comput Phys. (2014) 267:112–38. doi: 10.1016/j.jcp.2014.02.023
67. Bonazzoli M, Gaburro E, Dolean V, Rapetti F. High order edge finite element approximations for the time-harmonic Maxwell's equations. In: 2014 IEEE Conference on Antenna Measurements and Applications (CAMA). Antibes Juan-les-Pins: IEEE (2014). p. 1–4.
68. Boscheri W, Dumbser M, Balsara DS. High order Lagrangian ADER-WENO schemes on unstructured meshes – Application of several node solvers to hydrodynamics and Magnetohydrodynamics. Int J Numer Methods Fluids. (2014) 76:737–78. doi: 10.1002/fld.3947
69. Boscheri W, Dumbser M. An efficient quadrature-free formulation for high order Arbitrary-Lagrangian-Eulerian ADER-WENO finite volume schemes on unstructured meshes. J Sci Comput. (2016) 66:240–74. doi: 10.1007/s10915-015-0019-2
70. Boscheri W, Dumbser M. High order accurate direct Arbitrary-Lagrangian-Eulerian ADER-WENO finite volume schemes on moving curvilinear unstructured meshes. Comput Fluids. (2016) 136:48–66. doi: 10.1016/j.compfluid.2016.05.020
71. Boscheri W, Dumbser M, Loubere R. Cell centered direct Arbitrary-Lagrangian-Eulerian ADER-WENO finite volume schemes for nonlinear hyperelasticity. Comput Fluids. (2016) 134–35:111–29. doi: 10.1016/j.compfluid.2016.05.004
72. Peshkov I, Boscheri W, Loubère R, Romenski E, Dumbser M. Theoretical and numerical comparison of hyperelastic and hypoelastic formulations for Eulerian non–linear elastoplasticity. J Comput Phys. (2019) 387:481–521. doi: 10.1016/j.jcp.2019.02.039
73. Gaburro E, Dumbser M, Castro M. Direct Arbitrary-Lagrangian-Eulerian finite volume schemes on moving nonconforming unstructured meshes. Comput Fluids. (2017) 159:254–75. doi: 10.1016/j.compfluid.2017.09.022
74. Gaburro E, Castro M, Dumbser M. Well balanced Arbitrary-Lagrangian-Eulerian finite volume schemes on moving nonconforming meshes for the Euler equations of gasdynamics with gravity. Mon Notices R Astron Soc. (2018) 477:2251–75. doi: 10.1093/mnras/sty542
75. Springel V. E pur si muove: galilean-invariant cosmological hydrodynamical simulations on a moving mesh. Mon Notices R Astron Soc. (2010) 401:791–851. doi: 10.1111/j.1365-2966.2009.15715.x
76. Gaburro E. A unified framework for the solution of hyperbolic pde systems using high order direct arbitrary-lagrangian-eulerian schemes on moving unstructured meshes with topology change. Arch Comput Methods Eng. (2020). doi: 10.1007/s11831-020-09411-7
77. Gaburro E, Boscheri W, Chiocchetti S, Klingenberg C, Springel V, Dumbser M. High order direct Arbitrary-Lagrangian-Eulerian schemes on moving Voronoi meshes with topology changes. J Comput Phys. (2020) 109167. doi: 10.1016/j.jcp.2019.109167
78. Dumbser M, Zanotti O, Loubère R, Diot S. A posteriori subcell limiting of the discontinuous Galerkin finite element method for hyperbolic conservation laws. J Comput Phys. (2014) 278:47–75. doi: 10.1016/j.jcp.2014.08.009
79. Loubère R, Dumbser M, Diot S. A new family of high order unstructured MOOD and ADER finite volume schemes for multidimensional systems of hyperbolic conservation laws. Commun Comput Phys. (2014) 16:718–63. doi: 10.4208/cicp.181113.140314a
80. Zanotti O, Fambri F, Dumbser M, Hidalgo A. Space–time adaptive ADER discontinuous Galerkin finite element schemes with a posteriori sub–cell finite volume limiting. Comput Fluids. (2015) 118:204–24. doi: 10.1016/j.compfluid.2015.06.020
81. Dumbser M, Loubère R. A simple robust and accurate a posteriori sub–cell finite volume limiter for the discontinuous Galerkin method on unstructured meshes. J Comput Phys. (2016) 319:163–99. doi: 10.1016/j.jcp.2016.05.002
82. Boscheri W. An efficient high order direct ALE ADER finite volume scheme with a posteriori limiting for hydrodynamics and magnetohydrodynamics. Int J Numer Methods Fluids. (2017) 84:76–106. doi: 10.1002/fld.4342
83. Boscheri W, Loubère R. High order accurate direct Arbitrary-Lagrangian-Eulerian ADER-MOOD finite volume schemes for non-conservative hyperbolic systems with stiff source terms. Commun Comput Phys. (2017) 21:271–312. doi: 10.4208/cicp.OA-2015-0024
84. Fambri F, Dumbser M, Zanotti O. Space-time adaptive ADER-DG schemes for dissipative flows: Compressible Navier-Stokes and resistive MHD equations. Comput Phys Commun. (2017) 220:297–318. doi: 10.1016/j.cpc.2017.08.001
85. Tavelli M, Dumbser M, Charrier DE, Rannabauer L, Weinzierl T, Bader M. A simple diffuse interface approach on adaptive Cartesian grids for the linear elastic wave equations with complex topography. J Comput Phys. (2019) 386:158–89. doi: 10.1016/j.jcp.2019.02.004
86. Clain S, Diot S, Loubère R. A high-order finite volume method for systems of conservation laws Multi-dimensional Optimal Order Detection (MOOD). J Comput Phys. (2011) 230:4028–50. doi: 10.1016/j.jcp.2011.02.026
87. Diot S, Clain S, Loubère R. Improved detection criteria for the Multi-dimensional Optimal Order Detection (MOOD) on unstructured meshes with very high-order polynomials. Comput Fluids. (2012) 64:43–63. doi: 10.1016/j.compfluid.2012.05.004
88. Diot S, Loubère R, Clain S. The MOOD method in the three-dimensional case: very-high-order finite volume method for hyperbolic systems. Int J Numer Methods Fluids. (2013) 73:362–92. doi: 10.1002/fld.3804
89. Castro C, Käser M, Toro E. Space–time adaptive numerical methods for geophysical applications. Philos Trans R Soc A Math Phys Eng Sci. (2009) 367:4613–31. doi: 10.1098/rsta.2009.0158
90. Toro EF, Hidalgo A. ADER finite volume schemes for nonlinear reaction-diffusion equations. Appl Num Math. (2009) 59:73–100. doi: 10.1016/j.apnum.2007.12.001
91. Taube A, Dumbser M, Munz CD, Schneider R. A high-order discontinuous Galerkin method with time-accurate local time stepping for the Maxwell equations. Int J Num Model Electron Netw Devices Fields. (2009) 22:77–103. doi: 10.1002/jnm.700
92. Montecinos G, Castro CE, Dumbser M, Toro EF. Comparison of solvers for the generalized Riemann problem for hyperbolic systems with source terms. J Comput Phys. (2012) 231:6472–94. doi: 10.1016/j.jcp.2012.06.011
93. Montecinos GI, Toro EF. Reformulations for general advection-diffusion-reaction equations and locally implicit ADER schemes. J Comput Phys. (2014) 275:415–42. doi: 10.1016/j.jcp.2014.06.018
94. Toro EF, Montecinos GI. Advection-diffusion-reaction equations: hyperbolization and high-order ADER discretizations. SIAM J Sci Comput. (2014) 36:A2423–57. doi: 10.1137/130937469
95. Toro E, Montecinos G. Implicit, semi-analytical solution of the generalized Riemann problem for stiff hyperbolic balance laws. J Comput Phys. (2015) 303:146–72. doi: 10.1016/j.jcp.2015.09.039
96. Toro EF, Castro CE, Lee BJ. A novel numerical flux for the 3D Euler equations with general equation of state. J Comput Phys. (2015) 303:80–94. doi: 10.1016/j.jcp.2015.09.037
97. Busto S. Contributions to the Numerical Solution of Heterogeneous Fluid Mechanics Models. Universidade de Santiago de Compostela (2018).
98. Montecinos GI, López-Rios JC, Lecaros R, Ortega JH, Toro EF. An ADER-type scheme for a class of equations arising from the water-wave theory. Comput Fluids. (2016) 132:76–93. doi: 10.1016/j.compfluid.2016.04.012
99. Busto S, Toro EF, Vázquez-Cendón ME. Design and analysis of ADER-type schemes for model advection–diffusion–reaction equations. J Comput Phys. (2016) 327:553–75. doi: 10.1016/j.jcp.2016.09.043
100. Contarino C, Toro EF, Montecinos GI, Borsche R, Kall J. Junction-generalized Riemann problem for stiff hyperbolic balance laws in networks: an implicit solver and ADER schemes. J Comput Phys. (2016) 315:409–33. doi: 10.1016/j.jcp.2016.03.049
101. Busto S, Ferrín JL, Toro EF, Vázquez-Cendón ME. A projection hybrid high order finite volume/finite element method for incompressible turbulent flows. J Comput Phys. (2018) 353:169–92. doi: 10.1016/j.jcp.2017.10.004
102. Dematté R, Titarev VA, Montecinos GI, Toro EF. ADER methods for hyperbolic equations with a time-reconstruction solver for the generalized Riemann problem: the scalar case. Commun Appl Math Comput. (2019). doi: 10.1007/s42967-019-00040-x
103. Francois MM, Sun A, King WE, Henson NJ, Tourret D, Bronkhorst CA, et al. Modeling of additive manufacturing processes for metals: challenges and opportunities. Curr Opin Solid State Mater Sci. (2017) 21:198–206. doi: 10.1016/j.cossms.2016.12.001
104. Andreotti B, Forterre Y, Pouliquen O. Granular Media: Between Fluid and Solid. Cambridge University Press (2013). Available online at: http://www.edition-sciences.com/milieux-granulaires-entre-fluide-et-solide.htm.
105. Balmforth NJ, Frigaard IA, Ovarlez G. Yielding to stress : recent developments in viscoplastic fluid mechanics. Annu Rev Fluid Mech. (2014) 46:121–46. doi: 10.1146/annurev-fluid-010313-141424
106. Dumbser M. A simple two–phase method for the simulation of complex free surface flows. Comput Methods Appl Mech Eng. (2011) 200:1204–19. doi: 10.1016/j.cma.2010.10.011
107. Gaburro E, Castro M, Dumbser M. A well balanced diffuse interface method for complex nonhydrostatic free surface flows. Comput Fluids. (2018) 175:180–98. doi: 10.1016/j.compfluid.2018.08.013
108. Kemm F, Gaburro E, Thein F, Dumbser M. A simple diffuse interface approach for compressible flows around moving solids of arbitrary shape based on a reduced Baer-Nunziato model. arXiv [Preprint]. (2020) arXiv:2001.10326.
109. Gavrilyuk SL, Favrie N, Saurel R. Modelling wave dynamics of compressible elastic materials. J Comput Phys. (2008) 227:2941–69. doi: 10.1016/j.jcp.2007.11.030
110. Favrie N, Gavrilyuk SL, Saurel R. Solid–fluid diffuse interface model in cases of extreme deformations. J Comput Phys. (2009) 228:6037–77. doi: 10.1016/j.jcp.2009.05.015
111. Favrie N, Gavrilyuk SL. Diffuse interface model for compressible fluid - Compressible elastic-plastic solid interaction. J Comput Phys. (2012) 231:2695–723. doi: 10.1016/j.jcp.2011.11.027
112. Ndanou S, Favrie N, Gavrilyuk S. Multi–solid and multi–fluid diffuse interface model: applications to dynamic fracture and fragmentation. J Comput Phys. (2015) 295:523–55. doi: 10.1016/j.jcp.2015.04.024
113. de Brauer A, Iollo A, Milcent T. A cartesian scheme for compressible multimaterial hyperelastic models with plasticity. Commun Comput Phys. (2017) 22:1362–84. doi: 10.4208/cicp.OA-2017-0018
114. Michael L, Nikiforakis N. A multi-physics methodology for the simulation of reactive flow and elastoplastic structural response. J Comput Phys. (2018) 367:1–27. doi: 10.1016/j.jcp.2018.03.037
115. Jackson H, Nikiforakis N. A unified Eulerian framework for multimaterial continuum mechanics. J Comput Phys. (2020) 401:109022. doi: 10.1016/j.jcp.2019.109022
116. Barton PT. An interface-capturing Godunov method for the simulation of compressible solid-fluid problems. J Comput Phys. (2019) 390:25–50. doi: 10.1016/j.jcp.2019.03.044
117. Bungartz HJ, Mehl M, Neckel T, Weinzierl T. The PDE framework Peano applied to fluid dynamics: An efficient implementation of a parallel multiscale fluid dynamics solver on octree-like adaptive Cartesian grids. Comput Mech. (2010) 46:103–14. doi: 10.1007/s00466-009-0436-x
118. Weinzierl T, Mehl M. Peano-A traversal and storage scheme for octree-like adaptive Cartesian multiscale grids. SIAM J Sci Comput. (2011) 33:2732–60. doi: 10.1137/100799071
119. Boscheri W, Dumbser M. Arbitrary–Lagrangian–Eulerian Discontinuous Galerkin schemes with a posteriori subcell finite volume limiting on moving unstructured meshes. J Comput Phys. (2017) 346:449–79. doi: 10.1016/j.jcp.2017.06.022
120. Gaburro E. Well Balanced Arbitrary-Lagrangian-Eulerian Finite Volume Schemes on Moving Nonconforming Meshes for Non-conservative Hyperbolic Systems. University of Trento (2018).
121. Jiang G, Shu C. Efficient implementation of weighted ENO schemes. J Comput Phys. (1996) 126:202–28. doi: 10.1006/jcph.1996.0130
122. Balsara D, Shu C. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. J Comput Phys. (2000) 160:405–52. doi: 10.1006/jcph.2000.6443
123. Dumbser M, Käser M. Arbitrary high order non-oscillatory Finite Volume schemes on unstructured meshes for linear hyperbolic systems. J Comput Phys. (2007) 221:693–723. doi: 10.1016/j.jcp.2006.06.043
124. Zhang Y, Shu C. Third order WENO scheme on three dimensional tetrahedral meshes. Commun Comput Phys. (2009) 5:836–48.
125. Shu CW. High order WENO and DG methods for time-dependent convection-dominated PDEs: a brief survey of several recent developments. J Comput Phys. (2016) 316:598–613. doi: 10.1016/j.jcp.2016.04.030
126. Hank S, Gavrilyuk S, Favrie N, Massoni J. Impact simulation by an Eulerian model for interaction of multiple elastic-plastic solids and fluids. Int J Impact Eng. (2017) 109:104–11. doi: 10.1016/j.ijimpeng.2017.06.003
127. Hank S, Favrie N, Massoni J. Modeling hyperelasticity in non-equilibrium multiphase flows. J Comput Phys. (2017) 330:65–91. doi: 10.1016/j.jcp.2016.11.001
128. Stroud A. Approximate Calculation of Multiple Integrals. Englewood Cliffs, NJ: Prentice-Hall Inc. (1971).
129. Titarev VA, Tsoutsanis P, Drikakis D. WENO schemes for mixed–element unstructured meshes. Commun Comput Phys. (2010) 8:585–609. doi: 10.4208/cicp.040909.080110a
130. Tsoutsanis P, Titarev VA, Drikakis D. WENO schemes on arbitrary mixed-element unstructured meshes in three space dimensions. J Comput Phys. (2011) 230:1585–601. doi: 10.1016/j.jcp.2010.11.023
131. Levy D, Puppo G, Russo G. Compact central WENO schemes for multidimensional conservation laws. SIAM J Sci Comput. (2000) 22:656–72. doi: 10.1137/S1064827599359461
132. Dumbser M, Boscheri W, Semplice M, Russo G. Central weighted ENO schemes for hyperbolic conservation laws on fixed and moving unstructured meshes. SIAM J Sci Comput. (2017) 39:A2564–91. doi: 10.1137/17M1111036
133. Semplice M, Coco A, Russo G. Adaptive mesh refinement for hyperbolic systems based on third-order compact WENO reconstruction. J Sci Comput. (2016) 66:692–724. doi: 10.1007/s10915-015-0038-z
134. Hu C, Shu C. A high-order WENO finite difference scheme for the equations of ideal magnetohydrodynamics. J Comput Phys. (1999) 150:561–94. doi: 10.1006/jcph.1999.6207
135. Barth TJ, Jespersen DC. The Design and Application of Upwind Schemes on Unstructured Meshes. AIAA Paper 89-0366. (1989). p. 1–12.
136. Després B. Polynomials with bounds and numerical approximation. Numer Algorithms. (2017) 76:829–59. doi: 10.1007/s11075-017-0286-0
137. Campos-Pinto M, Charles F, Després B, Herda M. A projection algorithm on the set of polynomials with two bounds. arXiv preprint arXiv:190505546 (2019). doi: 10.1007/s11075-019-00872-x
138. Levy D, Puppo G, Russo G. Central WENO schemes for hyperbolic systems of conservation laws. Math Model Numer Anal. (1999) 33:547–71. doi: 10.1051/m2an:1999152
139. Levy D, Puppo G, Russo G. A third order central WENO scheme for 2D conservation laws. Appl Numer Math. (2000) 33:415–21. doi: 10.1016/S0168-9274(99)00108-7
140. Levy D, Puppo G, Russo G. A fourth-order central WENO scheme for multidimensional hyperbolic systems of conservation laws. SIAM J Sci Comput. (2002) 24:480–506. doi: 10.1137/S1064827501385852
141. Cravero I, Puppo G, Semplice M, Visconti G. CWENO: uniformly accurate reconstructions for balance laws. Math Comput. (2018) 87:1689–719. doi: 10.1090/mcom/3273
142. Boscheri W, Semplice M, Dumbser M. Central WENO subcell finite volume limiters for ADER discontinuous Galerkin schemes on fixed and moving unstructured meshes. Commun Comput Phys. (2019) 25:311–46. doi: 10.4208/cicp.OA-2018-0069
143. Jackson H. On the eigenvalues of the ADER-WENO Galerkin predictor. J Comput Phys. (2017) 333:409–13. doi: 10.1016/j.jcp.2016.12.058
144. Banach S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam Math. (1922) 3:133–81. doi: 10.4064/fm-3-1-133-181
145. Dal Maso G, LeFloch PG, Murat F. Definition and weak stability of nonconservative products. J Math Pures Appl. (1995) 74:483–548.
146. Parés C. Numerical methods for nonconservative hyperbolic systems: a theoretical framework. SIAM J Numer Anal. (2006) 44:300–21. doi: 10.1137/050628052
147. Castro MJ, Gallardo JM, Parés C. High-order finite volume schemes based on reconstruction of states for solving hyperbolic systems with nonconservative products. Applications to shallow-water systems. Math Comput. (2006) 75:1103–34. doi: 10.1090/S0025-5718-06-01851-5
148. Dumbser M, Toro EF. A simple extension of the Osher Riemann solver to non-conservative hyperbolic systems. J Sci Comput. (2011) 48:70–88. doi: 10.1007/s10915-010-9400-3
149. Toro EF, Vázquez-Cendón ME. Flux splitting schemes for the Euler equations. Comput Fluids. (2012) 70:1–12. doi: 10.1016/j.compfluid.2012.08.023
150. Hartmann R, Houston P. Adaptive discontinuous Galerkin finite element methods for the compressible Euler equations. J Comp Phys. (2002) 183:508–32. doi: 10.1006/jcph.2002.7206
151. Persson PO, Peraire J. Sub-cell Shock Capturing for Discontinuous Galerkin Methods. AIAA Paper 2006-112 (2006).
152. Cesenek J, Feistauer M, Horacek J, Kucera V, Prokopova J. Simulation of compressible viscous flow in time–dependent domains. Appl Math Comput. (2013) 219:7139–50. doi: 10.1016/j.amc.2011.08.077
153. Guermond JL, Nazarov M, Popov B, Tomas I. Second-order invariant domain preserving approximation of the Euler equations using convex limiting. SIAM J Sci Comput. (2018) 40:A3211–39. doi: 10.1137/17M1149961
154. Cockburn B, Shu CW. The Runge-Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. J Comput Phys. (1998) 141:199–224. doi: 10.1006/jcph.1998.5892
155. Qiu J, Shu C. Runge-Kutta discontinuous Galerkin method using WENO limiters. SIAM J Sci Comput. (2005) 26:907–29. doi: 10.1137/S1064827503425298
156. Qiu J, Shu CW. Hermite WENO schemes and their application as limiters for Runge-Kutta discontinuous Galerkin Method: one-dimensional case. J Comput Phys. (2004) 193:115–35. doi: 10.1016/j.jcp.2003.07.026
157. Balsara D, Altmann C, Munz CD, Dumbser M. A sub-cell based indicator for troubled zones in RKDG schemes and a novel class of hybrid RKDG+HWENO schemes. J Comput Phys. (2007) 226:586–620. doi: 10.1016/j.jcp.2007.04.032
158. Luo H, Baum JD, Löhner R. A hermite WENO-based limiter for discontinuous Galerkin method on unstructured grids. J Comput Phys. (2007) 225:686–713. doi: 10.1016/j.jcp.2006.12.017
159. Krivodonova L. Limiters for high-order discontinuous Galerkin methods. J Comput Phys. (2007) 226:879–96. doi: 10.1016/j.jcp.2007.05.011
160. Zhu J, Qiu J, Shu CW, Dumbser M. Runge-Kutta discontinuous Galerkin method using WENO limiters II: unstructured meshes. J Comput Phys. (2008) 227:4330–53. doi: 10.1016/j.jcp.2007.12.024
161. J Zhu CWS X Zhong, Qiu J. Runge-Kutta discontinuous Galerkin method using a new type of WENO limiters on unstructured meshes. J Comp Phys. (2013) 248:200–20. doi: 10.1016/j.jcp.2013.04.012
162. Boscheri W, Loubère R, Dumbser M. Direct Arbitrary-Lagrangian-Eulerian ADER-MOOD finite volume schemes for multidimensional hyperbolic conservation laws. J Comput Phys. (2015) 292:56–87. doi: 10.1016/j.jcp.2015.03.015
163. Sonntag M, Munz CD. Shock Capturing for discontinuous Galerkin methods using Finite Volume Subcells. In: Fuhrmann J, Ohlberger M, Rohde C, , editors. Finite Volumes for Complex Applications VII. Cham: Springer (2014). p. 945–53.
164. Rannabauer L, Dumbser M, Bader M. ADER-DG with a-posteriori finite-volume limiting to simulate tsunamis in a parallel adaptive mesh refinement framework. Comput Fluids. (2018) 173:299–306. doi: 10.1016/j.compfluid.2018.01.031
165. de la Rosa JN, Munz CD. Hybrid DG/FV schemes for magnetohydrodynamics and relativistic hydrodynamics. Comput Phys Commun. (2018) 222:113–35. doi: 10.1016/j.cpc.2017.09.026
166. Dumbser M, Peshkov I, Romenski E. A Unified Hyperbolic Formulation for Viscous Fluids and Elastoplastic Solids. In: Klingenberg C, Westdickenberg M, , editors. Theory, Numerics and Applications of Hyperbolic Problems II. HYP 2016. vol. 237 of Springer Proceedings in Mathematics and Statistics. Springer International Publishing (2018). p. 451–63.
167. Peshkov I, Romenski E, Dumbser M. Continuum mechanics with torsion. Continuum Mech Thermodyn. (2019) 31:1517–41. doi: 10.1007/s00161-019-00770-6
168. Romenski EI. Hyperbolic systems of thermodynamically compatible conservation laws in continuum mechanics. Math Comput Model. (1998) 28:115–30. doi: 10.1016/S0895-7177(98)00159-9
169. Peshkov I, Pavelka M, Romenski E, Grmela M. Continuum mechanics and thermodynamics in the Hamilton and the Godunov-type formulations. Continuum Mech Thermodyn. (2018) 30:1343–78. doi: 10.1007/s00161-018-0621-2
170. Godunov SK. An interesting class of quasilinear systems. Dokl Akad Nauk SSSR. (1961) 139:521–3.
171. Godunov S. Symmetric form of the magnetohydrodynamic equation. Numer Methods Mech Continuum Medium. (1972) 3:26–34.
172. Godunov SK, Romenski EI. Thermodynamics, conservation laws and symmetric forms of differential equations in mechanics of continuous media. Comput Fluid Dyn Rev. (1995) 95:19–31.
173. Godunov SK, Mikhaîlova TY, Romenskiî EI. Systems of thermodynamically coordinated laws of conservation invariant under rotations. Siberian Math J. (1996) 37:690–705. doi: 10.1007/BF02104662
174. Romensky EI. Thermodynamics and hyperbolic systems of balance laws in continuum mechanics. In: Toro EF, , editor. Godunov Methods: Theory and Applications. New York, NY: Springer US (2001). p. 745–61. Available online at: http://www.springer.com/gp/book/9780306466014
175. Hu C, Shu C. Weighted essentially non-oscillatory schemes on triangular meshes. J Comput Phys. (1999) 150:97–127. doi: 10.1006/jcph.1998.6165
176. Sambasivan S, Shashkov M, Burton DE. A finite volume cell-centered Lagrangian hydrodynamics approach for solids in general unstructured grids. Int J Numer Methods Fluids. (2013) 72:770–810.
177. Maire PH, Abgrall R, Breil J, LoubèRe R, Rebourcet B. A nominally second-order cell-centered Lagrangian scheme for simulating elastic-plastic flows on two-dimensional unstructured grids. J Comput Phys. (2013) 235:626–65. doi: 10.1016/j.jcp.2012.10.017
178. Burton DE, Morgan NR, Carney TC, Kenamond MA. Reduction of dissipation in Lagrange cell-centered hydrodynamics (CCH) through corner gradient reconstruction (CGR). J Comput Phys. (2015) 299:229–80. doi: 10.1016/j.jcp.2015.06.041
179. Barton PT, Drikakis D, Romenski EI. An Eulerian finite-volume scheme for large elastoplastic deformations in solids. Int J Numer Methods Eng. (2010) 81:453–84. doi: 10.1002/nme.2695
180. Barton PT, Obadia B, Drikakis D. A conservative level-set based method for compressible solid/fluid problems on fixed grids. J Comput Phys. (2011) 230:7867–90. doi: 10.1016/j.jcp.2011.07.008
181. Dobrev VA, Kolev TV, Rieben RN. High order curvilinear finite elements for elastic–plastic Lagrangian dynamics. J Comput Phys. (2014) 257:1062–80. doi: 10.1016/j.jcp.2013.01.015
182. Ferrari A, Dumbser M, Toro EF, Armanini A. A new 3D parallel SPH scheme for free surface flows. Comput Fluids. (2009) 38:1203–17. doi: 10.1016/j.compfluid.2008.11.012
183. Jackson H, Nikiforakis N. A numerical scheme for non-Newtonian fluids and plastic solids under the GPR model. J Comput Phys. (2019) 387:410–29. doi: 10.1016/j.jcp.2019.02.025
184. Schmidmayer K, Petitpas F, Daniel E, Favrie N, Gavrilyuk S. Iterated upwind schemes for gas dynamics. J Comput Phys. (2017) 334:468–96. doi: 10.1016/j.jcp.2017.01.001
185. Chiocchetti S, Peshkov I, Gavrilyuk S, Dumbser M. High order ADER schemes and GLM curl cleaning for a first order hyperbolic formulation of compressible flow with surface tension. arXiv [Preprint]. (2020). Available online at: https://arxiv.org/abs/2002.08818
186. Romenski E, Resnyansky AD, Toro EF. Conservative hyperbolic formulation for compressible two-phase flow with different phase pressures and temperatures. Q Appl Math. (2007) 65:259–79. doi: 10.1090/S0033-569X-07-01051-2
187. Romenski E, Drikakis D, Toro EF. Conservative models and numerical methods for compressible two-phase flow. J Sci Comput. (2010) 42:68–95. doi: 10.1007/s10915-009-9316-y
188. Abbate E, Iollo A, Puppo G. An asymptotic-preserving all-speed scheme for fluid dynamics and nonlinear elasticity. SIAM J Sci Comput. (2019) 41:A2850–79. doi: 10.1137/18M1232954
189. Tavelli M, Dumbser M. A pressure-based semi-implicit space-time discontinuous Galerkin method on staggered unstructured meshes for the solution of the compressible Navier-Stokes equations at all Mach numbers. J Comput Phys. (2017) 341:341–76. doi: 10.1016/j.jcp.2017.03.030
190. Ioriatti M, Dumbser M. A posteriori sub-cell finite volume limiting of staggered semi-implicit discontinuous Galerkin schemes for the shallow water equations. Appl Numer Math. (2019) 135:443–80. doi: 10.1016/j.apnum.2018.08.018
Keywords: Godunov-Peshkov-Romenski model, high order, finite volume, discontinuous Galerkin, diffuse interface
Citation: Busto S, Chiocchetti S, Dumbser M, Gaburro E and Peshkov I (2020) High Order ADER Schemes for Continuum Mechanics. Front. Phys. 8:32. doi: 10.3389/fphy.2020.00032
Received: 04 December 2019; Accepted: 04 February 2020;
Published: 12 March 2020.
Edited by:
Christian F. Klingenberg, Julius Maximilian University of Wrzburg, GermanyReviewed by:
Igor Petrov, Moscow Institute of Physics and Technology, RussiaAnna Carbone, Politecnico di Torino, Italy
Copyright © 2020 Busto, Chiocchetti, Dumbser, Gaburro and Peshkov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michael Dumbser, bWljaGFlbC5kdW1ic2VyJiN4MDAwNDA7dW5pdG4uaXQ=
 Saray Busto
Saray Busto Simone Chiocchetti
Simone Chiocchetti Michael Dumbser
Michael Dumbser Elena Gaburro
Elena Gaburro Ilya Peshkov
Ilya Peshkov