- 1Department of Mathematics, COMSATS University Islamabad, Attock Campus, Attock, Pakistan
- 2KMUTT-Fixed Point Research Laboratory, Department of Mathematics, Faculty of Science, King Mongkut's University of Technology Thonburi, Bangkok, Thailand
- 3KMUTT-Fixed Point Theory and Applications Research Group, Faculty of Science, Theoretical and Computational Science Center, King Mongkut's University of Technology Thonburi, Bangkok, Thailand
- 4Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Tiawan
- 5Center of Excellence in Theoretical and Computational Science, King Mongkut's University of Technology Thonburi, Bangkok, Thailand
- 6Department of Teacher Training in Electrical Engineering, Faculty of Technical Education, Renewable Energy Research Centre, King Mongkut's University of Technology North Bangkok, Bangkok, Thailand
Current research is intended to examine the hydro-magnetic peristaltic flow of copper-water nanofluid configured in a symmetric three-dimensional rotating channel having generalized complaint boundaries incorporating second-order velocity slip conditions and temperature-dependent viscosity effects. Strong magnetic field with Hall properties, viscous dissipation, thermal radiations, and heat source/sink phenomenon have been studied. Constitutive partial differential equations are modeled and then simplified into a coupled system of ordinary differential equations by employing lubrication approximation. Consequential governing model is tackled numerically, and the results for flow quantities and Nusselt number are physically interpreted via graphs and bar charts toward the assorted parameters. Interpreted numerical results indicate that velocity components are accelerated with augmentation in first- and second-order velocity slip parameters and variable viscosity parameter, while it is reduced with a rise in Grashof number possessing dominant effects in the central region. Also, the temperature of the fluid increases with an increase in temperature-dependent viscosity effect.
Introduction
Peristalsis is a transport process of a decisive kind for moving fluids inside a conduit that occurs due to its surface deformation. Analysis of peristalsis has gained plausible importance in the last few years due to its wide applications in medical and chemical fields. Peristalsis comes from the Greek word “Peristalsiskos,” which means spontaneous squeezing and grasping along the flexible walls of tabular structures. It is a self-regulating and necessary procedure that is precisely useful to move food in the digestive system, with commercial peristaltic pumping and blood pumping in the heart–lung machine, where it is essential to split the fluid from the walls of the pumping device and move forward without being infected due to the collision with the machinery. The idea of peristalsis has been pioneered by Shapiro et al. [1] and Latham [2], primarily. From then on, several researchers and scientists have studied the peristaltic transport under different aspects and assumptions. Representatively, mixed convection and Joule heating effects on peristaltic transport of water-based nanofluid by assuming convective boundary conditions have been examined by Hayat et al. [3]. Eventually, magneto-hydrodynamics (MHD) peristaltic transport of electrically conducting fluids is paramount in the medical field. Abbas et al. [4] have inspected peristalsis of blood transport carrying nanoparticles with magnetic field effects through a non-uniform channel, which is applicable in drug delivery. Further, magnetic field effects on ciliary-induced peristaltic motion of nanofluid with second law analysis have been investigated by Abrar et al. [5]. For strong magnetic field and rarefied medium, electric conductivity of the magnetic fluids becomes anisotropic due to which Hall current appears prominently and this has been initially presented by Hall [6]. Recently, Hall effects on peristaltic transport of Carreau fluid through a channel were examined by Hayat et al. [7]. The incompressible Eying–Powell fluid is used to fill the channel. A distinctive description in this regard is given in Hayat et al., Rashidi et al., Hasona and Qureshi et al. [8–12].
Fluids have a major role in augmentation of heat transfer rate in several physiological applications involving heat transfer in connection with peristalsis such as oxygenation, hemodialysis, photodynamic therapy, etc. In this regard, suspension of nanoparticles including metal oxides, metals, and carbide/nitride etc. are of the essence to boost up the thermal properties of ordinary fluids like water, engine oil, ethylene glycol, etc. and friction reduction, which enhances the bioactivity and bioavailability of therapeutics. In biomedical processes, nanotechnology is used as a substitute during envisioning accurate medication of rheumatoid arthritis and it makes selective targeting possible to damaged joints. Awais et al. [13] examined analytically and numerically the boundary layer Maxwell nanofluid transport over stretchable surface presuming the impacts of heat generation/absorption. Awais et al. [14] analyzed slippage phenomenon in the flow of non-Newtonian nanofluid over a stretchable surface. Hayat et al. [15] studied the nanofluid on the stretched surface. They analyzed the flow in the presence of magneto-hydrodynamics and chemical reactions. The generative/absorptive thermal effects have been analyzed. Several attempts in this regime have been made by investigators [16–20]. Recently, Shah et al. [21, 22] studied thermally and electrically conducting nanofluid and heat transfer in different geometries with their applications.
In many physiological and medical procedures, since no-slip boundary conditions do not remain authentic, slip effects are important [23–25]. Moreover, variable viscosity is significant when the physical properties of fluids vary significantly with the distance and temperature and thus studied intensively by researchers [26–29]. None of the above-cited attempts include combined effects of variable viscosity and second-order velocity slip through a channel with generalized wall properties; therefore, it is the subject of research in this study along with the peristaltic flow of nanofluid within a rotating frame. Modeled system of partial differential equations is a simplified lubrication approach and analyzed numerically by employing NDSolve command in MATHEMATICA based on the standard shooting method with fourth-order Runge-Kutta integration procedure. Several graphical illustrations and tables have been prepared to present the real insight of the current investigation.
Mathematical Formulation Of Problem
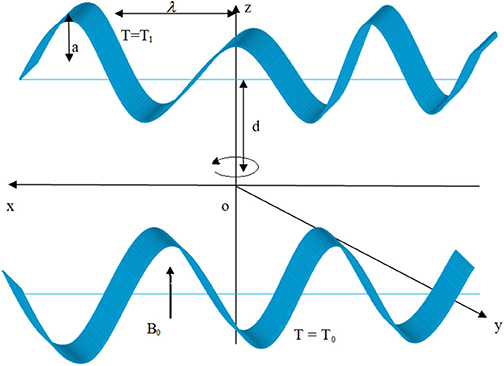
Consider peristaltic flow dynamics of (Cu-H2O) nanofluid in a homogeneous porous medium through complaint channel walls sculptured as spring-backed plates having temperature of upper/lower walls as T1/T0. The nanofluid and channel rotate with uniform angular speed Ω parallel to the z-axis (Figure 1). Flow occurs by expansion of waves having speed c, wavelength λ, and amplitude a parallel to the walls placed at z = ±η having the form:
in which t and d stand for time and half channel width, respectively. Moreover, magnetic field B0 is applied along the z-direction. In view of these facts, conservation laws of mass, momentum, and energy in the presence of generalized Hall properties, rotation, dissipative, radiative, internal heat generation/absorption, and buoyancy effects are of the form [30–33]:
where modified pressure involving centrifugal effect is given by
Moreover u, v, and w symbolize the velocities in the respective directions, while σf, k1, g, A1, m, σ*, k*, T, Tm, and Φ, respectively, represent the electrical conductivity, permeability of porous medium, gravitational force, effective thermal conductivity, Hall effect, Stefan–Boltzmann constant, mean absorption coefficient, fluid temperature, mean temperature of nanofluid, and internal heat generation/absorption effects. The relations for effective density ρeff, specific heat CPeff, thermal conductivity Keff, effective viscosity μeff with α as variable viscosity parameter and thermal expansion coefficient βeff for the dual phase flow model of the nanofluid are [29]:
As the wall properties decompose the pressure as rigidity, stiffness, and damping, thus expression for motion of generalized complaint boundaries is [29, 30]:
In the above relation, L is the operator that symbolizes the movement of elastic walls possessing viscous damping force, P0 represents the pressure outside the elastic walls due to muscular tension, τ expresses the longitudinal tension per unit area, m′ is mass of the plate, d′ is the wall damping coefficient, β′ is the flexural rigidity, and k is the stiffness effect. Utilizing the generalized complaint wall-pressure relation in Equation (3) with the assumption that P0 = 0, we get
Scaling transformations utilized in the above equations are
Here, α1, α2, β1, andβ2, respectively, express first-order velocity slip, second-order velocity slip, secondary velocity slip, and thermal slip parameters (T1, T0) are upper and lower wall temperatures while δ is wave number. Further, introducing stream function ψ such that and suppressing bar notations for ease, conservation laws with the assumption of long wavelength and small inertial forces, we reach:
In the above equations, denotes the Reynolds number, represents wave number, is the Taylor number, is the Hartman number, is radiation parameter, is the permeability parameter, is the Prandtl number, Br = EcPr expresses the Brinkman number, stands for the Eckert number, shows heat generation/absorption parameter, is the Hall parameter, and is the Grashof number. Moreover, the nanofluidics parameters A1 and A2 are expressed as
The wall properties for η = 1+εSin(2π(x−t)) with ε representing amplitude ratio parameter becomes:
where (E1, E2, E3, E4, E5) exposed the dimensionless wall parameters.
Numerical Results and Discussion
A series of analysis is physically interpreted in this section in order to understand behaviors of primary and secondary velocities, temperature, and heat exchange rate against involving parameters for x = 0.2, t = 0.1, ε = 0.3, ϕ = 0.01, E1 = 0.03, E2 = 0.02, E3 = 0.01, E4 = 0.03, E5 = 0.02.
Analysis of Axial Velocity
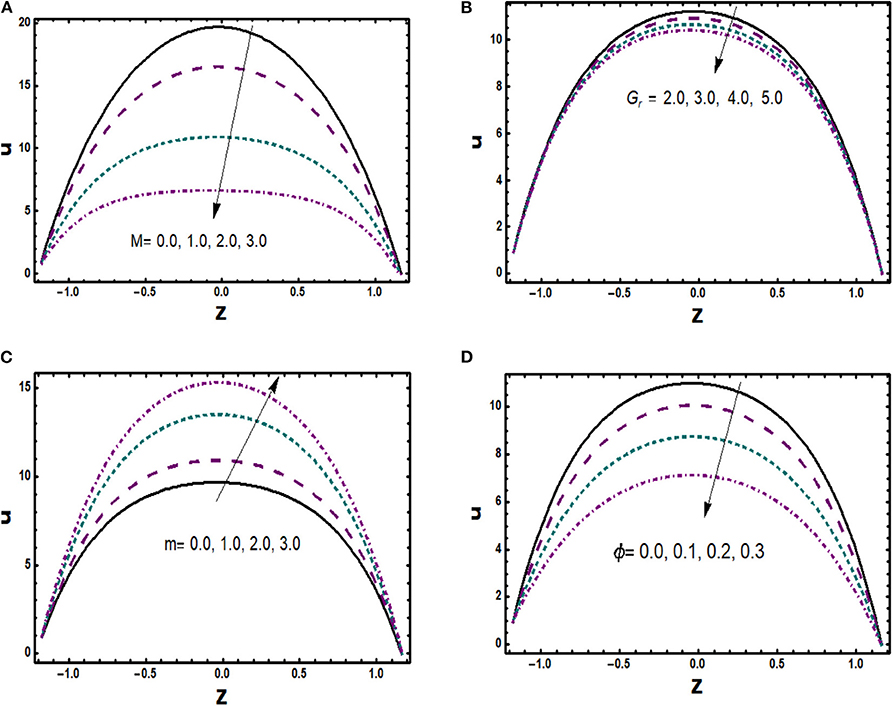
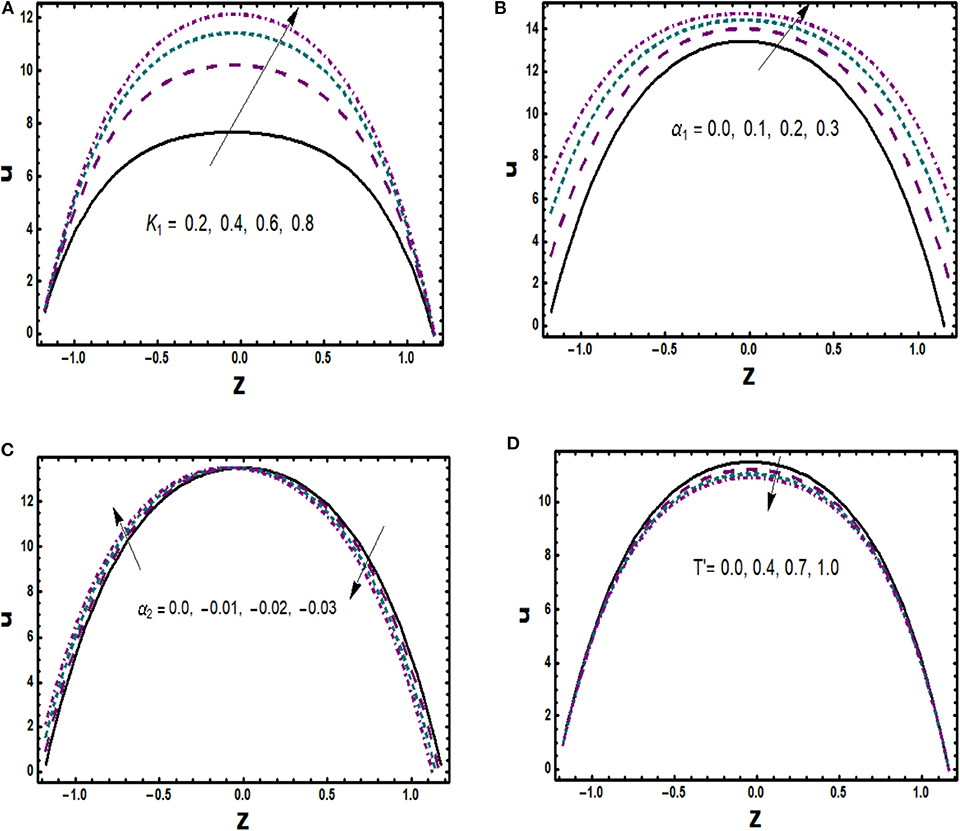
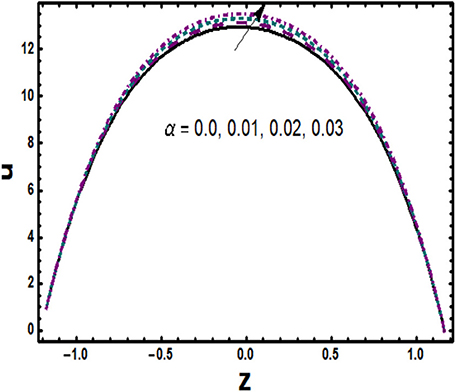
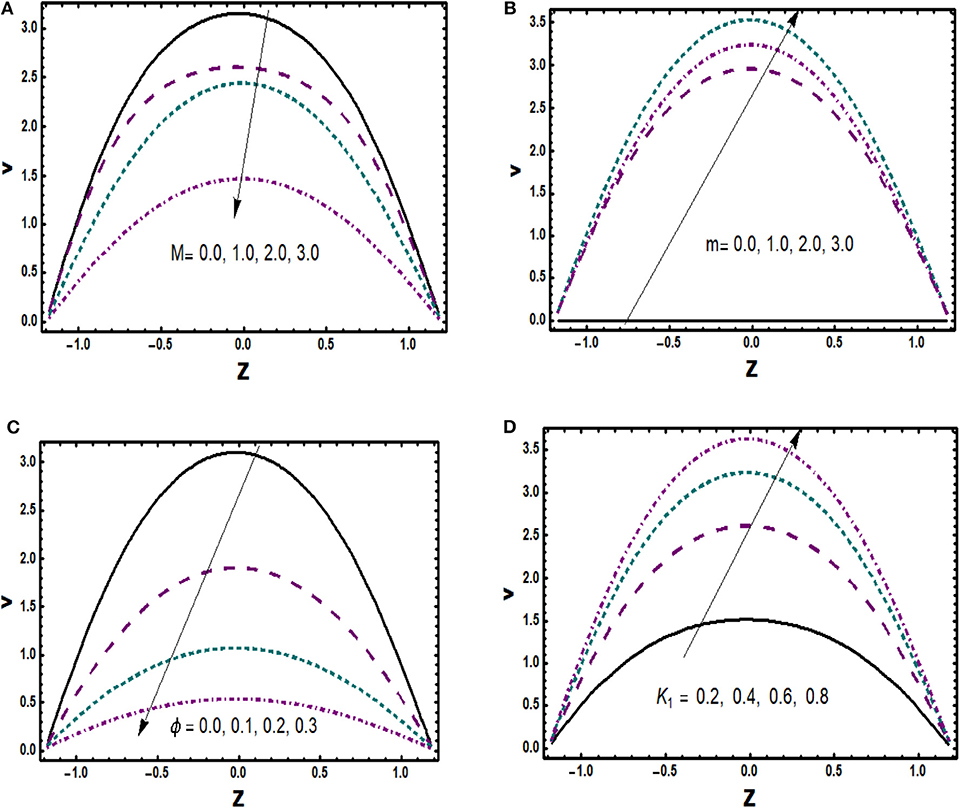
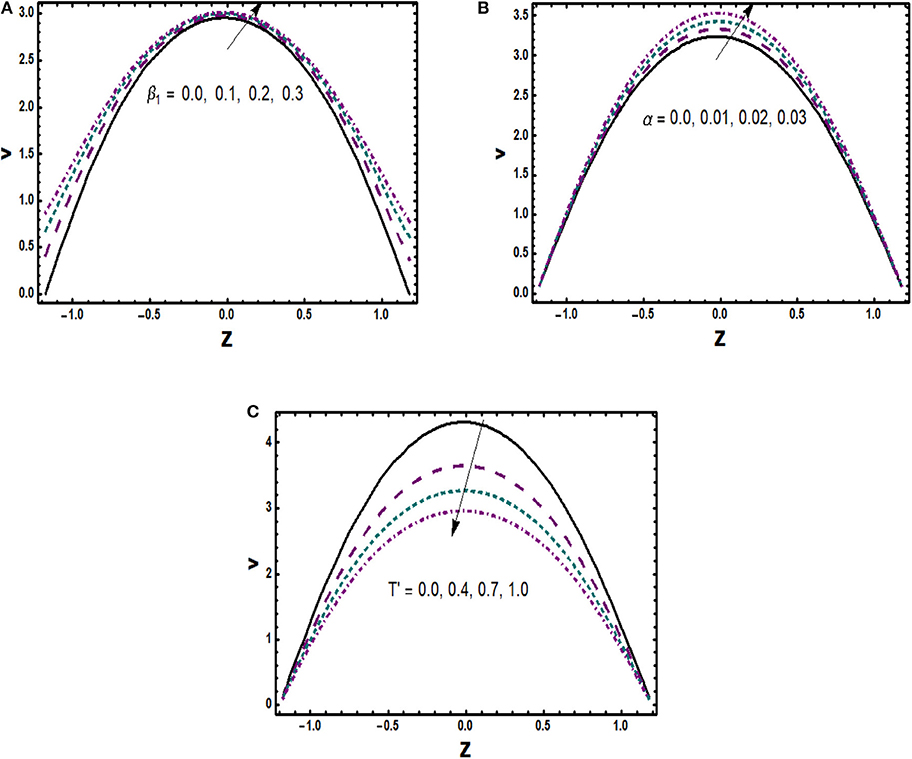
The physical behavior of the axial velocity component is exploited in Figures 2–4 for various substantial parameters with the numerical values α = 0.03, α1 = 0.01, α2 = −0.01, β1 = β2 = 0.02, m = 1.0, M = 2.0, Gr = 3.0, Br = 0.01, T′ = 1.0, R = 0.1, ε1 = 0.3, K1 = 0.5. Figure 2A depicts the consequence of applied magnetic field on velocity associated with Hartmann number M. Enhancement in values of M makes the impact of Lorentz force strong, which opposes the body forces with dominant retarding effects, and therefore, axial velocity is observed as a decreasing function of M. It is described in Figure 2B that velocity at the boundaries of channel shows almost a negligible variation against Gr, whereas it is trimmed down in the center of the channel, which clearly shows that thermal convection opposes the flow in an important manner. Variational trend of velocity toward Hall parameter m is noticed in Figure 2C. Effective viscosity of copper nanoparticles abbreviates with rise in values of m, which consequently reduces magnetic damping force, and thus, velocity seems to be accelerating. Furthermore, an augmentation in nanoparticle volume fraction (ϕ) offers more resistance to the fluid transport, which drops the flow velocity. This trend is represented in Figure 2D. Behavior of u(z) for non-identical values of permeability parameter K1 is illustrated in Figure 3A. Large values of porosity parameter lessen frictional effects as well as lead to high permeability, which causes flow rate to accelerate. The effect of hydrodynamic slip parameter α1 on velocity is depicted physically in Figure 3B. One can notice that as the values of slip parameter enlarge, fluid flows smoothly since it indicates that fluid velocity is unaffected by surface motion and that slippage reduces the resistive forces. A relevant behavior of second slip parameter α2 is exposed in Figure 3C as well. An increase in α2 accelerates flow in the vicinity of the lower half of the channel while a completely conflicting trend is seen in the region of the upper half. It is depicted in Figure 3D that velocity in axial direction is reduced for rising values of rotation parameter T′. It validates physically that a flow in the perpendicular direction is generated due to angular velocity with consequences in axial flow abbreviation. Moreover, it can be seen interestingly that velocity has its maximum values in absence of rotation. The effect of variable viscosity parameter is shown in Figure 4 in which velocity u(z) rises due to reducing frictional forces with increment in α.
Secondary Velocity
Effect of rotating motion induces a velocity component perpendicular to axial direction, which is known as secondary velocity v(z). In order to understand physical insight of secondary velocity against pertinent parameters for numerical values α = 0.03, α1 = 0.1, α2 = 0.1, β1 = β2 = 0.02, m = 1.0, M = 2.0, Br = 0.1, Gr = 3.0, T′ = 1.0, R = 0.1, ε1 = 0.3, K1 = 0.5, Figures 5, 6 are prepared. Figure 5A presents secondary velocity v(z) as a decreasing function of M whereas Hall effects enhance the secondary velocity as noticed in Figure 5B. Moreover, inspection of other plots in Figures 5, 6 signifies that physical behaviors of velocity v(z) for escalating values of ϕ, K1, β1, α, and T′ as well as motivation behind such behaviors are similar to those for axial velocity. Also, graphical estimation reveals that maximum velocity occurs in the middle region of the channel.
Temperature Distribution
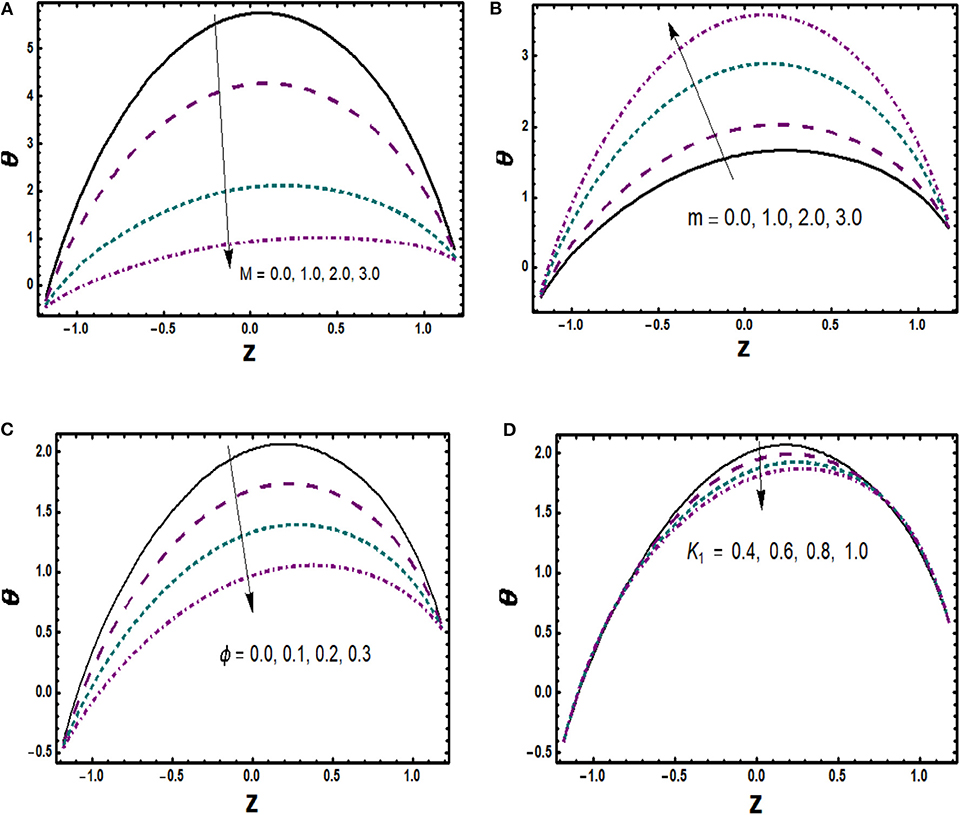
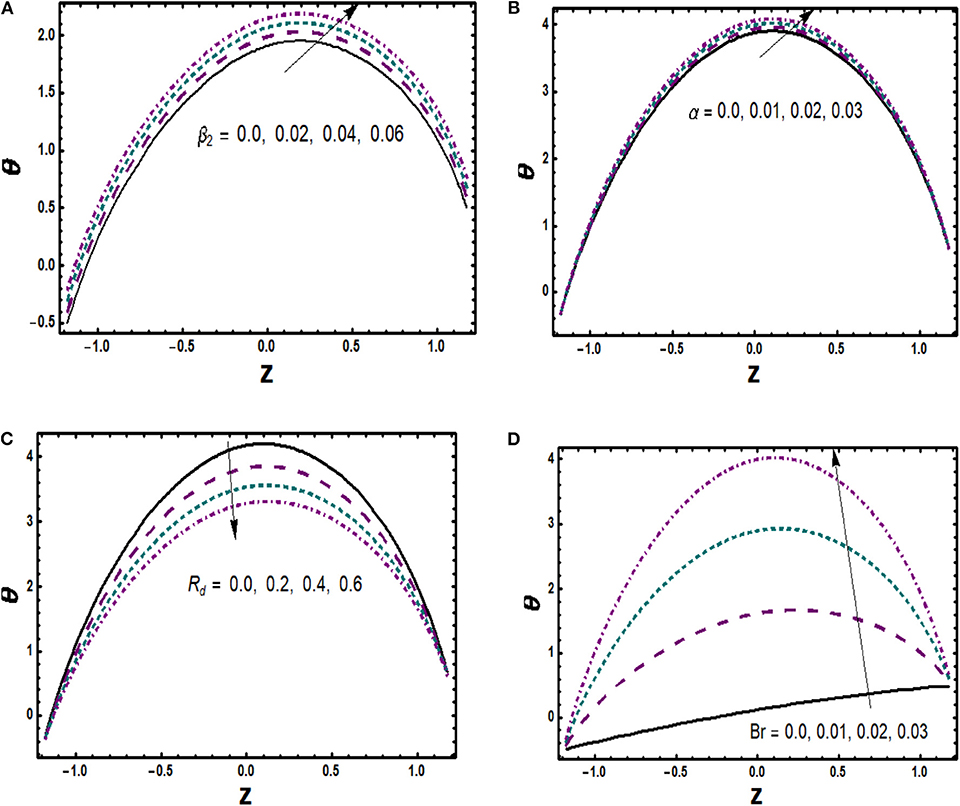
Variational trends of dimensionless temperature distribution toward the influence of substantial parameters in case of α = 0.02, α1 = 0.01, α2 = −0.01, β1 = β2 = 0.5, m = 2.0, M = 2.0, Gr = 3.0, Br=0.01, T′ = 1.0, R = 0.2, ε1 = 0.3, andK1 = 0.5 is plotted and presented in Figures 7–9. As demonstrated in Figure 7A, the temperature of the fluid decreases owing to the enhancing values of Hartmann number. This happens because magnetic field clustered the nanoparticles, thereby increasing viscous effects that reduce average kinetic energy leading to temperature rise. An increment in θ(z) corresponding to enlargement in Hall parameter is seen in Figure 7B. It is of factual significance that augmentation in m enhances electrical conductivity, i.e., number of free electrons to conduct electric current increases and correspondingly rising conduction rate leads to temperature increase. Figure 7C exposed a reduction in temperature for rise in ϕ due to increasing thermal exchange rate. More to the point, an increase in porosity parameter increases the permeability of channel walls and corresponds to larger time relaxation, which enhances resistive effects and, hence, temperature dropoff. This fact can be observed in Figure 7D. A corresponding enhancement in temperature profile vs. gradually mounting values of thermal slip parameter is observed in Figure 8A. This behavior is consistent with the physics of the problem that a rise in β2 leads to a reduction in retarding effects and dominates the temperature difference between fluid and boundaries of the channel due to which temperature rises accordingly. The purpose of Figure 8B is to explore the impact of the non-uniform viscosity parameter on θ(z), which serves to boost the temperature markedly due to the fact that α is inversely related to viscous forces and its growing values reduce such forces. Obstinately, Figure 8C signifies a contour of the variation in θ(z) for increasing values of Rd evolving. It is known that an increase in Rd values corresponds to a drop in mean absorption parameter prominently and in so doing refers to less energy absorption and temperature decreases accordingly. Further, Figure 8D portrays the variation in θ(z) toward Br. It is seen that temperature absolutely grows for the increase in Br due to increasing thermal energy generated by internal friction of fluid.
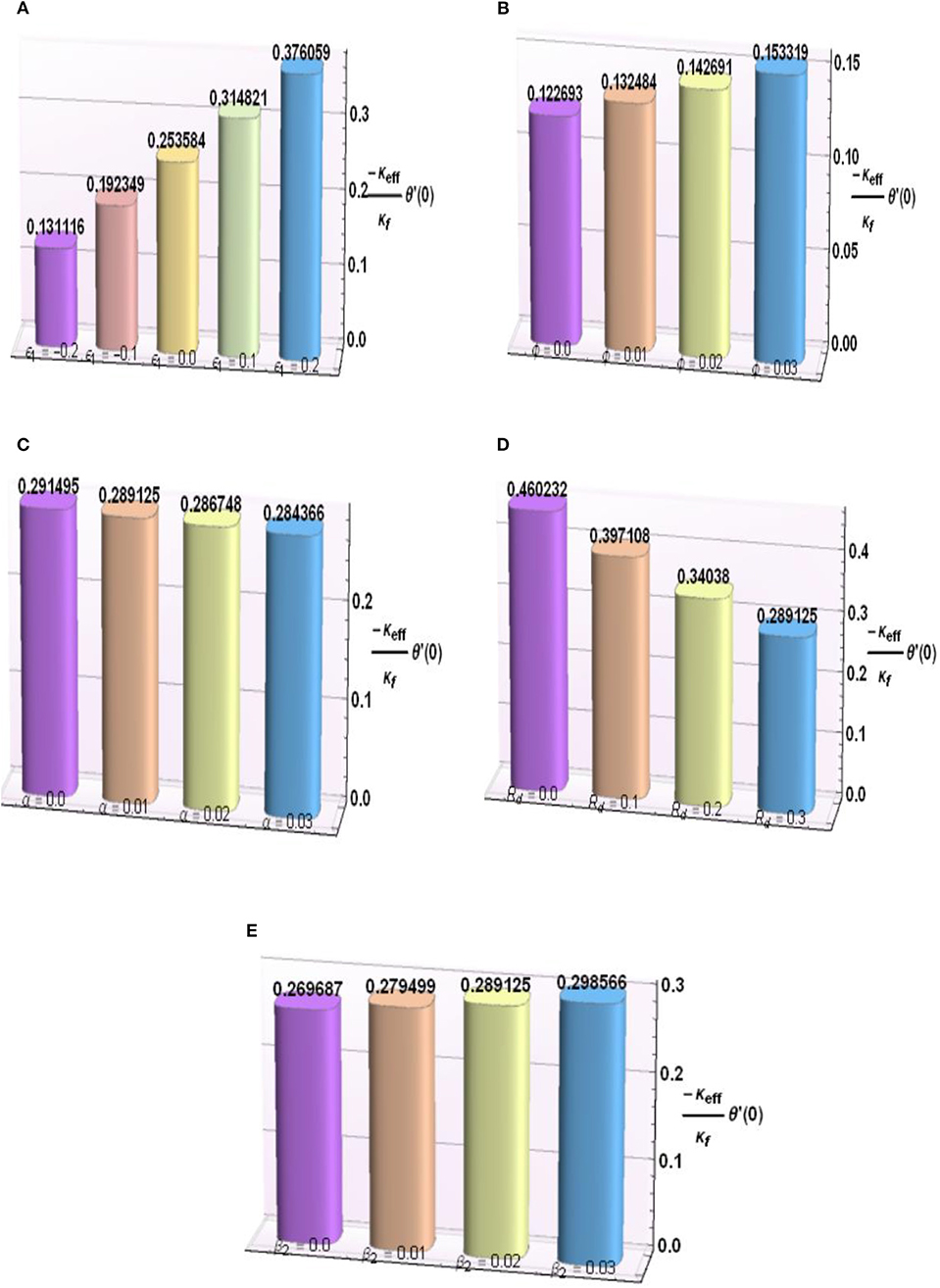
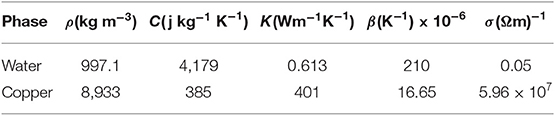
Deviation in a few of the emerging parameters for heat transfer rate is probed as well. For this purpose, bar charts are structured and exhibited in Figures 9A–E. An increment in rate of heat exchange for increasing values of ε1 and ϕ is expressed in Figures 9A,B due to internal heat production and ever-increasing thermal conduction, accordingly. Figures 9C,D, respectively, depict a decreasing trend in heat transfer rate as the values of αandRd become larger while an acceleration is reported for β2 as demonstrated in Figure 9E. Additionally, experimental numerical values of thermal properties are articulated in Table 1. A comparative analysis has been carried out and results are displayed in Table 2. A very good agreement is observed between existing results and those of Hayat et al. [27].
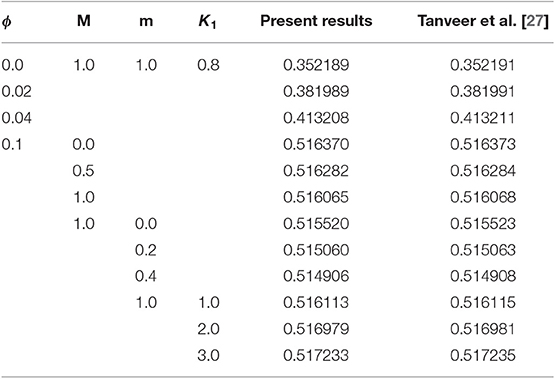
Table 2. Comparison of results for with Tanveer et al. [27] when α = α2 = E4 = E5 = ε1 = Gr = R = 0.
Concluding Remarks
Peristaltic flow dynamics of Cu-H2O nanofluid through channel with complaint walls having porous medium in a rotating frame is investigated in the presence of Hall current along with some physical factors. Major outcomes are recapped as:
➢ Enhancement in slip parameters α1, α2, and β1 has consequences in axial and secondary velocity acceleration while the impact of Gr shows a decrease in axial velocity.
➢ Variation in M and T′ corresponds to a decrease in velocities as well as temperature but the profiles show a conflicting trend toward m.
➢ Increase in values of K1 enhances velocities and drops fluid temperature, whereas consequences of ϕ depict a dropoff in velocities as well as temperature.
➢ Comparatively, both the axial and secondary velocities correspond to a similar variational trend.
➢ Dimensionless temperature distribution increases toward a rise in β2, Br, α, and ε1, whereas a conflicting variation is noticed for Rd.
➢ Heat transfer rate is maximum in the vicinity of the surface of the channel for boosting values of ε1, ϕ, and α, but it decreases for radiation and thermal slip parameters.
➢ Both velocity and temperature fields exhibit their maximum values in the central region of complaint walled channel.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This project was supported by the Theoretical and Computational Science (TaCS) Center under the Computational and Applied Science for Smart Innovation Research Cluster (CLASSIC), Faculty of Science, KMUTT.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Shapiro AH, Jafferin MY, Weinberg SL. Peristaltic pumping with long wavelengths at low Reynolds number. J Fluid Mech. (1969) 37:799–825. doi: 10.1017/S0022112069000899
2. Latham TW. Fluid motions in a peristaltic pump (Doctoral dissertation). Massachusetts Ins Tech. (1966). Available online at: http://dspace.mit.edu/handle/1721.1/7582.
3. Hayat T, Nawaz S, Alsaedi A, Rafiq M. Mixed convective peristaltic flow of water based nanofuids with joule heating and convective boundary conditions. PLoS ONE. (2016) 11:e0153537. doi: 10.1371/journal.pone.0153537
4. Abbas MA, Bai Y, Rashidi MM, Bhatti MM. Application of drug delivery in megnetohydrodynamics peristaltic blood flow of nano fluid in a non-uniform channel. J Mech Med Biol. (2016) 16:1650052. doi: 10.1142/S0219519416500524
5. Abrar MN, Haq RU, Awais M, Rashid I. Entropy analysis in a cilia transport of nanofluid under the influence of magnetic field. Nucl Eng Tech. (2017) 49:1680–8. doi: 10.1016/j.net.2017.09.007
6. Hall E. On a new action of the magnet on electric current. Amer J Math. (1879) 2:287–92. doi: 10.2307/2369245
7. Hayat T, Iqbal M, Yasmin H, Alsaadi F, Alotaibi N. Nonlinear flow of a Carreau fluid in the presence of Hall current and convective effect. Eur Phys J Plus. (2014) 129:107. doi: 10.1140/epjp/i2014-14107-2
8. Hayat T, Bibi A, Yasmin H, Ahmad B. Simultaneous effects of Hall current and homogeneous/heterogeneous reactions on peristalsis. J Taiwan Inst Chem Eng. (2016) 58:28–38. doi: 10.1016/j.jtice.2015.05.037
9. Hayat T, Iqbal M, Yasmin H, Alsaadi FE. Hall effects on peristaltic flow of couple stress fluid in an inclined asymmetric channel. J Biomath. (2014) 7:1450057. doi: 10.1142/S1793524514500570
10. Rashidi MM, Yang Z, Awais M, Nawaz M, Hayat T. Generalized magnetic field effects in Burgers nano-fluid model. PLoS ONE. (2017) 12:e0168923. doi: 10.1371/journal.pone.0168923
11. Hasona WM. Hall current effect on the peristaltic motion of synovial nanofluid with magnetohydrodynamic. Heat Trans Asian Res. (2019) 48:1–18. doi: 10.1002/htj.21469
12. Qureshi IH, Nawaz M, Shehzad A. Numerical study of dispersion of nanoparticles in magnetohydrodynamic liquid with Hall and ion slip currents. AIP Adv. (2019) 9:025219. doi: 10.1063/1.5084311
13. Awais M, Hayat T, Irum S, Alsaedi A. Heat generation/absorption effects in a boundary layer stretched flow of Maxwell nanofluid: analytical and Numerical solutions. PLoS ONE. (2015) 10:e0129814. doi: 10.1371/journal.pone.0129814
14. Awais M, Hayat T, Ali A, Irum S. Velocity, thermal and concentration slip effects on a magneto-hydrodynamic nano-fluid flow. Alex Eng J. (2016) 55:2107–14. doi: 10.1016/j.aej.2016.06.027
15. Hayat T, Rashid M, Imtaiz M, Alsaedi A. Magneto-hydrodynamic (MHD) stretched flow of nano-fluid with power-law velocity and chemical reaction. AIP Adv. (2015) 5:2158–3226. doi: 10.1063/1.4935649
16. Abbasi FM, Hayat T, Ahmad B, Chen GQ. Slip effect on mixed convective peristaltic transport of copper-water nano-fluid in an inclined channel. PLoS ONE. (2014) 9:e105440. doi: 10.1371/journal.pone.0105440
17. Awais M, Farooq S, Hayat T, Ahmad B. Comparative study of silver and copper water magneto nanoparticles with homogeneous-heterogeneous reactions in a tapered channel. Int J Heat Mass Trans. (2017) 115:108–14. doi: 10.1016/j.ijheatmasstransfer.2017.07.129
18. Awan SE, Khan ZA, Awais M, Rehman SU, Raja MAZ. Numerical treatment for hydro-magnetic unsteady channel flow of nanofluid with heat transfer. Results Phys. (2018) 9:1543–54. doi: 10.1016/j.rinp.2018.04.068
19. Awais M, Hayat T, Muqaddass N, Ali A, Aqsa Awan SE. Nanoparticles and nonlinear thermal radiation properties in the rheology of polymeric material. Results Phys. (2018) 8:1038–45. doi: 10.1016/j.rinp.2018.01.041
20. Khan WA, Ali M, Irfan M, Khan M, Shahzad M, Sultan F. A rheological analysis of nanofluid subjected to melting heat transport characteristics. Appl Nanosci. (2019) 1–10. doi: 10.1007/s13204-019-01067-5
21. Shah Z, Alzahrani EO, Dawar A, Ullah A, Khan I. Inuence of Cattaneo-Christov model on Darcy-Forchheimer flow of micropoler ferrouid over a stretching/shrinking sheet. Int Commun Heat Mass Transfer. (2020) 110:104385. doi: 10.1016/j.icheatmasstransfer.2019.104385
22. Shah Z, Khan A, Khan W, Alam MK, Islam S, Kumam P, et al. Micropolar gold blood nanofluid flow and radiative heat transfer between permeable channels. Comput Methods Programs Biomed. (2020) 186:105197. doi: 10.1016/j.cmpb.2019.105197
23. Hayat T, Awais M, Imtaiz A. Heat source/sink in a magneto-hydrodynamic non-Newtonian fluid flow in a porous medium: Dual solution. PLoS ONE. (2016) 11:e0162205. doi: 10.1371/journal.pone.0162205
24. Salahuddin T, Hussain A, Malik MY, Awais M, Khan M. Carreau nano-fluid impinging over a stretching cylinder with generalized slip effects: using finite difference scheme. Results Phys. (2017) 7:3090–9. doi: 10.1016/j.rinp.2017.07.036
25. Aly EH, Ebaid A. Effect of the velocity second slip boundary condition on the peristaltic flow of nanofluids in an asymmetric channel: exact solution. Abst Appl Anal. (2014) 2014:11. doi: 10.1155/2014/191876
26. Awais M, Bukhari U, Ali A, Yasmin H. Convective and peristaltic viscous fluid flow with variable viscosity. J Eng Thermophys. (2017) 26:69–78. doi: 10.1134/S1810232817010088
27. Tanveer A, Hayat T, Alsaedi A. Variable viscosity in peristalsis of Sisko fluid. Appl Math Mech Eng Ed. (2018) 39:501–12. doi: 10.1007/s10483-018-2313-8
28. Shah Z, Kumam P, Dawar A, Alzahrani EO, Thounthong P. Study of the couple stress convective micropolar fluid flow in a Hall MHD generator system. Front Phys. (2019) 7:171. doi: 10.3389/fphy.2019.00171
29. Shah Z, Babazadeh H, Kumam P, Shafee A, Thounthong P. Numerical simulation of magnetohydrodynamic nanofluids under the influence of shape factor and thermal transport in a porous media using CVFEM. Front Phys. (2019) 7:164. doi: 10.3389/fphy.2019.00164
30. Hayat T, Ayub S, Alsaedi A, Ahmad B. Numerical simulation of buoyancy peristaltic flow of Johnson-Segalman nanofluid in an inclined channel. Results Phys. (2018) 9:906–15. doi: 10.1016/j.rinp.2018.03.037
31. Hayat T, Rafique M, Alsaedi A. Investigation of Hall and slip conditions on peristaltic transport of Cu-water nanofluid in a rotating medium. Int J Heat Mass Trans. (2017) 112:129–41. doi: 10.1016/j.ijthermalsci.2016.10.004
32. Sharma RP, Raju MC, Makinde OD, Reddy PRK, Reddy PC. Buoyancy effects on unsteady MHD chemically reacting and rotating fluid flows past a plate in porous medium. Def Diff Forum. (2019) 392:1–9. doi: 10.4028/www.scientific.net/DDF.392.1
Keywords: nanofluid, peristalsis, rotation, slip conditions, hall effects, variable viscosity
Citation: Awais M, Kumam P, Parveen N, Ali A, Shah Z and Thounthong P (2020) Slip and Hall Effects on Peristaltic Rheology of Copper-Water Nanomaterial Through Generalized Complaint Walls With Variable Viscosity. Front. Phys. 7:249. doi: 10.3389/fphy.2019.00249
Received: 04 October 2019; Accepted: 23 December 2019;
Published: 31 January 2020.
Edited by:
Bruce Alan Wade, University of Louisiana at Lafayette, United StatesReviewed by:
Andreas Gustavsson, University of Seoul, South KoreaEbenezer Bonyah, University of Education, Winneba, Ghana
Copyright © 2020 Awais, Kumam, Parveen, Ali, Shah and Thounthong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Poom Kumam, cG9vbS5rdW1Aa211dHQuYWMudGg=; Zahir Shah, emFoaXIuc2hhQGttdXR0LmFjLnRo
 Muhammad Awais1
Muhammad Awais1 Aamir Ali
Aamir Ali Zahir Shah
Zahir Shah