Lump-Type and Bell-Shaped Soliton Solutions of the Time-Dependent Coefficient Kadomtsev-Petviashvili Equation

In this article, the lump-type solutions of the new integrable time-dependent coefficient (2+1)-dimensional Kadomtsev-Petviashvili equation are investigated by applying the Hirota bilinear technique and a suitable ansatz. The equation is applied in the modeling of propagation of small-amplitude surface waves in large channels or straits of slowly varying width, depth and non-vanishing vorticity. Applying the Bell's polynomials approach, we successfully acquire the bilinear form of the equation. We firstly find a general form of quadratic function solution of the bilinear form and then expand it as the sums of squares of linear functions satisfying some conditions. Most importantly, we acquire two lump-type and a bell-shaped soliton solutions of the equation. To our knowledge, the lump type solutions of the equation are reported for the first time in this paper. The physical interpretation of the results are discussed and represented graphically.

1. Introduction

Nonlinear equations (NLEs) have been the subject of concentrate in different parts of numerical physical sciences, for example, material science, science, and so forth. The explanatory arrangements of such conditions are of essential significance since a great deal of scientific physical models are depicted by NLEs [1]. Among the conceivable answers for NLEs, certain unique frame arrangements may depend just on a solitary blend of factors, for example, solitons. In soliton theory [2], optical solitons, painleve analysis, investigation of integrability of systems of equations, Hamiltonian structure, Bell's polynomials, Backlaund transformations, etc. are the hot topics in recent time. Lump solutions are important models to used to describe certain complicated physical phenomena in science [3]. Lump solution is a kind of special rational function solutions localized along all directions in the space. Lump solitons have been intensively studied and some of the results have been reported in [4–6]. The be integrable time-dependent coefficient (2+1)-dimensional Kadomtsev-Petviashvili model that will be studied in this work is given by Wazwaz [7]:

$\begin{array}{ll}{({\psi }_t+\psi {\psi }_x+{\psi }_{xxx})}_x+3{\psi }_{yy}+g(t){\psi }_{xx}=0,& (1)\end{array}$

where ψ(x, t, y) is a function of the temporal variable t and two scaled spatial variables x and y. g(t) is a functions of t. The equation is applied in the modeling of propagation of small-amplitude surface waves in large channels or straits of slowly varying width, depth and non-vanishing vorticity. (1) was proposed by WazWaz in [7] where the integrability property of the equation were explicitly demonstrated and the multiple complex and multiple real soliton solutions of the equation were reported. Variable-coefficients KP equations have been investigated thoroughly in the literature [8–11].

To our knowledge, the lump soliton solutions to (1) have not been studied using the Hirota Bilinear methods. In this article, by applying the concept of Bell polynomials [3, 4] and Hirota Bilinear approach [12–14], the lump soliton solutions of (1) will be derived. In addition, a Bell-shaped soliton solution will also be derived using an efficient ansatz [15].

2. Bell Polynomial

In this part, we recall some important terminologies about the Bell polynomials [12–14].

Let f = f(y₁, y₂, …, y_n) be a ℂ^∞ function, the multi-dimensional Bell polynomials are defined by the following:

$\begin{array}{ll}{Y}_{n_1{y}_1,\mathrm{...},m_r{y}_r}(f)\equiv Y_{m_1,\mathrm{...},m_r}(f_{l_1{y}_1},\mathrm{...},f_{l_r{y}_r})=e^{-f}{\partial }_{y_1}^{m_1}\mathrm{...}{\partial }_{y_r}^{m_r}{e}^f,& (2)\end{array}$

where $(f_{l_1{y}_1},\dots ,f_{l_r{y}_r})={\partial }_{y_1}^{l_1}\dots {\partial }_{y_r}^{l_r}(0\le l_i\le m_i,i=1,2,\dots r).$ Taking m = 1, Bell polynomials is given by:

$\begin{array}{l}{Y}_{my}(f)\equiv Y_m(f_1,\mathrm{...},f_m){\displaystyle \sum \frac{m!}{s_1!\mathrm{...}{s}_m!{(1!)}^{s_1}\mathrm{...}{(m!)}^{s_m}}}{f}_1^{s_1}\mathrm{...}{f}_n^{s_m},\\ \hfill m={\displaystyle \sum _{k=1}^{m}k}{s}_k.& (3)\end{array}$

The multi-dimensional Bell polynomials can be represented by Gilson et al. [14]:

$\begin{array}{l}{{Y}}_{m_1{y}_1,\mathrm{...}{m}_r{y}_r}(v,w)=Y_{m_1,\mathrm{...},m_r}(f){|}_{f_{l_1{y}_1},\mathrm{...},f_{l_r{y}_r}}\\ =\{\begin{array}{l}{v}_{l_1{y}_1},\mathrm{...},f_{l_r{y}_r},l_1+\mathrm{...}{l}_r\text{ is odd}\hfill \\ w_{l_1{y}_1},\mathrm{...},f_{l_r{y}_r},l_1+\mathrm{...}{l}_r\text{ is even}\hfill \end{array}& (4)\end{array}$

$\begin{array}{l}{{Y}}_y=v_y,{{Y}}_{2y}(v,w)=v_x^2+w_{2y},{{Y}}_{y,t}(v,w)=v_y{v}_t+w_{yt},\\ {{Y}}_{3y}(v,w)=v_{3y}+3v_y{w}_{2y}+v_y^2,\mathrm{...}& (5)\end{array}$

The conjunction between ${Y}$-polynomials and the Hirota bilinear operator are related by the following identity:

$\begin{array}{ll}{{Y}}_{m_1{y}_1,\mathrm{...},m_r{y}_r}(v=\text{ln}F/G,w=\text{ln}FG).{\left(FG\right)}^{-1}{D}_{y_1}^{m_1}\mathrm{...}{D}_{y_r}^{m_r}F.G,& (6)\end{array}$

where F and G are functions of y and t. Setting F = G, the identity (6) becomes:

$\begin{array}{l}{F}^{-2}{D}_{y_1}^{m_1}\mathrm{...}{D}_{y_r}^{m_r}F.F={Y}(0,2\text{ln}F)\\ =\{\begin{array}{c}0,m_1+\mathrm{...}{m}_r\text{ is odd}\hfill \\ {{Y}}_{m_1{y}_1,\mathrm{...}{m}_r{y}_r}(q),m_1+\mathrm{...}{m}_r\text{ is even}.\end{array}\\ & (7)\end{array}$

The first few ${P}$-polynomials can be represented by the following:

$\begin{array}{l}\hfill {{P}}_{2y}(q)=q_{2y},{{P}}_{yt}(q)=q_{yt},{{P}}_{4y}(q)=q_{4y}+3q_{2y}^2,\\ \hfill {{P}}_{6y}(q)=q_{6y}+15q_{2y}{q}_{4y}+15q_{2y}^3,\dots & (8)\end{array}$

The Bell polynomials ${Y}$_{m1y1, …mryr}(v, w) can be separated into certain polynomials and ${Y}$-polynomials:

$\begin{array}{l}\hfill {(FG)}^{-1}{D}_{y_1}^{m_1}\dots D_{y_r}^{m_r}F.G={{Y}}_{m_1{y}_1,\dots m_r{y}_r}(v,w){|}_{v=\text{ln}F/G,w=\text{ln}FG)}\\ \hfill ={\displaystyle \sum _{m_1+\dots +m_r=\text{even}}{\displaystyle \sum _{l_1=0}^{m_1}\dots }}{\displaystyle \sum _{l_r=0}^{m_r}{\displaystyle \prod _{i=0}^r\left(\begin{array}{c}{m}_i\\ l_i\end{array}\right)}}{P}_{l_1{y}_1,\dots ,l_r{y}_r}(q)Y_{(m_r-l_r)y_r}(v).& (9)\end{array}$

The main property of the Bell polynomials:

$\begin{array}{ll}{{Y}}_{m_1{y}_1,\dots n_r{y}_r}(v){|}_{v=\text{ ln }\psi ={\psi }_{m_1{y}_1,\dots ,m_r{y}_r}/\psi }& (10)\end{array}$

means that the binary Bell polynomials ${Y}$_{m1y1, …mryr}(v, w) can be linearized by applying the Hopf-Cole transformation v = lnψ, that is ψ = F/G

Theorem 1. By applying the transformation,

$\begin{array}{ll}\psi =12{(lnf)}_{xx},& (11)\end{array}$

(1) bilinearized into

$\begin{array}{ll}(D_x^4+g(t)D_x^2+D_t{D}_x+3D_y^2).f.f=0,& (12)\end{array}$

where f = f(x, t, y).

Proof: Introducing the potential field variable q on setting

$\begin{array}{ll}\psi =h(t)q_{xx},& (13)\end{array}$

where h = h(t) is a function of t. Substituting (13), we can obtain

$\begin{array}{ll}\frac{1}{2}h(t)q_{xx}^2+g(t)q_{xx}+3q_{yy}+q_{xxxx}+q_{xt}=0.& (14)\end{array}$

Integrating (14) with respect to x, setting h(t) = 6 and by means of formula (8), (14) can be converted to ${P}$-polynomials represented by:

$\begin{array}{ll}3{{P}}_{2y}(q)+g(t){{P}}_{2x}(q)+{{P}}_{4x}(q)+{{P}}_{xt}(q)=0.& (15)\end{array}$

By applying (10), we obtain:

$\begin{array}{ll}\psi =2\text{ln}f\iff \psi =h(t)q_{xx}=12{(\text{ln}f)}_{xx}.& (16)\end{array}$

3. Lump-Type Solitons to (1)

The Hirota bilinear form (12) of (1) is equivalent to the following:

$\begin{array}{ll}3f{f}_{yy}-2g(t)f_x{}^2+2fg(t)f_{xx}+6f_{xx}^2-8f_x{f}_{xxx}+2f{f}_{xxxx}-2f_x{f}_t+2f{f}_{xt}=0.& (17)\end{array}$

To derive the lump-type soliton of (1), we consider f in the following form [3]

$\begin{array}{ll}f=X^{T}BX+f_0,& (18)\end{array}$

where B = (a_ij)_4×4 is a symmetric matrix, X = (1, x, y, t)^T, a_ij and f₀ are constants. (18) can be expanded as:

$\begin{array}{l}f=a_{22}{x}^2+a_{44}{t}^2+a_{33}{y}^2+2a_{12}x+2a_{13}y+2a_{14}t+a_{23}xy\\ \hfill +2a_{24}tx+2a_{34}ty+a_{11}+f_0.& (19)\end{array}$

Putting (19) into (12) and performing all the necessary algebraic calculations by symbolic computations, we acquire the following system of algebraic expressions:

$\begin{array}{ll}6f_0{a}_{33}& +6a_{11}{a}_{33}-8a_{12}{a}_{14}+24a_{22}^2+4g(t)(-2a_{12}^2\\ & +(f_0+a_{11})a_{22})+4f_0{a}_{24}+4a_{11}{a}_{24}=0,& (20)\end{array}$

$\begin{array}{ll}-2a_{22}(2g(t)a_{22}+2a_{24}-3a_{33})=0,& (21)\end{array}$

$\begin{array}{ll}(-8g(t)a_{12}{a}_{22}-8a_{14}{a}_{22}+12a_{12}{a}_{33})=0,& (22)\end{array}$

$\begin{array}{ll}& (-4a_{14}{a}_{23}+8g(t)(a_{13}{a}_{22}-a_{12}{a}_{23})\\ +& 8a_{13}{a}_{24}+12a_{13}{a}_{33}-8a_{12}{a}_{34})=0,& (23)\end{array}$

$\begin{array}{ll}(-4g(t)a_{22}{a}_{23}+6a_{23}{a}_{33}-8a_{22}{a}_{34})=0,& (24)\end{array}$

$\begin{array}{ll}(4a_{24}{a}_{33}+6a_{33}^2-2g(t)(a_{23}^2-2a_{22}{a}_{33})-4a_{23}{a}_{34})=0,& (25)\end{array}$

$\begin{array}{ll}4(2g(t)(a_{14}{a}_{22}-2a_{12}{a}_{24})+3a_{14}{a}_{33}-2a_{12}{a}_{44})=0,& (26)\end{array}$

$\begin{array}{ll}(-8g(t)a_{22}{a}_{24}+12a_{24}{a}_{33}-8a_{22}{a}_{44})=0,& (27)\end{array}$

$\begin{array}{ll}(12a_{33}{a}_{34}+g(t)(-8a_{23}{a}_{24}+8a_{22}{a}_{34})-4a_{23}{a}_{44})=0,& (28)\end{array}$

$\begin{array}{ll}(2(-2a_{24}+3a_{33})a_{44}+g(t)(-8a_{24}^2+4a_{22}{a}_{44}))=0.& (29)\end{array}$

Solving (20) to (29), we acquire the following soliton parameters:

$\begin{array}{ll}\begin{array}{c}\{\begin{array}{l}{a}_{22}=\frac{a_{24}^2{a}_{33}}{a_{34}^2},\\ a_{13}=\frac{a_{14}{a}_{33}}{a_{34}},\\ a_{12}=\frac{a_{14}{a}_{24}{a}_{33}}{a_{34}^2},\\ a_{44}=\frac{a_{34}^2}{a_{33}},\\ a_{23}=\frac{2a_{24}{a}_{33}}{a_{34}},\\ g(t)=-\frac{\left(2a_{24}{a}_{33}-3a_{33}^2\right)a_{34}^2}{2a_{24}^2{a}_{33}^2},\\ f_0=-a_{11}+\frac{a_{33}\left(-2a_{24}^4+a_{14}^2{a}_{34}^2\right)}{a_{34}^4}.\end{array}\end{array}& (30)\end{array}$

where a₃₃ ≠ 0, a₂₄ ≠ 0, a₃₄ ≠ 0 are necessary and sufficient conditions which must be satisfied for the solution to exist. From (30), we obtain the following solution of f under the general quadratic function:

$\begin{array}{l}f=\frac{1}{a_{34}^4}\{-2a_{24}^4{a}_{33}+a_{24}^2{a}_{33}{a}_{34}^2{x}^2\\ +2a_{24}{a}_{34}^2(a_{14}{a}_{33}x+a_{34}(a_{33}y+t{a}_{34}))\\ +\frac{a_{34}^2{(a_{14}{a}_{33}+a_{34}(a_{33}y+a_{34}t))}^2}{a_{33}}\}.& (31)\end{array}$

Using (30), under the transformation (11), we acquire the following lump-type solution of (1).

$\begin{array}{lll}\psi (x,t,y)& =& \frac{12(f{f}_{xx}-f_x^2)}{f^2}\\ & =& \frac{12}{f^2{a}_{34}^6}\{2a_{24}^2(2a_{24}^4{a}_{33}^2+x^2{a}_{24}^2{a}_{33}^2{a}_{34}^2\\ & +& 2x{a}_{24}{a}_{33}{a}_{34}^2(a_{14}{a}_{33}+a_{34}(y{a}_{33}+t{a}_{34}))\\ & +& a_{34}^2{(a_{14}{a}_{33}+a_{34}(y{a}_{33}+t{a}_{34}))}^2)\}.& (32)\end{array}$

It should be noted that the positiveness of f cannot be guaranteed. To tackle this problem, we expand (18) as the sums of squares of linear function f and introduce the following theorem:

Theorem 2. (Cholesky Decomposition Theorem [3]). Let B = (a_ij) be a real symmetric positive matrix, then it can be simplified into the following:

$\begin{array}{ll}B=R{R}^T,& (33)\end{array}$

where R = (r_ij) is a triangular matrix. The relationship between elements in B and elements in R is given below:

$\begin{array}{l}{r}_{ij}=\{\begin{array}{c}{(a_{ii}-{\displaystyle {\sum }_{k=1}^{i-1}{r}_{ik}^2})}^2,(i=j),\hfill \\ \frac{1}{r_{ii}}(a_{ii}-{\displaystyle {\sum }_{k=1}^{i-1}{r}_{ik}}{r}_{jk}),(i>j),\hfill \\ 0,(i<j).\hfill \end{array}\hfill \\ \hfill & (34)\end{array}$

In accordance with Theorem 2, (18) can be rewritten as:

$\begin{array}{ll}\begin{array}{r}f=X^{T}R{R}^{T}X+f_0={(R^{T}X)}^T(R^{T}X)+f_0=\\ {(r_{11}+r_{12}x+r_{13}y+r_{14}t)}^2+{(r_{22}x+r_{23}y+r_{24}t)}^2\\ +{(r_{33}y+r_{34}t)}^2+r_{44}^2{t}^2+f_0.\end{array}& (35)\end{array}$

(35) guarantees the positive definiteness of f. Putting (35) into (12) and solving the result, we obtain the following soliton coefficients:

$\begin{array}{ll}\{\begin{array}{c}{r}_{23}=0,\hfill \\ r_{22}=0,\hfill \\ r_{33}=0,\hfill \\ r_{31}=0,\hfill \\ r_{24}=\sqrt{-r_{34}^2-r_{44}^2},\hfill \\ g(t)=\frac{3r_{13}^2-2r_{12}{r}_{14}}{2r_{12}^2},\hfill \\ f_0=-\frac{2r_{12}^4}{r_{13}^2}.\hfill \end{array}& (36)\end{array}$

Where r₂₃ ≠ 0, r₂₂ ≠ 0 are necessary and sufficient conditions which must be satisfied for the solutions to exist. From (36), we obtain the solution of f as:

$\begin{array}{ll}\begin{array}{c}f=-\frac{2r_{12}^4}{r_{13}^2}{t}^2+{(r_{11}+r_{12}x+r_{13}y+r_{14}t)}^2\\ \hfill +r_{34}^2{t}^2+t^2{r}_{44}^2+(-r_{34}^2-r_{44}^2).\end{array}& (37)\end{array}$

Putting (36) into (35) using (11), we acquire the following lump-type solution of (1) under positive quadratic function:

$\begin{array}{ll}\begin{array}{c}\psi (x,t,y)=\frac{12(f{f}_{xx}-f_x^2)}{f^2}=12\{-\frac{4r_{12}^2{(r_{11}+x{r}_{12}+y{r}_{13}+t{r}_{14})}^2}{{(-\frac{2r_{12}^4}{r_{13}^2}+{(r_{11}+x{r}_{12}+y{r}_{13}+t{r}_{14})}^2+t^2{r}_{34}^2+t^2{r}_{44}^2+t^2(-r_{34}^2-r_{44}^2))}^2}+\\ \hfill \frac{2r_{12}^2}{-\frac{2r_{12}^4}{r_{13}^2}+{(r_{11}+x{r}_{12}+y{r}_{13}+t{r}_{14})}^2+t^2{r}_{34}^2+t^2{r}_{44}^2+t^2(-r_{34}^2-r_{44}^2)}\}.\end{array}& (38)\end{array}$

4. Lump Solitons to (1)

4.1. Lump Solitons to (1) Using (32)

Setting the following soliton parameters a₂₄ = 1, a₃₃ = 2, a₁₄ = 1, a₃₄ = 3 in (32), we obtain the following lump solution to (1):

$\begin{array}{l}\psi (x,t,y)\\ =-\frac{864(8+36x^2+36x(2+3(3t+2y))+9{(2+3(3t+2y))}^2)}{{(-8+36x^2+36x(2+3(3t+2y))+9{(2+3(3t+2y))}^2)}^2}.& (39)\end{array}$

4.2. Lump Solitons to (1) Using (38)

Setting the following soliton parameters: r₁₁ = 1, r₁₂ = 2, r₁₃ = −1, r₄₄ = 1, r₃₄ = 3, r₁₄ = 1 in (38), we acquire the following lump solution to (1)

$\begin{array}{l}\psi (x,t,y)\\ =12\{\frac{8}{-32+{(1+t+2x-y)}^2}-\frac{16{(1+t+2x-y)}^2}{{(-32+{(1+t+2x-y)}^2)}^2}\}.& (40)\end{array}$

5. Bell-Shaped Soliton to (1)

The bell-shaped soliton solution of (1) may be derived using:

$\begin{array}{ll}\psi (x,t,y)=\rho {\text{sech}}^p\sigma ,& (41)\end{array}$

where σ = η(x + y − vt). Putting (41) into (1) yields:

$\begin{array}{l}pv{\eta }^2\rho \text{sech}{(\sigma )}^p-p{\eta }^4\rho \text{sech}{(\sigma )}^p+2p(1+p){\eta }^4\rho \text{sech}{(\sigma )}^p-\hfill \\ p(1+p)v{\eta }^2\rho \text{sech}{(\sigma )}^{2+p}\sinh {(\sigma )}^2+p(1+p){\eta }^4\rho \text{sech}{(\sigma )}^{2+p}\hfill \\ \sinh {(\sigma )}^2-2p{(1+p)}^2{\eta }^4\rho \text{sech}{(\sigma )}^{2+p}\sinh {(\sigma )}^2\hfill \\ +p^2{\eta }^2{\rho }^2\text{sech}{(\sigma )}^{2+2p}\sinh {(\sigma )}^2+3(-p{\eta }^2\rho \text{sech}{(\sigma )}^p\hfill \\ +p(1+p){\eta }^2\rho \text{sech}{(\sigma )}^{2+p}\sinh {(\sigma )}^2)+g(t)(-p{\eta }^2\rho \text{sech}{(\sigma )}^p\hfill \\ +p(1+p){\eta }^2\rho \text{sech}{(\sigma )}^{2+p}\sinh {(\sigma )}^2)+\rho \text{sech}{(\sigma )}^p\hfill \\ (-p{\eta }^2\rho \text{sech}{(\sigma )}^p+p(1+p){\eta }^2\rho \text{sech}{(\sigma )}^{2+p}\sinh {(\sigma )}^2)-p{\eta }^2\rho \cosh (\sigma )\hfill \\ (-(1+p){\eta }^2\text{sech}{(\sigma )}^{1+p}+(1+p)(2+p){\eta }^2\text{sech}{(\sigma )}^{3+p}\sinh {(\sigma )}^2)\hfill \\ -p\eta \rho \sinh (\sigma )(-(1+p){\eta }^3\text{sech}{(\sigma )}^{2+p}\sinh (\sigma )\hfill \\ +2(1+p)(2+p){\eta }^3\text{sech}{(\sigma )}^{2+p}\sinh (\sigma )\hfill \\ -(1+p)\eta \text{sinh}(\sigma )(\text{-}(\text{2+p}){\eta }^{\text{2}}\text{sch}{(\sigma )}^{\text{2+p}}\hfill \\ +(2+p)(3+p){\eta }^2\text{sech}{(\sigma )}^{4+p}\sinh {(\sigma )}^2)=0.\hfill & (42)\end{array}$

Equating the exponents 4 + p = 2 + 2p, we obtain p = 1. Plugging the obtained value of p into (42) yields:

$\begin{array}{rr}\hfill \begin{array}{c}\hfill 2{\eta }^2\rho (-3+v+8{\eta }^2-\rho -g(t))\text{sech}{(\sigma )}^2\\ \hfill +6{\eta }^2\rho (3-v-20{\eta }^2+2\rho +g(t))\text{sech}{(\sigma )}^{2}tanh{(\sigma )}^2\\ \hfill +10{\eta }^2(12{\eta }^2-\rho )\rho \text{sech}{(\sigma )}^{2}tanh{(\sigma )}^4=0.\end{array}& (43)\end{array}$

Equating the coefficients of linearly independent terms in (43) to zero, we get:

$\begin{array}{ll}\hfill \begin{array}{c}\hfill 2{\eta }^2\rho (-3+v+8{\eta }^2-\rho -g(t))=0,\\ \hfill 6{\eta }^2\rho (3-v-20{\eta }^2+2\rho +g(t))=0,\\ \hfill 10{\eta }^2(12{\eta }^2-\rho )\rho =0.\end{array}& (44)\end{array}$

Solving (44) yields:

$\begin{array}{ll}\eta =\frac{1}{2}\sqrt{\frac{\rho }{3}},g(t)=\frac{1}{3}(-9+3v-\rho ).& (45)\end{array}$

The bell-shaped soliton is represented by:

$\begin{array}{ll}\psi (x,t,y)=\rho {\text{sech}}^2\left[\frac{1}{2}\sqrt{\frac{\rho }{3}}(x+y-vt)\right].& (46)\end{array}$

Specifically, for the soliton (46) to exist, the condition ρ > 0 must hold.

6. Physical Interpretation of Results

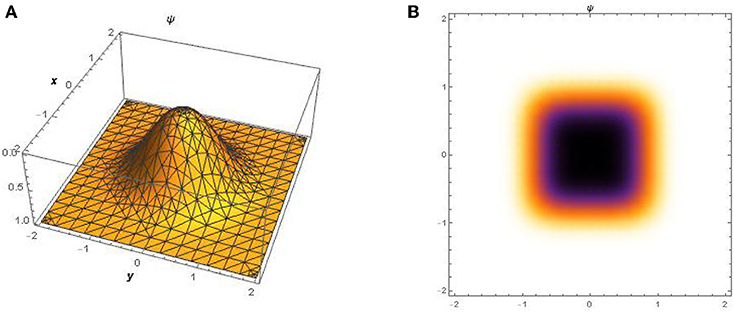
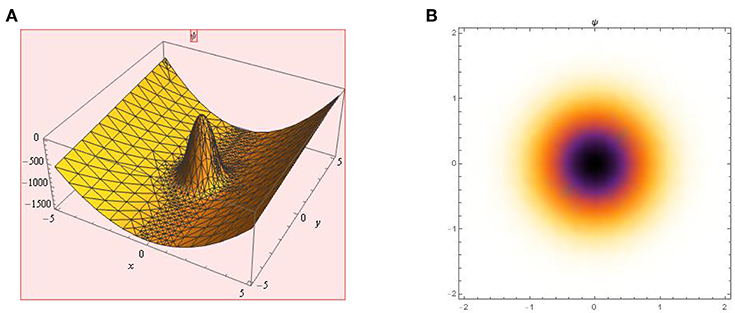
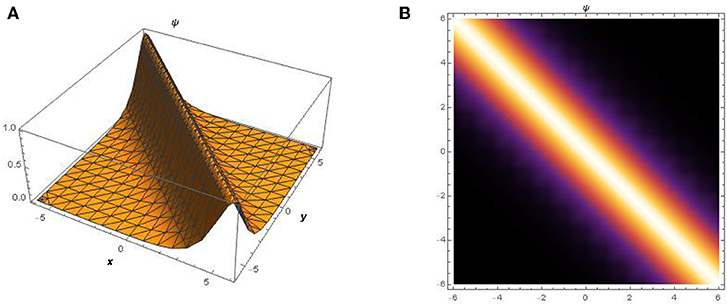
It is worth to mention that at for every t, the solution ψ = 12(lnf)_xx will approach 0 whenever (x, y) approach infinity in both solutions. The 3D and the density plot for the lump soliton (39) for t = 0 is shown in Figure 1. The 3D and the density plot for the lump soliton (40) for t = 0 is shown in Figure 2. The lump solitons (39) and (40) admits a pattern with one high peak and a deep hole hidden beneath the plane wave. Finally, the 3D and the density plot for the bell-shaped soliton (46) for t = 0 is shown in Figure 3.

FIGURE 1

Figure 1. Perspective view of the lump soliton (39) at t = 0. (A) 3D plot (B) Density plot.

FIGURE 2

Figure 2. Perspective view of the lump soliton (40) at t = 0. (A) 3D plot (B) Density plot.

FIGURE 3

Figure 3. Perspective view of the bell-shaped soliton (46) at t = 0. (A) 3D plot (B) Density plot.

7. Concluding Remarks

In this paper, with the aid of the Bell-polynomials approach, we have successfully derived the bilinear forms of an integrable time-dependent coefficient (2+1)-dimensional Kadomtsev-Petviashvili. We also studied the positive quadratic function solution to the model. Several constraint conditions that are necessary for the existence of the polynomial solutions were reported. Upon expanding the polynomials as sums of squares of linear functions, we acquire a lump-type solution possessing some arbitrary constraints. With the choice of different solution parameters, we have reported two forms of lump soliton solutions. We also utilized a suitable ansatz approach to derive a one soliton bell-shaped solution. To our knowledge, the results reported in this paper are new and introduced for the first time in the literature. Figures were given to describe the dynamics of the obtained results.

Author Contributions

All authors participated in the preparation and presentation of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (11571378, 11971493).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Whitham GB. Linear and Nonlinear Waves. New York, NY: John Whiley (1974).

Google Scholar

2. Hesegawa A, Kodama Y. Solitons in Optical Communication. Oxford: Oxford University Press (1995).

3. Li Q, Chaolu T, Wanga YH. Lump-type solutions and lump solutions for the (2+1)-dimensional generalized Bogoyavlensky-Konopelchenko equation. Comput Math Appl. (2019) 77:2077–85. doi: 10.1016/j.camwa.2018.12.011

CrossRef Full Text | Google Scholar

4. Yong X, Li X, Huang Y. General lump-type solutions of the (3+1)-dimensional Jimbo-Miwa equation. Appl Math Lett. (2018) 86:222–8. doi: 10.1016/j.aml.2018.07.001

CrossRef Full Text | Google Scholar

5. Ma WX, Qin ZY, Lu X. Lump solutions to dimensionally reduced p-gKP and p-gBKP equations. Nonlinear Dynam. (2016) 84:923–31. doi: 10.1007/s11071-015-2539-6

CrossRef Full Text | Google Scholar

6. Ma WX, You Y. Solving the Korteweg-de Vries equation by its bilinear form: Wronskian solutions. Trans Amer Math Soc. (2005) 357:1753–78.

Google Scholar

7. Wazwaz AM. Two new integrable Kadomtsev-Petviashvili equations with time-dependent coefficients: multiple real and complex soliton solutions. Waves Complex Random Media. (2018). doi: 10.1080/17455030.2018.1559962. [Epub ahead of print].

CrossRef Full Text | Google Scholar

8. Kadomtsev BB, Petviashvili VI. On the stability of solitary waves in weakly dispersive media. Sov Phys Dokl. (1970) 15:539–41.

Google Scholar

9. Tian FS, Zhang HQ. On the integrability of a generalized variable-coefficient forced Korteweg-de Vries equation in fluids. Stud Appl Math. (2013) 132:212–46. doi: 10.1111/sapm.12026

CrossRef Full Text | Google Scholar

10. Wazwaz AM. Multiple real and multiple complex soliton solutions for the integrable Sine-Gordon equation. Optik. (2013) 172:622–7. doi: 10.1016/j.ijleo.2018.07.080

CrossRef Full Text | Google Scholar

11. Wazwaz AM. Negative–order KdV equation and negative-order KP equation: multiple soliton solutions. Proc Natl Acad Sci Indian Sect A. (2017) 87:291–6. doi: 10.1007/s40010-017-0349-6

CrossRef Full Text | Google Scholar

12. Bell ET. Exponential polynomials. Ann Math. (1934) 35:258–77.

Google Scholar

13. Zhang TT, Ma PL, Xu MJ, Zhang XY, Tian SF. On Bell polynomials approach to the integrability of a (3 + 1)-dimensional generalized Kadomtsev Petviashvili equation. Modern Phys Lett B. (2015) 29:1550051. doi: 10.1142/S0217984915500517

CrossRef Full Text | Google Scholar

14. Gilson G, Lambert F, Nimmo JJC, Willox R. On the combinatorics of the Hirota D-operators. Proc R Soc Lond A. (1996) 452:223–34.

Google Scholar

15. Aliyu AI, Li Y, Baleanu D. Invariant subspace and classification of soliton solutions of the coupled nonlinear Fokas-Liu system. Front Phys. (2018) 7:39. doi: 10.3389/fphy.2019.00039

CrossRef Full Text | Google Scholar