
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Phys., 23 January 2020
Sec. Nuclear Physics
Volume 7 - 2019 | https://doi.org/10.3389/fphy.2019.00233
This article is part of the Research TopicThe Long-Lasting Quest for Nuclear Interactions: The Past, the Present and the FutureView all 16 articles
The present paper aims to provide a review of the relevance of quark degrees of freedom in the description of the nucleon-nucleon and, in general, of the baryon-baryon interaction. After a historical introduction, the second section of the paper will be dedicated to the first attempts to describe the short-range part of the NN potential in the so-called quark potential models. Here the importance of the symmetries of the 6-quark system will be emphasized. Then, we will discuss the concept of the constituent quark mass as originated by the breakdown of the chiral symmetry, in line with the articles of Manohar and Georgi [1] and the Instanton Liquid Model of Diakonov [2], and its consequences on the quark-quark interaction due to the presence of the Goldstone boson exchanges. Once the full quark-quark interaction is established, the description of the bound states (deuteron), the scattering states of the NN system, and nuclear matter in constituent quark models will be addressed. In this section, a discussion of the influence of NΔ, ΔΔ or NN* components will be included. The rest of the paper will be devoted to the extension of the model to another baryon-baryon system, namely the triton, hyperon-hyperon, and nucleon-antinucleon systems and references to other possible descriptions of the NN interaction in terms of quark degrees of freedom (bag models). The chapter will end with a concluding remark, and the success and limitations of the model described above will be summarized.
Upon the discovery of the compound nature of the nucleon it was suspected that the quark degrees of freedom had to be responsible for the properties of nucleon-nucleon interaction, at least of their short-range parts. However, due to the complexity of QCD (the underlying theory of the quark model), the implementation of these ideas was not straightforward. Although the deep inelastic scattering suggests that quarks are massless particles confined within the nucleons, the magnetic moments of the protons and neutrons could be explained by assuming an effective mass around 300 MeV for the quarks.
The apparent duality of the properties of the quarks gave rise to two types of models: the bags model (relativistic massless quarks confined within a cavity) and the potential model (no relativistic massive quarks confined within a potential). In both models, attempts were made to explain the properties of the short range of nuclear forces.
In 1975, Fairley and Squires [3, 4] tried to describe the deuteron using the MIT bag model. In the same year, Neudatchin et al. [5] proposed an explanation for the short-range repulsion due to the Pauli Exclusion Principle. Two years later, Neudatchin et al. [6] gave an algebraic reasoning to explain the hard core of nuclear forces in terms of six quarks states, assuming that the quark-quark interaction mixes the [6] and the [42] symmetries of the six-quark system, producing the node of the [42] state phase shifts and showing “hard-core like” behavior. More quantitative attempts were made by Liberman [7] (in a potential model) and [8] (in a bag model), though both calculations based on the Born-Oppenheimer approach [9] do not appear to be useful at the present time.
In 1980, three calculations appeared that used a more sophisticated scheme, the Resonant Group Method (RGM) [10, 11], which has been widely used in the treatment of the interaction between composite particles. The method allows you to make non-relativistic multichannel calculations and obtain phase shifts in a simple way. Within this framework, Oka and Yazaki [12] calculated the phase shifts for the 3S1 and 1S0 states of two nucleons, including the ΔΔ channel, thereby showing the presence of a strong repulsive force at short distance. This feature is due to an interplay between the Pauli principle and a spin-spin interaction between quarks. Similar calculations were performed by Ribeiro [13] and Toki [14], using, for the quark-quark interaction, a quadratic confinement plus a spin-spin force more or less related to the one-gluon exchange interaction derived by De Rújula [15]. They found a rather soft core (Toki) or hard core (Ribeiro) depending on the functional form of the spin-spin interaction and the election of the parameters, which, in these first stages of the calculation, are not clearly established.
The hope of being able to describe the short-range part of the nuclear forces in terms of the degrees of freedom of quarks suffered a heavy blow with the publication of the article of Harvey [16]. Harvey performed a similar calculation of the Liberman paper but did so using a quark-quark interaction similar to the one-gluon exchange, taking into account, besides the ΔΔ states, hidden color states, namely two three-quark color states coupled to color singlet's, in the two-nucleon system as required by completeness. The inclusion of these new states had dramatic effects: the repulsive core was transformed into a weak attraction. Although the use of the Born-oppenheimer approximation may be questionable, the need to include the configuration mixing remained very much in force. The situation was restored by the papers of Faessler et al. [17], which returned to the previous results that showed that obtaining a hard core, even if the hidden color states were included in the calculation provided, meant that the different parameters appearing in the calculation were chosen in a consistent way, as we will see later.
Once the question of the origin of the hard core was settled, the next objective was to achieve a description consistent with the quark degrees of freedom of all pieces of the nuclear forces. Two different ways have been used in the past to address this problem. The first one introduced an effective meson exchange potential (EMEP) into the Resonating Group Method equation [18–20]. The second one coupled the pion directly to the pairs [21, 22]. The difference between the two approaches is that the last one allowed for the study of the influence of the quark antisymmetrization on the one-pion exchange potential, which seems to be relevant in certain cases [23].
Although these methods succeeded to describe the NN and NY phase shift or the properties of the deuteron, its phenomenological nature leaves too many free parameters unconstrained by the theory, and the interplay between mesonic and quark degrees of freedom is worked out in a rather inconsistent way.
These problems have been partially solved by the introduction of the chiral (or constituent) quark models. These models are founded on the idea that the constituent (dynamical) quark mass is a consequence of the spontaneous breaking of the chiral symmetry of the QCD lagrangian. This SU(3)L × SU(3)R chiral symmetry is spontaneously broken to an SU(3)V symmetry at the scale ΛχSB, which is different from the confinement scale ΛQCD. The Goldstone theorem implies that there must exist an octet of Goldstone bosons coupled to the quark fields. There is no reason for these two scales to be the same. In fact, Manohar and Georgi [1] argued that ΛχSB is in fact greater than ΛQCD, which allows them to develop a field theory effective in the intermediate region, which includes quarks, gluons, and Goldstone boson fields.
A realistic mechanism for the chiral symmetry breaking is provided by instantons. Diakonov [2] showed that the light quarks in the liquid instanton vacuum acquired a momentum-dependent effective mass that breaks down the chiral symmetry of QCD spontaneously. This author ended up with an effective chiral Lagrangian, within which QCD was reduced at low energy, with quarks and Goldstone bosons fields. Based on this approach to QCD at low energy, in Fernandez et al. [24], the authors developed an improved quark-quark interaction that was suggested by instanton models that included π and σ exchanges as non-perturbative components and the one-gluon exchange as a perturbative one. The nucleon-nucleon potential derived from this model presents short-range repulsion and medium-range attraction besides the usual pion tail. The authors used this interaction to calculate the nucleon-nucleon phase shifts within the resonating group method, and a large number of observables were related to the N-N interaction. The results agreed reasonably well with experimental values. A similar approach has been pursued by the group of Beijing [25]. Further references of this period can be found in Myhrer and Wroldsen [26].
From the end of the twentieth century, the progress in the description of the nucleon-nucleon interaction based on quark degrees of freedom slowed down, and this was mainly due to the appearance of the effective field theories applied to the nucleon-nucleon interaction.
These theories are based on the Weinberg idea [27] that one has to write down the most general Lagrangian consistent with the symmetries of QCD, particularly the (spontaneously broken) chiral symmetry. Thus, in this formulation, which is seen as more fundamental than constituent quark models, the effective degrees of freedom, rather than quarks and gluons, are the Goldstone bosons of the broken symmetry and the nucleons. A detailed description of the progress of these theories in the last years can be found in the section dedicated to the nucleon-nucleon description in the framework of the effective field theories.
In these last years, there has nevertheless been progress in the field of the constituent quark models, which deserves a mention. Thus, several calculations have been done within the framework of the extended quark-delocalization color-screening model (QDCSM) [28], addressing problems with the intermediate range attraction (σ-exchange) [29] and the spin-orbit interaction [30]. On the other hand, Huang and Wang performed a calculation using the chiral SU(3) model in which the parameters of the nucleon-nucleon interaction are chosen consistently with the mass of octet and decuplet baryon ground states [31]. An improvement in the description of the nucleon-nucleon-meson vertices is achieved through the so-called Oxford potential [32], which uses the 3P0 model to calculate the form factors of these vertices, thus achieving a good description of the nucleon-nucleon phenomenology. Finally, during these years there has been impressive experimental progress in the discovery of the heavy baryons. This fact has produced a revival of the previous hyperon-nucleon calculations, thus extending the field to charmed and bottom baryon-nucleon interaction [33, 34].
By analogy with the short-range repulsion between two α particles, the short-range repulsion in the nucleon-nucleon interaction was naively expected to originate from the Pauli principle between quarks. In the case of the α − α scattering, the Pauli principle forbids eight particles to be in the 0S state. Therefore, one must put at least four particles in the 1P state, so the relative wave function between two α particles in a state with zero relative angular momentum must have a radial node inside the range of the nuclear forces. This node plays a role that is equivalent to a hard core.
However, the situation in the case of the nucleon-nucleon interaction is slightly different. Due to of the color degree of freedom, it is possible to have the six quarks in the lowest 0S so that the relative wave function between the two nucleons does not necessarily exhibit a node in the wave function.
Neudatchin et al. [6] was the first study to point out that the hard-core behavior can be still recovered in the quark model provided that the quark-quark interaction mixed the lowest 6-quark state with the first excited state. The relative wave function between the two nucleons would then be strongly suppressed in the inner region due to the node of the excited state, and the corresponding phase shifts would show 'hard-core like' behavior. In this sense, the validty of the analogy with the Pauli principle effects on the α − α system would be totally dependent on the character of the quark-quar interaction.
An interaction that can perform this task is the color magnetic part −g(r)(λiλj)(σiσj) of the one-gluon exchange interaction, as shown by De Rújula [15]. The expectation values of the operators σiσj and λiλj are positive (negative) for spatially symmetric (antisymmetric) qq pair states [15]. Then, the color magnetic part is attractive (due to the global minus sign of the interaction) for qq pairs, which are symmetric in color-spin space, and repulsive for qq pairs, which are antisymmetric.
The product wave function of two nucleons, each with a spatially symmetric three-quark state, gives the following S3 ⊗ S3 → S6 representations of the S6 symmetry group:
The [6]X and [42]X ([51]X, and [33]X) are symmetric (antisymmetric) for the whole exchange of the two nucleons. For the different spatial symmetries of the two nucleon states with l = 0 and isospin T = 0 ([33]T) or T = 1 ([42]T), the Pauli Principle requests the following color-space symmetries:
From these two equations one can see that, in both isospin cases, the state with spatial symmetry [6] have, in the color spin state, more antisymmetric than symmetric pairs, and they are therefore pushed up by the quark-quark color-magnetic interaction. However, the state with spatial symmetry [42]X has, in the color spin space, components with more symmetric than antisymmetric states, namely the [42]CS for the isospin T = 0 and the [33]CS and for the isospin T = 1. These states must be lowered by the color-magnetic interaction and can be mixed with the [6]X spatial symmetry.
Three important conclusions can be made from this kind of analysis. The first one is that the hard-core part of the nucleon-nucleon interaction is related to the node of the spatial [42]X component of the six-quark system. The second one is that the mixing of the [42]X and [6]X components is controlled by the strength parameter of the color-magnetic interaction. Finally, colorless objects, like nucleons, cannot exchange colored particles, like gluons, unless a quark is also exchanged. Therefore, the mechanism described above only works when the two nucleons overlap through a genuine short-range mechanism.
The effect of quark antisymmetrization also appears in other processes, such as the one-pion exchange process. Let assume for a moment that we can couple pions to qq pairs (we will come back to this point later on). The typical (σ · σ)(τ · τ) spin-isospin dependence of the one-pion exchange potential gets modified by the quark antisymmetrization operator , where Pij is the quark exchange operator, which is the product of the orbital exchange , the spin-isospin exchange , and the color exchange . As a consequence of the application of the antisymmetrization, it results in as a spin-isopin independent term, a (σ · σ), and a (τ · τ) term, besides the original (σ · σ)(τ · τ) term [22]. In the latter reference, following the model of Tegen and Weise [35], the author assumes that each nucleon consists of three massless quarks confined in a scalar potential M(r) = cr2. The NN potential was generated from a Born-Oppenheimer approximation using the quark wave functions obtained as a solution for the Dirac equation. The pions have been included in the model as a consequence of quark confinement that necessarily implies a breaking of the original chiral symmetry of the QCD Lagrangian of a free quark with zero mass. In this situation, the axial current of massless quarks confined by M(r) is not conserved.
To restore the chiral symmetry, one introduces a pseudoscalar, isovector field πλ(x) so that the generalized axial current:
is a conserved quantity.
Imposing PCAC, the later equation implies a Klein-Gordon equation for the pion field:
where fπ is the pion decay constant, and the summation runs over all quarks.
This last equation tells us that the πqq coupling is given by:
By employing this πqq one can calculate the one-pion exchange potential between nucleons using the Born-Oppenheimer approximation. The results of Shimizu [22] show that the effect of the quark antisymetrization on the one-pion is very large at short distances, producing a spin-isospin independent short-range repulsion that can be as important as the one generated by the color-magnetic piece of the one-gluon exchange potential. Besides the usual, part of the one-pion exchange potential with (σ · σ)(τ · τ) dependence becomes very weak. These results can be obtained with other models of the quark-pion coupling [21, 36].
The quark antisymmetrization can have an effect on the one-pion exchange interaction that is an observable consequence of the pion-dominated processes. One example is the confusing situation that arises with the interpretation of the p(n, p)n and p(p, Δ++)n charge-exchange reactions at intermediate energies in the forward direction using a meson-exchange model. A thorough study of the p(p, Δ++)n and p(n, p)n reactions has been done by Jain and Santra [37] from threshold to 5.5 GeV/c beam momentum. These authors use a one-boson exchange model for the transition potential in the framework of the distorted wave Born approximation (DWBA). The p(p, Δ++)n experimental data for the forward cross section in the considered energy region agree remarkably well with the theoretical results when only the one-pion exchange is included in the calculation. However the results for the p(n, p)n reaction greatly underestimate the experimental data.
The situation changes completely if the ρ-exchange is included in the transition potential. In this case, the p(n, p)n calculated cross section comes close to the experimental values. On the other hand, the inclusion of the ρ-exchange destroyed the former agreement in the p(p, Δ++)n independently of the choice of parameters.
These results can be understood in the following way. The p(p, Δ++)n reaction is dominated by the tensor terms of the transition potential due to the spin flip involved in the reaction, whereas the p(n, p)n process is dominated by the central potential. The central part of the OPE Born amplitude behaves like t/(t − m) (t = −q2), which gives a vanishing cross section in the forward direction. The finite value of the p(n, p)n cross section appears due to the modification of this behavior by the distortions in the DWBA treatment. The inclusion of the ρ-exchange in the transition potential contributes to enhancing the cross section in the p(n, p)n reaction but also reduces the tensor potential and destroy the agreement in the case of the p(p, Δ++)n reaction.
The solution to this conundrum can be found in the modification of the (σ · σ)(τ · τ) dependence of the one-pion exchange potential by the quark antisymmetrization [38]. As showed by Shimizu [22], quark antisymmetrization produces a sizable modification of the behavior of the central piece of the OPE potential but keeps the tensor piece almost unchanged. This fact explains simultaneously the p(p, Δ++)n reaction and the non-vanishing forward p(n, p)n cross section task that obviously cannot be done by the meson exchange models because the required modification of the central part of the interaction has, as a consequence, inconvenient changes in the tensor interaction.
The same mechanism provides a natural justification for the OPE-δ or poor's mans absorption procedure used to explain the behavior of the double-spin-flip helicity amplitudes for elastic nucleon-nucleon scattering. More details can be found in Fernández and Oset [39].
Two different approaches have been used in the literature to study the nucleon-nucleon interaction in the framework of the quark model. We have already referred to the first, namely, the Born-Oppenheimer approximation. In this approach, the distance between two nucleons is taken as a parameter, and one calculates the energy of the six-quark system from different distances. If the relative kinetic energy between the nucleons is subtracted, the remaining energy is identified with the nucleon-nucleon potential. However, as mentioned before, because of the color nature of the one-gluon exchange interaction, only those terms that include an additional quark exchange contribute to the nucleon-nucleon potential because it is not possible to exchange a colored object between two colorless objects. Then, the gluon exchange is only possible when the two nucleons overlap. This fact makes the potential highly non-local. Since the potential produced by the Born-Oppenheimer approximation is essentially local, it is difficult to admit that this potential is suitable to describe the short-range part of the N-N interaction.
The second approach, which has been widely used to describe the scattering problem of two composite objects and therefore seems to be the most appropriate method to incorporate the non-local effects, is the Resonating Group Method (RGM). This method was originally formulated by Wheeler [10] and applied to nuclear physics by Wildermuth and Tang [11]. The phase shifts of the two-nucleon interaction are usually calculated in the scheme developed by Kamimura [40].
The RGM assumes the wave function for two-nucleon (six quark) system can be written as:
The coordinates ξA = (ξ1, ξ2) and ξB = (ξ3, ξ4) are internal coordinates of the 19 three-quark clusters A and B in the Jacobi coordinate system [11]. RAB is the relative coordinate between the two nucleons. The internal nucleon wave function ϕN includes the color, spin, isospin, and orbital degrees of freedom. Once the quark-quark interaction is fixed, one should get ϕN as a solution of the three-body system. However, it is usually assumed that the internal orbital function is the 0S harmonic oscillator function with oscillator length b. The spin and isospin of each nucleon are coupled to total S and T.
The relative wave function χN(RAB), which is the only unknown of the problem, is calculated by solving the RGM equation:
where H is the total Hamiltonian of the six-quark system. It is usual to introduce the RGM Hamiltonian and normalization kernels in the following way:
Using this expression, Equation (9) can be written as:
which is usually referred to as the RGM equation.
From the asymptotic behavior of the relative wave function, one can easily calculate the corresponding phase shifts [40]. In the case of an S-wave, the phase shift can convert into an equivalent hard-core radius parameter r0 through the equation:
Another advantage of this formulation is that one can incorporate the modification of the nucleon wave function over short distances through standard coupling channel techniques. In this case, Equation (11) becomes a coupled-channel equation:
Ribeiro [13], Toki [14], Oka and Yazaki [12] and Faessler et al. [17] have employed the previous RGM method to describe the dispersion of N-N in terms of quark degrees of freedom using a coupled-channel calculation. However, for the sake of clarity, we will first discuss the short-range part of the N-N interaction in the channel approximation following [17], although the conclusion of the other calculation is very similar.
At short distances, the interaction between quarks is mediated by the exchange of gluons. However, gluons can interact with each other, which make the quark-quark interaction rather complicated to describe in an exact way. Usually, one assumes that the quark-quark potential V consist of two terms: the one-gluon exchange potential VOGEP, which describes the interaction at high momentum transfer, and the confining potential VCONF, which modelizes the multigluon interaction. In the one-channel approximation, VCONF does not contribute to the N-N interaction because nucleons are color singlets; however the stabilization of each nucleon should be taken into account, as we will see later.
Then, a typical Hamiltonian used in this kind of calculation is given by:
where m is the quark mass, pi is a momentum of the ith quark, and KG is the center of mass kinetic energy.
A detailed reduction for the OGE amplitude can be found in several textbooks, e.g., Berestetskii et al. [41], and we shall therefore only give the final expressions. One can start with the quark-gluon interaction Lagrangian:
where ψ(x) is the quark field, (i = 1, …8) are the eight gluon fields, λi the SU(3) generators, and g the quark gluon coupling constant. From this Lagrangian, one arrives, in the one-gluon approximation and the static limit, at a potential between quarks of the form:
where αs = g/4π and σi is the spin operator of the i-th quark.
There are no prescriptions to obtain an expression for the confining potential. Usually, this VCONF is chosen as:
where ac is the strength of the confining potential, λi the color SU(3) generator for the i-th quark, and, as before, rij is the distance between the i-th and the j-th quarks.
The orbital part of the quark wave function is assumed to be of Gaussian form:
where b is the size parameter related to the root mean square charge radius (rms-radius) of the proton through [17]. The model described above contains four parameters a, αs, mq, and b. In Faessler et al. [17], the parameter values are chosen so that they give reasonable values for the rms-radius of the proton, the magnetic moment of the proton, and the mass difference between the nucleon and the Δ. Although the rms-radius of the proton is around 0.8 fm, b is chosen as b = 0.5−0.6, taking into account the possible effect of the pion cloud. The quark mass is fixed in this calculation as mq = 336 MeV/c2 to be consistent with the observed proton and neutron magnetic moments. Once the quark mass and size parameter are fixed, the coupling constant αs is determined so that the nucleon and Δ mass difference comes out to be 294 MeV. However, this way of choosing the value of the parameters does not guarantee that we are describing the nucleon. In fact, one must satisfy the stability condition of the nucleon mass in terms of the size parameter:
This condition is used to determine the value of the remaining unfixed parameter, namely the strength of the confining potential a, to be 61.6 MeV/fm.
Figure 1 shows the result for the triplet S and the singlet S phase shifts for a value b = 0.6 fm. The behavior of the phase shifts corresponds with a hard-core potential of 0.45 fm for the triplet case and 0.52 fm for the singlet one. As b is actually a free parameter, Figure 2 shows the behavior of the hard-core radius calculated for several potentials available in the literature with different values of the parameter b. The common feature of all these potentials is that the coupling constant αs is readjusted for each value of b to reproduce the experimental NΔ mass difference.
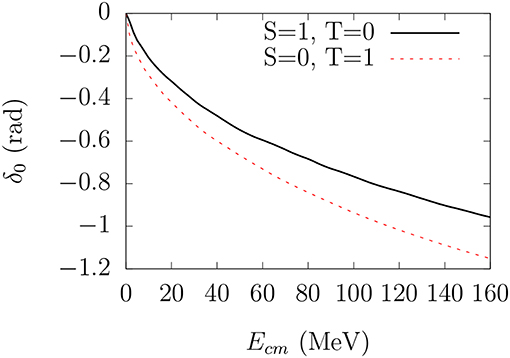
Figure 1. Singlet S and triplet S phase shifts as a function of the two-nucleon center of mas energy for the NN channel. The parameters of the quark-quark interaction are given in the text.
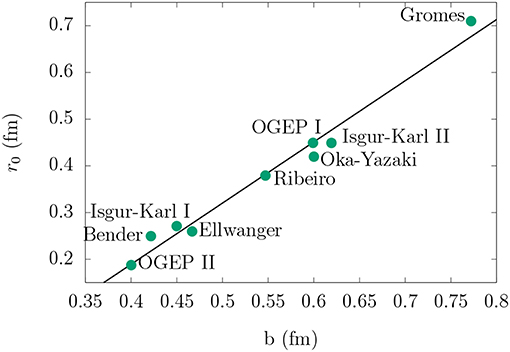
Figure 2. Hard-core radius r0 as a function of the oscillator length b for different quark-quark forces. The potentials are from ref OGEP I and OGEP II [17], Bender [42], Isgur-Karl I [43], Isgur-Karl II [44] Ellwanger [45], Ribeiro [13], Oka-Yazaki [12], and Gromes [46].
The general trend for all these calculations is an increasing of the hard-core radius with the oscillator length b. This fact agrees with the previous conclusions that the size of the hard core is related to the node at r = b in the [42] orbital configuration of the six-quark system.
So far, one has implicitly assumed that the nucleons remain unchangeable in their mutual interaction. However, this may not be the reality as different six-quark structures can come up when the two nucleons overlap. A possible candidate that might appear is the Δ(1232) resonance, which belongs together with the nucleon to the lowest orbital configuration of the three-quark system. The inclusion of the ΔΔ channel in a coupled-channel RGM calculation was done in Oka and Yazaki [12] and Faessler et al. [17]. They conclude that the ΔΔ channel does not appreciably modify the results.
More important could be the contribution of the so-called hidden color channels (CC). These channels are those in which the three-quark color wave function belongs to the color octet, rather than to the color singlet as the physical nucleon, even though the full six-quark system remains colorless. These three-quarks clusters are now sensitive to the confining force, and their dynamics are therefore different from the colorless cluster dynamics. The first calculation in which hidden color states were taken into account was made by Harvey [16] in the framework of the Born-Oppenheimer approximation. Harvey found that the three channels NN, ΔΔ, and CC coupled with each other rather strongly, and, as a result of the configuration mixing, the hard-core behavior of the NN potential disappeared. However, Faessler et al. [17, 47] showed, in an RGM coupled-channel calculation, that the inclusion of the CC channels does not produce a significant modification of the behavior of the S-wave phase shifts, the repulsion being only slightly weaker than in the case of only NN and ΔΔ were included.
The reason for this disagreement must be sought after in the treatment of the confinement parameter ac. The CC channel is the only channel sensible to the confining force; therefore, the election of the confinement strength is crucial to determining the final results. As we mentioned before in the Faessler's calculation, the confinement strength is adjusted to the minimum of the nucleon mass at a given rms-radius. Otherwise, Harvey chose the oscillator length b (fitted to the proton rms-radius) and the confinement strength (fitted to the baryon spectrum) independently. If we release the condition dM/db = 0 and allow the parameter ac to vary freely for a fixed value of b, the configuration mixing increases dramatically and the hard core even disappears when the value of ac is far enough from that which corresponds to the minimum condition (see Figure 3). This result is very understandable if one thinks of releasing the dM/db = 0 condition; we are not describing the physical nucleon anymore but some excited state of that couples strongly with the CC channels. Therefore, it is very important to choose the quark-quark interaction and the quark wave function in a self-consistent way in order to avoid unphysical coupling with the hidden color states.
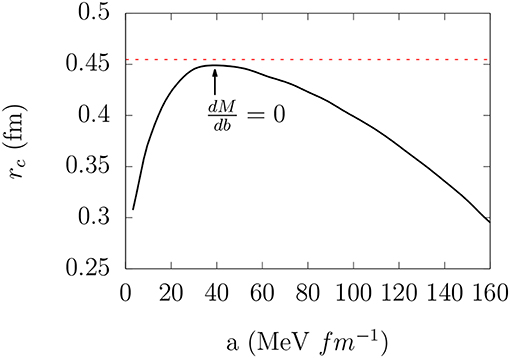
Figure 3. Triplet S hard-core radius r0 as a function of the confinement parameter a for one channel NN (dashed line) and three channels NN, ΔΔ, and CC (solid line) calculation. In the one channel case the hard-core radius is independent of a. The dependence with a in the three-channel calculation appears through the coupling with de hidden color states. The arrow shows the value of a which minimize the nucleon mass with respect to b.
The RGM calculations based on quark degrees of freedom that showed until now allowed for the understanding of the origin of the hard core of the nucleon-nucleon interaction, though it they are too naive to provide a quantitative description of the experimental phase shifts.
To go forward in the description of the experimental data one needs to include, in the RGM, Hamiltonian terms, which take care of the medium range attraction as well as the one-pion tail. Obviously, these terms should be related with a meson cloud surrounding the quark core and without any explicit assumption made about the coupling of mesons with the quark core. The most direct way is the introduction of effective meson exchange potentials (EMEP) in the renormalized RGM equations [18, 48, 49]. In this way, the so-called hybrid models appear.
The RGM equation can be symbolically written as:
This equation differs from the usual Schrödinger-type equation due to the presence of the normalization kernel . This term can be eliminated by the renormalization of χ, i.e.,
The equation for χr now can be written as:
This equation is called the renormalization RGM equation and is adequate to introduce the effective meson exchange potential VEMEP:
The description of the NN phase shifts with this modified RGM equation depends on the shape and the number of parameters included in the different VEMEP. Examples can be seen in the literature cited above.
In the last paragraph we argued that the chiral symmetry of the massless QCD Lagrangian is spontaneously broken by the bag surface in the bag model, thereby providing a scheme to couple quarks and pions. However, the spontaneous breaking of the chiral symmetry is not a characteristic of the bag model but a more general property of the QCD Lagrangian. In fact, if this symmetry were exact, we would observe degeneracy between states with opposite parity but with the same quantum numbers. For example, the ρ (1−, 775) meson would be degenerated with the axial a1 (1+, 1260) meson, the nucleon (1/2+, 940) would be degenerated with the (1/2−, 1535) resonance, etc. Since it is not the case, we conclude that the SU(3)L × SU(3)R symmetry is spontaneously broken. In a seminal article, Manohar and Georgi [1] argued that the chiral symmetry, spontaneously broken to an SU(3)v symmetry at same ΛχSB scale, does not necessarily have to match with the confinement scale ΛCONF. Therefore, one can develop an effective field theory in the intermediate region whose Lagrangian includes quarks and gluons fields and Goldstone bosons coupled to the quarks.
How the spontaneous breaking of the chiral symmetry comes about is still a topic of discussion. Diakonov and Petrov [50] suggested a theory of the light quarks in the instanton vacuum, which explained the spontaneous breakdown of chiral symmetry as being due to the delocalization of the would-be zero fermion modes in the field of individual instantons and allows for an effective chiral Lagrangian. The rationale of the model is that the quark propagator in the instanton vacuum develops a momentum-dependent dynamical mass (which we prefer to call constituent mass) that is related to the instanton density, N/V, and the average instanton size, , as:
so that the quark propagator has the form of a massive propagator:
where F(z) is a combination of the modified Bessel functions, which is equal to 1 at z = 0 and decreases rapidly with the momentum measured in units of the inverse of instanton size. Diakonov [51] estimated that the value of the dynamical mass at zero momentum is around 350 MeV/c2, which is in concordance with the values used in the non-relativistic quark model. Starting from these ideas, Diakonov [51] deduced an effective partition function:
from which an effective Lagrangian, invariant under chiral rotations (meaning, therefore, that it must contain chiral fields), can be expressed as:
where ψ is the quark spinor, is the Goldstone boson fields matrix, and M(q2) is the dynamical (constituent) mass that vanishes at large momenta and is frozen at low momenta for a value around 300 MeV.
The appearance of the constituent quark mass (or dynamical quark mass) related to the chiral symmetry justified, at least qualitatively, the non-relativistic quark model. Moreover, the Goldstone boson fields provide a natural coupling for quarks and pions.
The conclusions of the former section open the door to a complete description of the N-N interaction. They not only provide a justification for the constituent quark mass, as claimed by the phenomenology, but also explain how to include an important piece of the N-N interaction, namely the pion exchange.
Based on these ideas, a constituent quark model of the nucleon-nucleon interaction has been developed by the groups of Tubingen [24] and Salamanca [52, 53].
The starting point of the model is a non-relativistic reduction of the Lagrangian of Equation (27). Although the momentum dependence of the dynamical mass can be provided by the theory, it is more practical to simulate this behavior by parameterizing the dynamical mass as , where mq ≃ 300 MeV, and
The cut-off Λχ fixes the chiral symmetry breaking scale.
The Goldstone boson field matrix can be expanded in terms of boson fields,
The first term of the expansion generates the constituent quark mass while the second one gives rise to a one-pion exchange interaction between quarks. The main contribution of the third term comes from the two-pion exchange, which, in Fernandez et al. [24], has been simulated by means of a scalar σ−exchange potential.
Now it is straightforward to write the non-relativistic potentials generated in the static approximation in the following way,
where is the three-momentum transfer, the σ's (τ's) are the spin (isospin) Pauli matrices, and mq, mPS, and mS are the masses of the quark, pseudoscalar, and scalar bosons, respectively. The momentum states are normalized to 1.
It is well known that the long-range piece of the NN interaction is due to the one-pion exchange. Therefore, to reproduce accurately the long-range tail of the NN interaction, one need to identify the mass of the pseudoscalar field with the physical pion mass. Once the mass of the pseudoscalar field is fixed, the mass of the scalar field is obtained by the chiral relation [54].
In an early version of the model [24], the chiral Langrangian was linearized using the definitions
giving rise to the Hamiltonian:
The results of the two formulations are equivalent.
Below the chiral symmetry breaking scale, quarks still interact through gluon exchanges described by the Lagrangian:
where λc are the SU(3) color generators and the gluon field.
The corresponding non-relativistic reduction produces the one-gluon exchange potential:
where the λ's are the color Gell-Mann matrices and αs is the strong coupling constant.
Finally, the other QCD non-perturbative effect corresponds to confinement. This effect does not contribute to the N-N interaction because, taking into account the conclusion of the former sections, the model only includes color singlet three-quarks states.
As we will see below, the formulation of a realistic interaction of NN in terms of quark degrees of freedom has the advantage that nucleons and their resonances can be described in a unified way; only the wave function changes and the underlying interaction stays the same.
The works described above presented solutions of the RGM equations in coordinate space. However, it is more convenient to work in momentum space because, in this way, one avoids the problem of the rapid oscillations that the relative wave function exhibits in coordinate space at high energy. Moreover, the parametrization of the width of nucleon resonances is more naturally introduced, which simplified the equations in multichannel calculations.
With this approach, the usual ansatz for the quark radial wave function is:
where b fixes the size of the nucleon.
One could argue that the wave function of the three-quark clusters should be obtained consistently with the quark-quark interaction as the solution of the Schrödinger equation for the three-quark system. This calculation was carried out in Valcarce et al. [55] showing that the NN potential obtained in the Born-Oppenheimer approximation using the wave function coming from the full calculation were very similar to the one obtained with a Gaussian wave function for a certain value of the parameter b. This result legitimizes the use of Gaussian wave function to calculate RGM kernels The baryon total wave function, including the spin, isospin, and color degrees of freedom, can be written as,
where takes into account the internal spatial baryon degrees of freedom and is obtained from Equation (38) by removing the center of the mass wave function. Also, χB labels the totally symmetric spin-isospin wave function coupled to the quantum numbers of the baryon B, and is the color-singlet wave function. Built in this way, ψB is totally antisymmetric in quark exchanges.
From this expression, it easily to write the two-baryon wave function:
where, is the antisymmetrizer of the six-quark system, is the internal spatial wave function defined in Equation (39), denotes the spin-isospin wave function of baryons B1 and B2 coupled to a total spin-isospin ST, and is the product of the two color singlets.
The dynamics of the system is governed by the projection equation:
where,
with TCM being the center of mass kinetic energy, Vij the interaction described in the previous section, and mq the constituent quark mass.
In Equation (41) the variations are performed on the relative wave function . Then, integrating all the internal degrees of freedom, the projected Schrödinger equation for the relative wave function adopts the expression:
where E = ET − EA − EB is the relative energy of the clusters, and RGM VD( ) and RGMK( ) are the direct potential and the exchange kernel, respectively given by,
and
with
A similar expression can be found for the normalization exchange kernel, replacing with the identity operator. Equation (43) is readily generalized to a coupled-channel equation, starting from a sum of wave functions of the type of Equation (40) for the different baryon channels considered.
The solution of coupled-channel RGM equations is derived from Equation (43), a set of coupled Lippmann-Schwinger equations of the form:
where α labels the group of quantum numbers B1B2JLST, which defines a certain partial wave, is the projected potential that contains the direct potential and the RGM exchange kernels, and is the energy corresponding to a momentum p″, written as (in the non-relativistic case):
Here, μα is the reduced mass of the B1B2 system corresponding to the channel α, and ΔMα is the difference between the threshold of the B1B2 system and the one used as a reference, the NN system. The mass difference ΔMα is obtained from the interaction terms for quarks belonging to the same baryon, which relate to the total energy of the system ET and to the relative energy between clusters E.
The coupled-channel Lippmann-Schwinger equation is solved by a generalized version of the matrix inversion method of Machleidt [56] in order to include channels with different thresholds. Once the T matrix is calculated, the scattering matrix S is obtained for non-relativistic kinematics from the relationship:
with kα defined by:
so that, for channels above the threshold, .
For bound states, the integral equations do not have poles, and the problem is simplified. In this case, a discretized Schrödinger equation can be written in the form:
where i and j label the discretization of the integral and the quantum numbers of the different channels included in the calculation, and ψj is the value of the wave function in the channel and momentum corresponding to the index j.
Details of the calculation of the RGM Kernels and the solution of the equations for both bound and scattering states can be found in Entem et al. [52].
If the pseudoscalar field is to be identified with the one-pion exchange (OPE), a way to obtain the value of the coupling constant gch is to require that the pseudoscalar interaction should reproduce at long range the well-established OPE Yukawa potential. If the two nucleons are well separated, the central part of the pseudoscalar interaction between quarks given by Equation (30) generates an interaction between nucleons of the form,
where is the quark density Fourier transform of each nucleon normalized to . Compared with the standard OPE Yukawa potential,
and using , one finally obtains:
This gives the chiral coupling constant gch in terms of the πNN coupling constant, taken to be [57].
As discussed above, the parameter b describe the radius of the nucleon quark content, which is different from the nucleon charge radius and therefore cannot be directly measured. A value for this Gaussian parameter is determined by comparing the N-N potential obtained in a Born-Oppenheimer approximation using the nucleon wave function solution of Schrödinger equation, with the full quark-quark interaction and the one calculated with a single Gaussian of parameter b [55].
ΛχSB acts in the model as a cut-off for the pion interaction. Therefore, its value controls the NN tensor force, which is mainly due to the one-pion exchange. Then, the more clear way to determine the ΛχSB value is to resort to processes dominated by the one-pion tensor term. As discussed above, one such processes is the p(p, Δ++)n reaction. Fitting the missing mass spectrum of this reaction [58] estimated a value close to 4.2 fm −1 for ΛχSB.
Finally, the value of αs is estimated by means of the NΔ mass difference. It is worth noticing that, in this model, the pseudoscalar piece of the interaction contributes to approximately half of the total mass difference. The rest is attributed to the OGE, and the value of αs is adjusted to this value. The values of the parameters determined, as explained above, are given in Table 1.

Table 1. Model parameters from Entem et al. [52].
Once the model is completely defined, one can solve the scattering problem, obtaining the NN phase shifts and the bound state problem, namely the deuteron. The phase shifts calculation will include couplings to a ΔΔ channel for the isosinglet (T = 0) partial waves and to ΔΔ and NΔ channels for isotriplet (T = 1) partial waves. One of the great advantages of the description in terms of quark degrees of freedom is that this scheme allows us to treat the nucleon an its resonances Δ, N* in a single framework without having to increase the number of parameters. In Figures 4–10, one can see the comparison between the results of the model and the experimental data of Arndt et al. [59].
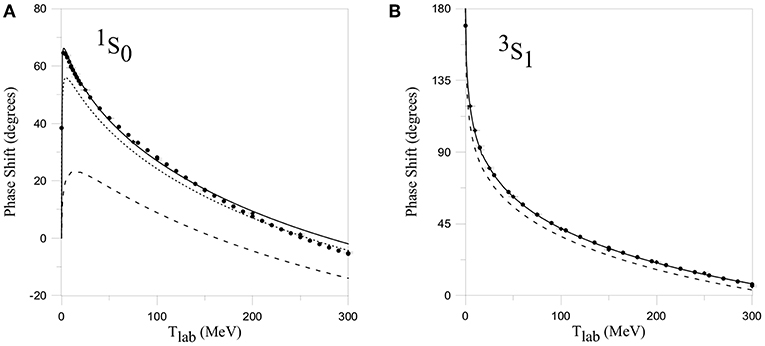
Figure 4. NN S wave phase-shifts for T = 1 (A) and T = 0 (B). Experimental points with and without error bars correspond to the energy independent and energy dependent solutions of Arndt et al. [59], respectively. The phase shifts are shown and the analysis correspond to neutron-proton. (A) Dashed line represents the calculation including NN channels only, dotted line includes also NΔ components, and solid line is the full calculation with NN, NΔ, and ΔΔ channels. (B) Dashed line is the calculation with NN only, and the solid line is the full calculation including NN and ΔΔ channels. Reprinted figure with permission from Entem et al. [52] Copyright (2000) by the American Physical Society.
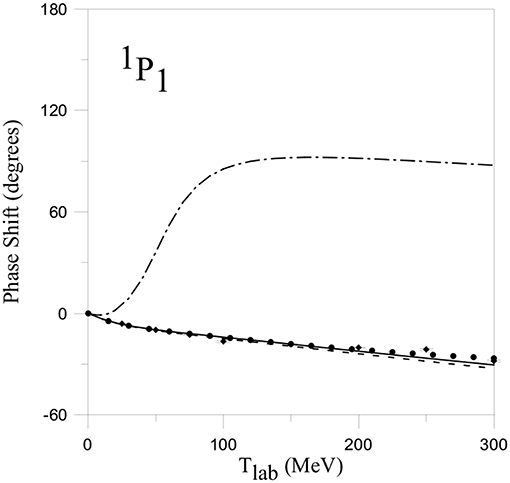
Figure 5. NN 1P1 phase-shift. Dashed and solid lines have the same meanings as in Figure 4B. Dashed-dotted line shows the effect of antisymmetry, corresponding to the result when all the exchange kernels are removed. Reprinted figure with permission from Entem et al. [52] Copyright (2000) by the American Physical Society.
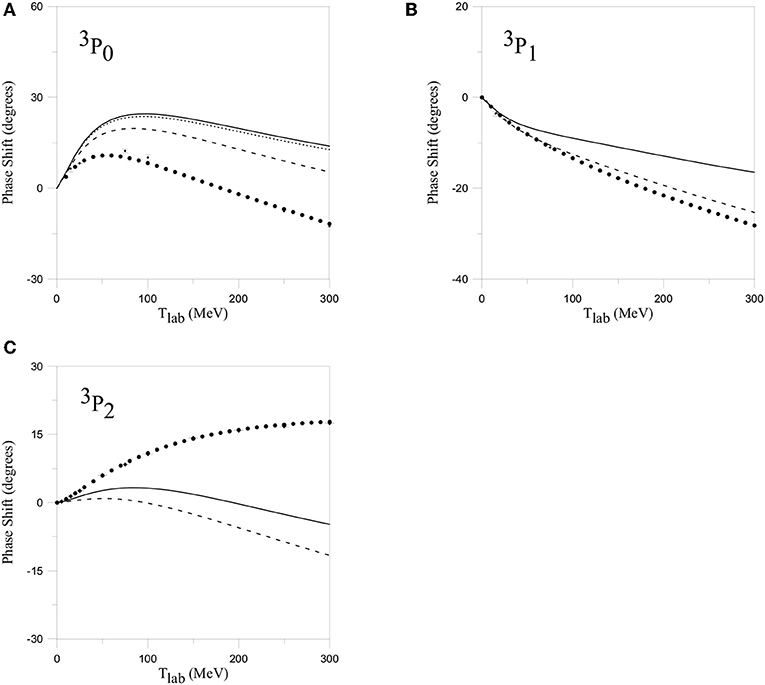
Figure 6. NN 3PJ phase-shifts. (A) Same meaning as in Figure 4A. (B,C) Dashed line corresponds to the result with NN channels only, and the solid line includes NN and NΔ channels. Reprinted figure with permission from Entem et al. [52] Copyright (2000) by the American Physical Society.
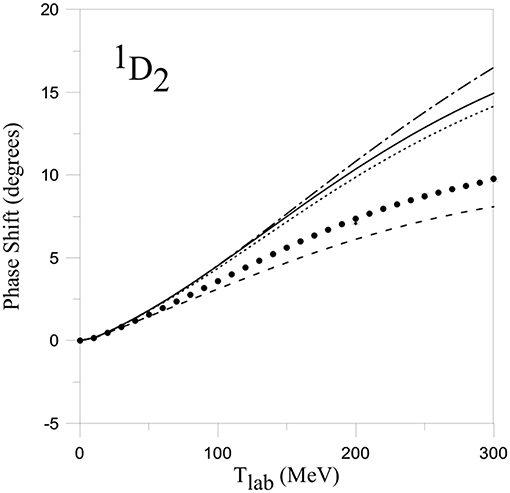
Figure 7. NN 1D2 phase-shift. Solid, dashed, and dotted lines have the same meanings as in Figure 4A. Dashed-dotted line represents the result without exchange kernels. Reprinted figure with permission from Entem et al. [52] Copyright (2000) by the American Physical Society.
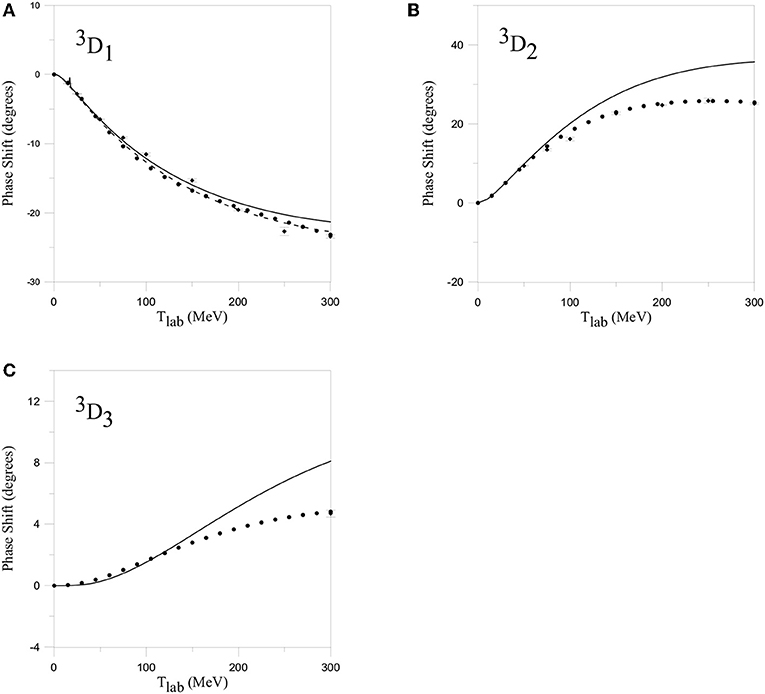
Figure 8. NN 3DJ phase-shifts. (A) Lines are labeled as in Figure 4B. (B,C) Solid line corresponds to the result with NN channels only. Reprinted figure with permission from Entem et al. [52] Copyright (2000) by the American Physical Society.
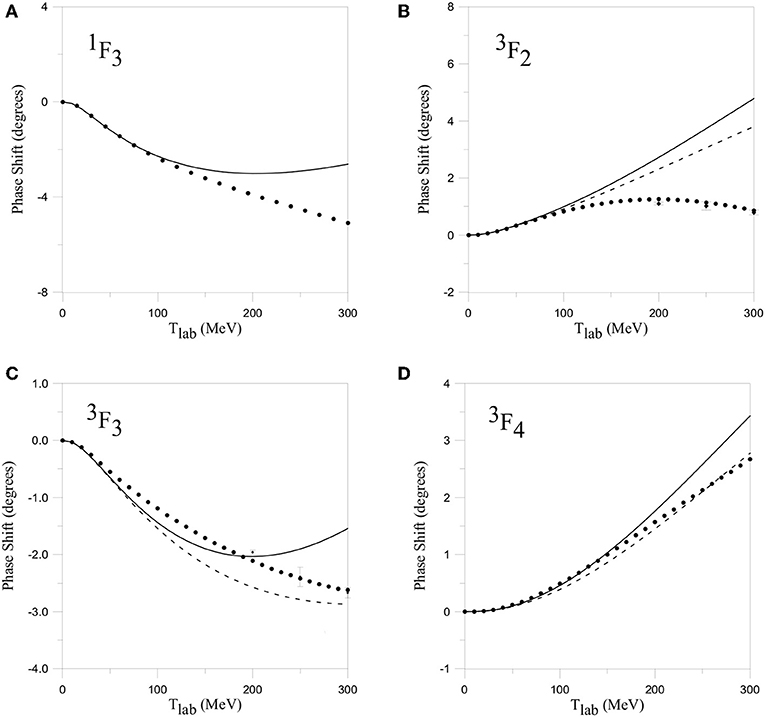
Figure 9. NN F phase-shifts. In the T = 0 sector (A), the solid line includes NN channels only. In the T = 1 sector (B,C,D), the dashed line corresponds to including NN channels only, and the solid line considers also NΔ channels. Reprinted figure with permission from Entem et al. [52] Copyright (2000) by the American Physical Society.
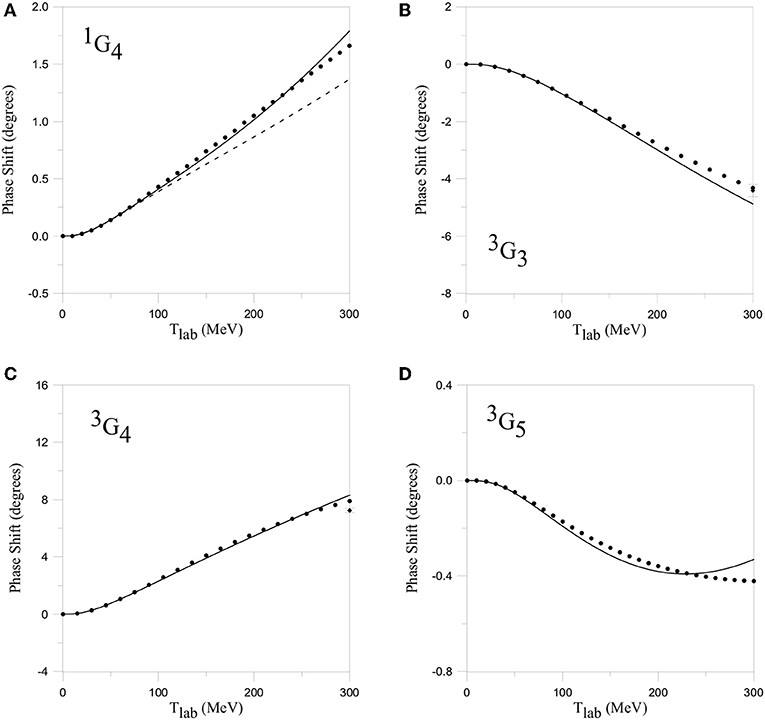
Figure 10. NN G phase shifts in the T = 0 (B,C,D) and T = 1 (A) sectors. Lines have the same meanings as in Figure 9. Reprinted figure with permission from Entem et al. [52] Copyright (2000) by the American Physical Society.
The first aspect that is interesting to remark upon is the result for the partial wave. This channel cannot be coupled to other NN channels by angular momentum selection rules, and it is therefore an ideal candidate to test the quark-quark interaction. As seen in Figure 4, the one channel NN calculation does not show enough attraction to reproduce the experimental data. A possible solution is to increase the strength of the σ exchange. However, in this model, the σ-quark coupling is related with the π-quark coupling by chiral symmetry and, hence, there is not freedom to fit the data. The required attraction is supplied by the coupling to the channel (dotted line) [60]. A complete agreement with the experimental data is obtained when the coupling to ΔΔ channels is included (solid line). For the isotriplet partial waves, the effect of the coupling to ΔΔ channels is very small, as shown here and as will be also seen for higher angular momentum partial waves.
The short-range repulsion of the potential is reproduced very well and without introducing any additional parameters. Although the presence of a pseudoscalar interaction reduces the value of αs in the OGE (the interaction usually advocated an explanation of the short-range repulsion of the NN potential), the strong spin-isospin independent repulsion produced by the effect of the quark antisymmetry on the one-pion exchange potential compensates for the lack of the OGE repulsion.
Table 2 shows the result for the low-energy scattering parameters. The agreement with the experimental results and other theoretical calculations is good, with the exception of the anp. One must be aware that the scattering length in the 1S0, due to the existence of an almost bound state in this partial wave, is extremely sensitive to small changes in the strength of the force. Moreover, the results of Table 2 have been calculated with the same set of parameters for the T = 0 and T = 1 channels. A non-significant change of the scalar boson mass in the T = 1 channel will drive the results to the experimental value. Further discussions of the scattering length problem in this model can be found in Entem et al. [66].
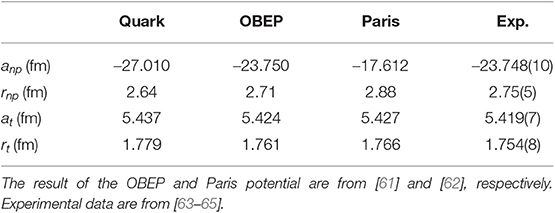
Table 2. Low-energy scattering parameters from Entem et al. [52].
The 1P1 wave is the only one that is not affected by the spin-orbit term of the interaction. This partial wave provides another example of the importance of the quark antisymmetrization in the model. In Figure 5 one can see that, if one removes the terms coming from the antisymmetrization, the interaction is attractive and, consequently, the phase shifts are positive. The one-gluon exchange interaction does not contribute due to its δ-like character, and the direct pseudoscalar is attractive for the 1P1 due to sign of the spin-isospin matrix elements. Only the repulsion coming from the quark antisymmetrization term of the one-pion exchange potential reproduces the correct experimental behavior.
As a general trend, the agreement between theory and experiment is reasonable for phase shifts with L > 1, although, as explained in Entem et al. [52], the interaction shows a lack of spin-orbit interaction.
The problem of the origin of the spin-orbit interaction in the constituent quark model is a long-standing problem that is rooted in the fact that the Galilei-invariant term of the spin-orbit piece, which comes from the one-gluon exchange interaction and is the best one founded for the description of the NN interaction, severely disturbs the description of the negative parity baryon spectrum [67].
Besides the one-gluon exchange, they are several possible sources of the spin-orbit term of the quark-quark interaction. Valcarce et al. [68] studied the spin-orbit terms generated by the one sigma exchange together with the Galilei-invariant spin-orbit terms coming from the one-gluon exchange. They found that the combination of scalar-meson-exchange interaction between quarks and the one-gluon exchange leads to a satisfactory description of the P-wave NN phase shifts and the baryon spectrum. A similar conclusion can be found in Takeuchi [69]. Another source of spin-orbit interaction is one arising as a relativistic effect from the confinement potential (the so-called Thomas term). In Koike [70], this interaction is studied using a particular model of confinement (flip-flop model). The spin-orbit force generated by one-gluon exchange and by a flip-flop model for confinement gives results that are qualitatively similar to those reported by Valcarce et al. [68].
Recent attempts to overcome this problem have been made by Chen et al. using an extension of the quark delocalization color screening model (QDCSM) [71], which includes a one-pion exchange with a short-range cutoff in the QDCSM Hamiltonian [28]. The quark delocalization is achieved by writing the wave function of each nucleon as a linear combination of left and right Gaussians in a two-center cluster model approximation where the mixing parameter ϵ is determined by the six quark dynamics. They obtain similar results as the Salamanca version of the constituent quark model [52] but replacing the σ-meson exchange by the quark delocalization and color-screening mechanism [29]. However, this new mechanism does not contribute to solving the spin-orbit problem [30].
One must conclude, therefore, that the situation of the spin-orbit force in quark potential models is still quite controversial. To remove the remaining uncertainties, a better understanding of the quark confinement is clearly needed (see also the discussion of this issue in Myhrer and Wroldsen [26]).
Besides the problem of the spin-orbit interaction, the constituent quark model description of the nucleon-nucleon interaction still has room for improvement. Although the Gaussian ansatz for the wave function is a reasonable and useful approximation, one may wonder what the result would be if a more accurate wave function was used. This has been done by Huang and Wang [31] in the framework of the SU(3) chiral model [72]. The authors constrained the adjustable parameters of the model by minimizing the masses of the octet and decuplet baryon ground states. These masses were calculated by using Gaussian trial wave functions where the size parameters are determined by a variational method, which guarantees that all baryons correspond to minimum states of the Hamiltonian model. The NN scattering phase shifts are in satisfactory agreement with the experimental data describing in a consistently unified way the single baryon properties and the baryon-baryon dynamics.
A still controversial and challenging problem is the inclusion of the vector-meson exchanges into the model. In a schematic model, Yazaki showed that the pseudo-scalar (π, η) and scalar (σ) meson exchange terms can be simply added to the quark exchange term without the risk of double counting, but the vector-meson (ρ, ω) exchange needs some care because it plays a role similar to the one-gluon exchange [48]. The same conclusion is obtained in Huang and Zhang [73]. These authors show, in a kaon-nucleon interaction in the extended chiral SU(3) quark model that includes vector-meson exchanges, that the role of the gluon is now nearly replaced by the vector-meson exchange. For heavy quarks, meson exchanges are questionable Because, in this sector, the chiral symmetry is explicitly broken by the quark masses. Hence, it seems that the one-gluon exchange should be a piece of the quark-quark interaction. However, which mechanism is the right one for describing the short-range quark-quark interactions is still an open question.
The quark scheme is also very suited to describing the nucleon-nucleon bound states and their possible baryon-baryon components. The deuteron has been traditionally described as an isospin singlet Jπ = 1+ two-nucleon system in even partial waves (i.e., 3S1 and 3D1). However, its structure could also be explained as a linear combination of pairs of baryonic resonances, provided they have the adequate total quantum numbers.
The usual way to treat the contribution of these resonances is to include them explicitly in a coupled-channel calculation. When this is done at the baryonic level, two problems immediately arise. If one uses for the nucleon-nucleon channel an effective potential that is fitted to the nucleon-nucleon scattering, it will already include contributions from the resonance intermediates N* or Δ. Therefore, one has to modify the normal nucleon-nucleon potential in order to account for the additional attraction coming from the channel coupling. Such procedures usually introduce an unwanted model dependence on the results obtained and are sometimes not fully consistent.
Examples of these concerns are the calculation of Haapakoski and Saarela [74] (ΔΔ components) and Rost [75] (NN* components). Both used a Reid Soft core potential for the NN channel and one-pion exchange potential for the NN* or ΔΔ channel. Rost realized that when NN* configurations are included, the NN potential must be modified because part of the attraction is produced by NN* components. It implicitly appears in the fit to the experimental data, and, now that the NN* are explicitly included in the coupled-channels calculation, it must be subtracted out to avoid double counting. This is done by modifying the values of the parameters responsible for the intermediate range attraction in the Reid potential. A similar problem appears in Haapakoski and Saarela [74] in their ΔΔ calculation. A second problem is that there is no guidance to construct the specific transition potential to the N* resonances, and one thus resorts to scaling some pieces (for example the one-pion exchange) of the nucleon-nucleon interaction, As shown by Juliá-Díaz et al. [76], however, the NN* interaction, due to quark antisymetrization, shows significant differences with respect to those obtained by a direct scaling of the nucleon-nucleon interaction.
These two difficulties are overcome in calculations based on quark degrees of freedom as the one performed in Entem et al. [52]. These authors assume that the deuteron can be described as a combination of different configurations, with two clusters of three quarks being the most important, in order of increasing mass, N(939)N(939), N(939)N*(1440), and Δ(1232)Δ(1232). Table 3 displays the different configurations and partial waves included in the calculation. The results of the calculation are shown in Table 4. In all cases, the deuteron binding energy is correctly reproduced, being Ed = –2.2246 MeV. There are a number of conclusions that can be drawn from this table. The first one is that the probability of the NN*(1440) components are significantly smaller than the ΔΔ ones, which is in agreement with the indirect estimations of Dorodnykh et al. [78]. As a consequence, the influence of these components on the value of the observables, such as the root mean square radius or AS, is negligible. Finally, the probability of the ΔΔ components (around 0.25%) agree with the upper limit established by Allasia et al. [79].

Table 3. Different channels and partial waves considered in the calculation of the deuteron properties from Juliá-Díaz et al. [77].
The nucleon-nucleon interaction described above can be applied to other systems, in the same way that they do other nucleon-nucleon potentials likes the ones based in boson exchanges. The most obvious system to extend the application of the quark model-based nucleon-nucleon interaction is the triton.
The interest of this calculation lies in the fact that the NN potential derived from the quark-quark interaction is non-local. This potential is generated using the Resonating Group Method so that the non-localities resulting from the internal structure of nucleons is persevered. These non-localities can produce off-shell behavior different to the quark model-based potential.
In Juliá-Díaz et al. [76], the triton binding energy was obtained from a Fadeev calculation, including only 1S0 and 3S1 – 3D1 NN partial waves, used for the NN interaction of the direct and exchange potential obtained in a fully RGM-based nucleon-nucleon calculation. The results for the triton observables are shown in Table 5 together with those obtained for conventional NN potentials. One can see that they are no significant differences between the three calculations, and so the quark model-based NN interaction can provide a realistic description of triton. A more complete calculation, which includes up to 50 channels in the Fadeev calculation and uses a different scheme for the quark-quark interaction, was developed by Fujiwara et al. [83], and it obtained a binding energy of Eb = −8.52 MeV.
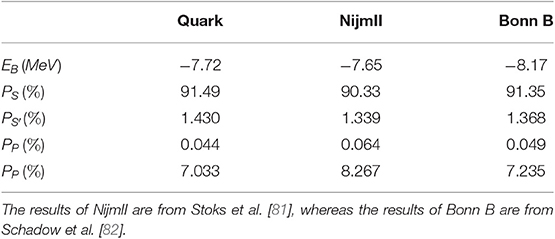
Table 5. Comparison of triton properties from Juliá-Díaz et al. [80].
Particularly attractive are those processes in which the quark model description involves completely different physics from the conventional one. One of these systems is the hyperon production process .
The experimental data shows two characteristic features of this production process. The first one is that the process that occurs predominately in a spin-triplet state. The second feature refers to the energy dependence of the cross section immediately after the threshold, which needs the inclusion of the calculation of partial waves higher than L = 0.
In the quark level description, the pair is produced from the state via the annihilation of a uū pair and the subsequent creation of an pair by s-channel exchanges. In a conventional description, meanwhile, this production relies on the t-channel meson exchanges, where at least kaon exchanges are needed. Examples of this different point of view can be found in Ortega et al. [84], Haidenbauer et al. [85] and references therein.
The two types of models involve completely different physics. Thus, the triplet-state dominance can easily be understood in quark models because the pair, which carry the spin, is produced by effective vector exchanges (gluons and Goldstone bosons), which gives rise to a spin 1 for the state. In meson exchange models, the tensor pieces of the K and K* mesons must be combined to produce the spin-triplet dominance, which may introduce a model dependence.
For the real part of the () interaction, both type of models use a G-parity transformation of some nucleon-nucleon (hyperon-nucleon) potential. The model of Haidenbauer et al. [85] is based in the OBEPF version of the one-boson exchange potential of Haidenbauer et al. [86] for the , whereas the corresponding interaction for the channel is derived from the hyperon-nucleon potential of Holzenkamp et al. [87]. The transition potential includes K and K* meson exchanges.
The quark-quark interaction used by Ortega et al. [84] is a generalization of the quark-quark interaction of Entem et al. [52]. It includes the exchange of π, K, η, σ, κ, and gluons in the t-channel and π, κ, η, and gluons in the annihilation s-channel. Initial and final state interactions are automatically included by the diagonal channel interactions.
Besides the interaction described above, both the and annihilate into mesons. These processes are very difficult to describe, and they are usually parameterized in both models by a complex potential, including spin- and isospin-dependent terms. The parameters of this potential are fitted to the cross sections (total, elastic, and charge exchange) and total cross section. Although both models reproduce the total and differential cross section with reasonable accuracy, completely different patters appear in the description of polarization observables, such as the depolarization observable Dnn, the Knn spin transfer, and the Ci,j spin correlation coefficients. The calculation of Haidenbauer et al. [85] concluded that the quark model seemed to be in better agreement with the Ci,j spin correlation coefficients data. There was no comparison with experimental data of Dnn, and the Knn spin transfer was performed, but the results show significant differences between the prediction of the two models. In Ortega et al. [84], the authors compared the results of the quark model calculation with a set of data on a different energy, concluding that the model seemed to show a reasonable agreement with the data. However, the scarcity and inaccuracy of existing data prevents us from forming any definitive conclusion.
The same scheme used to describe the nucleon-nucleon interaction in terms of degrees of quark freedom can be used to study the hyperon-nucleon interaction and the hyperon-hyperon interaction. Technically, this means extending the SU(2) flavor model to the SU(3) flavor model (or SU(6) spin flavor). Most of the parameters of the extended model are obtained from the nucleon-nucleon interaction and the rest from the low-energy cross section data of the hyperon-nucleon interaction.
Among the different works done in this line [88], we will refer to two of them, which use different approaches: the one develop by the Beijing group [89] and the one developed by the Kyoto group [49].
The model of Zhang et al. was an extension of the low-momentum effective Lagrangian coming from the instanton liquid picture of the QCD vacuum Equation (27) of Fernandez et al. [24] to a SU(3) model by the inclusion of an s-quark in the system. As a consequence, aside from the usual π and σ exchanges, K, η, and η′ exchanges appeared in a natural way. The 12 parameters of the model were fixed in the same way of Fernandez et al. [24], but the oscillator parameter bs was obtained by scaling the parameter bu as , were mu and ms are the constituent masses of the light and strange quark, respectively. The one-gluon exchange coupling constant for the light and strange quark were determined from the mass splitting of ΔN and ΛN, respectively. Finally, the strength of the confinements were obtained from the stability condition of nucleon Λ and Ξ.
Using this interaction, Zhang et al. [72, 89] studied the binding energy of the deuteron, the NN scattering phase shifts, and the hyperon-nucleon cross section in the framework of the RGM, obtaining results reasonably consistent with experiment.
The model of the Kyoto group follows the philosophy of the hybrids models. The effective qq interaction of the model consist of the one-gluon exchange Fermi-Breit interaction, a quark-confining potential, and other terms generated effective meson-exchange potentials (EMEP) from various meson-exchange mechanisms. They are various version of the model depending of the mesons included in the (EMEP). All of these versions can be found in the extensive review of Fujiwara et al. [88]. We will only mention the most recent version named fss2 [49], which, besides the scalar and pseudo-scalar meson exchanges, includes the vector meson exchanges as well. This potential reproduces the existing data of the NN and YN interactions quite well and, therefore, can predict all the interactions in the strangeness S = –2, –3, and –4 sectors without adding any extra parameters.
In the last years, the experimental progress in the phenomenology of heavy hadrons has increased the interest in the hadron-hadron interaction involving heavy flavors as well as the bound nuclear systems with heavy mesons. Due to the lack of experimental results, most works are devoted to looking for bound states or resonances or comparing phase shifts with lattice calculations, e.g., Miyamoto et al. [90, 91]. Thus, Huang et al. [33] the NΛc, NΛb, NΣc, and NΣb are investigated in the quark delocalization color screening model. The authors have shown that, although the interaction NΛc is attractive, it is not strong enough to form bound states. That is not the case of the NΣc interaction, which is able to form bound sates that become resonances with the coupling with the NΛc. The corresponding bottom states have similar properties.
A comparative study of charmed baryon-nucleon interaction is performed in Garcilazo et al. [34] based on different theoretical approaches and comparing them with a lattice calculation, forming a general qualitative agreement among the different approaches. However, more experimental efforts are necessary in this field to be able to drawn quantitative conclusions.
Finally, a NN interaction based on quark degrees of freedom has been applied to the description of the nuclear matter saturation point in Fukukawa et al. [92]. These authors derive the equation of states (EOS) of nuclear matter in the framework of the Bethe-Brueckner-Goldstone approach using the fss2 interaction of Fujiwara et al. [49]. The results showed that the nuclear matter saturation curves can be reproduced at the same level of the best NN interactions but without the need of the introduction of three-body forces or parameters different from the one used to reproduce the NN phase shifts and the deuteron properties. These results may be an indication that the effects of the three-body forces used in more traditional interactions are, to a large extend, automatically included when the quark degrees of freedom are explicitly introduced in the calculation.
Although the constituent quarks model, in its different versions, has been the most popular model to use to study the nucleon-nucleon interaction, there have been attempts to use other models for the same purpose, as the bag model is the most important. As we said in the introduction, the first attempts to describe this interaction using degrees of freedom from quarks were made by Fairley using the MIT bag model [93]. The ingredients of the model are very simple: relativistic quarks of three colors and two, three, or four flavors interacting through an octet of colored vector gluons. Quarks and gluons are confined to a finite volume by a uniform pressure. Non-strange quarks are massless, satisfying all quarks the Dirac equation inside the cavity.
The first serious effort to use the MIT bag model to describe the nucleon-nucleon interaction was carried out by DeTar [8]. In this model, the nucleon-nucleon interaction is obtained from the adiabatic deformation of a bag containing six quarks into two color singlet bags containing three each. The energy of the two three-quark bags is minimized with respect to two collective variables: a parameter that measures the separation of the three-quark subsystems and a second parameter related to the baryonic quadrupole moment that, in certain ways, takes into account the deformation of the three-quark bags in their mutual interaction. The obtained potential shows a soft core of about 300 MeV at short distances and it is attractive in the intermediate range. The soft core can be easily understood, as explained below.
In the MIT bag model, the color magnetic energy of n-quarks coupled to a color singlet and located in the same orbit is DeGrand et al. [94]:
where J is the angular momentum of the state and I the isospin. M00 is a model parameter that take the value 50 MeV in order to reproduce the Δ(1230)-nucleon mass difference. In the case J = 1 and I = 0 (calculated by DeTar), the color magnetic interaction when the two nucleons completely overlap was only 50 MeV, whereas each nucleon had a color magnetic energy of 150 MeV. This 250 MeV difference between the energy of two separated and merged nucleons accounted for the repulsion found by DeTar. The intermediate-range attraction obtained by DeTar could not have been predicted without a quantitative calculation and should be related with the strong color electrostatic attraction within the quark triplets [8].
The calculations in this model are sufficiently complex not to be able to advance much more in the calculation of the NN interaction. Moreover, the center of mass energy of the two bags is difficult to subtract, which can lead to double counting problems when calculating the nucleon-nucleon phase shifts. In order to solve the scattering problem of two bags, Jaffe and Low proposed the use of the P-matrix formalism [95]. These authors suggested that the energy of multiquarks states appears as poles of the P matrix, that is the logarithmic derivative of the hadronic wave function:
provided that the matching radius b is chosen to be consistent with that of the multiquark state. In this way, P-matrix poles are obtained from the experimental phase sifts and compared with the predictions of the bag model to form the multiquark states.
The Jaffe-Low hypothesis was tested for the NN system [96, 97], finding a qualitative explanation for the origin of the repulsive core and an overall agreement with the experimental data with an accuracy up to 10 − 15%. Possible improvements to the model include a better determination of the relationship between the bags parameter and the matching radius and the possibility of allowing for deformed bag shapes. This last point is technically complicated, although some advances have been made by expanding the wave function in an harmonic oscillator basis [98].
Bags models have also been used to generate boson-exchange interactions through a Fierz transformation of the gluon exchange between two bags, being that the form factors appearing in the OBE are defined as matrix elements of the vertex invariants with quark wave functions taken from the MIT bag model [99].
Throughout this chapter we have presented the achievements of the description of the nucleon-nucleon interaction in terms of quark degrees of freedom. At the scale of nuclear phenomena or low-energy hadron physics, the QCD running coupling constant is large, and, in this strong-coupling regime, non-perturbative methods are indispensable. But, so far, not much success has been achieved in this respect. Then, if one wants to explicitly keep the fundamental constituents in QCD, i.e., quarks and gluons, one is then led to the model non-perturbative QCD using ‘QCD-inspired’ models. One of these models, the constituent quark model, is experiencing a resurgence because of the recent studies of the NN interaction from first-principles lattice-QCD simulations near the physical quark masses that indicate that their behavior at short distances are qualitatively consistent with the constituent quark model [100, 101]. In particular, when a compact six-quark state is Pauli blocked, the baryon interaction is highly repulsive. However, when the channel is Pauli allowed, the interaction can be either attractive or repulsive, as predicted by the constituent quark model [102].
Leaving aside the fact that these models are not derived from the fundamental theory, the use of quark and gluon degrees of freedom allows us to better understand the physics underlying some phenomena, such as the hard core of the nuclear force or the role played by the quark antisymmetry, which in other models can be hidden in the parameters used. On the other hand, these models represent a complexity added to the calculations that make them less flexible in reproducing certain phenomenology.
The main advantages of these models is that they can describe a huge variety of phenomena, baryon and meson spectrum, baryon-baryon interactions, and few nucleons system (deuteron, triton,…), within an unified (and sometimes reduced) set of parameters with a quality comparable with the other models.
However, these models present the same caveats, such as their non-relativistic character; the way to set the values of the model parameters make it difficult to determine errors of the calculated observables and impossible to improving the model order by order.
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
This work has been funded by Ministerio de Economía, Industria y Competitividad under Contract No. FPA2016-77177-C2-2-P and by the EU STRONG-2020 project under the program H2020-INFRAIA-2018-1, grant agreement no. 824093.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
1. Manohar A, Georgi H. Chiral quarks and the non-relativistic quark model. Nuclear Phys B. (1984) 234:189–212.
2. Diakonov D. Instantons at work. Prog Part Nucl Phys. (2003) 51:173–222. doi: 10.1016/S0146-6410(03)90014-7
4. Fairley GT, Squires EJ. Nuclear forces and the quantization of M.I.T. bags. Acta Phys Polon. (1975) B6:893.
5. Neudatchin VG, Obukhovsky IT, Kukulin VI, Golovanova NF. Attractive potential with forbidden states for the N − N interaction. Phys Rev C. (1975) 11:128–36.
6. Neudatchin VG, Smirnov YF, Tamagaki R. An explanation of N-N “Repulsive Core” in terms of forbidden states based on the quark model. Progress Theor Phys. (1977) 58:1072–4.
11. Wildermuth K, Tang YC. A Unified Theory of the Nucleus. New York, NY; San Francisco, CA; London: Academic Press (1977).
13. Ribeiro JEFT. Microscopic calculation of the repulsive core in the elastic nucleon-nucleon scattering. Zeitschrift für Physik C Particles Fields. (1980) 5:27–35.
14. Toki H. Short range behaviour of the N-N potential within the quark model. Zeitschrift für Physik A Atoms Nuclei. (1980) 294:173–81.
15. De Rújula A, Georgi H, Glashow SL. Hadron masses in a gauge theory. Phys Rev D. (1975) 12:147–62.
16. Harvey M. Effective nuclear forces in the quark model with delta and hidden-color channel coupling. Nuclear Phys A. (1981) 352:326–42.
17. Faessler A, Fernandez F, Lübeck G, Shimizu K. The quark model and the nature of the repulsive core of the nucleon-nucleon interaction. Phys Lett B. (1982) 112:201–5.
18. Makato O, Koichi Y. Short-range part of the nuclear force and the deuteron in a quark model. Nuclear Phys A. (1983) 402:477–90.
19. Maltman K, Isgur N. Nuclear physics and the quark model: six quarks with chromodynamics. Phys Rev D. (1984) 29:952–77.
20. Fujiwara Y, Kohno M, Nakamoto C, Suzuki Y. Interactions between octet baryons in the SU6 quark model. Phys Rev C. (2001) 64:054001. doi: 10.1103/PhysRevC.64.054001
21. Faessler A, Fernandez F. The quark model and the nucleon-nucleon interaction. Phys Lett B. (1983) 124:145–8.
23. Fernández F. Neutron-proton charge exchange scattering in a one-pion-exchange model with quark exchange. Phys Lett B. (1987) 188:314–6.
24. Fernandez F, Valcarce A, Straub U, Faessler A. The nucleon-nucleon interaction in terms of quark degrees of freedom. J Phys G Nuclear Part Phys. (1993) 19:2013–26.
25. Yu YW, Zhang ZY, Shen PN, Dai LR. Quark-quark potential from chiral symmetry. Phys Rev C. (1995) 52:3393–8.
26. Myhrer F, Wroldsen J. The nucleon-nucleon force and the quark degrees of freedom. Rev Mod Phys. (1988) 60:629–61.
28. Lu XF, Ping JL, Wang F. The NN phase shifts in the extended quark-delocalization, color-screening model. Chin Phys Lett. (2003) 20:42–5. doi: 10.1088/0256-307X/20/1/313
29. Chen L, Pang H, Huang H, Ping J, Wang F. An Alternative approach to the sigma-meson-exchange in nucleon-nucleon interaction. Phys Rev. (2007) C76:014001. doi: 10.1103/PhysRevC.76.014001
30. Huang HX, Ping JL, Chen LZ, Wang F, Pang HR. Influence of spin-orbit force on nucleon-nucleon scattering in the quark delocalization colour screening model. Chin Phys Lett. (2008) 25:1617–20. doi: 10.1088/0256-307X/25/5/026
31. Huang F, Wang WL. Nucleon-nucleon interaction in a chiral SU(3) quark model revisited. Phys Rev. (2018) D98:074018. doi: 10.1103/PhysRevD.98.074018
32. Downum C, Stone J, Barnes T, Swanson E, Vidana I. Nucleon-nucleon interactions from the quark model. AIP Conf Proc. (2010) 1257:538–42. doi: 10.1063/1.3483388
33. Huang H, Ping J, Wang F. NΣcc and NΣbb resonances in the quark-delocalization color-screening model. Phys Rev C. (2013) 87:034002. doi: 10.1103/PhysRevC.87.034002
34. Garcilazo H, Valcarce A, Caramés TF. Charmed baryon-nucleon interaction. Eur Phys J. (2019) C79:598. doi: 10.1140/epjc/s10052-019-7110-z
35. Tegen R, Weise W. The nucleon axial form factor and the pion-nucleon vertex function. Zeitschrift für Physik A Atoms Nuclei. (1983) 314:357–64.
36. Bräuer K, Faessler A, Fernandez F, Shimizu K. Nucleon-nucleon interaction in a quark model with pions. Nuclear Phys A. (1990) 507:599–610.
37. Jain BK, Santra AB. Study of the p(p, n)Δ++ reaction in nuclei. Nuclear Phys A. (1990) 519:697–720.
38. Fernandez F, Valcarce A, Gonzalez P, Vento V. p(n, p)n and p(p, Δ++)n charge-exchange reactions in a constituent quark model. Phys Lett B. (1992) 287:35–9.
39. Fernández F, Oset E. A model of the double-spin-flip NN amplitude based on a one-pion exchange potential with quark exchange. Nuclear Phys A. (1986) 455:720–36.
40. Kamimura M. Chapter V. A coupled channel variational method for microscopic study of reactions between complex nuclei. Progress Theor Phys Suppl. (1977) 62:236–94.
41. Berestetskii VB, Pitaevskii LP, Lifshitz EM. Quantum Electrodynamics. v. 4. Oxford, UK: Elsevier Science (2012).
44. Isgur N, Karl G. Ground state baryons in a quark model with hyperfine interactions. Phys Rev. (1979) D20:1191–4.
45. Ellwanger U. Baryon mass splitting by the strong hyperfine interaction and SU(3) breaking. Nucl Phys. (1978) B139:422–32.
47. Faessler A, Fernandez F, Lübeck G, Shimizu K. The nucleon-nucleon interaction and the role of the [42] orbital six-quark symmetry. Nuclear Phys A. (1983) 402:555–68.
48. Yazaki K. Quark versus mesons in nuclear force and nuclear currents. Progress Part Nuclear Phys. (1990) 24:353–61.
49. Fujiwara Y, Fujita T, Kohno M, Nakamoto C, Suzuki Y. Resonating-group study of baryon-baryon interactions for the complete baryon octet: NN interaction. Phys Rev C. (2001) 65:014002. doi: 10.1103/PhysRevC.65.014002
50. Diakonov DI, Petrov VY. A theory of light quarks in the instanton vacuum. Nuclear Phys B. (1986) 272:457–89.
51. Diakonov D. Foundations of the constitutent quark model. Progress Part Nuclear Phys. (1996) 36:1–17.
52. Entem DR, Fernández F, Valcarce A. Chiral quark model of theNNsystem within a Lippmann-Schwinger resonating group method. Phys Rev C. (2000) 62. doi: 10.1103/PhysRevC.62.034002
53. Valcarce A, Garcilazo H, Fernandez F, Gonzalez P. Quark-model study of few-baryon systems. Rept Prog Phys. (2005) 68:965–1042. doi: 10.1088/0034-4885/68/5/R01
54. Scadron MD. SU(2) linear sigma model: its dynamical generation and phenomenological applications. Phys Atom Nucl. (1993) 56:1595–603.
55. Valcarce A, González P, Fernández F, Vento V. A consistent study of the low energy baryon spectrum and the nucleon-nucleon interaction within the chiral quark model. Phys Lett B. (1996) 367:35–9.
56. Machleidt R. One-boson-exchange potentials and nucleon-nucleon scattering. In: Langanke K, Maruhn JA, Koonin SE, editors. Computational Nuclear Physics 2: Nuclear Reactions. Berlin: Springer-Verlag (1993). p. 1–29.
57. Bergervoet JR, van Campen PC, Klomp RAM, de Kok JL, Rijken TA, Stoks VGJ, et al. Phase shift analysis of all proton-proton scattering data below Tlab=350 MeV. Phys Rev C. (1990) 41:1435–52.
58. Fernández F, Valcarce A, González P, Vento V. A quark-model description of the Δ-production in proton-proton collisions. Nuclear Phys A. (1994) 567:741–60.
59. Arndt RA, Heon Oh C, Strakovsky II, Workman RL, Dohrmann F. Nucleon-nucleon elastic scattering analysis to 2.5 GeV. Phys Rev C. (1997) 56:3005–13.
60. Valcarce A, Faessler A, Fernández F. Influence of the 5D0 nucleon-Δ channel on the 1S0 nucleon-nucleon phase shift in a quark model. Phys Lett B. (1995) 345:367–71.
61. Machleidt R. The Meson theory of nuclear forces and nuclear structure. Adv Nucl Phys. (1989) 19:189–376.
62. Lacombe M, Loiseau B, Richard JM, Vinh Mau R, Cote J, Pires P, et al. Parametrization of the Paris n n Potential. Phys Rev. (1980) C21:861–73.
63. Houk TL. Neutron-proton scattering cross section at a few electron volts and charge independence. Phys Rev. (1971) C3:1886–903.
64. Dilg W. Measurement of the neutron-proton total cross section at 132 eV. Phys Rev. (1975) C11:103–9.
65. Klarsfeld S, Martorell J, Sprung DWL. Deuteron properties and the nucleon nucleon interaction. J Phys. (1984) G10:165–79.
66. Entem DR, Fernández F, Valcarce A. Charge dependence and charge asymmetry of nuclear forces in chiral quark cluster models. Phys Lett B. (1999) 463:153–8.
68. Valcarce A, Buchmann A, Fernández F, Faessler A. Spin-orbit force in a quark model based nucleon-nucleon potential. Phys Rev C. (1995) 51:1480–7.
69. Takeuchi S. Effects of instantons on P-wave multiquark systems. Phys Rev Lett. (1994) 73:2173–5.
70. Koike Y. Nucleon-nucleon interaction with a flip-flop model for quark confinement. Nuclear Phys A. (1986) 454:509–26.
71. Wang F, Wu Gh, Teng Lj, Goldman JT. Quark delocalization, color screening, and nuclear intermediate range attraction. Phys Rev Lett. (1992) 69:2901–4.
72. Zhang ZY, Yu YW, Shen PN, Dai LR, Faessler A, Straub U. Hyperon-nucleon interactions in a chiral SU(3) quark model. Nuclear Phys A. (1997) 625:59–70.
73. Huang F, Zhang ZY. Kaon-nucleon interaction in the extended chiral SU(3) quark model. Phys Rev. (2005) C72:024003.
74. Haapakoski P, Saarela M. The double Δ(1236)-resonance in the deuteron. Phys Lett B. (1974) 53:333–6.
76. Juliá-Díaz B, Valcarce A, González P, Fernández F. Microscopic NN → NN*(1440) transition potential: determination of πNN*(1440) and σNN*(1440) coupling constants. Phys Rev C. (2002) 66:024005. doi: 10.1103/PhysRevC.66.024005
77. Juliá-Díaz B, Entem DR, Valcarce A, Fernández F. Deuteron NN*(1440) components from a chiral quark model. Phys Rev C. (2002) 66:047002. doi: 10.1103/PhysRevC.66.047002
78. Dorodnykh YL, Lykasov GI, Rzjanin MV, Cassing W. Probing the deuteron structure at small NN distances by subthreshold antiproton production. Phys Lett B. (1995) 346:227–32.
79. Allasia D, Angelini C, Baldini A, Bobisut F, Borg A, Capillupi P, et al. Search for a Δ(1236)-Δ(1236) structure of the deuteron. Phys Lett B. (1986) 174:450–2.
80. Juliá-Díaz B, Haidenbauer J, Valcarce A, Fernández F. Quark-model based study of the triton binding energy. Phys Rev C. (2002) 65:034001. doi: 10.1103/PhysRevC.65.034001
81. Stoks VGJ, Klomp RAM, Terheggen CPF, de Swart JJ. Construction of high quality N N potential models. Phys Rev. (1994) C49:2950–62.
82. Schadow W, Sandhas W, Haidenbauer J, Nogga A. Comparison of triton bound state properties using different separable representations of realistic potentials. Few Body Syst. (2000) 28:241–58. doi: 10.1007/s006010070023
83. Fujiwara Y, Miyagawa K, Suzuki Y, Kohno M, Nemura H. Three-nucleon bound state in the SU6 quark model for the baryon-baryon interaction. Nuclear Phys A. (2003) 721:C983–6. doi: 10.1016/S0375-9474(03)01265-X
84. Ortega PG, Entem DR, Fernández F. depolarization and spin transfer in a constituent quark model. Phys Lett B. (2011) 696:352–8. doi: 10.1016/j.physletb.2010.12.034
85. Haidenbauer J, Holinde K, Mull V, Speth J. Meson-exchange and quark-gluon transitions in the process. Phys Rev C. (1992) 46:2158–71.
86. Haidenbauer J, Holinde K, Johnson MB. Folded diagram nucleon-nucleon potential for application to the many body problem. Phys Rev. (1992) C45:2055–67.
87. Holzenkamp B, Holinde K, Speth J. A meson exchange model for the hyperon nucleon interaction. Nucl Phys. (1989) A500:485–528.
88. Fujiwara Y, Suzuki Y, Nakamoto C. Baryon-baryon interactions in the SU6 quark model and their applications to light nuclear systems. Progress Part Nucl Phys. (2007) 58:439–520.
89. Zhang ZY, Faessler A, Straub U, Glozman LYa. The Baryon baryon interaction in a modified quark model. Nucl Phys. (1994) A578:573–85.
90. Miyamoto T, Aoki S, Doi T, Gongyo S, Hatsuda T, Ikeda Y, et al. ΛcN interaction from lattice QCD and its application to Λc hypernuclei. Nucl Phys. (2018) A971:113–29. doi: 10.1016/j.nuclphysa.2018.01.015
91. Miyamoto T. Coupled-channel ΛcN − ΣcN interaction from lattice QCD. PoS. (2018) Hadron2017:146. doi: 10.22323/1.310.0146
92. Fukukawa K, Baldo M, Burgio GF, Monaco LL, Schulze HJ. Nuclear matter equation of state from a quark-model nucleon-nucleon interaction. Phys Rev C. (2015) 92:065802. doi: 10.1103/PhysRevC.92.065802
93. Chodos A, Jaffe RL, Johnson K, Thorn CB, Weisskopf VF. New extended model of hadrons. Phys Rev D. (1974) 9:3471–95.
94. DeGrand T, Jaffe RL, Johnson K, Kiskis J. Masses and other parameters of the light hadrons. Phys Rev D. (1975) 12:2060–76.
95. Jaffe RL, Low FE. Connection between quark-model eigenstates and low-energy scattering. Phys Rev D. (1979) 19:2105–18.
96. Simonov YA. The quark compound bag model and the Jaffe-low P-matrix. Phys Lett B. (1981) 107:1–4.
98. Furui S, Faessler A. Nucleon-nucleon scattering in the two-center MIT bag model with nonlocality and removal of the spurious relative motion. Nucl Phys A. (1983) 397:413–46.
99. Bakker BLG, Bozoian M, Maslow JN, Weber HJ. NN interaction from bag-model quark interchange. Phys Rev C. (1982) 25:1134–51.
100. Hatsuda T. Lattice quantum chromodynamics and baryon-baryon interactions. Front Phys. (2018) 13:132105. doi: 10.1007/s11467-018-0829-4
101. Park A, Lee SH, Inoue T, Hatsuda T. Baryon-baryon interactions at short distances–constituent quark model meets lattice QCD. arXiv:1907.06351. (2019).
Keywords: nucleon-nucleon interaction, nucleon-nucleon interactions (including antinucleons, deuterons, etc.), quark model, quark model baryon-baryon interaction, constituent quark cluster model
Citation: Fernández F, Ortega PG and Entem DR (2020) Quark Models of the Nucleon–Nucleon Interaction. Front. Phys. 7:233. doi: 10.3389/fphy.2019.00233
Received: 26 September 2019; Accepted: 12 December 2019;
Published: 23 January 2020.
Edited by:
Laura Elisa Marcucci, University of Pisa, ItalyReviewed by:
Roelof Bijker, National Autonomous University of Mexico, MexicoCopyright © 2020 Fernández, Ortega and Entem. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francisco Fernández, ZmR6QHVzYWwuZXM=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.