- Physical Chemistry and Soft Matter, Wageningen University and Research, Wageningen, Netherlands
Thoroughly mixing immiscible fluids creates droplets of one phase dispersed in a continuum of the other phase. In such emulsions, the individual droplets have rather mundane mechanical behavior. However, densely confining these suspended droplets generates a packing of particles with a spectacular diversity of mechanical behavior whose origins we are only beginning to understand. This mini review serves to survey a non-exhaustive range of experimental dense slow flow emulsion work. To embed these works in the context of the flow behavior of other structured fluids, we also discuss briefly the related non-local flow modeling attempts as one of the approaches that has been used successfully in describing emulsion flow properties and other materials.
1. Introduction
The mechanical behavior of fluids with an embedded “granular” phase is varied and complex [1–9]. Think of a wet sandy beach or foamy chocolate mousse. These materials are a bit elastic, but will flow when pushed. Wet sand will be hard enough to make a beach volleyball bounce, but the bubble packing in chocolate mousse can be easily swallowed. The overlap in phenomenology of these systems suggests that there exist concepts shared among all these materials. Think of the flow behavior of mayonnaise, a mixture of oil droplets in water. Such dense emulsions are highly viscous and even a bit elastic: they are so-called “yield stress” fluids and only flow when they are exposed to a stress above a certain level. All these systems have similarities that suggest underlying commonalities. We review here some experimental and modeling work on the slow flow behavior of emulsions, as it can serve as a model system for a wide range of disordered materials that are composed of a mix of a background fluid and particles.
Underlying commonalities are easy to find. For example, it seems intuitive that the flow resistance of a suspension of oil droplets in water increases with a higher volume fraction of oil droplets. The same intuition holds for particulate suspensions, colloidal gels and even foams. Volume fraction is thus an important parameter, but that is only a beginning of understanding. Indeed the viscosity of a hard particle suspension diverges at a particulate volume fraction of about 58% [10], with only recent advances of the understanding of the microscopics of this divergence [11]. Also for emulsions, the debate on the microscopic origin and the non-linear, even “critical” nature of the viscous or elastic behavior has been running for decades [12–17]. While the understanding of the micro-macro link in specific systems is progressing substantially, it seems fair to state that a perspective that connects these dots is still beyond the state of the art.
The flow behavior of structured fluids can be considered on the scale of particle contact time. When driving a sample of a structured fluid very slowly and at high volume fraction, interactions between particles are long-lived and the material acts as a solid. When driving a structured fluid at higher rates and/or lower densities, particle interactions are collision-like and short. When interactions are short lived, the material behavior typically obtains a rate dependence: inertia, collisions or the viscosity of the continuous phase starts to play a role. Note that dynamic shear thickening studies [18–21] show that even fast flowing suspensions can form long lived contacts between particles under certain conditions. Here, we will only consider flowing emulsions with long-lived contacts.
The richness in macroscopic flow behavior of structured fluids with long lived contacts is complemented with a diversity of their microscopic behavior. Many structured fluids display localized “plastic” reorganizing events when deformed [22–25]. Highly viscous or “glassy” flows induce non-thermal noise on the motion of their particulate content, non-Brownian diffusive particle dynamics and “dynamical heterogeneities” [26, 27]. In fluids that display “shear jamming,” highly anisotropic structural force features emerge [28–30]. The behavior of disordered fluids is extremely rich, and the references here cannot do justice to efforts from the past decades to try to capture the behavior of these systems. Experiments are evidently easier at lower rates and for emulsions not complicated by the dynamics of droplet rupture [31]. We therefore limit ourselves here to review the literature on slow emulsion flows. Emulsions are also a good model system because they are experimentally accessible: for most emulsions, droplets can be observed via standard microscopy techniques in a wide range of conditions. Additionally, emulsions have a number of physico-chemical ingredients that allows one to tune their microscopic and macroscopic properties.
2. Slow Flows
The most common way to describe the flow behavior of emulsions and other structured fluids is the phenomenological Herschel-Bulkley (HB) model [32, 33]:
Here, σHB denotes the shear stress, σ0 the yield stress, the local shear rate, k a proportionality constant representing some time scale [33] and n a power law index. The HB model effectively captures the macroscopic flow response of many systems [8, 16, 33–38]. In the slow flow limit, HB materials should therefore not display any motion when stress at which they are locally driven is below the yield stress. One might even naively argue that it is only the microscopic interactions that determine the yield stress value. Experiments have shown otherwise. Dense emulsions confined to a narrow flow geometry display flow in regions of the channel where they are exposed to a stress below their yield stress [39–41]. Observing such slow creeping flow behavior was not new; it had for example been observed for granular materials [42, 43] and metals [44, 45]. For emulsions it turns out to be possible to develop a so-called non-local or gradient continuum model that quantitatively captures the slow flow behavior [39, 40]. A “local” constitutive relation (e.g., for steady shear flow) describes the shear stress at a point in space as a function of the shear rate at the same point. In a non-local model, the constitutive relation also depends on spatial gradients of the stress and/or shear rate. Dimensional analysis alone will convince the reader that such a model must introduce coefficients with units of length. In this sense non-local models “know” about the size of microstructural features to which local models are blind. Gradient terms in a constitutive relation can be introduced phenomenologically, without an underlying microstructural model. And indeed there exists an extensive literature on empirical gradient and non-local flow models, largely developed by the engineering community. Recent work on emulsions and related yield stress fluids, however, has advanced hand-in-hand with a specific microscopic picture of how non-local effects emerge. Namely, plastic rearrangements are presumed to propagate mechanical noise, by which subsequent rearrangements can be triggered. The “kinetic elasto-plastic” model (KEP) [9, 46–49] is a prominent example of this approach. It should be noted however, that other modeling attempts also effectively capture the flow behavior of emulsions, such as lattice Boltzmann methods [50–52].
2.1. KEP at a Glance
The KEP perspective assumes that local flow behavior captured by the local dimensionless spatial velocity gradient also called shear rate , is determined by the rate at which local buildup of elastic stress dissipates via small “plastic events.” The intuitive picture is that such local plastic events in a flowing region can induce stress modifications at a finite length scale ξ away from these events, via the propagation of mechanical fluctuations. Such fluctuations can so induce rearrangements in regions of the materials where the local stress is below the yield stress. See Figure 1A for a sketch. This rearrangement perspective was made quantitative [48] by rewriting the Newtonian relation between the local shear force σ(r) at position r and the local flow rate via the concept of viscosity , with η the fluid viscosity. In a conventional Newtonian fluid η is a material parameter. In the KEP perspective, we want to capture the elastic nature of the complex fluid, but we also want to incorporate the plastic flow that occurs when we impose the existence of a local flow with, say, a moving boundary. We hence write that the local shear stress σ in a fluid is related to the rate of local plastic events. This plastic event rate is assumed to be proportional to the local shear rate and the so-called local “fluidity” f(r) through the relation . The fluidity f is thus an inverse viscosity, with the key distinction that fluidity is a field rather than a material constant. To determine the form of this field, it is necessary to describe its spatial evolution. To do this, one defines the “bulk” fluidity
that is obtained in homogeneous flow conditions. Local deviations from the bulk fluidity are then assumed to obey a diffusion equation
We readily see that the existence of a local finite fluidity diffuses into neighboring regions with a typical length scale ξ; having a finite local flow rate somewhere will thus induce flow elsewhere. The length scale ξ so captures the cooperativity between different flowing regions. In slow flows, the yield stress is approached from below, whence ξ depends on the distance to the yield stress σ0 of the fluid [48, 55]. The expression for ξ comes in a few forms in the literature; one common one is . The constants A, σ0 are all material parameters; their dependence on microscopic physics such as the friction coefficient μ or the volume fraction ϕ are not very clear, although it is believed that A is induced by steric hindrance effects [56]. Parameter d is a typical particle size. The exponent m is explicitly predicted when certain assumptions are made regarding the microscopics [48] but was also empirically determined to be 0.5−0.6 in a generalized fluidity model applied to granular flows [55, 57]. For confined frictionless emulsions, ξ was empirically found to depend on the volume fraction ϕ of the emulsion [39]. Cooperative effects are also present in complex fluids without a yield stress, albeit with a length scale that remains on the order of the particle size [58]. Several references here have already indicated that the generalization of this KEP based non-local modeling to granular flows is also possible both in two and three dimensions [38, 55, 59] including subtle “secondary rheology” effects [60]. Even wormlike micellar fluids [61] and cellulose solutions [62] have been effectively captured with gradient type models, and metal plasticity has for some time been described with gradient type models [63]. In the light of the phenomenological diversity, it is all the more exciting that there might be cross-fertilization possible in the understanding of complex disordered fluids, a process that is already ongoing [9].
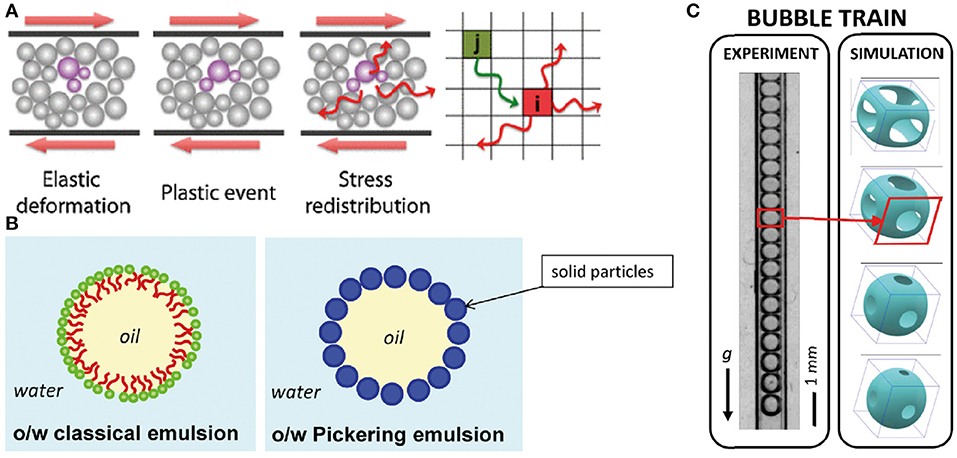
Figure 1. (A) The canonical kinetic elasto-plastic perspective in which induced flow generates non-local structural changes. From Bocquet et al. [48]. (B) Schematic of surfactant and particle stabilized oil in water (o/w) emulsions. From Chevalier and Bolzinger [53]. (C) Evidence for multiple contact dynamics in a simple train of bubbles. From Ginot et al. [54].
2.2. Flow Instabilities
It should be noted that the HB description of structured fluids is not always applicable. Suspensions of soft frictional particles have an effective friction coefficient that can get smaller with rate [64]. Such flow instabilities have been observed in multiple systems [65, 66] but were then linked to shear-induced weakening: the shear induces so much fluctuations that the yield stress is affected, even creating an additional critical point [67]. These experimental observations suggest that both microscopic interactions and fluctuations play a role in the flow behavior of structured fluids. The question is how to incorporate such microscopics in the non-local models that already exist. Finding the link between microscopics and non-local modeling link is challenging for several reasons, especially because of the central role of friction.
3. Microscopic interactions
Experiments on disordered fluids [28, 68], discrete element simulations [18, 69], and modeling [70] suggest that flow complexity in disordered fluids arises from the multitude of interparticle forces. For emulsions, the role of the many microscopic ingredients that determine the flow behavior has been captured in the review by Höhler and Cohen-Addad [33], such as interfacial energy, capillary pressure, long range molecular interactions, entropic effects and interfacial rheology; different surfactants can for example change the exponent n in the fast flow limit. However, it is not clear how the critical yield stress σ0, the main ingredient for the length scale ξ, arises from the microscopic physics [33]. The amplitude parameter A in the fluidity model for emulsions is currently a fit parameter whose physical meaning is not well-understood. Which microscopic mechanisms are responsible for these model parameters? There are many options; interparticle friction may be considered a player. Friction is conjectured to be at the heart of shear jamming [28], discontinuous shear thickening [18, 68], the viscosity divergence of hard sphere suspensions [11] and related to criticality in fluctuating granular flows [67].
3.1. The Many Faces of Friction
Friction is a phenomenon in which many lengths and time scales are relevant [71]. Contact friction is traditionally modeled with Amonton-Coulomb's law [72], which states that the frictional force FT tangential to a contact FT ≤ μFN is less than or equal to a fraction μ of the normal force FN on that contact. However, contact roughness, lubrication and elasticity complicate this perspective. The Stribeck curve [73, 74] summarizes much empirical work on lubricated friction; it indicates that the effective friction coefficient of a lubricated contact is rate dependent and can vary over orders of magnitude. There is also a role for contact elasticity coupled to to hydrodynamic effects [75–77] with roots in older work [78, 79]. Additionally, rate dependence in the contact laws is often observed [71], for example logarithmic strengthening [80, 81]. These complications make it challenging to model friction in standard numerical methods: frictional contacts often involve length scales much smaller than the particle diameter and time scales much shorter than a collisional contact time, presenting immediate challenges for the complete integration of their dynamics in numerical simulations. The relevance of such small lengthscales for slow collective particle dynamics is however evidenced by several works [26, 82].
In emulsions, the contact forces between two fluid droplets are expected to be purely viscous and vanish in the slow flow limit. However, even foams, consisting entirely out of fluids, are known to be very much affected by the friction between the foam bubbles [5]. For droplets in emulsions, very similar considerations hold [33]: emulsion droplets are usually stabilized against coalescence with small molecular surfactants, proteins or particles. The last case is also known as a Pickering emulsion [53]. See Figure 1B for a sketch. These ingredients add substantial complexity to the dynamics of two droplets rubbing against each other [83]. Amphiphilics are well-known to have complex phase behavior [84] at an interface. Droplets fully coated with surfactants of macromolecular or particulate nature are believed to have a yield stress [85]; emulsions can even be coated with colloidal particles [86], or the chemical composition of the interface can be modified to change interfacial mechanics [87] and the contact friction [88, 89]. In fact the mechanics of interfaces packed with particles has non-trivial dynamics of itself [90]. Interface mechanics may so provide emulsion droplet contacts with a static yield criterion, however small.
To illustrate the complexity of friction in structured fluids studies, it is helpful to consider that at the same time, numerous simulations have shown that even when one sets the interparticle friction coefficient to zero, the macroscopic friction coefficient of a structured fluid remains finite [91–94]. Even though numerical simulations of comparable systems have found contradicting relationships between the microscopic and macroscopic friction coefficient [93–95], the emergence of a non-zero macroscopic friction coefficient, where microscopically it is negligible, has been been confirmed in experiments [64]. Non-sphericity can further complicate the relation between the microscopic contact laws and the emergent frictional properties [92] but should be less important in slowly sheared emulsions, as the Laplace pressure will keep droplets in emulsions mostly spherical. The question remains: what is the role of friction, and other microscopic particle interactions, on the flow behavior of a structured fluids?
4. Fluctuations
KEP models rely on some form of “fluctuation” to propagate elastic events through a disordered medium, so fluctuations are also an ingredient that needs to be integrated in non-local modeling. In fact, particle velocities arising from thermal motion are a main ingredient of the kinetic part of the Irving-Kirkwood stress tensor and hence also a likely ingredient for any continuum theory that describes flow behavior of structured fluids. However, the particles in the dense structured fluids we discuss here do not show intrinsic thermal motion, in part because of their dissipative interactions. We should then note that microstructural disorder itself is already enough to cause ballistic-like diffusive motion in quasi-static flow [96], and additional velocity fluctuations at finite shear rates are thus to be expected. Particle velocity fluctuations are created in the presence of a mean flow itself and are generally quantified by the square of the RMS velocity fluctuations, but can also be based on breaking contacts [49]. The velocity fluctuations can be seen to represent the number of plastic events per unit of time. Such particle velocity fluctuation based “granular temperature” concepts have indeed been used since a long time [42, 97]. Hard particle simulations [98] suggest that the local velocity fluctuations with respect to the mean flow field are responsible for the fluidity field in the creep flow of granular materials driven below their yield stress. Emulsion flow experiments have provided a direct link between these velocity fluctuations and the fluidity field [99]. Even in the fast flow limit, flow induced velocity fluctuations have been observed to capture flow behavior in a range of geometries rather well [100].
The coupling of mean flow to velocity fluctuations depends on many microscopic parameters, including damping and interparticle friction. In the “emulsion” limit, where friction is low and rate dependent, one can expect different HB exponents than in dry granular materials, where friction is often assumed to be rate independent [15]. The value of the dry friction coefficient does not significantly affect the HB model [56] although in the limit of zero friction, the macroscopic friction remains finite as discussed above. This suggests that dissipation in structured fluids emerges from non-frictional sources such as velocity fluctuations. The coupling of the mean flow and its fluctuations also gives rise to different types of fluctuations [15, 101]. One might also believe that viscous damping suppresses the coupling between mean flow and fluctuations and the associated self-induced weakening, but the viscous damping needs to be strong enough: glass bead suspensions with water also show a logarithmic negative rate dependence [64]. Emulsions can also be composed of droplets that are smaller than a micrometer. For such emulsions, thermal fluctuations are large enough to affect droplet motion. It is not clear how thermal and mechanical noise are different in the way they affect the flow behavior of emulsions [9].
5. Challenges and opportunities
5.1. Anisotropy
The KEP fluidity based modeling for emulsions and other disordered fluids has a particularly obvious area for innovation. In many rheological experiments on sheared colloidal systems and granular media, structural anisotropy is important variable [28–30, 64, 91, 102, 102–108], e.g., the emergence of dilatancy [29, 109] and even in finite size frictionless systems [110]. Finding how anisotropy emerges from microscopics is an important next step to understand emulsion rheology. Such understanding should assist KEP advances: although the soft glassy rheology model has been extended into tensorial form [111] and KEP based granular flow modeling [55] has been successfully used to model three dimensional flows, anisotropy in either force or packing microstructure, is currently not a feature of KEP-based models.
5.2. Multiple Contacts
When emulsions have a yield stress, individual droplets will have multiple contacts. The pairwise interactions of droplets typically determined by the Laplace pressure induced by local surface curvature will therefore likely change. Such multiple contact dynamics has already been observed in foams [54, 112] (See Figure 1C) and soft granular materials [113–115] and is even considered to play a role in molecular systems [116]. These multiple contact effects act over lenghtscales larger than the particle diameter and thus bring long range correlations. Even though multiple contact dynamics has been shown to be relevant for static packings, it is not clear if or how such long range interactions are relevant during flow and/or for KEP style modeling approaches.
5.3. Experimental Perspectives
The fluidity requires knowledge of both local shear rates and the local stress dynamics. To link interparticle forces to fluidity, we must thus be able to probe fluidity-related variables inside a moving disordered fluid. This is challenging in experiments. Particle tracking will reveal spatial dynamics in packing microstructure, but this is not trivially connected to stress microstructure, due to the small deformations in emulsion droplets and the indeterminacy of frictional forces. Microstructure of stress evolution can be probed directly using particles that change their optical response under the influence of stress; however, this has only been probed in granular quasi-static experiments with no control or knowledge on boundary stresses [102, 117] and such techniques are not easily extended to emulsions. In emulsions, only full particle shape measurement experiments in dynamic conditions can reveal interparticle forces, yet this has so far only been done in flowing two dimensional emulsions [118, 119] and static packings [120, 121].
The relevance of microscopic interactions also provides new areas for experimental progress, for example for probing the role of friction. Friction is difficult to tune as a parameter in most disordered fluid experiments, especially with solid particles, where friction is complex as mentioned above. Moreover, most solid-solid friction coefficients are limited to a range of 0.05 and 1 [122]; numerical studies suggest that it is necessary to probe coefficients an order of magnitude lower [123, 124] to study the effect of friction. Typically, experimental studies that directly probe the relevance of macroscopic friction do not control friction but concern how a change in flow behavior can be linked to post-hoc observations of surface roughness [82, 125]. There have been many innovative studies on complex fluids with micron sized particles [16, 90, 126–128]. Despite the often sophisticated nature of these studies, the microstructural interactions between employed particles are a given, not a control parameter. When lowering the friction coefficient for hard particles is not an option, one can also increase it. To raise μ, changing particle shape [92] effectively increases the friction coefficients. Similarly, using surface bumpiness is also an effective numerical route to increase interparticle friction [124, 129], which has now also been used in experiments [130]. Some of these methods are available for emulsions as well: there are many surfactants and continuous phase fluids that one can choose to tune the interparticle dissipation. With control over microscopics, one future experiment would be to probe local stress and flow fields at fixed driving rate while directly varying μ.
6. Conclusion and Outlook
Continuum modeling of structured fluids in general and emulsions in particular has revealed the importance of the so-called non-local fluidity of the structured fluid, a dynamical order parameter equivalent to an inverse viscosity. Fluidity based modeling works, yet many questions remain unanswered. The major missing piece in our understanding of these complex “glassy” fluids is the connection between the “fluidity” and microscopic physics, such as particle interactions and fluctuations. Finding the connection between microscopics and the fluidity parameter would be a big leap forward in our understanding of these complex, glassy, disordered fluids.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
Funding from NWO IPP Program Controlling Multiphase Flow with program number 680-91-012 is gratefully acknowledged. This article was written during a research visit at the Naval Postgraduate School in Monterey, CA made possible by Office of Naval Research Global Visiting Scientist Program VSP 19-7-001.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Discussions with Brian Tighe have been very clarifying in all stages of the preparation of this manuscript and are gratefully acknowledged.
References
1. Forterre Y, Pouliquen O. Flows of dense granular media. Annu Rev Fluid Mech. (2008) 40:1–24. doi: 10.1146/annurev.fluid.40.111406.102142
2. Liu AJ, Nagel SR. The jamming transition and the marginally jammed solid. Annu Rev Cond Matt Phys. (2010) 1:347–69. doi: 10.1146/annurev-conmatphys-070909-104045
3. Van Hecke M. Jamming of soft particles: geometry, mechanics, scaling and isostaticity. J Phys Cond Matt. (2010) 22:033101. doi: 10.1088/0953-8984/22/3/033101
4. Brown E, Jaeger H. Shear thickening in concentrated suspensions: phenomenology, mechanisms and relations to jamming. Rep Prog Phys. (2014) 77:046602. doi: 10.1088/0034-4885/77/4/046602
5. Cohen-Addad S, Höhler R, Pitois O. Flow in foams and flowing foams. Annu Rev Fluid Mech. (2013) 45:241–67. doi: 10.1146/annurev-fluid-011212-140634
6. Denn MM, Morris JF. Rheology of non-Brownian suspensions. Annu Rev Chem Biomol Eng. (2014) 5:203–28. doi: 10.1146/annurev-chembioeng-060713-040221
7. Bonn D, Denn MM, Berthier L, Divoux T, Manneville S. Yield stress materials in soft condensed matter. Rev Modern Phys. (2017) 89:035005. doi: 10.1103/RevModPhys.89.035005
8. Vlassopoulos D, Cloitre M. Tunable rheology of dense soft deformable colloids. Curr Opin Coll Interface Science. (2014) 19:561–74. doi: 10.1016/j.cocis.2014.09.007
9. Nicolas A, Ferrero EE, Martens K, Barrat JL. Deformation and flow of amorphous solids: Insights from elastoplastic models. Rev Modern Phys. (2018) 90:045006. doi: 10.1103/RevModPhys.90.045006
10. Krieger IM, Dougherty TJ. A mechanism for non-Newtonian flow in suspensions of rigid spheres. J Rheol. (1959) 3:137–52. doi: 10.1122/1.548848
11. Boyer F, Guazzelli É, Pouliquen O. Unifying suspension and granular rheology. Phys Rev Lett. (2011) 107:188301. doi: 10.1103/PhysRevLett.107.188301
13. Olsson P, Teitel S. Critical scaling of shear viscosity at the jamming transition. Phys Rev Lett. (2007) 99:178001. doi: 10.1103/PhysRevLett.99.178001
14. Katgert G, Möbius ME, van Hecke M. Rate dependence and role of disorder in linearly sheared two-dimensional foams. Phys Rev Lett. (2008) 101:058301. doi: 10.1103/PhysRevLett.101.058301
15. Tighe BP, Woldhuis E, Remmers JJC, van Saarloos W, van Hecke M. Model for the scaling of stresses and fluctuations in flows near jamming. Phys Rev Lett. (2010) 105:088303. doi: 10.1103/PhysRevLett.105.088303
16. Paredes J, Michels MA, Bonn D. Rheology across the zero-temperature jamming transition. Phys Rev Lett. (2013) 111:015701. doi: 10.1103/PhysRevLett.111.015701
17. Goodrich CP, Liu AJ, Nagel SR. Solids between the mechanical extremes of order and disorder. Nat Phys. (2014) 10:578–81. doi: 10.1038/nphys3006
18. Seto R, Mari R, Morris JF, Denn MM. Discontinuous shear thickening of frictional hard-sphere suspensions. Phys Rev Lett. (2013) 111:218301. doi: 10.1103/PhysRevLett.111.218301
19. Comtet J, Chatté G, Niguès A, Bocquet L, Siria A, Colin A. Pairwise frictional profile between particles determines discontinuous shear thickening transition in non-colloidal suspensions. Nat Commun. (2017) 8:15633. doi: 10.1038/ncomms15633
20. Fall A, Huang N, Bertrand F, Ovarlez G, Bonn D. Shear thickening of cornstarch suspensions as a reentrant jamming transition. Phys Rev Lett. (2008) 100:018301. doi: 10.1103/PhysRevLett.100.018301
21. Brown E, Jaeger HM. Dynamic jamming point for shear thickening suspensions. Phys Rev Lett. (2009) 103:086001. doi: 10.1103/PhysRevLett.103.086001
22. Durian DJ. Foam Mechanics at the Bubble Scale. Phys Rev Lett. (1995) 75:4780–3. doi: 10.1103/PhysRevLett.75.4780
23. Schall P, Weitz DA, Spaepen F. Structural rearrangements that govern flow in colloidal glasses. Science. (2007) 318:1895–9. doi: 10.1126/science.1149308
24. Maloney CE, Lemaître A. Amorphous systems in athermal, quasistatic shear. Phys Rev E. (2006) 74:016118. doi: 10.1103/PhysRevE.74.016118
25. Schoenholz SS, Cubuk ED, Sussman DM, Kaxiras E, Liu AJ. A structural approach to relaxation in glassy liquids. Nat Phys. (2016) 12:469–71. doi: 10.1038/nphys3644
26. Lechenault F, Dauchot O, Biroli G, Bouchaud JP. Critical scaling and heterogeneous superdiffusion across the jamming/rigidity transition of a granular glass. EPL. (2008) 83:46003. doi: 10.1209/0295-5075/83/46003
27. Plagge J, Heussinger C. Melting a granular glass by cooling. Phys Rev Lett. (2013) 110:078001. doi: 10.1103/PhysRevLett.110.078001
28. Bi D, Zhang J, Chakraborty B, Behringer R. Jamming by shear. Nature. (2011) 480:355–8. doi: 10.1038/nature10667
29. Ren J, Dijksman JA, Behringer RP. Reynolds pressure and relaxation in a sheared granular system. Phys Rev Lett. (2013) 110:018302. doi: 10.1103/PhysRevLett.110.018302
30. Wandersman E, Van Hecke M. Nonlocal granular rheology: Role of pressure and anisotropy. EPL (2014) 105:24002. doi: 10.1209/0295-5075/105/24002
31. Taylor GI. The formation of emulsions in definable fields of flow. Proc R Soc Lond A. (1934) 146:501–23. doi: 10.1098/rspa.1934.0169
32. Herschel WH, Bulkley R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid Zeitschrift. (1926) 39:291–300. doi: 10.1007/BF01432034
33. Höhler R, Cohen-Addad S. Rheology of foams and highly concentrated emulsions. Curr Opin Coll Interface Sci. (2014) 19:536–48. doi: 10.1016/j.cocis.2014.11.003
34. Jop P, Forterre Y, Pouliquen O. A constitutive law for dense granular flows. Nature. (2006) 441:727–30. doi: 10.1038/nature04801
35. Dinkgreve M, Paredes J, Michels M, Bonn D. Universal rescaling of flow curves for yield-stress fluids close to jamming. Phys Rev E. (2015) 92:012305. doi: 10.1103/PhysRevE.92.012305
36. Dijksman JA, Wandersman E, Slotterback S, Berardi CR, Updegraff WD, van Hecke M, et al. From frictional to viscous behavior: three-dimensional imaging and rheology of gravitational suspensions. Phys Rev E. (2010) 82:060301. doi: 10.1103/PhysRevE.82.060301
37. Kawasaki T, Coslovich D, Ikeda A, Berthier L. Diverging viscosity and soft granular rheology in non-Brownian suspensions. Phys Rev E. (2015) 91:012203. doi: 10.1103/PhysRevE.91.012203
38. Bouzid M, Trulsson M, Claudin P, Clément E, Andreotti B. Nonlocal rheology of granular flows across yield conditions. Phys Rev Lett. (2013) 111:238301. doi: 10.1103/PhysRevLett.111.238301
39. Goyon J, Colin A, Ovarlez G, Ajdari A, Bocquet L. Spatial cooperativity in soft glassy flows. Nature. (2008) 454:84–7. doi: 10.1038/nature07026
40. Goyon J, Colin A, Bocquet L. How does a soft glassy material flow: finite size effects, non local rheology, and flow cooperativity. Soft Matter. (2010) 6:2668–78. doi: 10.1039/c001930e
41. Katgert G, van Hecke M. Jamming and geometry of two-dimensional foams. EPL. (2010) 92:34002. doi: 10.1209/0295-5075/92/34002
42. Komatsu TS, Inagaki S, Nakagawa N, Nasuno S. Creep motion in a granular pile exhibiting steady surface flow. Phys Rev Lett. (2001) 86:1757–60. doi: 10.1103/PhysRevLett.86.1757
43. Crassous J, Metayer JF, Richard P, Laroche C. Experimental study of a creeping granular flow at very low velocity. J Stat Mech. (2008) 2008:P03009. doi: 10.1088/1742-5468/2008/03/P03009
44. Andrade ENC. On the viscous flow in metals, and allied phenomena. Proc R Soc Lond A. (1910) 84:1–12.
45. Andrade ENdC. The flow in metals under large constant stresses. Proc R Soc Lond A. (1914) 90:329–42. doi: 10.1098/rspa.1914.0056
46. Sollich P, Lequeux F, Hébraud P, Cates ME. Rheology of soft glassy materials. Phys Rev Lett. (1997) 78:2020. doi: 10.1103/PhysRevLett.78.2020
47. Hébraud P, Lequeux F. Mode-coupling theory for the pasty rheology of soft glassy materials. Phys Rev Lett. (1998) 81:2934. doi: 10.1103/PhysRevLett.81.2934
48. Bocquet L, Colin A, Ajdari A. Kinetic theory of plastic flow in soft glassy materials. Phys Rev Lett. (2009) 103:036001. doi: 10.1103/PhysRevLett.103.036001
49. Mansard V, Colin A, Chaudhuri P, Bocquet L. A molecular dynamics study of non-local effects in the flow of soft jammed particles. Soft Matter. (2013) 9:7489–500. doi: 10.1039/c3sm50847a
50. Jansen F, Harting J. From bijels to pickering emulsions: a lattice Boltzmann study. Phys Rev E. (2011) 83:046707. doi: 10.1103/PhysRevE.83.046707
51. Benzi R, Sbragaglia M, Succi S, Bernaschi M, Chibbaro S. Mesoscopic lattice Boltzmann modeling of soft-glassy systems: theory and simulations. J Chem Phys. (2009) 131:104903. doi: 10.1063/1.3216105
52. Dollet B, Scagliarini A, Sbragaglia M. Two-dimensional plastic flow of foams and emulsions in a channel: experiments and lattice Boltzmann simulations. J Fluid Mech. (2015) 766:556–89. doi: 10.1017/jfm.2015.28
53. Chevalier Y, Bolzinger MA. Emulsions stabilized with solid nanoparticles: pickering emulsions. Coll Surf A Physicochem Eng Aspects. (2013) 439:23–34. doi: 10.1016/j.colsurfa.2013.02.054
54. Ginot G, Höhler R, Mariot S, Kraynik A, Drenckhan W. Juggling bubbles in square capillaries: an experimental proof of non-pairwise bubble interactions. Soft Matter. (2019) 15:4570–82. doi: 10.1039/C8SM02477D
55. Henann DL, Kamrin K. A predictive, size-dependent continuum model for dense granular flows. Proc Natl Acad Sci USA. (2013) 110:6730–5. doi: 10.1073/pnas.1219153110
56. Kamrin K, Koval G. Effect of particle surface friction on nonlocal constitutive behavior of flowing granular media. Comput Part Mech. (2014) 1:169–76. doi: 10.1007/s40571-014-0018-3
57. Tang Z, Brzinski TA, Shearer M, Daniels KE. Nonlocal rheology of dense granular flow in annular shear experiments. Soft Matter. (2018) 14:3040–8. doi: 10.1039/C8SM00047F
58. Saitoh K, Tighe BP. Nonlocal effects in inhomogeneous flows of soft athermal disks. Phys Rev Lett. (2019) 122:188001. doi: 10.1103/PhysRevLett.122.188001
59. Kamrin K, Koval G. Nonlocal constitutive relation for steady granular flow. Phys Rev Lett. (2012) 108:178301. doi: 10.1103/PhysRevLett.108.178301
60. Henann DL, Kamrin K. Continuum modeling of secondary rheology in dense granular materials. Phys Rev Lett. (2014) 113:178001. doi: 10.1103/PhysRevLett.113.178001
61. Masselon C, Salmon JB, Colin A. Nonlocal effects in flows of wormlike micellar solutions. Phys Rev Lett. (2008) 100:038301. doi: 10.1103/PhysRevLett.100.038301
62. De Kort DW, Veen SJ, Van As H, Bonn D, Velikov KP, Van Duynhoven JP. Yielding and flow of cellulose microfibril dispersions in the presence of a charged polymer. Soft Matter. (2016) 12:4739–44. doi: 10.1039/C5SM02869H
63. Aifantis EC. On the role of gradients in the localization of deformation and fracture. Int J Eng Sci. (1992) 30:1279–99. doi: 10.1016/0020-7225(92)90141-3
64. Workamp M, Dijksman JA. Contact tribology also affects the slow flow behavior of granular emulsions. J Rheol. (2019) 63:275–83. doi: 10.1122/1.5066438
65. Lu K, Brodsky E, Kavehpour H. Shear-weakening of the transitional regime for granular flow. J Fluid Mech. (2007) 587:347–72. doi: 10.1017/S0022112007007331
66. Dijksman JA, Wortel GH, van Dellen LTH, Dauchot O, van Hecke M. Jamming, yielding, and rheology of weakly vibrated granular media. Phys Rev Lett. (2011) 107:108303. doi: 10.1103/PhysRevLett.107.108303
67. Wortel G, Dauchot O, van Hecke M. Criticality in vibrated frictional flows at a finite strain rate. Phys Rev Lett. (2016) 117:198002. doi: 10.1103/PhysRevLett.117.198002
68. Chatté G, Comtet J, Niguès A, Bocquet L, Siria A, Ducouret G, et al. Shear thinning in non-Brownian suspensions. Soft Matter. (2018) 14:879–93. doi: 10.1039/C7SM01963G
69. Ikeda A, Berthier L, Sollich P. Unified study of glass and jamming rheology in soft particle systems. Phys Rev Lett. (2012) 109:018301. doi: 10.1103/PhysRevLett.109.018301
70. Wyart M, Cates M. Discontinuous shear thickening without inertia in dense non-Brownian suspensions. Phys Rev Lett. (2014) 112:098302. doi: 10.1103/PhysRevLett.112.098302
71. Muser MH, Urbakh M, Robbins MO. Statistical mechanics of static and low-velocity kinetic friction. Adv Chem Phys. (2003) 126:187–272. doi: 10.1002/0471428019.ch5
72. Amontons G. Remarques et Experiences Phisiques sur la Construction d'une Nouvelle Clepsidre, sur les Barometres, Termometres, & Higrometres. Paris: Chez Jean Jombert (1695).
74. Yoshitake T. Amontons' first experiment on friction - Looking back on 300 years of tribology. J Jpn Soc Tribol. (1999) 44:111–4.
75. Skotheim J, Mahadevan L. Soft lubrication. Phys Rev Lett. (2004) 92:245509. doi: 10.1103/PhysRevLett.92.245509
76. Gong JP. Friction and lubrication of hydrogels - its richness and complexity. Soft Matter. (2006) 2:544–52. doi: 10.1039/B603209P
77. Dunn AC, Sawyer WG, Angelini TE. Gemini interfaces in aqueous lubrication with hydrogels. Tribol Lett. (2014) 54:59–66. doi: 10.1007/s11249-014-0308-1
79. Archard JF. Elastic deformation and the Laws of Friction. Proc R Soc Lond A. (1957) 243:190–205.
81. Baumberger T, Caroli C. Solid friction from stick-slip down to pinning and aging. Adv Phys. (2006) 55:279–348. doi: 10.1080/00018730600732186
82. Schröter M, Goldman DI, Swinney HL. Stationary state volume fluctuations in a granular medium. Phys Rev E. (2005) 71:030301. doi: 10.1103/PhysRevE.71.030301
83. Bressy L, Hebraud P, Schmitt V, Bibette J. Rheology of emulsions stabilized by solid interfaces. Langmuir. (2003) 19:598–604. doi: 10.1021/la0264466
84. Chapman D, Urbina J, Keough KM. Biomembrane phase transitions studies of lipid-water systems using differential scanning calorimetry. J Biol Chem. (1974) 249:2512–21.
85. Sagis LM, Fischer P. Nonlinear rheology of complex fluid–fluid interfaces. Curr Opin Coll Interface Sci. (2014) 19:520–9. doi: 10.1016/j.cocis.2014.09.003
86. Rose S, Prevoteau A, Elzière P, Hourdet D, Marcellan A, Leibler L. Nanoparticle solutions as adhesives for gels and biological tissues. Nature. (2013) 505:382–5. doi: 10.1038/nature12806
87. Dollet B, Marmottant P, Garbin V. Bubble dynamics in soft and biological matter. Annu Rev Fluid Mech. (2019) 51:331–55. doi: 10.1146/annurev-fluid-010518-040352
88. de Beer S. Switchable friction using contacts of stimulus-responsive and nonresponding swollen polymer brushes. Langmuir. (2014) 30:8085–90. doi: 10.1021/la5013473
89. de Beer S, Kutnyanszky E, Schön PM, Vancso GJ, Müser MH. Solvent-induced immiscibility of polymer brushes eliminates dissipation channels. Nat Commun. (2014) 5:3781. doi: 10.1038/ncomms4781
90. Cicuta P, Stancik EJ, Fuller GG. Shearing or compressing a soft glass in 2D: time-concentration superposition. Phys Rev Lett. (2003) 90:236101. doi: 10.1103/PhysRevLett.90.236101
91. Peyneau PE, Roux JN. Frictionless bead packs have macroscopic friction, but no dilatancy. Phys Rev E. (2008) 78:011307. doi: 10.1103/PhysRevE.78.011307
92. Azema É, Radjai F, Saussine G. Quasistatic rheology, force transmission and fabric properties of a packing of irregular polyhedral particles. MechMat. (2009) 41:729–41. doi: 10.1016/j.mechmat.2009.01.021
93. Chialvo S, Sun J, Sundaresan S. Bridging the rheology of granular flows in three regimes. Phys Rev E. (2012) 85:021305. doi: 10.1103/PhysRevE.85.021305
94. Trulsson M, DeGiuli E, Wyart M. Effect of friction on dense suspension flows of hard particles. Phys Rev E. (2017) 95:012605. doi: 10.1103/PhysRevE.95.012605
95. Gallier S, Lemaire E, Peters F, Lobry L. Rheology of sheared suspensions of rough frictional particles. J Fluid Mech. (2014) 757:514–49. doi: 10.1017/jfm.2014.507
96. Li W, Rieser JM, Liu AJ, Durian DJ, Li J. Deformation-driven diffusion and plastic flow in amorphous granular pillars. Phys Rev E. (2015) 91:062212. doi: 10.1103/PhysRevE.91.062212
97. Losert W, Bocquet L, Lubensky T, Gollub JP. Particle dynamics in sheared granular matter. Phys Rev Lett. (2000) 85:1428. doi: 10.1103/PhysRevLett.85.1428
98. Zhang Q, Kamrin K. Microscopic description of the granular fluidity field in nonlocal flow modeling. Phys Rev Lett. (2017) 118:058001. doi: 10.1103/PhysRevLett.118.058001
99. Jop P, Mansard V, Chaudhuri P, Bocquet L, Colin A. Microscale rheology of a soft glassy material close to yielding. Phys Rev Lett. (2012) 108:148301. doi: 10.1103/PhysRevLett.108.148301
100. Pähtz T, Durán O, de Klerk DN, Govender I, Trulsson M. Local rheology relation with variable yield stress ratio across dry, wet, dense, and dilute granular flows. Phys Rev Lett. (2019) 123:048001. doi: 10.1103/PhysRevLett.123.048001
101. Radjai F, Roux S. Turbulentlike fluctuations in quasistatic flow of granular media. Phys Rev Lett. (2002) 89:064302. doi: 10.1103/PhysRevLett.89.064302
102. Majmudar TS, Behringer RP. Contact force measurements and stress-induced anisotropy in granular materials. Nature. (2005) 435:1079–82. doi: 10.1038/nature03805
103. Koumakis N, Laurati M, Egelhaaf S, Brady J, Petekidis G. Yielding of hard-sphere glasses during start-up shear. Phys Rev Lett. (2012) 108:098303. doi: 10.1103/PhysRevLett.108.098303
104. Rothenburg L, Bathurst R. Analytical study of induced anisotropy in idealized granular materials. Geotechnique. (1989) 39:601–14. doi: 10.1680/geot.1989.39.4.601
105. Peyneau PE, Roux JN. Solidlike behavior and anisotropy in rigid frictionless bead assemblies. Phys Rev E. (2008) 78:041307. doi: 10.1103/PhysRevE.78.041307
106. Azéma E, Radjai F. Internal structure of inertial granular flows. Phys Rev Lett. (2014) 112:078001. doi: 10.1103/PhysRevLett.112.078001
107. Azéma É, Radjaï F, Roux JN. Internal friction and absence of dilatancy of packings of frictionless polygons. Phys Rev E. (2015) 91:010202. doi: 10.1103/PhysRevE.91.010202
108. Chacko RN, Mari R, Fielding SM, Cates ME. Shear reversal in dense suspensions: the challenge to fabric evolution models from simulation data. J Fluid Mech. (2018) 847:700–34. doi: 10.1017/jfm.2018.279
109. Tighe BP. Shear dilatancy in marginal solids. Gr Matt. (2014) 16:203–8. doi: 10.1007/s10035-013-0436-6
110. Goodrich CP, Dagois-Bohy S, Tighe BP, van Hecke M, Liu AJ, Nagel SR. Jamming in finite systems: stability, anisotropy, fluctuations, and scaling. Phys Rev E. (2014) 90:022138. doi: 10.1103/PhysRevE.90.022138
111. Cates M, Sollich P. Tensorial constitutive models for disordered foams, dense emulsions, and other soft nonergodic materials. J Rheol. (2004) 48:193–207. doi: 10.1122/1.1634985
112. Höhler R, Cohen-Addad S. Many-body interactions in soft jammed materials. Soft Matter. (2017) 13:1371–83. doi: 10.1039/C6SM01567K
113. Šiber A, Ziherl P. Many-body contact repulsion of deformable disks. Phys Rev Lett. (2013) 110:214301. doi: 10.1103/PhysRevLett.110.214301
114. Brodu N, Dijksman JA, Behringer RP. Spanning the scales of granular materials through microscopic force imaging. Nat Commun. (2015) 6:6361. doi: 10.1038/ncomms7361
115. Brodu N, Dijksman JA, Behringer RP. Multiple-contact discrete-element model for simulating dense granular media. Phys Rev E. (2015) 91:032201. doi: 10.1103/PhysRevE.91.032201
116. Iuchi S, Izvekov S, Voth GA. Are many-body electronic polarization effects important in liquid water? J Chem Phys. (2007) 126:124505. doi: 10.1063/1.2710252
117. Zheng H, Dijksman JA, Behringer RP. Shear jamming in granular experiments without basal friction. EPL. (2014) 107:34005. doi: 10.1209/0295-5075/107/34005
118. Desmond KW, Young PJ, Chen D, Weeks ER. Experimental study of forces between quasi-two-dimensional emulsion droplets near jamming. Soft Matter. (2013) 9:3424–36. doi: 10.1039/c3sm27287g
119. Desmond KW, Weeks ER. Measurement of stress redistribution in flowing emulsions. Phys Rev Lett. (2015) 115:098302. doi: 10.1103/PhysRevLett.115.098302
120. Brujić J, Edwards SF, Hopkinson I, Makse HA. Measuring the distribution of interdroplet forces in a compressed emulsion system. Phys A Stat Mech Appl. (2003) 327:201–12. doi: 10.1016/S0378-4371(03)00477-1
121. Jorjadze I, Pontani LL, Brujic J. Microscopic approach to the nonlinear elasticity of compressed emulsions. Phys Rev Lett. (2013) 110:048302. doi: 10.1103/PhysRevLett.110.048302
122. Weast RC, Astle MJ, Beyer WH. CRC Handbook of Chemistry and Physics, Vol. 69. Boca Raton, FL: CRC Press (1988).
123. Shundyak K, van Hecke M, van Saarloos W. Force mobilization and generalized isostaticity in jammed packings of frictional grains. Phys Rev E. (2007) 75:010301. doi: 10.1103/PhysRevE.75.010301
124. Papanikolaou S, O'Hern CS, Shattuck MD. Isostaticity at frictional jamming. Phys Rev Lett. (2013) 110:198002. doi: 10.1103/PhysRevLett.110.198002
125. Pohlman NA, Severson BL, Ottino JM, Lueptow RM. Surface roughness effects in granular matter: influence on angle of repose and the absence of segregation. Phys Rev E. (2006) 73:031304. doi: 10.1103/PhysRevE.73.031304
126. Ivlev A, Morfill G. Acoustic modes in a collisional dusty plasma: effect of the charge variation. Phys Plasmas. (2000) 7:1094–102. doi: 10.1063/1.873917
127. Cheng X, McCoy JH, Israelachvili JN, Cohen I. Imaging the microscopic structure of shear thinning and thickening colloidal suspensions. Science. (2011) 333:1276–9. doi: 10.1126/science.1207032
128. Keim NC, Arratia PE. Mechanical and microscopic properties of the reversible plastic regime in a 2D jammed material. Phys Rev Lett. (2014) 112:028302. doi: 10.1103/PhysRevLett.112.028302
129. Romero V, Wandersman E, Debregeas G, Prevost A. Probing locally the onset of slippage at a model multicontact interface. Phys Rev Lett. (2014) 112:094301. doi: 10.1103/PhysRevLett.112.094301
Keywords: emulsion, non-local, yield stress fluids, surfactants, friction, anisotropy
Citation: Dijksman JA (2019) Connecting the Drops: Observing Collective Flow Behavior in Emulsions. Front. Phys. 7:198. doi: 10.3389/fphy.2019.00198
Received: 22 August 2019; Accepted: 08 November 2019;
Published: 26 November 2019.
Edited by:
Giancarlo Ruocco, Center for Life Nano Science (IIT), ItalyReviewed by:
Sauro Succi, Italian Institute of Technology (IIT), ItalyTheyencheri Narayanan, European Synchrotron Radiation Facility, France
Copyright © 2019 Dijksman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joshua A. Dijksman, am9zaHVhLmRpamtzbWFuQHd1ci5ubA==
 Joshua A. Dijksman
Joshua A. Dijksman