Outlier Mining Methods Based on Graph Structure Analysis

Outlier detection in high-dimensional datasets is a fundamental and challenging problem across disciplines that has also practical implications, as removing outliers from the training set improves the performance of machine learning algorithms. While many outlier mining algorithms have been proposed in the literature, they tend to be valid or efficient for specific types of datasets (time series, images, videos, etc.). Here we propose two methods that can be applied to generic datasets, as long as there is a meaningful measure of distance between pairs of elements of the dataset. Both methods start by defining a graph, where the nodes are the elements of the dataset, and the links have associated weights that are the distances between the nodes. Then, the first method assigns an outlier score based on the percolation (i.e., the fragmentation) of the graph. The second method uses the popular IsoMap non-linear dimensionality reduction algorithm, and assigns an outlier score by comparing the geodesic distances with the distances in the reduced space. We test these algorithms on real and synthetic datasets and show that they either outperform, or perform on par with other popular outlier detection methods. A main advantage of the percolation method is that is parameter free and therefore, it does not require any training; on the other hand, the IsoMap method has two integer number parameters, and when they are appropriately selected, the method performs similar to or better than all the other methods tested.

1. Introduction

When working with large databases, it is common to have entries that may not belong to the database. Sometimes this is because they were mislabeled, or some automatic process failed and introduced artifacts. On the other hand, anomalous items that appear not to belong, may actually be legitimate, just extreme cases of the variability of a large sample. All these elements are usually referred to as outliers [1, 2]. In general, outliers are observations that appear to have been generated by a different process than that of the other (normal) observations.

There are many definitions of what an outlier is, which vary with the system under consideration. For example, rogue waves (or freak waves), which are extremely high waves that might have different generating mechanisms than normal waves [3], have been studied in many fields [4–8], including hydrodynamics and optics. They are usually defined as the extremes in the tail of the distribution of wave heights, however, their precise definition varies, as in hydrodynamics a wave whose height is larger than three times the average can be considered extreme, while in optics, much higher waves compared to the average can be observed [9].

In the field of computer science, a practical definition of outlier elements is that they are those elements that, when they are removed from the training data set, the performance of a machine learning algorithm improves [10]. Outlier mining allows to identify and eliminate mislabeled data [11, 12]. In other situations, the outliers are the interesting points, for example to perform fraud detection [13, 14] or novelty detection [15]. The terms novelty detection, outlier detection and anomaly detection are sometimes used as synonyms in the literature [15, 16].

In spatial objects, the identification of anomalous regions that have distinct features from those of their surrounding regions can reveal valuable information [17–19]. This is the case of biomedical images where particular anomalies characterize the presence of a disease [20, 21]. For example, [22] recently proposed a generative adversarial network for detecting anomalies in OCT retinal images. Another relevant problem consists in anomaly detection in sequences of ordered events, a comprehensive review was provided in Chandola et al. [23], where three main types of formulations of the problem were identified: (i) to determine if a given sequence is anomalous with respect to a database of sequences; (ii) to determine if a particular segment is anomalous within a sequence; and (iii) to determine if the frequency of given event of sequence of events is anomalous with respect to the expected frequency.

With increasing computer power, neural networks are also an attractive option for detecting outliers [24, 25] and anomalies [26]. Hodge and Austin [2] have classified outlier detection methods in three groups: unsupervised (methods that use no prior knowledge of the data), supervised (methods which model both normal and outlier points), and semi-supervised (methods that model only normal points, or only outliers), although the latter can also include a broader spectrum of algorithms (for example a combination of fully unsupervised method and a supervised one). A recent review of outlier definitions and detection methods is presented in Zimek and Filzmoser [27].

We are interested in outlier detection in data that belong to a metric space [28–31]. In this type of dataset, a distance can be defined between items. A relevant example is a wireless sensor network, where localization is based on the distances between nodes and the presence of outliers in data results in localization inaccuracy [32, 33]. Abukhalaf et al. [34] presents a comprehensive survey of outlier detection techniques for localization in wireless sensor networks.

Here we propose two methods that use, as input, only the distances between items in the dataset. Both methods define a graph, or a network, where the nodes are the items of the dataset, and the links have associated weights which are the distances. Then, each method identifies outliers by analyzing the structure of the graph. The first method assigns to each item an outlier score based on the percolation (i.e., the fragmentation) of the graph. The second method uses the IsoMap algorithm [35] (a non-linear dimensionality reduction algorithm that learns the manifold in which the data is embedded in a reduced space), and assigns to each element an outlier score by comparing the geodesic distances with the distances in the reduced space.

Numerous algorithms have been proposed in the literature that use manifold embedding, or more in general, graph embedding, either explicitly or implicitly, to detect anomalies in data [36–41]. A comprehensive review of the literature is out of the scope of the present work, but here we discuss a few relevant examples. Agovic et al. [42, 43] and Wang et al. [44] used the IsoMap algorithm as a preprocessing step, before applying the actual outlier finding algorithm. Our approach differs fundamentally because we take into account how well or how poorly items fit in the manifold, which is disregarded by the cited methods, as they only perform outlier detection in the reduced space.

In Brito et al. [45] the authors use the distance matrix to build a graph where two nodes are connected if each of them is between the k's closest neighbors. For a sufficiently large value of k, the graph will be connected, while, for small values of k, disjoint clusters will appear. If the clusters that appear are large enough, they are considered as classes, while if they are small, they can be interpreted as outliers. In contrast to traditional k-NN algorithms, where the number of neighbors has to be determined a priori, the method proposed by Brito et al. [45] finds the value of k automatically. Nevertheless, the method is not truly parameter-free, as there are two parameters that have to be adjusted which depend on both the dimension and size of the dataset. We speculate that this graph fragmentation method identifies similar outliers as our percolation method, which has the advantage of being parameter free.

We demonstrate the validity of the percolation and IsoMap methods using several datasets, among them, a database of optical coherence tomography (OCT) images of the anterior chamber of the eye. OCT anterior chamber images are routinely used for the early diagnosis of glaucoma. We show that, when images with artifacts (outliers) are removed from the training dataset, the performance of the unsupervised ordering algorithm [46] improves significantly. We also compare the performance of these methods with the performance of other popular methods used in the literature. We show that our results are at worst comparable to those methods.

The paper is organized as follows, in section 2 we describe the proposed methods and also, other popular methods that we use for comparison. In section 3, we describe the datasets analyzed. In section 4 we present the results and in section 5, we summarize our conclusions.

2. Methods

In this section we describe the two proposed methods, which we refer to as percolation-based method and IsoMap-based method. Both methods require the definition of a distance measure between pairs of elements of the dataset. We also describe three other outlier mining methods, which we used for comparison.

We consider a dataset with N elements and let i and j be two elements, which have associated vectors with m features, $V_i=\left\{v_1^i\dots v_m^i\right\}$ and $V_j=\left\{v_1^j\dots v_m^j\right\}$. The distance between these elements can be defined as

$\begin{array}{ll}{D}_{ij}={\left({\displaystyle \sum _k}|v_k^i-v_k^j{|}^p\right)}^{1/p}& (1)\end{array}$

with p an integer number, taken equal to 2 (Euclidian distance) unless otherwise stated. The selection of an appropriate distance measure is of the utmost importance, since it must capture the similarities and differences of the data. Adding a preprocessing step before calculating the distance matrix may also be necessary to obtain significant distances.

2.1. Percolation-Based Method

The method is described in Figure 1 (a video is also included in the Supplementary Information). We begin by considering a fully connected graph, where the nodes are the elements of the set and where the links are weighted by the distance matrix D_ij. Now, we proceed in the following way: we remove the links one by one, from higher to lower weights (i.e., the link representing the highest distance between a pair of elements is removed first). If only a few links are removed, the graph will remain connected, but if one continues, the graph will start to break into different components. As it is well-known from percolation theory [47, 48], it is expected for most of the nodes to remain connected inside a single giant connected component (GCC), and for the rest of them to distribute into many small components. If we remove enough links, even the giant component disappears. This transition between the existence and non-existence of a giant component is known as a percolation transition, and is one of the most studied problems of statistical physics [49, 50]. Here, we are interested in the percolated state, i.e., when such a giant component exists. In particular, the nodes that do not belong to the GCC are candidates for being considered as outliers, as they are relatively distant to the rest of the graph.

FIGURE 1

Figure 1. Example of application of the percolation method. Starting with a fully connected graph (A) links are removed according to their distances (longer distances are removed first). In (B) some of the longest connections have been eliminated, but the graph remains fully connected, in (C) the first outlier is identified as the first element that becomes disconnected from the giant connected component, and in (D) two elements are disconnected. A video illustrating the procedure is presented in the Supplementary Information.

Following this idea, we can label each node with an outlier score (OS), defined as the weight of the link that, after being removed, separates the node from the GCC. Thus, the first elements to leave the GCC are the ones with the highest OS, while the last ones have the lowest OS.

For this method to correctly identify the outliers, we assume that normal points occupy more densely populated zones than outliers, thus having (normal points) local neighborhoods connected with small distances while outliers are connected to normal points via longer distances. Such outliers will become disconnected from the giant connected component sooner than the normal ones in the described procedure.

It is worth noting that the computation of the GCC can be performed efficiently using a variation of the union-find algorithm [51], thus making this method suitable for large datasets.

2.2. IsoMap-Based Method

The basic idea of this method is to use the well-known algorithm IsoMap [35] to perform dimensionality reduction on the raw data, and to analyze the manifold structure in the reduced space, assigning to each point an outlier score that measures how well it fits in the manifold.

The method consists of the following steps

- We apply IsoMap to the distance matrix D_ij (computed from the raw features) and obtain two matrices: 1) a new set of features for each element of the database, $V^i=\left\{{v^{\prime }}_1^i\dots {v^{\prime }}_r^i\right\}$ with i = 1…N and 2) a matrix of graph distances, $D_{ij}^G$ in the geodesic space as described in Tenenbaum et al. [35].

- Using the new set of features, we calculate a new distance matrix ${\tilde{D}}_{ij}$, using the Euclidean distance (Equation 1 with p = 2).

- The third step is to compare ${\tilde{D}}_{ij}$ with $D_{ij}^G$: for each element i we compute the similarity, ρ_i, between vectors $(D_{i1}^G,\dots D_{iN}^G)$ and $({\tilde{D}}_{i1},\dots {\tilde{D}}_{iN})$, using the Pearson correlation coefficient.

- The final step is to define the outlier score as $O{S}_i=1-{{\rho }_i}^2$. For “normal” elements, we expect high similarity, while for abnormal ones, we expect low similarity.

With this method, the assumption is that normal points lie in a low dimensional manifold embedded in the full-dimensional space, and outliers lie outside such manifold. If the parameters of the IsoMap are such that the low dimensional manifold structure is recovered successfully, the distances between points in the new set of features (${\tilde{D}}_{ij}$), the geodesic distances in the manifold, and the graph distances ($D_{ij}^G$ an approximation of the geodesic distance) should all be similar for normal points lying on the manifold. However, for outliers the geodesic distance is not defined and thus, the graph distances and the distances in the new set of features will disagree. When we compute the similarity, ρ_i, assessing this disagreement, normal points will have a high value ρ_i (near 1) and outliers a low value of ρ_i, therefore the outlier score should be high for outliers and low for normal points.

The parameters of this method, are the parameters of the IsoMap algorithm, namely, the dimensionality of the objective space (d) and neighborhood size (number of neighbors, k) to construct the graph. In this work, the parameters of the IsoMap were optimized (when a training set was available) by maximizing the average precision doing an extensive search in the parameter space.

2.3. Other Methods

We compared the performance of both methods with:

- The simplest way to define an outlier score: the distance to the center-of-mass (d2CM) in the original feature space, $V_i=\left\{v_1^i\dots v_m^i\right\}$. For “normal” elements, we expect short distance, while for abnormal ones, we expect high distance.

- A popular distance-based method, which will be referred to as Ramaswamy et al. [29]. This method is based on the distance of a point from its kth nearest neighbor, in the raw (original) high-dimensional feature space. The method assigns an outlier score to each point equal to its distance to its kth nearest neighbor.

- And a very popular method, One Class Support Vector Machine (OCSVM) which uses the inner product between the elements in the database to estimate a function that is positive in a subset of the input space where elements are likely to be found, and negative otherwise [52].

2.4. Implementation

All the methods were implemented and run in MatLab. The IsoMap method was build modifying the IsoMap algorithm implementation by Van Der Maaten et al. [53], the percolation method was implemented using graph objects in MatLab. With a simple database of 1,000 elements with 30 dimensions, the percolation method takes around 6 s to run and the IsoMap method takes around 18 s, while One Class Support Vector Machine takes around 0.2 s to run, Ramaswamy about 0.04 s to run, and distance to center of mass 0.01 s to run on an Intel i7-7700HQ laptop. Both methods could significantly improve their runtime by optimizing the code and translating it into a compiled language.

3. Data

We tested the above described methods in several databases. In the main text we present three examples: a database of anterior chamber Optical Coherent Tomography (OCT) images, a database of face images with added artifacts, and a database of credit card transactions. Additional synthetic examples are presented in the Supplementary Information.

3.1. Anterior Chamber OCT Images

This database consists of 1213 OCT images of the anterior chamber of the eye of healthy and non-healthy patients of the Instituto de Microcirugia Ocular in Barcelona. The database was analyzed in Amil et al. [46] where an unsupervised algorithm for ordering the images was proposed. The images had been classified in four categories (closed, narrow, open, and wide open) by two expert ophthalmologists. By using manually extracted features, and the features returned by the unsupervised algorithm, a similar separation in the four classes was found. Here we will demonstrate that the similarity is further improved when images containing artifacts (outliers) are removed from the dataset given to the unsupervised algorithm.

Examples taken from the database are shown in Figure 2.

FIGURE 2

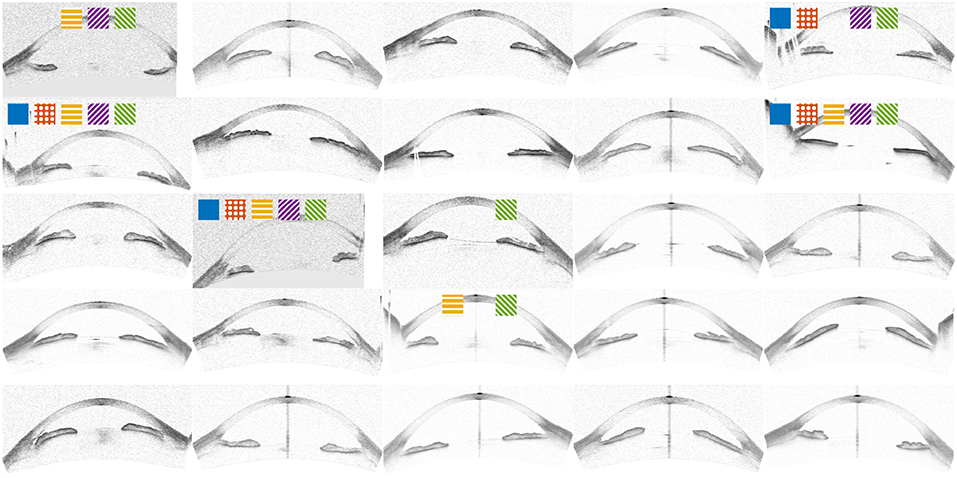
Figure 2. Example images from the OCT database, all except the first one were randomly sampled. Marked images correspond to top 15% outlier score for OCSVM (Blue), distance to center of mass (Orange), IsoMap (Yellow), Percolation (Purple), and Ramaswamy (Green). The first image corresponds to the marked improvement in Figure 4.

The distance matrix D_ij was calculated as described in detail in Amil et al. [46]: by comparing pixel-by-pixel, after pre-processing the images to adjust the alignment and to enhance the contrast. For the algorithms that don't use the distance matrix (OCSVM and distance to center of mass), the same pre-processing was used.

3.2. Face Database

This publicly available database [54], kindly provided by AT&T Laboratories Cambridge, is constituted by face images (photographs of 40 subjects with 10 different images per subject) with outliers that were added similarly to Ju et al. [55]: first we rescaled the images to 64 by 64 pixels, and then, we added a square of noise to one randomly selected image per subject. Examples are shown in Figure 3. When using the parameters proposed in Ju et al. [55] to generate the artifacts, all the methods have a perfect performance (average precision = 1), so we generated the artifacts in the following manner: We used only square artifacts whose size we varied from 0 (no artifact added) to 64 (the whole image), the square was placed randomly in the image and its content was gray-scale pixels whose gray-scale value was randomly sampled such that the distribution was the same as the gray-scale value distribution of the combination of all the images in the database. We also generated a database with outliers whose brightness was modify by simply multiplying all the image by a constant factor.

FIGURE 3

Figure 3. Example images from the face database. Eight original images at the top, and eight images with added artifacts at the bottom. Marked images correspond to top 10% outlier score for OCSVM (Blue), distance to center of mass (Orange), IsoMap (Yellow), Percolation (Purple), and Ramaswamy (Green).

For this database (and also for the databases analyzed in the Supplementary Information, which also have added outliers), we generated two independent sets for each square size: one was used to find, in the case of the IsoMap and Ramaswamy methods, the optimal parameters, and the second one was used for testing.

For this database, the distance matrix was calculated as the Euclidean pixel-by-pixel distance.

3.3. Credit Card Transactions

This publicly available database [56–61] contains credit card transactions made in September 2013 by European cardholders. It contains 284807 transactions made in 2 days, of which 492 correspond to frauds. In order to preserve confidentiality, for each transaction the data set only includes the amount of money in the transaction, a relative time, and 28 features that are the output of a principal component analysis (PCA) of all the other metadata related to the transaction. In our analysis we divided the total dataset into 8 sets of about 4,000 entries (due to computational constrains) according to the amount of the transaction and computed the distance as the euclidean distance using these 28 features.

4. Results

4.1. Anterior Chamber OCT Images

For the OCT database, there is no a priori definition of outliers (i.e., no ground truth), all the images were drawn from the same database. However, as a proxy for determining the performance of the outlier finding methods, we used the performance of the unsupervised methods proposed in Amil et al. [46] when ignoring the images identified as outliers.

As removing outliers should improve the performance of machine learning algorithms, we performed two tests: first, we recalculated the correlation metrics presented in Amil et al. ([46], Table 1), removing the first n outliers that were identified by each method. Second, to test the significance of the improved performance, we repeated the calculation, now removing random images. The results presented in Figure 4 confirm that removing the detected outliers improves the performance, while removing random images has no significant effect. We also see that IsoMap is the method that produces the highest improvement, while d2CM and OCSVM have low-significance performance improvement. For the IsoMap method we set the parameters to d = 10 and k = 15, while for the Ramaswamy method we used k = 6.

FIGURE 4

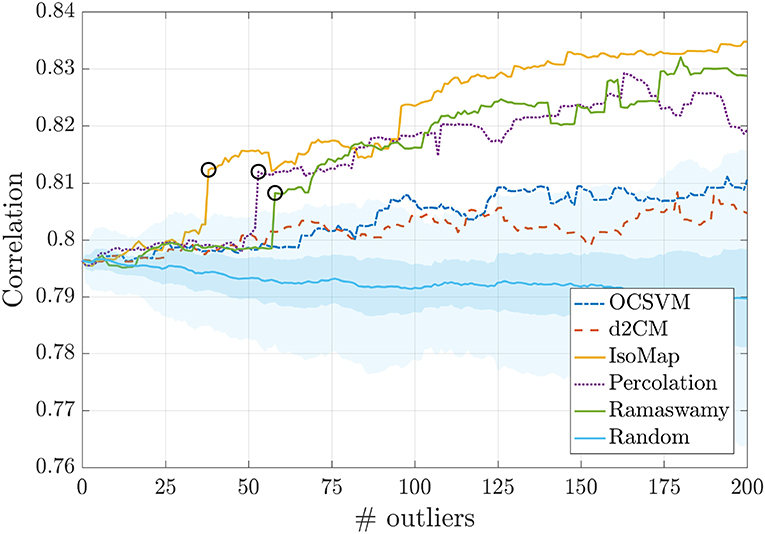
Figure 4. Performance of the OCT image ordering algorithm as a function of the number of outliers that are removed from the database. As expected, we see that the performance, which is measured by the correlation coefficient between the feature returned by the ordering (unsupervised) algorithm and the feature provided by manual expert annotation (mean angle), improves as the outliers detected are removed. The different lines indicate the method of outlier identification and the colored region indicates results when the images removed are randomly selected, one standard deviation is shown in dark coloring, while three standard deviations is shown in light coloring. In this case, as expected, no significant change in the performance is seen. For some methods a sharp improvement is observed when eliminating one specific image (marked with a black circle), this image corresponds to the first one shown in Figure 2.

4.2. Face Database

For this database, as explained in section 3.2, we generated artifacts artificially and tried to find the images presenting artifacts as outliers. We varied the size of the artifact generated to evaluate the robustness of the methods. For each size, we generated two different databases with artifacts (with the same parameters but different random seeds), we used the first one to optimize the parameters of IsoMap and Ramaswamy algorithms, and the second one to test the algorithms. We show the results of evaluating the performance on the second database for each square size in Figure 5A, we used the average precision based on the precision-recall curve as performance measure, this measure computed as the area under the precision-recall curve [62] is more appropriate than other more commonly used metrics for class imbalance scenarios. In Figure 5A we see that Ramaswamy tends to slightly outperform all other methods, in particular, the percolation-based method shifts from being the worst method (when the squares are small) to the second best (when the squares are large). In Figure 5D we show the performance of the IsoMap method as a function of its parameters, we depict two zones with better performance, one with fairly low dimensionality and a low number of neighbors (more neighbors translate to a more linear mapping), and another zone with greater dimensionality and almost the maximum possible number of neighbors. In general, performance is very sensitive to parameter variations. In Figure 5C we show how altering the brightness of some images can also be perceived as outliers due to the distance measure used (Euclidean pixel-by-pixel).

FIGURE 5

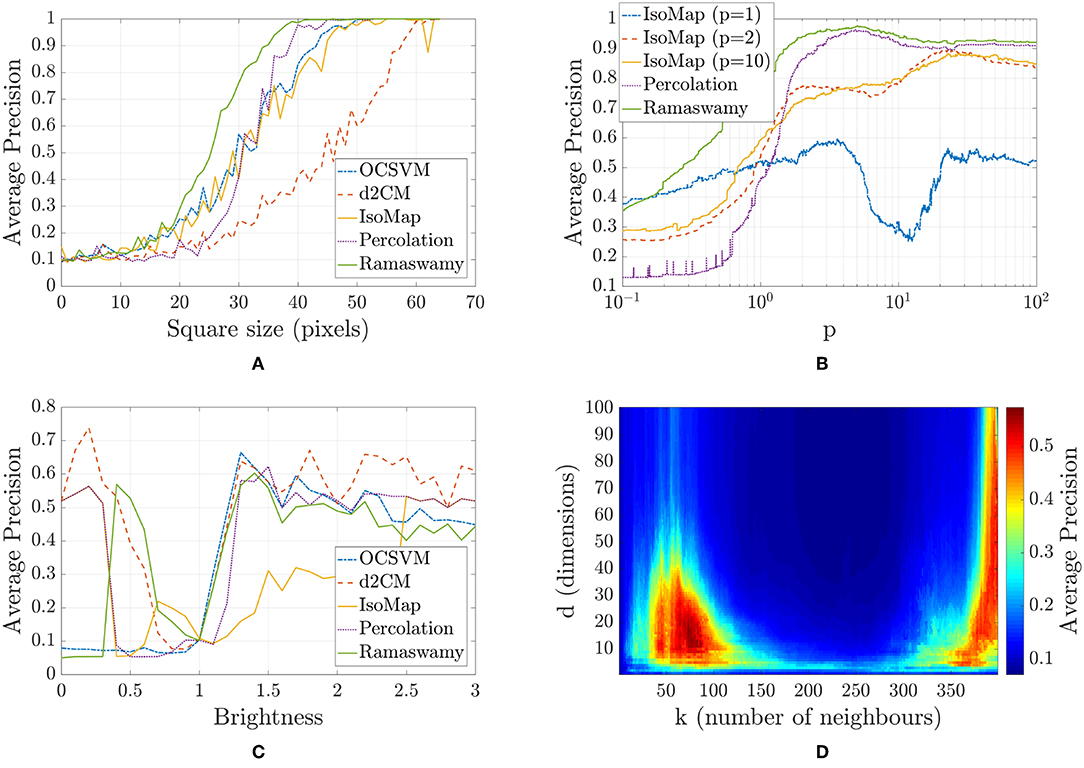
Figure 5. Analysis of the face database. (A) Average precision as a function of the square size for the different outlier finding methods, One Class Support Vector Machine (OCSVM) in blue, distance to center of mass (d2CM) in orange, IsoMap in yellow, Percolation-based method in purple, and Ramaswamy in green. The Average precision was calculated on databases independently generated from those used to set the parameters of the methods. (B) Average precision as a function of the distance measure for different outlier finding methods with a square size of 36 pixels, IsoMap (trained with p = 1) in blue, IsoMap (trained with p = 2) in orange, IsoMap (trained with p = 10) in yellow, Percolation-based method in purple, and Ramaswamy in green. The Average precision was calculated on databases independently generated from those used to set the parameters of the methods. (C) Average precision as a function of the brightness multiplier of the outliers. (D) Average precision in the training set as a function of the IsoMap parameters with a square size of 30 pixels.

Also, to evaluate how robust the methods are when changing the distance measure, we varied p in the Minkowski distance family (Equation 1), and evaluated the methods for the parameters optimized for p = 2 (Euclidean), p = 1 and p = 10, the average precision as a function of p for the distance-based methods is shown in Figure 5B. As we can see, for p > 4 Ramaswamy and Percolation-based perform similarly well, also, the parameters of Ramaswamy are very robust when changing p in the training set (the Ramaswamy method was also train with p = 1 and p = 10 obtaining the same parameters as for p = 2), while IsoMap is very sensitive to such changes.

We generated a different dataset whose outliers were images that, instead of having added noise, were multiplied by a constant (brightness) factor. We varied the brightness from 0 (the image being all black) to 3. The results of this study is shown in Figure 5C.

4.3. Credit Card Transactions

In this database the ground truth (the fraud credit card transactions) is known and thus, the performance of the different methods is, as in the prior example, quantified with the average precision based on the precision-recall curve.

The database was divided into several subsets according to the amount of money of each transaction (see Figure 6), each set (of around 4,000 transactions) was further randomly divided into two sets in order to use one for training and the other one for testing. The results are summarized in Figure 6 that displays the average precision for all testing sets. We can see that the performance of the methods is very heterogeneous.

FIGURE 6

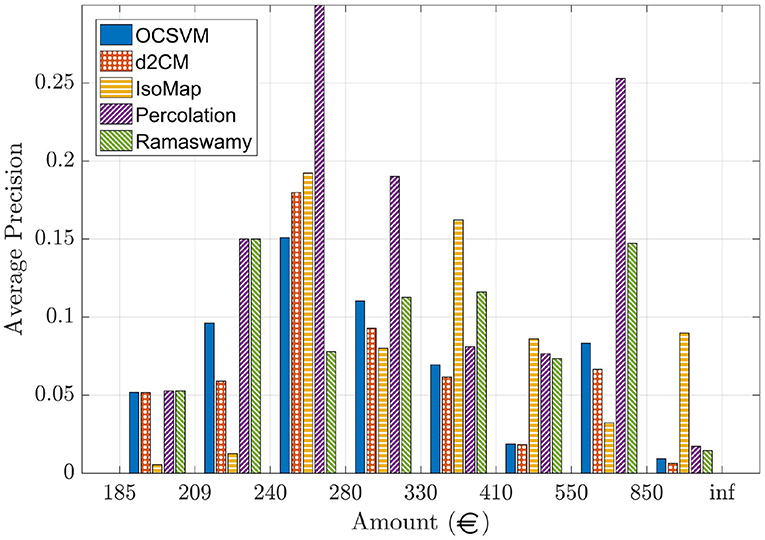
Figure 6. Performance of all the outlier finding methods for the credit card transactions on the test subsets for each amount range.

To try to understand the origin of the large variability, we conducted an additional experiment in which we considered groups of 3,900 normal transactions chosen at random (without considering the amount of the transaction) and 100 frauds also chosen at random, which were divided equally in training and test subsets. We repeat this experiment 8 times with different random seeds, and the results are presented in Figure 7 in this experiment the average precision of the methods was increased due to a larger fraction of frauds in the test sets.

FIGURE 7

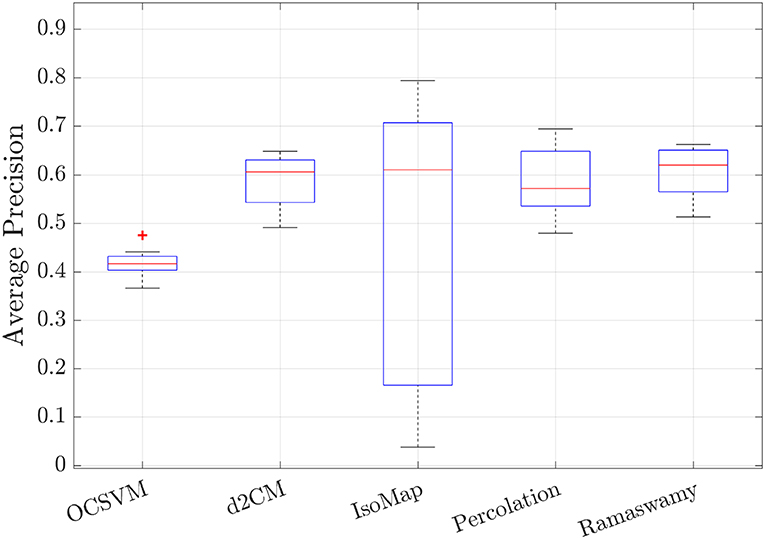
Figure 7. Performance of all the outlier finding methods for the credit card transactions on the test subsets of the random groups. The random groups were generated by randomly choosing 3,900 normal transactions and 100 frauds, and it was further randomly divided into two subsets, a training and a testing subsets.

4.4. Discussion

Figure 8 presents the comparison of the results obtained with the five methods used, for the three databases analyzed. Figure 8A summarizes the results for the OCT database, with the boxplot we can see the minimum, first quartile, median, third quartile, and maximum of the correlation coefficient when varying the amount of outliers considered (corresponds to Figure 4). Figure 8B summarizes, in a similar manner, the results for the face database showing the boxplot of the average precision values when varying the square size (corresponds to Figure 5A). Figure 8C summarizes the results for the credit card transactions showing the boxplot of the average precision values when changing the amount range (corresponds to Figure 6). As we can see in Figure 8, the IsoMap and Percolation methods perform well in the three databases; their performance being either better than or comparable to the performance of the other three methods. Additional examples presented in the Supplementary Information confirm the good performance of IsoMap and Percolation methods.

FIGURE 8

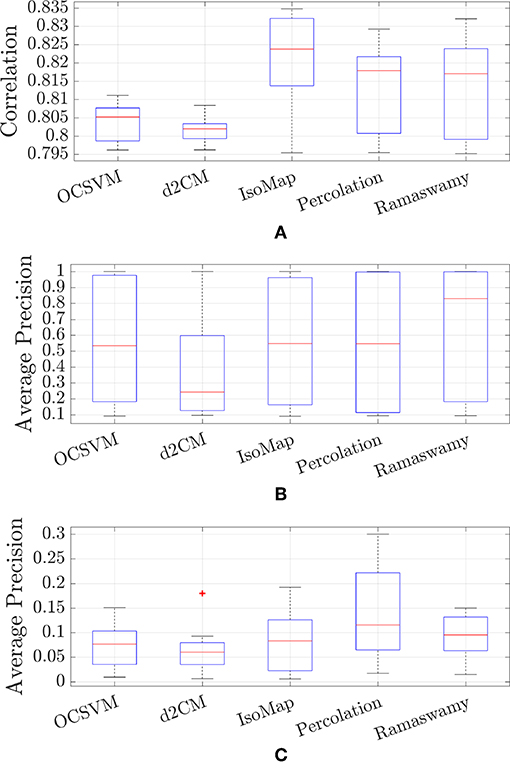
Figure 8. Box-plot summarizing the results of all the outlier finding methods in all the databases. (A) Anterior Chamber OCT images, (B) Face database (only testing groups), (C) Credit Card transactions (only testing groups).

Figure 5B shows how the performance of distance-based methods is affected by the definition of the distance. We can see that the performance of all the methods depends on the definition of the distance. The methods are also sensitive to changes in the preprocessing of the data, therefore, well-prepared data with a meaningful distance definition is needed for optimizing the performance of all methods.

It is important to consider how the two methods proposed here scale with the dimension of the data, d (i.e., the number of features of each sample), and the number of samples, N, in the database. Since both methods begin by calculating the distance matrix, the processing time is at least of the order dN² because the calculation of the distance between pairs of elements linearly increases with d and quadratically with N. Both methods need to store in memory the distance matrix and analize it, this imposes memory requirements that can limit their applicability for large datasets. In the case of IsoMap, this analysis is of order N². In the case of the percolation method, a threshold needs to be gradually varied in order to precisely identify the order in which the elements became disconnected from the giant component. This results in a runtime of the order of N² using the algorithm proposed in Newman and Ziff [51]. Regarding the dimensionality of the data, because both methods only need to hold in memory the N² distance matrix (and not the dN features of the N samples) they are suitable for very high dimensional data (where d≫N) because once the distances of an element to all other elements have been computed, the d features of that element will not be needed again.

5. Conclusions

We have proposed two methods for outlier mining that rely on the definition of a meaningful measure of distance between pairs of elements in the dataset, one being fully unsupervised without the need of setting any parameters, and other which has 2 integer number parameters that can be set using a labeled training set. Both methods define a graph (whose nodes are the elements of the dataset, connected by links whose weights are the distances between the nodes) and analyze the structure of the graph. The first method is based on the percolation of the graph, while the second method uses the IsoMap non-linear dimensionality reduction algorithm. We have tested the methods on several real and synthetic datasets (additional examples are presented in the Supplementary Information), and compared the performance of the proposed algorithms with the performance of a “naive” method (that calculates the distance to the center of mass) and two popular outlier finding methods, Ramaswamy and One Class Support Vector Machine (OCSVM).

Although the percolation algorithm performs comparably to (or slightly lower than) other methods, it has the great advantage of being parameter-free. In contrast, the IsoMap method has two parameters (natural numbers) that have to be selected appropriately. The performance of the methods varies with the dataset analyzed because the underlying assumption of what an outlier is, is different for the different methods. The percolation method assumes that the normal elements will be in one large cluster, with outliers being far from that cluster; IsoMap assumes that the normal elements lie on a manifold, and that outliers lie outside such manifold; the Ramaswamy and OCSVM methods assume that the outliers lie in a less densely populated sector of the space, while the “naive” method simply assumes that outliers are the furthest elements from the center of mass. These assumptions do not always hold, which results in the identification of normal elements as outliers. For example, in the OCT database there were some duplicated entries which were assigned by the Ramaswamy method the least outlier score, in spite of having a minor artifact.

The percolation algorithm is immune to duplicate entries, as it assigns the same outlier score as if there was only one element. On the other hand, the effect of duplicate entries on the IsoMap and “naive” methods is more difficult to asses, but is to be expected that if the duplicated elements are only few, they won't have a large effect in the manifold learned, or in the center of mass calculated.

The execution time of both methods scales at least as dN² where d is the number of features of each item and N is the number of items in the database (as dN² is the time needed to compute the distance matrix). Therefore, the methods are suitable for the analysis of small to medium-size databases composed of high-dimensional items.

Data Availability Statement

Some of the datasets analyzed in this manuscript are not publicly available. Requests to access such datasets should be directed to pamil@fisica.edu.uy.

Author Contributions

PA, NA, and CM designed the algorithms and wrote the manuscript. PA and NA implemented them. PA ran the test on the proposed databases.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

PA and CM acknowledge support by the BE-OPTICAL project (EU H2020-675512). CM also acknowledges support from the Spanish Ministerio de Ciencia, Innovación y Universidades (PGC2018-099443-B-I00) and ICREA ACADEMIA (Generalitat de Catalunya). NA and CM acknowledge the hospitality of the International Centre for Theoretical Physics-South American Institute for Fundamental Research (ICTP-SAIFR) where a collaboration was established and this work started.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00194/full#supplementary-material

Video S1. Video illustrating the whole percolation process. It starts with a fully connected graph where links are eliminated one by one according to the distance of the nodes in the original space.

References

1. Grubbs FE. Procedures for detecting outlying observations in samples. Technometrics. (1969) 11:1–21. doi: 10.1080/00401706.1969.10490657

CrossRef Full Text | Google Scholar

2. Hodge V, Austin J. A survey of outlier detection methodologies. Artif Intell Rev. (2004) 22:85–126. doi: 10.1023/B:AIRE.0000045502.10941.a9

CrossRef Full Text | Google Scholar

3. Onorato M, Residori S, Bortolozzo U, Montina A, Arecchi F. Rogue waves and their generating mechanisms in different physical contexts. Phys Rep. (2013) 528:47–89. doi: 10.1016/j.physrep.2013.03.001

CrossRef Full Text | Google Scholar

4. Solli D, Ropers C, Koonath P, Jalali B. Optical rogue waves. Nature. (2007) 450:1054–7. doi: 10.1038/nature06402

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhen-Ya Y. Financial rogue waves. Commun Theor Phys. (2010) 54:947. doi: 10.1088/0253-6102/54/5/31

CrossRef Full Text | Google Scholar

6. Shats M, Punzmann H, Xia H. Capillary rogue waves. Phys Rev Lett. (2010) 104:104503. doi: 10.1103/PhysRevLett.104.104503

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Katz RW, Parlange MB, Naveau P. Statistics of extremes in hydrology. Adv Water Resour. (2002) 25:1287–304. doi: 10.1016/S0309-1708(02)00056-8

CrossRef Full Text | Google Scholar

8. Chabchoub A, Hoffmann N, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett. (2011) 106:204502. doi: 10.1103/PhysRevLett.106.204502

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Akhmediev N, Kibler B, Baronio F, Belić M, Zhong WP, Zhang Y, et al. Roadmap on optical rogue waves and extreme events. J Opt. (2016) 18:063001. doi: 10.1088/2040-8978/18/6/063001

CrossRef Full Text | Google Scholar

10. Liu H, Shah S, Jiang W. On-line outlier detection and data cleaning. Comput Chem Eng. (2004) 28:1635–47. doi: 10.1016/j.compchemeng.2004.01.009

CrossRef Full Text | Google Scholar

11. Brodley CE, Friedl MA. Identifying and eliminating mislabeled training instances. In: Proceedings of the 13th National Conference on Artificial Intelligence. Portland, OR: AAAI Press (1996). p. 799–805.

Google Scholar

12. Brodley CE, Friedl MA. Identifying mislabeled training data. J Artif Intell Res. (1999) 11:131–67. doi: 10.1613/jair.606

CrossRef Full Text | Google Scholar

13. Aleskerov E, Freisleben B, Rao B. Cardwatch: a neural network based database mining system for credit card fraud detection. In: Proceedings of the IEEE/IAFE 1997 Computational Intelligence for Financial Engineering (CIFEr). IEEE (1997). p. 220–6.

Google Scholar

14. Cheng Q, Varshney PK, Michels JH, Belcastro CM. Fault detection in dynamic systems via decision fusion. IEEE Trans Aerospace Electron Syst. (2008) 44:227–42. doi: 10.1109/TAES.2008.4517001

CrossRef Full Text | Google Scholar

15. Pimentel MA, Clifton DA, Clifton L, Tarassenko L. A review of novelty detection. Signal Process. (2014) 99:215–49. doi: 10.1016/j.sigpro.2013.12.026

CrossRef Full Text | Google Scholar

16. Agrawal S, Agrawal J. Survey on anomaly detection using data mining techniques. Proc Comput Sci. (2015) 60:708–13. doi: 10.1016/j.procs.2015.08.220

CrossRef Full Text | Google Scholar

17. Kou Y, Lu CT, Chen D. Spatial weighted outlier detection. In: Proceedings of the 2006 SIAM International Conference on Data Mining. SIAM (2006). p. 614–8.

Google Scholar

18. Lu CT, Chen D, Kou Y. Detecting spatial outliers with multiple attributes. In: Proceedings 15th IEEE International Conference on Tools with Artificial Intelligence. Sacramento, CA: IEEE (2003). p. 122–8.

Google Scholar

19. Sun P, Chawla S. On local spatial outliers. In: Fourth IEEE International Conference on Data Mining (ICDM' 04). IEEE (2004). p. 209–16.

Google Scholar

20. Spence C, Parra L, Sajda P. Detection, synthesis and compression in mammographic image analysis with a hierarchical image probability model. In: Proceedings IEEE Workshop on Mathematical Methods in Biomedical Image Analysis (MMBIA 2001). IEEE (2001). p. 3–10.

Google Scholar

21. Taoum A, Mourad-Chehade F, Amoud H. Early-warning of ARDS using novelty detection and data fusion. Comput Biol Med. (2018) 102:191–9. doi: 10.1016/j.compbiomed.2018.09.030

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Schlegl T, Seeböck P, Waldstein SM, Langs G, Schmidt-Erfurth U. f-AnoGAN: fast unsupervised anomaly detection with generative adversarial networks. Med Image Anal. (2019) 54:30–44. doi: 10.1016/j.media.2019.01.010

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chandola V, Banerjee A, Kumar V. Anomaly detection for discrete sequences: a survey. IEEE Transn Knowl Data Eng. (2010) 24:823–39. doi: 10.1109/TKDE.2010.235

CrossRef Full Text | Google Scholar

24. Hawkins S, He H, Williams G, Baxter R. Outlier detection using replicator neural networks. In: International Conference on Data Warehousing and Knowledge Discovery. Aix-en-Provence: Springer (2002). p. 170–80.

Google Scholar

25. Chen J, Sathe S, Aggarwal C, Turaga D. Outlier detection with autoencoder ensembles. In: Proceedings of the 2017 SIAM International Conference on Data Mining. SIAM (2017). p. 90–8.

Google Scholar

26. Sabokrou M, Fayyaz M, Fathy M, Moayed Z, Klette R. Deep-anomaly: fully convolutional neural network for fast anomaly detection in crowded scenes. Comput Vision Image Understand. (2018) 172:88–97. doi: 10.1016/j.cviu.2018.02.006

CrossRef Full Text | Google Scholar

27. Zimek A, Filzmoser P. There and back again: outlier detection between statistical reasoning and data mining algorithms. Wiley Interdiscipl Rev Data Min Knowl Discov. (2018) 8:e1280. doi: 10.1002/widm.1280

CrossRef Full Text | Google Scholar

28. Knox EM, Ng RT. Algorithms for mining distancebased outliers in large datasets. In: Proceedings of the International Conference on Very Large Data Bases. Citeseer (1998). p. 392–403.

Google Scholar

29. Ramaswamy S, Rastogi R, Shim K. Efficient algorithms for mining outliers from large data sets. In: ACM Sigmod Record. Vol. 29. ACM (2000). p. 427–38.

Google Scholar

30. Angiulli F, Pizzuti C. Outlier mining in large high-dimensional data sets. IEEE Trans Knowl Data Eng. (2005) 17:203–15. doi: 10.1109/TKDE.2005.31

CrossRef Full Text | Google Scholar

31. Angiulli F, Fassetti F. Dolphin: an efficient algorithm for mining distance-based outliers in very large datasets. ACM Trans Knowl Discov. Data. (2009) 3:4. doi: 10.1145/1497577.1497581

CrossRef Full Text | Google Scholar

32. Yang Z, Wu C, Chen T, Zhao Y, Gong W, Liu Y. Detecting outlier measurements based on graph rigidity for wireless sensor network localization. IEEE Trans Vehicul Technol. (2012) 62:374–83. doi: 10.1109/tvt.2012.2220790

CrossRef Full Text | Google Scholar

33. Abukhalaf H, Wang J, Zhang S. Mobile-assisted anchor outlier detection for localization in wireless sensor networks. Int J Future Gen Commun Netw. (2016) 9: 63–76. doi: 10.14257/ijfgcn.2016.9.7.07

CrossRef Full Text | Google Scholar

34. Abukhalaf H, Wang J, Zhang S. Outlier detection techniques for localization in wireless sensor networks: a survey. Int J Future Gen Commun Netw. (2015) 8:99–114. doi: 10.14257/ijfgcn.2015.8.6.10

CrossRef Full Text | Google Scholar

35. Tenenbaum JB, De Silva V, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science. (2000) 290:2319–23. doi: 10.1126/science.290.5500.2319

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Pang Y, Yuan Y. Outlier-resisting graph embedding. Neurocomputing. (2010) 73:968–74. doi: 10.1016/j.neucom.2009.08.020

CrossRef Full Text | Google Scholar

37. Schubert E, Gertz M. Intrinsic t-stochastic neighbor embedding for visualization and outlier detection. In: International Conference on Similarity Search and Applications. Springer (2017). p. 188–203.

Google Scholar

38. Madabhushi A, Shi J, Rosen M, Tomaszeweski JE, Feldman MD. Graph embedding to improve supervised classification and novel class detection: application to prostate cancer. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Berlin, Heidelberg: Springer (2005). p. 729–37.

PubMed Abstract | Google Scholar

39. Cook DJ, Holder LB. Graph-based data mining. IEEE Intell Syst Appl. (2000) 15:32–41. doi: 10.1109/5254.850825

CrossRef Full Text | Google Scholar

40. Eberle W, Holder L. Anomaly detection in data represented as graphs. Intell Data Anal. (2007) 11:663–89. doi: 10.3233/IDA-2007-11606

CrossRef Full Text | Google Scholar

41. Rahmani A, Afra S, Zarour O, Addam O, Koochakzadeh N, Kianmehr K, et al. Graph-based approach for outlier detection in sequential data and its application on stock market and weather data. Knowl Based Syst. (2014) 61:89–97. doi: 10.1016/j.knosys.2014.02.008

CrossRef Full Text | Google Scholar

42. Agovic A, Banerjee A, Ganguly AR, Protopopescu V. Anomaly detection in transportation corridors using manifold embedding. In: Knowledge Discovery from Sensor Data. (2008). p. 81–105. Available online at: https://www.researchgate.net/profile/Auroop_Ganguly/publication/220571551_Anomaly_detection_using_manifold_embedding_and_its_applications_in_transportation_corridors/links/5400c3590cf2c48563aee68e/Anomaly-detection-using-manifold-embedding-and-its-applications-in-transportation-corridors.pdf

Google Scholar

43. Agovic A, Banerjee A, Ganguly A, Protopopescu V. Anomaly detection using manifold embedding and its applications in transportation corridors. Intell Data Anal. (2009) 13:435–55. doi: 10.3233/IDA-2009-0375

CrossRef Full Text | Google Scholar

44. Wang L, Li Z, Sun J. Improved ISOMAP algorithm for anomaly detection in hyperspectral images. In: Fourth International Conference on Machine Vision (ICMV 2011): Machine Vision, Image Processing, and Pattern Analysis. Vol. 8349. International Society for Optics and Photonics (2012). p. 834902.

Google Scholar

45. Brito M, Chavez E, Quiroz A, Yukich J. Connectivity of the mutual k-nearest-neighbor graph in clustering and outlier detection. Stat Probab Lett. (1997) 35:33–42.

Google Scholar

46. Amil P, González L, Arrondo E, Salinas C, Guell JL, Masoller C, et al. Unsupervised feature extraction of anterior chamber OCT images for ordering and classification. Sci Rep. (2019) 9:1157. doi: 10.1038/s41598-018-38136-8

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Barrat A, Barthélemy M, Vespignani A. Dynamical Processes on Complex Networks. Cambridge University Press (2008).

Google Scholar

48. Cohen R, Havlin S. Complex Networks: Structure, Robustness and Function. Cambridge University Press (2010).

Google Scholar

49. Stauffer D. Introduction to Percolation Theory: Revised Second Edition. Taylor & Francis (1994).

Google Scholar

50. Callaway DS, Newman MEJ, Strogatz SH, Watts DJ. Network robustness and fragility: percolation on random graphs. Phys Rev Lett. (2000) 85:5468–71. doi: 10.1103/physrevlett.85.5468

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Newman MEJ, Ziff RM. Fast Monte Carlo algorithm for site or bond percolation. Phys Rev E. (2001) 64:016706. doi: 10.1103/physreve.64.016706

CrossRef Full Text | Google Scholar

52. Schölkopf B, Platt JC, Shawe-Taylor J, Smola AJ, Williamson RC. Estimating the support of a high-dimensional distribution. Neural Comput. (2001) 13:1443–71. doi: 10.1162/089976601750264965

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Van Der Maaten L, Postma E, Van den Herik J. Dimensionality reduction: a comparative. J Mach Learn Res. (2009) 10:13. Available online at: http://www.math.chalmers.se/Stat/Grundutb/GU/MSA220/S18/DimRed2.pdf

Google Scholar

54. Samaria FS, Harter AC. Parameterisation of a stochastic model for human face identification. In: Proceedings of 1994 IEEE Workshop on Applications of Computer Vision. IEEE (1994). p. 138–42.

Google Scholar

55. Ju F, Sun Y, Gao J, Hu Y, Yin B. Image outlier detection and feature extraction via L1-Norm-Based 2D probabilistic PCA. IEEE Trans Image Process. (2015) 24:4834–46. doi: 10.1109/TIP.2015.2469136

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Dal Pozzolo A, Caelen O, Johnson RA, Bontempi G. Calibrating probability with undersampling for unbalanced classification. In: 2015 IEEE Symposium Series on Computational Intelligence. IEEE (2015). p. 159–66.

Google Scholar

57. Dal Pozzolo A, Caelen O, Le Borgne YA, Waterschoot S, Bontempi G. Learned lessons in credit card fraud detection from a practitioner perspective. Expert Syst Appl. (2014) 41:4915–28. doi: 10.1016/j.eswa.2014.02.026

CrossRef Full Text | Google Scholar

58. Dal Pozzolo A, Boracchi G, Caelen O, Alippi C, Bontempi G. Credit card fraud detection: a realistic modeling and a novel learning strategy. IEEE Trans Neural Netw Learn Syst. (2018) 29:3784–97. doi: 10.1109/TNNLS.2017.2736643

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Dal Pozzolo A. Adaptive Machine Learning for Credit Card Fraud Detection. (2015). Available online at: https://pdfs.semanticscholar.org/bcfb/f068dff507b9ef11240e69f96d24f5d89fc1.pdf.

Google Scholar

60. Carcillo F, Dal Pozzolo A, Le Borgne YA, Caelen O, Mazzer Y, Bontempi G. Scarff: a scalable framework for streaming credit card fraud detection with spark. Inform Fusion. (2018) 41:182–94. doi: 10.1016/j.inffus.2017.09.005

CrossRef Full Text | Google Scholar

61. Carcillo F, Le Borgne YA, Caelen O, Bontempi G. Streaming active learning strategies for real-life credit card fraud detection: assessment and visualization. Int J Data Sci Anal. (2018) 5:285–300. doi: 10.1007/s41060-018-0116-z

CrossRef Full Text | Google Scholar

62. Saito T, Rehmsmeier M. The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS ONE. (2015) 10:e0118432. doi: 10.1371/journal.pone.0118432

PubMed Abstract | CrossRef Full Text | Google Scholar