- 1AHEP Group, Institut de Física Corpuscular – CSIC/Universitat de València, Valencia, Spain
- 2Division of Theoretical Physics, University of Ioannina, Ioannina, Greece
- 3Department of Physics, Osaka University, Osaka, Japan
We review standard and non-standard neutrino physics probes that are based on nuclear measurements. We pay special attention on the discussion of prospects to extract new physics at prominent rare event measurements looking for neutrino-nucleus scattering, such as the coherent elastic neutrino-nucleus scattering (CEνNS) that may involve lepton flavor violation (LFV) in neutral-currents (NC). For the latter processes several appreciably sensitive experiments are currently pursued or have been planed to operate in the near future, like the COHERENT, CONUS, CONNIE, MINER, TEXONO, RED100, vGEN, Ricochet, NUCLEUS, etc. We provide a thorough discussion on phenomenological and theoretical studies, in particular those referring to the nuclear physics aspects in order to provide accurate predictions for the relevant experiments. Motivated by the recent discovery of CEνNS at the COHERENT experiment and the active experimental efforts for a new measurement at reactor-based experiments, we summarize the current status of the constraints as well as the future sensitivities on nuclear and electroweak physics parameters, non-standard interactions, electromagnetic neutrino properties, sterile neutrinos and simplified scenarios with novel vector Z′ or scalar ϕ mediators. Indirect and direct connections of CEνNS with astrophysics, direct Dark Matter detection and charge lepton flavor violating processes are also discussed.
1. Introduction
During the last few decades, intense research effort has been devoted to multidisciplinary neutrino searches involving physics within and beyond the standard model (SM) in the theory, phenomenology and experiments that drops in the interplay of particle, nuclear physics, astrophysics and cosmology.
Astrophysical and laboratory searches [1] offer unique opportunities to probe great challenges in modern-day physics such as the underlying physics of the fundamental electroweak interactions within and beyond the SM [2, 3] in the neutral and charged-current sector of semi-leptonic neutrino-nucleus processes [4–6]. To meet the sufficient energy and flux requirements, the relevant studies consider different low-energy neutrino sources including (i) Supernova (SN) neutrinos, (ii) accelerator neutrinos (from pion decay at rest, π-DAR) and (iii) reactor neutrinos, while interesting proposals aiming to use 51Cr and beta-beam neutrino sources have appeared recently. The detection mechanism of low-energy neutrino interactions with nucleons and nuclei is experimentally hard and limited by the tiny nuclear recoils produced by the scattering process. To this purpose, the nuclear detector materials are carefully selected to fulfill the requirement of achieving a-few-keV or sub-keV threshold capabilities. The detectors developed are based on cutting edge technologies such as scintillating crystals (CsI[Na], NaI[Tl]), p-type point-contact (PPC) germanium detectors, single-phase or double liquid noble gases (LAr, LXe) charged coupled devices (CCDs), cryogenic bolometers, etc.
The neutral-current coherent elastic neutrino nucleus scattering (CEνNS) was proposed about four decades ago [7–9], while it was experimentally confirmed in 2017 by the COHERENT Collaboration [10] at the Spallation Neutron Source, in good agreement with the SM expectation. The observation of CEνNS has opened up a new era, triggering numerous theoretical studies to interpret the available data [11] in a wide spectrum of new physics opportunities, with phenomenological impact on astroparticle physics, neutrino oscillations, dark matter (DM) detection, etc. (see [12] for various applications). In particular, the recent works have concentrated on non-standard interactions (NSI) [13–19], electromagnetic properties [20–23], sterile neutrinos [24–26], CP-violation [27] and novel mediators [28–31]. Nuclear and atomic effects are explored in Cadeddu et al. [32], Ciuffoli et al. [33], Huang and Chen [34], Aristizabal Sierra et al. [35], Papoulias et al. [36], Arcadi et al. [37], and Cadeddu et al. [38] which may have direct implications to the neutrino-floor [39–41] and to DM searches [42–44]. Being a rapidly developing field, there are several experimental programs aiming to observe CEνNS in the near future, such as the TEXONO [45], CONNIE [46], MINER [47], vGEN [48], CONUS [49], Ricochet [50], and NUCLEUS [51].
Future CEνNS measurements have good prospects to shed light on the exotic neutrino-nucleus interactions expected in the context of models describing flavor changing neutral-current (FCNC) processes [52] as well as to subleading NSI oscillation effects [53–57] and various open issues in nuclear astrophysics [58, 59]. The main goal of this review article is to provide an up-to-date status of the conventional and exotic neutrino physics probes of CEνNS and to summarize the necessary aspects for the interpretation of the experimental data. We focus on the theoretical modeling, calculations and analysis of the data that are relevant at the time of writing and we mainly concentrate on the theoretical and phenomenological physics aspects. For a recent review on the experimental advances of CEνNS, see Akimov et al. [60].
This review article has been organized as follows: section 2 provides the theoretical treatment of low-energy neutrino-nucleus processes for both coherent and incoherent channels and its connection to the more general lepton-nucleus case with a particular emphasis on the nuclear physics aspects. Section 3 presents the current status of constraints on SM and exotic physics parameters resulted from the analysis of the COHERENT data and discusses the projected sensitivities from future CEνNS measurements at π-DAR and reactor facilities. In section 4 we briefly summarize the most important connections of CEνNS with DM searches, charged lepton flavor violation (cLFV) and astrophysics. Finally, the main conclusions are given in section 5.
2. Theoretical Study of Neutrino-Nucleus Interaction
At low- and intermediate-energies, the neutrino being a key input to understand open issues in physics within and beyond the SM (see below), necessitated a generation of neutrino experiments for exploring neutrino scattering processes with nucleons and nuclei for both charged-current (inelastic) and neutral-current (coherent elastic and incoherent scattering) processes. Theoretically, the neutral-current neutrino-nucleus scattering we are interested here, is a well studied process for both coherent [61] an incoherent channels: [62, 63]. The accurate evaluation of the required transition matrix elements describing the various interaction channels of the electroweak processes between an initial and a final (many-body) nuclear state, is obtained on the basis of reliable nuclear wavefunctions. From a nuclear theory point of view, such results have been obtained by paying special attention on the accurate contruction of the nuclear ground state in the framework of the quasi-particle random phase approximation (QRPA), using schematic Skyrme [64] or realistic Bonn C-D pairing interactions [65]. Focusing on the latter method, the authors of Papoulias and Kosmas [61] solved iteratively the Bardeen-Cooper-Schrieffer (BCS) equations, achieving a high reproducibility of the available nuclear charge-density-distribution experimental data [66].
2.1. Coherent and Incoherent Neutrino-Nucleus Cross Sections
In the Donnelly-Walecka theory [67] all semi-leptonic nuclear processes at low and intermediate energies may be described by an effective interaction Hamiltonian through the leptonic and hadronic current densities,
where G = GF is the Fermi coupling constant for neutral-current processes and G = GF cos θc (θc is the Cabbibo angle) for charged-current processes. For partial scattering rates, the evaluation of the transition amplitudes 〈f | Ĥeff | i〉 are treated via a multipole decomposition analysis of the hadronic current (see the Appendix). Then, for a given set of an initial |Ji〉 and a final |Jf〉 nuclear state, the double differential SM cross section becomes [68]
with εf (|kf|) denoting the final energy (momentum) of the outgoing lepton, while ω = εi − εf stands for the excitation energy of the nucleus where εi is the initial lepton energy. For charged-current processes, the Fermi function F(Z, εf), takes into account the final state interaction of the outgoing charged particle, while for neutral-current processes such as coherent and incoherent neutrino-nucleus scattering it is F(Z, εf) = 1.
The individual cross sections in Equation (2) receive contributions from the so-called Coulomb , longitudinal , transverse electric and transverse magnetic operators for both vector and axial vector components (see the Appendix). The cross sections and are expressed in terms of the reduced matrix elements of the eight basic irreducible tensor operators [67]
Here, the + (−) sign refers to neutrino (antineutrino) scattering and θ represents the scattering angle, while the parameters a, b, d are expressed as
The 4-momentum transfer is trivially obtained from the kinematics of the process and in natural units reads
while for later convenience the magnitude of the 3-momentum transfer is defined as
For sufficiently small momentum transfer, i.e., q ≤ 1/R where R is the inverse nuclear radius1, CEνNS dominates (see Figure 1). In this case, only ground state to ground state (g.s. → g.s.) transitions occur and lead to the following simplifications: the kinematics of the reaction imply mf = 0 and |kf| = εf so that a = 1 and d = 0, while the momentum transfer can be cast in terms of the incoming neutrino energy Eν in the simple form
where the usual notation εi = εf ≡ Eν has been adopted. Note also that the excitation energy in this case is ω = 0 and , while angular momentum conservation implies that for CEνNS processes the only non-vanishing operator is the Coulomb, (see the Appendix for the definition of the operators ). Then the corresponding differential cross section is further simplified and takes the form
where the matrix element for g.s. → g.s. transitions is explicitly written in terms of the nuclear form factors for protons and neutrons , as
At CEνNS experiments the detection mechanism is sensitive to the tiny nuclear recoils generated in the aftermath of the scattering process. It is therefore reasonable to express the differential cross section with respect to the nuclear recoil energy TN, which in the low energy approximation TN ≪ Eν, reads
where and M is the mass of the nuclear isotope. The calculations of Papoulias and Kosmas [61] involved the BCS form factors for protons (neutrons)
with Nn = Z or N and represents the occupation probability amplitude of the j-th single nucleon level.
The method described above, involves realistic nuclear structure calculations making it more reliable compared to the use of phenomenological form factors, especially for accelerator neutrino sources (see the discussion in section 2.2). For the reader's convenience, Equation (11) is also expressed through the vector weak nuclear charge in the approximation of equal proton and neutron form factors, as [69]
where the vector weak charge is given by [70]
with the left- and right-handed couplings of u and d quarks to the Z-boson being
The latter expressions include the radiative corrections from the PDG [71]: , , λu, L = −0.0031, λd, L = −0.0025 and λd, R = 2λu, R = 3.7 ×10−5 while concerning the weak mixing-angle the adopted value is . Regarding the incoherent neutrino-nucleus cross section and for the sake of completeness we note that apart from the Donnelly-Walecka method given in Equation (2) a usefull formalism has been recently given in Bednyakov and Naumov [62].
The differential cross sections dσ/dTN and dσ/dcosθ are shown in the upper left and upper right panel of Figure 2, from where it can be seen that large differences appear if the form factor dependence is neglected. On the other hand at low neutrino energies, i.e., Eν ≤ 20MeV (relevant for reactor and solar neutrinos), the agreement of these two approximations is rather good. It is worth mentioning that forward scattering (θ = 0) leads to maximum dσ/dcosθ, as well as that for this particular case the form factor is by definition equal to unity due to the zero momentum transfer, see Equation (8). Finally the bottom panel illustrates a comparison of the CEνNS cross section by incorporating the nuclear form factors and by assuming F = 1.
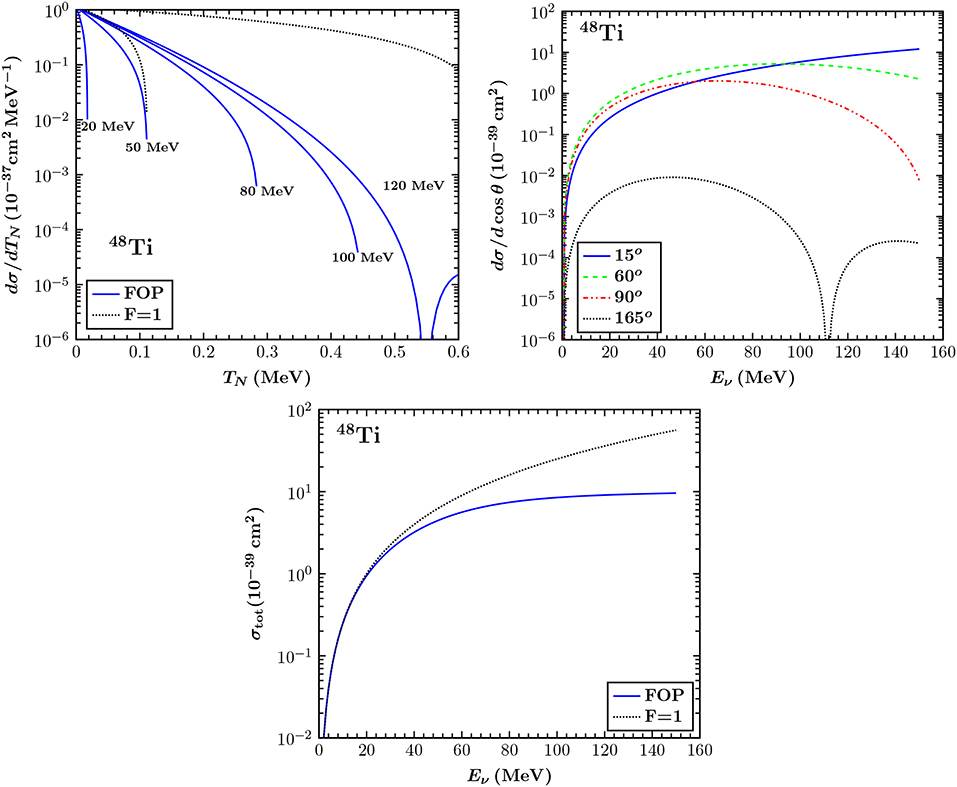
Figure 2. (Upper Left) The differential cross section dσ/dTN in terms of the nuclear recoil energy TN for different incident neutrino energies. The results are compared to the case of point-like nucleus (F = 1) for Eν = 50 and Eν = 120 MeV. (Upper Right) The differential cross section dσ/dcosθ as a function of the incoming neutrino energy Eν, for different scattering angles (for backward scattering the cross section vanishes). (Bottom) The CEνNS cross section σtot as a function of the neutrino energy. An asymptotic behavior is found at neutrino energies Eν ≥ 80 MeV or higher. Taken from Papoulias [72].
2.2. Theoretical Methods for Obtaining the Nuclear Form Factors
Electron scattering data provide high precision measurements of the proton charge density distribution [73]. The absence of similar data for neutron densities, restricts us to rely on the approximation of ρp(r) = ρn(r) and thus assume Fp(Q) = Fn(Q) ≡ F(Q) (see Equation 13). In the context of nuclear theory, it is possible to treat separately the proton and neutron nuclear form factors by employing non-trivial techniques. The most reliable methods for this purpose include the large-scale Shell-Model [74, 75], the QRPA [76], Microscopic Quasiparticle Phonon Model (MQPM) [77], the deformed Shell-Model (DSM) method [39] and others. Recently, crucial information on important nuclear parameters has been extracted from the analysis of the recent COHERENT data in Cadeddu et al. [32], Ciuffoli et al. [33], Huang and Chen [34], and Papoulias [78].
The point-nucleon charge density distribution ρ(r), is defined as the expectation value of the density operator [79]
where the + (−) sign refers to the point-proton (neutron) charge density distribution. Assuming the nuclear ground state to be approximately described by a Slater determinant constructed from single-particle wavefunctions, the distributions of Equation (16) are given by summing in quadrature the point-nucleon wavefunctions. According to Kosmas and Vergados [79], for closed (sub)shell nuclei the charge density distribution is assumed to be spherically symmetric while the interesting radial component (r = |r|) of the proton charge density distribution, ρp(r), can be cast in the form
where Rnlj(r) denotes the radial component of the single-particle wavefunction with quantum numbers n, l, and j. The nuclear form factor depends on the three momentum transfer squared q2 ≡ |q|2 and can be obtained via a Fourier transformation
where j0(x) = sinx/x denotes the zero-order Spherical Bessel function of first kind. The nuclear form factors lead to a suppression of the CEνNS cross section and subsequently to a suppression of the expected event rates (see [32] for a comparison with the COHERENT data). The uncertainties of the nuclear form factors are explored in Aristizabal Sierra et al. [35] where it is pointed out that studies looking for physics beyond the SM can be seriously affected by the uncertainty of the neutron form factor [80]. It is therefore important to treat with special care the nuclear form factors since new physics could be claimed or missed, if their uncertainties are not properly taken into account. In addition to the form factors obtained in the framework of the nuclear BCS method of Equation (12), below we present a summary of various form factor approximations widely considered in the literature.
(i) Form factors from available electron-scattering experimental data
The proton nuclear form factors , may be evaluated through a model independent analysis (e.g., by employing a Fourier-Bessel expansion) of the electron scattering data [66], having however the disadvantage of assuming .
(ii) Fractional occupation probabilities (FOP) in a simple Shell-Model
For Harmonic Oscillator (h.o.) wavefunctions the nuclear form factor for protons can be expressed in polynomial form [81, 82]
with Nmax = (2n + l)max denoting for the number of quanta of the highest occupied proton (neutron) level. In a similar manner, the radial nuclear charge density distribution ρp(r) is written in terms of the polynomials Π(r/b, Z) in the following compact form [81, 82]
with the definition χ = r/b (b stands for the h.o. size parameter). The explicit expressions for calculating the coefficients θλ and fλ are given in the Appendix.
The occupation probabilities entering Equations (18) and (19) are assumed equal to unity (zero) for the states below (above) the Fermi surface, e.g., the filling numbers of the states for closed (sub)shell nuclei are those predicted by the simple Shell-Model. Going one step further, Kosmas and Vergados [79] introduced depletion/occupation numbers to describe the occupation probabilities of the surface levels, which satisfy the relation
In this framework, there is a number of active surface nucleons (above or below the Fermi level) with non-vanishing occupation probability 0 ≤ αnlj ≤ 1 and a number of core levels with αnlj = 1. The parameters are properly adjusted so that a high reproducibility of the experimental data is achieved [66]. By introducing four parameters αi, i = 1, 2, 3, 4 in Equation (21) the polynomial Π(χ, Z) of Equation (20) reads
with λ = α1 + α2 − α3 − α4 (see [61] for the fitted values).
(iii) Use of effective expressions for the nuclear form factors
Besides calculations in the spirit of a nuclear structure model, a reliable description of the nuclear form factors (at least for low-energy reactor and solar neutrinos) may be obtained through the use of phenomenological approximations of the charge density distribution. The Helm-type density distribution is a convolution of a uniform nucleonic density with cut-off radius R0 (accounting for the interior density) with a Gaussian falloff with folding width s (surface thickness). The corresponding Helm form factor takes the analytical form as [83]
where is the 1st-order Spherical Bessel function. The first three moments can be analytically expressed as [84]
The surface thickness parameter is fixed to s = 0.9 by fitting muon spectroscopy data [85], having also the advantage of improving the matching between the Helm and the symmetrized Fermi (SF) distributions [86]. The SF approximation follows from a Woods-Saxon charge density distribution and is expressed through the half density radius c and the diffuseness parameter a, as [87]
with
while the surface thickness is written as t = 4aln 3 [32]. The corresponding first three moments of the SF form factor read [84]
The Klein-Nystrand (KN) distribution is obtained from the convolution of a Yukawa potential with range ak = 0.7 fm over a Woods-Saxon distribution (hard sphere with radius RA). The resulting KN form factor reads [88]
and is adopted by the COHERENT Collaboration, while in this case root mean square (rms) radius reads
Figure 3 presents the charge density distribution in the top panel and the corresponding nuclear form factors for 40Ar (interesting for LAr CEνNS detectors) and 48Ti (interesting for μ− → e− conversion in nuclei) in the lower panel, while the results are compared for the various methods used. A comparison of the form factors for 127I and 133Cs that are of interest for COHERENT, evaluated with the DSM method (not covered here), with those of the Helm, SF and KN parametrizations, is given in Papoulias et al. [36]. By incorporating realistic nuclear structure calculations on the basis of the BCS method, the SM CEνNS cross section is given in Figure 4 for a set of different isotopes throughout the periodic table. For heavier isotopes the form factor suppression is more pronounced and therefore the cross sections flatten more quickly, since the nuclear effects become significant even at low-energies.
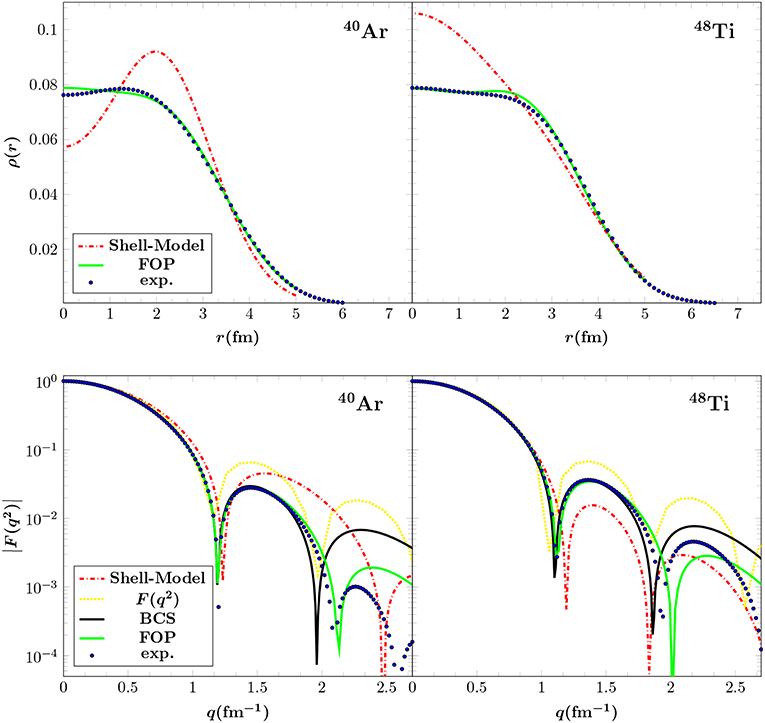
Figure 3. Charge density distribution (Top) and nuclear form factor (Bottom). The results refer to the 40Ar and 48Ti isotopes and are compared for different nuclear methods. Figure adapted from Papoulias and Kosmas [61] under the terms of the Creative Commons Attribution 4.0 International license.
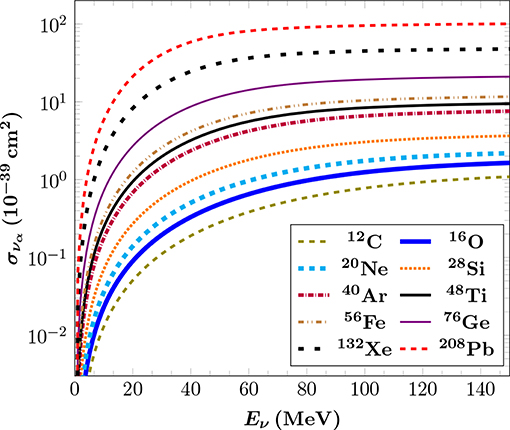
Figure 4. Integrated CEνNS cross sections for a set of nuclear targets ranging from light to heavy isotopes. Figure adapted from Papoulias and Kosmas [61] under the terms of the Creative Commons Attribution 4.0 International license.
3. Constraints Within and Beyond the SM From CEνNS
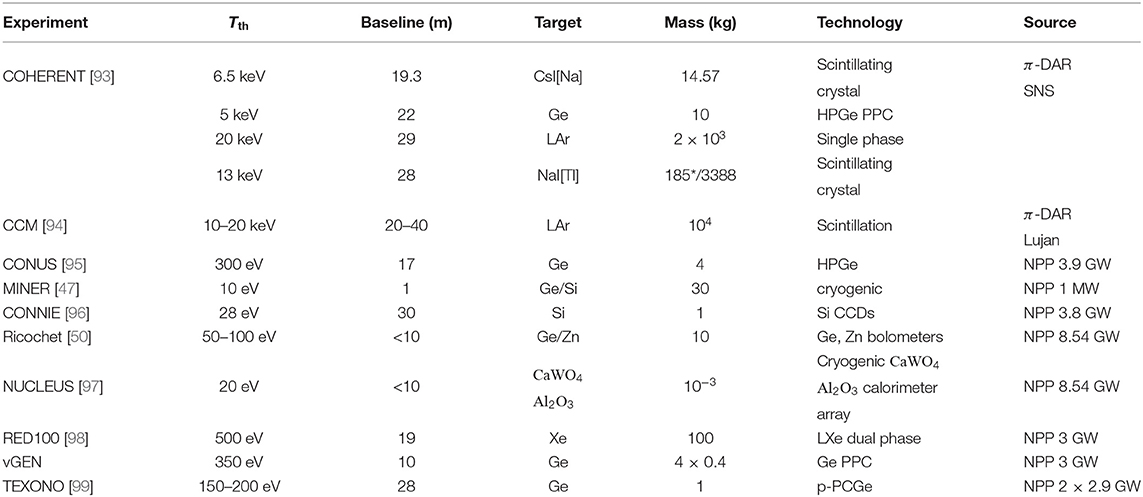
The observation of CEνNS by the COHERENT experiment with a π-DAR neutrino source is a portal to new physics triggering a considerable number of phenomenological studies at low-energies. New constraints have been put on neutrino, electroweak and nuclear physics parameters, that we devote an effort to summarize below. The experimental confirmation of CEνNS has also prompted a great rush in the experimental physics community and several projects are aiming to measure CEνNS using reactor neutrinos from nuclear power plants (NPP). It should be stressed that given the large potential of improvement in detector technology and control of systematics, it is feasible to further explore the low-energy and precision neutrino frontier. The CONUS experiment is currently running at the Brokdorf NPP (Germany) and has already released preliminary results while the COHERENT experiment has released new results from the engineering run with a LAr detector [89]. Moreover, a number of prominent experiments are in preparation such as: the MINER experiment at the TRIGA Nuclear Science Center at Texas A&M University (USA), the CONNIE project at the Angra NPP (Brazil), the NUCLEUS and Ricochet experiments at the Chooz NPP (France)2, the TEXONO program at the Kuo-Sheng NPP (Taiwan), the vGEN and RED100 experiments at the Kalinin NPP (Russia), the Coherent Captain-Mills (CCM) project at Los Alamos Neutron Science Center (LANSCE) as well as new proposals for a CEνNS measurement by employing a 51Cr source [91] and new possibilities in China3 (an exhaustive review of the CEνNS experimental developments is given in [60]). Finally, it has been recently discussed the possibility of measuring CEνNS at the European Spallation Source (ESS) [92]. Table 1 lists a summary of the current and future experimental projects, while Figure 5 demonstrates the differential event rate for the various target nuclei at π-DAR [see [100]] and at the various reactor CEνNS experiments neglecting detector efficiencies and quenching factors (QF).
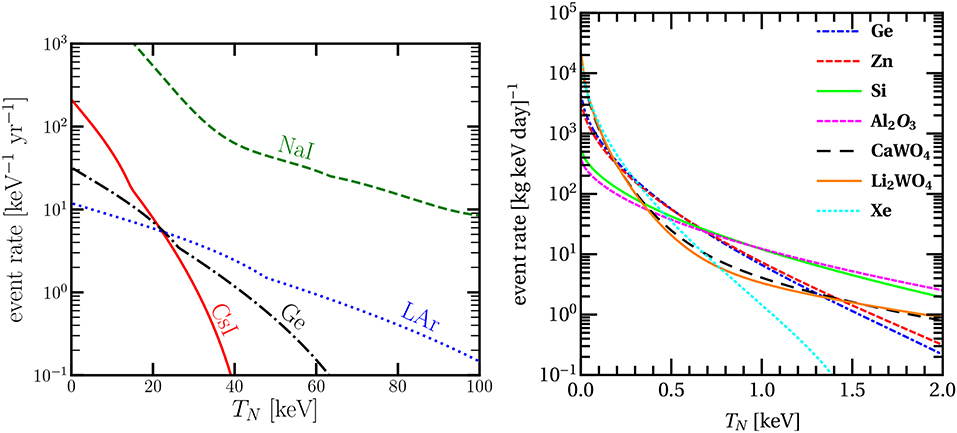
Figure 5. Expected CEνNS event rate for the different detector subsystems of the COHERENT experiment (Left) and for the different target nuclei relevant to reactor based experiments (Right). For the case of COHERENT the results are shown according to the setups of Table 1, while for reactor based experiments the calculation assumes 1 kg of each target located at 20 m from a 4 GW reactor NPP. The impact of QF and efficiency is ignored.
In reality however, these experiments are sensitive to an ionization energy (e.g., electron equivalent energy eVee) since a large portion of the nuclear recoil energy eVnr is lost to heat (conversion to phonons). The energy discrepancy has to be determined experimentally and is taken into account in terms of the QF. The latter quantity is crucial for such processes and depends on the nuclear recoil energy as well as on the target nucleus in question. Theoretically it follows the empirical form arising from the Lindhard theory [86]
with g(γ) = 3γ0.15 + 0.7γ0.6 + γ and , κ = 0.133Z2/3A−1/2. The left and right panels of Figure 6 quantify the effect of the QF in the case of CEνNS .
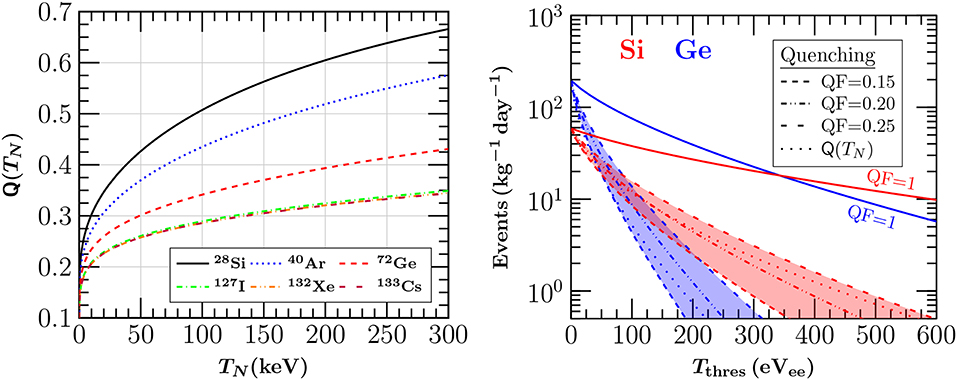
Figure 6. (Left) The QF as a function of the nuclear recoil energy. (Right) The impact of the QF on the expected number of events at a reactor based experiment assuming a typical neutrino flux of 1013cm−2s−1 for CEνNS off Silicon and Germanium detectors. The figure in the left panel has been adapted from Miranda et al. [22] under the terms of the Creative Commons Attribution 4.0 International license.
3.1. Electroweak and Nuclear Physics
The left panel of Figure 7 shows the expected number of events at the CsI[Na] detector of COHERENT and gives a comparison with the experimental data, from where it can be seen that a good agreement is reached. In Papoulias and Kosmas [21] the authors analyzed the CEνNS data and obtained a low-energy determination of the weak mixing angle, as illustrated in the right panel of Figure 7. The obtained constraint at 90% C.L. reads [21]
An interesting analysis combining atomic parity violating (APV) and CEνNS data was performed in Cadeddu and Dordei [101], while the prospects regarding the future reactor-based CEνNS experiments such as those presented in Table 1, have been extracted in Cañas et al. [102]. On the other hand, an improved determination of the CsI[Na] quenching factor can in principle lead to a significantly better agreement between the experimental results and the theoretical simulations [103], as well as to an improved sensitivity on the weak mixing angle [78].
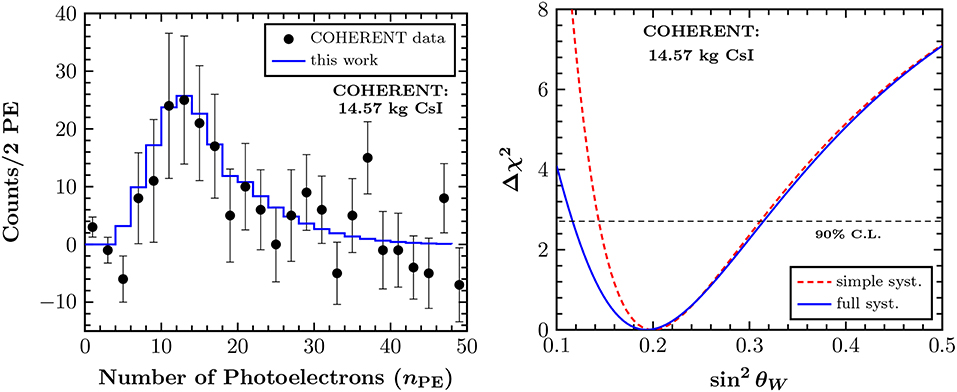
Figure 7. Comparison between the simulated number of CEνNS events and the experimental data by COHERENT (Left) and sensitivity of COHERENT on the weak mixing angle (Right). Figure adapted from Papoulias and Kosmas [21] under the terms of the Creative Commons Attribution 4.0 International license.
The discussion made in the previous section emphasized how the CEνNS cross section depends on the nuclear physics effects which are incorporated through the momentum variation of the relevant nuclear form factor. The authors of Aristizabal Sierra et al. [27] demonstrated how the intrinsic nuclear structure uncertainties may have a significant impact to searches beyond the SM such those regarding NSIs, sterile neutrinos and neutrino generalized interactions (GNIs). Starting from the form factor of Equation (18) and expanding in terms of even moments of the charge density distribution one arrives to a model independent expression [104]
with the k-th radial moment defined as
allowing the study of contributions of higher-order moments to nuclear form factors [33]. A sensitivity analysis of the two first moments with current and future COHERENT data is depicted in Figure 8 where the allowed regions are presented at 1σ, 90% and 99% C.L. The calculation in this case was restricted in the physical region [0,6] fm in order to obey the upper limit on Rn(208Pb) =5.75 ± 0.18 fm from the PREM experiment [105]. The future scenarios considered assume improved statistical uncertainties and more massive detectors in accord with the next generation COHERENT experiments [93] (see [36] for details), while as demonstrated in Patton et al. [104] multi-ton scale detectors will provide significant improvements.
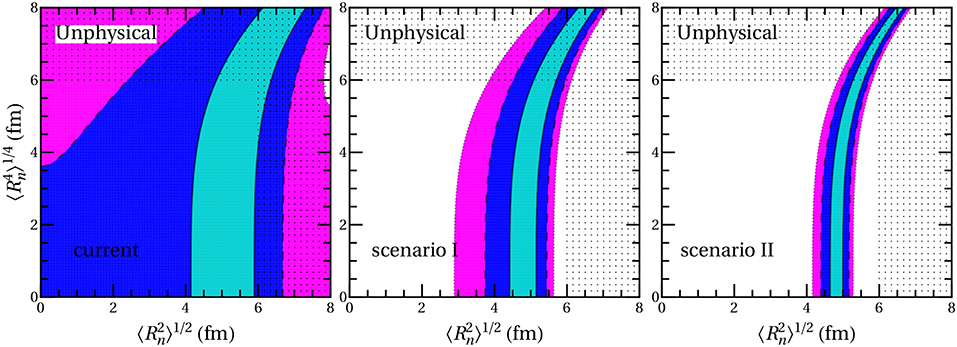
Figure 8. Sensitivity contours in the – plane from the COHERENT data assuming the current and possible future detector specifications (see the text). The allowed regions are shown at 1σ (turquoise), 90% C.L. (blue) and 99% C.L. (magenta). Taken from Papoulias et al. [36].
The average CsI neutron rms radius has been explored in Cadeddu et al. [32], Huang and Chen [36], and Papoulias et al. [34] using the energy spectrum of the available CEνNS data. The corresponding sensitivity profiles are presented in Figure 9, leading to the best fits at 90% C.L. [36]
while the potential of improvement through a more accurate determination of the QF is promising (see e.g., [78]). An independent analysis combining APV and CEνNS data was performed in Cadeddu et al. [106] leading to essentially similar results. Finally, it is worthwhile to mention the reported upper bound on the neutron skin fm [32].
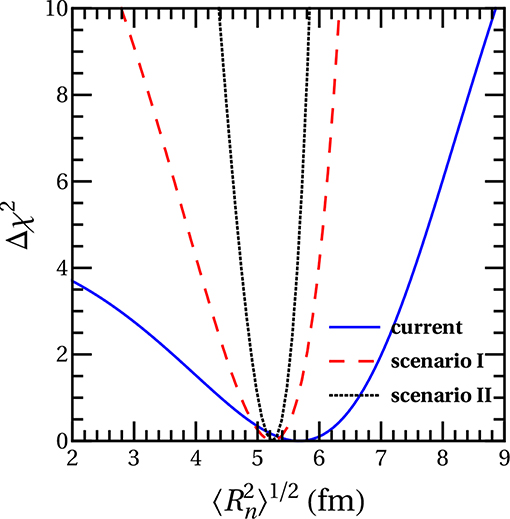
Figure 9. COHERENT sensitivity on the average nuclear rms radius of CsI assuming the current and possible future detector specifications. Taken from Papoulias et al. [36].
3.2. Non-standard and Generalized Neutrino Interactions
Non-standard interactions (NSI) [107] appear in several appealing SM extensions [108] involving four-fermion contact interaction, various seesaw realizations [109–111], left-right symmetry [112], gluonic operators [113], etc., constituting an interesting model independent probe of new physics. NSIs may have implications to SN [114], neutrino oscillations [57] and CEνNS [70, 115], while recently NSI terms were explored in the context of GNI [116] and effective field theory (EFT) operators [117, 118]. Finally the RG issue has been partly addressed in the context of NSI in Davidson and Gorbahn [119].
For sufficiently low energies vector-type NSIs arise from the effective four-fermion operators [56]
leading to new contributions to the CEνNS rate from exotic processes of the form
where α, β = {e, μ, τ} (α ≠ β), q denotes a first-generation quark q = {u, d} and P = {L, R} is the chiral projection operator. For the case of CEνNS the new interactions are taken into account through the NSI charge with the substitution in Equation (14). The latter contains flavor-preserving non-universal () and flavor changing () terms and is expressed as
implying that the NSI CEνNS cross section becomes flavor dependent.
There is a reach literature on NSI investigations with the recent COHERENT data. Assuming one nonvanishing coupling at a time, the authors of Papoulias and Kosmas [21] focused on the non-universal terms and obtained the sensitivity profiles shown in the left panel of Figure 10, while the corresponding allowed regions resulting from a combined analysis of the NSI couplings are illustrated in the upper panel of Figure 11 at 90% C.L. Regarding the future prospects of MINER, Ricochet, NUCLEUS and CONNIE, similar studies were conducted concentrating on the non-universal [120] and flavor-changing [121] terms. Indeed, a multitarget strategy can break degeneracies involved between up and down flavor-diagonal NSI terms that survives analysis of neutrino oscillation experiments [14]. Constraints on the corresponding parameters arising from leptoquarks [120], GNI [116], and EFT [117, 118] have been also reported. NSI constraints from CEνNS place meaningful constraints excluding a large part of the existing CHARM constraints and overlap with results coming out of LHC monojet searches (see [120] for a usefull comparison). Regarding the near-term future, a potential improvement on determination of the QF [103] may yield severe constraints. For example, updated bounds are possible by analyzing the number of events [78], the energy spectrum [122] as well as through a combined analysis of both energy and timing COHERENT data [123].
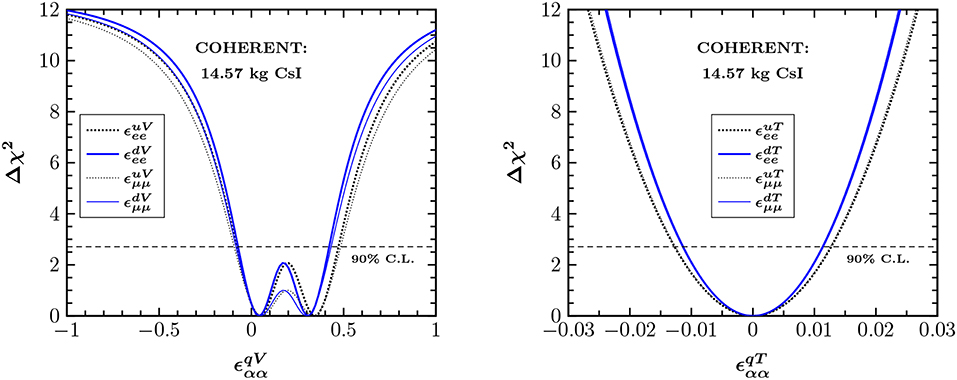
Figure 10. Sensitivity of COHERENT to vector (Left) and tensor (Right) NSI parameters. Thick (thin) curves correspond to the νe () beam. Figure adapted from Papoulias and Kosmas [21] under the terms of the Creative Commons Attribution 4.0 International license.
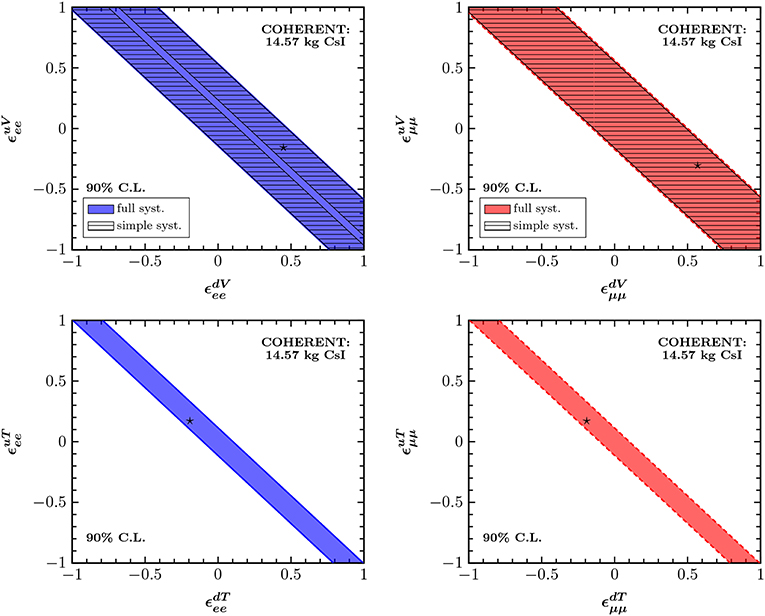
Figure 11. Sensitivity contours in the vector (Upper panel) and tensor (Lower panel) NSI parameter space. The results are presented at 90% C.L. assuming non-universal couplings only. The left (right) panel corresponds to the νe () beam, while the best-fit points are indicated by an asterisk ⋆. Figure adapted from Papoulias and Kosmas [21] under the terms of the Creative Commons Attribution 4.0 International license.
Novel tensor-type interactions are predicted in the general context of NSI [124] and GNI [116] which induce terms of the form
Such interactions violate the chirality constraint allowing for a wide class of new interactions, e.g., relevant to neutrino EM properties (see [125, 126]). Contrary to the vector NSI case, for tensorial interactions there is absence of interference with the SM interactions. In the approximation of a vector-type translation the corresponding tensor NSI charge has been expressed as [124]
while a more systematic interpretation has been carried out in Aristizabal Sierra et al. [116].
To account for the new contributions in the presence of tensorial NSI, the CEνNS cross is written [21]
with the tensor NSI factor defined as
From the analysis of the COHERENT data, the sensitivity profiles accounting to tensor NSIs, assuming one non-zero coupling at a time, are illustrated in the right panel of Figure 10 (see also [21]). The corresponding allowed regions coming out from a two parameter analysis are presented in the lower panel of Figure 11 at 90% C.L. The result is more stringent as compared to the analysis carried out in the framework of GNI for reasons discussed above. On the other hand, comparing with the vector NSI case the absence of SM-tensor NSI interference causes the allowed regions to appear with more narrow bands.
3.3. The Novel NSI Mediators Z′ (Vector) and ϕ (Scalar)
Theories beyond the SM with an additional U(1)′ symmetry have been comprehensively investigated. Regarding CEνNS related studies a novel massive mediator predicted in these concepts is expected to induce a detectable distortion to the nuclear recoil spectrum, provided that its mass is comparable to the momentum transfer. The study of models with new vector or scalar interactions that involve hidden sector particles may be also accessible at CEνNS experiments [127]. Such frameworks are interesting since they may play a central role in explaining anomalies with regards to B-meson decays at the LHCb experiment [128] and at DM searches [129].
We first examine the case of a new massive vector boson Z′. Restricting ourselves to the neutrino sector with only left-handed neutrinos the Lagrangian reads [130]
The arising cross sections imply a re-scaling of the SM one according to the expression
with the Z′ factor taking the form
Here, denotes the neutrino-vector coupling, while the respective Z′ charge reads [129]
However, in the general case the ν − Z′ coupling is flavor dependent . Denton et al. [16] has explored this possibility and concluded that for a sufficiently small momentum transfer with respect to , the new physics contributions can be addressed in the form of NSIs
where the Z′ has been integrated out. Unlike the NSI case that can only modify the energy spectrum by a global factor, the additional momentum dependence expected due to the new light mediators discussed here can be well encoded in the detected signature and subsequently lead to conclusive indications of the new physics nature.
We now turn our attention on new interactions induced by the presence of a CP-even mediator. In particular, we consider a new real scalar boson ϕ with mass Mϕ, based on the Lagrangian [130]
with and representing the scalar-quark and scalar-neutrino couplings, respectively. In this framework the SM CEνNS cross section acquires an additive contribution due to the boson exchange that can be quantified in terms of the respective cross section
with the scalar factor being
Analogously to the previous case, the corresponding scalar charge is defined as [130]
where the form factors capture the effective low-energy coupling of ϕ to the nucleon ( is the nucleon mass) for the quark q.
As discussed previously, different new physics signatures are expected to leave different imprints on the event and recoil spectrum. Contrary to the Z′ scenario discussed above, the Dirac structure of the vertex accounting for the scalar mediator is different (chirality-flipping) with respect to the SM one (chirality-conserving). Indeed, there is no interference between vector (or axial-vector) neutrino interactions and (pseudo-)scalar, tensor neutrino interactions [29, 131]. Therefore, the absence of interference between SM-scalar interactions gives rise to an overall modification of the expected CEνNS spectrum (see [129]). Moreover, comparing the vector and scalar cross sections it becomes evident that the corresponding signals are expected to be well distinguishable. The scalar effects are not pronounced at eV-thresholds, while on the contrary they are expected to be stronger at recoil energies of the order of keV. A thorough classification of the new physics signatures with respect to vector and scalar interactions is given in Aristizabal Sierra et al. [132] providing also key information on the possibility of breaking isospin-related degeneracies from combined measurements with different detector material.
Assuming universal couplings, one finds the equalities [130]
Using the COHERENT data, bounds have been put on the parameter planes and for the vector and scalar mediators, respectively [21]. In the left panel of Figure 12, the limits are shown at 90% C.L., where a degenerate area appears that cannot be excluded by the data is found due to the cancellations involved in Equation (44). However as shown in Liao and Marfatia [13] this degeneracy can be broken in the context of NSI, while for heavy mediator masses, ~50 MeV, it remains unbroken and depends on the ratio
For the case of light mediator masses , it holds
which implies that the bound is only sensitive to the coupling. The latter could be drastically improved by combining data from different detectors [133]. The case of a scalar field mediating CEνNS is explored in the right panel of Figure 12 where the extracted bounds in the plane are depicted at 90% C.L. Significant improvements are possible through powerful analyses that are based on both energy and timing COHERENT data [17] as well as by taking into account improved quenching factors [78]. The future of CEνNS experiments will offer a complementary probe to various existing limits in the low- and high-energy regime. The currently best results for a low-energy light vector mediator of have been recently reported by the CONNIE Collaboration [134]. The attainable sensitivity is expected to be competitive with existing bounds from neutrino-electron scattering, dark photon searches at BaBar and LHCb results (see [30, 120]). Before closing our discussion it is important to note that, very recently CP violating effects have been also analyzed with the current and future COHERENT data in the context of light vector mediator scenarios [27]. The latter have been also found to be applicable to reactor or solar/atmospheric neutrino searches with important implications on multi-ton dark matter detectors.
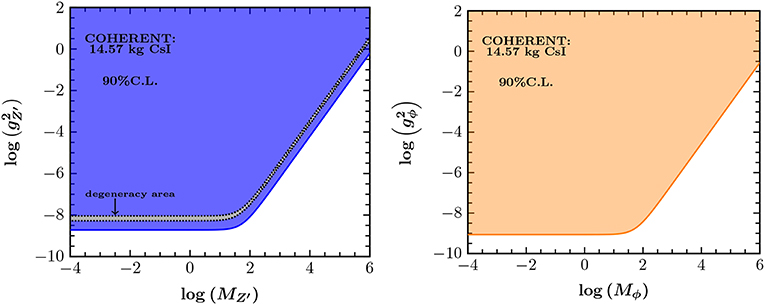
Figure 12. Excluded regions at 90% C.L. by the COHERENT experiment assuming simplified scenarios involving a Z′ vector mediator (Left panel) and a ϕ scalar mediator (Right panel). The mediator masses are in units of MeV. Figure adapted from Papoulias and Kosmas [21] under the terms of the Creative Commons Attribution 4.0 International license.
3.4. Studying Electromagnetic Neutrino Interactions
Non-trivial electromagnetic (EM) properties of massive neutrinos constitute an interesting probe to look for physics beyond the SM and at the same time they are crucial for distinguishing between the Dirac or Majorana nature of neutrinos [135]. The two main phenomenological parameters observable at a neutrino experiment are the effective neutrino magnetic moment and the neutrino charge radius (the possibility of a neutrino millicharge is explored in [23, 106]). Assuming Majorana neutrinos, the EM neutrino vertex is described by the electromagnetic field tensor Fαβ of the effective Hamiltonian [3, 136].
while for the case of Dirac neutrinos one has
It is important to note that for Majorana (Dirac) neutrinos λ = μ−iϵ is an antisymmetric complex (general complex) matrix. The two imaginary matrices μ (magnetic moment) and ϵ (electric dipole moment) obey the respective properties μT = −μ (μ = μ†) while ϵT = −ϵ (ϵ = ϵ†). It thus becomes evident that, unlike the Dirac case, for Majorana neutrinos the diagonal moments are vanishing .
For a low-energy neutrino scattering experiment the observable neutrino magnetic moment (flavor dependent) is in fact a combination of the neutrino transition magnetic moments (TMMs) discussed above. In the mass basis it reads [137]
In Equation (56) the following transformations have been introduced
where the 3−vectors 𝔞+ and 𝔞− denote positive and negative helicity states, respectively, while the magnetic moment matrix λ () in the flavor (mass) basis is written as [138]
with and being the TMMs in the flavor and mass basis, respectively, where ζα and ζi denote the corresponding CP-phases.
The potential EM neutrino properties appear in the form of an effective neutrino magnetic moment that is conveniently expressed in the mass basis according to Equation (56) in terms of fundamental parameters (TMMs, CP-violating phases and neutrino mixing angles). The latter induce an additive contribution to the SM cross section [139]
where the EM factor reads [21]
Here, the EM charge is written in terms of the fine structure constant aEM and the effective neutrino magnetic moment, as [115]
Moreover, the effect of a neutrino charge radius can be taken into consideration through a shift in the definition of the weak mixing angle [140]
where by it is denoted the low energy value of the weak mixing angle, e.g., .
The presence of a neutrino magnetic moment is expected to yield a distortion in the recoil spectrum during the CEνNS process, i.e., a detectable excess of events especially for low recoil energies. The left panel of Figure 13 shows the χ2 profile of the effective neutrino magnetic moment extracted by the first light of COHERENT data. A similar analysis has been performed in order to quantify the sensitivity of COHERENT on the neutrino charge radius as shown in the right panel of the same figure. Note that, an essential improvement due to a more accurate treatment of the QF is possible (see [78] for more details).
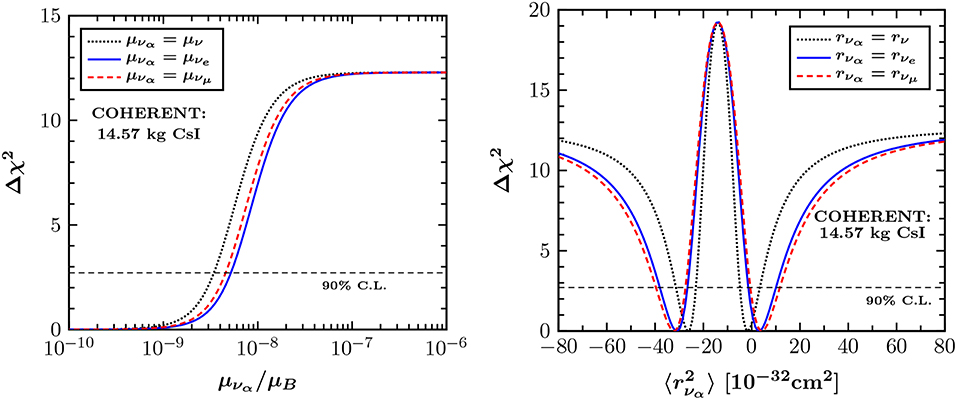
Figure 13. Constraints on electromagnetic neutrino properties by the COHERENT experiment. (Left) Sensitivity to the effective neutrino magnetic moment μνα. (Right) Sensitivity to the neutrino charge-radius . Figure adapted from Papoulias and Kosmas [21] under the terms of the Creative Commons Attribution 4.0 International license.
The authors of Miranda et al. [22] performed a comprehensive analysis on the sensitivity of various existing and future CEνNS experiments and extracted constraints on the different components Λi of the neutrino TMM matrix. In particular, their study focused on existing and next generation experimental setups of COHERENT as well as on the expected data from the future reactor-based experiments: CONUS, CONNIE, TEXONO, MINER, and RED100. In a similar manner, Billard et al. [120] extracted constraints focusing on the NUCLEUS and Ricochet detectors at the Chooz NPP, however assuming the effective neutrino magnetic moment. Miranda et al. [22] performed a systematic combined analysis with regards to the TMMs exploring also the effects of the CP violating phases of the complex matrix given in Equation (58). As a concrete example, Figure 14 shows the contours in the (|Λi|–|Λj|) parameter plane for the case of current and next generation reactor-based CEνNS experiments. It is worth mentioning that these bounds are comparable to existing ones from low energy solar neutrino data at Borexino phase-II [141]. Figure 15 shows the sensitivity contours in the plane that resulted from the COHERENT data. A similar analysis is performed in Papoulias [78] and Khan and Rodejohann [122], while for a comprehensive fit including energy and timing data the reader is referred to Cadeddu et al. [106].
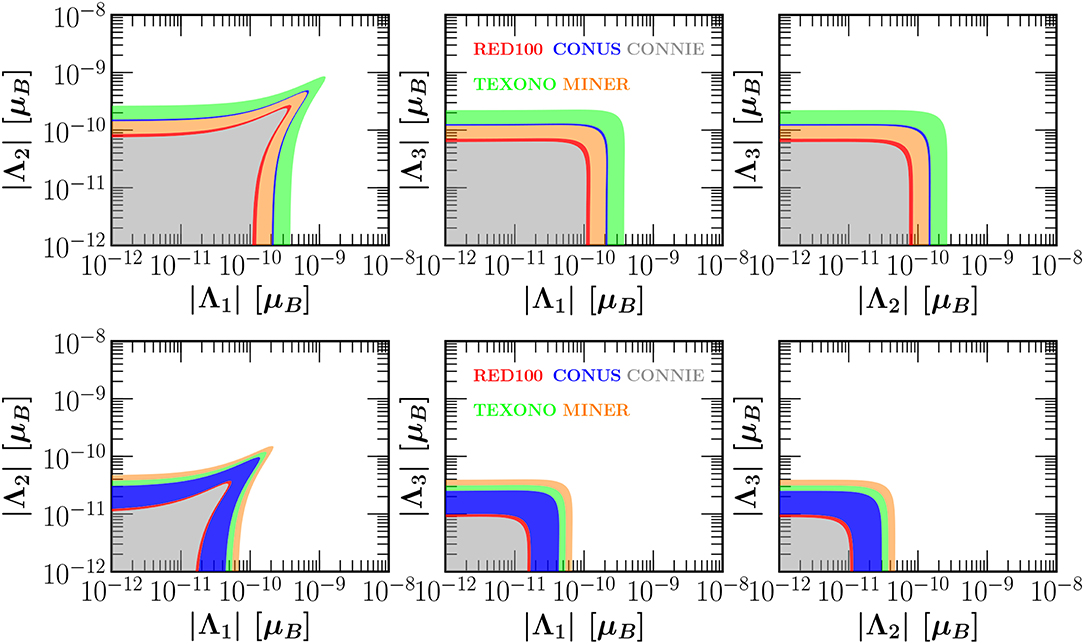
Figure 14. Sensitivity contours at 90% C.L. in the |Λi| − |Λj| parameter space that follow from the expected results of the current and future reactor based CEνNS experiments (see the text). The calculation assumes vanishing |Λk| and vanishing CP phases ζi. Figure adapted from Miranda et al. [22] under the terms of the Creative Commons Attribution 4.0 International license.
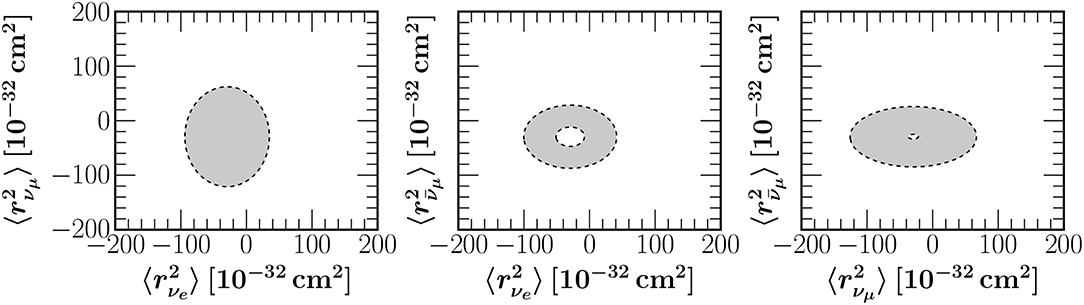
Figure 15. Sensitivity in the parameter space at 90% C.L. from the analysis of the COHERENT data. Taken from Papoulias [78].
3.5. The Existence of the Sterile Neutrinos
The three-neutrino paradigm has been put in rather solid grounds from the interpretation of solar and atmospheric oscillation data. On the other hand, controversial anomalies such as those coming from recent reactor data as well as existing anomalies implied by the LSND and MiniBooNE experiments inspired a reach phenomenology beyond the three-neutrino oscillation picture, based on the existence of a fourth sterile neutrino state with eV-scale mass (m1, 2, 3 ≪ m4) and tiny mixing angles. To accommodate sterile neutrinos the lepton mixing matrix is minimally extended so that the flavor eigenstates να, (α = e, μ, τ, s, ⋯ ) are related to the mass eigenstates νi (i = 1, 2, 3, 4, ⋯ ) by the unitary transformation . Then, for the short-baseline CEνNS experiments the survival probability of an active neutrino at a distance L is written [26]
with the abbreviation and the mass splittings under the approximation . At this point it should be stressed that neutrino-nucleus scattering experiments are favorable facilities to probe sterile neutrinos being complementary to dedicated experiments such as MINOS/MINOS+ [142], MiniBooNE [143], Daya-Bay [144], Juno [145], and NEOS [146]. Indeed, due to the purely neutral-current character of the CEνNS process it is not necessary to disentangle between active-sterile neutrino mixing [147].
The possibility of investigating sterile neutrinos in the simplest (3+1) scheme through the CEνNS process was examined for the first time in Anderson et al. [148], relying on an SNS source. A combined sterile neutrino analysis was performed in Kosmas et al. [24] highlighting the complementarity between accelerator and reactor neutrino sources, by focusing on COHERENT and TEXONO experiments, respectively (see Figure 16). Moreover, a detailed study of various reactor-based CEνNS proposals has been carried out in Cañas et al. [25], showing how such future measurements can be exploited to solve the reactor antineutrino anomaly. After the first observation of CEνNS by the COHERENT experiment, Papoulias and Kosmas [21] reported the first constraints under the assumption of a universal new mixing angle, extracting the conclusion that the current sensitivity is rather poor. By exploiting timing data the potential of a future measurement at the next generation of COHERENT with a 100 kg CsI detector has been demonstrated in Blanco et al. [26], concluding that the prospects of probing the exclusion regions in the (–) plane from the latest MiniBooNE [143] and LSND [149] are promising. Finally, focusing at CONUS in Berryman [150] it was shown that the complementarity between terrestrial-cosmological experiments may resolve the tension raised by astrophysical observations regarding the existence of sterile neutrinos.
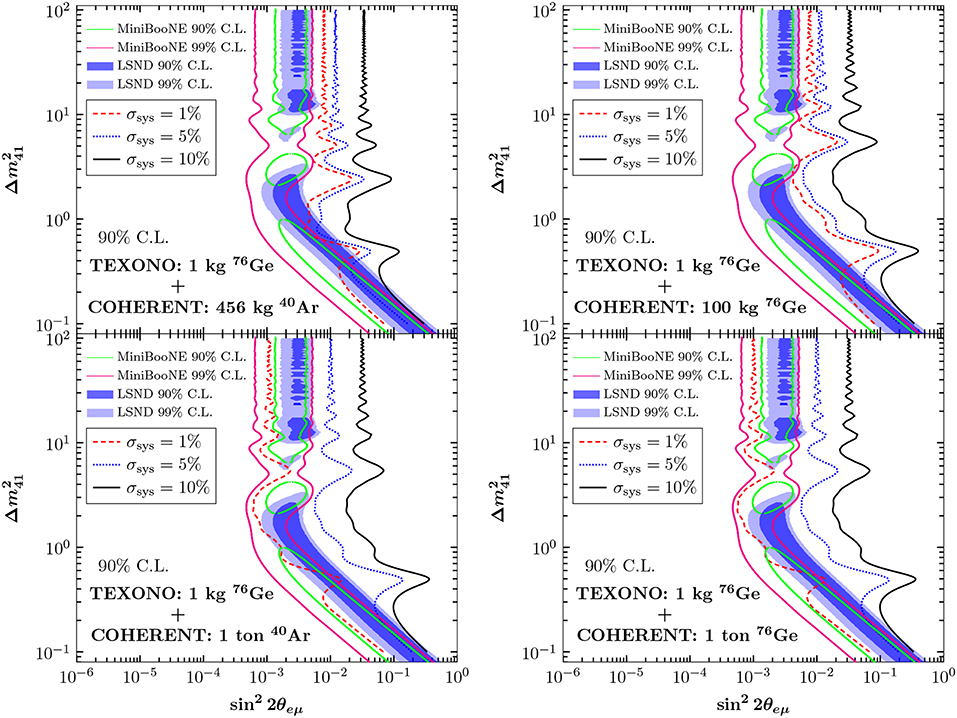
Figure 16. Exclusion curves at 90% C.L. in the (–) parameter plane from a combined analysis of COHERENT and TEXONO experiments. The results are compared to existing constraints from MiniBooNE and LSND. Figure reproduced from Kosmas et al. [24] with the permission of the American Physical Society and with updated results from MiniBooNE [143].
3.6. Summary of Constraints
Emphasis has been put on the physics beyond the SM by devoting a great part to the past and current research efforts and by concentrating on the various channels contributing to CEνNS processes and their interpretation. Through a χ2 sensitivity analysis, based on the recoil or timing spectra of the COHERENT data, the current limits are listed at 90% C.L. in Table 2. For a given parameter set , the best fit is found through the minimum value . The limits involve electroweak (weak-mixing angle), nuclear (nuclear radius), and physics beyond the SM (NSIs and EM neutrino properties). Significant improvements are expected through a more accurate determination of the QF and from a better control of the systematic uncertainties. The reported constraints on electroweak and NSIs have been extracted with various analysis methods, i.e., by combining existing APV measurements or global oscillation constraints with the recent COHERENT data, emphasizing the complementarity of CEνNS data in the low energy regime.
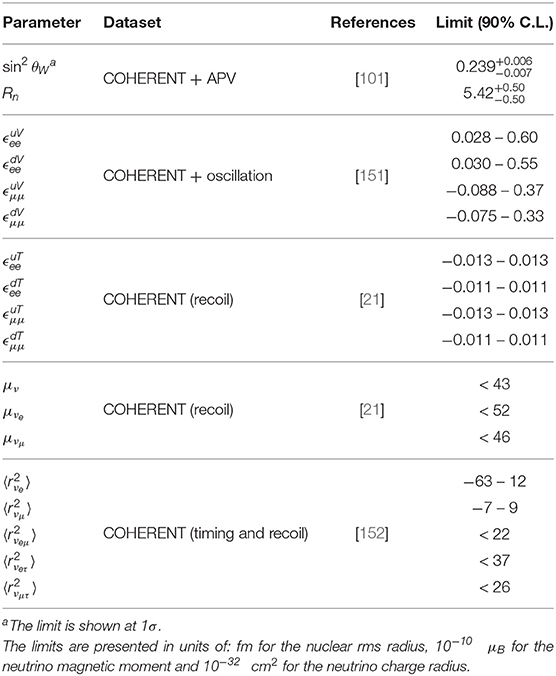
Table 2. Constraints on electroweak, nuclear and new physics parameters at 90% C.L. after the first CEνNS measurement by the COHERENT experiment.
4. Connection of CEνNS With Dark Matter, CLFV Processes and Astrophysics
Neutrino-nucleus scattering is one of the dominant processes taking place in SN environment and thus the emitted neutrinos can be an extremely useful tool for deep sky investigations. Moreover, SN constitute an ideal source for flavor physics applications since all flavors are involved. Going beyond the SM, potential FCNC under stellar conditions can modify the percentage of the neutrino flavors in the interior of massive stars [58]. The latter, may drastically affect a plethora of other processes governing the explosive-stellar nucleosynthesis [153], causing significant alteration of the evolution phenomena [114, 154]. If large enough, the modified neutrino energy-densities arriving at the terrestrial SN-neutrino detectors can be tested at CEνNS experiments [155]. It should be stressed that a SN neutrino burst can be well detected by the current technology DM detectors.
Direct Dark Matter detection experiments are expected to be sensitive to astrophysical neutrinos from the Sun, the Atmosphere and from core-collapse SN (e.g., diffuse supernova background, DSNB) [156, 157]. The neutrino-floor [158], being an irreducible background determines the criteria for using the appropriate detector material, threshold, mass, etc. Figure 17 illustrates the differential and integrated event rate of CEνNS expected at a ton-scale DM detector, calculated in the framewrok of the DSM assuming only SM interactions. Future precision measurements at such rare-event facilities may become sensitive to nuclear structure effects which in principle can be explored by experiments looking for CEνNS. Therefore precise information on the nuclear form factors becomes very relevant for DM detectors especially for those involving multi-ton mass scale [35]. For example, alterations are expected at high recoil energies of neutrino-induced interactions at direct DM detection searches [39] which on the other hand may be limited by the current uncertainties of the Atmospheric and DSNB neutrinos. Models involving light mediators are well testable at CEνNS searches and may offer a key solution to LMA-Dark [151, 159] as well as implications to DM searches [28, 133] and to the neutrino floor [40]. In the same spirit, combined analyses of oscillation and CEνNS data [15, 18] concluded that the LMA-D solution is excluded at 3.1σ (3.6σ) for NSI with up (down) quarks. Finally, it has been recently pointed out that potential DM-induced signatures from dark photon decay could be also detectable at CEνNS experiments, explaining an excess in the timing distribution of the COHERENT signal [44].
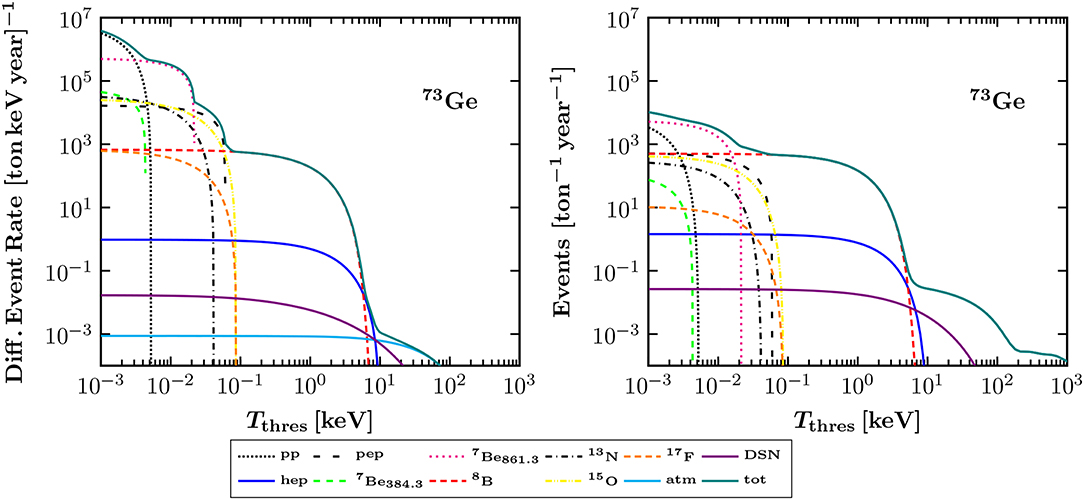
Figure 17. Differential event rate (Left) and total number of events above threshold (Right) expected due to CEνNS from solar, Atmospheric and DSNB neutrinos at a Germanium detector. Figure adapted from Papoulias et al. [39] under the terms of the Creative Commons Attribution 4.0 International license.
In the case of cLFV processes of μ → e transitions, especially coherent μ− → e− conversion in the field of nuclei has attracted much interest in the context of new physics mechanisms discussed in this article [160]. For example, μ → e conversion has been studied in the context of the inverse seesaw [109] and new Z′ mediators [161]. It is given by
which might have close relations to the process given in Equation (36) in the neutral sector. When the final nuclear state coincides the ground state this process could be a coherent channel, which in fact dominates by its enhancement by a factor of the square of the number of nucleons in nuclei. The cLFV processes are known to be highly suppressed in the SM even with lepton mixing due to the small neutrino masses, down to [162]. However, many theoretical models involving NSI predict sizable rates which the future experiments could reach [163]. The future experiments aiming to search for μ− → e− conversion are under preparation at J-PARC, Japan (COMET) [164] and Fermilab, in the USA (Mu2e) [165]. They expect to measure a characteristic peak of outgoing electrons (at energy Ee ≈ mμ) emitted from muonic atoms in a target. These experiments are aiming at sensitivities of the order of to , which is a factor of 10,000 or more improvement over the current experimental limits. Therefore they have excellent potential to establish or rule out the presence of new physics in the near future.
It is important to notice that theoretically the μ− → e− branching ratio depends on the nuclear form factor which can be probed from CEνNS measurements as discussed in Sect 3. For the relevant nuclei such as 27Al and 48Ti the nuclear form factors at have values 0.63 and 0.53, respectively, i.e., well far from the approximation of point like nucleus (see [81] for a detailed discussion). The incoherent channels of μ → e conversion can be studied with the matrix elements described in section 2 (see for example [82, 166]). Once μ− → e− conversion is observed, it holds significant potential for constraining the parameters of the NSI Lagrangian of the lepton-nucleus interactions [167]. It may shed light on FCNC processes in the leptonic sector [168–170], and particularly on the existence of the charged-lepton mixing which is analogous to neutrino oscillations at short baseline experiments.
5. Summary and Conclusions
In this review article, we made an attempt to summarize the main research efforts devoted to the conventional and exotic neutrino-nucleus interactions, in the recent years. The standard process of neutral-current neutrino-nucleus scattering, mediated by the neutral Z-boson boson presents two channels the elastic and inelastic scattering of neutrinos (and anti-neutrinos) off a nuclear isotope (A, Z), with A nucleons and Z protons. In the elastic process, the initial and final states of the target nucleus are the same and the detectable signal is an energy recoil, whereas in the case of the inelastic channel, the final nucleus is an excited state with the signal being a de-excitation product (gammas). We have mainly concentrated on beyond the SM neutrino-nucleus interactions, and especially on the prospects of extracting new physics from the operating prominent rare-event detectors looking for the coherent elastic neutrino-nucleus scattering. Such channels may involve lepton LFV in neutral-currents. This is motivated by the recent measurements of CEνNS events at the COHERENT experiment, the analysis and interpretation of which may imply the necessity of including non-standard neutrino-nucleus interactions. Toward this end, we discussed the impact of non-standard interactions and novel Z′ or ϕ mediators to the CEνNS event rates providing an estimation of the attainable sensitivities at current and future experiments. With regards to neutrino oscillations constraints on NSIs from neutral current interactions at CEνNS experiments are complementary since the former are only to sensitive to differences between the diagonal terms. It is furthermore expected that the next generation of the currently operating experiments like the COHERENT, TEXONO, MINER, CONUS, RED100, vGEN, Ricochet, NUCLEUS etc., will be of benefit to unravel open issues of the leptonic sector. The studies covered in this review article have evident connection with neutrino astronomy, SN physics, direct DM detection and cLFV processes. To understand these new interactions the proton and neutron weak nuclear form factors play key roles. This opens up the necessity of measuring the neutron nuclear form factors by appropriately designed and appreciably sensitive experiments such as those looking for CEνNS processes.
Author Contributions
DP: sensitivity analysis. TK: incoherent formalism. YK: experimental physics.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are grateful to Valentina De Romeri and Jorge Terol Calvo for fruitful discussions as well as to M. Cadeddu and F. Dordei for useful correspondence. DP is supported by the Spanish grants SEV-2014-0398 and FPA2017-85216-P (AEI/FEDER, UE), PROMETEO/2018/165 (Generalitat Valenciana) and the Spanish Red Consolider MultiDark FPA2017-90566-REDC. YK acknowledges support by the JSPS KAKENHI Grant No. 18H04231.
Footnotes
1. ^Typically 25-150 MeV for most nuclei.
2. ^BASKET [90] is a synergy of Ricochet and NUCLEUS that is developing a Li2WO4[Mo] Scintillating bolometer.
3. ^See e.g., talk by Ran Han: 10.5281/zenodo.3464505
References
1. Ejiri H, Suhonen J, Zuber K. Neutrino-nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys Rept. (2019) 797:1–102. doi: 10.1016/j.physrep.2018.12.001
2. Schechter J, Valle JWF. Neutrino masses in SU(2) x U(1) theories. Phys Rev D. (1980) 22:2227. doi: 10.1103/PhysRevD.22.2227
3. Schechter J, Valle JWF. Neutrino decay and spontaneous violation of lepton number. Phys Rev D. (1982) 25:774. doi: 10.1103/PhysRevD.25.774
4. Kosmas TS, Oset E. Charged current neutrino nucleus reaction cross-sections at intermediate-energies. Phys Rev C. (1996) 53:1409–15. doi: 10.1103/PhysRevC.53.1409
5. Ejiri H. Nuclear spin isospin responses for low-energy neutrinos. Phys Rept. (2000) 338:265–351. doi: 10.1016/S0370-1573(00)00044-2
6. Balasi KG, Langanke K, Martínez-Pinedo G. Neutrino–nucleus reactions and their role for supernova dynamics and nucleosynthesis. Prog Part Nucl Phys. (2015) 85:33–81. doi: 10.1016/j.ppnp.2015.08.001
7. Freedman DZ. Coherent neutrino nucleus scattering as a probe of the weak neutral current. Phys Rev D. (1974) 9:1389–92. doi: 10.1103/PhysRevD.9.1389
8. Tubbs DL, Schramm DN. Neutrino opacities at high temperatures and densities. Astrophys J. (1975) 201:467–88. doi: 10.1086/153909
9. Drukier A, Stodolsky L. Principles and applications of a neutral current detector for neutrino physics and astronomy. Phys Rev D. (1984) 30:2295. doi: 10.1103/PhysRevD.30.2295
10. Akimov D, Albert JB, An P, Awe C, Barbeau PS, Becker B, et al. Observation of coherent elastic neutrino-nucleus scattering. Science. (2017) 357:1123–6. doi: 10.1126/science.aao0990
11. Akimov D, Albert JB, An P, Awe C, Barbeau PS, Becker B, et al. COHERENT collaboration data release from the first observation of coherent elastic neutrino-nucleus scattering. arXiv:1804.09459.
12. Aristizabal Sierra D, Balantekin AB, Caratelli D, Cogswell B, Collar JI, Dahl CE, et al. Proceedings of the magnificent CEνNS workshop 2018. arXiv:1910.07450.
13. Liao J, Marfatia D. COHERENT constraints on nonstandard neutrino interactions. Phys Lett B. (2017) 775:54–7. doi: 10.1016/j.physletb.2017.10.046
14. Dent JB, Dutta B, Liao S, Newstead JL, Strigari LE, Walker JW. Accelerator and reactor complementarity in coherent neutrino-nucleus scattering. Phys Rev D. (2018) 97:035009. doi: 10.1103/PhysRevD.97.035009
15. Aristizabal Sierra D, Rojas N, Tytgat MHG. Neutrino non-standard interactions and dark matter searches with multi-ton scale detectors. JHEP. (2018) 1803:197. doi: 10.1007/JHEP03(2018)197
16. Denton PB, Farzan Y, Shoemaker IM. Testing large non-standard neutrino interactions with arbitrary mediator mass after COHERENT data. JHEP. (2018) 1807:037. doi: 10.1007/JHEP07(2018)037
17. Dutta B, Liao S, Sinha S, Strigari LE. Searching for beyond the standard model physics with COHERENT energy and timing data. Phys Rev Lett. (2019) 123:061801. doi: 10.1103/PhysRevLett.123.061801
18. Coloma P, Gonzalez-Garcia MC, Maltoni M, Schwetz T. COHERENT enlightenment of the neutrino dark side. Phys Rev D. (2017) 96:115007. doi: 10.1103/PhysRevD.96.115007
19. Gonzalez-Garcia MC, Maltoni M, Perez-Gonzalez YF, Zukanovich Funchal R. Neutrino discovery limit of dark matter direct detection experiments in the presence of non-standard interactions. JHEP. (2018) 1807:019. doi: 10.1007/JHEP07(2018)019
20. Kosmas TS, Miranda OG, Papoulias DK, Tortola M, Valle JWF. Probing neutrino magnetic moments at the Spallation Neutron Source facility. Phys Rev D. (2015) 92:013011. doi: 10.1103/PhysRevD.92.013011
21. Papoulias DK, Kosmas TS. COHERENT constraints to conventional and exotic neutrino physics. Phys Rev D. (2018) 97:033003. doi: 10.1103/PhysRevD.97.033003
22. Miranda OG, Papoulias DK, Tórtola M, Valle JWF. Probing neutrino transition magnetic moments with coherent elastic neutrino-nucleus scattering. JHEP. (2019) 1907:103. doi: 10.1007/JHEP07(2019)103
23. Parada A. New constraints on neutrino electric millicharge from elastic neutrino-electron scattering and coherent elastic neutrino-nucleus scattering. arXiv:1907.04942.
24. Kosmas TS, Papoulias DK, Tortola M, Valle JWF. Probing light sterile neutrino signatures at reactor and Spallation Neutron Source neutrino experiments. Phys Rev D. (2017) 96:063013. doi: 10.1103/PhysRevD.96.063013
25. Cañas BC, Garcés EA, Miranda OG, Parada A. The reactor antineutrino anomaly and low energy threshold neutrino experiments. Phys Lett B. (2018) 776:451–6. doi: 10.1016/j.physletb.2017.11.074
26. Blanco C, Hooper D, Machado P. Constraining sterile neutrino interpretations of the LSND and MiniBooNE anomalies with coherent neutrino scattering experiments. arXiv:1901.08094.
27. Aristizabal Sierra D, De Romeri V, Rojas N. CP violating effects in coherent elastic neutrino-nucleus scattering processes. JHEP. (2019) 09:069. doi: 10.1007/JHEP09(2019)069
28. Dent JB, Dutta B, Liao S, Newstead JL, Strigari LE, Walker JW. Probing light mediators at ultralow threshold energies with coherent elastic neutrino-nucleus scattering. Phys Rev D. (2017) 96:095007. doi: 10.1103/PhysRevD.96.095007
29. Farzan Y, Lindner M, Rodejohann W, Xu XJ. Probing neutrino coupling to a light scalar with coherent neutrino scattering. JHEP. (2018) 1805:066. doi: 10.1007/JHEP05(2018)066
30. Abdullah M, Dent JB, Dutta B, Kane GL, Liao S, Strigari LE. Coherent elastic neutrino nucleus scattering as a probe of a Z′ through kinetic and mass mixing effects. Phys Rev D. (2018) 98:015005. doi: 10.1103/PhysRevD.98.015005
31. Brdar V, Rodejohann W, Xu XJ. Producing a new fermion in coherent elastic neutrino-nucleus scattering: from neutrino mass to dark matter. JHEP. (2018) 1812:024. doi: 10.1007/JHEP12(2018)024
32. Cadeddu M, Giunti C, Li YF, Zhang YY. Average CsI neutron density distribution from COHERENT data. Phys Rev Lett. (2018) 120:072501. doi: 10.1103/PhysRevLett.120.072501
33. Ciuffoli E, Evslin J, Fu Q, Tang J. Extracting nuclear form factors with coherent neutrino scattering. Phys Rev D. (2018) 97:113003. doi: 10.1103/PhysRevD.97.113003
34. Huang XR, Chen LW. Neutron skin in CsI and low-energy effective weak mixing angle from COHERENT data. arXiv:1902.07625. (2019). doi: 10.1103/PhysRevD.100.071301
35. Aristizabal Sierra D, Liao J, Marfatia D. Impact of form factor uncertainties on interpretations of coherent elastic neutrino-nucleus scattering data. JHEP. (2019) 1906:141. doi: 10.1007/JHEP06(2019)141
36. Papoulias D, Kosmas T, Sahu R, Kota V, Hota M. Constraining nuclear physics parameters with current and future COHERENT data. arXiv:1903.03722.
37. Arcadi G, Lindner M, Martins J, Queiroz FS. New physics probes: atomic parity violation, polarized electron scattering and neutrino-nucleus coherent scattering. arXiv:1906.04755.
38. Cadeddu M, Dordei F, Giunti C, Kouzakov K, Picciau E, Studenikin A. Potentialities of a low-energy detector based on 4He evaporation to observe atomic effects in coherent neutrino scattering and physics perspectives. arXiv:1907.03302. (2019). doi: 10.1103/PhysRevD.100.073014
39. Papoulias DK, Sahu R, Kosmas TS, Kota VKB, Nayak B. Novel neutrino-floor and dark matter searches with deformed shell model calculations. Adv High Energy Phys. (2018) 2018:6031362. doi: 10.1155/2018/6031362
40. Bœhm C, Cerdeño DG, Machado PAN, Olivares-Del Campo A, Reid E. How high is the neutrino floor? JCAP. (2019) 1901:043. doi: 10.1088/1475-7516/2019/01/043
41. Link JM, Xu XJ. Searching for BSM neutrino interactions in dark matter detectors. JHEP. (2019) 08:004. doi: 10.1007/JHEP08(2019)004
42. Ge SF, Shoemaker IM. Constraining photon portal dark matter with texono and coherent data. JHEP. (2018) 1811:066. doi: 10.1007/JHEP11(2018)066
43. Ng KCY, Beacom JF, Peter AHG, Rott C. Solar atmospheric neutrinos: a new neutrino floor for dark matter searches. Phys Rev D. (2017) 96:103006. doi: 10.1103/PhysRevD.96.103006
44. Dutta B, Kim D, Liao S, Park JC, Shin S, Strigari LE. Dark matter signals from timing spectra at neutrino experiments. arXiv:1906.10745.
45. Wong HT. Neutrino-nucleus coherent scattering and dark matter searches with sub-keV germanium detector. Nucl Phys A. (2010) 844:229C–33C. doi: 10.1016/j.nuclphysa.2010.05.040
46. Aguilar-Arevalo A, Bertou X, Bonifazi C, Butner M, Cancelo G, Castaneda Vazquez A, et al. Results of the engineering run of the coherent neutrino nucleus interaction experiment (CONNIE). JINST. (2016) 11:P07024. doi: 10.1088/1748-0221/11/07/P07024
47. Agnolet G, Baker W, Barker D, Beck R, Carroll TJ, Cesar J, et al. Background studies for the MINER coherent neutrino scattering reactor experiment. Nucl Instrum Meth A. (2017) 853:53–60. doi: 10.1016/j.nima.2017.02.024
48. Belov V, Brudanin V, Egorov V, Filosofov D, Fomina M, Gurov Y, et al. The νGeN experiment at the Kalinin nuclear power plant. JINST. (2015) 10:P12011. doi: 10.1088/1748-0221/10/12/P12011
50. Billard J, Carr R, Dawson J, Figueroa-Feliciano E, Formaggio JA, Gascon J, et al. Coherent neutrino scattering with low temperature bolometers at chooz reactor complex. J Phys G. (2017) 44:105101. doi: 10.1088/1361-6471/aa83d0
51. Strauss R, Rothe J, Angloher G, Bento A, Gütlein A, Hauff d, et al. The ν-cleus experiment: a gram-scale fiducial-volume cryogenic detector for the first detection of coherent neutrino-nucleus scattering. Eur Phys J C. (2017) 77:506. doi: 10.1140/epjc/s10052-017-5068-2
52. Barranco J, Miranda OG, Moura CA, Valle JWF. Constraining non-standard interactions in nu(e) e or anti-nu(e) e scattering. Phys Rev D. (2006) 73:113001. doi: 10.1103/PhysRevD.73.113001
53. Friedland A, Lunardini C, Maltoni M. Atmospheric neutrinos as probes of neutrino-matter interactions. Phys Rev D. (2004) 70:111301. doi: 10.1103/PhysRevD.70.111301
54. Friedland A, Lunardini C, Pena-Garay C. Solar neutrinos as probes of neutrino matter interactions. Phys Lett B. (2004) 594:347. doi: 10.1016/j.physletb.2004.05.047
55. Friedland A, Lunardini C. A Test of tau neutrino interactions with atmospheric neutrinos and K2K. Phys Rev D. (2005) 72:053009. doi: 10.1103/PhysRevD.72.053009
56. Miranda OG, Nunokawa H. Non standard neutrino interactions: current status and future prospects. New J Phys. (2015) 17:095002. doi: 10.1088/1367-2630/17/9/095002
57. Farzan Y, Tortola M. Neutrino oscillations and non-standard interactions. Front Phys. (2018) 6:10. doi: 10.3389/fphy.2018.00010
58. Amanik PS, Fuller GM, Grinstein B. Flavor changing supersymmetry interactions in a supernova. Astropart Phys. (2005) 24:160–82. doi: 10.1016/j.astropartphys.2005.06.004
59. Esteban-Pretel A, Tomas R, Valle JWF. Interplay between collective effects and non-standard neutrino interactions of supernova neutrinos. Phys Rev D. (2010) 81:063003. doi: 10.1103/PhysRevD.81.063003
60. Akimov DYu, Belov VA, Bolozdynya A, Efremenko YuV, Konovalov AM, Kumpan AV, et al. Coherent elastic neutrino scattering on atomic nucleus: recently discovered type of low-energy neutrino interaction. Phys Usp. (2019) 62:166–78.
61. Papoulias DK, Kosmas TS. Standard and nonstandard neutrino-nucleus reactions cross sections and event rates to neutrino detection experiments. Adv High Energy Phys. (2015) 2015:763648. doi: 10.1155/2015/763648
62. Bednyakov VA, Naumov DV. Coherency and incoherency in neutrino-nucleus elastic and inelastic scattering. Phys Rev D. (2018) 98:053004. doi: 10.1103/PhysRevD.98.053004
63. Bednyakov VA, Naumov DV. On coherent neutrino and antineutrino scattering off nuclei. arXiv:1904.03119.
64. Almosly W, Carlsson BG, Suhonen J, Ydrefors E. Neutral-current supernova-neutrino cross sections for 204, 206, 208Pb calculated by Skyrme quasiparticle random-phase approximation. Phys Rev C. (2019) 99:055801. doi: 10.1103/PhysRevC.99.055801
65. Chasioti VC, Kosmas TS. A unified formalism for the basic nuclear matrix elements in semi-leptonic processes. Nucl Phys A. (2009) 829:234–52. doi: 10.1016/j.nuclphysa.2009.08.009
66. De Vries H, De Jager CW, De Vries C. Nuclear charge and magnetization density distribution parameters from elastic electron scattering. Atom Data Nucl Data Tabl. (1987) 36:495–536. doi: 10.1016/0092-640X(87)90013-1
67. Donnelly TW, Walecka JD. Semileptonic weak and electromagnetic interactions with nuclei: isoelastic processes. Nucl Phys A. (1976) 274:368–412. doi: 10.1016/0375-9474(76)90209-8
68. Donnelly TW, Peccei RD. Neutral current effects in nuclei. Phys Rept. (1979) 50:1. doi: 10.1016/0370-1573(79)90010-3
69. Lindner M, Rodejohann W, Xu XJ. Coherent neutrino-nucleus scattering and new neutrino interactions. JHEP. (2017) 1703:097. doi: 10.1007/JHEP03(2017)097
70. Barranco J, Miranda OG, Rashba TI. Probing new physics with coherent neutrino scattering off nuclei. JHEP. (2005) 512:21. doi: 10.1088/1126-6708/2005/12/021
71. Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F, et al. Review of particle physics. Phys Rev D. (2018) 98:030001.
72. Papoulias DK. Exotic lepton flavour violating processes in the field of nucleus. (Ph.D. thesis). Ioannina University (2016). Available online at: http://dx.doi.org/http://hdl.handle.net/10442/hedi/43131
73. Angeli I, Marinova KP. Table of experimental nuclear ground state charge radii: an update. Atom Data Nucl Data Tabl. (2013) 99:69–95. doi: 10.1016/j.adt.2011.12.006
74. Kortelainen M, Suhonen J, Toivanen J, Kosmas TS. Event rates for CDM detectors from large-scale shell-model calculations. Phys Lett B. (2006) 632:226–32. doi: 10.1016/j.physletb.2005.10.057
75. Toivanen P, Kortelainen M, Suhonen J, Toivanen J. Large-scale shell-model calculations of elastic and inelastic scattering rates of lightest supersymmetric particles (LSP) on I-127, Xe-129, Xe-131, and Cs-133 nuclei. Phys Rev C. (2009) 79:044302. doi: 10.1103/PhysRevC.79.044302
76. Papoulias DK, Kosmas TS. Nuclear aspects of neutral current non-standard ν-nucleus reactions and the role of the exotic μ−→e− transitions experimental limits. Phys Lett B. (2014) 728:482–8. doi: 10.1016/j.physletb.2013.12.028
77. Pirinen P, Suhonen J, Ydrefors E. Neutral-current neutrino-nucleus scattering off Xe isotopes. Adv High Energy Phys. (2018) 2018:9163586. doi: 10.1155/2018/9163586
78. Papoulias DK. COHERENT constraints after the Chicago-3 quenching factor measurement. arXiv:1907.11644.
79. Kosmas TS, Vergados JD. Nuclear densities with fractional occupation probabilities of the states. Nucl Phys A. (1992) 536:72–86. doi: 10.1016/0375-9474(92)90246-G
80. Amanik PS, McLaughlin GC. Nuclear neutron form factor from neutrino nucleus coherent elastic scattering. J Phys G. (2009) 36:015105. doi: 10.1088/0954-3899/36/1/015105
81. Kosmas TS, Vergados JD. Nuclear matrix elements for the coherent μ−e conversion process. Phys Lett B. (1988) 215:460–4. doi: 10.1016/0370-2693(88)91341-X
82. Kosmas TS, Vergados JD. Study of the flavor violating (μ−, e−) conversion in nuclei. Nucl Phys A. (1990) 510:641–70. doi: 10.1016/0375-9474(90)90353-N
83. Helm RH. Inelastic and elastic scattering of 187-Mev electrons from selected even-even nuclei. Phys Rev. (1956) 104:1466–75. doi: 10.1103/PhysRev.104.1466
84. Piekarewicz J, Linero AR, Giuliani P, Chicken E. Power of two: assessing the impact of a second measurement of the weak-charge form factor of 208Pb. Phys Rev C. (2016) 94:034316. doi: 10.1103/PhysRevC.94.034316
85. Fricke G, Bernhardt C, Heilig K, Schaller LA, Schellenberg L, Shera EB, et al. Nuclear ground state charge radii from electromagnetic interactions. Atom Data Nucl Data Tabl. (1995) 60:177–285. doi: 10.1006/adnd.1995.1007
86. Lewin JD, Smith PF. Review of mathematics, numerical factors, and corrections for dark matter experiments based on elastic nuclear recoil. Astropart Phys. (1996) 6:87–112. doi: 10.1016/S0927-6505(96)00047-3
87. Sprung DWL, Martorell J. The symmetrized Fermi function and its transforms. J Phys A. (1997) 30:6525–34.
88. Klein S, Nystrand J. Exclusive vector meson production in relativistic heavy ion collisions. Phys Rev C. (1999) 60:014903. doi: 10.1103/PhysRevC.60.014903
89. Akimov D, Albert JB, An P, Awe C, Barbeau PS, Becker B, et al. First constraint on coherent elastic neutrino-nucleus scattering in argon. arXiv:1909.05913.
90. Aliane A, Avetissovb ICh, Barinovab OP, de la Broisec X, Danevichd FA, Dumoulin L, et al. First test of a Li2WO4(Mo) bolometric detector for the measurement of coherent neutrino-nucleus scattering. Nucl Instrum Methods Phys Res A. 949:162784. doi: 10.1016/j.nima.2019.162784
91. Bellenghi C, Chiesa D, Di Noto L, Pallavicini M, Previtali E, Vignati M. Coherent elastic nuclear scattering of51 Cr neutrinos. Eur Phys J C. (2019) 79:727. doi: 10.1140/epjc/s10052-019-7240-3
92. Baxter D, Collar JI, Coloma P, Dahl CE, Esteban I, Ferrario P, et al. Coherent Elastic Neutrino-Nucleus Scattering at the European Spallation Source. arXiv:1911.00762 [physics.ins-det].
93. Akimov D, Albert JB, An P, Awe C, Barbeau PS, Becker B, et al. COHERENT 2018 at the spallation neutron source. arXiv:1803.09183.
94. Thornton R. Searching for Muon Neutrino Disappearance at LSND Neutrino Energies with CCM. (2019). Available online at: https://indico.cern.ch/event/782953/contributions/3444547/
95. Hakenmuller J, Buck C, Fülber K, Heusser G, Klages T, Lindner M, et al. Neutron-induced background in the CONUS experiment. Eur Phys J C. (2019) 79:699. doi: 10.1140/epjc/s10052-019-7160-2
96. Aguilar-Arevalo A, Bertou X, Bonifazi C, Cancelo G, Castañeda A, Cervantes Vergara B, et al. Exploring low-energy neutrino physics with the coherent neutrino nucleus interaction experiment (CONNIE). arXiv:1906.02200.
97. Angloher G, Ardellier-Desages F, Bento A, Canonica L, Erhart A, Ferreiro N, et al. Exploring CEνNS with NUCLEUS at the Chooz nuclear power plant. arXiv:1905.10258.
98. Akimov DY, Berdnikova AK, Belov VA, Bolozdynya AI, Burenkov AA, Dolgolenko AG, et al. Status of the RED-100 experiment. JINST. (2017) 12:C06018. doi: 10.1088/1748-0221/12/06/C06018
99. Wong HT, Li HB, Li J, Yue Q, Zhou ZY. Research program towards observation of neutrino-nucleus coherent scattering. J Phys. (2006) 39:266–8. doi: 10.1088/1742-6596/39/1/064
100. Rich GC. Measurement of Low-Energy Nuclear-Recoil Quenching Factors in CsI[Na] and Statistical Analysis of the First Observation of Coherent, Elastic Neutrino-Nucleus Scattering. PhD thesis, North Carolina U., 2017.
101. Cadeddu M, Dordei F. Reinterpreting the weak mixing angle from atomic parity violation in view of the Cs neutron rms radius measurement from COHERENT. Phys Rev D. (2019) 99:033010. doi: 10.1103/PhysRevD.99.033010
102. Cañas BC, Garcés EA, Miranda OG, Parada A. Future perspectives for a weak mixing angle measurement in coherent elastic neutrino nucleus scattering experiments. Phys Lett B. (2018) 784:159–62. doi: 10.1016/j.physletb.2018.07.049
103. Collar J, Kavner A, Lewis C. Response of CsI[Na] to nuclear recoils: impact on coherent elastic neutrino-nucleus scattering (CEνNS). arXiv:1907.04828.
104. Patton K, Engel J, McLaughlin GC, Schunck N. Neutrino-nucleus coherent scattering as a probe of neutron density distributions. Phys Rev C. (2012) 86:024612. doi: 10.1103/PhysRevC.86.024612
105. Horowitz CJ, Ahmed Z, Jen CM, Rakhman A, Souder PA, Dalton MM, et al. Weak charge form factor and radius of 208Pb through parity violation in electron scattering. Phys Rev C. (2012) 85:032501. doi: 10.1103/PhysRevC.85.032501
106. Cadeddu M, Dordei F, Giunti C, Li YF, Zhang YY. Neutrino, electroweak and nuclear physics from COHERENT elastic neutrino-nucleus scattering with refined quenching factor. arXiv:1908.06045.
107. Bhupal Dev PS, Babu KS, Denton PB, Machado PAN, Argüelles CA, Barrow JL, et al. Neutrino Non-Standard Interactions: A Status Report. (2019). arXiv:1907.00991 [hep-ph]. http://lss.fnal.gov/archive/2019/conf/fermilab-conf-19-299-t.pdf.
108. Babu KS, Dev PSB, Jana S, Thapa A. Non-Standard Interactions in Radiative Neutrino Mass Models. (2019). arXiv:1907.09498 [hep-ph].
109. Deppisch F, Kosmas TS, Valle JWF. Enhanced μ− - e− conversion in nuclei in the inverse seesaw model. Nucl Phys B. (2006) 752:80–92. doi: 10.1016/j.nuclphysb.2006.06.032
110. Malinsky M, Ohlsson T, Zhang H. Non-standard neutrino interactions from a triplet seesaw model. Phys Rev D. (2009) 79:011301. doi: 10.1103/PhysRevD.79.011301
111. Forero DV, Morisi S, Tortola M, Valle JWF. Lepton flavor violation and non-unitary lepton mixing in low-scale type-I seesaw. JHEP. (2011) 1109:142. doi: 10.1007/JHEP09(2011)142
112. Das SP, Deppisch FF, Kittel O, Valle JWF. Heavy neutrinos and lepton flavour violation in left-right symmetric models at the LHC. Phys Rev D. (2012) 86:055006. doi: 10.1103/PhysRevD.86.055006
113. Petrov AA, Zhuridov DV. Lepton flavor-violating transitions in effective field theory and gluonic operators. Phys Rev D. (2014) 89:033005. doi: 10.1103/PhysRevD.89.033005
114. Amanik PS, Fuller GM. Stellar collapse dynamics with neutrino flavor changing neutral currents. Phys Rev D. (2007) 75:083008. doi: 10.1103/PhysRevD.75.083008
115. Scholberg K. Prospects for measuring coherent neutrino-nucleus elastic scattering at a stopped-pion neutrino source. Phys Rev D. (2006) 73:033005. doi: 10.1103/PhysRevD.73.033005
116. Aristizabal Sierra D, De Romeri V, Rojas N. COHERENT analysis of neutrino generalized interactions. Phys Rev D. (2018) 98:075018. doi: 10.1103/PhysRevD.98.075018
117. Altmannshofer W, Tammaro M, Zupan J. Non-standard neutrino interactions and low energy experiments. arXiv:1812.02778.
118. Bischer I, Rodejohann W. General neutrino interactions from an effective field theory perspective. Nucl Phys B. (2019) 947:114746. doi: 10.1016/j.nuclphysb.2019.114746
119. Davidson S, Gorbahn M. Charged lepton flavour change and Non-Standard neutrino Interactions. arXiv:1909.07406.
120. Billard J, Johnston J, Kavanagh BJ. Prospects for exploring new physics in coherent elastic neutrino-nucleus scattering. JCAP. (2018) 1811:016. doi: 10.1088/1475-7516/2018/11/016
121. Miranda OG, Sanchez Garcia G, Sanders O. Coherent elastic neutrino-nucleus scattering as a precision test for the Standard Model and beyond: the COHERENT proposal case. Adv High Energy Phys. (2019) 2019:3902819. doi: 10.1155/2019/3902819
122. Khan AN, Rodejohann W. New physics from COHERENT data with improved Quenching Factors. arXiv:1907.12444.
123. Giunti C. General COHERENT constraints on neutrino non-standard interactions. arXiv:1909.00466.
124. Barranco J, Bolanos A, Garces EA, Miranda OG, Rashba TI. Tensorial NSI and unparticle physics in neutrino scattering. Int J Mod Phys A. (2012) 27:1250147. doi: 10.1142/S0217751X12501473
125. Healey KJ, Petrov AA, Zhuridov D. Nonstandard neutrino interactions and transition magnetic moments. Phys Rev D. (2013) 87:117301. doi: 10.1103/PhysRevD.87.117301
126. Papoulias DK, Kosmas TS. Neutrino transition magnetic moments within the non-standard neutrino–nucleus interactions. Phys Lett B. (2015) 747:454–9. doi: 10.1016/j.physletb.2015.06.039
127. Datta A, Dutta B, Liao S, Marfatia D, Strigari LE. Neutrino scattering and B anomalies from hidden sector portals. JHEP. (2019) 1:91. doi: 10.1007/JHEP01(2019)091
128. Abdullah M, Dalchenko M, Dutta B, Eusebi R, Huang P, Kamon T, et al. Bottom-quark fusion processes at the LHC for probing Z′ models and B -meson decay anomalies. Phys Rev D. (2018) 97:075035. doi: 10.1103/PhysRevD.97.075035
129. Bertuzzo E, Deppisch FF, Kulkarni S, Perez Gonzalez YF, Zukanovich Funchal R. Dark matter and exotic neutrino interactions in direct detection searches. JHEP. (2017) 1704:073. doi: 10.1007/JHEP04(2017)073
130. Cerdeño DG, Fairbairn M, Jubb T, Machado PAN, Vincent AC, Bœhm C. Physics from solar neutrinos in dark matter direct detection experiments. JHEP. (2016) 1605:118. doi: 10.1007/JHEP05(2016)118
131. Rodejohann W, Xu XJ, Yaguna CE. Distinguishing between Dirac and Majorana neutrinos in the presence of general interactions. JHEP. (2017) 5:24. doi: 10.1007/JHEP05(2017)024
132. Aristizabal Sierra D, Dutta B, Liao S, Strigari LE. Coherent elastic neutrino-nucleus scattering in multi-ton scale dark matter experiments: classification of vector and scalar interactions new physics signals. arXiv:1910.12437.
133. Shoemaker IM. COHERENT search strategy for beyond standard model neutrino interactions. Phys Rev D. (2017) 95:115028. doi: 10.1103/PhysRevD.95.115028
134. Aguilar-Arevalo A, Bertou X, Bonifazi C, Cancelo G, Cervantes-Vergara BA, Chavez C, et al. Light vector mediator search in the low-energy data of the CONNIE reactor neutrino experiment. arXiv:1910.04951.
135. Giunti C, Studenikin A. Neutrino electromagnetic interactions: a window to new physics. Rev Mod Phys. (2015) 87:531. doi: 10.1103/RevModPhys.87.531
136. Schechter J, Valle JWF. Majorana neutrinos and magnetic fields. Phys Rev D. (1981) 24:1883–9. doi: 10.1103/PhysRevD.24.1883
137. Grimus W, Schwetz T. Elastic neutrino electron scattering of solar neutrinos and potential effects of magnetic and electric dipole moments. Nucl Phys B. (2000) 587:45–66. doi: 10.1016/S0550-3213(00)00451-X
138. Tortola M. Constraining neutrino magnetic moment with solar and reactor neutrino data. arXiv:hep-ph/0401135.
139. Vogel P, Engel J. Neutrino electromagnetic form-factors. Phys Rev D. (1989) 39:3378. doi: 10.1103/PhysRevD.39.3378
140. Hirsch M, Nardi E, Restrepo D. Bounds on the tau and muon neutrino vector and axial vector charge radius. Phys Rev D. (2003) 67:033005. doi: 10.1103/PhysRevD.67.033005
141. Agostini M, Altenmüller K, Appel S, Atroshchenko V, Bagdasarian Z, Basilico D, et al. Limiting neutrino magnetic moments with Borexino Phase-II solar neutrino data. Phys Rev D. (2017) 96:091103.
142. Adamson P, Anghel I, Aurisano A, Barr G, Bishai M, Blake A, et al. Search for sterile neutrinos in MINOS and MINOS+ using a two-detector fit. Phys Rev Lett. (2019) 122:091803. doi: 10.1103/PhysRevLett.122.091803
143. Aguilar-Arevalo AA, Brown BC, Bugel L, Cheng G, Conrad JM, Cooper RL, et al. Significant excess of electronLike events in the MiniBooNE short-baseline neutrino experiment. Phys Rev Lett. (2018) 121:221801. doi: 10.1103/PhysRevLett.121.221801
144. Adey D, An FP, Balantekin AB, Band HR, Bishai M, Blyth S, et al. Measurement of the electron antineutrino oscillation with 1958 days of operation at daya bay. Phys Rev Lett. (2018) 121:241805. doi: 10.1103/PhysRevLett.121.241805
145. An F, An G, An Q, Antonelli V, Baussan E, Beacom J, et al. Neutrino physics with JUNO. J Phys G. (2016) 43:030401. doi: 10.1088/0954-3899/43/3/030401
146. Ko YJ, Kim BR, Kim JY, Han BY, Jang CH, Jeon EJ, et al. Sterile neutrino search at the NEOS experiment. Phys Rev Lett. (2017) 118:121802. doi: 10.1103/PhysRevLett.118.121802
147. Formaggio JA, Figueroa-Feliciano E, Anderson AJ. Sterile neutrinos, coherent scattering and oscillometry measurements with low-temperature bolometers. Phys Rev D. (2012) 85:013009. doi: 10.1103/PhysRevD.85.013009
148. Anderson AJ, Conrad JM, Figueroa-Feliciano E, Ignarra C, Karagiorgi G, Scholberg K, et al. Measuring active-to-sterile neutrino oscillations with neutral current coherent neutrino-nucleus scattering. Phys Rev D. (2012) 86:013004. doi: 10.1103/PhysRevD.86.013004
149. Aguilar-Arevalo A, Auerbach B, Burman RL, Caldwell DO, Church ED, Cochran AK, et al. Evidence for neutrino oscillations from the observation of anti-neutrino(electron) appearance in a anti-neutrino(muon) beam. Phys Rev D. (2001) 64:112007.
150. Berryman JM. Constraining sterile neutrino cosmology with terrestrial oscillation experiments. Phys Rev D. (2019) 100:023540. doi: 10.1103/PhysRevD.100.023540
151. Coloma P, Denton PB, Gonzalez-Garcia MC, Maltoni M, Schwetz T. Curtailing the dark side in non-standard neutrino interactions. JHEP. (2017) 1704:116. doi: 10.1007/JHEP04(2017)116
152. Cadeddu M, Giunti C, Kouzakov KA, Li YF, Studenikin AI, Zhang YY. Neutrino charge radii from COHERENT elastic neutrino-nucleus scattering. Phys Rev D. (2018) 98:113010. doi: 10.1103/PhysRevD.98.113010
153. Giannaka PG, Kosmas TS. Electron capture cross sections for stellar nucleosynthesis. Adv High Energy Phys. (2015) 2015:398796. doi: 10.1155/2015/398796
154. Stapleford CJ, Väänänen DJ, Kneller JP, McLaughlin GC, Shapiro BT. Nonstandard neutrino interactions in supernovae. Phys Rev D. (2016) 94:093007. doi: 10.1103/PhysRevD.94.093007
155. Biassoni M, Martinez C. Study of supernova ν -nucleus coherent scattering interactions. Astropart Phys. (2012) 36:151–5. doi: 10.1016/j.astropartphys.2012.05.009
156. Monroe J, Fisher P. Neutrino backgrounds to dark matter searches. Phys Rev D. (2007) 76:033007. doi: 10.1103/PhysRevD.76.033007
157. O'Hare CAJ. Dark matter astrophysical uncertainties and the neutrino floor. Phys Rev D. (2016) 94:063527. doi: 10.1103/PhysRevD.94.063527
158. Billard J, Strigari L, Figueroa-Feliciano E. Implication of neutrino backgrounds on the reach of next generation dark matter direct detection experiments. Phys Rev D. (2014) 89:023524. doi: 10.1103/PhysRevD.89.023524
159. Farzan Y. A model for large non-standard interactions of neutrinos leading to the LMA-Dark solution. Phys Lett B. (2015) 748:311–5. doi: 10.1016/j.physletb.2015.07.015
160. Kosmas TS, Vergados JD. (μ−, e−) conversion: a symbiosis of particle and nuclear physics. Phys Rept. (1996) 264:251–66. doi: 10.1016/0370-1573(95)00041-0
161. Farzan Y, Heeck J. Neutrinophilic nonstandard interactions. Phys Rev D. (2016) 94:053010. doi: 10.1103/PhysRevD.94.053010
162. Petcov ST. The processes μ –> e Gamma, μ –> e e anti-e, Neutrino' –> Neutrino gamma in the Weinberg-Salam Model with Neutrino Mixing. Sov J Nucl Phys. (1977) 25:340. [Erratum: Yad. Fiz. 25:1336 (1977)].
163. Kuno Y, Okada Y. Muon decay and physics beyond the standard model. Rev Mod Phys. (2001) 73:151–202. doi: 10.1103/RevModPhys.73.151
164. Lee M. COMET muon conversion experiment in J-PARC. Front Phys. (2018) 6:133. doi: 10.3389/fphy.2018.00133
166. Chiang HC, Oset E, Kosmas TS, Faessler A, Vergados JD. Coherent and incoherent (μ−, e−) conversion in nuclei. Nucl Phys A. (1993) 559:526–42. doi: 10.1016/0375-9474(93)90259-Z
167. Davidson S, Pena-Garay C, Rius N, Santamaria A. Present and future bounds on nonstandard neutrino interactions. JHEP. (2003) 303:11. doi: 10.1088/1126-6708/2003/03/011
168. Kitano R, Koike M, Okada Y. Detailed calculation of lepton flavor violating muon electron conversion rate for various nuclei. Phys Rev D. (2002) 66:096002. doi: 10.1103/PhysRevD.66.096002
169. Cirigliano V, Kitano R, Okada Y, Tuzon P. On the model discriminating power of μ —> e conversion in nuclei. Phys Rev D. (2009) 80:013002. doi: 10.1103/PhysRevD.80.013002
170. Davidson S, Kuno Y, Yamanaka M. Selecting μ → e conversion targets to distinguish lepton flavour-changing operators. Phys Lett B. (2019) 790:380–8. doi: 10.1016/j.physletb.2019.01.042
171. Edmonds AR. Angular Momentum in Quantum Mechanics. Reissue ed. Princeton, NJ: Princeton University Press (1996).
Appendix
A. Multipole Operators
The Donnelly-Walecka multipole decomposition method yields a set of eight linearly independent irreducible tensor operators which are typically expressed in terms of the Spherical Bessel functions, jl, and combined with the Spherical Harmonics, , or the vector Spherical Harmonics, [171]:
with
As a consequence of the V-A structure of electroweak interactions
four operators are associated to the vector component and four to the axial-vector component of the hadronic current
where κ = |q| denotes the 3-momentum transfer. Note that, the vector component yields the Coulomb , longitudinal LJM, transverse electric (normal parity π = (−)J) and transverse magnetic (abnormal parity π = (−)J+1), while regarding the axial-vector component , , have abnormal parity and has normal parity. The matrix elements of the above operators involve momentum dependence of the nucleon form factors , X = 1, A, P and μV(Q2)
It becomes evident that only seven are linearly independent
In the proton-neutron representation, , i = 1, 2, ⋯ , 7 can be written in closed form [65]
B. Coefficients for Calculating the Charge Density Distribution and Form Factors in the Context of FOP
The coefficients θλ of the polynomial Φ(|q|b, Z) are evaluated, as
In the latter expression, Γ(x) denotes the Gamma function while the definition of the index s is
and
The corresponding coefficients fλ are written as
As a concrete example the coefficients θλ and fλ for even-even nuclei up to 50Sn are listed in Table A1.
Keywords: coherent elastic neutrino-nucleus scattering (CENNS), non-standard interactions, electromagnetic neutrino properties, sterile neutrinos, novel mediators
Citation: Papoulias DK, Kosmas TS and Kuno Y (2019) Recent Probes of Standard and Non-standard Neutrino Physics With Nuclei. Front. Phys. 7:191. doi: 10.3389/fphy.2019.00191
Received: 23 July 2019; Accepted: 04 November 2019;
Published: 27 November 2019.
Edited by:
Frank Franz Deppisch, University College London, United KingdomReviewed by:
Yasaman Farzan, Institute for Research in Fundamental Sciences (IPM), IranChandan Hati, Technical University of Munich, Germany
Copyright © 2019 Papoulias, Kosmas and Kuno. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dimitrios K. Papoulias, ZGlwYXBvdUBpZmljLnV2LmVz
 Dimitrios K. Papoulias
Dimitrios K. Papoulias Theocharis S. Kosmas
Theocharis S. Kosmas Yoshitaka Kuno
Yoshitaka Kuno