Splitting and Motions of Dissipative Soliton Resonance Pulses in Mode-Locked Fiber Lasers

Lyu, Yanjia; Wei, Chen; Du, Wenxiong; Li, Heping; Liu, Yong

doi:10.3389/fphy.2019.00173

ORIGINAL RESEARCH article

Front. Phys., 01 November 2019

Sec. Optics and Photonics

Volume 7 - 2019 | https://doi.org/10.3389/fphy.2019.00173

This article is part of the Research Topic Soliton Build-up in Mode-Locked Lasers View all 6 articles

Splitting and Motions of Dissipative Soliton Resonance Pulses in Mode-Locked Fiber Lasers

$\nYanjia Lyu$ Yanjia Lyu

Chen Wei^*

Wenxiong Du

Heping Li

Yong Liu

State Key Laboratory of Electronic Thin Films and Integrated Devices, School of Optoelectronic Information, University of Electronic Science and Technology of China, Chengdu, China

We numerically investigated the splitting and motions of dissipative soliton resonance (DSR) pulses in an all-normal-dispersion Yb-doped fiber laser mode-locked by a non-linear optical loop mirror. At certain values of the system parameters, the initial single Gaussian pulse can evolve into an unstable DSR pulse with several dark solitons inside. After collisions of dark solitons, a big intensity dip occurs at the center of the DSR pulse, leading to the splitting of the DSR pulse. After splitting, the peak-to-peak separation between two DSR pulses increases at first and finally reaches a fixed value of 193 ps, indicating a steady-state multipulse operation The relative motions of separated DSR pulse originate from the phase shift.

Introduction

Passively mode-locked fiber lasers have attracted considerable attention due to their compact and stable performance for generating ultrafast pulse with high peak power [1–4]. As powerful tools, they also open an interest among researchers to explore new areas of soliton build-up dynamics [5–10]. Recently, a novel pulse formation known as dissipative soliton resonance (DSR) was initially found in the frame of complex cubic-quantic Ginzburg-Landau equation (CQGLE) in a specific parameter space [11]. Relying on the delicate and complicated balance of dispersion, non-linearity, loss, gain, non-linear gain saturation, and gain dispersion, the pulses in the DSR regime exhibit flat-top profiles and wave-breaking-free features. With increasing pump power, the DSR pulse keeps broadening its pulse width with a clamped peak power without suffering pulse breaking, which shows great potential for high-energy pulse generation in fiber lasers. During the past decade, the DSR phenomenon has been extensively investigated theoretically and experimentally with different dispersion regimes, mode-locking techniques and emission wavelengths [12–30]. It was found that the peak-power-clamping effect caused by reverse saturable absorption plays an important role in the formation of DSR pulses.

Although in the DSR regime light pulses are supposed to be wave-breaking-free, multipulse operation is still possible. In 2013, Komarov et al. have numerically demonstrated that an initial multipulse field with different amplitudes can evolve into a steady-state multipulse operation in DSR regime, where the number of pulses depends on the initial conditions [31]. In 2016, Armas-Rivera et al. have observed that a single DSR pulse splits into two equidistant trapezoidal-shaped DSR pulses by roundtrip at sufficiently high pump power [32]. In 2017, we have developed a harmonic DSR Er-dope fiber laser mode-locked by non-linear polarization rotation and numerically investigated its multipulse dynamics [33, 34]. Recently, Chowdhury et al. have observed DSR pulse splitting by rotating polarization controllers in an all-normal dispersion non-linear amplifying loop mirror based mode-locked Yb-doped fiber laser, and they have also numerically studied the multipulse dynamics of DSR with multipulse input field [35]. Very recently, Wang et al. have observed unusual evolutions of DSR in an all-normal dispersion fiber laser, where increasing pump power leads to pulse breaking and multipulse operation [36]. However, the entire splitting process from one single pulse to multiple DSR pulses and its mechanism has not been numerically demonstrated so far.

In this paper, we numerically investigated the DSR pulse splitting process in a non-linear optical loop mirror (NOLM) mode-locked Yb-doped fiber laser using the scalar non-linear Ginzburg-Landau equation. It is found that, with specific parameter selection, the initial single pulse can evolve into an unstable DSR pulse with several dark solitons inside, and then split into two stable DSR pulses with the same pulse properties (pulse shape, duration, peak power, chirp, and so on) and fixed peak-to-peak (PP) separation. This steady-state two DSR pulses operation can be attributed to energy quantization effect [37] and phase shift of pulses [38].

Numerical Model

The schematic of the proposed NOLM mode-locked Yb-doped fiber laser is shown in Figure 1. The cavity consists of a 1-m-long Yb-doped fiber (YDF), 5-m-long single mode fiber (SMF), a saturable absorber (SA) with a sinusoidal transmission function, and a 90:10 optical coupler (OC) with 10% output. To take every component in the cavity into account, our simulations are still based on the pulse tracing technique. The simulations start from a weak single Gaussian pulse. The pulse propagation in the fiber sections is modeled by a scalar non-linear Ginzburg-Landau equation:

\begin{array}{l} \frac{\partial A}{\partial z} = - \frac{i β_{2}}{2} \frac{\partial^{2} A}{\partial t^{2}} + i γ {| A |}^{2} A + \frac{g}{2} A + \frac{g}{2 Ω_{g}^{2}} \frac{\partial^{2} A}{\partial t^{2}} & (1) \end{array}

where A is the slowly varying electric field envelope, z is the propagation distance, and t is the pulse local time. β₂ and γ refer to the group velocity dispersion and the non-linearity of fiber, respectively. In the simulation all the fibers are assumed to have the same non-linearity of γ = 3 W⁻¹·km⁻¹, while the dispersion parameters are β_2,YDF = 20 ps²·km⁻¹, β_2,SMF = 22 ps²·km⁻¹, For the YDF, g is the saturable gain of the fiber and Ω_g = 40 nm is the gain bandwidth with a parabolic shape. For the SMF, g = 0. For the YDF, the gain saturation effect is considered as

\begin{array}{l} g = g_{0} exp (- \frac{1}{E_{s a t}} \int | A^{2} | d t) & (2) \end{array}

where g₀ = 3 m⁻¹ is the small signal gain coefficient, which relates to the doping concentration of the gain fiber; E_sat refers to the gain saturation energy, which relates to the pumping strength.

FIGURE 1

Figure 1. Schematic of the NOLM mode-locked Yb-doped fiber laser.

In our simulations, a simple model of NOLM is adopted, and its transmission function can be expressed as:

\begin{array}{l} T = \frac{1}{2} [1 - q cos (\frac{π (1 - Φ_{0}) {| A |}^{2}}{I_{s a t}} + Φ_{0} π)] & (3) \end{array}

where q is the modulation depth, Φ₀ accounts for linear bias, and I_sat is the saturation power. In our simulations, we set q = 0.4, Φ₀ = 0, and I_sat = 40 W.

Simulation Results and Discussion

Several previous theoretical works have studied the multipulse dynamics of DSR [31, 33, 35]. To generate multiple DSR pulses, all these simulations required a multipulse initial field, and during the evolution from the initial field to multiple DSR pulses, no pulse splitting process was found. To investigate the pulse splitting process of DSR, in our simulations we use only one single Gaussian pulse with weak peak power as the initial field.

The pulse splitting process of DSR was observed when the pump strength was selected as E_sat = 2 nJ. The 2D Color fill and 3D color map surface of the pulse evolution are shown in Figures 2A,B, respectively. From Figure 2A, we can obviously see that after a chaos process, one pulse splits into two stable DSR pulses. The PP separation between these two DSR pulses increases rapidly at the beginning of roundtrips, and eventually, it reaches a value of ~193 ps and keeps constant after the roundtrip number N > 4,000. Figure 2C shows the temporal profiles of the two DSR pulse at N = 5,000. The two DSR pulse have the same shape, pulse duration of ~41 ps, and peak power of ~5.5 W. As shown in Figure 2D, the two DSR pulses still have the same instantaneous frequency profiles. The pulses have non-zero linear frequency chirps across their flat-top part and exponential chirps at the edges, which are essential features of DSR.

FIGURE 2

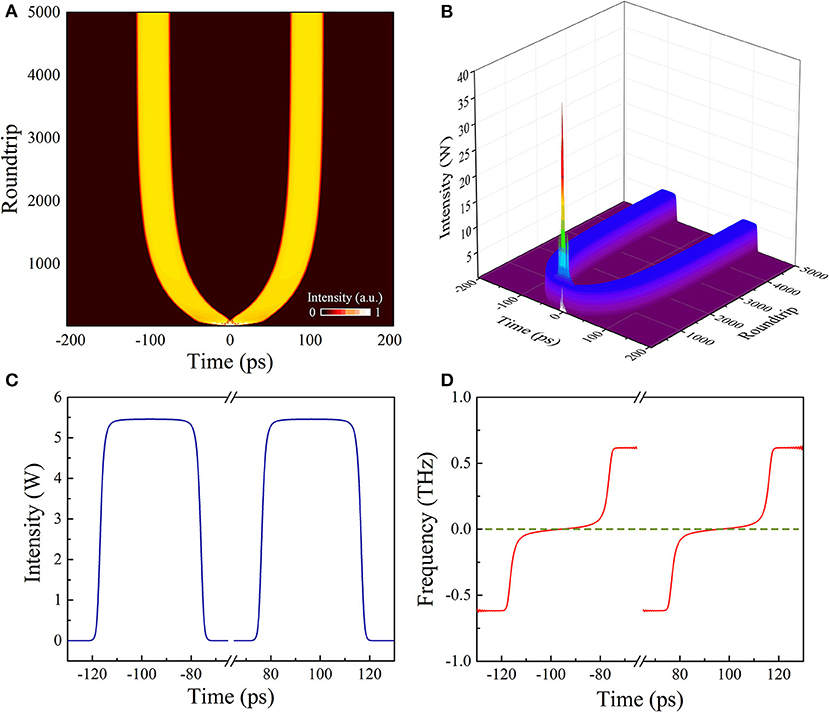
Figure 2. Pulse splitting process of DSR at E_sat = 2 nJ. (A) 2D Color fill, (B) 3D color map surface of evolutions. (C) Temporal profiles and (D) instantaneous frequency profiles at N = 5000.

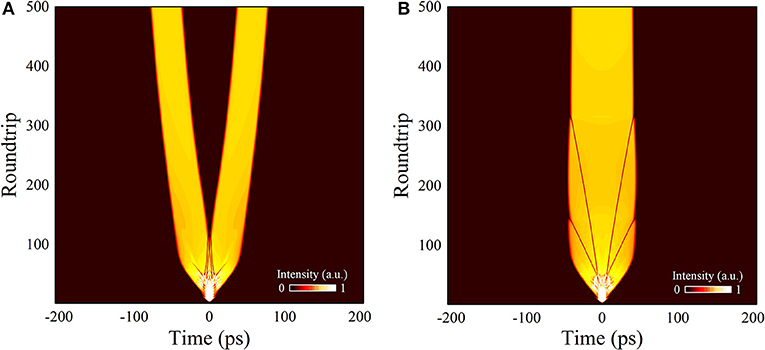
For better understanding the pulse splitting phenomenon in DSR regime, we focused on the evolutions of the first 500 roundtrips. Figures 3A,B show the pulse evolution of the first 500 roundtrips when E_sat was set to 2 nJ and 1.98 nJ, respectively. When E_sat = 2 nJ, after a chaos process the initial input pulse firstly evolves into an unstable DSR pulse with several dark solitons inside it. These dark solitons evolved from noise perturbations are commonly observed in dissipative soliton fiber lasers, since they are the stable solutions of the non-linear Schrodinger equation in the normal dispersion regime. When dark solitons are formed inside a dissipative soliton, the sloped background intensity will impose additional phase shifts on them, resulting in varying transverse velocities, which is proportional to the background intensity. Consequently, dark solitons in a dissipative soliton always walk off from the bright pulse and eventually decay with curved trajectories toward wings of the bright pulse [39]. However, in the DSR square-shaped pulse in our simulation, the formed dark solitons are on a quasi-cw background with almost constant intensity level, and thus no additional phase shift is imposed on them, making them move with constant transverse velocities (in other words, they have straight trajectories). This make the dark solitons possible to avoid decaying at the wings of the background pulse. Here, as shown in Figure 3A, although 2 gray solitons decay in the background, 4 dark solitons move straight toward the center of the background DSR pulse, and after collisions they finally converge into one big intensity dip when the roundtrip number N = 115. As a consequence, the left and right parts of the unstable broken DSR pulse are separated by this intensity dip, and these two parts become individual DSR pulses with the same properties. Since the dark solitons in the system originate from random spontaneous noise in the early build-up process of the DSR pulse, they would emerge from the background with varying position and blackness, which make it difficult to control the system parameters in our simulations to realize DSR pulse splitting. When we set system parameters (e.g., E_sat, β₂, and γ) to many other different values, even very close to the original values, the initial pulse always evolves into one stable single DSR pulse, in other words, the dark solitons decay at wings of the DSR pulse. As shown in Figure 3B, when E_sat = 1.98 nJ, the initial input pulse can still evolve into an DSR pulse with 4 dark solitons. However, in this case, all the dark solitons move straight toward the DSR pulse wings and eventually decay, leading to the formation of one stable DSR pulse. The results indicate that the DSR pulse splitting depends strongly on the system parameters, and the physical mechanism requires further investigation.

FIGURE 3

Figure 3. Pulse evolution of first 500 roundtrips at (A) E_sat = 2 nJ, (B) E_sat = 1.98 nJ.

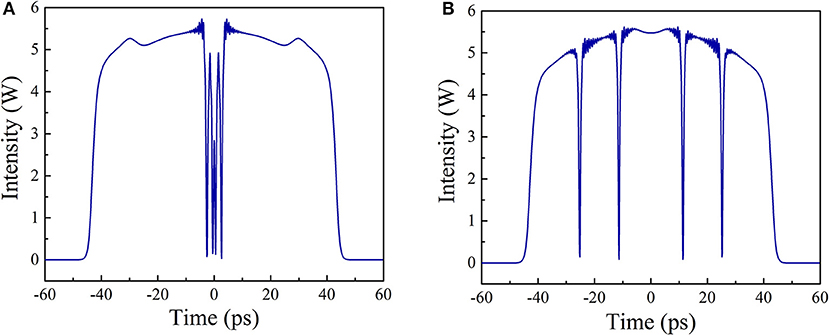
Figure 4A shows the pulse temporal profile at N = 100 and E_sat = 2 nJ. Here we observe the gathering of the 4 dark solitons at the center of the DSR pulse. As the collisions of dark solitons decrease the background intensity, their blackness also decrease. It is not surprising that they would eventually decay and form a big gap in the DSR pulse, leading to the splitting process. While for N = 100 and E_sat = 1.98 nJ, as shown in Figure 4B, the dark solitons are separated and have no chance of collisions. It should be noted that the splitting mechanism of DSR pulse here is entirely different from that of conventional soliton. Increasing pump strength cannot lead to the splitting of the DSR pulse but only leads to the broadening of the pulse width.

FIGURE 4

Figure 4. Pulse temporal profiles at N = 100 at (A) E_sat = 2 nJ, (B) E_sat = 1.98 nJ.

The relative motions of the two DSR pulses are similar to that of solitons in Liu [38], which can also be attributed to the phase shift arising from pulse interactions. When the phase shift is imposed on a pulse, the instantaneous frequency at the pulse peak, F_P, becomes non-zero, as the instantaneous frequency is the first derivative of phase. Figure 5A shows the temporal profile at N = 120 when E_sat = 2 nJ, where the broken DSR pulse is just separated into two symmetrical trapezoid-shaped DSR pulses. Figure 5B shows the corresponding instantaneous frequency at N = 120. Obviously, both pulses have almost linear frequency chirps with relatively large slopes across their pulse profiles. For the left trapezoid-shaped DSR pulse, its F_P < 0, and for the right one its F_P > 0, indicating that both pulses have phase shifts. After hundreds of roundtrips, as shown in Figure 5C, at N = 500 the trapezoid-shaped pulses transform to the typical square-shaped DSR pulses and they separate from each other. Figure 5D shows the corresponding instantaneous frequency at N = 500. Each pulse still has linear frequency chirp across the pulse profile, but the slope decrease and the F_P becomes closer to zero as compared with trapezoid-shaped DSR pulse at N = 120. As shown in Figures 2C,D, at N = 5,000, these two DSR pulses reach a steady-state multipulse operation with a fix PP separation of ~193 ps and the F_Pof each pulse is almost equals to zero.

FIGURE 5

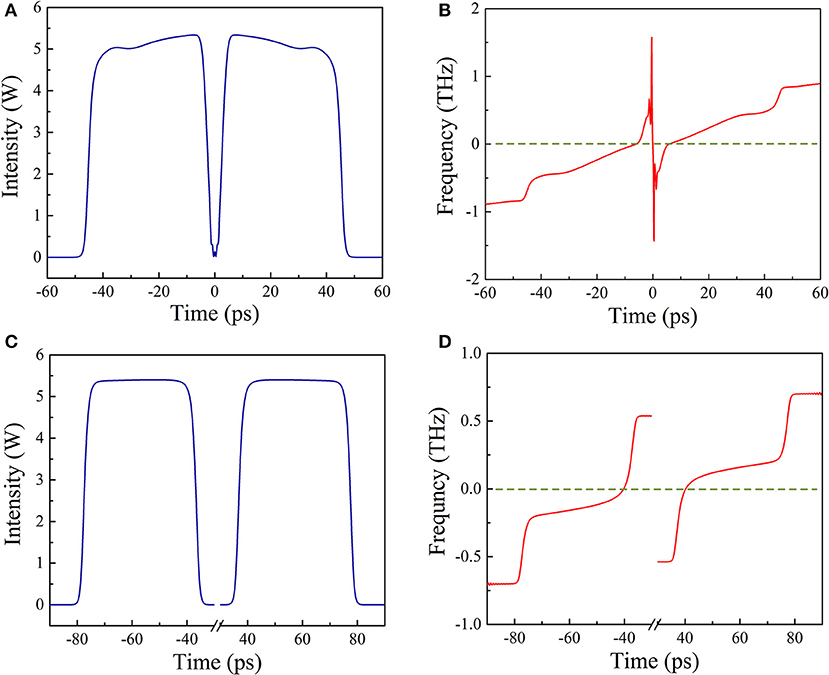
Figure 5. Pulse properties at different roundtrips when E_sat = 2 nJ. (A) Temporal profile at N = 120. (B) Instantaneous frequency profile at N = 120. (C) Temporal profile at N = 500. (D) Instantaneous frequency profile at N = 500.

Figures 6A,B show the evolutions of the F_P and pulse trajectory from N = 120 to N = 5,000. The absolute value of each F_P increases at the beginning, and then it keeps decreasing and eventually reaches zero at N = 4,000. Meanwhile, the PP separation between two pulses keeps increasing and gradually approaches ~193 ps at N = 4,000. When N > 4,000, the F_Pis fixed at 0 and PP separation is fixed at ~193 ps, indicating a steady-state multipulse operation. Obviously, the motions of two pulses are governed by the F_P or the phase shift, in other words.

FIGURE 6

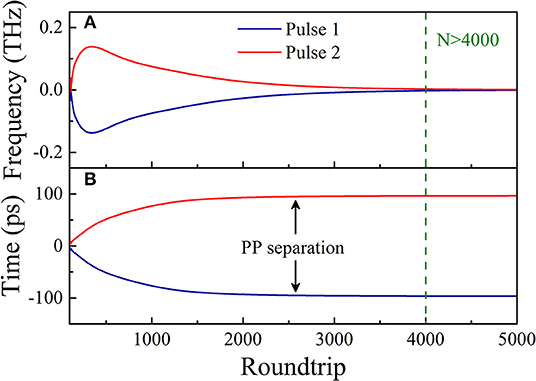
Figure 6. (A) Instantaneous frequency at pulse peak F_P and (B) pulse trajectory vs. roundtrip number N.

Conclusion

In conclusion, we have numerically studied the pulse splitting process and their motions in DSR regime in an Yb-doped fiber laser mode-locked by NOLM. Numerical simulations have demonstrated that with specific system parameters selection, one unstable DSR pulse with several dark solitons inside can split into two DSR pulse with the same properties due to the collisions and decay of dark solitons. The pulses can eventually reach a steady-state operation with a fixed separation. Similar to conventional solitons, the phase shift governs the relative motions of the separated DSR pulses. We believe that our simulation results can offer an insight into DSR pulse dynamics in mode-locked fiber lasers.

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Author Contributions

YLy contributed conception and design of the study. CW helped to evaluate and edit the manuscript. CW and YLi supervised the project. All the authors contributed to discussion on the results for this manuscript.

Funding

This work was supported by the National Nature Science Foundation of China (NSFC) (61435003, 61421002, 61875033, 61775031), Chengdu Science and Technology Huimin Project (2016-HM01-00269-SF), and China Scholarship Council (201706070044).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Zhao Y, Guo P, Li X, Jin Z. Ultrafast photonics application of graphdiyne in optical communication region. Carbon. (2019) 149:336–41. doi: 10.1016/j.carbon.2019.04.075