GeSn on Insulators (GeSnOI) Toward Mid-infrared Integrated Photonics

In recent years, Ge and Ge_1−xSn_x materials and devices have achieved rapid progress in integrated photonics. However, conventional heteroepitaxy of active photonic devices compromises the area on Si for CMOS electronics, limiting the scale of integration. Furthermore, it is not possible to grow GeSn epitaxially on amorphous and/or flexible substrates toward 3D photonic integration in mid-infrared (MIR) regime. Here, we present low-temperature crystallization of direct bandgap, high crystallinity Ge_1−xSn_x (0.08 < x < 0.26) on amorphous dielectrics insulators (GeSnOI) toward 3D and flexible MIR integrated photonics. Utilizing eutectically-enhanced crystallization (EEC), an extraordinarily large average grain size of ~100 μm has been achieved in blanket GeSn films crystallized on SiO₂ layers, flexible glass, and polyimide substrates alike. Furthermore, using Sn nanodot enhanced composition enhancement (NICE), we have achieved an average Sn composition as high as 26 at.% to further extend the optical response of GeSn toward λ = 3–5 μm. The achieved Sn composition of 8–26 at.% far exceeds that of the equilibrium solubility limit of <1 at.%, even though the crystallization temperature of 350–450°C far exceeds the typical epitaxial growth temperature of GeSn. This result indicates that crystallization from amorphous GeSn (a-GeSn) may offer better metastability compared to direct epitaxial growth of GeSn. Attesting to the high crystallinity, a peak optical gain of 2,900 cm⁻¹ with a lifetime approaching 0.1 ns is achieved at λ = 2,200–2,350 nm at 300 K. The gain lifetime is on the same order as epitaxial GeSn, and it is >100x longer than the direct gap transition in Ge, confirming the indirect-to-direct band gap transition in GeSn at ~9 at. Sn composition. Moreover, a prototype p-GeSn/n-Si photodiode from a-GeSn crystallization achieves 100 mA/W responsivity at λ = 2,050 nm and T = 300 K, approaching the level of some commercial PbS detectors. The device also demonstrates photovoltaic behavior and a low dark current density of 1 mA/cm² at −1 V reverse bias, comparable to epitaxial Ge/Si photodiodes. These results indicate that crystallization of GeSnOI offers a promising solution for active devices toward 3D MIR photonic integration and/or MIR photonics on flexible substrates.

Introduction

Integrated photonics has achieved rapid progress in the past two decades. An almost complete set of passive and active photonic components have been developed on the silicon-on-insulator (SOI) platform, including waveguides, couplers, splitters, filters, polarizers, (de)multiplexers, modulators, switches, and photodetectors [1, 2]. Many of these devices are being standardized in Silicon Photonics Process Design Kits (PDK) under the American Institute for Manufacturing Photonics (AIM Photonics)¹. Ge has played an important role in active photonic devices for integrated photonics [3–5] due to its pseudo direct bandgap behavior [6] and compatibility with Si complementary metal oxide semiconductor (CMOS) technology. More recently, Ge_1–xSn_x materials [7–13] and devices [14–20] have become an active field of research since an indirect-to-direct bandgap transition occurs at x~0.06–0.11 (depending on the level of strain). GeSn also brings about a great opportunity for integrated active photonic devices in mid-infrared (MIR) regime (λ = 3–5 μm) [21–24] for sensing and imaging applications since the direct bandgap can be decreased to <0.5 eV for x > 0.09.

So far, most of the Si-based integrated photonic devices, especially Ge and GeSn active devices, are achieved via planar electronic-photonic integration, where photonic components are integrated with CMOS circuitry on the same single-crystal Si layer (Figure 1a). However, heteroepitaxy of Ge and GeSn consumes real estate on single crystal Si, thereby significantly sacrificing CMOS area for photonic devices. This issue is manifested by the scanning electron microscopy (SEM) and transmission electron microscopy (TEM) images in the inset of Figure 1a, showing that the cross-sectional dimensions of a waveguide-integrated Ge photodetector is ~20 × bigger than CMOS transistor in 32 nm technology node due to the fundamental optical diffraction limit. Moreover, the planar integration approach has to introduce some modifications to existing CMOS process flow in order to accommodate the epitaxial growth as well as the vertical dimension of photonic devices [25], making it hard to implement in <45 nm CMOS technology nodes. In addition, it is not possible to epitaxially grow Ge or GeSn on amorphous substrates (such as polymers) for flexible integrated photonic circuits, either. Therefore, in large-scale electronic-photonic integration it would be ideal to adopt a monolithic 3D integration approach, moving the photonic circuits to the metal/dielectric interconnect level above the CMOS layer (Figure 1b). The ability to achieve high crystallinity Ge or GeSn on amorphous dielectrics would offer great flexibility in photonic integration since active photonic devices could be grown on any layer or substrate at any designated region.

FIGURE 1

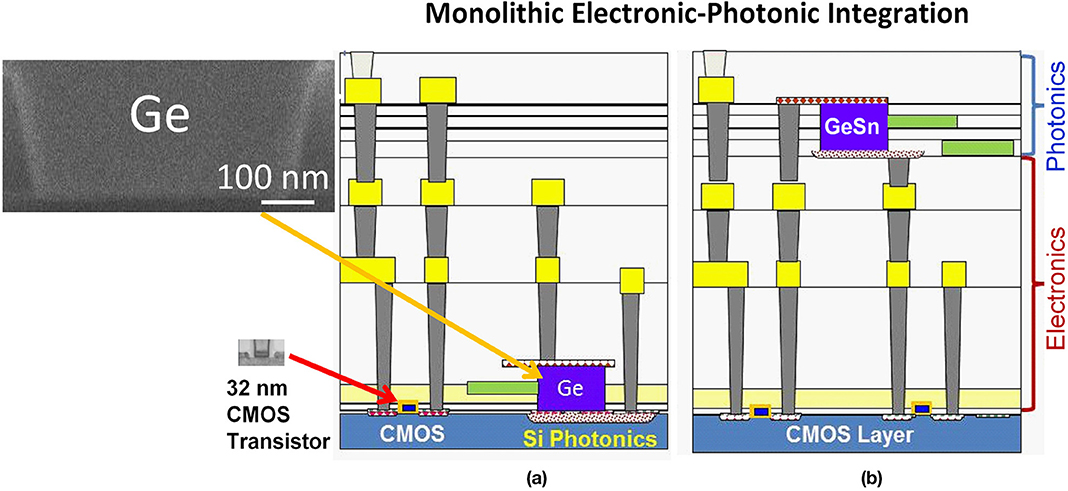
Figure 1. Schematics of monolithic electronic-photonic integration: (a) Planar integration of photonics with CMOS electronics on the same Si layer, and (b) 3D photonic integration with the photonic interconnect layer positioned well above the CMOS layer.

In this paper, we present low-temperature crystallization of direct bandgap, high crystallinity Ge_1–xSn_x with x up to 0.26 (i.e., 26 at.%) on amorphous dielectrics and flexible substrates toward monolithic 3D photonic integration and flexible MIR photonics. Utilizing eutectically enhanced crystallization (EEC) in Ge-Sn system, a very low nucleation rate and high lateral growth rate can be achieved, leading to an extraordinarily large grain size of ~100 μm in blanket GeSn films crystallized on thermally grown SiO₂ layers, flexible Willow glass, fused silica, and polyimide substrates alike. The crystallization temperature range of 380–450°C is also compatible with back-end-of-line CMOS processing and polyimide flexible substrates. Furthermore, using Sn nanodot induced composition enhancement (NICE), we have achieved an average Sn composition as high as 26 at.%. Attesting to the high material quality of crystallized GeSn, a high optical gain ~2,900 cm⁻¹ with a lifetime of 0.1 ns have been achieve at λ = 2,200–2,350 nm at room temperature from crystallized GeSn with 9 at.% Sn. The peak gain coefficient is comparable to III-V semiconductors. The gain lifetime is on the same order as epitaxial GeSn, and it is >100x longer than that of Ge, confirming the indirect-to-direct band gap transition in Ge_1–xSn_x at x ≥ 0.09. Furthermore, a prototype p-GeSn/n-Si photodiode achieves 100 mA/W responsivity at λ = 2,050 nm and 300 K, comparable to some PbS MIR photodetectors. The GeSn/Si photodiode also demonstrates photovoltaic behavior and a low dark current density of 1 mA/cm² at −1 V reverse bias, comparable to epitaxial Ge/Si photodiodes. These results indicate that GeSn crystallized on dielectrics offers a promising solution for active devices in 3D photonic integration.

Substrate-Independent GeSn Crystallization on Amorphous Insulators

The basic idea of crystallizing amorphous GeSn at low temperatures originates from the eutectic phase diagram of the Ge-Sn system [3, 10]. According to the equilibrium phase diagram, a Ge-rich solid phase is in equilibrium with a Sn-rich liquid phase at temperatures >231°C. While the exact temperature and solubility no longer applies to the crystallization of amorphous GeSn (a-GeSn) since it is not in thermodynamic equilibrium, the formation of a small amount of liquid Sn is indeed observed. During the crystallization process of a-GeSn thin films upon thermal annealing, which involves rearrangement of atoms into a long-range ordered diamond cubic structure, the Sn-rich liquid phase greatly enhances atomic diffusion, and subsequently, the lateral growth of the Ge-rich GeSn solid phase. Hence, crystallization of a-GeSn is expected to occur at a relatively low temperature with a fast lateral growth rate. This process is somewhat similar to liquid phase epitaxy except that there is no single crystal template. We call it “eutectically-enhanced crystallization” (EEC). Note that a dramatic difference between the crystallization of a-GeSn and the solidification of liquid-phase GeSn is that the incorporation of Sn into the Ge-rich solid phase could far exceed the equilibrium solubility (~1 at.%) in the former case because the initial state of a-GeSn is far from equilibrium. Furthermore, because of the lower surface energy of Sn compared to Ge, the Sn-rich liquid phase would segregate at the grain boundaries and on the surface of crystallized GeSn. Subsequently, the excess Sn can be easily and selectively etched away using HCl solution, leaving the crystallized GeSn for integrated photonic device fabrication [3, 10, 21, 26–29].

Blanket GeSn Thin Film Crystallization

To investigate the crystallization of GeSn thin films, a-Ge_1–xSn_x (0< x <0.20) thin films are deposited on thermally grown SiO₂ (5–10 nm thick) on Si, Corning's flexible Willow glass substrates [30], fused silica, and polyimide foils by co-evaporating Ge and Sn in a Kurt Lesker Lab 18 Physical Vapor Deposition (PVD) machine. The base vacuum of the system is better than 5 × 10⁻⁸ Torr before the co-evaporation process. Over the course of our studies, the purity of Sn evaporation sources has been improved from 99.999% (5Ns) to 99.99999% (7Ns), while semiconductor grade Ge has been used in all studies. The deposition rate of Ge is typically 0.08 nm/s, and the Sn deposition rate is adjusted to achieve different a-GeSn compositions. The deposited a-GeSn thin films are annealed at 380–450°C in N₂ for crystallization. Alternatively, the samples can be crystallized by rapid thermal annealing (RTA) or locally crystallized by a focused laser beam followed by furnace annealing. The excess Sn after the crystallization is etched away by 37.2% HCl:H₂O solution.

Irrespective of the substrate, we found the following common features of a-GeSn crystallization: (1) a high lateral growth rate vs. a very low nucleation rate, leading to an extraordinarily large average grain size of ~100 μm when crystallizing blanket Ge_1–xSn_x films with 0.08 < x < 0.15. (2) Well-defined crystallization temperature resembling thermodynamic phase transition. This feature is drastically different from the kinetics-dominated crystallization of amorphous Si. The crystallization temperature of a-GeSn decreases with the increase of Sn composition [10], and no crystallization will occur even at 5°C below the crystallization temperature after prolonged annealing for several hours. Once above the crystallization temperature, on the other hand, the crystallization can be completed within 90 s in RTA. This phenomenon is in line with the well-defined eutectic temperature in the Ge-Sn equilibrium phase diagram, although the actual crystallization temperature of a-GeSn is beyond the description of the phase diagram due to its non-equilibrium nature. (3) A strong (111) preferred orientation due to minimization of surface energy on amorphous layers [10, 21, 26, 27]. As will be discussed later, this preferred (111) orientation also has a beneficial effect on the strain engineering of GeSn toward direct gap semiconductors.

Figure 2a shows a top-view SEM image of a crystallized Ge_0.913Sn_0.087 film on 5 nm-thick thermally grown SiO₂ on Si. Grain boundaries can be clearly observed in the low magnification SEM image in Figure 2a, with huge grain sizes on the order of 0.1–1 mm, or 3–4 orders larger than the GeSn thin film thickness (316 nm in this case, as revealed in Figure 2b). This is an extraordinary result for semiconductor thin film crystallization, where typically the grain size is on the same order as the thickness of the thin film [31]. This observation indicates a slow nucleation rate vs. an extremely fast lateral growth rate during GeSn crystallization induced by the EEC mechanism. Electron backscatter diffraction (EBSD) analyses show that each grain predominantly consists of micro-twins as a result of lateral growth from the same nucleation center upon crystallization [10, 26, 27]. Figures 2b,c show the cross-sectional SEM image and the corresponding energy dispersion X-ray spectroscopy (EDS) mapping for compositional analyses, respectively. Ge and Sn are both distributed uniformly in the films without any Sn segregation. The Sn composition from the EDS mapping analysis is 8.7 ± 0.2 at.%. The biaxial tensile strain is determined to be ~0.2% by combining X-ray diffraction (XRD) with Raman spectroscopy analyses, as detailed in [21]. Furthermore, the strong (111) texture of the crystallized GeSn thin films leads to a relatively low Poisson's ratio and a higher dilatational strain under biaxial tensile stress due to the largest inter-planar spacing between (111) planes [21]. These factors favor indirect-to-direct gap transition [21], in contrast to compressive strain in their [001] oriented epitaxial counterparts.

FIGURE 2

Figure 2. (a) Low-magnification, top-view SEM image of a crystallized Ge_0.913Sn_0.087 thin film, showing a large average grain size on the order of mm scale. (b) Cross-sectional SEM image of the Ge_0.913Sn_0.087 film crystallized on thermally-grown 5 nm-thick SiO₂ on Si. The film thickness of GeSn is 316 nm. (c) The distribution of Ge and Sn atoms in the GeSn film in (b), as revealed by EDS mapping. Sn is evenly distributed in the film and no Sn clusters observed in the GeSn film.

Figure 3 further demonstrates that the EEC mechanism of a-GeSn is equally applicable to flexible Willow glass substrate, polyimide substrate, and fused silica substrate alike [26, 32]. Large grain sizes of 0.1–1 mm are maintained in all these cases for Ge_0.91Sn_0.09 thin films. In Figure 3b, the center of nucleation can also be clearly seen, from which the grain grows radially. The polyimide substrate also shows some micro wrinkles upon GeSn crystallization due to thermal stress. These wrinkles are similar to surface texturing used in solar cells and can potentially be engineered to enhance the absorption in GeSn. Furthermore, while it is impossible to directly measure the transmittance spectrum of epitaxial GeSn thin films on Si at λ < 1,200 nm due to the absorption of the Si substrate, the Ge_0.91Sn_0.09 thin films crystallized on transparent fused silica substrates reveals both the fundamental direct gap at λ~2,400 nm and the secondary direct gap at λ~1,150 nm in the transmittance spectrum (Figure 3d). Interestingly, in this case the second direct gap is almost exactly twice the first direct gap, which could make a significant impact on the performance of GeSn lasers due to up-conversion from the first to the second conduction valley through Auger process. These results not only demonstrate substrate-independent, high quality GeSn crystallization, but also show that such studies could offer more information about the band structure of GeSn inaccessible to their epitaxial counterparts. We will come to this point again in section Optical Gain Dynamics of Crystallized Direct Gap GeSnOI.

FIGURE 3

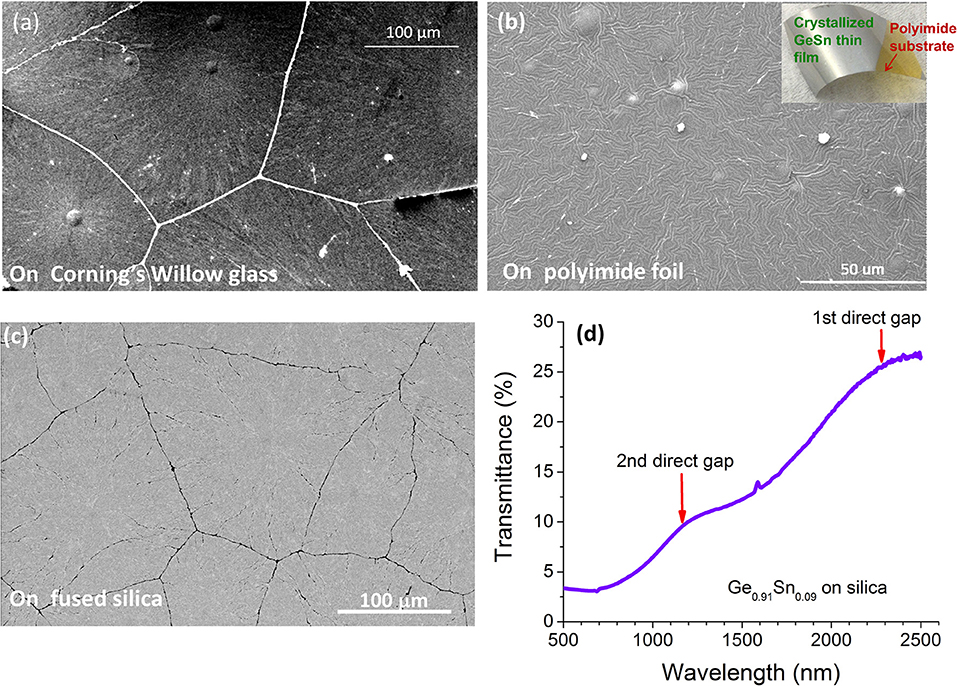
Figure 3. SEM images of Ge_0.91Sn_0.09 (~300 nm thick) crystallized on (a) flexible Willow glass substrates; (b) polyimide foils; and (c) fused silica substrate. The inset of (b) shows a photo of the corresponding sample. Panel (d) shows the transmittance spectrum of (c), where the 1st direct gap at λ~2,400 nm and the 2nd direct gap at λ~1,150 nm are clearly observed.

Controlling the Nucleation Location Upon GeSn Thin Film Crystallization

While large grains with high crystallinity are achieved in crystallizing blanket GeSn thin films, the nucleation remains a stochastic process and there is no control of the nucleation site. To pre-define the nucleation sites before crystallization annealing, we have developed three approaches: (1) Sn micropattern induced nucleation [32]; (2) laser seeded nucleation [26–28]; and (3) nanotip induced nucleation [26, 27].

Figures 4a,b show examples of Sn micropattern induced nucleation. In Figure 4a, a ~5 μm diameter Sn microdot is defined on top of a-GeSn by photolithography followed by crystallization annealing. Clearly, the Sn microdot serves as a nucleation center from which the Ge_0.91Sn_0.09 crystals grow radially. The Sn microdot also melts and dewets into smaller Sn nanodots upon crystallization annealing, as shown in the inset of Figure 4a. As discussed earlier, Sn can be removed selectively using HCl solution after crystallization, offering a convenient approach to define the nucleation sites on GeSn. Figure 4b further shows two Sn microstrips patterned on top of a-GeSn followed by crystallization annealing. Both Sn microstrips serve as nucleation centers for GeSn. Therefore, the GeSn grains grow perpendicular to the two Sn microstrips, respectively, and impinge each other almost exactly in the middle of the two Sn microstrips. This observation further confirms that Sn micropatterns on top of a-GeSn can be engineered to effectively control the nucleation and lateral growth of crystalline GeSn.

FIGURE 4

Figure 4. SEM images of Ge_0.91Sn_0.09 crystallization induced by Sn micropatterns: (a) nucleation site defined by a Sn microdot (b) nucleation and lateral growth induced by Sn microstrips.

An example of laser-seeded crystallization of Ge_0.89Sn_0.11 is shown in Figures 5a,b [27]. A laser beam at λ = 514 nm is scanned at one end of a 2 × 38 μm rectangular a-GeSn strip to seed the nucleation of GeSn before furnace annealing. The optical power at the sample surface is measured to be 2–3 mW during the laser annealing, and the focal spot is ~300 nm in diameter using a 100 × objective lens. The scan rate is ~1 μm/s. Subsequently, the a-GeSn microstrip with a laser seeded nucleation region on one end is annealed at 440°C for 30 min. Figure 5b shows the EBSD mapping of the crystallized strip. Two twinning grains are formed at first from the nucleation site seeded by laser annealing. During the lateral crystal growth along the length direction upon furnace annealing, one of the seed grains (pink) overgrows the other (blue) and becomes dominant. Remarkably, this grain spans almost the entire strip length of 38 μm, large enough for active photonic devices such as waveguide-coupled modulators or photodetectors. There are a few sporadic twin boundaries inside the microstrip, which are optoelectronically benign since these are coherent interfaces without dangling bonds to induce deep-level defect centers.

FIGURE 5

Figure 5. (a) SEM image of a 2 × 38 μm Ge_0.89Sn_0.11 microstrip laser annealed at one end (right hand side). The laser scanned along the direction of the width to form a seed for lateral crystal growth. (b) EBSD mapping of the strip after laser seeding and furnace annealing at 440°C for crystallization. A dominant grain (in pink) >35 μm long is clearly demonstrated. The twin boundaries are labeled in green. Grain boundaries with misorientation angles >15° are labeled in red. The color scale of the Euler angles for the EBSD mapping is also shown in the lower right corner. (c) SEM image of a trianglar Ge_0.885Sn_0.115 nanotaper pattern with tip radii on 10–150 nm nanometer scale. The radius of each tip/corner is labeled on the image. (d) Shows the corresponding EBSD mapping of (c) after crystallization. The nanotip on the left has a significantly smaller radius than the other two corners, leading to the growth of a large single crystal grain from this sharpest nanotip.

Figures 5c,d show an example of nanotip induced nucleation [26, 27]. When there is a high curvature surface, such as a nanotip on an a-GeSn micropattern (e.g., the nanotip on the left side of Figure 5c), the local phase transition/crystallization temperature decreases with the tip radius r as described by the Gibbs-Thomson Equation:

$\begin{array}{ll}{T}_m(r)=T_m(\infty )-\frac{2T_m(\infty ){\sigma }_{sl}}{\Delta H_f(\infty ){\rho }_{s}r}& (1)\end{array}$

Here T_m (r), T_m (∞), σ_sl, H_f (∞), and ρ_s are the nanotip crystallization temperature, bulk material crystallization temperature (i.e., r = ∞), solid/Sn liquid interfacial energy, heat of fusion of the phase transition, and the atomic density of the solid phase, respectively. Therefore, if we anneal an a-GeSn micropattern with a high curvature nanotip at a temperature between T_m (r) and T_m (∞), only the nanotip region will crystallize to form a single nucleus. This nucleus at the nanotip will subsequently seed the lateral growth of GeSn across the entire micropattern, leading to a piece of single crystal material. In Figure 5c, a GeSn microtaper pattern with different nanotip curvatures (r = 45, 103, and 185 nm, respectively) is annealed at 420°C for 30 min. Since the tip on the left has a much smaller radius than the other two, upon temperature ramping nucleation first starts at this nanotip. This is supported by the EBSD mapping in Figure 5d. An 18 μm-long single crystal grain (in blue) that occupies ~80% of the entire GeSn microtaper is formed, seeded by the high curvature nanotip on the left. There are grains growing from the other two tips on the right hand side, too, but their sizes much smaller than the dominant single crystal grain. A small amount of sporadic grains mostly form twin boundaries with the dominant single crystal grain. This result proves that the growth of single crystal GeSn on amorphous dielectric layers can indeed be seeded by the high curvature nanotip on an a-GeSn micropattern. Additionally, the microtaper structure in Figures 5c,d also facilitates mode conversion and optical coupling with waveguides, as has been applied to waveguide-coupled photodetectors [3, 33].

Sn Nanodot-Induced Composition Enhancement (NICE) in GeSn Crystallization

In crystallizing blanket a-GeSn thin films, the highest substitutional Sn composition achieved is ~10 at.% [10, 32], limited by surface and grain boundary segregation of Sn. RTA can help to suppress Sn segregation and increase the Sn composition to ~11 at.%. Using GeSn micropatterns and laser-seeded or nanotip-seeded crystallization, the Sn composition has been further increased to 14–15 at.% [27, 28] since most of the large-angle grain boundaries, which tend to induce Sn segregation, are eliminated. However, to extend the optical response of GeSn toward the MIR window at λ = 3–5 μm, an increase of Sn composition beyond 20 at.% is needed. To address this challenge, we have recently developed NICE growth approach [34, 35]. This method, counter-intuitively, is exactly opposite to the conventional approach of synthesizing diamond cubic GeSn. Since metallic β-Sn is thermodynamically more stable than diamond cubic α-Sn at >13°C in bulk materials, conventionally researchers try their best to avoid the nucleation of metallic β-Sn during GeSn growth. In sharp contrast, this novel NICE approach utilizes a “reverse nucleation” method to dissolve β-Sn nanodots below the critical size of nucleation into the Ge matrix, thereby achieving an average composition of 26 at.% Sn in Ge.

The fundamental principle of the NICE approach is schematically shown in Figure 6a. According to the well-known nucleation theory, the nucleus of β-Sn has to reach a critical size, r^*, in order to implement the phase separation from the diamond cubic matrix of Ge or GeSn (labeled as “α-GeSn” in Figure 6b). Any β-Sn nucleus smaller than r^* would dissolve back into the diamond cubic lattice to minimize the Gibbs free energy of the Ge-Sn system. This is because the nucleation of β-Sn creates new interfaces with the diamond cubic α-GeSn matrix, which increases the interfacial energy that dominates the total Gibbs free energy of nanostructure due to the large surface-to-volume ratio.

FIGURE 6

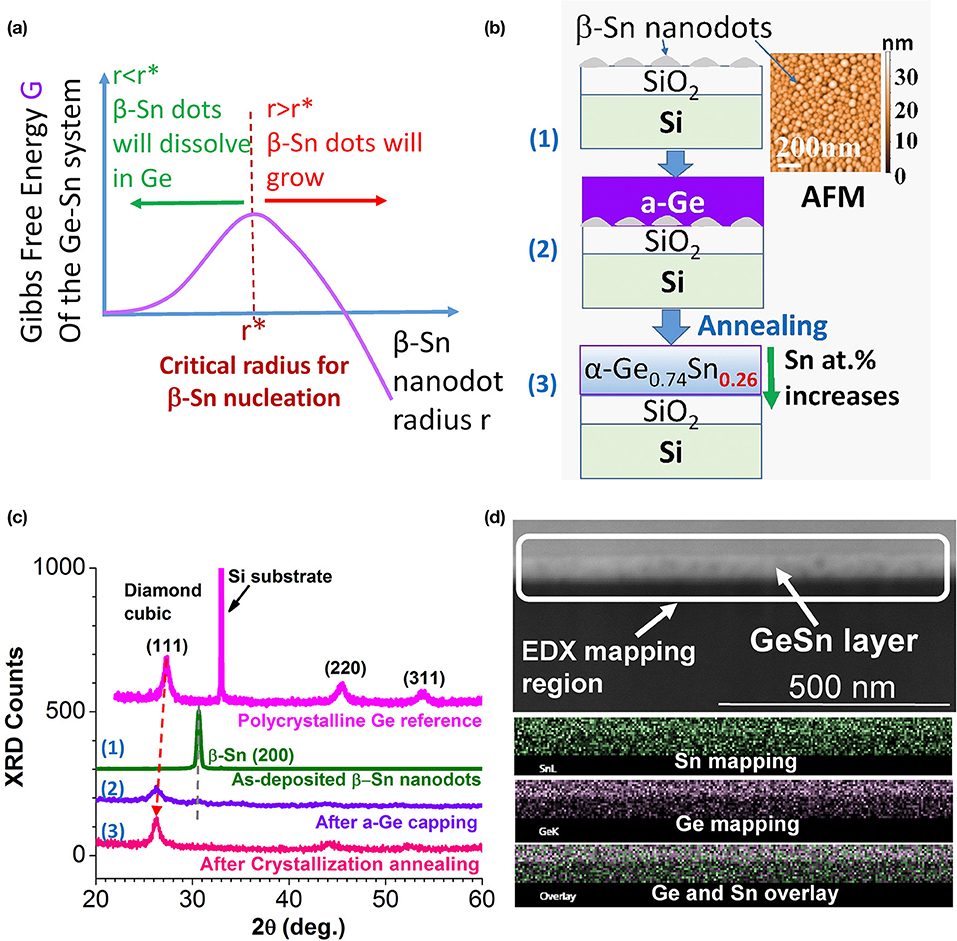
Figure 6. (a) Schematics showing the Gibb free energy of the Ge-Sn system vs. the radius of β-Sn (semimetal) nanodots. Below the critical size of nucleation r^*, the β-Sn nanodots should dissolve into Ge to minimize the interfacial energy. (b) Schematics showing the NICE fabrication process of crystalline diamond cubic α-GeSn with 26 at.% average Sn. (c) XRD data of a pure Ge reference sample and the Sn or GeSn samples corresponding to steps (1)–(3) in (b). (d) Cross-sectional SEM image (top) and the elemental EDS mapping of Sn, Ge, and Sn-Ge mapping overlay.

Based on this inspiration, if we can first deliberately make β-Sn nanodots with sizes smaller than r^*, they will be readily dissolved into Ge upon Ge deposition and crystallization annealing, thereby breaking through the existing solubility limit. As schematically shown in Figure 6b, we first deposit a layer of β-Sn nanodots (<50 nm in diameter and <30 nm in height, see the inset of Figure 6b) on SiO₂/Si, then cap the Sn nanodots with evaporated amorphous Ge (a-Ge). This process artificially creates a huge amount of Ge/Sn interfaces. Upon crystallization annealing at 300–500°C, these nanodots should dissolve into Ge and form crystalline GeSn with high Sn composition in order to eliminate the Ge/Sn interfaces and decrease the total Gibbs free energy (according to Figure 6a). Therefore, the NICE growth approach for high Sn composition is based on dissolving β-Sn nanodots into the diamond cubic lattice of Ge.

The preliminary demonstration of NICE growth is shown in Figures 6b–d. The inset of Figure 6b shows an AFM image of nominally 5 nm-thick β-Sn evaporated onto SiO₂/Si. Sn dewets on SiO₂ during the deposition, leading to the self-assembly of nanodots. The average diameter of the Sn dots is 45 nm and the height is ~30 nm. The XRD data of the as-deposited β-Sn nanodots are shown in Figure 6c [step (1)], demonstrating a strong (200) preferred orientation. Remarkably, after depositing nominally 20 nm-thick a-Ge on the β-Sn nanodots, the β-Sn (200) peak is already almost completely replaced by the (111) peak of nanocrystalline, diamond cubic structured GeSn [step (2)]. Moreover, after crystallization annealing at 450°C for 15 min, the β-Sn (200) peak completely disappears and the α-SnGe (111) peak becomes sharper due to improved crystallinity after annealing [step (3)]. Therefore, we can conclude that β-Sn is completely dissolved into the diamond cubic lattice of GeSn after the crystallization annealing, confirming our hypothesis based on the nucleation theory in Figure 6a. Compared to the pure Ge reference sample, the (111) peak of crystallized GeSn is drastically shifted to lower diffraction angle (indicating a larger lattice constant) due to the significant Sn alloying [Figure 6c, step (3)]. From the peak shift in the XRD data, we estimate an average composition of 26–27 at.% Sn in crystallized GeSn. Figure 6d further shows a cross-sectional SEM image and the corresponding EDS mapping of the crystallized GeSn sample grown by NICE approach. The Sn-rich region at the bottom and Ge-rich cap at the top can be clearly observed. An average Sn composition of 26 at.% Sn is confirmed, and the bottom Sn-rich region shows a Sn composition as high as ~40 at.%, indicating that NICE approach has a great potential to achieve even higher Sn composition for covering the entire MIR window of λ = 3–5 μm.

Optical Gain Dynamics of Crystallized Direct Gap GeSnOI

As an approach to evaluate the optoelectronic quality of crystallized GeSnOI discussed in section Substrate-Independent GeSn Crystallization on Amorphous Insulators as well as to elucidate some fundamental questions about the GeSn band structure near the indirect-to-direct gap transition, we performed ultrafast pump-probe optical gain dynamic measurements on the 0.2% tensile strained Ge_0.913Sn_0.087OI sample shown in Figure 2. This sample provides a composition close to the indirect-to-direct transition with high crystallinity and large grains on mm-scale so that grain boundaries have negligible effect on the pump-probe measurement. We aim at addressing two fundamental questions:

(1) Is the high lasing threshold observed from optically pumped GeSn lasers mainly due to the intrinsic band structure (i.e., insufficient directness of the bandgap) or is it because of extrinsic defects? Recently, optically pumped GeSn lasers have achieved dramatic progress [17, 19, 20, 22–24], yet the threshold pump power density increases from ~100 to 1,000 kW/cm² as the temperature increases from 77 to 180 K, orders of magnitude higher than bulk homojunction direct gap III-V lasers [36]. Even at 10 K, the threshold pump power density is still >>10 kW/cm², compared to < <1 kW/cm² from GaAs lasers. The threshold does not show significant decrease even at higher Sn compositions of 16–18 at.%, which are supposed to have better direct gap performance, even though the maximal operation lasing temperature does increases. Therefore, it is important to find out the key limiting factors of the lasing threshold.

(2) What is the intrinsic crossover composition for the indirect-to-direct bandgap transition in Ge_1–xSn_x? This issue is still controversial theoretically and experimentally, with the Sn content ranging from 6.5 to 10 at.% at the transition point from different reports [9, 13, 37–39]. The increase of the integrated photoluminescence (PL) intensity with the decrease of temperatures has been applied as an evidence to prove the direct fundamental bandgap of epitaxial Ge_1–xSn_x, in contrast to the behavior of direct gap emission in Ge. However, it has been found recently that there are possible pitfalls associated with this criterion. For example, Pezzoli et al. [40] reported that Ge_0.95Sn_0.05 coherently grown on Ge buffer layer (with −0.8% compressive strain) also shows a similar PL enhancement at lower temperatures in spite of its indirect gap nature. In fact, it is well-known that even indirect gap semiconductors (such as Si) tends to show higher PL intensity at lower temperatures due to less non-radiative recombination. On the other hand, demonstration of lasing can provide evidence for direct gap GeSn at low temperatures, but cannot directly prove that the same composition remains direct gap at room temperature since GeSn lasers operating at 300 K are still not available. Thus, direct measurement of the carrier dynamics and optical gain lifetime is required to undoubtedly determine the directness of the fundamental bandgap of Ge_1–xSn_x, especially at room temperature.

Femtosecond (fs) pump-probe studies provides an ideal approach to address these two fundamental questions. The peak optical gain measured at 0 time delay between the pump and probe pulses provides information about the maximal intrinsic optical gain from the direct band-to-band transitions since the measurement timescale of <60 fs is faster than any recombination process [41, 42]. On the other hand, the optical gain lifetime measurement provides affirmative information about the nature of the bandgap (indirect vs. direct) as well as any likely extrinsic factors (e.g., defects) that limits the injected carrier lifetime.

A challenge for ultrafast pump-probe measurement of GeSn, though, is that most of the epitaxial GeSn layers are grown on Ge buffers, which can complicate the pump-probe carrier dynamics analysis due to carrier diffusion between GeSn and the Ge buffer as well as non-linear effects in Ge such as two-photon absorption (TPA). Direct crystallization of high crystallinity GeSnOI provides a possible approach to circumvent the complication of Ge buffers. The thin SiO₂ layer also prevents photo-generated carrier diffusion from GeSn into the Si substrate, offering a more accurate evaluation of the injected carrier density. Therefore, ultrafast pump-probe measurements on our GeSnOI samples reveals important information about the optical gain and carrier dynamics inherent to GeSn.

Ultrafast Pump-Probe Measurement Setup

Our experiments are carried out using a setup similar to what has been described in [29] and [41]. In order to investigate the optical gain spectrum in the Ge_0.913Sn_0.087OI material, we first measure the power-dependent ultrafast pulse transmittance spectra (at high injection level) and compare it to the linear transmittance spectrum measured by a Jasco V-570 UV-VIS-IR spectrometer with a Jasco ISN-470 integrating sphere (at negligible injection level). For the ultrafast measurements, the incident light consist of broadband, <60 fs pulses covering the wavelength range of 1,850–2,400 nm. These are the idler pulses from an optical parametric amplifier (OPA, Spectra-Physics OPA-800C) pumped by high-energy pulses at λ = 800 nm seeded by a Spectra-Physics Tsunami Ti:Sapphire laser and amplified by Spectra-Physics Spitfire-Pro amplifier. In power-dependent ultrafast transmittance spectra measurements, the focal spot is in Gaussian profile with a beam waist of 90 μm, as measured by razor-blade method. In pump-probe measurements, the pump beam spot waist is increased to 200 μm in order to make sure that the probe spot overlaps with it in the center. Since the focal spot size is much smaller than the grain size of ~1 mm, we adjust the beam position so that it is focused within a single grain during the pump-probe measurement. The transmitted light was then detected by a thermoelectric (TE)-cooled (at −65°C) PbS detector with responsivity covering the wavelength range of 1–3 μm. The detector output was amplified by a lock-in amplifier triggered by the pulse repetition frequency of 1 kHz.

Figure 7a shows the spectrum of the <60 fs incident pulse used in this study. The higher energy photons near the peak wavelength of the pulse at λ~2,000 nm inject a large amount of carriers into the GeSn thin films, thereby inducing population inversion, optical bleaching and optical gain for the lower energy photons in the same pulse near the direct band gap of Ge_0.913Sn_0.087 at λ = 2,200–2,300 nm. This measurement is a good approach to probe the maximal transient gain with minimal time delay between the excitation of the higher energy photon and the transmission of the lower energy photons since they arrive at the sample within the duration of the <60 fs pulse. The peak wavelength of the incident pulse located at 2,000 nm is far away from the 2,200 to 2,300 nm wavelength range for transmittance spectra measurement, thereby avoiding any artifact in the gain spectrum due to its overlap with the peak of the pump pulse.

FIGURE 7

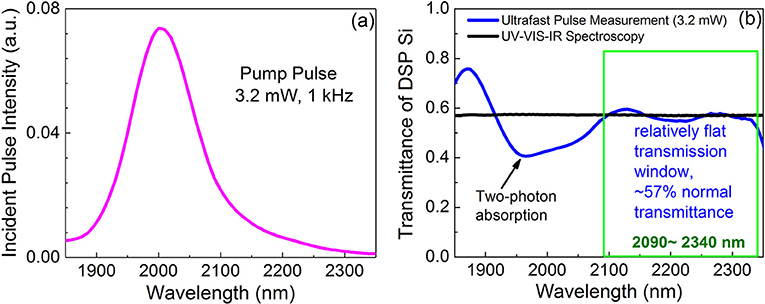
Figure 7. (a) The spectrum of the fs pump pulse with a peak at λ = 2,000 nm. The average power is 3.2 mW and the repetition rate is 1 kHz; (b) transmittance spectrum of a double side polished (DSP) Si wafer under the ultrafast pumping condition in (a) (blue line) compared to that measured by UV-VIS-IR spectroscopy (black line). While a dip due to two-photon absorption is observed at λ~1,950–2,050 nm, a relatively flat transmission window with negligible non-linear effect is identified in the range of 2,100–2,340 nm. We will use this range for GeSn optical gain and carrier dynamics studies.

To make sure that the incident pulse does not introduce any complicated non-linear effect in the double-side polished (DSP) Si substrate itself in the wavelength range of interest (λ = 2,200–2,300 nm), we first measured the fs pump transmittance spectrum of the Si DSP wafer as a reference, as shown in Figure 7b. Corresponding to the peak of the pumping wavelength, we see a dip at 1,950–2,050 nm due to strong TPA in DSP Si. On the other hand, the TPA coefficient β tends to be zero for wavelengths larger than 2,200 nm, corresponding to photon energies less than half of the Si band gap [43]. Indeed, the nearly flat transmittance spectrum in the wavelength range of 2,100–2,340 nm shows no non-linear effect from the DSP Si substrate, consistent with the linear transmittance spectrum measured by UV-VIS-IR spectroscopy. Therefore, this measurement confirms that the ultrafast transmittance data between 2,090 and 2,340 nm will be free of non-linear effects from the substrate, and that any optical gain in this wavelength range is attributed to the GeSn layer on top of Si.

Ultrafast Optical Gain and Carrier Dynamics Measurement of Ge_0.913Sn_0.087OI

Before analyzing the absorption spectra under ultrafast pulse pumping, we first derived the absorption coefficient spectrum of the Ge_0.913Sn_0.087OI sample from the transmittance spectrum measured by UV-VIS-IR spectrometer utilizing iterative self-consistent solution method based on transfer matrix method and Kramer-Kronig relation [41]. This analysis gives the baseline absorption of Ge_0.913Sn_0.087 without optical pumping, i.e., at an injected carrier density of Δn~0. The result is shown in Figure 8a. For direct gap optical absorption, it is well-known that

$\begin{array}{ll}{(\alpha hv)}^2\propto (hv-E_g),& (2)\end{array}$

Here α is the absorption coefficient, hv is the photon energy, and E_g is the direct bandgap. Since the 0.2% biaxial tensile strain splits the light hole (lh) and heavy hole (hh) bands at the center of the Brillouin zone (k = 0), the crystalized Ge_0.913Sn_0.087 shows a direct band gap of Eg^Γ(lh) = 0.502 eV and Eg^Γ(hh) = 0.531 eV. The obtained direct gaps are close to the expected value of 0.52 eV for 8.7% Sn based on the report of [37]. Figure 8c further shows that the derive absorption spectrum of Ge_0.913Sn_0.087 at λ = 2,000–2,500 nm is also similar to the data for epitaxial Ge₀.₉₂Sn_0.08 samples reported by [37]. Below its direct band gap of 0.54 eV, the absorption coefficient from the epitaxial Ge₀.₉₂Sn_0.08 layer is still high, e.g., 2,500 cm⁻¹ at 0.50 eV [37], which is believed to be Urbach tail absorption. Our crystalized Ge_0.913Sn_0.087 film has an additional 1,000 cm⁻¹ absorption at hv = 0.50 eV compared to its epitaxial counterpart in [37], partially due to higher Sn composition (~9 vs. 8 at.%) and partially due to Urbach tail below the direct gap that is clearly shown in Figure 8a. The Urbach tail absorption loss, probably originated from the nanoscale disorder of Sn distribution in the material, could be a limiting factor for the demonstration of low-threshold GeSn lasers.

FIGURE 8

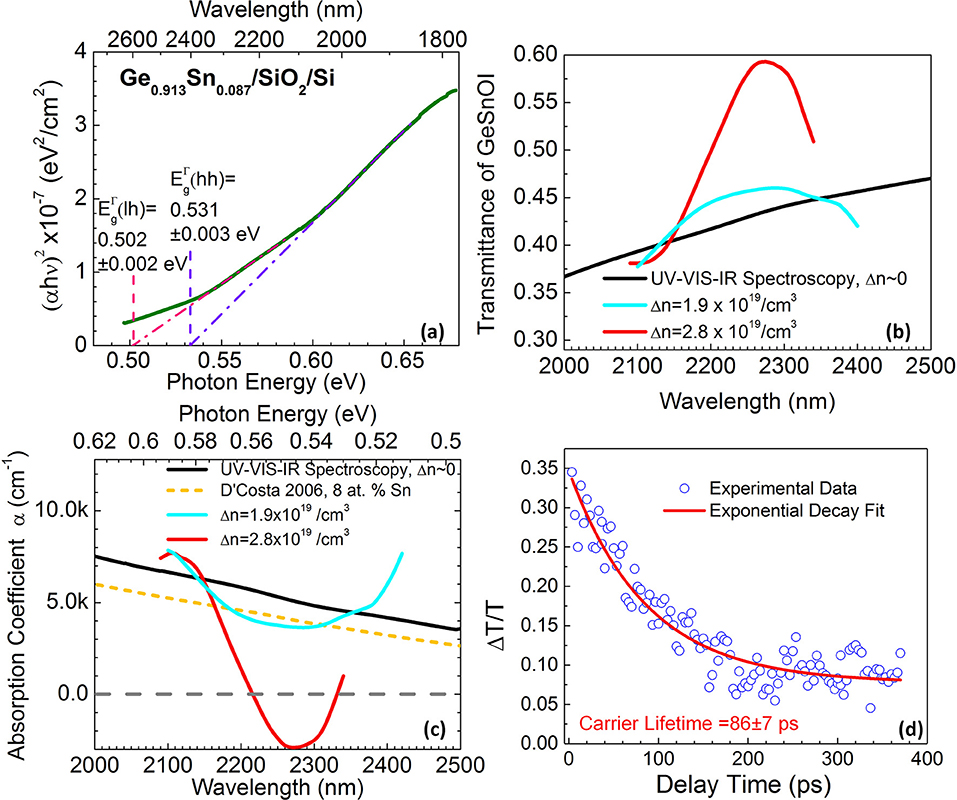
Figure 8. (a) Linear fit to (αhν)² vs. hν indicates that crystalized Ge_0.913Sn_0.087 has a direct band gap of ${\text{E}}_{\text{g}}^{\text{Γ}}$(lh) = 0.502 ± 0.002 eV and ${\text{E}}_{\text{g}}^{\text{Γ}}$(lh) = 0.531 ± 0.003 eV. Here α is absorption coefficient, and hν is photon energy. (b) Transmittance spectrum of the GeSnOI sample measured by UV-VIS-IR spectroscopy (black line) compared to the ultrafast pulse transmittance spectra of the same sample under injected carrier density of Δn = 1.9 × 10¹⁹/cm³ (cyan line) and Δn = 2.8 × 10¹⁹/cm³ (red line). (c) Comparison of derived absorption coefficients of crystalized Ge_0.913Sn_0.087OI with UV-VIS-IR spectroscopy (no pumping, black line), and under injected carrier densities Δn = 1.9 × 10¹⁹/cm³ (cyan line) and Δn = 2.8 × 10¹⁹/cm³ (red line). Negative absorption coefficient (below the dotted gray line) indicates a net optical gain. As a comparison, the linear absorption coefficient of epitaxial GeSn with 8 at.% Sn on Si reported by D'Costa et al. [37] is also shown (short dashed orange line). (d) Results of gain lifetime measurement plotting pump-induced change in transmittance (ΔT/T) vs. the delay time (Δt). The pump pulse is peaked at 2,000 nm, and the probe wavelength is 2,300 nm. The injected carrier density is estimated to be Δn = 4.8 × 10¹⁹ cm⁻³.

Next, we measured the ultrafast pulse transmittance spectra of the GeSnOI sample at different incident power/injection levels to reveal the intrinsic gain from the direct gap transition of GeSn using the pulse spectrum shown in Figure 7a. This captures the maximal optical gain within the 60 fs pulse width of the injection, practically before any carrier recombination could occur [41, 42], thereby revealing the nature of the intrinsic band structure. Figure 8b shows that, in the wavelength regime of 2,100–2,340 nm free of non-linear effects of the substrate (see Figure 7b), we clearly observe strongly enhanced transmittance peak (red curve) at an injected carrier density of Δn~2.8 × 10¹⁹ cm⁻³ from ultrafast pulse pumping compared to the regular transmittance (i.e., negligible injection level Δn~0) measured by UV-VIS-IR spectroscopy. The injected carrier density is estimated based on the input optical pulse power, the measured beam profile, and the measured thickness and optical absorption of GeSn at this wavelength. The transmittance is enhanced by ~37% at the peak wavelength of 2,270 nm at an injection level of Δn~2.8 × 10¹⁹ cm⁻³. The peak transmittance reaches 0.593 at 2,270 nm, even higher than that of the DSP Si substrate (0.572). As will be shown later in our quantitative analyses, this is due to the large optical gain in the GeSn thin film under high injection level. With a similar method, we also studied the case of lower injected carrier density. Under Δn = 1.9 × 10¹⁹/cm³, the transmittance becomes lower compared to the case of Δn = 2.8 × 10¹⁹/cm³, as expected. The peak transmittance occurs at a longer wavelength of λ = 2,290 nm compared to λ = 2,270 nm for Δn = 2.8 × 10¹⁹/cm³. Clearly, the transmittance peak blueshifts and the magnitude increases with the pump power. This is consistent with the band filling upon population inversion, again proving that the enhanced transmittance is due to the optical bleaching or gain in crystalized Ge_0.913Sn_0.087 films.

Further utilizing iterative self-consistent solution of the absorption spectra considering Kramer-Kronig relation and transfer matrix method [41], we are able to obtain the absorption/gain spectra at different injection levels, as shown in Figure 8c. Under Δn = 2.8 × 10¹⁹/cm³ injection, a net gain (i.e., negative absorption) is observed in the wavelength range of 2,220–2,330 nm at room temperature from the crystallized Ge_0.913Sn_0.087OI. The peak gain coefficient is ~2,900 cm⁻¹ at 2,270 nm, comparable to III-V semiconductors and promising for room-temperature lasing. On the other hand, under a lower injection level of Δn = 1.9 × 10¹⁹/cm³, only optical bleaching is observed with the absorption coefficient decreasing from 4,800 to 3,680 cm⁻¹ at 2,300 nm. This comparison indicates that Ge_0.913Sn₀.₀₈₇ needs ~10x larger injected carrier density for optical transparency than III-V semiconductors, i.e., Δn₀~2 × 10¹⁹/cm³ in GeSn vs. Δn₀~2 × 10¹⁸/cm³ in GaAs, possibly due to a larger optical loss (e.g., from free carriers and inter-valence band transitions). The high injection level needed for transparency could be one of the limiting factors of the lasing threshold.

To further study the carrier dynamics in GeSnOI, the ultrafast pulse with the peak positioned at 2,000 nm is used as the pump, and the probe wavelength is set at 2,300 nm. The experimental setup is similar to [29], except that the probe is shifted to longer wavelengths closer to the direct gap of Ge_0.913Sn_0.087 shown in Figure 8a, while the pump is shifted to shorter wavelengths to better distinguish from the probe. The probe pulse is incident vertically on the sample, while the pump pulse is incident at 60 degree angle. The beam profiles of the pump and probe spots on the surface of the sample are measured by razor-blade method and carefully overlapped, with the spot size of the pump pulse (200 μm) being ~2x that of the probe spot (90 μm). An aperture is placed immediately at the backside of the sample to block any astray light from the pump, thereby gathering the probe signal only. A neutral density (ND) filter is put in the probe path to achieve a pump-to-probe intensity ratio >8:1 and also to ensure no non-linear effect caused by the probe itself. The pump-induced change in the transmittance of the probe, ΔT, is normalized to the transmittance without pumping (T). ΔT/T is measured as a function of delay time Δt between the probe pulse and the pump pulse to evaluate the carrier dynamics and optical gain lifetime in the sample by varying the optical path length of the probe with a translation stage in the probe path.

At an injection level of Δn = 4.8 × 10¹⁹ cm⁻³ and a wavelength of λ = 2,300 nm, we observe ΔT/T as a function of the delay time Δt between the probe and pump, as shown in Figure 8d. ΔT/T is about 0.35 at Δt~0, corresponding to a net gain of 3,500 cm⁻¹ at 2,300 nm, and it decays exponentially with delay time Δt. Therefore, Figure 8d is a direct measurement of the gain lifetime. In the case of indirect gap intrinsic Ge, the phonon-assisted carrier scattering from the direct Γ valley to the indirect L valleys limits the gain lifetime to as short as ~200 fs [44–46]. In our case of Ge_0.913Sn_0.087OI, on the other hand, Figure 8d clearly shows a much longer gain lifetime of 86 ± 7 ps, nearly 3 orders of magnitude longer than indirect gap Ge. This result clearly confirms that 0.2% tensile strained Ge_0.913Sn_0.087 is indeed a direct gap semiconductor at room temperature. Measurements at other pumping wavelengths between 2,200 and 2,350 nm also indicate a gain lifetime on the order of 70–100 ps. Note that this gain lifetime is on the same order as the carrier lifetime of epitaxial GeSn lasers, i.e., 350 ps from [17]. This result demonstrates that the optoelectronic quality of crystallized GeSn is approaching their epitaxial counterparts. For laser applications, ideally the gain lifetime should reach several ns to achieve a reasonable threshold. Therefore, the short gain lifetime on the order of 0.1 ns in GeSn is another key limiting factor for lasing at room temperature. There are two possible reasons for the short gain lifetime in GeSn: (1) Auger recombination at high injection levels (Δn > 10¹⁹ cm⁻³) in small band gap GeSn (E_g~0.5 eV; see Figure 8a); (2) non-radiative recombination due to extrinsic defects in GeSn. Note that there could be some convolution between these two factors since defects could also assist Auger process.

Differential gain is another main parameter responsible for the quantum efficiency. It is the derivative of material gain vs. the injected carrier density evaluated near the lasing threshold. From Figures 8c,d, the maximal gain at Δt = 0 is enhanced from 2,500 to 3,600 cm⁻¹ at 2,300 nm when the injected carrier density is increases from 2.8 × 10¹⁹ to 4.8 × 10¹⁹ cm⁻³. This gives a differential gain of ~5.5 × 10⁻¹⁷ cm², one order of magnitude lower than bulk GaAs lasers.

In summary, our ultrafast pulse transmittance and pump-probe spectroscopy studies confirm that 0.2% tensile strained GeSn with 9 at.% Sn is already a direct gap semiconductor at room temperature. The direct band gap transition in GeSn leads to a large intrinsic gain of ~3,000 cm⁻¹, comparable to III-V semiconductors and promising for room-temperature lasing. However, a high transparency threshold of Δn₀ > 2 × 10¹⁹ cm⁻³, a short gain lifetime on the order of 100 ps, and a relatively small differential gain of Ge_0.91Sn_0.09 material pose challenges for the development of low-threshold room temperature GeSn lasers. The impact of these three major factors can be manifested by estimating the threshold current density for an ideal laser device assuming 100% optical confinement in the GeSn gain medium [47]:

$\begin{array}{ll}{J}_{th}=\frac{{\Delta n}_{0}qd}{{\tau }_r}+\frac{{\alpha }_i}{\Gamma }+\frac{1}{2\text{Γ}AL}ln(\frac{1}{R_1{R}_2})& (3)\end{array}$

Here τ_r is the carrier lifetime, d is the GeSn layer thickness, Δn₀ is the injected carrier density for transparency, q is the electron charge, α_i is the internal loss, Γ is the confinement factor, L is the cavity length, g is the differential gain at the transparency, $A=\frac{g{\tau }_r}{qd,}$ and R₁ and R₂ are the front and back mirror reflectivities. Based on the parameters obtained in our pump-probe studies and assuming ideal optical confinement in GeSn, we use the following values at λ = 2,300 nm: $\Delta n_0=2\times 10^{19}c{m}^{-3}$, τ_r = 100 ps, g = 5.5 × 10⁻¹⁷cm², q = 1.6 × 10⁻¹⁹ C, d = 300 nm, Γ = 1, ${\alpha }_i=1000c{m}^{-1}$ considering the Urbach tail absorption and the free carrier absorption, L = 200 μm, R₁ = 90%, and R₂ = 100%. The estimated threshold current density of GeSn lasers operating at room temperature would be ~2,000 kA/cm², equivalent to a threshold on the order of MW/cm² under optical pumping. This estimate of lasing threshold is consistent with the experimental result demonstrated recently at 270 K from a higher Sn composition [24]. Therefore, our ultrafast pump-probe analysis does reveal the major factors limiting the achievement of low threshold GeSn lasers at room temperature. Based on this analysis, we suggest that further reducing the defects in GeSn could get rid of the extrinsic absorption loss from the Urbach tail (which could still exist in epitaxial GeSn [37]) and increase the gain lifetime, thereby reducing the lasing threshold and truly employing the large intrinsic optical gain of direct gap GeSn. The relation between Auger recombination and extrinsic defect and intrinsic band structures (e.g., the transition between the first and second conduction valleys mentioned in section Blanket GeSn Thin Film Crystallization) needs further evaluation. Up-conversion spectroscopy could be applied to investigate the latter.

Prototype MIR Photodetectors Based on Crystallized GeSn

Based on the high crystallinity GeSnOI materials discussed in section Substrate-Independent GeSn Crystallization on Amorphous Insulators and tested optically in section Optical Gain Dynamics of Crystallized Direct Gap GeSnOI, we demonstrate a p-Ge_0.89Sn_0.11/n-Si p-n photodiode working at λ = 2,050 nm in Figure 9. The sample is prepared by RTA crystallization of 100 nm-thick a-GeSn on n-Si substrate at 450°C, leading to a Sn incorporation of 11 at.%. To maintain the beneficial features of GeSn crystallized on SiO₂ [e.g., (111) preferred orientation to enhance the beneficial effect of tensile strain [21]], we did not deliberately remove the native oxide on fresh Si wafers before the a-GeSn deposition. The active area of the device is 200 × 200 μm². The I-V characteristics of the device is shown in Figure 9a, with a clear rectifying behavior and a dark current as low as 200 nA at −1 V reserve bias. This corresponds to a dark current density of <1 mA/cm² at 1–2V reverse bias, approaching the level of epi Ge/Si photodiodes and better than most of the existing epitaxial GeSn photodetectors on Si (see Table 1). Figure 9b shows the responsivity of the device vs. applied voltage under the optical excitation of an LED emitting at λ = 2,050 nm. Clear photovoltaic behavior is observed, and full responsivity is observed at a low reverse bias of −1 V. Due to the limited thickness of the GeSn MIR absorber layer (~100 nm thick), the absorption at λ = 2,050 nm was measured to be ~9% by UV-VIS-IR spectrometer. Therefore, in the ideal case the responsivity would be 150 mA/W, compared to the experimental result of 100 mA/W (Figure 9b). This result indicates a carrier collection efficiency of ~67%. Note that the responsivity at 2,050 nm is already on the same order as some commercial PbS photodetectors. According to [58], the peak photoresponse of a PbS photoconductor at 2,200 nm wavelength under 15 V bias is 5 × 10⁴ V/W, with a load resistance = dark resistance = 0.25–2.5 MΩ. This translates to a responsivity of 20–200 mA/W (i.e., 5 × 10⁴ V/W divided by 0.25–2.5 MΩ). The fact that we already achieved 100 mA/W responsivity at a much lower bias of 1 V is clearly very competitive to the existing technology and high promising for future improvement. We will further investigate GeSn crystallization on n-type conductive oxides on flexible substrates in our future work to check if similar device performance can be maintained for flexible MIR photonics.

FIGURE 9

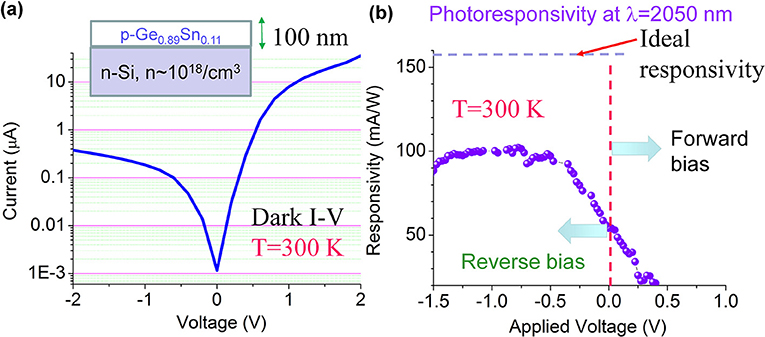
Figure 9. (a) I-V characteristics of the crystallized p-Ge_0.89Sn_0.11/n-Si photodiode. (b) Responsivity vs. applied voltage at an excitation wavelength of λ = 2,050 nm.

TABLE 1

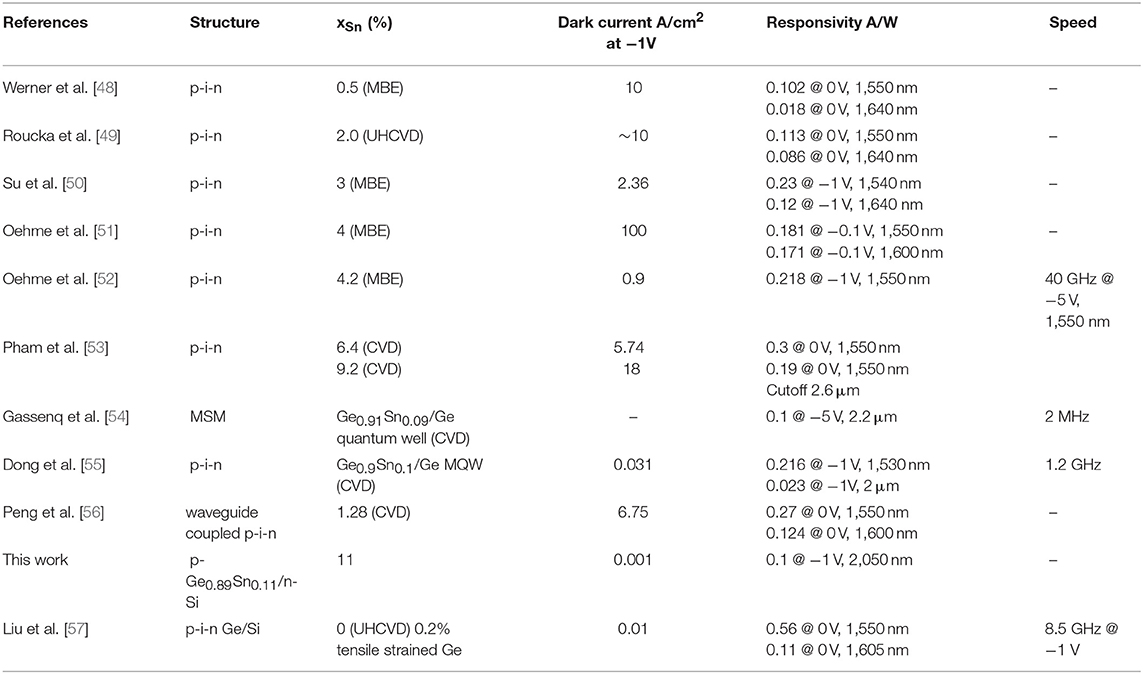
Table 1. Summary of the recent demonstration of GeSn detectors compared to free-space Ge p-i-n photodiodes.

Conclusions

In conclusion, we have demonstrated low-temperature crystallization of direct bandgap, high crystallinity Ge_1−xSn_x (0.08 < x <0.26) on amorphous dielectrics insulators (GeSnOI) toward 3D MIR photonic integration as well as flexible MIR photonics. Utilizing EEC, an extraordinarily large average grain size of ~100 μm has been achieved in blanket GeSn films crystallized on SiO₂ layers, flexible glass, fused silica, and polyimide substrates alike. Furthermore, using Sn nanodot enhanced composition enhancement, we have achieved an average GeSn composition as high as 26 at.% to further extend the optical response of GeSn toward λ = 3–5 μm. The achieved Sn composition of 8–26 at.% far exceeds that of the equilibrium solubility limit of <1 at.%, even though the crystallization temperature of 350–450°C far exceeds the typical epitaxial growth temperature of GeSn to prevent Sn segregation. This result indicates that crystallization from a-GeSn may offer better metastability compared to direct epitaxial growth of GeSn. Attesting to the high crystallinity, a peak optical gain of 2,900 cm⁻¹ with a lifetime on the order of 0.1 ns is achieved at λ = 2,200–2,350 nm at 300 K. The intrinsic gain coefficient is comparable to III-V semiconductors. The gain lifetime is on the same order as epitaxial GeSn, and it is >100x longer than the direct gap transition in Ge, confirming the indirect-to-direct band gap transition in GeSn at ~9 at. Sn composition. The study also suggests that further reducing the defects in GeSn could greatly reduce the Urbach tail absorption losses and increase the gain lifetime toward practical laser devices. Moreover, a prototype p-GeSn/n-Si photodiode from a-GeSn crystallization achieves 100 mA/W responsivity at λ = 2,050 nm and T = 300 K, approaching the level of some commercial PbS detectors. The device also demonstrates photovoltaic behavior and a low dark current density of 1 mA/cm² at −1 V reverse bias, comparable to epitaxial Ge/Si photodiodes. These results indicate that crystallization of GeSnOI offers a promising solution for active devices toward 3D MIR photonic integration and flexible MIR photonics.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

XW performed optical and ultrafast pump-probe characterization of the GeSn samples. She also contributed significantly to the write-up of this paper. AC and HL fabricated the GeSn materials and characterized their crystallinity and microstructures. AC and LJ fabricated and tested the photodetector devices with the help from SF. JP provided high purity Sn deposition source material. JL directed this research, analyzed the data with other co-authors, and coordinated the writing of this paper.

Funding

This work had been supported by the National Science Foundation under the grant number DMR-1255066. Additional support has been provided by Air Force Small Business Technology Transfer (STTR) program through prime contract # FA8650-18-C-1638.

Conflict of Interest

JP is the founder of Epitaxial Laboratory Inc. and a Research Affiliate at Dartmouth College.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would to thank Prof. Christopher Levey at Thayer School of Engineering for supporting the rapid thermal annealing equipment and Drs. Charles Daghlian and Maxime Guinel at the Dartmouth Electron Microscopy Facility Center for supporting the electron microscopy training.

Footnotes

1. ^http://www.aimphotonics.com/pdk

References

1. Soref RA. The past, present, and future of silicon photonics. IEEE J Sel Topics Quantum Electron. (2006) 12:1678–87. doi: 10.1109/JSTQE.2006.883151

CrossRef Full Text | Google Scholar

2. Subbaraman H, Xu X, Hosseini A, Zhang X, Zhang Y, Kwong D, et al. Recent advances in silicon-based passive and active optical interconnects. Opt Express. (2015) 23:2487–511. doi: 10.1364/OE.23.002487

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Liu J. Monolithically integrated Ge-on-Si active photonics. Photonics. (2014) 1:162–97. doi: 10.3390/photonics1030162

CrossRef Full Text | Google Scholar

4. Wada K, Kimerling LC. Photonics and Electronics With Germanium. Weinheim: Wiley-VCH (2015). doi: 10.1002/9783527650200

CrossRef Full Text | Google Scholar

5. Wang X, Liu J. Emerging technologies in Si active photonics. J Semicond. (2018) 39:051001. doi: 10.1088/1674-4926/39/6/061001

CrossRef Full Text | Google Scholar

6. Madelung O. (Ed.). Physics of Group IV Elements and III–V Compounds, Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology, Vol. 17a. Berlin: Springer (1982).

Google Scholar

7. Bauer M, Taraci J, Tolle J, Chizmeshya AVG, Zollner S, Smith DJ, et al. Ge-Sn semiconductors for band-gap and lattice engineering. Appl Phys Lett. (2002) 81:2992–94. doi: 10.1063/1.1515133

CrossRef Full Text | Google Scholar

8. Mathews J, Beeler RT, Tolle J, Xu C, Roucka R, Kouvetakis J, et al. Direct-gap photoluminescence with tunable emission wavelength in Ge_1−ySn_y alloys on silicon. Appl Phys Lett. (2010) 97:221912. doi: 10.1063/1.3521391

CrossRef Full Text | Google Scholar

9. Chen R, Lin H, Huo Y, Hitzman C, Kamins TI, Harris JS. Increased photoluminescence of strain-reduced, high-Sn composition Ge_1–xSn_x alloys grown by molecular beam epitaxy. Appl Phys Lett. (2011) 99:181125. doi: 10.1063/1.3658632

CrossRef Full Text | Google Scholar

10. Li H, Brouillet J, Salas A, Wang X, Liu J. Low temperature growth of high crystallinity GeSn on amorphous layers for advanced optoelectronics. Opt Mater Express. (2013) 3:1385–96. doi: 10.1364/OME.3.001385

CrossRef Full Text | Google Scholar

11. Bhargava N, Coppinger M, Prakash Gupta J, Wielunski L, Kolodzey J. Lattice constant and substitutional composition of GeSn alloys grown by molecular beam epitaxy. Appl Phys Lett. (2013) 103:041908. doi: 10.1063/1.4816660

CrossRef Full Text | Google Scholar

12. Oehme M, Kostecki K, Schmid M, Oliveira F, Kasper E, Schulze J. Epitaxial growth of strained and unstrained GeSn alloys up to 25% Sn. Thin Solid Films. (2014) 557:169–72. doi: 10.1016/j.tsf.2013.10.064

CrossRef Full Text | Google Scholar

13. Ghetmiri SA, Du W, Margetis J, Mosleh A, Cousar L, Conley BR, et al. Direct-bandgap GeSn grown on silicon with 2230 nm photoluminescence. Appl Phys Lett. (2014) 105:151109. doi: 10.1063/1.4898597

CrossRef Full Text | Google Scholar

14. Mathews J, Roucka R, Xie JQ, Yu SQ, Menéndez J, Kouvetakis J. Extended performance GeSn/Si(100) p-i-n photodetectors for full spectral range telecommunication applications. Appl Phys Lett. (2009) 95:133506. doi: 10.1063/1.3238327

CrossRef Full Text | Google Scholar

15. Gupta JP, Bhargava N, Kim S, Adam T, Kolodzey J. Infrared electroluminescence from GeSn heterojunction diodes grown by molecular beam epitaxy. Appl Phys Lett. (2013) 102:251117. doi: 10.1063/1.4812747

CrossRef Full Text | Google Scholar

16. Du W, Zhou Y, Ghetmiri SA, Mosleh A, Conley R, Nazzal A, et al. Room-temperature electroluminescence from Ge/Ge_1–xSn_x/Ge diodes on Si substrates. Appl Phys Lett. (2014) 104:241110. doi: 10.1063/1.4884380

CrossRef Full Text | Google Scholar

17. Wirths S, Geiger R, von den Driesch N, Mussler G, Stoica T, Mantl S, et al. Lasing in direct- bandgap GeSn alloy grown on Si. Nat Photonics. (2015) 9:88–92. doi: 10.1038/nphoton.2014.321

CrossRef Full Text | Google Scholar

18. Cong H, Xue C, Zheng J, Yang F, Yu K, Liu Z, et al. Silicon based GeSn p-i-n photodetector for SWIR detection. IEEE Photonics J. (2016) 8:6804706. doi: 10.1109/JPHOT.2016.2607687

CrossRef Full Text | Google Scholar

19. Stange D, Wirths S, Geiger R, Schulte-Braucks C, Marzban B, von den Driesch N, et al. Optically pumped GeSn microdisk lasers on Si. ACS Photonics. (2016) 3:1279–85. doi: 10.1021/acsphotonics.6b00258

CrossRef Full Text | Google Scholar

20. Al-Kabi S, Ghetmiri SA, Margetis J, Pham T, Zhou Y, Dou W, et al. An optically pumped 2.5 μm GeSn laser on Si operating at 110 K. Appl Phys Lett. (2016) 109:171105. doi: 10.1063/1.4966141

CrossRef Full Text | Google Scholar

21. Li H, Wang X, Liu J. Highly effective strain-induced band-engineering of (111) oriented, direct-gap GeSn crystallized on amorphous SiO₂ layers. Appl Phys Lett. (2016) 108:102101. doi: 10.1063/1.4943192

CrossRef Full Text | Google Scholar

22. Margetis J, Al-Kabi S, Du W, Dou W, Zhou Y, Pham T, et al. Si-based GeSn lasers with wavelength coverage of 2–3 μm and operating temperatures up to 180 K. ACS Photonics. (2017) 5:827–33. doi: 10.1021/acsphotonics.7b00938

CrossRef Full Text | Google Scholar

23. Reboud V, Gassenq A, Pauc N, Aubin J, Milord L, Thai QM, et al. Optically pumped GeSn micro-disks with 16% Sn lasing at 3.1 μm up to 180 K. Appl Phys Lett. (2017) 111:092101. doi: 10.1063/1.5000353

CrossRef Full Text | Google Scholar

24. Zhou Y, Dou W, Du W, Ojo S, Tran H, Ghetmiri SA, et al. Optically pumped GeSn lasers operating at 270 K with broad waveguide structures on Si. ACS Photonics. (2019) 6:1434–41. doi: 10.1021/acsphotonics.9b00030

CrossRef Full Text | Google Scholar

25. Beals M, Michel J, Liu J, Ahn D, Sparacin D, Sun R, et al. Process flow innovations for photonic device integration in CMOS. Proc SPIE. (2008) 6898:689804. doi: 10.1117/12.774576

CrossRef Full Text | Google Scholar

26. Li H, Brouillet J, Salas A, Chaffin I, Wang X, Liu J. Low temperature geometrically confined growth of pseudo single crystalline GeSn on amorphous layers for advanced optoelectronics. ECS Trans. (2014) 64:819–27. doi: 10.1149/06406.0819ecst

CrossRef Full Text | Google Scholar

27. Li H, Brouillet J, Salas A, Chaffin I, Wang X, Liu J. Pseudo single crystal, direct-band-gap Ge_0.89Sn_0.11 on amorphous dielectric layers towards monolithic 3D photonic integration. Appl Phys Lett. (2014) 105:201107. doi: 10.1063/1.4902349

CrossRef Full Text | Google Scholar

28. Li H, Cuervo Covian AV, Wang X, Liu J. High thermal stability of tensile strained direct gap GeSn crystallized on amorphous layers. ECS Trans. (2016) 75:623–32. doi: 10.1149/07508.0623ecst

CrossRef Full Text | Google Scholar

29. Wang X, Li H, Liu J. Power-dependent transient gain study on direct gap GeSn crystallized on amorphous layers. ECS Trans. (2016) 75:223–8. doi: 10.1149/07508.0223ecst

CrossRef Full Text | Google Scholar

30. Corning's flexible Willow glass laminate (2019). Available online at: https://www.corning.com/worldwide/en/innovation/corning-emerging-innovations/corning-willow-glass.html (accessed August 20, 2019).

Google Scholar

31. Thompson CV. Grain growth in thin films. Annu Rev Mater Sci. (1990) 20:245–68. doi: 10.1146/annurev.ms.20.080190.001333

CrossRef Full Text | Google Scholar

32. Li H. Group IV semiconductors for Si photonics and solar energy applications (Ph.D. thesis). Dartmouth College, Hanover, NH, United States (2016).

Google Scholar

33. Sun R, Beals M, Pomerene A, Cheng J, Hong CY, Kimerling LC, et al. Impedance matching vertical optical waveguide couplers for dense high index contrast circuits. Optics Express. (2008) 16:11682–90. doi: 10.1364/OE.16.011682

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Liu J, Wang X. Epitaxy-free direct bandgap GeSn materials and devices for facile 3D photonic integration. In: Conference on Lasers and Electro-Optics. San Jose, CA: OSA Technical Digest (Optical Society of America, 2018), paper STh4I.1 (2018). doi: 10.1364/CLEO_SI.2018.STh4I.1

CrossRef Full Text | Google Scholar

35. Cuervo Covian A, Zhou Y, Wang X, Yu SQ, Liu J. Sn Nanodots-induced composition enhancement (NICE) to achieve 26 at.% Sn in GeSn for mid-infrared integrated photonics. In: 2nd Joint ISTDM/ICSI 2019 Conference, 6/2-6/6, Madison, WI: University of Wisconsin-Madison (2019).

Google Scholar

36. Burns G, Dill FH Jr, Nathan MI. The effect of temperature on the properties of GaAs laser. Proc IEEE. (1963) 51:947–8. doi: 10.1109/PROC.1963.2345

CrossRef Full Text | Google Scholar

37. D'Costa VR, Cook CS, Birdwell AG, Littler CL, Canonico M, Zollner S, et al. Optical critical points of thin-film Ge_1−ySn_y alloys: a comparative Ge_1−ySn_y/Ge_1−xSi_x study. Phys Rev B. (2006) 73:125207. doi: 10.1103/PhysRevB.73.125207

CrossRef Full Text | Google Scholar

38. Jiang L, Gallagher JD, Senaratne CL, Aoki T, Mathews J, Kouvetakis J, et al. Compositional dependence of the direct and indirect band gaps in Ge_1−ySn_y alloys from room temperature photoluminescence: implications for the indirect to direct gap crossover in intrinsic and n-type materials. Semicond Sci Technol. (2014) 29:115028. doi: 10.1088/0268-1242/29/11/115028

CrossRef Full Text | Google Scholar

39. Polak MP, Scharoch P, Kudrawiec R. The electronic band structure of Ge_1−xSn_x in the full composition range: indirect, direct, and inverted gaps regimes, band offsets, and the Burstein-Moss effect. J Phys D Appl Phys. (2017) 50:195103. doi: 10.1088/1361-6463/aa67bf

CrossRef Full Text | Google Scholar

40. Pezzoli F, Giorgioni A, Patchett D, Myronov M. Temperature-dependent photoluminescence characteristics of GeSn epitaxial layers. ACS Photonics. (2016) 3:2004–9. doi: 10.1021/acsphotonics.6b00438

CrossRef Full Text | Google Scholar

41. Wang X, Kimerling LC, Michel J, Liu J. Large inherent optical gain from the direct gap transition of Ge thin films. Appl Phys Lett. (2013) 102:131116. doi: 10.1063/1.4800015

CrossRef Full Text | Google Scholar

42. Xu X, Wang X, Nishida K, Takabayashi K, Sawano K, Shiraki Y, et al. Ultralarge transient optical gain from tensile-strained, n-doped germanium on silicon by spin-on dopant diffusion. Appl Phys Express. (2015) 8:092101. doi: 10.7567/APEX.8.092101

CrossRef Full Text | Google Scholar

43. Bristow AD, Rotenberg N, van Driel HM. Two-photon absorption and Kerr coefficients of silicon for 850-2200 nm. App Phys Lett. (2007) 90:191104. doi: 10.1063/1.2737359

CrossRef Full Text | Google Scholar

44. Mak G, van Driel HM. Femtosecond transmission spectroscopy at the direct band edge of germanium. Phys Rev B. (1994) 49:16817–20. doi: 10.1103/PhysRevB.49.16817

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Lange C, Köster NS, Chatterjee S, Sigg H, Chrastina D, Isella G, et al. Ultrafast nonlinear optical response of photoexcited Ge/SiGe quantum wells: evidence for a femtosecond transient population inversion. Phys Rev B. (2009) 79:201306 (R). doi: 10.1103/PhysRevB.79.201306

CrossRef Full Text | Google Scholar

46. Claussen SA, Tasyurek E, Roth JE, Miller DAB. Measurement and modeling of ultrafast carrier dynamics and transport in germanium/silicon-germanium quantum wells. Opt Express. (2010) 18:25596–607. doi: 10.1364/OE.18.025596

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Chuang SL. Physics of Optoelectronic Devices. Volume 22 of Wiley Series in Pure and Applied Optics, New York, NY: Wiley (1995).

Google Scholar

48. Werner J, Oehme M, Schmid M, Schirmer A, Kasper E, Schulze J. Germanium-tin p-i-n photodetectors integrated on silicon grown by molecular beam epitaxy. Appl Phys Lett. (2011) 98:061108. doi: 10.1063/1.3555439

CrossRef Full Text | Google Scholar

49. Roucka R, Mathews J, Weng C, Beeler R, Tolle J, Menéndez J, et al. High-performance near-IR photodiodes: a novel chemistry-based approach to Ge and Ge–Sn devices integrated on silicon. IEEE J Quantum Electron. (2011) 47:213–22. doi: 10.1109/JQE.2010.2077273

CrossRef Full Text | Google Scholar

50. Su S, Cheng B, Xue C, Wang W, Cao Q, Xue H, et al. GeSn p-i-n photodetector for all telecommunication bands detection. Opt Express. (2011) 19:6400–5. doi: 10.1364/OE.19.006400

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Oehme M, Schmid M, Kaschel M, Gollhofer M, Widmann D, Kasper E, et al. GeSn p-i-n detectors integrated on Si with up to 4% Sn. Appl Phys Lett. (2012) 101:141110. doi: 10.1063/1.4757124

CrossRef Full Text | Google Scholar

52. Oehme M, Kostecki K, Ye K, Bechler S, Ulbricht K, Schmid M, et al. GeSn-on-Si normal incidence photodetectors with bandwidths more than 40 GHz. Opt Express. (2014) 22:839–46. doi: 10.1364/OE.22.000839

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Pham T, Du W, Tran H, Margetis J, Tolle J, Sun G, et al. Systematic study of Si-based GeSn photodiodes with 2.6 μm detector cutoff for short-wave infrared detection. Opt Express. (2016) 24:4519–31. doi: 10.1364/OE.24.004519

CrossRef Full Text | Google Scholar

54. Gassenq A, Gencarelli F, Van Campenhout J, Shimura Y, Loo R, Narcy G, et al. GeSn/Ge heteostructure short-wave infrared photodetectors on Silicon. Opt Express. (2012) 20:27297–303. doi: 10.1364/OE.20.027297

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Dong Y, Wang W, Xu S, Lei D, Gong X, Guo X, et al. Two-micro-wavelength germanium-tin photodiodes with low dark current and gigahertz bandwidth. Opt Express. (2017) 25:15818–27. doi: 10.1364/OE.25.015818

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Peng YH, Cheng HH, Mashanov VI, Chang GE. GeSn p-i-n waveguide photodetectors on silicon substrates. Appl Phys Lett. (2014) 105:231109. doi: 10.1063/1.4903881

CrossRef Full Text | Google Scholar

57. Liu J, Cannon DD, Wada K, Ishikawa Y, Jongthammanurak S, Danielson DT, et al. Tensile strained Ge p-i-n photodetectors on Si platform for C and L band telecommunications. Appl Phys Lett. (2005) 87:011110. doi: 10.1063/1.1993749

CrossRef Full Text | Google Scholar

58. Thorlabs (2019). Available online at: https://www.thorlabs.com/drawings/674eb64b187d9912-43AED979-5056-0103-7954CD792A847D84/FDPS3X3-Manual.pdf

Google Scholar