Mathematical Model for Simulating the Movement of Water Droplet on Artificial Leaf Surface

To understand the mechanism of how a droplet of pesticide, nutrient or water is imbibed via the leaf surface, a simple model-based mathematics for simulating a realistic water droplet motion over the artificial leaf surface is introduced. The preliminary object of this model is to reconstruct the leaf surface, so an interpolation finite element method so-called hybrid Clough–Tocher (CT) radial basis function (RBF) with a cubic polynomial (CT-MRBFC) has recently been proposed by the authors [1] for this purpose. The surface consists of a triangular element over which the method of CT-MRBFC is applied. In the presented droplet motion model, the forces that influence the motion are supposed to be the internal force due to the drag force and external force caused by gravity. As outcomes of the proposed model, the droplet model captures realism fairly well and generates a genuine motion over the surface. More significantly, the droplet movements pursue the surface contours and falls from the leaf mesh depending on the model parameters. Furthermore, the droplet height is computed over every triangle and the droplet vanishes or stops moving if a set tolerance is greater than the droplet height.

Introduction

Modeling and simulating a droplet motion on the leaf structure are significant research module of plant spray retention. Therefore, a simple model is presented mathematically for this procedure using a specific kind of leaf called the Anthurium leaf. A vital aspect of the presented approach is to create the leaf surface using a surface fitting technique.

When a droplet moves on a compact surface, it might spread out or drop off the surface, and these actions depend on the surface inclination and nature, the size and the speed of the drop, and the surface viscosity and tension. Nonetheless, the droplet destination in reality has more possibilities. For example, an experiment was performed [2], and the results included prompt splash, deposition, partial rebound and corona splash. Qualitative description is given by Yarin [3]. Droplet spreading leads to viscous identification, which was studied by Kim et al. [4] and Thoroddsen and Sakakibara [5]. A significant fact is that the mechanics of the fluid of these results is fairly sophisticated and needs powerful mathematical modeling.

The aim of the current research is to propose a basic mathematical model in order to provide a droplet motion over an artificial leaf surface. The driven model is one-dimensional, where a polygonal path is used to describe the droplet movement as curved arcs. The proposed droplet model generates a real droplet movement on the leaf surface. Furthermore, the droplet movement follows the surface contours, stops moving at times similar with the timeframe or fall off the surface (see Figures 5–7).

Although this paper formulates its contribution via visualizing and simulating the genuine motion of a droplet on an artificial leaf surface, a certain possible significant phenomena's are not addressed here, for instance using the Navier–Stokes equations to illustrate the time-dependent droplet profile.

In line to simulate the movement of a droplet on the actual leaf surface, we need first to create the surface using the methods of surface fitting. Loch [6] used the finite element method to construct the surface. The authors previously [7–14] suggested a new hybrid CT-MRBFC technique [15–18] for this goal. The proposed techniques are based on 3D data points collected from the surface of a real Anthurium leaf using a scanner. Moreover, the authors [19] proposed a comparison between some methods based on surface fitting and concluded that the best is the hybrid multiquadric RBF-CT. Kempthorne [20, 21] suggested smoothing D²-splines to create the cotton and wheat leaf surface. In this paper, we adapted our proposed CT-MRBFC method [1] to reconstruct the surface of the Anthurium leaf from 3D real scattered points.

This paper is outlined as follows. A literature review of leaf surface reconstruction and droplet simulation is given in the next section. In section Artificial Leaf Surface Model Using the CT-MRBFC Method, a concise explanation of the hybrid CT-MRBFC method to construct the Anthurium leaf is clarified. An outline of the water droplet model is given in section Water Droplet Model. Moreover, the forces that influence the movement of the droplet are assumed to be external, including gravity, and internal, including the drag (friction) force. The droplet motion is computed over every triangle where the surface consists of a triangular mesh, and as a result the model seems to capture reality fairly well. Lastly, the conclusion and prospects for future research are given in section Results and Future Work.

Relevant Literature

The water droplets animation has been studied by a few researchers [21–24] since the 1980s. Nevertheless, in the 1990s, a few methods addressed the phenomenon of droplets flowing on surfaces. For example [25], modeled droplet shapes using meta-balls on a flat surface [26, 27], used meta-balls to model water flows by suggesting a volume-preserving technique [21], proposed a physical model to model droplets morphing [28], studied droplet animation on a glass plate, but the model failed to capture the droplet movements on a curved surface [29, 30], proposed a model for the water droplet animation on curved surface where the wetting and merging phenomenon are addressed in the model [31]. Suggested a physical model based on a bump map surface to capture the trend of the droplet flows where a solid sphere is considered to model the droplet. An efficient model to simulate the motion and the shape of droplet movements was proposed by Jonsson [32] where the adhesion, friction, roughness and gravity forces are considered in the droplet motion. A few researchers have considered the fluid dynamics to produce a realistic motion of fluids. For example, Chen [21, 22, 33–35] applied the Navier–Stokes equations to simulate the flow of water droplets.

Artificial Leaf Surface Model Using The CT-MRBFC Method

As stated earlier, we cannot start the simulation of a droplet on a leaf surface until the virtual leaf surface is constructed. Previously the authors [7–14] proposed some surface fitting methods to construct the artificial surface of different types of leaves. In this research paper we applied the hybrid CT-MRBFC technique proposed by the author [1] to obtain an accurate and continuous surface. The mixture of these two methods permits us to approximate the CT triangle-required gradients by the multiquadric radial basis function that enhanced a cubic polynomial; more information about the construction of this method can be found in Oqielat [1]. Moreover, the Anthurium leaf data sampled using laser scanner and the collected data points comprised 4,688 surface points and 79 boundary points, shown in Figure 1. The Point Picker software was used by Loch [6] and Losasso et al. [36] to determine the boundary points. Generally, two steps are required in turn to use the hybrid CT-MRBFC method, which include a new reference plane for the scanned leaf data points and leaf surface triangulation. Next, we will briefly explain these two steps.

FIGURE 1

Figure 1. The 4,688 Anthurium leaf data points (black dots) and the 79 boundary points (red dots).

The collected Anthurium leaf data do not agree with the xy-plane; moreover, there is the possibility for multivalued and vertical surface for the scanned data. Consequently, to resolve this issue we utilized an orthogonal distance regression plane (ODRP), and afterward the coordinate system was rotated to obtain the reference plane; the following paragraphs summarize the reference plane construction, see Oqielat [14] for more details.

Given ${\psi }_i={(x_i,y_i,z_i)}^T,i=1,2,\dots ,N$, leaf data points, apply the ODRP to fit the leaf points:

$\begin{array}{ll}\prime \gamma \left(x,y\right)=a_{1}x+a_{2}y+a_3.& (1)\end{array}$

The distance from a plane to a point can be used as starting point, then the coefficients a₁, a₂, and a₃ that minimize can be found

$\prime \gamma \left(a_1,a_2,a_3\right)={\displaystyle \sum _{i=1}^N\frac{{\left|a_1{x}_i+a_2{y}_i+a_3\right|}^2}{a_1^2+a_2^2}}$

to obtain the best fit.

Rewrite U as

$\prime \gamma \left(a_1,a_2\right)={\displaystyle \sum _{i=1}^N\frac{{\left|a_1(x_i-x_0)+a_2(y_i-y_0)\right|}^2}{a_1^2+a_2^2}},$

then the Rayleigh quotient is given by

$\prime \gamma \left(v\right)=\frac{v^{T}Av}{v^{T}v}$

where $v^T=\left[a_1,a_2\right]$,

$M=\left[\begin{array}{cc}(x_1-x_0)& (y_1-y_0)\\ (x_2-x_0)& (y_2-y_0)\\ ⋮& ⋮\\ (x_N-x_0)& (y_N-y_0)\end{array}\right],$

and (x₀, y₀) are the centroid of the data. Finally, the leaf data points after being projected to the proposed plane are given by

$\begin{array}{ll}{\psi }^{\prime }=R{\left(x_i,y_i,z_i\right)}^T,i=1,2,\dots ,N.& (2)\end{array}$

where R = R_x.R_y is a rotation matrix. This matrix rotates the plane unit normal vector about the x-axis and y-axis—more information can be found in Oqielat [1].

As mentioned earlier, the hybrid CT-MRBFC method is employed to construct the Anthurium leaf surface. Therefore, Anthurium leaf surface triangulation is required. To decrease the computational expense of this method, we selected a subset of the Anthurium leaf data set to create the triangulation. Subsequently, EasyMesh [37] was applied to construct the surface triangulation, see Oqielat [1] for more details. EasyMesh produces Delaunay triangulations in 2D, as shown in Figure 2.

FIGURE 2

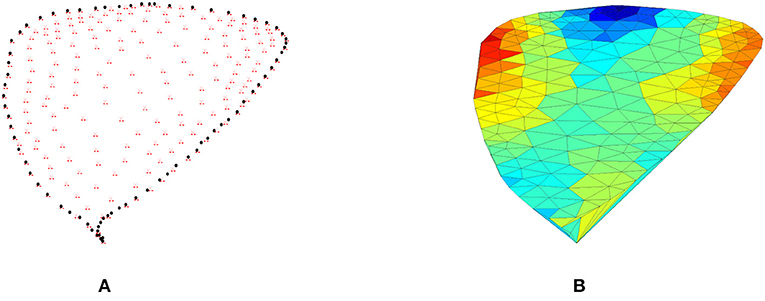
Figure 2. (A) The red represents the triangle vertices and the black dots represent the boundary points. (B) The Anthurium surface triangulation generated using EasyMesh.

Finally, after we constructed the new reference plane and the leaf surface triangulation, the hybrid CT-MRBFC technique was used to create the surface of the Anthurium leaf shown in Figure 3.

FIGURE 3

Figure 3. (A) Shows the real Anthurium leaf. (B) Shows the Anthurium leaf model constructed using hybrid CT-MRBFC.

Water Droplet Model

The triangular elements form the primary component of the droplet model. The advantages of using the triangulations are the animation and location of the droplet are straightforward to compute over each triangle and the droplet location can be determined at any time on the surface. Such droplet simulations can be expensive computationally if we use a large number of triangles, so a subset of the leaf points is implemented to obtain less triangles, which represent the main surface features (see Figure 2).

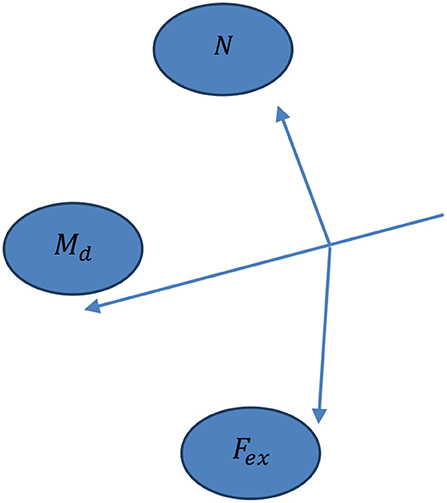
In the droplet model, the forces that influence motion that are considered to be external forces (F_ex) include gravity (F_G) and internal forces (F_in) includes drag (friction) force (F_f). The force of gravity is projected in the movement direction (M_d), see Figure 4, as follows:0

FIGURE 4

Figure 4. The droplet movement direction M_d with gravity F_ex and normal N forces.

$\begin{array}{ll}{M}_d=F_G-(F_G.N)N& (3)\end{array}$

where N is the surface unit normal vector [32]. Let δ = (x, y, Z(x, y)) denote the interest surface, where Z(x, y) is the surface value for (x, y), then the surface normal is the cross product of the tangent vectors ${\delta }_x={(1,0,Z_x)}^T$ and ${\delta }_y={(0,1,Z_y)}^T$. Therefore, the surface unit vector is defined as follows:

$\begin{array}{ll}N=\frac{(-Z_x,-Z_y,1)}{\sqrt{Z_x^2+Z_y^2+1}}.& (4)\end{array}$

where Z_x, Z_y and 1 are the components of the surface normal vector. The force of friction F_f is treated as a retarding force with a fixed negative factor (λ) consequent of the roughness of the surface [32]:

$\begin{array}{ll}{F}_f=-\lambda v\left(t\right),& (5)\end{array}$

where the droplet velocity at time t is denoted by v(t). The droplet begins to move down on the surface if the F_ex exceeds the F_in.

As stated earlier, the Anthurium surface is characterized by a triangular mesh over which the droplet transfer occurs. The droplet height is computed on every triangle to find the droplet height along its triangular path. Furthermore, the droplet movement is stopped if a set tolerance (κ = 10⁻⁵) is greater than the droplet height (see Figure 7), otherwise the droplet continues its movement to the following triangle (see Figures 5,6).

FIGURE 5

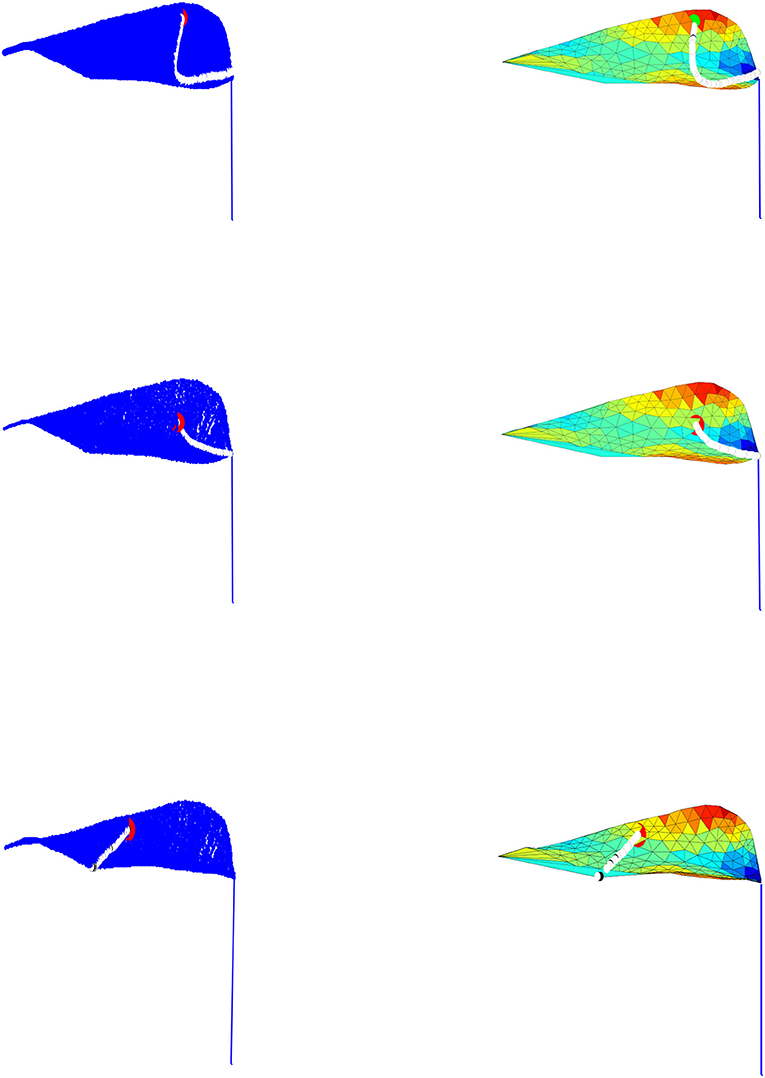
Figure 5. The figures given on the left column represent the droplet motion employed by our model across the constructed leaf, while the figures given on the right column show the corresponding droplet movement on the leaf triangulation.

The Water Droplet Movements Over the Surface

We proposed in this paper a single droplet model to simulate the droplet motion over the leaf surface. Moreover, in the future the model will be extended to a multiple droplet model. However, the current model offers several advantages—it is easy to control the droplet motion and location at any given time. The same notation used by the authors [38] has been adopted in this article along with new notations for vectors. The droplet movements at any given time (T) are defined by employing the Newton's second law F = ma therefore the droplet has mass (m), position (p), velocity (v) and acceleration (a). Thus, taking into account the internal and external forces acting on the droplet, the droplet motion model is derived as follows:

$\begin{array}{ll}m{M}_d-\lambda v\left(T\right)=m{v}^{\prime }\left(T\right),& (6)\end{array}$

which is a linear first order differential equation. We estimated the friction coefficient to be λ ~ O(10⁻⁸) (kg m/s²) using Stokes's law for a sphere of radius r = 0.001(m), moreover we supposed the droplet mass to be constant.

As mentioned before, the virtual surface of the leaf consists of a triangular element (Figure 2) and the droplet moves down over this surface. To start our simulation, first we should identify the initial position (p₀), time (t₀), velocity (v₀), the transit time (T_t), the frame time (F_t) and the initial triangle which is found using tsearch (Matlab command). Then Equation (3) is used to specify the movement direction and permit the droplet to move to the flowing triangle. Suppose T_n is the entrance time of the droplet of nth triangle, we computed the time that the droplet needs to move to the following triangle as [T_n, T_n + T_t] and we stored the accumulated transit time. The new position and new velocity of the droplet over the new triangle are calculated using Equations (8, 7), respectively. Finally, if the time frame is greater than the transit time, and the droplet height is greater than a defined tolerance (κ = 10⁻⁵), then the droplet moves to the following triangle.

The equation of water droplet velocity (7) and position (8) at any time is obtained by solving Equation (6) as follows:

$\begin{array}{ll}v\left(T\right)=v_0\left(T_n\right)e^{-\frac{\lambda }{m}T}+\frac{m}{\lambda }{M}_d^n-\frac{m}{\lambda }{M}_d^n{e}^{-\frac{\lambda }{m}T},& (7)\end{array}$

$\begin{array}{ll}p\left(T\right)=p_0\left(T_n\right)+\frac{m}{\lambda }{M}_d^{n}T+\left(v_0\left(T_n\right)-\frac{m}{\lambda }{M}_d^n\right)\left(-\frac{m}{\lambda }{e}^{-\frac{\lambda }{m}T}+\frac{m}{\lambda }\right),& (8)\end{array}$

where $M_d^n$, p₀(T_n) and v₀(T_n) are the droplet movement direction, the initial position, and velocity, respectively, at time T_n of the nth triangle. Assume that, at time T_n, the droplet arrives to the nth triangle, then the transit and exit time are denoted, respectively, by T_t and T_e = T_n + T_t and the exit position p(T_e) and exit velocity v(T_e) are also computed.

Now, to compute T_t we intersect the droplet trajectory (Equation 8 with the three edges of the triangle, Equation 9) by means of a Newton algorithm. The triangle edge equation is given by

$\begin{array}{ll}{E}_i\left(\kappa \right)=r_i+\kappa (r_j-r_i),& (9)\end{array}$

and it has three components ${(E_x,E_y,E_z)}^T$, 0 ≤ κ ≤ 1. The r_i, r_j are the two vertices of the triangle edge. The point of intersection (T, κ) is then obtained using Newton algorithm by solving the following non-linear system:

$\begin{array}{ll}{{K}}_i\left(T,\kappa \right)=p_i\left(T\right)-E_i\left(\kappa \right)=0,i=1,2,3.& (10)\end{array}$

Using Equation (8), the path of the droplet can be followed over any triangle by increasing T_t till T_e is reached. Moreover, the velocity projected in the movement direction to guarantee that the droplet stays on the surface and the initial velocity updated each time the droplet enters the nth triangle. As stated, before we used tsearch to find the new triangle to which the droplet transfers, whereas the droplet leaves the leaf surface if we cannot locate such a triangle. The following algorithm describes the droplet flow simulating on the Anthurium leaf surface:

ALGORITHM 4.1.

Algorithm 4.1. Water droplet flow simulation

The MATLAB software is used to perform our simulation over the leaf surface given in Figures 2, 3. As exhibited in Figures 5–7, the droplet model captures the movement fairly well and produces genuine motion of the droplet on the surface; moreover the droplet movements follow the surface contours and fall from the leaf mesh depending on the model parameters. Additionally, the droplet stops moving at times consistent with timeframe and if a set tolerance is greater than the droplet height.

FIGURE 6

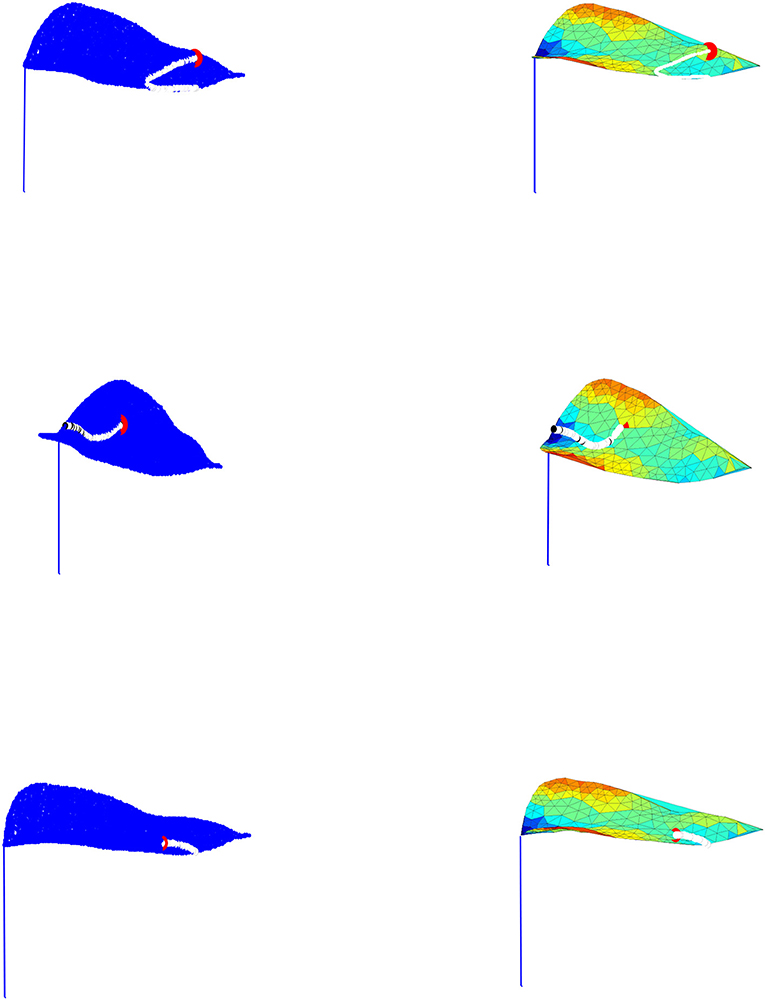
Figure 6. The figures given on the left column represent the droplet motion using our model across the constructed leaf, while the figures given on the right column show the corresponding droplet movement on the leaf triangulation.

FIGURE 7

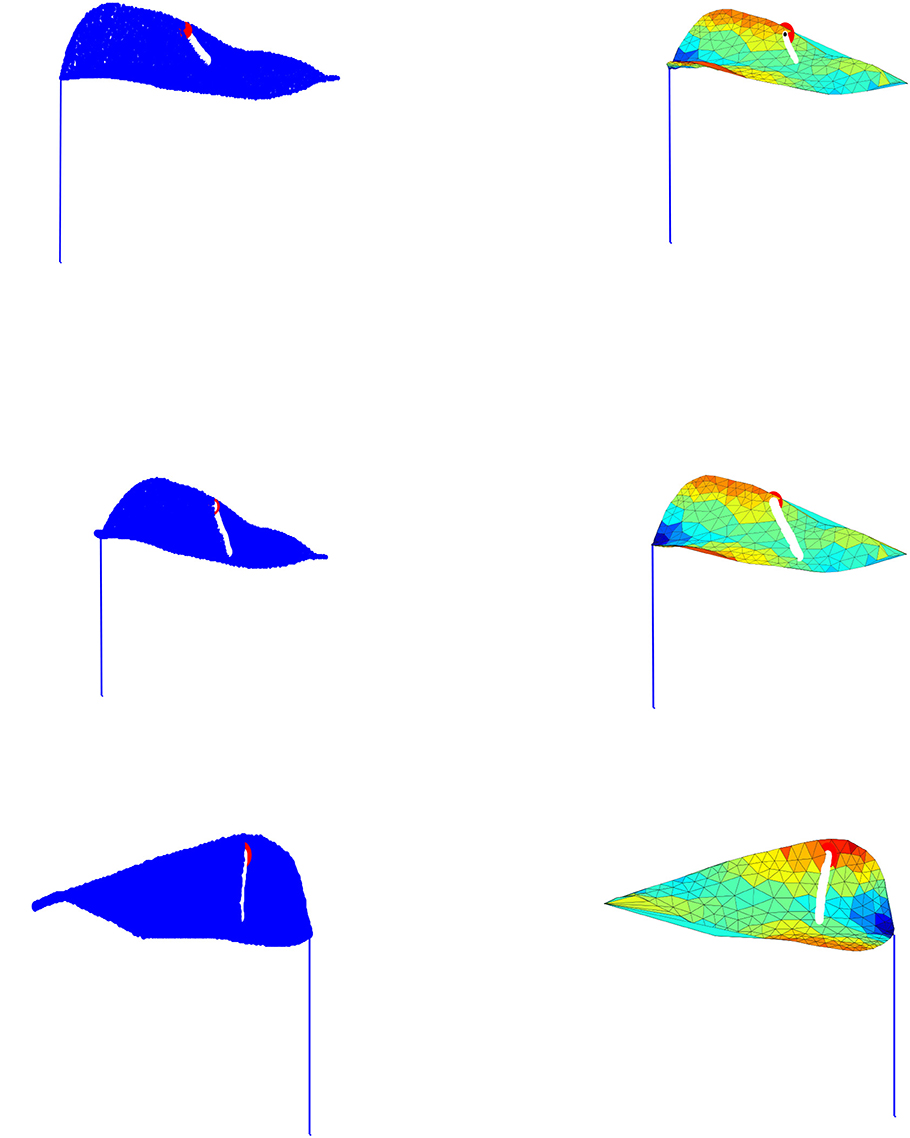
Figure 7. The figures given on the left column represent the droplet motion by implementing the stopping tolerance in our model across the constructed leaf, while the figures given on the right column show the corresponding droplet movement on the leaf triangulation.

The droplet motion shown in Figures 5–7. is classified into four cases as follows:

Case 1: If the droplet is located close to the leaf upper edge, then the droplet crosses the surface and passes the leaf vein till it gets to the lower edge of the leaf and falls off the surface. However, this is due to the droplet large velocity.

Case 2: If the droplet is placed on the upper leaf side it transfers across the triangular element till it gets to the vein of the leaf, then it continues to move alongside the vein because of the internal force controlled by the external force.

Case 3: When the droplet is closed to the surface edge, as expected, it ultimately falls off the surface.

Case 4: Figure 7 shows that the droplet movement is stopped somewhere on the surface before it reaches the leaf edge because the specified tolerance (κ = 10⁻⁵) is greater than the droplet height and the time frame is less than the transit time.

Results and Future Work

In this article, we presented a mathematical model for simulating droplet motion of the Anthurium leaf. Two forces supposed to influence the droplet motion in our model included the external force due to gravity and internal force due to drag force. The model flexibility permits the researcher to understand how a water droplet transfers over a virtual leaf surface and how a small adjustment in the main parameters creates diverse movements of the droplet over the surface. Furthermore, the droplet model captures realism fairly well and produces genuine motion of the droplet on the surface of the leaf. More importantly, the droplet movements follow the surface contours and falls from the leaf mesh depending on the model parameters as well as the droplet stops moving at times consistent with time frame.

The model can be extended to create a more physical simulation by including additional forces and dominant factors that affect the motion of the droplet, such as spraying and adhesion [39–41]. Moreover, the physical leaf surface properties can be included as well as the paths of several droplets, which is important in modeling of a pesticide implementation to plant [42, 43].

Data Availability

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Oqielat MN. Application of interpolation finite element methods to a real 3D leaf data. J KSU Sci. (2018). doi: 10.1016/j.jksus.2018.04.006. [Epub ahead of print].

CrossRef Full Text | Google Scholar

2. Rioboo R, Tropea C, Marengo M. Outcomes from a drop impact on solid surfaces. Atom Sprays. (2001) 11:155−66. doi: 10.1615/AtomizSpr.v11.i2.40

CrossRef Full Text | Google Scholar

3. Yarin AL. Drop impact dynamics: splashing, spreading, receding, bouncing. Ann Rev Fluid Mech. (2006) 38:159−92. doi: 10.1146/annurev.fluid.38.050304.092144

CrossRef Full Text | Google Scholar

4. Kim HY, Feng ZC, Chun JH. Instability of a liquid jet emerging from a droplet upon collision with a solid surface. Phys Fluids. (2000) 12:531−41. doi: 10.1063/1.870259

CrossRef Full Text | Google Scholar

5. Thoroddsen ST, Sakakibara J. Evolution of the fingering pattern of an impacting drop. Phys Fluids. (1998) 10:1359. doi: 10.1063/1.869661

CrossRef Full Text | Google Scholar

6. Loch BI. Surface fitting for the modelling of plant leaves (Ph.D. thesis). University of Queensland (2004).

Google Scholar

7. Oqielat MN, Belward JA, Turner IW, and Loch BI “A Hybrid Clough-Tocher radial basis function method for modelling leaf surfaces. In: MODSIM 2007 International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand (Christchurch) (2007).

Google Scholar

8. Oqielat MN, Turner IW, and Belward JA. A Hybrid Clough-Tocher method for surface fitting with application to leaf data. Appl Math Model. (2009) 33:2582−95. doi: 10.1016/j.apm.2008.07.023

CrossRef Full Text | Google Scholar

9. Oqielat MN, Ogilat ON. Application of gaussion radial basis function with cubic polynomial for modelling leaf surface. J Math Anal. (2018) 9:78–87. Available online at: http://www.ilirias.com/jma/repository/docs/JMA9-2-8.pdf

Google Scholar

10. Oqielat MN, Ogilat O, Bataineh AS. Approximation of radial basis function with linear polynomial: comparison and application. In: International Conference on Applied Physics and Mathematics (ICAPM). Sydney (2018).

11. Turner IW, Belward JA, Oqielat MN. Error bounds for least squares gradient estimates. SIAM J Sci Comput. (2010) 32:2146–66. doi: 10.1137/080744906

CrossRef Full Text | Google Scholar

12. Oqielat MN. Surface fitting methods for modelling leaf surface from scanned data. J KSU Sci. (2017) 31:215–21. doi: 10.1016/j.jksus.2017.03.008

CrossRef Full Text | Google Scholar

13. Oqielat MN, Ogilat ON, Al-Oushoush N, Bataineh AS. Radial basis function method for modelling leaf surface from real leaf data. Aus J Basic Appl Sci. (2017) 11:103–11. Available online at: http://www.ajbasweb.com/old/ajbas/2017/October/103-111.pdf

14. Oqielat MN. Scattered data approximation using radial basis function with a cubic polynomial reproduction for modelling leaf surface. J Taibah Univ Sci. (2018) 12:331–7. doi: 10.1080/16583655.2018.1469293

CrossRef Full Text | Google Scholar

15. Clough RW, Tocher JL. Finite element stiffness matrices for analysis of plate bending. In: Proceedings of the Conference on Matrix Methods in Structural Mechanics (Ohio) (1965). p. 515–45.

16. Lancaster P, Salkauskas K. Curve and Surface Fitting: An Introduction. London; Orlando, FL; San Diego, CA: Society for Industrial and Applied Mathematics (1986).

Google Scholar

17. Hardy RL. Theory and applications of the multiquadric bi-harmonic method. Comput Math Appl. (1990) 19:163–208. doi: 10.1016/0898-1221(90)90272-L

CrossRef Full Text | Google Scholar

18. Rippa S. An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Adv Comput Math. (1999) 19:193–210.

Google Scholar

19. Oqielat MN. Comparison of surface fitting methods for modelling leaf surfaces. Ital J Pure Appl Math. (2018) 40:215–226. Available online at: http://ijpam.uniud.it/journal/onl_2018-40.htm

20. Kempthorne DM, Turner IW, Belward JB, McCue SW, Barry M, Young J, et al. Surface reconstruction of wheat leaf morphology from three-dimensional scanned data. Funct. Plant Biol. (2015) 42:444. doi: 10.1071/FP14058

CrossRef Full Text

21. Kempthorne DM, Turner IW, Belward JB. A comparison of techniques for the reconstruction of leaf surfaces from scanned data. SIAM J Sci Comput. (2015) 36:B969–88. doi: 10.1137/130938761

CrossRef Full Text | Google Scholar

22. Foster N, Fedkiw R. Practical animation of liquids. In: Proceedings of ACM SIGGRAPH'01 (Orlando, FL) (2001).

Google Scholar

23. Foster N, Metaxas D. Realistic animation of liquids. Graph Models Image Process. (1996) 58:471–83. doi: 10.1006/gmip.1996.0039

CrossRef Full Text | Google Scholar

24. Fournier A, Reeves WT. A simple model of ocean waves. In: SIGGRAPH'86 Conference Proceedings (Los Angeles, CA) (1986).

Google Scholar

25. Peachey DR. Modeling waves and surf. In: ACM GRAPHITE 86 Conference Proceedings (Los Angeles, CA) (1986).

Google Scholar

26. Yu Y, Jung H, Cho H. A new water droplet model using meta ball in the gravitational field. Comput Graph. (1999) 23:213–22. doi: 10.1016/S0097-8493(99)00031-X

CrossRef Full Text | Google Scholar

27. Tong R, Kaneda K, Yamashita H. A volume preserving approach for modeling and animating water flows generated by meta-balls. Visual Comput. (2002) 18:469–80. doi: 10.1007/s003710100164

CrossRef Full Text | Google Scholar

28. Lin L, Shenghui L, RuoFeng T, JinXiang D. Water droplet morphing combining rigid transformation. In: Sunderam VS, van Albada GD, Sloot PMA, Dongarra JJ, editors. Computational Science–ICCS. Berlin; Heidelberg: Springer (2005). p. 671–8.

Google Scholar

29. Kaneda K, Kagawa T, Yamashita H. Animation of water droplets on a glass plate. In: Proceedings of Computer Animation (Anaheim, CA) (1993).

Google Scholar

30. Kaneda K, Ikeda S, Yamashita H. Animation of water droplets moving down a surface. J Visualizat Comput Animat. (1999)10:15–26. doi: 10.1002/(SICI)1099-1778(199901/03)10:1<15::AID-VIS192>3.0.CO;2-P

CrossRef Full Text | Google Scholar

31. Kaneda K, Zuyama Y, Yamashita H, Nishita T. Animation of water droplet flow on curved surfaces. In: Proceedings of Pacific Graphics (Seoul) (1996).

Google Scholar

32. Jonsson M. Animation of water droplet flow on structured surfaces. In: SIGRAD'2002 Conference Proceedings (Orlando, FL) (2002).

Google Scholar

33. Fournier P, Habibi A, Poulin P. Simulating the flow of liquid droplets. In: Proceedings of Graphics Interface (Vancouver, BC) (1998).

Google Scholar

34. Chen Q. Water animation with disturbance model. IEEE Computer Society (Kauai, HI) (2001).

Google Scholar

35. Enright D, Marschner S, Fedkiw R. Animation and rendering of complex water surfaces. In: Proceedings of ACM GRAPHITE (Melbourne, VIC) (2002).

Google Scholar

36. Losasso F, Gibou F, Fedkiw R. Simulating water and smoke with an octree data structure. ACM Trans Graph. (2004) 23:457–62. doi: 10.1145/1186562.1015745

CrossRef Full Text | Google Scholar

37. Hanan J, Loch B, McAleer T. Processing laser scanner plant data to extract structural information. Proceedings of FSPM04 (Montpellier) (2004). p. 9–12.

Google Scholar

38. Oqielat MN, Turner IW, Belward JA, McCue SW. Modelling water droplet movements on a leaf surface. Math. Comput. Simulat. (2011) 81:1553−71. doi: 10.1016/j.matcom.2010.09.003

CrossRef Full Text | Google Scholar

39. Niceno B. EasyMesh. (2003). Available online at: https://www-dinma.univ.trieste.it/nirftc/research/easymesh (accessed July, 2001).

Google Scholar

40. Forster W, Zabkiewicz J, Kimberley M. A universal spray droplet adhesion model. Trans ASAE. (2005) 48:1321–30. doi: 10.13031/2013.19179

CrossRef Full Text | Google Scholar

41. Forster W, Zabkiewicz J, Riederer M. Spray formulation deposit on leaf surfaces and xenobiotic mass uptake. In: Proceedings of the 7th International Symposium on Adjuvants for Agrochemicals, Document Transformation Technologies. Cape Town (2004).

Google Scholar

42. Zabkiewicz J, Forster W, Mercer G. Spray adhesion and retention crop: formulation interactions. In: 11th IUPAC International Congress of Pesticide Chemistry. Kobe (2006).

Google Scholar

43. Hanan J, Renton M, Yorston E. Simulating and visualising spray deposition in plant canopies. In: ACM GRAPHITE. Melbourne (2003).

Google Scholar