Polymerization Induces Non-Gaussian Diffusion

Recent theoretical modeling offers a unified picture for the description of stochastic processes characterized by a crossover from anomalous to normal behavior. This is particularly welcome, as a growing number of experiments suggest the crossover to be a common feature shared by many systems: in some cases the anomalous part of the dynamics amounts to a Brownian yet non-Gaussian diffusion; more generally, both the diffusion exponent and the distribution may deviate from normal behavior in the initial part of the process. Since proposed theories work at a mesoscopic scale invoking the subordination of diffusivities, it is of primary importance to bridge these representations with a more fundamental, “microscopic” description. We argue that the dynamical behavior of macromolecules during simple polymerization processes provide suitable setups in which analytic, numerical, and particle-tracking experiments can be contrasted at such a scope. Specifically, we demonstrate that Brownian yet non-Gaussian diffusion of the center of mass of a polymer is a direct consequence of the polymerization process. Through the kurtosis, we characterize the early-stage non-Gaussian behavior within a phase diagram, and we also put forward an estimation for the crossover time to ordinary Brownian motion.

1. Introduction

Diffusion in crowded and complex systems such as biological cells is usually very heterogeneous, and anomalous behavior—where the mean square displacement of tracers varies non linearly with time—is envisaged [1–3]. Over the last few years a new class of diffusive processes has been reported, where the mean square displacement is found to grow linearly in time like in standard, Brownian diffusion, but with a corresponding probability density function (PDF) which is strongly non-Gaussian [4–16]. This behavior, termed Brownian yet non-Gaussian diffusion [6, 8], occurs quite robustly in a wide range of systems, including beads diffusing on lipid tubes [6] or in networks [6, 7], the motion of tracers in colloidal, polymeric or active suspensions [4, 17–19] and in biological cells [12, 20, 21], as well as the motion of individuals in heterogeneous populations such as nematodes [5]. Similar effects on the PDF are also observed in the anomalous diffusion [22] of labeled messenger RNA molecules in living E.coli and S.cervisiae cells. In the majority of cases, at larger time the form of the PDF crosses over to the normal, Gaussian one. Therefore, such change cannot be simply due to the heterogeneity of the tracers, unless some of their properties vary with time. More plausibly, the anomalous-to-Gaussian transition might be induced by temporal fluctuations of the diffusion coefficient, due to rearrangements of properties of tracers or of the surrounding medium. To mimic such behaviors, models in which the diffusion varies with time by obeying a stochastic equation have been introduced and solved both analytically and numerically. These models are referred in the literature as “diffusing diffusivity models” [23–32], and it has been shown that for short times they are intimately related to the idea of superstatistics [33]. In the latter approach, an ensemble of particles is assumed to be characterized by different diffusion coefficients and it is then described as a mixture of Gaussian PDFs, weighted by the distribution of the diffusivities. As a result, the ensemble dynamics is still Brownian, yet the PDF of particle displacements corresponds to a Gaussian mixture and it is thus not Gaussian anymore.

Although diffusing diffusivity models qualitatively reproduce the experimental observations, they work at a mesoscopic scale and without a visible connection to the underlying molecular processes. It is therefore becoming increasingly relevant to find strategies that bridge the gap between the paradigm of diffusing diffusivity and the microscopic realm, in order to fully understand this form of anomalous diffusion. In this paper we show how the diffusion of polymers during a polymerization process offers one possible mechanism to realize this connection¹. It is well known from polymer theory [36] that the motion of the center of mass of a linear chain is Brownian, but with a diffusivity constant which is inversely proportional to N^α, where N is the number of monomers and α an exponent ranging from 1/2 (Rouse model) to 2 (reptation model). During an equilibrated polymerization processes the number N fluctuates in time and its statistics can be obtained through the exact solution of its stationary master equation. By using a continuous approximation for this temporally homogeneous birth-death Markov process [37], it emerges that in the limit of large systems such process converges to an Ornstein-Uhlenbeck, as it is assumed in most of the diffusing diffusivity models [24]. The time scale of the Ornstein-Uhlenbeck process is linearly proportional to the volume of the system and this guarantees that the non-Gaussian behavior can be accessible experimentally by tuning such parameter.

2. Polymerization Process

Polymers are made of relatively simple subunits (monomers) assembled with one another through different mechanisms and geometries. The result is a macromolecule which may contain from a few tens (in the case oligomers), to several thousand monomer units [38], or even millions as in the case of DNA and RNA molecules. From a biological point of view, the polymerization process occurs regularly either within or outside the cell [39]. In particular, cells might trigger polymerization by several mechanisms such as the de novo nucleation of new filaments, the uncapping of existing barbed ends (actin) and rescuing a depolymerizing filament (commonly observed for microtubules).

In order to guarantee the existence of equilibrium conditions, here we consider a polymerization process occurring in a closed volume with a fixed total number of monomers N_t. For sake of simplicity, in what follows we suppose that one filament only can nucleate and that subunits may bind reversibly onto both ends of the chain. At each end, the addition and deletion of monomers can be represented as [40]

$\begin{array}{l}{A}_N+A_1\underset{k_{-}}{\overset{k_{+}}{\rightleftharpoons }}{A}_{N+1},& (1)\end{array}$

where A_N is the filament with N subunits, and k₊, k₋ are the rate constants for association and dissociation, respectively. Hence,

$\begin{array}{ll}{N}_{\text{t}}=N(t)+M(t),& (2)\end{array}$

where M(t) = c(t)V is the number of monomeric subunits, c its concentration and V the system volume. The probability of a filament with n monomers at time t given n₀ units at time t₀, P_N(n, t|n₀, t₀) satisfies the (forward) master equation of a temporally homogeneous birth-death Markov process [37]:

$\begin{array}{l}{\partial }_t{P}_N(n,t|n_0,t_0)=[W_{-}(n+1)P_N(n+1,t|n_0,t_0)\\ -W_{+}(n)P_N(n,t|n_0,t_0)]\\ +[W_{+}(n-1)P_N(n-1,t|n_0,t_0)\\ -W_{-}(n)P_N(n,t|n_0,t_0)],& (3)\end{array}$

with stepping functions

$\begin{array}{l}{W}_{+}(n)=2k_{+}c(n)(1\le n\le N_{\text{t}}),\\ W_{-}(1)=0,W_{-}(2)=k_{-},W_{-}(n)=2k_{-}(3\le n\le N_{\text{t}}),& (4)\end{array}$

and c(n) = (N_t − n)/V. Through these choices, we are assuming with certainty the existence in solution of a filament with at least one monomer. The factor 2 in W₊ models a linear polymer which grows at both ends without developing branching; W₋ is instead concerned with the possible bonds which may break down. Equilibrium is reached under detailed balance W₋(n) = W₊(n) (3 ≤ n ≤ N_t), corresponding to a polymer composed by

$\begin{array}{l}{N}_{\text{eq}}=N_{\text{t}}-\frac{k_{-}}{k_{+}}V\equiv \lambda N_{\text{t}}(5)\end{array}$

monomers, and to a number

$\begin{array}{ll}{M}_{\text{eq}}=\frac{k_{-}}{k_{+}}V\equiv (1-\lambda )N_{\text{t}}& (6)\end{array}$

of single monomers in solution. We remark that the rate constants k₊, k₋ are specific to the polymerization chemical reactions. Given a certain kind of polymer, the average polymer size and the average number of single monomers in solution are thus controlled by the total number of subunits N_t and by the volume of the system V, which are quantities easily controlled in experiments. In the following analysis, we find it convenient to replace the volume with the fraction 0 < λ < 1 of N_t that compose the polymer at equilibrium; clearly, V = (1 − λ) N_tk₊/k₋.

As we prove in the Appendix, for any given N_t and independently from n₀, the stationary solution $P_N(n)\equiv {lim}_{t\to \infty }{P}_N(n,t|n_0,t_0)$ reads

$\begin{array}{l}{P}_N(1)=\frac{1}{{N}(N_{\text{t}},\lambda )}\frac{(1-\lambda )N_{\text{t}}}{2(N_{\text{t}}-1)}\\ P_N(2)=\frac{1}{{N}(N_{\text{t}},\lambda )}\\ P_N(n)=\frac{2}{{N}(N_{\text{t}},\lambda )}\frac{(N_{\text{t}}-2)!}{{\left[(1-\lambda )N_{\text{t}}\right]}^{N_{\text{t}}-2}}\frac{{\left[(1-\lambda )N_{\text{t}}\right]}^{N_{\text{t}}-n}}{(N_{\text{t}}-n)!}(3\le n\le N_{\text{t}}),& (7)\end{array}$

with a normalization factor

$\begin{array}{l}{N}(N_{\text{t}},\lambda )=\frac{N_{\text{t}}[(11-4\lambda )\lambda -9]+2}{2(N_{\text{t}}-1)}\\ +\frac{2(N_{\text{t}}-2)!}{{\left[(1-\lambda )N_{\text{t}}\right]}^{N_{\text{t}}-2}}\frac{\Gamma (N_{\text{t}}+1,(1-\lambda )N_{\text{t}})}{\Gamma (N_{\text{t}}+1)}{\text{e}}^{(1-\lambda )N_{\text{t}}},& (8)\end{array}$

Γ(·, ·) being the upper incomplete gamma function [41],

$\Gamma (N_{\text{t}}+1,(1-\lambda )N_{\text{t}})\equiv {\displaystyle {\int }_{(1-\lambda )N_{\text{t}}}^{\infty }\text{d}}t{t}^{N_{\text{t}}}{\text{e}}^{-t},(9)$

and Γ(·) the Euler gamma function. We may observe that with (1 − λ)N_t → 0 the two Gamma functions in the normalization factor become equal and simplify to 1; in this limit, probabilities for small n are suppressed. Indeed, in section 4 we show that P_N(n) becomes close to a Gaussian for large λ and N_t. In view of the inverse power-law relation with the diffusion coefficient of the center of mass, it is however the behavior for small n which affects the probability of large diffusivities, triggering in turn strong deviations from ordinary diffusion which are described in the following Section.

3. Brownian Yet Non-Gaussian Diffusion of the Center of Mass

From polymer physics we know that the center of mass R_G of a macromolecules with N subunits diffuses with a coefficient $D(N)=D_0/N^{\alpha }$, D₀ being a diffusion coefficient specific of the considered subunit. This means

$\begin{array}{ll}\text{d}{R}_G(t)=\sqrt{6D(N(t))}\text{d}B(t),& (10)\end{array}$

with B(t) a (three-dimensional) Wiener process (Brownian motion). Reference values for the exponent α are:

• α = 1/2 in the Rouse model [36, 42], where the polymer is composed of N equivalent beads with neither excluded-volume nor hydrodynamic interaction;

• α = 1 for the Zimm model [36, 43], where hydrodynamic is taken into account;

• α = 2 for the reptation model which describes tagged polymer motion in entangled polymer solutions [36, 44].

In view of the previous analysis, we understand that polymerization confers a random character to R_G, providing a clear microscopic origin to the “diffusing diffusivity” process we are going to detail next.

From Equation (7) we readily obtain the stationary distribution for the diffusion coefficient of the polymer's center of mass,

$\begin{array}{l}{P}_D(D_n)={\displaystyle \sum _{n^{\prime }=1}^{N_{\text{t}}}{P}_N}(n^{\prime }){\delta }_{D_n,\frac{D_0}{{n^{\prime }}^{\alpha }}}\\ =P_N\left(\frac{D_0^{\alpha }}{D_n^{\alpha }}\right)(1\le n\le N_{\text{t}},D_n=D_0/n^{\alpha }),(11)\end{array}$

and its first moment

$D_{\text{av}}\equiv \mathbb{E}[D_n]={\displaystyle \sum _{n=1}^{N_{\text{t}}}{P}_D}(D_n)D_n.(12)$

Imagine now to perform a particle-tracking experiment at constant N_t and V and to monitor the position of R_G in stationary conditions. At a given initial instant the polymer possesses a size n, and thus a diffusion coefficient $D_n=D_0/n^{\alpha }$ with probability given by Equation (12). For time smaller than the characteristic decay τ of the autocorrelation of the process N(t), the experimental PDF amounts then to a Gaussian mixture (also called “superstatistics”) [6, 23, 33] weighted by Equation (12). In addition, its second moment grows linearly with time as in the ordinary Brownian motion. Such a phenomenon of “Brownian yet non Gaussian diffusion” [6, 8] has been recently modeled at a mesoscopic scale in terms of diffusing diffusivity models [23–32]. It is only at time larger than τ that ordinary (Gaussian) Brownian motion is recovered, with a diffusion coefficient D_av. Before giving an estimate of τ for our model (see next section), we study the early time non-Gaussianity in the full phase diagram [N_t, λ], together with its dependence on α.

The non-Gaussian behavior distinctive of R_G(t) at time 0 ≤ t ≪ τ can be properly characterized by referring to one of its Cartesian coordinates, say x. The PDF of the x-displacements takes the form

$\begin{array}{ll}{p}_X(x,t)={\displaystyle \sum _{n=1}^{N_{\text{t}}}{P}_N}\left(\frac{D_0^{\alpha }}{D_n^{\alpha }}\right)\frac{\exp \left(-\frac{x^2}{4\pi D_{n}t}\right)}{\sqrt{4\pi D_{n}t}}.& (13)\end{array}$

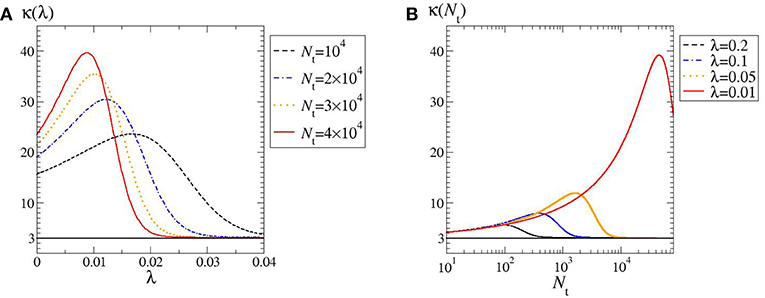
In Figure 1 we plot Equation (13) for α = 1 and different values of λ and N_t. At first sight, non-Gaussianity increases with decreasing N_t and λ; below we however show that the behavior is not monotonic. To measure deviations from Gaussianity we consider the kurtosis of p_X(x, t),

$\begin{array}{ll}\kappa \equiv \frac{\mathbb{E}\left[{\left(X-\mathbb{E}[X]\right)}^4\right]}{{\left(\mathbb{E}\left[{\left(X-\mathbb{E}[X]\right)}^2\right]\right)}^2}& (14)\end{array}$

(κ = 3 for any Gaussian variable). In our case it is straightforward to see that

$\begin{array}{ll}\kappa =3\frac{\mathbb{E}\left[D^2\right]}{{\left(\mathbb{E}\left[D\right]\right)}^2}=3\frac{\mathbb{E}\left[N^{-2\alpha }\right]}{{\left(\mathbb{E}\left[N^{-\alpha }\right]\right)}^2},& (15)\end{array}$

independently of D₀. Notice instead the strong dependence of κ from α; moreover, κ > 3 (positive excess kurtosis or leptokurtic PDF). In order to illustrate regions of more pronounced non-Gaussianity and to discuss their dependence on α in Figure 2 we draw the kurtosis level curves within a (λ, N_t)-phase diagram. Note that, for a given pair (N_t, λ), higher values of the exponent α give rise to larger kurtosis (compare Figures 2A,B).

FIGURE 1

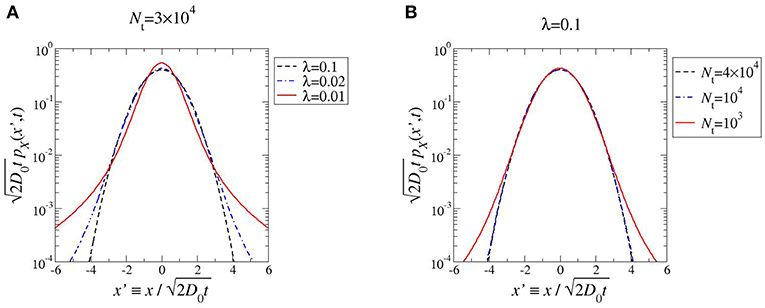
Figure 1. PDF of the x-coordinate of R_G for 0 ≤ t ≪ τ, at fixed N_t (A), and fixed λ (B). The PDF is rescaled such that the variance is unity; recall that in a log-linear plot Gaussian PDFs have parabolic shape. In both cases, α = 1.

FIGURE 2

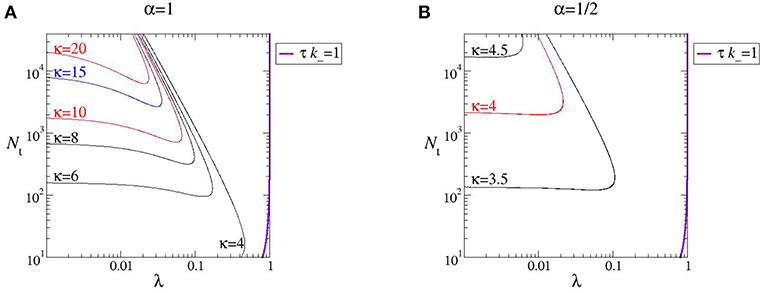
Figure 2. Phase diagram of the early-stage non-Gaussianity for (A) α = 1 and (B) α = 1/2. The thick, violet, line at the right end of both plots corresponds to τk₋ = 1 (please refer to text for details).

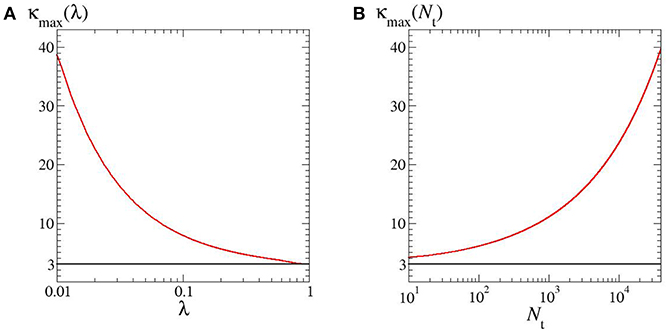
As quoted, by looking at the plots in Figure 1 one may expect the kurtosis to steadily increase by decreasing λ and N_t. The structure of the phase diagram implies instead the existence of a maximum kurtosis, both at given λ and N_t. Indeed, for any horizontal or vertical line traced through the phase diagram (Figure 2) it is possible to find a family of kurtosis level curves each intersecting the line in two distinct points. Between each couple of intersection points the kurtosis first raises and then decreases, thus reaching a maximum value. This is highlighted in Figure 3. Albeit within a small portion of the phase space, the maximum kurtosis can be extremely high, as reported in Figure 4; for instance, k_max ≃ 40 corresponds to an average polymer size of order N_eq ≃ 350 with $N_{\text{t}}\simeq 10^4$.

FIGURE 3

Figure 3. Kurtosis as a function of: (A) λ; (B) N_t. In both cases, α = 1.

FIGURE 4

Figure 4. Maximum kurtosis as a function of: (A) λ; (B) N_t. In both cases, α = 1.

4. Crossover to Brownian, Gaussian Diffusion

The stationary distribution in Equation (7) is exact, but it does not provide information about the decay time-scale τ of initial conditions for the process N(t). To get such an insight, we next workout a continuous approximation for the polymerization process. In the gedankenexperiment reported above, τ is the persistence time scale of the randomly chosen initial diffusion coefficient for R_G, corresponding in turn to the typical duration of the leptokurtic PDF for the diffusion of the center of mass.

We start by noticing that around equilibrium, for N_t ≫ 1 and N_eq ≫ M_eq (large λ), N(t) can be approximated as a continuous Markov process with Langevin equation [37]

$\begin{array}{ll}\text{d}N(t)=2\frac{k_{+}}{V}\left[N_{\text{eq}}-N(t)\right]\text{d}t+\sqrt{2\frac{k_{+}}{V}\left[2N_{\text{t}}-N_{\text{eq}}-N(t)\right]}\text{d}B(t),& (16)\end{array}$

where B(t) is a Wiener process (Brownian motion). Taking further advantage of the large N_eq assumption, we then introduce the rescaled quantity $\tilde{N}\equiv N/N_{\text{eq}}$, obeying

$\begin{array}{l}\text{d}\stackrel{\sim }{N}(t)=2\frac{k_{+}}{V}\left[1-\stackrel{\sim }{N}(t)\right]\text{d}t\\ +{\left(\frac{1}{N_{\text{eq}}}\right)}^{1/2}\sqrt{2\frac{k_{+}}{V}\left[2\frac{N_{\text{t}}}{N_{\text{eq}}}-1-\stackrel{\sim }{N}(t)\right]}\text{d}B(t),(17)\end{array}$

to which we may apply the weak noise approximation. Indeed, one may straightforwardly prove [37] that for large N_eq Equation (18) is satisfied by the approximate solution

$\begin{array}{l}\stackrel{\sim }{N}(t)\simeq \stackrel{\sim }{n}(t)+{\left(\frac{1}{N_{\text{eq}}}\right)}^{1/2}Y(t),(18)\end{array}$

with $\tilde{n}(t)$ a deterministic process satisfying

$\begin{array}{ll}\frac{\text{d}\stackrel{\sim }{n}(t)}{\text{d}t}=2\frac{k_{+}}{V}\left[1-\stackrel{\sim }{n}(t)\right],& (19)\end{array}$

and Y(t) the stochastic process defined by the Langevin equation

$\begin{array}{ll}\text{d}Y(t)=-2\frac{k_{+}}{V}Y(t)\text{d}t+\sqrt{2\frac{k_{+}}{V}\left[2\frac{N_{\text{t}}}{N_{\text{eq}}}-1-\stackrel{\sim }{n}(t)\right]}\text{d}B(t).& (20)\end{array}$

The solution of the deterministic process,

$\begin{array}{ll}\stackrel{\sim }{n}(t)=1+[\stackrel{\sim }{n}(0)-1]{\text{e}}^{-\frac{t}{\tau }},& (21)\end{array}$

asymptotically tends to 1 with a characteristic decay time

$\begin{array}{ll}\tau \equiv \frac{V}{2k_{+}}=\frac{(1-\lambda )N_{\text{t}}}{2k_{-}}.& (22)\end{array}$

Correspondingly, the long-time behavior of Y(t) is that of an Ornstein-Uhlenbeck process:

$\begin{array}{ll}Y(t\to \infty )=\mathbb{N}\left(0,\frac{N_{\text{t}}}{N_{\text{eq}}}-1\right),& (23)\end{array}$

where ℕ(μ, σ²) is a Gaussian variable with mean μ and variance σ². Hence, the stationary solution of $\tilde{N}$ is

$\begin{array}{ll}\stackrel{\sim }{N}(t\to \infty )=\mathbb{N}\left(1,\frac{M_{\text{eq}}}{N_{\text{eq}}^2}\right).& (24)\end{array}$

For the polymer size $N=\tilde{N}{N}_{\text{eq}}$, this implies

$\begin{array}{ll}N(t\to \infty )=\mathbb{N}\left(N_{\text{eq}},M_{\text{eq}}\right).& (25)\end{array}$

We thus appreciate that, to be self consistent, the continuous approximation requires large values of N_t to blur out discreteness, and N_eq ≫ M_eq so that the negative support of the Gaussian PDF corresponds to a negligible probability. Figure 5 shows that when N_t and λ are both large the weak noise approximation of the stationary distribution P_N(n) is almost indistinguishable from the exact solution. On the other hand, decreasing either N_t or λ the approximation fails concomitantly with the fact that the Gaussian probability of negative n-values becomes significant. Depending on the specific cut in phase-space, the approximation may or may not work well in correspondence to the maximum kurtosis (compare red full lines in Figures 5A,B).

FIGURE 5

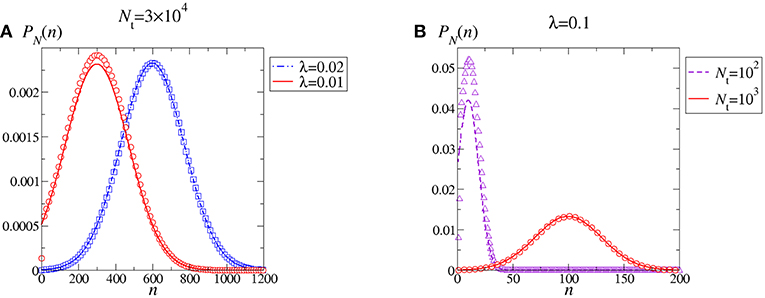
Figure 5. Stationary PDF of the polymerization process. Comparison between the exact PDF in Equation (7) (symbols) and the continuous, weak noise approximation associated to Equation (25) (curves). Values for the parameters N_t and λ have been chosen to facilitate comparison with Figure 1. Specifically, continuous red curves correspond to choices in Figure 1. By decreasing either λ at fixed N_t (A) or N_t at fixed λ (B) the weak noise approximation breaks down.

When applicable, the important result conveyed by the continuous, weak noise approximation is that through Equation (22) it establishes the time scale of the decay of the autocorrelation of N(t). It would be nice to give an explicit representation of τ in terms of the control parameters (λ, N_t); however, Equation (22) shows that it further depends on the dissociation rate constant k₋, which is specific to the chosen polymer. To get a qualitative insight, in Figure 2 we have added the line

$\begin{array}{ll}\tau k_{-}=\frac{(1-\lambda )N_{\text{t}}}{2}=1,& (26)\end{array}$

representing the locus of points for which τ is equal to the inverse of k₋. Notice that the largest kurtosis level curve lay at the left of the line, a region which is also characterized by τ > 1/k₋. Hence, the farther left of the line the longer lasts the Brownian yet non-Gaussian diffusion stage.

5. Conclusions

We have been able to analytically characterize the stochastic motion of the center of mass of a fluctuating filament undergoing a simple polymerization process. Depending on experimentally accessible parameters such as the the total monomers in the solution N_t and the system volume V (equivalently, the fraction λ of total monomers composing the filament in equilibrium), the center of mass displays at early times a Brownian, yet non-Gaussian, diffusion. To our knowledge, this is one of the first example in which this anomalous behavior is directly linked to a microscopic prototype: the effect originates from the fluctuations of N (due to polymerization) and from the relation $D(N)=D_0/N^{\alpha }$ which distinguishes many microscopic models of polymeric diffusion. By studying the kurtosis of the early-time displacement PDF along the x-coordinate we quantified deviations from Gaussian behavior in the phase diagram (λ, N_t), highlighting the dependence on the exponent α. Remarkably, the kurtosis is not monotonic and displays a maximum at either λ or N_t fixed. Finally, on the basis of a continuum (weak noise) approximation for the stochastic process N(t), we put forward an estimation for the time τ(λ, N_t) at which the anomalous behavior crosses over to ordinary Brownian motion. Since the weak noise approximation is not applicable in the whole (λ, N_t) phase diagram, and also in view of the non-monotonic behavior of the kurtosis, further studies approaching the determination of τ are welcome.

In parallel with the analytical results, we proposed a gedankenexperiment in which the anomalous behavior could be detected. As a further perspective, we may notice that if we shift the focus on the diffusion of a tagged monomer (in place of the center of mass of the polymer), in the early stage of the process a subdiffusive behavior coupled to non-Gaussianity is expected to be observed, with a crossover to a Brownian regime at the Rouse time [36]. This analysis is intended to be the subject of future work.

In conclusion, we believe that this work provides a valuable analytical backdrop to Brownian yet non-Gaussian diffusion, a fascinating phenomenon reported to occur in many physical systems. To fully understand this anomalous behavior, it is essential to ground it on a microscopic spring. This is the case for the presented model, but we are confident than others more will come along these lines.

Data Availability

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

FB and FS acknowledge financial support from a 2019 PRD project of the Physics and Astronomy Department of the University of Padova, Italy (BIRD 191017).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank M. Baiesi, G. Falasco, and A.L. Stella for useful discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00124/full#supplementary-material

Footnotes

1. ^Along different lines, connections between polymerization processes and anomalous diffusion have been pointed out in Oshanin and Moreau [34] and Sposini et al. [35].

References

1. Metzler R, Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys Rep. (2000) 339:1–77. doi: 10.1016/S0370-1573(00)00070-3

CrossRef Full Text | Google Scholar

2. Sanabria H, Kubota Y, Waxham MN. Multiple diffusion mechanisms due to nanostructuring in crowded environments. Biophys J. (2007) 92:313–22. doi: 10.1529/biophysj.106.090498

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Höfling F, Franosch T. Anomalous transport in the crowded world of biological cells. Rep Prog Phys. (2013) 76:046602. doi: 10.1088/0034-4885/76/4/046602

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Weeks ER, Crocker JC, Levitt AC, Schofield A, Weitz DA. Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science. (2000) 287:627–31. doi: 10.1126/science.287.5453.627

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Hapca S, Crawford JW, Young IM. Anomalous diffusion of heterogeneous populations characterized by normal diffusion at the individual level. J R Soc Interf. (2008) 6:111–22. doi: 10.1098/rsif.2008.0261

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Wang B, Anthony SM, Bae SC, Granick S. Anomalous yet brownian. Proc Natl Acad Sci U.S.A. (2009) 106:15160–4. doi: 10.1073/pnas.0903554106

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Toyota T, Head DA, Schmidt CF, Mizuno D. Non-Gaussian athermal fluctuations in active gels. Soft Matter. (2011) 7:3234–9. doi: 10.1039/c0sm00925c

CrossRef Full Text | Google Scholar

8. Wang B, Kuo J, Bae SC, Granick S. When Brownian diffusion is not Gaussian. Nat Mater. (2012) 11:481. doi: 10.1038/nmat3308

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Guan J, Wang B, Granick S. Even hard-sphere colloidal suspensions display Fickian yet non-Gaussian diffusion. ACS Nano. (2014) 8:3331–6. doi: 10.1021/nn405476t

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Ghosh SK, Cherstvy AG, Metzler R. Deformation propagation in responsive polymer network films. J Chem Phys. (2014) 141:08B6141. doi: 10.1063/1.4893056

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang D, Hu R, Skaug MJ, Schwartz DK. Temporally anticorrelated motion of nanoparticles at a liquid interface. J Phys Chem Lett. (2014) 6:54–9. doi: 10.1021/jz502210c

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Stylianidou S, Kuwada NJ, Wiggins PA. Cytoplasmic dynamics reveals two modes of nucleoid-dependent mobility. Biophys J. (2014) 107:2684–92. doi: 10.1016/j.bpj.2014.10.030

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Samanta N, Chakrabarti R. Tracer diffusion in a sea of polymers with binding zones: mobile vs. frozen traps. Soft Matter. (2016) 12:8554–63. doi: 10.1039/C6SM01943A

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Dutta S, Chakrabarti J. Anomalous dynamical responses in a driven system. Europhys Lett. (2016) 116:38001. doi: 10.1209/0295-5075/116/38001

CrossRef Full Text | Google Scholar

15. Metzler R. Gaussianity fair: the riddle of anomalous yet non-Gaussian diffusion. Biophys J. (2017) 112:413. doi: 10.1016/j.bpj.2016.12.019

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Cherstvy AG, Nagel O, Beta C, Metzler R. Non-Gaussianity, population heterogeneity, and transient superdiffusion in the spreading dynamics of amoeboid cells. Phys Chem Chem Phys. (2018) 20:23034–54. doi: 10.1039/C8CP04254C

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Kegel WK, van Blaaderen A. Direct observation of dynamical heterogeneities in colloidal hard-sphere suspensions. Science. (2000) 287:290–3. doi: 10.1126/science.287.5451.290

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Leptos KC, Guasto JS, Gollub JP, Pesci AI, Goldstein RE. Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys Rev Lett. (2009) 103:198103. doi: 10.1103/PhysRevLett.103.198103

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Xue C, Zheng X, Chen K, Tian Y, Hu G. Probing non-Gaussianity in confined diffusion of nanoparticles. J Phys Chem Lett. (2016) 7:514–9. doi: 10.1021/acs.jpclett.5b02624

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Parry BR, Surovtsev IV, Cabeen MT, OHern CS, Dufresne ER, Jacobs-Wagner C. The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity. Cell. (2014) 156:183–94. doi: 10.1016/j.cell.2013.11.028

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Munder MC, Midtvedt D, Franzmann T, Nüske E, Otto O, Herbig M, et al. A pH-driven transition of the cytoplasm from a fluid-to a solid-like state promotes entry into dormancy. Elife. (2016) 5:e09347. doi: 10.7554/eLife.09347

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lampo TJ, Stylianidou S, Backlund MP, Wiggins PA, Spakowitz AJ. Cytoplasmic RNA-protein particles exhibit non-Gaussian subdiffusive behavior. Biophys J. (2017) 112:532–42. doi: 10.1016/j.bpj.2016.11.3208

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chubynsky MV, Slater GW. Diffusing diffusivity: a model for anomalous, yet Brownian, diffusion. Phys Rev Lett. (2014) 113:098302. doi: 10.1103/PhysRevLett.113.098302

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Chechkin AV, Seno F, Metzler R, Sokolov IM. Brownian yet non-Gaussian diffusion: from superstatistics to subordination of diffusing diffusivities. Phys Rev X. (2017) 7:021002. doi: 10.1103/PhysRevX.7.021002

CrossRef Full Text | Google Scholar

25. Jain R, Sebastian K. Diffusing diffusivity: a new derivation and comparison with simulations. J Chem Sci. (2017) 129:929–37. doi: 10.1007/s12039-017-1308-0

CrossRef Full Text | Google Scholar

26. Jain R, Sebastian K. Diffusing diffusivity: rotational diffusion in two and three dimensions. J Chem Phys. (2017) 146:214102. doi: 10.1063/1.4984085

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Tyagi N, Cherayil BJ. Non-Gaussian Brownian diffusion in dynamically disordered thermal environments. J Phys Chem B. (2017) 121:7204–9. doi: 10.1021/acs.jpcb.7b03870

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Matse M, Chubynsky MV, Bechhoefer J. Test of the diffusing-diffusivity mechanism using near-wall colloidal dynamics. Phys Rev E. (2017) 96:042604. doi: 10.1103/PhysRevE.96.042604

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Jain R, Sebastian K. Diffusing diffusivity: fractional Brownian oscillator model for subdiffusion and its solution. Phys Rev E. (2018) 98:052138. doi: 10.1103/PhysRevE.98.052138

CrossRef Full Text | Google Scholar

30. Sposini V, Chechkin AV, Seno F, Pagnini G, Metzler R. Random diffusivity from stochastic equations: comparison of two models for Brownian yet non-Gaussian diffusion. New J Phys. (2018) 20:043044. doi: 10.1088/1367-2630/aab696

CrossRef Full Text | Google Scholar

31. Sposini V, Chechkin A, Metzler R. First passage statistics for diffusing diffusivity. J Phys A. (2018) 52:04LT01. doi: 10.1088/1751-8121/aaf6ff

CrossRef Full Text | Google Scholar

32. Grebenkov D. A unifying approach to first-passage time distributions in diffusing diffusivity and switching diffusion models. J Phys A Math Theor. (2019) 52:174001. doi: 10.1088/1751-8121/ab0dae

CrossRef Full Text | Google Scholar

33. Beck C, Cohen EG. Superstatistics. Physica A. (2003) 322:267–75. doi: 10.1016/S0378-4371(03)00019-0

CrossRef Full Text | Google Scholar

34. Oshanin G, Moreau M. Influence of transport limitations on the kinetics of homopolymerization reactions. J Chem Phys. (1995) 102:2977–85. doi: 10.1063/1.468606

CrossRef Full Text | Google Scholar

35. Sposini V, Metzler R, Oshanin G. Single-trajectory spectral analysis of scaled Brownian motion. New J Phys. (2019) 21:073043–2985. doi: 10.1088/1367-2630/ab2f52

CrossRef Full Text | Google Scholar

36. Doi M, Edwards SF. The Theory of Polymer Dynamics. Vol. 73. Oxford: Oxford University Press (1992).

PubMed Abstract | Google Scholar

37. Gillespie DT. Markov Processes: An Introduction for Physical Scientists. San Diego, CA: Academic Press (1992).

Google Scholar

38. Flory PJ. Thermodynamics of high polymer solutions. J Chem Phys. (1942) 10:51–61. doi: 10.1063/1.1723621

CrossRef Full Text | Google Scholar

39. Paul R. Modeling biological cells. Chem Modell. (2012) 9:61–91. doi: 10.1039/9781849734790-00061

CrossRef Full Text | Google Scholar

40. Boal DH. Mechanics of the Cell. Cambridge: Cambridge University Press (2002).

Google Scholar

41. Abramowitz M, Stegun IA. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. Vol. 55. Washington, DC: Courier Corporation (1965).

Google Scholar

42. Weber SC, Spakowitz AJ, Theriot JA. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Phys Rev Lett. (2010) 104:238102. doi: 10.1103/PhysRevLett.104.238102

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Ermak DL, McCammon JA. Brownian dynamics with hydrodynamic interactions. J Chem Phys. (1978) 69:1352–60. doi: 10.1063/1.436761

CrossRef Full Text | Google Scholar

44. Doi M, Edwards S. Dynamics of concentrated polymer systems. Part 1. Brownian motion in the equilibrium state. J Chem Soc Far Trans 2 Mol Chem Phys. (1978) 74:1789–801. doi: 10.1039/F29787401789

CrossRef Full Text | Google Scholar