- Department of Physics, Ben Gurion University of the Negev, Beer-Sheva, Israel
We show that kinematic collisionless relaxation in the macroscopic electric and magnetic fields plays the main role in the formation of the downstream ion distributions in a super-critical shock with ion reflection present. It is done by comparison of a theoretically predicted magnetic profile with the magnetic profile of a shocks observed by MMS mission. It is shown that pressure balance remains the main constraint for the shock stability.
1. Introduction
Collisionless shocks are one of the most fundamental phenomena in plasmas and one of the most efficient accelerators of charged particles in the visible Universe. The large variety processes, leading to the energy redistribution by a shock, occurs at a larger variety of the spatial scales. Yet, the outcome of all these processes depends crucially on the narrow shock transition where the incident upstream flow brakes down. The only place where the structure of this transitions can be explored via in situ measurements is the heliosphere. At least a part of the heliosphere is accessible to a fleet of scientific spacecraft, the sizes of which are much smaller than the transition width to allow local measurements of the magnetic and electric fields and particle distributions as well. In the heliospheric conditions all known shocks are magnetized, that is, magnetic field plays the decisive role in the shock formation and properties. The magnetic field jump serves at the major signature of the shock front. Despite vast improvement of the quality of particle and electric field measurements, the magnetic field measurements remain by far the best by precision and resolution. It is therefore natural that in most cases magnetic observations not only are used to describe the shock structure but also for comparison of theory and observations, even if the theoretically predicted magnetic profile is a result of particle dynamics.
In an ideal MHD a shock is a discontinuity [1]. Real shock have finite width. Dissipative MHD predicts that the shock width is determined by the corresponding dissipative coefficients [2–4]. Up to the critical Mach number, depending on the shock angle and upstream pressure, a shock can be maintained by resistivity or resistivity with thermal conductivity in the so-called subcritical regime. Super-critical dissipative MHD shocks require viscosity [4]. Subcritical shocks are expected to have a monotonically increasing magnetic profile, while super-critical shocks rely on ion reflection and become non-monotonic. In the post-MHD two-fluid theory shocks possess dispersive profiles with upstream oscillations ahead of the main magnetic field jump (ramp) [5]. Yet, dissipation is needed to have these oscillations damp farther from the shock. Downstream oscillations of the magnetic field also require dissipation which is inserted by hand in all theses approaches.
Real observed shocks, even subcritical ones, rarely have monotonic profiles [6–13]. Moreover, the shock width is smaller than the upstream ion convective gyroradius, so that the ion behavior inside the transition region is essentially kinetic and hydrodynamics is no longer a useful approach since the equation of motion is not known a priori. For a long while it was believed that overshoots of the downstream magnetic field are signatures of super-criticality, that is, of ion reflection [14–17], and are produced by reflected ions [10, 12, 14, 18–21]. Observations of a very low-Mach number subcritical shock with an overshoot followed by a trail of coherent magnetic oscillations, spatially periodic at the ion dynamical scale [22], have shown that ion motion in the macroscopic electric and magnetic fields of the shock front plays the main role in the formation of the magnetic profile. Similar oscillations have been observed at many other shocks [23, 24]. It appeared that ions begin to gyrate coherently upon crossing the shock front, which causes spatially periodic oscillations of ion pressure downstream. In a steady shock the sum of the magnetic pressure and plasma pressure should be constant throughout the shock, which means that oscillations of ion pressure would cause oscillations of the magnetic field in the opposite phase. The pressure oscillations gradually damp out because of the gyrophase mixing and gyrotropization of the downstream ion distribution. The whole process, named kinematic collisionless relaxation, was shown theoretically [22, 25–27], numerically [25, 28], and observationally [29, 30] to be responsible for the downstream magnetic field profiles of low-Mach number shocks. It was used theoretically to predict the shapes of observed shocks with unprecedented precision [30]. Until recently, it was believed that the kinematic collisionless relaxation cannot be observed in super-critical shocks, even if it plays there a significant role (which was also casted a doubt upon). Yet, there are no differences between sub- and super-critical shocks from the point of view of equations of motion for ions. Therefore, it is unreasonable to expect that the major effect suddenly disappears upon crossing a borderline. The objective of the present paper is to check whether main features of a super-critical shock with substantial ion reflection can be explained by kinematic collisionless relaxation. In this approach we choose an observed quasi-perpendicular shock with high resolution measurements of the magnetic field and clear presence of a reflected ion population. We identify the features of magnetic profile which we expect to be related to ion gyration. We perform an advanced test particle analysis (ATPA) [31] in a simple model shock front with a limited number of basic parameters similar to those of the observed shock: the shock angle θBn, the magnetic compression Bd/Bu, and the upstream kinetic-to-magnetic pressure ratios βi and βe. ATPA allows to determine the magnetic field profile which would be consistent with the ion distributions formed in this shock. Comparison of the features of the ATPA predicted magnetic profile with the observed one will show what can be attributed to the mechanism of the kinematic collisionless relaxation. The model fields are taken one-dimensional and stationary so that waves and time-dependence of the profile are not included. If a major feature/mechanism is missing in the analysis then comparison of the derived magnetic field with the observed one will fail, that is, they will be essentially different.
2. The Observed Shock
We have chosen an intetplanetary super-critical shock observed by MMS on 2018-01-08 [32]. All spacecraft observed the same transition so that one can conclude that the shock was reasonably planar and steady. In what follows we shall use the magnetic profile measured by MMS-3. The shock crossing occurred at 06:41:11 UT. The shock profile is plotted over the ion spectrogram is shown in Figure 1.
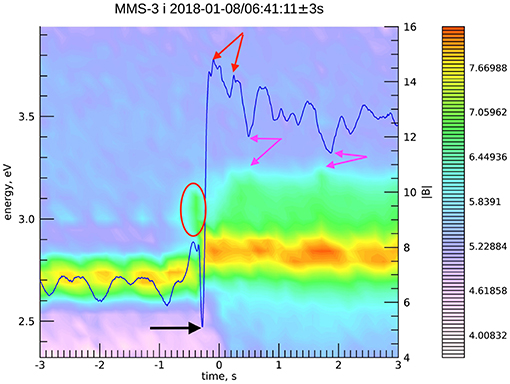
Figure 1. Quasi-perpendicular shock crossing by MMS-3 at 2018-01-08/06:41:11. The magnetic profile is shown in the background of the ion spectrogram (log of energy).
Reflected ions are clearly seen in the spectrogram. In the downstream part pressure oscillations can be also seen which anti-correlate with the magnetic field. The shock is a quite typical supercritical quasi-perpendicular shock with Bd/Bu ≈ 2. The shock angle is estimated as , while the ion kinetic-to-magnetic pressure ratio is βi ≈ 0.35. The forthcoming analysis will also use βe ≈ 1.2. These parameters are taken from Table 1 in [32] where the ion temperature is inferred from Wind measurements.
We identify the following features which we may be possibly related to ion dynamics in the macroscopic fields of the shock front: (a) the reflected ions ahead of the ramp (shown by the orange oval), (b) the overshoot behind the ramp which is the strongest magnetic peak and the decreasing subsequent peaks (red arrows), and (c) the magnetic depression just ahead of the ramp (black arrow). The magenta arrows show the positions where the anti-correlation of the ion distribution and the magnetic field can be seen by eye. The magnetic oscillations do not exhibit clean spatial periodicity and monotonic damping as in laminar shocks [22, 30].
3. The Analysis
We perform advanced test particle analysis of the shock. Namely, we start with a model shock profile in the form
with Bx = BucosθBn, By∝dBz/dx, and Ex∝dBz/dx, and . The coefficients of proportionality for By and Ex are constrained by the chosen values of the normal incidence frame cross-shock potential sNIF and the de Hoffman-Teller potential sHT [21, 33, 34]. Initially Maxwellian distributed (in the upstream plasma frame) ions with were traced in the model fields. Here M is the Alfvenic Mach number. Ion motion was found to be not sensitive to the latter which was kept sHT = 0.1 in the subsequent analysis. The magnetic field is further derived from the condition
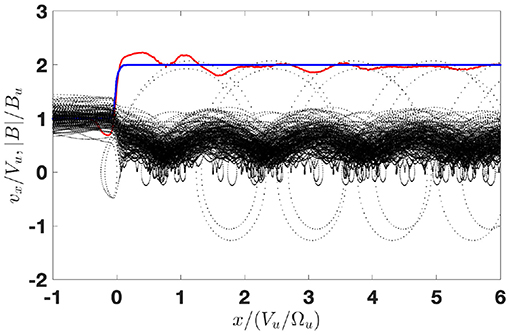
where the ion pressure was determined numerically from the numerically found ion distribution and for the electron pressure the polytropic equation of state was used, together with the quasineutrality. The derived magnetic field is the one which is predicted by the theory. The parameters M, sNIF, and D were varied for adjustment until the asymptotic predicted field be equal to the model downstream value. Figure 2 shows the initial model magnetic field (blue line) and the predicted magnetic field magnitude obtained from (2) (red line). The parameters of this run are: the Alfvenic Mach number M = 2.8, the cross-shock potential sNIF = 0.55, and the ramp width D = 0.4(c/ωpi), where c/ωpi is the ion inertial length. Variation of the parameters within 5% of these values gave similar results. This set is chosen as a representative one. We note that for the chosen angle and β the corresponding fast magnetosonic Mach number is Mf ≈ 1.83 which is rather close to the value Mg ≈ 1.9 estimated by Cohen et al. [32]. The coordinate is normalized on the upstream ion convective gyroradius rg = Vu/Ωu, where Vu is the upstream plasma speed in NIF and Ωu = eBu/mic is the upstream gyrofrequency. The magnetic field is normalized on Bu. The basic features of the magnetic field, as identified above, are clearly caught by the calculation: there is a clear overshoot with subsequently decreasing oscillations of the magnetic field at the downstream side of the profile and a magnetic dip just ahead of the ramp. Figure 3 shows orbits of 1% of ions randomly chosen from the initial Maxwellian. The velocities are normalized on Vu. The reflected ions are clearly seen as well as the competing contributions of the directly transmitted and reflected ions into downstream ion pressure and the resulting effect of the magnetic field. Figure 4 shows the ion distribution in the vx − vy plane accumulated in the spatial region of the width of 0.5(Vu/Ωu) just upstream of the middle of the ramp. The reflected ions are clearly seen as a distinct population. The maximum density of reflected ions is about 10% of the upstream density and is achieved at the magnetic depression as was predicted earlier [31] and can be seen in Figure 1.
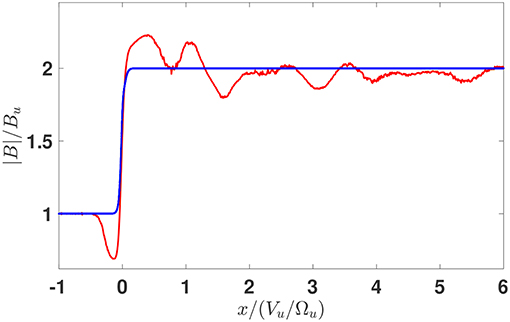
Figure 2. The model magnetic field (blue) and the predicted magnetic field (red). The adjusted parameters are: M = 2.8, sNIF = 0.55, and D = 0.4(c/ωpi).
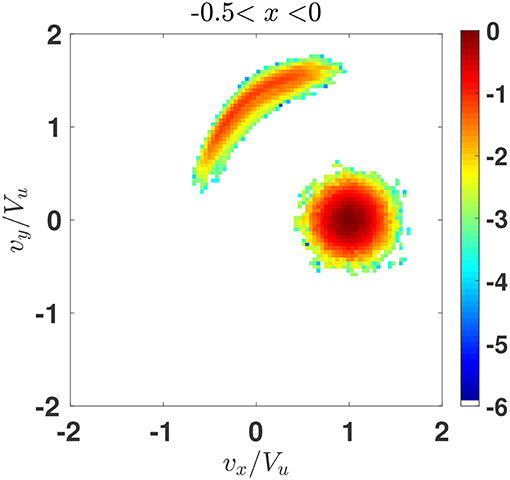
Figure 4. Ion distribution projected on the plane vx − vy, accumulated in the spatial region of the width of 0.5rg toward upstream from the middle of the ramp.
4. Discussion and Conclusions
Obviously, ATPA cannot reproduce exactly the observed shock profile. Supercritical shocks are not exactly planar and time-independent and ion dynamics should be affected by deviations from planarity and time-dependent fields. Moreover, even if the shock were exactly one-dimensional and stationary, the measurements are not precise and the shock parameters are known only approximately. In addition, our knowledge of the detailed shape of the fields inside the shock is far from being complete. Therefore, it does not make sense to try to exactly fit the predicted profile to the observed one, and this certainly was not the objective. However, it is reasonable to check what major features of the magnetic profile can be explained by theory. By comparing theoretical predictions with an observed interplanetary super-critical shock we have shown that the overshoot with subsequent damping oscillations, even not spatially periodic, as well as the magnetic dip just ahead of the ramp, appear naturally due to the gyration of the directly transmitted and reflected ions in the macroscopic fields of the shock front. The role of time-dependent fields and/or non-planarity is secondary: they may affect the amplitude of the oscillations, the peak-to-peak distance, and the damping rate (gyrotropization) but only mildly. The very existence of the above mentioned features is due to the kinematic collisionless relaxation. At this stage we do not have quantitative predictions of the overshoot amplitude or spatial parameters. This will require additional study as well as the issue of the increasing importance of the time-dependent features with the increase of the Mach number.
Data Availability
The MMS data was retrieved and processed using the SPEDAS software [35].
Author Contributions
The whole study and writing is done by MG.
Funding
This study was supported in part by the Israel Science Foundation (Grant No. 368/14).
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. de Hoffmann F, Teller E. Magneto-hydrodynamic shocks. Phys Rev. (1950) 80:692–703. doi: 10.1103/PhysRev.80.692
2. Edmiston JP, Kennel CF. A parametric survey of the first critical Mach number for a fast MHD shock. J Plasma Phys. (1984) 32:429–41. doi: 10.1017/S002237780000218X
3. Kennel CF. Critical mach numbers in classical magnetohydrodynamics. J Geophys Res. (1987) 92:13427–37. doi: 10.1029/JA092iA12p13427
4. Kennel CF. Shock structure in classical magnetohydrodynamics. J Geophys Res. (1988) 93:8545–57. doi: 10.1029/JA093iA08p08545
5. Sagdeev RZ. Cooperative phenomena and shock waves in collisionless plasmas. Rev Plasma Phys. (1966) 4:23.
6. Greenstadt EW, Scarf FL, Russell CT, Formisano V, Neugebauer M. Structure of the quasi-perpendicular laminar bow shock. J Geophys Res. (1975) 80:502. doi: 10.1029/JA080i004p00502
7. Greenstadt EW, Scarf FL, Russell CT, Gosling JT, Bame SJ, Paschmann G, et al. A macroscopic profile of the typical quasi-perpendicular bow shock - Isee 1 and 2. J Geophys Res. (1980) 85:2124–30. doi: 10.1029/JA085iA05p02124
8. Russell C, Hoppe M, Livesey W, Gosling J. Isee-1 and-2 observations of laminar bow shocks- velocity and thickness. Geophys Res Lett. (1982) 9:1171. doi: 10.1029/GL009i010p01171
9. Livesey WA, Kennel CF, Russell CT. ISEE-1 and -2 observations of magnetic field strength overshoots in quasi-perpendicular bow shocks. Geophys Res Lett. (1982) 9:1037–40. doi: 10.1029/GL009i009p01037
10. Russell CT, Hoppe MM, Livesey WA. Overshoots in planetary bow shocks. Nature. (1982) 296:45–8. doi: 10.1038/296045a0
11. Mellott MM, Greenstadt EW. The structure of oblique subcritical bow shocks - ISEE 1 and 2 observations. J Geophys Res. (1984) 89:2151–61. doi: 10.1029/JA089iA04p02151
12. Mellott MM, Livesey WA. Shock overshoots revisited. J Geophys Res. (1987) 92:13661. doi: 10.1029/JA092iA12p13661
13. Farris M, Russell C, Thomsen M. Magnetic structure of the low beta, quasi-perpendicular shock. J Geophys Res. (1993) 98:15285–94. doi: 10.1029/93JA00958
14. Gosling JT, Thomsen MF, Bame SJ, Feldman WC, Paschmann G, Sckopke N. Evidence for specularly reflected ions upstream from the quasi-parallel bow shock. Geophys Res Lett. (1982) 9:1333–6. doi: 10.1029/GL009i012p01333
15. Sckopke N, Paschmann G, Bame SJ, Gosling JT, Russell CT. Evolution of ion distributions across the nearly perpendicular bow shock - Specularly and non-specularly reflected-gyrating ions. J Geophys Res. (1983) 88:6121–36. doi: 10.1029/JA088iA08p06121
16. Burgess D, Wilkinson WP, Schwartz SJ. Ion distributions and thermalization at perpendicular and quasi-perpendicular supercritical collisionless shocks. J Geophys Res. (1989) 94:8783–92. doi: 10.1029/JA094iA07p08783
17. Sckopke N, Paschmann G, Brinca AL, Carlson CW, Luehr H. Ion thermalization in quasi-perpendicular shocks involving reflected ions. J Geophys Res. (1990) 95:6337–52. doi: 10.1029/JA095iA05p06337
18. Woods LC. On the structure of collisionless magneto-plasma shock waves at super-critical Alfvén-Mach numbers. J Plasma Phys. (1969) 3:435. doi: 10.1017/S0022377800004517
19. Woods LC. On double-structured, perpendicular, magneto-plasma shock waves . Plasma Phys. (1971) 13:289–302. doi: 10.1088/0032-1028/13/4/302
20. Leroy MM, Winske D, Goodrich CC, Wu CS, Papadopoulos K. The structure of perpendicular bow shocks. J Geophys Res. (1982) 87:5081–94. doi: 10.1029/JA087iA07p05081
21. Scudder JD, Aggson TL, Mangeney A, Lacombe C, Harvey CC. The resolved layer of a collisionless, high beta, supercritical, quasi-perpendicular shock wave. I - Rankine-Hugoniot geometry, currents, and stationarity. J Geophys Res. (1986) 91:11019–52. doi: 10.1029/JA091iA10p11019
22. Balikhin MA, Zhang TL, Gedalin M, Ganushkina NY, Pope SA. Venus Express observes a new type of shock with pure kinematic relaxation. Geophys Res Lett. (2008) 35:L01103. doi: 10.1029/2007GL032495
23. Russell CT, Jian LK, Blanco-Cano X, Luhmann JG. STEREO observations of upstream and downstream waves at low Mach number shocks. Geophys Res Lett. (2009) 36:03106. doi: 10.1029/2008GL036991
24. Kajdič P, Blanco-Cano X, Aguilar-Rodriguez E, Russell CT, Jian LK, Luhmann JG. Waves upstream and downstream of interplanetary shocks driven by coronal mass ejections. J Geophys Res. (2012) 117:A06103. doi: 10.1029/2011JA017381
25. Ofman L, Balikhin M, Russell CT, Gedalin M. Collisionless relaxation of ion distributions downstream of laminar quasi-perpendicular shocks. J Geophys Res. (2009) 114:09106. doi: 10.1029/2009JA014365
26. Gedalin M. Collisionless relaxation of non-gyrotropic downstream ion distributions: dependence on shock parameters. J Plasma Phys. (2015) 81:905810603. doi: 10.1017/S0022377815001154
27. Gedalin M, Friedman Y, Balikhin M. Collisionless relaxation of downstream ion distributions in low-Mach number shocks. Phys Plasmas. (2015) 22:072301. doi: 10.1063/1.4926452
28. Ofman L, Gedalin M. Two-dimensional hybrid simulations of quasi-perpendicular collisionless shock dynamics: gyrating downstream ion distributions. J Geophys Res. (2013) 118:1828–36. doi: 10.1029/2012JA018188
29. Gedalin M, Zhou X, Russell CT, Drozdov A, Liu TZ. Ion dynamics and the shock profile of a low-mach number shock. J Geophys Res. (2018) 141:5.
30. Pope SA, Gedalin M, Balikhin MA. The first direct observational confirmation of kinematic collisionless relaxation in very-low mach number shocks near the earth. J Geophys Res. (2019) 165:3–15. doi: 10.1029/2018JA026223
31. Gedalin M. Transmitted, reflected, quasi-reflected, and multiply reflected ions in low-Mach number shocks. J Geophys Res. (2016) 121:10. doi: 10.1002/2016JA023395
32. Cohen IJ, Schwartz SJ, Goodrich KA, Ahmadi N, Ergun RE, Fuselier SA, et al. High-resolution measurements of the cross-shock potential, ion reflection, and electron heating at an interplanetary shock by MMS. J Geophys Res. (2019) 90:12095.
33. Goodrich CC, Scudder JD. The adiabatic energy change of plasma electrons and the frame dependence of the cross-shock potential at collisionless magnetosonic shock waves. J Geophys Res. (1984) 89:6654–62. doi: 10.1029/JA089iA08p06654
34. Schwartz SJ, Thomsen MF, Bame SJ, Stansberry J. Electron heating and the potential jump across fast mode shocks. J Geophys Res. (1988) 93:12923–31. doi: 10.1029/JA093iA11p12923
Keywords: collisionless shocks, heliospheric shocks, bow shock, particle acceleration, plasma heating, magnetic fields in space
Citation: Gedalin M (2019) Kinematic Collisionless Relaxation of Ions in Supercritical Shocks. Front. Phys. 7:114. doi: 10.3389/fphy.2019.00114
Received: 31 May 2019; Accepted: 31 July 2019;
Published: 14 August 2019.
Edited by:
Vladislav Izmodenov, Space Research Institute (RAS), RussiaReviewed by:
Anton Artemyev, Space Research Institute (RAS), RussiaHarald Kucharek, University of New Hampshire, United States
Copyright © 2019 Gedalin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michael Gedalin, Z2VkYWxpbkBiZ3UuYWMuaWw=
 Michael Gedalin
Michael Gedalin