Numerical Solutions for Time-Fractional Cancer Invasion System With Nonlocal Diffusion

This article studies the existence and uniqueness of a weak solution of the time-fractional cancer invasion system with nonlocal diffusion operator. Existence and uniqueness results are ensured by adapting the Faedo-Galerkin method and some a priori estimates. Further, finite element numerical scheme is implemented for the considered system. Finally, various numerical computations are performed along with the convergence analysis of the scheme.

1. Introduction

In the past few decades, a large number of mathematical models have been applied for biological studies. In addition, mathematical models give a deeper conceptual understanding of behavioral dynamics of complex systems. Some of the advantages of mathematical models include cost efficient experiments, which can be performed speedily without disturbing biological variants. Cancer is a disease defined by a normal cell which starts replicating out-of-control. Over the years, cancer modeling has gained popularity with applied mathematicians because of its challenges, resulting in numerous research findings on the dynamics of tumor invasion. Some of these propositions are available in the literature to acquaint oneself with the developments in cancer modeling (see for instance [1–4]).

On the other hand, fractional differential equations (FDEs) have been extensively used for constructing biological models and other areas of science and engineering. We refer the following monographs [5–7] and research articles [8–12] that have explored recent developments using FDEs. Biological phenomena have an anomalous diffusion property which includes heterogeneous systems that are witnessed in porous materials (see for example [13, 14]). Linear and nonlinear models of anomalous diffusion, which have been experimented by researchers could not do justice to the biological phenomena. But the fractional models have contributed to replicate the biological phenomena with a greater accuracy. Diffusions in biological tissue has characterized as anomalous. Therefore, it has been shown to be best described using fractional calculus tools. It means equations involving non-integer derivatives and integrals. Cancer models adapting fractional differential equations are studied by Ahmed et al. [15] and Iyiola and Zaman [16] and also see the references there in.

Theoretical and numerical analysis of fractional partial differential equations (FPDEs), concerned with only very few articles, are available in the literature. Alikhanov [17] applied the method of energy inequalities to obtain the existence of solutions for a time-fractional boundary value problem of the diffusion-wave equation. Jiao and Zhou [18] established an existence result for a fractional boundary value problem with the application of the critical point theory. Further, Zhou et al. [19] analyzed the time-fractional reaction-diffusion equation under nonlocal boundary condition. Zhou and Peng [11] established the existence, uniqueness and regularity of time-fractional Navier-Stokes equations. Further, they ensured the existence of weak solutions and also provided the sufficient conditions for optimal controls in Zhou and Peng [12]. Finite volume method [20–22], meshless method [23, 24], finite difference method [25–28], finite element method [29–31] and the spectral method [32–35] are widely preferred numerical methods in the literature to solve fractional partial differential equations. Finite element methods have become popular for numerical simulations of time-fractional diffusion equations due to their good approximation and feasibility to work with any domains. Recently, Esen et al. [36] studied the numerical solutions of time-fractional diffusion equations and diffusion-wave equations using Galerkin finite element method. Jin et al. [29] analyzed the numerical solutions of multiple time-fractional derivative using the Galerkin finite element method. Wang et al. [37] combined second-order time approximation with the finite element method to solve nonlinear fractional Cable equation. Liu et al. [38] used fully discrete mixed finite element scheme to study the second order convergence for nonlinear time-fractional diffusion problem with fourth-order derivative term. Jin et al. [39] solved proposed Crank-Nicolson-Galerkin finite element scheme to solve the linear time FPDEs. Kumar et al. [40] proposed Crank-Nicolson-Galerkin finite element scheme to solve the time-fractional nonlinear diffusion equation using Newton's algorithm. However, according to author's knowledge there is no paper available in the literature to study the fractional order cancer invasion system using finite element method.

Recently fractional reaction-diffusion systems are applied for many applications in science and engineering. Fractional models are proposed and used in chemical reactions, propagation phenomena, transport systems, pattern formation processes and spatiotemporal distribution of species [41–45] and references therein. In this connection, we are interested to study and analyze the time-fractional cancer invasion model with nonlocal diffusion operator. Existence and uniqueness of a weak solution and various numerical simulations are presented for the below considered model. We considered a mathematical model proposed in Solis and Delgadillo [46] with four unknown variables namely two cancer cells density, normal cells density and acidification medium concentration. Further, we extend the same model for fractional differential equations and we show the importance of fractional derivatives using numerical simulations. The dynamics of cancer invasion system with time-fractional is governed by the following nonlocal diffusion system:

$\begin{array}{ll}\begin{array}{l}{\partial }_t^{\alpha }{u}_1-d_1\left(l(u_1)\right)\Delta u_1=\\ u_1(1-u_1)-{\beta }_1{u}_1{u}_2-\rho u_1-{\gamma }_1{u}_1{u}_3\text{ in }{Q}_T,\\ {\partial }_t^{\alpha }{u}_2-d_2\left(l(u_2)\right)\Delta u_2=\\ r_2{u}_2(1-u_2)-{\beta }_2{u}_1{u}_2+\rho u_1-{\delta }_1{u}_2{u}_3\text{ in }{Q}_T,\\ {\partial }_t^{\alpha }{u}_3=r_3{u}_3(1-u_3)\\ -{\gamma }_2{u}_1{u}_3-{\delta }_2{u}_2{u}_3-\sigma u_3{u}_4\text{ in }{Q}_T,\\ {\partial }_t^{\alpha }{u}_4-d_4\left(l(u_4)\right)\Delta u_4=\\ \xi (u_1+u_2-u_4)\text{ in }{Q}_T,\end{array}\}& (1.1)\end{array}$

with initial and boundary conditions

$\begin{array}{l}{u}_j(x,0)=u_{j,0}(x),j=1,2,3,4\text{ in }\Omega ,\\ u_i(x,t)=0,i=1,2,4\text{ in }{\Sigma }_T,\end{array}$

where Q_T = Ω × (0, T), Σ_T = ∂Ω × (0, T), T > 0 is final time and α ∈ (0, 1]. Here, Ω is a bounded domain in ℝ^N with smooth boundary ∂Ω. The unknown functions u₁(x, t) and u₂(x, t), respectively, describe the density of two types of cancer cells. Further, u₃(x, t) and u₄(x, t), respectively, represent the density of normal cells and medium acidification concentration due to excess H⁺ ions. The constants β₁ and β₂, respectively, denote the rates of interaction and the positive constant ρ delineates the intrinsic mutation rate of cancer cells. Furthermore, γ₁ and δ₁ represent the rate of consumption of cancer cell populations. The proliferation rate of cancer cells is given by r₂ ≥ 0 and r₃ ≥ 0. Here, ξ represents the production rate of the H⁺ions. Moreover, γ₂ and δ₂, respectively, denote the interaction rate of two types of cancer cells with normal cells and σ denotes the degradation rate of normal cells due to acidification. In (1.1), the diffusion rates d_i: ℝ → ℝ are the Lipschitz continuous functions with d_i(ξ) ≥ m_i > 0 where i = 1, 2, 4. Further, d_i, i = 1, 2, 4 are taken to be depend on the whole of each population in the domain rather than on the local density. From a physical point of view of biological models, especially migration of cancer cells through normal cell is more like movement in a porous medium. Therefore, we consider the cell random motility to be a function of unknowns, see for example Szymańska et al. [47]. Therefore, it is more realistic to work with density dependent diffusion like nonlocal diffusion instead of linear diffusion function. Further, we assume that linear continuous nonlocal operator l(s) ∈ xs(L²(Ω))′ where s ∈ ℝ. This work investigates existence and uniqueness of a weak solution and numerical solutions for the time-fractional cancer invasion system (1.1).

It should be remarked that throughout the paper, we use the Caputo sense fractional derivatives for time. The main advantage the Caputo derivative, we can use initial conditions as in integer order derivatives. However, for more details we refer the interested readers to the book [48].

The rest of the manuscript is arranged as follows. In section 2, we present some preliminaries of fractional calculus and existence and uniqueness of weak solution of (1.1) using the Faedo-Galerkin approximation method and priori estimates. In section 3, we give the variational formulation of (1.1), finite element discretization and temporal discretization. Finally, in section 4, we present the convergence study of the numerical scheme and some computations with various numerical experiments.

2. Existence and Uniqueness

The goal of this section is to prove existence and uniqueness of a weak solution of nonlocal density dependent diffusion cancer invasion parabolic system with time-fractional derivative (1.1). By adopting the Faedo-Galerkin approximation method and deriving uniform a priori estimates for approximation solution, we show the existence of a weak solution in appropriate solution space. Here, we use the same notations and definitions as in Zhou et al. [19, 49]. Further, in order to avoid too many notations, we use a generic constant C instead of different constants.

Theorem 2.1 ([6]). Consider the fractional ordinary differential equation (FODE)

$\begin{array}{ll}\begin{array}{l}{}_0{}^{C}D{ }_x^{\alpha }u(x)=f(x,u(x)),0<x<T,\\ u(0)=b_0,\end{array}\}& (2.1)\end{array}$

where 0 < α < 1 and b₀ ∈ ℝ be a given constant. Suppose U be an open and connected set in ℝ and Ω = [0, T] × U. Assume that f(x, y):(0, T) × U → ℝ be a continuous function satisfying the Lipschitz condition. Then for any (x₀, y₀) ∈ Ω, there exists h > 0 such that the real interval [x₀ − h, x₀ + h] ⊂ (0, T) and there exists a unique solution u(x): [x₀ − h, x₀ + h] → U for (2.1) such that u(x) ∈ C[x₀ − h, x₀ + h], and for any x ∈ [x₀ − h, x₀ + h].

Lemma 2.1. Suppose u:[0, T] → X where X: = L²(Ω) is a real Hilbert space. Assume that there exists fractional derivative of u in the Caputo sense, then the following inequality holds true:

$(u(t),{}_0{}^{C}D{ }_t^{\alpha }(u(t)))\ge \frac{1}{2}{}_0{}^{C}D{ }_t^{\alpha }\Vert u{\Vert }_X^2.$

Lemma 2.2. Let α ∈ (0, 1) and a non-negative integrable function c₁(t) for t ∈ [0, T] satisfies the inequality

$\begin{array}{ll}{}_0{}^{C}D{ }_t^{\alpha }u(t)\le c_1(t),& (2.2)\end{array}$

for almost all t ∈ [0, T]. Then

$\begin{array}{ll}u(t)\le u(0)+\frac{1}{\Gamma (\alpha )}{\displaystyle {\int }_0^t{(t-s)}^{\alpha -1}}{c}_1(s)ds.& (2.3)\end{array}$

Lemma 2.3 ([50], p.9). Let α ∈ (0, 1). Suppose u, v are two integrable functions, v is nondecreasing and g is a continuous function in [a, b]. If

$u(t)\le v(t)+g(t){\displaystyle {\int }_a^t}{(t-s)}^{\alpha -1}u(s)ds,\forall t\in \left[a,b\right],$

then

$u(t)\le v(t)E_{\alpha }[g(t)\Gamma (\alpha ){(t-a)}^{\alpha }],$

where E_α(·) is one parameter Mittag-Leffler function.

Lemma 2.4. Let α ∈ (0, 1). Suppose u(·) is a non-negative, absolute continuous function on [0, T], which satisfies for a.e. t the following differential inequality

$\begin{array}{ll}{}_0{}^{C}D{ }_t^{\alpha }u(t)\le Cu(t),& (2.4)\end{array}$

for constant C ≥ 0. Then

$u(t)\le u(0)E_{\alpha }\left[C{t}^{\alpha }\right].$

Proof. From (2.4),

$u(t)\le u(0)+\frac{C}{\Gamma (\alpha )}{\displaystyle {\int }_0^t}{(t-s)}^{\alpha -1}u(s)ds,$

where we use the Lemma 2.2 Using the Lemma 2.3, we get

$u(t)\le u(0)E_{\alpha }\left[C{t}^{\alpha }\right].$

Assume that X₀, X₁, X are Hilbert spaces. The Fourier transform of u : ℝ → X₁ is defined by $û(\tau )={\int }_{-\infty }^{\infty }{e}^{-2i\theta t\tau }u(t)dt$ (See [51]). Then, we have

${ }_{-\infty }^C{D}_t^{\alpha }\widehat{u}(\tau )=(2i\theta \tau {)}^{\alpha }\widehat{u}(\tau ).$

For 0 < α ≤ 1, define a Hilbert space

${{W}}^{\alpha }(ℝ,X_0,X_1)=\left\{u\in L^2(ℝ,X_0)\underset{-\infty }{\overset{C}{:}}{D}_t^{\alpha }\in L^2(ℝ,X_1)\right\}$

endowed with the norm

$\Vert u{\Vert }_{{{W}}^{\alpha }}={\left\{\Vert u{\Vert }_{L^2(ℝ,X_0)}^2+\Vert {\tau }^{\alpha }\widehat{u}{\Vert }_{L^2(ℝ,X_1)}^2\right\}}^{\frac{1}{2}}.$

For any set J ⊂ ℝ, define a subspace ${{W}}_J^{\alpha }$ of ${{W}}^{\alpha }$ (see p. 274, [49]) as with support contained in J:

$\begin{array}{l}{{W}}_J^{\alpha }(ℝ,X_0,X_1)=\left\{v\in {{W}}^{\alpha }(ℝ,X_0,X_1):supp(v)\subset J\right\},\end{array}$

Further, we use the space

$V:=H_0^1(\Omega )\times H_0^1(\Omega )\times L^2(\Omega )\times H_0^1(\Omega );$

throughout the article.

Theorem 2.2 ([51]). Assume that X₀ ↪ X ↪ X₁ is continuous and X₀ ↪ X is compact. Then for any bounded set J and α > 0, ${{W}}_J^{\alpha }(ℝ,X_0,X_1)\hookrightarrow L^2(ℝ,X)$ is compact.

Without loss of generality, we rewrite the nonlocal density dependent diffusion cancer invasion parabolic system (1.1) with time-fractional derivative in the following form:

$\begin{array}{ll}\begin{array}{ll}{\partial }_t^{\alpha }{u}_1-d_1(l(u_1))\Delta u_1+G_1(x,t,u_1,u_2,u_3)=(1-\rho )u_1\hfill & \text{in }{Q}_T,\hfill \\ {\partial }_t^{\alpha }{u}_2-d_2(l(u_2))\Delta u_2+G_2(x,t,u_1,u_2,u_3)=r_2{u}_2+\rho u_1\hfill & \text{in }{Q}_T,\hfill \\ {\partial }_t^{\alpha }{u}_3+G_3(x,t,u_1,u_2,u_3,u4)=r_3{u}_3\hfill & \text{in }{Q}_T,\hfill \\ {\partial }_t^{\alpha }{u}_4-d_4(l(u_4))\Delta u_4=\xi (u_1+u_2-u_4)\hfill & \text{in }{Q}_T,\hfill \end{array}\}& (2.5)\end{array}$

where

$\begin{array}{l}\begin{array}{l}{G}_1(x,t,u_1,u_2,u_3)=u_1(u_1+{\beta }_1{u}_2+{\gamma }_1{u}_3),\hfill \\ G_2(x,t,u_1,u_2,u_3)=u_2({\beta }_2{u}_1+r_2{u}_2+{\delta }_1{u}_3),\hfill \\ G_3(x,t,u_1,u_2,u_3,u_4)=u_3({\gamma }_2{u}_1+{\delta }_2{u}_2+r_3{u}_3+\sigma u_4).\hfill \end{array}\end{array}$

Theorem 2.3. Suppose the initial conditions u_j,0, j = 1, 2, 3, 4 are in L²(Ω). Then the system (2.5) admits a weak solution u₁, u₂, u₃, u₄, which satisfies the following conditions:

$\begin{array}{l}{u}_1,u_2,u_4\in L^{\infty }(0,T;L^2(\Omega ))\cap L^2(0,T;H_0^1(\Omega )),\\ u_3\in L^{\infty }(0,T;L^2(\Omega )),\end{array}$

such that for every ${\varphi }_j\in L^2(0,T;H_0^1(\Omega )),j=1,2,3,4,$

$\begin{array}{l}{\displaystyle {\int }_0^T{\partial }_t^{\alpha }}(u_1,{\varphi }_1)dt+d_1(l(u_1)){\displaystyle {\int }_{Q_T}\nabla }{u}_1\nabla {\varphi }_{1}dxdt\\ +{\displaystyle {\int }_{Q_T}{G}_1}(x,t,u_1,u_2,u_3){\varphi }_{1}dxdt\\ =(1-\rho ){\displaystyle {\int }_{Q_T}{u}_1}{\varphi }_{1}dxdt,\\ {\displaystyle {\int }_0^T{\partial }_t^{\alpha }}(u_2,{\varphi }_2)dt+d_2(l(u_2)){\displaystyle {\int }_{Q_T}\nabla }{u}_2\nabla {\varphi }_{2}dxdt\\ +{\displaystyle {\int }_{Q_T}{G}_2}(x,t,u_1,u_2,u_3){\varphi }_{2}dxdt\\ ={\displaystyle {\int }_{Q_T}(r_2{u}_2+\rho u_1)}{\varphi }_{2}dxdt,\\ {\displaystyle {\int }_0^T{\partial }_t^{\alpha }}(u_3,{\varphi }_3)dt+{\displaystyle {\int }_{Q_T}{G}_3}(x,t{u}_1,u_2,u_3,u_4){\varphi }_{3}dxdt\\ ={\displaystyle {\int }_{Q_T}{r}_3}{u}_3{\varphi }_{3}dxdt,\\ {\displaystyle {\int }_0^T{\partial }_t^{\alpha }}(u_4,{\varphi }_4)dt+d_4(l(u_4)){\displaystyle {\int }_{Q_T}\nabla }{u}_4\nabla {\varphi }_{4}dxdt\\ ={\displaystyle {\int }_{Q_T}\xi }(u_1+u_2-u_4){\varphi }_{4}dxdt.& (2.6)\end{array}$

Now, we use the following regularized system in order to find weak solutions of the system (2.5). For ϵ > 0,

$\begin{array}{ll}\begin{array}{ll}{\partial }_t^{\alpha }{u}_1^{ϵ}-d_1(l(u_1^{ϵ}))\Delta u_1^{ϵ}+G_{1,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ})=u_1^{ϵ}-\rho u_1^{ϵ}\hfill & \text{in }{Q}_T,\hfill \\ {\partial }_t^{\alpha }{u}_2^{ϵ}-d_2(l(u_2^{ϵ}))\Delta u_2^{ϵ}+G_{2,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ})=r_2{u}_2^{ϵ}+\rho u_1^{ϵ}\hfill & \text{in }{Q}_T,\hfill \\ {\partial }_t^{\alpha }{u}_3^{ϵ}+G_{3,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ},u_4^{ϵ})=r_3{u}_3^{ϵ}\hfill & \text{in }{Q}_T,\hfill \\ {\partial }_t^{\alpha }{u}_4^{ϵ}-d_4(l(u_4^{ϵ}))\Delta u_4^{ϵ}=\xi (u_1^{ϵ}+u_2^{ϵ}-u_4^{ϵ})\hfill & \text{in }{Q}_T,\hfill \end{array}\}& (2.7)\end{array}$

with initial and boundary conditions

$\begin{array}{l}{u}_j^{ϵ}(x,0)=u_{j,0}^{ϵ}(x),j=1,2,3,4\text{in}\Omega ,\\ u_i^{ϵ}(x,t)=0,i=1,2,4\text{in }{\Sigma }_T,\end{array}$

where $G_{j,ϵ}=\frac{G_j}{1+ϵ\left|G_j\right|},j=1,2,3.$

We apply the Faedo-Galerkin method to solve (2.7). Let {e_l} be a denumerable orthogonal base of $H_0^1(\Omega )$ orthonormal with respect to L²(Ω). We consider the sequence of finite dimensional spaces S_n = span {e_l, l ≤ n}. Let ${\displaystyle u_{j,n}^{ϵ}(x,t)=\sum _{l=1}^n{c}_{j,n,l}(t)e_l(x),j=1,2,3,4,}$ be the weak solution of system (2.7), where c_j,n,l(t), j = 1, 2, 3, 4 are unknowns of the nonlinear FODE system,

$\begin{array}{l}{\displaystyle {\int }_{\Omega }{\partial }_t^{\alpha }}{u}_{1,n}^{ϵ}{e}_{m}dx+d_1(l(u_{1,n}^{ϵ})){\displaystyle {\int }_{\Omega }\nabla }{u}_{1,n}^{ϵ}\nabla e_{m}dx\\ +{\displaystyle {\int }_{\Omega }{G}_{1,ϵ}}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})e_{m}dx=(1-\rho ){\displaystyle {\int }_{\Omega }{u}_{1,n}^{ϵ}}{e}_{m}dx,\\ {\displaystyle {\int }_{\Omega }{\partial }_t^{\alpha }}{u}_{2,n}^{ϵ}{e}_{m}dx+d_2(l(u_{2,n}^{ϵ})){\displaystyle {\int }_{\Omega }\nabla }{u}_{2,n}^{ϵ}\nabla e_{m}dx\\ +{\displaystyle {\int }_{\Omega }{G}_{2,ϵ}}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})e_{m}dx\\ ={\displaystyle {\int }_{\Omega }(r_2{u}_{2,n}^{ϵ}+\rho u_{1,n}^{ϵ})}{e}_{m}dx,\\ {\displaystyle {\int }_{\Omega }{\partial }_t^{\alpha }}{u}_{3,n}^{ϵ}{e}_{m}dx+{\displaystyle {\int }_{\Omega }{G}_{3,ϵ}}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ})e_{m}dx\\ ={\displaystyle {\int }_{\Omega }{r}_3}{u}_{3,n}^{ϵ}{e}_{m}dx,\\ {\displaystyle {\int }_{\Omega }{\partial }_t^{\alpha }}{u}_{4,n}^{ϵ}{e}_{m}dx+d_4(l(u_{4,n}^{ϵ})){\displaystyle {\int }_{Q_T}\nabla }{u}_{4,n}^{ϵ}\nabla e_{m}dx\\ ={\displaystyle {\int }_{\Omega }\xi }(u_{1,n}^{ϵ}+u_{2,n}^{ϵ}-u_{4,n}^{ϵ})e_{m}dx,& (2.8)\end{array}$

for all e_m ∈ S_n. Thus, we get

$\begin{array}{l}{}_0{}^{C}D{ }_t^{\alpha }{c}_{1,n,m}(t)=-d_1\left(l(u_{1,n}^{ϵ})\right){\displaystyle {\int }_{\Omega }\nabla }{u}_{1,n}^{ϵ}\nabla e_{m}dx\\ -{\displaystyle {\int }_{\Omega }{G}_{1,ϵ}}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})e_{m}dx+(1-\rho ){\displaystyle {\int }_{\Omega }{u}_{1,n}^{ϵ}}{e}_{m}dx,\\ =:F_1^m(t,\{c_{1,n,l}{\}}_{l=1}^n,\{c_{2,n,l}{\}}_{l=1}^n,\{c_{3,n,l}{\}}_{l=1}^n,\{c_{4,n,l}{\}}_{l=1}^n),\\ {}_0{}^{C}D{ }_t^{\alpha }{c}_{2,n,m}(t)=-d_2\left(l(u_{2,n}^{ϵ})\right){\displaystyle {\int }_{\Omega }\nabla }{u}_{2,n}^{ϵ}\nabla e_{m}dx\\ -{\displaystyle {\int }_{\Omega }{G}_{2,ϵ}}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})e_{m}dx+{\displaystyle {\int }_{\Omega }(r_2{u}_{2,n}^{ϵ}+\rho u_{1,n}^{ϵ})}{\varphi }_{2,n}dx,\\ =:F_2^m(t,\{c_{1,n,l}{\}}_{l=1}^n,\{c_{2,n,l}{\}}_{l=1}^n,\{c_{3,n,l}{\}}_{l=1}^n,\{c_{4,n,l}{\}}_{l=1}^n),\\ {}_0{}^{C}D{ }_t^{\alpha }{c}_{3,n,m}(t)=-{\displaystyle {\int }_{\Omega }{G}_{3,ϵ}}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ})e_{m}dx\\ +{\displaystyle {\int }_{\Omega }{r}_3}{u}_{3,n}^{ϵ}{e}_{m}dx,\\ =:F_3^m(t,\{c_{1,n,l}{\}}_{l=1}^n,\{c_{2,n,l}{\}}_{l=1}^n,\{c_{3,n,l}{\}}_{l=1}^n,\{c_{4,n,l}{\}}_{l=1}^n),\\ {}_0{}^{C}D{ }_t^{\alpha }{c}_{4,n,m}(t)=-d_4\left(l(u_{4,n}^{ϵ})\right){\displaystyle {\int }_{\Omega }\nabla }{u}_{4,n}^{ϵ}\nabla e_{m}dx+\\ {\displaystyle {\int }_{\Omega }\xi }(u_{1,n}^{ϵ}+u_{2,n}^{ϵ}-u_{4,n}^{ϵ})e_{m}dx,\\ =:F_4^m(t,\{c_{1,n,l}{\}}_{l=1}^n,\{c_{2,n,l}{\}}_{l=1}^n,\{c_{3,n,l}{\}}_{l=1}^n,\{c_{4,n,l}{\}}_{l=1}^n).& (2.9)\end{array}$

Further, it is east to see that all $F_j^m,j=1,2,3,4$ are continuous functions of c_j,n,l(t). From the Theorem 2.1, the system (2.9) has a local solution c_j,n,l(t), j = 1, 2, 3, 4 on some interval [0, t_n), 0 < t_n < T. The extension of these solutions to the whole interval [0, T] is a consequence of the following apriori estimates.

Lemma 2.5. Assume the hypothesis of Theorem 2.3. Then there exists a constant C > 0 is independent on n such that

$\begin{array}{ll}\begin{array}{l}\parallel (u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ}){\parallel }_{L^{\infty }(0,T;L^2(\Omega ))}\\ \le C, \parallel (u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{4,n}^{ϵ}){\parallel }_{L^2(0,T;H_0^1(\Omega ))}\le C,\\ \parallel G_{1,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})u_{1,n}^{ϵ}{\parallel }_{L^1(Q_T)}\\ +\parallel G_{2,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})u_{2,n}^{ϵ}{\parallel }_{L^1(Q_T)}\\ +\parallel G_{3,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ})u_{3,n}^{ϵ}{\parallel }_{L^1(Q_T)}\le C.\end{array}\}& (2.10)\end{array}$

Proof. Now, we set ${\displaystyle {\varphi }_{j,n}(x,t)=\sum _{l=1}^n{b}_{j,n,l}(t)e_l(x),j=1,2,3,4}$. the coefficients {b _{j, n, l}}, j = 1, 2, 3, 4. are absolutely continuous functions. Then, from (2.8), the Faedo-Galerkin approximation solution satisfy the following weak formulation

$\begin{array}{l}{\displaystyle {\int }_{\Omega }}{\partial }_t^{\alpha }{u}_{1,n}^{ϵ}{\varphi }_{1,n}dx+d_1\left(l(u_{1,n}^{ϵ})\right){\displaystyle {\int }_{\Omega }}\nabla u_{1,n}^{ϵ}\nabla {\varphi }_{1,n}dx\\ +{\displaystyle {\int }_{\Omega }}{G}_{1,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ}){\varphi }_{1,n}dx\\ =(1-\rho ){\displaystyle {\int }_{\Omega }}{u}_{1,n}^{ϵ}{\varphi }_{1,n}dx,\\ {\displaystyle {\int }_{\Omega }}{\partial }_t^{\alpha }{u}_{2,n}^{ϵ}{\varphi }_{2,n}dx+d_2\left(l(u_{2,n}^{ϵ})\right){\displaystyle {\int }_{\Omega }}\nabla u_{2,n}^{ϵ}\nabla {\varphi }_{2,n}dx\\ +{\displaystyle {\int }_{\Omega }}{G}_{2,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ}){\varphi }_{2,n}dx\\ ={\displaystyle {\int }_{\Omega }}(r_2{u}_{2,n}^{ϵ}+\rho u_{1,n}^{ϵ}){\varphi }_{2,n}dx,\\ {\displaystyle {\int }_{\Omega }}{\partial }_t^{\alpha }{u}_{3,n}^{ϵ}{\varphi }_{3,n}dx+{\displaystyle {\int }_{\Omega }}{G}_{3,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ}){\varphi }_{3,n}dx\\ ={\displaystyle {\int }_{\Omega }}{r}_3{u}_{3,n}^{ϵ}{\varphi }_{3,n}dx,\\ {\displaystyle {\int }_{\Omega }}{\partial }_t^{\alpha }{u}_{4,n}^{ϵ}{\varphi }_{4,n}dx+d_4\left(l(u_{4,n}^{ϵ})\right){\displaystyle {\int }_{Q_T}}\nabla u_{4,n}^{ϵ}\nabla {\varphi }_{4,n}dx\\ ={\displaystyle {\int }_{\Omega }}\xi (u_{1,n}^{ϵ}+u_{2,n}^{ϵ}-u_{4,n}^{ϵ}){\varphi }_{4,n}dx.& (2.11)\end{array}$

Choosing ${\varphi }_{j,n}=u_{j,n}^{ϵ},j=1,2,3,4,$, respectively, in the above system (2.11) and summing the resulting terms, we get

$\begin{array}{l}\frac{1}{2}{}_0{}^{C}D{ }_t^{\alpha }{\displaystyle {\int }_{\Omega }{\displaystyle \sum _{j=1}^4|}}{u}_{j,n}^{ϵ}{|}^{2}dx+{\displaystyle {\int }_{\Omega }(m_1|\nabla u_{1,n}^{ϵ}{|}^2+m_2|\nabla u_{2,n}^{ϵ}{|}^2+m_4|\nabla u_{4,n}^{ϵ}{|}^2)}dx\\ +{\displaystyle {\int }_{\Omega }{G}_{1,ϵ}}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})u_{1,n}^{ϵ}dx+{\displaystyle {\int }_{\Omega }{G}_{2,ϵ}}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})u_{2,n}^{ϵ}dx\\ +{\displaystyle {\int }_{\Omega }{G}_{3,ϵ}}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ})u_{3,n}^{ϵ}dx\le C{\displaystyle {\int }_{\Omega }{\displaystyle \sum _{j=1}^4|}}{u}_{j,n}^{ϵ}{|}^{2}dx,\end{array}$

where C is the positive constant which does not depend on n and t. Further, using the Lemma 2.3, we have,

$\begin{array}{ll}{\displaystyle {\int }_{\Omega }{\displaystyle \sum _{j=1}^4{|u_{j,n}^{ϵ}|}^2}}dx\le C,& (2.12)\end{array}$

for some positive constant C depending only on the given data and independent of n. From (2.12), we get

$\begin{array}{l}{\Vert (u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ})\Vert }_{L^{\infty }(0,T;L^2(\Omega ))}\le C,\\ {\Vert (u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{4,n}^{ϵ})\Vert }_{L^2(0,T;H_0^1(\Omega ))}\le C.& (2.13)\end{array}$

Using the results (2.12) and (2.13), we get

$\begin{array}{l}\parallel G_{1,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})u_{1,n}^{ϵ}{\parallel }_{L^1(Q_T)}\\ +\parallel G_{2,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})u_{2,n}^{ϵ}{\parallel }_{L^1(Q_T)}\\ +\parallel G_{3,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ})u_{3,n}^{ϵ}{\parallel }_{L^1(Q_T)}\le C.& (2.14)\end{array}$

Lemma 2.6. Assume the hypothesis of Theorem 2.3. Then $\left\{{ũ}_{1,n}^{ϵ},{ũ}_{2,n}^{ϵ},{ũ}_{4,n}^{ϵ}\right\}$ is bounded set of ${{W}}^{\alpha }(ℝ,H_0^1(\Omega ),L^2(\Omega ))$, where

$\begin{array}{ll}{\tilde{z}}_{ϵ,n}(x,t)=\{\begin{array}{ll}{z}_{ϵ,n}(x,t)\hfill & t\in [0,T],\hfill \\ 0\hfill & ℝ\backslash [0,T].\hfill \end{array}& (2.15)\end{array}$

Proof. In order to prove the result, Theorem 2.2 with Lemma 2.5, we have to show that

$\begin{array}{ll}{\displaystyle {\int }_{-\infty }^{\infty }}|\tau {|}^{2\gamma }|{\widehat{u}}_{j,n}^{ϵ}(\tau )|d\tau \le C,j=1,2,4,& (2.16)\end{array}$

for some γ > 0, where ${û}_{j,n}^{ϵ},j=1,2,4$ denote the Fourier transform of ${ũ}_{j,n}^{ϵ},j=1,2,4$.

Now, rewritten is defined as in (2.7),

$\begin{array}{ll}\begin{array}{l}({}_0{}^{C}D{ }_t^{\alpha }{\tilde{u}}_{1,n}^{ϵ},{\varphi }_j)=\langle {\tilde{F}}_1^n,{\varphi }_j\rangle +(u_{1,n}(0),{\varphi }_j)-\infty I_t^{1-\alpha }{\delta }_0\\ -(u_{1,n}(T),{\varphi }_j)-\infty I_t^{1-\alpha }{\delta }_T,\\ ({}_0{}^{C}D{ }_t^{\alpha }{\tilde{u}}_{2,n}^{ϵ},{\varphi }_j)=\langle {\tilde{F}}_2^n,{\varphi }_j\rangle +(u_{2,n}(0),{\varphi }_j)-\infty I_t^{1-\alpha }{\delta }_0\\ -(u_{2,n}(T),{\varphi }_j)-\infty I_t^{1-\alpha }{\delta }_T,\\ ({}_0{}^{C}D{ }_t^{\alpha }{\tilde{u}}_{4,n}^{ϵ},{\varphi }_j)=\langle {\tilde{F}}_4^n,{\varphi }_j\rangle +(u_{4,n}(0),{\varphi }_j)-\infty I_t^{1-\alpha }{\delta }_0\\ -(u_{4,n}(T),{\varphi }_j)-\infty I_t^{1-\alpha }{\delta }_T,\end{array}\}& (2.17)\end{array}$

where ${\tilde{F}}_i^n$ is defined as in (2.15),

$\begin{array}{l}{F}_1^n=d_1(l(u_1^{ϵ}))\Delta u_1^{ϵ}-G_{1,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ})+u_1^{ϵ}-\rho u_1^{ϵ},\\ F_2^n=d_2(l(u_2^{ϵ}))\Delta u_2^{ϵ}-G_{2,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ})+r_2{u}_2^{ϵ}+\rho u_1^{ϵ},\\ F_4^n=d_4(l(u_4^{ϵ}))\Delta u_4^{ϵ}+\xi (u_1^{ϵ}+u_2^{ϵ}-u_4^{ϵ}).\end{array}$

Here δ₀ and δ_T denote the Dirac distribution at 0 and T. Indeed, it is classical that since ũ_m has discontinuities at 0 and T, the Caputo derivatives of ũ_n is given by Zhou and Peng [12] and Zhou et al. [19]. Substitute ${\varphi }_{j,n}={û}_{j,n}^{ϵ}j=1,2,4,$, respectively, in (2.11), and using the Fourier transform, we get

$\begin{array}{ll}\begin{array}{l}{(2i\pi \tau )}^{\alpha }|{\widehat{u}}_{1,n}^{ϵ}(\tau ){|}^2=\langle {\widehat{F}}_1^n,{\widehat{u}}_{1,n}^{ϵ}\rangle +(u_{1,n}(0),{\widehat{u}}_{1,n}^{ϵ}(\tau )){(2i\pi \tau )}^{\alpha -1}\\ -(u_{1,n}(T),{\widehat{u}}_{1,n}^{ϵ}(\tau ))e^{-2i\pi T\tau },\\ {(2i\pi \tau )}^{\alpha }|{\widehat{u}}_{2,n}^{ϵ}(\tau ){|}^2=\langle {\widehat{F}}_2^n,{\widehat{u}}_{2,n}^{ϵ}\rangle +(u_{2,n}(0),{\widehat{u}}_{2,n}^{ϵ}(\tau )){(2i\pi \tau )}^{\alpha -1}\\ -(u_{2,n}(T),{\widehat{u}}_{2,n}^{ϵ}(\tau ))e^{-2i\pi T\tau },\\ {(2i\pi \tau )}^{\alpha }|{\widehat{u}}_{4,n}^{ϵ}(\tau ){|}^2=\langle {\widehat{F}}_4^n,{\widehat{u}}_{4,n}^{ϵ}\rangle +(u_{4,n}(0),{\widehat{u}}_{4,n}^{ϵ}(\tau )){(2i\pi \tau )}^{\alpha -1}\\ -(u_{4,n}(T),{\widehat{u}}_{4,n}^{ϵ}(\tau ))e^{-2i\pi T\tau }.\end{array}\}& (2.18)\end{array}$

It is obvious that the boundedness of solution shows that,

$\begin{array}{l}{\displaystyle \underset{\tau \in ℝ}{sup}}\parallel {\widehat{F}}_i^n(\tau ){\parallel }_{H^{-1}(\Omega )}\le C,\forall n,i=1,2,4,\end{array}$

where C > 0 is a positive constant. On account of $\left\{(u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{4,n}^{ϵ})\right\}$ is bounded set in L^∞(0, T; L²(Ω)), we get

$\begin{array}{l}\hfill (|u_{1,n}(0)|,|u_{2,n}(0)|,|u_{4,n}(0)|)\\ \le C\text{and }(|u_{1,n}(T)|,|u_{2,n}(T)|,|u_{4,n}(T)|)\le C,\end{array}$

and from (2.18), we get

$\begin{array}{l}\begin{array}{c}|\tau {|}^{\alpha }|{\widehat{u}}_{i,n}^{ϵ}(\tau ){|}^2\le C\text{ max}\left\{1,|\tau {|}^{\alpha -1}\right\}\parallel {\widehat{u}}_{i,n}^{ϵ}(\tau )|{\parallel }_{H_0^1(\Omega )},i=1,2,4.\end{array}\end{array}$

For γ fixed, $\gamma <\frac{\alpha }{4}$, we see that

$\begin{array}{l}|\tau {|}^{2\gamma }\le C(\gamma )\frac{1+|\tau {|}^{\alpha }}{1+|\tau {|}^{\alpha -2\gamma }}.\end{array}$

Accordingly

$\begin{array}{l}{\displaystyle {\int }_{-\infty }^{\infty }}|\tau {|}^{2\gamma }|{\widehat{u}}_{i,n}^{ϵ}(\tau ){|}^{2}d\tau \le C(\gamma ){\displaystyle {\int }_{-\infty }^{\infty }}\frac{1+|\tau {|}^{\alpha }}{1+|\tau {|}^{\alpha -2\gamma }}|{\widehat{u}}_{i,n}^{ϵ}{|}^{2}d\tau \\ \le C_1(\gamma ){\displaystyle {\int }_{-\infty }^{\infty }}\parallel {\widehat{u}}_{i,n}^{ϵ}{\parallel }_{H_0^1(\Omega )}^{2}d\tau \\ +C_2(\gamma ){\displaystyle {\int }_{-\infty }^{\infty }}\frac{|\tau {|}^{\alpha -1}\Vert {\widehat{u}}_{i,n}^{ϵ}(\tau ){\Vert }_{H_0^1(\Omega )}}{1+|\tau {|}^{\alpha -2\gamma }}d\tau .\end{array}$

Applying the Parseval identity, the first integral is bounded as n → ∞, and we have to prove that

$\begin{array}{ll}{\displaystyle {\int }_{-\infty }^{\infty }}\frac{|\tau {|}^{\alpha -1}\parallel {\widehat{u}}_{i,n}^{ϵ}(\tau ){\parallel }_{H_0^1(\Omega )}}{1+|\tau {|}^{\alpha -2\gamma }}d\tau \le C.& (2.19)\end{array}$

From the Schwarz inequality, we prove (2.19) as follows.

$\begin{array}{l}{\displaystyle {\int }_{-\infty }^{\infty }}\frac{|\tau {|}^{\alpha -1}\parallel {\widehat{u}}_{i,n}^{ϵ}(\tau ){\parallel }_{H_0^1(\Omega )}}{1+|\tau {|}^{\alpha -2\gamma }}d\tau \le {\left({\displaystyle {\int }_{-\infty }^{\infty }}\frac{d\tau }{{(1+|\tau {|}^{\alpha -2\gamma })}^2}\right)}^{\frac{1}{2}}\\ \left({\displaystyle {\int }_{-\infty }^{\infty }}|\tau {|}^{2\alpha -2}\parallel {\widehat{u}}_{i,n}^{ϵ}(\tau ){\parallel }_{H_0^1(\Omega )}^{2}d\tau \right),\end{array}$

the first integral is finite due to $\gamma <\frac{1}{4}$. On the other hand, it follows from the Parseval identity that

$\begin{array}{l}{{{\displaystyle \int }}^{\text{}}}_{-\infty }^{\infty }|\tau {|}^{2\alpha -2}{\Vert {\widehat{u}}_{i,n}^{ϵ}(\tau )\Vert }_{H_0^1(\Omega )}^{2}d\tau ={{{\displaystyle \int }}^{\text{}}}_{-\infty }^{\infty }{({\Vert {}_{-\infty }I{ }_t^{1-\alpha }{\tilde{u}}_{i,n}^{ϵ}(t)\Vert }_{ H_0^1(\Omega )})}^{2}dt\\ ={{{\displaystyle \int }}^{\text{}}}_0^T{\Vert { }_0{I}_t^{1-\alpha }{u}_{i,n}^{ϵ}(t)\Vert }_{H_0^1(\Omega )}^{2}dt\\ \le {\left(\frac{T^{1-\alpha }}{\Gamma (2-\alpha )}\right)}^2{{{\displaystyle \int }}^{\text{}}}_0^T{\Vert u_{i,n}^{ϵ}(t)\Vert }_{H_0^1(\Omega )}^{2}dt.\hfill \end{array}$

From the above integral, we understand that (2.19) is true. Thus, $\left\{{ũ}_{1,n}^{ϵ},{ũ}_{2,n}^{ϵ},{ũ}_{4,n}^{ϵ}\right\}$ is bounded set of ${{W}}^{\alpha }(ℝ,H_0^1(\Omega ),L^2(\Omega ))$.

Theorem 2.4. Suppose the hypotheses of Theorem 2.3 hold true, then the regularized system (2.7) possesses a weak solution $(u_1^{ϵ},u_2^{ϵ},u_3^{ϵ},u_4^{ϵ})$, which satisfies the following conditions:

$\begin{array}{l}{u}_1^{ϵ},u_2^{ϵ},u_4^{ϵ}\in L^{\infty }(0,T;L^2(\Omega ))\cap L^2(0,T;H_0^1(\Omega )),\\ u_3^{ϵ}\in L^{\infty }(0,T;L^2(\Omega )),\end{array}$

such that for every ${\varphi }_j\in L^2(0,T;H_0^1(\Omega )),j=1,2,3,4,$

$\begin{array}{l}{\int }_0^T{\partial }_t^{\alpha }(u_1^{ϵ},{\varphi }_1)dt+d_1\left({\int }_{\Omega }{u}_1^{ϵ}dx\right){\int }_{Q_T}\nabla u_1^{ϵ}\nabla {\varphi }_{1}dxdt\\ +{\int }_{Q_T}{G}_{1,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ}){\varphi }_{1}dxdt=(1-\rho ){\int }_{Q_T}{u}_1^{ϵ}{\varphi }_{1}dxdt,\\ {\int }_0^T{\partial }_t^{\alpha }(u_2^{ϵ},{\varphi }_2)dt+d_2\left({\int }_{\Omega }{u}_2^{ϵ}dx\right){\int }_{Q_T}\nabla u_2^{ϵ}\nabla {\varphi }_{2}dxdt\\ +{\int }_{Q_T}{G}_{2,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ}){\varphi }_{2}dxdt={\int }_{Q_T}(r_2{u}_2^{ϵ}+\rho u_1^{ϵ}){\varphi }_{2}dxdt,\\ {\int }_0^T{\partial }_t^{\alpha }(u_3^{ϵ},{\varphi }_3)dt+{\int }_{Q_T}{G}_3(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ},u_4^{ϵ}){\varphi }_{3}dxdt\\ ={\int }_{Q_T}{r}_3{u}_3^{ϵ}{\varphi }_{3}dxdt,\\ {\int }_0^T{\partial }_t^{\alpha }(u_4^{ϵ},{\varphi }_4)dt+d_4\left({\int }_{\Omega }{u}_4^{ϵ}dx\right){\int }_{Q_T}\nabla u_4^{ϵ}\nabla {\varphi }_{4}dxdt\\ ={\int }_{Q_T}\xi (u_1^{ϵ}+u_2^{ϵ}-u_4^{ϵ}){\varphi }_{4}dxdt.\end{array}$

Proof. By Lemma 2.5, Lemma 2.6 and Theorem 2.2, we can extract the subsequences of $(u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ})$ such that as n → ∞, we get

$\begin{array}{l}(u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ},u_{4,n}^{ϵ})\rightharpoonup (u_1^{ϵ},u_2^{ϵ},u_3^{ϵ},u_4^{ϵ})\text{weak }\ast \text{ in }{L}^{\infty }(0,T;L^2(\Omega )),\\ (u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{4,n}^{ϵ})\rightharpoonup (u_1^{ϵ},u_2^{ϵ},u_4^{ϵ})\text{weakly in }{L}^2(0,T;H_0^1(\Omega )).\end{array}$

It is enough, we show that

$d_j(l(u_{j,n}^{ϵ}))\to d_j(l(u_j^{ϵ}))\text{in }{L}^2(0,T),\forall T>0,j=1,2,4.$

Since d_j is continuous functions, it is enough to show that

$l(u_{j,n}^{ϵ})\to l(u_j^{ϵ})\text{strongly in }{L}^2(0,T).$

Now,

${\displaystyle {\int }_0^T}|l(u_{j,n}^{ϵ})-l(u_j^{ϵ}){|}^{2}dt={\displaystyle {\int }_0^T}|l(u_{j,n}^{ϵ}-u_j^{ϵ}){|}^{2}dt\le C{\displaystyle {\int }_0^T}|u_{j,n}^{ϵ}-u_j^{ϵ}{|}^{2}dt.$

This result concludes that

$d_j(l(u_{j,n}^{ϵ}))\to d_j(l(u_j^{ϵ}))\text{in }{L}^2(0,T),\forall T>0,j=1,2,4.$

Substitute ϕ_1,n = v and integrate the first equation of (2.11) from 0 to t and 0 to t₀, respectively. Then, subtract the resulting equation, we get

$\begin{array}{l}(u_{1,n}^{ϵ}(t_0),v)-(u_{1,n}^{ϵ}(t),v)\\ ={\displaystyle {\int }_0^{t_0}{(t_0-s)}^{\alpha -1}}-(t-s{)}^{\alpha -1}((d_1(l(u_{1,n}^{ϵ}))\nabla u_{1,n}^{ϵ},\nabla v)\\ +(G_{1,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})-(1-\rho )u_{1,n}^{ϵ},v)ds\\ -{\displaystyle {\int }_0^{t_0}{(t-s)}^{\alpha -1}}((d_1(l(u_{1,n}^{ϵ}))\nabla u_{1,n}^{ϵ},\nabla v)\\ +(G_{1,ϵ}(x,t,u_{1,n}^{ϵ},u_{2,n}^{ϵ},u_{3,n}^{ϵ})-(1-\rho )u_{1,n}^{ϵ},v)ds.\end{array}$

Using the Lemma 2.6 and the Lebesgue dominated convergence theorem, we can prove that $(u_1^{ϵ}(t),v)-(u_1^{ϵ}(t_0),v)\to 0$ as t → t₀ as in Zhou and Peng [12] and Zhou et al. [19]. Similarly, it can be show that $(u_2^{ϵ}(t),v)-(u_2^{ϵ}(t_0),v)\to 0$ as t → t₀, $(u_3^{ϵ}(t),v)-(u_3^{ϵ}(t_0),v)\to 0$ as t → t₀ and $(u_4^{ϵ}(t),v)-(u_4^{ϵ}(t_0),v)\to 0$ as t → t₀.

Now, we prove the Theorem 2.3 and some priori estimates and compactness results.

Lemma 2.7. Assume that the assumptions of Theorem 2.3 are satisfied, then

$\begin{array}{ll}\begin{array}{l}\Vert u_1^{ϵ},u_2^{ϵ},u_3^{ϵ},u_4^{ϵ}{\Vert }_{L^{\infty }(0,T;L^2(\Omega ))}\le C,\Vert u_1^{ϵ},u_2^{ϵ},u_4^{ϵ}{\Vert }_{L^2(0,T;H_0^1(\Omega ))}\le C,\\ \Vert G_{1,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ})u_1^{ϵ}{\Vert }_{L^1(Q_T)}+\Vert G_{2,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ})u_2^{ϵ}{\Vert }_{L^1(Q_T)}\\ +\Vert G_{3,ϵ}(x,t,u_1^{ϵ},u_2^{ϵ},u_3^{ϵ},u_4^{ϵ})u_3^{ϵ}{\Vert }_{L^1(Q_T)}\le C.\end{array}\}& (2.20)\end{array}$

Proof. Let us presume $u_j^{-ϵ}=sup(0,-u_j^{ϵ}),j=1,2,3,4$. Multiplying the first equation (2.7) by $u_1^{-ϵ}$and integrating over Ω, we get

$\begin{array}{l}\frac{1}{2}{}_0{}^{C}D{ }_t^{\alpha }{{{\displaystyle \int }}^{\text{}}}_{\Omega }|u_1^{-ϵ}{|}^{2}dx+m_1{{{\displaystyle \int }}^{\text{}}}_{\Omega }|\nabla u_1^{-ϵ}{|}^{2}dx\\ +{{{\displaystyle \int }}^{\text{}}}_{\Omega }{G}_{1,ϵ}(x,t,u_1^{-ϵ},u_2^{-ϵ},u_3^{-ϵ})u_1^{-ϵ}dxleq{{{\displaystyle \int }}^{\text{}}}_{\Omega }(1-\rho )|u_1^{-ϵ}{|}^{2}dx.\end{array}$

Using the assumptions of the given data, we get

$\frac{1}{2}{}_0{}^{C}D{ }_t^{\alpha }\underset{\Omega }{{{\displaystyle \int }}^{\text{}}}|u_1^{-ϵ}{|}^{2}dx\le 0.$

This concludes that the solution $u_1^{ϵ}$ is a nonnegative solution. Similarly, we can claim that solution $u_2^{ϵ},u_3^{ϵ},u_4^{ϵ}$ are nonnegative. We prove (2.20) as in Lemma 2.5, by replacing $u_{i,n}^{ϵ}$ by $u_j^{ϵ},j=1,2,3,4.$

Lemma 2.8. Assume the hypothesis of Theorem 2.3 are hold true. Then $\left\{{ũ}_1^{ϵ},{ũ}_2^{ϵ},{ũ}_4^{ϵ}\right\}$ is bounded set of ${{W}}^{\alpha }(ℝ,H_0^1(\Omega ),L^2(\Omega ))$, where

${\tilde{z}}_{ϵ}(x,t)=\{\begin{array}{cc}{z}_{ϵ}(x,t)& t\in [0,T],\\ 0\hfill & ℝ\backslash [0,T].\end{array}$

Proof. As similar as proof of the Lemma 2.6.

Proof of Theorem 2.3: From Lemma 2.7, Lemma 2.8 and Theorem 2.2, we understand that sequences have convergent subsequences which are still denoted by $(u_1^{ϵ},u_2^{ϵ},u_3^{ϵ},u_4^{ϵ})$. Then there exists (u₁, u₂, u₃, u₄) as n → ∞, we get

$\begin{array}{l}(u_1^{ϵ},u_2^{ϵ},u_3^{ϵ},u_4^{ϵ})\rightharpoonup (u_1,u_2,u_3,u_4)\text{weak }*\text{ in }{L}^{\infty }(0,T;L^2(\Omega )),\\ (u_1^{ϵ},u_2^{ϵ},u_4^{ϵ})\rightharpoonup (u_1,u_2,u_4)\text{weakly in }{L}^2(0,T;H_0^1(\Omega )).\end{array}$

This concludes the proof of the Theorem 2.3.

Theorem 2.5. The solution (u₁, u₂, u₃, u₄) of system (1.1) is unique.

Proof. Let (v₁, v₂, v₃, v₄) and (ṽ₁, ṽ₂, ṽ₃, ṽ₄) be any two solutions of (1.1). Now, we consider u_i = v_i − ṽ _i, i = 1, 2, 3, 4 and choose ϕ_i = u_i, i = 1, 2, 3, 4 in (2.6), we get

$\begin{array}{l}\frac{1}{2}{}_0{}^{C}D{ }_t^{\alpha }{\displaystyle {\int }_{\Omega }{|u_1(x,t)|}^{2}dx}+{\displaystyle {\int }_{\Omega }(d_1(l(v_1))\nabla v_1}\\ -d_1(l({\tilde{v}}_1)\nabla {\tilde{v}}_1))\nabla u_{1}dx+{\displaystyle {\int }_{\Omega }(G_1(}x,t,v_1,v_2,v_3)\\ -G_1(x,t,{\tilde{v}}_1,{\tilde{v}}_2,{\tilde{v}}_3))u_{1}dx\le (1-\rho ){\displaystyle {\int }_{\Omega }{|u_1|}^2}dx,\\ \frac{1}{2}{}_0{}^{C}D{ }_t^{\alpha }{\displaystyle {\int }_{\Omega }{|u_2(x,t)|}^{2}dx}+{\displaystyle {\int }_{\Omega }(d_2(l(v_2))\nabla v_2}\\ -d_2(l({\tilde{v}}_2)\nabla {\tilde{v}}_2))\nabla u_{2}dx+{\displaystyle {\int }_{\Omega }(G_2(}x,t,v_1,v_2,v_3)\\ -G_1(x,t,{\tilde{v}}_1,{\tilde{v}}_2,{\tilde{v}}_3))u_{1}dx\\ \le r_2{\displaystyle {\int }_{\Omega }{|u_2|}^2}dx+\rho {\displaystyle {\int }_{\Omega }{u}_1{u}_{2}dx,}\\ \frac{1}{2}{}_0{}^{C}D{ }_t^{\alpha }{\displaystyle {\int }_{\Omega }{|u_3(x,t)|}^{2}dx}+{\displaystyle {\int }_{\Omega }(G_3(}x,t,v_1,v_2,v_3,v_4)\\ -G_1(x,t,{\tilde{v}}_1,{\tilde{v}}_2,{\tilde{v}}_3,{\tilde{v}}_4))u_{3}dx\le r_3{\displaystyle {\int }_{\Omega }{|u_3|}^2}dx,\\ \frac{1}{2}{}_0{}^{C}D{ }_t^{\alpha }{\displaystyle {\int }_{\Omega }{|u_2(x,t)|}^{2}dx}+{\displaystyle {\int }_{\Omega }(d_4(l(v_4))\nabla v_4}\\ -d_2(l({\tilde{v}}_4)\nabla {\tilde{v}}_4))\nabla u_{4}dx\\ \le \xi {\displaystyle {\int }_{\Omega }(u_1+u_2-u_4)}{u}_{4}dx.\end{array}$

Using the Lipschitz assumptions of d_i, i = 1, 2, 4, the non-negativity and boundedness of solutions of (2.7) with the Young inequality, we obtain

$\begin{array}{l}\frac{1}{2}{{\displaystyle \int }}_{\Omega }|u_1(x,t){|}^{2}dx\le \frac{1}{2}{{\displaystyle \int }}_{\Omega }|u_1(x,0){|}^{2}dx\\ +\frac{C}{\Gamma (\alpha )}\left({{\displaystyle \int }}_{Q_t}{(t-s)}^{\alpha -1}(|u_1{|}^2+|u_2{|}^2+|u_3{|}^2+|u_4{|}^2)dxds\right),\\ \frac{1}{2}{{\displaystyle \int }}_{\Omega }|u_2(x,t){|}^{2}dx\le \frac{1}{2}{{\displaystyle \int }}_{\Omega }|u_2(x,0){|}^{2}dx\\ +\frac{C}{\Gamma (\alpha )}\left({{\displaystyle \int }}_{Q_t}{(t-s)}^{\alpha -1}(|u_1{|}^2+|u_2{|}^2+|u_3{|}^2+|u_4{|}^2)dxds\right),\\ \frac{1}{2}{{\displaystyle \int }}_{\Omega }|u_3(x,t){|}^{2}dx\le \frac{1}{2}{{\displaystyle \int }}_{\Omega }|u_3(x,0){|}^{2}dx\\ +\frac{C}{\Gamma (\alpha )}\left({{\displaystyle \int }}_{Q_t}{(t-s)}^{\alpha -1}(|u_1{|}^2+|u_2{|}^2+|u_3{|}^2+|u_4{|}^2)dxds\right),\\ \frac{1}{2}{{\displaystyle \int }}_{\Omega }|u_4(x,t){|}^{2}dx\le \frac{1}{2}{{\displaystyle \int }}_{\Omega }|u_4(x,0){|}^{2}dx\\ +\frac{C}{\Gamma (\alpha )}\left({{\displaystyle \int }}_{Q_t}{(t-s)}^{\alpha -1}(|u_1{|}^2+|u_2{|}^2+|u_3{|}^2+|u_4{|}^2)dxds\right).\end{array}$

Summing up the above inequalities and using the Lemma 2.3, we get

${\displaystyle {\int }_{\Omega }{\displaystyle \sum _{j=1}^4{u}_j}}|u_j(x,t){|}^{2}dx\le {\displaystyle {\int }_{\Omega }{\displaystyle \sum _{j=1}^4|u_j(x,0){|}^2}}dx{E}_{\alpha }[C{t}^{\alpha }].$

This concludes the proof of the theorem.

3. Finite Element Scheme

In this section, we present a finite element scheme for the considered model (1.1). Here, first we present a weak formulation for time-fractional cancer invasion system (1.1), where the time-fractional derivative is the Caputo derivative. Further, the spatial and temporal discretization are presented. Furthermore, an iteration fixed point type is proposed to handle the nonlinear terms of the system as in Ganesan and Shangerganesh [52, 53] and Ganesan and Tobiska [54].

3.1. Finite Element Semi-discretization

Let ${{T}}_h$ be a partition of Ω into non overlapping triangles $T_k\in {{T}}_h$ cells, and use the piecewise linear (P1) finite elements on each cell. Now, let V_h ⊂ V be a conforming finite element subspace of V with basis function ${\left\{{\varphi }_k\right\}}_{k=1}^{{N}}$ such that V_h = span{ϕ_k}, where ${N}$ is the number of degrees of freedom. Then the semidiscrete problem, based on (2.6) is to find a solution w_h ∈ V_h such that for a.e t ∈ (0, T), for all ψ ∈ V_h

$\begin{array}{ll}({\partial }_t^{\alpha }{w}_h,\psi )+{B}(w_h,\psi )={F}(w_h,\psi ),& (3.1)\end{array}$

where ${B}(w_h,\psi )=\left(\begin{array}{l}{b}_{u_1}(u_{1,h};u_{1,h};u_{2,h};u_{3,h},{\psi }_1)\\ b_{u_2}(u_{2,h};u_{1,h};u_{2,h};u_{3,h},{\psi }_2)\\ b_{u_3}(u_{3,h};u_{1,h};u_{2,h};u_{3,h};u_{4,h},{\psi }_3)\\ b_{u_4}(u_{4,h};u_{4,h},{\psi }_4)\end{array}\right)$ & ${F}(w_h,\psi )=\left(\begin{array}{l}0\\ f_1(u_{1,h},{\psi }_2)\\ 0\\ f_2(u_{1,h},u_{2,h},{\psi }_4)\end{array}\right).$

Further,

$\begin{array}{l}{b}_{u_1}(u_{1,h};u_{1,h};u_{2,h};u_{3,h},{\psi }_1)={\displaystyle {\int }_{\Omega }{d}_1}\left(l(u_{1,h})\right)\nabla u_{1,h}\nabla {\psi }_{1}dx\\ +{\displaystyle {\int }_{\Omega }{u}_{1,h}}(u_{1,h}+{\beta }_1{u}_{2,h}\\ +\rho +{\gamma }_1{u}_{3,h}-1){\psi }_{1}dx,\\ b_{u_2}(u_{2,h};u_{1,h};u_{2,h};u_{3,h},{\psi }_2)={\displaystyle {\int }_{\Omega }{d}_2}\left(l(u_{2,h})\right)\nabla u_{2,h}\nabla {\psi }_{2}dx\\ +{\displaystyle {\int }_{\Omega }{u}_{2,h}}(r_2{u}_{2,h}+{\beta }_2{u}_{1,h}\\ +{\delta }_1{u}_{3,h}-r_2){\psi }_{2}dx,\\ b_{u_3}(u_{3,h};u_{1,h};u_{2,h};u_{3,h};u_{4,h},{\psi }_3)={\displaystyle {\int }_{\Omega }{u}_{3,h}}(r_3{u}_{3,h}+{\gamma }_2{u}_{1,h}\\ +{\delta }_2{u}_{2,h}+\sigma u_{4,h}-r_3){\psi }_{3}dx,\\ b_{u_4}(u_{4,h};u_{1,h};u_{2,h};u_{4,h},{\psi }_4)={\displaystyle {\int }_{\Omega }{d}_4}\left(l(u_{4,h})\right)\nabla u_{4,h}\nabla {\psi }_{4}dx\\ +{\displaystyle {\int }_{\Omega }\xi }{u}_{4,h}{\psi }_{4}dx,\\ f_1(u_{1,h},{\psi }_2)={\displaystyle {\int }_{\Omega }\rho u_{1,h}{\psi }_{2}dx,f_2(u_{1,h},u_{2,h},{\psi }_4)}\text{}\\ ={\displaystyle {\int }_{\Omega }\xi (u_{1,h}+u_{2,h}){\psi }_{4}dx.}\end{array}$

Furthermore, using the basis ${\left\{{\varphi }_k\right\}}_{k=1}^{{N}}$, we describe the discrete solution w_h ∈ V_h, in terms of the basis of V_h as

$u_{j,h}={\displaystyle \sum _{k=1}^{{N}}}{u}_{j,k}(t){\varphi }_k(x),j=1,2,3,4,$

where u_j,k(t), j = 1, 2, 3, 4, t ∈ [0, T], are the unknown coefficients to be determined. Thus, we have

$\begin{array}{ll}{{M}}_0^C{D}_t^{\alpha }\omega (t)+{A}\omega =F,& (3.2)\end{array}$

where $\omega =(u_{1,1},u_{2,2},\dots ,u_{1,{N}},u_{2,1},u_{2,2},\dots ,u_{2,{N}},u_{3,1},u_{3,2},\dots ,u_{3,{N}},u_{4,1},u_{4,2},\dots ,u_{4,{N}})$ is unknown vector. Further, mass matrix M, stiffness matrices A and known vectors F₁, F₂ are given by

$\begin{array}{l}{M}=\left[\begin{array}{llll}M\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & M\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & M\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & M\hfill \end{array}\right],(M{)}_{\mathfrak{p}\mathfrak{q}}={\displaystyle {\int }_{{{T}}_h}{\varphi }_{\mathfrak{p}}}(x){\varphi }_{\mathfrak{q}}(x),\\ {A}=\left[\begin{array}{l}{A}^{(U_1)}\hfill \\ A^{(U_2)}\hfill \\ A^{(U_3)}\hfill \\ A^{(U_4)}\hfill \end{array}\right],\\ (A^{(U_1)}{)}_{\mathfrak{p}\mathfrak{q}}={\displaystyle {\int }_{{{T}}_h}{d}_1}\left(l\left({\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{1,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)\right)\right)\nabla {\varphi }_{\mathfrak{p}}(x)\nabla {\varphi }_{\mathfrak{q}}(x)dx\\ +{\displaystyle {\int }_{{{T}}_h}({\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{1,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)+{\beta }_1{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{2,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)}\\ +\rho +{\gamma }_1{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{3,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)-1){\varphi }_{\mathfrak{p}}(x){\varphi }_{\mathfrak{q}}(x)dx,\\ (A^{(U_2)}{)}_{\mathfrak{p}\mathfrak{q}}={\displaystyle {\int }_{{{T}}_h}{d}_2}\left(l\left({\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{2,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)\right)\right)\\ \nabla {\varphi }_{\mathfrak{p}}(x)\nabla {\varphi }_{\mathfrak{q}}(x)dx\\ +{\displaystyle {\int }_{{{T}}_h}(r_2{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{2,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)+{\beta }_2{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{1,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)}\\ +{\delta }_1{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{3,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)-r_2){\varphi }_{\mathfrak{p}}(x){\varphi }_{\mathfrak{q}}(x)dx,\\ (A^{(U_3)}{)}_{\mathfrak{p}\mathfrak{q}}={\displaystyle {\int }_{{{T}}_h}(r_3{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{3,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)+}\\ {\gamma }_2{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{1,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)+{\delta }_2{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{2,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)\\ +\sigma {\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{4,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)-r_3){\varphi }_{\mathfrak{p}}(x){\varphi }_{\mathfrak{q}}(x)dx,\\ (A^{(U_4)}{)}_{\mathfrak{p}\mathfrak{q}}={\displaystyle {\int }_{{{T}}_h}{d}_1}\left(l\left({\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{4,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x)\right)\right)\\ \nabla {\varphi }_{\mathfrak{p}}(x)\nabla {\varphi }_{\mathfrak{q}}(x)dx,\\ F=\left[\begin{array}{l}0\hfill \\ F_1\hfill \\ 0\hfill \\ F_2\hfill \end{array}\right],(F_1)={\displaystyle {\int }_{{{T}}_h}\rho }{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{1,\mathfrak{k}}}(t){\varphi }_k(x){\varphi }_{\mathfrak{q}}(x)dx,\\ (F_2)={\displaystyle {\int }_{{{T}}_h}\xi }({\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{1,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x){\varphi }_{\mathfrak{q}}(x)\\ +{\displaystyle \sum _{\mathfrak{k}=1}^{{N}}{u}_{2,\mathfrak{k}}}(t){\varphi }_{\mathfrak{k}}(x){\varphi }_{\mathfrak{q}}(x))dx.\end{array}$

The system (3.2) is a FODE system. Solvability of (3.2) can be achieved as in Theorem 2.3 and Theorem 2.5.

3.1.1. Temporal Discretization and Linearization

We present now the time discretization of (3.2). Let 0 = t₀ < t₁ < t₂ < ··· < t_𝔑 = T be a decomposition of the considered time interval [0, T] and δ_t = t_𝔯 − t_𝔯−1, 𝔯 = 1, 2, 3, …, 𝔑 represents the uniform time step. We discretize the Caputo fractional time derivative be using finite difference scheme as in Lin and Xu [55] and Sun and Wu [56]. The approximation is given by

$\begin{array}{ll}{\partial }_t^{\alpha }u(x,t_{𝔯})=\frac{{\delta }_t^{-\alpha }}{\Gamma (2-\alpha )}{\displaystyle \sum _{𝔩=0}^{𝔯}}{a}_{𝔩}(u(x,t_{𝔯+1-𝔩})-u(x,t_{𝔯-𝔩})),& (3.3)\end{array}$

$a_{𝔩}={(𝔩+1)}^{\alpha -1}-{(𝔩)}^{\alpha -1},𝔩=1,2,3,\dots ,𝔯.$

Substitute (3.3) in (3.1), we have

$\begin{array}{ll}\left(\frac{{\delta }_t^{-\alpha }}{\Gamma (2-\alpha )}{\displaystyle \sum _{𝔩=0}^{𝔯}}{a}_{𝔩} {(w}_{𝔯+1-𝔩}-w_{𝔯-𝔩} ),\varphi \right)+{B}(w_{𝔯+1},\varphi )={F}(w_{𝔯+1},\varphi ),& (3.4)\end{array}$

where $a_{𝔩}={(𝔩+1)}^{\alpha -1}-{(𝔩)}^{\alpha -1}$, 𝔯 = 1, 2, 3, …, 𝔑 and ψ ∈ V. Moreover, we use fixed point iteration technique to control the nonlinear terms of the given system. Initiate with $u_{j,n+1}^0=u_{j,n},j=1,2,3,4$, then the nonlinear terms in (3.4) can be written as

$\begin{array}{l}{b}_{u_1}(u_{1,𝔯+1}^{𝔪};u_{1,n+1}^{𝔪};u_{2,𝔯+1}^{𝔪};u_{3,𝔯+1}^{𝔪},\varphi )\simeq b_{u_1}\\ (u_{1,𝔯+1}^{𝔪};u_{1,𝔯+1}^{𝔪-1};u_{2,𝔯+1}^{𝔪-1};u_{3,𝔯+1}^{𝔪-1},\varphi ),\\ b_{u_2}(u_{2,𝔯+1}^{𝔪};u_{1,𝔯+1}^{𝔪};u_{2,𝔯+1}^{𝔪};u_{3,𝔯+1}^{𝔪},\varphi )\simeq b_{u_2}\\ (u_{1,𝔯+1}^{𝔪};u_{1,𝔯+1}^{𝔪-1};u_{2,𝔯+1}^{𝔪-1};u_{3,𝔯+1}^{𝔪-1},\varphi ),\\ b_{u_3}(u_{3,𝔯+1}^{𝔪};u_{1,𝔯+1}^{𝔪};u_{2,𝔯+1}^{𝔪};u_{3,𝔯+1}^{𝔪};u_{3,𝔯+1}^{𝔪},\varphi )\simeq b_{u_3}\\ (u_{3,𝔯+1}^{𝔪};u_{1,𝔯+1}^{𝔪-1};u_{2,𝔯+1}^{𝔪-1};u_{3,𝔯+1}^{𝔪-1};u_{4,𝔯+1}^{𝔪-1},\varphi ),\end{array}$

for 𝔪 = 1, 2, 3, …. In addition, we iterate until the residual is less than the prescribed threshold value (10⁻¹⁰) or the given maximal number of iterations is reached. In computations, the fixed point iteration converges within six or seven iterations for the prescribed residual value. Furthermore, the number of fixed point iteration increases when δ_t is increased.

4. Numerical Experiment

In this section, we perform series of numerical computations to understand the impact of α in cancer invasion system. Here, all numerical computations are performed in the unit square domain Ω = [0, 1] × [0, 1]. We used Freefem++ [57] for finite element scheme and UMFPACK [58, 59] is used to solve the resulting algebraic system. All computations are carried out by using Intel (R) Core (TM) i7-7700 CPU with 3.60GHz and 8 GB RAM.

4.1. Convergence Study

We consider the cancer invasion model (2.5)

$\begin{array}{ll}\begin{array}{c}{\partial }_t^{\alpha }{u}_1-d_1(l(u_1))\Delta u_1-u_1(1-u_1)+{\beta }_1{u}_1{u}_2+\rho u_1+{\gamma }_1{u}_1{u}_3=f_{u_1},\hfill \\ {\partial }_t^{\alpha }{u}_2-d_2(l(u_2))\Delta u_2-r_2{u}_2(1-u_2)+{\beta }_2{u}_1{u}_2-\rho u_1+{\delta }_1{u}_2{u}_3=f_{u_2},\hfill \\ {\partial }_t^{\alpha }{u}_3-r_3{u}_3(1-u_3)+{\gamma }_2{u}_1{u}_3+{\delta }_2{u}_2{u}_3+\sigma u_3{u}_4=f_{u_3},\hfill \\ {\partial }_t^{\alpha }{u}_4-d_4(l(u_4))\Delta u_4-\xi (u_1+u_2-u_4)=f_{u_4},\hfill \end{array}\}& (4.1)\end{array}$

where f_u1, f_u2, f_u3, and f_u4 are forcing terms. They are chosen such that following smooth solutions are satisfies (4.1).

$\begin{array}{lll}\hfill u_1& =\hfill & (1+t^2)((x-x^2)(y-y^2)),\hfill \\ \hfill u_2& =\hfill & (1+t)((x-x^2)(y-y^2)),\hfill \\ \hfill u_3& =\hfill & (1+3t^2)((x-x^2)(y-y^2)),\hfill \\ \hfill u_4& =\hfill & (1+t^2)((x-x^2)(y-y^2)).\hfill \end{array}$

Moreover, we fixed d_i(l(u_i)) = D_i sin (l(u_i)) where $l(u)={{\displaystyle \int }}_{\Omega }udx.$ Further all other parameters of the model are chosen as

$\begin{array}{l}\hfill D_1=0.0035,D_2=0.035,D_4=0.0002,\\ \hfill {\beta }_1=0.0015,{\beta }_2=0.0015,{\gamma }_1=0.0015,{\gamma }_2=0.003,\\ \hfill r_2=0.0012,r_3=0.001,\\ \hfill \xi =0.1,{\delta }_1=0.25,{\delta }_2=0.35,\rho =0.0015,\sigma =0.001.\end{array}$

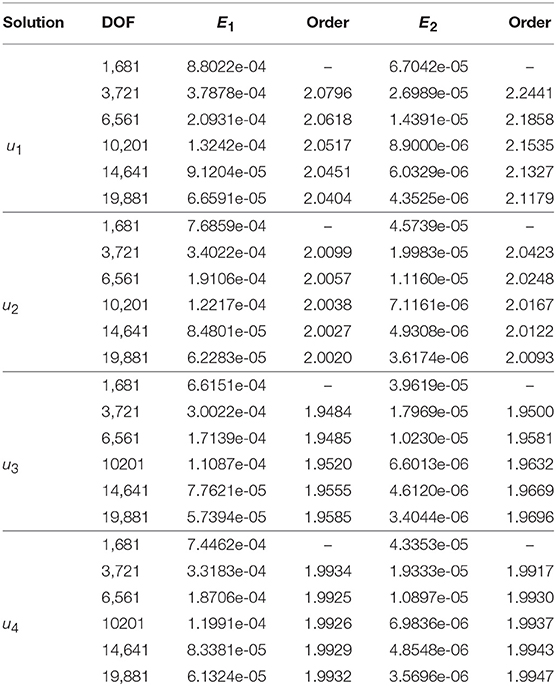
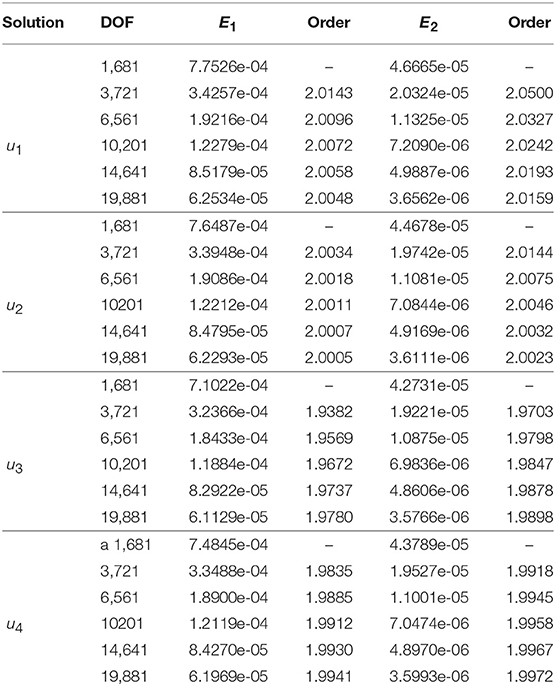
A set of finite element computations on uniformly refined meshes with ${\delta }_t=h^{\frac{2}{2-\alpha }}$ are performed. In order to compare the discretization errors at different mesh levels and verify the order of convergence of numerical scheme, the following errors are computed for each unknowns u_j, j = 1, ··· , 4 of the system.

$\begin{array}{l}{E}_1:=L^2(0,T;L^2(\Omega ))={\left({\displaystyle {\int }_0^T}\left({\Vert u(t)-u_h(t)\Vert }_{L^2(\Omega )}^2\right)dt\right)}^{\frac{1}{2}},\\ E_2:=L^{\infty }(0,T;L^2(\Omega ))=\underset{i=1,2,3,\dots ,n}{\sup }{\Vert u(t^i)-u_h(t^i)\Vert }_{L^2(\Omega )}.\end{array}$

First, for α = 0.4 then the obtained numerical errors and corresponding convergence rates are depicted in Table 1. Then, for α = 0.7 obtained results are shown in Table 2. Tables 1, 2 clearly shows that existence of second order convergence for the errors E₁ and E₂, respectively, for all unknowns of the system.

TABLE 1

Table 1. Errors and order of convergence when α = 0.4.

TABLE 2

Table 2. Errors and order of convergence when α = 0.7.

4.2. Numerical Results and Discussion

We understand the influence of fractional derivative on cancer invasion system (1.1) by performing numerical simulations with different values of α. All computations are performed until at end time T = 20. Further, uniform time step size δ_t is taken as 0.1. We discretize the unit square domain using triangular elements with characteristic element length 140 × 140 and a uniform mesh size h = 0.0101015. We used 19881 degrees of freedom for each unknown in all computations with total 79,524 degrees of freedom. We assumed the homogeneous Dirichlet boundary conditions for all unknowns with the following initial conditions.

$\begin{array}{l}{u}_1(x,0)=1.01exp\left(\frac{-{(x-0.5)}^2-{(y-0.5)}^2}{{ϵ}_1}\right),u_2(x,0)=0,\hfill \\ u_3(x,0)=1-0.99exp\left(\frac{-{(x-0.5)}^2-{(y-0.5)}^2}{{ϵ}_1}\right),\hfill \\ u_4(x,0)=1.01exp\left(\frac{-{(x-0.5)}^2-{(y-0.5)}^2}{{ϵ}_2}\right),\hfill \end{array}$

where ϵ₁ = 0.005, and ϵ₂ = 0.075. We performed simulations for α = 0.1, 0.4, 0.7, 1 and all other parameters are taken of the model of the previous section 4.1.

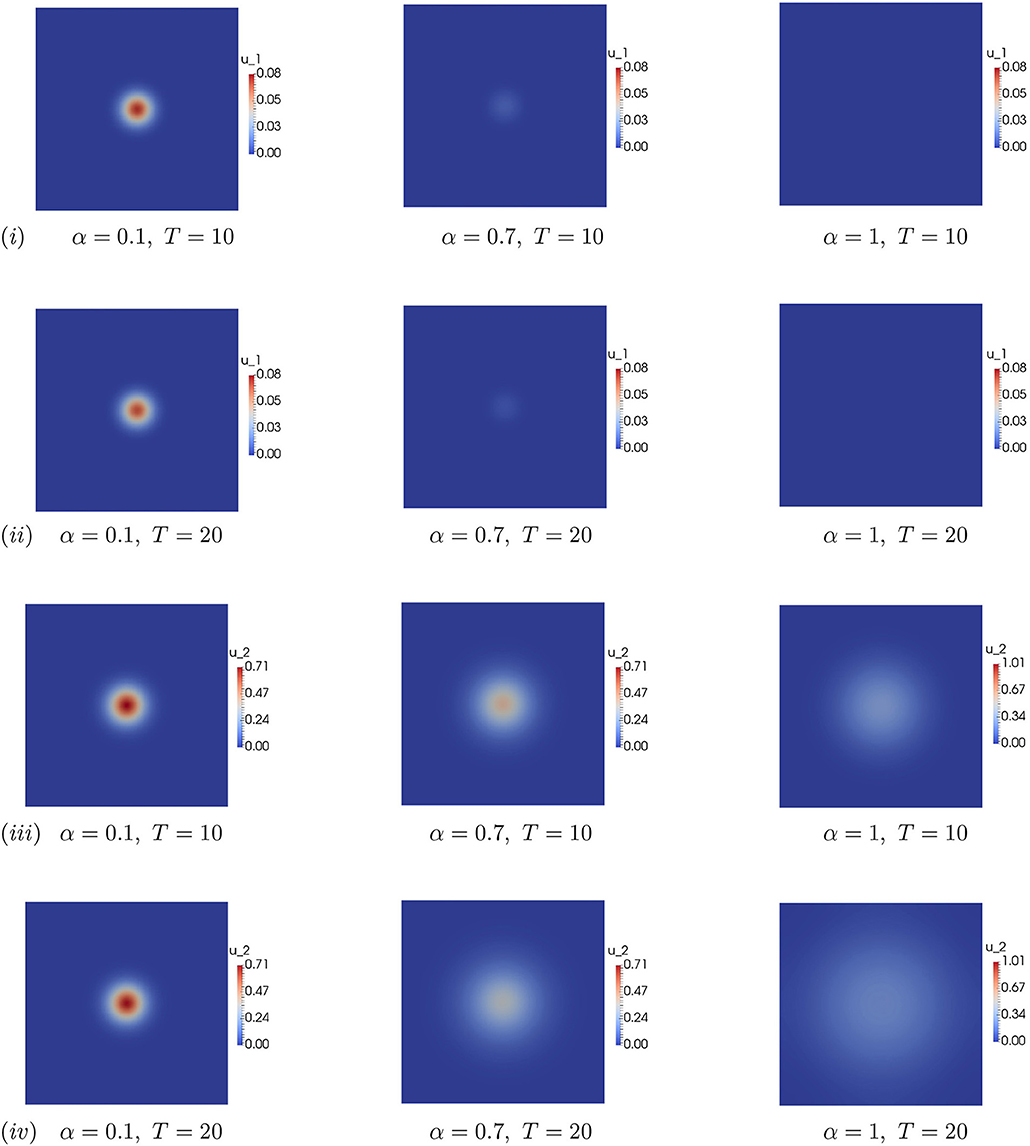
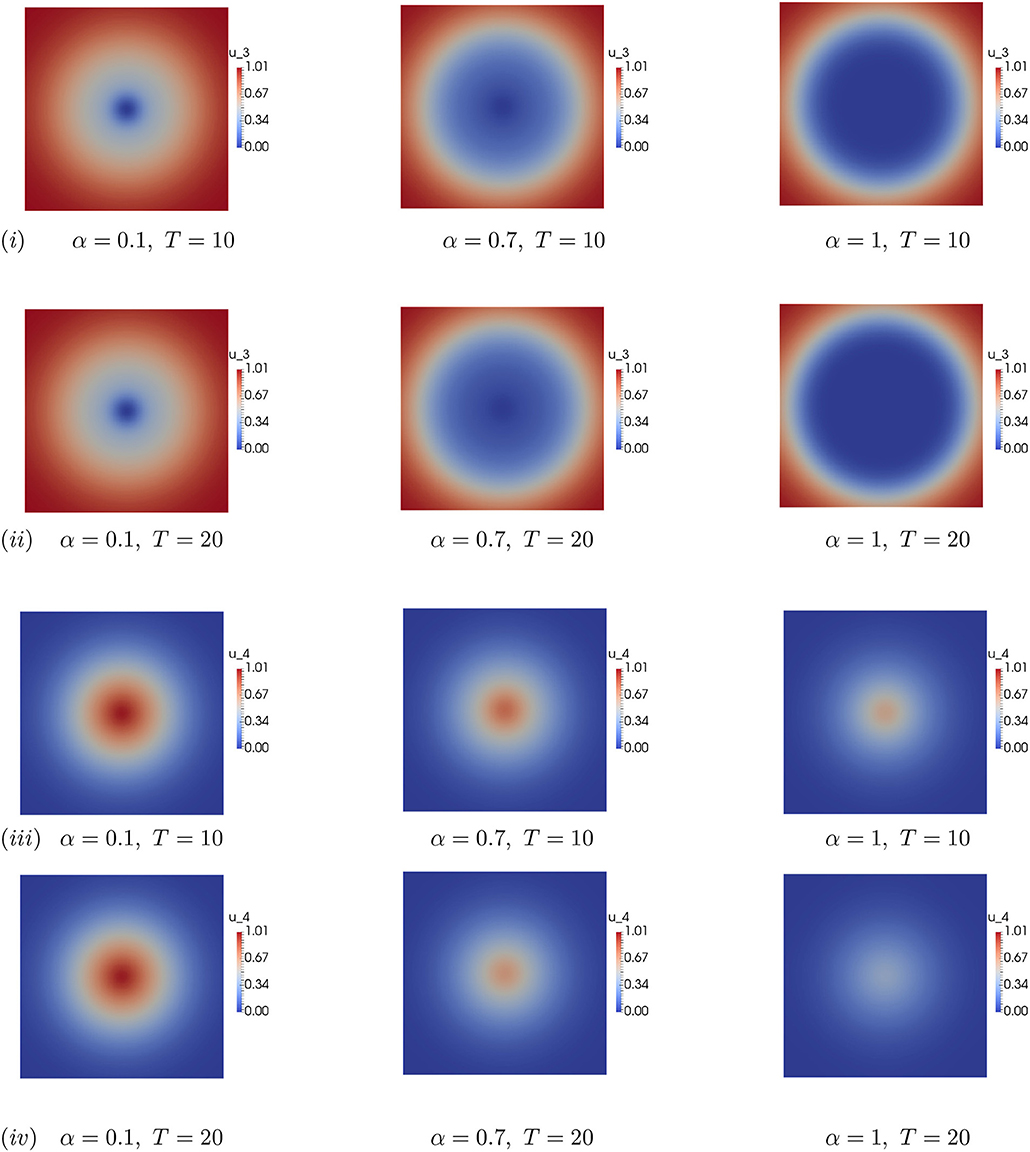
Now numerical simulations are carried out to analyse the influence of fractional parameter α on the cancer invasion system (2.5). The first two rows of Figure 1 show the comparison between the fractional derivatives when α = 0.1&0.7 and the integer order derivative for cancer density u₁ at time T = 10&20. Similarly rows (iii) & (iv) of Figure 1 show the effects on cancer density u₂ at time T = 10&20. Differences on the evolution of u₁ and u₂ can be observed depending on the value of α. We observed huge morphological changes in the invasion of cancer cells with fractional derivatives than the integer order derivative. We note that investigations with different fractional order derivatives suggest that they have relatively little impact on general properties of the cancer invasion system. Fractional derivative equips the distinct sequence of cancer cells (type I and II) migration toward the normal cell domain, see Figure 1 when α = 0.1&0.7. Similar pattern changes also observed in the evolution of normal cells density (u₃) and acidification concentration (u₄) due to the influence of fractional derivatives, see Figure 2 (i) − (iv).

FIGURE 1

Figure 1. Evaluation of u₁ and u₂ at T = 10, 20 with the different values of α = 0.1, 0.7, and 1.

FIGURE 2

Figure 2. Evaluation of u₃ and u₄ at T = 10, 20 with the different values of α = 0.1, 0.7, and 1.

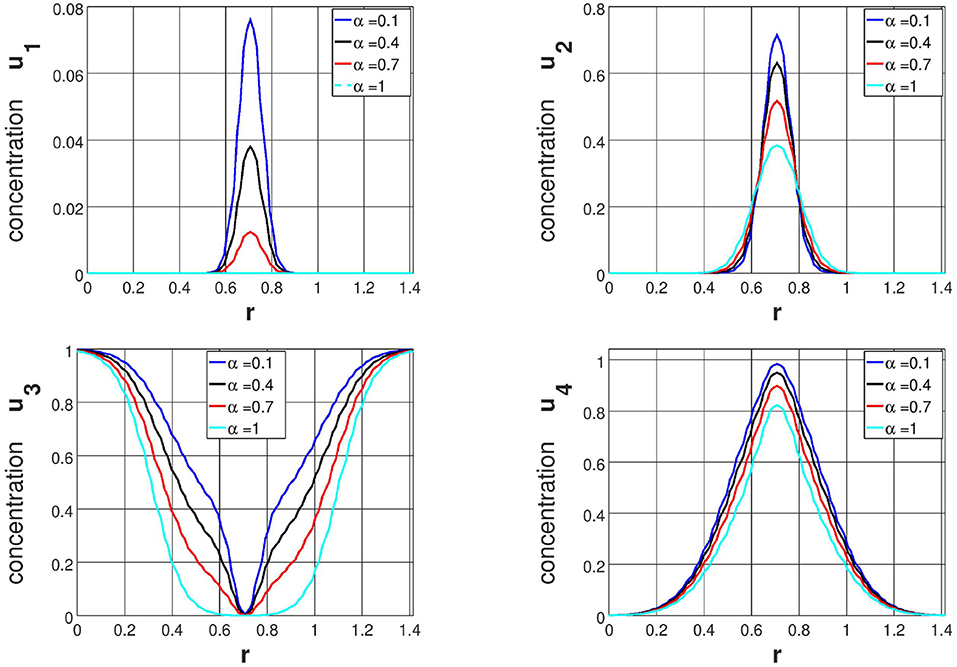
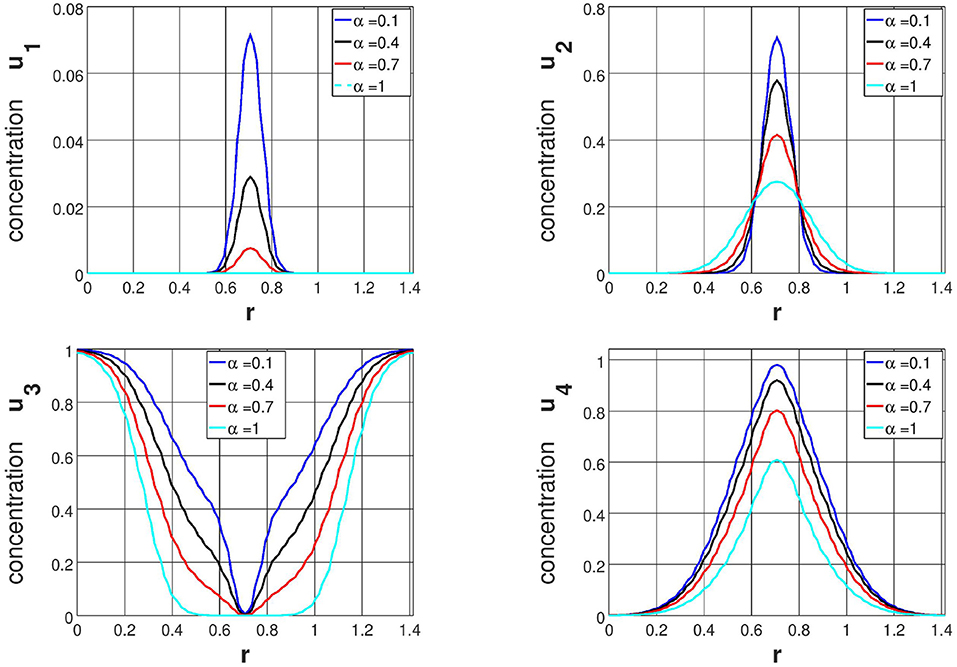
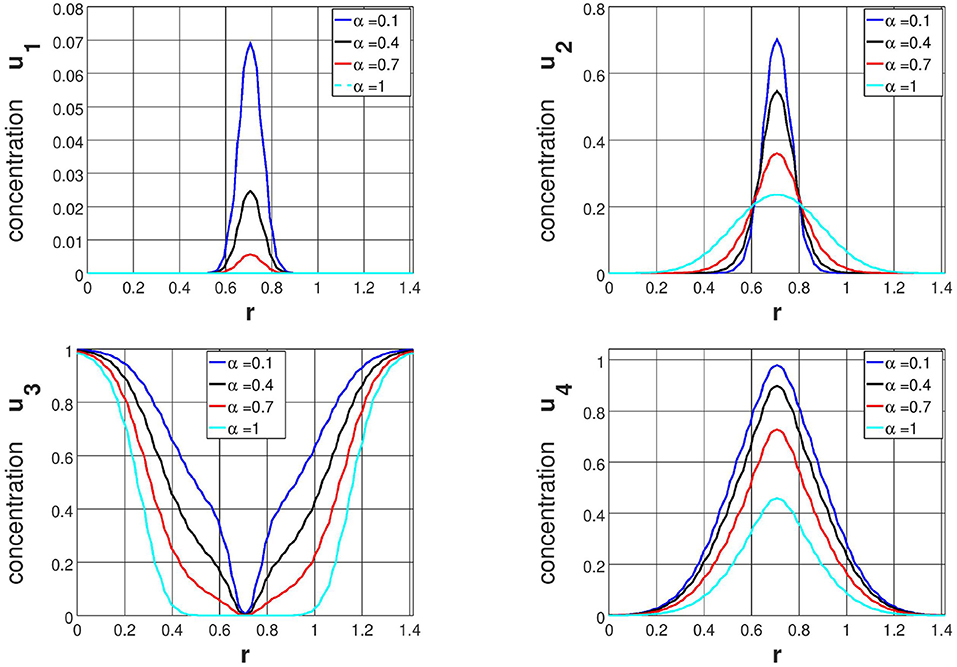
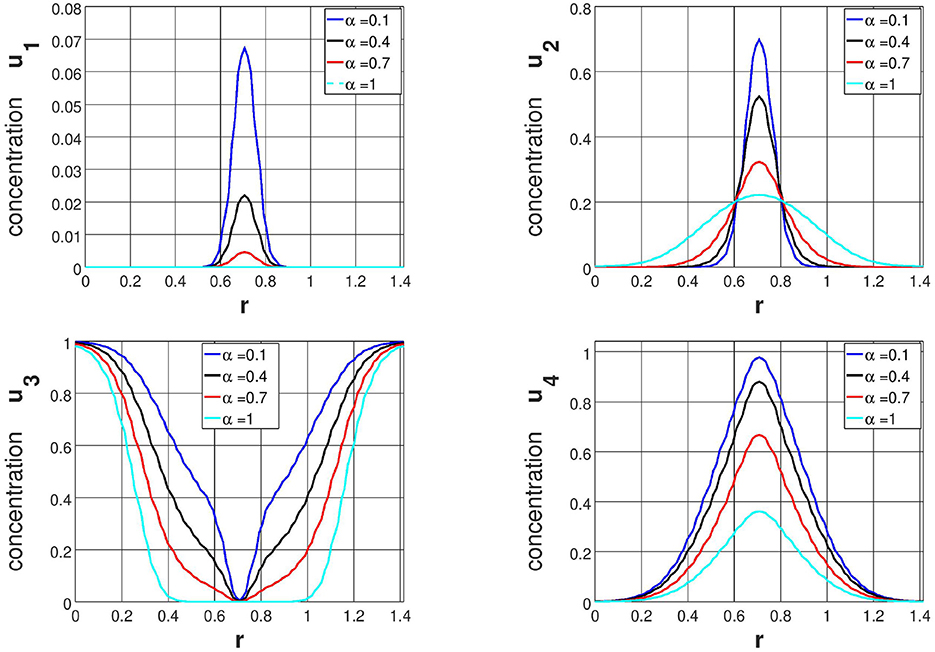
Further, the influence of fractional derivatives α = 0.1, 0.4&0.7 compared with α = 1.0 on the evolution of cancer density u₁&u₂, normal density u₃ and acidification concentration u₄ are discussed along the y = x. Numerical results are depicted in Figures 3–6 at time T = 5, 10, 15, and 20. From the these figures (Figures 3–6), it is clear that density of cancer cells (both type I and II) increasing when α decreases. At the same instance, acidification concentration (due to H⁺ions) u₄ increases, when α decreases. By comparing all these numerical results, we understand that fractional derivatives increase the population of cancer cells at some position of the domain. Therefore, by comparing all the simulation results in Figures 1–6, it is not difficult to find the that fractional derivatives change the invasion of cancer cells toward normal cells by comparing with integer order derivatives. Therefore, we conclude that proposed computational model can be employed to foresee the location and the shape of the tumor at a particular instance during cancer growth and invasion.

FIGURE 3

Figure 3. Evaluation of u₁, u₂, u₃, and u₄ at t = 5 along the line y = x.

FIGURE 4

Figure 4. Evaluation of u₁, u₂, u₃, and u₄ at t = 10 along the line y = x.

FIGURE 5

Figure 5. Evaluation of u₁, u₂, u₃, and u₄ at t = 15 along the line y = x.

FIGURE 6

Figure 6. Evaluation of u₁, u₂, u₃, and u₄ at t = 20 along the line y = x.

Data Availability

All datasets generated for this study are included in the manuscript and the supplementary files.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Araujo RP, MceLwain DLS. A history of the study of solid tumour growth: the contribution of mathematical modelling. Bull Math Biol. (2004) 66:1039–91. doi: 10.1016/j.bulm.2003.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Clatz O, Sermesant M, Bondiau PY, Delingette H, Warfield SK, Malandain G, et al. Realistic simulation of the 3D growth of brain tumors in MR images coupling diffusion with biomechanical deformation. IEEE Trans Med Imaging. (2005) 24:1334–46. doi: 10.1109/TMI.2005.857217

CrossRef Full Text | Google Scholar

3. Enderling H, Chaplain MAJ. Mathematical modeling of tumor growth and treatment. Curr Pharm Des. (2014) 20:4934–40. doi: 10.2174/1381612819666131125150434

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Tracqui P. Biophysical models of tumor growth. Rep Prog Phys. (2009) 72:056701. doi: 10.1088/0034-4885/72/5/056701

CrossRef Full Text | Google Scholar

5. Hilfer R. Applications of Fractional Calculus in Physics. Singapore: World Scientific (2000).

6. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of the Fractional Differential Equations. Amsterdam: Elsevier (2006).

Google Scholar

7. Zhou Y. Basic Theory of Fractional Differential Equations. Singapore: World Scientific (2014).

8. Henry BI, Wearne SL. Fractional reaction-diffusion. Phys A. (2000) 276:448–55. doi: 10.1016/S0378-4371(99)00469-0

CrossRef Full Text | Google Scholar

9. Henry BI, Langlands T, Wearne S. Turing pattern formation in fractional activator-inhibitor systems. Phys Rev E. (2005) 72:026101. doi: 10.1103/PhysRevE.72.026101

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Magin RL. Fractional calculus models of complex dynamics in biological tissues. Comput Math Appl. (2010) 59:1586–93. doi: 10.1016/j.camwa.2009.08.039

CrossRef Full Text | Google Scholar

11. Zhou Y, Peng L. On the time-fractional Navier-Stokes equations. Comput Math Appl. (2017) 73:874–91. doi: 10.1016/j.camwa.2016.03.026

CrossRef Full Text | Google Scholar

12. Zhou Y, Peng L. Weak solutions of the time-fractional Navier-Stokes equations and optimal control. Comput Math Appl. (2017) 73:1016–27. doi: 10.1016/j.camwa.2016.07.007

CrossRef Full Text | Google Scholar

13. Berkowitz B, Scher H. Anomalous transport in random fracture networks. Phys Rev Lett. (1997) 79:4038–41. doi: 10.1103/PhysRevLett.79.4038

CrossRef Full Text | Google Scholar

14. Caputo M. Linear models of dissipation whose q is almost frequency independent. J Geophys. (1967) 13:529–39. doi: 10.1111/j.1365-246X.1967.tb02303.x

CrossRef Full Text | Google Scholar

15. Ahmed E, Hashis AH, Rihan FA. On fractional order cancer model. J Fract Calc Appl. (2012) 3:1–6.

Google Scholar

16. Iyiola OS, Zaman FD. A fractional diffusion equation model for cancer tumor. Am Inst Phys Adv. (2014) 4:107121. doi: 10.1063/1.4898331

CrossRef Full Text | Google Scholar

17. Alikhanov AA. A priori estimates for solutions of boundary value problems for fractional-order equations. Differ Equ. (2010) 46:660–6. doi: 10.1134/S0012266110050058

CrossRef Full Text | Google Scholar

18. Jiao F, Zhou Y. Existence results for fractional boundary value problem via critical point theory. Int J Bifurcation Chaos. (2012) 22:1–17. doi: 10.1142/S0218127412500861

CrossRef Full Text | Google Scholar

19. Zhou Y, Shangerganesh L, Manimaran J, Debbouche A. A class of time fractional reaction-diffusion equation with nonlocal boundary condition. Math Meth Appl Sci. (2018) 41:2987–99. doi: 10.1002/mma.4796

CrossRef Full Text | Google Scholar

20. Hejazi H, Moroney T, Liu F. Stability and convergence of a finite volume method for the space fractional advection-dispersion equation. J Comput Appl Math. (2014) 255:684–97. doi: 10.1016/j.cam.2013.06.039

CrossRef Full Text | Google Scholar

21. Jia JH, Wang H. A preconditioned fast finite volume scheme for a fractional differential equation discretized on a locally refined composite mesh. J Comput Phys. (2015) 299:842–62. doi: 10.1016/j.jcp.2015.06.028

CrossRef Full Text | Google Scholar

22. Liu F, Zhuang P, Turner I, Burrage K, Anh V. A new fractional finite volume method for solving the fractional diffusion equation. Appl Math Model. (2014) 38:3871–8. doi: 10.1016/j.apm.2013.10.007

CrossRef Full Text | Google Scholar

23. Dehghan M, Abbaszadeh M, Mohebbi A. Analysis of a meshless method for the time fractional diffusion-wave equation. Numer Algor. (2016) 73:445–76. doi: 10.1007/s11075-016-0103-1

CrossRef Full Text | Google Scholar

24. Hosseini VR, Shivanian E, Chen W. Local radial point interpolation (MLRPI) method for solving time fractional diffusion-wave equation with damping. J Comput Phys. (2016) 312:307–32. doi: 10.1016/j.jcp.2016.02.030

CrossRef Full Text | Google Scholar

25. Alikhanov AA. A new difference scheme for the time fractional diffusion equation. J Comput Phys. (2015) 280:424–38. doi: 10.1016/j.jcp.2014.09.031

CrossRef Full Text | Google Scholar

26. Li CP, Zeng FH. Finite difference methods for fractional differential equations. Int J Bifur Chaos. (2012) 22:427–32. doi: 10.1142/S0218127412300145

CrossRef Full Text | Google Scholar

27. Sun H, Sun ZZ, Gao GH. Some temporal second order difference schemes for fractional wave equations, Numer. Methods Partial Differ. Equ. (2016) 32:970–1001. doi: 10.1002/num.22038

CrossRef Full Text | Google Scholar

28. Zhang YN, Sun ZZ, Liao HL. Finite difference methods for the time fractional diffusion equation on non-uniform meshes. J Comput Phys. (2014) 265:195–210. doi: 10.1016/j.jcp.2014.02.008

CrossRef Full Text | Google Scholar

29. Jin B, Lazarov R, Liu Y, Zhou Z. The Galerkin finite element method for a multi-term time-fractional diffusion equation. J Comput Phys. (2015) 281:825–43. doi: 10.1016/j.jcp.2014.10.051

CrossRef Full Text | Google Scholar

30. Jin B, Lazarov R, Pasciak J, Zhou Z. Error analysis of semidiscrete finite element methods for inhomogeneous time-fractional diffusion. IMA J Numer Anal. (2015) 35:561–82. doi: 10.1093/imanum/dru018

CrossRef Full Text | Google Scholar

31. Jin B, Lazarov R, Zhou Z. Error estimates for a semidiscrete finite element method for fractional order parabolic equations. SIAM J Numer Anal. (2013) 51:445–66. doi: 10.1137/120873984

CrossRef Full Text | Google Scholar

32. Le KN, McLean W, Mustapha K. Numerical solution of the time-fractional Fokker-Planck equation with general forcing. SIAM J Numer Anal. (2016) 54:1763–84. doi: 10.1137/15M1031734

CrossRef Full Text | Google Scholar

33. Li XJ, Xu CJ. A space-time spectral method for the time fractional diffusion equation. SIAM J Numer Anal. (2009) 47:2108–31. doi: 10.1137/080718942

CrossRef Full Text | Google Scholar

34. Zheng M, Liu F, Turner I, Anh V. A novel high order space-time spectral method for the time fractional Fokker-Planck equation. SIAM J Scient Comput. (2015) 37:A701–24. doi: 10.1137/140980545

CrossRef Full Text | Google Scholar

35. Zheng M, Liu F, Anh V, Turner I. A high-order spectral method for the multi-term time-fractional diffusion equations. Appl Math Model. (2016) 40:4970–85. doi: 10.1016/j.apm.2015.12.011

CrossRef Full Text | Google Scholar

36. Esen A, Ucar Y, Yagmurlu N, Tasbozan O. A Galerkin finite element method to solve fractional diffusion and fractional diffusion-wave equations. Math Model Anal. (2013) 18:260–73. doi: 10.3846/13926292.2013.783884

CrossRef Full Text | Google Scholar

37. Wang YJ, Liu Y, Li H, Wang JF. Finite element method combined with second-order time discrete scheme for nonlinear fractional Cable equation. Eur Phys J Plus. (2016) 131:61. doi: 10.1140/epjp/i2016-16061-3

CrossRef Full Text | Google Scholar

38. Liu N, Liu Y, Li H, Wang J. Time second-order finite difference/finite element algorithm for nonlinear time-fractional diffusion problem with fourth-order derivative term. Comput Math Appl. (2018) 75:3521–36. doi: 10.1016/j.camwa.2018.02.014

CrossRef Full Text | Google Scholar

39. Jin B, Li B, Zhou Z. An analysis of the Crank Nicolson method for subdiffusion. IMA J Numer Anal. (2017) 38:518–41. doi: 10.1093/imanum/drx019

CrossRef Full Text | Google Scholar

40. Kumar D, Chaudhary S, Kumar VVKS. Galerkin finite element schemes with fractional Crank-Nicolson method for the coupled time-fractional nonlinear diffusion system. Comput Appl Math. (2019) 38:123. doi: 10.1007/s40314-019-0889-2

CrossRef Full Text | Google Scholar

41. Owolabi KM. Mathematical analysis and numerical simulation of patterns in fractional and classical reaction-diffusion systems. Chaos Solit Fract. (2016) 93:89–98. doi: 10.1016/j.chaos.2016.10.005

CrossRef Full Text | Google Scholar

42. Owolabi KM, Atangana A. Numerical approximation of nonlinear fractional parabolic differential equations with Caputo-Fabrizio derivative in Riemann-Liouville sense. Chaos Solit Fract. (2017) 99:171–9. doi: 10.1016/j.chaos.2017.04.008

CrossRef Full Text | Google Scholar

43. Owolabi KM. Robust and adaptive techniques for numerical simulation of non-linear partial differential equations of fractional order. Commun Nonlin Sci Numer Simul. (2017) 44:304–17. doi: 10.1016/j.cnsns.2016.08.021

CrossRef Full Text | Google Scholar

44. Owolabi KM. Mathematical modelling and analysis of two-component system with Caputo fractional derivative order. Chaos Solit Fract. (2017) 103:544–54. doi: 10.1016/j.chaos.2017.07.013

CrossRef Full Text | Google Scholar

45. Owolabi KM, Atangana A. Analysis and application of new fractional Adams Bashforth scheme with Caputo-Fabrizio derivative. Chaos Solit Fract. (2017) 105:111–9. doi: 10.1016/j.csfx.2019.100007

CrossRef Full Text | Google Scholar

46. Solis FJ, Delgadillo SE. Evolution of a mathematical model of an aggressive-invasive cancer under chemotherapy. Comput Math Appl. (2015) 69:545–58. doi: 10.1016/j.camwa.2015.01.013

CrossRef Full Text | Google Scholar

47. Szymańska Z, Morales C, Lachowicz M, Chaplain MAJ. Mathematical modelling of cancer invasion of tissue: the role and effect of nonlocal interactions. Math Models Methods Appl Sci. (2009) 19:257–81. doi: 10.1142/S0218202509003425

CrossRef Full Text | Google Scholar

48. Podlubny I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, Vol.198. Elsevier; Academic Press (1999).

Google Scholar

49. Zhou Y, Manimaran J, Shangerganesh L, Debbouche A. Weakness and Mittag-Leffler stability of solutions for time-fractional Keller-Segel models. Int J Nonlin Sci Num. (2018) 19:753–61. doi: 10.1515/ijnsns-2018-0035

CrossRef Full Text | Google Scholar

50. Almeida R. A Gronwall inequality for a general Caputo fractional operator. arXiv: 1705.10079 (2017). doi: 10.7153/mia-2017-20-70

CrossRef Full Text | Google Scholar

51. Temam R. Navier-Stokes Equations: Theory and Numerical Analysis. Amsterdam: North-Holland (1979). doi: 10.1115/1.3424338

CrossRef Full Text | Google Scholar

52. Ganesan S, Shangerganesh L. Galerkin finite element method for cancer invasion mathematical model. Comput Math Appl. (2017) 73:2603–17. doi: 10.1016/j.camwa.2017.04.006

CrossRef Full Text | Google Scholar

53. Ganesan S, Shangerganesh L. A biophysical model for tumor invasion. Commun Nonlin Sci Numer Simul. (2017) 46:135–52. doi: 10.1016/j.cnsns.2016.10.013

CrossRef Full Text | Google Scholar

54. Ganesan S, Tobiska L. An accurate finite element scheme with moving meshes for computing 3d-axisymmetric interface flows. Int J Numer Meth Fluids. (2008) 57:119–138. doi: 10.1002/fld.1624

CrossRef Full Text | Google Scholar

55. Lin Y, Xu C. Finite difference/spectral approximations for the time-fractional diffusion equation. J Comput Phys. (2007) 225:1533–52. doi: 10.1016/j.jcp.2007.02.001

CrossRef Full Text | Google Scholar

56. Sun ZZ, Wu X. A fully discrete scheme for a diffusion wave system. Appl Numer Math. (2006) 56:193–209. doi: 10.1016/j.apnum.2005.03.003

CrossRef Full Text | Google Scholar

57. Hecht F. New development in freefem++. J Numer Math. (2012) 20:251–65. doi: 10.1515/jnum-2012-0013

CrossRef Full Text | Google Scholar

58. Davis TA. Algorithm 832: UMFPACK V4.3-an unsymmetric-pattern multifrontal method. ACM Trans Math Softw. (2004) 30:196–9. doi: 10.1145/992200.992206

CrossRef Full Text | Google Scholar

59. Davis TA. A column pre-ordering strategy for the unsymmetric-pattern multifrontal method. ACM Trans Math Softw. (2004) 30:167–95. doi: 10.1145/992200.992205

CrossRef Full Text