Decoding the Nature of Dark Matter at Current and Future Experiments

Determination of the nature of Dark Matter (DM) is one of the most fundamental problems of particle physics and cosmology. If DM is light enough and interacts with Standard Model particles directly or via some mediators with a strength beyond the gravitational one, it can be probed at particle accelerators or in complementary direct and indirect DM searches in non-collider experiments. In the absence of such signals at present we can prepare ourselves for its discovery and identification. Generic signature from DM produced in particles collisions is missing transverse energy, MET, originating from DM particles escaping detector. Using effective field theory approach one can show that, depending on the structure and DM spin, effective operators have different MET distributions. This provides potential to distinguish certain classes of effective field theory (EFT) operators and related spin of DM at the LHC. This observation can be directly applied to theories beyond EFT paradigm as we demonstrate for Supersymmetry and inert two Higgs doublet model (i2HDM) as two examples. At the same time direct and indirect DM searches strongly complement collider searches for DM with large masses and pointing that collider and non-collider DM searches have unique power to probe the nature of Dark Matter. We also highlight prospects of new collider signature from DM such as disappearing charge tracks which are characteristic for wide class of DM theories. Finally, we advocate the importance of the joint framework which would join efforts of HEP community and allow to effectively identify the underlying theory of DM.

1. Introduction

Understanding the nature of Dark Matter (DM) is one of the greatest puzzles of modern particle physics and cosmology. Although overwhelming observational evidences from galactic to cosmological scales point to the existence of DM [1–3], after decades of experimental effort only its gravitational interaction has been experimentally confirmed. Currently, no information is available on the DM properties, such as its spin, mass, interactions other than gravitational, symmetry responsible for its stability, number of states associated to it, and possible particles that would mediate the interactions between DM and the standard model (SM) particles.

If DM is light enough and interacts with SM particles directly or via some mediators with a strength beyond the gravitational one, its elusive nature can be detected or constrained in different ways: (a) from direct production at colliders, resulting in a signature exhibiting an observed SM object, such as jet, Higgs, Z, W, photon, or top-quark(s) that recoils against the missing energy from the DM pair [4–8]; (b) via the relic density constraint obtained through the observations of cosmic microwave background (CMB) anisotropies, such as those of WMAP and PLANCK collaborations [1, 9, 10]; (c) from DM direct detection (DD) experiments, which are sensitive to elastic spin independent (SI) or spin dependent (SD) DM scattering off nuclei [11–14]; (d) from DM indirect detection searches, that look for SM particles produced in the decay or annihilation of DM present in the cosmos, both with high energy observables (gamma-rays, neutrinos, charge cosmic rays) produced in the local Universe [15–20], and by studying the effects of energy produced by DM annihilation in the early universe on the properties of the CMB spectrum [1, 21, 22].

It is clear that decoding the nature of DM requires the respective signal at least in one of the search experiments. We do not have one yet. However, even without having the signal at the moment we can already conclude on what kind of DM models are excluded. Moreover, by exploring different signatures of one particular model, their correlation and interplay we can prepare ourselves to discovery of DM and their identification.

2. Contact Interactions

Let us start our discussion with the three simplest scenarios for the DM particles: complex scalars (ϕ), Dirac fermions (χ), and complex vectors (V_μ) within the effective field theory (EFT) approach. In the EFT approach we parametrize the DM interactions with the SM quarks and gluons with the effective coupling and the scale describing operators of dimension six or five. In Table 1 we have summarized a minimal set of independent dimension-5 and dimension-6 operators for complex scalar, Dirac fermion, and complex vector DM coupling to quarks and gluons, adopting the widely used notations of Goodman et al. [23], Kumar et al. [24], and Belyaev et al. [25]. Since different operators have different energy behavior and respective different invariant mass distributions: typically softer for majority operators with scalar DM, intermediate for fermion DM and the hardest for vector DM and because of relation of M_inv(DM, DM) and $E_{\text{T}}^{\text{miss}}$ slope one can distinguish several operators and related underlying theories using the shape of the $E_{\text{T}}^{\text{miss}}$ signal: C1-C2,C5-C6,D9-D10,V1-V2,V3-V4,V5-V6, and V11-12 pairs among each other [25].

TABLE 1

Table 1. Minimal basis of dimension 5 and 6 operators for complex scalar DM (ϕ), Dirac fermion DM (χ) or complex vector DM (V^μ) interacting with SM quarks (q) or gluons.

Notice the presence of the coupling g_* in the definition of the effective operators, which we insert according to the Naive Dimensional Analysis [26]. Moreover, for the vector DM case we choose the parametrization suggested in Belyaev et al. [25] that takes into account the high energy behavior of the scattering amplitudes that are enhanced by an energy factor (E/m_DM) for every longitudinal vector DM polarization. These operators are gauge invariant and provides the minimal and simplistic description of underlying theory of DM. The scale Λ is related to the mass of the mediator, while coupling g^* is related to the product of DM and SM couplings to the mediator.

These operators provide monojet-signature, the shapes of $E_{\text{T}}^{\text{miss}}$ distributions for which is presented in Figure 1 from Belyaev et al. [25] for DM mass of 10 GeV. One can observe a big difference in $E_{\text{T}}^{\text{miss}}$ shapes of the groups of the operators, primarily split into groups of operators with scalar, femion and vector DM. The origin of the different $E_{\text{T}}^{\text{miss}}$ shapes from different operators can be related to a combination of effects. First, for a fixed Lorentz structure of the SM part of the EFT operators, the same invariant mass distribution of the DM pair, M_inv(DM, DM), uniquely defines the shape of the $E_{\text{T}}^{\text{miss}}$ distribution. Moreover, with the increase of M_inv(DM, DM), the $E_{\text{T}}^{\text{miss}}$ shape falls less and less steeply (again, for a given SM component of the EFT operator).

FIGURE 1

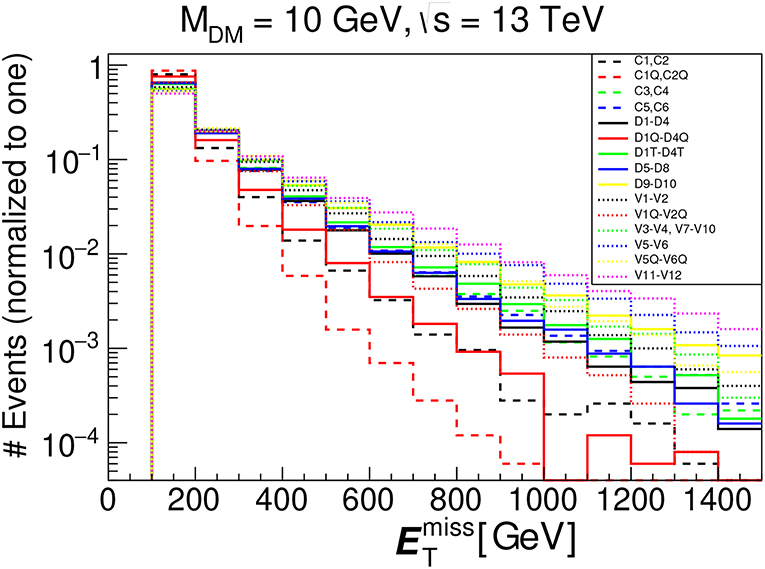
Figure 1. $E_{\text{T}}^{\text{miss}}$ parton level distributions for a representative subset of the EFT operators from Table 1 for 13 TeV LHC energy and M_DM = 10 GeV.

It was found in Belyaev et al. [25] that the reason why the bigger invariant mass of DM is correlated with flatter $E_{\text{T}}^{\text{miss}}$ behavior is related to phase space and parton density effects: when M_inv(DM, DM) is small, the radiation of a high p_T jet will “cost” a large relative shift in x, the transferred momentum of the parton, leading to a rapidly falling $E_{\text{T}}^{\text{miss}}$ distribution; on the contrary, when M_inv(DM, DM) is large, the radiation of a high p_T jet will “cost" a small relative shift in x, which will lead to a more slowly falling $E_{\text{T}}^{\text{miss}}$ distribution in comparison to the first case.

Therefore if one theory predicts higher values of the invariant mass of DM-pair, M(DM, DM), than the other theory, one expects the flatter $E_{\text{T}}^{\text{miss}}$ distribution for the first one. In Figure 2 we present M(DM, DM) distributions for all EFT operators in Table 1 where one clearly observes that the mean values of M(DM, DM) distributions for vector DM operators are larger than those for most of fermion DM operators which are in their turn have higher mean value of M(DM, DM) than most of scalar DM operators. Now we can see the connection of M(DM, DM) distributions shape and the slope of the $E_{\text{T}}^{\text{miss}}$ which was presented in Figure 1.

FIGURE 2

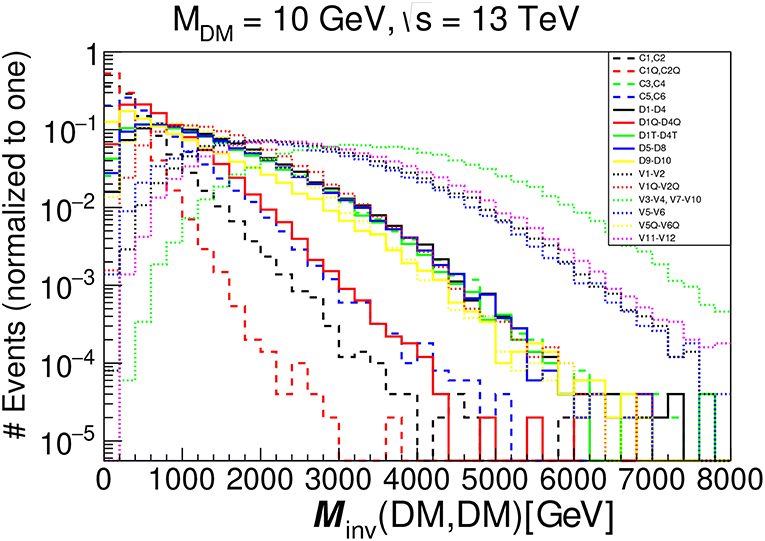
Figure 2. Invariant mass of DM pair distributions normalized to unity for EFT operators in Table 1 for 13 TeV LHC energy, M_DM = 10 GeV and p_{T, jet} ≥ 100 GeV cut applied.

One should stress that non-collider DM searches play an important complementary role in probing DM parameter space. As an example in Figure 3 (left) we present the non-collider constraints for the operators D2, which exhibit pseudo-scalar interactions of fermion Dirac DM with quarks.

FIGURE 3

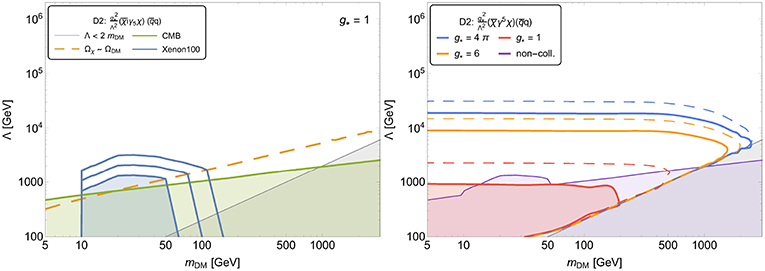
Figure 3. (Left) Non-collider constraints on D2 operator with fermion DM: (i) SI DM DD searches (shaded blue region below the lowest blue contour), (ii) constraints from relic density (above the yellow dashed line), (iii) constraints from the CMB (shaded green area), and (iv) constraints from the validity of the EFT (Λ > 2m_DM). (Right) LHC monojet constraints on D2 EFT operator. The area inside the red, orange and blue solid curves is excluded by current LHC data at 95% CL for g_⋆ = 1, 6, and 4π, respectively. The projected LHC limits for 300 fb⁻¹ are indicated by dashed thin lines. The combined exclusion regions from CMB and DM DD searches for g_⋆ = 1 are given by the light-purple area. See details and complete set of plots in Belyaev et al. [27].

One can see that even for momentum-suppressed operator D2 (because of its pseudo-scalar nature) DM DD constraints from Xenon [28] play an important role which is comparable to collider constraints, presented in Figure 3 (right). It is important to stress that both LHC and DM DD searches set an upper limit on value of Λ. The LHC limit is of the order of 1 TeV for present LHC data while DM DD searches the limit strongly depend on the operator. For example for non-suppressed operators conserving parity the limit on Λ is about 3 orders of magnitude above the LHC one. On the other hand LHC limit is beyond DM DD searches for operators with suppressed elastic scattering cross sections on the nuclei (C2,C4,C6,D2,D3,D4,D6-10,V2,V4-V10). Moreover, for operators with pseudo-vector currents which have suppressed DM DD rates, one should take into account effect of their running from TeV energy scale at the LHC down to low energy scale at DM DD experiments, due to which an operator acquires non-negligible vector component [29–31].

3. Beyond EFT

The analysis of $E_{\text{T}}^{\text{miss}}$ shape presented here can be applied to different scenarios, beyond the EFT approach in general, where the DM mediator is not produced on-the-mass-shell, such as the case of t-channel mediator or mediators with mass below 2M_DM, where the M_inv(DM, DM) is not fixed. This case covers a wide range of theories.

As an example in Figure 4 (left) the normalized shape for $E_{\text{T}}^{\text{miss}}$ distribution from $pp\to {\chi }_1^{+}{\chi }_1^{-}/{\chi }_1^{\pm }{\chi }_1^0\to {\chi }_1^0{\chi }_1^0+\text{soft leptons}/\text{jets}$ Minimal Supersymmetric Model(MSSM) signal and its dominant irreducible background $Z+jet\to \nu \bar{\nu }+jet$ (Zj) is presented for LHC@13TeV [32]. The model parameter space in the compressed chargino-neutralino scenario driven by small μ parameter is essentially characterized only by DM (${\chi }_1^0$) and chargino (${\chi }_1^{+}$) masses and mildly depends on the value of tanβ.

FIGURE 4

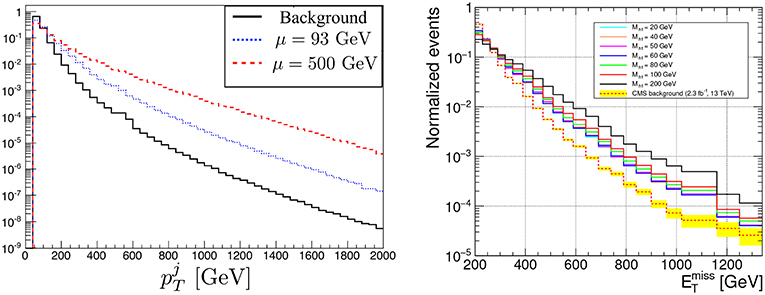
Figure 4. (Left) Normalized signal (dotted blue and dashed red) and Zj background (solid black) parton-level $p_T^j$ distributions for the 13 TeV LHC for the NSUSY scenario: normalized signal and Zj background distributions. See details in Barducci et al. [32]. (Right) Normalized $E_{\text{T}}^{\text{miss}}$ from h₁h₂j i2HDM signal vs. background for $\sqrt{s}=$ 13 TeV. See details in Belyaev et al. [33].

In the Figure 4 (right) we present $E_{\text{T}}^{\text{miss}}$ from h₁h₂j inert two Higgs doublet model (i2HDM) signal alongside the estimated (by CMS) experimental background for $\sqrt{s}=$ 13 TeV. The parameter space of the model, details of which can be found for example in Belyaev et al. [33], is characterized by DM mass (h₁), the mass of the second neutral scalar (h₂), the mass of the charged scalar (h⁺) and the DM-Higgs boson coupling. However, the h₁h₂j production cross section depends only on two parameters–h₁ and h₂ masses in analogy to the above SUSY scenario. An important feature of the signal vs. background shapes in these completely different theory cases is that the background falls more rapidly with $E_{\text{T}}^{\text{miss}}$, and the difference in the slope with respect to the signal is bigger for higher DM mass. This behavior has the same explanation as for EFT study case above—it is related to the bigger invariant mass of the invisible system for the signal—M(DM, DM) than for the background—M_Z. This feature is very instrumental to increase signal-to-background ratio (S/B) (which is typically below 1% for low $E_{\text{T}}^{\text{miss}}$ cuts) by increasing the value of $E_{\text{T}}^{\text{miss}}$ or by performing the signal-background shape analysis [33].

The role of non-collider DM searches is also crucial in case of these two complete and consistent models. And an example in Figure 5 we present the projected LHC reach for MSSM monojet signal in the $\Delta M=m_{{\chi }_1^{+}}-m_{{\chi }_1^0}$, $M_{DM}=m_{{\chi }_1^0}$ parameter space together with LUX and Xenon1T DM DD exclusion [32]. One can see that LHC would be able cover neutralino DM mass only below 250 GeV (with the assumption that S/B of the order of 3% will be under control) even with 3 ab⁻¹ total integrated luminosity. But coverage of this region is important as well as LHC-Xenon1T complementarity: LHC will be able to cover the region inaccessible by Xenon1T in small ΔM region, while Xenon1T is able to cover m_DM well beyond the LHC reach for ΔM > 3 − 5 GeV. In case of i2HDM model collider sensitivity with mono-jet signature is even more limited because of the lower production rates of the scalar DM, h₁, or its inert partners (h₂ and h⁺) and expected LHC reach is below 100 GeV for M_h1.

FIGURE 5

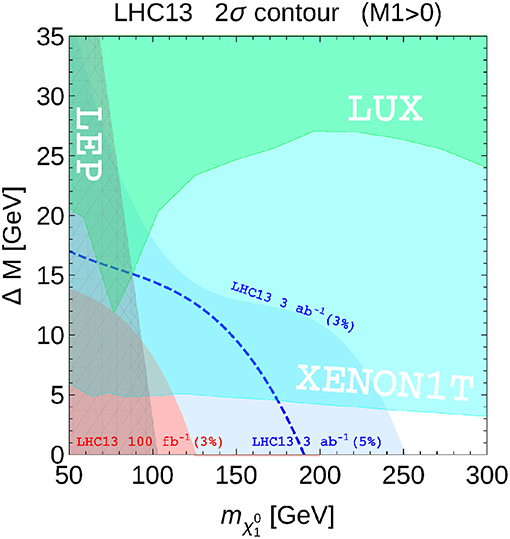
Figure 5. Exclusion contour lines for the 13 TeV LHC at the end of the LHC Run2 (light red region) and of the HL-LHC (light blue region). The region excluded by LUX and Xenon1T are also shown, together with the LEP limit. See details in Barducci et al. [32].

4. Beyond Mono-X Signature

While mono-X (with X being jet, γ, Z, H, t etc.) DM signatures at colliders are the most general ones, their rates are typically very low (usually at the percent level or even lower). Besides several other interesting but model-specific DM signature studies, one should stress one signature which can be also considered as quite generic one. In case when DM, D⁰, is embedded into electroweak multiplet and its mass split from the charged odd particle(s), D⁺, is generated only radiatively (preserving gauge invariance), the one can find that the value of this mass split is of the order of 0.2 GeV. In this case D⁺ has a very small width and respectively large life-time. D⁺ being long lived particle (LLP) dominantly decays into DM and very soft pion: D⁺ → D⁰π⁰. Production of D⁺ in pairs or in association with DM leads then to the typical signature from charged LLP: disappearing charged track (DCT) as soon as the track from LLP is long enough (from few cm to a meter). In case of such signature the S/B ratio is much higher than in case of mono-jet signal and therefore, substantially bigger DM masses can be probed with charged LLPs from DM sector [34–36]. As an example, we would like to present here results for the minimal vector triplet DM (V⁰) model [36] which predicts the right amount of DM for M_DM in the 3-4 TeV range depending on DM coupling to the Higgs boson.

In this model the SM is supplemented by a new massive vector boson V_μ in the adjoint representation of SU(2)_L, e.g., by two new massive vector particles: V⁰ and V^±. If V_μ transforms homogeneously (i.e., $V_{\mu }\to g_L^{†}{V}_{\mu }{g}_L$ where g_L∈SU(2)_L) and Z₂ symmetry is imposed (which links the quartic V coupling to the gauge coupling constant and makes theory unitary is unitary before EW symmetry breaking and in the absence of the Higgs boson as found in Zerwekh [37]) then Lagrangian can be written as:

$\begin{array}{l}{L}={{L}}_{SM}-Tr\left\{D_{\mu }{V}_{\nu }{D}^{\mu }{V}^{\nu }\right\}+Tr\left\{D_{\mu }{V}_{\nu }{D}^{\nu }{V}^{\mu }\right\}\\ -\frac{g^2}{2}Tr\left\{\left[V_{\mu },V_{\nu }\right]\left[V^{\mu },V^{\nu }\right]\right\}\\ -igTr\left\{W_{\mu \nu }\left[V^{\mu },V^{\nu }\right]\right\}+{\tilde{M}}^{2}Tr\left\{V_{\nu }{V}^{\nu }\right\}\\ +a\left({\Phi }^{†}\Phi \right)Tr\left\{V_{\nu }{V}^{\nu }\right\}\end{array}$

where D_μ = ∂_μ − ig[W_μ, ] is the usual SU(2)_L covariant derivative in the adjoint representation and ${{L}}_{SM}$ represents the SM Lagrangian. The main difference with respect to the model in Zerwekh [37] is that the SU(2)_L symmetry is broken by the Higgs mechanism and the associated gauge bosons have mass. We thus allow for a coupling of V to the Higgs scalar field Φ. Due to the Z₂ symmetry the neutral new vector boson, V⁰ is stable and therefore is the perfect DM candidate. The mass split, ΔM, between V⁰ and V^± is generated radiatively and its value is just above the pion mass which makes V^± long lived. In Figure 6 we present ΔM as a function of M_V, which was calculated in Belyaev et al. [36].

FIGURE 6

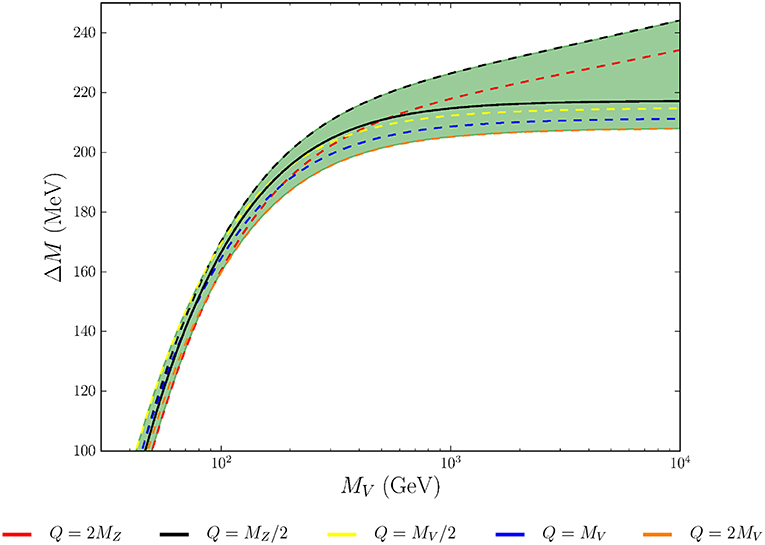
Figure 6. The one-loop radiatively induced mass splitting between the charged and neutral components of the vector DM. The solid lines represent ΔM computed at fixed values of the renormalization scale Q. The shaded green band indicates the range of values obtained by varying Q continuously between min{M_V/2, M_Z/2} and max{2M_V, 2M_Z} and thus constitutes an estimate of the uncertainty on ΔM. The solid black line is the one-loop mass splitting, with all higher order terms truncated [36].

In Figure 7 we present results for spin-independent cross-section for V⁰-nucleon elastic scattering as a function of M_V and for representative values of a. It is very important to note that Xenon1T experiment combined with DM relic density constraints excludes DM mass above 4 TeV.

FIGURE 7

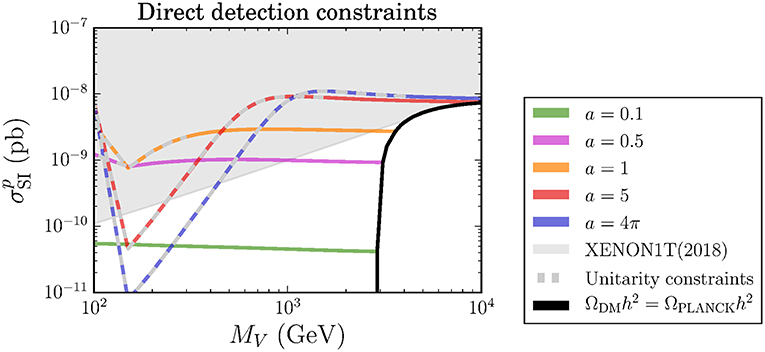
Figure 7. Spin-independent cross-section for V⁰-nucleon elastic scattering as a function of M_V and for representative values of a. The continuous black curve represents the elastic cross-section computed with the values of M_V and a that saturate the measured DM relic density. The gray dashing highlights the parameter space where perturbative unitarity loss occurs at too low scale. See details in Belyaev et al. [36].

At the same time the production rate σ_eff for σ(pp → V^±V⁰) + 2σ(pp → V⁺V⁻) process which leads to the disappearing charge track signatures (that is why pp → V⁺V⁻ process comes with coefficient 2 which is equal to the number of disappearing charged tracks it provides) are high enough to probe this process at colliders. In particular, the current LHC@13TeV limit on M_V is about 1.4 TeV as one can see from Figure 8. Moreover, one can also see from this figure that 100 TeV collider will be able to exclude DM mass below 4 TeV, thus allowing to probe the entire parameter space of the model. One should also note that in case of i2HDM, DCT signature also allows to substantially enhance LHC potential and probe DM mass upto about 500 GeV [34] which is much higher than 100 GeV—the maximum DM mass which can be probed via mono-jet signature.

FIGURE 8

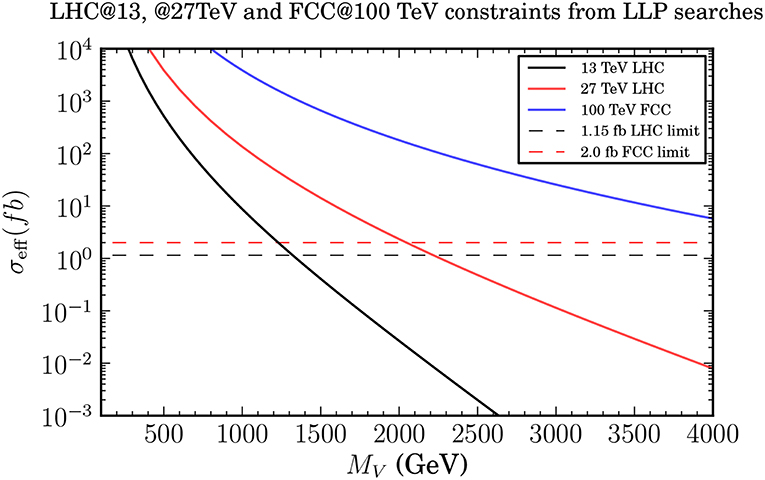
Figure 8. The effective cross-sections ${\sigma }_{eff}=\sigma (pp\to V^{\pm }{V}^0)+2\sigma (pp\to V^{+}{V}^{-})$ at leading order for the vector isotriplet model for 13 and 27 TeV LHC energies and for a 100 TeV future collider. The dashed lines corresponds to collider sensitivity. See details in Belyaev et al. [36].

5. Toward Decoding Framework

There is no framework at the moment which can solve the reverse engineering task—the task of decoding the nature of DM. It is not surprising why—we are all eagerly looking for the signal first of all and busy with the interpreting and exploring our own models. The huge amount of work has been done on the model building, phenomenology and experimental searches as well as on building different tools, examples of which has been given above. And there is really huge potential of combining different methods and signatures to probe different models. What is missing is the framework which joins all these pieces in one tool which would help us to decode underlying theory, in particular its part related to DM. The task of decoding of the whole underlying theory sounds probably too ambitious to the author, while decoding of its DM part sound more realistic since it contain specific and possibly much smaller piece of the theory. This framework requires the database of models, database of various signatures and set of tools which will be able to effectively explore not only parameter space of each particular model, but also the model parameter space and compare predicted signatures with the observed ones. Such a framework would allow objectively judge about preferred model or set of models which would fit signal best of all. An example of the prototype of such a framework actually already exists in the form of High Energy Physics Model Data Base (HEPMDB) (https://hepmdb.soton.ac.uk) [38], created at Southampton University in 2011. At the moment HEPMDB is created as a web-server accessible to everybody and is able to:

1. collect HEP models for all multipurpose Matrix Element (ME) generators in the form of Feynman rules and parameters written in the format specific for a given package;

2. collect models' sources which can be used to generate HEP models for various ME generators using FeynRules [39] or LanHEP [40];

3. allow users to perform simulations for their own models or models available at HEPMDB using the full power of the High Performance Computing (HPC) IRIDIS cluster standing behind the HEPMDB itself. Connection to HPC cluster is one of the key features of the HEPMDB: it provides a web interface to various ME generators (CalcHEP[41], Madgraph [42], and Whizard [43]) which can then also be run directly on the HPC cluster avoiding problems related to installing the actual software, which can sometimes be quite cumbersome;

4. collect simulated events and plot distributions using web interface.

Though the signature database at HEPMDB is at the development stage, users can indicate some essential features of the signatures which model can provide, such as presence of resonance, $E_{\text{T}}^{\text{miss}}$ etc. The next step of development of HEPMDB will include an addition of various packages to event analysis. Probably the most important feature of HEPMDB is that it can be developed by the whole HEP community—any registered user can add his/her own model and signature which would be used for identification of underlying theory when the experimental signal will be observed.

6. Conclusions

In the absence of DM signal we can still do a lot—we can prepare ourselves for its discovery and identification. $E_{\text{T}}^{\text{miss}}$ shape is quite instrumental in understanding the underlying theory at colliders, while direct and indirect DM searches are very powerful in complementing collider searches especially in the parameter space with large DM mass. We also advocate the usage of new DM signatures such as disappearing charge tracks which allows to substantially extend collider exploration of large DM mass. Moreover, we would like to stress the crucial role of 100 TeV pp collider which is likely to exclude substantial amount of thermal DM models. We show that collider and non-collider DM searches have a unique power to decode the nature of Dark Matter on the examples of several appealing DM theories. Such complementarity and usage of different signatures would allow us to decode the nature of DM, signals from which we are expecting in the near future. Finally, we advocate the importance of the framework which would combine the experience of HEP community and would allow to identify effectively the underlying theory of DM from the experimental signal which we will hopefully observe in the near future.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

AB acknowledges partial support from the STFC grant ST/L000296/1 and Soton-FAPESP grant. AB also thanks the NExT Institute and Royal Society International Exchange grant IE150682.

References

1. Ade PAR, Aghanim N, Arnaud M, Ashdown M, Aumont J, Baccigalupi C, et al. Planck 2015 results. XIII. Cosmological parameters. Astron Astrophys. (2016) 594:A13. doi: 10.1051/0004-6361/201525830

CrossRef Full Text | Google Scholar

2. Blumenthal GR, Faber SM, Primack JR, Rees MJ. Formation of galaxies and large scale structure with cold dark matter. Nature (1984) 311:517–25. doi: 10.1038/311517a0

CrossRef Full Text | Google Scholar

3. Bullock JS, Kolatt TS, Sigad Y, Somerville RS, Kravtsov AV, Klypin AA, et al. Profiles of dark haloes. Evolution, scatter, and environment. Mon Notices R Astron Soc. (2001) 321:559–75. doi: 10.1046/j.1365-8711.2001.04068.x

CrossRef Full Text | Google Scholar

4. Aaboud M, Aad G, Abbott B, Abdinov O, Abeloos B, Abidi SH, et al. Search for dark matter and other new phenomena in events with an energetic jet and large missing transverse momentum using the ATLAS detector. J High Energy Phys. (2018) 1:126. doi: 10.1007/JHEP01

CrossRef Full Text | Google Scholar

5. CMS Collaboration. Search for new physics in final states with an energetic jet or a hadronically decaying W or Z boson using 35.9 fb⁻¹ of data at √s = 13  TeV CMS-PAS-EXO-16-048 (2017).

6. ATLAS Collaboration. Search for Dark Matter in Events with a Hadronically Decaying Vector Boson and Missing Transverse Momentum in pp Collisions at √s = 13 TeV with the ATLAS Detector ATLAS-CONF-2018-005 (2018).

Google Scholar

7. ATLAS Collaboration. Search for Dark Matter at p √s = 13 in final states containing an energetic photon and large missing transverse momentum with the ATLAS detector. Eur Phys J. (2017) C77:393. doi: 10.1140/epjc/s10052-017-4965-8

CrossRef Full Text | Google Scholar

8. CMS Collaboration. Search for dark matter produced in association with a single top quark or a top quark pair in proton-proton collisions at √s = 13 TeV. J High Energy Phys. (2019) 3:141. doi: 10.1007/JHEP03(2019)141

CrossRef Full Text | Google Scholar

9. Hinshaw G, Larson D, Komatsu E, Spergel DN, Bennett CL, Dunkley J, et al. Nine-Year wilkinson microwave anisotropy probe (WMAP) observations: cosmological parameter results. Astrophys J Suppl. (2013) 208:19. doi: 10.1088/0067-0049/208/2/19

CrossRef Full Text | Google Scholar

10. Aghanim N, Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 results. VI. Cosmological parameters. arXiv:1807.06209 (2018).

Google Scholar

11. Goodman MW, Witten E. Detectability of certain dark matter candidates. Phys Rev. (1985) D31:3059–63. doi: 10.1103/PhysRevD.31.3059

CrossRef Full Text | Google Scholar

12. Aprile E, Aalbers J, Agostini F, Alfonsi M, Amaro FD, Anthony M, et al. First dark matter search results from the XENON1T experiment. Phys Rev Lett. (2017) 119:181301. doi: 10.1103/PhysRevLett.119.181301

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Akerib DS, Alsum S, Araújo HM, Bai X, Bailey AJ, Balajthy J, et al. Results from a search for dark matter in the complete LUX exposure. Phys Rev Lett. (2017) 118:021303. doi: 10.1103/PhysRevLett.118.021303

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Cui X, Abdukerim A, Chen W, Chen X, Chen Y, Dong B, et al. Dark matter results from 54-Ton-Day exposure of PandaX-II experiment. Phys Rev Lett. (2017) 119:181302. doi: 10.1103/PhysRevLett.119.181302

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Slatyer TR. TASI Lectures on Indirect Detection of Dark Matter. In: Theoretical Advanced Study Institute in Elementary Particle Physics: Anticipating the Next Discoveries in Particle Physics (TASI 2016). Boulder, CO (2017).

Google Scholar

16. Ackermann M, Albert AM, Anderson B, Atwood WB, Baldini L, Barbiellini G, et al. Searching for dark matter annihilation from milky way dwarf spheroidal galaxies with six years of Fermi large area telescope data. Phys Rev Lett. (2015) 115:231301. doi: 10.1103/PhysRevLett.115.231301

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zitzer B. A Search for Dark Matter from Dwarf Galaxies using VERITAS. The 34th International Cosmic Ray Conference. ICRC2015 (2016).

Google Scholar

18. Ahnen ML, Ansoldi S, Antonelli LA, Antoranz P, Babic A, Banerjee B, et al. Limits to dark matter annihilation cross-section from a combined analysis of MAGIC and Fermi-LAT observations of dwarf satellite galaxies. J Cosmol Astropart Phys. (2016) 1602:039. doi: 10.1088/1475-7516/2016/02/039

CrossRef Full Text | Google Scholar

19. Abdallah H, Abramowski A, Aharonian F, Ait Benkhali F, Akhperjanian AG, Angüner E, et al. Search for dark matter annihilations towards the inner Galactic halo from 10 years of observations with H.E.S.S. Phys Rev Lett. (2016) 117:111301. doi: 10.1103/PhysRevLett.117.111301

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Abramowski A, Acero F, Aharonian F, Akhperjanian AG, Anton G, Balenderan S, et al. Search for photon-linelike signatures from dark matter annihilations with H.E.S.S. Phys Rev Lett. (2013) 110:041301. doi: 10.1103/PhysRevLett.110.041301

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Galli S, Iocco F, Bertone G, Melchiorri A. CMB constraints on Dark Matter models with large annihilation cross-section. Phys Rev. (2009) D80:023505. doi: 10.1103/PhysRevD.80.023505

CrossRef Full Text | Google Scholar

22. Galli S, Iocco F, Bertone G, Melchiorri A. Updated CMB constraints on Dark Matter annihilation cross-sections. Phys Rev. (2011) D84:027302. doi: 10.1103/PhysRevD.84.027302

CrossRef Full Text | Google Scholar

23. Goodman J, Ibe M, Rajaraman A, Shepherd W, Tait TM, Yu H-B. Constraints on dark matter from colliders. Phys Rev. (2010) D82:116010. doi: 10.1103/PhysRevD.82.116010

CrossRef Full Text | Google Scholar

24. Kumar J, Marfatia D, Yaylali D. Vector dark matter at the LHC. Phys Rev. (2015) D92:095027. doi: 10.1103/PhysRevD.92.095027

CrossRef Full Text | Google Scholar

25. Belyaev A, Panizzi L, Pukhov A, Thomas M. Dark Matter characterization at the LHC in the Effective Field Theory approach. J High Energy Phys. (2017) 4:110. doi: 10.1007/JHEP04(2017)110

CrossRef Full Text | Google Scholar

26. Contino R, Falkowski A, Goertz F, Grojean C, Riva F. On the validity of the effective field theory approach to SM precision tests. J High Energy Phys. (2016) 7:144. doi: 10.1007/JHEP07(2016)144

CrossRef Full Text | Google Scholar

27. Belyaev A, Bertuzzo E, Caniu Barros C, Eboli O, Grilli Di Cortona G, Iocco F, et al. Interplay of the LHC and non-LHC Dark Matter searches in the Effective Field Theory approach. Phys Rev. (2019) D99:015006. doi: 10.1103/PhysRevD.99.015006

CrossRef Full Text | Google Scholar

28. Aprile E, Aalbers J, Agostini F, Alfonsi M, Althueser L, Amaro FD, et al. Dark matter search results from a one Ton-year exposure of XENON1T. Phys Rev Lett. (2018) 121:111302. doi: 10.1103/PhysRevLett.121.111302

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Hill RJ, Solon MP. Universal behavior in the scattering of heavy, weakly interacting dark matter on nuclear targets. Phys Lett. (2012) B707:539–45. doi: 10.1016/j.physletb.2012.01.013

CrossRef Full Text | Google Scholar

30. Frandsen MT, Haisch U, Kahlhoefer F, Mertsch P, Schmidt-Hoberg K. Loop-induced dark matter direct detection signals from gamma-ray lines. J Cosmol Astropart Phys. (2012) 1210:033. doi: 10.1088/1475-7516/2012/10/033

CrossRef Full Text | Google Scholar

31. Vecchi L. WIMPs and Un-Naturalness. arXiv:1312.5695 (2013).

Google Scholar

32. Barducci D, Belyaev A, Bharucha AKM, Porod W, Sanz V. Uncovering natural supersymmetry via the interplay between the LHC and direct dark matter detection. J High Energy Phys. (2015) 7:066. doi: 10.1007/JHEP07(2015)066.

CrossRef Full Text | Google Scholar

33. Belyaev A, Fernandez Perez Tomei TR, Mercadante PG, Moon CS, Moretti S, Novaes SF, et al. Advancing LHC probes of dark matter from the inert two-Higgs-doublet model with the monojet signal. Phys Rev. (2019) D99:015011. doi: 10.1103/PhysRevD.99.015011

CrossRef Full Text | Google Scholar

34. Belyaev A, Cacciapaglia G, Ivanov IP, Rojas-Abatte F, Thomas M. Anatomy of the inert two higgs doublet model in the light of the LHC and non-LHC dark matter searches. Phys Rev. (2018) D97:035011. doi: 10.1103/PhysRevD.97.035011

CrossRef Full Text | Google Scholar

35. Mahbubani R, Schwaller P, Zurita J. Closing the window for compressed Dark Sectors with disappearing charged tracks. J High Energy Phys. (2017) 6:119. doi: 10.1007/JHEP06(2017)119

CrossRef Full Text | Google Scholar

36. Belyaev A, Cacciapaglia G, Mckay J, Marin D, Zerwekh AR. Minimal Spin-one Isotriplet Dark Matter. Phys. Rev. (2019) D99:115003. doi: 10.1103/PhysRevD.99.115003

CrossRef Full Text | Google Scholar

37. Zerwekh AR. On the quantum chromodynamics of a massive vector field in the adjoint representation. Int J Mod Phys. (2013) A28:1350054. doi: 10.1142/S0217751X13500541

CrossRef Full Text | Google Scholar

38. Bondarenko M, Belyaev A, Blandford J, Basso L, Boos E, Bunichev V, et al. High Energy Physics Model Database: Towards Decoding of the Underlying Theory (within Les Houches 2011: Physics at TeV Colliders New Physics Working Group Report) (2012).

39. Alloul A, Christensen ND, Degrande C, Duhr C, Fuks B. FeynRules 2.0 - A complete toolbox for tree-level phenomenology. Comput Phys Commun. (2014) 185:2250–300. doi: 10.1016/j.cpc.2014.04.012

CrossRef Full Text | Google Scholar

40. Semenov A. LanHEP - A Package for Automatic Generation of Feynman Rules From the Lagrangian. Updated version 3.1. arXiv:1005.1909 (2010).

Google Scholar

41. Belyaev A, Christensen ND, Pukhov A. CalcHEP 3.4 for collider physics within and beyond the Standard Model. Comput Phys Commun. (2013) 184:1729–69. doi: 10.1016/j.cpc.2013.01.014

CrossRef Full Text | Google Scholar

42. Alwall J, Herquet M, Maltoni F, Mattelaer O, Stelzer T. MadGraph 5: Going Beyond. J High Energy Phys. (2011) 06:128. doi: 10.1007/JHEP06(2011)128

CrossRef Full Text

43. Kilian W, Ohl T, Reuter J. WHIZARD: Simulating Multi-Particle Processes at LHC and ILC. Eur Phys J. (2011) C71:1742. doi: 10.1140/epjc/s10052-011-1742-y

CrossRef Full Text | Google Scholar