Neutrinoless Double Beta Decay Experiments With TeO2 Low-Temperature Detectors

Neutrinoless double beta decay (0νββ) is a powerful tool to investigate Lepton Number Violation (LNV), and the only practical way to assess the nature of the neutrinos. It can therefore provide unique information about the Physics Beyond the Standard Model. If observed, 0νββ would unambiguously demonstrate that neutrinos are Majorana particles and would provide a precise measurement of their mass. Among the many experimental techniques used in the search for this rare process, low-temperature detectors represent one of the most promising choices: they show an excellent energy resolution and can scale to very large masses. In this work, we review the most relevant experiments based on TeO₂ bolometers that have been developed and taking data at the Laboratori Nazionali del Gran Sasso (LNGS), Italy, since the early 90's. This 30-years-old effort has led to the design and construction of the CUORE detector, currently taking data at LNGS. The use of low-temperature detectors allows to study the 0νββ of ¹³⁰Te on both ground and excited states, and to explore different decay mechanisms (“standard” light neutrino exchange, Majoron emission, …). At the same time, the investigation of other rare nuclear physics processes is also possible, such as the two-neutrino double beta decay of ¹³⁰Te as well as the rare decays (¹²⁰Te and ¹²³Te). Next generation bolometric experiments anticipate top leading sensitivities. The corresponding challenges in the development of ton-scale, low background detectors are highlighted.

1. Introduction

Neutrinoless double beta decay (0νββ) [1] is a hypothesized nuclear transition, forbidden in the framework of the Standard Model (SM). In this extremely rare process, a pair of free electrons is created in the transformation from a nucleus (A, Z) into its daughter (A, Z + 2), namely:

$\begin{array}{ll}(A,Z)\to (A,Z+2)+2{\text{e}}^{-}.& (1)\end{array}$

Similar transitions could proceed through the emission of a pair of positrons, double electron capture (EC), or EC plus single emission of a positron, with the nucleus changing from (A, Z) to (A, Z − 2). All these variations are equally interesting when discussing of new Physics, since they all manifest a non-conservation of the number of leptons (see section 6). The observation of one of these processes would therefore demonstrate that the lepton number is not a symmetry of Nature. Such a scenario would open the way to a possible explanation of the Baryon Asymmetry of the Universe via Leptogenesis, thus solving another big mystery of Nature [2]. 0νββ is a fundamental tool to study neutrinos, since it can exist only if they are Majorana particles (the transition could not take place otherwise) and it can provide us with precious information on the neutrino absolute mass scale and ordering, a major clue nowadays.

The experimental search for 0νββ is based on the detection and exact measurement of the sum of the kinetic energies of the two emitted electrons or positrons. In fact, since the energy of the recoiling nucleus is negligible, the sum of the two leptons' kinetic energy must be equal to the Q-value of the transition, Q_ββ, and it should appear in the energy spectrum as a monochromatic peak.

The experimental parameter extracted from the data is the half-life of the decay of the isotope under study, $t_{1/2}^{0\nu }$. In the fortunate case of a 0νββ peak showing up in the energy spectrum, this parameter can be deduced from the radioactive decay law:

$\begin{array}{ll}{t}_{1/2}^{0\nu }=ln2T\epsilon \frac{N_{\beta \beta }}{N_{\text{peak}}}& (2)\end{array}$

where T is the measuring time, ε is the detection efficiency, N_ββ is the number of ββ-decaying nuclei under observation, and N_peak is the number of counts at the peak. If no peak is detected, the sensitivity of a given 0νββ experiment, $S_{1/2}^{0\nu }$, is usually defined as the minimum half-life compatible with the background fluctuations n_B at a given confidence level. In the assumption that the background counts scale linearly with the mass of the detector ¹, we have at 1σ:

$\begin{array}{ll}{n}_B=\sqrt{MTB\Delta }& (3)\end{array}$

where M is the detector mass, B is the background level per unit mass, energy, and time in the region of interest (ROI) around Q_ββ and Δ is the FWHM energy resolution (used conventionally as the region over which to integrate B). Therefore, starting from Equation (2), it is easy to obtain the expression:

$\begin{array}{ll}{S}_{1/2}^{0\nu }=ln2\epsilon \frac{1}{n_{\sigma }}\frac{x\eta N_A}{{{M}}_A}\sqrt{\frac{MT}{B\Delta }}& (4)\end{array}$

where x is the stoichiometric multiplicity of the element containing the ββ candidate, η is the ββ candidate isotopic abundance, N_A is the Avogadro number, ${{M}}_A$ is the compound molecular mass and n_σ is the number of sigmas corresponding to the requested C. L. . Despite its simplicity, this expression clearly shows the role of the basic experimental parameters: improving one or more of these quantities will enhance the sensitivity on $t_{1/2}^{0\nu },$ and this is what drives the experimental decisions and efforts in the search for 0νββ.

Equation (4) isn't valid anymore if the background level is so low that the expected number of background events in the ROI collected during the experiment is nearly zero. This is the so called “zero background” experimental condition. The transition between the two regimes takes place when the expected number of counts is of the order of unity:

$\begin{array}{ll}MTB\Delta ={O}(1).& (5)\end{array}$

In this case, we replace the background term in Equation (3) with n_L, i.e., the maximum number of counts compatible with zero at a given C. L. (in the assumption of Poisson statistics). The new expression for the sensitivity thus becomes:

$\begin{array}{ll}{S}_{1/2,0\text{bkg}}^{0\nu }=ln2T\epsilon \frac{x\eta N_A}{{{M}}_A}\frac{MT}{n_L}.& (6)\end{array}$

Every future experiment on 0νββ has as one of its major goals the reach of the zero background condition (see the discussion in section 7) since, as it can be seen by comparing Equations (4) and (6), the sensitivity increases faster in the latter case, namely linearly with the exposure (the product of the detector mass times the live time).

Within the natural isotopic composition of the different elements, we find 69 ββ-unstable nuclides present [3]. However, only a small subset is of any practical experimental interest for the study of 0νββ. In fact, the choice for a suitable candidate is driven by multiple important requirements:

1. a high Q_ββ, since this corresponds to a higher decay probability, due to the higher Phase Space Factor, and to a lower beta-gamma natural radioactive background,

2. a good detector energy and time resolutions, together with a long enough half-life of the 2νββ half-life, to avoid excessive background counts from this dominating channel;

3. a large natural isotopic abundance or an affordable possibility to isotopically enrich the material;

4. the compatibility with a well-established detection technique.

Unfortunately each of these requests implies often contradictory constraints and a compromise solution is usually unavoidable. As a result, the list of isotopes commonly under study includes [4]: ⁴⁸Ca, ⁷⁶Ge, ⁸²Se, ⁹⁶Zr, ¹⁰⁰Mo, ¹¹⁶Cd, ¹³⁰Te, ¹³⁶Xe, and ¹⁵⁰Nd. Among these, ¹³⁰Te presents important advantages (Table 1) and it results to be a very favorable choice. The Q_ββ of ¹³⁰Te lies in between the Compton edge and the full-energy peak of the 2615 keV γ-line from ²⁰⁸Tl and therefore in a quite low natural background region, while the long 2νββ half-life (about 8·10²⁰ yr [9]) limits the hiding effects of the unavoidable background from this process over the sought peak.

TABLE 1

Table 1. Relevant features of ¹³⁰Te for the search of 0νββ.

The isotopic abundance of ¹³⁰Te is more than 30% in natural Te, a value by far larger than that of all the other above-mentioned isotopes, and a further enrichment is viable, as it has been successfully demonstrated [11]. At the same time, ¹³⁰Te can be part of many different detectors: scintillators [12], solid state detectors [13, 14], as passive source in a tracker-calorimeter detector [15] or in a liquid scintillator [16]. But the most powerful application for the ¹³⁰Te 0νββ study remains at present the use of TeO₂ thermal detectors.

2. Bolometric Technique

Bolometers are calorimeters in which the energy released in a crystal, acting as absorber, by an interacting particle is converted into phonons and measured via temperature variation. These detectors can operate only at cryogenic temperatures of about 10 or few tens of mK. The elementary excitation energy transferred to the lattice phonon system is of the order of 10meV, which corresponds, in the typical detectors used for 0νββ searches, to a temperature increase of about a few tens/hundreds of μK per MeV.

The idea behind the phonon-mediated particle detection is very simple: the specific heat C of a dielectric and diamagnetic crystal cooled down to the millikelvin region can be so low that appreciable temperature increases are induced even by the tiny energy released during a single particle interaction. At these temperatures, C is proportional to the cube of the ratio between the operating and the Debye temperatures of the absorber crystal. In a very intuitive approach, a bolometer can be sketched as a device consisting of an energy absorber thermally linked to a thermometer (Figure 1). A weak thermal link, of conductance G, between the detector and a heat sink kept at constant temperature T_S is needed in order to restore the original temperature after the impinging of the particle. Of course, the real situation is much more complex. For example, the parameters C and G should not be considered as global quantities, but rather as the sum of many contributions, each with its specific behavior. Anyway, this simple thermal model will suffice in order to get a general idea about the operation of these devices.

FIGURE 1

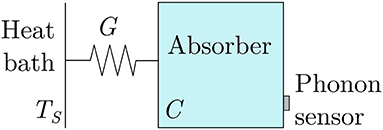
Figure 1. Simplified bolometer thermal model. The detector is modeled as a single object with heat capacity C coupled to the heat sink (at constant temperature T_S) through the thermal conductance G. The phonon sensor plays no active role.

If a certain amount of energy E is released in the absorber, it will produce a change in temperature ΔT equal to the ratio between E and C. Let T(t) be the absorber temperature as a function of the time t and let us assume that

$\begin{array}{ll}\Delta T\equiv |T(t)-T_S|\ll T_S\forall t,& (7)\end{array}$

so that C and G can be considered constant quantities. The temperature variation can then be described by the time evolution

$\begin{array}{ll}\Delta T(t)=\frac{E}{C}{\text{e}}^{-t/\tau }\text{ where }\tau \equiv \frac{C}{G}.& (8)\end{array}$

The characteristic time of the thermal pulse can be very long, up to few seconds, depending on the values of C and G. From Equation (8) we can see that, to get a large signal amplitude, C has to be as small as possible. C is therefore a crucial parameter in the design of the detector.

For what concerns the intrinsic energy resolution of a thermal detector, the only limiting factor are the fluctuations of the internal energy of the system due to the continuous phonon exchange between the absorber and the heat sink. At the thermal equilibrium, the mean number of phonons will be N = C(T)/k_B, each with mean energy ε = k_B T [17], and therefore:

$\begin{array}{ll}\Delta E\propto \epsilon \sqrt{N}=\xi \sqrt{k_{\text{B }}C(T)T^2}.& (9)\end{array}$

The factor ξ is a dimensionless factor that depends on the details of the real detector and it can become of the order of unity with a proper optimization work. Equation (9) tells that the intrinsic energy resolution of bolometers can be as low as few eV even for crystal masses of the order of 1 kg, provided that the temperature is sufficiently low. This description shows that the resolution is independent of the energy released in the absorber. It holds only if we can assume that the system has reached a complete thermalization before the readout. In general, this is not always the case. For example, when the thermometer detects the out-of-equilibrium high-energy phonons directly produced by the particle interaction in the absorber, the energy resolution will be dominated by the fluctuation in the number of produced elementary quanta (phonons or quasi-particles, depending on the specific device). However, all the TeO₂ bolometers developed in the last 30 years for 0νββ search have been using semiconductor thermistors glued on the absorber crystals, for which the hypothesis of complete phonon thermalization before readout is quite correct.

In reality, the effective energy resolution of thermal detectors is generally dominated by the “extrinsic” noise generated by a variety of uncorrelated sources that cannot be fully eliminated [18, 19]. Among these we can cite the thermal noise (i.e., noise due to temperature instabilities of the heat sink), the Johnson noise, or any kind of noise related to the electronics readout and the cryogenic system. At the end, the combination of these multiple factors usually results in an energy resolution of the order of few keV at 1 MeV (see section 4), a value still competitive with that of the best performing detectors.

Besides the excellent performance, another important advantage of bolometers is the very broad choice for the absorber material. Indeed, for almost any element it is possible to identify a compound suitable for a bolometric application. This is the case, for example, of Tellurium. In its metallic form, Te is unable to stand thermal cycles [20]. Instead, the compound Tellurium dioxide, TeO₂ has demonstrated to be an excellent choice, as it will be shown in sections 4 and 5.

The main disadvantages of bolometers are their intrinsic slow response and insensitivity to the nature of the interacting particles. However, the former can be mitigated by a proper choice of field of the application, such as rare-event searches, while the latter can take advantage by the acquisition of additional information. Hybrid detectors, characterized by the simultaneous measurement of heat and ionization or scintillation/Čerenkov light, had been proposed since long time [21]. These have already been successfully implemented in a number of experiments aiming at the detection of Dark Matter candidates [22–24]. At the same time, by exploiting the broad variety of available materials offered by the bolometric approach, a number of successful R&D's [11, 25–31] has demonstrated the effectiveness of this technique in the identification of the contributions from alpha emissions. This allows to get rid of one of the most dangerous background sources in experiments looking for 0νββ, and it is thus paving the road to future low background experiments. Correspondingly, very sensitive light bolometric detectors have been developed [32–35] and implemented in medium-scale demonstrators [30, 36, 37] to demonstrate the viability of the technique. Molybdenum if at the moment the favorite choice even if tellurium is still a viable alternative.

3. TeO₂ Bolometers for 0νββ Studies

As mentioned, the main component of a bolometer is the crystal acting as absorber and, in this regard, TeO₂ is a particularly suitable material. TeO₂ is the most stable oxide of Te [38] and presents good thermal properties for cryogenic particle detectors. TeO₂ crystals are dielectric and diamagnetic, with a relatively high value of the Debye temperature (Θ_D = (232 ± 7) K [39]). This leads to very low heat capacity at cryogenic temperatures which, we recall, is fundamental if you want a high energy resolution bolometer. Since the thermal expansion of TeO₂ is very close to that of copper [40, 41], its use in the mechanical support structure does not introduce excessive strain on the crystals during cool down.

TeO₂ crystals have mechanical and optical characteristics that match very well the requirements for thermal detectors. At the same time, significant developments in preparing powder out of this compound and in growing the crystals allow nowadays the production of almost perfect (bubble-free, crack-free and twin-free) crystal boules from which crystals with masses of the order of 750 g [42, 43] or more [44, 45] can be routinely obtained. TeO₂ satisfies also the tight requirements imposed on radiopurity: thanks to dedicated production lines for the raw powder synthesis, the crystal growth and the surface processing, crystals with bulk contamination of the order of 10⁻⁶ Bqkg⁻¹ for ²³⁸U and ²³²Th, and with surface contamination levels of a few 10⁻⁹ Bq cm⁻² for both ²³⁸U and ²³²Th [46, 47], are now achievable [43, 46].

The other key component of a bolometer is the phonon sensor. The type of device used in all the ¹³⁰Te cryogenic detectors reviewed in this work has always been Ge thermistors. In general, semiconductor thermistors consist of small Ge crystals with a region doped near the metal-insulator transition (MIT). The resistance presents therefore a steep slope as a function of the temperature, with a logarithmic sensitivity, A ≡ | d log R(T) / d log T |, that can reach values close to 5–10. To reach a very uniform and large dopant distribution, together with an accurate net dopant concentration, the Neutron Transmutation Doping (NTD) [48] technique can be used. The semiconductor slab, from where the thermistors will be afterwards obtained, is bombarded with a high intensity neutron flux, which induces nuclear transformations of some of the natural Ge isotopes. This leads to the formation of a compensated doped semiconductor, with n- and p- dopants present at a similar concentration level near the MIT. For brevity, these doped semiconductors are usually referred to as simply “NTDs.” The resistivity as a function of the temperature follows the exponential law

$\begin{array}{ll}\rho ={\rho }_{0}exp{\left(\frac{T_0}{T}\right)}^{\gamma }& (10)\end{array}$

where ρ₀ and T₀ are parameters that depend on the doping level and compensation. For NTDs γ is typically 1/2 [49].

The resistance variations of the thermistor are transformed into a readable voltage signal using a constant bias current I_B generated by means of the bias circuit shown in Figure 2. The DC power supply is closed on a load resistor R_L in series with the thermistor R_bol, with R_L ≫ R_bol. In this way I_B is practically independent of the value of R_bol. Once a certain bias current is circulating, a voltage drop V_bol(T) = I_B R_bol(T) crosses the thermistor. The consequent power dissipation P = I_B V_bol produces a rise of the bolometer temperature T_bol and acts back on the resistance R_bol(T), lowering it, and therefore reducing the voltage drop. This in turn reduces the dissipated power, until an equilibrium is reached:

$\begin{array}{ll}{T}_{\text{bol}}=T_S+\frac{P}{G}.& (11)\end{array}$

This phenomenon causes the V-I relation, called “load curve,” to deviate from the simple Ohm law and leads to a behavior that is often referred to as “electrothermal feedback.” The (I_B, V_bol) pair, once the equilibrium is reached, corresponds to a precise working point for the thermistor and any instantaneous temperature variation will be translated into a voltage pulse. The relationship between the electrical pulse height ΔV_bol and the energy deposition E in the crystal is obtained by solving the circuit of Figure 2:

$\begin{array}{ll}\Delta V_{\text{bol}}~\frac{E}{C·T_{\text{bol}}}·\sqrt{P·R_{\text{bol}}}& (12)\end{array}$

where P is the power dissipated in the thermistor R_bol by Joule effect.

FIGURE 2

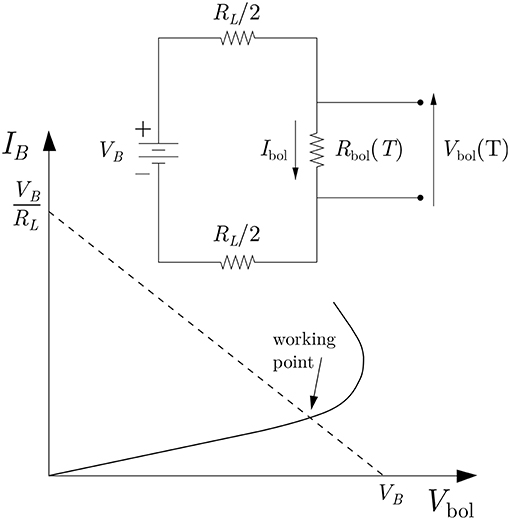
Figure 2. (Top) Electric scheme of the biasing system used for the NTD readout. (Bottom) Typical load curve of a semiconductor thermistor. The working point is set as the intersection between the V-I characteristic curve and the load line V_bol = V_B − I_B R_L.

The highest sensitivity in the conversion of the thermal pulse into an electric voltage signal is obtained when the working point is selected close to the inversion on the load curve (see Figure 2). Its value is way larger than the one that would be obtained by selecting a working point in the linear part of the load curve. To make a concrete example, an energy deposition of 1MeV in a 750 g TeO₂ absorber at 10 mK typically produces a temperature increase ΔT ~ 100 μK, with a related voltage drop ΔV_bol ~ 100 μV.

An additional crucial component of a thermal detector is the pulser system. When bolometers are operated over long periods, keeping a stable detector's response becomes mandatory, even in presence of temperature fluctuations of the cryogenic setup. In these cases, a pulser able to periodically deliver a fixed and extremely precise amount of energy to the detector [50, 51], represents an effective approach to deal with this issue. Of course, the system must generate a pulse as similar as possible to that corresponding to a real event. Such control pulses can be obtained by injecting calibrated amounts of energy through the interaction of well-known energetic charged particles, or by means of light pulses transmitted via optical fibers, or by Joule-heating of a resistive element thermally coupled to the absorber crystal. The variation of the detector response to the same energy deposition can then be used to correct (off-line) the effects of most of the cryogenic instabilities.

In the TeO₂ bolometers covered by this review, the chosen solution has been to glue on the crystal a resistive element consisting in a heavily doped (well above the MIT region) Si semiconductor, which thus exhibits a low-mobility metallic behavior [52]. This special “heater” satisfies two important requirements: to have a resistance free from temperature and applied voltage dependence, and a negligible heat capacity if compared to that of the crystal. This solution offers the clear advantage of a complete control on the off-line detector's response correction: the pulses can be released periodically and their rate and amplitudes can be chosen looking at the specific needs of the experiment. In order to provide an energy release as prompt as a real particle interaction would be, the relaxation time of the heat toward the crystal has to be much shorter than all the thermal time constants of the detector, while the signal generation of particle interactions and Joule-heating has to be similar enough to ensure that the pulse amplitude dependence on time, baseline level and other operation conditions, will be the same for the two processes.

Finally, the remaining components of any cryogenic detector are both the mechanical and electrical connections. Regarding the former, the mechanical holder of the TeO₂ crystals and the main thermal connection to the heat bath have been relying since long time on the use of more or less complex PTFE clamps and copper structures. By taking advantage of the different thermal contraction of these materials and of the crystals, it has been possible to fasten the system as a whole. Concerning the latter, electrical contacts are obtained by means of 25 or 50 μm-thick gold wires bonded on the thermistor and on the Si heater.

4. Past Experiments

A long sequence of measurements based on TeO₂ thermal detectors began to take place starting from 1991. The original group was led by E. Fiorini and comprised only a few researchers. Early runs were carried out with crystals with very small mass, from 6 g to 73 g [53–56]. Apart from the study of 0νββ, these runs were intended to investigate the background level achievable with the bolometric technique, whose use was relatively new in the field. A large effort was thus paid to the mitigation of the background contamination of the whole experimental apparatus, by constantly improving the material selection and the design of the detector components.

These bolometric measurements found a favorable environment in the Laboratori Nazionali del Gran Sasso of I. N. F. N. (LNGS) in Italy². With a rock coverage of about 3600 m w. e. and a mostly calcareous composition [57], this facility is able to guarantee very low muon and neutron fluxes, at the level of 3·10⁻⁸ cm⁻² s⁻¹ [58] and 4·10⁻⁶ cm⁻² s⁻¹ [59], respectively, thus offering suitable conditions for the search for 0νββ.

The results obtained on the 0νββ half-life of ¹³⁰Te immediately showed to be competitive and world-leading. In less than 2 years since the start of the experimental activity, it was possible to improve the limit coming from a direct search from $t_{1/2}^{0\nu }>2.8·10^{18}\text{ yr}$ (obtained with a CdTe detector [13]) to $t_{1/2}^{0\nu }>2.7·10^{21}\text{ yr}$ at 90%C. L. [56], and to pass the most stringent at the time, i.e., $t_{1/2}^{0\nu }>2.6·10^{21}\text{ yr}$, coming from an inclusive double beta decay study (0νββ + 2νββ) of ¹³⁰Te with the geochemical method [60].

A significant improvement was represented by the use of a 3 × 3 × 6cm³ TeO₂ crystal of 334 g of mass [61] (at the time, the largest thermal detector ever operated in the world), that became the unitary element of the first bolometric array with large-mass crystals. In particular, a detector constituted by 4 bolometers was operated in 1994 [62], while a tower made of 20 bolometers (5 floors of 4 crystals each) was assembled and operated since 1997 [63]. The latter experiment was named MiDBD (Milan Double Beta Decay) and opened the competitive era of bolometers in the world leadership ride for 0νββ searches.

MiDBD proved that an energy resolution of 5 keV at Q_ββ was within reach and achieved a very low background of less than 1 counts keV⁻¹ kg⁻¹ yr⁻¹ in the Region of Interest (ROI), around Q_ββ. After few years of operation, the original detector was dismounted and remounted in a new and significantly improved configuration [64]. The new crystal assembly was much more compact and it was therefore possible to reinforce the detector shielding with additional lead. Moreover the new design required less support material for the crystals (copper and PTFE), thus allowing to reduce the background even more thanks to less passive material mass and surface and a more effective anti-coincidence analysis. With a total exposure of 4.25 kg yr, MiDBD set the limit $t_{1/2}^{0\nu }>2.1·10^{23}\text{ yr}$ at 90%C. L. .

In parallel with the operation of MiDBD, an important technological improvement was obtained with the massive production of very high quality crystals of ~ 750 g and their successful operation as bolometers [65]. These 5 × 5 × 5cm³ TeO₂ crystals were proposed as “bricks” of an extremely ambitious project: a bolometer array of 1000 cryogenic detectors, the Cryogenic Underground Observatory for Rare Events, alias CUORE [66]. The unitary element of such a big array was supposed to be a tower of 4-crystal floors, similar to MiDBD but with bigger crystals.

As an intermediate step toward CUORE, a single tower, named Cuoricino (Italian for “small CUORE”) was designed and operated. Apart from being a proof of concept for CUORE, Cuoricino was with full honors a standalone experiment. The tower, the new world largest cryogenic detector ever in operation, consisted of 44 5 × 5 × 5cm³ crystals, and 18 3 × 3 × 6cm³ crystals coming from MiDBD, for a total TeO₂ mass of 40.7 kg. These crystals were disposed into 13 floors, 11 4-crystal modules housing the larger crystals and 2 9-crystal modules housing the smaller ones.

The detector was successfully run for over 5 years. The best performance, both in terms of background counts and resolution, was reached with the 5 cm-side bolometers, which achieved (0.153 ± 0.006) counts keV⁻¹ kg⁻¹ yr⁻¹ in the ROI ³ and a FWHM resolution of (5.8 ± 2.1)keV [70] at the Q_ββ. Cuoricino improved the previous limit on 0νββ set by MiDBD by more than one order of magnitude: $t_{1/2}^{0\nu }>2.8·10^{24}\text{ yr}$ at 90%C. L. . At the same time, this detector showed that it was possible to operate massive and complex bolometric detector arrays almost continuously.

In view of the forthcoming CUORE experiment, a big effort was paid to the investigation of the background sources. Thanks to Cuoricino, it was definitely confirmed that the major contribution to the counts in the ROI was produced by “degraded” alphas, i.e., alpha particles that deposit only part of their total energy in the detector, as expected in crystal or copper/PTFE surface events. Several dedicated R&D setups were put into operation in an ancillary cryostat at LNGS to investigate the individual contributions to the background, in order to address the issue of its reduction in the most effective way. These studies led to an improved detector design and cleaning protocol for both the crystals and the support materials. In addition, a completely industrialized assembly line was realized in order to transform the over 10,000 ultra-clean pieces into CUORE towers [71]: all the construction processes had to be performed into sealed glove boxes constantly flushed with N₂ to prevent the re-contamination of the various components by any exposure to air (and thus to Rn).

The final test for CUORE consisted in operating as a standalone experiment a prototype tower, CUORE-0, produced and assembled following all the new procedures, protocols and prescriptions. The CUORE-0 tower [70] comprised 52 5 × 5 × 5cm³ crystals, arranged in 13 4-crystal floors, for a total mass of 39kg of TeO₂. The collected data allowed ultimately to check all the improvements achieved since Cuoricino. In particular, for what concerns the background, a significant reduction was obtained, spanned over the whole energy range, with a factor ~3 reduction in the Q_ββ region. The counts in the ROI were (0.058 ± 0.004 (stat.) ± 0.002 (syst.)) counts keV⁻¹ kg⁻¹ yr⁻¹ and the α continuum above 2615keV was a factor ~ 7 smaller than that obtained with Cuoricino.

The combined limit of Cuoricino and CUORE-0, whose results are comparable due to the better performance of the latter despite its shorter live time, was $t_{1/2}^{0\nu }>4.0·10^{24}$ at 90%C. L. [67], among the stringent ones on the 0νββ process.

5. Present: The CUORE Experiment

CUORE [72] consists of 19 CUORE-0-like towers. The number of TeO₂ crystals is 988, for a total mass of 742kg (Figure 3). Given the natural isotopic abundance, this corresponds to ~ 206kg of ¹³⁰Te. CUORE is by far the largest bolometer array operated.

FIGURE 3

Figure 3. The CUORE detector with the experiment logo. Reproduced with permission from the CUORE Collaboration. See original in the official CUORE experiment website. Available online at: https://cuore.lngs.infn.it/en.

After the design and realization of the assembly line, the full detector construction took about 2 years. The installation inside the CUORE cryostat could be performed after the completion of the commissioning of the cryogenic system. In the meanwhile, the individual towers were stored in sealed containers constantly flushed with clean N₂ gas, inside the CUORE cleanroom. This prevented any contamination of the crystals and frames from Rn. The installation was performed during summer 2016. This extremely delicate task (the fragile detector is completely “bare”) was carried out in a controlled cleanroom environment continuously flushed with Rn-free filtered air [73]. The background target level in the ROI was set to 0.01 counts keV⁻¹ kg⁻¹ yr⁻¹, reflecting the expected outcome of the extensive background reduction program.

CUORE also benefited from the completely new cryostat. The CUORE cryostat is a huge custom-made dilution refrigerator cooled down by multiple Pulse Tube units [74, 75]. Its design had to satisfy a set of very stringent experimental requirements: high cooling power and cryogenic reliability, low noise detector environment and extremely low radioactivity content. In particular, the cryostat is composed of six nested high-purity-copper vessels. The innermost vessel encloses the experimental volume, which is ~ 1m³ (Figure 4). The detector is attached to a dedicated suspension system that strongly reduces the amount of transmitted vibrations, which represent a noise source. In order to mitigate the radioactive background, almost 7 t of lead are integrated in the structure. The largest part of the shielding is made of ancient Roman lead [76]. In addition, the whole apparatus is protected from the external environmental radioactivity by a 80-ton composed shield made of polyethylene, H₃BO₃ and lead.

FIGURE 4

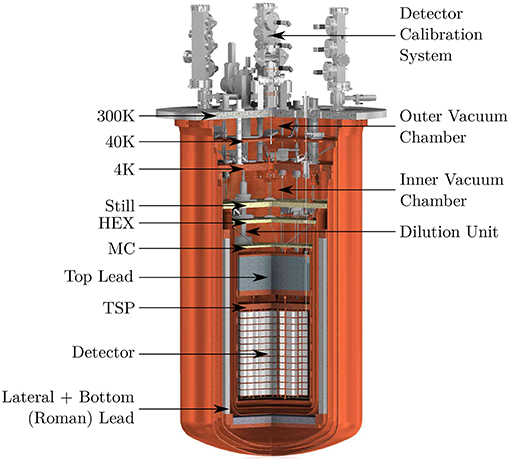
Figure 4. The CUORE cryostat. The different thermal stages, the lead shields, the vacuum chambers and the cooling units are indicated. See original in the official CUORE experiment website. Available online at: https://cuore.lngs.infn.it/en.

CUORE, which started the data-taking in spring 2017, will collect data until reaching a total of 5yr live time. The successful cool down and operation of CUORE marks an important step in the application of thermal detectors for rare-event searches, by bringing it to the ton-scale. It also opens the way to the use this technologies to future large-mass bolometer arrays.

5.1. CUORE Background

The experience acquired in running the previous TeO₂ experiments, supported by a complete Monte Carlo simulation of the detector (and of the shielding) that has been developed and fine-tuned step-by-step since MiDBD, allowed the implementation of a background model for CUORE-0 first [9], and then for CUORE [77]. Three dominant sources have been identified as contributors to the Background Index (BI):

• multi-Compton events from the γs line of ²⁰⁸Tl (2615 keV), coming from the ²³²Th contamination of the cryogenic system;

• ²³⁸U and ²³²Th α-emitting contamination (with related decay products), coming from the surface of the TeO₂ crystals. This also include the surface contamination ²¹⁰Pb (with the long half-life of ~ 22.3yr) from the environmental ²²²Rn;

• α-emitting contamination coming from the surfaces of the inert materials facing the crystals, mostly the copper frames.

The strategy adopted in CUORE in order to reduce these contributions consisted in the optimization, i.e., reduction, of the amount of inert material employed for the detector frames and structure and in the improved design of the shields. This was done in addition to the dedicated cleaning treatments, both for crystals and copper. The resulting effectiveness has been demonstrated by CUORE-0, which observed a reduced background with respect to Cuoricino of about a factor 3 in the ROI. This success was actually limited by the use of the same cryogenic infrastructure of the Hall A cryostat (about 25-years-old during the run CUORE-0).

The selection and procurement of all the materials then used in the construction of the CUORE detector and cryostat was preceded by a broad screening campaign. This study employed different material assay techniques and considered both bulk and surface contamination (these could have occurred during the part handling and machining, and/or due to air exposure). Furthermore, a specific analysis of material activation for TeO₂ was performed. This helped to confirm that the overall exposure to cosmic radiation following the production and transportation of the crystals did not constitute a major issue for CUORE [78].

In the end, the sources that were believed could give a sizable contribution to the CUORE BI were identified with:

• ²³⁸U and ²³²Th (and their progeny) coming from crystals and holders;

• cosmogenically activated isotopes from crystals and copper parts closest to the detector;

• ²³⁸U and ²³²Th coming from cryostat vessels and lead shields.

The projection of the total BI resulted in $(1.02\pm 0.03{\text{(stat)}}_{-0.10}^{+0.23}\text{(syst)})·10^{-2}$ counts keV⁻¹ kg⁻¹ yr⁻¹. A detailed list of the individual contributions is reported in Figure 5. The dominant entry is represented by the degraded αs coming from the surface contaminants of the detector frames.

FIGURE 5

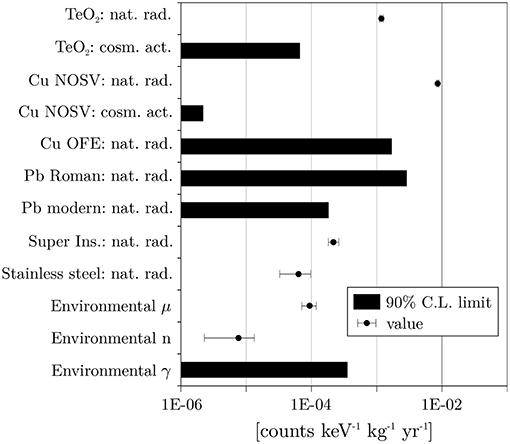
Figure 5. Histogram with the main BI components expected for CUORE. The bars indicate upper limits (90% C. L.), while the markers derived values (with 1σ uncertainty). The thick line marks the CUORE background target. Figure from Alduino et al. [77].

The ultimate validation (or rejection) of the projected background model for CUORE will come from the CUORE data themselves, provided that sufficiently high statistics will be collected.

5.2. CUORE First Results

At the end of 2017, CUORE released the first results on the 0νββ search. The total TeO₂ exposure was 86.3kg yr [69]. The background was found in line with the expectations: (1.4 ± 0.2)·10⁻² counts keV⁻¹ kg⁻¹ yr⁻¹, while the average bolometer energy resolution at Q_ββ was (7.7±0.5)keV. The latter parameter saw an improvement during the data-acquisition campaign and room for further a improvement down to ~ 5keV is still present, thanks to improved cryogenic stability and data analysis.

The final spectra in ROI region for MiDBD, Cuoricino and CUORE-0 spectra are reported in Figure 6, together with the initial CUORE spectrum. The combined limit of CUORE, CUORE-0 and Cuoricino on the ¹³⁰Te 0νββ half-life is 1.5·10²⁵ yr [69]. It follows the corresponding limits in ¹³⁶Xe and ⁷⁶Ge, namely 1.1·10²⁶ yr at 90%C. L. by the KamLAND-Zen Collaboration [79] and 8.0·10²⁵ yr at 90%C. L. by the GERDA Collaboration [80]. Eventually, CUORE is expected to raise its half-life limit sensitivity at 9.0·10²⁵ yr at 90%C. L. [81], therefore ensuring the central role played by thermal detectors in the forthcoming future.

FIGURE 6

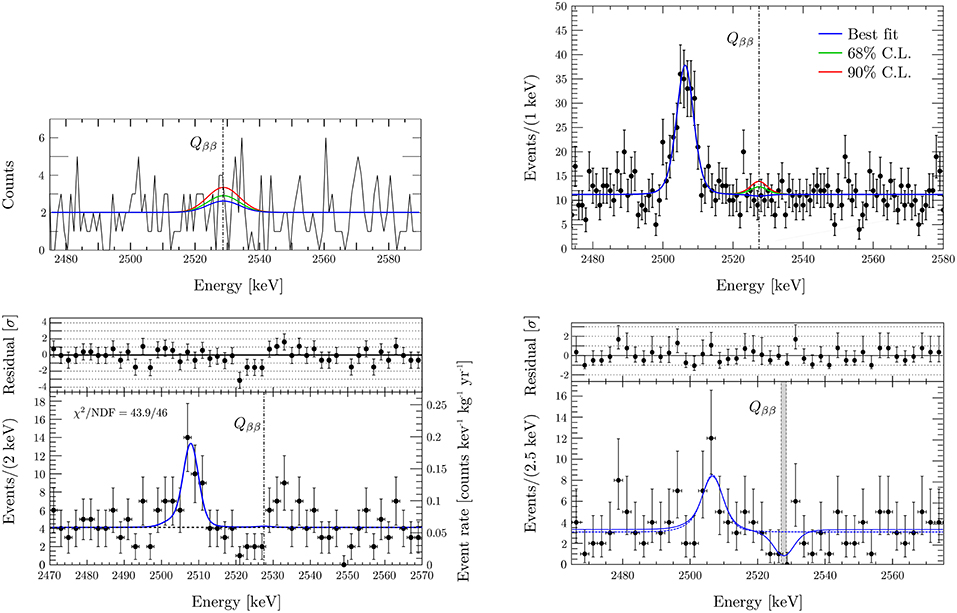
Figure 6. (From Left to Right, Top to Bottom) MiDBD, Cuoricino, CUORE-0 and CUORE (first data release) best-fit model in the ROI region. No peak is found at Q_ββ (that at ~ 2507 keV is attributed to ⁶⁰Co). Figures from Arnaboldi et al. [64], with permission from Elsevier, Alfonso et al. [67], with permission from Elsevier, Andreotti et al. [68], with permission from the American Physical Society, and Alduino et al. [69], with permission from the American Physical Society (see the references for details).

5.3. Constraints on the Neutrino Mass

The huge impact on Particle Physics that the observation of 0νββ would have is of course not related to the interest on an extremely rare nuclear decay, that would put another important tile in the framework of Nuclear Physics and would challenge theoreticians to explain the observed half-life, but to the consequences that the observation or even the limits posed on its half-life would have on neutrino physics.

The connection between 0νββ and some neutrino properties can be extracted from the Majorana effective mass definition:

$\begin{array}{ll}{m}_{\beta \beta }\equiv \left|{\text{e}}^{i{\alpha }_1}|U_{\text{e}1}^2|m_1+{\text{e}}^{i{\alpha }_2}|U_{\text{e}2}^2|m_2+|U_{\text{e}3}^2|m_3\right|& (13)\end{array}$

where m_i are the masses of the neutrino eigenstates ν_i, α_{1, 2} are the Majorana phases and U_ei are the elements of the PMNS mixing matrix that define the composition of the electron neutrino: $|{\nu }_{\text{e}}\rangle ={{\sum }^{\text{}}}_{i=1}^3{U}_{\text{e}i}^{*}|{\nu }_i\rangle$.

If a 0νββ would be observed, the measurement of $t_{1/2}^{0\nu }$ would translate into a value of m_ββ, while an experimental limit on $t_{1/2}^{0\nu }$ will always correspond to an upper bound on m_ββ. In order to operate this conversion, it is necessary to pass through quantities obtained by theoretical calculations of atomic and nuclear physics. Within the hypothesis of “ordinary” neutrinos as mediators of the 0νββ transition, a convenient parametrization for $t_{1/2}^{0\nu }$ can be:

$\begin{array}{ll}{\left[t_{1/2}^{0\nu }\right]}^{-1}=\frac{m_{\beta \beta }^2}{m_{\text{e}}^2}{G}_{0\nu }|{{M}}_{0\nu }{|}^2& (14)\end{array}$

where G_0ν is the Phase Space Factor (PSF), ${{M}}_{0\nu }$ is the Nuclear Matrix Element (NME), and m_e is the electron mass, conventionally taken as normalization factor for m_ββ.

By inverting Equation (14) and by choosing proper values for the isotope of interest for PSF [82] and NME (e.g., [83]), it is thus possible to obtain the limits on m_ββ starting from the experimental sensitivities.

There has been a lot of discussions in the last years on the correct value of the axial-vector coupling constant to be used in the calculation of the NME and for this reason you will now often find Equation (14) unfolded, with the dependence from ${g_{\text{A}}}^4$ made explicit. Since we still lack of a unanimous guideline on the value to be used for g_A in nuclear decays in general and in 0νββ in particular, we will stick to the conventionally used value of g_{A, nucl} ≃ 1.27, the value observed in neutron decay, leaving it hidden inside the NME.

When passing from $t_{1/2}^{0\nu }$ to m_ββ, the uncertainties in the theoretical calculations should be taken into account. The PSFs have been recently recalculated [82] with accurate precision for most of the nuclei of interest for 0νββ. The present uncertainty is about 7%. For the NMEs, the situation is more complicated. A relatively small intrinsic error of ≲ 20% [83, 84] is presently assessed by the most recent calculations within the same theoretical approach. But the disagreement between the results from different models is still quite large, up to a factor ~ 3.

For this reason, any experimental limit on $t_{1/2}^{0\nu }$ will actually correspond to a range of values for m_ββ, that will translate into a horizontal band in the usual representation of m_ββ as a function of the mass of the lightest neutrino m_lightest [85, 86]. An example is shown in Figure 7. The two branches that appear in these type of plots correspond to the two (mutually exclusive) scenarios of Normal and Inverted Hierarchy (NHand IH) of the neutrino mass spectrum. The broadness of the branches depends on the adopted approach in discussing the theoretical uncertainties.

FIGURE 7

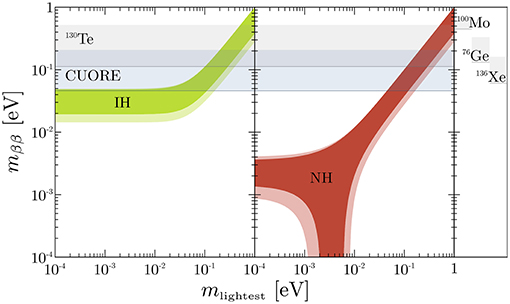
Figure 7. Predictions on m_ββ from oscillations as a function of the mass of the lightest neutrino in the two cases of NH and IH. The shaded areas correspond to the 3σ regions after propagation of the uncertainties on the oscillation parameters [87]. The horizontal gray band shows the current 0νββ limit of ¹³⁰Te after the first CUORE data release [69], while the blue band shows the projected CUORE sensitivity [81]. To the side, the current limits on the 0νββ half-life for ⁷⁶Ge [80], ¹⁰⁰Mo [88] and ¹³⁶Xe [79] are reported.

As for the experiments with T_eO₂ discussed in this paper, their limits on m_ββ, calculated using the PSF from Kotila and Iachello [82] and the NME from Barea et al. [83], are shown in Table 2. As can be seen, the evolution of the limit on the decay half-life of the 0νββ of ¹³⁰Te proceeded in parallel with the technological improvements on the bolometric detectors: mass, energy resolution, background.

TABLE 2

Table 2. Main characteristics of the TeO₂ bolometric experiments searching for the 0νββ of ¹³⁰Te.

In Figure 7 the bands coming from some of the most studied isotopes are plotted. The constraint from ¹³⁰Te, i.e., the current CUORE limit on m_ββ < (110−520)meV [69], is already compatible with that from ⁷⁶Ge, while the projected CUORE sensitivity should reach (or pass) the most stringent present limit, coming from ¹³⁶Xe, approaching the Inverted Hierarchy region.

6. Other Studies

Although 0νββ of ¹³⁰Te is the main objective of TeO₂ bolometers, a number of other processes is open to experimental investigation. The excellent energy resolution and the anticipated low background rates allow competitive sensitivities for many of them. The accessible processes include alternative modes of double beta decay as well as more exotic processes predicted by some extensions of the SM.

Indeed, natural tellurium includes ββ -active isotopes other than ¹³⁰Te , namely ¹²⁰Te and ¹²⁸Te , and the ββ transitions to excited states can provide unique information on the 0νββ mechanism. On the other hand, the precise measurement of the 2νββ half-lives is crucial to test the constraints of the ββ nuclear matrix elements.

Among the exotic processes, the experimental investigation of the validity limits of fundamental principles such as the charge conservation or the CPT/Lorentz invariance deserve particular attention since most of our theoretical construction is based on them. On an equal footing, the search for Dark Matter candidates (which, by the way, began with the first 0νββ experiments), is still a subject on which TeO₂ bolometers can provide competitive results.

6.1. Alternative Double Beta Decays

Thanks to a larger available energy, the best 0νββ experimental sensitivity is generally for the transition to the ground state of the daughter nucleus. However double beta decay may occur (in both 2ν and 0ν modes) also to an excited state of the daughter nucleus. In the case of 0νββ, these transitions can disclose the exotic mechanisms (e.g., RH currents) which mediate the decay [89, 90], while for 2νββ they can provide unique insight to the details of the mechanisms responsible for the nuclear transition [91, 92]. From the experimental point of view, most of the interest is motivated by the fact that in a close packed array, like those developed for TeO₂ bolometers, the strong signature provided by the simultaneous detection of one or two gammas can lead to an almost background-free search. In this respect, the transitions to 0⁺ states are favored while states with larger spin (e.g., 2⁺) are generally suppressed by angular momentum conservation. The adopted strategy exploits multiple coincidence patterns to select topological configurations characterized by a lower background contribution [93]. In this respect, particularly interesting is the 0νββ transition of ¹³⁰Te to the 0⁺ excited state at 1793.5 keV of ¹³⁰Xe whose de-excitation is characterized by a cascade of multiple high energy gamma's which provide distinctive signatures.

Up to date, no evidence for any of the ββ transitions of tellurium isotopes to 0⁺ and 2⁺ excited states of xenon has been observed. In all the cases, the most stringent limits come from TeO₂ bolometers [63, 93–96]. The 90% C. L. half-life limits by the combined Cuoricino + CUORE-0 are [93]:

$\begin{array}{ll}{\tau }_{0^{+}}^{0\nu }>1.4·10^{24}\text{ yr and }{\tau }_{0^{+}}^{2\nu }>2.5·10^{23}\text{ yr}.& (15)\end{array}$

¹³⁰Te is certainly the most favorable isotope for ββ searches (see section 5.3).

Two other tellurium isotopes are however also ββ -active: ¹²⁸Te and ¹²⁰Te . ¹²⁰Te can β⁺EC decay to ¹²⁰Sn with a transition energy of 1730 keV [97]. Despite β⁺β⁺, β⁺EC and EC EC modes are generally less appealing because of the lower available energy, they can only be mediated by peculiar mechanisms and can therefore provide unique details on the decay [98, 99]. Although no calculation of the nuclear matrix element is presently available in the literature for ¹²⁰Te , the expected 0νβ⁺EC half-lives for other most commonly investigated isotopes are a few orders of magnitude larger with respect to 0νββ, making the search for this decay mode very appealing. In addition, the presence of the positron with the consequent emission of a pair of back-to-back 511 keV gammas provides extremely clean signatures (Figure 8) which reduce the background contributions and compensate for the low isotopic abundance of ¹²⁰Te (0.09%). The decay scheme is:

$\begin{array}{ll}{}^{120}\text{T}\text{e}+{\text{e}}^{-}\to {}^{120}\text{S}{\text{n}}^{*}+{\beta }^{+}\to {}^{120}\text{S}\text{n}+X+{\beta }^{+}\to {}^{120}\text{S}\text{n}+X+2\gamma ,& (16)\end{array}$

where the asterisk indicates an atomic excited state while X stays for the products of atomic de-excitation (X-rays or Auger electrons). In TeO₂ bolometers the latter amounts to the captured electron binding energy and adds to the positron energy. The signature is therefore the coincidence of a fixed amount of energy deposition and two 511 keV γs. No evidence for ¹²⁰Te decay has been observed so far, and again the stringent limits is set by TeO₂ bolometers, namely the combined Cuoricino + CUORE-0 [100, 101]:

$\begin{array}{ll}{t}_{1/2}^{0\nu }({}^{120}\text{T}\text{e})>2.7·{10}^{21}\text{ yr }(90\%\text{ C}.\text{L}.).& (17)\end{array}$

¹²⁸Te ββ transitions have been investigated since a long time. The large natural isotopic abundance of this isotope, 31.74%, is in fact very appealing. However the very low transition energy, 866.6 keV [97], leads to a generally poor sensitivity and weakens the interest for this search. On the other hand, its very large 2νββ half-life [102] is out of reach even for a ton-sized arrays like CUORE.

FIGURE 8

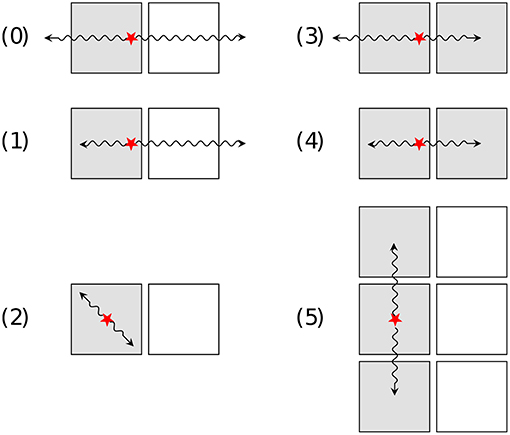
Figure 8. Signatures of the 0νβ⁺EC decay of ¹²⁰Te in CUORE-0. The red stars indicated the energy depositions by the β⁺ , while the arrows represent the resulting annihilation 511-keV γ rays. The shaded squares show the crystals which see an energy deposition. Figure from Alduino et al. [100], with permission from the American Physical Society.

Exotic 0νββ forms, characterized by the emission of a massless Goldstone boson, called Majoron, were originally introduced within SM extensions in which neutrino masses are obtained as a manifestation of the spontaneous break of the lepton number symmetry [103]. The precise measurements of the Z invisible width at LEP, has greatly disfavored the original Majoron triplet and pure doublet. Several new models have been developed [104, 105], which predict different (continuous) spectral shapes for the sum energies of the emitted electrons. This extends from zero to the transition energy $Q_{\beta \beta }:dN/dT\propto {(Q_{\beta \beta }-T)}^n$, where T is the electron summed kinetic energy and the spectral index n depends on the decay details (Figure 9). Single Majoron emissions are characterized by n = 1−3, while double Majoron decays can have either n = 3 or n = 7. The precise measurement of n allows to discriminate between the processes and 2νββ (n = 5). As for any process characterized by continuous spectra, the experimental sensitivity is mainly limited by the background contributions and the detector mass. Several experiments looking for 0νββ have focused their attention on these exotic searches [106–109]. In the case of TeO₂ bolometers, stringent half-life limits on these exotic decays have been set by past arrays [63], namely

$\begin{array}{ll}{\tau }_{\text{Majoron}}^{0\nu }>1.4·10^{21}\text{ yr }(n=1)\text{ and }>7.0·10^{20}\text{ yr }(n=2)& (18)\end{array}$

while competitive results are anticipated by future extensions of the technology based on the simultaneous detection of Čerenkov light and aiming at unprecedented reductions of the background [110, 111].

FIGURE 9

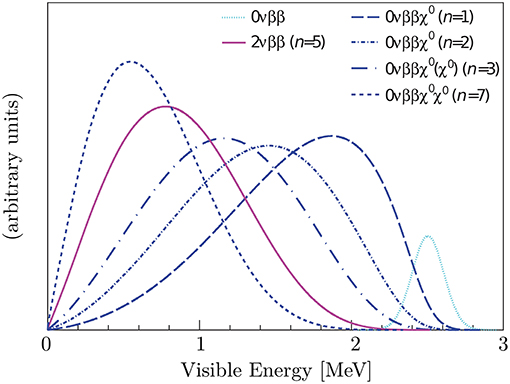
Figure 9. Visible 0νββ with Majoron emission energy spectra for different spectral index n in the case of ¹³⁶Xe. The line at Q_ββ, charaterized by the KamLAND-Zen detector resolution, indicates the position of the 0νββ peak without Majoron emission. Figure from Gando et al. [106], with permission from the American Physical Society.

2νββ is a direct transition between isobaric nuclei differing by two units of nuclear charge and corresponds to two simultaneous beta decays:

$\begin{array}{ll}(A,Z)\to (A,Z+2)+2{\text{e}}^{-}+2{\bar{\nu }}_{\text{e}}.& (19)\end{array}$

It is an allowed process within the SM and was originally proposed based on the observed trend of nuclear masses in isobaric multiplets [112]. 2νββ is the slowest nuclear decay ever discovered. It has actually been observed in a number of candidate nuclei. Most of the interest for this decay mode arises from its similarity with 0νββ (compare Equation 19 to Equation 11). Indeed, the calculation of the nuclear matrix elements for the latter are the main source of uncertainty in the extraction of the relevant neutrino parameters and it is expected that 2νββ experimental results could provide relevant insight into the details of these calculations (see section 5.3). However, in practice the 2νββ experimental results have further complicated the situation: the measured 2νββ half-lives have outlined an evident disagreement with calculations. An explanation is still missing as well as how this disagreement affects 0νββ calculations.

From the experimental point of view, the 2νββ represents an irreducible source of background for the 0νββ searches. The finite energy resolution of the detector produces a smearing of the spectrum which brings some 2νββ events in the 0νββ region. Thanks to the excellent energy resolution of bolometers and to the relatively long 2νββ half-life of ¹³⁰Te , this will not be a concern even for next generation TeO₂ experiments. However, a potential issue for thermal detectors is constituted by the random coincidences of 2νββ events [113, 114]. The resulting pile-up would not be disentangled due to the bad time resolution which, in the case of TeO₂ bolometers with NTD thermistors, is of the order of 1 ms at best. Nonetheless, this contribution is estimated to be < 10⁻⁴ counts keV⁻¹t⁻¹ yr⁻¹ for a 1 t TeO₂ experiment with enriched crystals [115], or even less in case a light signal would also be recorded (see section 7), and it is thus negligible.

TeO₂ thermal detectors have provided the most precise measurements of ¹³⁰Te 2νββ half-life [9, 64, 116]. Figure 10 shows the fit obtained with the background simulation in CUORE-0 (left panel) and CUORE first data release (right panel). The contribution of the 2νββ is clearly visible in both spectra. In particular, in CUORE, this accounts for nearly all of the signal in the range (1–2) MeV. The extracted value for the ¹³⁰Te 2νββ is [116]:

$\begin{array}{ll}{t}_{1/2}^{2\nu }=\left(7.9\pm 0.1(\text{stat}.)\pm 0.2(\text{syst}.)\right)·10^{20}\text{ yr}.& (20)\end{array}$

FIGURE 10

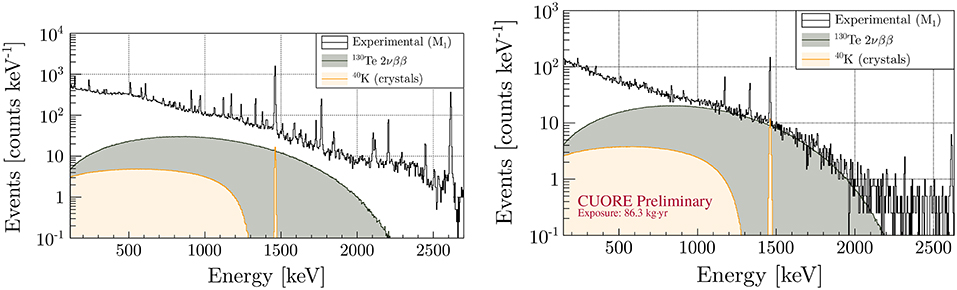
Figure 10. CUORE-0 (Left) and CUORE first data release (Right) spectra compared to the 2νββ contribution predicted by the reference fits. The ⁴⁰K peak from the crystal contamination (the radioactive source that has the strongest correlation with the 2νββ) is also reported. Figures from Alduino et al. [9] and Ouellet [116].

6.2. Violation of Fundamental Principles

The decay of an atomic electron is probably the most sensitive test of electric charge conservation. Charge Non Conservation (CNC) can be obtained by including additional interactions of leptons and photons which can lead to the decay of the electron:

$\begin{array}{ll}\text{e}\to \gamma {\nu }_{\text{e}}\text{ or e}\to {\nu }_{\text{e }}{\nu }_{\text{X }}{\bar{\nu }}_{\text{X}}.& (21)\end{array}$

These modes conserve all known quantities but electric charge. An additional possibility is connected with CNC involving interactions with nucleons. Discussions of CNC in the context of gauge theories can be found in a number of Beyond SM gauge theories [117–119].

Referring to Equation (21), while the signature of the three-neutrino mode is quite poor, the coincidence between the decay γ and the atomic de-excitation X-rays can give rise to interesting topological configurations. These can help to lower the background contributions and look particularly suited for bolometric arrays with a high granularity. The most stringent limits on CNC have been obtained as side results in experiments characterized by large masses and very low backgrounds [120, 121]. Indeed, the large detection efficiency, low threshold and excellent energy resolution of TeO₂ bolometers are crucial to detect the low energy de-excitation X-rays or Auger electrons. The sensitivity has been so far limited by the available mass so that competitive results are anticipated by CUORE and future developments of this technique.

Lorentz invariance and CPT violations arising from the spontaneous breaking of the underlying space-time symmetry are interesting theoretical feature that can be parametrized within SM extensions [122–124]. Lorentz-violating effects in the neutrino sector can thus appear both in the 2ν and 0ν decay modes [125]. A distortion of the two-electron summed energy is expected for 2νββ due to an extra term in the phase space factor, while 0νββ could be directly induced by a Lorentz-violating term. The experimental signature is therefore very similar to the one expected for Majoron searches with a deformation of the 2νββ spectrum [125]. This investigation has been recently performed by the EXO Collaboration on ¹³⁶Xe [126]. A similar study is foreseen for CUORE, and dedicated analysis tools have already been developed [127].

The Pauli Exclusion Principle (PEP) is one of the basic principles of Physics, upon which modern atomic and nuclear physics are built. Despite its well known success, the exact validity of PEP is still an open question, and an experimental verification is thus extremely important [128]. Indeed, a number of experimental investigations have been carried out both in the nuclear and atomic sector [129–132]. Each time, the signature is a transition to an already occupied (atomic or nuclear) level which is clearly prohibited by the PEP. Dedicated searches to the PEP exploit the continuous filling of atomic levels with fresh electrons in order to measure the corresponding X-ray transitions to occupied levels. Instead, most of the low activity experiments uses large masses and/or low background rates to search for the emission of specific “wrong energy” electromagnetic or nuclear radiation from atoms or nuclei. TeO₂ bolometers, belonging to the latter category, take advantage of the excellent energy resolution to isolate the seeked X-ray lines. However, sensitivity has been so far mainly limited by the detector mass and competitive results are therefore expected only for future generation ton-sized arrays. Unfortunately, a model linking the various experimental observations is still missing and a comparison of the sensitivities is therefore difficult, and must carefully take into account the assumptions underlying the specific search [133].

Baryon number (B) conservation is an empirical symmetry of the SM and its violation is predicted by a number of extensions. In particular, some of these theoretical frameworks, which allow for small neutrino masses, anticipate ΔB = 3 transitions in which three baryons can simultaneously disappear from the nucleus, often leaving an unstable isotope [134]. The coincidence between the tri-nucleon decay and the radioactive decay of the daughter nuclei is thus a robust signature for TeO₂ arrays and can help to get rid of the backgrounds. The dominant ΔB = 3 decay modes are:

$\begin{array}{ll}\text{ppp}\to {\text{e}}^{+}{\pi }^{+}{\pi }^{+},\text{ ppn}\to e^{+}{\pi }^{+},\text{ pnn}\to {\text{e}}^{+}{\pi }^0,\text{ nnn}\to \bar{\nu }{\pi }^0.& (22)\end{array}$

These can be experimentally investigated by exploiting the decay specific energy and time constraints. Recently, results on the search for instability of bound nucleons have been reported for ¹³⁶Xe [135] and for ⁷⁶Ge [136]. The half-life limits range, depending on the decay mode, around 10²³ yr in the former case, and around 10²⁵ yr in the latter one.

6.3. The Rare Nuclear Decay of ¹²³Te

Primordial radionuclides are nuclides characterized by lifetimes longer than the time passed since their formation. Therefore, they are still surviving today. Besides the progenitors of the natural decay series, ²³²Th, ²³⁵U and ²³⁸U, this set comprises: ⁴⁰K, ⁸⁷Rb, ¹¹⁵In, ¹²³Te, ¹³⁸La, ¹⁴⁴Nd, ¹⁴⁷Sm, ¹⁴⁸Sm, ¹⁷⁴Hf, ¹⁷⁶Lu, ¹⁸⁷Re, and ¹⁹⁰Pt. Their rare nuclear decays are generally of interest not only for nuclear spectroscopy but also for the implications of the very long lifetime in geochronology and ore dating. Furthermore, despite expected to occur based on the available mass measurements, the β decays of few isobaric doublets are still missing experimental observation and are often characterized by conflicting results.

This is the case for ¹²³Te , which is expected to decay by EC to the ground state of ¹²³Sb with a second forbidden unique transition (Q = 51.3 keV). Indeed, published lower limits on the lifetime of this decay [137, 138] are in contradiction with the positive result of 1.23·10¹³ yr, quoted in most of the papers on the subject [139]. The reason for the disagreement is still unclear, but it is probably due to limits imposed by the original experimental technique. If the limits were confirmed, or even more stringent ones would be set, then ¹²³Te could be characterized by the longest natural single β transition, a fact of obvious interest for nuclear physics.

The main advantage of TeO₂ thermal detectors is to implement a pure calorimetric approach, characterized by a distinctive signature in which the signal corresponds to an energy release equal to the binding energy of the captured electron. The most probable capture is then from the L3 atomic shell, with an energy of 4.1 keV. The EC decay of ¹²³Te has been investigated in a number of TeO₂ bolometric measurements. Initial limits on the suppressed K-capture [138] has been later improved when technological improvements have contributed to lower the detector threshold, thus allowing the study of the L-capture processes [140]. Here a signal corresponding to another highly suppressed L1 capture has been observed leaving the question of the ¹²³Te decay existence still open. It is expected that CUORE (and possible future TeO₂ developments), thanks to the increased mass and lower background will finally contribute to provide a definite answer.

7. Looking Ahead

CUORE is not the ultimate bolometric experiment searching for 0νββ. On the contrary, it represents a crucial step toward the forthcoming generation of experiments. Thanks to the knowledge acquired by running the first ton-scale bolometric detector, we are now aware of where and how to intervene in order to further increase the sensitivity. It appear realistic to imagine a next-generation 0νββ experiment hosted inside the CUORE cryogenic infrastructure.

As discussed in section 2, thermal detectors offer a wide choice for the possible absorber materials, hence isotopes different from ¹³⁰Te can be as well considered due to their “intrinsic” properties and/or to the more favorable characteristics of the outcoming detector. Indeed, such scenario is an open possibility concerning a post-CUORE experiment (see [115]). Anyhow, TeO₂ still remains a valid choice, and the following discussion will focus on the search for 0νββ of ¹³⁰Te with this latter compound.

As shown in section 1, the detector sensitivity for the search of 0νββ is determined by the live time of the experiment, the mass of isotope under observation, the detector energy resolution and the background level. These are therefore the key quantities to address to improve the sensitivity. In particular, all next-generation forthcoming experiments aim at reaching the zero background condition, and this sets very stringent requirements on the detector features and performance, i.e., the relation in Equation (5) must hold.

In order to increase the total mass of ¹³⁰Te, we could in principle allocate more crystals by further optimizing the detector design. However, we must keep in mind that this option is eventually constrained by the experimental volume available in the CUORE cryostat. Alternatively (or combined), we could use TeO₂ crystals enriched in ¹³⁰Te: this would correspond to an increase in the isotope mass of almost a factor 3. The results in this direction are promising. Apart from the pioneering studies on enriched crystals with MiDBD and CUORICINO, the recent bolometric run of two TeO₂ crystals enriched at ~ 92% in ¹³⁰Te showed that performance comparable to CUORE-0 are within reach [11]. Specifically, these crystals (of mass ~ 435g each) exhibited a FWHM energy resolution of 6.5 and 4.3keV (at the ²⁰⁸Tl line). Moreover, no contamination in ²³²Th was observed, while a small contamination of ²³⁸U was present, still more than 10 times larger than that of the CUORE crystals. Therefore, some extreme purification procedure should be foreseen to avoid spoiling the excellent results achieved by the CUORE crystal quality. Some work in this direction has already started.

Concerning the live time of a future 0νββ experiment, given that it is quite unlikely that the data taking will last longer than a few years, it is important to maximize the experimental duty cycle in order to, in turn, maximize the exposure. A value larger than 80% has already been achieved by CUORE-0. Furthermore, the use of mechanical cryo-cooler in the CUORE cryostat (see section 5) additionally increases the total duty cycle compared to a LHe bath cryostat, such as the one used until CUORE-0, avoiding the need of refill. It sounds reasonable to expect to keep a duty cycle of about 80% also for a future experiment.

As discussed in section 2, bolometers fully exploit the potentiality of solid state detectors. Energy resolutions of the order of the per mille at the Q_ββ, quite close to those of HPGe detectors, can be achieved.

Trying to improve the single detector performance—remind that the effective resolution of a bolometer is due to various noise sources, while in principle intrinsic value for CUORE-like bolometers should be of the order of some tens of eV—requires a deeper understanding of the thermal behavior. Studies aiming at reproducing the actual response of the CUORE bolometers have been carried out [141–143], while a large amount of data is becoming available thanks to CUORE. This will provide important information in this direction. However, we do not really know the level of improvement we can expect and, especially, when this will provide a practical contribution to the experimental search. The value of 5keV, achieved by CUORE-0, still is a valid target for a forthcoming experiment.

The mitigation of the background is leading way toward the zero background condition. It actually represents the largest challenge we will deal with and it in fact is the target of most of the R&D projects which studying the optimal configuration/technology for a new generation bolometric detector. As it will be shown, there is still room for a significant improvement from the 0.01counts keV⁻¹ kg⁻¹ yr⁻¹ of CUORE.

7.1. Active Rejection of Background

In CUORE, the study of coincidences among events generated in nearby crystals allows to discard a significant fraction of α interactions and multi-Compton scatters of γs by rejecting simultaneous signals (within 10 ms) [69]. The main limitation of this method is that, in this way, it is only possible to identify events that deposit energy in multiple crystals. Therefore, despite the rejection efficiency is still high thanks to the detector compactness, the goal for a next-generation detector is to perform an active reduction of background against α events.

A very promising approach in this sense foresees a simultaneous readout of heat and light signals. In fact, by measuring the ratio of the emitted light over the dissipated energy (heat), it is possible to discriminate between β/γ and α events with the same energy, since the scintillation light is strongly quenched in the latter case. The combined readout can be obtained by coupling the main bolometer to a thin, large-area Ge or Si light detector (acting as well as a bolometer). The light collection can be maximized by wrapping the main crystal with a reflecting foil (Figure 11).

FIGURE 11

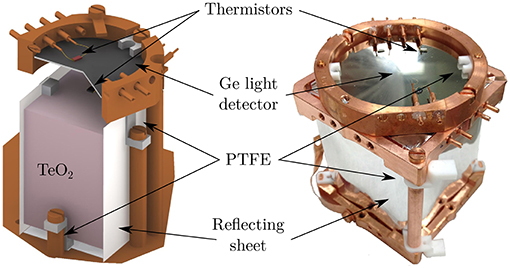
Figure 11. Example of TeO₂ bolometers coupled to light detectors, allowing for a simultaneous measurement of heat + light signals. The crystals are wrapped with a reflecting foil to maximize light collection. Figures from Artusa et al. [11] and Casali et al. [144].

Despite this approach is limited to scintillating compounds, and noticeable results have already been obtained (see e.g.,[30, 145, 146]), it can also be applied to TeO₂ crystals. In this case, the low luminescence of paratellurite is, at least partially, compensated by the suitable optical properties of the crystal to act as excellent Čerenkov radiators [147]. The Čerenkov emission threshold is ~ 400MeV for α particles while only ~ 50keV for electrons: no light emission is thus expected from the α background, allowing for a complete rejection. At the same time, ~ 125 photons in the range (350−600) nm are expected for electron pair emitted in the 0νββ process, showing the challenge of this approach, even if it is feasible.

7.2. CUPID

The CUPID project, acronym for CUORE Upgrade with Particle IDentification [110] aims at constructing a bolometric 0νββ experiment with sensitivity on $t_{1/2}^{0\nu }$ of the order of (10²⁷ − 10²⁸) yr at 90% C. L., starting from the experience and the expertise acquired by running CUORE. The largest efforts of CUPID is put into the identification of an effective strategy for a dramatic reduction of the background in the 0νββ ROI. In the case of TeO₂, the background suppression is pursued by developing high-quality light detectors, with sufficiently elevated performance to effectively identify Čerenkov emission.

Among the different technologies under investigation, we find the use of transition edge sensors [148, 149], microwave kinetic inductance detectors [150, 151], or Neganov-Trofimov-Luke (NTL) amplified light detectors [11, 33, 111, 149, 152, 153]. The results coming out from the several R&D programs are encouraging. As a remarkable example, in Bergé et al. [111] the authors demonstrate a complete event-by-event αvs. β/γ discrimination in a TeO₂ CUORE-like bolometer by employing a NTL-assisted Ge bolometer for the light collection (Figure 12).

FIGURE 12

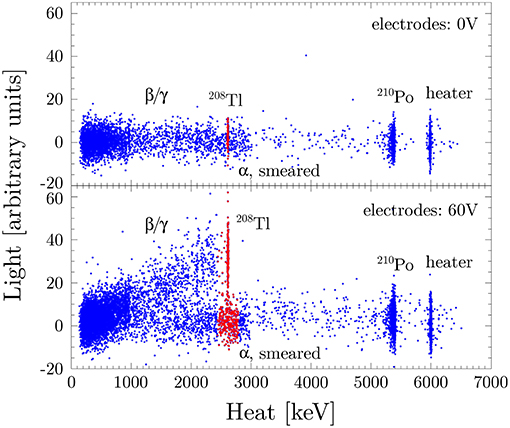
Figure 12. Heat vs. light scatter plots obtained with a CUORE bolometer in coincidence with a NTL Ge light detector. (Top) The light detector is operated as a “standard” bolometric light detector, i.e., without applying any electrode voltage bias. (Bottom) The light detector working in a signal amplification regime, by applying 60 V as electrode bias. This results in a clear separation between α and β/γ signals. Figure from Bergé et al. [111], with permission from the American Physical Society.

At the same time, additional studies within the CUPID frame aim at tagging of surface events. Surface events can represent a problem if they become a significant background component, since in thermal detector there is no dead layer and the crystal surface is as sensitive as the bulk. In order to mitigate this background, an effective solution could be represented by the addition of a passive element on the bolometer surface. The coating may be obtained by deposition of a superconducting Al film, which would affect the shape of the signal events generated a few mm from the surface, thus making it possible be able to discriminate between bulk and surface events [154]. Alternatively, by wrapping the crystal with a scintillating foil, surface events could be identified by the measurement of scintillation light (which would be collected in addition to the Čerenkov light) generated by the interaction with the foil [155]. These solutions, together with strategies for the mitigation of the environmental radioactivity [156], could in principle translate into a dramatic reduction of the BI, of about two orders of magnitude with respect to CUORE. The level of 0.1 counts keV⁻¹t⁻¹ yr⁻¹ is compatible with the zero background condition (see section 5.2) for a ton-size bolometric experiment.

8. Summary

TeO₂ thermal detectors satisfy the experimental requirements needed by a competitive search for 0νββ. This very important process—its discovery would directly address the open issues of the lepton number conservation and the Majorana nature of the neutrino—is in fact under study in a bunch of candidate isotopes, including ¹³⁰Te.

A long series of successful measurements at LNGS allowed to continuously improve the sensitivity on the half-life of the ¹³⁰Te 0νββ. Today, the CUORE experiment is providing one of the most stringent limits in the field, namely 1.5·10²⁵ yr at 90% C. L. . At the same time, TeO₂ thermal detectors were used in different studies of rare nuclear processes, spanning from different 0νββ modes to the investigation of fundamental Physics laws.

Numerous R&Ds are paving the way for a next generation bolometric experiment searching for 0νββ with zero background and enhanced sensitivity, in the range of (10²⁷ − 10²⁸) yr, showing that TeO₂ thermal detectors could continue to play a central role.

Author Contributions

Each of the three authors has given an equivalent contribution to the writing of the different sections of the paper. However, each section has been reviewed, complemented, and corrected by the other authors. CB and OC have mainly conveyed their 30 year long experience in the field, while SD, stimulated by his direct contribution to the CUORE-0 and CUORE effort, has contributed a lot of enthusiasm in re-discovering and creating a new interest for the series of results which have lead to the modern approach to low temperature detectors for double beta decay.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This review reports the successful results achieved by the CUORE (and previously Cuoricino) Collaborations. We therefore thank the numerous researchers and members of the technical staff of the institutions involved in this scientific enterprise.

Footnotes

1. ^This is true for instance if impurities are uniform inside the detector. But this might not be always the case. For example, if the main background component is superficial, it is the surface over volume ratio that matters. Also, the external background does not scale with the mass since the outer layers of the detector act as a shielding for the core part.

2. ^https://www.lngs.infn.it/en

3. ^The ROI can be intended as the 100 keV-wide region around Q_ββ, namely (2470−2570) keV. In that energy region the 2505 keV ⁶⁰Co sum peak (see Figure 6) appears, but does not contribute to the background in the ROI.

References

1. Furry WH. On transition probabilities in double beta-disintegration. Phys Rev. (1939) 56:1184–93. doi: 10.1103/PhysRev.56.1184

CrossRef Full Text | Google Scholar

2. Fukugita M, Yanagida T. Baryogenesis without grand unification. Phys Lett B. (1986) 174:45. doi: 10.1016/0370-2693(86)91126-3

CrossRef Full Text | Google Scholar

3. Tretyak VI, Zdesenko YG. Tables of double beta decay data: an update. At Data Nucl Data Tables. (2002) 80:83–116. doi: 10.1006/adnd.2001.0873

CrossRef Full Text | Google Scholar

4. Giuliani A, Poves A. Neutrinoless double-beta decay. Adv High Energy Phys. (2012) 2012:857016. doi: 10.1155/2012/857016

CrossRef Full Text | Google Scholar

5. Rahaman S, Elomaa VV, Eronen T, Hakala J, Jokinen A, Kankainen A, et al. Double-beta decay Q values of Cd-116 and Te-130. Phys Lett B. (2011) 703:412–6. doi: 10.1016/j.physletb.2011.07.078

CrossRef Full Text | Google Scholar

6. Redshaw M, Mount BJ, Myers E, Avignone FT. Masses of Te-130 and Xe-130 and Double-beta-Decay Q Value of Te-130. Phys Rev Lett. (2009) 102:212502. doi: 10.1103/PhysRevLett.102.212502

CrossRef Full Text | Google Scholar

7. Scielzo ND, Caldwell S, Savard G, Clark JA, Deibel CM, Fallis J, et al. Double-β decay Q values of ¹³⁰Te, ¹²⁸Te, and ¹²⁰Te. Phys Rev C. (2009) 80:025501. doi: 10.1103/PhysRevC.80.025501

CrossRef Full Text | Google Scholar

8. Nesterenko DA, Blaum K, Block M, Droese C, Eliseev S, Herfurth F, et al. Double−β transformations in isobaric triplets with mass numbers A = 124, 130, and 136. Phys Rev C. (2012) 86:044313. doi: 10.1103/PhysRevC.86.044313

CrossRef Full Text | Google Scholar

9. Alduino C, Alfonso K, Artusa DR, Avignone FT, Azzolini O, Banks TI, et al. Measurement of the two-neutrino double beta decay half-life of ¹³⁰Te with the CUORE-0 experiment. Eur Phys J C. (2017) 77:13. doi: 10.1140/epjc/s10052-016-4498-6

CrossRef Full Text | Google Scholar

10. Meija J, Coplen TB, Berglund M, Brand WA, De Biv̀re P, Grŏning M, et al. Isotopic compositions of the elements 2013 (IUPAC Technical Report). Pure Appl Chem. (2016) 88:293–306. doi: 10.1515/pac-2015-0503

CrossRef Full Text | Google Scholar

11. Artusa DR, Avignone FT, Beeman JW, Dafinei I, Dumoulin L, Ge Z, et al. Enriched TeO₂ bolometers with active particle discrimination: towards the CUPID experiment. Phys Lett B. (2017) 767:321–9. doi: 10.1016/j.physletb.2017.02.011

CrossRef Full Text | Google Scholar

12. Zdesenko YG. On lepton charge conservation in the double β decay of ¹³⁰Te. JETP Lett. (1980) 32:58.

Google Scholar

13. Mitchell LW, Fisher PH. Rare decays of cadmium and tellurium. Phys Rev C. (1988) 38:895–9. doi: 10.1103/PhysRevC.38.895

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ebert J, Fritts M, Gehre D, Goßling C, Hagner C, Heidrich N, et al. Results of a search for neutrinoless double-β decay using the COBRA demonstrator. Phys Rev C. (2016) 94:024603. doi: 10.1103/PhysRevC.94.024603

CrossRef Full Text | Google Scholar

15. Arnold R, Augier C, Baker J, Barabash AS, Basharina-Freshville A, Blondel S, et al. Measurement of the double beta decay half-life of ¹³⁰Te with the NEMO-3 detector. Phys Rev Lett. (2011) 107:062504. doi: 10.1103/PhysRevLett.107.062504

CrossRef Full Text | Google Scholar

16. Biller SD. Probing Majorana neutrinos in the regime of the normal mass hierarchy. Phys Rev D (2013) 87:071301. doi: 10.1103/PhysRevD.87.071301

CrossRef Full Text | Google Scholar

17. Moseley SH, Mather JC, McCammon D. Thermal detectors as x-ray spectrometers. J Appl Phys. (1984) 56:1257. doi: 10.1063/1.334129

CrossRef Full Text | Google Scholar

18. Mather J. Bolometer noise: nonequilibrium theory. J Appl Opt. (1982) 21:1125. doi: 10.1364/AO.21.001125

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mather J. Bolometers: ultimate sensitivity, optimization, and amplifier coupling. J Appl Opt. (1984) 23:584. doi: 10.1364/AO.23.000584

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Alessandrello A, Brofferio C, Camin DV, Cremonesi O, Fiorini E, Giuliani A, et al. A Cryogenic tellurium detector for rare events and gamma-rays. Phys Lett B. (1990) 247:442–7. doi: 10.1016/0370-2693(90)90923-T

CrossRef Full Text | Google Scholar

21. Alessandrello A, Bashkirov V, Brofferio C, Bucci C, Camin DV, Cremonesi O, et al. A scintillating bolometer for experiments on double beta decay. Phys Lett B. (1998) 420:109–13. doi: 10.1016/S0370-2693(97)01544-X

CrossRef Full Text | Google Scholar

22. Abdelhameed AH, Angloher G, Bauer P, Bento A, Bertoldo E, Bucci C, et al. First results from the CRESST-III low-mass dark matter program (2019). arXiv [Preprint]. arXiv:1904.00498. Available online at: https://arxiv.org/abs/1904.00498 (submitted March 31, 2019).

Google Scholar

23. Arnaud Q, Armengaud E, Augier C, Benot A, Bergé L, Billard J, et al. Optimizing EDELWEISS detectors for low-mass WIMP searches. Phys Rev D. (2018) 97:022003. doi: 10.1103/PhysRevD.97.022003

CrossRef Full Text | Google Scholar

24. Agnese R, Anderson AJ, Aramaki T, Asai M, Baker W, Balakishiyeva D, et al. New results from the search for low-mass weakly interacting massive particles with the CDMS low ionization threshold experiment. Phys Rev Lett. (2016) 116:071301. doi: 10.1103/PhysRevLett.116.071301

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Arnaboldi C, Beeman JW, Cremonesi O, Gironi L, Pavan M, Pessina G, et al. CdWO₄ scintillating bolometer for Double Beta Decay: light and Heat anticorrelation, light yield and quenching factors. Astropart Phys. (2010) 34:143–50. doi: 10.1016/j.astropartphys.2010.06.009

CrossRef Full Text | Google Scholar

26. Arnaboldi C, Capelli S, Cremonesi O, Gironi L, Pavan M, Pessina G, et al. Characterization of ZnSe scintillating bolometers for double beta decay. Astropart Phys. (2011) 34:344–53. doi: 10.1016/j.astropartphys.2010.09.004

CrossRef Full Text | Google Scholar

27. Gironi L, Arnaboldi C, Beeman JW, Cremonesi O, Danevich FA, Degoda VY, et al. Performance of ZnMoO₄ crystal as cryogenic scintillating bolometer to search for double beta decay of molybdenum. J Intrum. (2010) 5:P11007. doi: 10.1088/1748-0221/5/11/P11007

CrossRef Full Text | Google Scholar

28. Beeman JW, Bellini F, Cardani L, Casali N, Dafinei I, Di Domizio S, et al. Performances of a large mass ZnSe bolometer to search for rare events. J Intrum. (2013) 8:P05021. doi: 10.1088/1748-0221/8/05/P05021

CrossRef Full Text | Google Scholar

29. Cardani L, Cardani L, Casali N, Nagorny S, Pattavina L, Piperno G, et al. Development of a Li₂MoO₄ scintillating bolometer for low background physics. J Intrum. (2013) 8:P10002. doi: 10.1088/1748-0221/8/10/P10002

CrossRef Full Text | Google Scholar

30. Armengaud E, Augier C, Barabash AS, Beeman JW, Bekker TB, Bellini F, et al. Development of ¹⁰⁰Mo-containing scintillating bolometers for a high-sensitivity neutrinoless double-beta decay search. Eur Phys J C. (2017) 77:785. doi: 10.1140/epjc/s10052-017-5343-2

CrossRef Full Text | Google Scholar

31. Nagorny S, Pattavina L, Kosmyna MB, Nazarenko BP, Nisi S, Pagnanini L, et al. ^archPbMoO₄ scintillating bolometer as detector to searches for the neutrinoless double beta decay of ¹⁰⁰Mo. J Phys Conf Ser. (2017) 841:012025. doi: 10.1088/1742-6596/841/1/012025

CrossRef Full Text | Google Scholar

32. Colantoni I, Cardani L, Casali N, Cruciani A, Bellini F, Castellano MG, et al. Design and fabrication of the second-generation KID-based light detectors of CALDER. J Low Temp Phys. (2018) 193:726–31. doi: 10.1007/s10909-018-1905-4

CrossRef Full Text | Google Scholar

33. Gironi L, Biassoni M, Brofferio C, Capelli S, Carniti P, Cassina L, et al. Cerenkov light identification with Si low-temperature detectors with sensitivity enhanced by the Neganov-Luke effect. Phys Rev C. (2016) 94:054608. doi: 10.1103/PhysRevC.94.054608

CrossRef Full Text | Google Scholar

34. Beeman JW, Bellini F, Casali N, Cardani L, Dafinei I, Di Domizio S, et al. Characterization of bolometric Light Detectors for rare event searches. J Instrum. (2013) 8:P07021. doi: 10.1088/1748-0221/8/07/P07021

CrossRef Full Text | Google Scholar

35. Novati V, Artusa DR, Avignone FT, Beeman JW, Dafinei I, Dumoulin L, et al. An innovative bolometric Cherenkov-light detector for a ouble beta decay search. Nucl Instrum Meth A. (2018) 912:82–4. doi: 10.1016/j.nima.2017.10.058

CrossRef Full Text | Google Scholar

36. Azzolini O, Barrera MT, Beeman JW, Bellini F, Beretta M, Biassoni M, et al. First result on the neutrinoless double-β decay of ⁸²Se with CUPID-0. Phys Rev Lett. (2018) 120:232502. doi: 10.1103/PhysRevLett.120.232502

CrossRef Full Text | Google Scholar

37. Alenkov V, Bae HW, Beyer J, Boiko RS, Boonin K, Buzanov O, et al. First results from the AMoRE-Pilot neutrinoless double beta decay experiment (2019).

Google Scholar

38. Dutton WA, Charles Cooper W. The Oxides and Oxyacids of Tellurium. Chem Rev. (1966) 66:657–75. doi: 10.1021/cr60244a003

CrossRef Full Text | Google Scholar

39. Barucci M, Brofferio C, Giuliani A, Gottardi E, Peroni I, Ventura G. Measurement of low temperature specific heat of crystalline TeO₂ for the optimization of bolometric detectors. J Low Temp Phys. (2001) 123:303–14. doi: 10.1023/A:1017555615150

CrossRef Full Text | Google Scholar

40. White GK, Collocott S, Collins JG. Thermal properties of paratellurite (TeO₂) at low temperatures. J Phys Condensed Matter. (1990) 2:7715–8. doi: 10.1088/0953-8984/2/37/015

CrossRef Full Text | Google Scholar

41. Kroeger FR, Swenson CA. Absolute linear thermal-expansion measurements on copper and aluminum from 5 to 320 K. J Appl Phys. (1977) 48:853–64. doi: 10.1063/1.323746

CrossRef Full Text | Google Scholar

42. Chu Y, Li Y, Ge Z, Wu G, Wang H. Growth of the high quality and large size paratellurite single crystals. J Cryst Growth (2006) 295:158–61. doi: 10.1016/j.jcrysgro.2006.08.009

CrossRef Full Text | Google Scholar

43. Arnaboldi C, Brofferio C, Bryant A, Bucci C, Canonica L, Capelli S, et al. Production of high purity TeO₂ single crystals for the study of neutrinoless double beta decay. J Cryst Growth. (2010) 312:2999–3008. doi: 10.1016/j.jcrysgro.2010.06.034

CrossRef Full Text | Google Scholar

44. Arnaboldi C, Brofferio C, Bucci C, Gorla P, Pessina G, Pirro S. 1.3 kg bolometers to search for rare events. Nucl Instrum Meth A. (2005) 554:300–5. doi: 10.1016/j.nima.2005.07.060

CrossRef Full Text | Google Scholar

45. Cardani L, Gironi L, Beeman JW, Dafinei I, Ge Z, Pessina G, et al. Performance of a large TeO₂ crystal as a cryogenic bolometer in searching for neutrinoless double beta decay. J Instrum. (2012) 7:P01020. doi: 10.1088/1748-0221/7/01/P01020

CrossRef Full Text | Google Scholar

46. Alessandria F, Andreotti E, Ardito R, Arnaboldi C, Avignone FT, Balata M, et al. CUORE crystal validation runs: results on radioactive contamination and extrapolation to CUORE background. Astropart Phys. (2012) 35:839–49. doi: 10.1016/j.astropartphys.2012.02.008

CrossRef Full Text | Google Scholar

47. Alessandria F, Ardito R, Artusa DR, Avignone FT, Azzolini O, Balata M, et al. Validation of techniques to mitigate copper surface contamination in CUORE. Astropart Phys. (2013) 45:13–22. doi: 10.1016/j.astropartphys.2013.02.005

CrossRef Full Text | Google Scholar

48. Haller EE, Palaio NP, Rodder M, Hansen WL, Kreysa E. NTD germanium: a novel material for low temperature bolometers. In: Larrabee RD, editor. Neutron Transmutation Doping of Semiconductor Materials. Boston, MA: Springer US (1984). p. 21–36. doi: 10.1007/978-1-4613-2695-3_2

CrossRef Full Text | Google Scholar

49. Shklovskii BI, Efros AL. Electronic Properties of Doped Semiconductors. Berlin; Heidelberg: Springer (1984). doi: 10.1007/978-3-662-02403-4

CrossRef Full Text | Google Scholar

50. Alessandrello A, Brofferio C, Bucci C, Cremonesi O, Giuliani A, Margesin B, et al. Methods for response stabilization in bolometers for rare decays. Nucl Instrum Meth A (1998) 412:454–64. doi: 10.1016/S0168-9002(98)00458-6

CrossRef Full Text | Google Scholar

51. Arnaboldi C, Giachero A, Gotti C, Pessina G. A very high performance stabilization system for large mass bolometer experiments. Nucl Instrum Meth A. (2011) 652:306–9. doi: 10.1016/j.nima.2010.09.151

CrossRef Full Text | Google Scholar

52. Andreotti E, Brofferio C, Foggetta L, Giuliani A, Margesin B, Nones C, et al. Production, characterization, and selection of the heating elements for the response stabilization of the CUORE bolometers. Nucl Instrum Meth A. (2012) 664:161–70. doi: 10.1016/j.nima.2011.10.065

CrossRef Full Text | Google Scholar

53. Alessandrello A, Alessandrello A, Brofferio C, Camin DV, Cremonesi O, Fiorini E, et al. Large mass, low temperature, low background detectors. Nucl Instrum Meth A. (1992) 315:263–6. doi: 10.1016/0168-9002(92)90713-E

CrossRef Full Text | Google Scholar

54. Giuliani A, Alessandrello A, Brofferio C, Camin DV, Cremonesi O, Fiorini E, et al. A low temperature TeO₂ detector to search for double beta decay of ¹³⁰Te. In: Hegarty S, Potter K, Quercigh E, editors. Proceedings of the Joint International Lepton Photon Symposium at High Energies (15th) and European Phys. Soc. Conf. on High-energy Phys. Singapore: World Scientific, (1992). p. 670–672.

55. Alessandrello A, Brofferio C, Camin DV, Cremonesi O, Fiorini E, Gervasio G, et al. A search for neutrinoless double beta decay of ¹³⁰Te with a bolometric detector. Nucl Phys B. (1992) 28A:229–32. doi: 10.1016/0920-5632(92)90177-T

CrossRef Full Text | Google Scholar

56. Alessandrello A, Brofferio C, Camin DV, Cremonesi O, Fiorini E, Gervasio G, et al. Milano experiment on 0−ν ββ decay of ¹³⁰Te with a thermal detector. Nucl Phys B. (1993) 31:83–7. doi: 10.1016/0920-5632(93)90118-P

CrossRef Full Text | Google Scholar

57. Catalano PG, Cavinato G, Salvini F, Tozzi M. Structural analysis of the Gran Sasso Laboratories of INFN (in Italian). Mem Soc Geol It. (1986) 35:647–55.

58. Ambrosio M, Antolini R, Auriemma G, Baker R, Baldini A, Barbarino GC, et al. Vertical muon intensity measured with MACRO at the Gran Sasso Laboratory. Phys Rev D. (1995) 52:3793–802. doi: 10.1103/PhysRevD.52.3793

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Best A, Görres J, Junker M, Kratz KL, Laubenstein M, Long A, et al. Low energy neutron background in deep underground laboratories. Nucl Instrum Meth. A. (2016) 812:1–6. doi: 10.1016/j.nima.2015.12.034

CrossRef Full Text | Google Scholar

60. Kirsten T, Richter H, Jessberger E. Rejection of Evidence for Nonzero Neutrino Rest Mass from Double Beta Decay. Phys Rev Lett. (1983) 50:474–7. doi: 10.1103/PhysRevLett.50.474

CrossRef Full Text | Google Scholar

61. Alessandrello A, Brofferio C, Camin DV, Cremonesi O, Fiorini E, Garcia E, et al. A New search for neutrinoless ββ decay with a thermal detector. Phys Lett B. (1994) 335:519–25. doi: 10.1016/0370-2693(94)90388-3

CrossRef Full Text | Google Scholar

62. Alessandrello A, Brofferio C, Cremonesi O, Garcia E, Giuliani A, Nucciotti A, et al. First tests on a large mass, low temperature array detector. Nucl Instrum Meth A. (1995) 360:363–6. doi: 10.1016/0168-9002(94)01723-9

CrossRef Full Text | Google Scholar

63. Alessandrello A, Brofferio C, Cremonesi O, Fiorini E, Giuliani A, Nucciotti A, et al. New experimental results on double beta decay of ¹³⁰Te. Phys Lett B. (2000) 486:13–21. doi: 10.1016/S0370-2693(00)00747-4

CrossRef Full Text | Google Scholar

64. Arnaboldi C, Brofferio C, Bucci C, Capelli S, Cremonesi O, Fiorini E, et al. A Calorimetric search on double beta decay of ¹³⁰Te. Phys Lett B. (2003) 557:167–75. doi: 10.1016/S0370-2693(03)00212-0

CrossRef Full Text | Google Scholar

65. Alessandrello A, Brofferio C, Cremonesi O, Fiorini E, Giuliani A, Nucciotti A, et al. A massive thermal detector for alpha and gamma spectroscopy. Nucl Instrum Meth A. (2000) 440:397–402. doi: 10.1016/S0168-9002(99)00928-6

CrossRef Full Text | Google Scholar

66. Fiorini E. CUORE: a cryogenic underground observatory for rare events. Phys Rep. (1998) 307:309–17. doi: 10.1016/S0370-1573(98)00060-X

CrossRef Full Text | Google Scholar

67. Alfonso K, Artusa DR, Avignone FT, Azzolini O, Balata M, Banks TI, et al. Search for neutrinoless double-beta decay of ¹³⁰Te with CUORE-0. Phys Rev Lett. (2015) 115:102502. doi: 10.1103/PhysRevLett.115.102502

CrossRef Full Text | Google Scholar

68. Andreotti E, Arnaboldi C, Avignone FT, Balata M, Bandac I, Barucci M, et al. ¹³⁰Te neutrinoless double-beta decay with CUORICINO. Astropart Phys. (2011) 34:822–31. doi: 10.1016/j.astropartphys.2011.02.002

CrossRef Full Text | Google Scholar

69. Alduino C, Alfonso K, Andreotti E, Arnaboldi C, Avignone FT, Azzolini O, et al. First results from CUORE: a search for lepton number violation via 0νββ Decay of ¹³⁰Te. Phys Rev Lett. (2018) 120:132501. doi: 10.1103/PhysRevLett.120.132501

CrossRef Full Text | Google Scholar

70. Alduino C, Alfonso K, Artusa DR, Avignone FT, Azzolini O, Balata M, et al. CUORE-0 detector: design, construction and operation. J Instrum. (2016) 11:P07009. doi: 10.1088/1748-0221/11/07/P07009

CrossRef Full Text | Google Scholar

71. Buccheri E, Capodiferro M, Morganti S, Orio F, Pelosi A, Pettinacci V. An assembly line for the construction of ultra-radio-pure detectors. Nucl Instrum Meth A. (2014) 768:130–40. doi: 10.1016/j.nima.2014.09.046

CrossRef Full Text | Google Scholar

72. Artusa DR, Avignone FT, Azzolini O, Balata M, Banks TI, Bari G, et al. Searching for neutrinoless double-beta decay of ¹³⁰Te with CUORE. Adv High Energy Phys. (2015) 2015:879871. doi: 10.1155/2015/879871

CrossRef Full Text | Google Scholar

73. Benato G, G Biare D, Bucci C, Di Paolo L, Drobizhev A, Kadel RW, et al. Radon mitigation during the installation of the CUORE 0νββ decay detector. J Instrum. (2018) 13:P01010. doi: 10.1088/1748-0221/13/01/P01010

CrossRef Full Text | Google Scholar

74. Dell'Oro S. Optimization of the CUORE detector during the commissioning phase. (Ph. D. thesis). INFN - Gran Sasso Science Institute, l'Aquila, Italy (2017).

Google Scholar

75. Alduino C, Alessandria M F Balata, Biare D, Biassoni M, Bucci C, et al. The CUORE cryostat: a 10 mK infrastructure for large bolometric arrays. (2019). arXiv [Preprint]. arXiv:1904.05745.

Google Scholar

76. Alessandrello A, Arpesella C, Brofferio C, Bucci C, Cattadori C, Cremonesi O, et al. Measurements of internal radioactive contamination in samples of roman lead to be used in experiments on rare events. Nucl. Instrum. Meth. B. (1998) 142:163–72. doi: 10.1016/S0168-583X(98)00279-1

CrossRef Full Text | Google Scholar

77. Alduino C, Alfonso K, Artusa DR, Avignone FT, Azzolini O, Banks TI, et al. The projected background for the CUORE experiment. Eur Phys J C (2017) 77:543. doi: 10.1140/epjc/s10052-017-5080-6

CrossRef Full Text | Google Scholar

78. Barghouty AF, Brofferio C, Capelli S, Clemenza M, Cremonesi O, Cebrián S, et al. Measurements of proton-induced radionuclide production cross sections to evaluate cosmic-ray activation of tellurium. Nucl Instrum Meth B. (2013) 295:16–21. doi: 10.1016/j.nimb.2012.10.008

CrossRef Full Text | Google Scholar

79. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H, et al. Search for majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen. Phys Rev Lett. (2016) 117:082503. doi: 10.1103/PhysRevLett.117.109903

CrossRef Full Text | Google Scholar

80. Agostini M, Bakalyarov AM, Balata M, Barabanov I, Baudis L, Bauer C, et al. Improved limit on neutrinoless double-β decay of ⁷⁶Ge from GERDA phase II. Phys Rev Lett. (2018) 120:132503. doi: 10.1103/PhysRevLett.120.132503

CrossRef Full Text | Google Scholar

81. Alduino C, Alfonso K, Artusa DR, Avignone FT, Azzolini O, Banks TI, et al. CUORE sensitivity to 0νββ decay. Eur Phys J C. (2017) 77:532. doi: 10.1140/epjc/s10052-017-5098-9

CrossRef Full Text | Google Scholar

82. Kotila J, Iachello F. Phase space factors for double-β decay. Phys Rev C (2012) 85:034316. doi: 10.1103/PhysRevC.85.034316

CrossRef Full Text | Google Scholar

83. Barea J, Kotila J, Iachello F. 0νββ and 2νββ nuclear matrix elements in the interacting boson model with isospin restoration. Phys Rev C. (2015) 91:034304. doi: 10.1103/PhysRevC.91.034304

CrossRef Full Text | Google Scholar

84. Simkovic F, Rodin V, Faessler A, Vogel P. 0νββ and 2νββ nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration. Phys Rev C. (2013) 87:045501. doi: 10.1103/PhysRevC.87.045501

CrossRef Full Text | Google Scholar

85. Vissani F. Signal of neutrinoless double beta decay, neutrino spectrum and oscillation scenarios. J High Energy Phys. (1999) 6:022. doi: 10.1088/1126-6708/1999/06/022

CrossRef Full Text | Google Scholar

86. Dell'Oro S, Marcocci S, Vissani F. New expectations and uncertainties on neutrinoless double beta decay. Phys Rev D. (2014) 90:033005. doi: 10.1103/PhysRevD.90.033005

CrossRef Full Text | Google Scholar

87. Capozzi F, Lisi E, Marrone A, Montanino D, Palazzo A. Neutrino masses and mixings: Status of known and unknown 3ν parameters. Nucl Phys B. (2016) 908:218–34. doi: 10.1016/j.nuclphysb.2016.02.016

CrossRef Full Text | Google Scholar

88. Arnold R, Augier C, Baker J, Barabash AS, Basharina-Freshville A, Blondel S, et al. Result of the search for neutrinoless double-β decay in ¹⁰⁰Mo with the NEMO-3 experiment. Phys Rev D. (2015) 92:072011. doi: 10.1103/PhysRevD.92.072011

CrossRef Full Text | Google Scholar

89. Tomoda T. 0⁺ → 2⁺0νββ decay triggered directly by the Majorana neutrino mass. Phys Lett B. (2000) 474:245–50. doi: 10.1016/S0370-2693(00)00025-3

CrossRef Full Text | Google Scholar

90. Simkovic F, Faessler A. Distinguishing the 0νββ-decay mechanisms. Prog Part Nucl Phys. (2002) 48:201–9. doi: 10.1016/S0146-6410(02)00125-4

CrossRef Full Text | Google Scholar

91. Aunola M, Suhonen J. Systematic study of beta and double beta decay to excited final states. Nucl Phys A. (1996) 602:133–66. doi: 10.1016/0375-9474(96)00087-5

CrossRef Full Text | Google Scholar

92. Suhonen J, Civitarese O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys Rep. (1998) 300:123–214. doi: 10.1016/S0370-1573(97)00087-2

CrossRef Full Text | Google Scholar

93. Alduino C, Alfonso K, Artusa DR, Avignone FT, Azzolini O, Banks TI, et al. Double-beta decay of ¹³⁰Te to the first 0⁺ excited state of ¹³⁰Xe with CUORE-0 (2018). arXiv [Preprint]. arXiv:1811.10363.

Google Scholar

94. Alessandrello A, Brofferio C, Camin DV, Cremonesi O, Fiorini E, Giuliani A, et al. Preliminary results on double beta decay of ¹³⁰Te with an array of twenty cryogenic detectors. Phys Lett B. (1998) 433:156–62. doi: 10.1016/S0370-2693(98)00645-5

CrossRef Full Text | Google Scholar

95. Andreotti E, Arnaboldi C, Avignone FT, Balata M, Bandac I, Barucci M, et al. Search for double-β decay of ¹³⁰Te to the first 0⁺ excited state of ¹³⁰Xe with the CUORICINO experiment bolometer array. Phys Rev C. (2012) 85:045503.

Google Scholar

96. Pozzi S. Search for double-beta decay of ¹³⁰Te to the excited states of ¹³⁰Xe in CUORE-0. (Ph. D. thesis). Università degli Studi di Milano-Bicocca, Milano, Italy (2017).

Google Scholar

97. Wang M, Audi G, Kondev FG, Huang WJ, Naimi S, Xu X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin Phys C. (2017) 41:030003. doi: 10.1088/1674-1137/41/3/030003

CrossRef Full Text | Google Scholar

98. Vergados JD. Lepton-violating β⁻β⁻, β⁺β⁺ decays, (e⁻, e⁺) conversion and double electron capture in gauge theories. Nucl Phys B. (1983) 218:109–44. doi: 10.1016/0550-3213(83)90477-7

CrossRef Full Text | Google Scholar

99. Kotila J, Barea J, Iachello F. Neutrinoless double-electron capture. Phys Rev C. (2014) 89:064319. doi: 10.1103/PhysRevC.89.064319

CrossRef Full Text | Google Scholar

100. Alduino C, Alfonso K, Artusa DR, Avignone FT, Azzolini O, Bari G, et al. Search for neutrinoless β⁺EC decay of ¹²⁰Te with CUORE-0. Phys Rev C. (2018) 97:055502. doi: 10.1103/PhysRevC.97.055502

CrossRef Full Text | Google Scholar

101. Andreotti E, Arnaboldi C, Avignone FT, Balata M, Bandac I, Barucci M, et al. Search for β⁺/ec double beta decay of ¹²⁰Te. Astropart Phys. (2011) 34:643–8. doi: 10.1016/j.astropartphys.2010.12.011

CrossRef Full Text | Google Scholar

102. Takaoka N, Motomura Y, Nagao K. Half-life of ¹³⁰Te double-β decay measured with geologically qualified samples. Phys Rev C (1996) 53:1557. doi: 10.1103/PhysRevC.53.1557

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Gelmini GB, Roncadelli M. Left-handed neutrino mass scale and spontaneously broken lepton number. Phys Lett B. (1981) 99:411–5. doi: 10.1016/0370-2693(81)90559-1

CrossRef Full Text | Google Scholar

104. Burgess CP, Cline JM. New class of Majoron-emitting double-β decays. Phys Rev D. (1994) 49:5925–44. doi: 10.1103/PhysRevD.49.5925

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Bamert P, Burgess CP, Mohapatra RN. Multi-majoron modes for neutrinoless double-beta decay. Nucl Phys B. (1995) 449:25–48. doi: 10.1016/0550-3213(95)00273-U

CrossRef Full Text | Google Scholar

106. Gando A, Gando Y, Hanakago H, Ikeda H, Inoue K, Kato R, et al. Limits on majoron-emitting double-β decays of ¹³⁶Xe in the KamLAND-Zen experiment. Phys Rev C. (2012) 86:021601. doi: 10.1103/PhysRevC.86.021601

CrossRef Full Text | Google Scholar

107. Elliott SR, Hahn AA, Moe MK. Limit on neutrinoless double-beta decay with majoron emission in ⁸²Se. Phys Rev Lett. (1987) 59:1649–51. doi: 10.1103/PhysRevLett.59.1649

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Arnold R, Augier C, Baker J, Barabash AS, Brudanin V, Caffrey AJ, et al. Limits on different majoron decay modes of ¹⁰⁰Mo and ⁸²Se for neutrinoless double beta decays in the NEMO−3 experiment. Nucl Phys A. (2006) 765:483–94. doi: 10.1016/j.nuclphysa.2005.11.015

CrossRef Full Text | Google Scholar

109. Arnold R, Augier C, Barabash AS, Basharina-Freshville A, S B, Blot S, et al. Detailed studies of ¹⁰⁰Mo two-neutrino double beta decay in NEMO-3. arXiv [Preprint]. arXiv:1903.08084 (2019).

110. Wang G, Chang CL, V Y, Ding J, Novosad V, Bucci C, et al. CUPID: CUORE (cryogenic underground observatory for rare events) upgrade with particle iDentification. arXiv [Preprint]. arXiv:1504.03599 (2015).

111. Bergé L, Chapellier M, de Combarieu M, Dumoulin L, Giuliani A, Gros M, et al. Complete event-by-event α/γ(β) separation in a full-size TeO₂ CUORE bolometer by simultaneous heat and light detection. Phys Rev C. (2018) 97:032501. doi: 10.1103/PhysRevC.97.032501

CrossRef Full Text | Google Scholar

112. Goeppert-Mayer M. Double beta-disintegration. Phys Rev. (1935) 48:512–6. doi: 10.1103/PhysRev.48.512

CrossRef Full Text | Google Scholar

113. Beeman JW, Danevich FA, Degoda VY, Galashov EN, Giuliani A, Kobychev VV, et al. A next generation neutrinoless double beta decay experiment based on ZnMoO₄ scintillating bolometers. Phys Lett B. (2012) 710:318–23. doi: 10.1016/j.physletb.2012.03.009

CrossRef Full Text | Google Scholar

114. Chernyak DM, Danevich FA, Giuliani A, Olivieri E, Tenconi M, Tretyak VI. Random coincidence of 2ν2β decay events as a background source in bolometric 0ν2β decay experiments. Eur Phys J C. (2012) 72:1989. doi: 10.1140/epjc/s10052-012-1989-y

CrossRef Full Text | Google Scholar

115. Artusa DR, Avignone FT, Azzolini O, Balata M, Banks TI, Bari G, et al. Exploring the neutrinoless double beta decay in the inverted neutrino hierarchy with bolometric detectors. Eur Phys J C. (2014) 74:3096. doi: 10.1140/epjc/s10052-014-3096-8

CrossRef Full Text | Google Scholar

116. Ouellet J. Latest Results from the CUORE Experiment. In: Proceedings of the International Conference Neutrino-2018. (2018). doi: 10.5281/zenodo.1286904

CrossRef Full Text | Google Scholar

117. Voloshin MB, Okun LB. On the electric charge conservation. JETP Lett. (1978) 28:145.

Google Scholar

118. Okun LB, Zeldovich YB. Paradoxes of unstable electron. Phys Lett B. (1978) 78:597–600. doi: 10.1016/0370-2693(78)90648-2

CrossRef Full Text | Google Scholar

119. Ignatiev AY, Kuzmin VA, Shaposhnikov ME. Is the electric charge conserved? Phys Lett B. (1979) 84:315–8. doi: 10.1016/0370-2693(79)90048-0

CrossRef Full Text | Google Scholar

120. Belli P, Bernabei R, Dai CJ, Ignesti G, Incicchitti A, Montecchia F, et al. Quest for electron decay ${\text{e}}^{-}\to {\nu }_e\gamma$ with a liquid xenon scintillator. Phys Rev D. (2000) 61:117301. doi: 10.1103/PhysRevD.61.117301

CrossRef Full Text | Google Scholar

121. Agostini M, Appel S, Bellini G, Benziger J, Bick D, Bonfini G, et al. A test of electric charge conservation with Borexino. Phys Rev Lett. (2015) 115:231802. doi: 10.1103/PhysRevLett.115.231802

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Colladay D, Kostelecký VA. CPT violation and the standard model. Phys Rev D. (1997) 55:6760–74. doi: 10.1103/PhysRevD.55.6760

CrossRef Full Text | Google Scholar

123. Colladay D, Kostelecký VA. Lorentz-violating extension of the Standard Model. Phys Rev D. (1998) 58:116002. doi: 10.1103/PhysRevD.58.116002

CrossRef Full Text | Google Scholar

124. Kostelecký VA. Gravity, Lorentz violation, and the Standard Model. Phys Rev D. (2004) 69:105009. doi: 10.1103/PhysRevD.69.105009

CrossRef Full Text | Google Scholar

125. Diaz JS. Limits on Lorentz and CPT violation from double beta decay. Phys Rev D. (2014) 89:036002. doi: 10.1103/PhysRevD.89.036002

CrossRef Full Text | Google Scholar

126. Albert JB, Barbeau PS, Beck D, Belov V, Breidenbach M, Brunner T, et al. First Search for Lorentz and CPT Violation in Double Beta Decay with EXO-200. Phys Rev D. (2016) 93:072001. doi: 10.1103/PhysRevD.93.072001

CrossRef Full Text | Google Scholar

127. Nutini I. The CUORE experiment: detector optimization and modelling and CPT conservation limit. (Ph. D. thesis). INFN - Gran Sasso Science Institute, l'Aquila, Italy (2019).

128. Greenberg OW. On the surprising rigidity of the Pauli exclusion principle. Nucl Phys B Proc Suppl. (1989) 6:83–9. doi: 10.1016/0920-5632(89)90405-2

CrossRef Full Text | Google Scholar

129. Belli P, Bernabei R, Dai CJ, He HL, Ignesti G, Incicchitti A, et al. New experimental limit on the electron stability and non-paulian transitions in Iodine atoms. Phys Lett B. (1999) 460:236–41. doi: 10.1016/S0370-2693(99)00783-2

CrossRef Full Text | Google Scholar

130. Bellini G, Bonetti S, Buizza Avanzini M, Caccianiga B, D'Angelo D, Franco D, et al. New experimental limits on the Pauli-forbidden transitions in ¹²C nuclei obtained with 485 days Borexino data. Phys Rev C. (2010) 81:034317. doi: 10.1103/PhysRevC.81.034317

CrossRef Full Text | Google Scholar

131. Abgrall N, Arnquist FT I J Avignone, Barabash AS, Bertrand FE, Bradley AW, et al. Search for Pauli exclusion principle violating atomic transitions and electron decay with a p-type point contact germanium detector. Eur Phys J C. (2016) 76:619. doi: 10.1140/epjc/s10052-016-4467-0

CrossRef Full Text | Google Scholar

132. Shi H, Milotti E, Bartalucci S, Bazzi M, Bertolucci S, Bragadireanu AM, et al. Experimental search for the violation of Pauli exclusion principle. Eur Phys J C. (2018) 78:319. doi: 10.1140/epjc/s10052-018-5802-4

PubMed Abstract | CrossRef Full Text | Google Scholar

133. Elliott SR, LaRoque BH, Gehman VM, Kidd MF, Chen M. An improved limit on pauli-exclusion-principle forbidden atomic transitions. Found Phys. (2012) 42:1015–30. doi: 10.1007/s10701-012-9643-y

CrossRef Full Text | Google Scholar

134. Babu KS, Gogoladze I, Wang K. Gauged baryon parity and nucleon stability. Phys Lett B. (2003) 570:32–8. doi: 10.1016/j.physletb.2003.07.036

CrossRef Full Text | Google Scholar

135. Albert JB, Anton G, Badhrees I, Barbeau PS, Bayerlein R, Beck D, et al. Search for nucleon decays with EXO-200. Phys Rev D. (2018) 97:072007. doi: 10.1103/PhysRevD.97.072007

CrossRef Full Text | Google Scholar

136. Alvis SI, Arnquist IJ, Avignone FT, Barabash AS, Barton CJ, Bertrand FE, et al. Search for tri-nucleon decay in the majorana demonstrator. arXiv:1812.01090 (2018).

137. Heintze J. On the question of the natural radioactivity of ⁵⁰V, ¹¹³In and ¹²³Te (in German). Z Naturforsch A. (1955) 10:77. doi: 10.1515/zna-1955-0113

CrossRef Full Text | Google Scholar

138. Alessandrello A, Arnaboldi C, Brofferio C, Capelli S, Cremonesi O, Fiorini E, et al. New limits on naturally occurring electron capture of ¹²³Te. Phys Rev. C. (2003) 67:014323. doi: 10.1103/PhysRevC.67.014323

CrossRef Full Text | Google Scholar

139. Watt DE, Glover RN. A search for radioactivity among the naturally occurring isobaric pairs. Philos Mag. (1962) 7:105–14. doi: 10.1080/14786436208201861

CrossRef Full Text | Google Scholar

140. Alessandria F, Ardito R, Artusa DR, Avignone FT, Azzolini O, Balata M, et al. The low energy spectrum of TeO₂ bolometers: results and dark matter perspectives for the CUORE-0 and CUORE experiments. J Cosm Astropart Phys. (2013) 1:038. doi: 10.1088/1475-7516/2013/01/038

CrossRef Full Text | Google Scholar

141. Pedretti M. The single module for Cuoricino and CUORE detectors: tests, construction and modeling. (Ph. D. thesis). Università dell'Insubria, Como, Italy (2004).

142. Vignati M. Model of the response function of CUORE bolometers. (Ph. D. thesis). Università di Roma-La Sapienza (2010).

Google Scholar

143. Santone D. Pulse shape analysis of CUORE-0 bolometers for a better comprehension of detector response. (Ph. D. thesis). Università dell'Aquila, l'Aquila, Italy (2017).

144. Casali N, Vignati M, Beeman JW, Bellini F, Cardani L, Dafinei I, et al. TeO₂ bolometers with Čerenkov signal tagging: towards next-generation neutrinoless double beta decay experiments. Eur Phys J C. (2015) 75:12. doi: 10.1140/epjc/s10052-014-3225-4

CrossRef Full Text | Google Scholar

145. Kim GB, Choi S, Danevich FA, Fleischmann A, Kang CS, Kim HJ, et al. A CaMoO₄ crystal low temperature detector for the AMoRE neutrinoless double beta decay search. Adv High Energy Phys. (2015) 2015:817530. doi: 10.1155/2015/817530

CrossRef Full Text | Google Scholar

146. Artusa DR, Balzoni A, Beeman JW, Bellini F, Biassoni M, Brofferio C, et al. First array of enriched Zn⁸²Se bolometers to search for double beta decay. Eur Phys J C. (2016) 76:364. doi: 10.1140/epjc/s10052-016-4223-5

PubMed Abstract | CrossRef Full Text | Google Scholar

147. Tabarelli de Fatis T. Cerenkov emission as a positive tag of double beta decays in bolometric experiments. Eur Phys J C. (2010) 65:359–61. doi: 10.1140/epjc/s10052-009-1207-8

CrossRef Full Text | Google Scholar

148. Schäffner K, Angloher G, Bellini F, Casali N, Ferroni F, Hauff D, et al. Particle discrimination in TeO₂ bolometers using light detectors read out by transition edge sensors. Astropart Phys. (2015) 69:30–6. doi: 10.1016/j.astropartphys.2015.03.008

CrossRef Full Text | Google Scholar

149. Willers M, Feilitzsch FV, Gutlein A, Munster A, Lanfranchi JC, Oberauer L, et al. Neganov-Luke amplified cryogenic light detectors for the background discrimination in neutrinoless double beta decay search with TeO₂ bolometers. J Instrum. (2015) 10:P03003. doi: 10.1088/1748-0221/10/03/P03003

CrossRef Full Text | Google Scholar

150. Battistelli ES, Bellini F, Bucci C, Calvo M, Cardani L, Casali N, et al. CALDER: neutrinoless double-beta decay identification in TeO₂ bolometers with kinetic inductance detectors. Eur Phys J C. (2015) 75:353. doi: 10.1140/epjc/s10052-015-3575-6

CrossRef Full Text | Google Scholar

151. Bellini F, Cardani L, Casali N, Colantoni I, Cruciani A, Bellini F, Castellano MG, et al. High sensitivity phonon-mediated kinetic inductance detector with combined amplitude and phase read-out. Appl Phys Lett. (2017) 110:033504. doi: 10.1063/1.4974082

CrossRef Full Text | Google Scholar

152. Pattavina L, Casali N, Dumoulin L, Giuliani A, Mancuso M, de Marcillac P, et al. Background suppression in massive TeO₂ bolometers with Neganov' Luke amplified light detectors. J Low Temp Phys. (2016) 184:286–91. doi: 10.1007/s10909-015-1404-9

CrossRef Full Text | Google Scholar

153. Biassoni M, Brofferio C, Capelli S, Cassina L, Clemenza M, Cremonesi O, et al. Large area Si low-temperature light detectors with Neganov' Luke effect. Eur Phys J C. (2015) 75:480. doi: 10.1140/epjc/s10052-015-3712-2

CrossRef Full Text | Google Scholar

154. Nones C, Bergé L, Dumoulin L, Marnieros S, Olivieri E. Superconducting aluminum layers as pulse shape modifiers: an innovative solution to fight against surface background in neutrinoless double beta decay experiments. J Low Temp Phys. (2012) 167:1029–34. doi: 10.1007/s10909-012-0558-y

CrossRef Full Text | Google Scholar

155. Canonica L, Biassoni M, Brofferio C, Bucci C, Calvano S, Di Vacri ML, et al. Rejection of surface background in thermal detectors: the ABSuRD project. Nucl Instrum Meth A. (2013) 732:286–9. doi: 10.1016/j.nima.2013.05.114

CrossRef Full Text | Google Scholar

156. Wang G, Chang CL, Yefremenko V, Ding J, Novosad V, Bucci C, et al. R&D towards CUPID (CUORE upgrade with particle iDentification). arXiv [Preprint]. arXiv:1504.03612 (2015).

Google Scholar