The Symmetry Energy of the Nuclear EoS: A Study of Collective Motion and Low-Energy Reaction Dynamics in Semiclassical Approaches

In the framework of mean-field based transport approaches, we discuss recent results concerning collective motion and low-energy heavy ion reactions involving neutron-rich systems. We focus on aspects which are particularly sensitive to the isovector terms of the nuclear effective interaction and the corresponding symmetry energy. As far as collective excitations are concerned, we discuss the mixed nature of dipole oscillations in neutron-rich systems. On the other hand, for reactions close to the Coulomb barrier, we investigate the structure of pre-equilibrium collective dipole oscillations, focusing on their sensitivity to the symmetry energy behavior below normal density. Nucleon emission is also considered within the same context. The possible impact of other relevant terms of the nuclear effective interaction on these mechanisms is also examined. From this analysis we expect to put further constraints on the nuclear Equation of State, of crucial importance also in the astrophysical context.

1. Introduction

Collective patterns exhibited by complex systems can bear important information on relevant properties of the particle interaction. In nuclei, the investigation of the giant resonances, whose collective nature is well established, is therefore of primary importance [1]. A prominent example in this context is the giant dipole resonance (GDR), which can be described in terms of protons and neutrons oscillating as a whole against each other.

Stimulated by the advent of new radioactive beam facilities, a large amount of research has been devoted in recent years to the features of unstable nuclei and their collective multipole response. In the case of nuclei with some neutron excess, a strong fragmentation of strength has been observed in the isovector dipole response, mainly located at lower energy with respect to the GDR [2–11]. These low-lying excitations, which are referred in the literature as Pygmy Dipole Resonance (PDR), have been the object of intense discussion [12–23], proving to be, like the GDR, an important probe of crucial information of the nuclear effective interaction, especially concerning its isovector component and the corresponding contribution to the Equation of State (EoS) [24–26], namely the symmetry energy.

Collective oscillations of neutrons against protons might occur also in low-energy reactions involving charge-asymmetric systems, at least during the pre-equilibrium stage. If the N/Z ratios of the reaction partners are appreciably different, then neutron and proton centers of mass of the involved composite system do not coincide in the early phase of the fusion path and charge equilibration mechanisms take place. As a result, together with the incoherent exchange of nucleons between the reacting ions, a dynamical dipole (DD) mode, also known as pre-equilibrium GDR [27–34], is observed along the symmetry axis of the dinuclear system.

Since the transient composite system might experience large prolate deformation with respect to the equilibrium configuration of the final compound nucleus, the corresponding pre-equilibrium radiation carries out fundamental information about the density distribution and the shape of the di-nuclear complex. It is worth noting that this mechanism may also provide a cooling effect, which could favor superheavy element formation [35, 36].

Apart from the strong influence of different parameters, such as mass and charge asymmetry, collision centrality and energy [27, 33, 37], collective oscillations which characterize the DD turn out to be mainly ruled by the isovector channel of the nuclear effective interaction, which yields once again the restoring force. However, within the selected beam energy (around 10 MeV/A), where the DD mechanism is better evidenced, other pre-equilibrium effects, such as nucleon and light particle emission, can occur, leading to a reduction of the initial charge asymmetry of the colliding nuclei and contributing to cooling down the system. Likewise the DD mechanism, also the N/Z ratio of the pre-equilibrium nucleon emission, has been proposed as a probe of the symmetry energy behavior below normal density [33, 34, 38].

In this article we review recent studies devoted to the investigation, within a semi-classical transport approach, of collective excitations in isolated nuclei and of pre-equilibrium effects, such as dipole radiation and nucleon emission, occurring in nuclear reactions at low beam energy [39, 40]. The nuclear effective interaction is described by Skyrme-like parameterizations, which are mainly tuned on the features of selected nuclei, especially in spin-isospin channels [41, 42]. We will explore the sensitivity of the mechanisms considered to specific properties of the effective interaction and, in the case of nuclear reactions, also to the strength of two-body (n-n) collision cross section. In particular, from our combined analysis, we aim to get a consistent picture of the impact of the density dependence of the symmetry energy on dipole excitations in neutron-rich systems and on the features of pre-equilibrium DD oscillations, together with nucleon emission. We stress the general interest of this study, considering the leading role played by the symmetry energy in nuclear structure problems (the neutron skin thickness, for instance) [43–45] and its impact in the astrophysical context [46, 47].

2. Theoretical Framework

We adopt here the same theoretical and numerical treatments illustrated in Zheng et al. [39] and Zheng et al. [40], namely calculations are based on the semi-classical Boltzmann-Nordheim-Vlasov (BNV) model [48, 49].

Within such a framework, the evolution of the system is investigated by solving the two dynamical coupled equations [24]:

$\begin{array}{ll}\frac{\partial f_q(\text{r},\text{p},t)}{\partial t}+\frac{\partial {ϵ}_q}{\partial \text{p}}\frac{\partial f_q(\text{r},\text{p},t)}{\partial \text{r}}-\frac{\partial {ϵ}_q}{\partial \text{r}}\frac{\partial f_q(\text{r},\text{p},t)}{\partial \text{p}}=I_{coll}[f_n,f_p],& (1)\end{array}$

where f_q and ϵ_q, with q = n, p, are the distribution functions and the single particle energies of neutrons and protons, respectively. In the spirit of the density functional theory, the single particle energy, which includes the mean-field potential, can be derived from an energy density functional, ${\epsilon }$ [50]. The latter quantity, in the case of Skyrme-like interactions, is written as Raduta et al. [51]:

$\begin{array}{l}{\epsilon }=\frac{{\hslash }^2}{2m}\tau +C_0{\rho }^2+D_0{\rho }_3^2+C_3{\rho }^{\alpha +2}+D_3{\rho }^{\alpha }{\rho }_3^2+C_{eff}\rho \tau \\ +D_{eff}{\rho }_3{\tau }_3+C_{surf}{(▽\rho )}^2+D_{surf}{(▽{\rho }_3)}^2,& (2)\end{array}$

where (ρ = ρ_n + ρ_p, ρ₃ = ρ_n − ρ_p) and (τ = τ_n + τ_p, τ₃ = τ_n − τ_p) denote isoscalar and isovector density and kinetic energy densities, respectively, and the standard Skyrme parameters have been properly combined into the coefficients C_.., D_... In the calculations, the Coulomb contribution is also included [39]. The effect of the residual two-body correlations is taken into account in the collision integral, I_coll[f_n, f_p], employing the isospin, energy- and angular-dependent free nucleon-nucleon cross section. The test-particle (t.p.) method [52] is adopted to integrate Equation (1). However, the finite number of t.p. considered requires setting a maximum cutoff of 50 mb for the n-n cross section [53, 54], to quench spurious collisions that may originate from an inaccurate evaluation of Pauli blocking effects.

The model illustrated here is able to describe nuclear dynamics at low beam energies, from fusion to quasi-fission and deep-inelastic processes [33, 55, 56]. Moreover, the features of zero-sound excitations are well reproduced, both in nuclear matter and finite nuclei [24, 39, 57], though quantum effects, such as shell effects, cannot be accounted for.

Among the different channels of the effective interaction, we are mainly interested in the isovector terms. Thus, we introduce the definition of the symmetry energy per nucleon, $E_{sym}/A=C(\rho )I^2$, where I = ρ₃/ρ is the asymmetry parameter. The coefficient C(ρ) can be expressed in terms of the Skyrme coefficients:

$\begin{array}{ll}C(\rho )=\frac{{\epsilon }_F}{3}+D_0\rho +D_3{\rho }^{\alpha +1}+\frac{2m}{{\hslash }^2}\left(\frac{C_{eff}}{3}+D_{eff}\right){\epsilon }_F\rho ,& (3)\end{array}$

where ε_F denotes the Fermi energy and m is the nucleon mass.

In our calculations we will employ the recently introduced SAMi-J Skyrme effective interactions. The details of the SAMi fitting protocol and the derivation of the corresponding parameters can be found in Roca-Maza et al. [41]. As a key feature, the SAMi-J family has been produced to allow for different values of the symmetry energy at normal density, J = C(ρ₀), from 27 to 35 MeV, but keeping the same optimal values of the main isoscalar nuclear matter properties and of the main features of selected finite nuclei. In this way, these interactions mainly differ in the isovector channel and are thus well suited to explore the impact of isovector terms on a given observable.

It is worth noting here that, by construction, the Skyrme mean-field potential U_q is associated with a quadratic dependence on the momentum. This behavior is a good approximation for low momenta, such as in the situation explored in our study [58]. Actually, for the SAMi-J interactions, a rather flat momentum dependence is observed for the symmetry potential, according to the small splitting, $m_n^{*}-m_p^{*}=0.023mI$, between neutron and proton effective masses. Moreover, an effective isoscalar mass m*(I = 0) = 0.67m MeV is predicted by these interactions.

In the following, we will consider three SAMi-J parametrizations: SAMi-J27, SAMi-J31 and SAMi-J35 [41]. Since the fitting procedure involves the properties of finite nuclei, the coefficient C(ρ) gets the same value, i.e., C(ρ_c) ≈ 22 MeV at the density ρ_c ≈ 0.6ρ₀, that approximately represents the average density of nuclei of intermediate mass. Consequently, each parameterization is characterized by a different symmetry energy value, J, at normal density, as indicated in the corresponding interaction name.

The values of the slope parameter ${L=3{\rho }_0\frac{dC(\rho )}{d\rho }|}_{{}_{\rho ={\rho }_0}}$ are reported in Table 1. The corresponding density dependence of C(ρ) is displayed in Figure 1A.

TABLE 1

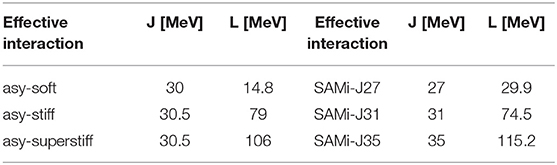
Table 1. The values of the symmetry energy J and its slope L at normal density are reported for the Skyrme interactions adopted in our study.

FIGURE 1

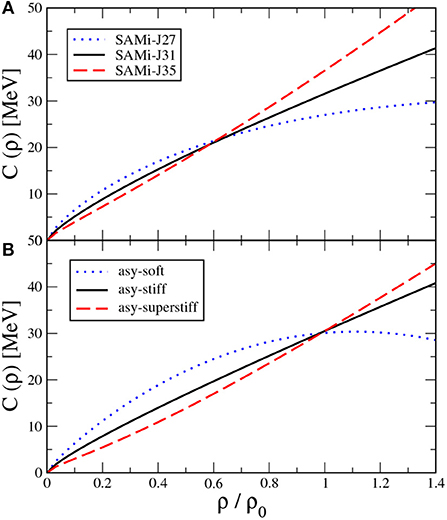
Figure 1. (Color online) Density dependence of the symmetry energy for the EoS with (upper panel) or without (lower panel) momentum dependence (ρ₀ = 0.16 fm⁻³). Readapted from Zheng et al. [40].

We will also adopt momentum-independent Skyrme interactions (C_eff = D_eff = 0, m* = m), characterized by an incompressibility modulus K = 200 MeV [59] and widely employed in the literature [38, 39, 59].

In order to distinguish these interactions from the SAMi-J family introduced above, which is momentum-dependent (MD), in the following we will indicate them as momentum-independent (MI) interactions. Concerning the symmetry energy, several trends are considered, as shown in Figure 1, lower, leading to different values of the slope L, but close values of the symmetry energy at normal density (J ≈ 30 MeV) (see also Table 1) [59]. As we will show in the following, the possibility to probe several interactions in the transport dynamics allows one to define the density regime explored in low-energy nuclear reactions and to test the impact of density dependent terms, such as the symmetry energy, on reaction observables.

The ground state of the considered nuclei is determined by solving Equation (1) in the stationary limit. Since we work with test particles which are usually associated with wave packets of finite width, some surface contributions are already implicitly taken into account, both in the initialization and in the dynamics, in addition to the surface terms of the SAMI-J interactions. In our case, in particular, we adopt triangular functions [49]. We find that the optimal reproduction of the experimental features (binding energy and charge radius) of selected nuclei is attained when suppressing the explicit surface terms, i.e., C_surf = D_surf = 0. Therefore, we will adopt this choice in the following.

3. Dipole Excitations in Neutron-Rich Systems

For the study of collective motion in nuclei, we neglect the collision integral in Equation (1). Thus, we are lead to consider the Vlasov equation, which represents the semi-classical limit of Time-Dependent Hartree-Fock (TDHF) and, for small oscillations, of the Random Phase Approximation (RPA) equations. In our calculations, a number of 1, 500 t.p. per nucleon is considered, ensuring a good spanning of the phase space. We will consider the following neutron-rich nuclei, spanning three mass regions: ⁶⁸Ni (N/Z = 1.43), ¹³²Sn (N/Z = 1.64), ²⁰⁸Pb (N/Z = 1.54).

3.1. Ground State Properties

The numerical procedure that we adopt to define the ground state gives charge radius and binding energy values which agree rather well with the predictions of Hartree-Fock calculations [41] and allow getting a reasonable reproduction of experimental values [60], as one observes in Table 2 in the case of the MD parameterizations. MI calculations overestimate the binding energy if one imposes having similar neutron and proton density profiles as obtained in the MD case (see Table 2). The values reported for the neutron skin thickness are also in good agreement with previous results obtained with the Sly4 Skyrme interaction [63], though the latter predicts smaller neutron and proton radii with respect to our results. On the other hand, a more diffuse neutron skin is observed in the case of the Relativistic Mean Field (RMF) calculations reported in Sarriguren et al. [63] (see also [44, 45] for further details). Isoscalar and isovector density profiles are shown in Figure 2 for the system ¹³²Sn and the three SAMi-J parameterizations adopted in our analysis. As evidenced in the left panel, a more diffuse density profile is obtained when increasing the slope parameter L. From the inspection of the isovector density (right panel), it appears that this effect can be ascribed to the development of a neutron skin. Indeed a larger slope L (see for instance the SAMi-J35 parametrization) is associated with a steeper variation of the symmetry energy around normal density, thus favoring the migration of the neutron excess toward the low-density nuclear surface. Similar behavior is seen for the ⁶⁸Ni and ²⁰⁸Pb ground state configuration and also in the case of the MI interactions [59]. The trend observed for the dependence of the neutron skin thickness on the symmetry energy features is in agreement with previous investigations with other models [7, 43–45].

TABLE 2

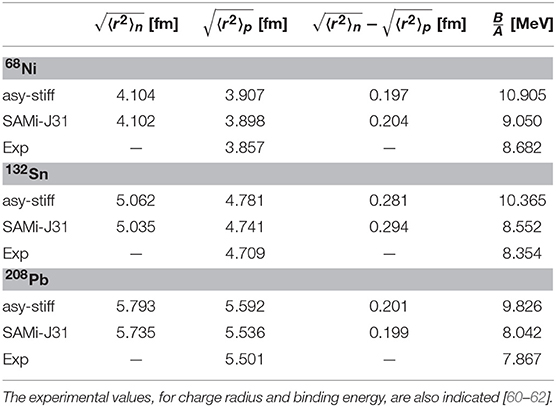
Table 2. Neutron and proton root mean square radii, their difference, and binding energy for the three systems considered in our study, as obtained with asy-stiff (MI) and SAMi-J31 (MD) interaction.

FIGURE 2

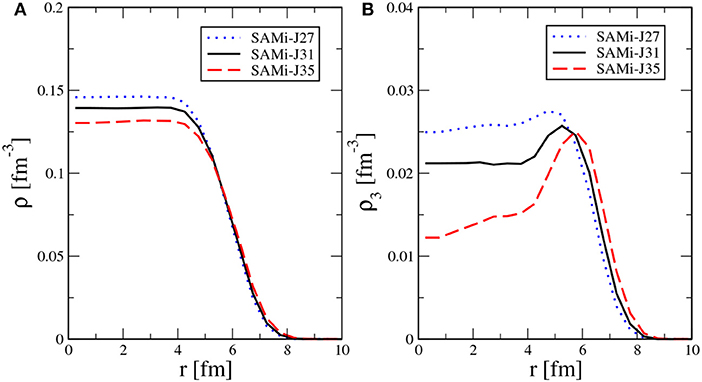
Figure 2. (Color online) The isoscalar (A) and isovector (B) density profiles of ¹³²Sn for the three SAMi-J parameterizations adopted in our study. Readapted from Zheng et al. [39].

3.2. Collective Dipole Response: Isoscalar-Isovector Mixing

We concentrate our analysis on the E1 (isoscalar and isovector) response of nuclear systems. Thus, we inject at the initial time the instantaneous excitation $V_{ext}={\eta }_k\delta (t-t_0){\widehat{D}}_k$, at t = t₀, along the z direction [64, 65], following the time evolution of the system until t = t_max. Here ${\widehat{D}}_k$ indicates the operator inducing dipole excitations of isoscalar or isovector type (k = S or V, respectively):

$\begin{array}{lll}{\widehat{D}}_S& ={\displaystyle \sum _i}\left(r_i^2-\frac{5}{3}\langle r^2\rangle \right)z_i;& (4)\end{array}$

$\begin{array}{lll}{\widehat{D}}_V& ={\displaystyle \sum _i}\left[{\tau }_i\frac{N}{A}-(1-{\tau }_i)\frac{Z}{A}\right]z_i,& (5)\end{array}$

where τ_i = 0(1) for neutrons (protons) and 〈r² 〉 refers to the mean square radius of the system under study. It should be noticed that, in the general case of asymmetric systems (with different N and Z numbers), the operator ${\widehat{D}}_V$ also contains an isoscalar component.

The strength function S_k(E) is evaluated considering the Fourier transform of D_k(t), which is the expectation value of the time-dependent dipole moment:

$\begin{array}{ll}{S}_k(E)=\frac{Im(D_k(\omega ))}{\pi {\eta }_k},& (6)\end{array}$

where $D_k(\omega )={\int }_{t_0}^{t_{max}}{D}_k(t)e^{i\omega t}dt$, with E = ℏω.

Introducing a gentle perturbation on the ground state of the considered nucleus, we follow the time oscillations of the dipole moment, solving Equation (1), until the final time t_max = 1, 800 fm/c. A filtering procedure, as described in Reinhard et al. [66], was applied in order to cure the problems connected to the finite calculation time. To this purpose, a smooth cut-off function was introduced such that $D_k(t)\to D_k(t){cos}^2(\frac{\pi t}{2t_{max}})$.

As discussed in Zheng et al. [39], whereas in symmetric matter one can isolate pure isoscalar and isovector excitations, in asymmetric systems a mixing is generally observed, owing to the different amplitude of neutron and proton oscillations. It is quite interesting to try to get deeper insight into this effect and its dependence on the features of the effective interaction employed.

3.3. Sensitivity to System Size and Effective Interaction

Let us first discuss how the response of the system evolves in the three mass regions considered in this work. For the results shown in the following, we only consider the IS(IV) response generated by a corresponding IS(IV) perturbation.

Figure 3 represents dipole oscillations and corresponding strength, as a function of the excitation energy E, as obtained for the system ¹³²Sn and the SAMi-J31 interaction. The (Figures 3A–D) correspond to an initial IS perturbation with η_S = 0.5 MeV fm⁻², whereas an initial IV perturbation with η_V = 25 MeV has been considered in Figures 3E–H.

FIGURE 3

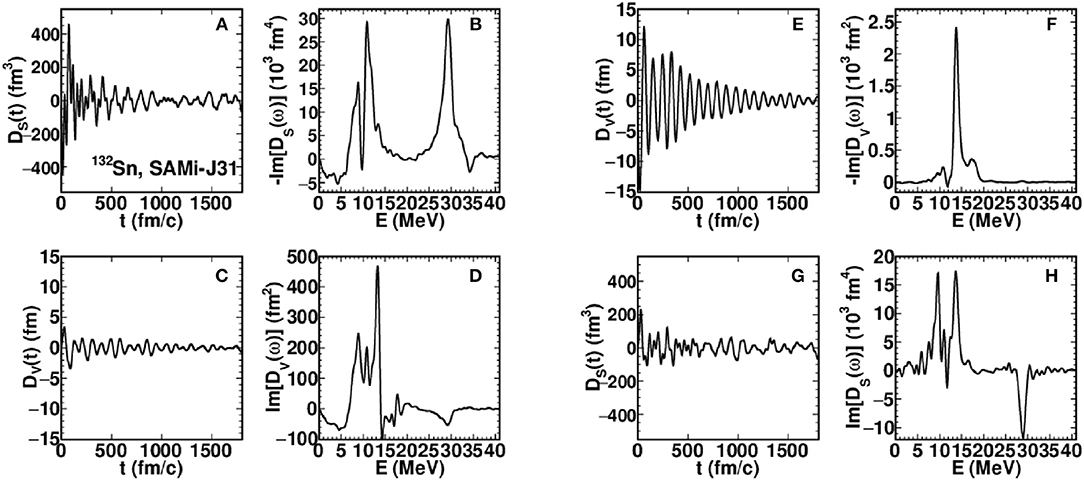
Figure 3. The dipole oscillations and corresponding response functions for ¹³²Sn and the SAMi-J31 interaction. Panels from (A–D) represent the results obtained with the initial IS perturbation and panels from (E–H) show the results obtained with the initial IV perturbation. Readapted from Zheng et al. [39].

The mixing between isoscalar and isovector excitations is rather evident. Indeed, the IS perturbation (Figures 3A,B) also excites oscillations of the IV dipole moment (Figures 3C,D). In a similar way, when an IV perturbation is applied (Figures 3E,F), one also gets an isoscalar response (Figures 3G,H).

Let us start our discussion by looking at the features of the isovector response (Figure 3F). Here we easily identify the IV GDR peak, with E_GDR ≈ 14 MeV. On the left, the low-energy region (the so called PDR region) is moderately populated, with some strength located between E₁ = 9 MeV and E₂ = 11 MeV. Interestingly, the contribution of the latter region is enhanced when looking at the IS projection (Figure 3H), where the corresponding strength now acquires a similar amplitude as compared to the GDR. This observation already suggests that these low-energy modes are mostly of isoscalar nature and is confirmed by the results obtained considering an initial IS perturbation (Figures 3A,B). Indeed, in Figure 3B one observes two important peaks with energies close to E₁ and E₂, together with a moderate strength contribution in the IV GDR region (E_GDR ≈ 14 MeV). Considerable strength is also located in the high-energy region of the spectrum (E ≈ 29 MeV) and can be attributed to the IS GDR mode. One can notice that this mode also has some mixed character. In fact, a sizable (negative) contribution appears, at this energy, also in the IS projection corresponding to an initial IV perturbation (see Figure 3F).

From the results discussed above, one can conclude that in asymmetric systems the normal modes are of quite mixed nature, so that they can be excited, though with different strength, by both IS and IV perturbations. Thus it is appropriate to discuss essentially in terms of isoscalar-like (i.e., mostly isoscalar) and isovector-like (i.e., mostly isovector) modes. In particular, our analysis suggests that the modes located in the PDR region are isoscalar-like; they contribute to the IV response because of their mixed character [39]. The dependence of these effects on the features of the nuclear effective interaction is discussed in the next section.

In Figure 4 we show, for the SAMi-J31 effective interaction, the strength function corresponding to the IS (Figure 4, Left) and IV (Figure 4, Right) dipole response as a function of the excitation energy E. As a general remark, we observe that the response is shifted to lower energy regions when increasing the system mass. Let us start discussing the IS response, whose spectrum is generally characterized by two main region of contributions: a large peak in the strength, which is associated with the compressional IS GDR mode and is located at high energy, above 25 MeV for all the nuclei under study, and a quite fragmented response, which is observed in the low-energy domain, in all cases below 15 MeV. The isoscalar-like nature of the isolated high-energy mode is considered well established, while its spreading width is still under investigation, although a significant dependence on the size of the nucleus is already evidenced in Figure 4. Concerning the low-lying energy modes, despite of the fragmentation, one can generally observe the emergence of two main peaks of comparable height with respect to the strength of the IS GDR, in agreement with previous results deduced within other semi-classical studies [57], where these excitations have been predominantly interpreted as surface modes. However, it is worth noting here that, owing to the coupling induced in neutron-rich systems discussed above, these oscillations are then responsible also for the strength observed in the PDR region of the isovector response. This correspondence holds for the three nuclei considered, including the largest system, ²⁰⁸Pb, where the low-lying IS peaks tend to merge together. The features regarding the low-energy part of the dipole spectrum can therefore be addressed by looking also at the IV response. In this case, however, we observe—for all nuclei—that the IV projection of the PDR is quite smaller than the IV GDR (about one order of magnitude), in agreement with previous RPA calculations [67]. We conclude that the PDR region is mainly populated by isoscalar low-energy modes, which generally involve mostly nucleons belonging to the nuclear surface [39]. Thus the position and the relative importance of the different low-lying energy modes may reflect the shape (i.e., the volume/surface relative contributions) of the density profile of the nucleus considered.

FIGURE 4

Figure 4. (Color online) The strength function vs. excitation energy for the three nuclei under study with SAMi-J31 interaction. The left panel refers to the IS strength, the right panel to the IV strength. The curves are normalized to the Energy Weighted Sum Rule (EWSR) of the IS (left) or IV (right) strength of the system ¹³²Sn, respectively. Readapted from Zheng et al. [39].

The reliability of our results is demonstrated by the good reproduction of the experimental data related to the IV GDR. Also the PDR region is reasonably reproduced, though a systematic overestimation is present in our calculations. This discrepancy might be attributable to the semi-classical treatment of surface effects. Indeed, these low-lying energy modes are mostly related to the oscillations of the most external nucleons. An improvement within the semi-classical framework can probably be achieved through a fine tuning of the coefficients C_{sur f} and D_{sur f} in the Skyrme parameterizations.

To better explore this issue, in Figure 5 we compare the IV dipole response extracted within our semi-classical Vlasov model to the results of standard TDHF calculations [68]. Despite the general good agreement, especially for the heavier systems, of the main IV GDR peak energy resulting from semi-classical and quantal approaches, significant differences between the two calculations are observed for the low-lying dipole modes. This comparison supports the conclusion that Vlasov results, in the PDR region, are affected by our numerical treatment of surface effects and by the lack of gradient terms of intrinsic quantal nature. A deeper investigation of the detailed structure of these excitations, both in semi-classical and quantal approaches, must thus be envisaged. However, though the exact energy location of the PDR region is not well reproduced, it is still worth examining the dependence of the response in this region on the effective interaction employed.

FIGURE 5

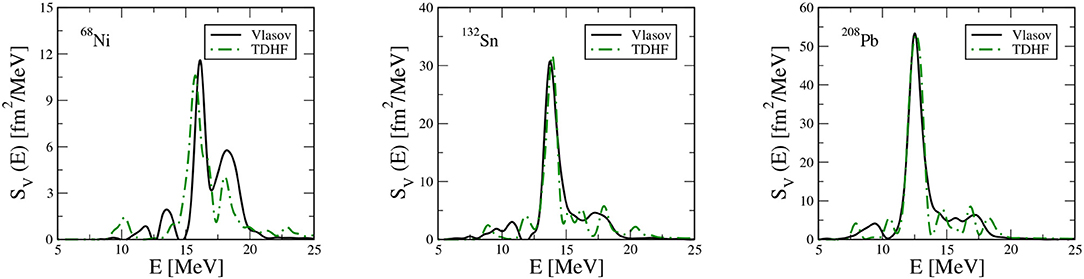
Figure 5. (Color online) The IV strength function versus excitation energy for ⁶⁸Ni (Left), ¹³²Sn (Central) and ²⁰⁸Pb (Right) with SAMi-J31 interaction, as obtained within the semi-classical Vlasov model or through a quantal TDHF calculation. Readapted from Zheng et al. [39].

We will focus on the description of ¹³²Sn. Let us look in particular at the change introduced in the spectrum when employing different SAMi-J parameterizations. We offer a reminder that this allows us to appreciate the sensitivity to the isovector channel of the interaction. Qualitatively, looking at the central panel of Figure 6, it appears that the different peaks arising in the low-energy region of the IV dipole response become higher for larger L values. Moreover, the left panel indicates also that the IS response of the lowest energy mode increases with L. This is expected on the basis that a larger symmetry energy slope L leads to a larger coupling between isoscalar and isovector modes, as pointed out by calculations in asymmetric nuclear matter [24]. Moreover, as seen in Figure 2, stiffer symmetry energy leads to thicker neutron skin. Thus, surface modes become more important, with a sizable isovector component as well, owing to the neutron enrichment of the surface region. We conclude that the strength of the dipole response located in the PDR region is quite sensitive to the symmetry energy parameterization and, in particular, to its slope L. On the other hand, almost no sensitivity to the isovector channel is seen for the energy position of the PDR strength, as it is expected for IS-like excitations.

FIGURE 6

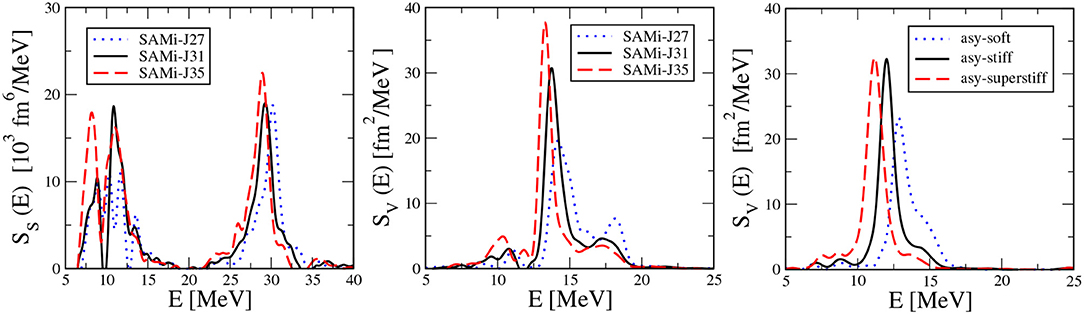
Figure 6. (Color online) The IS (Left) and IV (Central) strength function versus excitation energy for ¹³²Sn and the three considered SAMi-J interactions. Right : the same as for the Central, but employing momentum-independent interactions. Readapted from Zheng et al. [39].

Other interesting features of the IV response can be discussed by taking into account also the results related to the MI Skyrme interactions, represented in the right panel of Figure 6, still for ¹³²Sn. As far as the energy of the IV GDR is concerned, one can see that it does not evolve much in the SAMi-J case, whereas it shows a pronounced sensitivity to the interaction in the MI case, being smaller for the asy-superstiff parameterization. This suggests that the GDR energy reflects the value of the symmetry energy close to ρ_c = 0.6 ρ₀, which indeed can be taken as the average density of medium-heavy nuclei. In fact, the three SAMi-J interactions have equal symmetry energy at ρ_c (see Figure 1A), whereas in the MI case (Figure 1B) the symmetry energy is smaller for the stiffer interaction. It is of particular interest to compare the results of the asy-stiff and SAMi-J31 parameterizations, which show a close density behavior of the symmetry energy (see Figure 1). In spite of this, one observes a higher frequency in the MD case. This can be ascribed to momentum-dependent effects, thus evidencing an interesting interplay between symmetry energy and other terms of the effective interaction in shaping the features of the nuclear response.

Finally, a quite pronounced IV peak is observed in the energy region above the GDR, whose strength looks sensitive to the stiffness of the interaction. As confirmed by the analysis of the transition densities, discussed below, this peak is associated with volume IV excitations.

3.4. Transition Densities

Additional information on the nature of the nuclear excitations, namely on the mixing of IS and IV components, is gained through the study of the associated transition densities. The latter describe how neutrons and protons move in response to the external perturbation, thus helping to identify the volume/surface character of the different modes [39]. The transition densities, δρ_q, essentially correspond to the density oscillations, around the ground state configuration, induced by the initial perturbation. They can be calculated separately for neutrons and protons. Exploiting the cylindrical symmetry of the system and making the same assumptions (linear response regime) as in Urban [57], one can write: δρ_q(r, cos θ, t) = δρ_q(r, t) cos θ. Thus, at each time step, the transition densities can be finally extracted by performing an angular average, just as a function of the radial coordinate r.

As discussed above, different modes are excited by the delta function perturbation, V_ext, associated with the operator ${\widehat{D}}_k$. Thus, the observed transition densities will reflect the superposition of the different oscillations. As explained in Zheng et al. [39], in order to extract the contribution of a given mode, of energy E, to the transition densities, one can consider the Fourier transform of δρ_q(r, t):

$\begin{array}{ll}\delta {\rho }_q(r,E)\propto {\displaystyle {\int }_{t_0}^{\infty }}dt\delta {\rho }_q(r,t)sin\frac{Et}{\hslash }.& (7)\end{array}$

Owing to the finite calculation time, the sine function is multiplied by the same damping factor, as considered for the strength function S_k(E).

Since we are dealing with asymmetric systems, it is convenient to evaluate, for each mode, isoscalar and isovector transition densities (or, equivalently, neutron and proton transition densities). Then we expect the isoscalar component to be dominant in the case of isoscalar-like excitation, where neutrons and protons oscillate in phase, though with different amplitude. On the other hand, isovector-like oscillations should be associated with a dominant isovector component of the transition density.

In Figure 7, we display the isoscalar and isovector transition densities associated with the lowest energy peak observed in the IS response (the PDR peak), for ¹³²Sn and the three SAMi-J parameterizations adopted. As shown in Figure 4, this excitation contributes also to the IV response. The curves in Figure 7 clearly manifest the isoscalar nature of the pygmy mode. Indeed, the amplitude of the isoscalar density fluctuation is predominant overall, in contrast with the isovector one, which is generally rather small. However, a significant isovector density oscillation seems to involve the external part, where its contribution equals the isoscalar one. In fact, as a consequence of the neutron skin development, in this radial region only the neutron practically oscillate, and this fluctuation is responsible for the observed IV projection in the PDR region. Moreover, the interactions characterized by a large slope L lead to an increase of both IS and IV transition densities (which practically coincide) in the surface region. Indeed, as discussed above, for increasing L, the system develops a thicker neutron skin, thus the surface region becomes rather neutron rich and isovector effects are correspondingly enhanced in this region. Hence, the analysis of the transition densities confirms the interpretation of the strength observed in the PDR region discussed above.

FIGURE 7

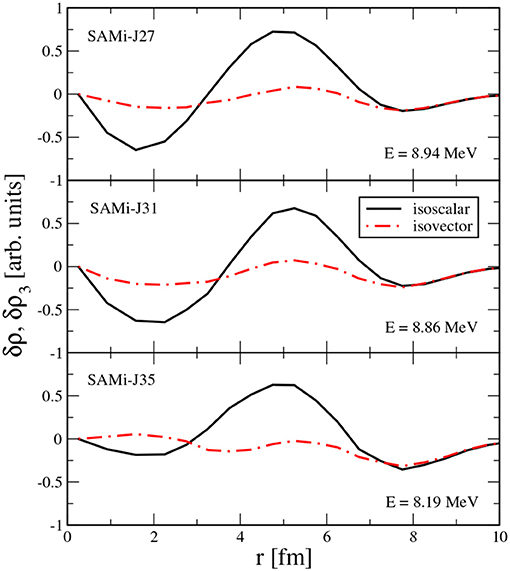
Figure 7. (Color online) Radial dependence of the isoscalar and isovector transition density for the lowest energy dipole mode, for ¹³²Sn and three SAMi-J interactions. Readapted from Zheng et al. [39].

Figure 8 shows the results relative to other modes, which give a relevant contribution to the dipole strength, for the system ¹³²Sn and the SAMi-J31 interaction. IS (IV) initial perturbations are considered in the left (right) panel. Let us comment first the features of the low-energy modes. As one can see in Figure 8, Left A, the transition densities of the second peak identified in the IS response (around E₂ = 11 MeV, see Figure 6) indicate that neutron and proton densities are in phase, though some mismatch is present. The mode has an isoscalar-like character, but with some mixing, leading to a contribution also to the IV response.

FIGURE 8

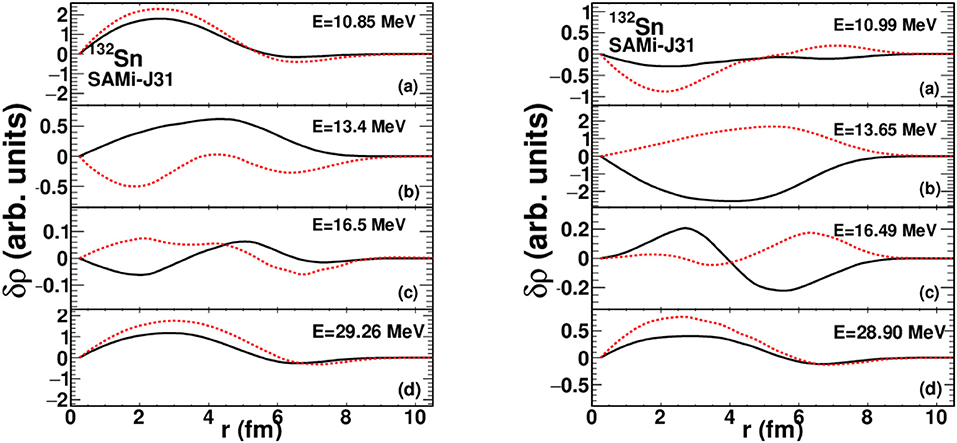
Figure 8. (Color online) Left: the transition densities are displayed as a function of the radial coordinate r for different excitation energies in ¹³²Sn. An initial IS perturbation and the SAMi-J31 interaction are considered. Dashed lines refer to neutrons, full lines to protons. Right: similar to the Left, but employing an initial IV perturbation. Readapted from Zheng et al. [39].

Indeed, when the same energy region is explored through IV excitations (Figure 8, Right A), the difference between protons and neutrons becomes stronger. We note that the feature described above, namely the splitting of the PDR strength into an isoscalar contribution (at lower energy) and an isovector (more energetic) component has been reported also in recent theoretical and experimental analyses [16–18].

Turning now to discuss the highest energy isoscalar mode (Figure 8D) we observe transition densities of considerable amplitude also in the internal part of the system. This confirms that this mode can actually be associated with the IS dipole compression mode, of robust isoscalar nature. By comparing left and right panels, one can also notice that the features of this mode are practically not affected by the initial perturbation.

Concerning the modes that are essentially isovector-like (Figures 8B,C), one can see that also in this case the transition densities associated with IS or IV excitations are quite similar (compare left and right panels). The transition densities nicely indicate that, whereas the standard GDR (Figure 8B) is essentially a surface mode, the higher energy mode (Figure 8C) deeply involves the nucleons belonging to the internal part, exhibiting a double oscillation, typical of Steinwedel-Jensen volume modes.

4. Results for Reaction Dynamics

Let us move now to discuss reaction dynamics between charge asymmetric systems, where charge equilibration takes place [40]. Full BNV calculations are performed for the reaction ¹³²Sn+⁵⁸Ni at 10 MeV/A, considering several impact parameters leading to incomplete fusion and employing both MD and MI interactions. A proper number of t.p. (600 t.p./nucleon) is adopted to ensure a reasonable spanning of f_q in phase space, as well as an acceptable computing time. Considering ¹³²Sn as a projectile induces a sizable charge asymmetry in the entrance channel, also allowing to explore possible reaction effects related to the neutron skin thickness, whose dependence on L has been already addressed in the previous section [39] and shown in Figure 2. Moreover, considering projectile (P) and target (T) with different N/Z ratios [${(\frac{N}{Z})}_P=1.64$ and ${(\frac{N}{Z})}_T=1.07$ in the case considered], neutron and proton centers of mass do not coincide, thus creating an initial dipole moment which may trigger DD oscillations along the rotating reaction symmetry axis. Another interesting aspect of nuclear reactions at energies just above the Coulomb barrier is that pre-equilibrium nucleon emission starts to take place. The two pre-equilibrium effects, namely nucleon and γ-ray emission, will be therefore addressed in the following [40].

4.1. The DD Emission

We first discuss dipole oscillations following a collective bremsstrahlung analysis [27, 36, 38]. Similarly to Equation 5, the dipole moment is defined in coordinate space as:

$\begin{array}{ll}D(t)=\frac{NZ}{A}(R_p-R_n),& (8)\end{array}$

where A = A_T + A_P is the total mass of the dinuclear system and Z = Z_T + Z_P (N = N_T + N_P) is the proton (neutron) number. R_n and R_p denote the center of mass of neutrons and protons, respectively. For the system considered, when the two nuclei touch each other, the dipole moment is equal to D_i = 45.1 fm. The DD emission probability of photons with energy E_γ is given by (E_γ = ℏω):

$\begin{array}{ll}\frac{dP}{d{E}_{\gamma }}=\frac{2e^2}{3\pi \hslash c^3{E}_{\gamma }}|D^{″}(\omega ){|}^2,& (9)\end{array}$

where D″(ω) is the Fourier transform of the dipole acceleration D″(t) [27]. We will show the results for the average DD evolution, as obtained by considering 10 events for each specific calculation. This allows one to avoid spurious oscillations caused by the numerical noise associated with the finite number of test particles. We expect that, according to both mean-field and two-body collisional effects, the DD oscillations will be damped. Since microscopic calculations suggest that in-medium effects quench the two-body nucleon cross section [69], we also performed simulations multiplying the latter quantity by a global factor f_cs. Two cases (i.e., f_cs = 0, corresponding to Vlasov calculations, and f_cs = 0.5) are considered. Hence in the following we will explore, in addition to mean-field effects, also the influence of collisional damping and nucleon emission on the dipole oscillations.

In Figure 9, Left, we plot the time evolution of the DD, at b = 2 fm, as obtained for the SAMi-J31 EoS and with the different choices of f_cs. The initial dipole moment is quite large because at the initial time considered, the distance between the centers of mass of the two nuclei is 14 fm. First of all, it can be interesting to compare the results related to the Vlasov case (f_cs = 0) with the oscillations displayed in Figure 3. A considerable damping of the dipole oscillations is observed in Figure 9, owing to possible non-linear effects and to nucleon emission, which cools down the system and reduces the initial charge asymmetry. One can also notice that the DD oscillations with the free n-n cross section (f_cs = 1) are damped faster than in the calculations associated with smaller f_cs values. As a result, when neglecting the in-medium suppression of the n-n cross section, dipole oscillations are fully damped within about 600 fm/c. The corresponding power spectrum, |D″(ω)|², which enters the expression of the photon emission probability [see Equation (9)] is also represented in Figure 9, Right. One can notice that the peak centroid is located at smaller energy with respect to the IV GDR in isolated nuclei. This is due to the elongated shape of the system at the initial reaction stage. Moreover, one observes that the centroids of the power spectra do not depend too much on the cross section choice. However, a slight shift to lower energies is observed especially in the f_cs = 0 case, indicating that, in absence of two-body collisions, the systems maintain the elongated shape for a longer time. Dissipation effects are clearly larger for the larger cross section and the DD strength correspondingly decreases. The calculations for the other impact parameters indicate that the DD signal is quenched in more peripheral events, though similar features are observed with respect to the results for central collisions discussed above.

FIGURE 9

Figure 9. (Color online) Left: The time evolution of DD for the SAMi-J31 EoS at b = 2 fm. Right: the corresponding power spectrum of the dipole acceleration. Results are plotted for different choices of the n-n cross section (see text). Readapted from Zheng et al. [40].

4.2. Sensitivity to the Effective Interaction

Once the effect of the two-body collisional damping is clarified, we can look at the role of different ingredients of the nuclear effective interaction, in determining the energy spectrum, analogous with the study of collective dipole modes carried out in section Sensitivity to System Size and Effective Interaction. The value of f_cs = 1 will be fixed therefore in the following, while all interactions introduced in Figure 1 will be taken into account. The results are displayed in Figure 10, for MI (Figure 10, Left) and MD (Figure 10, Right) interactions, respectively.

FIGURE 10

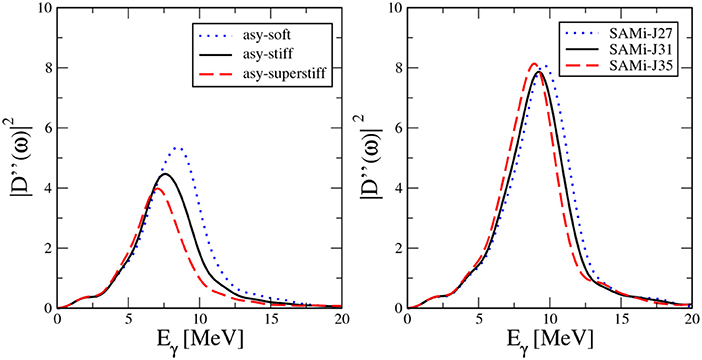
Figure 10. (Color online) Power spectrum of the dipole acceleration as obtained by employing MI (Left) or MD (Right) interaction, for f_cs = 1 and b = 2 fm (see text). Readapted from Zheng et al. [40].

Several differences emerge between the power spectra obtained in the two cases which are actually consistent with what we have already discussed in section Sensitivity to System Size and Effective Interaction. Indeed the peak centroid is insensitive to the effective interaction in the MD case, where a sizable dependence is observed in the MI case. As already stressed above, the restoring force of IV dipole oscillations is essentially ruled by the symmetry energy. Thus, we conclude that the DD features are also determined by the symmetry energy value in the density region around ρ_c ≈ 0.6 ρ₀, the crossing point of the SAMi-J interactions. The lower frequency of the oscillations, with respect to the standard GDR, is due to the elongated shape of the system. In the MI case, the frequency of the power spectrum is higher for the asy-soft case, in connection to the larger value taken by the symmetry energy below normal density (see Figure 1B). One can also observe that a higher peak energy is also associated with a higher magnitude of the power spectrum, consistent with previous studies [38]. Moreover, the MD calculations are characterized by higher magnitude and frequency of the power spectrum, with respect to the MI results. As already stressed in the case of the small amplitude excitations (see Figure 6), this result is related to the influence of the effective mass on the features of collective dipole modes, for which it is well known that MD interactions yield a larger EWSR, which can better reproduce the experimental data [39]. As discussed in Zheng et al. [40], the results illustrated above can be grasped, in a rather schematic manner, in terms of the damped oscillator model. Indicated by τ and ω₀ damping time and oscillation frequency, respectively, the Fourier transform of the dipole acceleration can be written as Baran et al. [38]:

$\begin{array}{ll}|D^{″}(\omega ){|}^2=\frac{{({\omega }_0^2+1/{\tau }^2)}^2{D}_i^2}{{(\omega -{\omega }_0)}^2+1/{\tau }^2}.& (10)\end{array}$

From the above equation, it is clear that the DD emission is governed by the size of the initial dipole D_i, as expected, but it also reflects the amplitude of the oscillation frequency ω₀. This is fully in line with the results of Figure 10, Left: a larger energy centroid also corresponds to a larger strength. One can also realize that a short damping rate, 1/τ, leading to strong two-body collisional effects, quenches the strength [see the denominator of Equation (10)], as is shown in Figure 9.

4.3. Nucleon Emission

Let us discuss here the nucleon emission characterizing the pre-equilibrium stage. As we will show in the following, nucleon and light particle emission may carry out important information on selected properties of the nuclear effective interaction. Indeed, for reactions at Fermi energies, the isotopic content of such emission has already been shown to reflect the behavior of the symmetry energy at subsaturation density. This is in fact the density region explored during the expansion phase of the nuclear composite system, when this emission mainly occurs [24, 25, 70]. The nucleons emitted escape from the dense compact system, so that they can be traced back just looking at the particles belonging to low-density regions (ρ < 0.01 fm⁻³) at the final calculation time, t_max = 600 fm/c. One observes that a larger nucleon emission is associated with MD interactions. This can be attributed to the fact that the most energetic particles feel a less attractive mean-field potential when momentum-dependent effects are turned on. Larger f_cs values also lead to an enhanced pre-equilibrium emission, owing to the increased n-n collision number. On the contrary, the N/Z ratio decreases in the MD case and also in the calculations associated with a larger n-n cross section. Thus, it appears that, on top of the expected sensitivity to the symmetry energy, the N/Z ratio also reflects some isoscalar features, such as effective mass and n-n collisions. When the pre-equilibrium emission becomes more abundant, the relative importance of isospin effects may become smaller and hence the N/Z ratio approaches 1. This dependence on several aspects of the effective interation is seen also for the DD emission, as discussed above. However, one can pin down the sensitivity to the symmetry energy by inspecting in deeper detail the results corresponding to the three parameterizations considered in our study, either in the MI or MD case, with a given f_cs choice. For instance, in the case of f_cs = 1, the N/Z ratio obtained in central collisions evolves from 2.049 to 1.774 when going from the asy-soft to the asy-superstiff symmetry energy parameterizations, whereas it changes from 1.433 to 1.687 in correspondence to the SAMi-J27 and SAMi-J35 interactions, respectively. Bearing in mind that the N/Z ratio increases with the symmetry energy value (owing to the increased neutron repulsion), one can conclude that, in low-energy nuclear reactions, the pre-equilibrium emission mainly tests the density region in between ρ_c and ρ₀. This statement is corroborated by the opposite trend of N/Z with respect to the slope, as obtained in the MI and MD cases. Indeed, the crossing point of the symmetry energy (see Figure 1) is different for the two types of interactions, so that the ordering of the symmetry energy strength with L, in the density region considered, is opposite in the two cases. Therefore, combining the study of DD and pre-equilibrium nucleon emission, one has the possibility to probe the effective interaction in the low-density range [ρ_c, ρ₀].

4.4. Global Analysis

The results discussed above indicate that the selected pre-equilibrium mechanisms, i.e., γ radiation and nucleon emission, are influenced by several ingredients of the nuclear effective interaction. A deeper insight into this issue is obtained by performing a more global analysis in order to explore mutual correlations between the features of the interaction and some proper observables [70]. The correlation coefficient C_XY between the variable X and observable Y is usually defined as:

$\begin{array}{lll}{C}_{XY}& =\frac{cov(X,Y)}{s(X)s(Y)}& (11)\end{array}$

$\begin{array}{lll}cov(X,Y)& =\frac{1}{n-1}{\displaystyle \sum _{i=1}^n}(X_i-\bar{X})(Y_i-Ȳ),& (12)\end{array}$

where cov(X, Y) denotes the covariance, Ā and s(A) indicate average value and variance of A (=X or Y), respectively. These quantities are calculated from the considered set of MI and MD calculations, with different symmetry energy and n-n cross section parameterizations. It should be noticed that a linear correlation between X and Y leads to C_XY = ±1, whereas, in the absence of correlations, one gets C_XY = 0. Inspired by the results that have been presented so far, we select three observables, which can be investigated experimentally [33, 70]: the centroid (E_centr) and the integral of the DD emission strength, and the N/Z ratio of the nucleons emitted. Three model parameters, which have been shown to impact significantly these observables, are considered: the symmetry energy slope L, the effective mass m* and the f_cs value. The correlations between the model parameters and the observables are presented in Figure 11 (see the solid bars) [40]. In this analysis, we intend to use the L parameter to characterize the low-density behavior of the symmetry energy. Thus, the correlation functions have been evaluated excluding the SAMi-J27 and SAMi-J35 interactions. Indeed, within the SAMi-J family, the symmetry energy takes the same value below normal density (at ρ = ρ_c, see Figure 1), and this feature could blur the sensitivity to L. One can see that an appreciable sensitivity to the slope L can be identified for the DD centroid energy and for the N/Z of the pre-equilibrium emission. A negative correlation is observed (denoted by the blue color); indeed, both the centroid energy and the pre-equilibrium N/Z decrease for stiffer (i.e., with larger L) interactions, as discussed above. On the other hand, for the integral of the DD power spectrum, the sensitivity to L is overwhelmed by the huge dependence of the results on effective mass and n-n cross section. For the sake of completeness, calculations have been performed also considering the full set of MD and MI interaction (dashed bars in Figure 11). As one can see, this does not change the conclusions drawn above. This analysis underlines and better quantifies the concurrent impact of several aspects of the effective interaction on observables which, by construction, should be particularly sensitive to the isovector terms, namely to the symmetry energy. In particular, it appears that it would be rather difficult to pin down the sensitivity to the symmetry energy without fixing, at the same time, other ingredients, such as the effective mass and the strength of the residual interaction.

FIGURE 11

Figure 11. (Color online) Negative (positive) correlations functions between model parameters and observables are indicated by blue (red) bars. Solid and shaded bars refer to different sets of calculations included in the analysis (see text for more details). Readapted from Zheng et al. [40]. The centroid of the DD emission strength, its integral and the N/Z ratio of the nucleons emitted are considered in (A–C), respectively.

5. Conclusions

To summarize, in this work we have performed, within a semi-classical transport approach, a combined study of collective modes in neutron-rich nuclei and pre-equilibrium dipole radiation in low-energy nuclear reactions. Within the latter framework, pre-equilibrium nucleon emission has also been discussed. The aim of our investigation was indeed to assess the sensitivity of several observables involved in the reaction dynamics to the main ingredients of the nuclear effective interaction as well as to the in-medium n-n cross section.

Concerning the analysis of collective excitations in neutron rich-systems, we aimed at gaining better insight into the features of the low-lying IV dipole response which is experimentally observed in several neutron-rich nuclei [13]. Interesting features of the E1 nuclear response have been evidenced by exploring three mass regions and considering a variety of effective interactions, mainly differing in the isovector channel. Inspecting both IS and IV response of the systems investigated, our analysis indicates the emergence, in neutron rich systems, of a strong mixing between isoscalar and isovector excitations, analogous to the one discussed for infinite nuclear matter [24], in agreement with previous semi-classical [57] or RPA [67] investigations. PDR excitations are mainly of isoscalar nature; however, because of mixing effects, some strength is observed also in the IV response, whose amplitude is rather sensitive to the slope L of the symmetry energy around saturation. This observation is associated with the appearance of a thicker neutron skin, in neutron-rich systems, for increasing L values. Hence our analysis confirms the important contribution of the study of low-lying dipole excitations to the symmetry energy debate. At last, it is also worth noting that our results give a centroid energy of the IV GDR that is quite close to the experimental value as well as to RPA calculations [67], also reflecting the value of the symmetry energy below normal density.

Moreover, the results discussed here, in particular the link between the PDR strength, the neutron enrichment of the nuclear surface and the IS/IV mixing of the collective excitations, can be useful for the experimental search of the PDR and for a more accurate estimate of the corresponding strength. The latter, in turn, can provide information about the neutron skin thickness of the nucleus considered, complementary to more direct measurements.

As far as the study of pre-equilibrium dipole and nucleon emission is concerned, considering a variety of effective interactions in the calculations, we have asserted that these observables are also quite appropriate to explore the symmetry energy behavior below normal density, in the density range [0.6ρ₀, ρ₀]. However, though sensitive to the isovector channel of the interaction, we have brought out that these mechanisms strongly depend also on isoscalar terms, such as n-n correlations and momentum-dependent terms. A significant dependence on the latter terms, i.e., on the effective mass, is observed also for the collective excitations investigated in section 3 [71]. Moreover, the sensitivity to several ingredients of the effective interaction has been recently pointed out also for the competition between fusion and quasifission processes in heavy ion reactions close to the Coulomb barrier [72].

Our analysis suggests that a consistent study of collective excitations and low-energy reaction dynamics may open the possibility, by a parallel investigation of different observables, to constrain at once the details of effective interaction and n-n cross section, together with the low-density behavior of the symmetry energy.

Author Contributions

SB and HZ have been mostly involved in the semi-classical calculations leading to the results discussed in the manuscript. MC has supervised this work. SB, MC, and HZ have contributed to the writing of the manuscript and to the general interpretation of the results.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This project has received funding from the European Union's Horizon 2020 research and innovation program under grant agreement N. 654002.

References

1. Harakeh MN, van der Woude A. Giant Resonances, Oxford Studies in Nuclear Physics, Vol. 24. New York, NY: Oxford University (2001).

Google Scholar

2. Hartmann T, Enders J, Mohr P, Vogt K, Volz S, Zilges A. Measurement of the dipole and electric quadrupole strength distributions up to 10 MeV in the doubly magic nuclei ⁴⁰Ca and ⁴⁸Ca. Phys Rev Lett. (2000) 85:274–7. doi: 10.1103/PhysRevLett.85.274

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Hartmann T, Enders J, Mohr P, Vogt K, Volz S, Zilges A. Dipole and electric quadrupole excitations in ^{40, 48}Ca. Phys Rev C. (2002) 65:034301. doi: 10.1103/PhysRevC.65.034301

CrossRef Full Text | Google Scholar

4. Kondo T, Utsunomiya H, Goriely S, Daoutidis I, Iwamoto C, Akimune H, et al. Total and partial photoneutron cross sections for Pb isotopes. Phys Rev C. (2012) 86:014316. doi: 10.1103/PhysRevC.86.014316

CrossRef Full Text | Google Scholar

5. Adrich P, Klimkiewicz A, Fallot M, Boretzky K, Aumann T, Cortina-Gil D, et al. Evidence for pygmy and giant dipole resonances in ¹³⁰Sn and ¹³²Sn. Phys Rev Lett. (2005) 95:132501. doi: 10.1103/PhysRevLett.95.132501

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Klimkiewicz A, Paar N, Adrich P, Fallot M, Boretzky K, Aumann T, et al. Nuclear symmetry energy and neutron skins derived from pygmy dipole resonances. Phys Rev C. (2007) 76:051603(R). doi: 10.1103/PhysRevC.76.051603

CrossRef Full Text | Google Scholar

7. Carbone A, Colò G, Bracco A, Cao L-G, Bortignon PF, Camera F, et al. Constraints on the symmetry energy and neutron skins from pygmy resonances in ⁶⁸Ni and ¹³²Sn. Phys Rev C. (2010) 81:041301(R). doi: 10.1103/PhysRevC.81.041301

CrossRef Full Text | Google Scholar

8. Wieland O, Bracco A. The pygmy dipole resonance in ⁶⁸Ni and the neutron skin. Prog Part Nucl Phys. (2011) 66:374–8. doi: 10.1016/j.ppnp.2011.01.037

CrossRef Full Text | Google Scholar

9. Tamii A, Poltoratska I, von Neumann-Cosel P, Fujita Y, Adachi T, Bertulani CA, et al. Complete electric dipole response and the neutron skin in ²⁰⁸Pb. Phys Rev Lett. (2011) 107:062502. doi: 10.1103/PhysRevLett.107.062502

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Rossi DM, Adrich P, Aksouh F, Alvarez-Pol H, Aumann T, Benlliure J, et al. Measurement of the dipole polarizability of the unstable neutron-rich nucleus ⁶⁸Ni. Phys Rev Lett. (2013) 111:242503. doi: 10.1103/PhysRevLett.111.242503

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Toft HK, Larsen AC, Bürger A, Guttormsen M, Görgen A, Nyhus HT, et al. Evolution of the pygmy dipole resonance in Sn isotopes. Phys Rev C. (2011) 83:044320. doi: 10.1103/PhysRevC.83.044320

CrossRef Full Text | Google Scholar

12. Aumann T, Nakamura T. The electric dipole response of exotic nuclei. Phys Scr. (2013) T 152:014012. doi: 10.1088/0031-8949/2013/T152/014012

CrossRef Full Text | Google Scholar

13. Savran D, Aumann T, Zilges A. Experimental studies of the Pygmy Dipole Resonance. Prog Part Nucl Phys. (2013) 70:210–45. doi: 10.1016/j.ppnp.2013.02.003

CrossRef Full Text | Google Scholar

14. Paar N, Vretenar D, Khan E, Colò G. Exotic modes of excitation in atomic nuclei far from stability. Rep Prog Phys. (2007) 70:691–793. doi: 10.1088/0034-4885/70/5/R02

CrossRef Full Text | Google Scholar

15. Lanza EG, Vitturi A, Andrés MV, Catara F, Gambacurta D. Excitations of pygmy dipole resonances in exotic and stable nuclei via Coulomb and nuclear fields. Phys Rev C. (2011) 84:064602. doi: 10.1103/PhysRevC.84.064602

CrossRef Full Text | Google Scholar

16. Crespi FCL, Bracco A, Nicolini R, Mengoni D, Pellegri L, Lanza EG, et al. Isospin character of low-lying pygmy dipole states in ²⁰⁸Pb via inelastic scattering of ¹⁷O Ions. Phys Rev Lett. (2014) 113:012501. doi: 10.1103/PhysRevLett.113.012501

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Lanza EG, Vitturi A, Litvinova E, Savran D. Dipole excitations via isoscalar probes: The splitting of the pygmy dipole resonance in ¹²⁴Sn. Phys Rev C. (2014) 89:041601. doi: 10.1103/PhysRevC.89.041601

CrossRef Full Text | Google Scholar

18. Endres J, Savran D, Butler PA, Harakeh PA, Harissopulos S, Herzberg R-D, et al. Structure of the pygmy dipole resonance in ¹²⁴Sn. Phys Rev C. (2012) 85:064331. doi: 10.1103/PhysRevC.85.064331

CrossRef Full Text | Google Scholar

19. Repko A, Reinhard P-G, Nesterenko VO, Kvasil J. Toroidal nature of the low-energy E1 mode. Phys Rev C. (2013) 87:024305. doi: 10.1103/PhysRevC.87.024305

CrossRef Full Text | Google Scholar

20. Papakonstantinou P, Hergert H, Roth R. Isoscalar and neutron modes in the E1 spectra of Ni isotopes and the relevance of shell effects and the continuum. Phys Rev C. (2015) 92:034311. doi: 10.1103/PhysRevC.92.034311

CrossRef Full Text | Google Scholar

21. Knapp F, Lo Iudice N, Veselỳ P, Andreozzi F, De Gregorio G, Porrino A. Dipole response in ²⁰⁸Pb within a self-consistent multiphonon approach. Phys Rev C. (2015) 92:054315. doi: 10.1103/PhysRevC.92.054315

CrossRef Full Text | Google Scholar

22. Knapp F, Lo Iudice N, Veselỳ P, Andreozzi F, De Gregorio G, Porrino A. Dipole response in ¹³²Sn within a self-consistent multiphonon approach. Phys Rev C. (2014) 90:014310. doi: 10.1103/PhysRevC.90.014310

CrossRef Full Text | Google Scholar

23. Auerbach N, Stoyanov C, Anders MR, Shlomo S. Isoscalar and isovector dipole strength distributions in nuclei and the Schiff moment. Phys Rev C. (2014) 89:014335. doi: 10.1103/PhysRevC.89.014335

CrossRef Full Text | Google Scholar

24. Baran V, Colonna M, Greco V, Di Toro M. Reaction dynamics with exotic nuclei. Phys Rep. (2005) 410:335–466. doi: 10.1016/j.physrep.2004.12.004

CrossRef Full Text | Google Scholar

25. Li B-A, Chen L-W, Ko CM. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys Rep. (2008) 464:113–281. doi: 10.1016/j.physrep.2008.04.005

CrossRef Full Text | Google Scholar

26. Giuliani G, Zheng H, Bonasera A. The many facets of the (non-relativistic) Nuclear Equation of State. Prog Part Nucl Phys. (2014) 76:116–64. doi: 10.1016/j.ppnp.2014.01.003

CrossRef Full Text | Google Scholar

27. Baran V, Brink DM, Colonna M, Di Toro M. Collective Dipole Bremsstrahlung in Fusion Reactions. Phys Rev Lett. (2001) 87:182501. doi: 10.1103/PhysRevLett.87.182501

CrossRef Full Text | Google Scholar

28. Simenel C, Chomaz Ph, de France G. Quantum Calculation of the Dipole Excitation in Fusion Reactions. Phys Rev Lett. (2001) 86:2971–4. doi: 10.1103/PhysRevLett.86.2971

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Umar AS, Oberacker VE. ⁶⁴Ni+¹³²Sn fusion within the density-constrained time-dependent Hartree-Fock formalism. Phys Rev C. (2007) 76:014614. doi: 10.1103/PhysRevC.76.014614

CrossRef Full Text | Google Scholar

30. Wu HL, Tian WD, Ma YG, Cai XZ, Chen JG, Fang DQ, et al. Dynamical dipole γ radiation in heavy-ion collisions on the basis of a quantum molecular dynamics model. Phys Rev C. (2010) 81:047602. doi: 10.1103/PhysRevC.81.047602

CrossRef Full Text | Google Scholar

31. Flibotte S, Chomaz Ph, Colonna M, Cromaz M, DeGraaf J, Drake TE, et al. Pre-equilibrium effects in the population of giant dipole resonances. Phys Rev Lett. (1996) 77:1448–51. doi: 10.1103/PhysRevLett.77.1448

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Papa M, Tian W, Giuliani G, Amorini F, Cardella G, Di Pietro A, et al. Pre-equilibrium γ-ray emission induced in the ⁴⁰Ca+⁴⁸Ca system at 10 MeV/nucleon and isospin equilibration processes. Phys Rev C. (2005) 72:064608. doi: 10.1103/PhysRevC.72.064608

CrossRef Full Text | Google Scholar

33. Pierroutsakou D, Martin B, Agodi C, Alba R, Baran V, Boiano A, et al. Dynamical dipole mode in fusion reactions at 16 MeV/nucleon and beam energy dependence. Phys Rev C. (2009) 80:024612. doi: 10.1103/PhysRevC.80.024612

CrossRef Full Text | Google Scholar

34. Giaz A, Corsi A, Barlini S, Kravchuk VL, Wieland O, Colonna M, et al. Measurement of dynamical dipole γ-ray emission in the N/Z-asymmetric fusion reaction ¹⁶O+¹¹⁶Sn at 12 MeV/nucleon. Phys Rev C. (2014) 90:014609. doi: 10.1103/PhysRevC.90.014609

CrossRef Full Text | Google Scholar

35. Simenel C, Chomaz Ph, de France G. Fusion process studied with a preequilibrium giant dipole resonance in time-dependent Hartree-Fock theory. Phys Rev C. (2007) 76:024609. doi: 10.1103/PhysRevC.76.024609

CrossRef Full Text | Google Scholar

36. Parascandolo C, Pierroutsakou D, Alba R, Del Zoppo A, Maiolino C, Santonocito D, et al. Evidence of dynamical dipole excitation in the fusion-evaporation of the ⁴⁰Ca+¹⁵²Sm heavy system. Phys Rev C. (2016) 93: 044619. doi: 10.1103/PhysRevC.93.044619

CrossRef Full Text | Google Scholar

37. Baran V, Cabibbo M, Colonna M, Di Toro M, Tsoneva N. The dynamical dipole mode in dissipative heavy-ion collisions. Nucl Phys A. (2001) 679:373–92. doi: 10.1016/S0375-9474(00)00365-1

CrossRef Full Text | Google Scholar

38. Baran V, Rizzo C, Colonna M, Di Toro M, Pierroutsakou D. Dynamical dipole mode in fusion reactions with exotic nuclear beams. Phys Rev C. (2009) 79:021603(R). doi: 10.1103/PhysRevC.79.021603

CrossRef Full Text | Google Scholar

39. Zheng H, Burrello S, Colonna M, Baran V. Dipole response in neutron-rich nuclei with new Skyrme interactions. Phys Rev C. (2016) 94:014313. doi: 10.1103/PhysRevC.94.014313

CrossRef Full Text | Google Scholar

40. Zheng H, Burrello S, Colonna M, Baran V. Pre-equilibrium effects in charge-asymmetric low-energy reactions. Phys Lett B. (2017) 769:424–9. doi: 10.1016/j.physletb.2017.04.002

CrossRef Full Text | Google Scholar

41. Roca-Maza X, Colò G, Sagawa H. New Skyrme interaction with improved spin-isospin properties. Phys Rev C. (2012) 86:031306(R).

Google Scholar

42. Roca-Maza X, Brenna M, Agrawal BK, Bortignon PF, Colò G, Li-Gang Cao NP, et al. Giant quadrupole resonances in ²⁰⁸Pb, the nuclear symmetry energy, and the neutron skin thickness. Phys Rev C. (2013) 87:034301. doi: 10.1103/PhysRevC.87.034301

CrossRef Full Text | Google Scholar

43. Piekarewicz J, Agrawal BK, Colò G, Nazarewicz W, Paar N, Reinhard P-G, et al. Electric dipole polarizability and the neutron skin. Phys Rev C. (2012) 85:041302(R). doi: 10.1103/PhysRevC.85.041302

CrossRef Full Text | Google Scholar

44. Gaidarov MK, Antonov AN, Sarriguren P, Moya de Guerra E. Surface properties of neutron-rich exotic nuclei: a source for studying the nuclear symmetry energy. Phys Rev C. (2011) 84:034316. doi: 10.1103/PhysRevC.84.034316

CrossRef Full Text | Google Scholar

45. Gaidarov MK, Antonov AN, Sarriguren P, Moya de Guerra E. Symmetry energy of deformed neutron-rich nuclei. Phys Rev C. (2012) 85:064319. doi: 10.1103/PhysRevC.85.064319

CrossRef Full Text | Google Scholar

46. Steiner AW, Prakash M, Lattimer JM, Ellis PJ. Isospin asymmetry in nuclei and neutron stars. Phys Rep. (2005) 411:325–75. doi: 10.1016/j.physrep.2005.02.004

CrossRef Full Text | Google Scholar

47. Burrello S, Gulminelli F, Aymard F, Colonna M, Raduta AdR. Heat capacity of the neutron star inner crust within an extended nuclear statistical equilibrium model. Phys Rev C. (2015) 92:055804. doi: 10.1103/PhysRevC.92.055804

CrossRef Full Text | Google Scholar

48. Bonasera A, Gulminelli F, Molitoris J. The Boltzmann equation at the borderline. A decade of Monte Carlo simulations of a quantum kinetic equation. Phys Rep. (1994) 243:1–124. doi: 10.1016/0370-1573(94)90108-2

CrossRef Full Text | Google Scholar

49. Guarnera A, Colonna M, Chomaz Ph. 3D stochastic mean-field simulations of the spinodal fragmentation of dilute nuclei. Phys Lett B. (1996) 373:267–74. doi: 10.1016/0370-2693(96)00152-9

CrossRef Full Text | Google Scholar

50. Colonna M, Di Toro M, Larionov AB. Collective modes in asymmetric nuclear matter. Phys Lett B. (1998) 428:1–7. doi: 10.1016/S0370-2693(98)00383-9

CrossRef Full Text | Google Scholar

51. Raduta AdR, Aymard F, Gulminelli F. Clusterized nuclear matter in the (proto-)neutron star crust andthe symmetry energy. Eur Phys J A. (2014) 50:24. doi: 10.1140/epja/i2014-14024-y

CrossRef Full Text | Google Scholar

52. Wong CY. Dynamics of nuclear fluid. VIII. Time-dependent Hartree-Fock approximation from a classical point of view. Phys Rev C. (1982) 25:1460–75. doi: 10.1103/PhysRevC.25.1460

CrossRef Full Text | Google Scholar

53. Baran V, Colonna M, Di Toro M, Greco V, Zielinska-Pfabéc M, Wolter HH. Isospin effects in nuclear fragmentation. Nucl Phys A. (2002) 703:603–32. doi: 10.1016/S0375-9474(01)01671-2

CrossRef Full Text | Google Scholar

54. Rizzo J, Colonna M, Ono A. Comparison of multifragmentation dynamical models. Phys Rev C. (2007) 76:024611. doi: 10.1103/PhysRevC.76.024611

CrossRef Full Text | Google Scholar

55. Rizzo C, Baran V, Colonna M, Corsi A, Di Toro M. Symmetry energy effects on fusion cross sections. Phys Rev C. (2011) 83:014604. doi: 10.1103/PhysRevC.83.014604

CrossRef Full Text | Google Scholar

56. Rizzo C, Colonna M, Baran V, Di Toro M. Exotic break-up modes in heavy ion reactions at low energies. Phys Rev C. (2014) 90:054618. doi: 10.1103/PhysRevC.90.054618

CrossRef Full Text | Google Scholar

57. Urban M. Pygmy resonance and torus mode within Vlasov dynamics. Phys Rev C. (2012) 85:034322. doi: 10.1103/PhysRevC.85.034322

CrossRef Full Text | Google Scholar

58. Li X-H, Guo W-J, Li B-A, Chen L-W, Fattoyev FJ, Newton WG. Neutron–proton effective mass splitting in neutron-rich matter at normal density from analyzing nucleon–nucleus scattering data within an isospin dependent optical model. Phys Lett B. (2015) 743:408–14. doi: 10.1016/j.physletb.2015.03.005

CrossRef Full Text | Google Scholar

59. Baran V, Colonna M, Di Toro M, Croitoru A, Dumitru D. Connecting the pygmy dipole resonance to the neutron skin. Phys Rev C. (2013) 88:044610. doi: 10.1103/PhysRevC.88.044610

CrossRef Full Text | Google Scholar

60. De Vries H, De Jager CW, De Vries C. Nuclear charge-density-distribution scattering. Atom Data Nucl Data Tables. (1987) 36:495–536. doi: 10.1016/0092-640X(87)90013-1

CrossRef Full Text | Google Scholar

61. Audi G, Wapstra AH. The 1995 update to the atomic mass evaluation. Nucl Phys A. (1995) 595:409–80.

Google Scholar

62. Angeli I, Marinova KP. Table of experimental nuclear ground state charge radii: an update. Atom Data Nucl Data Tables (2013) 99:69–95. doi: 10.1016/j.adt.2011.12.006

CrossRef Full Text | Google Scholar

63. Sarriguren P, Gaidarov MK, de Guerra EM, Antonov AN. Nuclear skin emergence in Skyrme deformed Hartree-Fock calculations. Phys Rev C. (2007) 76:044322. doi: 10.1103/PhysRevC.76.044322

CrossRef Full Text | Google Scholar

64. Calvayrac F, Reinhard PG, Suraud E. Spectral signals from electronic dynamics in sodium clusters. Ann Phys. (1997) 225:125–62. doi: 10.1006/aphy.1996.5654

CrossRef Full Text | Google Scholar

65. Baran V, Frecus B, Colonna M, Di Toro M. Pygmy dipole resonance: Collective features and symmetry energy effects. Phys Rev C. (2012) 85:051601. doi: 10.1103/PhysRevC.85.051601

CrossRef Full Text | Google Scholar

66. Reinhard P-G, Stevenson PD, Almehed D, Maruhn JA, Strayer MR. Role of boundary conditions in dynamic studies of nuclear giant resonances and collisions. Phys Rev E. (2006) 73:036709. doi: 10.1103/PhysRevE.73.036709

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Roca-Maza X, Pozzi G, Brenna M, Mizuyama K, Colò G. Low-lying dipole response: isospin character and collectivity in ⁶⁸Ni, ¹³²Sn, and ²⁰⁸Pb. Phys Rev C. (2012) 85:024601. doi: 10.1103/PhysRevC.85.024601

CrossRef Full Text | Google Scholar

68. Lacroix D, Ayik S, Chomaz P. Nuclear collective vibrations in extended mean-field theory. Prog Part Nucl Phys. (2004) 52:497–563. doi: 10.1016/j.ppnp.2004.02.002

CrossRef Full Text | Google Scholar

69. Li GQ, Machleidt R. Microscopic calculation of in-medium nucleon-nucleon cross sections. Phys Rev C. (1993) 48:1702–12. doi: 10.1103/PhysRevC.48.1702

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Zhang YX, Tsang MB, Li ZX. Covariance analysis of symmetry energy observables from heavy ion collision. Phys Lett B. (2015) 749:262–6. doi: 10.1016/j.physletb.2015.07.064

CrossRef Full Text | Google Scholar

71. Kong H-Y, Xu J, Chen L-W, Li B-A, Ma Y-G. Constraining simultaneously nuclear symmetry energy and neutron-proton effective mass splitting with nucleus giant resonances using a dynamical approach. Phys Rev C. (2017) 95:034324. doi: 10.1103/PhysRevC.95.034324

CrossRef Full Text | Google Scholar

72. Zheng H, Burrello S, Colonna M, Lacroix D, Scamps G. Connecting the nuclear equation of state to the interplay between fusion and quasifission processes in low-energy nuclear reactions. Phys Rev C. (2018) 98:024622. doi: 10.1103/PhysRevC.98.024622

CrossRef Full Text | Google Scholar