Double β Decay and the Axial Strength

Quenching of the weak axial strength g_A is discussed and relations of this quenching to the nuclear matrix elements of double beta decays are highlighted. An analysis of Gamow-Teller transitions in the mass range A = 62 − 142 is presented and its results are compared with those of many previous works. The enhancement of the axial charge is discussed for first-forbidden pseudoscalar β transitions. Higher-forbidden β transitions are introduced and their role in determining the effective value of g_A is examined, in particular from the point of view of the β-decay half-lives and the shapes of electron spectra of forbidden non-unique β transitions.

1. Introduction

Double β decay (ββ decay) has been under intensive discussion for the last decades from the point of view of both nuclear theory and ββ-decay experiments. The interesting decay mode is the neutrinoless ββ (0νββ) decay which is mediated, e.g., by a massive Majorana neutrino, which is exchanged between the two decaying nucleons. Thus the 0νββ decay implies also the breaking of lepton-number conservation. The high stakes involved in the detection of 0νββ decay have made the associated theoretical and experimental aspects highly important, in particular the calculation of the involved nuclear matrix elements (NMEs). The NMEs of 0νββ decays have been computed for decades using a number of different nuclear-structure approaches (for older calculations see the review [1] and for the more recent ones see [2, 3]). Most of these calculations have been done by using the framework of the QRPA (quasiparticle random-phase approximation [4]). Also many calculations have been performed using the interacting shell model (ISM, see e.g., [5–7]) and the microscopic interacting boson model (IBM-2, see e.g., [8]).

Besides the problems with the calculations of the NMEs of 0νββ decay there is an other severe problem, namely the one related to the value of the weak axial coupling g_A. For low-energy processes, like the β decay or the two-neutrino ββ (2νββ) decay [1], the nucleonic charged weak current is simply

$\begin{array}{ll}{j}_{\text{N}}^{\mu }={\bar{N}}_f(x)\left(g_{\text{V}}{\gamma }^{\mu }-g_{\text{A}}{\gamma }^{\mu }{\gamma }^5\right)N_i(x),& (1)\end{array}$

where N_i (N_f) is the initial-state (final-state) nucleon spinor and γs are the usual Dirac matrices. Here g_V = 1.0 is the weak vector coupling and its value is protected by the CVC (Conserved Vector Current) hypothesis [9]. The value g_A = 1.27 of the weak axial coupling has been obtained from the decay of free neutron [10], N_i = n in (1), into free proton, N_f = p in (1). For the 0νββ decay the values of these weak couplings are altered by the high energy scale (q ~ 100 MeV) of the exchanged momentum q between the decaying nucleons and the Majorana neutrino. In addition, induced currents become involved in the decay (see e.g., [11]). The evolution of the value of g_A with the magnitude of the exchanged momentum q has been discussed in Menéndez et al. [12] and an extensive discussion of the effective value of g_A has been carried out in the review [13].

For the two-neutrino ββ decay from the initial 0⁺ state ($0_i^{+}$) to the final 0⁺ state ($0_f^{+}$) the decay rate is directly proportional to the fourth power of g_A as given by

$\begin{array}{c}2\nu \beta \beta -\text{rate}(0_i^{+}\to 0_f^{+})\propto {\displaystyle |M_{\text{GT}}^{(2\nu )}{|}^2}\\ ={\displaystyle |{\displaystyle \sum _n}\frac{g_{\text{A}}{M}_{\text{L}}(1_n^{+})\times g_{\text{A}}{M}_{\text{R}}(1_n^{+})}{(\frac{1}{2}\left[\text{Δ}+E(1_n^{+})\right]-M_i)/m_e+1}{|}^2,}& (2)\end{array}$

where Δ is the nuclear mass difference between the initial and final 0⁺ ground states, M_i is the mass of the initial nucleus, m_e the electron rest mass and $E(1_n^{+})$ is the absolute energy of the nth 1⁺ state. Furthermore, $g_{\text{A}}{M}_{\text{L}}(1_n^{+})$ is the left-branch NME and $g_{\text{A}}{M}_{\text{R}}(1_n^{+})$ the right-branch NME for the nth 1⁺ state, as shown schematically in Figure 1. The NMEs $M_{\text{L}}(1_n^{+})$ and $M_{\text{R}}(1_n^{+})$ are the usual Gamow-Teller NMEs. In this case the low-momentum form (1) of the nucleon current is applicable and the quenching of g_A can be studied through allowed Gamow-Teller β decays of low-energy nuclear states, as described in section 3 of this article.

FIGURE 1

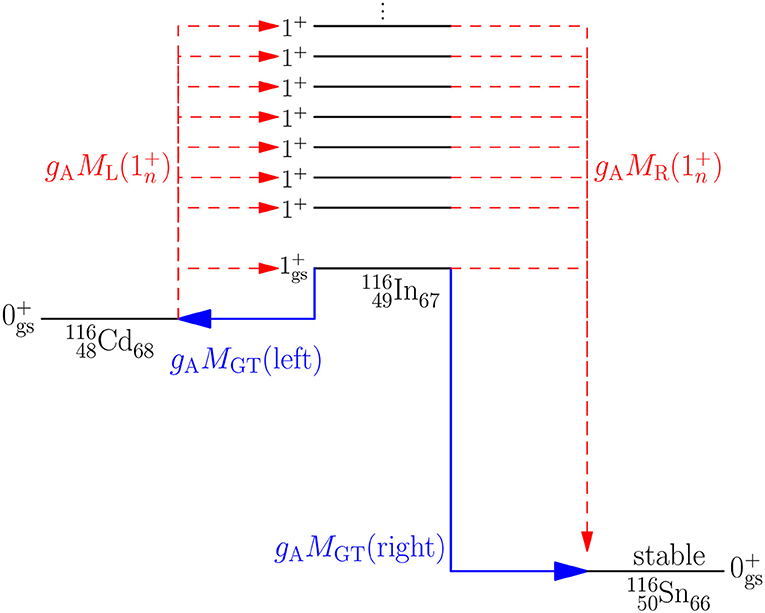
Figure 1. Schematic representation of the β and 2νββ transitions in the mass A = 116 triplet. Shown are the 0⁺ ground state of the initial nucleus ¹¹⁶Cd, the 0⁺ ground state of the final nucleus ¹¹⁶Sn and the 1⁺ states of the intermediate nucleus ¹¹⁶In of the 2νββ decay. Also the left-branch and right-branch NMEs for both decay modes are presented.

For the 0νββ decay from the initial 0⁺ state ($0_i^{+}$) to the final 0⁺ state ($0_f^{+}$) the decay rate is given by

$\begin{array}{ll}0\nu \beta \beta -\text{rate}(0_i^{+}\to 0_f^{+})\propto {\displaystyle |M_{\text{GT}}^{(0\nu )}-M_{\text{F}}^{(0\nu )}+M_{\text{T}}^{(0\nu )}{|}^2,}& (3)\end{array}$

where the Fermi NME $M_{\text{F}}^{(0\nu )}$ is proportional to $g_{\text{V}}^2$ and the Gamow-Teller and tensor NMEs, $M_{\text{GT}}^{(0\nu )}$ and $M_{\text{T}}^{(0\nu )}$, are proportional to $g_{\text{A}}^2$. The Gamow-Teller NME is the leading one and has the constitution

$\begin{array}{ll}{M}_{\text{GT}}^{(0\nu )}={\displaystyle \sum _{J^{\pi }}}{\left(g_{\text{A},0\nu }(J^{\pi })\right)}^2(0_f^{+}||{{O}}_{\text{GT}}^{(0\nu )}(J^{\pi })||0_i^{+}),& (4)\end{array}$

where the sum is over all multipole states J^π in the intermediate nucleus and the effective axial couplings for 0νββ decay, $g_{\text{A},0\nu }(J^{\pi })$, are, in principle, multipole dependent. All the details of the 0νββ-decay transitions are included in the operator ${{O}}_{\text{GT}}^{(0\nu )}(J^{\pi })$. The low-q limit of these couplings is

$\begin{array}{ll}{g}_{\text{A},0\nu }(J^{\pi })\stackrel{q\to 0}{\to }{g}_{\text{A}}(J^{\pi }),& (5)\end{array}$

where q is the exchanged momentum. For the J^π = 1⁺ multipole this low-q limit is the “usual” axial coupling

$\begin{array}{ll}{g}_{\text{A}}\equiv g_{\text{A}}(1^{+}),& (6)\end{array}$

relevant for the Gamow-Teller and 2νββ decays. For the sake of simplicity, the notation g_A will be used also for the other multipoles $g_{\text{A}}(J^{\pi })$. The g_A for higher multipoles can be studied through half-lives and electron spectral shapes of forbidden β decays, as discussed in section 4 of this article.

2. Nuclear Models

In this section we briefly describe the many-body aspects of the nuclear models which are mentioned later in this article. These models have been used to study the β-decay and ββ-decay NMEs and the associated effective values of the axial coupling. It should be noted here that these are not the only models that can (potentially) describe these features. These other nuclear models can be based on modern energy-density functionals or thermofield-dynamics formalism, as also on Monte-Carlo shell model, etc. A comprehensive list of these nuclear models and the associated references are given in section 5.4. of the very recent review article [14].

• ISM: The ISM (interacting shell model) is a many-body framework that uses a limited single-particle valence space, typically one harmonic-oscillator major shell or one nuclear major shell. In the ISM one forms all the possible many-nucleon configurations in a given single-particle valence space, each configuration described by one Slater determinant, and diagonalizes the nuclear (residual) Hamiltonian in the basis formed by these Slater determinants. In this way the many-body features are taken into account exactly but only in a restricted valence space, typically leaving out one or two spin-orbit-partner orbitals from the model space.

• Spherical pnQRPA: The proton-neutron version of the QRPA (pnQRPA) uses two-quasiparticle excitations that are built from a proton and a neutron quasiparticle. Here only the spherical pnQRPA, based on a spherical nuclear mean field, is described. The pnQRPA model framework enables description of odd-odd nuclei starting from an even-even reference nucleus where the quasiparticles are created, e.g., through the BCS (Bardeen-Cooper-Schrieffer) procedure [15]. The advantage of the pnQRPA theory is that it can include large single-particle valence spaces in the calculations and there arise no problems associated with spin-orbit-partner orbitals since they can easily be accommodated in the valence space. On the other hand, the pnQRPA has a limited configuration space. Schematic or G-matrix-based boson-exchange Hamiltonians have widely been used in the pnQRPA calculations. A frequently used extension of the pnQRPA framework is the renormalized QRPA (RQRPA) [16, 17]. One particular problem with the pnQRPA calculations is the determination of the value of the particle-particle interaction parameter g_pp, used to scale the particle-particle part of the proton-neutron two-body interaction matrix elements [18, 19]. Usually the value of this parameter has been determined by using β-decay or 2νββ-decay data. The particle-hole parameter, g_ph, of the proton-neutron two-body interaction is usually determined by adjusting the parameter such that the phenomenological or experimental energy of the Gamow-Teller giant resonance is reproduced [20, 21]. The spherical pnQRPA has been applied to the description of ββ decays (see e.g., [22–25]) and it has also been used in β-decay studies (see e.g., [26–28]).

• MQPM: The microscopic quasiparticle-phonon model (MQPM) describes states of odd-A nuclei starting from the adjacent even-even reference nuclei. The MQPM states are generated by combining proton or neutron one-quasiparticle excitations of the reference nucleus with three-quasiparticle excitations built by coupling a proton or neutron quasiparticle to a QRPA phonon. A QRPA phonon is a proton-proton-plus-neutron-neutron excitation of an even-even reference nucleus. The MQPM creation operator creates a state |kjm〉 in an odd-A nucleus by the action

$\begin{array}{ll}|kjm\text{〉}={\text{Γ}}_k^{†}(jm)|\mathrm{\text{QRPA〉 }},& (7)\end{array}$

with the excitation operator given by

$\begin{array}{ll}{\text{Γ}}_k^{†}(jm)={\displaystyle \sum _n}{X}_n^k{a}_{njm}^{†}+{\displaystyle \sum _{a\omega }}{X}_{a\omega }^k{[a_a^{†}{Q}_{\omega }^{†}]}_{jm},& (8)\end{array}$

where $Q_{\omega }^{†}$ is a QRPA phonon creation operator [15] and the a^† operators create BCS quasiparticles. Since the MQPM states (8) contain the three-quasiparticle components special care should be taken when solving the MQPM equations of motion for the amplitudes $X_n^k$ and $X_{a\omega }^k$ in order to handle the over-completeness and non-orthogonality of the quasiparticle-phonon basis. For details see Toivanen and Suhonen [29, 30].

• IBM-2: The interacting boson model (IBM) is a theory framework based on s and d bosons which have as their microscopic paradigms the 0⁺ and 2⁺ angular-momentum-coupled collective fermion pairs present in nuclei. An extension of the IBM is the microscopic IBM (IBM-2) where the proton and neutron degrees of freedom are explicit. The IBM-2 is a sort of phenomenological version of the ISM, containing the seniority aspect and the restriction to one magic shell in terms of the single-particle valence space. The Hamiltonian and the transition operators are constructed from the s and d bosons as lowest-order boson expansions with coupling coefficients to be determined by fits to experimental data on low-lying energy levels and E2 γ transitions. However, the fitting does not use the spin or isovector data available from β decays. The extension to the microscopic interacting boson-fermion model (IBFM-2) [31] enables the description of odd-A nuclei. Here problems arise from the interactions between the bosons and the extra fermion in the Hamiltonian, and from the transition operators containing a host of phenomenological parameters to be determined in some meaningful way.

3. Quenching of G_A in Gamow-Teller β Decays

The half-life of allowed Gamow-Teller β decays can be written as

$\begin{array}{ll}{t}_{1/2}=\frac{\kappa }{\tilde{C}},& (9)\end{array}$

where $\tilde{C}$ is the integrated shape function and the constant κ has the value [32]

$\begin{array}{ll}\kappa =\frac{2{\pi }^3{\hslash }^7\text{ln }2}{m_e^5{c}^4{(G_{\text{F}}cos{\theta }_{\text{C}})}^2}=6147\text{ s },& (10)\end{array}$

θ_C being the Cabibbo angle. In order to simplify the formalism it is usual to introduce unitless kinematic quantities $w_e=W_e/m_e{c}^2$, $w_0=W_0/m_e{c}^2$, and $p=p_{e}c/(m_e{c}^2)=\sqrt{w_e^2-1}$, where W_e is the total energy of the emitted charged lepton (electron or positron), p_e is the electron/positron momentum and W₀ is the end-point energy, i.e., the total energy of the emitted leptons, and hence the maximum energy of the emitted electron/positron. With the unitless quantities the integrated shape function can be expressed as

$\begin{array}{ll}\tilde{C}={\displaystyle {\int }_1^{w_0}}C(w_e)p{w}_e{(w_0-w_e)}^2{F}_0(Z_f,w_e)d{w}_e,& (11)\end{array}$

where F₀(Z_f, w_e) is the Fermi function taking into account the interaction of the final-state charged lepton with the positive charge of the final nucleus (with charge number Z_f). The integration is performed over the total scaled energy of the emitted electron/positron.

The shape factor C(w_e) of Equation (11) can be expressed for the pure¹ Gamow-Teller J_i → J_f = J_i ± 1 transitions as

$\begin{array}{ll}C(w_e)=\frac{1}{2J_i+1}{\left(g_{\text{A}}{M}_{\text{GT}}\right)}^2,& (12)\end{array}$

where M_GT is the Gamow-Teller NME (assumed to be real, as usual) and J_i (J_f) the angular momentum of the initial (final) state. Here the axial coupling g_A is the low-q limit (6). Since the shape factor (12) does not depend on the lepton variables it can be taken out of the shape function (11) and the rest constitutes the universal phase-space factor

$\begin{array}{ll}{f}_0={\displaystyle {\int }_1^{w_0}}p{w}_e{(w_0-w_e)}^2{F}_0(Z_f,w_e)d{w}_e,& (13)\end{array}$

usually quoted for the allowed (Fermi and Gamow-Teller) β decays. At this point it should be noted that a new method of calculation of these phase-space factors was introduced in Stoica et al. [33]. These phase-space results contribute to calculations of β-decay rates for nuclei far away from the stability line. Using the phase-space factor f₀, the half-life (9) can be expressed in a more familiar form using the reduced transition probability B_GT:

$\begin{array}{ll}{t}_{1/2}{f}_0=\frac{\kappa }{B_{\text{GT}}};B_{\text{GT}}=\frac{1}{2J_i+1}{\left(g_{\text{A}}{M}_{\text{GT}}\right)}^2.& (14)\end{array}$

What is usually quoted in literature are the log ft values

$\begin{array}{ll}logft={log}_{10}(f_0{t}_{1/2}),& (15)\end{array}$

which are 10-base logarithms of the product of the half-life and the universal phase-space factor.

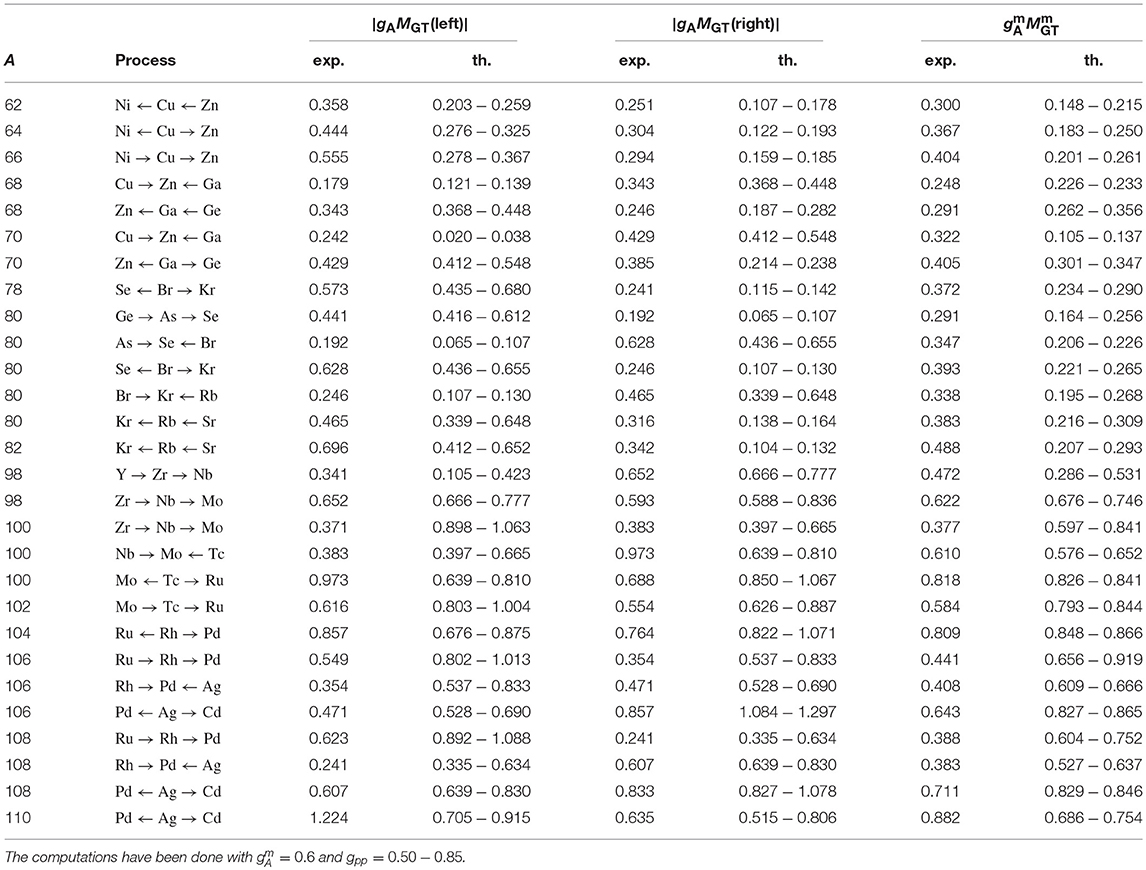
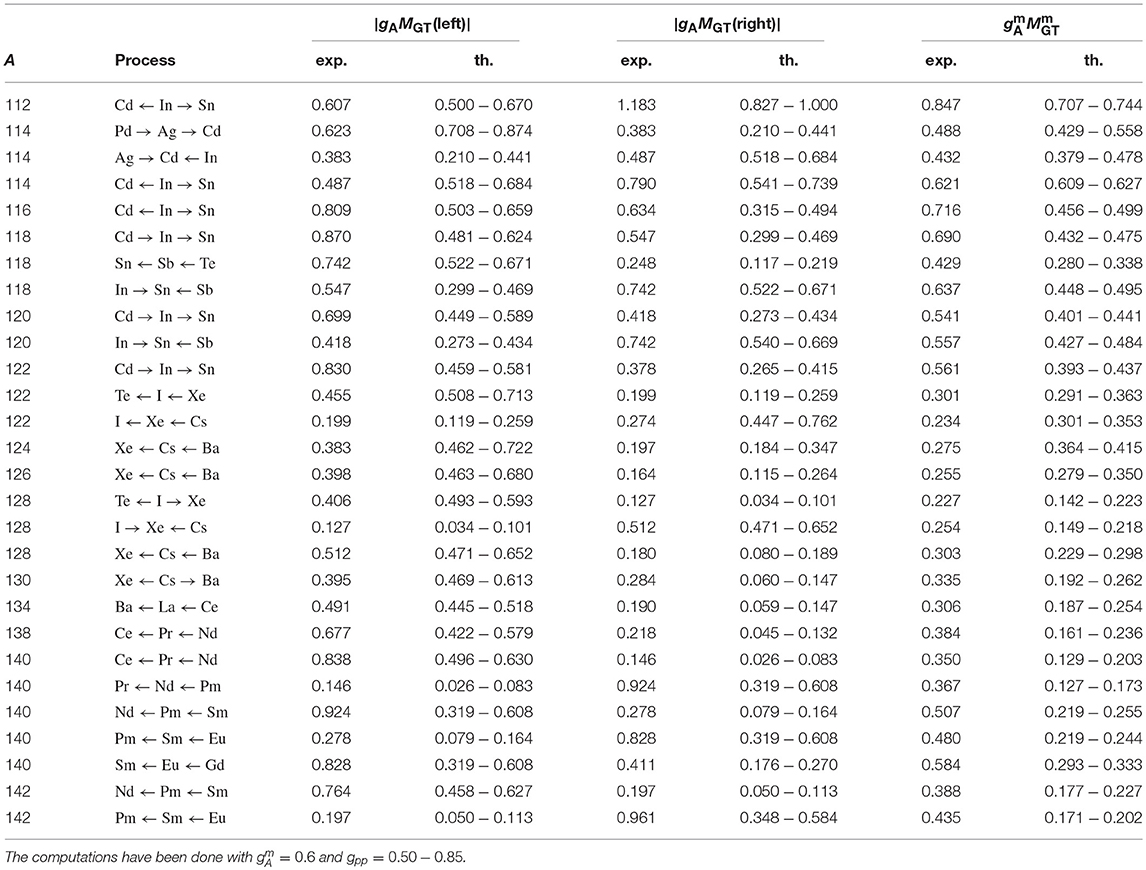
By using Equations (14) and (15) one can extract from the experimental log ft value the magnitude of the experimental Gamow-Teller NME in the form |g_AM_GT|. Here one has to note that only the product of the NME and the weak axial coupling g_A can be extracted. These products can be extracted from both the left-branch, |g_AM_GT(left)|, and right-branch, |g_AM_GT(right)|, β decays as shown schematically in Figure 1. These extracted products are shown in Tables 1, 2 for the left (third column) and right (fifth column) transitions from/to the central nucleus of the triplet of nuclei of column two. A sample of these triplets are shown in Figure 2. There four mass triplets A = 110, 116, 128, 136 are displayed with a central nucleus feeding the lateral ones, thus constituting the left-branch and right-branch of β transitions. These triplets host also double beta decays, with β⁻β⁻ decays for the masses A = 110, 116, 128 and double electron-capture (EC) decay for A = 136. For the double EC decay the log ft of the right-branch decay is not known and thus this triplet is omitted from the subsequent decay analysis whereas all the other triplets are included. In the figure it is also shown that there is no available data on the decays of the low-lying 2⁻ states in these triplets. These decays are relevant for the first-forbidden unique β transitions of section 4.2, mediated by a rank-2 tensor. They are also quite important for the neutrinoless ββ-decay NMEs.

TABLE 1

Table 1. Experimental and computed geometric means of the NMEs for A = 62 − 110.

TABLE 2

Table 2. Experimental and computed geometric means of the NMEs for A = 112 − 142.

FIGURE 2

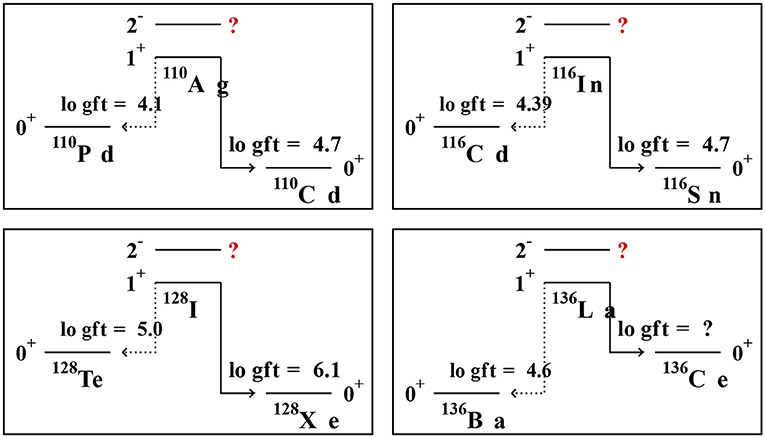
Figure 2. Experimental log ft values of the left-branch and right-branch β transitions in four triplets of nuclei. It is also shown that no data on the decays of the 2⁻ states are available in these triplets.

As can be seen in Tables 1, 2, the extracted experimental left-branch and right-branch NMEs differ sometimes considerably from each other and these differences are rather erratic. In order to stabilize this behavior one may use the geometric mean $g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}$ of the left and right NMEs:

$\begin{array}{ll}{g}_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}=\sqrt{\left|g_{\text{A}}{M}_{\text{GT}}(\mathrm{\text{left}})\right|\times \left|g_{\text{A}}{M}_{\text{GT}}(\mathrm{\text{right}})\right|},& (16)\end{array}$

where the geometric mean of both the left-branch and right-branch NMEs and axial couplings has been computed. The corresponding experimental NMEs are shown in column seven in Tables 1, 2. These NMEs do not behave quite as wildly as the individual left-branch and right-branch NMEs.

The experimental left-branch, right-branch and mean NMEs can be compared with the corresponding computed NMEs listed in columns four, six and eight in Tables 1, 2. The computed NMEs are obtained by using the pnQRPA (see section 2) in the following single-particle model spaces:

$\begin{array}{l}0d-1s-0f-1p-0g_{9/2}\mathrm{\text{for }}A=62-68,\\ 0f-1p-0g-2s-1d-0h_{11/2}\mathrm{\text{for }}A=70-84,\\ 0f-1p-0g-2s-1d-0h\mathrm{\text{for }}A=90-108,\\ 0f-1p-0g-2s-1d-0h-1f-2p\mathrm{\text{for }}A=110-144.& (17)\end{array}$

These single-particle valence spaces have been chosen such that they are expected to capture the relevant features of the low-lying states in the triplets of nuclei, such that the involved left-branch and right-branch β transitions are described as well as possible within the framework of the pnQRPA model. In the course of the calculations the pairing parameters were fitted to reproduce the experimental pairing gaps extracted from the available data [34] on nucleon separation energies. The particle-hole parameter g_ph was fitted to reproduce the empirical location of the giant Gamow-Teller resonance (see [35] for fitting also to more general spin-multipole resonances).

The particle-particle parameter g_pp and the strength of the axial coupling were left as free parameters in the calculations. According to the Gamow-Teller β-decay study [36], performed for a number of nuclei in the mass range A = 100 − 136, a good overall value for the particle-particle parameter is g_pp ≈ 0.7. In the present study we vary the values of this parameter in the range g_pp = 0.50 − 0.85 to have a feeling of the effects of the variation of g_pp on the values of the computed NMEs. This variation is shown in Tables 1, 2, in columns four and six for the left-branch and right-branch NMEs, and in the last column for the mean NMEs (16). The variations in the values of the individual NMEs are usually (much) larger than in the values of the mean NMEs, thus justifying the use of the geometric mean of the left-branch and right-branch NMEs, instead of the individual NMEs. For the mean strength of the axial coupling we have taken the constant overall value $g_{\text{A}}^{\text{m}}=0.6$ which was found to be a good average value in the study [36] for the A = 100 − 136 mass range. Our adopted values of g_pp = 0.67 (plus the variation in g_pp described above) and g_A = 0.6 are also in good agreement with the average values of these parameters deduced from the extensive analyses of the Gamow-Teller β decays conducted in the study [37].

A further comparison of the calculated and experimental Gamow-Teller NMEs has been conducted in Figures 3–6. In these figures the computed values of the mean NMEs (16) are presented for g_pp = 0.67 (solid line with open circles) and the hatched area represents the variations in these values induced by the adopted range g_pp = 0.50 − 0.85 of variations in the value of the particle-particle interaction parameter. The extracted experimental NMEs are represented by a dashed line with filled circles.

FIGURE 3

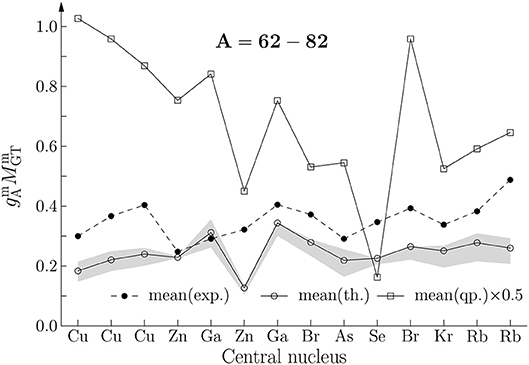
Figure 3. Mean experimental and theoretical NMEs $g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}$ (Table 1, last two columns) for the mass range A = 62 − 82. The hatched area describes the uncertainty of the calculations (the range g_pp = 0.50 − 0.85 in Table 1). Also the NMEs in the two-quasiparticle approximation have been plotted for comparison (note the scaling of these NMEs by a factor one-half in order to save vertical space in the figure).

From Figures 3–6 one notices that in the mass range A = 62 − 82 (Figure 3) the magnitude of the computed mean NME is almost everywhere slightly below that of the experimental one whereas in the mass region A = 98 − 110 (Figure 4) the magnitude of the computed mean NME is above that of the experimental mean NME. In both mass regions the staggering of the computed and experimental mean NMEs is similar. In the mass range A = 112 − 124 (Figure 5) the experimental mean NME is mostly larger than the computed one but the staggering of both are quite similar. For the heaviest triplets, A = 126 − 142 (Figure 6), the values of the experimental mean NMEs are larger than those of the computed ones, the difference increasing with increasing mass. Still, in the staggering similarities between the two NMEs are to be seen.

FIGURE 4

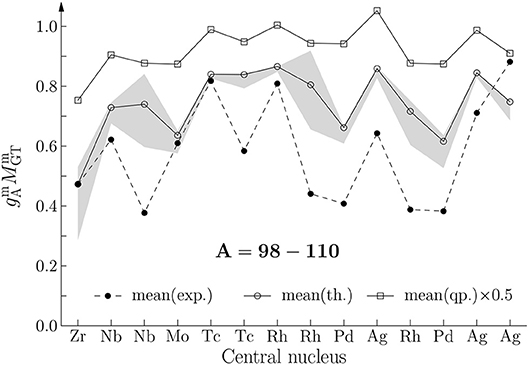
Figure 4. The same as in Figure 3 for the mass range A = 98 − 110.

FIGURE 5

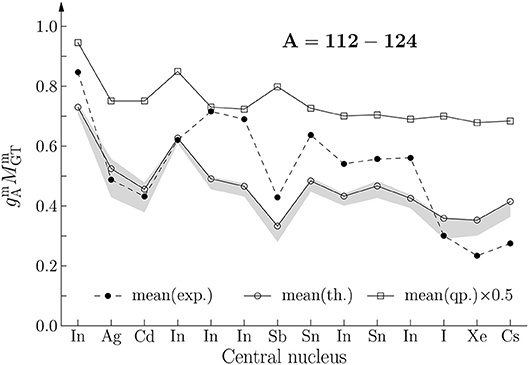
Figure 5. The same as in Figure 3 for the mass range A = 112 − 124, with the mean NMEs corresponding to Table 2.

FIGURE 6

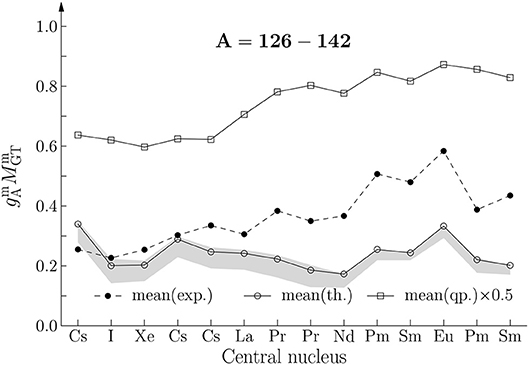
Figure 6. The same as in Figure 5 for the mass range A = 126 − 142.

In Figures 3–6 also the magnitudes of the proton-neutron two-quasiparticle NMEs are presented (solid line with open squares) for comparison. The corresponding spin-orbit-partner configurations give the strongest contributions to the mean NMEs and these configurations are

$\begin{array}{l}0f_{5/2}-0f_{7/2}\mathrm{\text{for }}A=62-70,\\ 0g_{7/2}-0g_{9/2}\mathrm{\text{for }}A=78-128,\\ 0h_{9/2}-0h_{11/2}\mathrm{\text{for }}A=130-142.& (18)\end{array}$

Here it should be noted that these configurations are not the same as the leading contributions quoted in the study [38] since there the two-quasiparticle configurations closest to the respective Fermi surfaces were taken. The magnitudes of the two-quasiparticle mean NMEs are far too large implying a strong quenching of the mean NME when going from the simple two-quasiparticle approximation to the more sophisticated pnQRPA model. This large reduction can be associated with spin-isospin correlations missing in the two-quasiparticle approximation but taken into account in the pnQRPA framework, as discussed extensively in Ejiri and Suhonen [38]. In the two-quasiparticle NMEs there are also some staggering in the magnitude, but usually (much) less than in the pnQRPA and experimental NMEs. Sometimes this staggering is out of phase with the pnQRPA staggering (and the experimental one) indicating that the spin-isospin correlations are crucial in order to reproduce the trends of the experimental mean NMEs.

The error bars of the magnitudes of the computed NMEs, caused by the variation g_pp = 0.50 − 0.85, are shown as hatched areas in Figures 3–6. In general, the relative variation is rather modest, in particular in the mass range A = 112 − 124 (Figure 5). The largest absolute variations are seen around the masses A = 100, A = 106 and A = 108. Generally, the upper limit of the hatched area is close to the best NME value (solid line with open circles) since this maximum NME is obtained for the lowest value g_pp = 0.50 and for this value of g_pp the NME is already saturated close to its maximum value at g_pp = 0.0.

To give yet an other view to the comparison of the experimental and computed NMEs, one can calculate the mean value and the RMS (Root-Mean-Square) deviation of the NMEs in the four mass ranges of Figures 3–6. The result is

$\begin{array}{l}{g}_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}(\mathrm{\text{exp}})=0.35\pm 0.06g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}(\mathrm{\text{th}})=0.24\pm 0.06\mathrm{\text{for }}A=62-82,\\ g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}(\mathrm{\text{exp}})=0.58\pm 0.18g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}(\mathrm{\text{th}})=0.72\pm 0.14\mathrm{\text{for }}A=98-110,\\ g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}(\mathrm{\text{exp}})=0.52\pm 0.18g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}(\mathrm{\text{th}})=0.45\pm 0.12\mathrm{\text{for }}A=112-124,\\ g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}(\mathrm{\text{exp}})=0.37\pm 0.10g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}(\mathrm{\text{th}})=0.22\pm 0.06\mathrm{\text{for }}A=126-142.& (19)\end{array}$

These ranges have been shown in Figure 7 for easy comparison. The figure shows clearly that the computed mean NMEs are smaller than the experimental ones for small (A = 62 − 82) and large (A = 126 − 142) mass numbers, whereas for the intermediate masses (A = 98 − 124) they largely overlap with the experimental ones. This means that with an overall constant $g_{\text{A}}^{\text{m}}$ one cannot reproduce the values of the experimental mean NMEs.

FIGURE 7

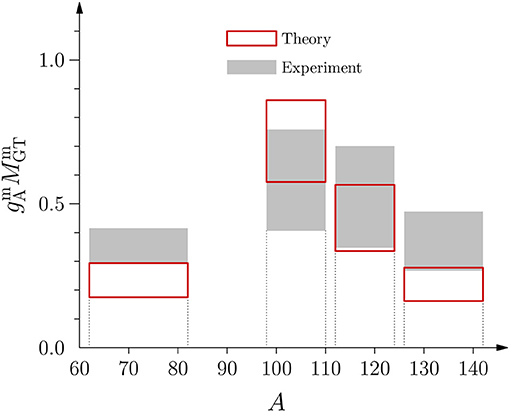
Figure 7. Ranges of the experimental and theoretical mean NMEs for different mass ranges as deduced from (19).

If one would like to match the experimental and computed average $g_{\text{A}}^{\text{m}}{M}_{\text{GT}}^{\text{m}}$ in the different mass ranges one would need a different effective value of the weak axial coupling in each of them. Matching the computed NMEs with the data leads to the following effective $g_{\text{A}}^{\text{m}}$ values

$\begin{array}{l}{g}_{\text{A}}^{\text{m}}=0.90(A=62-82);g_{\text{A}}^{\text{m}}=0.49(A=98-110);\\ g_{\text{A}}^{\text{m}}=0.70(A=112-124);g_{\text{A}}^{\text{m}}=1.01(A=126-142).& (20)\end{array}$

One can compare these values of effective g_A ($g_{\text{A}}^{\text{eff}}$ in Figure 8) with other recent calculations in different theory frameworks. This has been done in Figure 8. In the figure the present pnQRPA results are displayed by blue horizontal solid lines. These are contrasted against the ISM-computed (for the ISM, see section 2) results of Martínez-Pinedo et al. (ISM calculations of rates of β decays [42], gray rectangle marked M-P1996 in the figure), Siiskonen et al. (ISM calculations of muon-capture transitions of different exchanged momenta with effective transition operators [44], circles with cross inside in the figure), Caurier et al. (based mainly on analyses of 2νββ decays [5], solid red horizontal lines), Horoi et al. (based mainly on analyses of 2νββ decays in the A = 124 − 136 region [6], horizontal dashed line in the figure), Kumar et al. (systematic examination of β decays with the ISM [43], dark rectangles in the A = 52 − 80 regions in the figure), Iwata et al. (ISM analysis of the ββ decays of ⁴⁸Ca [7], cross at A = 48 in the figure). The studies of Faessler et al. [40] and Suhonen and Civitarese [41], marked by vertical black and green line segments, respectively, are pnQRPA studies of nuclei (¹⁰⁰Mo, ¹¹⁶Cd, and ¹²⁸Te) with available data on the rates of both β and 2νββ decays The analyses were performed in the aim of constraining the values of both g_A and g_pp simultaneously. The solid line with the zig-zag behavior is the result of the pnQRPA analysis of Suhonen [39] in the aim to constrain the possible values of g_A and 0νββ NMEs in order to have a feeling of their effects on the sensitivity of the present and future 0νββ experiments.

FIGURE 8

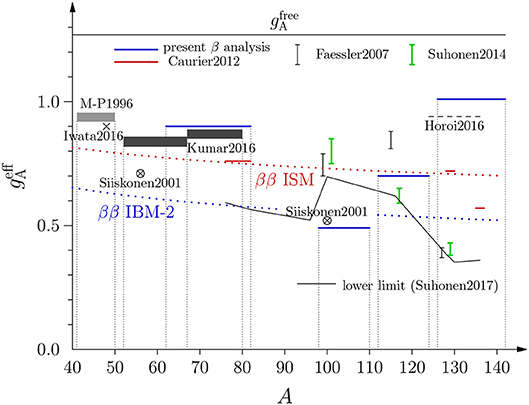
Figure 8. Effective values of g_A in different theoretical β and 2νββ analyses for the nuclear mass range A = 41 − 142. The quoted references of 2νββ studies are Suhonen2017 [39], Caurier2012 [5], Faessler2007 [40], Suhonen2014 [41] and Horoi2016 [6]. These studies are contrasted with the ISM β-decay studies of M-P1996 [42], Iwata2016 [7], Kumar2016 [43] and Siiskonen2001 [44]. The red and blue dotted lines show the results of the analysis in Barea et al. [8] and quoted in Equation (21).

The red (ββ ISM) and blue (ββ IBM-2) dotted lines show the results of the 2νββ analyses of Barea et al. [8] yielding the fits

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(\mathrm{\text{IBM-2}})=1.269A^{-0.18};g_{\text{A}}^{\text{eff}}(\mathrm{\text{ISM}})=1.269A^{-0.12},& (21)\end{array}$

where A is the mass number and IBM-2 stands for the microscopic interacting boson model (see section 2). The IBM-2 results have been obtained by using the closure approximation for the analyzed 2νββ transitions since there are no spin-isospin degrees of freedom in IBM-2 and thus the intermediate nuclei of 2νββ decays cannot be reached.

Interesting conclusions can be drawn from the calculations shown in Figure 8. For the mass range A = 41 − 82 the present result for the effective value of g_A is in striking agreement with the many shell-model calculations in the region, consistently producing the value $g_{\text{A}}^{\text{eff}}\approx 0.9$. The same can be said about the mass regions A = 112 − 124 and A = 126 − 142 where the ISM results of Barea et al. [8] and Horoi and Neacsu [6] are quite close to the present effective values $g_{\text{A}}^{\text{eff}}\approx 0.7$ and $g_{\text{A}}^{\text{eff}}\approx 1.0$. In the A = 126 − 142 region the ISM analyses of Caurier et al. [5] and the IBM-2 analyses of Barea et al. [8] produce smaller values of $g_{\text{A}}^{\text{eff}}\approx 0.6-0.7$ and there is a strong tension between the different ISM analyses. The present results are in line with the pnQRPA results of Suhonen and Civitarese [41] and Faessler et al. [40] for ¹¹⁶Cd but far off from the results of these studies for ¹²⁸Te. It seems that the fit to the average value of the mean experimental β-decay NMEs brings the results of the pnQRPA analysis closer to those of the ISM, in particular for the heavy end of the presently discussed nuclei. The mass range A = 98 − 110 is the most interesting: Here a very small value $g_{\text{A}}^{\text{eff}}\approx 0.5$ is required both by the present study and the ISM study of Siiskonen et al. [44]. Also the IBM-2 result of Barea et al. [8] is consistent with these results whereas the interpolated ISM result of Barea et al. [8] and the results of Suhonen and Civitarese [41] and Faessler et al. [40] for ¹⁰⁰Mo are in the range $g_{\text{A}}^{\text{eff}}\approx 0.7-0.8$.

4. Quenching of G_A in Forbidden β Decays

In forbidden β transitions the low-q limit (5) can be studied for different multipoles J^π. In this section we denote all these weak axial couplings as g_A for simplicity.

4.1. Theoretical Background

4.1.1. Forbidden Non-unique β Decays

The half-life of a forbidden non-unique β decay can be written in the same way as that of the allowed β decay in (9). The corresponding integrated shape function can be expressed as written in Equation (11) but the shape factor C(w_e) of Equation (12) has to be replaced by a much more complicated expression:

$\begin{array}{l}C(w_e)={\displaystyle \sum _{k_e,k_{\nu },K}}{\text{λ}}_{k_e}{\displaystyle [M_K{(k_e,k_{\nu })}^2}\\ {\displaystyle +m_K{(k_e,k_{\nu })}^2-\frac{2{\gamma }_{k_e}}{k_e{w}_e}{M}_K(k_e,k_{\nu })m_K(k_e,k_{\nu })]},& (22)\end{array}$

where the notation of unitless leptonic quantities was discussed in the context of Equation (11). The factor λ_ke contains the generalized Fermi function F_ke−1 [45] as the ratio

$\begin{array}{ll}{\text{λ}}_{k_e}=\frac{F_{k_e-1}(Z_f,w_e)}{F_0(Z_f,w_e)},& (23)\end{array}$

Z_f being the charge number of the final nucleus. The indices k_e and k_ν (k_e, k_ν = 1,2,3…) are related to the partial-wave expansion of the electron (e) and neutrino (ν) wave functions, K is the order of forbiddenness of the transition, and ${\gamma }_{k_e}=\sqrt{k_e^2-{(\alpha Z_f)}^2}$, α ≈ 1/137 being the fine-structure constant. The nuclear-physics information is carried by the quantities M_K(k_e, k_ν) and m_K(k_e, k_ν), which are conglomerations of different NMEs and leptonic phase-space factors. For more information on the integrated shape function, see Behrens and Bühring [45] and Mustonen et al. [46].

The shape factor C(w_e) can be decomposed into vector, axial-vector, and mixed vector-axial-vector parts. In this decomposition the shape factor is

$\begin{array}{ll}C(w_e)=g_{\text{A}}^2\left[C_{\text{A}}(w_e)+\frac{g_{\text{V}}}{g_{\text{A}}}{C}_{\text{VA}}(w_e)+{\left(\frac{g_{\text{V}}}{g_{\text{A}}}\right)}^2{C}_{\text{V}}(w_e)\right],& (24)\end{array}$

where the quantities C_A, C_V and C_VA are complicated expressions including Coulomb functions, nuclear matrix elements, etc. This is the decomposition used in Haaranen et al. [47, 48] and Kostensalo et al. [49] and it enables studies of the effects caused by the ratio g_V/g_A on the shape factor. Integrating Equation (24) over the electron kinetic energy, we get an analogous expression for the integrated shape function (11)

$\begin{array}{ll}\tilde{C}=g_{\text{A}}^2\left[{\tilde{C}}_{\text{A}}+\frac{g_{\text{V}}}{g_{\text{A}}}{\tilde{C}}_{\text{VA}}+{\left(\frac{g_{\text{V}}}{g_{\text{A}}}\right)}^2{\tilde{C}}_{\text{V}}\right],& (25)\end{array}$

where the factors ${\tilde{C}}_{\text{A}}$, ${\tilde{C}}_{\text{V}}$ and ${\tilde{C}}_{\text{VA}}$ in Equation (25) do not depend on the electron kinetic energy.

4.1.2. First-Forbidden Non-unique β Decays

For the first-forbidden non-unique β decays the shape factor (22) has to be supplemented with a ΔJ = |J_i − J_f| = 0 term $C^{(1)}(w_e)$ [26, 45, 50, 51], where J_i (J_f) is the initial-state (final-state) spin of the mother (daughter) nucleus. In the papers (see [52–54]) the shape factor for first forbidden decays has been given in the form

$\begin{array}{ll}C(w_e)=k+ka{w}_e+kb/w_e+kc{w}_e^2,& (26)\end{array}$

where k, ka, kb, and kc contain the Coulomb functions, nuclear matrix elements and weak coupling constants. Writing the shape factor in this form is often useful for comparing the theoretical and experimental shape factors. It should be noted that the shape factors of Equations (24) and (26) are different but equivalent ways of expressing the shape factor but in the first one the terms with the same product of weak coupling constants have been collected, while in the latter the terms with the same power of electron kinetic energy w_e are combined.

4.1.3. Forbidden Unique β Decays

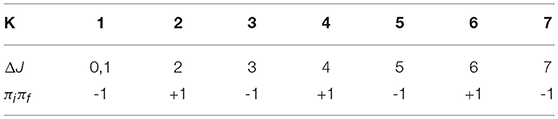
An important special case of forbidden β decays are the forbidden unique decays for which the theory simplifies considerably. The classification of forbidden unique decays by change in parity and angular momentum is presented in Table 3. For the non-unique case these are presented in Table 4.

TABLE 3

Table 3. The change in angular momentum and parity in a Kth forbidden unique β decay.

TABLE 4

Table 4. The change in angular momentum and parity in a Kth forbidden non-unique β decay.

For unique β-decay transitions the half-life (9) can be expressed analogously to (14), valid for the Gamow-Teller β transitions. Thus we have

$\begin{array}{ll}{t}_{1/2}=\frac{\kappa }{f_{\text{Ku}}{B}_{\text{Ku}}};B_{\text{Ku}}=\frac{1}{2J_i+1}{\left(g_{\text{A}}{M}_{\text{Ku}}\right)}^2,& (27)\end{array}$

where f_Ku is the phase-space factor and g_AM_Ku is the nuclear matrix element. The phase-space factor f_Ku for the Kth forbidden unique β^± decay can be written as

$\begin{array}{l}{f}_{\text{Ku}}={\left(\frac{3}{4}\right)}^K\frac{(2K)!!}{(2K+1)!!}{\displaystyle {\int }_1^{w_0}}{C}_{\text{Ku}}(w_e)p_e{w}_e{(w_0-w_e)}^2\\ \times F_0(Z_f,w_e)\text{d}{w}_e& (28)\end{array}$

and the corresponding shape factor can be written as (see e.g., [15, 55])

$\begin{array}{ll}{C}_{\text{Ku}}(w_e)={\displaystyle \sum _{k_e+k_{\nu }=K+2}}\frac{{\text{λ}}_{k_e}{p}_e^{2(k_e-1)}{(w_0-w_e)}^{2(k_{\nu }-1)}}{(2k_e-1)!(2k_{\nu }-1)!}.& (29)\end{array}$

The notation was explained in the context of the allowed and forbidden non-unique β transitions, around Equations (11) and (22) and the ratio λ_ke was given in Equation (23).

The NME in (27) can be expressed as

$\begin{array}{ll}{M}_{\text{Ku}}={\displaystyle \sum _{ab}}{M}^{\text{Ku}}(ab)({\psi }_f||{[c_a^{†}{\tilde{c}}_b]}_{K+1}||{\psi }_f),& (30)\end{array}$

where the factors M^Ku(ab) are the single-particle matrix elements and the quantities $({\psi }_f||{[c_a^{†}{\tilde{c}}_b]}_{K+1}||{\psi }_f)$ are the one-body transition densities with ψ_i being the initial-state wave function and ψ_f the final-state wave function. The operator $c_a^{†}$ is a creation operator for a nucleon in the orbital a and the operator ${\tilde{c}}_a$ is the corresponding annihilation operator. The single-particle matrix elements are given (in the Biedenharn-Rose phase convention [15]) by

$\begin{array}{ll}{M}_{\text{Ku}}(ab)=\sqrt{4\pi }(a||r^K{[Y_K\sigma ]}_{K+1}{i}^k||b),& (31)\end{array}$

where Y_K is a spherical harmonic of rank K, r the radial coordinate, and a and b stand for the single-particle orbital quantum numbers. The NME is given explicitly in Suhonen [15].

4.2. First-Forbidden β Decays

The shape factor C(w_e) of Equation (22) contains complicated combinations of both (universal) kinematic factors and nuclear form factors [26–28]. The nuclear form factors can be related to the corresponding NMEs using the impulse approximation [45]. For the first-forbidden non-unique decays the relevant NMEs are those of the transition operators denoted here by ${O}(0^{-})$ [rank-0 tensors], ${O}(1^{-})$ [rank-1 tensors] and ${O}(2^{-})$ [rank-2 tensors]. The ${O}(0^{-})$ operators mediate pseudoscalar transitions, ${O}(1^{-})$ pseudovector transitions and ${O}(0^{-})$ pseudotensor transitions. In the non-relativistic reduction there are six matrix elements corresponding to the operators

$\begin{array}{ll}{O}(0^{-}):g_{\text{A}}\frac{\sigma ·{\text{p}}_e}{M_{\text{N}}},\text{ i}{g}_{\text{A}}\frac{\alpha Z_f}{2R}(\sigma ·\text{r}),& (32)\end{array}$

$\begin{array}{ll}{O}(1^{-}):g_{\text{V}}\frac{{\text{p}}_e}{M_{\text{N}}},g_{\text{A}}\frac{\alpha Z_f}{2R}(\sigma \times \text{r}),g_{\text{V}}\frac{\alpha Z_f}{2R}\text{r},& (33)\end{array}$

$\begin{array}{ll}{O}(2^{-}):\frac{\text{i}}{\sqrt{3}}{g}_{\text{A}}{\left[\sigma \text{r}\right]}_2\sqrt{{\text{p}}_e^2+{\text{q}}_{\nu }^2},& (34)\end{array}$

where r is the coordinate vector and p_e (q_ν) is the electron (neutrino) momentum, and the square brackets in the ${O}(2^{-})$ operator denote angular-momentum coupling. The nuclear matrix elements related to the first forbidden decays are suppressed relative to the Gamow-Teller matrix elements by the small momenta of the leptons, the large nucleon mass, and the small value of the fine-structure constant α.

The quenching of the effective value of g_A in first-forbidden decays in the lead region was observed in the late 1960's in a study by Bohr and Mottelson [56]. In this study the so-called ξ approximation, discussed in Behrens and Bühring [45], Schopper [50], and Bohr and Mottelson [56], was adopted. The wave functions were assumed to be dominated by certain single-particle configurations around the double-magic ²⁰⁸Pb nucleus. For the decays mediated by the rank-1 operators ${O}(1)$ in Equation (33), the obtained effective values of the weak coupling constants were

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(1^{-})=0.46-0.56,& (35)\end{array}$

$\begin{array}{ll}{g}_{\text{V}}^{\text{eff}}(1^{-})=0.3-0.7.& (36)\end{array}$

The effective value of the vector coupling constant deviates significantly from the canonical value g_V = 1, pointing to large nuclear-model-dependent effects. Also the value of the axial coupling is quite low.

Next we discuss more recent and complete studies of the quenching or enhancement of the weak couplings in the first-forbidden β transitions.

4.2.1. Rank-0 Tensors

The mesonic enhancement of the γ₅ NME (σ · p_e of Equation (32) in the non-relativistic limit) was discussed in Kubodera et al. [57] for the pseudoscalar 0⁺ ↔ 0⁻ β transitions. The enhancement of the γ₅ NME stems from the renormalization of the pion-decay constant and the nucleon mass M_N in nuclear medium [58] and exchange of heavy mesons [59, 60]. The γ₅ NME is accompanied by a pseudo-scalar axial coupling g_A(γ₅). The effective value of this coupling can be expressed in terms of an enhancement factor ϵ_MEC through the relation

$\begin{array}{ll}{g}_{\text{A}}({\gamma }_5)=({ϵ}_{\text{MEC}})g_{\text{A}},& (37)\end{array}$

where g_A is the usual axial-vector coupling strength. Related to this, a fundamental enhancement factor ϵ_MEC = 1.4 − 1.7, insensitive to nuclear-structure aspects, was predicted [61, 62]. In the paper of Kirchbach and Reinhardt [63] enhancements of 40 − 50% were predicted for singe-particle transitions between s_1/2 and p_1/2 orbitals. This work was extended by Towner [60] to include several single-particle transitions in multiple mass regions from light nuclei to A ≈ 208. Enhancement factors

$\begin{array}{ll}{ϵ}_{\text{MEC}}=1.6-1.8(A=16-208)& (38)\end{array}$

were obtained.

The mesonic enhancement was considered also in the framework of the interacting shell model for A = 11 − 16. In the studies Millener and Alburger [64] and Warburton et al. [65] some 40 − 50% enhancement of the axial charge was found. Further systematic studies in the A = 11 − 16 [66] and A = 205 − 212 [53, 67, 68] regions reported mesonic enhancement factors of

$\begin{array}{ll}{ϵ}_{\text{MEC}}=\{\begin{array}{l}1.61\pm 0.03(A=11-16)\\ 2.01\pm 0.05(A=205-212).\end{array}& (39)\end{array}$

Interestingly, in the lead-region practically no quenching of the σ · r operator was found with $g_{\text{A}}/g_{\text{A}}^{\text{free}}(0^{-})=0.97\pm 0.06$, as reported in Warburton [53, 67, 68]. The value of ϵ_MEC in the lead region was derived by Kubodera and Rho [58] by adopting an effective Lagrangian incorporating approximate chiral and scale invariance of QCD. The result of Kubodera and Rho was

$\begin{array}{ll}{ϵ}_{\text{MEC}}=2.0\pm 0.2(A\approx 208),& (40)\end{array}$

which agrees well with the phenomenological shell-model result (39). In addition, separate studies for ⁵⁰K [69] and ⁹⁶Y [70] yielded enhancement factors 1.52±0.07 and 1.75±0.30. However, in the case of ⁵⁰K there was no estimate of the theoretical error so the reported uncertainty is purely experimental.

Mesonic enhancement of the axial-charge matrix element, as well as the quenching of g_A, was systematically studied in the previously less studied A ≈ 95 and A ≈ 135 regions by the present authors [71]. In this systematic shell-model study of the two regions, using state-of-the-art two-body interactions, a single effective value of $g_{\text{A}}^{\text{eff}}$ for all axial-vector operators was used. The mesonic enhancement was found to depend on the chosen effective value of g_A. Since the mesonic enhancement has been found to vary between 40 % and 100 %, the effective value of g_A was extracted for several different values of ϵ_MEC. In the A = 92 − 97 region the results were

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(0^{-})=\{\begin{array}{l}0.94\pm 0.08({ϵ}_{\text{MEC}}=1.4)\\ 0.77\pm 0.07({ϵ}_{\text{MEC}}=1.7)\\ 0.65\pm 0.06({ϵ}_{\text{MEC}}=2.0).\end{array}& (41)\end{array}$

In the A = 133 − 139 region the results were quite similar:

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(0^{-})=\{\begin{array}{l}0.87\pm 0.04({ϵ}_{\text{MEC}}=1.4)\\ 0.75\pm 0.03({ϵ}_{\text{MEC}}=1.7)\\ 0.66\pm 0.03({ϵ}_{\text{MEC}}=2.0).\end{array}& (42)\end{array}$

This is quite strong evidence of the quenching of g_A in first-forbidden decays, since significant quenching is found regardless of the exact strength of the mesonic enhancement. In Kubodera and Rho [58] it was pointed out that the mesonic enhancement should be larger for heavier nuclei, which is in line with the earlier shell-model results [53, 67, 68]. In Kostensalo and Suhonen [71] this was used to extract the effective value of g_A by fitting all the available data from the previous studies. The fit of this study is shown in Figure 9. As can be seen from the figure, a suitably increasing mesonic enhancement as a function of A is seen only when g_A ≈ 0.70. The linear fit obtained for the whole mass region A = 11 − 212 reads

$\begin{array}{ll}{ϵ}_{\text{MEC}}=1.576+2.08\times 10^{-3}A.& (43)\end{array}$

FIGURE 9

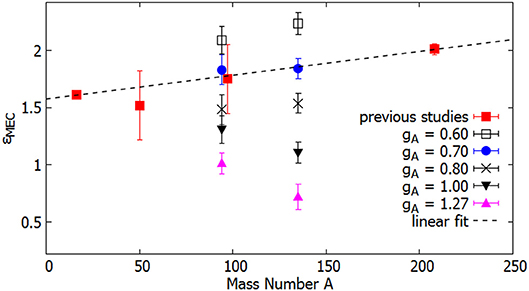
Figure 9. Mesonic enhancement factors ϵ_MEC of the previous studies and the study of Kostensalo and Suhonen [71] as a function of the mass number A. The red squares represent the previous systematic studies done in the A ≈ 16 and A ≈ 208 regions and the separate studies done for ⁵⁰K and ⁹⁶Y. The other points represent the results of Kostensalo and Suhonen [71] for different effective values of g_A. The linear fit is an error-weighted fit, where the results of the previous studies and the study [71] with g_A = 0.70 are used.

4.2.2. Rank-1 Tensors

Since the early findings (35) and (36) of Bohr and Mottelson [56], the effective values of the weak coupling constants related to rank-1 operators ${O}(1^{-})$ in (33) have been studied also separately using the available data on the corresponding pseudovector transitions. In Warburton [53, 67] the effective values

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(1^{-})\approx 0.6;g_{\text{V}}^{\text{eff}}(1^{-})\approx 0.6(\text{Warburton})& (44)\end{array}$

were obtained in the lead region, where the heavy quenching was attributed to core-polarization effects. The shell model study of Rydström et al. [72] of the transition ${}^{205}\text{Pb}(1/2^{-}){\to }^{205}\text{Tl}(1/2_{\text{g}.\text{s}.}^{+})$ yielded similar results:

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(1^{-})\approx 0.43\text{−}0.65;g_{\text{V}}^{\text{eff}}(1^{-})\approx 0.38\text{−}0.85.(\mathrm{\text{Rydström }}etal.)& (45)\end{array}$

In the work Zhi [52] half-lives of a number of nuclei at the magic neutron numbers N = 50, 82, 126 were analyzed by comparing the results of large-scale shell-model calculations with experimental data. Both Gamow-Teller and first-forbidden β decays were included in the analysis. By performing a least-squares fit to the experimental data the following quenched weak couplings were extracted

$\begin{array}{ll}{O}(0^{-}):g_{\text{A}}({\gamma }_5)=1.61;g_{\text{A}}(\sigma ·\text{r})=0.66,& (46)\end{array}$

$\begin{array}{ll}{O}(1^{-}):g_{\text{A}}^{\text{eff}}(1^{-})\approx 0.48;g_{\text{V}}^{\text{eff}}(1^{-})\approx 0.65,& (47)\end{array}$

$\begin{array}{ll}{O}(2^{-}):g_{\text{A}}^{\text{eff}}(2^{-})\approx 0.53.& (48)\end{array}$

For the rank-1 operators the obtained effective value on g_V is quite far from the CVC value g_V = 1.0 [9]. In the recent work of Hayen et al. [73] the first-forbidden decays related to the cumulative reactor antineutrino spectrum were studied in the ISM. In this short letter type article it was not possible to give the details related to the calculations, so they are presented here for the first time. In the A = 86 − 97 region the interaction glepn [70] was used and in the region A = 133 − 142 the (unpublished) interaction jj56pnb of Alex Brown was used. For the decays with ΔJ = 1 the half-lives could not be reproduced with any reasonable g_A, with the exception of the decay ${}^{134m}\text{Sb}(7^{-}){\to }^{134}\text{Te}(6_2^{-})$ for which g_A = 0.34(12) works, if the CVC hypothesis g_V = 1 was not broken. Since there were so few decays calculated in different model spaces, it was not meaningful to start fitting the values of both g_A and g_V to this data. However, this might be an interesting research topic in the future. Since the previous studies, discussed above, point to g_A ≈ g_V, we set the two coupling constants to be equal and then fitted this value to the experimental data. As can be seen from Table 5 the recent calculations seem to also point to heavy quenching g_A = g_V ≈ 0.5 for the first-forbidden rank-1-tensor-mediated β decays in medium-heavy nuclei.

TABLE 5

Table 5. Values of the weak couplings g_A = g_V needed to reproduce the experimental half-lives of the listed β transitions, mediated by rank-1 tensors (33) of the first-forbidden β decay.

4.2.3. Rank-2 Tensor

The quenching of g_A related to the pseudotensor transitions mediated by the rank-2 operator (34) is best studied in the context of first-forbidden unique ground-state-to-ground-state decays in even-A nuclei, as this is the only operator at work in the leading order. In the early work [74] a systematic schematic analysis of the first-forbidden unique β decays was performed from the point of view of suppression factors stemming from the effect of E1 (electric dipole) giant resonance in the final odd-odd nucleus. In Towner et al. [75] the suppression mechanism of the first-forbidden and third-forbidden β decays of light nuclei (A ≤ 50) was studied by using simple shell-model estimates and first-order perturbation theory. The hindrance was traced to the repulsive T = 1 (isospin 1) particle-hole force.

In the work Ejiri et al. [76] 19 first-forbidden unique ground-state-to-ground-state β-decay transitions were studied. The interesting transitions are the ones where a central nucleus (here only ⁸⁴Kr) is fed by a left-branch and a right-branch 2⁻ → 0⁺ transition or a central nucleus (⁷⁴As, ⁸⁶Rb, ¹²²Sb and ¹²⁶I) is feeding the neighboring even-even nuclei by left-branch and right-branch 2⁻ → 0⁺ transitions. By denoting the associated left-branch and right-branch NMEs by g_AM_L and g_AM_R, respectively, one can compute the geometric mean (16) of these MNEs and compare with experimental data.

In Ejiri et al. [76] a g_ph- and g_pp-renormalized Bonn-A G matrix (one-meson-exchange nucleon-nucleon interaction adapted to nuclear matter by enforcing the Pauli principle) was used as the two-nucleon interaction in a pnQRPA framework. The two-quasiparticle and pnQRPA mean NMEs were compared with the ones extracted from the measured comparative half-lives. The analysis yielded

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(2^{-})\approx 0.57& (49)\end{array}$

for the effective axial-vector coupling strength using the pnQRPA wave functions. This in excellent agreement with the result of Zhi et al. given in (48). The average of the values of the leading two-quasiparticle NMEs gives in turn

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(2^{-})\approx 0.23& (50)\end{array}$

implying the ratio

$\begin{array}{ll}k=\frac{M_{\text{pnQRPA}}^{\text{m}}}{M_{\text{qp}}^{\text{m}}}\approx 0.4& (51)\end{array}$

and thus a drastic nuclear many-body effect when going from the two-quasiparticle level of approximation to the more sophisticated pnQRPA level. The 2qp-NME to pnQRPA-NME comparison is the only one where a clean separation between the nuclear-medium effects and the nuclear-model effects can be achieved, the nuclear-model effect being responsible for the (in this case large) shift in the values of the NMEs.

4.3. Higher-Forbidden Decays

4.3.1. Higher-Forbidden Non-unique Decays

The shape factors of forbidden non-unique β decays are rather complex combinations of different NMEs and phase-space factors. Furthermore, their dependence on the weak couplings g_V and g_A is very nontrivial as shown by the decomposition (24) and its integrated version (25).

In Haaranen et al. [47] the spectrum-shape method (SSM) was proposed. In this method the computed β-electron spectra can be used to determine the values of the weak coupling strengths by comparing the computed spectra with the measured one for forbidden non-unique β decays. In this work it was found that the computed β-electron spectra were very sensitive to the effective value of g_A in the 4th-forbidden non-unique ground-state-to-ground-state β-decay transitions ¹¹³Cd(1/2⁺) → ¹¹³In(9/2⁺) and ¹¹⁵In(9/2⁺) → ¹¹⁵Sn(1/2⁺). The related calculations were done in the frameworks of the MQPM and the ISM (see section 2). It was also found that for all values of g_A the best fits to the spectrum-shape and half-life data were obtained by using the canonical value g_V = 1.0 for the vector coupling strength. This result is in conflict with the results for the first-forbidden non-unique pseudovector decays, where quenched values for g_V were obtained (see section 4.2.2).

The work in Haaranen et al. [47] was extended in Haaranen et al. [48] by including the microscopic interacting boson-fermion model (IBFM-2) (see section 2), in the calculations. Interestingly all three models gave g_A ≈ 0.92 when the SSM method was applied to the transition ¹¹³Cd(1/2⁺) → ¹¹³In(9/2⁺) where the experimental spectrum shape was available. For the three models, in the whole range of electron energies, the two components, C_V(w_e) and C_A(w_e) are roughly of the same size whereas the magnitude of the component C_VA(w_e) is practically the sum of the previous two, but with opposite sign. Hence, for the whole range of electron energies there is a delicate balance between the three terms, and their sum is much smaller than the magnitudes of the individual components. However, the half-life comparisons were not in line with the SSM analyses, giving g_A ≈ 0.65 for ISM and MQPM and g_A ≈ 0.10 for IBFM-2. The possible cure to this could be to independently vary the weak couplings for multipole operators of different rank as was described for the first-forbidden β transitions in section 4.2.

The works [47, 48] were continued by the works [49, 77] where both the MQPM and ISM frameworks were used as theory tools. It was found that the spectrum shapes of the third- and fourth-forbidden non-unique decays depend strongly on the value of g_A, whereas the first- and second-forbidden decays were practically insensitive to the variations in g_A. Furthermore, the g_A-driven evolution of the normalized β spectra was found to be quite universal, largely insensitive to small changes of the nuclear mean field and the adopted residual many-body Hamiltonian. This makes SSM a robust tool for extracting information on the effective values of weak couplings.

All the potentially interesting nuclei for the application of the spectrum-shape method found in Kostensalo et al. [49] and Kostensalo and Suhonen [77] had mass numbers A = 87 − 115 and were second-, third-, or fourth-forbidden. In order to better understand the evolution of the quenching of g_A it would be preferable to have also lighter and heavier nuclei to study. Also, in these papers there were no first-forbidden decays discovered for with the SSM could be applicable. However, in Kostensalo and Suhonen [78] the first potential heavy candidate, the ground-state-to-ground-state decay of ²¹⁰Bi was pointed out. This decay is also first-forbidden and its spectrum is given in Figure 10.

FIGURE 10

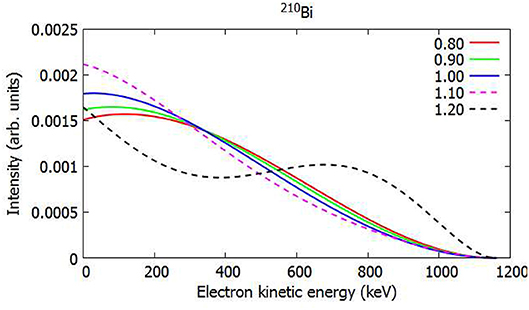
Figure 10. Normalized ISM-computed electron spectrum for the first-forbidden non-unique β⁻ decay of ²¹⁰Bi. The value g_V = 1.0 was assumed and the color coding represents the value of g_A.

In Kostensalo and Suhonen [71] a modest g_A dependence was reported in the spectra of the decays ⁹³Y(1/2⁻) → ⁹³Zr(1/2⁺) and ¹³⁸Cs(3⁻) → ¹³⁸Ba(3⁺), as can bee seen in Figure 11. In the spectrum on ⁹³Y some dependence on the value of ϵ_MEC is also seen, which opens up the possibility for investigating the mesonic enhancement of the axial-charge matrix element using the SSM.

FIGURE 11

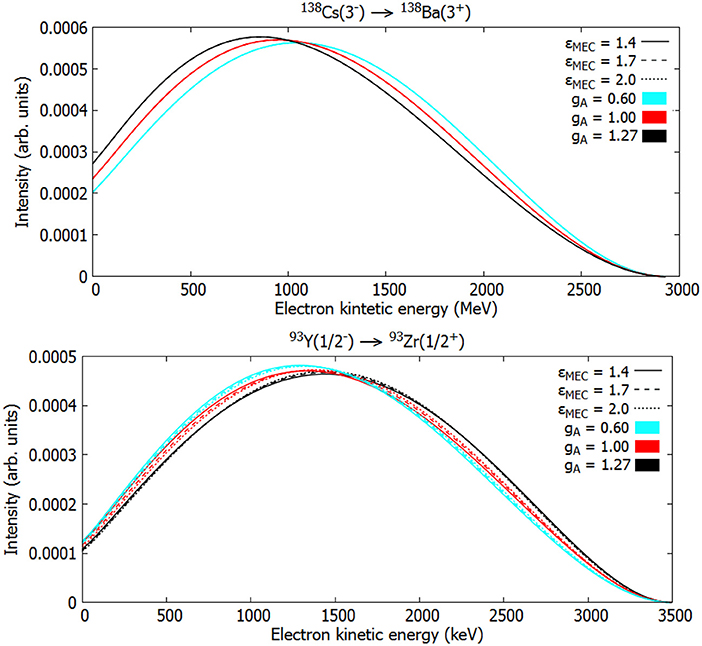
Figure 11. Normalized ISM-computed electron spectra for the first-forbidden non-unique β⁻ decays of ¹³⁸Cs and ⁹³Y. The value g_V = 1.0 was assumed and the color coding represents the value of g_A and the dash coding the value of the mesonic enhancement factor ϵ_MEC.

Concerning the lighter nuclei, so far there are not any good candidates yet discovered. However, our recent shell-model calculation in the full fp shell using the interaction gxpf1a [79, 80] shows that the second-forbidden ground-state-to-ground-state decay of ⁵⁹Fe possesses the necessary g_A dependence, as can be seen from Figure 12. The branching ratio on the other hand is only 0.18 % [81], which complicates the measurement of this spectrum to the required precision. In any case, this discovery gives us hope that there might be some good candidates for the SSM also in this mass region.

FIGURE 12

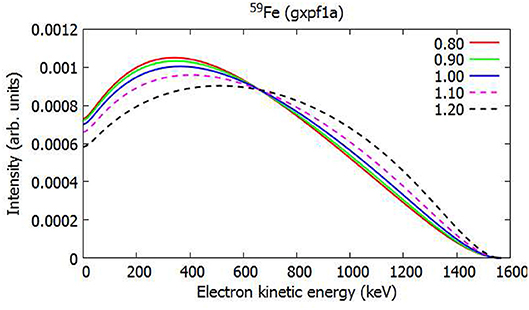
Figure 12. Normalized ISM-computed electron spectrum for the second-forbidden non-unique β⁻ decay of ⁵⁹Fe. The value g_V = 1.0 was assumed and the color coding represents the value of g_A.

The main issue with the SSM is the quality of the theoretical wave functions. However, the spectral shapes have been found to depend very little on the details of the wave functions making it possibly a very robust tool [49, 78]. The best candidates for the SSM found so far are, unfortunately, decay transitions between mid-shell nuclei, such as ¹¹³Cd, which are not easy to describe theoretically. Even though the SSM seems to be robust, in order to make strong claims about the effective value of g_A it would be preferable to have precise wave functions. In the case of the β⁻-decay transition ⁹⁸Tc(6⁺) → ⁹⁸Ru(4⁺) our recent calculations using the glepn interaction [70] have given results which are in good agreement with the available spectroscopic data. For the 2⁺ state in ⁹⁸Ru the calculated magnetic dipole moment +0.445μ_N is in agreement with the experimental value +0.8(6)μ_N [82] and the electric quadrupole moment −0.129e²b agrees with the experimental value -0.03(14)e²b [83] also. The interaction also manages to predict that the 4⁺, 5⁺, 6⁺ states in ⁹⁸Tc are below 70 keV, though does not get the ordering quite right. Furthermore, the experimental half-life of the β decay is reproduced with a reasonable g_A = 0.96. In comparison, the calculation carried out in Kostensalo and Suhonen [77], using the interaction by Gloeckner [84], fails to reproduce the half-life 4.2(3) × 10⁶ yr with any effective value of g_A giving 2.1 × 10⁶ yr for g_A = 1.04 and less for all other values. As can be seen from Figure 13 the two Hamiltonians still predict very similar spectral shape evolution regardless of the failures in half-life prediction.

FIGURE 13

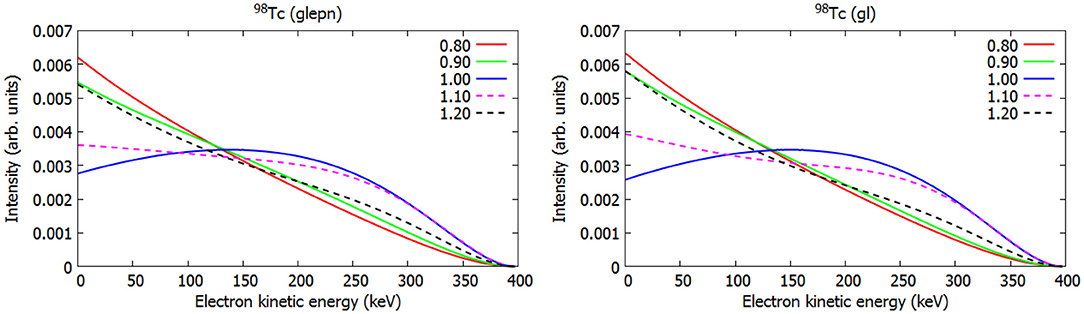
Figure 13. Normalized ISM-computed electron spectra for the second-forbidden non-unique β⁻ transition ⁹⁸Tc(6⁺) → ⁹⁸Ru(4⁺) using two different Hamiltonians. The branching to this decay channel is 100%. The value g_V = 1.0 was assumed and the color coding represents the value of g_A.

On the experimental side advances have been made by measuring the ¹¹³Cd spectrum to high accuracy [85]. When compared with the spectral shapes given in Haaranen et al. [48] the following effective values of g_A were obtained

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(\mathrm{\text{ISM}})=0.915\pm 0.021,& (52)\end{array}$

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(\mathrm{\text{MQPM}})=0.911\pm 0.009,& (53)\end{array}$

$\begin{array}{ll}{g}_{\text{A}}^{\text{eff}}(\mathrm{\text{IBFM-2}})=0.943\pm 0.090,& (54)\end{array}$

which are in excellent agreement with each other.

4.3.2. Higher-Forbidden Unique Decays

Early studies of the quenching in the second- and third-forbidden unique β decays were performed in Towner et al. [75] and Warburton et al. [86]. In Towner et al. [75] the suppression mechanism of the first-forbidden and third-forbidden β decays of light nuclei (A ≤ 50) was studied by using simple shell-model estimates and first-order perturbation theory. The hindrance of the decay transitions was argued to result from the repulsive T = 1 (isospin 1) particle-hole force. In Warburton et al. [86] the second- and third-forbidden unique β decays were studied using a simple interacting shell model and the unified model (deformed shell model) for six β transitions in the A = 10, 22, 26, 40 nuclei. The incentive for the studies was the hindrance of certain measured β transitions. A later study of second-forbidden unique β decays in the mass range A = 10 − 54 was performed in Martínez-Pinedo and Vogel [87] by using the ISM. A reasonable correspondence with the measured half-lives was achieved by using the free value of the axial coupling but a quenched value would have improved the correspondence.

The quenching related to the virtual β transitions of the 0νββ decay can be studied at the low-q limit (5) by using the theoretical machinery of section 4.1. In Kostensalo and Suhonen [88] this machinery was applied to 148 potentially measurable second-, third-, fourth-, fifth-, sixth- and seventh-forbidden unique beta transitions. The calculations were done using realistic single-particle model spaces and G-matrix-based microscopic two-body interactions. The results of Kostensalo and Suhonen [88] could shed light on the magnitudes of the NMEs corresponding to the high-forbidden unique 0⁺ ↔ J^π = 3⁺, 4⁻, 5⁺, 6⁻, 7⁺, 8⁻ virtual transitions taking part in the 0νββ decays.

In the work of Kostensalo and Suhonen [88] the expected half-lives of the studied β-decay transitions were derived by comparison with the analyses performed for the Gamow-Teller and first-forbidden unique β transitions in the works [38, 76]. An example of such predictions is given in Figure 14. In the figure one sees that the expected half-lives are very long and hard to measure. On the β⁻ side the fourth-forbidden and seventh-forbidden decay transitions are masked by the strong β⁻ branches to the excited states of ¹³⁶Ba.

FIGURE 14

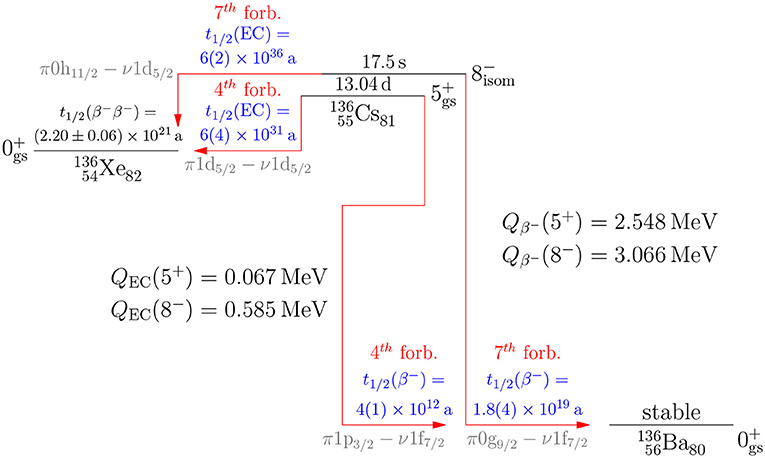
Figure 14. Predicted half-lives and their error estimates (in parenthesis) for β⁻ and EC (electron-capture) transitions in the isobaric chain A = 136. The spin-parity assignment, life-time and decay energies (Q values) of the 5⁺ ground (gs) state and 8⁺ isomeric (isom) state of ¹³⁶Cs are experimental data and taken from ENSDF [89]. The 2νββ half-life is taken from Barabash [90]. In addition to the predicted half-lives the degree of forbiddenness and the leading single-particle transition are shown.

5. Conclusions

Double β decay is a hot issue in modern day's particle, neutrino and nuclear physics. To gain the full benefit from the potential results of the running and future ββ-decay experiments, accurate evaluation of the involved nuclear matrix elements is crucial. This evaluation calls for reliable nuclear many-body approaches in order to produce realistic wave functions for ββ calculations. Beyond this, systematic estimation of the effective value of the weak axial coupling, g_A, is necessary. The value of this coupling plays a notable role in both the two-neutrino and neutrinoless ββ decays.

The effective value of g_A can be studied at low momentum-exchange limit by using data on β and two-neutrino ββ decays. Data on Gamow-Teller 0⁺ ↔ 1⁺ β transitions are relatively abundant and the most clean-cut to compare with calculations, thus enabling systematic studies of the quenching of g_A within different nuclear-structure frameworks. The β-decay analyses (see Figure 8) suggest that effective values $g_{\text{A}}^{\text{eff}}\approx 0.9$ for masses A ≤ 82, around $g_{\text{A}}^{\text{eff}}\approx 0.5$ in the mass A = 98 − 110 region, around $g_{\text{A}}^{\text{eff}}\approx 0.7$ in the mass A = 112 − 124 region and close to $g_{\text{A}}^{\text{eff}}\approx 1.0$ for the masses A = 126 − 142 are appropriate.

Available data on first-forbidden unique β decays offer a straightforward systematic way to access the quenching of g_A beyond the allowed β decays. A recent analysis (see section 4.2.2) suggests $g_{\text{A}}^{\text{eff}}(2^{-})\approx 0.5-0.6$. A more involved analysis has to be performed for the first-forbidden non-unique β decays owing to the meson-exchange enhancement of the weak axial charge, combined with the quenching of g_A. A recent study (see Figure 9) suggests enhancement factors ϵ_MEC obeying the simple linear law of Equation (43) all through the mass region A = 16 − 208. Higher-forbidden non-unique β transitions offer yet another way to study, at low-momentum-transfer limit, the quenching of g_A in virtual transitions to high-angular-momentum intermediate states in the neutrinoless ββ decay. In particular, the shapes of electron spectra in these transitions can, in selected cases and once more experimental data are available, offer a viable alternative to access the quenching of g_A. Here a study, combining theory with data of a recent experiment, suggests values around $g_{\text{A}}^{\text{eff}}\approx 0.9$ for the 4th-forbidden β decay of ¹¹³Cd (see Equations (52)–(54)).

Data Availability

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work has been partially supported by the Academy of Finland under the Academy project no. 318043. JK acknowledges the financial support from Jenny and Antti Wihuri Foundation.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^Without the allowed Fermi J_i → J_f = J_i transitions.

References

1. Suhonen J, Civitarese O. Weak interaction and nuclear structure aspect of nuclear double beta decay. Phys Rep. (1998) 300:123–214. doi: 10.1016/S0370-1573(97)00087-2

CrossRef Full Text | Google Scholar

2. Suhonen J, Civitarese O. Review of the properties of the 0νβ⁻β⁻ nuclear matrix elements. J Phys G Nucl Part Phys. (2012) 39:124005. doi: 10.1088/0954-3899/39/12/124005

CrossRef Full Text | Google Scholar

3. Engel J, Menendez J. Status and future of nuclear matrix elements for neutrinoless double beta decay: a review. Rep Prog Phys. (2017) 60:046301. doi: 10.1088/1361-6633/aa5bc5

CrossRef Full Text | Google Scholar

4. Suhonen J, Civitarese O. Double-beta-decay nuclear matrix elements in the QRPA framework. J Phys G Nucl Part Phys. (2012) 39:085105. doi: 10.1088/0954-3899/39/8/085105

CrossRef Full Text | Google Scholar

5. Caurier E, Nowacki F, Poves A. Shell model description of the ββ decay of ¹³⁶Xe. Phys Lett B. (2012) 711:62–4. doi: 10.1016/j.physletb.2012.03.076

CrossRef Full Text | Google Scholar

6. Horoi M, Neacsu A. Shell model predictions for ¹²⁴Sn double-β decay. Phys Rev C. (2016) 93:024308. doi: 10.1103/PhysRevC.93.024308

CrossRef Full Text | Google Scholar

7. Iwata Y, Shimizu N, Otsuka T, Utsuno Y, Menéndez J, Honma M, et al. Large-scale shell-model analysis of the neutrinoless ββ decay of ⁴⁸Ca. Phys Rev lett. (2016) 116:112502. doi: 10.1103/PhysRevLett.116.112502

CrossRef Full Text | Google Scholar

8. Barea J, Kotila J, Iachello F. Nuclear matrix elements for double-β decay. Phys Rev C. (2013) 87:014315. doi: 10.1103/PhysRevC.87.014315

CrossRef Full Text | Google Scholar

9. Feynman RP, Gell-Mann M. Theory of the fermi interaction. Phys Rev. (1958) 109:193–8. doi: 10.1103/PhysRev.109.193

CrossRef Full Text | Google Scholar

10. Patrignani C, Agashe K, Aielli G, Amsler C, Antonelli M, Asner DM, et al. (Particle Data Group). Review of particle physics. Chin Phys C. (2016) 40:100001. doi: 10.1088/1674-1137/40/10/100001

CrossRef Full Text | Google Scholar

11. Šimkovic F, Pantis G, Vergados JD, Faessler A. Additional nucleon current contributions to neutrinoless double β decay. Phys Rev C. (1999) 60:055502. doi: 10.1103/PhysRevC.60.055502

CrossRef Full Text | Google Scholar

12. Menéndez J, Gazit D, Schwenk A. Chiral two-body currents in nuclei: Gamow-Teller transitions and neutrinoless double-beta decay. Phys Rev Lett. (2011) 107:062501. doi: 10.1103/PhysRevLett.107.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Suhonen J. Value of the axial-vector coupling strength in β and ββ decays: a review. Front Phys. (2017) 5:55. doi: 10.3389/fphy.2017.00055

CrossRef Full Text | Google Scholar

14. Ejiri H, Suhonen J, Zuber K. Neutrino-nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys Rep. (in press). doi: 10.1016/j.physrep.2018.12.001

CrossRef Full Text

15. Suhonen J. From Nucleons to Nucleus: Concepts of Microscopic Nuclear Theory. Theoretical and Mathematical Physics. Berlin: Springer (2007).

Google Scholar

16. Toivanen J, Suhonen J. Renormalized proton-neutron QRPA and its application to double beta decay. Phys Rev Lett. (1995) 75:410–3. doi: 10.1103/PhysRevLett.75.410

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Toivanen J, Suhonen J. Study of several double-beta-decaying nuclei using the renormalized proton-neutron quasiparticle random-phase approximation. Phys Rev C. (1997) 55:2314–23. doi: 10.1103/PhysRevC.55.2314

CrossRef Full Text | Google Scholar

18. Vogel P, Zirnbauer MR. Suppression of the two-neutrino double-beta decay by nuclear-structure effects. Phys Rev Lett. (1986) 57:3148–51. doi: 10.1103/PhysRevLett.57.3148

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Civitarese O, Faessler A, Tomoda T. Suppression of the two-neutrino double β decay. Phys Lett B (1987) 194:11–14. doi: 10.1016/0370-2693(87)90760-X

CrossRef Full Text | Google Scholar

20. Suhonen J, Faessler A, Taigel T, Tomoda T. Suppression of the β⁺ decays of ¹⁴⁸Dy, ¹⁵⁰Er and ¹⁵²Yb. Phys Lett B. (1988) 202:174–8. doi: 10.1016/0370-2693(88)90002-0

CrossRef Full Text | Google Scholar

21. Suhonen J, Taigel T, Faessler A. pnQRPA calculation of the β⁺/EC quenching for several neutron-deficient nuclei in mass regions A = 94 − 110 and A = 146 − 156. Nucl Phys A. (1988) 486:91–117. doi: 10.1016/0375-9474(88)90041-3

CrossRef Full Text | Google Scholar

22. Kortelainen M, Suhonen J. Nuclear matrix elements of 0νββ decay with improved short-range correlations. Phys Rev C. (2007) 76:024315. doi: 10.1103/PhysRevC.76.024315

CrossRef Full Text | Google Scholar

23. Šimkovic F, Faessler A, Rodin V, Vogel P, Engel J. Anatomy of the 0νββ nuclear matrix elements. Phys Rev C. (2008) 77:045503. doi: 10.1103/PhysRevC.77.045503

CrossRef Full Text | Google Scholar

24. Šimkovic F, Rodin V, Faessler A, Vogel P. 0νββ and 2νββ nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration. Phys Rev C. (2013) 87:045501. doi: 10.1103/PhysRevC.87.045501

CrossRef Full Text | Google Scholar

25. Hyvärinen J, Suhonen J. Nuclear matrix elements for 0νββ decays with light or heavy Majorana-neutrino exchange. Phys Rev C. (2015) 91:024613. doi: 10.1103/PhysRevC.91.024613

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Suhonen J. Calculation of allowed and first-forbidden beta-decay transitions of odd-odd nuclei. Nucl Phys A. (1993) 563:205–24. doi: 10.1016/0375-9474(93)90602-T

CrossRef Full Text | Google Scholar

27. Nabi JU, Cakmak N, Stoica S, Iftikhar Z. First-forbidden transitions and stellar β-decay rates of Zn and Ge isotopes. Phys Scr. (2015) 90:115301. doi: 10.1088/0031-8949/90/11/115301

CrossRef Full Text | Google Scholar

28. Nabi JU, Cakmak N, Iftikhar Z. First-forbidden β-decay rates, energy rates of β-delayed neutrons and probability of β-delayed neutron emissions for neutron-rich nickel isotopes. Eur Phys J A. (2016) 52:5. doi: 10.1140/epja/i2016-16005-6

CrossRef Full Text | Google Scholar

29. Toivanen J, Suhonen J. Microscopic quasiparticle-phonon description of odd-A Xe isotopes. J Phys G Nucl Part Phys. (1995) 21:1491–7. doi: 10.1088/0954-3899/21/11/007

CrossRef Full Text | Google Scholar

30. Toivanen J, Suhonen J. Microscopic quasiparticle-phonon description of odd-mass ^127−133Xe isotopes and their β decay. Phys Rev C. (1998) 57:1237–45. doi: 10.1103/PhysRevC.57.1237

CrossRef Full Text | Google Scholar

31. Iachello F, Van Isacker P. The Interacting Boson-Fermion Model. Cambridge: Cambridge University Press (1991).

Google Scholar

32. Hardy JC, Towner IS, Koslowsky VT, Hagberg E, Schmeing H. Superallowed 0⁺ → 0⁺nuclear β-decays: a critical survey with tests of CVC and the standard model. Nucl Phys A. (1990) 509:429–60. doi: 10.1016/0375-9474(90)90086-2

CrossRef Full Text | Google Scholar

33. Stoica S, Mirea M, Nitescu O, Nabi JU, Ishfaq M. New phase space calculations for β-decay half-lives. Adv High Energy Phys. (2016) 2016:8729893. doi: 10.1155/2016/8729893

CrossRef Full Text | Google Scholar

34. Audi G, Kondev FG, Wang M, Pfeiffer B, Sun X, Blachot J, et al. The NUBASE2012 evaluation of nuclear properties. Chin Phys C. (2012) 36:1157–2014. doi: 10.1088/1674-1137/36/12/001

CrossRef Full Text | Google Scholar

35. Jokiniemi L, Ejiri H, Frekers D, Suhonen J. Neutrinoless ββ nuclear matrix elements using isovector spin-dipole J^π = 2⁻ data. Phys Rev C. (2018) 98:024608. doi: 10.1103/PhysRevC.98.024608

CrossRef Full Text | Google Scholar

36. Pirinen P, Suhonen J. Systematic approach to β and 2νββ decays of mass A = 100 − 136 nuclei. Phys Rev C. (2015) 91:054309. doi: 10.1103/PhysRevC.91.054309

CrossRef Full Text | Google Scholar

37. Deppisch FF, Suhonen J. Statistical analysis of β decays and the effective value of g_A in the proton-neutron quasiparticle random-phase approximation framework. Phys Rev C. (2016) 94:055501. doi: 10.1103/PhysRevC.94.055501

CrossRef Full Text | Google Scholar

38. Ejiri H, Suhonen J. GT neutrino-nuclear responses for double beta decays and astro-neutrinos. J Phys G Nucl Part Phys. (2015) 42:055201. doi: 10.1088/0954-3899/42/5/055201

CrossRef Full Text | Google Scholar

39. Suhonen J. Impact of the quenching of g_A on the sensitivity of 0νββ experiments. Phys Rev C. (2017) 96:055501. doi: 10.1103/PhysRevC.96.055501

CrossRef Full Text | Google Scholar

40. Faessler A, Lisi E, Fogli GL, Rodin V. Overconstrained estimates of neutrinoless double beta decay within the QRPA. J Phys G Nucl Part Phys. (2008) 35:075104. doi: 10.1088/0954-3899/35/7/075104

CrossRef Full Text | Google Scholar

41. Suhonen J, Civitarese O. Single and double beta decays in the A = 100, A = 116 and A = 128 triplets of isobars. Nucl Phys A. (2014) 924:1–23. doi: 10.1016/j.nuclphysa.2014.01.004

CrossRef Full Text | Google Scholar

42. Martínez-Pinedo G, Poves A, Caurier E, Zuker AP. Effective g_A in the pf shell. Phys Rev C. (1996) 53:R2602–5. doi: 10.1103/PhysRevC.53.R2602

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Kumar V, Srivastava PC, Li H. Nuclear β⁻-decay half-lives for fp and fpg shell nuclei. J Phys G Nucl Part Phys. (2016) 43:105104. doi: 10.1088/0954-3899/43/10/105104

CrossRef Full Text | Google Scholar

44. Siiskonen T, Hjorth-Jensen M, Suhonen J. Renormalization of the weak hadronic current in the nuclear medium. Phys Rev C. (2001) 63:055501. doi: 10.1103/PhysRevC.63.055501

CrossRef Full Text | Google Scholar

45. Behrens H, Bühring W. Electron Radial Wave Functions and Nuclear Beta Decay. Oxford: Clarendon (1982).

46. Mustonen MT, Aunola M, Suhonen J. Theoretical description of the fourth-forbidden non-unique β decays of ¹¹³Cd and ¹¹⁵In. Phys Rev C. (2006) 73:054301. doi: 10.1103/PhysRevC.73.054301

CrossRef Full Text | Google Scholar

47. Haaranen M, Srivastava PC, Suhonen J. Forbidden nonunique β decays and effective values of weak coupling constants. Phys Rev C. (2016) 93:034308. doi: 10.1103/PhysRevC.93.034308

CrossRef Full Text | Google Scholar

48. Haaranen M, Kotila J, Suhonen J. Spectrum-shape method and the next-to-leading-order terms of the β-shape factor. Phys Rev C. (2017) 95:024327. doi: 10.1103/PhysRevC.95.024327

CrossRef Full Text | Google Scholar

49. Kostensalo J, Haaranen M, Suhonen J. Electron spectra in forbidden β decays and the quenching of the weak axial-vector coupling constant g_A. Phys Rev C. (2017) 95:044313. doi: 10.1103/PhysRevC.95.044313

CrossRef Full Text | Google Scholar

50. Schopper HF. Weak Interactions and Nuclear Beta Decay. Amsterdam: North-Holland (1966).

Google Scholar

51. Ydrefors E, Mustonen MT, Suhonen J. MQPM description of the structure and beta decays of the odd A=95,97 Mo and Tc isotopes. Nucl Phys A. (2010) 842:33–47. doi: 10.1016/j.nuclphysa.2010.04.005

CrossRef Full Text | Google Scholar

52. Zhi Q, Caurier E, Cuenca-García JJ, Langanke K, Martínez-Pinedo G, Sieja K. Shell-model half-lives including first-forbidden contributions for r-process waiting-point nuclei. Phys Rev C. (2013) 87:025803. doi: 10.1103/PhysRevC.87.025803

CrossRef Full Text | Google Scholar

53. Warburton EK. First-forbidden β decay in the lead region and mesonic enhancement of the weak axial current. Phys Rev C. (1991) 44:233–60. doi: 10.1103/PhysRevC.44.233

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Warburton EK, Towner IS. Renormalization of the axial charge at A ≈ 132. Phys Lett B. (1992) 294:1–6. doi: 10.1016/0370-2693(92)91629-N

CrossRef Full Text | Google Scholar

55. Gove NB, Martin MJ. Log-f tables for beta decay. Atomic Data Nucl Data Tables. (1971) 10:205–19. doi: 10.1016/S0092-640X(71)80026-8

CrossRef Full Text | Google Scholar

56. Bohr A, Mottelson B. Nuclear Structure, Vol. 1. New York, NY: Benjamin (1969).

PubMed Abstract

57. Kubodera K, Delorme J, Rho M. Axial currents in nuclei. Phys Rev Lett. (1978) 40:755–8. doi: 10.1103/PhysRevLett.40.755

CrossRef Full Text | Google Scholar

58. Kubodera K, Rho M. Axial-charge transitions in heavy nuclei and in-medium effective chiral lagrangians. Phys Rev Lett. (1991) 67:3479–82. doi: 10.1103/PhysRevLett.67.3479

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Kirchbach M, Riska DO, Tsushima K. The axial exchange charge operator and the nucleon-nucleon interaction. Nucl Phys A. (1992) 542:616–30. doi: 10.1016/0375-9474(92)90260-Q

CrossRef Full Text | Google Scholar

60. Towner IS. Enhancement in axial-charge matrix elements from meson-exchange currents. Nucl Phys A. (1992) 542:631–58. doi: 10.1016/0375-9474(92)90261-H

CrossRef Full Text | Google Scholar

61. Towner IS, Khanna FC. Role of 2p-2h states in weak 0⁺ − 0⁻ transitions in A = 16 nuclei. Nucl Phys A. (1981) 372:331–48. doi: 10.1016/0375-9474(81)90039-7

CrossRef Full Text | Google Scholar

62. Delorme J. Meson degrees of freedom in nuclei. Nucl Phys A. (1982) 374:541–55. doi: 10.1016/0375-9474(82)90263-9

CrossRef Full Text | Google Scholar

63. Kirchbach M, Reinhardt H. On the meson-exchange correction to the axial-charge density for ns_1/2 ↔n'p_1/2 β-transitions. Phys Lett B. (1988) 208:79–83. doi: 10.1016/0370-2693(88)91207-5

CrossRef Full Text | Google Scholar

64. Millener DJ, Alburger DE, Warburton EK, Wilkinson DH. Decay scheme of ¹¹Be. Phys Rev C. (1982) 26:1167–85. doi: 10.1103/PhysRevC.26.1167

CrossRef Full Text | Google Scholar

65. Warburton EK, Alburger DE, Millener DJ. Shapes of the ¹⁶N and ¹⁵C beta spectra and extraction of matrix elements for ¹⁵C(^β−)¹⁵N(g.s.). Phys Rev C. (1984) 29:2281–9. doi: 10.1103/PhysRevC.29.2281

CrossRef Full Text | Google Scholar

66. Warburton EK, Towner IS, Brown BA. First-forbidden β decay: Meson-exchange enhancement of the axial charge at A~16. Phys Rev C. (1994) 49:824–39. doi: 10.1103/PhysRevC.49.824

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Warburton EK. Core polarization effects on spin-dipole and first-forbidden β-decay operators in the lead region. Phys Rev C. (1990) 42:2479–86. doi: 10.1103/PhysRevC.42.2479

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Warburton EK. Mesonic enhancement of the weak axial-vector current evaluated from β decay in the lead region. Phys Rev Lett. (1991) 66:1823–6. doi: 10.1103/PhysRevLett.66.1823

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Warburton EK. In-medium and core-polarization effects in ⁵⁰K(0⁻) $\stackrel{{\beta }^{-}}{\to }$ ⁵⁰Ca(0⁺). Phys Rev C. (1991) 44:1024–9. doi: 10.1103/PhysRevC.44.1024

CrossRef Full Text | Google Scholar

70. Mach H, Warburton EK, Gill RL, Casten RF, Becker JA, Brown BA, et al. Meson-exchange enhancement of the first-forbidden ⁹⁶Y^g(0⁻) → ⁹⁶Zr^g(0⁺) β transition: β decay of the low-spin isomer of ⁹⁶Y. Phys Rev C. (1990) 41:226–42. doi: 10.1103/PhysRevC.41.226

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Kostensalo J, Suhonen J. Mesonic enhancement of the weak axial charge and its effect on the half-lives and spectral shapes of first-forbidden J⁺ ↔ J⁻ decays. Phys Lett B. (2018) 781:480–4. doi: 10.1016/j.physletb.2018.02.053

CrossRef Full Text | Google Scholar

72. Rydström L, Blomqvist J, Liotta RJ, Pomar C. Structure of proton-deficient nuclei near ²⁰⁸Pb, Nucl Phys A. (1990) 512:217–40.

Google Scholar

73. Hayen L, Kostensalo J, Severijns N, Suhonen J. First-forbidden transitions in the reactor anomaly. arXiv:1805.12259 [nucl-th] (2018).

Google Scholar

74. Ejiri H, Ikeda K, Fujita JI. Hindrance factors for beta decays of heavy nuclei. Phys Rev. (1968) 176:1277–88. doi: 10.1103/PhysRev.176.1277

CrossRef Full Text | Google Scholar

75. Towner IS, Warburton EK, Garvey GT. Hindrance phenomena in unique first- and third-forbidden β-decay. Ann Phys. (1971) 66:674–96. doi: 10.1016/0003-4916(71)90074-1

CrossRef Full Text | Google Scholar

76. Ejiri H, Soukouti N, Suhonen J. Spin-dipole nuclear matrix elements for double beta decays and astro-neutrinos. Phys Lett B. (2014) 729:27–32. doi: 10.1016/j.physletb.2013.12.051

CrossRef Full Text | Google Scholar

77. Kostensalo J, Suhonen J. g_A-driven shapes of electron spectra of forbidden β decays in the nuclear shell model. Phys Rev C. (2017) 96:024317. doi: 10.1103/PhysRevC.96.024317

CrossRef Full Text | Google Scholar

78. Kostensalo J, Suhonen J. Beta-spectrum shapes of forbidden β decays. Int J Mod Phys A. (2018) 33:1843008. doi: 10.1142/S0217751X1843008X

CrossRef Full Text | Google Scholar

79. Honma M, Otsuka T, Brown BA, Mizusaki T. New effective interaction for pf-shell nuclei and its implications for the stability of the N = Z = 28 closed core. Phys Rev C. (2004) 69:034335. doi: 10.1103/PhysRevC.69.034335

CrossRef Full Text | Google Scholar

80. Honma M, Otsuka T, Brown BA, Mizusaki T. Shell-model description of neutron-rich pf-shell nuclei with a new effective interaction gxpf 1. Eur Phys J A. (2005) 25:499–502. doi: 10.1140/epjad/i2005-06-032-2

CrossRef Full Text | Google Scholar

81. Baglin CM. Nuclear data sheets for A = 59. Nucl Data Sheets. (2002) 95:215–386. doi: 10.1006/ndsh.2002.0004

CrossRef Full Text | Google Scholar

82. Hubler GK, Kugel HW, Murnick DE. Nuclear magnetic moments of very short-lived states via the transient-field implantation perturbed-angular-correlation technique. Phys Rev C. (1974) 9:1954–64. doi: 10.1103/PhysRevC.9.1954

CrossRef Full Text | Google Scholar

83. Maynard M, Palmer DC, Cresswell JR, Forsyth PD, Hall I, Martin DGE. Relative measurement of the quadrupole moments of the first excited states of the even isotopes of Ru, Pd and Cd. J Phys G Nucl Phys. (1977) 3:1735. doi: 10.1088/0305-4616/3/12/012

CrossRef Full Text | Google Scholar

84. Gloeckner DH. Shell-model systematics of the zirconium and niobium isotopes. Nucl Phys A. (1975) 253:301–23. doi: 10.1016/0375-9474(75)90484-4

CrossRef Full Text | Google Scholar

85. Bodenstein-Dresler L, Chu Y, Gehre D, Gössling C, Heimbold A, Herrmann C, et al. Quenching of g_A deduced from the β-spectrum shape of ¹¹³Cd measured with the COBRA experiment. arXiv:1806.02254 [nucl-ex] (2018).

86. Warburton EK, Garvey GT, Towner IS. Unique second- and third-forbidden β decay. Ann Phys. (1970) 57:174–200. doi: 10.1016/0003-4916(70)90275-7

CrossRef Full Text | Google Scholar

87. Martínez-Pinedo G, Vogel P. Shell model calculation of the β⁻ and β⁺ partial half-lives of ⁵⁴Mn and other unique second forbidden β decays. Phys Rev Lett. (1998) 81:281–4. doi: 10.1103/PhysRevLett.81.281

CrossRef Full Text | Google Scholar

88. Kostensalo J, Suhonen J. Spin-multipole nuclear matrix elements in the pn quasiparticle random-phase approximation: implications for β and ββ half-lives. Phys Rev C. (2017) 95:014322. doi: 10.1103/PhysRevC.95.014322

CrossRef Full Text | Google Scholar

89. ENSDF at NNDC site. Available online at: http://www.nndc.bnl.gov/

90. Barabash AS. Average and recommended half-life values for two neutrino double beta decay. Nucl Phys A (2015) 935:52–64. doi: 10.1016/j.nuclphysa.2015.01.001

CrossRef Full Text | Google Scholar