
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 12 March 2019
Sec. Nuclear Physics
Volume 7 - 2019 | https://doi.org/10.3389/fphy.2019.00025
We study the contribution of the chromo-electric field to the total energy of the hadrons. We analyze the case of quarks considered as extended sources of the field. Specific forms of the interaction potential of the quarks are obtained. Moreover, the color charge distribution of these sources allows to determine the zero-point energy that is commonly introduced, as a free (independent) parameter, in the total quark model Hamiltonian of the hadronic systems. The ground states of charmonium () and nucleon (qqq) are studied in more detail: their mass is calculated within a relativized dynamical model and the expectation value of the chromo-electric field energy is consistently obtained.
According to Quantum Chromo-Dynamics (QCD) the chromo-electric and chromo-magnetic fields, brought by the eight gluons, transmit the interaction among the quarks and contribute to the total energy of the hadrons. Due to the difficulties to solve analytically the QCD field equations, approximate techniques have been developed to study these fields and the energy associated with them.
In the first place, lattice simulations have been developed in order to determine non-perturbatively the chromo-electric and chromo-magnetic fields produced by static quarks [1–4].
At general level, we note that interesting analytical calculations have been carried out within Coulomb Gauge QCD [5, 6].
It is necessary to recall that the spectroscopy of hadronic systems (baryons and mesons) has been also successfully studied by means of various forms of Quark Models (QMs), partially related to QCD, that can be grouped in the following categories: Bag Models (BMs), see for example references [7–11]; Constituent Quark Models (CQMs), see for example, for charmonium and so-called higher quarkonia, referenes [12–31]; for baryons, see for example references [32–46]; Quark Diquark Models (QDMs), see for example references [47–61]. In the BMs the calculation of the chromo-electric and chromo-magnetic fields has been performed taking into account the specific boundary conditions on the surface of the bag [7, 8].
On the other hand, the results for the hadronic spectra given by the CQMs and QDMs are usually obtained directly by means of phenomenological interaction potentials, so that the specific form of the produced fields and the energy associated with them are not studied in detail.
However, the experimental discovery at LHCb, in 2015, of two new hadronic peaks, the and the [62], has stimulated new interest on the theoretical study of the quark interaction, enphasizing the role of the chromo-electric field produced by the quarks.
Even though in the present work we shall not develop directly a specific model for those peaks, it is necessary to summarize here the state of the art of this phenomenology, in particular with respect to the chromo-electric field energy.
In the first place, we recall that those peaks have been interpreted as new resonances given by pentaquark configurations. This interpretation has been developed in the framework of the so-called hadro-quarkonium model, defined more specifically, in this case, as baryo-charmonium model; for an orientation about this model, see references [63–71]. But, in this concern, it is necessary to recall that also other theoretical interpretations have been proposed: in Guo et al. [72, 73], Liu et al. [74], and Mikhasenko [75], it has been suggested that these peaks have a non-resonant nature related to the rescattering of known particles, in the triangle diagram, near kinematical thresholds. We note that, in any case, robust theoretical models should be developed to explain these exotic experimental observations.
With respect to the interest of the present study and considering, for example, the baryo-charmonium model of Ferretti et al. [63], we note that a configuration has been introduced, where q represents a light quark. The (multi-gluon) interaction between the compact, heavy state and the light-quark baryonic qqq field is written in terms of the QCD multipole expansion, retaining only the leading E1 term of the chromo-electric field [64, 65]. The final effective interaction (obtained by means of further approximations) depends on the chromo-electric polarizability and on the chromo-electric field energy of the baryonic state qqq.
We note that, in this model, based on QCD and on effective field theories, the interaction is not written directly at quark level. In particular, an approximated estimation is taken for the chromo-electric field energy.
This situation suggests the possibility of a different calculation, in the framework of the CQM, provided that a sensible definition of the chromo-electric field energy is obtained.
The hadro-quarkonium model has been also used in Ferretti [76], in another context, to study some hadronic resonances that cannot be described accurately by CQMs as standard excitations. Also in this case, a variety of different theoretical interpretations has been proposed, including (as in the pentaquark case discussed above) kinematical effects related to rescattering. A careful discussion of this phenomenology is given in Molina et al. [31], where the mass of these resonances is compared to the results of a fully relativistic Dirac quark model in which the theoretical uncertainties of the predicted masses are also taken into account.
We recall that in the hadro-quarkonium model of Dubynskiy and Voloshin [64] and Ferretti [76], the effective interaction between a compact state and the light-meson state (analogously to the baryo-charmonium case, discussed above) depends on the chromo-electric polarizabilty and on the chromo-electric field energy of the light meson.
We observe that also this physical problem could be studied with a CQM in which the chromo-electric field energy is correctly determined.
For completeness, we finally recall that hidden-charm tetraquark spectroscopy has been also studied in Naeem Anwar et al. [77] by means of a generalized CQM.
As discussed above, in the baryo-charmonium and hadro-charmonium models, the chromo-electric field energy represents a necessary element to perform the complete calculation of the quark effective interaction. We recall that, lattice techniques [2] have been also used to determine the quarkonium chromo-electric polarizability matrix elements.
We can now specify the aim of the present work, that is to study the chromo-electric field energy within the framework of the CQM, defining at the same time a phenomenological quark interaction.
We disregard here the three gluon interaction terms. This approximation is usually made in an implicit way in the CQMs and is discussed in more detail in the BMs [7, 8].
According to another standard approximation, see for example references [8, 65], we also disregard the chromo-magnetic field contributions (smaller than those given by the chromo-electric field), that would give rise to the spin-spin interaction terms, as shown, for example, in DeGrand et al. [7].
Finally, we neglect the electromagnetic interaction between the quarks because it is much smaller than their strong interaction. Furthermore, the theoretical uncertainties related to the quark model formulation are, in any case, bigger than the contributions of the electromagnetic interaction.
As it will discussed in section 2, if point-like quarks were considered as sources of the chromo-eletric field, it would be not possible to obtain a finite result for the energy associated to that field. More precisely, with point-like quarks, the chromo-electric field energy, would be, as such, an infinite, ill-defined, and useless quantity. To avoid this difficulty, the (positive) infinite contributions of the quark self-energy should be “subtracted” and only the negative attractive (pure) Coulombic interaction term would remain. But this conclusion would be in contrast to the widely accepted result shown in Voloshin [65] (and used in the hadro-quarkonium model), in which the chromo-electric field energy is a positive, finite quantity.
Moreover, we note that in many quark models the Coulombic interaction term is often regularized to avoid the short-distance divergence (obtaining an interaction that is not purely Coulombic) and a zero-point energy is added to improve the reproduction of the hadronic spectra.
In the present work we make the hypothesis that these properties of the quark effective interaction can be directly obtained by considering the quarks as extended particles. The extended nature of the constituent quarks has been already proposed for the study of hadronic systems; see, for example, [78].
The quarks represent the sources of the chromo-electric field, with specific color charge distributions and, within that hypothesis, their self-energies are finite and must not be subtracted, so that the total chromo-electric field energy is a positive, well-defined quantity whose general properties will be derived and analyzed in the same section 2. The total chromo-electric field energy developed here is given by the sum of two contributions: the quark finite self-energies and the attractive interaction term between the two quarks. This total energy is substantially different with respect to the electromagnetic interaction of point-like particles: in the case of positronium, the electric field self-energy produced by the electron and positron, would be infinite and, in consequence, is subtracted, leaving no effect on the observable quantities. On the other hand, in the case of nuclei, that are extended objects, the electrostatic repulsion of the protons gives rise to well-known, observable contributions to the rest mass of the nuclei. The analogy with this effect can illustrate the meaning of the finite self-energy introduced in this work.
In the present model, the total chromo-electric field energy is then used as a quantum operator that represents the total potential of the CQM. In this way, we can study the ground states of charmonium ( state) and nucleon (qqq state) that will be examined in sections 3 and 4, respectively. We make the hypothesis that, in the ground states, the confining interaction can be disregarded. This hypothesis should hold better for charmonium than for nucleon. A complete model is necessary to understand completely the hadronic bound state interaction. In the present, preliminar work, with a simple relativistic dynamical model, we reproduce the experimental masses of those ground states and fix, for a given value of the effective coupling constant αs, the dimensional parameter d of the color charge distribution.
In Appendix A we show the formal details of the derivation of the self-energy and of the interaction energy. The quark model developed here is, obviously, not complete: spin-spin effects and, moreover, a confining interaction should be added to study the excited states of the spectra.
Throughout this paper we shall use the word quark to indicate, in a generic way, both a quark and an antiquark. The word antiquark will be used only in specific cases, when strictly necessary. Furthermore, the natural set of units ℏ = c = 1 will be used.
In this section we specify the general formalism of our model. Considering that we work in the framework of the CQM, we disregard, as discussed before, the three gluon interaction that is given by QCD.
The model developed in the following represents an extension of electrostatics, related to U(1) charge symmetry, to a color quark effective interaction, related to SU(3) color symmetry. As a reference for the concepts and metods of electrostatics, we follow a standard textbook [79], unless otherwise stated.
As a first step, we introduce the differential form of the Gauss's low for the chromo-electric field:
In the previous equation the upper index a = 1, …, 8 denotes the eight color components of the field; the lower index i indicates the quark that produces the field. In more detail, represents the chromo-electric field at the spatial point , produced by the i-th quark, located at . At variance with standard formulation of electrostatics, we prefer to write explicitly the dependence on αs that represents the (effective) strong coupling constant. Furthermore, represents the color charge density; this quantity has the dimensions of L−3; finally, we have introduced the color operators, defined by means of the Gell-Mann matrices as . For the following calculations, we also recall some standard expressions for the color operators:
when only the quark i is considered. For two different quarks (i, j) we introduce the color expectation value Gh, in the following way:
where the index h can represent a meson (h = m) or a baryon (h = b). Specifically, for a meson we have:
and for a baryon:
In the previous equations, a meson (m) is represented as a quark and an antiquark in a colorless state, and a baryon (b) as three quarks, also in a colorless state. Note that, in both cases, Gh is negative.
In the static limit, we also take into account the irrotational character of the chromo-electric field:
In this way, with Equations (1–4), we have generalized the standard Maxwell theory of the electrostatic field to the case of a field with an effective SU(3) color symmetry in which the non-abelian contributions have been disregarded. For clarity, we recall that, to recover the expression corresponding to the electromagnetic interaction, one should eliminate the color index a, replace with the adimensional charge ei of the particle, with its sign, and, finally, replace αs with the fine structure constant αem.
We analyze now in more detail some possible forms of the distributions for the color charge density, assuming for brevity, up to Equation (16), that the quark is located at the origin, that is .
For a point-like particle, one would have:
that gives the standard point-like color distribution.
In the case of an extended distribution (that represents the main object of this study), we assume that:
a) the distribution is spherically symmetric;
b) it depends on a parameter d, with the dimensions of L.
In consequence, by introducing the adimensional quantity s = x/d, we can write the charge density as:
being the adimensional color charge distribution. In the present work we shall study in more detail three specific forms of extended (normalized) distributions:
i) The exponential distribution, with
ii) The Gaussian distribution, with
iii) The step-wise (spherical) distribution, with
In order to write the chromo-electric field produced by the color distributions introduced above, we note that the field is always radial (given that spherical distributions are considered); furthermore, we introduce the charge contained in a sphere of radius x:
by using the standard substitution s′ = x′/d, we can write the charge Q(x) by means of a manifestly adimensional expression, in the following way:
In consequence, the chromo-electic field, by means of the Gauss theorem, can be written in the following general form, as:
with
For a point-like distribution, one has:
so that the standard expression for the Coulombic field is recovered.
For the extended distributions one has to integrate Equation (11) with the specific expressions of Equations (7,8,9). The following results for the color charge are obtained.
i) For the exponential distribution, one has:
ii) For the Gaussian distribution, one has:
being and Φ(u) the standard error function.
iii) For the step-wise distribution, one has:
For the calculation of the total chromo-electric field energy we shall follow the standard procedure of electrostatics [79]. Considering the field produced by the quarks i, j, the total energy can be written as the spatial integral of the square of the chromo-electric field at the point :
where the notation < > refers here to the color state ( or qqq) of the system. Wi, j is evidently a non-negative quantity. We have calculated directly total energy Wi, j by using the chromo-electric field expression of Equations (12a, 12b) performing numerically the integration over ; the obtained result, for the extended color charge distributions, is a non-negative, finite function of the interquark distance , being .
However, some manipulations will help to understand the physical meaning of the different contributions and will also speed the quantum calculations of sections 3 and 4. In the first place, expanding Equation (17), we obtain:
The first two terms of Equation (18) give the self-energies of the color charge distributions of the two quarks i, j; this contribution will be denoted in the following as:
The last term of Equation (18) represents the interaction contribution, depending on r, and will be denoted as . Synthetically, we write:
In this work we also assume that the two sources have the same color charge distribution.
In the first place, we discuss the self-energies. Their contribution is divergent in the case of a point-like distribution [79]; the analogous contribution in classical and quantum electrodynamics, in that case, is “subtracted”. On the other hand, for extended distributions, a finite result is obtained. The details of the derivation are shown in Appendix A. Synthetically, we recall here that the self-energy represents the straightforward generalization of the uniformly charged sphere energy (in electrostatics) to the case of a color charge distribution, not necessarily uniform. From Equation (A7), the result can be written in the following general form:
with
In Equation (21a) the factor 4/3, taken from Equation (2), holds for both mesonic and baryonic states. Furthermore, the factor 2 has been highlighted here to recall that the contributions of the distributions of the two quarks are taken; Ŵself is an adimensional constant that depends on the specific form of the distribution. In particular, the calculation gives the following results:
note that the very well-known result (3/5) for the step-wise uniform distribution is obtained.
In the second place, we now consider the interaction energy between the two color charge distributions. To study this contribution we introduce the adimensional relative distance vector between the two quarks: . With standard handlings [79], explicitly shown in Appendix A, the interaction energy obtained in Equation (A13), can be written in the following form:
with the adimensional function
obviously the final result does not depend on the angles of . Note that is a negative function, expressing the attractive character of the chromo-electric interaction, both in mesons and baryons.
The function Û(ξ) is calculated numerically for thedifferent distributions.
We note that for r >> d one recovers the Coulombic form:
For r → 0 one has:
In the first place we discuss the case of a quark and an antiquark in a meson. By using Equation (3b) for Gm, and Equations (21a, 23a), the total chromo-electric field energy takes the form:
This expression, that includes Wself, gives rise, considered as a whole, to a potential that is vanishing at r = 0 and grows up to the constant value Wself as r → ∞. This potential is calculated numerically and compared, for a check, with the direct numerical calculation of Equation (18).
For clarity, in Figure 1 we plot the adimensional factor
for the three distributions. We also show in Figure 2 the ratio X(ξ) = Y(ξ)/(2Ŵself).
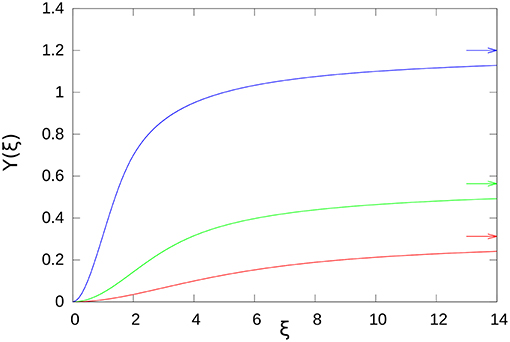
Figure 1. Adimensional interaction functions Y(ξ) for exponential (red), Gaussian (green), and step-wise (blue) distributions. The arrows on the right indicate the corresponding asymptotic values 2Ŵ.
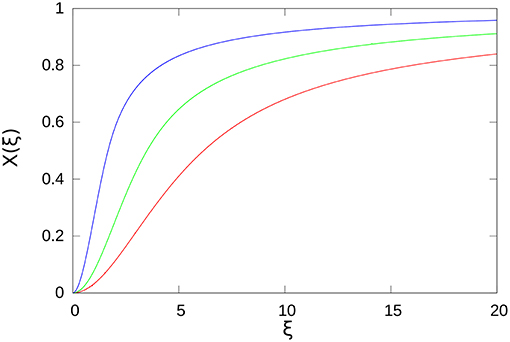
Figure 2. Adimensional ratio functions X(ξ) for the three distributions, plotted with the same colors as in Figure 1.
We now consider a couple of quarks (qq) in a baryon state (qqq). The procedure is similar to the case but using Gb of Equation (3c). To calculate the total chromo-electric energy of the hadron one has to sum up the contributions of the interaction energies of the three couples of quarks and the self-energies of the three quarks. To obtain correctly (i.e., without double counting) that result [see also Equation (33) of section 4], the total chromo-electric energy of one couple of quarks is written as:
Comparing with Equation (26), we find that:
This result is in accordance with general properties of hadronic interactions, as discussed, for example, in Richard [46].
Finally, we highlight that for extended color charge distributions, the chromo-electric field energy, given by Equations (26, 28) is a positive quantity, in accordance with the initial definition, given in Equation (17). The positive (finite) self-energy contributions play a crucial role to obtain this result that, on the other hand, cannot be obtained for a point-like distribution.
In this section we study the charmonium ground state by using the chromo-electric field energy obtained in section 2. More precisely, we consider the chromo-electric energy as a quantum operator function of the quark-antiquark distance operator . We also assume that the chromo-electric field energy represents the main contribution to the potential energy of the ground state of charmonium, disregarding the confining interaction and the chromo-magnetic interaction. Considering this latter approximation, the spin-spin mass splitting between the state ηc, with spin S = 0, and the state J/ψ, with S = 1, is not reproduced by the present calculation. Assuming that this splitting could be calculated apart, perturbatively, by means of a spin-spin interaction of the form:
with the use of the standard Landé formula, one has for the two charmonium states introduced above:
Taking the experimental values of the masses of the two states [80], one obtains the value of the unperturbed mass that will be reproduced in this work, that is .
We consider, in the Center of Mass, a very simple relativized Hamiltonian, of the following form:
We calculate the ground state eigenvalue E0 of this Hamiltonian by means of a variational procedure with a harmonic oscillator basis [22]. Recalling that the interaction potential, of Equation (26), only depends on the parameters αs and d, the condition allows to determine, for a given αs, the corresponding value of d. In the present CQM approch, αs represents a purely phenomenological parameter. For a rough orientation about some possible numerical values, see, for example, references [19, 24, 31]. Here we explore tentatively the interval 0.2 ≤ αs ≤ 1.0 and find the value of the parameter d (of the selected color charge distribution) that gives the fixed value of . Finally, for the quark charm mass, we take the numerical value mq = 1.275 GeV, that represents the QCD current mass value [80]. In any case, the phenomenological values of the quark mass in CQMs do not differ very much form the QCD value.
The results for d as a function of αs are shown in Figure 3. We note that a growing function of αs is obtained. The results for the expectation values of the chromo-electric field energy in charmonium are shown in Figure 4 where we plot the expectation values of W(r), that is < W > = < ψc|W(r)|ψc >, calculated with the ground state charmonium wave function |ψc >. A decreasing function of αs is obtained.
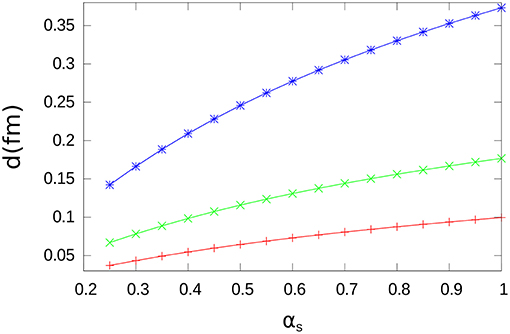
Figure 3. The parameter d is plotted as a function of αs. The results of the numerical calculation are indicated by points, joined by lines for convenience. As before, red, green, and blue refer to exponential, Gaussian, and step-wise distributions, respectively.
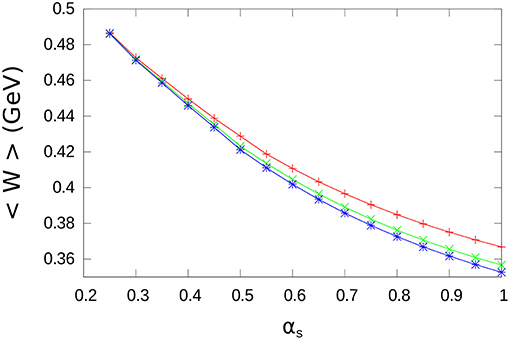
Figure 4. The expectation values of the potential energy W(r) are plotted as a function of αs with the values of d shown in Figure 3. The results of the numerical calculation are indicated by points, joined by lines for convenience. As before, red, blue, and green refer to exponential, Gaussian, and step-wise distributions, respectively.
Finally, we highlight that, for a given value of αs, the results for the chromo-electric energy < W > are not very different for the exponential, Gaussian, and step-wise distributions. The differences increase for growing values of αs. At αs = 1.0, the maximum difference for < W > between the exponential and the step-wise distribution is only 0.014 GeV that represents, in any case, only a small amount with respect to < W >.
In this section we study the ground state energy of the nucleon (qqq) state. Analogously to the charmonium case, we take a relativized Hamiltonian of the form:
In the first (kinetic) term the sum is performed over the three quarks, in the second (interaction) term over the three couples of quarks. The calculation is done in the Center of Mass, that is with the condition
We use the standard Jacobi coordinates ρ, λ and their conjugate momenta . For the nucleon ground state we take a completely symmetric spatial wave function that depends on the hyperradius as defined, for example, in Giannini [40].
As in the case of charmonium, we use a variational procedure, in the harmonic oscillator basis, to calculate the eigenvalue E0. In the Hamiltonian of Equation (33) we have not included any chromo-magnetic term. Due to this approximation, the spin-spin splitting between the N(939) and Δ(1232) is not reproduced. Analogously to the charmonium case, we determine the “unperturbed“ value Mqqq = 1.086 GeV as the three quark ground state mass to be reproduced.
With the same procedure discussed in the charmonium case, for a given value of αs, we determine (for the three extended distributions considered in this work) the value of d that gives Mqqq. We have explored the interval , where represents the minimum value of αs that gives the bound state mass Mqqq. We have also calculated the expectation value of the chromo-electric field energy, that is given by the expression where |ψqqq > represents the (qqq) ground state wave function.
At variance with respect to the charmonium case, the quark mass mq (for the quarks up, down) cannot be fixed unambigously but is generally considered as a model dependent quantity with very different values. The QCD quark mass is mq = 0.0035GeV [80]. On the other hand, in non-relativistic CQMs it was customary to take mq ≃ Mqqq/3; in relativized models smaller values are often considered: for example, in a hyperspherical interaction model [45], the value mq = 0.100GeV was taken; in a quark-diquark interacting model [61], for the quark not belonging to the diquark, the value mq = 0.140GeV has been used. Considering this situation, we have explored here tentatively the range 0.040 GeV ≤ mq ≤ 0.200 GeV.
The results for d as a function of αs are shown in Figures 5, 7 and Figure A1; furthermore, the results for the corresponding values of < W >, are shown in Figures 6, 8 and Figure A2. The specific values of mq = 0.040GeV, mq = 0.120GeV and mq = 0.200GeV have been chosen for these figures.
As in the case of charmonium, d is a growing function of αs, while < W > decreases when αs increases.
We note that for a given distribution and a fixed value of αs, < W > decreases when higher values of mq are taken.
Quite different walues of d are obtained for the three extended color charge distributions; however, the maximum difference for < W > (between the exponential and the step-wise distribution) at αs = 4.5, is only a small fraction of < W >: 0.035GeV, 0.024GeV, 0.014GeV, for mq = 0.040GeV, mq = 0.120GeV and mq = 0.200GeV, respectively.
Finally, we note that the values of αs that give a bound state for the qqq system are higher than the values that give a bound charmonium.
The previous results indicate that our preliminar model for the quark interaction is able to reproduce, in principle, the ground state of the nucleon. To obtain further information, it would be necessary to study the whole spectroscopy of this system and to analyze its electromagnetic form factors. In the case of the nucleon, the confining interaction may be more relevant than in the case of charmonium, so that it is strictly necessary to include it in a complete model for this system.
In this work we have shown that the chromo-electric field energy can be calculated without inconsistencies, in the framework of the CQM, for mesons and baryons, by taking extended (i.e., not point-like) distributions for the color charge sources. In this context, the chromo-electric field energy directly represents the interaction operator for the hadronic interaction in the CQM. This interaction has the very interesting properties of being regular for vanishing interquark distance and of containing (automatically) a zero-point energy contribution.
Starting from the interaction operator studied in this work, a full model should be constructed for the hadronic systems in order to analyze all the resonances of the spectra and, for the nucleon case, the elastic and inelastic electromagnetic form factors.
In the full model, the introduction of confining interaction and the use of a complete vector interaction to reproduce the spin-spin splittings, are mandatory. We have shown that it is possible to reduce the number of free parameters of the quark interaction; in particular we refer to the zero-point energy for which a possible physical interpretation has been given as the self-energy term of the chromo-electric field. The calculation of the chromo-electric field energy can also help to construct more consistent and sound models for the exotic tetraquark and pentaquark configurations.
MD performed all the theoretical calculations, wrote and tested the computer programs, prepared the figures, and wrote the manuscript.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer JF declared a past co-authorship with the author to the handling editor.
1. Baker M, Cea P, Chelnokov V, Cosmai L, Cuteri F, Papa A. The nonperturbative color field in the SU(3) flux tube. arXiv:1810.07133 (2018).
2. Polyakov MV, Schweitzer P. Determination of the J/ψ chromoelectric polarizability from lattice data. Phys Rev. (2018) D98:034030. doi: 10.1103/PhysRevD.98.034030
3. Cea P, Cosmai L, Cuteri F, Papa A. Flux tubes at finite temperature. J High Energ Phys. (2016) 33:1–23. doi: 10.1007/JHEP06(2016)033
4. Okiharu F, Woloshyn RM. A study of colour field distributions in the baryon. Nucl Phys Proc Suppl. (2004) 129:745–7. doi: 10.1016/S0920-5632(03)02700-2
5. Bowman PO, Szczepaniak AP. Chromoelectric flux tubes. Phys Rev. (2004) D70:016002. doi: 10.1103/PhysRevD.70.016002
6. Szczepaniak AP, Krupinski P. Coulomb energy and gluon distribution in the presence of static sources. Phys Rev. (2006) D73:034022. doi: 10.1103/PhysRevD.73.034022
7. DeGrand T, Jaffe RL, Johnson K, Kiskis J. Masses and other parameters of the light hadrons. Phys Rev. (1975) D12:2060–76. doi: 10.1103/PhysRevD.12.2060
8. Haxton WS, Heller L. Heavy-quark-antiquark potential in the MIT bag model. Phys Rev. (1980) D22:1198–208. doi: 10.1103/PhysRevD.22.1198
9. Chodos A, Jaffe RL, Johnson K, Thorn CB, Weisskopf VF. New extended model of hadrons. Phys Rev. (1974) D9:3471–95. doi: 10.1103/PhysRevD.9.3471
10. Chodos A, Jaffe RL, Johnson K, Thorn CB. Baryon structure in the bag theory. Phys Rev. (1974) D10:2599–604. doi: 10.1103/PhysRevD.10.2599
12. Eichten E, Gottfried K, Kinoshita T, Lane KD, Yan TM. Charmonium: the model. Phys Rev. (1978) D17:3090–117. doi: 10.1103/PhysRevD.17.3090
13. Ono S, Törnqvist NA. Continuum mixing and coupled channel effects in and quarkonium. Z Phys. (1984) C23:59–66. doi: 10.1007/BF01558041
14. Heikkila K, Törnqvist NA, Ono S. Heavy and quarkonium states and unitarity effects. Phys Rev. (1984) D29:110–20. doi: 10.1103/PhysRevD.29.110
15. Godfrey S, Isgur N. Mesons in a relativized quark model with chromodynamics. Phys Rev. (1985) D32:189–231. doi: 10.1103/PhysRevD.32.189
16. Eichten EJ, Lane K, Quigg C. Charmonium levels near threshold and the narrow state X(3872) → π+π−J/ψ. Phys Rev. (2004) D69:094019. doi: 10.1103/PhysRevD.69.094019
17. Barnes T, Godfrey S, Swanson ES. Higher charmonia. Phys Rev. (2005) D72:054026. doi: 10.1103/PhysRevD.72.054026
18. Ebert D, Faustov RN, Galkin VO. Masses of heavy tetraquarks in the relativistic quark model. Phys Lett. (2006) B634:214–9. doi: 10.1016/j.physletb.2006.01.026
19. Radford SF, Repko WW. Potential model calculations and predictions for heavy quarkonium. Phys Rev. (2007) D75:074031. doi: 10.1103/PhysRevD.75.074031
20. Pennington MR, Wilson DJ. Decay channels and charmonium mass shifts. Phys Rev. (2007) D76:077502. doi: 10.1103/PhysRevD.76.077502
21. Barnes T, Swanson ES. Hadron loops: General theorems and application to charmonium. Phys Rev. (2008) C77:055206. doi: 10.1103/PhysRevC.77.055206
22. De Sanctis M, Quintero P. Charmonium spectrum with a generalized Fermi-Breit equation. Eur Phys J. (2010) A46:213–22. doi: 10.1140/epja/i2010-11032-y
23. Ferretti J, Galatà G, Santopinto E, Vassallo A. Bottomonium self-energies due to the coupling to the meson-meson continuum. Phys Rev. (2012) C86:015204. doi: 10.1103/PhysRevC.86.015204
24. Ferretti J, Galatà G, Santopinto E. Interpretation of the X(3872) as a charmonium state plus an extra component due to the coupling to the meson-meson continuum. Phys Rev. (2013) C88:015207. doi: 10.1103/PhysRevC.88.015207
25. Brambilla N, Groher M, Martinez HE, Vairo A. Effective string theory and the long-range relativistic corrections to the quark-antiquark potential. Phys Rev. (2014) D90:114032. doi: 10.1103/PhysRevD.90.114032
26. Ferretti J, Galatà G, Santopinto E. Quark structure of the X(3872) and χb(3P) resonances. Phys Rev. (2014) D90:054010. doi: 10.1103/PhysRevD.90.054010
27. Ferretti J, Santopinto E. Higher mass bottomonia. Phys Rev. (2014) D90:094022. doi: 10.1103/PhysRevD.90.094022
28. Lu Y, Naeem Anwar M, Zou BS. Coupled-channel effects for the bottomonium with realistic wave functions. Phys Rev. (2016) D94:034021. doi: 10.1103/PhysRevD.94.034021
29. Lu Y, Naeem Anwar M, Zou BS. How large is the contribution of excited mesons in coupled-channel effects? Phys Rev. (2017) D95:034018.
30. Lu Y, Naeem Anwar M, Zou BS. X(4260) revisited: a coupled channel perspective. Phys Rev. (2017) D96:114022.
31. Molina D, De Sanctis M, Fernández-Ramírez C. Charmonium spectrum with a Dirac potential model in the momentum space. Phys Rev. (2017) D95:094021. doi: 10.1103/PhysRevD.95.094021
32. Isgur N, Karl G. P-wave baryons in the quark model. Phys Rev. (1978) D18:4187–205. doi: 10.1103/PhysRevD.18.4187
33. Isgur N, Karl G. Positive-parity excited baryons in a quark model with hyperfine interactions. Phys Rev. (1979) D19:2653–677. doi: 10.1103/PhysRevD.19.2653
34. Isgur N, Karl G. Ground-state baryons in a quark model with hyperfine interactions. Phys Rev. (1979) D20:1191–4. doi: 10.1103/PhysRevD.20.1191
35. Capstick S, Isgur N. Baryons in a relativized quark model with chromodynamics. Phys Rev. (1986) D34:2809–35. doi: 10.1103/PhysRevD.34.2809
36. Bijker R, Iachello, Leviatan A. Algebraic models of hadron structure. I. Nonstrange baryons. Ann Phys. (1994) 236:69–116. doi: 10.1006/aphy.1994.1108
37. Santopinto E, Iachello F, Giannini MM. Nucleon form factors in a simple three-body quark model. Eur Phys J. (1998) A1:307–16. doi: 10.1007/s100500050065
38. Bijker R, Iachello, Leviatan A. Algebraic models of hadron structure: II. Strange baryons. Ann Phys. (2000) 284: 89–133. doi: 10.1006/aphy.2000.6064
39. Bijker R, Iachello F, Santopinto E. Algebraic treatment of the hyper-Coulomb problem. J Phys. (1998) A31:9041–54. doi: 10.1088/0305-4470/31/45/004
40. Giannini MM, Santopinto E, Vassallo A. Hypercentral constituent quark model and isospin dependence. Eur Phys J. (2001) A12:447–52. doi: 10.1007/s10050-001-8668-y
41. Glozman LY, Riska DO. The Spectrum of the nucleons and the strange hyperons and chiral dynamics. Phys Rept. (1996) 268:263–303. doi: 10.1016/0370-1573(95)00062-3
42. Glozman LY, Plessas W, Varga K, Wagenbrunn RF. Unified description of light- and strange-baryon spectra. Phys Rev. (1998) D58:094030. doi: 10.1103/PhysRevD.58.094030
43. Wagenbrunn RF, Boffi S, Klink W, Plessas W, Radici M. Covariant nucleon electromagnetic form factors from the Goldstone-boson-exchange quark model. Phys Lett. (2001) B511:33–9. doi: 10.1016/S0370-2693(01)00622-0
44. Boffi S, Glozman LY, Klink W, Plessas W, Radici M, Wagenbrunn RF. Covariant electroweak nucleon form factors in a chiral constituent-quark model. Eur Phys J. (2002) A14:17–22. doi: 10.1140/epja/iepja1403
45. De Sanctis M, Giannini MM, Santopinto E, Vassallo A. Electromagnetic form factors and the hypercentral constituent quark model. Phys Rev. (2007) C76:062201(R). doi: 10.1103/PhysRevC.76.062201
46. Richard JM. The nonrelativistic three-body problem for baryons. Phys Rept. (1992) 212:1–76. doi: 10.1016/0370-1573(92)90078-E
47. Ida M, Kobayashi R. Baryon resonances in a quark model. Prog Theor Phys. (1966) 36:846–7. doi: 10.1143/PTP.36.846
48. Lichtenberg DB, Tassie LJ. Baryon mass splitting in a boson-fermion model. Phys Rev. (1967) 155:1601–6. doi: 10.1103/PhysRev.155.1601
49. Anselmino M, Predazzi E, Ekelin S, Fredriksson S, Lichtenberg DB. Diquarks. Rev Mod Phys. (1993) 65:1199–234. doi: 10.1103/RevModPhys.65.1199
51. Wilczek F. Diquarks as inspiration and as objects. In: Shifman M, Vainshtein A, Wheater J, editors. From Fields to Strings, Vol. 1. World Scientific Oxford: Publishing Co. Pte. Ltd. (2005). p. 77–93. doi: 10.1142/9789812775344_0007
52. Selem A, Wilczek F. New trends in HERA physics. In: Grindhammer G, Ochs W, Kniehl BA, Kramer G, editors. Proceedings, Ringberg Workshop. Tegernsee: World Scientific Publishing Co. Pte. Ltd. (2006). p. 337–56.
53. Santopinto E. Interacting quark-diquark model of baryons. Phys Rev. (2005) C72:022201(R). doi: 10.1103/PhysRevC.72.022201
54. Forkel H, Klempt E. Diquark correlations in baryon spectroscopy and holographic QCD. Phys Lett. (2009) B679:77–80. doi: 10.1016/j.physletb.2009.07.008
55. Anisovich AV, Anisovich VV, Matveev MA, Nikonov VA, Sarantsev AV, Vulfs TO. Searching for the quark–diquark systematics of baryons composed by light quarks q = u, d. Int J Mod Phys. (2010) A25:2965–95. doi: 10.1142/S0217751X10049050
56. Anisovich AV, Anisovich VV, Matveev MA, Nikonov VA, Sarantsev AV, Vulfs TO. Quark–diquark systematics of baryons and the SU(6) symmetry for light states. Int J Mod Phys. (2010) A25:3155–71. doi: 10.1142/S0217751X10049177
57. Ferretti J, Vassallo A, Santopinto E. Relativistic quark-diquark model of baryons. Phys Rev. (2011) C83:065204. doi: 10.1103/PhysRevC.83.065204
58. Santopinto E, Ferretti J. Strange and nonstrange baryon spectra in the relativistic interacting quark-diquark model with a Gürsey and Radicati-inspired exchange interaction. Phys Rev. (2015) C92:025202. doi: 10.1103/PhysRevC.92.025202
59. De Sanctis M, Ferretti J, Santopinto E, Vassallo A. Electromagnetic form factors in the relativistic interacting quark-diquark model of baryons. Phys Rev. (2011) C84:055201. doi: 10.1103/PhysRevC.84.055201
60. Galatà G, Santopinto E. Hybrid quark-diquark baryon model. Phys Rev. (2012) C86:045202. doi: 10.1103/PhysRevC.86.045202
61. De Sanctis M, Ferretti J, Santopinto E, Vassallo A. Relativistic quark-diquark model of baryons with a spin-isospin transition interaction: non-strange baryon spectrum and nucleon magnetic moments. Eur Phys J. (2016) A52:121. doi: 10.1140/epja/i2016-16121-3
62. Aaij R, Adeva B, Adinolfi M, Affolder A, Ajaltouni Z, Akar S. Observation of J/ψp Resonances Consistent with Pentaquark States in Decays. Phys Rev Lett. (2015) 115:072001. doi: 10.1103/PhysRevLett.115.072001
63. Ferretti J, Santopinto E, Naem Anwar M, Bedolla MA. The baryo-quarkonium picture for hidden-charm and bottom pentaquarks and LHCb Pc(4380) and Pc(4450) states. arXiv:1807.01207 (2018).
64. Dubynskiy S, Voloshin MB. Hadro-charmonium. Phys Lett. (2008) B666:344–6. doi: 10.1016/j.physletb.2008.07.086
65. Voloshin MB. Charmonium. Prog Part Nucl Phys. (2008) 61:455–511. doi: 10.1016/j.ppnp.2008.02.001
66. Eides MI, Petrov VY, Polyakov MV. Narrow nucleon-ψ(2S) bound state and LHCb pentaquarks. Phys Rev. (2016) D93:054039. doi: 10.1103/PhysRevD.93.054039
67. Eides MI, Petrov VY, Polyakov MV. Pentaquarks with hidden charm as hadroquarkonia. Eur Phys J. (2018) C78:36. doi: 10.1140/epjc/s10052-018-5530-9
68. Perevalova IA, Polyakov MV, Schweitzer P. LHCb pentaquarks as a baryon-ψ(2S) bound state: Prediction of isospin-3/2 pentaquarks with hidden charm. Phys Rev. (2016) D94:054024. doi: 10.1103/PhysRevD.94.054024
69. Alberti M, Bali GS, Collins S, Knechtli F, Moir G, Söldner W. Hadroquarkonium from lattice QCD. Phys Rev. (2017) D95:074501. doi: 10.1103/PhysRevD.95.074501
70. Cleven M, Guo FK, Hanhart C, Wang Q, Zhao Q. Employing spin symmetry to disentangle different models for the XYZ states. Phys Rev. (2015) D92:014005. doi: 10.1103/PhysRevD.92.014005
71. Brambilla N, Krein G, Tarrús Castellà J, Vairo A. Long-range properties of 1S bottomonium states. Phys Rev. (2016) D93:054002 doi: 10.1103/PhysRevD.93.054002
72. Guo FK, Meißner UG, Wang W, Yang Z. How to reveal the exotic nature of the Pc(4450). Phys Rev. (2015) D92:071502(R). doi: 10.1103/PhysRevD.92.071502
73. Guo FK, Meißner UG, Nieves J, Yang Z. Remarks on the Pc structures and triangle singularities. Eur Phys J. (2016) A52:318. doi: 10.1140/epja/i2016-16318-4
74. Liu XH, Wang Q, Zhao Q. Understanding the newly observed heavy pentaquark candidates. Phys Lett. (2016) B757:231–6. doi: 10.1016/j.physletb.2016.03.089
76. Ferretti J. ηc- and J/ψ-isoscalar meson bound states in the hadro-charmonium picture. Phys Lett. (2018) B782:702–6. doi: 10.1016/j.physletb.2018.06.032
77. Naeem Anwar M, Ferretti J, Santopinto E. Spectroscopy of the hidden-charm and tetraquarks. Phys. Rev. D. (2018) 98:094015. doi: 10.1103/PhysRevD.98.094015
78. Semay C, Silvestre-Brac B. Potential models and meson spectra. Nucl Phys. (1997) A618:455–82. doi: 10.1016/S0375-9474(97)00060-2
79. Jackson JD. Classical Electrodynamics, 2nd Edn. New York, NY: John Wiley & Sons (1975). p. 45–9.
80. Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F. Particle data group. Phys Rev. (2018) D98:030001. doi: 10.1103/PhysRevD.98.030001
We derive here the self-energy Wself of the quark distribution and the interaction energy .
Starting from Equation (18), the self-energy of the quark i, is:
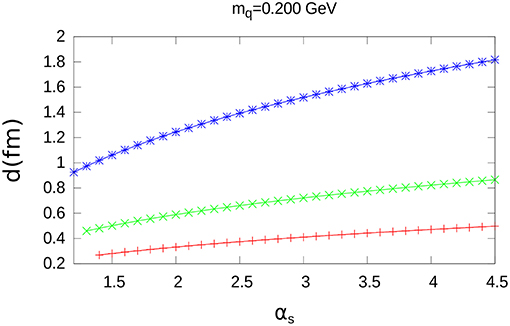
Figure A1. Value of d as a function of αs. The same conventions as in the previous figures are used.
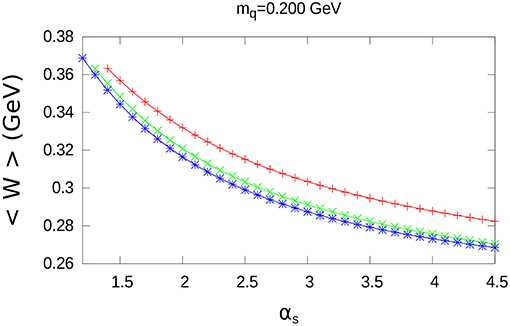
Figure A2. Value of W as a function of αs. The same conventions as in the previous figures are used.
Note that the expression of the first line does not really depend on the position ; in consequence, it has been easily rewritten in the form shown in the second line. We can now express the chromo-electric field by means of Equations (12a,12b) with the charge Q(x) of Equation (10). Also, we make use of Equation (2) for the color operators. In this way, we obtain:
We introduce the following auxiliary functions:
and their derivatives:
where the definition of Q(x) in Equation (10) has been used. With the help of Equations (A3a) and (A4b), we write the self-enery in the form:
We integrate by parts the first term, obtaining
The first term of Equation (A6) represents the result of the calculation, that has been easily performed by using the spherical symmetry of the color charge distribution. The second term of Equation (A6) is vanishing.
At x → ∞, Q(x) → 1, as it can be easily verified in Equations (14), (15) and (16) for the three cases studied in this work. Physically, at infinity, where no free color charges are present, one has only the total color charge of the quark.
At x → 0, for ρ(x) ~ constant, as it is for the three cases of this work, Q(x) ~ x3 and also this contribution is vanishing. If a singular distribution were considered, for example with the behavior ρ(x) ~ x−k, one can find with simple calculations that the condition to obtain a vanishing contribution is: k ≤ 2.
For equal color distributions, one has , so that for a pair of quarks
By means of the adimensional quantities introduced in the text: and substituting s = x/d, the final result of Equations (21a) and (21b) is easily obtained.
The calculation of the interaction energy is performed with standard techniques of electrostatics. Taking into account Equation (4), the chromo-electric field generated by a color charge distribution can be written in the form:
By using the standard equation for the Dirac delta function
one can immediately check that the field of Equation (A8) satisfies the Maxwell Equation (1).
With the expression of the field given by Equation (A8), we write the chromo-electric interaction energy:
where we have used the color expectation value Gh introduced in Equation (3a).
By using the first Green's identity (with the hypothesis of vanishing fields at infinity) and Equation (A9), we obtain:
Then, with the substitutions
one finally has:
By substituting , replacing and using the adimensional color distribution , one obtains the result of Equations (23a) and (23b).
Keywords: quark models, chromo-electric field, quark interactions, charmonium, nucleon
PACS numbers: 12.39.-x, 12.39.Ki, 12.39.Pn, 12.39Jh
Citation: De Sanctis M (2019) Chromo-Electric Field Energy in Quark Models. Front. Phys. 7:25. doi: 10.3389/fphy.2019.00025
Received: 30 November 2018; Accepted: 14 February 2019;
Published: 12 March 2019.
Edited by:
Michele Viviani, Istituto Nazionale di Fisica Nucleare (INFN), ItalyReviewed by:
Andrea Celentano, Istituto Nazionale di Fisica Nucleare (INFN), ItalyCopyright © 2019 De Sanctis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Maurizio De Sanctis, bWRlc2FuY3Rpc0B1bmFsLmVkdS5jbw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.