Local vs. Long-Range Infection in Unidimensional Epidemics

We study the effects of local and distance interactions in the unidimensional contact process (CP). In the model, each site of a lattice is occupied by an individual, which can be healthy or infected. As in the standard CP, each infected individual spreads the disease to one of its first-neighbors with rate λ, and with unitary rate, it becomes healthy. However, in our model, an infected individual can transmit the disease to an individual at a distance ℓ apart. This step mimics a vector-mediated transmission. We observe the host-host interactions do not alter the critical exponents significantly in comparison to a process with only Lévy-type interactions. Our results confirm, numerically, early field-theoretic predictions.

1. Introduction

The contact process (CP) [1] is a stochastic epidemics model with spatial structure [2]. In the CP, each individual inhabits a site on a d−dimensional lattice and can be in one of two states: healthy or infected. Each infected individual transmits the disease to one of its nearest-neighbors with rate λ, or become healthy with a unitary rate. When the transmission rate λ is varied, the system undergoes a phase transition between disease-free and endemic phases.

Apart from its interest as an elementary spatial model of epidemic spreading, the critical behavior of the CP (and its variations) is interesting in the study of non-equilibrium universality classes. The disease-free state is an absorbing state, a frozen state with no fluctuations [3–7]. Non-equilibrium phase transitions into absorbing states have been a topic of much interest in recent decades. In addition to their connection with epidemics, they appear in a wide variety of problems, such as heterogeneous catalysis [8], interface growth [9], population models, and ecology [10]. Recent experimental realizations in the liquid crystal electroconvection [11], driven suspensions [12], and superconducting vortices [13] have heightened interest in absorbing transitions.

It is expected that absorbing state phase transitions in models with a positive unidimensional order parameter, short-range interactions, and without additional symmetries or quenched disorder belong generically to the universality class of directed percolation (DP)[14, 15]. Including long-range interactions in spreading processes can provide more realistic models, instead of short-range models as the original CP, for example, to model spreading of vector-borne diseases [16]. One of the first approaches was the model proposed by Grassberger [17], based on the original idea presented in Mollison [18]. In his model, the infection probability obeys a Lévy flight decaying as a power-law relation 1/r^α+d with the distance r, where d is the spatial dimension of the system and α is a control parameter. Simulational [19, 20] and field-theoretical renormalization group analysis [21] revealed that such anomalous directed percolation presents critical exponents varying continuously with the parameter α.

A generalized version of the unidimensional CP where inactive (healthy) sites can be activated (infected) over long distance was introduced by Ginelli et al. [22, 23], inspired by pinning-depinning transitions in non-equilibrium wetting phenomena. In such model, an active site infects an inactive with rate q/ℓ^α, where q is the coordination number and ℓ is the distance between both sites. Depending on the value of the control parameter α, the contact process with long-range interactions exhibits a rich phase diagram, with distinct universality classes and discontinuous phase transitions [20, 22–24]. The robustness of these discontinuous phase transitions was studied in Fiore and de Oliveira [25]. More recent studies focused on the effects of quenched disorder [26] and diffusion [27]. Inspired by diseases that can spread via host-host in addition to long-distance spreading, in this work, we examine the effects of an additional local infection in the unidimensional CP with Lévy flights.

The remainder of this paper is organized as follows. In section 2 we introduce the model and methods used in our analysis. In section 3 we present our results. Section 4 is devoted to discussion and conclusions.

2. Model and Methods

To begin, we modify the standard contact process to include long distance infection. An infected host, placed at a site i on the lattice, is signed by a state variable σ_i = 1. It infects one of its healthy (signed by σ_j = 0) nearest-neighbors with rate λ_h, or become healthy with rate μ = 1. In addition, the infected host can infect a healthy individual located at some distance, with rate λ_v. Here, λ_v and λ_h are the control parameters that govern the epidemic spreading. Each flight is described by using a Lévy distribution [28], which is characterized by an exponent α. These events are schematically represented in Figure 1. Note that the evolution occurs in two independent steps, one concerning direct host-host infection, and the other, vector-mediated infection, related to the flights.

FIGURE 1

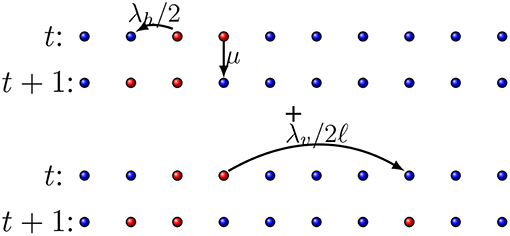
Figure 1. Transition rates for the model. Red circles represent infected and the blue ones represent the healthy individuals. (Top) Local infection (An infected individual transmites the disease to one of its first neighbors with rate λ_h/2, or become healthy with rate μ.). (Bottom) Long-distance infection (An infected individual transmites the disease to another individual with rate λ_v/2ℓ, where ℓ is the distance between the individuals).

This model can be interpreted as a prototypical model for diseases which can spread via vectors which can transmit the pathogen over long distances, and also by direct host-host contact. Since the CP is a spatial lattice model, it is in a core of models used in Ecology to investigate criticality in process determined by the local structure (configuration of trees) [29]. In nature, it is possible to occur long-range infections, as, for example in orchards where flying parasites contaminate the trees almost instantaneously in a widespread manner if the timescale of the flights of the parasites is much shorter than the mesoscopic timescale of the epidemic process itself [30]. We should remark, however that our model is not suitable for modeling the spreading of human diseases such as the Zika virus, which is transmitted by mosquitoes, and by parental or sexual contact [31–33]. The length of intrinsic and extrinsic incubation periods of human vector-mediated diseases can be up to 2 weeks, and it is an essential factor that determines the transmission dynamics. In addition, differently from trees, the human contact network is not a lattice, but instead a complex network, which also affects drastically the epidemic spreading [34–36]. Both factors should be introduced in the model in a future work, if one intends modeling such diseases.

In the simulation scheme, each step is divided in two events: (i) local, where an infected individual infects one of its neighbors (chosen at random) with probability q = λ_h/(1 + λ_h) or it becomes healthy with probability ν = 1/(1 + λ_h); (ii) long-range, where an individual is infected with probability $q^{\prime }={\lambda }_v/(1+{\lambda }_v)$, or nothing happens with probability $v^{\prime }=1/(1+{\lambda }_v)$. To improve efficiency, we maintain a list of infected individuals, and time is updated as Δt = 1/N_inf at each iteration (here N_inf is the number of infected individuals).

The implementation of the vector flies consider a Lévy-distributed random variables. The strategy to obtain such random flies is based on a non-linear transformation of Gaussian random variables [37]. This strategy is based on the following recipe: (i) First, a random variable V distributed homogeneously on (−π/2, π/2) is generated. (ii) Second, an exponential variable W with unity mean is generated. (iii) Finally, we compute the random variable ℓ [38], following

$\begin{array}{rc}\ell =\frac{sin(\alpha V)}{{\left[cos(V)\right]}^{\frac{1}{\alpha }}}{\left\{\frac{cos\left[(1-\alpha )V\right]}{W}\right\}}^{\frac{1-\alpha }{\alpha }},& (1)\end{array}$

where α is a control parameter of the length of the flies (this results in random flies with probability distribution function of length decaying as ℓ^{−(1 + α)}) [38].

We have done dynamical and stationary simulations. The dynamical simulations follow the system stochastic evolution from spreading (where the system is initialized with a “seed”, i.e., only one site is infected at t = 0), and initial decay studies (here the system evolves from a full infected lattice). On the other hand, in the stationary simulations, we are interested in the (long-time) time independent behavior. Stationary analysis nearby the critical point of systems with transitions into absorbing states are hard to be done due to strong finite size effects. This is consequence of that, in conventional simulations, small systems quickly become trapped in the absorbing state (in this case, we can say of a quasistationary state (since the only true stationary state is the absorbing one). In order to circumvent such difficulties, we employ a simulation method that yields quasistationary (QS) properties directly [39, 40]. The method is based in maintaining, and gradually updating, a list of M configurations visited during the evolution; when a transition to the absorbing state is imminent, the system is instead placed in one of the saved configurations. Otherwise, the evolution is exactly that of a conventional simulation. This procedure results in an unbiased sampling of the quasistationary distribution of the process, and improve the statistics.

3. Results and Discussion

In order to analyze the dynamical scaling of the model at criticality, we employed initial decay simulations in a unidimensional lattice of L sites (with periodic boundary conditions). The initial decay studies use an initial configuration with all sites occupied. The order parameter $\rho (t)=\frac{1}{L}\sum {\sigma }_i$ is the density of active sites, i.e., the fraction of infected individuals. At the critical point, one expects to observe a power-law behavior of the density

$\begin{array}{rc}\rho (t)=t^{-\delta },& (2)\end{array}$

until it saturates at its QS value. The larger the system size, the longer the period of power-law decay, and the more precise the resulting estimate for the critical exponent δ. In the initial decay studies, we have used systems with size up to L = 10⁸, and averages are taken over up to 10⁶ runs.

From the spreading simulations, we observe there is a critical value of (λ_h,λ_v) above which the activity survives, while for values below such critical point, the system becomes trapped in the absorbing state. The phase diagram obtained in the λ_h × λ_v plane is plotted in Figure 2. As expected, the absorbing phase is larger when α increases, since small values of α favor the epidemic spreading.

FIGURE 2

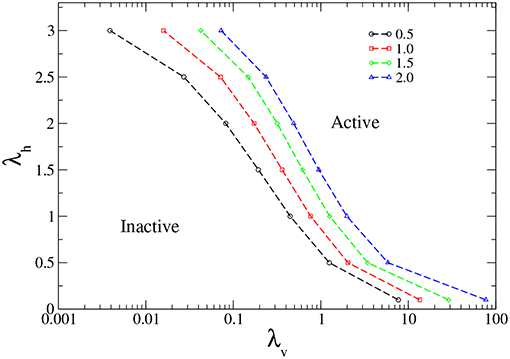
Figure 2. Phase diagram in the λ_v × λ_h plane, showing the inactive and active phases, for α = 0.5, 1.0, 1.5, and 2.0 (from left to right).

In Figure 3, we show the critical decay of the density of active sites, for distinct values of λ_h and α = 1.5. In all cases, we observe a power law decay at criticality. Analysis from the data obtained yields the values of the critical exponent (δ) reported in Table 1. The inset in Figure 3 shows that ρ/t^δ converges to a constant value, therefore confirming the accuracy of the exponents obtained. We note the transient behavior is longer for larger values of λ_h. Also, the increase of λ_h alters only slightly the value of the exponent δ. Figure 4 shows the evolution of the average density of infected sites for distinct values of α. Increasing α, we observe a slower decay, as expected, since in such case, the flights are short-ranged. Increasing α, the results become close to the original CP, with the critical exponent δ converging to the DP value, δ = 0.159, as shown in Table 1.

FIGURE 3

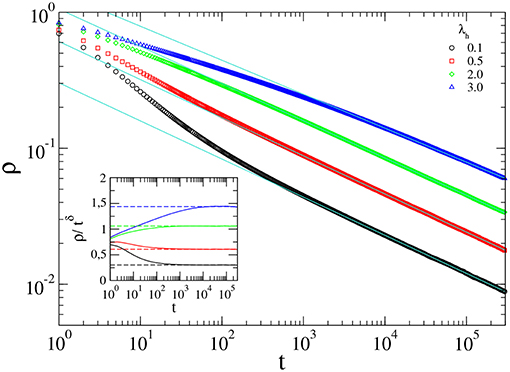
Figure 3. Decay of ρ from an initial configuration with all sites infected for distinct values of λ_h, for α = 1.5. The straight lines are linear regressions from the data. The inset shows that ρ/t^δ converges to constant values in all cases, confirming the accuracy of the regressions.

TABLE 1

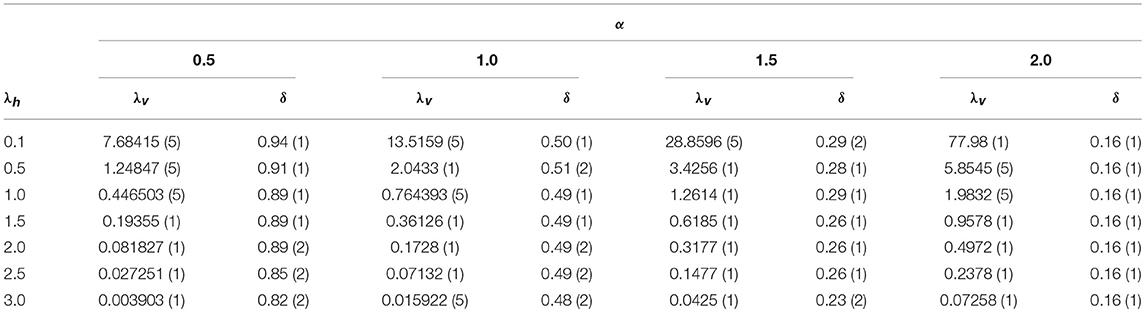
Table 1. Critical values of the control parameter, ${\lambda }_v^{*}$, and critical exponent δ as a function of λ_h for α = 0.5, 1.0, 1.5, and 2.0.

FIGURE 4

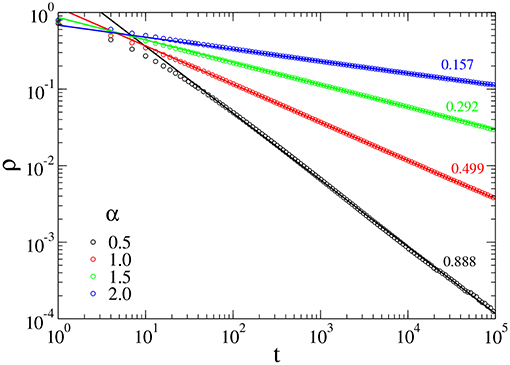
Figure 4. Decay of the density of infected sites ρ from an initial configuration with all sites infected for distinct values of α, with λ_h = 1.0. The straight lines are linear regressions from the data.

From the data in Table 1, we observe that higher values of α recover the DP critical behavior, which presents δ = 0.15947 [3]. On the other hand, decreasing the value of α, the exponent δ approaches the mean-field value δ = 1. The critical exponent δ varies continuously between these limits. We observe that the effects of λ_h are more pronounced for lower values of α, since the exponent δ varies from 0.95 to 0.82 when α = 0.5. We note, however, that α = 0.5 is a crossover point, where the dynamical behavior is often plagued by huge corrections to scaling. Otherwise, for higher values of α the exponent does not alter significantly. Finally, in comparison with the results for the CP with only Lévy-type infection (i.e, with λ_h = 0.0) [19], we observe the non-universal critical exponents are closer the DP values (for the same value of α) when the host-host infection is introduced. For example, in [19] it was found δ = 0.21 for α = 2.0 and δ = 0.94 for α = 0.5, in contrast to δ = 0.16 and δ = 0.82, respectively, in the present work with λ_h = 3.0.

Now, we turn to the static, long-time behavior, represented by the quasi-stationary state. In the QS simulations, we have used system sizes ranging from L = 10² to L = 10⁵. Each simulation ran until t = 10⁸, and averages were taken over 10³ runs. We used a list of size M = 2, 000. At the critical point, the finite-size theory [3] implies the quasistationary order parameter ρ_qs decays with the system size as a power law

$\begin{array}{rc}{\rho }_{qs}~L^{-\beta /{\nu }_{\perp }}.& (3)\end{array}$

In Figure 5, we show the QS density of infected sites (ρ_qs) as a function of the system size L, for α = 1.5. We observe that at criticality, ρ_qs scales as a power law with exponent ratio β/ν_⊥ = 0.45, 0.42, 0.42, 0.43, 0.42, 0.41, and 0.44 for λ_h = 0.1, 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0, respectively. Hence, we can conclude that the exponent β/ν_⊥ is independent of λ_h.

FIGURE 5

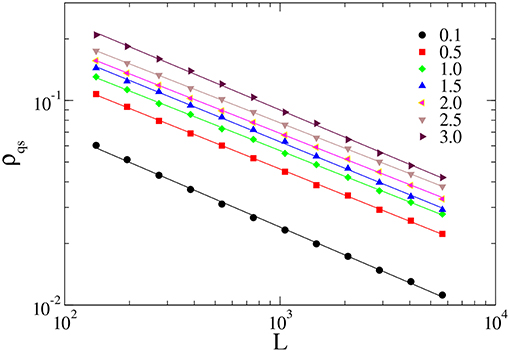
Figure 5. Finite size scaling of the QS density ρ_qs, for α = 1.0 and λ_h = 0.1, 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0.

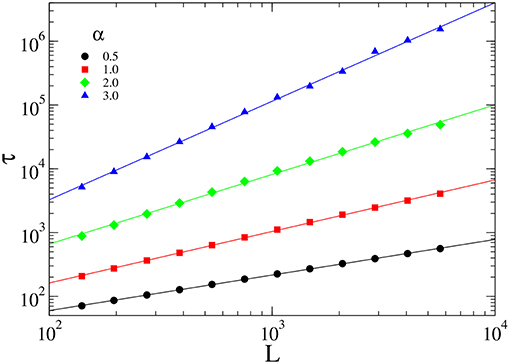
In Figure 6, we evaluate the behavior of the lifetime τ of the QS state at the criticality, which is expected to scale as

$\begin{array}{rc}\tau ~L^z,& (4)\end{array}$

with z = ν_∥/ν_⊥ (here, we evaluate the lifetime as the time between two consecutive visits to the absorbing state). Analysis from the data yields z = 0.84, 0.83, 0.83, 0.80, 0.82, 0.84, and 0.83 for λ_h = 0.1, 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0, respectively. Therefore, this exponent also is not affected by the host-host interaction. Results of the QS simulations for distinct values of α are reported in Table 2. We observe that in all cases the critical exponents obtained from the QS simulations are not significantly affected by the host-host infection.

FIGURE 6

Figure 6. Finite size scaling of the QS lifetime τ_qs, for α = 1.5 and λ_h = 0.5, 1.0, 2.0, and 3.0.

TABLE 2

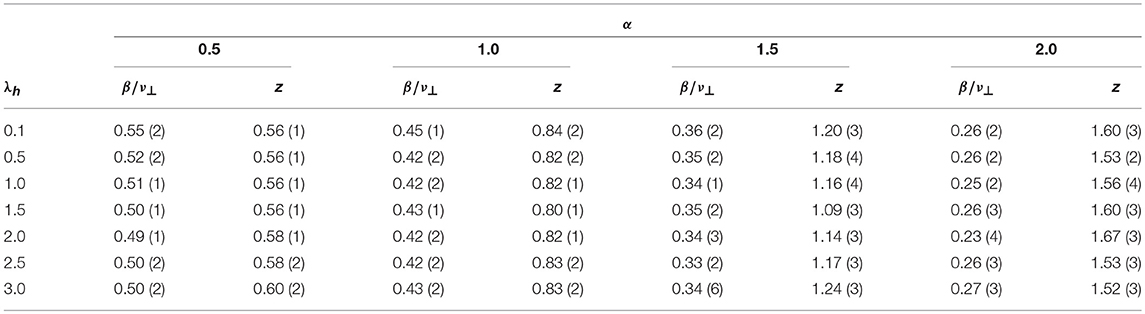
Table 2. Critical values of the control parameter, ${\lambda }_v^{*}$, and critical exponent δ as a function of λ_h for α = 0.5, 1.0, 1.5 and 2.0.

In resume, we conclude that the introduction of a local host-host interaction in epidemics with Lévy-type long-range interactions does not affect the long-time critical behavior. On the other hand, we observe an anomalous spreading observed for the dynamical critical exponent for α = 0.5.

4. Conclusions

We have proposed a variation of the contact process that includes both local (host-host) and long-distance (vector-mediated) interactions. We observe the host-host interactions does not alter the static and dynamical critical exponents significantly in comparison to a process with only Lévy-type interactions. Our results are in agreement with early field-theoretic results [30], which revealed that the relative strength of short-and long-range interactions do not affect the critical behavior. Our results also show an anomalous spreading, with the dynamical exponent varying continuously with the host-host infection rate, when α = 0.5. However, we should remark that at this crossover point, the dynamical behavior is affected by huge corrections to scaling, and we cannot discard that this difference could vanish for sufficient long times (note that the static simulations show the same set of exponents for all values of α). Finally, in the limit in which the host-host infection vanishes, our model reduces to the anomalous contact process proposed in [19], and our results in this limit confirm the critical behavior obtained previously in the literature.

A promising extension of the present work includes the study of the model under the influence of temporal disorder [41, 42], that could, for example, affect only the vector-mediated infection, reflecting seasonal variations [16]. Another critical issue is the effect of local interaction in the robustness of the discontinuous phase transition exhibited by some classes of long-range models [22, 23, 43].

Data Availability

All datasets generated for this study are included in the manuscript and/or the supplementary files.

Author Contributions

SA and MdO conceived the study. PS and SA performed the simulations. PS, SA, and MdO analyzed the data and wrote the paper. All authors reviewed the manuscript.

Funding

This work was partially supported by Brazilian agencies CNPq and FAPEMIG.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Harris TE. Contact interactions on a lattice. Ann Probab. (1974) 2:969. doi: 10.1214/aop/1176996493

CrossRef Full Text | Google Scholar

2. Durrett R. Stochastic spatial models. SIAM Rev. (1994) 41:677. doi: 10.1137/S0036144599354707

CrossRef Full Text | Google Scholar

3. Marro J, Dickman R. Nonequilibrium Phase Transitions in Lattice Models. Cambridge:Cambridge University Press (1999).

Google Scholar

4. Henkel M, Hinrichsen H, Lubeck S. Non-Equilibrium Phase Transitions Volume I: Absorbing Phase Transitions. Dordrecht: Springer-Verlag (2008).

Google Scholar

5. Ódor G. Universality In Nonequilibrium Lattice Systems: Theoretical Foundations. Singapore: World Scientific (2007).

Google Scholar

6. Hinrichsen H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv Phys. (2000) 49:815. doi: 10.1080/00018730050198152

CrossRef Full Text | Google Scholar

7. Ódor G. Universality classes in nonequilibrium lattice systems. Rev Mod Phys (2004) 76:663. doi: 10.1103/RevModPhys.76.663

CrossRef Full Text | Google Scholar

8. Ziff RM, Gulari E, Barshad Y. Kinetic phase transitions in an irreversible surface-reaction model. Phys Rev Lett. (1986) 56:2553.10033028

PubMed Abstract | Google Scholar

9. Tang LH, Leschhorn H. Pinning by directed percolation. Phys Rev A (1992) 45:R8309.

PubMed Abstract | Google Scholar

10. de Oliveira MM, Santos RV, Dickman R. Symbiotic two-species contact process. Phys Rev E (2012) 86:011121. doi: 10.1103/PhysRevE.86.011121

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Takeuchi KA, Kuroda M, Chaté H, Sano M. Directed percolation criticality in turbulent liquid crystals. Phys Rev Lett. (2007) 99:234503. doi: 10.1103/PhysRevLett.99.234503

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Corté L, Chaikin PM, Gollub JP, Pine DJ. Random organization in periodically driven systems. Nat Phys. (2008) 4:420. doi: 10.1038/nphys891

CrossRef Full Text | Google Scholar

13. Okuma S, Tsugawa Y, and Motohashi A. Transition from reversible to irreversible flow: absorbing and depinning transitions in a sheared-vortex system. Phys Rev B (2011) 83:012503. doi: 10.1103/PhysRevB.83.012503

CrossRef Full Text | Google Scholar

14. Janssen HK. On the nonequilibrium phase transition in reaction-diffusion systems with an absorbing stationary state. Z Phys B (1981) 42:151.

Google Scholar

15. Grassberger P. On phase transitions in schlooglś second model. Z Phys B (1982) 47:365.

Google Scholar

16. Botari T, Alves SG, Leonel ED. Explaining the high number of infected people by dengue in Rio de Janeiro in 2008 using a susceptible-infective-recovered model. Phys Rev E (2011) 83:037101. doi: 10.1103/PhysRevE.83.037101

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Grassberger P. “Spreading of epidemic processes leading to fractal structures” In: Fractals in Physics. Pietronero L, Tosatti E editors. Amsterdam: Elsevier (1986).

Google Scholar

18. Mollison D. Spatial contact models for ecological and epidemic spread. J R Stat Soc Ser B Methodol (1977) 39:283.

Google Scholar

19. Hinrichsen H, Howard M. A model for anomalous directed percolation. Eur Phys J B (1999) 7:635.

Google Scholar

20. Hinrichsen H. Non-equilibrium phase transitions with long-range interactions. J Stat Mech Theor Exp. (2007) 2007:P07006. doi: 10.1088/1742-5468/2007/07/P07006

CrossRef Full Text | Google Scholar

21. Janssen HK, Oerding K, van Wijland F, Hilhorst HJ. Lévy-flight spreading of epidemic processes leading to percolating clusters, Eur Phys J B (1999) 7:137. doi: 10.1007/s100510050596

CrossRef Full Text | Google Scholar

22. Ginelli F, Hinrichsen H, Livi R, Mukamel D, Politi A. Directed percolation with long-range interactions: modeling nonequilibrium wetting. Phys Rev E (2005) 71:026121. doi: 10.1103/PhysRevE.71.026121

PubMed Abstract | CrossRef Full Text | Google Scholar

23. FGinelli F, Hinrichsen H, Livi R, Mukamel D, Torcini A. Contact processes with long range interactions. J Stat Mech Theor Exp. (2006) 2006:P08008. doi: 10.1088/1742-5468/2006/08/P08008

CrossRef Full Text | Google Scholar

24. Fiore CE de Oliveira MJ. Contact process with long-range interactions: a study in the ensemble of constant particle number. Phys Rev E (2007) 76:041103. doi: 10.1103/PhysRevE.76.041103

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Fiore CE de Oliveira MJ. Robustness of first order phase transitions in one-dimensional long-range contact processes. Phys Rev E (2013) 87:042101. doi: 10.1103/PhysRevE.87.042101

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Juhász R, Kovács IA, Iglói F. Long-range epidemic spreading in a random environment. Phys Rev E (2015) 91:032815. doi: 10.1103/PhysRevE.91.032815

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Pedro TB, Figueiredo W, Ferreira AL. Mean-field theory for the long-range contact process with diffusion. Phys Rev E (2015) 92:032131. doi: 10.1103/PhysRevE.92.032131

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Montroll EW, West BJ. Fluctuation Phenomena. Montroll EW, Lebowitz JL editors. Amsterdam: North-Holland (1979).

Google Scholar

29. Pascual M, Guichard F. Criticality and disturbance in spatial ecological systems. Trends Ecol Evol. (2005) 20:88. doi: 10.1016/j.tree.2004.11.012

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Janssen H-K, Stenull O. Field theory of directed percolation with long-range spreading. Phys Rev E (2008) 78:061117. doi: 10.1103/PhysRevE.78.061117

PubMed Abstract | CrossRef Full Text | Google Scholar

31. D'Ortenzio E, Matheron S, Yazdanpanah Y, de Lamballerie X, Hubert B, Piorkowski G, et al. Evidence of sexual transmission of zika virus. N Engl J Med. (2016) 374:2195. doi: 10.1056/NEJMc1604449

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Coelho FC, Durovni B, Saraceni V, Lemos C, Codeco CT, Camargo S, et al. Higher incidence of zika in adult women than adult men in rio de janeiro suggests a significant contribution of sexual transmission from men to women. Int J Infect Dis. (2016) 51:128. doi: 10.1016/j.ijid.2016.08.023

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Towers S, Brauer F, Castillo-Chavez C, Falconar AKI, Mubayi A, Romero-Vivas CME. Estimate of the reproduction number of the 2015 zika virus outbreak in Barranquilla, Colombia, and estimation of the relative role of sexual transmission. Epidemics (2016) 17:50. doi: 10.1016/j.epidem.2016.10.003

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Moore C, Newman MEJ. Epidemics and percolation in small-world networks. Phys Rev E (2000) 61:5678. doi: 10.1103/PhysRevE.61.5678

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Parshani R, Carmi S, Havlin S. Epidemic threshold for the susceptible-infectious-susceptible model on random networks. Phys Rev Lett. (2010) 104:258701. doi: 10.1103/PhysRevLett.104.258701

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks, Rev Mod Phys. (2015) 87:925. doi: 10.1103/RevModPhys.87.925

CrossRef Full Text | Google Scholar

37. Janicki A, Weron A. Computer simulation of attractors in stochastic models with α-stable noise. Math Comput Simul. (1995) 39:9. doi: 10.1016/0378-4754(95)00132-H

CrossRef Full Text | Google Scholar

38. Klafter J, Sokolov M. First Steps in Random Walks. New York, NY: Oxford University Press (2011).

Google Scholar

39. de Oliveira MM, Dickman R. How to simulate the quasistationary state. Phys Rev E (2005) 71:016129. doi: 10.1103/PhysRevE.71.016129

CrossRef Full Text | Google Scholar

40. Dickman R, de Oliveira MM. Quasi-stationary simulation: the subcritical contact process. Braz J Phys. (2006) 36:685. doi: 10.1590/S0103-97332006000500020

CrossRef Full Text | Google Scholar

41. de Oliveira MM, Fiore CE. Temporal disorder does not forbid discontinuous absorbing phase transitions in low-dimensional systems. Phys Rev E (2016) 94:052138. doi: 10.1103/PhysRevE.94.052138

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Solano CMD, de Oliveira MM, Fiore CE. Comparing the influence of distinct kinds of temporal disorder in a low-dimensional absorbing transition model. Phys Rev E (2016) 94:042123. doi: 10.1103/PhysRevE.94.042123

PubMed Abstract | CrossRef Full Text | Google Scholar

43. de Oliveira MM, da Luz MGE, Fiore CE. Generic finite size scaling for discontinuous nonequilibrium phase transitions into absorbing states. Phys Rev E (2015) 92:062126. doi: 10.1103/PhysRevE.92.062126

PubMed Abstract | CrossRef Full Text | Google Scholar