A Nonequilibrium-Potential Approach to Competition in Neural Populations

Energy landscapes are a highly useful aid for the understanding of dynamical systems, and a particularly valuable tool for their analysis. For a broad class of rate neural-network models of relevance in neuroscience, we derive a global Lyapunov function which provides an energy landscape without any symmetry constraint. This newly obtained “nonequilibrium potential” (NEP)—the first one obtained for a model of neural circuits—predicts with high accuracy the outcomes of the dynamics in the globally stable cases studied here. Common features of the models in this class are bistability—with implications for working memory and slow neural oscillations—and population bursts, associated with signal detection in neuroscience. Instead, limit cycles are not found for the conditions in which the NEP is defined. Their nonexistence can be proven by resorting to the Bendixson–Dulac theorem, at least when the NEP remains positive and in the (also generic) singular limit of these models. This NEP constitutes a powerful tool to understand average neural network dynamics from a more formal standpoint, and will also be of help in the description of large heterogeneous neural networks.

1. Introduction

The analysis of dissipative, autonomous¹ dynamic flows (especially high-dimensional ones) can be greatly simplified, if a function can be constructed to provide an “energy landscape” to the problem. Note that only in very few cases can a nonlinear dynamical system be analytically solved; for instance, if the system itself is a quadratic form, one can use the Wei–Norman (Lie-algebraic) method to reduce it to a linear one (see e.g., [1]). Energy landscapes not only help visualize the systems' phase space and its structural changes as parameters are varied, but allow predicting the rates of activated processes [2–4]. Some fields that benefit from the energy landscape approach are optimization problems [5], neural networks [6], protein folding [7], cell nets [8], gene regulatory networks [9, 10], ecology [11], and evolution [12].

For continuous-time flows, the possibility of this “Lyapunov function”—with its distinctive property $\stackrel{·}{\Phi }<0$ outside the attractors—was suggested in the context of the general stability problem of dynamical systems [13] and in a sense, it adds a quantitative dimension to the qualitative theory of differential equations. The linearization of the flow around its attractors always provides such a function, but its validity breaks down well inside their own basin. Instead, finding a global Lyapunov function is not an easy problem². If only the information of the (deterministic) dynamical system is to be used, this function can be found for the so-called “gradient flows”—purely irrotational flows in 3D, exact (longitudinal) forms in any dimensionality. But since for general relaxational flows (having nontrivial Helmholtz–Hodge decomposition) the integrability conditions are not automatically met, some more information is needed.

A hint of what information is needed comes from recalling that dynamical systems are models and as such, they leave aside a multitude of degrees of freedom—deemed irrelevant to the model, but nonetheless coupled to the “system.” A useful framework to deal with them is the one set forward by Langevin [15], which makes the dynamical flow into a stochastic process (thus nonautonomous, albeit driven by a stationary “white noise” process).

What Graham and his collaborators [16, 17] realized more than 30 years ago is that even in the deterministic limit, this space enlargement can eventually help meet the integrability conditions. Given an initial state x_i of a (continuous-time, dissipative, autonomous) dynamic flow ẋ = f (x), its conditional probability density function (pdf) P(x, t|x_i, 0) when submitted to a (Gaussian, centered) white noise ξ(t) with variance γ, namely³

$\dot{x}=f(x)+\xi (t)\text{, with }\langle \xi (t)\rangle =0\text{ and }\langle \xi (t)\xi (t^{\prime })\rangle =2\gamma \delta (t-t^{\prime })$

obeys the Fokker–Planck equation (FPE)

$\begin{array}{l}{\partial }_{t}P(x,t|x_i,0)+{\partial }_{x}J(x,t|x_i,0)=0\text{, with }J(x,t|x_i,0)\\ =D^{(1)}(x)P-{\partial }_x\left[D^{(2)}(x)P\right]\end{array}$

in terms of the “drift” D⁽¹⁾ = f (x) and “diffusion” D⁽²⁾ = γ Kramers–Moyal coefficients [18–20]. Being the flow nonautonomous but dissipative, one can expect generically situations of statistical energy balance in which the pdf becomes stationary, ∂_tP_st(x) = 0, thus independent of the initial state. Then by defining $\Phi (x):=-{\displaystyle {\int }_x^{x_0}f(y)dy}$, it is immediate to find $P_{\text{st}}(x)={N}(x_0)exp\left[-\Phi (x)/\gamma \right]$.

For an n–component dynamic flow submitted to m ≤ n (Gaussian, uncorrelated, centered) white noises ξ_i(t) with common variance γ,

$\stackrel{.}{x}=f(x)+\sigma \Xi (t),\langle \Xi (t)\rangle =0,\langle \Xi (t){\Xi }^T(t^{\prime })\rangle =2\gamma I\delta (t-t^{\prime })$

(σ is an n × m constant matrix) the nonequilibrium potential (NEP) has been thus defined [16] as

$\Phi (x)=-\underset{\gamma \to 0}{\lim }\gamma \ln P_{\text{st}}(x;\gamma ).\begin{array}{cc}& (1)\end{array}$

That implies $P_{\text{st}}(\text{x};\gamma )\propto exp\left[-\Phi (\text{x};\gamma )/\gamma \right]+{O}(\gamma )$, which replaced into the stationary n–variable FPE ∇·[f(x)P_st(x) − γQ∇P_st(x)] = 0 (with Q : = σσ^T = Q^T) yields in the $\underset{\gamma \to 0}{lim}$ the equation

$f^{\text{T}}(x)\nabla \Phi +{\left(\nabla \Phi \right)}^{\text{T}}Q\nabla \Phi =0,\begin{array}{cc}& (2)\end{array}$

from which Φ(x) can in principle be found. In an attractor's basin, asymptotic stability imposes D : = det Q > 0. In fact, for m = n (restriction adopted hereafter) it is D = (det σ)², which in turn requires σ to be nonsingular. Using Equation (2),

$\dot{\Phi }={\stackrel{.}{x}}^{\text{T}}\nabla \Phi =f^{\text{T}}(x)\nabla \Phi =-{\left(\nabla \Phi \right)}^{\text{T}}Q\nabla \Phi <0$

for γ → 0. Hence, Φ(x) is a Lyapunov function for the deterministic dynamics.

Equation (2) has the structure of a Hamilton–Jacobi equation. This trouble can be circumvented if we can decompose f(x) = d(x) + r(x), with d(x) : = −Q∇Φ the dissipative part of f(x)⁴. Then Equation (2) reads r^T(x)∇Φ = 0, and r(x) is the conservative part of f(x). Note that d(x) is still irrotational (in the sense of the Helmholtz decomposition) but is not an exact form (the Hodge decomposition is made in the enlarged space).

For n = 2 we may write r(x) = κ Ω∇Φ, with Ω the N = 1 symplectic matrix. Hence f(x) = −(Q − κΩ)∇Φ, with det(Q − κΩ) = D + κ² > 0, and thus

$\nabla \Phi =-{(Q-\kappa \Omega )}^{-1}f(x).\begin{array}{cc}& (3)\end{array}$

For arbitrary real σ_ij we can parameterize

$\sigma =\left(\begin{array}{cc}\sqrt{{\lambda }_1}\cos {\alpha }_1& \sqrt{{\lambda }_1}\sin {\alpha }_1\\ \sqrt{{\lambda }_2}\cos {\alpha }_2& \sqrt{{\lambda }_2}\sin {\alpha }_2\end{array}\right)$

and define $\lambda :=\sqrt{{\lambda }_1{\lambda }_2}cos({\alpha }_1-{\alpha }_2)$ (note that the condition D > 0 imposes α₂ ≠ α₁). Then

$Q-\kappa \Omega =\left(\begin{array}{cc}{\lambda }_1& \lambda -\kappa \\ \lambda +\kappa & {\lambda }_2\end{array}\right),$

and Equation (3) reads

$\nabla \Phi :=\left(\begin{array}{c}{\partial }_1\Phi \\ {\partial }_2\Phi \end{array}\right)=-\frac{1}{\det (Q-\kappa \Omega )}\left(\begin{array}{c}{\lambda }_2{f}_1(x)-(\lambda -\kappa )f_2(x)\\ -(\lambda +\kappa )f_1(x)+{\lambda }_1{f}_2(x)\end{array}\right)$

(∂_k is a shorthand for ∂/∂x_k). If a set {λ₁, λ₂, λ, κ} can be found such that Φ(x) fulfills the integrability condition ∂₂∂₁Φ = ∂₁∂₂Φ, then a NEP exists. Early successful examples are the complex Ginzburg–Landau equation (CGLE) [21, 22] and the FitzHugh–Nagumo (FHN) model [23, 24]⁵. This scheme has been later reformulated [29], extended [30], and exploited in many interesting cases [6–12].

The goal of this work is to show that a NEP exists for a broad class of rate models of neural networks, of the type proposed by Wilson and Cowan [31]. The Wilson–Cowan model has been used to model many different dynamics, brain areas, and neural-network structures in the brain. Therefore, the derivation of a NEP has potential implications for many problems in computational neuroscience. Section 2 is devoted to an analysis of the model and variations of section 3, to the derivation of the NEP in some of the cases studied in section 2, which are of high relevance in neuroscience. Section 4 undertakes a thorough discussion of our findings, and section 5 collects our conclusions.

2. The Wilson–Cowan Model

Elucidating the architecture and dynamics of the neocortex is of utmost importance in neuroscience. But despite ongoing titanic efforts like the Human Brain Project or the BRAIN initiative, we are still very far from that goal. Given that the dynamics of single typical neurons has been relatively well described (in some cases even by analytical means), a fundamental approach can be practiced for small neural circuits. This means describing them as networks of excitable elements (neurons) connected by links (synapses), and solving the network dynamics by hybrid (analytical-numerical) techniques. However, the time employed in the analytical solution has poor scaling with size. Hence, this approach becomes unworkable for more than a few recurrently interconnected neurons, and one has to rely only on numerical simulations.

Fortunately—as evidenced since long ago by the existence (as in a medium) of wavelike excitations—the huge connectivity of the neocortex enables coarse-grained or mean-field descriptions, which provide more concise and relevant information to understand the mesoscopic dynamics of the system⁶. Frequently obtained via mean-field techniques and commonly referred to as rate models or neural mass models, coarse-grained reductions have been widely used in the theoretical study of neural systems [31, 33–35]. In particular, the one proposed by Wilson and Cowan [31] has proved to be very useful in describing the macroscopic dynamics of neural circuits. This level of description is able to capture many of the dynamical features associated with several cognitive and behavioral phenomena, such as working memory [33, 36] or perceptual decision making [35, 37]. It is also possible to use a rate model approach to study the dynamics of networks constituted by heterogeneous neurons [38, 39], thus recovering part of the complexity lost in the averaging. Disposing of an “energy function” (not restricted to symmetric couplings) for rate-level dynamics of neural networks would be a major added advantage.

The Wilson–Cowan model describes the evolution of competing populations x₁, x₂ of excitatory and inhibitory neurons, respectively. The model is defined by [31]

$\begin{array}{rc}{\tau }_1{ẋ}_1=-x_1+({\nu }_1-r_1{x}_1)s_1(i_1),{\tau }_2{ẋ}_2=-x_2+({\nu }_2-r_2{x}_2)s_2(i_2),& (4)\end{array}$

where x₁ and x₂ represent the coarse-grained activity of an excitatory and an inhibitory neural population, respectively, and the monotonically increasing (sigmoidal) response functions

$\begin{array}{rc}{s}_k(i_k):=\frac{1}{1+exp\left[-{\beta }_k(i_k-i_k^0)\right]}-\frac{1}{1+exp({\beta }_k{i}_k^0)}& (5)\end{array}$

are such that s_k(0) = 0, and range from $-{\left[1+exp({\beta }_k{i}_k^0)\right]}^{-1}$ for i_k → −∞ to $1-{\left[1+exp({\beta }_k{i}_k^0)\right]}^{-1}$ for i_k → ∞. So the first crucial observation about the model is that it is asymptotically linear.

The currents i_k are in turn linearly related to the x_k:

$\text{i}(\text{x}):=J\text{x}+\text{M}=\left(\begin{array}{cc}{j}_{11}& -j_{12}\\ j_{21}& -j_{22}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)+\left(\begin{array}{c}{\mu }_1\\ {\mu }_2\end{array}\right).$

All the parameters are real and moreover, the j_kl are positive (j₁₁ and j₂₂ are recurrent interactions, j₁₂ and j₂₁ are cross-population interactions). The above definitions are such that for M = 0, x = 0 is a stable fixed point. To avoid confusions in the following, note that det J = −(j₁₁j₂₂ − j₁₂j₂₁).

Wilson and Cowan [31] found interesting features as e.g., staircases of bistable regimes and limit cycles. A thorough analysis of the model's bifurcation structure has been undertaken in Borisyuk and Kirillov [40]. The authors create a two-parameter structural portrait by fixing all the parameters but μ₁ and j₂₁ and find that the μ₁−j₂₁ plane turns out to be partitioned into several regions by:

• a fold point bifurcation curve (the number of fixed points changes by two when crossed),

• an Andronov–Hopf bifurcation curve (separates regions with stable and unstable foci),

• a saddle separatrix loop (a limit cycle on one side, none on the other), and

• a double limit cycle curve (the number of limit cycles changes by two).

The uncoupled case (j₁₂ = j₂₁ = 0) is clearly a gradient system, with potential

$\begin{array}{l}\Phi (x)=\frac{1}{{\tau }_1}\left\{\frac{x_1^2}{2}-\frac{1}{j_{11}}\left[F_1(i_1)-F_1({\mu }_1)\right]\right\}\\ +\frac{1}{{\tau }_2}\left\{\frac{x_2^2}{2}-\frac{1}{j_{22}}\left[F_2(i_2)-F_2({\mu }_2)\right]\right\},\end{array}$

where i₁ = j₁₁x₁ + μ₁ and i₂ = −j₂₂x₂ + μ₂. Functions F_k differ only in the values of their parameters. Their functional expression, involving polylogs, is uninteresting besides being complicated. Much more insight is obtained by observing the global features:

• for i_k → −∞, Equation (4) become ${\tau }_k{ẋ}_k=-x_k-({\nu }_k-r_k{x}_k){\left[1+exp({\beta }_k{i}_k^0)\right]}^{-1}$,

• for i_k → ∞, ${\tau }_k{ẋ}_k=-x_k+({\nu }_k-r_k{x}_k)(1-{\left[1+exp({\beta }_k{i}_k^0)\right]}^{-1})$.

So it seems interesting to look at them in the limit β_k → ∞ (k = 1, 2),

$\begin{array}{lll}{\tau }_1{ẋ}_1& =& -x_1+({\nu }_1-r_1{x}_1)\theta (i_1-i_1^0),\\ {\tau }_2{ẋ}_2& =& -x_2+({\nu }_2-r_2{x}_2)\theta (i_2-i_2^0),\end{array}$

θ(x) being Heaviside's unit step function. Unfortunately, neither Equation (4) nor their singular limit fulfill the above mentioned integrability condition.

In practice however, the names of Wilson and Cowan are associated to the broader class of rate models. In the following we shall show that the model defined by

$\begin{array}{rc}{\tau }_1{ẋ}_1=-x_1+s_1(i_1),{\tau }_2{ẋ}_2=-x_2+s_2(i_2)& (6)\end{array}$

does admit a NEP—for any functional forms of the nonlinear single-variable functions s_k(i_k)⁷—provided global stability is assured.

3. Nonequilibrium Potential

For the model defined by Equation (6), it is $\text{f}(\text{x})=\left(\begin{array}{c}\frac{1}{{\tau }_1}\left[-x_1+s_1(i_1)\right]\\ \frac{1}{{\tau }_2}\left[-x_2+s_2(i_2)\right]\end{array}\right)$. The condition ∂₂∂₁Φ = ∂₁∂₂Φ, namely

$\begin{array}{l}\frac{{\lambda }_2}{{\tau }_1}\left[-j_{12}{s}_1^{\prime }(i_1)\right]-\frac{\lambda -\kappa }{{\tau }_2}\left[-1-j_{22}{s}_2^{\prime }(i_2)\right]\\ =-\frac{\lambda +\kappa }{{\tau }_1}\left[-1+j_{11}{s}_1^{\prime }(i_1)\right]+\frac{{\lambda }_1}{{\tau }_2}\left[j_{21}{s}_2^{\prime }(i_2)\right],\end{array}$

boils down to

$j_{12}{\lambda }_2=j_{11}(\lambda +\kappa ),j_{22}(\lambda -\kappa )=j_{21}{\lambda }_1,\frac{\lambda -\kappa }{{\tau }_2}=\frac{\lambda +\kappa }{{\tau }_1}$

(and these in turn to j₂₁ j₁₁ τ₁ λ₁ = j₁₂ j₂₂ τ₂ λ₂) so that λ₂, λ and κ can be expressed in terms of λ₁, which sets the global scale of Φ(x):

${\lambda }_2=\frac{j_{21}}{j_{22}}\frac{j_{11}}{j_{12}}\frac{{\tau }_1}{{\tau }_2}{\lambda }_1,\lambda =\frac{j_{21}}{j_{22}}\frac{{\tau }_1+{\tau }_2}{2{\tau }_2}{\lambda }_1,\kappa =\frac{j_{21}}{j_{22}}\frac{{\tau }_1-{\tau }_2}{2{\tau }_2}{\lambda }_1.$

Since r(x) = κ Ω∇Φ, τ₁ = τ₂ suffices to render the flow purely dissipative (albeit not gradient). From this, a good choice is ${\lambda }_1:=\frac{j_{22}}{j_{21}}{\tau }_2\rho$. In summary,

$Q-\kappa \Omega =\rho \left(\begin{array}{cc}\frac{j_{22}}{j_{21}}{\tau }_2& {\tau }_2\\ {\tau }_1& \frac{j_{11}}{j_{12}}{\tau }_1\end{array}\right),det(Q-\kappa \Omega )=-\frac{{\rho }^2{\tau }_1{\tau }_2}{j_{12}{j}_{21}}detJ,$

and Equation (3) becomes

$\begin{array}{rc}\nabla \Phi =\frac{j_{12}{j}_{21}}{\rho {\tau }_1{\tau }_{2}detJ}\left(\begin{array}{c}\frac{j_{11}}{j_{12}}\left[-x_1+s_1(i_1)\right]-\left[-x_2+s_2(i_2)\right]\\ -\left[-x_1+s_1(i_1)\right]+\frac{j_{22}}{j_{21}}\left[-x_2+s_2(i_2)\right]\end{array}\right).& (7)\end{array}$

Integrating Equation (7) over any path from x = 0, yields

$\begin{array}{l}\Phi (x)=-\frac{j_{11}{j}_{21}{x}_1^2-2j_{12}{j}_{21}{x}_1{x}_2+j_{12}{j}_{22}{x}_2^2}{2\rho {\tau }_1{\tau }_2\det J}\\ +\frac{j_{21}\left[S_1(i_1)-S_1({\mu }_1)\right]-j_{12}\left[S_2(i_2)-S_2({\mu }_2)\right]}{\rho {\tau }_1{\tau }_2\det J}.& (8)\end{array}$

4. Theoretical Analysis

The first—crucial—observation is that being s_k(i_k) sigmoidal functions, Equation (8) is at most quadratic. Global stability thus imposes detJ < 0, i.e., j₁₁j₂₂ > j₁₂j₂₁. But note that matrix J also determines the paraboloid's cross section⁸.

If the form $x^{T}Ax,A=\left(\begin{array}{cc}{j}_{11}{j}_{21}& -j_{12}{j}_{21}\\ -j_{12}{j}_{21}& j_{12}{j}_{22}\end{array}\right)$ in the first term of Equation (8) could be straightforwardly factored out, then one could tell what its section is by watching whether the factors are real or complex. A more systematic approach is to reduce x^TAx to canonical form by a similarity transformation that involves the normalized eigenvectors of A. Then the inverse squared lengths of the principal axes are the eigenvalues ${\lambda }_{1,2}=\frac{1}{2}(j_{11}{j}_{21}+j_{12}{j}_{22})\pm \sqrt{\frac{1}{4}{(j_{11}{j}_{21}+j_{12}{j}_{22})}^2+j_{12}{j}_{21}detJ}$ of A. Since the j_kl are positive and detJ < 0, the second term is lesser than the first and the cross section is definitely elliptic. Although global stability rules out detJ > 0, we can conclude that the instability proceeds through a pitchfork (codimension one) bifurcation along the minor principal axis (because of the double role of detJ), not a Hopf (codimension two) one.

For the remaining terms, we note that Equation (7) can be written as $\nabla \Phi =\frac{1}{\rho {\tau }_1{\tau }_{2}detJ}\left(\begin{array}{cc}{j}_{21}& 0\\ 0& -j_{12}\end{array}\right)J(\text{x}-\text{s})$and recall that s_k(i_k) have sigmoidal shape. So at large |x|, the component $-\frac{1}{\rho {\tau }_1{\tau }_{2}detJ}\left(\begin{array}{cc}{j}_{21}& 0\\ 0& -j_{12}\end{array}\right)J\text{s}$ will tend to different constants—according to the signs of i_k—so the asymptotic contribution of these terms will be piecewise linear, namely a collection of half planes.

The reduction to the uncoupled case can be safely done by writing j₁₂ = ϵ and j₂₁ = αϵ:

$\begin{array}{l}\Phi (x)=\frac{j_{11}\alpha ϵx_1^2-2\alpha {ϵ}^2{x}_1{x}_2+j_{22}ϵx_2^2}{2\rho {\tau }_1{\tau }_2(j_{11}{j}_{22}-\alpha {ϵ}^2)}\\ -\frac{\alpha ϵ\left[S_1(i_1)-S_1({\mu }_1)\right]-ϵ\left[S_2(i_2)-S_2({\mu }_2)\right]}{\rho {\tau }_1{\tau }_2(j_{11}{j}_{22}-\alpha {ϵ}^2)}.\end{array}$

To first order as ϵ → 0, one retrieves

$\begin{array}{l}\Phi (x)\approx \frac{ϵ}{\rho {\tau }_1{j}_{11}}\{\frac{\alpha j_{11}}{{\tau }_2{j}_{22}}\left[\frac{x_1^2}{2}-\frac{1}{j_{11}}\left[S_1(i_1)-S_1({\mu }_1)\right]\right]\\ +\frac{1}{{\tau }_2}\left[\frac{x_2^2}{2}-\frac{1}{j_{21}}\left[S_2(i_2)-S_2({\mu }_2)\right]\right]\},\end{array}$

so by choosing $\alpha =\frac{{\tau }_2{j}_{22}}{{\tau }_1{j}_{11}}$ and $\rho =\frac{ϵ}{{\tau }_1{j}_{11}}$,

$\begin{array}{l}\Phi (x)\approx \frac{1}{{\tau }_1}\left\{\frac{x_1^2}{2}-\frac{1}{j_{11}}\left[S_1(i_1)-S_1({\mu }_1)\right]\right\}\\ +\frac{1}{{\tau }_2}\left\{\frac{x_2^2}{2}-\frac{1}{j_{21}}\left[S_2(i_2)-S_2({\mu }_2)\right]\right\}.\end{array}$

A popular choice—that can be cast in the form of Equation (5)—is $s_k(i_k):=\frac{{\nu }_k}{2}(1+tanh{\beta }_k{i}_k)$, β_k > 0, for which⁹

$\begin{array}{rc}{S}_k(i_k)-S_k({\mu }_k)=\frac{{\nu }_k}{2}\left[i_k-{\mu }_k+{\beta }_k^{-1}ln\frac{cosh{\beta }_k{i}_k}{cosh{\beta }_k{\mu }_k}\right].& (9)\end{array}$

Its β_k → ∞ limit, ν_kθ(i_k) with

$\begin{array}{rc}{S}_k(i_k)-S_k({\mu }_k)={\nu }_k\left[i_k\theta (i_k)-{\mu }_k\theta ({\mu }_k)\right],& (10)\end{array}$

highlights the cores of the response functions while keeping the global landscape¹⁰.

As a check of Equation (8), we show in the next subsections the mechanism whereby Equation (6) can sustain bistability.

4.1. Analytically, for Steplike Response Function s_k(i_k): = ν_kθ(i_k)

• For μ_k < 0 (k = 1, 2), there is no question that x = 0 is a fixed point (we may call it the “off” node); Equation (8) reduces to its first term and Φ(0) = 0.

• By suitably choosing the half planes—taking advantage of the relative sign in the numerator of the second term in Equation (8)—another fixed point $\text{N}:={({\nu }_1,{\nu }_2)}^T$ (the “on” node) can be induced¹¹ if (JN)_k > −μ_k, k = 1, 2 (namely j₁₁ν₁−j₁₂ν₂ > −μ₁, j₂₁ν₁ − j₂₂ν₂ > − μ₂) with

$\Phi (\text{N})=\frac{j_{11}{j}_{21}{\nu }_1^2-2j_{12}{j}_{21}{\nu }_1{\nu }_2+j_{12}{j}_{22}{\nu }_2^2}{2\rho {\tau }_1{\tau }_2\det J}+\frac{j_{21}{\nu }_1{\mu }_1-j_{12}{\nu }_2{\mu }_2}{\rho {\tau }_1{\tau }_2\det J}.$

If μ₁ is varied (as in [31, 40]), equistability is achieved for

${\mu }_1=\frac{1}{2}\left[\frac{j_{12}{\nu }_2}{j_{21}{\nu }_1}(j_{21}{\nu }_1-j_{22}{\nu }_2+2{\mu }_2)-(j_{11}{\nu }_1-j_{12}{\nu }_2)\right].\begin{array}{cc}& (11)\end{array}$

The intersection of the cores of the s_k(i_k)¹² is a (singular in this limit) saddle point. Figure 1B illustrates this situation for the parameters quoted in the caption (the choice obeys to the fact that global stability makes condition j₂₁ν₁ −j₂₂ ν₂ > −μ₂ rather stringent).

• As μ_k → 0, k = 1, 2, this saddle point moves toward the “off” node. After a (direct) saddle-node bifurcation, only the “on” node at x_k = ν_k remains, since conditions (JN)_k > −μ_k, k = 1, 2 are better satisfied, see Figure 1A.

FIGURE 1

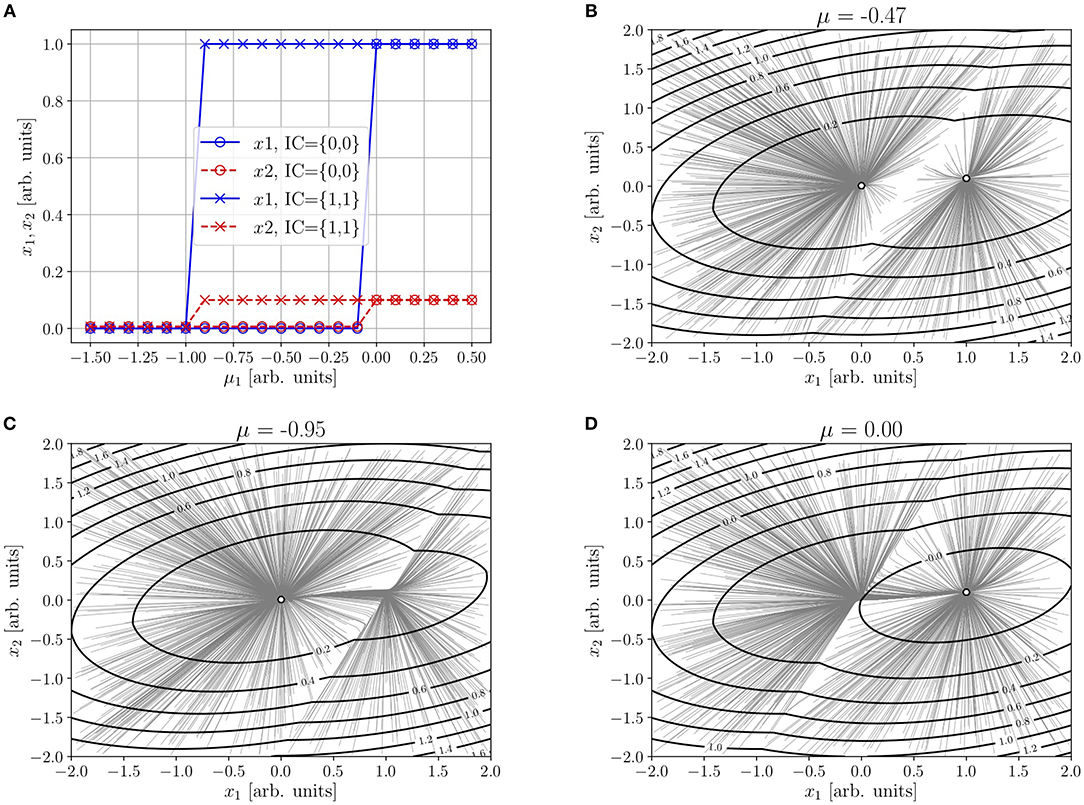
Figure 1. Illustration of the analytical results in section 4.1, for ρ = 1, τ₁ = τ₂ = 1, μ₂ = −0.01, ν₁ = 1, ν₂ = 0.1, j₁₁ = 1, j₂₂ = 0.5, j₁₂ = 0.5, j₂₁ = 0.1. (A) Abscissas (solid line) and ordinates (dashed line) of the “off” (circle) and “on” (cross) nodes of Equation (6) with s_k(i_k): = ν_kθ(i_k), as functions of μ₁. Trajectories from random initial conditions and contour plot of the NEP—Equation (8), with S_k(i_k)−S_k(μ_k) given by Equation (10)—in the equistable case given by Equation (11) (B), and near the “off” (C) and “on” (D) saddle-node bifurcations.

If there is room for some spreading of the core, as seen in Figures 1B–D, the former result remains valid for whatever analytical form of the response functions. In such a case, the saddle point will be analytical.

In the singular limit s_k(i_k) : = ν_kθ(i_k) we deal with in this subsection, we can prove rigorously the nonexistence of limit cycles (at least for large μ_k < 0, k = 1, 2). The Bendixson–Dulac theorem states that if there exists a ${{C}}^1$ function Φ(x) (called the Dulac function) such that div(Φf) has the same sign almost everywhere¹³ in a simply connected region of the plane, then the plane autonomous system $\stackrel{·}{\text{x}}=\text{f}(\text{x})$ has no nonconstant periodic solutions lying entirely within the region. Because of Equation (2),

$\text{div}(\Phi \text{f})={\text{f}}^{\text{T}}(\text{x})\nabla \Phi +\Phi \text{div}\text{f}=-{(\nabla \Phi )}^{\text{T}}Q\nabla \Phi +\Phi \text{div}\text{f}.$

Clearly, divf < 0 almost everywhere [i.e., except at the cores of the s_k(i_k)]. For μ_k < 0 (k = 1, 2) and large, Φ(x) will be essentially the quadratic form in the first term of Equation (8), so it meets the conditions to be a Dulac function in a simply connected region of the plane.

4.2. Numerically, For a (More) Realistic Example

For the integrable version (r₁ = r₂ = 0) of Equations (4)–(5), it is

$\begin{array}{l}{S}_k(i_k)-S_k({\mu }_k)={\nu }_k[(i_k-{\mu }_k)\frac{\exp [{\beta }_k{i}_k^0]}{1+\exp [{\beta }_k{i}_k^0]}\\ +{\beta }_k^{-1}\ln \frac{1+\exp [-{\beta }_k(i_k-i_k^0)]}{1+\exp [-{\beta }_k({\mu }_k-i_k^0)]}]& (12)\end{array}$

(recall that μ = i(x = 0)). Here, because of the condition s_k(0) = 0, the “off” node will move as μ₁ is varied. Figure 2 considers the integrable version of Figures 4 and 5 in [31] (the only ones for which det J < 0). The parameters specified by the authors are j₁₁ = 12, j₁₂ = 4, j₂₁ = 13, j₂₂ = 11, β₁ = 1.2, $i_1^0=2.8$, β₂ = 1, $i_2^0=4$, μ₂ = 0. The values of τ₁ and τ₂ (as well as ν₁ and ν₂, not specified by the authors) have been chosen as 1 throughout¹⁴.

FIGURE 2

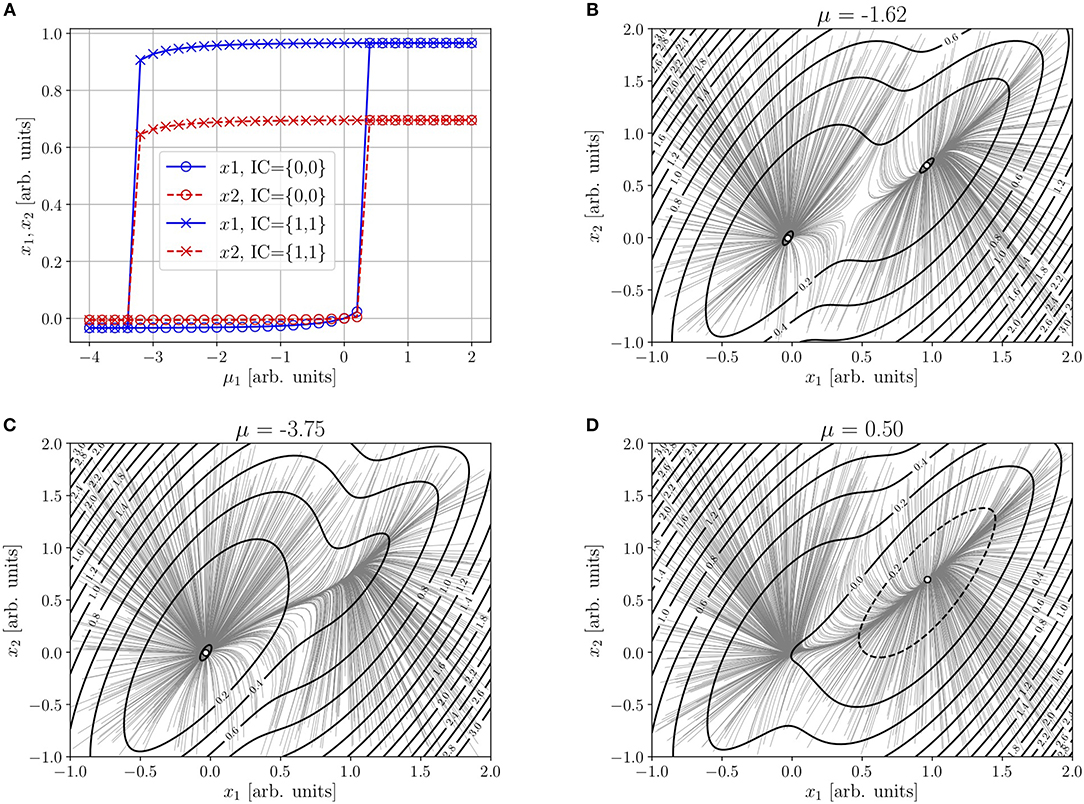
Figure 2. (A) Abscissas (solid line) and ordinates (dashed line) of the “off” (circle) and “on” (cross) nodes of Equations (4)–(5) (with r₁ = r₂ = 0) as functions of μ₁. (B) Trajectories from random initial conditions and contour plot of the NEP—Equation (8), with S_k(i_k)−S_k(μ_k) given by Equation (12)—near the equistable case μ₁ = −1.7 (B), and near the “off” (C), and “on” (D) saddle-node bifurcations. Remaining parameters: ρ = 1, τ₁ = τ₂ = 1, ν₁ = ν₂ = 1, μ₂ = 0, j₁₁ = 12, j₁₂ = 4, j₂₁ = 13, j₂₂ = 11, β₁ = 1.2, $i_1^0=2.8$, β₂ = 1, and $i_2^0=4$.

Frame (a), as well as the trajectories from random initial conditions (uniform distribution) in frames (b)–(d), of Figures 1, 2 are the result of a 4th order Runge–Kutta integration of Equation (6), after 100,000,000 iterations with Δt = 10⁻⁴. In the contour plots of Φ(x) of frames (b)–(d) of Figure 2, S_k(i_k) − S_k(μ_k) is given by Equation (12). Even though the details differ between Figures 1, 2, the structural picture (in particular, the inverse-direct saddle-node mechanism) remains the same.

5. Different Relaxation Times

When τ₁ ≠ τ₂, then

$\text{r}(\text{x})=\frac{j_{12}{j}_{21}}{2\rho detJ}\left(\frac{1}{{\tau }_1}-\frac{1}{{\tau }_2}\right)\left(\begin{array}{c}\left[-x_1+s_1(i_1)\right]-\frac{j_{22}}{j_{21}}\left[-x_2+s_2(i_2)\right]\\ \frac{j_{11}}{j_{12}}\left[-x_1+s_1(i_1)\right]-\left[-x_2+s_2(i_2)\right]\end{array}\right)$

and d(x) = f(x) − r(x). However Φ(x) can remain the same, as far as τ₁τ₂ does not change. So whereas the contour plots of the NEP in Figure 3 reproduce those of Figures 2C,D, the displayed set of trajectories (from random initial conditions within suitably selected tiny patches) have r(x)≠0 and consequently, many of them perform a large excursion toward the attractor.

FIGURE 3

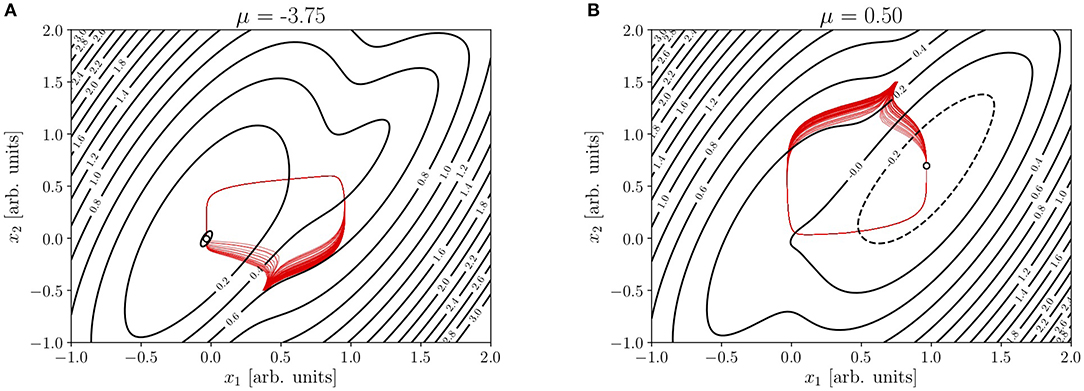
Figure 3. (A,B) Contour plot of the NEP in Figures 2C,D, together with trajectories (in red) from random initial conditions within suitably selected tiny patches. Parameters: ρ = 1, τ₁ = 0.5, τ₂ = 2, ν₁ = ν₂ = 1, μ₂ = 0, j₁₁ = 12, j₁₂ = 4, j₂₁ = 13, j₂₂ = 11, β₁ = 1.2, $i_1^0=2.8$, β₂ = 1, and $i_2^0=4$.

Excitable events such as those described here by the NEP, in which the activity of excitatory neurons in the population shows a sharp peak, are known in the computational neuroscience literature as “population bursts.” These are brief events of high excitatory activity in the neural system being modeled. In neural network models composed of interconnected spiking neurons, they reflect a sudden rise in spiking activity at the level of the whole population (or a significant part of it), in such a way that a high proportion of neurons in the network fire at least one action potential during a short time window. Spiking neurons participating in the population burst are therefore transiently synchronized. In spite of not being able to properly capture synchronous phenomena, the Wilson–Cowan model may capture this phenomenon as a transient peak of activity that is later shut down by inhibition. But for more realistic models, additional biophysical mechanisms (such as actual spiking dynamics, refractory period of neurons or short-term adaptation) have to be considered since they are likely involved in population bursts on real neural systems [41]. Population bursts have several computational uses; for example, they can be used to transmit temporally precise information to other brain areas, even in the presence of noise or heterogeneity [38].

6. Conclusions

Rate- (also called neural mass-) models have been a useful approach to neural networks for half a century. Today, their simplicity (not short of comprehensivity) makes them ideal to fulfill the node dynamics in, for instance, connectome-based brain networks. So the availability of an “energy function” for rate models is expected to be welcome news.

Dynamical systems of the form given by Equation (6) admit a NEP regardless of the functional forms of the nonlinear single-variable functions s_k(i_k). Throughout this work, the latter are assumed to have the same functional form, of sigmoidal shape. But neither condition is necessary to satisfy the integrability condition.

A crucial observation about rate models—even the one put forward by Wilson and Cowan [31], and given by Equations (4)–(5)—is that they are asymptotically linear, so their eventual NEP can be at most quadratic. Then in principle, global stability rules out some coupling configurations. Obviously, this requirement can be relaxed if the rate model fulfills the node dynamics of a neural network, for what matters in that case is the network's global stability.

The here obtained NEP provides a more quantitative intuition on the phenomenon of bistability, that has been naturally found in real neural systems. Neural bistability underlies e.g., the persistent activity which is commonly found in neurons of the prefrontal cortex, a mechanism that is thought to maintain information during working memory tasks [36, 42]. In the presence of neural noise and other adaptation mechanisms, bistability is also a useful hypothesis to explain slow irregular dynamics or “up” and “down” dynamics, also observed across cortex and modeled using bistable dynamics [43–45].

Our results open the door to considering the calculation of nonequilibrium potentials of rate-based neural network models, and in particular considering the implications of different biologically realistic dynamics in such potentials. One interesting possibility is to consider in our model the effect of short-term synaptic plasticity effects. Short-term plasticity has been shown to impact computational properties of neural systems, such as their signal detection abilities [46–48], their pattern storage capacity [49, 50], or the statistics of neural bistable dynamics [44, 45]. We would expect, for example, that changes in the ability of neural systems to detect weak signals due to short-term plasticity could be reflected in changes in the nonequilibrium potential landscape, making population bursts easier to be triggered by weak stimuli. Changes in the statistics of neural bistable dynamics, or ‘up-down' transitions, could be reflected in swifts of the dwells in the landscape, and also on the statistics of real experimental data.

Finally, it is worth mentioning that the here obtained NEP—valid as argued for generic transfer functions s_k(i_k)—opens the door to the potential use of more generic rate models in the field of artificial neural networks and deep learning. By identifying the NEP with the cost function to be minimized, gradient descent algorithms can be used to train networks of generic Wilson–Cowan units for different tasks. This implies that more realistic and less computationally expensive neural population models can be trained and used for behavioral tasks, a topic that has gathered attention recently [51, 52].

Author Contributions

All the listed authors have made substantial and direct intellectual contribution to this work, and approve its publication. In particular, JM proposed the idea, contributed preliminary analytical calculations, and provided key information from the field of neuroscience.

Funding

RD acknowledges support from UNMdP http://dx.doi.org/10.13039/501100007070, under Grant 15/E779–EXA826/17. NM acknowledges a Doctoral Fellowship from CONICET http://dx.doi.org/10.13039/501100002923.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

JM thanks warmly A. Longtin for his support during the early stages of this work. ID and HW thank, respectively, IFIMAR and IFISC for their hospitality. NM thanks HW and IFISC for their hospitality during his research visit.

Footnotes

1. ^The framework can also be applied to nonautonomous flows, as far as their explicit time-dependence can be regarded as slow in comparison with the relaxation times toward the system's attractors (adiabatic approximation).

2. ^By this we mean that we know no systematic methods other than the one we describe here. Of course, there is always room for heuristically finding a global Lyapunov function for some systems, even those containing dynamical variables that exert feedback control (see e.g.,[14]).

3. ^We follow the usual notation in physics, which strictly means dx = f(x)dt + dW(t) in terms of the Wiener process $W(t)={\displaystyle {\int }_t^0\xi (s)ds}$. Note that dx−dW(t) is still a (deterministic) dynamic flow, which implies some kind of connection in the x−W bundle (but not the one of gauge theory).

4. ^Had we written ẋ = f(x) + σξ(t) for n = 1, then $\Phi (x):=-{\sigma }^{-2}{\displaystyle {\int }_x^{x_0}f(y)dy}$

5. ^The knowledge of a NEP for FHN units has greatly simplified the dynamical analysis of reaction–diffusion [2–4] and network [25–27] FHN models, as well as the study of stochastic resonance in some extended systems [3, 28].

6. ^Note that the usually large connectivity of general networks already enables mean-field descriptions (see e.g.,[32]). But the connectivity of the neocortex is overwhelmingly larger than that.

7. ^With our mind in neurophysiology applications, we shall assume s_k(i_k) to have the same functional form, of sigmoidal shape. But neither condition is necessary to satisfy the integrability condition.

8. ^Incidentally, note that $j_{11}{j}_{21}{x}_1^2-2j_{12}{j}_{21}{x}_1{x}_2+j_{12}{j}_{22}{x}_2^2\equiv {(J\text{x})}_1{(J\text{x})}_2-x_1{x}_{2}detJ$.

9. ^Using s_k(i_k): = tanhi_k, Tsodyks et al. have reported a paradoxical increase in x₁ as a result of an increase in μ₂. Unfortunately, this occurs for det J > 0. What we can assure is that there is a saddle point involved.

10. ^For μ_k ≠ 0, Equation (10) can be arrived at from Equation (9) given that for β_k → ∞, ${\beta }_k^{-1}lncosh{\beta }_{k}x\to \left|x\right|-ln2$. Once Equation (10) is obtained, one can let μ_k → 0.

11. ^(through an inverse saddle-node bifurcation at the “on” location: in one variable, $\frac{x^2}{2}-a(x-a)\theta (x-a)$ resets the slope to zero at x = a).

12. ^(located at the solution $\frac{j_{22}{\mu }_1-j_{12}{\mu }_2}{detJ},\frac{j_{21}{\mu }_1-j_{11}{\mu }_2}{detJ}$ of Jx+M = 0)

13. ^Everywhere except possibly in a set of measure 0.

14. ^This has the additional advantage that the flow is purely dissipative, facilitating dynamical conclusions from the landscape.

References

1. Shang Y. Analytical solution for an in-host viral infection model with time-inhomogeneous rates. Acta Phys Pol B (2015) 46:1567–77. doi: 10.5506/APhysPolB.46.1567

CrossRef Full Text | Google Scholar

2. Wio HS. Nonequilibrium potential in reaction–diffusion systems. in: Garrido P, Marro J, editors. 4th Granada Seminar in Computational Physics. Dordrecht: Springer (1997). p. 135–93.

Google Scholar

3. Wio HS, Deza RR. Aspects of stochastic resonance in reaction–diffusion systems: the nonequilibrium-potential approach. Eur Phys J Special Topics (2007) 146:111–26. doi: 10.1140/epjst/e2007-00173-0

CrossRef Full Text | Google Scholar

4. Wio HS, Deza RR, López JM. An Introduction to Stochastic Processes and Nonequilibrium Statistical Physics, revised edition. Singapore: World Scientific (2012).

Google Scholar

5. Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science (1983) 220:671–80. doi: 10.1126/science.220.4598.671

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Yan H, Zhao L, Hu L, Wang X, Wang E, Wang J. Nonequilibrium landscape theory of neural networks. Proc Natl Acad Sci USA (2013) 110:E4185–94. doi: 10.1073/pnas.1310692110

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wang J, Oliveira RJ, Chu X, Whitford PC, Chahine J, Han W, et al. Topography of funneled landscapes determines the thermodynamics and kinetics of protein folding. Proc Natl Acad Sci USA (2012) 109:15763–8. doi: 10.1073/pnas.1212842109

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wang J, Huang B, Xia X, Sun Z. Funneled landscape leads to robustness of cell networks: yeast cell cycle. PLoS Comput Biol. (2006) 2:e147. doi: 10.1371/journal.pcbi.0020147

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Kim KY, Wang J. Potential energy landscape and robustness of a gene regulatory network: toggle switch. PLoS Comput Biol. (2007) 3:e60. doi: 10.1371/journal.pcbi.0030060

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Wang J, Xu L, Wang E, Huang S. The potential landscape of genetic circuits imposes the arrow of time in stem cell differentiation. Biophys J. (2010) 99:29–39. doi: 10.1016/j.bpj.2010.03.058

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Li C, Wang E, Wang J. Potential landscape and probabilistic flux of a predator prey network. PLoS Comput Biol. (2011) 6:e17888. doi: 10.1371/journal.pone.0017888

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zhang F, Xu L, Zhang K, Wang E, Wang J. The potential and flux landscape theory of evolution. J Chem Phys. (2012) 137:065102. doi: 10.1063/1.4734305

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Lyapunov AM. The General Problem of the Stability of Motion (in russian). Kharkiv: Mathematical Society of Kharkov (1892). English transl.: Int. J. Control (1992) 55:531–772.

14. Shang Y. Global stability of disease-free equilibria in a two-group SI model with feedback control. Nonlin Anal. (2015) 20:501–8. doi: 10.15388/NA.2015.4.3

CrossRef Full Text | Google Scholar

15. Langevin P. Sur la théorie du mouvement Brownien. C R Acad Sci. (1908) 146:530.

Google Scholar

16. Graham R. Weak noise limit and nonequilibrium potentials of dissipative dynamical systems. In: Tirapegui E, Villarroel D, editors. Instabilities and Nonequilibrium Structures. Dordrecht: Reidel (1987). p. 271–90.

Google Scholar

17. Graham R, Tél T. Steady-state ensemble for the complex Ginzburg–Landau equation with weak noise. Phys Rev A (1990) 42:4661. doi: 10.1103/PhysRevA.42.4661

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Risken H. The Fokker-Planck Equation: Methods of solution and applications. 2nd ed. Berlin: Springer (1996).

Google Scholar

19. Gardiner CW. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. Berlin: Springer (2004).

Google Scholar

20. van Kampen NG. Stochastic Processes in Physics and Chemistry. Amsterdam: North-Holland (1990).

Google Scholar

21. Descalzi O, Graham R. Gradient expansion of the nonequilibrium potential for the supercritical Ginzburg–Landau equation. Phys Lett A (1992) 170:84. doi: 10.1016/0375-9601(92)90777-J

CrossRef Full Text | Google Scholar

22. Montagne R, Hernández-García E, San Miguel M. Numerical study of a Lyapunov functional for the complex Ginzburg–Landau equation. Physica D (1996) 96:47. doi: 10.1016/0167-2789(96)00013-9

CrossRef Full Text | Google Scholar

23. Izús GG, Deza RR, Wio HS. Exact nonequilibrium potential for the FitzHugh–Nagumo model in the excitable and bistable regimes. Phys Rev E (1998) 58:93–8. doi: 10.1103/PhysRevE.58.93

CrossRef Full Text | Google Scholar

24. Izús GG, Deza RR, Wio HS. Critical slowing-down in the FitzHugh–Nagumo model: a non-equilibrium potential approach. Comp Phys Comm. (1999) 121–122:406–7. doi: 10.1016/S0010-4655(99)00368-9

CrossRef Full Text | Google Scholar

25. Izús GG, Sánchez AD, Deza RR. Noise-driven synchronization of a FitzHugh–Nagumo ring with phase-repulsive coupling: a perspective from the system's nonequilibrium potential. Physica A (2009) 388:967–76. doi: 10.1016/j.physa.2008.11.031

CrossRef Full Text | Google Scholar

26. Sánchez AD, Izús GG. Nonequilibrium potential for arbitrary-connected networks of FitzHugh–Nagumo elements. Physica A (2010) 389:1931–44. doi: 10.1016/j.physa.2010.01.013

CrossRef Full Text | Google Scholar

27. Sánchez AD, Izús GG, dell'Erba MG, Deza RR. A reduced gradient description of stochastic-resonant spatiotemporal patterns in a FitzHugh–Nagumo ring with electric inhibitory coupling. Phys Lett A (2014) 378:1579–83. doi: 10.1016/j.physleta.2014.03.048

CrossRef Full Text | Google Scholar

28. Wio HS, Von Haeften B, Bouzat S. Stochastic resonance in spatially extended systems: the role of far from equilibrium potentials. Physica A (2002) 306:140–56. doi: 10.1016/S0378-4371(02)00493-4

CrossRef Full Text | Google Scholar

29. Ao P. Potential in stochastic differential equations: novel construction. J Phys A (2004) 37:L25–30. doi: 10.1088/0305-4470/37/3/L01

CrossRef Full Text | Google Scholar

30. Wu W, Wang J. Landscape framework and global stability for stochastic reaction diffusion and general spatially extended systems with intrinsic fluctuations. J Phys Chem B (2013) 117:12908–34. doi: 10.1021/jp402064y

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. (1972) 12:1–24. doi: 10.1016/S0006-3495(72)86068-5

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Shang Y. Impact of self-healing capability on network robustness. Phys Rev E (2015) 91:042804. doi: 10.1103/PhysRevE.91.042804

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Amit DJ, Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex (1997) 7:237–52. doi: 10.1093/cercor/7.3.237

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comp Neurosci. (2000) 8:183–208. doi: 10.1023/A:1008925309027

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Wong K, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. J Neurosci. (2006) 26:1314–28. doi: 10.1523/JNEUROSCI.3733-05.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Wang XJ. Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. (2001) 24:455–63. doi: 10.1016/S0166-2236(00)01868-3

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Wang XJ. Probabilistic decision making by slow reverberation in cortical circuits. Neuron (2002) 36:955–68. doi: 10.1016/S0896-6273(02)01092-9

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Mejías JF, Longtin A. Optimal heterogeneity for coding in spiking neural networks. Phys Rev Lett. (2012) 108:228102. doi: 10.1103/PhysRevLett.108.228102

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Mejías JF, Longtin A. Differential effects of excitatory and inhibitory heterogeneity on the gain and asynchronous state of sparse cortical networks. Front Comput Neurosci. (2014) 8:107. doi: 10.3389/fncom.2014.00107

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Borisyuk RM, Kirillov AB. Bifurcation analysis of a neural network model. Biol Cybern. (1992) 66:319–25. doi: 10.1007/BF00203668

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Tsodyks M, Uziel A, Markram H. Synchrony generation in recurrent networks with frequency-dependent synapses. J Neurosci. (2000) 20:RC50. doi: 10.1523/JNEUROSCI.20-01-j0003.2000

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Funahashi S, Bruce CJ, Goldman-Rakic PS. Mnemonic coding of visual space in the monkey's dorsolateral prefrontal cortex. J Neurophysiol. (1989) 61:331–49. doi: 10.1152/jn.1989.61.2.331

PubMed Abstract | CrossRef Full Text | Google Scholar

43. McCormick DA. Neuronal networks: flip-flops in the brain. Curr Biol. (2005) 15:R294–6. doi: 10.1016/j.cub.2005.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Holcman D, Tsodyks M. The emergence of up and down states in cortical networks. PLoS Comput Biol. (2006) 2:174–81. doi: 10.1371/journal.pcbi.0020023

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Mejías JF, Kappen HJ, Torres JJ. Irregular dynamics in up and down cortical states. PLoS ONE (2010) 5:e13651. doi: 10.1371/journal.pone.0013651

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Mejías JF, Torres JJ. The role of synaptic facilitation in spike coincidence detection. J Comput Neurosci. (2008) 24:222–34. doi: 10.1007/s10827-007-0052-8

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Mejías JF, Torres JJ. Emergence of resonances in neural systems: the interplay between adaptive threshold and short-term synaptic plasticity. PLoS ONE (2011) 6:e17255. doi: 10.1371/journal.pone.0017255

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Torres JJ, Marro J, Mejías JF. Can intrinsic noise induce various resonant peaks? New J Phys. (2011) 13:053014. doi: 10.1088/1367-2630/13/5/053014

CrossRef Full Text | Google Scholar

49. Mejías JF, Torres JJ. Maximum memory capacity on neural networks with short-term synaptic depression and facilitation. Neural Comput. (2009) 21:851–71. doi: 10.1162/neco.2008.02-08-719

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Mejías JF, Hernández-Gómez B, Torres JJ. Short-term synaptic facilitation improves information retrieval in noisy neural networks. Europhys Lett. (2012) 97:48008. doi: 10.1209/0295-5075/97/48008

CrossRef Full Text | Google Scholar

51. Mante V, Sussillo D, Shenoy KV, Newsome WT. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature (London). (2013) 503:78–84. doi: 10.1038/nature12742

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Song HF, Yang GR, Wang XJ. Training excitatory-inhibitory recurrent neural networks for cognitive tasks: a simple and flexible framework. PLoS Comput Biol. (2016) 12:e1004792. doi: 10.1371/journal.pcbi.1004792

PubMed Abstract | CrossRef Full Text | Google Scholar