Spin-2 Twisted Duality in (A)dS

Starting from the dual Lagrangians recently obtained for (partially) massless spin-2 fields in the Stueckelberg formulation, we write the equations of motion for (partially) massless gravitons in (A)dS in the form of twisted-duality relations. In both cases, the latter admit a smooth flat limit. In the massless case, this limit reproduces the gravitational twisted-duality relations previously known for Minkowski spacetime. In the partially-massless case, our twisted-duality relations preserve the number of degrees of freedom in the flat limit, in the sense that they split into a decoupled pair of dualities for spin-1 and spin-2 fields. Our results apply to spacetimes of any dimension greater than three. In four dimensions, the twisted-duality relations for partially massless fields that appeared in the literature are recovered by gauging away the Stueckelberg field.

1. Introduction and Conventions

Electric-magnetic duality, the symmetry of vacuum Maxwell equations under the exchange of electric and magnetic fields that interchanges dynamical equations with Bianchi identities, has counterparts in other physical systems, including supersymmetric field theories, linearised gravity and free higher-spin gauge theories. In supersymmetric Yang-Mills theories, electric-magnetic duality—see Olive and West [1] and references therein—acts as a strong/weak duality and, as such, has found applications in the study of non-perturbative phenomena like confinement (see e.g., [2]). In extended supergravity theories it is part of the U-duality symmetry and, since the pioneering work [3], it has been extensively studied.

If the dimension of spacetime is bigger than four, electric-magnetic duality actually links different descriptions of the same physical system. For linearised gravity on a flat background in n dimensions, for instance, it relates the Fierz-Pauli description in terms of the tensor h_ab with a description in terms of an irreducible mixed-symmetry tensor T_{a1 … an−3|b}, completely antisymmetric in its first n−3 indices. This link has however been established only at the linearised level: non-linear Einstein gravity cannot be reproduced in the dual mixed-symmetry picture by means of local interactions [4, 5]. The problems encountered in the attempts to lift gravitational dualities from the linearised formulation in flat background to the interacting level suggest that the study of electric-magnetic duality in curved backgrounds may be particularly promising. Positive results about interaction vertices for mixed-symmetry fields are indeed available in this context [6] and may indicate a way to extend the duality to the interacting theory.

Recently Boulanger et al. [7], built manifestly covariant action principles in the Stueckelberg formulation for dual massless, partially massless and massive spin-2 fields in maximally symmetric spacetimes of arbitrary dimensions n > 3, such that the degrees of freedom are preserved in the flat limit. The action principles for the dual fields were also related to the standard ones for such field theories by building on the previous works [8–19]. See also Mignaco [20] for references on earlier works.

In this Letter we focus on the massless and partially-massless cases and formulate the field equations derived from the actions of Boulanger et al. [7] as twisted-duality relations. In the massless case, our twisted-duality relation—see Equation 2.34—generalizes to (A)dS backgrounds the twisted-duality relation written in Hull [21, 22] for linearised Einstein gravity in flat spacetimes. Our duality relation actually smoothly reproduces the latter duality relation in the flat limit, thanks to the crucial role played by the Stueckelberg fields.

In the case of a partially-massless spin-2 field [23], the twisted-duality relation that we obtain—see Equation 3.35—has a smooth flat limit that reproduces a couple of twisted-duality relations in flat background, one for a massless spin-2 field and the other for a massless spin-1 field, thereby correctly accounting for the degrees of freedom of a partially-massless spin-2 field. Moreover, keeping the cosmological constant non-zero and setting the dimension of spacetime to n = 4, our twisted-duality relation reproduces the one given in Hinterbichler [24], upon eliminating the Stueckelberg field.

Twisted-duality relations are interesting for many reasons. In particular they relate, for a pair of dual theories, the Bianchi identities of one system to the field equations of the dual one, and vice versa. In the present work, we show that the field equations of two dual theories are formulated as a twisted-duality equation, although we note that the latter is not obtained from a variational principle that is manifestly spacetime covariant. Forgoing the latter requirement, for linearised Einstein theory around flat spacetime Bunster et al. [25] gave an action principle that yields the twisted self-duality conditions as equations of motion, keeping the graviton and its dual on equal footing. Finally, let us mention that, for the fully nonlinear Einstein-Hilbert theory, an action principle was given in Boulanger and Hohm [26] where both the graviton and its dual appear inside the action, albeit not on an equal footing and together with extra auxiliary fields. For recent interesting works where twisted (self) duality relations play a central role and for more references, see Henneaux et al. [27–29] and Lekeu [30].

As for our conventions, we work on constant-curvature spacetimes with either negative or positive cosmological constant Λ. We denote the number of spacetime dimensions by n and define the quantity ${\lambda }^2=\frac{-2\sigma \Lambda }{(n-1)(n-2)}$, σ = ±1, that is always positive. When the background is AdS_n one has σ = 1, while σ = −1 for dS_n. The commutator of covariant derivatives gives $\left[{\nabla }_a,{\nabla }_b\right]V_c=-\sigma {\lambda }^2(g_{ac}{V}_b-g_{bc}{V}_a)$, where g_ab is the background (A)dS_n metric. The symbols ϵ_{a1 ⋯ an} and ${ϵ}^{a_1\cdots a_n}$ denote the totally antisymmetric tensors obtained from the corresponding densities upon multiplication and division by $\sqrt{-g}$.

2. Massless Spin-2 Twisted Duality

2.1. Fierz-Pauli Formulation

In the Fierz-Pauli formulation for a massless spin-2 field around a maximally-symmetric spacetime of dimension n, the Lagrangian (where we omit the factor $\sqrt{-g}$ for the sake of conciseness) is given by

$\begin{array}{cc}\begin{array}{l}{L}^{FP}=-\frac{1}{2}{\nabla }_{\text{}a}{h}_{bc}{\nabla }^a{h}^{bc}+{\nabla }_{\text{}a}{h}_{bc}{\nabla }^c{h}^{ba}+\frac{1}{2}{\nabla }_{\text{}a}h{\nabla }^{a}h\\ -{\nabla }_{\text{}a}h{\nabla }_b{h}^{ab}-\frac{(n-1)\sigma {\lambda }^2}{2}\left(2h_{ab}{h}^{ab}-h^2\right).\end{array}& \left(2.1\right)\end{array}$

It is invariant, up to a total derivative, under the gauge transformations¹

$\begin{array}{cc}\begin{array}{l}\delta h_{ab}=2{\nabla }_{\text{}(a}{\xi }_{b)}.\hfill \end{array}& \left(2.2\right)\end{array}$

The primary gauge-invariant quantity for the Fierz-Pauli theory is given by

$\begin{array}{cc}\begin{array}{l}{K}^{ab|mn}=-\frac{1}{2}({\nabla }^a{\nabla }^{[m}{h}^{n]b}-{\nabla }^b{\nabla }^{[m}{h}^{n]a}+{\nabla }^m{\nabla }^{[a}{h}^{b]n}\\ -{\nabla }^n{\nabla }^{[a}{h}^{b]m})+\sigma {\lambda }^2\left(g^{a[m}{h}^{n]b}-g^{b[m}{h}^{n]a}\right).\end{array}& \left(2.3\right)\end{array}$

It possesses the same symmetries as the components of the Riemann tensor,

$\begin{array}{cc}\begin{array}{ll}{K}_{[ab|c]d}\hfill & \equiv 0,\hfill \end{array}& \left(2.4\right)\end{array}$

and obeys the differential Bianchi identity

$\begin{array}{cc}\begin{array}{ll}{\nabla }^{[a}{K}^{bc]|mn}\hfill & \equiv 0.\hfill \end{array}& \left(2.5\right)\end{array}$

The field equations derived from the Lagrangian ${{L}}^{FP}$ imply the tracelessness of the curvature:

$\begin{array}{cc}\begin{array}{l}{K}_{mn}:=g^{ab}{K}_{ma|nb}\approx 0,\hfill \end{array}& \left(2.6\right)\end{array}$

where weak equalities are used throughout this paper to indicate equalities that hold on the surface of the solutions to the equations of motion. More precisely, defining $K=g^{ab}{K}_{ab}$, the left-hand side of the field equations read

$\begin{array}{cc}\begin{array}{l}\frac{\delta L^{FP}}{\delta h^{ab}}\equiv -2\left(K_{ab}-\frac{1}{2}{g}_{ab}K\right).\hfill \end{array}& \left(2.7\right)\end{array}$

By virtue of the differential Bianchi identity for the curvature, one also finds that, on-shell, the curvature has vanishing divergence:

$\begin{array}{cc}\begin{array}{l}{\nabla }^m{K}_{mn|ab}\approx 0.\hfill \end{array}& \left(2.8\right)\end{array}$

To summarize, the important equations in this section are 2.4, 2.5, and 2.6. The latter relation was derived from the Lagrangian ${{L}}^{FP}$. For the purpose of deriving a twisted-duality relation, we can actually forget the origin of 2.6 and focus on the three Equations 2.4, 2.5, and 2.6.

2.2. Dual Formulation

We start from the dual formulation of the massless spin-2 theory as given by the Lagrangian ${{L}}_0(Ŷ,W)$ in Equation (20) of Boulanger et al. [7]:

$\begin{array}{cc}\begin{array}{l}{L}_0(\widehat{Y},W)=\frac{1}{{\lambda }^2}[\frac{1}{2}{\nabla }_{\text{}c}{W}^{abc|d}{\nabla }^e{W}_{dbe|a}+\lambda {\widehat{Y}}^{ab|c}{\nabla }^e{W}_{cbe|a}\\ +\frac{\sigma }{2(n-2)}{\nabla }_{\text{}b}{\widehat{Y}}^{ab|c}{\nabla }^d{\widehat{Y}}_{cd|a}+\frac{{\lambda }^2}{2}{\widehat{Y}}^{ab|c}{\widehat{Y}}_{ac|b}].\end{array}& \left(2.9\right)\end{array}$

This Lagrangian describes the propagation of the same degrees of freedom as the Fierz-Pauli one in Equation 2.1. It has been built in two steps: a Lagrangian depending only on the field Ŷ_ab|c (that is a traceless combination of the components of the spin connection) is obtained by eliminating the vielbein from the first-order formulation of linearised gravity in (A)dS. The full Lagrangian 2.9 then results from the Stueckelberg shift

$\begin{array}{cc}{\widehat{Y}}^{bc|}{}_a\to {\widehat{Y}}^{bc|}{}_a+\frac{1}{\lambda }{\nabla }_{\text{}d}{W}^{bcd|}{}_a.& \left(2.10\right)\end{array}$

The Lagrangian 2.9 possesses as many differential gauge symmetries as the Lagrangian obtained in Boulanger et al. [13] that describes dual (linearised) gravity in Minkowski background.

We now define the following quantities

$\begin{array}{cc}{R}_{ab|}{}^{cd}:=2{\nabla }_{\text{}[a|}\text{}\left({\nabla }_{\text{}e}{W}^{cde}{}_{|b]}+\lambda {\widehat{Y}}^{cd}{}_{|b]}\right),& \left(2.11\right)\end{array}$

$\begin{array}{cc}{K}_{ab|}{}^d:=2{\nabla }_{\text{}[a|}{\nabla }_c{\widehat{Y}}^{cd}{}_{|b]}+2\sigma (n-2)\lambda \left({\nabla }_{\text{}c}{W}^{cd}{}_{[a|b]}+\lambda {\widehat{Y}}^d{}_{[a|b]}\right),& \left(2.12\right)\end{array}$

together with their various non-vanishing traces

$\begin{array}{cc}{R}_{a|}{}^c=R_{ab|}{}^{cb},K_a=K_{ab|}{}^b.& \left(2.13\right)\end{array}$

Further introducing the traceless tensor V_ab|^cd encoding the traceless projection of R_ab|^cd,

$\begin{array}{cc}{V}_{ab|}{}^{cd}=R_{ab|}{}^{cd}-\frac{4}{n-2}{\delta }^{[c}{}_{[a}{R}_{b]|}{}^{d]},& \left(2.14\right)\end{array}$

we find that V_ab|^cd is invariant under the following gauge transformations:

$\begin{array}{cc}\delta {\widehat{Y}}^{bc|}{}_a\text{ }=\text{}{\nabla }_{\text{}d}{\zeta }^{bcd|}{}_a\text{}+\text{}{\nabla }_{\text{}a}{\Lambda }^{bc}\text{}+\text{}\frac{2}{n-1}{\delta }_a{}^{[b}{\nabla }_{\text{}d}{\Lambda }^{c]d}+(n-3)\sigma \lambda {\chi }^{bc}{}_a,& \left(2.15\right)\end{array}$

$\begin{array}{cc}\delta W^{bcd|}{}_a={\nabla }_{\text{}e}{\upsilon }^{bcde|}{}_a+{\nabla }_{\text{}a}{\chi }^{bcd}-\frac{3}{n-2}{\delta }_a{}^{[b}{\nabla }_{\text{}e}{\chi }^{cd]e}-\lambda {\zeta }^{bcd|}{}_a.& \left(2.16\right)\end{array}$

Finally, the traceless tensor

$\begin{array}{cc}{X}_{ab|}{}^c:=K_{ab|}{}^c+\frac{2}{n-1}{\delta }^c{}_{[a}{K}_{b]}& \left(2.17\right)\end{array}$

is also found to be gauge invariant.

As in Boulanger et al. [7], one can also express the fields W and Ŷ in terms of their Hodge duals, that we denote by C and T:²

$\begin{array}{cc}\begin{array}{l}{W}^{abc|}{}_d=-\frac{1}{(n-3)!}{ϵ}^{e[n-3]abc}{C}_{e[n-3]|d},\\ {\widehat{Y}}^{ab|}{}_d=-\frac{1}{(n-2)!}{ϵ}^{e[n-2]ab}{T}_{e[n-2]|d}.\end{array}& \left(2.18\right)\end{array}$

The corresponding curvatures are obtained from the previous gauge-invariant tensors V and X as follows:

$\begin{array}{cc}\begin{array}{lll}{K}_{a[n-2]|bc}^C\hfill & =\frac{1}{2!}{ϵ}_{a[n-2]de}{V}_{bc|}{}^{de},\hfill & K_{a[n-1]|bc}^T={ϵ}_{a[n-1]d}{X}_{bc|}{}^d.\hfill \end{array}& \left(2.19\right)\end{array}$

In components, the curvature tensors read

$\begin{array}{cc}{K}_{a[n-2]|}^C{}^{bc}=2(n-2){(-1)}^{n-1}{\nabla }^{[b}{\nabla }_{\text{}a}{C}_{a[n-3]|}{}^{c]}+2\lambda {\nabla }^{[b}{T}_{a[n-2]|}{}^{c]}+\dots ,& \left(2.20\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}{K}_{a[n-1]|}^T{}^{bc}= 2(n-1){\left(-1\right)}^n{\nabla }^{[b}{\nabla }_{\text{}a}{T}_{a[n-2]|}{}^{c]}\hfill \\ -2\sigma \lambda (n-1){\left(n-2\right)}^2{\delta }^{[b}{}_a{\nabla }_{\text{}a}{C}_{a[n-3]|}{}^{c]}\hfill \\ \text{}+2\sigma {\lambda }^2(n-1)(n-2)T_{a[n-2]|}{}^{[b}{\delta }_a{}^{c]}\text{}+\dots ,\hfill \end{array}& (2.21)\end{array}$

where the ellipses denote terms that are necessary to ensure GL(n)-irreducibility of the curvatures K^C_a[n−2]|bc and K^T_a[n−1]|bc on the two-column Young tableaux of types [n−2, 2] and [n–1, 2], respectively. Pictorially, they are represented by

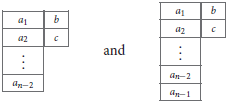
Indeed, tracelessness of V_bc|^de and X_ab|^c implies that the Hodge dual tensors $K_{a\left[n-2\right]|bc}^C$ and $K_{a\left[n-1\right]|bc}^T$ obey the following algebraic Bianchi identities:

$\begin{array}{cc}{K}_{a[n-2]|ac}^C\equiv 0,K_{a[n-1]|ac}^T\equiv 0.& \left(2.22\right)\end{array}$

The two curvatures are linked via the following differential Bianchi identities:

$\begin{array}{cc}{\nabla }_{\text{}a}{K}_{a[n-2]|}^C{}^{bc}\equiv \lambda \frac{{(-1)}^n(n-3)}{(n-1)(n-2)}{K}_{a[n-1]|}^T{}^{bc},& \left(2.23\right)\end{array}$

$\begin{array}{cc}{\nabla }^{[b}{K}^C{{}_{a[n-2]|}}^{cd]}\equiv \lambda \frac{1}{n-2}{K}^T{{}_{a[n-2]}}^{[b|cd]}.& \left(2.24\right)\end{array}$

These are equivalent to the following two identities:

$\begin{array}{cc}{\nabla }_{\text{}d}{V}_{ab|}{}^{cd} \equiv -\lambda \frac{n-3}{n-2}{X}_{ab|}{}^c,{\nabla }_{\text{}[b}{V}_{cd]|}{}^{ij} \equiv \lambda \frac{2}{n-2}{\delta }_{[b}{}^{[i}{X}_{cd]|}{}^{j]}.& \left(2.25\right)\end{array}$

The equations of motion for the dual gauge fields C_a[n−3]|b and T_a[n−2]|b derived from the Lagrangian ${{L}}_0(C,T)$—obtained by substituting 2.18 in 2.9 and given in Equation (23) of Boulanger et al. [7]—can be written in terms of the traces of the gauge-invariant curvatures $K_{a\left[n-2\right]|b\left[2\right]}^C$ and $K_{a\left[n-1\right]|b\left[2\right]}^T$. Explicitly, one has

$\begin{array}{cc}\frac{\delta L_0}{\delta C_{a[n-3]|b}}\equiv \frac{1}{{\lambda }^2(n-3)!}\left(K_C{{}^{a[n-3]c|}}_c{}^b+\frac{n-3}{2}{K}_C{{}^{a[n-4]cd|}}_{cd}{g}^{ab}\right)\approx 0,& \left(2.26\right)\end{array}$

$\begin{array}{cc}\frac{\delta L_0}{\delta T_{a[n-2]|b}}\equiv \frac{\sigma }{{\lambda }^2{(n-2)}^2(n-3)!}\left(K_T{{}^{a[n-2]c|}}_c{}^b+\frac{n-2}{2}{K}_T{{}^{a[n-3]cd|}}_{cd}{g}^{ab}\right)\approx 0.& \left(2.27\right)\end{array}$

The field equations 2.26 and 2.27 can easily be obtained by starting from the field equations of the Lagrangian ${{L}}_0(W,Ŷ)$ and then expressing the fields W^abc|_d and Ŷ^ab|_c in terms of their Hodge duals C_a[n−3]|b and C_a[n−3]|b in terms of their Hodge duals T_a[n−2]|b and T_a[n−2]|b, respectively. More in details, the left-hand sides of the field equations derived from ${{L}}_0(W,Ŷ)$ read

$\begin{array}{cc}\frac{\delta L_0(W,\widehat{Y})}{\delta W^{abc|}{}_d}=\frac{1}{2{\lambda }^2}{V}_{[ab|c]}{}^d,\frac{\delta L_0(W,\widehat{Y})}{\delta {\widehat{Y}}^{ab|}{}_d}=-\frac{\sigma }{2(n-2){\lambda }^2}{X}_{ab|}{}^d,& \left(2.28\right)\end{array}$

and the gauge invariant tensors X and V can be expressed as

$\begin{array}{l}{X}_{ab|}{}^d=-\frac{1}{(n-1)!}{ϵ}^{c[n-1]d}{K}^T{}_{c[n-1]|ab},\\ V_{ab|}{}^{cd}=-\frac{1}{(n-2)!}{ϵ}^{e[n-2]cd}{K}^C{}_{e[n-2]|ab}.\end{array}$

The field equations 2.26 and 2.27 imply the tracelessness of the curvatures:

$\begin{array}{cc}\begin{array}{lll}{K}_C{{}^{a[n-3]c|}}_c{}^b\hfill & \approx 0,\hfill & K_T{{}^{a[n-2]c|}}_c{}^b\approx 0.\hfill \end{array}& \left(2.30\right)\end{array}$

In fact, from a result in representation theory of the orthogonal group—see the theorem on p. 394 of Hamermesh [31]—, the second equation above implies that

$\begin{array}{cc}{K}^T{}_{a[n-1]|bc}\approx 0.& \left(2.31\right)\end{array}$

The curvature for the field T thus vanishes on shell, consistently with the observation that this field does not propagate any degrees of freedom in the flat limit [7, 19].

Upon using the first and second differential Bianchi identities 2.23 and 2.24, we also find the following two relations that are true on shell:

$\begin{array}{cc}{\nabla }_{\text{}a}{K}_{a[n-2]|}^C{}^{bc}\approx 0,{\nabla }^{[b}{K}_{a[n-2]|}^C{}^{cd]}\approx 0.& \left(2.32\right)\end{array}$

These equations, together with 2.30, imply that the divergences of the curvature K^C vanish on shell:

$\begin{array}{cc}{\nabla }^a{K}_{ab[n-3]|cd}^C\approx 0,{\nabla }^b{K}_{a[n-2]|bc}^C\approx 0.& \left(2.33\right)\end{array}$

To summarise, the important equations of this section are the equations of motion 2.30 and the Bianchi identities 2.22, 2.23 and 2.24. In the following section we will relate them to the field equations and the Bianchi identities of the Fierz-Pauli formulation via a twisted-duality relation.

2.3. Massless Twisted Duality

The twisted-duality relations for the massless spin-2 theory around (A)dS backgrounds are

$\begin{array}{cc}{K}_{a[n-2]|bc}^C\approx \frac{1}{2}{ϵ}_{a[n-2]ij}{K}^{ij|}{}_{bc}.& \left(2.34\right)\end{array}$

As usual for twisted-duality relations, the Bianchi identities in a formulation of the theory are mapped to the field equations of the dual formulation, and vice versa, as we now explain in details.

First, the algebraic Bianchi identity 2.22 for the left-hand side of the twisted-duality relation 2.34 implies that the trace of K_ab|cd vanishes on-shell, which is the field equation 2.6 in the metric formulation. The converse is true: If one takes the trace of the relation 2.34, the right-hand side vanishes by virtue of the algebraic Bianchi identity 2.4. This implies that the trace of the left-hand side of 2.34 vanishes, which enforces the field equation 2.30 in the dual formulation.

Second, starting again from the twisted-duality equation 2.34, the differential Bianchi identity 2.24 on the second column of K^C combined with the Bianchi differential identity 2.5 imply the on-shell vanishing of K^T, that is, 2.31. Using this result, the differential Bianchi identity 2.23 on the first column of K^C gives the first equation of 2.32 that implies in its turn, via 2.34, the field equation 2.8 in the metric formulation of the massless spin-2 theory. The converse is also true: acting on the twisted-duality relation 2.34 with ∇^a gives identically zero, from the right-hand side and as a consequence of the differential Bianchi identity 2.5 for the curvature in the metric formulation of linearised gravity around (A)dS. This implies the first field equation 2.33 for the dual graviton. Moreover, acting on 2.34 with ∇_d and antisymmetrising over the three indices {b, c, d} gives identically zero from the right-hand side of 2.34, as a consequence of 2.5. That implies the field equation 2.31 (and therefore the second field equation 2.32) by virtue of the identity 2.24. Finally, the field equation 2.8 is mapped to the second field equation in 2.33.

Third, the twisted-duality relation 2.34 exactly reproduces, in the limit where the cosmological constant goes to zero, the twisted-duality relations given by Hull [22] for linearised gravity in flat spacetime, see also section 4 of Bekaert and Boulanger [32].

3. Partially-Massless Spin-2 Twisted Duality

3.1. Standard Stueckelberg Formulation

We consider the Stueckelberg Lagrangian for a partially-massless, symmetric spin-2 field in which both signatures are allowed (making AdS manifestly non-unitary at the classical level):

$\begin{array}{cc}\begin{array}{l}{L}_{PM}=-\frac{1}{2}{\nabla }_{\text{}a}{h}_{bc}{\nabla }^a{h}^{bc}+{\nabla }_{\text{}a}{h}_{bc}{\nabla }^c{h}^{ba}+\frac{1}{2}{\nabla }_{\text{}a}h{\nabla }^{a}h-{\nabla }_{\text{}a}h{\nabla }_b{h}^{ab}\\ -\frac{(n-1)\sigma {\lambda }^2}{2}\left(2h_{ab}{h}^{ab}\text{}-\text{}{h}^2\right)+\sigma {\nabla }_{\text{}[a}{A}_{b]}{\nabla }^{[a}{A}^{b]}\text{}+\text{}(n-1){\lambda }^2{A}_a{A}^a\\ -2\tilde{m}{A}_a\left({\nabla }^{a}h-{\nabla }_{\text{}b}{h}^{ab}\right)+\sigma {\tilde{m}}^2\left(h_{ab}{h}^{ab}-h^2\right),\end{array}& \left(3.1\right)\end{array}$

where the partially massless theory really appears in the limit

$\begin{array}{cc}{\tilde{m}}^2 \to \frac{(n-2){\lambda }^2}{2}.& \left(3.2\right)\end{array}$

The last two lines in the expression 3.1 are new terms in comparison with the Lagrangian for a strictly massless spin-2 field in (A)dS, see 2.1. In the limit 3.2, the Lagrangian ${{L}}_{PM}$ is invariant, up to total derivatives, under the gauge transformations

$\begin{array}{cc}\delta h_{ab}=2{\nabla }_{\text{}(a}{\xi }_{b)}+\frac{2\tilde{m}}{n-2}{g}_{ab}ϵ,\delta A_a={\nabla }_aϵ+2\sigma \tilde{m}{\xi }_a.& \left(3.3\right)\end{array}$

The quantity

$\begin{array}{cc}{H}_{ab}=h_{ab}-\frac{\sigma }{\tilde{m}}{\nabla }_{(a}{A}_{b)}& \left(3.4\right)\end{array}$

is invariant under the gauge transformations with parameter ξ_a, but not under the gauge transformations with parameter ϵ. A fully gauge-invariant quantity is provided by the antisymmetrised curl of H_ab. Indeed, defining

$\begin{array}{cc}\begin{array}{l}{K}_{ab|c}:=2{\nabla }_{\text{}c}{\nabla }_{\text{}[a}{A}_{b]}-4\sigma {\lambda }^2{g}_{c[a}{A}_{b]}-4\sigma \tilde{m}{\nabla }_{\text{}[a}{h}_{b]c}\equiv -4\sigma \tilde{m}{\nabla }_{\text{}[a}{H}_{b]c},\hfill \end{array}& \left(3.5\right)\end{array}$

we have that ${{K}}_{ab|c}$ is fully gauge invariant in the partially massless limit 3.2, hence so is ∇_[aH_b]c. We further define the derived quantity Q^ab|mn as follows:

$\begin{array}{cc}\begin{array}{l}{Q}^{ab|mn}\text{}=\text{ }-\text{}\frac{1}{2}\left({\nabla }^a{\nabla }^{[m}{H}^{n]b}\text{}-\text{}{\nabla }^b{\nabla }^{[m}{H}^{n]a}\text{}+\text{}{\nabla }^m{\nabla }^{[a}{H}^{b]n}\text{}-\text{}{\nabla }^n{\nabla }^{[a}{H}^{b]m}\right)\\ +(1-\frac{2{\tilde{m}}^2}{(n-2){\lambda }^2})\sigma {\lambda }^2\left(g^{a[m}{H}^{n]b}-g^{b[m}{H}^{n]a}\right).\end{array}& \left(3.6\right)\end{array}$

It possesses the symmetries of the components of the Riemann tensor, like K_ab|cd in the massless case. The second line of the above expression is identically vanishing in the limit 3.2, so that Q^ab|mn is indeed a composite object purely built out of the gauge-invariant quantity ∇_[aH_b]c. The writing that we adopted in 3.6 facilitates the relation between K_ab|cd and Q_ab|cd. The interest in defining 3.6 rests in the fact that the field equations for h_ab read

$\begin{array}{cc}\begin{array}{l}\frac{\delta L_{PM}}{\delta h^{ab}}\equiv -2G_{ab},\text{\hspace{1em}where\hspace{1em}}{G}_{ab}:=(Q_{ac|b}{}^c-\frac{1}{2}{g}_{ab}{Q}^{cd|}{}_{cd}).\hfill \end{array}& \left(3.7\right)\end{array}$

As a consequence, the field equations for h_ab imply that the curvature Q_ab|cd is traceless on-shell, as it was for K_ab|cd in the strictly massless case.

The Noether identities associated with the gauge parameter ξ_a give the left-hand side of the field equations for the vector A_a:

$\begin{array}{cc}\begin{array}{ll}\frac{\delta L_{PM}}{\delta A^a}\hfill & \equiv -\frac{2\sigma }{\tilde{m}}{\nabla }^b{G}_{ab}.\hfill \end{array}& \left(3.8\right)\end{array}$

The non-vanishing of the covariant divergence of G_ab is also related to the Bianchi identity

$\begin{array}{cc}\begin{array}{l}{\nabla }^{[a}{Q}^{bc]|}{}_{mn}\equiv -\frac{\tilde{m}}{n-2}{\delta }^{[a}{}_{[m}{K}^{bc]|}{}_{n]},\hfill \end{array}& \left(3.9\right)\end{array}$

where the gauge-invariant quantity ${{K}}_{ab|c}$ was defined above in 3.5 and satisfies the identity ${{K}}_{\left[ab|c\right]}\equiv 0$. In terms of ${{K}}_{ab|c}$, the left-hand side of the field equations for A_a reads

$\begin{array}{cc}\begin{array}{l}\frac{\delta L_{PM}}{\delta A^a}\equiv \sigma K_{ab|}{}^b,\hfill \end{array}& \left(3.10\right)\end{array}$

so that the field equations for A_a imply that the curvature ${{K}}_{ab|c}$ is traceless on-shell.

3.2. Dual Formulation

We now consider the dual formulation of the partially-massless spin-2 theory that is described by the Lagrangian ${{L}}_{PM}(W,U)$ in Equation (39) of Boulanger et al. [7]:

$\begin{array}{cc}\begin{array}{l}{L}_{PM}(W,U)=-\frac{1}{2{\lambda }^2}{\nabla }_{\text{}d}{W}^{bcd|a}{\nabla }^e{W}_{abe|c}+\frac{\sigma }{\tilde{m}}{U}_{abc}{\nabla }_d{W}^{abd|c}\\ -\frac{\sigma }{2(n-2){\tilde{m}}^2}{\nabla }_{\text{}c}{U}^{abc}{\nabla }^d{U}_{abd}-\frac{{\lambda }^2}{2{\tilde{m}}^2}{U}^{abc}{U}_{abc}.\end{array}& \left(3.11\right)\end{array}$

A Lagrangian depending only on the field W_abc|d has first been obtained by solving the equations of motion given by the variation of the vielbein in a first-order formulation of the partially-massless theory. In analogy with the massless case, the additional field U^abc has then been introduced by a Stueckelberg shift.

Starting from 3.11 one can define the following quantities

$\begin{array}{cc}{R}_{ab|}{}^{cd}:=2{\nabla }_{\text{}[a|}\text{}\left({\nabla }_{\text{}e}{W}^{cde}{}_{|b]}-\frac{\sigma {\lambda }^2}{\tilde{m}}{U}_{|b]}{}^{cd}\right),& \left(3.12\right)\end{array}$

$\begin{array}{cc}{K}_{ab|}^U{}^c:=2{\nabla }_{\text{}[a}{\nabla }^e{U}_{b]}{{}^c}_e+2(n-2)\tilde{m}\left({\nabla }_{\text{}e}{W}^{ec}{}_{[a|b]}-\frac{\sigma {\lambda }^2}{\tilde{m}}{U}_{ab}{}^c\right),& \left(3.13\right)\end{array}$

together with the successive traces

$\begin{array}{cc}{R}_{a|}{}^c=R_{ab|}{}^{cb},R=R_{a|}{}^a\equiv 0,K_a^U=K_{ab|}^U{}^b\equiv 0.& \left(3.14\right)\end{array}$

In a similar manner to the massless case, we introduce the traceless tensor ${V}$_ab|^cd according to

$\begin{array}{cc}{V}_{ab|}{}^{cd}=R_{ab|}{}^{cd}-\frac{4}{n-2}{\delta }^{[c}{}_{[a}{R}_{b]|}{}^{d]},& \left(3.15\right)\end{array}$

and we find that the tensors ${V}$_ab|^cd and ${{K}}_{abc}^U$ are invariant under the following gauge transformations:

$\begin{array}{cc}\delta W^{bcd|}{}_a=\text{}{\nabla }_{\text{}e}{\upsilon }^{bcde|}{}_a\text{}+\text{}{\nabla }_{\text{}a}{\chi }^{bcd}-\frac{3}{n-2}{\delta }_a{}^{[b}{\nabla }_{\text{}e}{\chi }^{cd]e}-\frac{\sigma {\lambda }^2}{\tilde{m}}{\rho }^{bcd}{}_a,& \left(3.16\right)\end{array}$

$\begin{array}{cc}\delta U^{abc}={\nabla }_{\text{}d}{\rho }^{abcd}-(n-3)\tilde{m}{\chi }^{abc}.& \left(3.17\right)\end{array}$

Also in this case, we then express W and U in terms of their Hodge duals

$\begin{array}{cc}\begin{array}{lll}{W}^{abc|}{}_d\hfill & \text{}=\text{}-\frac{1}{(n-3)!}{ϵ}^{e[n-3]abc}{C}_{e[n-3]|d},\text{}\hfill & U^{abc}\text{}=\text{}-\frac{1}{(n-3)!}{ϵ}^{d[n-3]abc}{A}_{d[n-3]}.\hfill \end{array}& \left(3.18\right)\end{array}$

The curvature tensor for C is defined, as in the massless case, by

$\begin{array}{cc}\begin{array}{l}{K}_{a[n-2]|bc}^C=\frac{1}{2!}{ϵ}_{a[n-2]de}{V}_{bc|}{}^{de}.\hfill \end{array}& \left(3.19\right)\end{array}$

We also define the curvature ${\tilde{K}}^{a\left[n-2\right]|}$ via

$\begin{array}{cc}\begin{array}{l}{K}^U{{}_{ab|}}^c={(-1)}^{n-1}\frac{2}{(n-2)!}{ϵ}_{d[n-2][a}{}^c{\tilde{K}}^{d[n-2]|}{}_{b]}.\hfill \end{array}& \left(3.20\right)\end{array}$

In order to invert this relation, we first compute

$\begin{array}{cc}\frac{{(-1)}^n}{2}{ϵ}^{d[n-2]ab}{K}^U{}_{ab|c}={\tilde{K}}^{d[n-2]|}c-(n-2){\delta }^d{}_c{\tilde{K}}^{ed[n-3]{|}_e}& (3.21)\end{array}$

and take the trace of the above relation, which produces

$\begin{array}{cc}{\tilde{K}}^{{}^{ab[n-3]|}}a=\frac{1}{4}{ϵ}^{b[n-3]cde}{K}^U{}_{cd|e}.& \left(3.22\right)\end{array}$

Inserting this relation back in 3.21 gives

$\begin{array}{cc}\tilde{K}\begin{array}{l}{{}^{a[n-2]|}}_b=\frac{{(-1)}^n}{2}{ϵ}^{a[n-3]cde}({\delta }^a{}_e{K}^U{}_{cd|b}-\frac{n-2}{2}{\delta }^a{}_b{K}^U{}_{cd|e}).\hfill \end{array}& \left(3.23\right)\end{array}$

Explicitly, we have

$\begin{array}{cc}\begin{array}{l}{\tilde{K}}^{a[n-2]|b}=(n-2)({\nabla }^b{\nabla }^a{A}^{a[n-3]}+(n-2)\tilde{m}{\nabla }^a{C}^{a[n-3]|b}\\ -\sigma (n-2){\lambda }^2{g}^{ab}{A}^{a[n-3]}),\end{array}& \left(3.24\right)\end{array}$

which is gauge invariant under [7]

$\begin{array}{cc}\begin{array}{l}\delta C_{a[n-3]|b}={\left(-1\right)}^{n-1}(n-3)({\nabla }_{\text{}a}{\tilde{\upsilon }}_{a[n-4]|b}-\frac{\sigma {\lambda }^2}{\tilde{m}}{g}_{ba}{\tilde{\rho }}_{a[n-4]})\hfill \\ +\frac{n-3}{n-2}({\nabla }_{\text{}b}{\tilde{\chi }}_{a[n-3]}+{(-1)}^n{\nabla }_{\text{}a}{\tilde{\chi }}_{a[n-4]b}) ,\hfill \end{array}& (3.25)\end{array}$

$\begin{array}{cc}\delta A_{a[n-3]}=(n-3)\left({(-1)}^{n-1}{\nabla }_{\text{}a}{\tilde{\rho }}_{a[n-4]}-\tilde{m}{\tilde{\chi }}_{a[n-3]}\right).& \left(3.26\right)\end{array}$

The curvatures obey the following algebraic Bianchi identities

$\begin{array}{cc}\begin{array}{lll}{K}^C{}_{a[n-2]|ab}\hfill & \equiv 0,\hfill & {\tilde{K}}_{a[n-2]|a}\equiv 0,\hfill \end{array}& \left(3.27\right)\end{array}$

which means that ${K}$^C_a[n−2]|bc and ${\tilde{{K}}}_{a\left[n-2\right]|b}$ are projected on the following GL(n)-irreducible Young tableaux

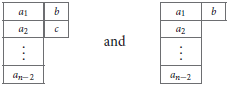
The left-hand sides of the equations of motion derived from the Lagrangian 3.11 are given by

$\begin{array}{cc}\begin{array}{lll}\frac{\delta {ℒ}_{PM}}{\delta W_{abc|}{}^d}\hfill & =\frac{1}{2{\lambda }^2}{V}^{[ab|c]}{}_d,\hfill & \frac{\delta {ℒ}_{PM}}{\delta U_{abc}}=\frac{\sigma }{2(n-2){\tilde{m}}^2}{K}_U^{[ab|c]}.\hfill \end{array}& \left(3.28\right)\end{array}$

Combining with what we obtained above, the field equations therefore imply

$\begin{array}{cc}\begin{array}{lll}{\tilde{K}}_{a[n-3]b|}{}^b\hfill & \approx 0,\hfill & K^C{{}_{a[n-3]b|}}^{bc}\approx 0.\hfill \end{array}& \left(3.29\right)\end{array}$

The Bianchi identities read

$\begin{array}{cc}\begin{array}{lll}{\nabla }_d{V}_{ab|}{}^{cd}\hfill & \equiv -\frac{\sigma {\lambda }^2(n-3)}{(n-2)\tilde{m}}{K}^U{{}_{ab|}}^c,\hfill & {\nabla }_{[a}{V}_{bc]|}{}^{de}\equiv \frac{2\sigma {\lambda }^2}{\tilde{m}(n-2)}{\delta }^{[d}{}_{[a}{K}^U{{}_{bc]|}}^{e]}.\hfill \end{array}& \left(3.30\right)\end{array}$

In terms of the curvatures ${{K}}^C$ and $\tilde{{K}}$, they become

$\begin{array}{cc}{\nabla }_a{K}^C{{}_{a[n-2]|}}^{bc}\equiv {(-1)}^n\frac{2\sigma {\lambda }^2(n-3)}{\tilde{m}(n-2)}{\delta }^{[b}{}_a{\tilde{K}}_{a[n-2]|}{}^{c]},& \left(3.31\right)\end{array}$

$\begin{array}{cc}{\nabla }^{[a}{K}^C{{}_{d[n-2]|}}^{bc]}\equiv -\frac{2\sigma {\lambda }^2}{\tilde{m}}{\tilde{K}}^{[a}{{}_{d[n-3]|}}^b{\delta }^{c]}{}_d.& \left(3.32\right)\end{array}$

By taking a trace of the Bianchi identity and using the field equations, one therefore deduces that

$\begin{array}{cc}{\nabla }^b{K}^C{}_{a[n-2]|bc}\approx {(-1)}^n\frac{(n-3)\sigma {\lambda }^2}{(n-2)\tilde{m}}{\tilde{K}}_{a[n-2]|c},& \left(3.33\right)\end{array}$

$\begin{array}{cc}{\nabla }^b{K}^C{{}_{a[n-3]b|}}^{cd}\approx -\frac{2\sigma {\lambda }^2}{(n-2)\tilde{m}}{\tilde{K}}^{[c}{{}_{a[n-3]|}}^{d]}.& \left(3.34\right)\end{array}$

3.3. Partially-Massless Twisted Duality

The twisted duality that mixes the field equations and Bianchi identities of the two dual theories, the one for ${{L}}_{PM}(h_{ab},A_a)$ on the one hand, and the one for ${{L}}_{PM}(C_{a\left[n-3\right]|b},A_{a\left[n-3\right]})$ on the other hand, is

$\begin{array}{cc}\begin{array}{l}{K}_{a[n-2]|bc}^C\approx \frac{1}{2}{ϵ}_{a[n-2]ij}{Q}^{ij|}{}_{bc}.\hfill \end{array}& \left(3.35\right)\end{array}$

This equation plays the same role as 2.34 in the strictly massless case.

What is new in the partially massless case compared to the massless case is that the flat limit of 3.35 is not enough to describe all degrees of freedom of a partially massless field. In fact, the twisted-duality relation 3.35 also induces a duality relation between the curvatures ${\tilde{{K}}}_{a\left[n-2\right]|b}$ and ${{K}}_{ab|c}$. This can be viewed by acting on 3.35 with ∇_a and contracting the result with ϵ^a[n−1]d. One then uses 3.31 and the trace of 3.9, taking into account that, on shell, the traces of the four curvatures ${\tilde{{K}}}_{a\left[n-2\right]|b}$, ${{K}}_{a\left[n-2\right]|bc}^C$, Q_ab|cd and ${{K}}_{ab|c}$ vanish. We obtain

$\begin{array}{cc}\begin{array}{l}{\tilde{K}}_{a[n-2]|b}\approx {(-1)}^{n-1}\frac{\sigma {\tilde{m}}^2}{4{\lambda }^2}{ϵ}_{a[n-2]cd}{K}^{cd|}{}_b,\hfill \end{array}& \left(3.36\right)\end{array}$

where we stress that 3.35 and 3.36 are equivalent for non-zero cosmological constant.

Now, taking the flat limit of both 3.35 and 3.36, we obtain two decoupled twisted-duality relations for the two decoupled pairs of fields (C_a[n−3]|b, h_ab) and (A_a[n−3], A_a). Both together, they propagate the correct degrees of freedom for a partially massless spin-2 field in the flat limit, as was found and discussed in section 4.3 of Boulanger et al. [7]. The flat limit of 3.36 gives

$\begin{array}{cc}\begin{array}{l}{\partial }_b{\tilde{F}}_{a[n-2]}\approx {(-1)}^n\frac{(n-2)\sigma }{8}{ϵ}_{a[n-2]cd}{\partial }_b{F}^{cd},\hfill \end{array}& \left(3.37\right)\end{array}$

where ${\tilde{F}}_{a\left[n-2\right]}=(n-2){\partial }_a{A}_{a\left[n-3\right]}$ and F_ab = 2∂_[aA_b] are the field strengths for A_b[n−3] and A_b, respectively. In the flat limit, these latter quantities are gauge invariant, therefore the gradient ∂_b on both sides of the above relation 3.37 can be stripped off to give, up to an unessential coefficient that can be absorbed into a redefinition of A_a[n−3], the usual electric-magnetic duality between a 1-form and its dual (n−3)-form in dimension n.

As a consistency check for the second duality relation 3.36, one can start from the twisted-duality relation 3.35 and this time take the curl of ${{K}}^C$ on its second column of indices, which yields

$\begin{array}{cc}\begin{array}{l}{\nabla }^{[b}{K}^C{{}_{a[n-2]|}}^{cd]}\approx \frac{1}{2}{ϵ}_{a[n-2]ij}{\nabla }^{[b}{Q}^{cd]|}{}_{ij}.\hfill \end{array}& \left(3.38\right)\end{array}$

We then use the Bianchi identities 3.32 and 3.9 and take a trace, taking into account the field equation 3.29, which allows us to obtain the relation

$\begin{array}{cc}\begin{array}{l}{\tilde{K}}_{a[n-3][b|c]}\approx {(-1)}^{n-1}\frac{\sigma {\tilde{m}}^2}{4{\lambda }^2}{ϵ}_{a[n-3]ij[b}{K}^{ij|}{}_{c]},\hfill \end{array}& \left(3.39\right)\end{array}$

which is fully consistent with 3.36.

Finally, we come back to the twisted-duality relation 3.36 and gauge fix to zero both A_a and A_a[n−3] since they are Stueckelberg fields as long as λ is different from zero. In these gauges for the dual formulations, our second twisted-duality relation 3.36 becomes

$\begin{array}{cc}\begin{array}{l}(n-2){\nabla }_a{C}_{a[n-3]|}{}^b\approx \frac{{(-1)}^n}{2}{ϵ}_{a[n-2]cd}{\nabla }^c{h}^{db},\hfill \end{array}& \left(3.40\right)\end{array}$

while the first twisted-duality relation 3.35 is just its curl, as one can readily check. This duality relation makes immediate contact with the one proposed for the specific case n = 4 in Equation (2.3) of Hinterbichler [24]. Relation 3.40 identifies the dual curvature ${\tilde{F}}_{ab|c}$ in Hinterbichler [24] with 4∇_[aC_b]|c, the curl of the dual potential C_b|c = C_c|b. Note that, once the Stueckelberg fields A_a and A_a[n−3] have been set to zero, one cannot take a smooth flat limit any longer in the sense that physical degrees of freedom are lost in the flat limit.

The advantage of our Stueckelberg formulation for the twisted-duality relation is that the identification of the helicity degrees of freedom is manifest and does not require any specific system of coordinates to be seen. In the original Stueckelberg formulation, h_ab and A_a carry the helicity two and one degrees of freedom, and the twisted-duality relations 3.35 and 3.36 identify these degrees of freedom with the dual fields C_a[n−2]|b and A_a[n−3], respectively, in a manifestly covariant way.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We performed or checked several computations with the package xTras [33] of the suite of Mathematica packages xAct. The work of NB has been supported in part by a FNRS PDR grant (number T.1025.14), while the work of AC has been supported in part by the NCCR SwissMAP, funded by the Swiss National Science Foundation. AC and LT are, respectively, a Research Associate and a Research Fellow of the Fund for Scientific Research-FNRS, Belgium.

Footnotes

1. ^Indices enclosed between (square) round brackets are (anti)symmetrised, and dividing by the number of terms involved is understood (strength-one convention). Moreover, we will use a vertical bar to separate groups of antisymmetrised indices, see e.g., Equation 2.3.

2. ^We substitute groups of antisymmetrised indices with a label denoting the total number of indices, e.g., ϵ_a1⋯an≡ϵ_a[n]. Moreover, repeated indices denote an antisymmetrisation, e.g., A_aB_a≡A_[a1B_a2].

References

1. Olive DI, West PC. Duality and supersymmetric theories. Cambridge: Cambridge University Press (1999).

Google Scholar

2. Strassler MJ. On confinement and duality. In: Proceedings of the 2001 Spring School on Superstrings and Related Matters. Trieste (2001). Available online at: http://users.ictp.it/ ~pub_off/lectures/lns007/Strassler/Strassler.pdf

Google Scholar

3. Cremmer E, Julia B. The SO(8) supergravity. Nucl Phys. (1979) B159:141. doi: 10.1016/0550-3213(79)90331-6

CrossRef Full Text | Google Scholar

4. Bekaert X, Boulanger N, Henneaux M. Consistent deformations of dual formulations of linearized gravity: a no go result. Phys Rev D (2003) 67:044010. doi: 10.1103/PhysRevD.67.044010

CrossRef Full Text | Google Scholar

5. Bekaert X, Boulanger N, Cnockaert S. No self-interaction for two-column massless fields. J Math Phys. (2005) 46:012303. doi: 10.1063/1.1823032

CrossRef Full Text | Google Scholar

6. Boulanger N, Skvortsov ED. Higher-spin algebras and cubic interactions for simple mixed-symmetry fields in AdS spacetime. J High Energy Phys. (2011) 9:63. doi: 10.1007/JHEP09(2011)063

CrossRef Full Text | Google Scholar

7. Boulanger N, Campoleoni A, Cortese I. Dual actions for massless, partially-massless and massive gravitons in (A)dS. Phys Lett. (2018) B782:285–90. doi: 10.1016/j.physletb.2018.05.046

CrossRef Full Text | Google Scholar

8. Curtright TL, Freund PG. Massive dual fields. Nucl Phys. (1980) B172:413–24. doi: 10.1016/0550-3213(80)90174-1

CrossRef Full Text | Google Scholar

9. Fradkin E, Tseytlin AA. Quantum equivalence of dual field theories. Ann Phys. (1985) 162:31. doi: 10.1016/0003-4916(85)90225-8

CrossRef Full Text | Google Scholar

10. West PC. E(11) and M theory. Class Quant Grav. (2001) 18:4443–60. doi: 10.1088/0264-9381/18/21/305

CrossRef Full Text | Google Scholar

11. Zinoviev Y. On massive high spin particles in AdS. arXiv:hep-th/0108192.

12. West PC. Very extended E(8) and A(8) at low levels, gravity and supergravity. Class Quant Grav. (2003) 20:2393–406. doi: 10.1088/0264-9381/20/11/328

CrossRef Full Text | Google Scholar

13. Boulanger N, Cnockaert S, Henneaux M. A note on spin s duality. J High Energy Phys. (2003) 6:60. doi: 10.1088/1126-6708/2003/06/060

CrossRef Full Text | Google Scholar

14. Matveev A, Vasiliev M. Dual formulation for higher spin gauge fields in (A)dS(d). Phys Lett. (2005) B609:157–66. doi: 10.1016/j.physletb.2005.01.032

CrossRef Full Text | Google Scholar

15. Zinoviev Y. On dual formulations of massive tensor fields. J High Energy Phys. (2005) 510:75. doi: 10.1088/1126-6708/2005/10/075

CrossRef Full Text | Google Scholar

16. Zinoviev Y. On dual formulation of gravity. J High Energy Phys. (2006) 10:9. doi: 10.1088/1126-6708/2006/10/009

CrossRef Full Text | Google Scholar

17. Gonzalez B, Khoudeir A, Montemayor R, Urrutia LF. Duality for massive spin two theories in arbitrary dimensions. J High Energy Phys. (2008) 9:58. doi: 10.1088/1126-6708/2008/09/058

CrossRef Full Text | Google Scholar

18. Khoudeir A, Montemayor R, Urrutia LF. Dimensional reduction as a method to obtain dual theories for massive spin two in arbitray dimensions. Phys Rev. (2008) D78:65041. doi: 10.1103/PhysRevD.78.065041

CrossRef Full Text | Google Scholar

19. Basile T, Bekaert X, Boulanger N. Note about a pure spin-connection formulation of general relativity and spin-2 duality in (A)dS. Phys Rev. (2016) D93:124047. doi: 10.1103/PhysRevD.93.124047

CrossRef Full Text | Google Scholar

20. Mignaco JA. Electromagnetic duality, charges, monopoles, topology, .…Braz J Phys. (2001) 31:235–46. doi: 10.1590/S0103-97332001000200014

CrossRef Full Text | Google Scholar

21. Hull C. Strongly coupled gravity and duality. Nucl Phys. (2000) B583:237–59. doi: 10.1016/S0550-3213(00)00323-0

CrossRef Full Text | Google Scholar

22. Hull C. Duality in gravity and higher spin gauge fields. J High Energy Phys. (2001) 109:27. doi: 10.1088/1126-6708/2001/09/027

CrossRef Full Text | Google Scholar

23. Deser S, Nepomechie RI. Gauge invariance versus masslessness in de Sitter space. Ann Phys. (1984) 154:396. doi: 10.1016/0003-4916(84)90156-8

CrossRef Full Text | Google Scholar

24. Hinterbichler K. Manifest duality invariance for the partially massless graviton. Phys Rev. (2015) D91:026008. doi: 10.1103/PhysRevD.91.026008

CrossRef Full Text | Google Scholar

25. Bunster C, Henneaux M, Hörtner S. Twisted self-duality for linearized gravity in D dimensions. Phys Rev. (2013) D88:064032. doi: 10.1103/PhysRevD.88.064032

CrossRef Full Text | Google Scholar

26. Boulanger N, Hohm O. Non-linear parent action and dual gravity. Phys Rev. (2008) D78:064027. doi: 10.1103/PhysRevD.78.064027

CrossRef Full Text | Google Scholar

27. Henneaux M, Lekeu V, Leonard A. Chiral tensors of mixed young symmetry. Phys Rev. (2017) D95:084040. doi: 10.1103/PhysRevD.95.084040

CrossRef Full Text | Google Scholar

28. Henneaux M, Lekeu V, Leonard A. The action of the (free) (4, 0)-theory. J High Energy Phys. (2018) 1:114. doi: 10.1007/JHEP01(2018)114

CrossRef Full Text | Google Scholar

29. Henneaux, M, Lekeu, V, Matulich, J, and Prohazka, S The action of the (free) ??? theory in six spacetime dimensions. J High Energy Phys. (2018) 6:57. doi: 10.1007/JHEP06(2018)057

CrossRef Full Text | Google Scholar

30. Lekeu V. Aspects of Electric-Magnetic Dualities in Maximal Supergravity. PhD thesis, Université Libre de Bruxelles (2018).

31. Hamermesh M. Group Theory and Its Application to Physical Problems (Dover Books on Physics). Dover Publications.

32. Bekaert X, Boulanger N. Tensor gauge fields in arbitrary representations of GL(D,R): duality and Poincare lemma. Commun Math Phys. (2004) 245:27–67. doi: 10.1007/s00220-003-0995-1

CrossRef Full Text | Google Scholar

33. Nutma T. xTras: a field-theory inspired xAct package for mathematica. Comput Phys Commun. (2014) 185:1719–38. doi: 10.1016/j.cpc.2014.02.006

CrossRef Full Text | Google Scholar