Multiscale Molecular Dynamics Simulation of Plasma Processing: Application to Plasma Sputtering

Molecular dynamics is an atomistic tool that is able to treat dynamics of atom/molecules/cluster assemblies mainly in the condensed and liquid phases. The goal of the present article is to provide a new methodology for describing all phenomena of plasma processing and beyond such as gas phase chemistry as well. Simulations of condensed matter and liquid processes by molecular dynamics are now readily accessible provided the interaction potentials are available, so quantitative parameters can be deduced as diffusion coefficient, etc. The situation is less clear for gas phase processes while they operate on larger space and time scales than for condensed phases and at lower specie densities. The present article is proposing a new methodology for describing plasma core interactions in taking into account experimental space and time scales. This is illustrated on a plasma sputtering process and deposition in a single simulation.

Introduction

Multiscale modeling of plasma processing and more generally of chemical processing can be considered as a “holy Grail” quest. Numerous work have been carried out since the 90' [1–21]. The ultimate goal is to treat in a “quick way” all the length and time scales of the processing, i.e., from nanometer to centimeter or even meter and from picosecond to hours. It is worth noting that such approaches have mainly concerned interaction with materials. Coupling between scales is achieved in a hierarchical way: The fundamental growth mechanisms, both in gas phase and at the materials interface, occur on the atomic scale. But, the geometry of the deposition/etching/treatment reactor and the associated operating parameters directly affect the chemical composition of the gas/plasma and the temperature at the growth surface, if any. The properties are, in turn, controlled by both atomic- and microstructural-scale features. This approach provides the missing link between chemical vapor deposition reactor design/operating conditions and the material structure/properties in the case of film growth. A tricky challenge is to use atomic scale simulation methods for enabling multiscale analysis. Kinetic Monte-Carlo methods are now relevant for describing a wide range of time and space scales [9, 12, 16, 22–25], including plasma materials processing reactors [26–28]. Recently Molecular Dynamics simulations (MDs), which are calculating all the trajectories of an ensemble of particle, have overcome the barrier of describing long time phenomena or rare infrequent events [29–34]. Indeed, MDs are highly demanding computational resources while “exactly” solving Newton or Langevin equations of motion, which, a priori prevents to reach long time dynamics without including additional ad-hoc powerful procedures. Moreover, the recent availability of (reactive) many-body potential [35, 36] has increased the interest of carrying MD simulations of complex systems both in materials science and in plasma/gas phases.

For going further, the present manuscript aims to provide a method for a full description of all steps of plasma processing, from gas phase to thin film growth or materials treatments.

Multiscale Molecular Dynamics

Molecular Dynamics Principles

Molecular Dynamics simulation (MD) is a powerful techniques for describing atomic and molecular processes at the nanoscales. It is solving the equation of motion using Newton equations of motion (or Langevin dynamics which includes energy dissipation through an additional friction term):

$\frac{{\partial }^2}{\partial t^2}\overrightarrow{r_i}=\frac{1}{m_i}{\overrightarrow{f}}_{\text{}i},{\overrightarrow{f}}_{\text{}i}=-\frac{\partial }{\partial r}V({\overrightarrow{r}}_{\text{}1}(t),{\overrightarrow{r}}_{\text{}i}(t),\cdots ,{\overrightarrow{r}}_{\text{}N}(t))(1)$

where ${\vec{r}}_i(t)$ is the position of atom i at time t with mass m_i, and V is the interaction potential between all N involved species. So solving such a set of equations requires the knowledge of the interaction potentials V and a set of initial conditions, preferably matching experimental situations.

It is widely recognized, using massively parallel programming and computers, that MDs are able to solve multi-million atom system dynamics (which corresponds to a volume of the order of 100 × 100 × 100 nm³) over several nanosecond time-scale with many body-interactions. In such a form MDs, today, are not able to go further in size and time scale. Recent advances either by coupling Monte-Carlo approaches or accelerated dynamics allowed to move time scales up to several seconds [34, 37]. Nevertheless, for addressing large reactor scales, it is necessary to find a way for rescaling experimental conditions toward simulation sizes and accessible computational time.

First of all, it is interesting to point out in which situations MDs are able to give relevant macroscopic information, ideally only depending on the interaction potential quality.

In condensed and liquid matter, distances between atoms or molecules are small enough for defining a simulation box identical to a representative part of the real system. For illustrating this, let us consider a single crystal, e.g., platinum. Pt density is 65 at. nm⁻³ so in a 10 × 10 × 10 nm³ cell there are already enough atoms for calculating average macroscopic quantity with enough precision, provided accurate interaction potentials are available, which is the case for Pt. For example self Pt diffusion coefficient can be calculated as well as numerous other quantities. In liquid, say water, there are 33 H₂O molecules per nm⁻³, so it is also possible to have a large number of molecules in a simulation box for reaching macroscopic quantities with enough precision, also if interaction potentials are of sufficient precision. In this case, time –dependent quantities are also deduced with enough accuracy while no hypothesis on space and time scales are done.

The situation in diluted media, among them plasmas, is quite different. For example, the density of a gas at atmospheric pressure, P = 1. 10⁵ Pa, is 2.4 10⁻² nm⁻³, so it is quite difficult to have a tractable simulation box with a significant atom/molecule number, say 50–1,00,000. Moreover low pressure plasma processing involves pressure as low as 0.1–10 Pa, which drastically lowers the possibility of handling molecular dynamics.

A second difficulty is arising when considering plasma—materials interaction: the fluxes of species on material surfaces. Typical fluxes for deposition/etching/surface treatment are typically of the order of 1. 10¹⁵ cm⁻².s⁻¹, which is close to one surface layer of a flat material surface per second. Such low flux is not reachable by MDs: it is not possible to directly wait for 1 s when the integration time interval for solving Equation (1) is in the range 0.1–5 femtosecond. This problem can be simply overcome by considering that the time interval for releasing an atom/molecule toward a surface should be large enough for allowing energy relaxation between two consecutive impacts on the surface. When choosing correctly this time interval, the results should not change when increasing it [38, 39]. But the true time of experiments is not recovered, and thus consequently macroscopic rates as etching, depositions rates, etc., also do not.

Pushing MDS Toward Multiscale Description of Plasma Processing

Considering all points listed above, realizing multiscale modeling based on MDs requires to be able to describe gas phase reactions in a realistic way and with a suitable time scale.

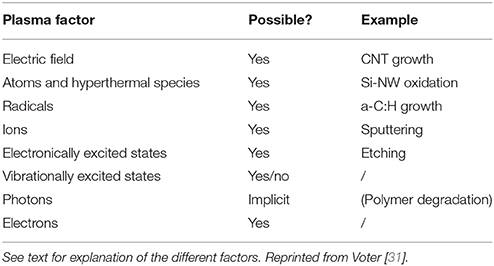
First of all, plasma is a complex medium including electrons, ions, ionic or neutral radicals, and excited states (electronic, rotational, and vibrational) of these latter species. The most difficult species to include in MDs are electrons and excited states [31]. Nevertheless, interaction potentials aiming at describing electron motion in MDs have been proposed: these are eFF [40, 41] and eReaxFF [42] force fields. Both are suitable for including electrons in simulations. eFF allows excited atomic states to be treated so monoatomic plasmas are reachable, while eReaxFF is explicitly treating electrons in chemical reactions using the reactive potential. At this stage electronic excited states can be included in MDs, and chemical reactions involving (ionic) radical, electron collisions, etc, are expected to work. A pending question is the description of vibrationally excited molecules and radicals. Vibrational excited states are quantified and their chemical reactivity, as occurring in plasma chemistry, is thus difficult to capture using classical MDs. Nevertheless some attempts have been done with a relative success [43] and are opening the way for new studies. Two ways are explored: increasing potential energy of the molecule by stretching the bonds to an appropriate length or increasing velocities of the atoms of the molecule which results in increasing kinetic energy of the atoms of the molecules resulting in oscillations with larger bond length. As a summary, Table 1 is displaying capabilities of MDs in including the nature and state of plasma species.

TABLE 1

Table 1. Different plasma factors that can be accounted for in MD simulations.

If we consider that all these issues specific to plasmas are solved or are giving a first approximation for starting MDs of physics/chemistry inside a reactor, a last work should be done: how to describe chemical reactions and or collisions at low pressure for which distances between interacting species are large, even when mean free path is lower than reactor size for allowing collisions and then reactions. If we recall that during two collisions, neutral species are traveling in a straight line while ions have an ambipolar diffusion in the electric fields (such a motion can be simulated using MDs), nothing happens except radiative de-excitation, if any. So the way for having a correct description of the plasma core is to build a simulation box with the same collision number and with a distance between plasma species greater than twice the largest interaction cutoff length. Recall that, the collision number is proportional in experiments and simulations, to the pressure-distance product through the relation:

$\begin{array}{rc}{n}_{coll}=\frac{Pd\sigma }{k_B{T}_g}& (2)\end{array}$

T_g is gas temperature, n is the number of collisions that take place in the gas, d is the reactor or simulation box size, P is the gas pressure in the is the reactor or simulation box, and σ is the collision cross section. Equating the collision number in simulation box (SB, label sim) and in the reactor (label exp) leads to the relation:

$\begin{array}{rc}{P}_{\text{exp}}{d}_{\text{exp}}=P_{sim}{d}_{sim}& (3)\end{array}$

Noticing that the SB volume can written as V_sim = S_simd_simwhere S_sim is the area normal to d_sim. If d_sim is along z axis then S_simis in the xy plane. Using $P_{sim}=\frac{N_{sim}}{V_{sim}}·k_B{T}_g$, with N_sim being the number of atoms in the SB, Equation (3) can be rewritten as:

$\begin{array}{rc}{N}_{sim}=\frac{P_{\text{exp}}}{k_B{T}_g}·S_{sim}·d_{\text{exp}}& (4)\end{array}$

which does not depend on d_sim. Nevertheless, d_sim can be calculated keeping in mind that the species in the gas/plasma phase should not be closer than the largest interaction cutoff r_cut used in the simulations. The distance l between gas/plasma phase species can thus be estimated to:

$\begin{array}{l}l={\left[\frac{S_{sim}·d_{sim}}{N_{sim}}\right]}^{1/3}>r_{cut},\text{ and thus}\\ d_{sim}>\frac{N_{sim}}{S_{sim}}·{r_{cut}}^3& (5)\end{array}$

And so the correct number of species in the simulation box can be deduced for matching experimental conditions. Moreover, if concentration, temperature, etc. gradients are present in the reactor, the gas/plasma can be divided in representative cells as in Figure 1, including substrate for thin film deposition/etching/treatments, if any. Each of these cells is associated with a simulation box of a size preserving the collision number, with different parameters, pressure and/or temperature for example. The dynamics is calculated in the considered box and at a relevant simulation time, the created species are allowed to move toward a neighboring simulation box describing the neighboring cell in the experimental setup (see Figure 1). So the full simulation box will be made of individual boxes communicating in the same way as in the experimental reactor. Each individual boxes is the “model” of its experimental counterpart and is appearing in the same ordering as the cells in the experiments. This mapping is displayed as a simplified 2D picture in Figure 1.

FIGURE 1

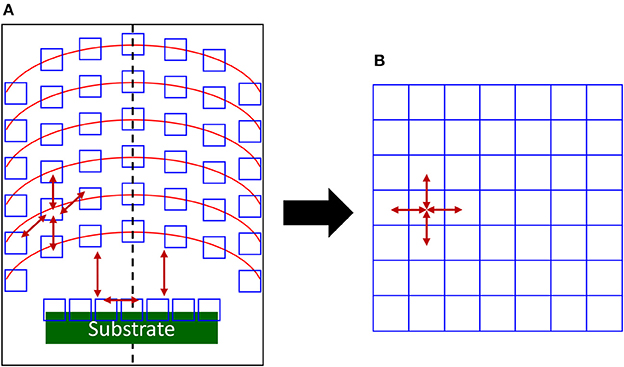
Figure 1. 2D schematics of the mapping of (A) a plasma reactor illustrating gradients at different reactor heights (red lines). Relevant experimental cells are open blue squares and arrows indicates species exchange between cells. The specific region of the substrate is green with its own cells interacting with the plasma phase. The dashed line is displaying the symmetry axis in this case and (B) to the corresponding full simulation box with communicating primary simulation boxes. Arrows gives the possible communications between the cells for covering all the experimental situations. Only a few are present for clarity.

When succeeding in this mapping, there is a remaining issue to be solved: converting the simulation time to the experiment time, in the gas/plasma phase.

It should be recalled that during the flight between two collisions, nothing happens that changes velocities and direction of the particles and that the velocity in simulations and experiments should be the same. As shown in Figure 2, if we are always considering that the collision number is the same in an experimental cell and its corresponding simulation cell, the unaffected velocity v between two collisions can be written as:

$\begin{array}{rc}v=\frac{d_{\text{exp}}}{t_{\text{exp}}}=\frac{d_{sim}}{t_{sim}},when{d}_{\text{exp}},d_{sim}>2\rho & (6)\end{array}$

where we define the traveled distances d_exp, d_sim and elapsed times t_exp, t_sim between two collisions, respectively for experiments and simulations. So d_exp, d_sim are the collision (interaction) mean free paths. ρ is the interaction distance, assumed for simplicity to be the same for the plasma species. Generalizing to different interaction lengths ρ_i is straight forward.

FIGURE 2

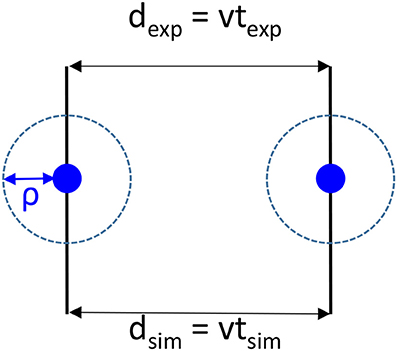
Figure 2. Schematics of the collision between two species (blue discs) both in simulations and in experiments and definitions of the interaction distance ρ, the distances d_exp, d_sim and times t_exp, t_sim between two collisions, respectively for experiments and simulations. v is the velocity which should be the same in experiments and simulations.

Thus the expected experimental time can be deduced from MDs as:

$\begin{array}{rc}{t}_{\text{exp}}=\frac{d_{\text{exp}}}{d_{sim}}.t_{sim},when{d}_{\text{exp}},d_{sim}>2\rho & (7)\end{array}$

When particle are interacting, then the interaction duration are the same in both experiments and simulations, because distances between species become identical:

$\begin{array}{rc}{t}_{\text{exp}}=t_{sim},when{d}_{\text{exp}},d_{sim}\le 2\rho & (8)\end{array}$

Accessing the “experimental time” will thus allow to directly calculate the reaction rate coefficients in the gas/plasma phase, while usually classical MDs is rather able to calculate reaction probability, which can be connected to reaction rates using relevant approximations.

This description of the plasma core reactivity is thus providing, in a space and time resolved way, the consistent source of species that will impact on the substrate surface and reactor walls leading to deposition/etching and/or other relevant surface interactions.

Such methodology is not limited to plasma processing, and it can be applied for any chemical processing, provided interaction potentials are available.

Application to Plasma Sputtering

For validating the method on a simple case, this MD procedure is applied for describing plasma sputtering deposition, including sputtering, transport of the sputtered atoms through the plasma phase and deposition on a substrate. At this stage including all plasma processes (electron collision using electric force fields, excited states, etc.) is beyond the scope of this article. The sputtering of a platinum target in an argon plasma with subsequent deposition onto a porous carbon is addressed, while both processes have been previously and separately studied using MD [44, 45] and experimentally [46, 47].

The simulation box is thus built as a porous carbon substrate, a platinum target, an argon gas in between. The simulations box size is 12 × 12 × 136 nm³, with periodic boundary conditions in the xy plane. The total number of atoms in the SB is 170,056, including 68,160 carbon atoms, 96,100 Pt atoms and 5,796 argon atoms among them 500 are randomly selected during the simulation to become Ar ions directed toward the Pt substrate with the cathode fall kinetic energy. The total Ar atom number is calculated using Equation (4) with experimental argon pressure P_Ar = 2.5 Pa (n_coll = 8), with a target to substrate distance of d = 6.5 cm [46, 47] and temperature T of 300 K.

The impinging Ar ion energy on the Pt target is chosen to be 500 eV: this allows significant sputtering of Pt atoms [45]. They are released toward porous carbon substrate every 2 ps. Ar gas atoms are thermostated at 300 K: this is mimicking energy transfers to the reactor wall after Ar⁺ – Ar and Pt – Ar collisions. Pt target is divided in 3 zones. The top of the crystal is made of 0.6 nm thickness zone with motionless atoms for preventing Pt target motion under Ar ion impact. A 7 nm thickness zone is thermostated for dissipating the energy released by the impinging Ar ions. The remaining zone, 2.4 nm thickness, is composed of free moving atoms. They are not thermostated for allowing correct escape kinetic energy of sputtered Pt [45]. The model porous carbon [48] is divided in two zones: the bottom zone with motionless carbon atoms, 0.6 nm thickness prevents porous carbon substrate motion under impact of depositing Pt atoms. The remaining part is thermostated at 300 K mimicking substrate temperature control, here at 300 K. As a summary, Figure 4 illustrates the MD simulation initial configuration.

The Pt interaction potential is the Embedded Atom Model (EAM) function [45, 49, 50], the Tersoff potential is used for C-C interactions [51]. Repulsive interaction of Ar with Pt, C, Ar are of the Moliere form Graves and Brault [52]. Pt-C interaction are modeled by an improved Lennard-Jones potential [44, 53]. The equations of motion (1) are integrated using velocity—Verlet algorithm, with a timestep of 0.1 fs. Such a short timestep is necessary for describing Ar ion—Pt interactions. The LAMMPS software [54]¹ is used for running the simulations. Damping time for Berendsen thermostats used for dissipating energy in the plasma region through Ar gas and in the carbon substrate and platinum target is 1 ps (see Figure 3). The total calculation time is 2 ns: during the first ns, the Ar ions are impinging the Pt target and sputtered Pt atoms are traveling toward the surface. An additional calculation time of 1 ns is needed for allowing last created Pt atoms to interact with the carbon substrate.

FIGURE 3

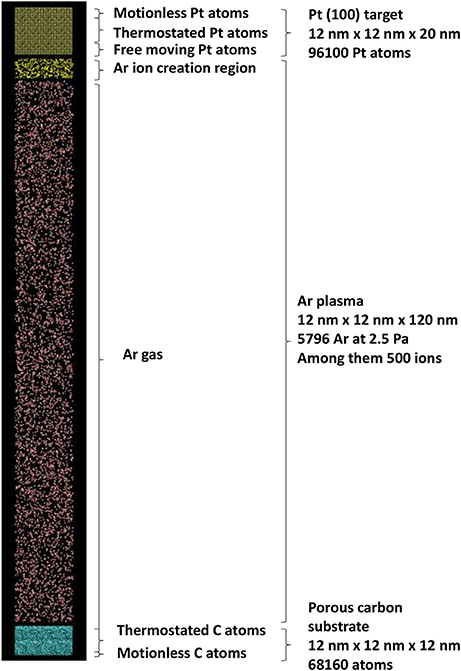
Figure 3. Schematics of the simulation cell with the initial positions of all species involved in sputtering plasma simulation.

Figure 4 is presenting the snapshots at 2 ns elapsed time (2 10⁷ iterations) for this present simulation of the full sputtering deposition process (Figures 4a–c) and with the snapshots obtained using simulations described in Xie et al. [44] (Figures 4d–f). In the latter case, the deposition occurs without Ar gas and for which the initial velocity distribution is calculated from the Thompson distribution at the substrate position [44], which is expected to take into account the collision between traveling Pt atoms and Ar background between target and substrate. The comparison between these two sets of snapshots (a–c and d–f) shows that cluster size distribution and density are the same, as well as the depth profiles. So it can be concluded that the reactor model is able to reproduce the deposition process. Moreover, it should be recalled that the Pt clusters morphologies were in agreement with experimental findings [44].

FIGURE 4

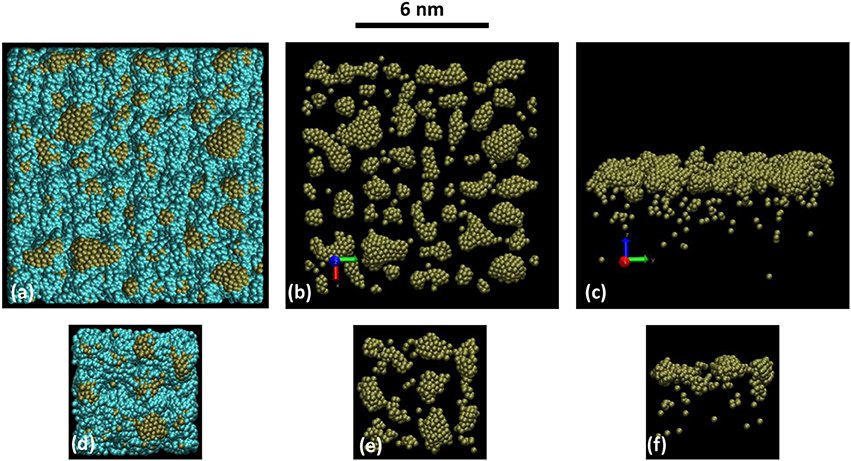
Figure 4. Snapshot views of (a–c) the present simulation after 2 ns calculation time: with the substrate 12 × 12 × 6 nm³ (a) without the substrate top (b) and side (c) views. Gas phase Ar close to the substrate are removed for clarity. And (d–f) from calculations presented in Xie et al. [44], on a 6 × 6 × 6 nm³ similar porous substrate (d) without the substrate top (e) and side (f) views. The scale bar on the top of the figures holds for all pictures. The number of Pt atoms per unit area is the same. Blue and brown colored atoms are C and Pt respectively.

So it can be deduced that the sputtering model of sputtering reactor presented here is accounting for a correct description of sputtering, transport and deposition of Pt onto porous carbon. It should be mentioned this is showing that the transport from the target to the substrate is correctly taken into account. This is establishing that the assumption of considering the collision number as a prescribed input of the model is correct. Even if the present model does not includes electron collisions, this is a first step that is assessing the interest of the approach. When there is no electron, say in chemical vapor deposition, this work gives the way for treating reactivity in the plasma core and the interaction with the materials. This will be achieved by a simulation box, with relevant dimensions calculated using Equations (4–5) filled with molecules of interest, interacting with the chosen substrate.

Conclusion

MDs capabilities in materials science are increasing with the availability of new reactive many-body potentials, macroscopic parameters are readily accessible and comparison with experiments is more and more efficient. For gases and plasmas, the connection between MDs and experiments is difficult due to the too diluted matter preventing direct realistic large scale simulation to be carried out. In the present article, when highlighting that considering the collision number in both MDS and experiments, a direct link can be established between MDS and experimental results allowing recovery of macroscopic time dependent coefficients (reactions, deposition, etching rates, etc.). A general procedure for describing plasma (chemical) processing is presented, suggesting a possible way for recovering reaction rates based on distance scaling between experiment and simulation conditions. As example, a sputtering model is presented which includes sputtering, transport, and deposition making use of the conservation of the collision number. It correctly describes the overall sputtering process, consistent with previous experimental findings. Future work will include electron collisions in the gas phase.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a shared affiliation, though no other collaboration, with the author.

Footnotes

1. ^http://lammps.sandia.gov

References

1. Srolovitz DJ, Dandy DS, Butler JE, Battaile CC, Paritosh. The integrated multiscale modelling of diamond chemical vapor deposition. JOM (1997). 49:42–7. doi: 10.1007/BF02914350

CrossRef Full Text | Google Scholar

2. Jensen KF, Rodgers ST, Venkataramani R. Multiscale modelling of thin film growth. Curr Opin Solid State Mater Sci. (1998) 3:562–9. doi: 10.1016/S1359-0286(98)80026-0

CrossRef Full Text | Google Scholar

3. Maroudas D. Multiscale modelling of hard materials: challenges and opportunities for chemical engineering. AIChE J. (2000) 46:878–82. doi: 10.1002/aic.690460502

CrossRef Full Text | Google Scholar

4. Merchant TP, Gobbert MK, Cale TS, Borucki LJ. Multiple scale integrated modelling of deposition processes. Thin Solid Films (2000) 365:368–75. doi: 10.1016/S0040-6090(99)01055-X

CrossRef Full Text | Google Scholar

5. Baumann FH, Chopp DL, de la Rubia TD, Gilmer GH, Greene JE, Huang H, et al. Multiscale Modelling of thin-film deposition: applications to Si device processing. MRS Bull. (2001) 26:182–9. doi: 10.1557/mrs2001.40

CrossRef Full Text | Google Scholar

6. Wadley HN, Zhou X, Johnson R, Neurock M. Mechanisms, models and methods of vapor deposition. Progr Mater Sci. (2001) 46:329–77. doi: 10.1016/S0079-6425(00)00009-8

CrossRef Full Text | Google Scholar

7. Cale TS, Bloomfield MO, Richards DF, Jansen KE, Gobbert MK. Integrated multiscale process simulation. Comp Mater Sci. (2002) 23:3–14. doi: 10.1016/S0927-0256(01)00216-6

CrossRef Full Text | Google Scholar

8. Sukharev V. Multiscale modelling of plasma etch processing. Vacuum (2002) 65:281–9. doi: 10.1016/S0042-207X(01)00432-8

CrossRef Full Text | Google Scholar

9. Dollet A. Multiscale modelling of CVD film growth—a review of recent works. Surface Coat Technol. (2004) 177–178:245–51. doi: 10.1016/j.surfcoat.2003.09.040

CrossRef Full Text | Google Scholar

10. Braatz RD, Alkire RC, Seebauer E, Rusli E, Gunawan R, Drews TO, et al. Perspectives on the design and control of multiscale systems. J Proc Control (2006) 16:193–204. doi: 10.1016/j.jprocont.2005.06.001

CrossRef Full Text | Google Scholar

11. Kleijn CR, Dorsman R, Kuijlaars KJ, Okkerse M, van Santen H. Multi-scale modelling of chemical vapor deposition processes for thin film technology. J Cryst Growth (2007) 303:362–80. doi: 10.1016/j.jcrysgro.2006.12.062

CrossRef Full Text | Google Scholar

12. Dkhissi A, Estève A, Mastail C, Olivier S, Mazaleyrat G, Jeloaica L, et al. Multiscale Modelling of the atomic layer deposition of HfO₂ thin film grown on silicon: how to deal with a kinetic monte carlo procedure. J Chem Theor Comp. (2008) 4:1915–27. doi: 10.1021/ct8001249

CrossRef Full Text | Google Scholar

13. Cheimarios N, Kokkoris G, Boudouvis AG. Multiscale modelling in chemical vapor deposition processes: coupling reactor scale with feature scale computations. Chem Eng Sci. (2010) 65:5018–28. doi: 10.1016/j.ces.2010.06.004

CrossRef Full Text | Google Scholar

14. Bogaerts A, Eckert M, Mao M, Neyts E. Computer modelling of the plasma chemistry and plasma-based growth mechanisms for nanostructured materials. J Phys D Appl Phys. (2011) 44:174030. doi: 10.1088/0022-3727/44/17/174030

CrossRef Full Text | Google Scholar

15. Vasenkov AV, Fedoseyev AI, Kolobov VI, Choi HS, Hong KH, Kim K, et al. Computational framework for modeling of multi-scale processes. J Comp Theor Nanosci. (2006) 3:453–8. doi: 10.1166/jctn.2006.005

CrossRef Full Text | Google Scholar

16. Tsalikis DG, Baig C, Mavrantzas VG, Amanatides E, Mataras D. A hybrid kinetic Monte Carlo method for simulating silicon films grown by plasma-enhanced chemical vapor deposition. J Chem Phys. (2013) 139:204706. doi: 10.1063/1.4830425

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Neyts EC, Bogaerts A. Understanding plasma catalysis through modelling and simulation—a review. J Phys D Appl Phys. (2014) 47:224010. doi: 10.1088/0022-3727/47/22/224010

CrossRef Full Text | Google Scholar

18. Crose M, Sang-Il Kwon J, Nayhouse M, Ni D, Christofides PD. Multiscale modelling and operation of PECVD of thin film solar cells. Chem Eng Sci. (2015) 136:50–61. doi: 10.1016/j.ces.2015.02.027

CrossRef Full Text | Google Scholar

19. Cheimarios N, Kokkoris G, Boudouvis AG. A multi-parallel multiscale computational framework for chemical vapor deposition processes. J Comp Sci. (2016) 15:81–5. doi: 10.1016/j.jocs.2015.08.011

CrossRef Full Text | Google Scholar

20. Elliott SD, Dey G, Maimaiti Y, Ablat H, Filatova EA, Fomengia GN. Modelling mechanism and growth reactions for new nanofabrication processes by atomic layer deposition. Adv Mater. (2016) 28:5367–80. doi: 10.1002/adma.201504043

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Crose M, Kwon JS-I, Tran A, Christofides PD. Multiscale modelling and run-to-run control of PECVD of thin film solar cells. Renew Energy (2017) 100:129–40. doi: 10.1016/j.renene.2016.06.065

CrossRef Full Text | Google Scholar

22. Rosenthal L, Strunskus T, Faupel F, Abraham JW, Bonitz M. Kinetic Monte Carlo simulations of cluster growth and diffusion in metal-polymer nanocomposites. In: Bonitz M, Lopez J, Becker K, Thomsen H, editors. Complex Plasmas. Cham: Springer International Publishing (2014). p. 321–70.

Google Scholar

23. Bal KM, Neyts EC. On the time scale associated with Monte Carlo simulations. J Chem Phys. (2014) 141:204104. doi: 10.1063/1.4902136

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Barbato A, Cavallotti C. Challenges of introducing quantitative elementary reactions in multiscale models of thin film deposition. Phys Status Sol. (2010) 247:2127–46. doi: 10.1002/pssb.200945454

CrossRef Full Text | Google Scholar

25. Marinov D, Teixeira C, Guerra V. Deterministic and Monte Carlo methods for simulation of plasma-surface interactions: deterministic and monte carlo methods for simulation. Plasma Proc Polymers. (2017) 14:1600175. doi: 10.1002/ppap.201600175

CrossRef Full Text | Google Scholar

26. Van Aeken K, Mahieu S, Depla D. The metal flux from a rotating cylindrical magnetron: a Monte Carlo simulation. J Phys D Appl Phys. (2008) 41:205307. doi: 10.1088/0022-3727/41/20/205307

CrossRef Full Text | Google Scholar

27. Strijckmans K, Depla D. A time-dependent model for reactive sputter deposition. J Phys D Appl Phys. (2014) 47:235302. doi: 10.1088/0022-3727/47/23/235302

CrossRef Full Text | Google Scholar

28. Bultinck E, Bogaerts A. Characterization of an Ar/O2 magnetron plasma by a multi-species Monte Carlo model. Plasma Sour Sci Technol. (2011) 20:045013. doi: 10.1088/0963-0252/20/4/045013

CrossRef Full Text | Google Scholar

29. Voter AF. A method for accelerating the molecular dynamics simulation of infrequent events. J Chem Phys. (1997) 106:4665–77. doi: 10.1063/1.473503

CrossRef Full Text | Google Scholar

30. Voter AF. Hyperdynamics: accelerated molecular dynamics of infrequent events. Phys Rev Lett. (1997) 78:3908–11. doi: 10.1103/PhysRevLett.78.3908

CrossRef Full Text | Google Scholar

31. Soerensen MR, Voter AF. Temperature-accelerated dynamics for simulation of infrequent events. J Chem Phys. (2000) 112:9599–606. doi: 10.1063/1.481576

CrossRef Full Text | Google Scholar

32. Perez D, Uberuaga BP, Shim Y, Amar JG, Voter AF. Chapter 4 accelerated molecular dynamics methods: introduction and recent developments. In: Annual Reports in Computational Chemistry. Elsevier (2009). p. 79–98. Available online at: http://linkinghub.elsevier.com/retrieve/pii/S1574140009005040

Google Scholar

33. Bal KM, Neyts EC. Merging metadynamics into hyperdynamics: accelerated molecular simulations reaching time scales from microseconds to seconds. J Chem Theor Comp. (2015) 11:4545–54. doi: 10.1021/acs.jctc.5b00597

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Plimpton SJ, Thompson AP. Computational aspects of many-body potentials. MRS Bull. (2012) 37:513–21. doi: 10.1557/mrs.2012.96

CrossRef Full Text | Google Scholar

35. Neyts EC, Brault P. Molecular dynamics simulations for plasma-surface interactions. Plasma Proc Polym. (2017) 14:1600145. doi: 10.1002/ppap.201600145

CrossRef Full Text | Google Scholar

36. Bal KM, Neyts EC. Direct observation of realistic-temperature fuel combustion mechanisms in atomistic simulations. Chem Sci. (2016) 7:5280–6. doi: 10.1039/C6SC00498A

CrossRef Full Text | Google Scholar

37. Pentecoste L, Brault P, Thomann A-L, Desgardin P, Lecas T, Belhabib T, et al. Low energy and low fluence helium implantations in tungsten: Molecular dynamics simulations and experiments. J Nucl Mater. (2016) 470:44–54. doi: 10.1016/j.jnucmat.2015.12.017

CrossRef Full Text | Google Scholar

38. Xie L, Brault P, Bauchire J-M, Thomann A-L, Bedra L. Molecular dynamics simulations of clusters and thin film growth in the context of plasma sputtering deposition. J Phys D Appl Phys. (2014) 47:224004. doi: 10.1088/0022-3727/47/22/224004

CrossRef Full Text | Google Scholar

39. Su JT, Goddard WA. Excited electron dynamics modeling of warm dense matter. Phys Rev Lett. (2007) 99:185003. doi: 10.1103/PhysRevLett.99.185003

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Jaramillo-Botero A, Su J, Qi A, Goddard WA. Large-scale, long-term nonadiabatic electron molecular dynamics for describing material properties and phenomena in extreme environments. J Comp Chem. (2011) 32:497–512. doi: 10.1002/jcc.21637

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Islam MM, Kolesov G, Verstraelen T, Kaxiras E, van Duin ACT. eReaxFF: a pseudoclassical treatment of explicit electrons within reactive force field simulations. J Chem Theor Comp. (2016) 12:3463–72. doi: 10.1021/acs.jctc.6b00432

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Somers W Atomic, Scale Simulations of the Interactions of Plasma Species on Nickel Catalyst Surfaces. University of Antwerp. Available online at: https://www.uantwerpen.be/images/uantwerpen/container2642/files/PhD-theses/Somers.pdf (Accessed September 2015).

43. Xie L, Brault P, Coutanceau C, Caillard A. Berndt J, Neyts E. Efficient amorphous platinum catalyst cluster growth on porous carbon: a combined molecular dynamics and experimental study. Appl. Cat. B. (2015) 62:21–6. doi: 10.1016/j.apcatb.2014.06.032

CrossRef Full Text

44. Brault P, Chuon S, Bauchire JM. Molecular dynamics simulations of platinum plasma sputtering: a comparative case study. Front Phys. (2016) 4:20. doi: 10.3389/fphy.2016.00020

CrossRef Full Text | Google Scholar

45. Cavarroc M, Ennadjaoui A, Mougenot M, Brault P, Escalier R, Tessier Y, et al. Performance of plasma sputtered Fuel Cell electrodes with ultra-low Pt loadings. Electro Commun. (2009) 11:859–61. doi: 10.1016/j.elecom.2009.02.012

CrossRef Full Text | Google Scholar

46. Brault P, Caillard A, Baranton S, Mougenot M, Cuynet S, Coutanceau C. One-step synthesis and chemical characterization of Pt C nanowire composites by plasma sputtering. ChemSusChem (2013) 6:1168–71. doi: 10.1002/cssc.201300236

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Pikunic J, Clinard C, Cohaut N, Gubbins KE, Guet JM, Pellenq RJM, et al. Structural modeling of porous carbons: constrained reverse Monte Carlo method. Langmuir (2003) 19:8565. doi: 10.1021/la034595y

CrossRef Full Text | Google Scholar

48. Brault P, Neyts E. Molecular dynamics simulations of supported metal nanocatalyst formation by plasma sputtering. Cataly Today (2015) 256:3–12. doi: 10.1016/j.cattod.2015.02.004

CrossRef Full Text | Google Scholar

49. Foiles S, Baskes M, Daw M. Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys. Rev. B (1986) 33:7983.

Google Scholar

50. Tersoff J. Modeling solid-state chemistry: interatomic potentials for multicomponent systems. Erratum Phys Rev B (1990) 41:3248. doi: 10.1103/PhysRevB.39.5566

CrossRef Full Text | Google Scholar

51. Graves DB, Brault P. Molecular dynamics for low temperature plasma–surface interaction studies. J. Phys D Appl Phys. (2009) 42:194011. doi: 10.1088/0022-3727/42/19/194011

CrossRef Full Text | Google Scholar

52. Morrow BH, Striolo A. Assessing how metal–carbon interactions affect the structure of supported platinum nanoparticles. Mol Simul. (2009) 35:795–803. doi: 10.1080/08927020902787812

CrossRef Full Text | Google Scholar

53. Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comp Phys. (1995) 117:1–19.

Google Scholar

54. Voter AF. Parallel replica method for dynamics of infrequent events. Phys Rev B. (1998) 57:R13985–8.

Google Scholar