- Wellcome Centre for Human Neuroimaging, Institute of Neurology, University College London, London, United Kingdom
To infer the causes of its sensations, the brain must call on a generative (predictive) model. This necessitates passing local messages between populations of neurons to update beliefs about hidden variables in the world beyond its sensory samples. It also entails inferences about how we will act. Active inference is a principled framework that frames perception and action as approximate Bayesian inference. This has been successful in accounting for a wide range of physiological and behavioral phenomena. Recently, a process theory has emerged that attempts to relate inferences to their neurobiological substrates. In this paper, we review and develop the anatomical aspects of this process theory. We argue that the form of the generative models required for inference constrains the way in which brain regions connect to one another. Specifically, neuronal populations representing beliefs about a variable must receive input from populations representing the Markov blanket of that variable. We illustrate this idea in four different domains: perception, planning, attention, and movement. In doing so, we attempt to show how appealing to generative models enables us to account for anatomical brain architectures. Ultimately, committing to an anatomical theory of inference ensures we can form empirical hypotheses that can be tested using neuroimaging, neuropsychological, and electrophysiological experiments.
Introduction
This paper is based upon the notion that brain function can be framed as Bayesian inference (Kersten et al., 2004; Knill and Pouget, 2004). Under this view, our brains possess an internal (generative) model of our environment that we use to predict sensory data, and to explain current data in terms of their causes (Friston et al., 2006). Another way of putting this is that we have prior beliefs about the state of the world, and beliefs about how this gives rise to sensations. On encountering data, we update our beliefs to form a posterior belief about the world. This has interesting implications for neuroanatomy. Specifically, for most generative models, it is possible to specify belief updating, evidence accumulation or inference, in terms of the passing of local messages between variables in the generative model (Wainwright and Jordan, 2008). In machine learning, this gives rise to efficient inference schemes; including predictive coding (Rao and Ballard, 1999), variational message passing (Winn and Bishop, 2005; Dauwels, 2007), belief propagation (Yedidia et al., 2005; Pearl, 2014), and expectation propagation (Minka, 2001). In neuroscience, local message passing provides a useful way to interpret synaptic communication. This implies that the dependencies between variables in a probabilistic generative model should be reflected in the anatomy of the brain.
The good regulator theorem (Conant and Ashby, 1970) provides a useful perspective on the form generative models must take. It states that any system capable of regulating its environment must be a model of that environment. This means the model used by the brain must be constrained by what it tries to regulate; i.e., the body and its surroundings. By appealing to the form of the real-world processes that generate sensory data, we can attempt to construct generative models like those that the brain uses, and to use the inferential message passing those models imply to interpret known neuroanatomy. To do so, we need to understand the relationship between models and messages.
The key notion that underwrites this is the Markov blanket (Pearl, 2014)—a statistical boundary that renders one set of variables conditionally independent from another. Importantly, if we know everything about a variable's Markov blanket, knowledge about things outside the blanket becomes uninformative about things inside the blanket, and vice versa. For example, if we know the state of the surface of an object, the outside world offers no useful information about its interior. If we knew everything about the present, the past would add nothing to our predictions about the future. The concept of a Markov blanket is central to recent formulations of self-organization (Friston, 2013; Kirchhoff et al., 2018) and, in the present context, for anatomy. Here, the conditional dependency structure is important, as it means a population of neurons representing a given variable only need receive connections from those populations representing its Markov blanket.
Throughout, we will see that anatomy and generative models offer constraints upon one another that limit the space of plausible brain architectures. Ensuring mutual and internal consistency in these domains represents the kind of conceptual analysis necessary to form meaningful hypotheses in neuroscience (Nachev and Hacker, 2014). This is supported by the complete class theorems (Wald, 1947; Daunizeau et al., 2010) that ensure the validity of treating neural computations as Bayes optimal, and allow us to frame questions in terms of the generative models used for inference, and the physical (biological) substrates of these inferences.
This is not the first attempt to map inferential computations to the anatomy of the brain, and builds upon several existing accounts of neuroanatomy in terms of predictive coding architectures (Bastos et al., 2012; Shipp, 2016). The novel aspects of this article come from recent theoretical advances that address categorical inferences (Friston et al., 2012b, 2015), planning (Attias, 2003; Botvinick and Toussaint, 2012; Kaplan and Friston, 2018), and the inferences that underwrite the activity of the ascending neuromodulatory systems (Yu and Dayan, 2005; Friston et al., 2014; Parr and Friston, 2017c). In addition, our focus is upon the form of generative models and their constituent Markov blankets, while previous accounts have often focused upon the anatomy implied by specific inferential procedures. The ideas we present here transcend specific variational inference schemes and, for this reason, we avoid committing to a particular scheme in this paper. This is to emphasize that the conditional independencies in the generative model are the key constraints over anatomy.
The organization of this review is as follows. First, we overview the notion of a generative model and introduce some of the general principles that will be necessary for understanding the rest of the paper. Following this, we try to ground these abstract ideas by illustrating their implications in the domains of perceptual inference, planning, neuromodulation, and movement. We conclude by considering some specific and testable hypotheses.
Generative Models and Markov Blankets
A generative model is a probabilistic description of how a given type of data might have been generated. It expresses prior beliefs about unobserved hidden states (or latent variables), the probabilistic dependencies between these states, and a likelihood that maps hidden states (i.e., causes) to sensory data (i.e., consequences). Such models can be used to predict new sensory data, and to infer the hidden states that could have caused observed data (Beal, 2003). While we rely upon several formal, mathematical, concepts in this paper, most of these formalisms can be expressed clearly through graphical models (Pearl, 1998). Inspired by recent papers that express electrical networks (Vontobel and Loeliger, 2003), analytical physics (Vontobel, 2011), and Quantum mechanics (Loeliger and Vontobel, 2017) using factor graphs, we adopt the same formalism to address computational neuroanatomy. Specifically, we use Forney-style factor graphs (Forney, 2001; Loeliger, 2004) as illustrated in Figure 1. This graphical notation provides a way to visualize any function that, like a probability distribution, may be decomposed into a product of factors. We use this notation for the generative models we will use in this paper. Each of these factors is plotted as a square node, and these are connected by an “edge” (line) if they are both functions of the same random variable. These graphs have previously been applied in the life sciences; notably, in theoretical neurobiology (de Vries and Friston, 2017; Friston et al., 2017a), and in biomedical engineering (Laar and Vries, 2016). One of the key advantages of these graphs is that they make the Markov blankets of each variable visually obvious.
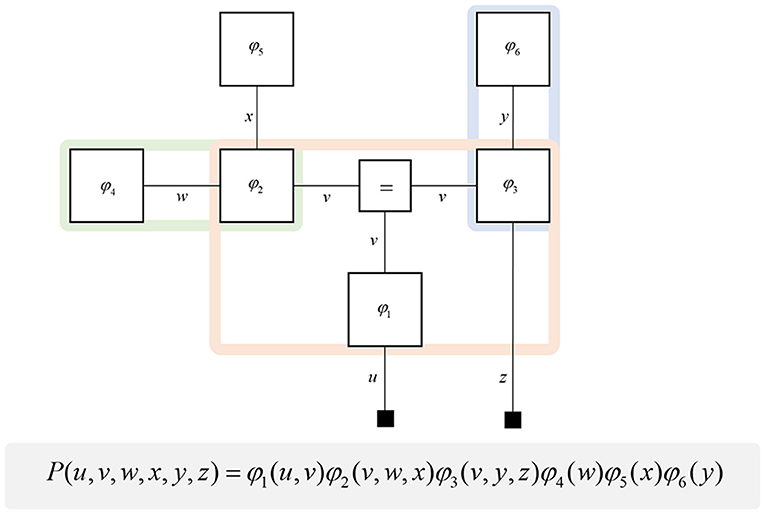
Figure 1. Forney factor graphs. The graphical model in this figure represents the (arbitrary) probability distribution shown below. Crucially, this distribution can be represented as the product of factors (ϕ) that represent prior and conditional distributions. By assigning each factor a square node, and connecting those factors that share random variables, we construct a graphical representation of the joint probability distribution. The “ = ” node enforces equality on all edges (lines) that connect to it. Small black squares represent observable data. This figure additionally illustrates a simple method for determining the Markov blanket of a variable (or set of variables). By drawing a line around all of the factor nodes connected to a variable, we find that the edges we intersect represent all of the constituents of the Markov blanket. For example, the green line shows that the blanket of w comprises x and v. The pink line shows the Markov blanket of v, which contains u, w, x, y, and z. The blue line indicates that v and z make up the blanket of y.
A common rhetoric for describing directed causal relationships is that “parent” variables cause “child” variables. Using these terms, a Markov blanket for a given variable may be thought of as its parents, children, and the parents of its children (Pearl, 2014). While this is a simple rule to follow, it becomes even easier to identify blankets when adopting a factor graph formalism. This is because the constituents of a Markov blanket are the set of variables that share factors with those variables insulated by the blanket. Figure 1 illustrates a procedure that identifies all the components of the Markov blanket associated with a random variable, simply by drawing a line around the factors it participates in. Anatomically, these blanket components should correspond to the neuronal populations that project to that population housing representations of the original variable.
One further concept that will be useful in what follows is the idea of “closing a box” (Loeliger, 2004) or finding the partition function (Forney and Vontobel, 2011) of part of the graph. This simply means summing (or integrating) over all of the variables represented by edges within a subgraph. Figure 2 demonstrates this idea by taking the graph of Figure 1 and converting it to a simpler graph by summing over all variables within a dashed box. For some generative models, this summation (or integration) may not be computationally or analytically feasible. However, we can approximate partition functions using free energy functionals (Dayan et al., 1995; Beal, 2003), as indicated in Figure 2. This becomes very important in active inference, which expresses brain function in terms of a principle of least action, that tries to minimize free energy over time (Friston et al., 2010). This is equivalent to pursuing behavior that gives rise to data consistent with the partition function of the brain's generative model; a process sometimes referred to as “self-evidencing” (Hohwy, 2016). This appeals to evidence in the technical sense (the probability that data could have been generated by a given model), which can be expressed as a partition function bounded by a free energy. A self-evidencing system is then one that acts to maximize the evidence for its model of its environment.
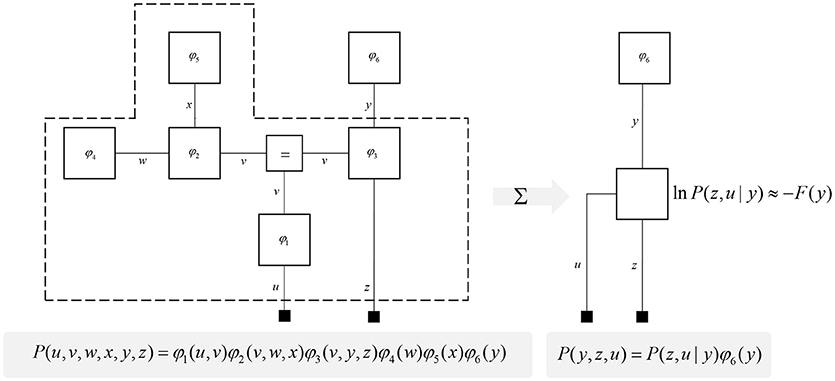
Figure 2. Partition functions and free energy. This schematic illustrates a useful operation known as “closing the box” or taking a partition function of part of a graph. By summing (or integrating) over all variables on edges within the dashed box, we can reduce this portion of the graph to a single factor that plays the part of a (marginal) likelihood. While it is not always feasible to perform the summation explicitly, we can approximate the marginal likelihood with a negative free energy. This affords an efficient method for evaluating subregions of the graph. Taking the partition function, or computing the free energy, for the whole graph allows us to evaluate the evidence sensory data affords the generative model.
In the following sections, we will unpack the idea of a generative model and its constituent Markov blankets in several domains. Before doing so, it is worth emphasizing the domain generality of this sort of approach. The ideas here have been applied, explicitly or implicitly, across applications as diverse as agency (Friston et al., 2012b), simple forms of pictographic language (Friston et al., 2017c), and interpersonal interactions (Moutoussis et al., 2014). Ultimately, all of these rely upon the idea of the passing of local messages across graphs that represent generative models. The differences in each domain depend upon the specific form of the underlying generative model—but, crucially, not the principles of message passing and implicit functional architectures. In other words, the tenets of belief updating covered in this review should, in principle, apply to any perceptual or cognitive domain and their associated neuronal systems. Furthermore, the generative models illustrated below do not exist in isolation. Rather, it is the association between each part of the brain's generative model that facilitates complex behaviors requiring interplay between perception and action.
Perceptual Inference
Dynamic Generative Models
To start, we consider some of the simplest generative models that capture useful features of the environment. Broadly, there are two important categories (Friston et al., 2017a): those that describe the evolution of variables in discrete time (Mirza et al., 2016), and those that describe continuous dynamics (Friston et al., 2011). Trajectories in discrete time can be characterized by a sequence of values over time. Assuming a Markovian system, the value at any position in the sequence depends upon that at the previous time. During each time step, the current state of the world gives rise to a sensory observation. These probabilistic dependencies are illustrated in the factor graph on the left of Figure 3. As the Markov blanket of the present state includes the proximal past, future, and sensory observations, we only need messages derived from these to infer the present (Beal, 2003).
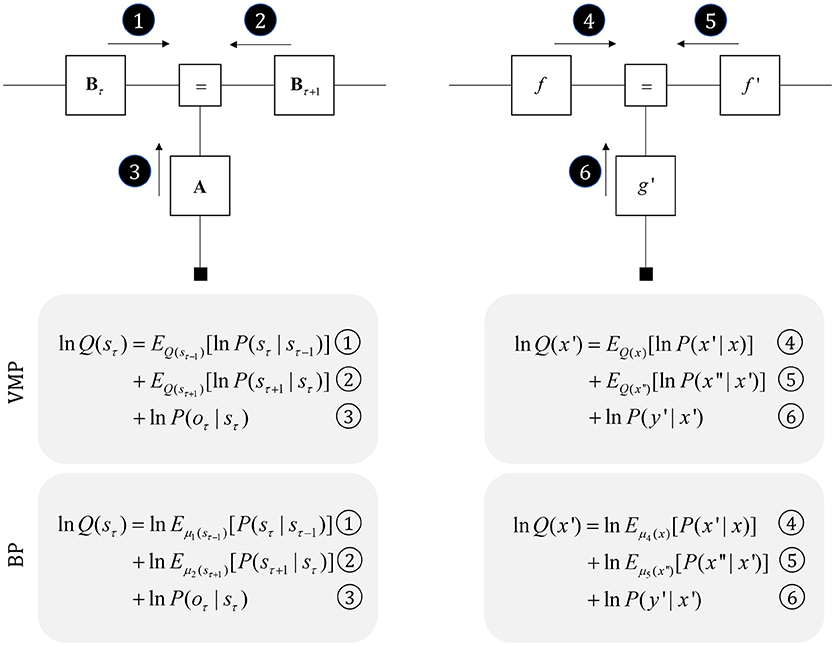
Figure 3. Perception as inference. This figure shows two generative models that describe hidden state trajectories, and the data they generate. On the left, we show evolution of discrete states (s), represented as the “edges” (lines) connecting the square nodes, with probabilistic transitions B from one state to the next. Each of these states gives rise to a discrete observation (o), as determined by a likelihood mapping A. On the right, we show the analogous factor graph for continuous dynamics, in which states are described in terms of their positions (x), velocities (x′), accelerations (x″), etc., coupled by flows (f) (rates of change) and give rise to continuous observations (y) determined by a likelihood mapping (g). Numbered black circles indicate the messages that would need to be passed to infer the current state (left) or velocity (right). The equations below show how these could be combined to form a belief about these variables using two different inference schemes (variational message passing and belief propagation). That the same message passing architecture applies in both cases emphasizes the importance of the generative model and its Markov blankets. The precise form of these message passing schemes is unimportant from the perspective of this paper, but for technical details on variational message passing schemes, we refer readers to Winn and Bishop (2005), Dauwels (2007), and for belief propagation (Loeliger, 2004; Yedidia et al., 2005), and to the Appendix, which provides a brief outline of these schemes. Table 1 provides a short glossary for some of the mathematical notation used in this and subsequent figures.
It is also possible to represent trajectories in continuous time using a sequence of numbers, but these no longer express states at each time step. Instead, we can represent the coefficients of a Taylor series expansion of the trajectory. These are the current position, velocity, acceleration, and subsequent temporal derivatives—sometimes referred to as “generalized coordinates of motion” (Friston et al., 2010). This formalism is a very general way to represent trajectories, and encompasses similar formulations used for control systems (Baltieri and Buckley, 2018). On the right of Figure 3, we illustrate that this representation takes the same graphical form as the discrete case. The Markov blanket of the velocity includes the position, acceleration, and the rate of change of the data. Messages from each of these, under certain assumptions (Friston et al., 2007), take the form of squared precision-weighted prediction errors. The gradients of these are the messages passed by predictive coding schemes (Rao and Ballard, 1999; Friston and Kiebel, 2009).
Generative models that evolve continuous time or discrete time likely coexist in the brain, mirroring the processes generating sensory data. While, at the level of sensory receptors, data arrive in continuous time, they may be generated in a sequential, categorical manner at a deeper level of hierarchical structure. For example, a continuous model may be necessary for low level auditory processing, but language processing depends upon being able to infer discrete sequences of words (which may themselves make up discrete phrases or sentences).
Neuronal Architectures
Before detailing the neuronal network that could perform these inferences, it is worth acknowledging the limitations of the generative model alone in trying to understand neuroanatomy at the microcircuit level. It may be that the brain makes use of auxiliary variables that, while in the service of inference, are not themselves sufficient statistics or messages. Probably the simplest example of this kind of variable is a prediction error, which quantifies the difference between the optimal solution and the current estimate of a continuous state (e.g., luminance contrast). In a biological setting, with inferences that play out in continuous time, gradient descents using prediction errors offer a plausible way to describe inferential dynamics (Rao and Ballard, 1999; Friston and Kiebel, 2009; Friston et al., 2017d). Figure 4 illustrates how we could represent the factor graph for discrete systems in neuronal network form, relating the messages highlighted in Figure 3 to axonal connections between populations of neurons. This represents input to prediction error cells in cortical layer IV that subtract current expectations, encoded in superficial layers, from the three incoming messages (which together represent the optimal expectation). These errors then drive changes in the superficial cells to update expectations (Miller, 2003; Shipp, 2016).
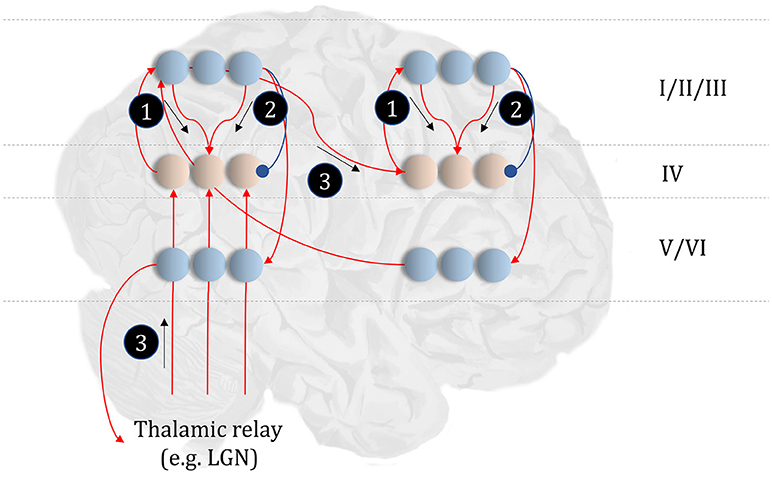
Figure 4. The anatomy of perceptual inference. The neuronal network illustrated in this figure could be used to perform inferences about the model of Figure 3. Neurons in cortical layer IV represent the spiny stellate cells that receive input from relay nuclei of the thalamus, and from lower cortical areas. The appropriate thalamic relay depends upon the system in question. In the context of the visual system, it is the lateral geniculate nucleus (LGN). In the somatosensory or auditory systems, it is the ventral posterior nucleus or the medial geniculate nucleus, respectively. Layer IV cells in this network signal prediction errors, computed by comparing the optimal estimate (obtained by combining the messages from its Markov blanket) with the current belief, represented in superficial cortical layers. Assuming a logarithmic code (as in Figure 3), this involves subtracting (blue connection) the current estimates of the sufficient statistics from the sum (red connections) of the incoming messages. The numbered circles indicate the same messages as in Figure 3. We could also represent messages 4, 5, and 6 in exactly the same way.
The move from the factor graph representation in Figure 3 to the neuronal network of Figure 4 proceeds as follows. First, each state (connecting line) in the factor graph is represented within a neuronal population in superficial levels of the network. The three units represented in Figure 4 correspond to beliefs about the state at three time-points. In the factor graph, these are the lines connected to the left B-factor (past state), the right B-factor (future state), and the line connecting the two (current state). We additionally include prediction error units in layer IV that relate to each of the belief states. As the prediction errors drive belief updating, they must receive the messages indicated in Figure 3, shown as connections from those populations from which the messages are derived in Figure 4. So far, we have accounted for layer IV and the superficial layers superimposed upon the posterior sensory cortices. The additional cortical column superimposed upon the frontal cortices replicates the same structure, but treats the states at the lower level as if they were sensory data.
Sensory input may come directly from sensory thalamic nuclei, or may come via sensory cortical areas (Thomson and Bannister, 2003). Both of these are shown in Figure 4, introducing the idea that the models in Figure 3 can form a repeating hierarchical pattern. This implies lower level hidden states may be generated from higher level states, where higher levels are defined as those that are further from sensory input. A consequence of this is bidirectional message passing between hierarchical levels (Friston et al., 2017c). This follows because a model that allows lower level states to be generated by higher level states mandates that each set of states sits in the Markov blanket of the other. An important feature of hierarchies in the brain is their temporal organization. As we ascend a cortical hierarchy, the temporal scale represented by each neuronal population generally increases (Hasson et al., 2008; Kiebel et al., 2008; Murray et al., 2014; Vidaurre et al., 2017). Those regions that sit near the top of these hierarchies are those associated with “delay period” activity or working memory (Funahashi et al., 1989; Goldman-Rakic, 1995); each defined by the persistence of a representation over a timescale that transcends that of stimulus presentation. To make the concept of a temporal hierarchy—or deep temporal models—more intuitive, consider the hierarchies inherent in reading: words are made up of letters, perceived over a fast time scale. Words themselves make up sentences, and paragraphs, each of which take longer to construct. Given the separation of timescales in real-world processes, like reading, the good regulator theorem (Conant and Ashby, 1970) implies generative models in the brain should adopt the same organization. As such, we could interpret a neuronal population at a higher level as encoding a short trajectory at the lower level, much as a sentence represents a short sequence of words. To illustrate this in Figure 4, we have only shown connections between the higher level cortical column and the first neuron in the sequence at the lower level. This is consistent with the generative models used to simulate reading (Friston et al., 2017c) and classic working memory tasks (Parr and Friston, 2017d) using active inference.
Empirical Constraints
This neuronal network illustrates a very important point. The architectures suggested by theoretical considerations must be constrained by our knowledge of real neuroanatomy (Douglas and Martin, 2004; Shipp, 2007). For example, sensory thalamic projections to the cortex, including those from the lateral geniculate nucleus, target the spiny stellate cells in (granular) layer IV of the cortex (Zeki and Shipp, 1988; Felleman and Van Essen, 1991; Callaway and Wiser, 2009). These cells project to more superficial layers, which themselves project to higher cortical regions. Connections from higher to lower regions of cortex (Bai et al., 2004), or from cortex to sensory thalamus (Olsen et al., 2012), arise from deep layers; notably layer VI (Thomson, 2010). To conform to this anatomy, the most obvious (but perhaps not only) solution is to assume that cells encoding the expectations are duplicated in the deep layers, illustrating the importance of mutual constraints between theory and known anatomy.
A similar constraint comes from neuropsychological research (Heinke and Humphreys, 2003; Testolin and Zorzi, 2016; Parr et al., 2018b). Not only should the networks we propose be internally consistent in both anatomical and theoretical domains, but they should give rise to similar deficits when disrupted; i.e., when the associated structures are lesioned. For example, if we were to remove message 3 (Figure 4) through a disconnection, or damage to the associated sensory organ, our prediction would be that internally generated influences (messages 1 and 2) would dominate perception. This is entirely consistent with conditions such as Charles Bonnet syndrome (Teunisse et al., 1996; Menon et al., 2003; Reichert et al., 2013), in which people with retinal damage experience complex visual hallucinations; something also associated with hypometabolism of early visual areas as observed with Lewy body dementia (Motohiro et al., 1987; Khundakar et al., 2016). Similarly, people with loss of proprioceptive or somatosensory input from an amputated limb can continue to experience percepts relating to absent body parts (Frith et al., 2000; De Ridder et al., 2014). These phantom phenomena are highly consistent with the theoretically derived architecture of Figure 4 (De Ridder et al., 2014). We will appeal to similar examples throughout, to illustrate the face validity of this anatomical process theory.
While the anatomy of Figure 4 might be suitable for describing trilaminar archicortical regions (Wesson and Wilson, 2011), such as the olfactory cortex and hippocampus, isocortical regions subdivide into six, histologically distinct, layers. To understand the need for additional inferential machinery, we note that perceptual inference is not a passive process. Sensory data depends to a large extent upon the orientation and position of mobile receptive epithelia (Parr and Friston, 2017a). This emphasizes the fact that an important class of latent variable is the set of hidden states over which we have control. These include the positions of body parts, and give rise to multiple data modalities (notably, visual, and proprioceptive). This provides an interesting perspective on the connections between frontal and posterior cortices, as the former houses representations of controllable variables, while the latter receives data about their sensory consequences (Shulman et al., 2009; Szczepanski et al., 2013; Limanowski and Blankenburg, 2018). Descending connections from frontal to parietal areas can then be thought of as predictions about the sensory input expected contingent upon a given action (Zimmermann and Lappe, 2016), endorsing an enactive perspective (Bruineberg et al., 2016; Kiverstein, 2018) on perceptual inference. In the context of the visual system, this implies visual space might be represented in terms of saccadic sensorimotor contingencies [i.e., “what I would see if I were to look there” (Parr and Friston, 2017a)]. The brain's ability to select future sensory data implies beliefs about the future, and about how it will choose to sample these data; i.e., planning.
Planning
Partition Functions and (Expected) Free Energy
One way to think about planning is that it represents the selection from several possible behavioral trajectories, or models of future action (Kaplan and Friston, 2018). This implies a set of models or policies that differ only in the state transitions they imply. We can represent this graphically by augmenting Figure 3 with a “policy” variable that represents which trajectory is in play. The edge related to this variable connects to the B factors, encoding transitions, and to an E factor, that represents a prior belief about which policy to engage in. To infer the appropriate behavioral policy, we can appeal to the idea of “closing the box” as in Figure 2, taking the partition function of the sequence of states, conditioned upon a policy, and their outcomes. As discussed in the section Generative models and Markov blankets partition functions are a way of summarizing part of a graphical model and may be approximated by a free energy functional. This suggests we can perform inference by passing messages in the subgraph within the dashed lines in Figure 5, computing posterior beliefs about the constituent variables conditioned upon a behavioral policy. These posteriors can then be used to calculate the free energy of each policy, providing evidence for or against each hypothesized trajectory. This treats planning as an inferential (Attias, 2003; Botvinick and Toussaint, 2012) model selection process.
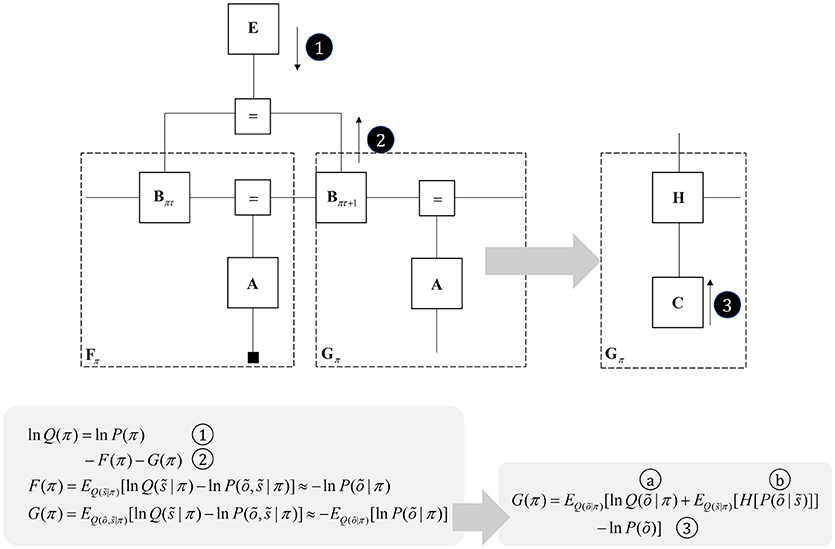
Figure 5. Planning as inference. This figure illustrates the use of partition functions to evaluate regions of the graph (see also Figure 2). Crucially, while we can approximate a partition functions based upon past data using a free energy functional, we do not yet have data from the future. This means we instead need an expected free energy, to approximate the partition function under posterior predictive beliefs. The panel below the graph illustrates how we can re-express the expected free energy such that we can represent this portion of the graph in terms of two new factors: a marginal belief about future outcomes and a likelihood that becomes an expected entropy after taking the expectation. As G depends upon beliefs about outcomes, but not upon the outcomes themselves, we can compute this prior to observing data. In some accounts of active inference, this is made explicit by treating C as a prior that connects to a factor G (that acts as if it were a likelihood generating policies from outcomes). The circled numbers and letters here are consistent with those in Figure 6. For technical accounts of these equations, please see Friston et al. (2017d), Parr and Friston (2018c).
Once we acknowledge the need for beliefs about the future, we run into a problem. By definition, sensory data from the future have not yet been collected, and we cannot compute their associated free energy. We can resolve this by using beliefs about the future to compute predictions about the sort of data expected under each policy. Averaging with respect to this “posterior predictive” density (probability distribution) allows us to compute an expected free energy (Figure 5) that approximates the partition function for future states and observations (Friston et al., 2015). This takes an interesting form when we use Bayes rule to re-express the generative model within the dashed box (gray arrow). Here, we have used the fact that the joint distribution over states and outcomes can be expressed either as the product of a prior and a likelihood, or as a posterior and a marginal distribution over the data (C). If we assume that the latter does not depend upon the policy, this acquires an important interpretation. As plans depend upon the negative expected free energy, those policies that give rise to data consistent with C become more likely to be selected. This allows us to think of this marginal distribution as encoding preferences or goals. Figure 5 illustrates this with a decomposition of the expected free energy (Friston et al., 2015) into a goal directed (message 3) and an uncertainty resolving (information gain) term (“a” and “b”). The consequence of this is that the best behavioral policies are those that balance exploitative (goal-directed) imperatives with explorative (information seeking) drives (Parr and Friston, 2017c).
Free energy approximations to model evidence (or expected model evidence) depend upon how closely beliefs (Q) approximate posterior distributions. This means that we must perform the message passing of Figures 3, 4 to ensure good approximations before using the free energy to adjudicate between policies that select new data as in Figure 5. We have previously argued (Friston et al., 2017d; Parr and Friston, 2018b) that these scheduling constraints may form the basis for theta rhythms in the brain, as this is the frequency at which we tend to sample the world around us (e.g., through saccadic eye movements). This implies that between actions we optimize posterior beliefs so that they can be used to compute free energy functionals to evaluate the next action.
The Basal Ganglia
The basal ganglia are a complex network of subcortical structures (Lanciego et al., 2012). They are engaged in a set of hierarchically organized cortico-subcortical loops, thought to underwrite planning and behavioral policy selection (Haber, 2003; Yin and Knowlton, 2006; Graybiel and Grafton, 2015; Jahanshahi et al., 2015). The anatomy of cortico-basal ganglia communication depends upon two distinct circuits, referred to as the direct and indirect pathways. Each has an opposing influence upon behavior, with the direct pathway facilitating, and the indirect suppressing, voluntary behaviors (Freeze et al., 2013). It is tempting to associate the two different messages (Figure 5) required to compute beliefs about policies with each of these pathways, as in Figure 6.
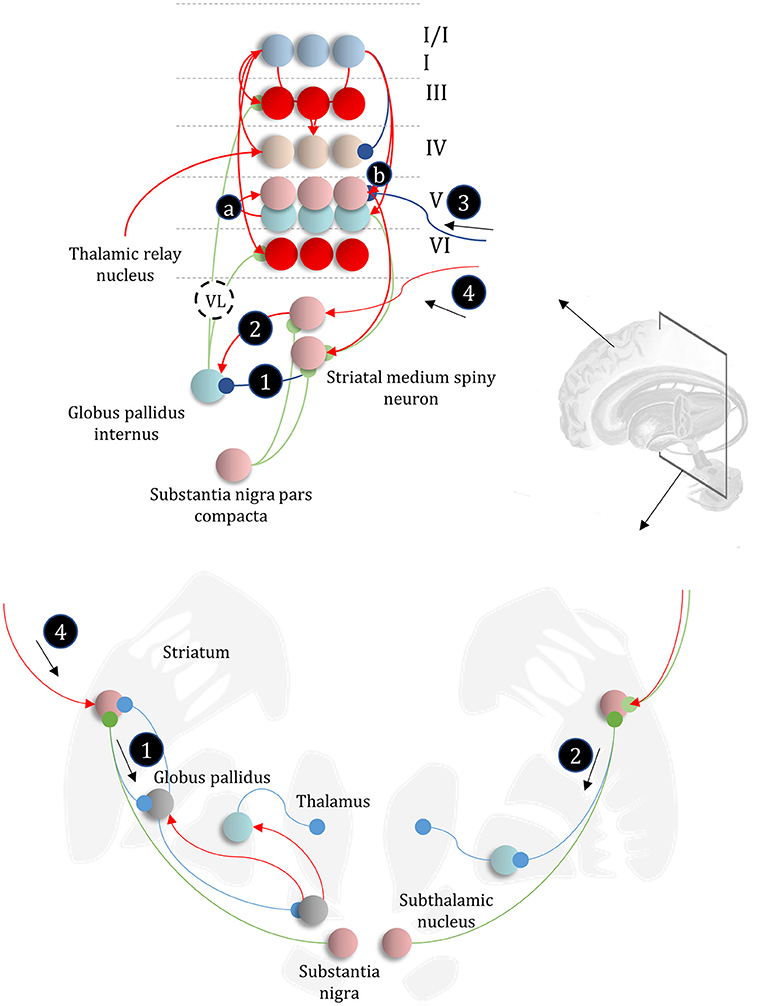
Figure 6. The basal ganglia. In the upper part of this figure, we show the same network as in Figure 4, but augmented such that it includes layer V cells encoding the gradients of the expected free energy and posterior predictive beliefs. These project to direct pathway medium spiny neurons and combine to give the expected free energy. This has a net inhibitory influence over the output nuclei (the globus pallidus internus and the substantia nigra pars reticulata), while the indirect pathway has a net excitatory effect. These are consistent with messages 2 and 3, respectively (the numbering is consistent with Figures 5, 7). Once the direct and indirect messages are combined at the globus pallidus internus, this projects via the thalamic fasciculus to the ventrolateral (VL) and ventral anterior nuclei of the thalamus. These modulate signals in the cortex, consistent with averaging beliefs about states under different policies, to compute average beliefs about the states (red neurons). Once we consider the hierarchical organization of this system (Figure 7), we need beliefs about preferences, derived from states at the higher level (message 3) combined with a posterior predictive belief (a) and an expected entropy term (b) to compute the gradient of the expected free energy. We additionally require a cortical input to the indirect pathway neurons, representing an empirical prior belief about policies (message 4—see Figure 7 for details). The coronal view of the basal ganglia, in the lower part of the figure, shows the connectivity of the direct (right) and indirect (left) pathways, to illustrate their consistency with the network above, but including the additional synapses that are not accounted for in the message passing. The substantia nigra pars compacta is included, and this modulates the weighting of messages 2 and 3. Please see the section below on Neuromodulation for details as to the emergence of dopaminergic phenomena from a generative model. In summary, the layers of the cortical microcircuit shown here represent beliefs about states under a given policy (I/II), beliefs about states averaged over policies (III), state prediction errors (IV), expected free energy gradients and predicted outcomes (V), and beliefs about states averaged over policies (VI).
The striatum, consisting of the caudate and putamen, is the main input nucleus of the basal ganglia (Shipp, 2017). It is the origin of the direct and indirect pathways, associated with the initiation and inhibition of behavioral policies, respectively. Each pathway is associated with phenotypically distinct striatal medium spiny neurons. They are often characterized pharmacologically, with facilitatory D1-dopamine receptors predominating in direct pathway neurons, and suppressive D2-dopamine receptors on indirect pathway neurons (Smith et al., 1998); allowing dopamine to modulate the balance between these two pathways. However, the phenotypic differences extend beyond pharmacology to include anatomical connectivity, morphology, and electrophysiological properties (Gertler et al., 2008).
The differences between direct and indirect pathway medium spiny neurons are consistent with the form of the messages required to compute posterior beliefs about policies. While the direct pathway neurons have an inhibitory effect on the output nuclei of the basal ganglia, the indirect pathway has a net excitatory effect. The latter depends upon an additional GABAergic (inhibitory) synapse from the globus pallidus externus to the subthalamic nucleus (Jahanshahi et al., 2015), which has (excitatory) glutamatergic projections to the globus pallidus internus, converging with the direct pathway (Figure 6). Morphologically, D1-expressing neurons are well suited to combining input from many cortical areas to compute a free energy (or expected free energy) functional (Gertler et al., 2008). Compared to their D2-expressing counterparts, they have an extensive dendritic arbor, accompanied by a relatively high action potential threshold, suggesting their firing is highly context dependent, drawing from a wide range of cortical areas. Given the representation of posterior beliefs in the cortex (Figure 4), this suggests direct pathway medium spiny neurons are very well placed to compute the free energy expected under a given policy (i.e., message 2 in Figure 5).
In contrast, indirect pathway striatal neurons have a smaller dendritic arbor (Gertler et al., 2008). This is consistent with message 1 in Figure 5, that does not depend upon cortically held beliefs (Parr and Friston, 2017b). The idea that the message from these neurons is independent of the cortex is clearly a step too far, as these cells do receive some cortical input. One way to resolve this is to note that the factor E, while playing the role of a prior, becomes an empirical prior1 once we move to a hierarchical network (Figure 7). This is because we can treat prior beliefs about policies as conditioned upon the outcomes at a higher level. In other words, habitual behaviors are dependent upon a slowly changing context. Interpreting cortical input to the indirect pathway as a descending signal from higher cortical regions is consistent with the difference in the distribution of cortical input to the direct vs. indirect pathways (Wall et al., 2013). The latter tends to receive more input from frontal regions, often thought to sit higher in cortical hierarchies (Felleman and Van Essen, 1991) than the sensory regions projecting to the direct pathway neurons. Endorsing a hierarchical aspect to basal ganglia function, the striatum reflects the hierarchical structure of the cortex in the connections it receives, its interactions with the midbrain, and the behaviors it modulates. For example, dorsolateral parts of the striatum receive dopaminergic input from the substantia nigra pars compacta and cortical input from sensorimotor cortices (Haber, 2003). In contrast, the ventral striatum receives dopaminergic input from the ventral tegmental area, and cortical input from limbic cortices.
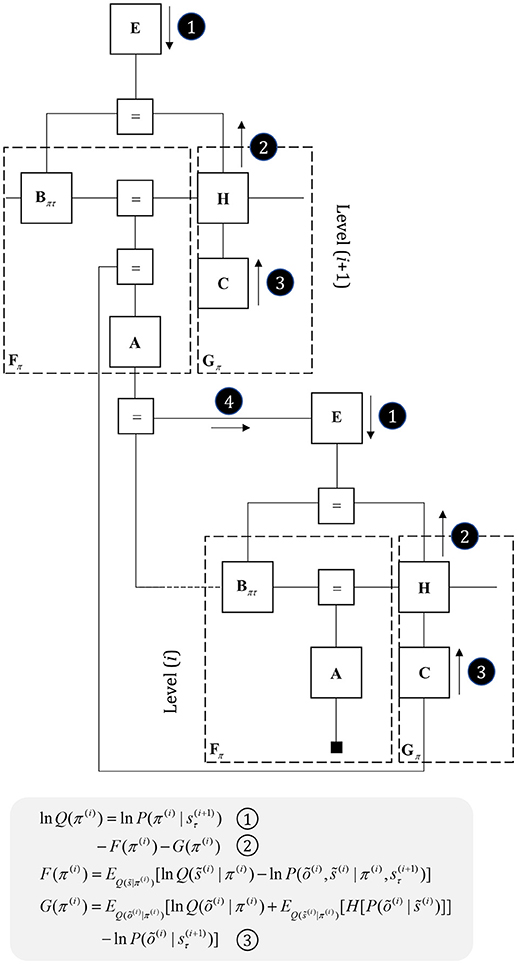
Figure 7. Hierarchical models. This figure illustrates the extension of Figure 5 to two hierarchical levels; although this pattern could be recursively extended to an arbitrary number of levels. There are three points at which the levels interact. The first is a mapping from the outcomes of the higher level to the initial states at the lower level (A to “ = ” to B). An example of this might be a mapping from a sentence level representation to the first word of that sentence. The second associates higher level outcomes with low level empirical priors over policies (A to “ = ” to E). Finally, we allow the low-level preferences to depend upon higher level states (“ = ” to C).
Cortico-Subcortical Networks
In addition to providing a computational hypothesis for basal ganglia function that formalizes the notion that they are engaged in planning (i.e., policy evaluation), we can now refine the cortical anatomy of Figure 4 to include the signals required to compute the expected free energy in the striatum (Friston et al., 2017c). In Figure 6, we show the addition of two cell populations in layer V. These represent posterior predictive beliefs about the sensory outcomes of a given policy, and the gradient of the expected free energy with respect to these beliefs. The latter is an auxiliary variable, like the prediction errors of Figure 4. It is computed based upon the C factor, the entropy2 of the likelihood (a) (weighted by beliefs about states), and posterior predictive beliefs about outcomes (b) (Friston et al., 2017a). Weighting the expected free energy gradients by these predicted outcomes allows us to compute the expected free energy associated with a given policy. The reason for restricting these cell populations to cortical layer V is that the cortical input to striatal medium spiny neurons arises almost exclusively from this layer (Shipp, 2007; Wall et al., 2013). There are several types of layer V pyramidal cell, two of which project to the striatum (Kim et al., 2015). One of these additionally projects to subcortical regions, including the superior colliculus, and we will return to this in the section on Movement. A further modification of the anatomy of Figure 4 is that we have included beliefs about states under a given policy (layers I and II), and beliefs about states averaged over all policies (layers III and VI) (FitzGerald et al., 2014). The latter are the sources of ascending and descending messages, and are computed by weighting conditional beliefs from superficial layers by beliefs about policies from the output nuclei of the basal ganglia (via the ventrolateral nucleus of the thalamus McFarland and Haber, 2002).
While the computational anatomy appears to be consistent with known basal ganglia circuitry, there are several outstanding questions that need resolution. The first of these is the number of synapses between the indirect pathway neurons and the output nuclei. The upper and lower parts of Figure 6 emphasize this, with the inclusion of intermediate synapses in the lower part. While the direct pathway involves a single synapse between the striatum and globus pallidus internus (or substantia nigra pars reticulata), the indirect pathway is trisynaptic. A single additional inhibitory synapse makes intuitive sense, as this converts a net inhibition to an excitation (consistent with message 2 in Figure 6). However, the additional excitatory synapse appears redundant. A plausible theory—that accounts for this—relies upon the timing of messages in each pathway (Nambu, 2004). This suggests that a short latency signal from the direct pathway disinhibits a select set of policies, based upon the highly specific contextual signals it receives from the cortex. This is followed by a much broader inhibition of a priori implausible policies by the slower indirect pathway. The timing of these signals is thought to contribute to a center-surround pattern of activity in the basal ganglia outputs which ensures precise posterior beliefs about policies. We could also argue that, if the indirect pathway receives slowly changing contextual input from higher cortical areas, it makes sense that its signals should play out over a longer time-span. The presence of recurrent connectivity within the indirect pathway, including arkypallidal neurons (Mallet et al., 2012) from the external globus pallidus to the striatum, reinforces this idea, as this could sustain these representations over a longer time.
A second question concerns the role of the hyperdirect pathway (Nambu et al., 2002), which provides a subthalamic input, and why it is necessary to have an additional cortical input. A plausible, if speculative, role for this pathway is in signaling when to implement each new policy, as these cortico-subthalamic axons arise from motor neuron collaterals (Giuffrida et al., 1985). Given the highly non-specific terminations of the hyperdirect pathway in the basal ganglia outputs, it seems more likely that this signals when an action has taken place, as opposed to contributing directly to policy selection. This is consistent with the theta cycle at which new actions (e.g., saccades) are performed (although the components of these actions may be much faster), and its correlates in the subthalamic nucleus during sensorimotor tasks (Zavala et al., 2017). The hyperdirect pathway may then use motor signals to entrain the pacemaker circuits associated with this nucleus (e.g., subthalamopallidal networks) that include neurons oscillating at a theta frequencies (Plenz and Kital, 1999). Speculatively, this could be an important part of the scheduling of the message passing involved in planning, compared to that for state inferences. Failures of scheduling may underwrite aspects of conditions like Parkinson's disease (Cagnan et al., 2015).
Pathologies of the Basal Ganglia
Disorders of basal ganglia nuclei are well characterized. It is a useful test of the validity of the proposed anatomy to see whether deficits in these computational units are consistent with behaviors observed in neurological practice. Parkinson's disease is a common disorder in which degeneration of neurons in the substantia nigra pars compacta lead to dopamine deficits in the striatum (Albin et al., 1989). This leads to an akinetic rigid syndrome, characterized by a difficulty initiating movements (Clarke, 2007). If we interpret dopamine as weighting the balance of messages derived from expected free energy compared to empirical priors (Friston et al., 2014; FitzGerald et al., 2015; Schwartenbeck et al., 2015), the loss of dopamine could lead to excessive reliance on these slowly changing priors that do not take account of changes in context over the timescale necessary for movement. We have previously demonstrated behaviors that become increasingly random as the contribution from the expected free energy is down-weighted in the presence of flat priors (Parr and Friston, 2017d). Under the more realistic priors required for (for example) maintenance of postural stability (Dokka et al., 2010), it is easy to see how an excessive reliance upon these might lead to akinesia and rigidity. This suggests Parkinson's disease could be thought of as a syndrome of excessive reliance upon slowly changing beliefs at higher hierarchical levels to direct behavior (Jávor-Duray et al., 2017). Reliance upon higher levels might account for the bradykinesia and bradyphrenia of this disorder (Mayeux, 1987), as faster processes lose their influence over (motor and mental) behavior. In contrast, increasing dopamine levels might decrease the influence of higher levels, leading to shorter term planning and impulsive behaviors of the sort associated with pro-dopaminergic Parkinson's medications (Cools et al., 2003; Michele and Anna Rita, 2012).
An intriguing feature of Parkinson's disease is that, in certain contexts, patients can perform complex fluent motor behavior; e.g., cycling (Snijders and Bloem, 2010). This phenomenon, known as kinesia paradoxa (Banou, 2015), typically relies upon some form of cueing (Glickstein and Stein, 1991), signaling a behavioral context. The hierarchy of Figure 7 offers a framework in which we can try to understand this effect. While dopaminergic deficits limit the influence of message 2 on policy selection, there is another route by which sensory data can influence behavior. Although somewhat circuitous, messages may be passed up to the higher level, allowing inference about slowly changing hidden states. These then influence lower level policies via message 4. This indicates that understanding the structure of message passing architectures might afford opportunities for the design of rehabilitative therapies or medical devices (Ferrarin et al., 2004) that make use of alternative routes through the set of Markov blankets comprising a generative model.
While Parkinson's disease represents reduced direct pathway influences, there are other syndromes that occur if the indirect pathway is damaged. These provide support for the idea that the indirect pathway uses prior beliefs to prevent the performance of implausible behavioral policies. One such syndrome is hemiballismus, resulting from damage to the subthalamic nucleus (Hawley and Weiner, 2012). This syndrome is characterized by involuntary ballistic movements that the indirect pathway fails to suppress. This is consistent with a policy that has a relatively low expected free energy, despite being implausible according to healthy prior beliefs. Crucially, while disconnections in the indirect pathway lead to fast involuntary movements, reduced direct pathway influences lead to slowing of movements. The difference in time scales adds further weight to the hypothesis that indirect pathway signals derive from slower hierarchical levels.
Other Subcortical Networks
The ideas in this section may be generalizable to other subcortical structures. Specifically, some nuclei of the amygdala resemble those of the basal ganglia, but appear to have a role in regulating autonomic, as opposed to skeletomotor, policies (Swanson and Petrovich, 1998; Kimmerly et al., 2005). The central and medial nuclei appear to be extensions of the striatum and may send and receive analogous messages, suggesting these nuclei compute the expected free energy of alternative autonomic policies. The output of these amygdala regions target the periaqueductal gray matter (Hopkins and Holstege, 1978; Bandler and Shipley, 1994) and hypothalamic regions (Petrovich et al., 2001) that regulate the balance between the sympathetic and parasympathetic nervous systems. This view of these structures is highly consistent with inferential accounts of autonomic regulation (Owens et al., 2018). That the same computational role associated with the basal ganglia generalizes to provide a hypothesis for the function of some amygdala nuclei suggests that similar explanations might hold for other subcortical structures. The generative model we have considered so far leads us to anticipate that any planning or decision-making process, whether in the domain of skeletomotor, autonomic, or mental (Metzinger, 2017; Limanowski and Friston, 2018) action, implies an anatomical network for the evaluation of expected partition functions, or free energies, for alternative courses of action.
Neuromodulation
Precision and Attention
In addition to knowing which variables are causally related to which others, our brains must be able to infer how reliable these relationships are. In the previous section, we discussed the role of dopamine in modulating the indirect and direct pathways, but without specifying its role in the generative model. We have suggested that dopamine increases the influence of message 2 relative to message 1 (Figure 7); i.e., changes the weighting of priors and likelihoods. This implies it plays the role of a precision parameter. Precision quantifies the confidence, associated with a given probabilistic distribution. Associating a high precision with prior beliefs means that these are the dominant influence in forming a posterior belief. Lower precisions of prior beliefs favor other messages, including those derived from sensory data. We could then think of dopamine as encoding the imprecision of prior beliefs about policies or, as the precision of the partition functions used to evaluate the evidence for different policies. While the latter is the more common formulation in papers on active inference (Friston et al., 2014), we adopt the former here for (graphical) notational convenience. Either would lead to increased direct pathway activation with increased dopamine.
We can generalize the idea that dopamine modulates the balance between prior and posterior influences over policies by considering the confidence ascribed to other factors in the generative model. Figure 8 illustrates this idea explicitly by assigning precision parameters to each factor. Prior beliefs about these parameters are expressed in factors Γ, Ω, and Z, with precisions (γ, ω, ζ) on the edges connecting to these factors E, B, and A (Parr and Friston, 2017c). The capacity to estimate the precision of these conditional distributions is thought to underwrite attentional processing (Feldman and Friston, 2010). The reason for this is that assigning a high precision (or confidence) to a given probabilistic mapping implies that one variable is highly informative about the other. For example, if we were to hold very precise beliefs about transitions (i.e., a minimally volatile world), the past would be very informative about the present. Similarly, precise beliefs about the likelihood of observing data affords those data the potential to drive belief updating about causative states. In short, increasing precision increases the influence that the messages passed across a factor have on beliefs about variables either side of it. Biologically, this is consistent with modulation of the gain of the synapses carrying these messages. We will use attention, synaptic gain, and precision synonymously in this paper.
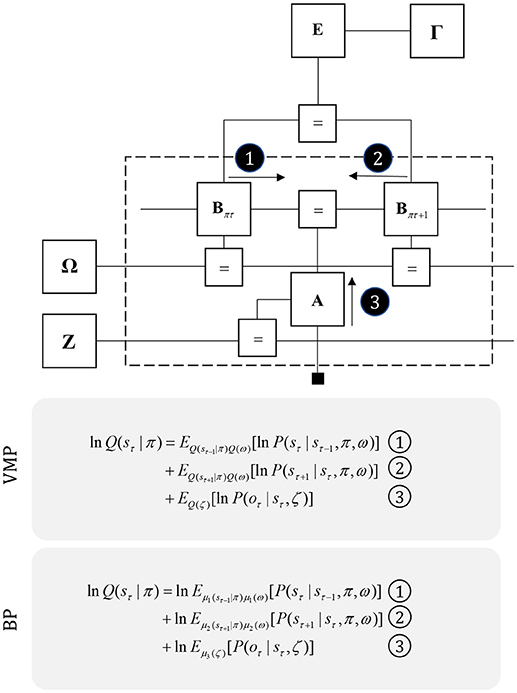
Figure 8. Precision and uncertainty. This figure shows the graph of Figure 5, but supplemented with precision parameters and prior factors over these precisions. These encode confidence in policies (γ), transitions (ω), and likelihoods (ζ). The priors for these are the factors Γ, Ω, and Z, respectively. Note that the messages required to update beliefs about the hidden states are almost identical to those of Figure 3, but are now averaged over beliefs about the precision. Messages from the past (1) and future (2) are contextualized by the transition precision, while those from sensory input (3) are modulated by the likelihood precision. As in Figure 3, we provide the form of the variational and belief propagation messages implied by this model to illustrate the commonalities between their forms. Again, this is due to the structure of the Markov blankets of each state, which now includes precision parameters.
Neuromodulators
It is likely that there is a range of mechanisms that give rise to attentional gain-control in the brain, from neuromodulators acting via NMDA receptor pathways (Law-Tho et al., 1993) to communication through coherence (Fries, 2015). While acknowledging that they are only part of the story, we will focus upon the role of ascending neuromodulators (Table 2) in controlling synaptic gain. Figure 9 illustrates the neuronal network implied by the message passing of Figure 8, combined with the network of Figure 6. The additions to this are the subcortical nodes projecting to the cortex. We have associated projections from the locus coeruleus with beliefs about the precision of transitions, consistent with previous theoretical work (Dayan and Yu, 2006; Parr and Friston, 2017c), and with empirical studies (Marshall et al., 2016). The locus coeruleus is the primary source of noradrenaline to the cortex (Aston-Jones and Cohen, 2005), and much of its phenomenology has been reproduced in simulations that associate it with error signals when predicting state transitions (Sales et al., 2018). Error signals of this sort can be interpreted as encoding an increase in the estimated volatility (imprecision) of state transitions.
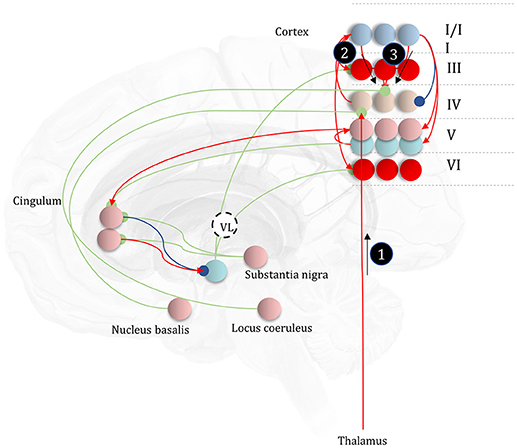
Figure 9. The anatomy of uncertainty. This schematic extends the network of Figure 6 to include modulatory variables, consistent with the factor graph of Figure 8. Specifically, we have now included subcortical regions that give rise to ascending neuromodulatory projections. This includes the locus coeruleus in the pons, which gives rise to noradrenergic signals. Axons from this structure travel through the dorsal noradrenergic bundle to reach the cingulum, a white matter bundle that allows dissemination of signals to much of the cortex. Here, we show these axons modulating messages 2 and 3, representing the past and future, respectively. The nucleus basalis of Meynert is the source of cholinergic signals to the cortex (again, via the cingulum). These modulatory connections target thalamocortical inputs to layer IV (i.e., message 1). Finally, the substantia nigra pars compacta (and the ventral tegmental area) projects via the medial forebrain bundle to the striatum, supplying it with dopaminergic terminals. This modulates the balance between prior and marginal likelihood influences over policy evaluation that we hypothesize correspond to indirect and direct pathway activity, respectively. As before, the layers of the cortical microcircuit shown here represent beliefs about states under a given policy (I/II), beliefs about states averaged over policies (III), state prediction errors (IV), expected free energy gradients and predicted outcomes (V), and beliefs about states averaged over policies (VI).
The cholinergic system appears a good candidate for the encoding of likelihood precision, given its known role in regulating the gain of sensory evoked responses (Gil et al., 1997; Disney et al., 2007). This implies there should be acetylcholine receptors in those cortical layers receiving messages computed from the likelihood, as in Figure 9. Consistent with this, nicotinic acetylcholine receptors are found presynaptically on thalamocortical terminals targeting layer IV (Sahin et al., 1992; Lavine et al., 1997). Although omitted in Figure 9, the connections labeled “a” and “b” in Figures 5, 6 also depend upon likelihood distributions, and so should be subject to cholinergic input. As the message passing would predict, cholinergic influences are also found in the deeper layers housing these connections (Eckenstein et al., 1988; Arroyo et al., 2014). Both pharmacological (Vossel et al., 2014; Marshall et al., 2016) and neuroimaging (Moran et al., 2013) studies in humans support the hypothesis that the cholinergic system is engaged in precision estimation. This idea additionally lends itself to further testable predictions. A pharmacologically induced decrease in cholinergic activity (e.g., using hyoscine) might then reduce the amplitude of measured electrophysiological responses to sensory stimuli, consistent with increased reliance upon prior beliefs compared to sensory evidence. An attenuated sensory drive toward belief updating might also impair the performance of sensory discrimination tasks (e.g., dot-motion tasks). A further prediction is that a noradrenergic blockade could rescue this performance, as reducing the precision of transition probabilities could restore the relative balance between (empirical) prior and likelihood beliefs.
Neurobiological theories based upon active inference frequently implicate dopamine in the encoding of the precision of beliefs about policies (Friston et al., 2014; FitzGerald et al., 2015). The anatomy of projections originating from the midbrain, compared to the cortex, supports this interpretation. Dopaminergic neurons from the substantia nigra pars compacta and the ventral tegmental area preferentially target the necks of dendritic spines (but also the cell body and axons) of medium spiny neurons (Freund et al., 1984; Yager et al., 2015), while cortical input targets the heads of these, consistent with the notion that dopaminergic signals modulate the gain of these signals rather than providing a driving input. Neuroimaging provides evidence in favor of dopaminergic encoding of precision of beliefs about policies (Schwartenbeck et al., 2015).
While we have focused upon three modulatory transmitters, there are clearly many more to be accounted for in this computational framework (Iglesias et al., 2016; Avery and Krichmar, 2017). One notable omission is serotonin. This transmitter has been linked to various psychiatric conditions, and forms the basis for a range of pharmacological interventions (Andrews et al., 2015). As an illustration of the constraints enforced by the computational anatomy so far, we can use existing knowledge about laminar expressions of serotonin to speculate upon a plausible role. Serotonergic activity is heavily implicated in modulation of layer V pyramidal cells (Aghajanian and Marek, 1999; Lambe et al., 2000; Elliott et al., 2018); especially in the medial prefrontal cortex. Notably, the amygdala receives extensive input from this cell layer (Cho et al., 2013), and cortical region (Marek et al., 2013; Mukherjee et al., 2016).
Drawing from the idea that some nuclei of the amygdala could be an autonomic analog of the basal ganglia (Swanson and Petrovich, 1998) (see the section Planning for details), we can hypothesize that serotonin is somehow involved in modulating policy selection in response to interoceptive signals. The involvement of layer V suggests two mechanisms by which this might occur. The inputs to this layer in Figure 6 include those that depend upon the likelihood (labeled “a” and “b”) and descending messages representing the top-down influence via the C factor (i.e., context sensitive preferences); i.e., message 3 in Figure 6. Notably, both of these are functions of predicted outcomes, which in this case would be interoceptive modalities. This suggests two alternative hypotheses for the computational role of serotonin. Either it plays an analogous role to ζ, the likelihood precision (i.e., an interoceptive version of acetylcholine), or it could modulate an equivalent precision parameter encoding the fidelity of the mapping from high level states (context) to interoceptive preferences. Either of these hypotheses complement the recent trend toward embodied psychiatry (Seth, 2013; Barrett et al., 2016; Petzschner et al., 2017; Khalsa et al., 2018), and longstanding theories concerning the connection between mood and interoceptive sensations (James, 1884; Ondobaka et al., 2017).
Inferring Uncertainty
For simplicity, we have only included the unidirectional connections from neuromodulatory systems to the cortex and basal ganglia in Figure 9. The form of Figure 8 demonstrates that the Markov blankets of these precision parameters include the variables encoded by the pre and postsynaptic neurons of the synapses they modulate. For the two cortically-projecting systems, this implicates axons signaling in the reverse direction in the cingulum, perhaps targeting the prefrontal cortex (which projects to both the nucleus basalis and the locus coeruleus). For the mesostriatal system, this suggests reciprocal interactions between the dopaminergic midbrain and the striatum, consistent with known anatomical loops between these structures (Haber, 2003), and the striosome compartments of the striatum that seem specialized in relaying signals to the dopaminergic midbrain (Fujiyama et al., 2011).
Pathologies of Synaptic Gain
There are many disorders thought to be due to abnormalities of precision estimation (Friston, 2017; Friston et al., 2017b; Parr et al., 2018b) and synaptic gain, including but not limited to Lewy body dementia, Autism, and Parkinson's disease. Theoretical accounts of the first of these typically implicate abnormalities in estimating likelihood precision (Collerton et al., 2005; Parr et al., 2018a). Recent accounts of autism suggest a failure to properly estimate the precision of transitions (Lawson et al., 2014, 2017). As discussed in the section Planning, Parkinson's disease reflects degeneration of the dopaminergic system, leading to failure to represent the precision of beliefs about policies. The above conditions show changes in neurotransmitter function consistent with the computational anatomy of Figure 9. In Lewy body dementia, there is a dramatic decrease in cholinergic activity in the cortex (Perry et al., 1994; Graff-Radford et al., 2012), effectively releasing the cortex from the constraints imposed by sensory input (message 1). This could account for the complex visual hallucinations associated with this condition. Pupillary analysis in autism indicates attenuated responses to (normally) surprising stimuli (Lawson et al., 2017). Given the relationship between pupillary dilatation and the activity of the locus coeruleus (Koss, 1986), this implies abnormalities in noradrenergic signaling, limiting the influence that beliefs about the past (message 2) and the future (message 3). This could lead to an excessive reliance upon message 1, and a failure to use prior beliefs to contextualize this sensory evidence. Theoretical accounts of this sort (Palmer et al., 2015, 2017) have been used to account for the resistance to visual illusions (Happé, 1996) and the superior visual search performance observed in autistic individuals (Shah and Frith, 1983; Simmons et al., 2009).
Movement
Predictions and Motor Commands
The graphs and neuronal networks of the preceding sections have all focused upon the discrete dynamics outlined on the left of Figure 3. While this is appropriate for planning sequences of actions, these models are not suited to implementing these actions as movements. The reason for this is that movement necessarily involves continuous variables (muscle length, velocity) that evolve in continuous time, as indicated on the right of Figure 3 (Parr and Friston, 2018b). The same is true of low-level sensory processes, as data arrives in continuous time. Fortunately, the structure of the message passing is almost identical in the two cases (Friston et al., 2017a). Again, they correspond to reciprocal connections between neurons representing prediction errors (free energy gradients) and posterior expectations [for more details on this, please see (Bastos et al., 2012; Shipp, 2016)]. This means we can use the same sorts of architectures to make predictions about the continuous signals from muscle proprioceptors. Active inference takes this one step further. Once we have a prediction as to the sensory data coming from a muscle, this generates a prediction error. There are two ways in which this prediction error may be resolved. First, we could update expectations to be more consistent with this. Second, we could use the error to drive a movement that renders proprioceptive data consistent with the prediction (Adams et al., 2013). Under this view, motor commands and proprioceptive predictions become synonymous. Brainstem and spinal cord reflexes can then be seen as mechanisms to resolve prediction errors. An interesting consequence of this is that, given errors are resolved at this level, there should be no residual error at the level of the motor cortex, as all of its expectations are fulfilled at spinal levels. As such, cells in the motor cortex representing prediction error may be redundant. This reasoning has been used to account for the impoverished (granular) layer IV in primary motor cortex (Shipp et al., 2013), sometimes referred to as “agranular” cortex for this reason. However, it seems that some prediction error must still be unresolved, as there is evidence for some granular cells in motor cortex (García-Cabezas and Barbas, 2014; Barbas and García-Cabezas, 2015).
In addition to accounting for anatomical findings, models based upon this form of active inference have reproduced a range of complex motor phenomena, including handwriting (Friston et al., 2011), limb movements (Friston et al., 2010), smooth pursuit (Adams et al., 2012), and saccadic eye movements (Friston et al., 2012a). They are capable of reproducing plausible electrophysiological and pathological behaviors that are consistent with (clinical) neuroanatomy. For example, we have previously reproduced the activity of collicular “build-up” cells (Ma et al., 1991; Munoz and Wurtz, 1995) and pathological phenomena, including internuclear ophthalmoplegia (Virgo and Plant, 2017), using the same generative model (Parr and Friston, 2018a).
Translating Policies Into Movements
The success of continuous state space generative models in accounting for motor behavior appears to imply a disconnect between movement and planning, with the latter more easily accounted for using discrete time models. This suggests there must be some interface between the two, where decisions, selected from a discrete repertoire, are translated into beliefs about continuous variables. Figure 10 illustrates this idea, with a discrete model that gives rise to empirical priors for a continuous model, via a η factor. This corresponds to a Bayesian model average, where several hypothetical continuous variables are weighted by the probabilities of their associated categorical outcomes (Friston et al., 2017a). By computing the approximate partition function (negative free energy) for the continuous region, we can approximate the evidence for each categorical outcome. As the continuous dynamics play out over time, the log evidence must be integrated over that duration. The idea that complex motor behavior may be constructed from short sequences of simpler dynamics resonates with ideas implemented in control systems and robotics (Schaal, 2006).
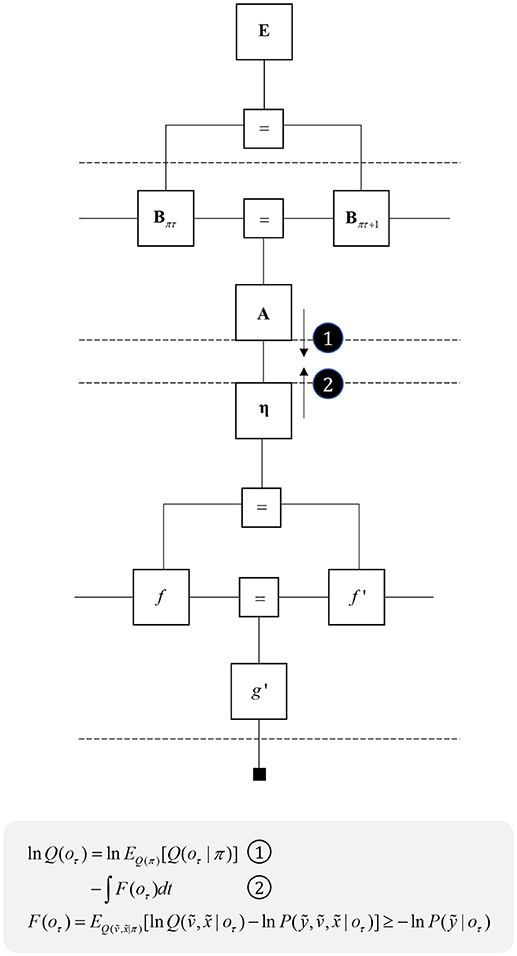
Figure 10. Decisions and movement. This graph illustrates how beliefs about categorical variables may influence those about continuous variables (message 1) and vice versa (message 2). The upper part of the graph is the same as that from Figure 5, while the lower part is that from the right of Figure 2. The additional η factor represents the empirical prior for a hidden cause, v, that determines the dynamics of x, much as the policies at the higher level determine the dynamics of state transitions. The equations below show that we can treat the descending message as a Bayesian model average, incorporating posterior predictive beliefs about outcomes under policies, averaged over policies. The ascending message is the free energy integrated over time for each outcome. This effectively treats each outcome as an alternative hypothesis for the continuous dynamics at the lower level.
Discretized Encoding of Continuous Space
Translating from discrete to continuous variables implies that there must be an interface at which a discretized encoding of space is mapped to a continuous encoding. In the oculomotor system, the superior colliculus may represent an interface of this sort (Parr and Friston, 2018b). It contains a population of cells that are retinotopically mapped to regions of visual space (Sparks, 1986), but the brainstem oculomotor regions it projects to appear to encode continuous variables. It is ideally placed to map empirical priors, derived from cortical beliefs, to predictions about eye position and the status of oculomotor muscles. Its cortical input is derived from cells in layer V (Fries, 1985; Kim et al., 2015), possibly those encoding posterior predictive beliefs about discrete outcomes under each policy (Figure 6). The superior colliculus additionally receives input from the substantia nigra pars reticulata (Hikosaka and Wurtz, 1983), which could encode posterior beliefs about policies in line with Figure 6. This means the superior colliculus receives the inputs required to perform a Bayesian model average over policies to derive empirical priors over outcomes, and over the causes of continuous dynamics (message 1 in Figures 10, 11).
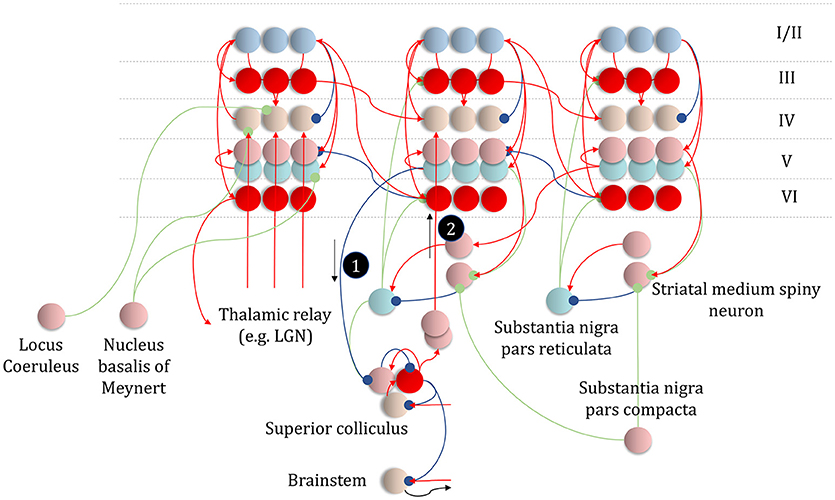
Figure 11. An anatomy of inference. This schematic summarizes the networks we have discussed so far, but adds in the messages of Figure 10, with empirical priors propagated by message 1. These are subtracted from expectation neurons to give error signals, then used to update expectations. Expectations are used to derive predictions about sensory data. These are subtracted from the incoming data to calculate sensory errors, used to update current expectations, but also to drive brainstem reflexes through action (black arrow) to change sensory data (e.g., by moving the eyes). Message 2 derives from the expectations, which are used to compute the integral of the free energy over time. The relative evidence for each outcome is then propagated to layer IV cells in the cortex, acting as if it were sensory data. As before, the layers of the cortical microcircuit shown here represent beliefs about states under a given policy (I/II), beliefs about states averaged over policies (III), state prediction errors (IV), expected free energy gradients and predicted outcomes (V), and beliefs about states averaged over policies (VI).
While the superior colliculus may play the role of discrete-continuous interface in the oculomotor system, other structures must play analogous roles for different motor outputs. These are likely to share features of anatomy and physiology with the colliculus. Following the pattern above, these structures should receive input from cortical layer V, and from the output nuclei of the basal ganglia. Furthermore, they should encode continuous variables in a discretized fashion, with different neurons representing discrete elements of a continuous scale. A network that includes the ventrolateral (motor) thalamus and the primary motor cortex represent a candidate that meets these criteria (Bosch-Bouju et al., 2013). The motor thalamus receives cortical layer V and basal ganglia input, and projects to motor cortical regions. This suggests the combined cortico-subcortical input to these thalamic nuclei could represent message 1 in Figure 10. Thalamic projections to primary motor cortex might then be the axonal substrate of the η factor. The motor cortex is known to contain discretized maps of space (Georgopoulos et al., 1986), while the spinal motor neurons it projects to elicit continuous changes in muscle length, depending upon their firing rates (Connelly et al., 1999; Conwit et al., 1999; Kirk and Rice, 2017). This implies the motor thalamus and motor cortex might together play the same role for limb and trunk movements as the subpopulations within the superior colliculus do for eye movements.
Figure 11 places these ideas in the context of the neuronal networks from previous sections, showing a hierarchy of three cortical areas, one of which gives rise to projections to the superior colliculus. This would be consistent with a hierarchy implicating occipito-parietal areas at the lowest level (left column) that project to, and receive projections from, frontal oculomotor areas (middle) known to project to the superior colliculus (Künzle and Akert, 1977). These then share reciprocal connections with dorsolateral parts of the prefrontal cortex, involved in the longer-term planning of eye movements required for delayed oculomotor responses (Fuster et al., 1982; Funahashi et al., 1989). The laminar specific terminations in Figure 11 conform to those required for message passing in the generative models we have described, and are highly consistent with those observed in the cerebral cortex and associated structures (Shipp, 2007).
Discussion
The preceding sections have reviewed recent attempts to understand the anatomy of the brain in terms of the inferential computations it must perform. We have argued that the key determinant for anatomical connectivity is the structure of the generative model the brain uses to make these inferences. This allows us to express hypotheses about computational neuroanatomy in a graphical notation that can be built up from relatively few simple building blocks, as described above. This framework is sufficiently general that we can use it to understand perceptual inference, planning, attentional gain, and movement. These can all be combined within the same factor graph, enabling the expression of systems-level hypotheses about brain-wide networks.
This article has focused on some very specific but ubiquitous features of computational anatomy that emerge under a factor graph treatment—with special attention to known neuroanatomy, neurophysiology, and neuropsychology. There are clear and obvious architectural features that are predicted under a graphical treatment of neuronal message passing; for example, the very existence of sparse neuronal (axonal) connections and the hierarchical organization of cortical and subcortical structures. The very existence of the brain as a network or graph that possesses hierarchically nested Markov blankets—and engages in sparse message passing [unlike the liver or blood (Friston and Buzsaki, 2016)]—could be understood as a prediction of the process theories that arise under active inference and Bayesian brain. Crucially, the formal approach offered by these process theories forces us to ensure consistency in theories about different aspects of brain function. For example, the assignment of posterior predictive beliefs and expected free energy gradients to cortical layer V in the section on Planning had to be consistent with the kinds of signals propagated to the superior colliculus, and the motor thalamus, from this same cortical layer in the section on Movement. This represents one of many constraints that can be simply articulated using the graphical formalisms described here.
Not only do these ideas have to be internally consistent (minimally complex in relation to one another), they must accurately account for a range of observed phenomena, including the consequences of anatomical lesions. We have outlined a few examples throughout that illustrate this, including abnormalities of perception resulting from disconnections (e.g., Charles Bonnet syndrome), disorders of policy evaluation (e.g., Parkinson's disease), and failures of attentional gain (e.g., Lewy body disease). It is also important to realize that, as messages are propagated across the graph, deficits in one part of the graph have implications for all other parts. A disorder that offers a clear example of this kind of diaschisis (Price et al., 2001; Carrera and Tononi, 2014) is visual neglect (Parr and Friston, 2017a). This neuropsychological syndrome is associated with right hemispheric lesions (Halligan and Marshall, 1998), which can occur at various anatomical sites, and results in a failure to perform exploratory saccades to the left side of visual space (Husain et al., 2001; Fruhmann Berger et al., 2008; Karnath and Rorden, 2012).
The heterogeneity of anatomical lesions giving rise to neglect illustrates that the same processes of policy (i.e., saccadic) selection can be disrupted by multiple distant lesions. We have previously shown through simulation (Parr and Friston, 2017b) that disruption of policy priors (E), proprioceptive preferences (C), or the likelihood mapping fixation locations to predicted visual data (A) can all bias saccadic policy selection. This is unsurprising when we consider the factor graph of Figure 5, as messages across each of these factors either directly or indirectly influences beliefs about policies. Lesions in the proposed neurobiological substrates (Parr et al., 2018b) of each of these factors have been associated with visual neglect (Karnath et al., 2002; Bartolomeo, 2012). Although not commonly observed in clinical practice, experimental manipulation of almost every part of the anatomy presented here can induce or alleviate neglect-like saccadic behavior, including unilateral collicular inactivation (Schiller et al., 1980, 1987), chemical ablation of the substantia nigra pars compacta (Kato et al., 1995; Kori et al., 1995), and noradrenergic modulation (Malhotra et al., 2006).
The above represent criteria for the face validity of anatomical process theories. To go further, it is necessary to make empirical predictions based upon these theories. We have highlighted three novel ideas that have arisen from the form of the generative models used here, which could be interrogated in empirical studies. First, if we interpret the direct and indirect pathways of the basal ganglia in terms of partition functions and empirical priors, respectively, this has important consequences for learned behaviors. While it is possible to optimize the parameters of a conditional probability (E), the same cannot be done for the partition function; although it is possible to optimize those distributions that make up that function. This suggests that learned automatic behaviors depend upon plastic changes involving the indirect, more than the direct, pathway. Selective ablation or optogenetic suppression (Freeze et al., 2013) of the direct pathway would, under this hypothesis, preserve certain context dependent automatic behaviors. In other words, it should be possible to reproduce the phenomenon of kinesia paradoxa by facilitating the indirect at the expense of the direct pathway, perhaps while presenting slowly changing exteroceptive cues with a learned behavioral association.
Second, we touched upon hypothetical computational roles for serotonin that would be consistent with its anatomical and laminar distribution in the cortex under the computational anatomy discussed above. This scheme offers the potential to frame these, anatomically derived, computational hypotheses in terms of simulated behavior. To test whether serotonergic modulations are best explained as manipulations of interoceptive sensory precision, or the precision of preferences, we would need to design a task in which simulating manipulations of each of these parameters would give rise to different behavioral outputs. Fitting these parameters to behavior under different levels of pharmacological manipulation would allow us to evaluate the relative evidence for each of these hypotheses. For a recent example of this sort of approach, inferring computational parameters (including precision of preferences) for visual exploration, see Mirza et al. (2018).
Finally, we considered the role of the motor thalamocortical networks, and suggested that these might represent the sort of discrete-continuous interface that we have previously associated with the superior colliculus. This predicts that there should be a very different sort of deficit resulting from the pathway into the ventrolateral thalamus compared to that following lesions to motor cortical outputs. The former might involve deficits in choice of movement, or difficulty initiating movements. The latter are more likely to give rise to impairments in the motor trajectories themselves. Of course, it is important to emphasize again that lesions to any neuroanatomical structure, or equivalently, to any part of a generative model, will have wide-reaching consequences due to the propagation of inferential messages.
The above represent theoretically motivated hypotheses that may be evaluated in relation to empirical evidence. These are potentially falsifiable (in a frequentist statistical sense), or could be shown to be relatively poor hypotheses compared to an alternative explanation (in a Bayesian sense). It is worth emphasizing that the inferential framework described here is not subject to these same tests. This (active) inference formulation simply provides a formal language and notation in which hypotheses about neuronal processes can be articulated and evaluated. The formulation of the brain's inferential computations as graphs and Markov blankets is therefore not in competition with, or an endorsement of, other approaches to understanding brain function. It accommodates those approaches that appeal to chaotic dynamical systems (Korn and Faure, 2003), as these may be written in to the flows of Figures 3, 10 (Friston and Ao, 2012), and is predicated upon probabilistic dynamics of the sort that motivate the use of mathematical tools developed in stochastic (and quantum) physics (Seifert, 2012; Korf, 2014) for understanding brain function.
Clearly the account given in this paper is far from complete. We have omitted important structures from this, including the cerebellum and second order thalamic nuclei, like the pulvinar. These have not escaped treatment under the framework of active inference. The pulvinar, have been associated with generative models that treat prior beliefs over precisions as empirical priors, conditioned upon hidden states (Kanai et al., 2015). This sort of state-dependent precision is vital in accounting for phenomena such as figure-ground segregation. The cerebellum has been associated with inferences and learning in the continuous domain (Friston and Herreros, 2016), enabling Pavlovian conditioning of eye-blink responses. For an account of the cerebellum consistent with our computational anatomy, it is worth noting that the cerebellum projects to both the ventrolateral nucleus of the thalamus, and to the superior colliculus. These are the regions we have associated with discrete-continuous interfaces, and therefore with the η factor of Figure 10. This raises the possibility that one of the roles of the cerebellum is to optimize the mapping between discrete motor sequences, and the trajectories at each point in the sequence. This resonates with features of cerebellar disease, including “past-pointing,” where patients are able to recognize a target and initiate a limb movement toward it, but fail to map the location of the target effectively into continuous space, and miss when trying to point to it. Future work developing the anatomical process theory of active inference must rise to the challenge of synthesizing these phenomena within this broader theory.
Conclusion
In this paper, we have emphasized the idea that generative models, and their constituent Markov blankets, represent a useful way to express hypotheses about brain connectivity. We have reviewed recent attempts to apply this framework to a range of anatomical networks, illustrating their face validity and internal consistency. There may be other plausible mappings between the connectivity implied by the Markov blankets of a generative model and the anatomy of the brain, which could make use of different auxiliary variables to the free energy gradients (prediction errors) we have assumed. Similarly, there are other plausible generative models that the brain may use, and these may involve different Markov blankets. For this reason, we emphasize not only current anatomical theories, but also a theoretically rigorous graphical framework in which questions about computational anatomy can be clearly posed. Under this framework, there are two broad lines of enquiry. First, what are the generative models the brain employs to make inferences about the world? Second, what is the mapping between the network implied by a given generative model and the connections of the brain? These questions constrain one another, as a good hypothesis for a computational neuroanatomy will imply a plausible generative model that contains Markov blankets consistent with brain connectivity.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Rosetrees Trust (Award Number 173346) to TP. KF is a Wellcome Principal Research Fellow (Ref: 088130/Z/09/Z).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fncom.2018.00090/full#supplementary-material
Footnotes
1. ^An empirical prior arises in hierarchical models, when a higher level provides constraints on a lower-level. It is called an empirical prior because the reciprocal message passing means that the prior is informed by the (empirical) data at hand. In other words, hierarchical models endow (empirical) priors with context-sensitivity.
2. ^The (Shannon) entropy is the dispersion of a probability distribution, and may be thought of as quantifying uncertainty about the variable described by the distribution.
References
Adams, R. A., Perrinet, L. U., and Friston, K. (2012). Smooth pursuit and visual occlusion: active inference and oculomotor control in Schizophrenia. PLoS ONE 7:e47502. doi: 10.1371/journal.pone.0047502
Adams, R. A., Shipp, S., and Friston, K. J. (2013). Predictions not commands: active inference in the motor system. Brain Struct. Funct. 218, 611–643. doi: 10.1007/s00429-012-0475-5
Aghajanian, G. K., and Marek, G. J. (1999). Serotonin, via 5-HT2A receptors, increases EPSCs in layer V pyramidal cells of prefrontal cortex by an asynchronous mode of glutamate release. Brain Res. 825, 161–171. doi: 10.1016/S0006-8993(99)01224-X
Albin, R. L., Young, A. B., and Penney, J. B. (1989). The functional anatomy of basal ganglia disorders. Trends Neurosci. 12, 366–375. doi: 10.1016/0166-2236(89)90074-X
Andrews, P. W., Bharwani, A., Lee, K. R., Fox, M., and Thomson, J. A. (2015). Is serotonin an upper or a downer? The evolution of the serotonergic system and its role in depression and the antidepressant response. Neurosci. Biobehav. Rev. 51, 164–188. doi: 10.1016/j.neubiorev.2015.01.018
Arnsten, A. F. T., and Li, M. (2005). Neurobiology of executive functions: catecholamine influences on prefrontal cortical functions. Biol. Psychiatry 57, 1377–1384. doi: 10.1016/j.biopsych.2004.08.019
Arroyo, S., Bennett, C., and Hestrin, S. (2014). Nicotinic modulation of cortical circuits. Front. Neural Circuits 8:30. doi: 10.3389/fncir.2014.00030
Aston-Jones, G., and Cohen, J. D. (2005). An integrative theory of locus coruleus-norepinephrine function: adaptive gain and optimal performance. Annu. Rev. Neurosci. 28, 403–450. doi: 10.1146/annurev.neuro.28.061604.135709
Attias, H. (2003). “Planning by probabilistic inference,” in Proceedins of the 9th International Workshop on Artificial Intelligence and Statistics (Key West, FL).
Avery, M. C., and Krichmar, J. L. (2017). Neuromodulatory systems and their interactions: a review of models, theories, and experiments. Front. Neural Circuits 11:108. doi: 10.3389/fncir.2017.00108
Bai, W. Z., Ishida, M., and Arimatsu, Y. (2004). Chemically defined feedback connections from infragranular layers of sensory association cortices in the rat. Neuroscience 123, 257–267. doi: 10.1016/j.neuroscience.2003.08.056
Baltieri, M., and Buckley, C. L. (2018). A probabilistic interpretation of PID controllers using active inference. bioRxiv. doi: 10.1007/978-3-319-97628-0_2
Bandler, R., and Shipley, M. T. (1994). Columnar organization in the midbrain periaqueductal gray: modules for emotional expression? Trends Neurosci. 17, 379–389. doi: 10.1016/0166-2236(94)90047-7
Banou, E. (2015). Kinesia Paradoxa: A Challenging Parkinson's Phenomenon for Simulation. GeNeDis 2014. Cham: Springer International Publishing.
Barbas, H., and García-Cabezas, M. Á. (2015). Motor cortex layer 4: less is more. Trends Neurosci. 38, 259–261. doi: 10.1016/j.tins.2015.03.005
Barrett, L. F., Quigley, K. S., and Hamilton, P. (2016). An active inference theory of allostasis and interoception in depression. Philos. Trans. R. Soc. B: Biol. Sci. 371:1708. doi: 10.1098/rstb.2016.0011
Bartolomeo, P. M., Thiebaut de Schotten, and Chica, A. B. (2012). Brain networks of visuospatial attention and their disruption in visual neglect. Front. Hum. Neurosci. 6:110. doi: 10.3389/fnhum.2012.00110
Bastos, A. M., Usrey, W. M., Adams, R. A., Mangun, G. R., Fries, P., and Friston, K. J. (2012). Canonical microcircuits for predictive coding. Neuron 76, 695–711. doi: 10.1016/j.neuron.2012.10.038
Beal, M. J. (2003). Variational Algorithms for Approximate Bayesian Inference. London: University of London United Kingdom.
Bosch-Bouju, C., Hyland, B. I., and Parr-Brownlie, L. C. (2013). Motor thalamus integration of cortical, cerebellar and basal ganglia information: implications for normal and parkinsonian conditions. Front. Comput. Neurosci. 7:163. doi: 10.3389/fncom.2013.00163
Botvinick, M., and Toussaint, M. (2012). Planning as inference. Trends Cogn. Sci. 16, 485–488. doi: 10.1016/j.tics.2012.08.006
Bruineberg, J., Kiverstein, J., and Rietveld, E. (2016). The anticipating brain is not a scientist: the free-energy principle from an ecological-enactive perspective. Synthese 195, 1–28. doi: 10.1007/s11229-016-1239-1
Cagnan, H., Duff, E. P., and Brown, P. (2015). The relative phases of basal ganglia activities dynamically shape effective connectivity in Parkinson's disease. Brain 138, 1667–1678. doi: 10.1093/brain/awv093
Callaway, E. M., and Wiser, A. K. (2009). Contributions of individual layer 2–5 spiny neurons to local circuits in macaque primary visual cortex. Vis. Neurosci. 13, 907–922. doi: 10.1017/S0952523800009159
Carrera, E., and Tononi, G. (2014). Diaschisis: past, present, future. Brain 137, 2408–2422. doi: 10.1093/brain/awu101
Cho, Y. T., Ernst, M., and Fudge, J. L. (2013). Cortico–amygdala–striatal circuits are organized as hierarchical subsystems through the primate amygdala. J. Neurosci. 33, 14017–14030. doi: 10.1523/JNEUROSCI.0170-13.2013
Collerton, D., Perry, E., and McKeith, I. (2005). Why people see things that are not there: a novel Perception and Attention Deficit model for recurrent complex visual hallucinations. Behav. Brain Sci. 28, 737–757. doi: 10.1017/S0140525X05000130
Conant, R. C., and Ashby, W. R. (1970). Every good regulator of a system must be a model of that system. Int. J. Syst. Sci. 1, 89–97. doi: 10.1080/00207727008920220
Connelly, D. M., Rice, C. L., Roos, M. R., and Vandervoort, A. A. (1999). Motor unit firing rates and contractile properties in tibialis anterior of young and old men. J. Appl. Physiol. 87, 843–852. doi: 10.1152/jappl.1999.87.2.843
Conwit, R. A., Stashuk, D., Tracy, B., McHugh, M., Brown, W. F., and Metter, E. J. (1999). The relationship of motor unit size, firing rate and force. Clin. Neurophysiol. 110, 1270–1275. doi: 10.1016/S1388-2457(99)00054-1
Cools, R., Barker, R. A., Sahakian, B. J., and Robbins, T. W. (2003). l-Dopa medication remediates cognitive inflexibility, but increases impulsivity in patients with Parkinson's disease. Neuropsychologia 41, 1431–1441. doi: 10.1016/S0028-3932(03)00117-9
Daunizeau, J., den Ouden, H. E. M., Pessiglione, M., Kiebel, S. J., Stephan, K. E., and Friston, K. J. (2010). Observing the observer (I): meta-bayesian models of learning and decision-making. PLoS ONE 5:e15554. doi: 10.1371/journal.pone.0015554
Dauwels, J. (2007). “On variational message passing on factor graphs. Information Theory, 2007. ISIT 2007,” in IEEE International Symposium on IEEE (Nice).
Dayan, P., Hinton, G. E., Neal, R. M., and Zemel, R. S. (1995). The Helmholtz machine. Neural Comput. 7, 889–904. doi: 10.1162/neco.1995.7.5.889
Dayan, P., and Yu, A. J. (2006). Phasic norepinephrine: a neural interrupt signal for unexpected events. Netw. Comput. Neural Syst. 17, 335–350. doi: 10.1080/09548980601004024
De Ridder, D., Vanneste, S., and Freeman, W. (2014). The Bayesian brain: phantom percepts resolve sensory uncertainty. Neurosci. Biobehav. Rev. 44(Suppl. C), 4–15. doi: 10.1016/j.neubiorev.2012.04.001
de Vries, B., and Friston, K. J. (2017). A factor graph description of deep temporal active inference. Front. Comput. Neurosci. 11:95. doi: 10.3389/fncom.2017.00095
Disney, A. A., Aoki, C., and Hawken, M. J. (2007). Gain modulation by nicotine in macaque V1. Neuron 56, 701–713. doi: 10.1016/j.neuron.2007.09.034
Dokka, K., Kenyon, R. V., Keshner, E. A., and Kording, K. P. (2010). Self versus environment motion in postural control. PLoS Comput. Biol. 6:e1000680. doi: 10.1371/journal.pcbi.1000680
Douglas, R. J., and Martin, K. A. C. (2004). Neuronal circuits of the neocortex. Annu. Rev. Neurosci. 27, 419–451. doi: 10.1146/annurev.neuro.27.070203.144152
Eckenstein, F. P., Baughman, R. W., and Quinn, J. (1988). An anatomical study of cholinergic innervation in rat cerebral cortex. Neuroscience 25, 457–474. doi: 10.1016/0306-4522(88)90251-5
Elliott, M. C., Tanaka, P. M., Schwark, R. W., and Andrade, R. (2018). Serotonin differentially regulates L5 pyramidal cell classes of the medial prefrontal cortex in rats and mice. eNeuro 5:ENEURO.0305-0317.2018. doi: 10.1523/ENEURO.0305-17.2018
Feldman, H., and Friston, K. (2010). Attention, uncertainty, and free-energy. Front. Hum. Neurosci. 4:215. doi: 10.3389/fnhum.2010.00215
Felleman, D. J., and Van Essen, D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47. doi: 10.1093/cercor/1.1.1
Ferrarin, M., Brambilla, M., Garavello, L., Di Candia, A., Pedotti, A., and Rabuffetti, M. (2004). Microprocessor-controlled optical stimulating device to improve the gait of patients with Parkinson's disease. Med. Biol. Eng. Comput. 42, 328–332. doi: 10.1007/BF02344707
FitzGerald, T., Dolan, R., and Friston, K. (2014). Model averaging, optimal inference, and habit formation. Front. Hum. Neurosci. 8:457. doi: 10.3389/fnhum.2014.00457
FitzGerald, T. H., Dolan, R. J., and Friston, K. (2015). Dopamine, reward learning, and active inference. Front. Comput. Neurosci. 9:136. doi: 10.3389/fncom.2015.00136
Forney, G. D. (2001). Codes on graphs: normal realizations. IEEE Trans. Inform. Theory 47, 520–548. doi: 10.1109/18.910573
Forney, G. D. Jr., and Vontobel, P. O. (2011). Partition functions of normal factor graphs. arXiv preprint arXiv:1102.0316.
Freeze, B. S., Kravitz, A. V., Hammack, N., Berke, J. D., and Kreitzer, A. C. (2013). Control of basal ganglia output by direct and indirect pathway projection neurons. J. Neurosci. 33, 18531–18539. doi: 10.1523/JNEUROSCI.1278-13.2013
Freund, T. F., Powell, J. F., and Smith, A. D. (1984). Tyrosine hydroxylase-immunoreactive boutons in synaptic contact with identified striatonigral neurons, with particular reference to dendritic spines. Neuroscience 13, 1189–1215. doi: 10.1016/0306-4522(84)90294-X
Fries, P. (2015). Rhythms for cognition: communication through coherence. Neuron 88, 220–235. doi: 10.1016/j.neuron.2015.09.034
Fries, W. (1985). Inputs from motor and premotor cortex to the superior colliculus of the macaque monkey. Behav. Brain Res. 18, 95–105. doi: 10.1016/0166-4328(85)90066-X
Friston, K., Adams, R. A., Perrinet, L., and Breakspear, M. (2012a). Perceptions as hypotheses: saccades as experiments. Front. Psychol. 3:151. doi: 10.3389/fpsyg.2012.00151
Friston, K., and Ao, P. (2012). Free energy, value, and attractors. Comput. Math. Methods Med. 2012, 27. doi: 10.1155/2012/937860
Friston, K., and Buzsaki, G. (2016). The functional anatomy of time: what and when in the brain. Trends Cogn. Sci. 20, 500–511. doi: 10.1016/j.tics.2016.05.001
Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P., and Pezzulo, G. (2017d). Active inference: a process theory. Neural Comput. 29, 1–49. doi: 10.1162/NECO_a_00912
Friston, K., and Herreros, I. (2016). Active inference and learning in the cerebellum. Neural Comput. 28, 1812–1839. doi: 10.1162/NECO_a_00863
Friston, K., and Kiebel, S. (2009). Predictive coding under the free-energy principle. Philos. Trans. R. Soc. B Biol. Sci. 364, 1211. doi: 10.1098/rstb.2008.0300
Friston, K., Kilner, J., and Harrison, L. (2006). A free energy principle for the brain. J. Physiol. Paris 100, 70–87. doi: 10.1016/j.jphysparis.2006.10.001
Friston, K., Mattout, J., and Kilner, J. (2011). Action understanding and active inference. Biol. Cybern. 104, 137–160. doi: 10.1007/s00422-011-0424-z
Friston, K., Mattout, J., Trujillo-Barreto, N., Ashburner, J., and Penny, W. (2007). Variational free energy and the Laplace approximation. Neuroimage 34, 220–234. doi: 10.1016/j.neuroimage.2006.08.035
Friston, K., Rigoli, F., Ognibene, D., Mathys, C., Fitzgerald, T., and Pezzulo, G. (2015). Active inference and epistemic value. Cogn. Neurosci. 6, 187–214. doi: 10.1080/17588928.2015.1020053
Friston, K., Samothrakis, S., and Montague, R. (2012b). Active inference and agency: optimal control without cost functions. Biol. Cybern. 106, 523–541. doi: 10.1007/s00422-012-0512-8
Friston, K., Schwartenbeck, P., FitzGerald, T., Moutoussis, M., Behrens, T., and Dolan, R. J. (2014). The anatomy of choice: dopamine and decision-making. Philos. Trans. R. Soc. B Biol. Sci. 369:20130481. doi: 10.1098/rstb.2013.0481
Friston, K., Stephan, K., Li, B., and Daunizeau, J. (2010). Generalised filtering. Math. Prob. Eng. 2010:621670. doi: 10.1155/2010/621670
Friston, K. J. (2017). Precision psychiatry. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2, 640–643. doi: 10.1016/j.bpsc.2017.08.007
Friston, K. J., Daunizeau, J., Kilner, J., and Kiebel, S. J. (2010). Action and behavior: a free-energy formulation. Biol. Cybern. 102, 227–260. doi: 10.1007/s00422-010-0364-z
Friston, K. J., Parr, T., and de Vries, B. (2017a). The graphical brain: belief propagation and active inference. Netw. Neurosci. 1, 381–414. doi: 10.1162/NETN_a_00018
Friston, K. J., Redish, A. D., and Gordon, J. A. (2017b). Computational nosology and precision psychiatry. Comput. Psychiatry. 1, 2–23. doi: 10.1162/CPSY_a_00001
Friston, K. J., Rosch, R., Parr, T., Price, C., and Bowman, H. (2017c). Deep temporal models and active inference. Neurosci. Biobehav. Rev. 77, 388–402. doi: 10.1016/j.neubiorev.2017.04.009
Frith, C. D., Blakemore, S. J., and Wolpert, D. M. (2000). Abnormalities in the awareness and control of action. Philos. Trans. R. Soc. B Biol. Sci. 355, 1771–1788. doi: 10.1098/rstb.2000.0734
Fruhmann Berger, M., Johannsen, L., and H.-Karnath, O. (2008). Time course of eye and head deviation in spatial neglect. Neuropsychology 22, 697–702. doi: 10.1037/a0013351
Fujiyama, F., Sohn, J., Nakano, T., Furuta, T., Nakamura, K. C., Matsuda, W., et al. (2011). Exclusive and common targets of neostriatofugal projections of rat striosome neurons: a single neuron-tracing study using a viral vector. Eur. J. Neurosci. 33, 668–677. doi: 10.1111/j.1460-9568.2010.07564.x
Funahashi, S., Bruce, C. J., and Goldman-Rakic, P. S. (1989). Mnemonic coding of visual space in the monkey's dorsolateral prefrontal cortex. J. Neurophysiol. 61, 331. doi: 10.1152/jn.1989.61.2.331
Fuster, J. M., Bauer, R. H., and Jervey, J. P. (1982). Cellular discharge in the dorsolateral prefrontal cortex of the monkey in cognitive tasks. Exp. Neurol. 77, 679–694. doi: 10.1016/0014-4886(82)90238-2
García-Cabezas, M. Á., and Barbas, H. (2014). Area 4 has layer IV in adult primates. Eur. J. Neurosci. 39, 1824–1834. doi: 10.1111/ejn.12585
Georgopoulos, A., Schwartz, A., and Kettner, R. (1986). Neuronal population coding of movement direction. Science 233, 1416–1419. doi: 10.1126/science.3749885
Gertler, T. S., Chan, C. S., and Surmeier, D. J. (2008). Dichotomous anatomical properties of adult striatal medium spiny neurons. J. Neurosci. 28, 10814. doi: 10.1523/JNEUROSCI.2660-08.2008
Gil, Z., Connors, B. W., and Amitai, Y. (1997). Differential Regulation of Neocortical Synapses by Neuromodulators and Activity. Neuron 19, 679–686. doi: 10.1016/S0896-6273(00)80380-3
Giuffrida, R., Li Volsi, G., Maugeri, G., and Perciavalle, V. (1985). Influences of pyramidal tract on the subthalamic nucleus in the cat. Neurosci. Lett. 54, 231–235. doi: 10.1016/S0304-3940(85)80084-7
Glickstein, M., and Stein, J. (1991). Paradoxical movement in Parkinson's disease. Trends Neurosci. 14, 480–482. doi: 10.1016/0166-2236(91)90055-Y
Goldman-Rakic, P. S. (1995). Cellular basis of working memory. Neuron 14, 477–485. doi: 10.1016/0896-6273(95)90304-6
Graff-Radford, J., Boeve, B. F., Pedraza, O., Ferman, T. J., Przybelski, S., Lesnick, T. G., et al. (2012). Imaging and acetylcholinesterase inhibitor response in dementia with Lewy bodies. Brain 135, 2470–2477. doi: 10.1093/brain/aws173
Graybiel, A. M., and Grafton, S. T. (2015). The striatum: where skills and habits meet. Cold Spring Harb. Perspect. Biol. 7:a021691. doi: 10.1101/cshperspect.a021691
Haber, S. N. (2003). The primate basal ganglia: parallel and integrative networks. J. Chem. Neuroanat. 26, 317–330. doi: 10.1016/j.jchemneu.2003.10.003
Halligan, P. W., and Marshall, J. C. (1998). Neglect of awareness. Conscious. Cogn. 7, 356–380. doi: 10.1006/ccog.1998.0362
Happé, F. G. E. (1996). Studying weak central coherence at low levels: children with autism do not succumb to visual illusions. A research note. J. Child Psychol. Psychiatry 37, 873–877. doi: 10.1111/j.1469-7610.1996.tb01483.x
Hasson, U., Yang, E., Vallines, I., Heeger, D. J., and Rubin, N. (2008). A hierarchy of temporal receptive windows in human cortex. J. Neurosci. 28, 2539–2550. doi: 10.1523/JNEUROSCI.5487-07.2008
Hawley, J. S., and Weiner, W. J. (2012). Hemiballismus: current concepts and review. Parkinsonism Relat. Disord. 18, 125–129. doi: 10.1016/j.parkreldis.2011.08.015
Heinke, D., and Humphreys, G. W. (2003). Attention, spatial representation, and visual neglect: simulating emergent attention and spatial memory in the selective attention for identification model (SAIM). Psychol. Rev. 110, 29–87. doi: 10.1037/0033-295X.110.1.29
Hikosaka, O., and Wurtz, R. H. (1983). Visual and oculomotor functions of monkey substantia nigra pars reticulata. IV. Relation of substantia nigra to superior colliculus. J. Neurophysiol. 49, 1285. doi: 10.1152/jn.1983.49.5.1285
Hopkins, D. A., and Holstege, G. (1978). Amygdaloid projections to the mesencephalon, pons and medulla oblongata in the cat. Exp. Brain Res. 32, 529–547. doi: 10.1007/BF00239551
Husain, M., Mannan, S., Hodgson, T., Wojciulik, E., Driver, J., and Kennard, C. (2001). Impaired spatial working memory across saccades contributes to abnormal search in parietal neglect. Brain 124, 941–952. doi: 10.1093/brain/124.5.941
Iglesias, S., Tomiello, S., Schneebeli, M., and Stephan, K. E. (2016). Models of neuromodulation for computational psychiatry. Wiley Interdisc. Rev. Cogn. Sci. 8:e1420. doi: 10.1002/wcs.1420
Jahanshahi, M., Obeso, I., Rothwell, J. C., and Obeso, J. A. (2015). A fronto-striato-subthalamic-pallidal network for goal-directed and habitual inhibition. Nat. Rev. Neurosci. 16, 719–732. doi: 10.1038/nrn4038
Jávor-Duray, B. N., Vinck, M. M., van der Roest, M., Bezard, E., Berendse, H. W., Boraud, T., et al. (2017). Alterations in functional cortical hierarchy in hemiparkinsonian rats. J. Neurosci. 37, 7669. doi: 10.1523/JNEUROSCI.3257-16.2017
Kanai, R., Komura, Y., Shipp, S., and Friston, K. (2015). Cerebral hierarchies: predictive processing, precision and the pulvinar. Philos. Trans. R. Soci. B Biol. Sci. 370:1668. doi: 10.1098/rstb.2014.0169
Kaplan, R., and Friston, K. J. (2018). Planning and navigation as active inference. Biol. Cybern.. doi: 10.1007/s00422-018-0753-2
Karnath, H.-O., and Rorden, C. (2012). The anatomy of spatial neglect. Neuropsychologia 50, 1010–1017. doi: 10.1016/j.neuropsychologia.2011.06.027
Karnath, H. O., Himmelbach, M., and Rorden, C. (2002). The subcortical anatomy of human spatial neglect: putamen, caudate nucleus and pulvinar. Brain 125, 350–360. doi: 10.1093/brain/awf032
Kato, M., Miyashita, N., Hikosaka, O., Matsumura, M., Usui, S., and Kori, A. (1995). Eye movements in monkeys with local dopamine depletion in the caudate nucleus. I. Deficits in spontaneous saccades. J. Neurosci. 15, 912.
Kersten, D., Mamassian, P., and Yuille, A. (2004). Object perception as bayesian inference. Annu. Rev. Psychol. 55, 271–304. doi: 10.1146/annurev.psych.55.090902.142005
Khalsa, S. S., Adolphs, R., Cameron, O. G., Critchley, H. D., Davenport, P. W., Feinstein, J. S., et al. (2018). Interoception and mental health: a roadmap. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 3, 501–513. doi: 10.1016/j.bpsc.2017.12.004
Khundakar, A. A., Hanson, P. S., Erskine, D., Lax, N. Z., Roscamp, J., Karyka, E., et al. (2016). Analysis of primary visual cortex in dementia with Lewy bodies indicates GABAergic involvement associated with recurrent complex visual hallucinations. Acta Neuropathol. Commun. 4:66. doi: 10.1186/s40478-016-0334-3
Kiebel, S. J., Daunizeau, J., and Friston, K. J. (2008). A hierarchy of time-scales and the brain. PLoS Comput. Biol. 4:e1000209. doi: 10.1371/journal.pcbi.1000209
Kim, E. J., Ashley Juavinett, L., Espoir Kyubwa, M., Matthew Jacobs, W., and Edward Callaway, M. (2015). Three types of cortical layer 5 neurons that differ in brain-wide connectivity and function. Neuron 88, 1253–1267. doi: 10.1016/j.neuron.2015.11.002
Kimmerly, D. S., O'Leary, D. D., Menon, R. S., Gati, J. S., and Shoemaker, J. K. (2005). Cortical regions associated with autonomic cardiovascular regulation during lower body negative pressure in humans. J. Physiol. 569(Pt 1), 331–345. doi: 10.1113/jphysiol.2005.091637
Kirchhoff, M., Parr, T., Palacios, E., Friston, K., and Kiverstein, J. (2018). The Markov blankets of life: autonomy, active inference and the free energy principle. J. R. Soc. Interface 15:20170792. doi: 10.1098/rsif.2017.0792
Kirk, E. A., and Rice, C. L. (2017). Contractile function and motor unit firing rates of the human hamstrings. J. Neurophysiol. 117, 243–250. doi: 10.1152/jn.00620.2016
Kiverstein, J. (2018). Free energy and the self: an ecological–enactive interpretation. Topoi 1–16. doi: 10.1007/s11245-018-9561-5
Knill, D. C., and Pouget, A. (2004). The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. 27, 712–719. doi: 10.1016/j.tins.2004.10.007
Korf, J. (2014). Quantum and multidimensional explanations in a neurobiological context of mind. Neuroscientist 21, 345–355. doi: 10.1177/1073858414542250
Kori, A., Miyashita, N., Kato, M., Hikosaka, O., Usui, S., and Matsumura, M. (1995). Eye movements in monkeys with local dopamine depletion in the caudate nucleus. II. Deficits in voluntary saccades. J. Neurosci. 15, 928.
Korn, H., and Faure, P. (2003). Is there chaos in the brain? II. Experimental evidence and related models. Comptes Rendus Biol. 326, 787–840. doi: 10.1016/j.crvi.2003.09.011
Koss, M. C. (1986). Pupillary dilation as an index of central nervous system α2-adrenoceptor activation. J. Pharmacol. Methods 15, 1–19. doi: 10.1016/0160-5402(86)90002-1
Künzle, H., and Akert, K. (1977). Efferent connections of cortical, area 8 (frontal eye field) in Macaca fascicularis. A reinvestigation using the autoradiographic technique. J. Comp. Neurol. 173, 147–163.
Laar, T. V. D., and Vries, B. D. (2016). A probabilistic modeling approach to hearing loss compensation. IEEE/ACM Trans. Audio Speech Lang. Process. 24, 2200–2213. doi: 10.1109/TASLP.2016.2599275
Lambe, E. K., Goldman-Rakic, P. S., and Aghajanian, G. K. (2000). Serotonin induces EPSCs preferentially in layer V pyramidal neurons of the frontal cortex in the rat. Cereb. Cortex 10, 974–980. doi: 10.1093/cercor/10.10.974
Lanciego, J. L., Luquin, N., and Obeso, J. A. (2012). Functional neuroanatomy of the basal ganglia. Cold Spring Harb. Perspect. Med. 2:a009621. doi: 10.1101/cshperspect.a009621
Lavín, C., San Martín, R., and Rosales Jubal, E. (2013). Pupil dilation signals uncertainty and surprise in a learning gambling task. Front. Behav. Neurosci. 7:218. doi: 10.3389/fnbeh.2013.00218
Lavine, N., Reuben, M., and Clarke, P. (1997). A population of nicotinic receptors is associated with thalamocortical afferents in the adult rat: laminal and areal analysis. J. Comp. Neurol. 380, 175–190. doi: 10.1002/(SICI)1096-9861(19970407)380:2<175::AID-CNE3>3.0.CO;2-0
Lawson, R. P., Mathys, C., and Rees, G. (2017). Adults with autism overestimate the volatility of the sensory environment. Nat. Neurosci. 20, 1293–1299. doi: 10.1038/nn.4615
Lawson, R. P., Rees, G., and Friston, K. J. (2014). An aberrant precision account of autism. Front. Hum. Neurosci. 8:302. doi: 10.3389/fnhum.2014.00302
Law-Tho, D., Crepel, F., and Hirsch, J. C. (1993). Noradrenaline decreases transmission of NMDA- and non-NMDA-receptor mediated monosynaptic EPSPs in rat prefrontal neurons in vitro. Eur. J. Neurosci. 5, 1494–1500. doi: 10.1111/j.1460-9568.1993.tb00217.x
Liao, H.-I., Yoneya, M., Kidani, S., Kashino, M., and Furukawa, S. (2016). Human pupillary dilation response to deviant auditory stimuli: effects of stimulus properties and voluntary attention. Front. Neurosci. 10:43. doi: 10.3389/fnins.2016.00043
Limanowski, J., and Blankenburg, F. (2018). Fronto-parietal brain responses to visuotactile congruence in an anatomical reference frame. Front. Hum. Neurosci. 12:84. doi: 10.3389/fnhum.2018.00084
Limanowski, J., and Friston, K. (2018). ‘Seeing the Dark’: grounding phenomenal transparency and opacity in precision estimation for active Inference. Front. Psychol. 9:643. doi: 10.3389/fpsyg.2018.00643
Loeliger, H. A. (2004). An introduction to factor graphs. IEEE Signal Process. Mag. 21, 28–41. doi: 10.1109/MSP.2004.1267047
Loeliger, H. A., and Vontobel, P. O. (2017). Factor graphs for quantum probabilities. IEEE Trans. Inform. Theory 63, 5642–5665. doi: 10.1109/TIT.2017.2716422
Ma, T. P., Graybiel, A. M., and Wurtz, R. H. (1991). Location of saccade-related neurons in the macaque superior colliculus. Exp. Brain Res. 85, 21–35. doi: 10.1007/BF00229983
Malhotra, P. A., Parton, A. D., Greenwood, R., and Husain, M. (2006). Noradrenergic modulation of space exploration in visual neglect. Ann. Neurol. 59, 186–190. doi: 10.1002/ana.20701
Mallet, N., Benjamin Micklem, R., Henny, P., Matthew Brown, T., Williams, C., J Bolam, P., et al. (2012). Dichotomous organization of the external globus pallidus. Neuron 74, 1075–1086. doi: 10.1016/j.neuron.2012.04.027
Marek, R., Strobel, C., Bredy, T. W., and Sah, P. (2013). The amygdala and medial prefrontal cortex: partners in the fear circuit. J. Physiol. 591, 2381–2391. doi: 10.1113/jphysiol.2012.248575
Marshall, L., Mathys, C., Ruge, D., de Berker, A. O., Dayan, P., Stephan, K. E., et al. (2016). Pharmacological fingerprints of contextual uncertainty. PLoS Biol. 14:e1002575. doi: 10.1371/journal.pbio.1002575
Mayeux, R. P. (1987). Clinical and biochemical correlates of bradyphrenia in Parkinson's disease. Neurology 37, 1693–1693-a.
McFarland, N. R., and Haber, S. N. (2002). Thalamic relay nuclei of the basal ganglia form both reciprocal and nonreciprocal cortical connections, linking multiple frontal cortical areas. J. Neurosci. 22, 8117. doi: 10.1523/JNEUROSCI.22-18-08117.2002
Menon, G. J., Rahman, I., Menon, S. J., and Dutton, G. N. (2003). Complex visual hallucinations in the visually impaired: the charles bonnet syndrome. Surv. Ophthalmol. 48, 58–72. doi: 10.1016/S0039-6257(02)00414-9
Metzinger, T. (2017). “The problem of mental action - predictive control without sensory sheets,” in Philosophy and Predicitive Processing, eds T. Metzingerand and W. Wiese (Frankfurt: MIND Group), 1–26. doi: 10.15502/9783958573208
Michele, R., and Anna Rita, B. (2012). Impulsive and compulsive behaviors during dopamine replacement treatment in Parkinson's disease and other disorders. Curr. Drug Saf. 7, 63–75. doi: 10.2174/157488612800492726
Miller, K. D. (2003). Understanding layer 4 of the cortical circuit: a model based on cat V1. Cerebral Cortex 13, 73–82. doi: 10.1093/cercor/13.1.73
Minka, T. P. (2001). “Expectation propagation for approximate bayesian inference,” in Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence. Seattle, WA: Morgan Kaufmann Publishers Inc.
Mirza, M. B., Adams, R. A., Mathys, C., and Friston, K. J. (2018). Human visual exploration reduces uncertainty about the sensed world. PLoS ONE 13:e0190429. doi: 10.1371/journal.pone.0190429
Mirza, M. B., Adams, R. A., Mathys, C. D., and Friston, K. J. (2016). Scene construction, visual foraging, and active inference. Front. Comput. Neurosci. 10:56. doi: 10.3389/fncom.2016.00056
Moran, R. J., Campo, P., Symmonds, M., Stephan, K. E., Dolan, R. J., and Friston, K. J. (2013). Free energy, precision and learning: the role of cholinergic neuromodulation. J. Neurosci. 33, 8227–8236. doi: 10.1523/JNEUROSCI.4255-12.2013
Motohiro, K., Sabina, P., Danielle, D., Danielle, R., Henri, C., Bernard, M., et al. (1987). Cortical hypometabolism and its recovery following nucleus basalis lesions in baboons: a PET study. J. Cereb. Blood Flow Metab. 7, 812–817.
Moutoussis, M., Trujillo-Barreto, N. J., El-Deredy, W., Dolan, R. J., and Friston, K. J. (2014). A formal model of interpersonal inference. Front. Hum. Neurosci. 8:160. doi: 10.3389/fnhum.2014.00160
Mukherjee, P., Sabharwal, A., Kotov, R., Szekely, A., Parsey, R., Barch, D. M., et al. (2016). Disconnection between amygdala and medial prefrontal cortex in psychotic disorders. Schizophr. Bull. 42, 1056–1067. doi: 10.1093/schbul/sbw012
Munoz, D. P., and Wurtz, R. H. (1995). Saccade-related activity in monkey superior colliculus. I. Characteristics of burst and buildup cells. J. Neurophysiol. 73:2313–2333. doi: 10.1152/jn.1995.73.6.2313
Murray, J. D., Bernacchia, A., Freedman, D. J., Romo, R., Wallis, J. D., Cai, X., et al. (2014). A hierarchy of intrinsic timescales across primate cortex. Nat. Neurosci. 17, 1661–1663. doi: 10.1038/nn.3862
Nachev, P., and Hacker, P. (2014). The neural antecedents to voluntary action: a conceptual analysis. Cogn. Neurosci. 5, 193–208. doi: 10.1080/17588928.2014.934215
Nambu, A. (2004). A new dynamic model of the cortico-basal ganglia loop. Progress Brain Rese. Else. 143, 461–466. doi: 10.1016/S0079-6123(03)43043-4
Nambu, A., Tokuno, H., and Takada, M. (2002). Functional significance of the cortico–subthalamo–pallidal ‘hyperdirect’ pathway. Neurosci. Res. 43, 111–117. doi: 10.1016/S0168-0102(02)00027-5
Olsen, S. R., Bortone, D. S., Adesnik, H., and Scanziani, M. (2012). Gain control by layer six in cortical circuits of vision. Nature 483:47–52. doi: 10.1038/nature10835
Ondobaka, S., Kilner, J., and Friston, K. (2017). The role of interoceptive inference in theory of mind. Brain Cogn. 112, 64–68. doi: 10.1016/j.bandc.2015.08.002
Owens, A. P., Friston, K. J., Low, D. A., Mathias, C. J., and Critchley, H. D. (2018). Investigating the relationship between cardiac interoception and autonomic cardiac control using a predictive coding framework. Auton. Neurosci. 210, 65–71. doi: 10.1016/j.autneu.2018.01.001
Palmer, C. J., Lawson, R. P., and Hohwy, J. (2017). Bayesian approaches to autism: towards volatility, action, and behavior. Psychol. Bull. 143, 521–542. doi: 10.1037/bul0000097
Palmer, C. J., Paton, B., Kirkovski, M., Enticott, P. G., and Hohwy, J. (2015). Context sensitivity in action decreases along the autism spectrum: a predictive processing perspective. Proc. Royal Soc. B Biol. Sci. 282:20141557. doi: 10.1098/rspb.2014.1557
Parr, T., Benrimoh, D. A., Vincent, P., and Friston, K. J. (2018a). Precision and False Perceptual Inference. Front. Integr. Neurosci. 12:39. doi: 10.3389/fnint.2018.00039
Parr, T., and Friston, K. J. (2017a). The active construction of the visual world. Neuropsychologia 104, 92–101. doi: 10.1016/j.neuropsychologia.2017.08.003
Parr, T., and Friston, K. J. (2017b). The computational anatomy of visual neglect. Cereb. Cortex. 28, 777–790. doi: 10.1093/cercor/bhx316
Parr, T., and Friston, K. J. (2017c). Uncertainty, epistemics and active inference. J. Royal Soc. Inter. 14:136. doi: 10.1098/rsif.2017.0376
Parr, T., and Friston, K. J. (2017d). Working memory, attention, and salience in active inference. Sci. Rep. 7:14678. doi: 10.1038/s41598-017-15249-0
Parr, T., and Friston, K. J. (2018a). Active inference and the anatomy of oculomotion. Neuropsychologia 111. 334–343 doi: 10.1016/j.neuropsychologia.2018.01.041
Parr, T., and Friston, K. J. (2018b). The discrete and continuous brain: from decisions to movement—and back again. Neural Comput. 30, 2319–2347. doi: 10.1162/neco_a_01102
Parr, T., and Friston, K. J. (2018c). Generalised free energy and active inference: can the future cause the past? bioRxiv. 1–22. doi: 10.1101/304782
Parr, T., Rees, G., and Friston, K. J. (2018b). Computational neuropsychology and bayesian inference. Front. Hum. Neurosci. 12:61. doi: 10.3389/fnhum.2018.00061
Pearl, J. (1998). “Graphical models for probabilistic and causal reasoning,” in Quantified Representation of Uncertainty and Imprecision, ed P. Smets (Dordrecht: Springer Netherlands), 367–389.
Pearl, J. (2014). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. San Francisco, CA: Elsevier.
Perry, E. K., Haroutunian, V., Davis, K. L., Levy, R., Lantos, P., Eagger, S., et al. (1994). Neocortical cholinergic activities differentiate lewy body dementia from classical Alzheimer's disease. Neuroreport 5, 747–749. doi: 10.1097/00001756-199403000-00002
Petrovich, G. D., Canteras, N. S., and Swanson, L. W. (2001). Combinatorial amygdalar inputs to hippocampal domains and hypothalamic behavior systems. Brain Res. Rev. 38, 247–289. doi: 10.1016/S0165-0173(01)00080-7
Petzschner, F. H., Weber, L. A. E., Gard, T., and Stephan, K. E. (2017). Computational psychosomatics and computational psychiatry: toward a joint framework for differential diagnosis. Biol. Psychiatry 82, 421–430. doi: 10.1016/j.biopsych.2017.05.012
Plenz, D., and Kital, S. T. (1999). A basal ganglia pacemaker formed by the subthalamic nucleus and external globus pallidus. Nature 400, 677–682. doi: 10.1038/23281
Price, C., Warburton, E., Moore, C., Frackowiak, R., and Friston, K. (2001). Dynamic diaschisis: anatomically remote and context-sensitive human brain lesions. J. Cogn. Neurosci. 13, 419–429. doi: 10.1162/08989290152001853
Rao, R. P., and Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 2, 79–87. doi: 10.1038/4580
Reichert, D. P., Seriès, P., and Storkey, A. J. (2013). Charles bonnet syndrome: evidence for a generative model in the cortex? PLoS Comput. Biol. 9:e1003134. doi: 10.1371/journal.pcbi.1003134
Sahin, M., Bowen, W. D., and Donoghue, J. P. (1992). Location of nicotinic and muscarinic cholinergic and μ-opiate receptors in rat cerebral neocortex: evidence from thalamic and cortical lesions. Brain Res. 579, 135–147. doi: 10.1016/0006-8993(92)90752-U
Sales, A. C., Friston, K. J., Jones, M. W., Pickering, A. E., and Moran, R. J. (2018). Locus Coeruleus tracking of prediction errors optimises cognitive flexibility: an active inference model. bioRxiv:340620. doi: 10.1101/340620
Schaal, S. (2006). “Dynamic movement primitives-a framework for motor control in humans and humanoid robotics,” in Adaptive Motion of Animals and Machines, eds H. Kimura, K. Tsuchiya, A. Ishiguro, and H. Witte (Tokyo: Springer), 261–280. doi: 10.1007/4-431-31381-8_23
Schiller, P. H., Sandell, J. H., and Maunsell, J. H. (1987). The effect of frontal eye field and superior colliculus lesions on saccadic latencies in the rhesus monkey. J. Neurophysiol. 57, 1033– 1049. doi: 10.1152/jn.1987.57.4.1033
Schiller, P. H., True, S. D., and Conway, J. L. (1980). Deficits in eye movements following frontal eye-field and superior colliculus ablations. J. Neurophysiol. 44, 1175–1189. doi: 10.1152/jn.1980.44.6.1175
Schwartenbeck, P., FitzGerald, T. H. B., Mathys, C., Dolan, R., and Friston, K. (2015). The dopaminergic midbrain encodes the expected certainty about desired outcomes. Cereb. Cortex. 25, 3434–3445. doi: 10.1093/cercor/bhu159
Seifert, U. (2012). Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Progress Phys. 75:126001. doi: 10.1088/0034-4885/75/12/126001
Seth, A. K. (2013). Interoceptive inference, emotion, and the embodied self. Trends Cogn. Sci. 17, 565–573. doi: 10.1016/j.tics.2013.09.007
Shah, A., and Frith, U. (1983). An islet of ability in autistic children: a research note. J. Child Psychol. Psychiatry 24, 613–620. doi: 10.1111/j.1469-7610.1983.tb00137.x
Shipp, S. (2007). Structure and function of the cerebral cortex. Curr. Biol. 17, R443–R449. doi: 10.1016/j.cub.2007.03.044
Shipp, S. (2016). Neural elements for predictive coding. Front. Psychol. 7:1792. doi: 10.3389/fpsyg.2016.01792
Shipp, S. (2017). The functional logic of corticostriatal connections. Brain Struct. Funct. 222, 669–706. doi: 10.1007/s00429-016-1250-9
Shipp, S., Adams, R. A., and Friston, K. J. (2013). Reflections on agranular architecture: predictive coding in the motor cortex. Trends Neurosci. 36, 706–716. doi: 10.1016/j.tins.2013.09.004
Shulman, G. L., Astafiev, S. V., Franke, D., Pope, D. L. W., Snyder, A. Z., McAvoy, M. P., et al. (2009). Interaction of stimulus-driven reorienting and expectation in ventral and dorsal fronto-parietal and basal ganglia-cortical networks. J. Neurosci. 29, 4392–4407. doi: 10.1523/JNEUROSCI.5609-08.2009
Simmons, D. R., Robertson, A. E., McKay, L. S., Toal, E., McAleer, P., and Pollick, F. E. (2009). Vision in autism spectrum disorders. Vision Res. 49, 2705–2739. doi: 10.1016/j.visres.2009.08.005
Smith, Y., Bevan, M., Shink, E., and Bolam, J. (1998). Microcircuitry of the direct and indirect pathways of the basal ganglia. Neuroscience 86, 353–387.
Snijders, A. H., and Bloem, B. R. (2010). Cycling for freezing of gait. N. Engl. J. Med. 362:e46. doi: 10.1056/NEJMicm0810287
Sparks, D. L. (1986). Translation of sensory signals into commands for control of saccadic eye movements: role of primate superior colliculus. Physiol. Rev. 66, 118–171. doi: 10.1152/physrev.1986.66.1.118
Swanson, L. W., and Petrovich, G. D. (1998). What is the amygdala? Trends Neurosci. 21, 323–331. doi: 10.1016/S0166-2236(98)01265-X
Szczepanski, S. M., Pinsk, M. A., Douglas, M. M., Kastner, S., and Saalmann, Y. B. (2013). Functional and structural architecture of the human dorsal frontoparietal attention network. Proc. Natl. Acad. Sci. U.S.A. 110, 15806–15811. doi: 10.1073/pnas.1313903110
Testolin, A., and Zorzi, M. (2016). Probabilistic models and generative neural networks: towards an unified framework for modeling normal and impaired neurocognitive functions. Front. Comput. Neurosci. 10:73. doi: 10.3389/fncom.2016.00073
Teunisse, R. J., Zitman, F. G., Cruysberg, J. R. M., Hoefnagels, W. H. L., and Verbeek, A. L. M. (1996). Visual hallucinations in psychologically normal people: charles bonnet's syndrome. Lancet 347, 794–797. doi: 10.1016/S0140-6736(96)90869-7
Thomson, A. (2010). Neocortical layer 6, a review. Front. Neuroanat. 4:13. doi: 10.3389/fnana.2010.00013
Thomson, A. M., and Bannister, A. P. (2003). Interlaminar connections in the neocortex. Cereb. Cortex 13, 5–14. doi: 10.1093/cercor/13.1.5
Vidaurre, D., Smith, S. M., and Woolrich, M. W. (2017). Brain network dynamics are hierarchically organized in time. Proc. Natl. Acad. Sci. 114:12827. doi: 10.1073/pnas.1705120114
Virgo, J. D., and Plant, G. T. (2017). Internuclear ophthalmoplegia. Pract. Neurol. 17:149. doi: 10.1136/practneurol-2016-001428
Vontobel, P. O. (2011). “A factor-graph approach to Lagrangian and Hamiltonian dynamics,” in 2011 IEEE International Symposium on Information Theory Proceedings (St. Petersburg: IEEE).
Vontobel, P. O., and Loeliger, H. A. (2003). “Factor graphs and dynamical electrical networks,” in Proceedings 2003 IEEE Information Theory Workshop (Cat. No.03EX674) (Paris: IEEE).
Vossel, S., Bauer, M., Mathys, C., Adams, R. A., Dolan, R. J., Stephan, K. E., et al. (2014). Cholinergic stimulation enhances bayesian belief updating in the deployment of spatial attention. J. Neurosci. 34, 15735–15742. doi: 10.1523/JNEUROSCI.0091-14.2014
Wainwright, M. J., and Jordan, M. I. (2008). Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn. 1. 1–305. doi: 10.1561/2200000001
Wald, A. (1947). An essentially complete class of admissible decision functions. Anna. Mathemat. Statist. 18, 549–555. doi: 10.1214/aoms/1177730345
Wall, N., De La Parra, R. M., Callaway, E. M., and Kreitzer, A. C. (2013). Differential innervation of direct- and indirect-pathway striatal projection neurons. Neuron 79, 347–360. doi: 10.1016/j.neuron.2013.05.014
Wesson, D. W., and Wilson, D. A. (2011). Sniffing out the contributions of the olfactory tubercle to the sense of smell: hedonics, sensory integration, and more? Neurosci. Biobehav. Rev. 35, 655–668. doi: 10.1016/j.neubiorev.2010.08.004
Yager, L. M., Garcia, A. F., Wunsch, A. M., and Ferguson, S. M. (2015). The ins and outs of the striatum: role in drug addiction. Neuroscience 301, 529–541. doi: 10.1016/j.neuroscience.2015.06.033
Yedidia, J. S., Freeman, W. T., and Weiss, Y. (2005). Constructing free-energy approximations and generalized belief propagation algorithms. IEEE Trans. Inform. Theory 51, 2282–2312. doi: 10.1109/TIT.2005.850085
Yin, H. H., and Knowlton, B. J. (2006). The role of the basal ganglia in habit formation. Nat. Rev. Neurosci. 7, 464–476. doi: 10.1038/nrn1919
Yu, A. J., and Dayan, P. (2005). Uncertainty, neuromodulation, and attention. Neuron 46, 681–692. doi: 10.1016/j.neuron.2005.04.026
Zavala, B., Damera, S., Dong, J. W., Lungu, C., Brown, P., and Zaghloul, K. A. (2017). Human subthalamic nucleus theta and beta oscillations entrain neuronal firing during sensorimotor conflict. Cereb. Cortex. 27, 496–508. doi: 10.1093/cercor/bhv244
Zeki, S., and Shipp, S. (1988). The functional logic of cortical connections. Nature 335, 311–317. doi: 10.1038/335311a0
Zhang, Z., Cordeiro Matos, S., Jego, S., Adamantidis, A., and Séguéla, P. (2013). Norepinephrine drives persistent activity in prefrontal cortex via synergistic α1 and α2 adrenoceptors. PLoS ONE 8:e66122. doi: 10.1371/journal.pone.0066122
Keywords: Bayesian, neuroanatomy, active inference, generative model, message passing, predictive processing
Citation: Parr T and Friston KJ (2018) The Anatomy of Inference: Generative Models and Brain Structure. Front. Comput. Neurosci. 12:90. doi: 10.3389/fncom.2018.00090
Received: 24 August 2018; Accepted: 25 October 2018;
Published: 13 November 2018.
Edited by:
Yilei Zhang, Nanyang Technological University, SingaporeReviewed by:
Jamie Sleigh, University of Auckland, New ZealandGopikrishna Deshpande, Auburn University, United States
Adam Ponzi, Okinawa Institute of Science and Technology Graduate University, Japan
Jan Lauwereyns, Kyushu University, Japan
Copyright © 2018 Parr and Friston. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Thomas Parr, dGhvbWFzLnBhcnIuMTJAdWNsLmFjLnVr
 Thomas Parr
Thomas Parr Karl J. Friston
Karl J. Friston