- 1Institute of Physiology, University Medical Center Mainz, Johannes Gutenberg University Mainz, Mainz, Germany
- 2Interdisciplinary Centre for 3Rs in Animal Research, Faculty of Medicine, Justus Liebig University Giessen, Giessen, Germany
- 3Institute of Clinical Neuroanatomy, Neuroscience Center, Goethe University Frankfurt, Frankfurt, Germany
Giant depolarizing potentials (GDPs) represent a typical spontaneous activity pattern in the immature hippocampus. GDPs are mediated by GABAergic and glutamatergic synaptic inputs and their initiation requires an excitatory GABAergic action, which is typical for immature neurons due to their elevated intracellular Cl- concentration ([Cl-]i). Because GABAA receptors are ligand-gated Cl- channels, activation of these receptors can potentially influence [Cl-]i. However, whether the GABAergic activity during GDPs influences [Cl-]i is unclear. To address this question we performed whole-cell and gramicidin-perforated patch-clamp recordings from visually identified CA3 pyramidal neurons in immature hippocampal slices of mice at postnatal days 4–7. These experiments revealed that the [Cl-]i of CA3 neurons displays a considerable heterogeneity, ranging from 13 to 70 mM (average 38.1 ± 3.2 mM, n = 36). In accordance with this diverse [Cl-]i, GDPs induced either Cl--effluxes or Cl--influxes. In high [Cl-]i neurons with a negative Cl--driving force (DFCl) the [Cl-]i decreased after a GDP by 12.4 ± 3.4 mM (n = 10), while in low [Cl-]i neurons with a positive DFCl [Cl-]i increased by 4.4 ± 0.9 mM (n = 6). Inhibition of GDP activity by application of the AMPA receptor antagonist CNQX led to a [Cl-]i decrease to 24.7 ± 2.9 mM (n = 8). We conclude from these results, that Cl--fluxes via GABAA receptors during GDPs induced substantial [Cl-]i changes and that this activity-dependent ionic plasticity in neuronal [Cl-]i contributes to the functional consequences of GABAergic responses, emphasizing the concept that [Cl-]i is a state- and compartment-dependent parameter of individual cells.
Introduction
Spontaneous neuronal activity transients are a hallmark of developing neuronal systems and play an essential role for several developmental processes like neuronal migration, myelinization, cortical regionalization, or the establishment of neuronal connectivity (for review Spitzer, 2006; Ben-Ari and Spitzer, 2010; Griguoli and Cherubini, 2017; Kirischuk et al., 2017). Such spontaneous activity transients can be generated in the sensory periphery, but are also intrinsic to developing neuronal networks (for review Ben Ari, 2001; Khazipov and Luhmann, 2006; Blankenship and Feller, 2010; Kilb et al., 2011). The fact that even synaptic networks of cultured neurons develop correlated activity transients (Rolston et al., 2007; Sun et al., 2010) suggests that the formation of circuits capable of mediating recurrent activity is probably an innate feature of the neuronal nature. One striking example for spontaneous, repetitive activity transients are hippocampal giant depolarizing potentials (GDPs) (Ben-Ari et al., 1989). Such GPDs have also been observed in the immature neocortex (Allene et al., 2008), thalamus (Pangratz-Fuehrer et al., 2007), and the embryonic spinal cord (Czarnecki et al., 2014).
Giant depolarizing potentials represent recurrent, synaptically evoked suprathreshold depolarizations, which rely on GABAergic and glutamatergic transmission (Ben-Ari et al., 1989; Blankenship and Feller, 2010). GDPs require a depolarizing GABAergic action (Sipila et al., 2006b; Cherubini et al., 2011). Such depolarizing GABAergic responses are typical for immature neurons (for review Ben-Ari, 2002; Ben-Ari et al., 2012; Watanabe and Fukuda, 2015; Kirmse et al., 2018) and reflect an elevated intracellular Cl- concentration ([Cl-]i) maintained by a Cl- uptake via the isoform 1 of the Na+-dependent K+-Cl--Cotransporter (NKCC1) (Rohrbough and Spitzer, 1996; Yamada et al., 2004; Achilles et al., 2007; Blaesse et al., 2009). The membrane depolarization via synaptic and extrasynaptic GABAA receptors, which is augmented via an activation of persistent Na+ currents (Sipila et al., 2006a; Valeeva et al., 2010), facilitates the onset of neuronal activity underlying GDPs (Sipila et al., 2005). Subsequently, hippocampal neurons start burst firing and this activity is transmitted via GABAA and AMPA receptors to adjacent interneurons and pyramidal neurons (Khazipov et al., 1997; Bolea et al., 1999). A subset of GABAergic interneurons, with a high synaptic connectivity and a putative origin in the medial ganglionic eminence, serve as hub neurons with specific importance during the generation of GDPs (Bonifazi et al., 2009; Wester and McBain, 2016).
In accordance with these observations, GDPs are characterized by an initial phase of depolarizing GABAergic post-synaptic currents (PSCs) and subsequent AMPA mediated PSCs which synergistically drive the depolarization (Khalilov et al., 2015). When the depolarization surpasses the GABA equilibrium potential (EGABA) the GABAergic currents become outwardly directed, promoting an inhibitory action of GABA that limits the amount of depolarization/activation and thus the synchronization between pyramidal neurons (Khalilov et al., 2015). Finally, activation of Ca2+-dependent K+ channels and post-synaptic GABAB receptors decreases the excitability and the firing frequency of pyramidal neurons (Sipila et al., 2006a; Khalilov et al., 2017), which reduce AMPA and GABA post-synaptic potentials (PSPs) and thus terminates GDPs.
Since GABAA receptors are ligand-gated anion-channels with a high permeability for Cl- ions (Farrant and Kaila, 2007), Cl--fluxes through activated GABAA receptors can influence [Cl-]i on a shorter time scale (Kaila et al., 1989; Bracci et al., 2001; Isomura et al., 2003; Jedlicka and Backus, 2006; Jedlicka et al., 2011; Lillis et al., 2012; Sato et al., 2017). The resulting activity-dependent [Cl-]i increase upon massive GABAergic stimulation, in combination with the HCO3- permeability of GABAA receptors, leads to a shift from hyperpolarizing/inhibitory to depolarizing/excitatory GABAergic action (Staley et al., 1995; Sun et al., 2001; Isomura et al., 2003, but see Kaila et al., 1997 for more complex events involved in this hyperpolarizing-depolarizing shift). This process has been termed ionic plasticity (Blaesse et al., 2009; Raimondo et al., 2012; Kaila et al., 2014a). The relation between Cl- influx, dendritic volume/morphology and the capacity of Cl- extrusion systems determines the size of such activity-dependent Cl- transients (Staley and Proctor, 1999; Wright et al., 2011; Mohapatra et al., 2016). In the immature system, with high [Cl-]i and depolarizing GABAergic events, the GABA-mediated Cl- efflux causes a transient decline in [Cl-]i that temporarily attenuates the amplitude of subsequent GABAergic responses, thereby reducing or omitting possible excitatory effects (Achilles et al., 2007; Gonzalez-Islas et al., 2010; Kolbaev et al., 2011b). However, it has remained unclear whether GDPs lead to detectable [Cl-]i changes.
In order to elucidate whether the massive GABAergic activity during a GDP influences [Cl-]i in the immature hippocampus, we performed whole-cell and gramicidin-perforated patch-clamp recordings from visually identified CA3 pyramidal neurons in hippocampal slices from mice at postnatal day 4–7. These experiments revealed that the [Cl-]i in pyramidal neurons is altered following a GDP. The direction and amount of [Cl-]i changes depends on the cell’s individual [Cl-]i, with a [Cl-]i decrease in high [Cl-]i neurons and a [Cl-]i increase at low [Cl-]i neurons. Inhibition of GDP activity leads to a decreased [Cl-]i. These results indicate that ongoing GDP activity induces ionic plasticity in immature hippocampal neurons and emphasize the concept that neuronal [Cl-]i has to be considered as a state- and compartment-dependent parameter of individual cells (Wright et al., 2011).
Materials and Methods
Slice Preparation
All experiments were conducted in accordance with EU directive 86/609/EEC for the use of animals in research and the NIH Guide for the Care and Use of Laboratory Animals, and were approved by the local ethical committee (Landesuntersuchungsanstalt RLP, Koblenz, Germany). All efforts were made to minimize the number of animals and their suffering. Time pregnant C57Bl/6 mice were obtained from Janvier Labs (Saint Berthevin, France) and housed in the local animal facility. Newborn pups of postnatal days [P] 4–7 were deeply anesthetized with enflurane (Ethrane, Abbot Laboratories, Wiesbaden, Germany). After decapitation, the brains were quickly removed and immersed for 2–3 min in ice-cold standard artificial cerebrospinal fluid (ACSF, composition see below). Horizontal slices (400 μm thickness) including the hippocampus were cut on a vibratome (Microm HM 650 V, Thermo Fischer Scientific, Schwerte, Germany). The slices were stored in an incubation chamber filled with oxygenated ACSF at room temperature before they were transferred to the recording chamber.
Solutions and Drugs
The bathing solution consisted of (in mM) 125 NaCl, 25 NaHCO3, 1.25 NaH2PO5, 1 MgCl2, 2 CaCl2, 2.5 KCl, 10 glucose and was equilibrated with 95% O2/5% CO2 at least 1 h before use (pH 7.4, osmolarity 306 mOsm). Two pipette solutions for whole-cell recordings were used: for a pipette Cl- concentration ([Cl-]p) of 10 mM the solution was composed of (in mM) 128 K-gluconate, 2 KCl, 4 NaCl, 1 CaCl2, 11 EGTA, 10 K-HEPES, 2 Mg2-ATP, 0.5 Na-GTP, and 2 lidocaine-N-ethyl chloride (pH adjusted to 7.4 with KOH and osmolarity to 306 mOsm with sucrose). For a [Cl-]p of 50 mM the solution contained (in mM) 86 K-gluconate, 44 KCl, 4 NaCl, 1 CaCl2, 11 EGTA, 10 K-HEPES, 2 Mg2-ATP, 0.5 Na-GTP. Pipette solution for gramicidin-perforated patch experiments consisted of (in mM) 10 Na-gluconate, 120 KCl, 1 CaCl2, 2 MgCl2, 11 EGTA, and 10 K-HEPES. For gramicidin-perforated patch-clamp recordings 10 μg/ml Gramicidin D (Sigma, St. Louis, MO, United States) was added from a stock solution (2 mg/ml in DMSO) on the day of experiment. Gramicidin D, bumetanide, and lidocaine-N-ethyl chloride was obtained from Sigma-Aldrich and 6-Cyano-7-nitroquinoxaline-2,3-dione (CNQX) was obtained from Biotrend (Cologne, Germany). CNQX and bumetanide were used from a dimethylsulfoxide (DMSO, Sigma-Aldrich) stock solution. The DMSO concentration of the final solution never exceeded 0.1%.
Data Acquisition and Analysis
Whole-cell and gramicidin-perforated patch-clamp recordings were performed as described previously (Kyrozis and Reichling, 1995; Kolbaev et al., 2011b) at 31 ± 1°C in a submerged-type recording chamber attached to the fixed stage of a microscope (BX51 WI, Olympus). Pyramidal neurons in the stratum pyramidale of the CA3 region were identified by their location and morphological appearance in infrared differential interference contrast image. Patch-pipettes (5–12 MΩ) were pulled from borosilicate glass capillaries (2.0 mm outside, 1.16 mm inside diameter, Science Products, Hofheim, Germany) on a vertical puller (PP-830, Narishige) and filled with the pipette solutions (composition see above).
Signals were recorded with a discontinuous voltage-clamp/current-clamp amplifier (SEC05L, NPI, Tamm, Germany), low-pass filtered at 3 kHz and stored and analyzed using an ITC-1600 AD/DA board (HEKA) and TIDA software. All voltages were corrected post hoc for liquid junction potentials of -9 mV for 10 mM [Cl-]p, -6 mV for 50 mM [Cl-]p, and -3 mV for the perforated-patch solution (Achilles et al., 2007). Input resistance and capacitance were determined from a series of hyperpolarizing current steps. Action potential amplitude was calculated from the threshold (as determined by eye) and action potential duration was measured at half-maximal amplitude. Spontaneous post-synaptic currents (sPSCs) were detected and analyzed according to their amplitude and shape by appropriate settings using Minianalysis Software (Synaptosoft, Fort Lee, NJ, United States). Charge transfer is the total amount of charges that flow during an event. For PSCs it was determined in Minianalysis by integration of the currents between calculated onset and termination time points. Charge transfer of GDPs was determined in TIDA by integration of the current deflection from the holding current between the starting and endpoint of a GDP, as defined by eye.
The GABA reversal potential (EGABA) was determined from the GABAergic currents induced by focal pressure application of 100 μM GABA via a micropipette (tip diameter ca. 1–2 μm, placed 50–100 μm from the soma in the stratum radiatum, puff duration 5–10 ms) during a voltage ramp protocol (from -3 to -63 mV; Figures 3A,B). For this purpose the current of a control voltage ramp was subtracted from the current of the voltage ramp delivered in the presence of GABA. The voltage ramp was applied during a quasi-stationary phase of the GABAergic response (Figure 3B). The Em value at which this differential current reverses was considered as EGABA (Figures 3C–E). Because for the central aim of this study it was not possible to pharmacologically block voltage-dependent Na+ currents with TTX, the voltage ramp protocol was preceded by a 100 ms long depolarizing phase at -3 mV to inactivate voltage-dependent Na+ currents (Figure 3B).
In order to take the contribution of HCO3- ions to the reversal potential of GABAA receptors into account (Farrant and Kaila, 2007), we calculated [Cl-]i from EGABA with the Goldman-Hodgkin-Katz equation:
For the calculation of [Cl-]i from EGABA we used a [Cl-]e of 133.5 mM, an extracellular HCO3- concentration ([HCO3-]e) of 24 mM and a [HCO3-]i of 14.1 mM. The [HCO3-]i was calculated with the Henderson–Hasselbalch equation using a CO2 pressure of 38 mmHg (corresponding to 5% CO2 at 760 Torr), an intracellular pH of 7.2 (Ruusuvuori et al., 2010), a Henry coefficient of 0.318 and a pKs of 6.128 (Mitchell et al., 1965). A relative HCO3- permeability (PHCO) of 0.44, which has been determined for GABAA receptors in hippocampal neurons (Fatima-Shad and Barry, 1993), was used and PCl was defined as 1. The driving-force of Cl- (DFCl) was calculated from the difference between the average Em during a GDP and ECl (DFCl = Em – EGABA). To calculate GABAergic (gGABA) and glutamatergic conductances (gGlu) the peak amplitudes of GDP associated currents (IGDP) were divided by the estimated driving force at the given holding potentials using Ohm’s law [for GABA: gGABA = IGDP/(Em - ERevGABA); for glutamate: gGlu = IGDP/(Em - ERevGABA)].
All values are given as mean ± SEM. If not explicitly noted, Student’s t-test was used for statistical analysis (Systat 11). Significance was assigned at p-levels of 0.05 (∗), 0.01 (∗∗), and 0.001 (∗∗∗).
Microcontroller-Based GDP Detection
To enable the online determination of [Cl-]i at distinct latencies after a GDP we used a microcontroller (Arduino Uno1) connected to the inputs and outputs of the NPI amplifier. A threshold crossing algorithm comparing a floating average of 50 Em datapoints (to avoid triggering by single action potential) with a manually preset threshold potential was used to detect a GDP (Figure 3F). The time point when Em falls below the threshold was defined as end of a GDP. After a defined interval (0.1–20 s) the microcontroller provided a signal that switches the amplifier to voltage-clamp mode and delivers the ramp protocol used for the determination of EGABA (Figures 3A–E). The used program code for the Arduino microcontroller is available at https://forum.arduino.cc/index.php?topic=564489.0.
Compartmental Modeling
For morphological reconstruction some CA3 pyramidal cells were filled with biocytin (0.5–1%, Sigma-Aldrich) under whole-cell conditions as described in detail before (Horikawa and Armstrong, 1988; Schröder and Luhmann, 1997). Reconstruction and morphological analysis of the biocytin-labeled neurons were performed from 60x oil-immersion images using Fiji2. A reconstructed CA3 pyramidal cell was imported into the NEURON simulation program3 (Figures 5A,B). The following passive parameters were used: Ra (specific axial resistance) = 34.5 Ωcm; Rm (specific membrane resistance) = 2 kΩcm2; Cm (specific membrane capacitance) = 1 μFcm-2.
GABAA synapses were simulated as a post-synaptic parallel Cl- and HCO3- conductance with exponential rise and exponential decay (Jedlicka et al., 2011):
where P is a fractional ionic conductance that was used to split the GABAA conductance (gGABA) into Cl- and HCO3- conductance. ECl and EHCO3 were calculated from Nernst equation. The GABAA conductance was modeled using a two-term exponential function, using separate values of rise time (0.5 ms) and decay time (80 ms) (Santhakumar et al., 2005). Parameters used in our simulations were as follows: [Cl-]o = 133.5 mM, [HCO3-]i = 14.1 mM, [HCO3-]o = 24 mM, temperature = 31°C, p = 0.44 (Fatima-Shad and Barry, 1993).
For the experiments used to model the impact of access resistance (Rs) or dendritic filtering on the determination of the reversal potential we considered static [Cl-]i and [HCO3-]i ([Cl-]i = 30 mM; [HCO3-]i = 14.4 mM) and implemented a single-electrode voltage-clamp process to the soma, using Rs values of 0.5, 5, 10, 20, and 40 MΩ. A GABA synapse with a decay time of 100 ms and a peak conductance of 10 nS was used to emulate the GABA application protocol.
For the modeling of the GDP-induced [Cl-]i and [HCO3-]i changes we calculated ion diffusion and uptake by standard compartmental diffusion modeling (De Schutter and Smolen, 1998; De Schutter, 2010; Mohapatra et al., 2014, 2016). To simulate intracellular Cl- and HCO3- dynamics, we adapted our previously published model (Jedlicka et al., 2011). Longitudinal Cl- and HCO3- diffusion along dendrites was modeled as the exchange of anions between adjacent compartments. For radial diffusion, the volume was discretized into a series of four concentric shells around a cylindrical core (De Schutter and Smolen, 1998) and Cl- or HCO3- was allowed to flow between adjacent shells (Hines and Carnevale, 2000). The free diffusion coefficient of Cl- inside neurons was set to 2 μm2/ms (Kuner and Augustine, 2000). Since the cytoplasmatic diffusion constant for HCO3- is to our knowledge unknown, we also used a value of 2 μm2/ms. To simulate transmembrane transport of Cl- and HCO3-, we implemented an exponential relaxation process for [Cl-]i and [HCO3-]i to resting levels [Cl-]irest or [HCO3-]irest with a time constant τIon.
Cl- transport was modeled as bimodal process, for [Cl-]i < [Cl-]irest τ was set to 174s to emulate an NKCC1-like Cl- transport mechanism. For [Cl-]i > [Cl-]irest τ was set to 321s to emulate passive Cl- efflux (both values obtained from unpublished experiments on immature rat CA3 hippocampal neurons). The impact of GABAergic Cl- currents on [Cl-]i and [HCO3-]i was calculated as:
To simulate the GABAergic activity during a GDP, 534 GABA synapses with a peak conductance of 0.789 nS and a decay of 80 ms were randomly distributed in the dendritic compartment of the reconstructed neurons. This number of GABAergic inputs generates a charge transfer of 88 pA (at initial [Cl-]i of 10 mM and under VC conditions at 0 mV) similar to the charge transfer recorded experimentally under this condition (see section “Properties of GDPs”). To simulate AMPA synapses, additional 107 Exp2syn processes with a peak conductance of 0.509 nS, a reversal potential of 0 mV, a rise time of 0.1 ms, and a decay of 11 ms were randomly distributed. GABA and AMPA inputs were activated stochastically using a normal distribution that emulates the distribution of glutamatergic/GABAergic PSCs observed in the present study. We analyzed the mean [Cl-]i and [HCO3-]i of all dendrites to simulate the experimental procedure for EGABA determination, in which GABA was applied to the dendritic compartment.
Results
Properties of the Recorded Cells
The average resting membrane potential (RMP) of the CA3 pyramidal cells under whole cell condition was -52.1 ± 0.8 mV (n = 116), their input resistance (Rin) at RMP was 0.9 ± 0.1 GΩ and their membrane time constant amounted to 86 ± 8.3 ms, corresponding to a membrane capacitance of 152 ± 24.3 pF. Upon depolarization above a membrane potential (Em) of -42.4 ± 0.68 mV, these cells were capable to fire action potentials with an amplitude of 54.9 ± 1.3 mV (n = 72) and a duration of 2.7 ± 0.4 ms. Comparable results were observed under gramicidin-perforated patch conditions. In these experiments the average resting membrane potential was -53.6 ± 0.24 mV (n = 24), the input resistance was 1.75 ± 0.13 GΩ and the membrane time constant amounted to 105.9 ± 11.4 ms, corresponding to a membrane capacitance of 65 ± 9.1 pF. Upon Em depolarization above -46.2 ± 1.2 mV these cells fired action potentials with an amplitude of 36 ± 2 mV (n = 22) and a duration of 3.6 ± 0.4 ms.
Properties of GDPs
Giant depolarizing potentials were present in 96 of in total 111 cells (corresponding to 86.5%) from 73 slices/44 animals investigated with different recording conditions. In the first set of experiments we used a high Cl- pipette solution ([Cl-]p = 50 mM) to characterize the properties of spontaneous network events. Under this condition in all 13 cells (from 13 slices/6 animals) spontaneous massive depolarizing events with an average amplitude of 24.9 ± 1.2 mV (n = 130 GDPs in 13 cells) and a duration of 1.24 ± 0.04 s were observed (Figures 1A,B). While these depolarizing events were subthreshold in three cells, they reliably evoked 6.4 ± 0.4 APs (n = 104 GDPs in 10 cells) in the remaining cells. Since the amplitude, duration and appearance of these depolarizing events mimic the properties of GDPs (Ben-Ari et al., 1989; Khalilov et al., 2015), we considered them as GDPs. These GDPs occurred at a rate of 1.3 ± 0.13 min-1 (n = 13 cells).
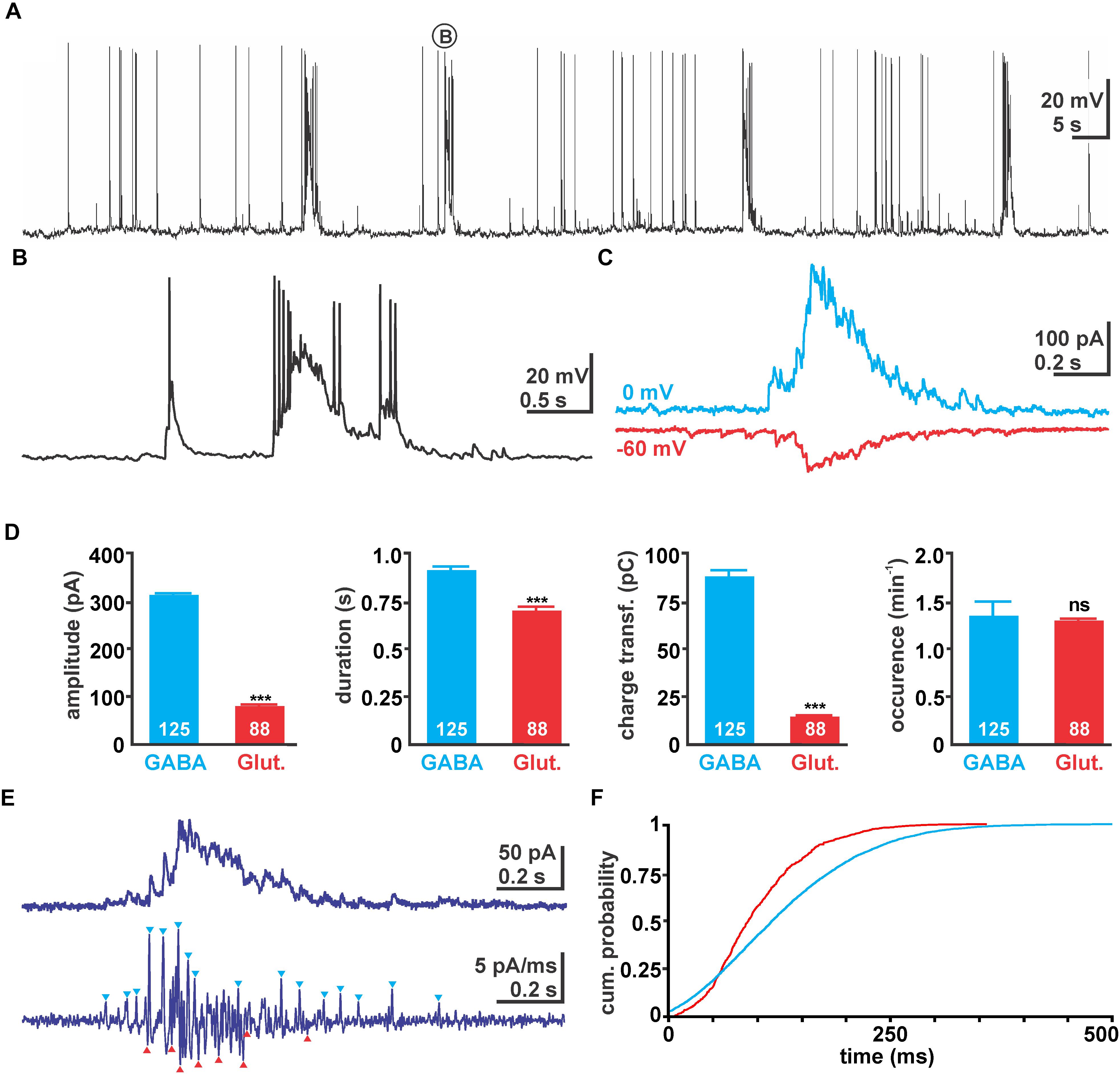
FIGURE 1. Properties of giant depolarizing potential (GDP) activity in immature hippocampal slices. (A) Typical voltage traces recorded with 50 mM [Cl-]p. Note the occurrence of massive depolarizing shifts triggering several action potentials (APs). (B) One typical GDP as indicated in (A) in higher temporal resolution. (C) Typical GDP associated currents recorded with 10 mM [Cl-]p at 0 mV (blue traces) and –60 mV (red traces), reflecting GABAergic and glutamatergic currents, respectively. Note that the traces were recorded from the same neuron in two independent experiments and have been manually aligned. (D) Statistical evaluation of absolute current amplitude, duration, charge transfer, and occurrence of GDP associated GABAergic and glutamatergic currents. Glutamatergic currents have smaller amplitude and mediate less charge transfer. Values in the bar diagrams represent mean ± SEM, number of experiments are given in the bars, ∗∗∗ indicates a p-level of <0.001. (E) Typical current recording using 10 mM [Cl-]p at –30 mV. Since from this trace GABAergic outward currents and glutamatergic inward currents could not be separated easily (upper trace), the first derivative of this recording was calculated (lower trace). From this trace several outward and inward currents could be identified (blue/red arrowheads). (F) Cumulative probability plot of the identified GABAergic (blue, 4004 events) and glutamatergic (red, 699 events) post-synaptic events (PSCs) during a GDP calculated from 105 GDPs in 15 recordings. Note the earlier onset of GABAergic PSCs and that glutamatergic PSCs terminated much earlier.
To investigate the contribution of synaptic events underlying these GDPs, we next performed voltage-clamp recordings using a [Cl-]p of 10 mM. For this purpose GABAergic and glutamatergic synaptic events were isolated at 0 mV (close to the reversal potential of glutamatergic currents) and at -60 mV (close to the calculated reversal potential of GABAergic currents at a [Cl-]p of 10 mM), respectively. At a holding potential of 0 mV in total 125 GDPs associated inward currents (IGDP) were identified (n = 17 cells), occurring at a rate of 1.35 ± 0.15 min-1 (Figure 1C). These IGDP had an average amplitude of 309.5 ± 3.5 pA (n = 125), a duration of 0.91 ± 0.02 s and conveyed an average charge transfer of 88 ± 3.3 pC (Figure 1D). At a holding potential of -60 mV in total 88 IGDP from 15 cells could be recorded. They had an average amplitude of 79.3 ± 3.7 pA (n = 88), a duration of 0.7 ± 0.02 s, conveyed an average charge transfer of 14.6 ± 0.7 pC, and occurred at a rate of 1.3 ± 0.2 min-1 (Figures 1C,D). These peak currents correspond to conductances of 5.1 ± 0.1 nS for the GABAergic and 1.3 ± 0.06 nS for the glutamatergic GDP component.
In order to analyze the temporal relation between GABAergic and glutamatergic synaptic inputs during a GDP, we performed voltage-clamp recordings at -30 mV, which in theory would enable identification of glutamatergic inward and GABAergic outward currents. However, as from the raw current traces GABAergic outward currents and glutamatergic inward current could not be separated (Figure 1E), we had to identify the onset of GABAergic and glutamatergic events from the first derivative of the current trace (Figure 1E). The cumulative probability distribution of those identified GABAergic (n = 4003 events) and glutamatergic events (n = 699) revealed that glutamatergic events start slightly delayed to GABAergic synaptic inputs and also terminated significantly earlier (p < 0.001, Kolmogorov–Smirnov test, 2351 events) (Figure 1F), although these events reflect only a fraction of all synaptic events during a GDP.
Relation Between GDPs and Spontaneous Synaptic Events
In order to estimate how much synaptic inputs underlie a GDP, we next analyzed the properties of spontaneous post-synaptic events (sPSCs) that occurred clearly outside of GDPs (Figure 2A). Voltage-clamp recordings using a [Cl-]p of 10 mM revealed that at -60 mV (close to the calculated reversal potential of GABAergic currents) sPSCs had an average amplitude of 18.3 ± 1.3 pA (n = 17 cells), a rise time of 3.5 ± 0.2 ms, a decay time of 10.8 ± 1.5 ms and a charge transfer of 131.5 ± 14.4 fC. These putatively glutamatergic sPSCs occurred at a frequency of 5.8 ± 1.2 Hz (Figure 2B).
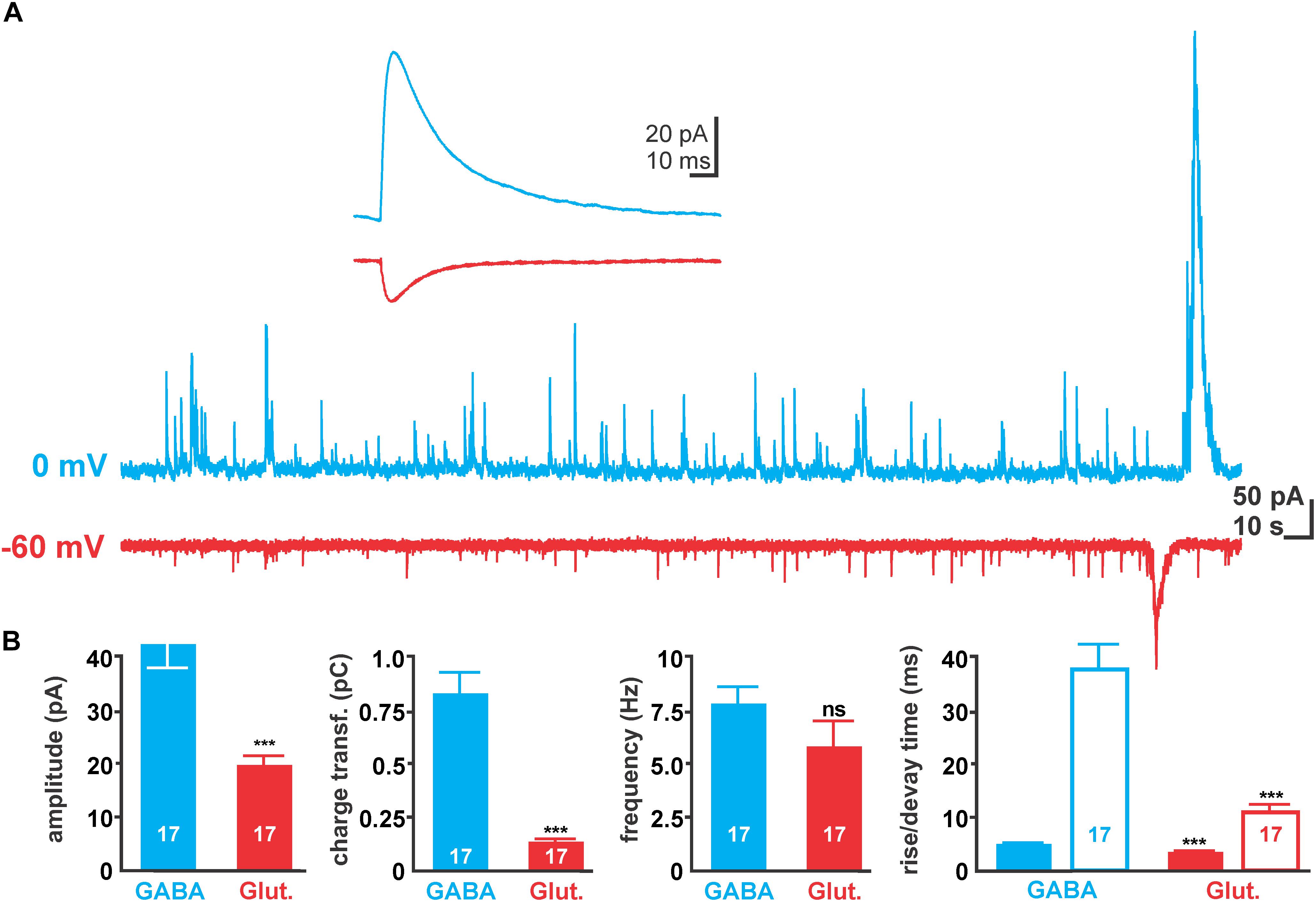
FIGURE 2. Properties of spontaneous synaptic activity in immature hippocampal slices. (A) Typical spontaneous post-synaptic currents (sPSCs) recorded with 10 mM [Cl-]p at 0 mV (blue traces) and –60 mV (red traces), reflecting GABAergic and glutamatergic sPSCs, respectively. Note the large current deflections at the end of the traces, which represent GDP-associated currents and were excluded from analysis. (B) Statistical evaluation of amplitude, charge transfer, frequency, and kinetic properties of GABAergic and glutamatergic sPSCs. Glutamatergic currents have smaller amplitude and mediate less charge transfer due to their smaller amplitude and faster decay time (open bars). Bars represent mean ± SEM, numbers of experiments are given in the bars, ∗∗∗ indicates a p-level of <0.001.
At a holding potential of 0 mV (close to the calculated reversal potential of glutamatergic currents) putatively GABAergic sPSCs (Figure 2A) with a significantly (p < 0.001) larger amplitude of 46.9 ± 3.1 pA (n = 17 cells), longer rise (4.9 ± 0.2 ms) and decay (37.3 ± 3.7 ms) times and a larger charge transfer (872.3 ± 96.2 fC) were observed (Figure 2B). These putatively GABAergic sPSCs occurred at a frequency of 7.8 ± 0.8 Hz.
The average amplitudes of GABAergic and glutamatergic sPSCs correspond under these conditions to a unitary conductance of 0.78 and 0.3 nS, respectively. Comparison of charge transfer at holding potentials of 0 mV suggests that 101 GABAergic synaptic inputs mediate the same charge transfer as the GABAergic component of an average GDP. And the comparison of charge transfer at holding potentials of -60 mV suggests that 107 glutamatergic synaptic inputs mediate the same charge transfer as the glutamatergic component of an average GDP.
GDPs Induced Transient [Cl-]i Alterations
As a variety of studies demonstrated that excessive GABAergic stimulation can alter [Cl-]i (Kaila et al., 1989; Staley et al., 1995; Jedlicka and Backus, 2006; Achilles et al., 2007; Kolbaev et al., 2011b), we assumed that the Cl--fluxes underlying the GABAergic currents during a GDP may be sufficient to induce significant alterations in [Cl-]i. To address this question, we determined the [Cl-]i shifts after a GDP had occurred. In order to maintain the [Cl-]i undisturbed the experiments were performed under gramicidin-perforated patch-clamp conditions (Kyrozis and Reichling, 1995). These experiments demonstrated that the average [Cl-]i of CA3 pyramidal neurons amounted to 38.1 ± 3.2 mM (n = 36), however with a considerable scatter between ca. 13 and 70 mM. Application of the NKCC1 inhibitor bumetanide (10 μM) significantly (p < 0.001) reduced the [Cl-]i to 21.4 ± 2.7 mM (n = 9). In the presence of bumetanide a slow [Cl-]i decline with a time constant of 280s occurred, indicating that passive Cl--fluxes are rather small. In addition, the coefficient of variation (CV) in [Cl-]i droped from 0.51 under control conditions to 0.37 in the presence of bumetanide, indicating a more homogenous distribution of [Cl-]i.
Under gramicidin-perforated patch-clamp conditions GDPs had an average depolarization of -46.9 ± 0.5 mV (n = 119 GDPs from 19 neurons) and lasted for 1.09 ± 0.07 s. To quantify possible GDP-induced [Cl-]i changes, [Cl-]i was determined between 0.5 and 10 s after the termination of a GDP by a ramp-protocol under voltage-clamp conditions (Figure 3). Beginning and end of each GDP were detected by threshold-crossing algorithms implemented in a microcontroller (Figure 3F).
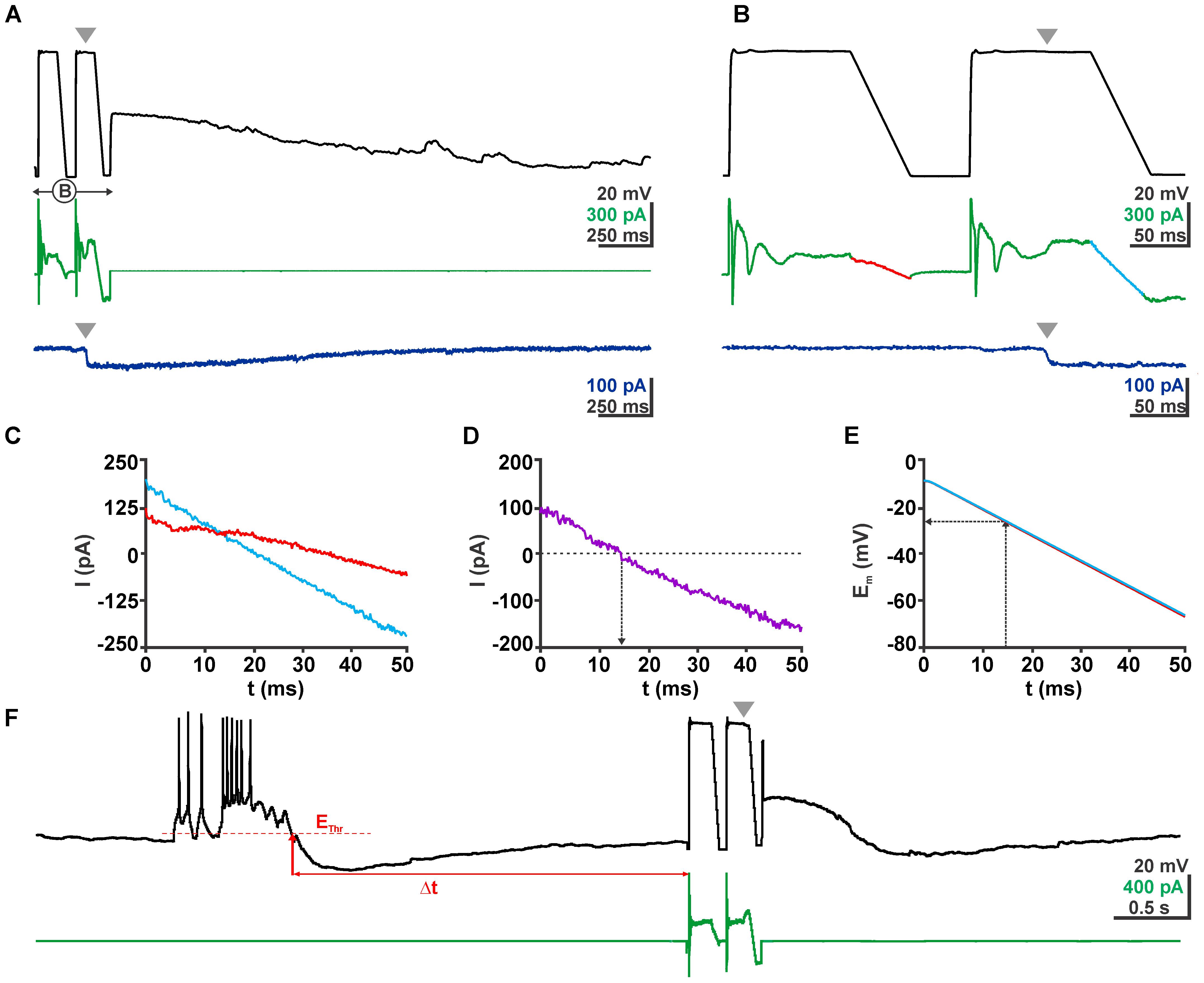
FIGURE 3. Determination of EGABA using a voltage ramp protocol. (A) Voltage (black trace) and current (green trace) traces of a typical clamp protocol used to determine EGABA. Voltage ramps between –3 and –63 mV were given from a 100 ms long depolarizing phase to inactivate fast Na+ currents. The second voltage ramp was delivered during the quasi-stationary phase of GABAergic response evoked by a short application of 100 μM GABA pulse (gray arrowhead). The dark blue trace in the bottom depicts the current response of the same cell without a voltage ramp protocol to illustrate the stationarity of the GABAergic current during the voltage ramp. (B) The ramp interval as shown in (A) at a higher temporal resolution. (C) Current traces from (B) recorded in the absence (red) and presence (blue) of GABA. (D) The difference between both current traces reverses at 13 ms. (E) Voltage traces recorded in the absence (red) and presence (blue) of GABA. Note that both traces are virtually identical. From these traces the reversal potential was determined. (F) Voltage and current traces of an experiment illustrating the procedures of a GDP triggered ramp protocol. From a continuous recording in current-clamp mode the microcontroller identified a GDP that crossed the threshold (EThr), the end of this GDP was determined as the time point when Em recovers to EThr. After a defined latency (Δt) the microcontroller provided a pulse to the amplifier to switch to VC mode and run the ramp protocol.
These experiments demonstrated that obvious changes in the [Cl-]i were observed within the first 1–5 s after a GDP (Figure 4A). On the other hand, the average [Cl-]i decreased 1–2 s after a GDP only by 6.1 ± 3.0 mM (n = 16 cells, p = 0.06). However, in individual neurons considerable [Cl-]i changes occurred during this interval (Figure 4B). From this figure it is obvious that GDPs led to a [Cl-]i decrease in neurons that had initially a high [Cl-]i, while they increased [Cl-]i in neurons with a low [Cl-]i.
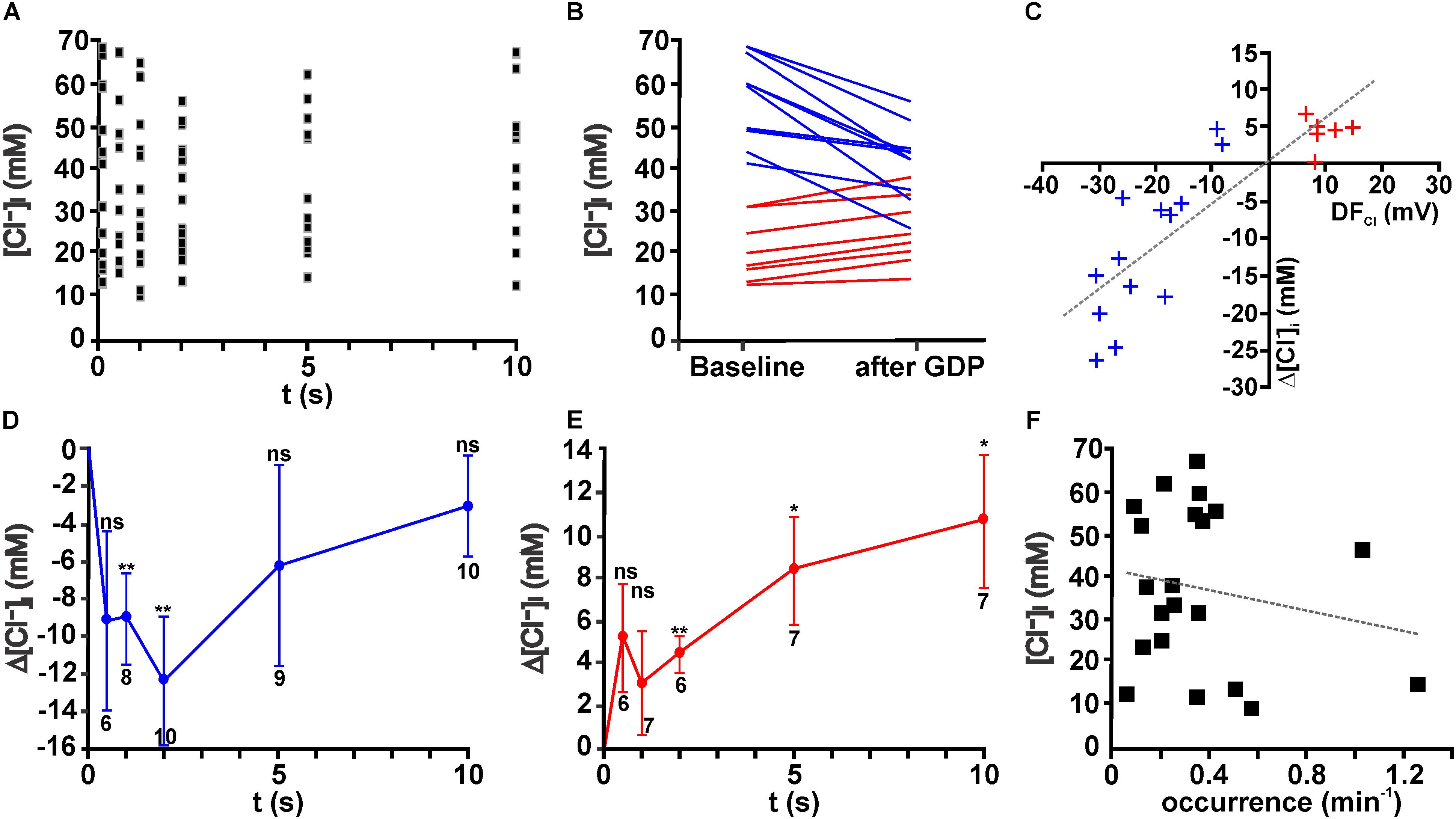
FIGURE 4. Giant depolarizing potentials lead to substantial [Cl-]i changes. (A) Scatter plot of [Cl-]i determined at given intervals after a GDP in 19 neurons. Note that the [Cl-]i values tend to decrease between 1 and 5 s. (B) [Cl-]i of individual neurons at baseline conditions and 1–2 s after a GDP. Note the obvious alteration in [Cl-]i. Cells that respond with a [Cl-]i increase are represented by red lines and [Cl-]i decreases by blue lines. (C) Plot of the GDP induced [Cl-]i change (Δ[Cl-]i) against the estimated driving force (DFCl) for individual neurons. Blue symbols represent cells with a negative DFCl, red symbols cells with a positive DFCl. Note the obvious correlation between both values. (D) Average [Cl-]i changes observed at different intervals after GDP termination for all cells with a negative DFCl. In these neurons a significant [Cl-]i decrease occurs that peaked 2 s after GDP termination. (E) Average [Cl-]i changes observed at different intervals after GDP termination for all cells with a positive DFCl. In these neurons a significant [Cl-]i increase occurs. (F) Plot of [Cl-]i against the frequency of GDPs. No significant correlation between both values was detected. Data points in (D,E) represent mean ± SEM, numbers of experiments are given in the diagrams, ∗ indicates a p-level of <0.05 and ∗∗ indicates a p-level of <0.01.
In order to quantify these different responses, we next estimated the driving-force of Cl- (DFCl) during a GDP from the difference between the average Em during a GDP and ECl. Regression analysis for the [Cl-]i changes against the DFCl revealed a significant (R2 = 0.713, F = 49.74, p < 0.001) correlation between DFCl and the [Cl-]i changes after a GDP (Figure 4C). Therefore we subdivided neurons in groups with positive DFCl and negative DFCl, respectively. In both groups a significant [Cl-]i change occurred after a GDP (Figures 4D,E). In the neurons with positive DFCl the maximal [Cl-]i decrease in the first 2 s after a GDP amounted to 12.4 ± 3.4 mM (n = 10, p = 0.0057, Figure 4D), while GDPs induced in the neurons with negative DFCl a relatively long lasting [Cl-]i increase (Figure 4E), which 2 s after a GDP amounted to 4.4 ± 0.9 mM (n = 6, p = 0.0039). Further analysis suggested that neither the initial [Cl-]i, nor the distribution of neurons showing Cl- influx/efflux or the amount of GPD-induced [Cl-]i changes depend on the age of the animals (data not shown).
Inhibition of GDP Activity Reduces [Cl-]i
Since these results demonstrated that GDPs lead to long lasting [Cl-]i changes, which in particular in case of [Cl-]i increases showed no evident back regulation in the first 10 s, we postulated that ongoing GDP activity can contribute to the initial [Cl-]i of immature hippocampal CA3 pyramidal neurons. Indeed, after inhibition of GDP activity for ≥30 min by bath application of 10 μM CNQX (Bolea et al., 1999), the average [Cl-]i amounted to 24.7 ± 2.9 mM (n = 8), which is significantly (p = 0.0035) smaller than the initial [Cl-]i under control conditions (38.1 ± 3.2 mM, n = 36). In addition, the CV in the [Cl-]i droped from 0.51 under control conditions to 0.33 in the presence of CNQX, indicating a more homogenous distribution of [Cl-]i. In summary, these results indicate that ongoing GDP activity led in general to an increased [Cl-]i, suggesting that the association of a high Cl- conductance and a depolarized Em during a GDP in combination with slow passive efflux rates of Cl- favors an accumulation of Cl- in these neurons. In order to evaluate whether the frequency of GDP activity influences [Cl-]i of CA3 pyramidal neurons under control conditions, the average occurrence of GDPs was plotted against the initial [Cl-]i in these cells (Figure 4F). This analysis revealed that initial [Cl-]i and the occurrence of GDPs are not correlated (R2 = 0.036, F = 0.72, p = 0.407). This observation indicates that the [Cl-]i of an individual cell cannot directly be related to the frequency of GDP activity in the slices. In addition, neither the amplitude of GDPs not their duration are significantly correlated with [Cl-]i (data not shown).
Compartmental Modeling
The observation that Rin was higher and the membrane capacitance was lower in the gramicidin-perforated patch-clamp recordings suggests that the access resistances (Rs) was under perforated-patch conditions higher than in whole-cell recordings. To investigate to which extend such differences in Rs can affect the determination of [Cl-]i we employed compartmental modeling using a reconstructed immature CA3 pyramidal neuron (Figures 5A,B, see section “Materials and Methods” for details). Therefore we estimated the influence of Rs on the determination of EGABA using a voltage-ramp protocol. Implementation of a voltage ramp protocol via a simulated single-electrode process with defined Rs values of 0.5, 5, 10, 20, and 40 MΩ on a neuron with a [Cl-]i of 30 mM led to EGABA values of -28.6, -28.7, -28.8, -28.9, and -29.0 mV, respectively (Figures 5B–D). This simulation suggests that EGABA is only marginally affected by Rs.
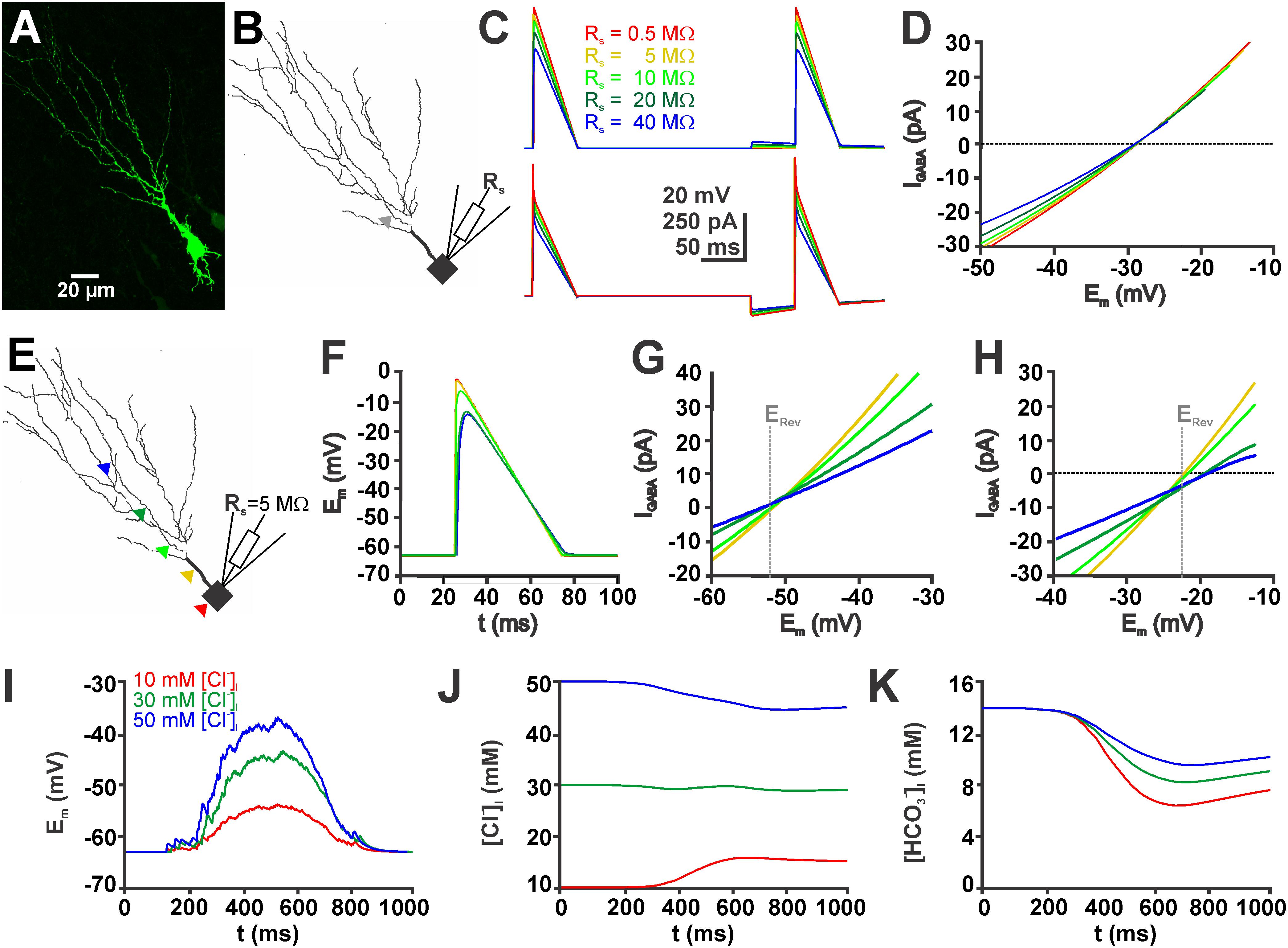
FIGURE 5. Simulations in a biophysically realistic compartmental model of a CA3 pyramidal cell replicate the dependence of GDP-induced [Cl-]i changes on initial [Cl-]i. (A) Biocytin labeled CA3 neuron in a P4 mouse slice. (B) Somatodendritic reconstruction of this cell. The gray arrowhead indicates the site of the GABAergic synapse used in (C,D). Voltage-clamp was simulated using the single-electrode voltage-clamp process of NEURON. (C) Voltage (top) and current (bottom) traces of voltage ramps applied in the absence and presence of GABA using five different values for the access resistance (Rs). (D) Current-voltage plot of the GABAergic currents (IGABA, as archived by subtraction of the current traces) at different Rs values. Note that although the slope of the curves clearly depends on Rs, the currents reverse at comparable values. (E) Location of five different GABAergic synapses (color coded) on the reconstructed neurons. (F) Voltage responses during a voltage ramp at the sites of GABA application (as indicated in E). Note the apparent dendritic filtering. (G) Current-voltage plot upon GABAergic stimulation at the sites illustrated in (E) for a neuron with 10 mM [Cl-]i. (H) Current-voltage plot upon GABAergic stimulation for a neuron with 50 mM [Cl-]i. The gray line in (G,H) marks the calculated reversal potential (ERev). Note the apparent divergence of the measured ERev at distal application sites. (I) Voltage trace of a simulated GDP (see section “Materials and Methods” for details) using three different initial [Cl-]i. (J) GDP-induced [Cl-]i changes at different initial [Cl-]i. Note the Cl- influx at low [Cl-]i, Cl--efflux at high [Cl-]i and small [Cl-]i changes at intermediate [Cl-]i. (K) GDP-induced [HCO3-]i changes under conditions with different initial [Cl-]i. Note that HCO3- influx depend on [Cl-]i.
Next we used the compartmental modeling to estimate to which extend space-clamp problems will affect the determination of [Cl-]i by EGABA. These simulations revealed that the Em values during the voltage ramp are attenuated in distant dendrites (Figures 5E,F). Accordingly, EGABA, determined by a voltage ramp applied via a simulated single-electrode (Rs = 5 MΩ) was shifted in the distal dendrites (Figures 5G,H). In a simulated neuron with a defined and static [Cl-]i of 50 mM the determined [Cl-]i were shifted to higher values. If the GABA synapse was located in the most proximal dendrite a [Cl-]i of 50.8 mM was determined, while if the GABA synapse was located in a distal dendrite the estimated [Cl-]i increased to 59.1 mM. A similar shift was observed for neurons with a defined [Cl-]i of 10 mM. Here, stimulation at proximal synapse resulted in a determined [Cl-]i of 10.4 mM and at distal dendrites to a determined [Cl-]i of 9.6 mM. These experiments indicate that space-clamp problems can considerably affect [Cl-]i calculated from EGABA.
Finally, we used compartmental modeling to estimated the GDP-induced [Cl-]i changes (Figures 5I,J). These in silico experiments revealed that simulated GDP activity induced a [Cl-]i decrease by 5.5 mM in neurons with an initial high [Cl-]i of 50 mM, a [Cl-]i decrease by 1.1 mM in neurons with an intermediate [Cl-]i of 30 mM, and a [Cl-]i increase by 5.7 mM in neurons with an initial low [Cl-]i of 10 mM. In addition, this model also allowed to estimate the [HCO3-]i changes that occur by activation of GABAA receptors during a GDP (Figure 5K). These modeling studies indicate that the [Cl-]i changes were paralleled by a considerable [HCO3-]i decrease to 6.5 mM in the high [Cl-]i neurons, to 8.3 mM in the intermediate [Cl-]i neurons, and to 9.6 mM in the high [Cl-]i neurons (Figure 5K). In summary, these results suggest that in addition to [Cl-]i, also [HCO3-]i shows a considerable ionic plasticity, leading to a decreased DFHCO3.
Discussion
The main aim of the present study was to reveal, whether GDPs lead to detectable [Cl-]i changes. The main findings of this study can be summarized as follows: (i) The [Cl-]i of CA3 pyramidal neurons in immature hippocampal slices displays a considerable heterogeneity, ranging from 13 to 70 mM. (ii) GDPs induced considerable [Cl-]i shifts by several mM, with either Cl--effluxes or Cl--influxes occurring in individual cells. (iii) The direction and amount of the GDP-mediated [Cl-]i shifts depends on the DFCl during the GDP. (iv) Inhibition of GDP activity results in a decrease of the steady-state [Cl-]i. We conclude from these results that the Cl--fluxes associated with GABAergic activity during GDPs induced significant [Cl-]i changes, which attenuate excitatory GABAergic responses and influence the initial [Cl-]i in hippocampal neurons.
The [Cl-]i in CA3 neurons recorded by perforated patch recordings revealed an obvious large scatter in the present study. From these values it could be assumed that both, inhibitory and excitatory GABAergic responses coexist in CA3 neurons at the same developmental stage, as has been reported in other brain structures (Chavas and Marty, 2003). However, this large scatter of [Cl-]i is in line with a series of previous publications that reported similar distributions in the initial [Cl-]i of immature hippocampal (Dzhala et al., 2012), but also neocortical neurons (Glykys et al., 2009; Sato et al., 2017). On the other hand, Valeeva et al. (2013) described considerably smaller [Cl-]i using non-invasive electrophysiological measurements. In accordance with the established role of NKCC1 for the maintenance of a high [Cl-]i in neurons (Rohrbough and Spitzer, 1996; Blaesse et al., 2009), bath application of the loop diuretic bumetanide significantly decreased [Cl-]i and also reduced the scatter in [Cl-]i.
We could not exclude, that part of the rather large scatter in the initial [Cl-]i observed in the present publication may to some extent be related to perforated-patch recordings from neurons that have been affected by the slicing procedure (Dzhala et al., 2012). In addition, our modeling studies demonstrate that [Cl-]i determined from EGABA are critically affected by space-clamp problems within the dendritic compartment. Thus we cannot exclude that a considerably part of the scatter in [Cl-]i and in particular the high [Cl-]i in some neurons are caused by insufficient voltage-clamp conditions at the site of GABAergic stimulation. However, while this obstruction influences the absolute [Cl-]i values, it doesn’t affect the main observation of this study, that GDPs induce considerable [Cl-]i shifts. Because we used identical stimulation parameters before and after a GDP, the influence of space-clamp errors should be identical for both [Cl-]i values. In contrast, Rs seems to have only a marginal effect on the determination of EGABA, which is mainly caused by the fact that during a voltage ramp protocol IGABA, and thus the voltage-error caused by Rs, is minimal at EGABA.
And finally, our modeling studies demonstrate that the [Cl-]i changes were paralleled by a considerable [HCO3-]i decline of several mM. These putative [HCO3-]i changes were not considered in the calculation of [Cl-]i from EGABA. If these estimated reduced [HCO3-]i was used in the Goldman Equation we calculated slightly reduced [Cl-] values of 48.1 mM for a [Cl-]i of 50 mM, of 27.5 mM for a [Cl-]i of 30 mM and of 6.7 mM for a [Cl-]i of 10 mM. However, the validity of such corrections for [HCO3-]i shifts critically depend on the [HCO3-]i values in individual neurons, which cannot be determine experimentally. Because our modeling results indicate that consideration of these [HCO3-]i changes for the calculation of [Cl-]i resulted in a slight, but consistent underestimation of [Cl-]i, we suggest that the main implications of the present results, namely that GDPs lead to considerable [Cl-]i changes and that the direction of these [Cl-]i changes depends on the initial [Cl-]i, are still valid. On the other hand, the absolute values for these changes represents probably only an estimate of the [Cl-]i changes in the dendritic compartment.
In any way, the mean [Cl-]i value of our recordings is in good agreement with the values expected to be recorded in neurons residing sufficiently deep below the slice surface to be unaffected by the slicing procedure (Dzhala et al., 2012) and the in-toto, unsliced hippocampal preparation shows a comparable wide distribution of [Cl-]i between 5 and 50 mM (Dzhala et al., 2012). In addition, we considered the first [Cl-]i value that was determined in a cell as initial [Cl-]i. However, we cannot exclude that this cell experienced a GDP before the recording interval started (about 30–60 s before [Cl-]i determination). Finally, our results revealed that inhibition of GDP activity reduced not only the initial [Cl-]i, but also the variance in these values, indicating that probably also different frequency or different amounts of GABAergic inputs during GDPs may contribute to the scatter in [Cl-]i.
From the observation that EGABA and [Cl-]i was increased in superficial neurons of the traumatized slice surface, it has been suggested that part of the excitatory GABAergic action may represent a “slicing artifact” (Dzhala et al., 2012). However, GDPs have also been observed in whole-hippocampal preparations (Leinekugel et al., 1998), which excludes that they represent “slicing artifacts” caused by artificially increased [Cl-]i in traumatized neurons (Valeeva et al., 2013). In fact, GDPs are also present under in vivo conditions (Khazipov et al., 2001; Leinekugel et al., 2002), suggesting that GABAA receptors may provide the excitatory drive required to trigger GDPs also in vivo. These observations in the immature hippocampus are in contrast to recent in vivo recordings from immature neocortical neurons, which revealed that GABAA receptor-mediated responses are indeed depolarizing, but most probably provide an inhibitory effect on immature neocortical neurons (Kirmse et al., 2015; Valeeva et al., 2016).
While the GABAergic conductance underlying GDPs determined in our study is in agreement with published values (Khalilov et al., 2015), the glutamatergic component is considerably higher than the published values. In addition, there is an obvious discrepancy between our conclusion that comparable numbers of GABAergic and glutamatergic synaptic inputs underlie a GDP (drawn from the comparison of charge transfer), while the detection of synaptic inputs from the first derivative of the current trace at -30 mV revealed much less identified glutamatergic synaptic events. However, the latter method detects clearly not all events, but, in particular during the phase of maximal inputs, only the most prominent ones. Therefore we assume that a considerable portion of GABAergic events and a larger fraction of the glutamatergic events remained undetected in this analysis. Nevertheless, we still consider that this analysis provides a good estimate for the temporal relation between GABAergic and glutamatergic inputs. Our findings are also in good agreement with previous studies demonstrating that GABAergic inputs precede the onset of glutamatergic inputs (Mohajerani and Cherubini, 2005; Khalilov et al., 2015).
The main observation of the present study is that GDPs induced considerable [Cl-]i shifts. Such ionic plasticity in [Cl-]i transients has been found after a variety of pathophysiological impacts (Lillis et al., 2012; Kaila et al., 2014b; Sato et al., 2017) and physiological processes (Bracci et al., 2001; Chub et al., 2006; Gonzalez-Islas et al., 2010; Kolbaev et al., 2011b). While in the present study the overall effect was partially masked by the variability in initial [Cl-]i, considerable GDP-induced [Cl-]i shifts were observed in individual neurons. Due to the large variability in the initial [Cl-]i and thus in the DFCl both, Cl--influx and Cl--efflux were mediated by activated GABAA receptors. Therefore, GDPs induced a [Cl-]i reduction in neurons with a negative DFCl (resulting mainly from a high [Cl-]i) and an [Cl-]i increase in neurons with a positive DFCl (resulting mainly from a low [Cl-]i). The [Cl-]i increase of ∼4 mM observed in low [Cl-]i neurons after a GDP in the present study is in line with the ∼ 4 mM [Cl-]i increase induced in the dendritic compartments of adult hippocampal neurons upon moderate electrical stimulation (43 single pulses at 23 Hz) (Berglund et al., 2008).
In order to evaluate whether the recorded GABAergic currents during a GDP can indeed lead to the observed GDP-induced [Cl-]i changes, we implemented a biophysically realistic compartmental model that allows dynamic [Cl-]i and [HCO3-]i changes. Simulating GDPs in a reconstructed immature CA3 pyramidal cell with a burst of GABAergic inputs that resembles the unitary GABAergic conductance and the total charge transfer during a GDP resulted in considerable dendritic [Cl-]i changes. The amount of these [Cl-]i changes is roughly comparable to the experimentally determined values. Our modeling studies also demonstrate that the [Cl-]i changes were paralleled by considerably [HCO3-]i decreases by several mM. Such a [HCO3-]i decrease will lead to a decreased DFHCO3 and thus affects EGABA. This observation supports the concept that also [HCO3-]i changes contribute to ionic plasticity after GABAergic stimulation (Staley and Proctor, 1999; Blaesse et al., 2009; Raimondo et al., 2012), in particular in the immature brain where the replenishment of [HCO3-]i via carbonic anhydrase VII is reduced (Rivera et al., 2005).
The GDP-induced shifts in [Cl-]i affect the DFCl and thus the functional consequences of subsequent GABAA receptor activation. However, it is important to consider that the [Cl-]i of the arbitrary neuron investigated by patch-clamp is most probably not decisive for the generation of GDP activity in a slice, but that GDPs are initiated in few hub neurons (Bonifazi et al., 2009; Wester and McBain, 2016). While the [Cl-]i increase in low [Cl-]i neurons attenuates the inhibitory effect of GABA in these neurons (Staley and Proctor, 1999; Raimondo et al., 2012), the [Cl-]i decrease in high [Cl-]i neurons reduced depolarizing GABAergic responses and their putative excitatory effect (Kolbaev et al., 2011a,b). Although the small GDP-induced [Cl-]i decline in the whole population of recorded neurons suggests that these [Cl-]i shifts may only marginally reduce the global excitatory effect of GABA on network excitability, the [Cl-]i decline in the high [Cl-]i neurons will clearly attenuate the excitatory potential of GABA in these cells. In addition, the GDP-induced [HCO3-]i decline, which was suggested from our modeling studies, reduces the inwardly directed DFHCO3 and would thus additionally attenuate an excitatory effect of GABA.
As the initiation of GDPs (Sipila et al., 2005) as well as the positive feedback during the “onset” phase (Khalilov et al., 2015) depend on excitatory GABAergic inputs, we propose that these high [Cl-]i neurons may be particularly relevant for the establishment of GDPs. Therefore we assume that the transient, GDP-mediated [Cl-]i decline in CA3 pyramidal neurons with high [Cl-]i will considerably attenuate the excitatory effect of GABA during a GDP. This effect adds to the dynamic model of Khalilov et al. (2015), which demonstrated that during the peak (or “catharsis”) phase of the GDP DFCl becomes positive, thus providing an inhibitory effect that is essential to limit excitatory influences.
Interestingly, it has been observed that interneurons of the mature hippocampus are much more susceptible to activity-dependent shifts in EGABA than pyramidal neurons (Lamsa and Taira, 2003), suggesting that ionic plasticity during a GDP is more pronounced in these cells. Therefore the typically shunting depolarization provoked by GABAA receptors in hippocampal interneurons (Banke and McBain, 2006), might be shifted to excitatory effects during a GDP. And since a subpopulation of GABAergic interneurons serve as hub neurons that orchestrate GDP activity (Bonifazi et al., 2009; Picardo et al., 2011), the resulting decline in the GABAergic inhibitory drive on GABAergic interneurons will probably impact the frequency of GABAergic inputs to pyramidal neurons during GDPs.
In addition, the [Cl-]i dynamics and the resulting decreased excitatory drive of GABAergic inputs may contribute to the termination phase of the GDP, in addition to other processes that have been shown to terminate GDPs (Sipila et al., 2006a; Khalilov et al., 2017). The calculation from Khalilov et al. (2015) proposed depolarizing GABAergic current during the repolarization phase, because their assumption of a constant [Cl-]i resulted in stable EGABA values. Therefore DFGABA will become negative when Em falls below EGABA during the repolarization. The collapse of [Cl-]i during a GDP observed in the present study may explain a reduced GABAergic depolarization/excitation during this phase, which will support the termination of a GDP.
In the developing spinal cord GABA-dependent spontaneous neuronal activity induces a collapse of the Cl- gradient, which temporarily attenuates the excitatory drive provided by GABAA receptors, and the subsequent slow Cl- accumulation that reestablishes GABAergic excitation underlies the low frequency of this recurrent activity (Chub and O’Donovan, 2001; Chub et al., 2006). Thus the dynamics of hippocampal [Cl-]i homeostasis after a GDP may also determine the frequency of GDPs. The breakdown of [Cl-]i in the high [Cl-]i neurons and in hub neurons will reduce excitatory GABAergic responses (Kolbaev et al., 2011a), which not only contributes to the shutoff of GDPs, but also prevents the generation of new excitatory network events. With the [Cl-]i re-accumulation via NKCC1, GABAergic responses regain their excitatory potential. At the time point when the net GABAergic effect becomes sufficiently excitatory again, it can contribute to the generation of the next GDP. We assume that neurons with a low [Cl-]i do not contribute to the initiation of GDP activity, thus the GDP-induced [Cl-]i-increase in these neurons probably doesn’t play an essential role in the generation of GDPs.
The observation that the peak of [Cl-]i changes occurred with several seconds delay to the end of the GDP most probably reflects the time required for a diffusional equilibration within the dendrites (Kuner and Augustine, 2000) and is in line with previously reported delays of 2–5 s between electrical stimulation and the peak of dendritic [Cl-]i responses (Berglund et al., 2008, see also Jedlicka et al., 2011). While this rather slow propagation of [Cl-]i transients limits the spatial extend of ionic plasticity, it doesn’t exclude that GDPs induces in the vicinity of GABAergic synapses sufficiently high [Cl-]i alterations to affect GABAergic transmission.
The KCC2-dependent back-regulation of [Cl-]i after an activity dependent increase in mature neurons occurred within several seconds (Lamsa and Taira, 2003; Jin et al., 2005). However, as the Cl--loader NKCC1 probably modulates a less effective transmembrane transport, [Cl-]i back regulation upon activity-dependent Cl- loss in immature neurons seems to take longer time, even up to some minutes (Achilles et al., 2007). Thus the observed slow recovery of the GDP-induced Cl--loss in high [Cl-]i neurons is in agreement with the relatively slow time constant of NKCC1 mediated Cl- uptake. The recovery upon GDP-induced [Cl-]i increases in the low [Cl-]i group appeared to be even slower, indicating that it is mainly mediated by [Cl-]i diffusion toward the soma and the ineffective passive transmembrane fluxes observed in immature hippocampal neurons. This observation was supported by the slow [Cl-]i decline observed in the presence of the NKCC1 inhibitor bumetanide.
The fact that recovery rates after [Cl-]i increases were slower than after [Cl-]i losses also suggests that ongoing GDP activity may increase basal [Cl-]i. Indeed, we observed that inhibition of GDP activity significantly reduces initial [Cl-]i. This result demonstrates that the [Cl-]i in immature neurons depends substantially on GABAergic activity due to the slow kinetics of activity dependent [Cl-]i transients. However, GDPs may also effect [Cl-]i homeostasis by post-translational modification of KCC2 and NKCC1 transporters (Blaesse et al., 2009; Kaila et al., 2014a).
In summary, our results indicate that the [Cl-]i and thus the physiological effects of GABAergic inputs critically depend on prior GABAergic activity. Therefore, in immature hippocampal neurons ionic plasticity must be considered to explain [Cl-]i and thus the functional state of GABAergic transmission at each single time point. These observations also foster the concept that neuronal [Cl-]i has to be considered as a state- and compartment-dependent parameter of individual cells (Wright et al., 2011).
Author Contributions
WK and HL designed this study. AL performed all recordings. AL and WK analyzed the data. WK, AL, and PJ performed computational modeling. AL, HL, PJ, and WK wrote the manuscript.
Funding
This study was supported by funding from the Deutsche Forschungsgemeinschaft (DFG) to WK and HL and a FTN stipend to AL. This manuscript is part of the Ph.D. thesis of AL.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to thank Beate Krumm for her excellent technical assistance and Emma Wong for suggesting the Arduino microcontroller.
Footnotes
References
Achilles, K., Okabe, A., Ikeda, M., Shimizu-Okabe, C., Yamada, J., Fukuda, A., et al. (2007). Kinetic properties of Cl uptake mediated by Na+-dependent K+-2Cl cotransport in immature rat neocortical neurons. J. Neurosci. 27, 8616–8627. doi: 10.1523/JNEUROSCI.5041-06.2007
Allene, C., Cattani, A., Ackman, J. B., Bonifazi, P., Aniksztejn, L., Ben Ari, Y., et al. (2008). Sequential generation of two distinct synapse-driven network patterns in developing neocortex. J. Neurosci. 28, 12851–12863. doi: 10.1523/JNEUROSCI.3733-08.2008
Banke, T. G., and McBain, C. J. (2006). GABAergic input onto CA3 hippocampal interneurons remains shunting throughout development. J. Neurosci. 26, 11720–11725. doi: 10.1523/JNEUROSCI.2887-06.2006
Ben Ari, Y. (2001). Developing networks play a similar melody. Trends Neurosci. 24, 353–360. doi: 10.1016/S0166-2236(00)01813-0
Ben-Ari, Y. (2002). Excitatory actions of GABA during development: the nature of the nurture. Nat. Rev. Neurosci. 3, 728–739. doi: 10.1038/nrn920
Ben-Ari, Y., Cherubini, E., Corradetti, R., and Gaiarsa, J.-L. (1989). Giant synaptic potentials in immature rat CA3 hippocampal neurones. J. Physiol. 416, 303–325. doi: 10.1113/jphysiol.1989.sp017762
Ben-Ari, Y., and Spitzer, N. C. (2010). Phenotypic checkpoints regulate neuronal development. Trends Neurosci. 33, 485–492. doi: 10.1016/j.tins.2010.08.005
Ben-Ari, Y., Woodin, M. A., Sernagor, E., Cancedda, L., Vinay, L., Rivera, C., et al. (2012). Refuting the challenges of the developmental shift of polarity of GABA actions: GABA more exciting than ever! Front. Cell. Neurosci. 6:35. doi: 10.3389/fncel.2012.00035
Berglund, K., Schleich, W., Wang, H., Feng, G. P., Hall, W. C., Kuner, T., et al. (2008). Imaging synaptic inhibition throughout the brain via genetically targeted Clomeleon. Brain Cell Biol. 36, 101–118. doi: 10.1007/s11068-008-9031-x
Blaesse, P., Airaksinen, M. S., Rivera, C., and Kaila, K. (2009). Cation-chloride cotransporters and neuronal function. Neuron 61, 820–838. doi: 10.1016/j.neuron.2009.03.003
Blankenship, A. G., and Feller, M. B. (2010). Mechanisms underlying spontaneous patterned activity in developing neural circuits. Nat. Rev. Neurosci. 11, 18–29. doi: 10.1038/nrn2759
Bolea, S., Avignone, E., Berretta, N., Sanchez-Andres, J. V., and Cherubini, E. (1999). Glutamate controls the induction of GABA-mediated giant depolarizing potentials through AMPA receptors in neonatal rat hippocampal slices. J. Neurophysiol. 81, 2095–2102. doi: 10.1152/jn.1999.81.5.2095
Bonifazi, P., Goldin, M., Picardo, M. A., Jorquera, I., Cattani, A., Bianconi, G., et al. (2009). GABAergic hub neurons orchestrate synchrony in developing hippocampal networks. Science 326, 1419–1424. doi: 10.1126/science.1175509
Bracci, E., Vreugdenhil, M., Hack, S. P., and Jefferys, J. G. R. (2001). Dynamic modulation of excitation and inhibition during stimulation at gamma and beta frequencies in the CA1 hippocampal region. J. Neurophysiol. 85, 2412–2422. doi: 10.1152/jn.2001.85.6.2412
Chavas, J., and Marty, A. (2003). Coexistence of excitatory and inhibitory GABA synapses in the cerebellar interneuron network. J. Neurosci. 23, 2019–2031. doi: 10.1523/JNEUROSCI.23-06-02019.2003
Cherubini, E., Griguoli, M., Safiulina, V., and Lagostena, L. (2011). The Depolarizing action of GABA controls early network activity in the developing hippocampus. Mol. Neurobiol. 43, 97–106. doi: 10.1007/s12035-010-8147-z
Chub, N., Mentis, G. Z., and O’Donovan, M. J. (2006). Chloride-sensitive MEQ fluorescence in chick embryo motoneurons following manipulations of chloride and during spontaneous network activity. J. Neurophysiol. 95, 323–330. doi: 10.1152/jn.00162.2005
Chub, N., and O’Donovan, M. J. (2001). Post-episode depression of GABAergic transmission in spinal neurons of the chick embryo. J. Neurophysiol. 85, 2166–2176. doi: 10.1152/jn.2001.85.5.2166
Czarnecki, A., Le Corronc, H., Rigato, C., Le Bras, B., Couraud, F., Scain, A. L., et al. (2014). Acetylcholine controls GABA-, glutamate-, and glycine-dependent giant depolarizing potentials that govern spontaneous motoneuron activity at the onset of synaptogenesis in the mouse embryonic spinal cord. J. Neurosci. 34, 6389–6404. doi: 10.1523/JNEUROSCI.2664-13.2014
De Schutter, E. (2010). “Modeling intracellular calcium dynamics,” in Computational Modeling Methods for Neuroscientists, ed. E. De Schutter (London: MIT Press), 93–105.
De Schutter, E., and Smolen, P. (1998). “Calcium Dynamics in Large Neuronal Models,” in Methods in Neuronal Modeling, eds C. Koch and I. Segev (London: MIT Press), 211–250.
Dzhala, V., Valeeva, G., Glykys, J., Khazipov, R., and Staley, K. (2012). Traumatic alterations in GABA signaling disrupt hippocampal network activity in the developing brain. J. Neurosci. 32, 4017–4031. doi: 10.1523/JNEUROSCI.5139-11.2012
Farrant, M., and Kaila, K. (2007). The cellular, molecular and ionic basis of GABA(A) receptor signalling. Prog. Brain Res. 160, 59–87. doi: 10.1016/S0079-6123(06)60005-8
Fatima-Shad, K., and Barry, P. H. (1993). Anion permeation in GABA- and glycine-gated channels of mammalian cultured hippocampal neurons. Proc. Biol. Sci. 253, 69–75. doi: 10.1098/rspb.1993.0083
Glykys, J., Dzhala, V. I., Kuchibhotla, K. V., Feng, G., Kuner, T., Augustine, G., et al. (2009). Differences in cortical versus subcortical GABAergic signaling: a candidate mechanism of electroclinical uncoupling of neonatal seizures. Neuron 63, 657–672. doi: 10.1016/j.neuron.2009.08.022
Gonzalez-Islas, C., Chub, N., Garcia-Bereguiain, M. A., and Wenner, P. (2010). GABAergic synaptic scaling in embryonic motoneurons is mediated by a shift in the chloride reversal potential. J. Neurosci. 30, 13016–13020. doi: 10.1523/JNEUROSCI.1659-10.2010
Griguoli, M., and Cherubini, E. (2017). Early correlated network activity in the hippocampus: its putative role in shaping neuronal circuits. Front. Cell. Neurosci. 11:255. doi: 10.3389/fncel.2017.00255
Hines, M. L., and Carnevale, N. T. (2000). Expanding NEURON’s repertoire of mechanisms with NMODL. Neural Comput. 12, 995–1007. doi: 10.1162/089976600300015475
Horikawa, K., and Armstrong, W. E. (1988). A versatile means of intracellular labeling: injection of biocytin and its detection with avidin conjugates. J. Neurosci. Methods 25, 1–11. doi: 10.1016/0165-0270(88)90114-8
Isomura, Y., Sugimoto, M., Fujiwara-Tsukamoto, Y., Yamamoto-Muraki, S., Yamada, J., and Fukuda, A. (2003). Synaptically activated Cl- accumulation responsible for depolarizing GABAergic responses in mature hippocampal neurons. J. Neurophysiol. 90, 2752–2756. doi: 10.1152/jn.00142.2003
Jedlicka, P., and Backus, K. H. (2006). Inhibitory transmission, activity-dependent ionic changes and neuronal network oscillations. Physiol. Res. 55, 139–149.
Jedlicka, P., Deller, T., Gutkin, B. S., and Backus, K. H. (2011). Activity-dependent intracellular chloride accumulation and diffusion controls GABA(A) receptor-mediated synaptic transmission. Hippocampus 21, 885–898. doi: 10.1002/hipo.20804
Jin, X., Huguenard, J. R., and Prince, D. A. (2005). Impaired Cl- extrusion in layer V pyramidal neurons of chronically injured epileptogenic neocortex. J. Neurophysiol. 93, 2117–2126. doi: 10.1152/jn.00728.2004
Kaila, K., Lamsa, K., Smirnov, S., Taira, T., and Voipio, J. (1997). Long-lasting GABA-mediated depolarization evoked by high-frequency stimulation in pyramidal neurons of rat hippocampal slice is attributable to a network-driven, bicarbonate-dependent K+ transient. J. Neurosci. 17, 7662–7672. doi: 10.1523/JNEUROSCI.17-20-07662.1997
Kaila, K., Pasternack, M., Saarikoski, J., and Voipio, J. (1989). Influence of GABA-gated bicarbonate conductance on potential, current and intracellular chloride in crayfish muscle fibres. J. Physiol. 416, 161–181. doi: 10.1113/jphysiol.1989.sp017755
Kaila, K., Price, T. J., Payne, J. A., Puskarjov, M., and Voipio, J. (2014a). Cation-chloride cotransporters in neuronal development, plasticity and disease. Nat. Rev. Neurosci. 15, 637–654. doi: 10.1038/nrn3819
Kaila, K., Ruusuvuori, E., Seja, P., Voipio, J., and Puskarjov, M. (2014b). GABA actions and ionic plasticity in epilepsy. Curr. Opin. Neurobiol. 26, 34–41. doi: 10.1016/j.conb.2013.11.004
Khalilov, I., Minlebaev, M., Mukhtarov, M., Juzekaeva, E., and Khazipov, R. (2017). Postsynaptic GABA(B) receptors contribute to the termination of giant depolarizing potentials in CA3 neonatal rat hippocampus. Front. Cell. Neurosci. 11:179. doi: 10.3389/fncel.2017.00179
Khalilov, I., Minlebaev, M., Mukhtarov, M., and Khazipov, R. (2015). Dynamic changes from depolarizing to hyperpolarizing GABAergic actions during giant depolarizing potentials in the neonatal rat hippocampus. J. Neurosci. 35, 12635–12642. doi: 10.1523/JNEUROSCI.1922-15.2015
Khazipov, R., Esclapez, M., Caillard, O., Bernard, C., Khalilov, I., Tyzio, R., et al. (2001). Early development of neuronal activity in the primate hippocampus in utero. J. Neurosci. 21, 9770–9781. doi: 10.1523/JNEUROSCI.21-24-09770.2001
Khazipov, R., Leinekugel, X., Khalilov, I., Gaiarsa, J. L., and Ben-Ari, Y. (1997). Synchronization of GABAergic interneuronal network in CA3 subfield of neonatal rat hippocampal slices. J. Physiol. 498, 763–772. doi: 10.1113/jphysiol.1997.sp021900
Khazipov, R., and Luhmann, H. J. (2006). Early patterns of electrical activity in the developing cerebral cortex of human and rodents. Trends Neurosci. 29, 414–418. doi: 10.1016/j.tins.2006.05.007
Kilb, W., Kirischuk, S., and Luhmann, H. J. (2011). Electrical activity patterns and the functional maturation of the neocortex. Eur. J. Neurosci. 34, 1677–1686. doi: 10.1111/j.1460-9568.2011.07878.x
Kirischuk, S., Sinning, A., Blanquie, O., Yang, J. W., Luhmann, H. J., and Kilb, W. (2017). Modulation of neocortical development by early neuronal activity: physiology and pathophysiology. Front. Cell. Neurosci. 11:379. doi: 10.3389/fncel.2017.00379
Kirmse, K., Hubner, C. A., Isbrandt, D., Witte, O. W., and Holthoff, K. (2018). GABAergic transmission during brain development: multiple effects at multiple stages. Neuroscientist 24, 36–53. doi: 10.1177/1073858417701382
Kirmse, K., Kummer, M., Kovalchuk, Y., Witte, O. W., Garaschuk, O., and Holthoff, K. (2015). GABA depolarizes immature neurons and inhibits network activity in the neonatal neocortex in vivo. Nat. Commun. 6:7750. doi: 10.1038/ncomms8750
Kolbaev, S. N., Achilles, K., Luhmann, H. J., and Kilb, W. (2011a). Effect of depolarizing GABA(A)-mediated membrane responses on excitability of Cajal-Retzius cells in the immature rat neocortex. J. Neurophysiol. 106, 2034–2044. doi: 10.1152/jn.00699.2010
Kolbaev, S. N., Luhmann, H. J., and Kilb, W. (2011b). Activity-dependent scaling of GABAergic excitation by dynamic Cl- changes in Cajal-Retzius cells. Pflugers Arch. 461, 557–565. doi: 10.1007/s00424-011-0935-4
Kuner, T., and Augustine, G. J. (2000). A genetically encoded ratiometric indicator for chloride: capturing chloride transients in cultured hippocampal neurons. Neuron 27, 447–459. doi: 10.1016/S0896-6273(00)00056-8
Kyrozis, A., and Reichling, D. B. (1995). Perforated-patch recording with gramicidin avoids artifactual changes in intracellular chloride concentration. J. Neurosci. Methods 57, 27–35. doi: 10.1016/0165-0270(94)00116-X
Lamsa, K., and Taira, T. (2003). Use-dependent shift from inhibitory to excitatory GABAA receptor action in SP-O interneurons in the rat hippocampal CA3 area. J. Neurophysiol. 90, 1983–1995. doi: 10.1152/jn.00060.2003
Leinekugel, X., Khalilov, I., Ben Ari, Y., and Khazipov, R. (1998). Giant depolarizing potentials: the septal pole of the hippocampus paces the activity of the developing intact septohippocampal complex in vitro. J. Neurosci. 18, 6349–6357. doi: 10.1523/JNEUROSCI.18-16-06349.1998
Leinekugel, X., Khazipov, R., Cannon, R., Hirase, H., Ben Ari, Y., and Buzsaki, G. (2002). Correlated bursts of activity in the neonatal hippocampus in vivo. Science 296, 2049–2052. doi: 10.1126/science.1071111
Lillis, K. P., Kramer, M. A., Mertz, J., Staley, K. J., and White, J. A. (2012). Pyramidal cells accumulate chloride at seizure onset. Neurobiol. Dis. 47, 358–366. doi: 10.1016/j.nbd.2012.05.016
Mitchell, R. A., Herbert, D. A., and Carman, C. T. (1965). Acid-Base constants and temperature coefficients for cerebrospinal fluid. J. Appl. Physiol. 20, 27–30. doi: 10.1152/jappl.1965.20.1.27
Mohajerani, M. H., and Cherubini, E. (2005). Spontaneous recurrent network activity in organotypic rat hippocampal slices. Eur. J. Neurosci. 22, 107–118. doi: 10.1111/j.1460-9568.2005.04198.x
Mohapatra, N., Deans, H. T., Santamaria, F., and Jedlicka, P. (2014). “Modeling ion concentrations,” in Encyclopedia of Computational Neuroscience, eds D. Jaeger and R. Jung (New York, NY: Springer), 1–6. doi: 10.1007/978-1-4614-7320-6_239-2
Mohapatra, N., Tonnesen, J., Vlachos, A., Kuner, T., Deller, T., Nagerl, U. V., et al. (2016). Spines slow down dendritic chloride diffusion and affect short-term ionic plasticity of GABAergic inhibition. Sci. Rep. 6:23196. doi: 10.1038/srep23196
Pangratz-Fuehrer, S., Rudolph, U., and Huguenard, J. R. (2007). Giant spontaneous depolarizing potentials in the developing thalamic reticular nucleus. J. Neurophysiol. 97, 2364–2372. doi: 10.1152/jn.00646.2006
Picardo, M. A., Guigue, P., Bonifazi, P., Batista-Brito, R., Allene, C., Ribas, A., et al. (2011). Pioneer GABA cells comprise a subpopulation of hub neurons in the developing hippocampus. Neuron 71, 695–709. doi: 10.1016/j.neuron.2011.06.018
Raimondo, J. V., Markram, H., and Akerman, C. J. (2012). Short-term ionic plasticity at GABAergic synapses. Front. Synaptic Neurosci. 4:5. doi: 10.3389/fnsyn.2012.00005
Rivera, C., Voipio, J., and Kaila, K. (2005). Two developmental switches in GABAergic signalling: the K+–Cl- cotransporter KCC2 and carbonic anhydrase CAVII. J. Physiol. 562, 27–36. doi: 10.1113/jphysiol.2004.077495
Rohrbough, J., and Spitzer, N. C. (1996). Regulation of intracellular Cl- levels by Na+-dependent Cl- cotransport distinguishes depolarizing from hyperpolarizing GABAA receptor-mediated responses in spinal neurons. J. Neurosci. 16, 82–91. doi: 10.1523/JNEUROSCI.16-01-00082.1996
Rolston, J. D., Wagenaar, D. A., and Potter, S. M. (2007). Precisely timed spatiotemporal patterns of neural activity in dissociated cortical cultures. Neuroscience 148, 294–303. doi: 10.1016/j.neuroscience.2007.05.025
Ruusuvuori, E., Kirilkin, I., Pandya, N., and Kaila, K. (2010). Spontaneous network events driven by depolarizing GABA action in neonatal hippocampal slices are not attributable to deficient mitochondrial energy metabolism. J. Neurosci. 30, 15638–15642. doi: 10.1523/JNEUROSCI.3355-10.2010
Santhakumar, V., Aradi, I., and Soltesz, I. (2005). Role of mossy fiber sprouting and mossy cell loss in hyperexcitability: a network model of the dentate gyrus incorporating cell types and axonal topography. J. Neurophysiol. 93, 437–453. doi: 10.1152/jn.00777.2004
Sato, S. S., Artoni, P., Landi, S., Cozzolino, O., Parra, R., Pracucci, E., et al. (2017). Simultaneous two-photon imaging of intracellular chloride concentration and pH in mouse pyramidal neurons in vivo. Proc. Natl. Acad. Sci. U.S.A. 114, E8770–E8779. doi: 10.1073/pnas.1702861114
Schröder, R., and Luhmann, H. J. (1997). Morphology, electrophysiology and pathophysiology of supragranular neurons in rat primary somatosensory cortex. Eur. J. Neurosci. 9, 163–176. doi: 10.1111/j.1460-9568.1997.tb01364.x
Sipila, S. T., Huttu, K., Soltesz, I., Voipio, J., and Kaila, K. (2005). Depolarizing GABA acts on intrinsically bursting pyramidal neurons to drive giant depolarizing potentials in the immature hippocampus. J. Neurosci. 25, 5280–5289. doi: 10.1523/JNEUROSCI.0378-05.2005
Sipila, S. T., Huttu, K., Voipio, J., and Kaila, K. (2006a). Intrinsic bursting of immature CA3 pyramidal neurons and consequent giant depolarizing potentials are driven by a persistent Na current and terminated by a slow Ca-activated K current. Eur. J. Neurosci. 23, 2330–2338. doi: 10.1111/j.1460-9568.2006.04757.x
Sipila, S. T., Schuchmann, S., Voipio, J., Yamada, J., and Kaila, K. (2006b). The cation-chloride cotransporter NKCC1 promotes sharp waves in the neonatal rat hippocampus. J. Physiol. 573, 765–773.
Spitzer, N. C. (2006). Electrical activity in early neuronal development. Nature 444, 707–712. doi: 10.1038/nature05300
Staley, K. J., and Proctor, W. R. (1999). Modulation of mammalian dendritic GABAA receptor function by the kinetics of Cl- and HCO3- transport. J. Physiol. 519, 693–712. doi: 10.1111/j.1469-7793.1999.0693n.x
Staley, K. J., Soldo, B. L., and Proctor, W. R. (1995). Ionic mechanisms of neuronal excitation by inhibitory GABAA receptors. Science 269, 977–981. doi: 10.1126/science.7638623
Sun, J. J., Kilb, W., and Luhmann, H. J. (2010). Self-organization of repetitive spike patterns in developing neuronal networks in vitro. Eur. J. Neurosci. 32, 1289–1299. doi: 10.1111/j.1460-9568.2010.07383.x
Sun, M. K., Zhao, W. Q., Nelson, T. J., and Alkon, D. L. (2001). Theta rhythm of hippocampal CA1 neuron activity: gating by GABAergic synaptic depolarization. J. Neurophysiol. 85, 269–279. doi: 10.1152/jn.2001.85.1.269
Valeeva, G., Abdullin, A., Tyzio, R., Skorinkin, A., Nikolski, E., Ben-Ari, Y., et al. (2010). Temporal coding at the immature depolarizing GABAergic synapse. Front. Cell. Neurosci. 4:17. doi: 10.3389/fncel.2010.00017
Valeeva, G., Tressard, T., Mukhtarov, M., Baude, A., and Khazipov, R. (2016). An optogenetic approach for investigation of excitatory and inhibitory network GABA actions in mice expressing channelrhodopsin-2 in GABAergic neurons. J. Neurosci. 36, 5961–5973. doi: 10.1523/JNEUROSCI.3482-15.2016
Valeeva, G., Valiullina, F., and Khazipov, R. (2013). Excitatory actions of GABA in the intact neonatal rodent hippocampus in vitro. Front. Cell. Neurosci. 7:20. doi: 10.3389/fncel.2013.00020
Watanabe, M., and Fukuda, A. (2015). Development and regulation of chloride homeostasis in the central nervous system. Front. Cell. Neurosci. 9:371. doi: 10.3389/fncel.2015.00371
Wester, J. C., and McBain, C. J. (2016). interneurons differentially contribute to spontaneous network activity in the developing hippocampus dependent on their embryonic lineage. J. Neurosci. 36, 2646–2662. doi: 10.1523/JNEUROSCI.4000-15.2016
Wright, R., Raimondo, J. V., and Akerman, C. J. (2011). Spatial and temporal dynamics in the ionic driving force for GABA(A) receptors. Neural Plast. 2011:728395. doi: 10.1155/2011/728395
Keywords: development, Cl- homeostasis, gramicidin-perforated patch-clamp, post-synaptic currents, ionic plasticity, GABA(A) receptors
Citation: Lombardi A, Jedlicka P, Luhmann HJ and Kilb W (2018) Giant Depolarizing Potentials Trigger Transient Changes in the Intracellular Cl- Concentration in CA3 Pyramidal Neurons of the Immature Mouse Hippocampus. Front. Cell. Neurosci. 12:420. doi: 10.3389/fncel.2018.00420
Received: 20 August 2018; Accepted: 26 October 2018;
Published: 20 November 2018.
Edited by:
Yehezkel Ben-Ari, Neurochlore, FranceReviewed by:
Davide Pozzi, Humanitas Research Hospital, ItalyStefano Taverna, San Raffaele Hospital (IRCCS), Italy
Christine R. Rose, Heinrich Heine Universität Düsseldorf, Germany
Michel Joseph Roux, INSERM, U964 Institut de Génétique et de Biologie Moléculaire et Cellulaire (IGBMC), France
Copyright © 2018 Lombardi, Jedlicka, Luhmann and Kilb. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Werner Kilb, d2tpbGJAdW5pLW1haW56LmRl
 Aniello Lombardi
Aniello Lombardi Peter Jedlicka
Peter Jedlicka Heiko J. Luhmann
Heiko J. Luhmann Werner Kilb
Werner Kilb