Isotopic Fractionation Associated With Sulfate Import and Activation by Desulfovibrio vulgaris str. Hildenborough

The use of stable isotopes to trace biogeochemical sulfur cycling relies on an understanding of how isotopic fractionation is imposed by metabolic networks. We investigated the effects of the first two enzymatic steps in the dissimilatory sulfate reduction (DSR) network – sulfate permease and sulfate adenylyl transferase (Sat) – on the sulfur and oxygen isotopic composition of residual sulfate. Mutant strains of Desulfovibrio vulgaris str. Hildenborough (DvH) with perturbed expression of these enzymes were grown in batch culture, with a subset grown in continuous culture, to examine the impact of these enzymatic steps on growth rate, cell specific sulfate reduction rate and isotopic fractionations in comparison to the wild type strain. Deletion of several permease genes resulted in only small (∼1‰) changes in sulfur isotope fractionation, a difference that approaches the uncertainties of the measurement. Mutants that perturb Sat expression show higher fractionations than the wild type strain. This increase probably relates to an increased material flux between sulfate and APS, allowing an increase in the expressed fractionation of rate-limiting APS reductase. This work illustrates that flux through the initial steps of the DSR pathway can affect the fractionation imposed by the overall pathway, even though these steps are themselves likely to impose only small fractionations.

Introduction

Dissimilatory sulfate reduction (DSR) is associated with the oxidation of organic matter in modern and ancient oceans, and is essential to regulating the redox state of the Earth’s surface. The sulfur cycle represents one of the oldest biologically mediated chemical cycles on earth (Shen et al., 2001; Canfield, 2004; Fike et al., 2015). The marine sulfur cycle can be tracked through time by examining the stable isotopic compositions of seawater sulfate and reduced sedimentary sulfur phases, such as pyrite or organic sulfur. Sulfur and oxygen stable isotope ratios in sulfate and other sulfur-bearing species are largely a product of the biogeochemical sulfur cycle, although they can also be affected by abiotic processes like hydrothermal activity and photochemical reactions in the atmosphere. DSR is particularly influential on the sulfur isotope ratios (Jørgensen, 1982; Canfield, 2001; Brunner et al., 2005; Canfield et al., 2010; Sim et al., 2011a, 2019; Leavitt et al., 2013) because sulfur isotopic fractionations (³⁴ε_{sulfate–sulfide}) generated by DSR can be very large – with observations recording and models predicting values ranging up to 72‰ (Habicht and Canfield, 1997; Wortmann et al., 2001; Brunner and Bernasconi, 2005; and as reported in Sim et al., 2011a). However, the actual fractionations imposed during DSR are usually smaller, and depend on a number of environmental and biological factors such as sulfate reduction rate, sulfate concentration, temperature and the fluxes and fractionations imposed by the particular set of enzymes in a given organism (Thode et al., 1951; Rudnicki et al., 2001; Farquhar et al., 2003; Bradley et al., 2011, 2016; Sim et al., 2011b; Leavitt et al., 2013). Therefore, an essential approach to understanding the fractionations involves defining the fluxes of sulfur molecules through the DSR pathway, the fractionations of isotopes at each enzymatic step, and the controls on these in various organisms.

In sulfate-reducing bacteria (SRB) carrying out DSR, four critical enzymatically catalyzed steps (Figure 1) are involved: (i) import of sulfate into the cell by sulfate transporters, (ii) the “activation” of sulfate to the intermediate adenylyl 5′-phosphosulfate (APS) by sulfate adenylyl transferase (Sat, EC 2.7.7.4, also called ATP sulfurylase), (iii) the reduction of APS to sulfite by adenylyl-sulfate reductase (ApsR, EC 1.8.99.2, also called APS reductase), and (iv) the reduction of sulfite to sulfide (and potentially to thionates) by the multi-subunit dissimilatory sulfite reductase (Dsr, EC 1.8.99.5) (Brunner and Bernasconi, 2005; Wing and Halevy, 2011; Leavitt et al., 2015; Santos et al., 2015; Bradley et al., 2016; Sim et al., 2019).

FIGURE 1

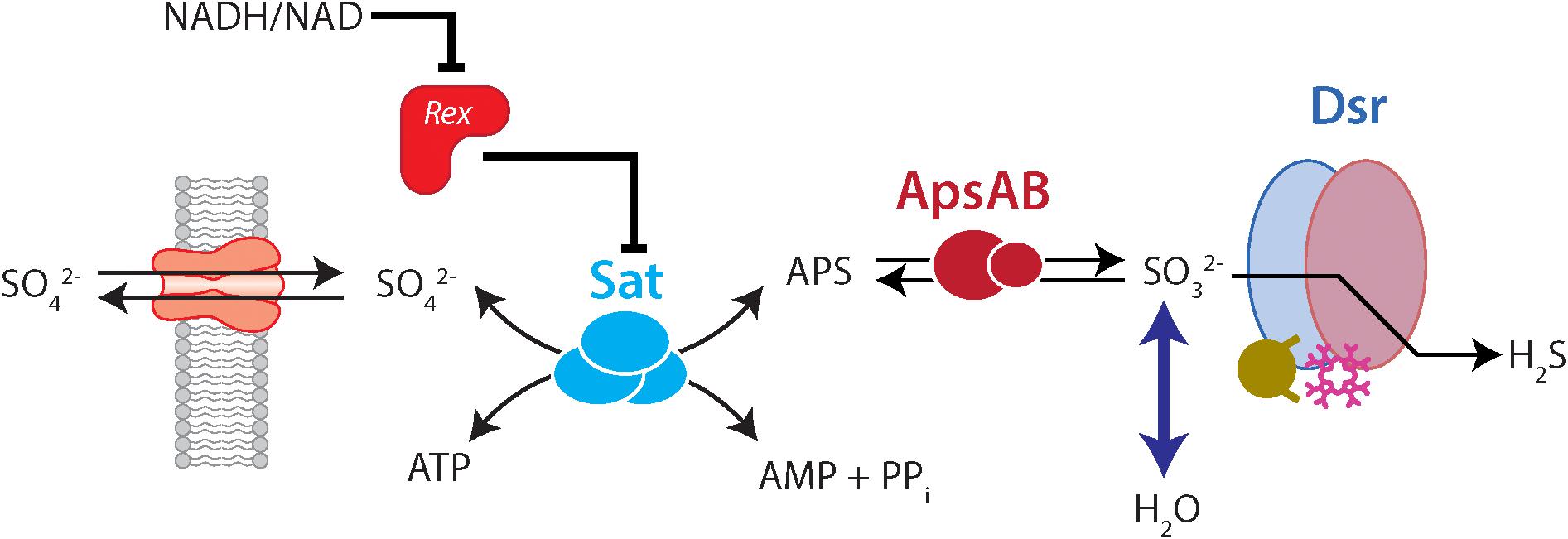
Figure 1. The dissimilatory sulfate reduction pathway, indicating the role of Rex in regulating Sat and isotopic fractionation. Forward reactions are left-to-right, while right-to-left indicates reversal. In the forward (reductive) direction, sulfate enters the cell through transporters. Sat catalyzes the reaction of sulfate with ATP to the products APS, AMP, and pyrophosphate (PP_i). APS is reduced to sulfite, and sulfite is reduced to sulfide via a complex interaction with Dsr. Exchange of oxygen isotopes happens between sulfite and water. Rex represses Sat expression. However, when the cellular redox state (as expressed by NADH/NAD) is high, Rex un-represses Sat, and Sat is more highly expressed. This would allow more flux through Sat. In our mutant strains this is likely to result in a higher intracellular APS concentration, which may allow for more expression of fractionation by ApsR.

The sulfur isotope ratio of residual sulfate produced by DSR is a consequence of the fractionation imposed by the enzymes in DSR. However, isotopic fractionations expressed by individual steps are not well constrained. The intrinsic sulfur isotope effects for two enzymes of the DSR metabolic network have recently been measured in vitro. Under experimental conditions, DsrAB imposed a fractionation factor (³⁴ε_{reactant–product}) of 15.3 ± 2‰ (Leavitt et al., 2015) and ApsR had a ³⁴ε of 20.1 ± 0.8‰ (Sim et al., 2019). However, these enzymatic constraints cannot fully explain the bank of observations.

The stable isotope ratio of oxygen in residual sulfate during DSR is a consequence of fractionation (¹⁸ε) resulting from both reductive and oxidative reactions (Brunner et al., 2005; Farquhar et al., 2008; Turchyn et al., 2010; Wankel et al., 2014). Sulfate does not exchange oxygen isotopes with water at biologically relevant pH and temperature ranges (Chiba and Sakai, 1985; Brunner et al., 2005). However, DSR promotes an increase in the relative amount of ¹⁸O in residual sulfate through two mechanisms: (i) discrimination against the heavier isotope during sulfate reduction (Brunner et al., 2005; Antler et al., 2013), and (ii) equilibrium exchange between water and sulfite (Betts and Voss, 1970; Farquhar et al., 2008; Wankel et al., 2014). Back-reactions from sulfite to sulfate can carry this equilibrium signature into sulfate (Lloyd, 1968; Fritz et al., 1989; Brunner et al., 2005; Turchyn et al., 2010; Antler et al., 2013; Wankel et al., 2014).

The isotopic consequences of the first steps in DSR – sulfate import and activation – have not been closely examined. These steps are unlikely to have large direct sulfur isotope effects, since they are not associated with forming or breaking bonds to sulfate sulfur. However, they may still affect the overall sulfur isotope fractionation during DSR by perturbing flux through the metabolic network. In this study, we begin to examine these effects by comparing a model sulfate reducing organism [Desulfovibrio vulgaris str. Hildenborough (DvH)] to mutant strains in which these early steps of sulfate reduction have been perturbed.

The import of sulfate into the cytoplasm of cells is modulated by sulfate permeases. The specificity and affinity of these transporters is not well documented (e.g., Price et al., 2018). Many SRB possess multiple sulfate permeases, and some data hint that differences in permeases among strains may have isotopic consequences. For example, Desulfovibrio alaskensis str. G20 and DvH show very different ³⁴ε under identical growth conditions under low millimolar sulfate concentrations (Bradley et al., 2016). One interpretation of this observation is that these strains are adapted to different concentrations of ambient sulfate – with D. vulgaris having high-affinity sulfate transporters adapted to low sulfate conditions, and D. alaskensis having low-affinity sulfate transporters adapted to high sulfate conditions. According to this interpretation, under low sulfate conditions D. vulgaris would have a higher intracellular sulfate concentration and therefore express higher ³⁴ε. D. alaskensis has eleven annotated sulfate transporters (Kuehl et al., 2014), and DvH has three (Clark et al., 2006). However, a recent study showed that across 23 different bacterial genera 48% of ABC transport proteins were incorrectly annotated or failed to accurately describe the transported substrates (Price et al., 2018). The genomes of 44 sulfate-reducing archaea and bacteria were recently examined for putative sulfate transporters and provide important targets for future research directions (Marietou et al., 2018). This analysis, published after our experiments were conducted and analyzed, revealed that instead of three putative sulfate transporters, DvH actually possesses thirteen transporter type proteins that could be associated with sulfate reduction (Marietou et al., 2018). Under conditions in which a strain is perturbed such that the only altered variable is the sulfate transport rate (i.e., a permease mutant with an unchanged growth phenotype), we would predict more quantitative reduction of imported sulfate, and lower ¹⁸ε and ³⁴ε. Under real-world experimental conditions, we need to account for complexity resulting from other changes to growth.

To study the importance of sulfate transport, we employed a mutant strain (ΔPerm) of DvH in which three proteins previously annotated as sulfate transport proteins (gene loci DVU0053, DVU0279, and DVU1999) were deleted from the genome (Keller et al., 2009). This triple-knockout mutant was predicted to be deficient in sulfate transport relative to the wild type, although it is still capable of sulfate reduction. We compared ΔPerm to the wild type (WT) strain and to three strains in which ΔPerm was complemented with each individual permease (DVU0053, DVU0279, and DVU1999). Of these three genes, DVU0053, closely aligns phylogenetically with other known sulfate transporters in the SulP family of proteins (Marietou et al., 2018), while DVU0279 is most closely related to dicarboxylic acid transporters, and DVU1999 is associated with bicarbonate transporters (Marietou et al., 2018). Of the remaining ten putative sulfate transporters in DvH, many are likely involved in phosphate transportation, three are putative sulfite transporters, and only one other (DVU2958) aligns with highly conserved sulfate transporters (Marietou et al., 2018).

After transport into the cytoplasm, sulfate is converted to adenosine 5′-phosphosulfate (APS) by Sat. This requires an investment of cellular energy in the form of ATP. Cells optimize the production of APS by modulating Sat expression through a redox-sensitive transcriptional repressor, Rex (Ravcheev et al., 2012; Christensen et al., 2015). Rex modulates transcription in response to the intracellular ratio of NADH/NAD⁺ through attachment to a DNA binding site upstream of its target gene (Gyan et al., 2006; Kuehl et al., 2014). This Sat expression optimization may be an adaptation to minimize APS hydrolysis, which would expend ATP investment. Perturbation of this regulatory feedback may result in increased intracellular APS production. This could result in an increased intracellular APS pool, which could result in a larger fractionation being expressed during APS reduction to sulfite (and an overall larger cellular ¹⁸ε and ³⁴ε). A larger pool of intracellular APS or higher rates of Sat expression could also result in more back-reaction from sulfite to sulfate.

To study the consequences of Rex on isotopic fractionation, we compared a wild type DvH to a mutant strain lacking Rex (Δrex) and to a mutant strain lacking the Rex binding site (IR1and2) (Christensen et al., 2015). The Δrex strain cannot transcriptionally repress Sat with Rex, and Sat transcripts in this strain are ∼11 times more abundant than in the wild type strain under growth conditions similar to our experiments (Christensen et al., 2015). However, Rex may interact with other regions of the genome, and so the phenotype of this strain may be more complicated than the perturbation to Sat expression alone (Christensen et al., 2015). The IR1and2 strain perturbs the Rex binding site and still contains Rex, but since Rex cannot bind to DNA upstream of Sat it cannot transcriptionally repress Sat expression. This mutant specifically impairs the mechanism for Sat repression, and shows a mean transcript level for Sat ∼4.6 higher than wild type (Christensen et al., 2015). We examined the ¹⁸ε and ³⁴ε of these mutant strains relative to the wild type strain.

Materials and Methods

Strains and Batch Growth Conditions

Seven strains of D. vulgaris: WT, ΔPerm, Perm53, Perm279, Perm1999, Δrex, and IR1and2, were obtained from J. D. Wall (University of Missouri) (Table 1). The construction of the mutants has been previously reported (Keller et al., 2009; Korte et al., 2014; Christensen et al., 2015). All seven strains were grown in triplicate batch culture at 30°C in the dark. Each seventy-milliliter butyl rubber sealed serum bottle contained 60 mL of MO media (as defined in Zane et al., 2010) without added yeast extract, of which 5 mL was derived from the inoculum. The remaining volume was a headspace of oxygen-free nitrogen gas. Fresh media contained 25 mM lactate as the electron donor and 28 mM sulfate as the electron acceptor. A 97.6% H₂¹⁸O (Berry & Associates/ICON Isotopes) spike was added to the media water of the Rex-related mutants (Δrex and IR1and 2) and a WT to achieve a δ¹⁸O_H2O of +130‰ vs. VSMOW and permit the profiling of back reactions through the DSR network. The bottles were autoclaved after the addition of the ¹⁸O-enriched water. Sterile and anaerobic protocols and conditions were maintained throughout growth and sampling. Inocula were grown under the same conditions as the experimental strains, but without the ¹⁸O spike.

TABLE 1

Table 1. Strains of Desulfovibrio vulgaris str. Hildenborough used in this study.

Batch Sampling

The experimental matrix contained 144 experimental bottles (36 WT and 18 of each mutant strain) and 17 killed controls, with 60 ml of culture in each bottle. After inoculation of each strain, three sample bottles were each harvested at 6 time points.

Harvested material was divided into two portions. At the time of harvest, a 15 mL aliquot was removed from each bottle, from which a 0.5 mL sub-sample was used to measure optical density at 600 nm using a Thermo Nanodrop 2000c. The remaining 14.5 mL were centrifuged at 5000 rpm for 15 min at 5°C. The supernatant was decanted and stored at −20°C. The cell pellet was re-suspended in 0.75 mL 10 mM PBS buffer, transferred to a microcentrifuge tube, and centrifuged at 10,000 rpm for 10 min at room temperature. The cell pellet was stored at −20°C and the PBS buffer was discarded.

To the remaining 45 mL of culture in the sealed serum bottle, we injected 4 mL of 1 M (sulfate free) ZnCl₂ using a needle and syringe. This mixture was shaken vigorously, then allowed to react for a minimum of 10 min in order to ensure that both gaseous and aqueous sulfide was converted to ZnS. The butyl septum and aluminum seal were then removed. Two 1.5 mL aliquots were removed for the measurement of dissolved ion concentrations (see below). The remaining 46 mL of media and ZnCl₂ were centrifuged at 5000 rpm for 15 min at 5°C. The ZnS pellet was retained and the supernatant was transferred to a new tube. The ZnS pellets were each rinsed three times with 45 mL MilliQ water, homogenized, centrifuged at 5000 rpm for 15 min at 5°C, then the supernatant was discarded. The washed ZnS pellet was re-suspended in 25 mL MilliQ water and reacted with 4 mL 2M AgNO₃ for more than 96 h in the dark, in order to completely convert the ZnS to Ag₂S. The supernatant remaining from the ZnS precipitation was allowed to react with 3.5 mL 1M BaCl₂ for more than 96 h in the dark in order to ensure complete conversion of aqueous sulfate into the insoluble BaSO₄.

Ag₂S and BaSO₄ solutions were each centrifuged at 5000 rpm for 10 min at 5°C. The supernatants were discarded. The pellets were then homogenized three times in 45 mL of MilliQ water and centrifuged again at 5000 rpm for 10 min at 5°C, with the supernatant being discarded after each centrifugation. The Ag₂S pellet was then homogenized and reacted with 15 mL 1 M NH₄OH. The solution was centrifuged at 5000 rpm for 10 min at 5°C. The supernatant was discarded and the resultant pellet was twice rinsed with 45 mL of MilliQ water, followed by centrifugation at 5000 rpm for 10 min at 5°C. The prepared BaSO₄ and Ag₂S pellets were dried in an oven at 70°C overnight, homogenized, and weighed for isotopic analysis.

Batch Rate Estimations

In batch culture, we calculated cellular growth rates and cell-specific sulfate reduction rate (csSRR). Growth rates for each strain were calculated from the slopes of the linear regression of the natural logarithm of the optical densities (OD₆₀₀) of the cells growing in exponential phase versus time. The csSRR up to time of harvest was calculated using the concentrations of sulfate and the OD₆₀₀ at time of harvest. The average OD₆₀₀ over the exponential growth period was taken as

$$\mathrm{Average}\mathrm{optical}\mathrm{density}={\displaystyle \frac{c_t}{kt\left[1-e^{kt}\right]}}$$

where c_t is the optical density at harvest, k is the specific growth rate, and t is the time elapsed since inoculation. OD₆₀₀ was converted to cell number using a calibration previously established for D. vulgaris (Leavitt et al., 2013). Sulfate consumption per cell was converted to mean csSRR in units of fmol sulfate/cell/day.

Chemostat Design and Growth Conditions

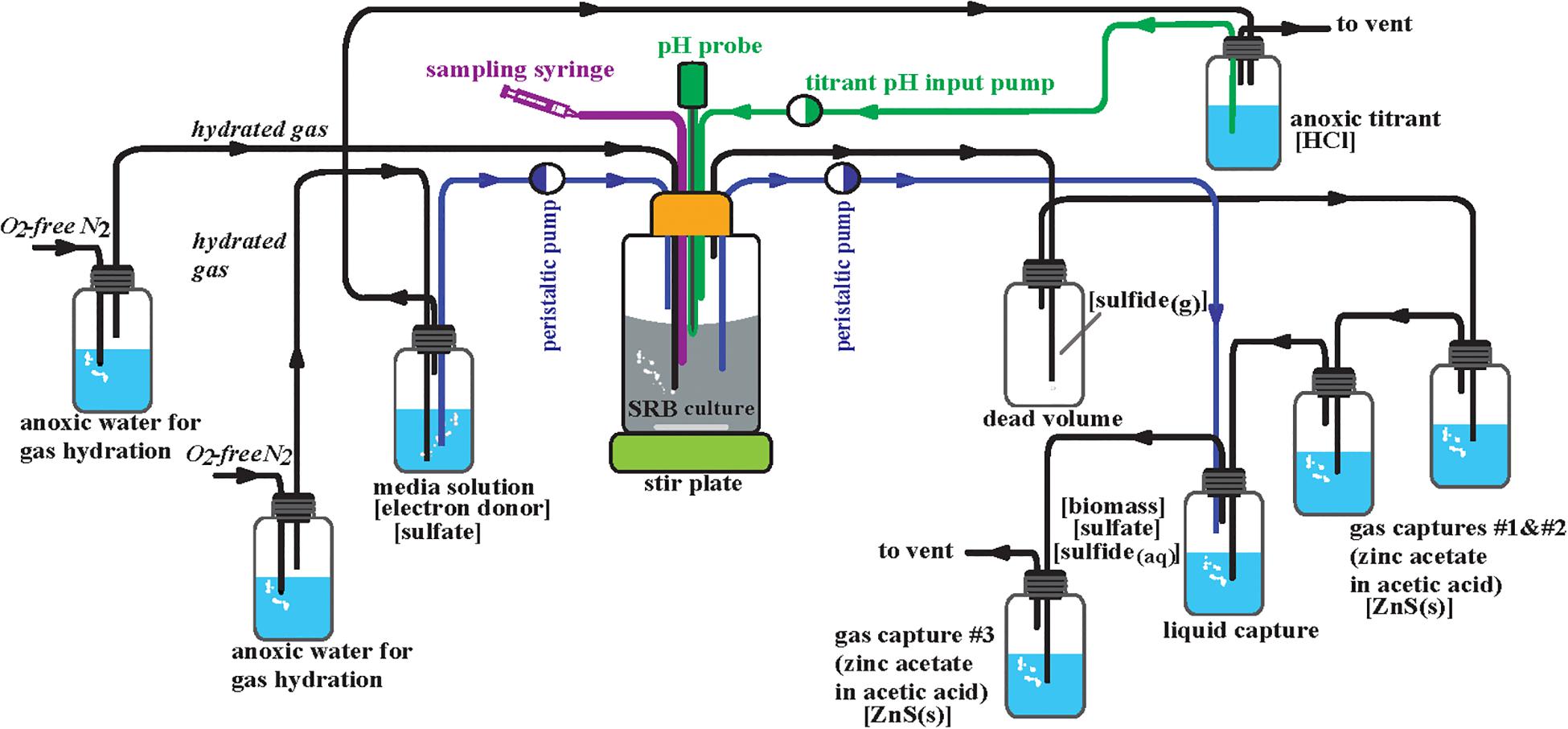
The WT and Δrex strains were cultivated in separate anoxic continuous cultivation reactors run in parallel under chemically static conditions (chemostats) (Figure 2). The initial design of these is described in Leavitt et al. (2013, 2016). MO media (described above) for each strain were prepared under anoxic conditions (10 L per strain), autoclaved, kept under sterile conditions, and kept anoxic by a constant flux of 0.22 μm filter sterile ultra high purity (>99.999%) anoxic N₂ gas at an influent pressure of 2.5 psi. This gas stream was used maintain anoxic conditions of the 1 M HCl titrant via constant flushing of the titrant headspace. The growth chambers (reactors) were maintained at a working volume of 300 mL. Prior to inoculation the reactors were autoclaved with 300 mL of MO media. Sterile and anoxic conditions were maintained throughout the course of the experiment. A constant stream of 0.22 μm filter sterile ultra high purity (>99.999%) anoxic N₂ gas was supplied to each reactor at an influent pressure of 6.5 psi that flowed in series to all of the gas and liquid traps. Inoculation occurred for each strain from a 10 mL aliquot of batch culture in MO media. These inocula were grown from freezer stock then transferred three times and harvested at exponential phase. Each reactor was connected to a series of three gas traps, each containing 50 mL of 1 M zinc acetate to precipitate ZnS: two following the dead volume for evolved H₂S gas from the reactor and one following the liquid capture of spent media and cells from the reactor, insuring quantitative conversion of ZnS (Figure 2). Each reactor was also connected to a liquid trap where spent media and cells accumulated containing excess 1 M BaCl₂ at a pH of 4 which immediately halts biologic activity and precipitates BaSO₄. Sulfide was maintained well below detection limits (<30 μM, see below) in this liquid trap via constant gas purging and connection in tandem to the third zinc trap. The pH of the reactors was maintained at 7.15 ± 0.4. An Etatron DLX pH-RX/MBB metering pump, activated by a pH probe, supplied anoxic and sterile 1 M HCl for titration of each reactor. Dilution rate was altered by adjusting the pump rate of an Ismatec SC0816 peristaltic pump containing 0.64 mm two-stop PVC Tygon tubing. Five steady-state dilution rates were examined: 0.008 ± 0.0002, 0.011 ± 0.0006, 0.015 ± 0.0005, 0.022 ± 0.0004, and 0.051 ± 0.0024 hr^–1. In chemostats at steady state, the growth rate (μ) is equal to the dilution rate. These dilution rates relative to μ_max were 0.096 ± 0.002, 0.133 ± 0.008, 0.181 ± 0.004, 0.265 ± 0.002, and 0.614 ± 0.027 for the WT and 0.129 ± 0.003, 0.177 ± 0.010, 0.242 ± 0.005, 0.355 ± 0.003, and 0.823 ± 0.035 for Δrex (Table 2). The onset of steady state was defined by constant cell density, as monitored by the optical density at 600 nm (OD₆₀₀) of the reactor. Once steady state was achieved, a minimum of three flush volumes [the volume required to replace all of the liquid in the reactor] occurred before sampling commenced. After these three flush volumes, the gas and liquid traps were switched with new traps containing fresh material to start steady state sample collection.

FIGURE 2

Figure 2. Schematic design for the chemostats.

TABLE 2

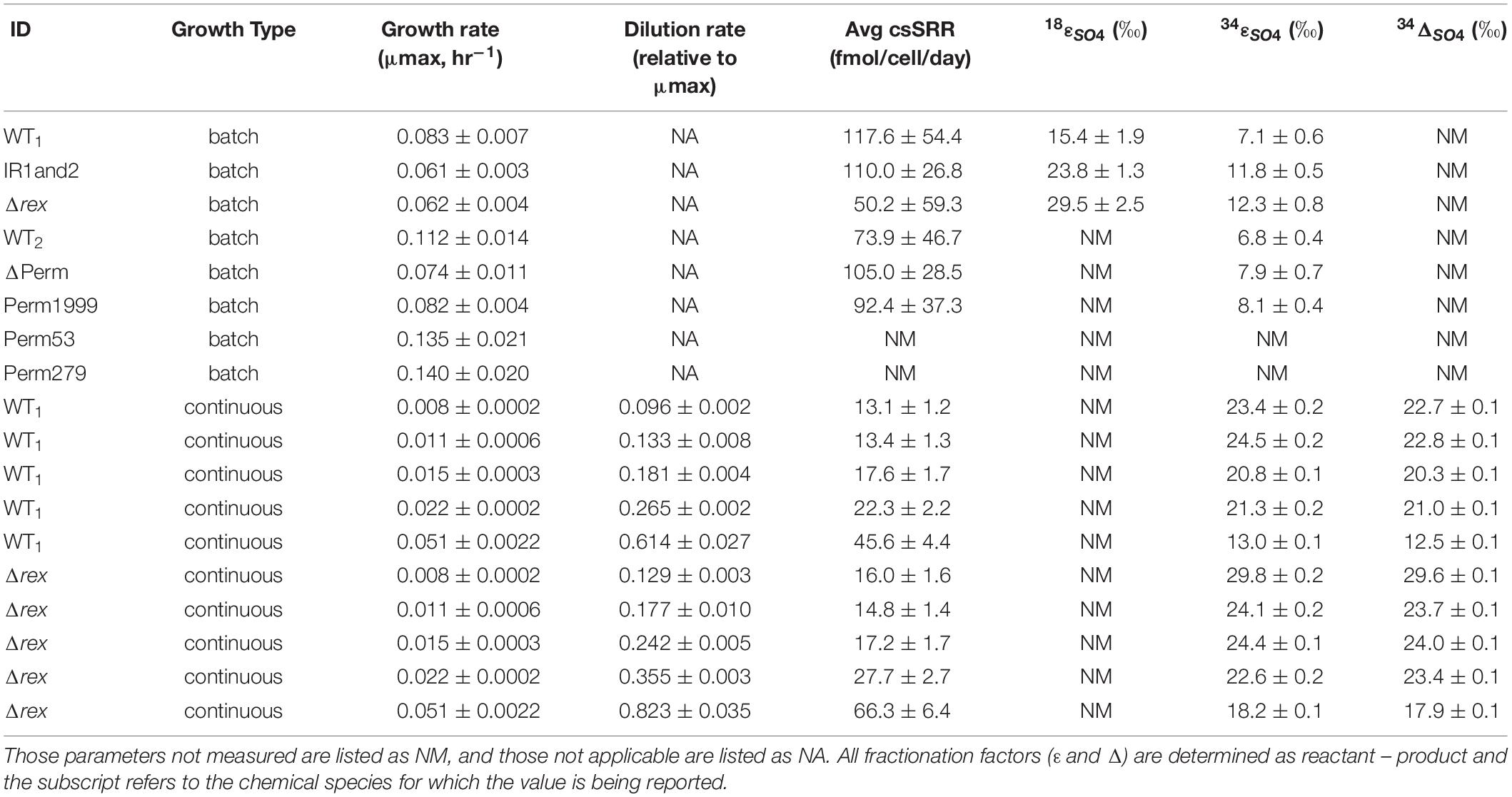
Table 2. Average growth rate, cell-specific sulfate reduction rate (csSRR), and isotopic fractionation factors for the wild type (WT and WT₂), Rex-promoter Sat mutant (IR1and2), Rex mutant (Δrex), triple permease knockout mutant (ΔPerm), and the three mutants with an individual permease complemented back into the triple knockout (Perm1999, Perm53, and Perm279) displayed with errors in measurements or uncertainties (±).

Chemostat Sampling

Steady-state sampling included samples directly from the reactor, gas and liquid traps. Sampling from all three locations provided an assessment of isotopic consistency, shown in Table 2. A 20 mL aliquot was taken from the reactor, placed in two 15 mL centrifuge tubes, and centrifuged at 5,000 rpm for 10 min at 4°C. The resulting cell pellet was resuspended with 0.75 mL 10 mM PBS in microcentrifuge tubes, centrifuged at 12,000 rpm for 6 min, the supernatant discarded and pellet frozen at −20°C. The supernatant of each 10 mL sample was reacted with 2.5 mL 1 M ZnCl₂ for 25 min and centrifuged at 5,000 rpm for 10 min at 4°C. The resultant ZnS was retained for later isotope analysis. A 1.5 mL aliquot was taken from the supernatant of the centrifuged reactor sample for IC analysis (described below) and stored at −20°C. The remaining liquid was reacted with 1.5 mL of 1 M BaCl₂ and allowed to react for at least 24 h, then centrifuged at 5,000 rpm for 10 min at 4°C. The resultant BaSO₄ was retained for isotope analysis. The accumulated precipitated ZnS was harvested from the gas traps in three 50 mL centrifuge tubes, and centrifuged at 5,000 rpm for 10 min at 4°C. The ZnS pellets were combined, rinsed 3x with MilliQ water then reacted with excess 1 M AgNO₃ to generate Ag₂S and allowed to react for at least 24 h in the dark. These Ag₂S pellets were washed 3x with MilliQ water with homogenization and centrifugation in between the washing steps. The washed Ag₂S was then reacted with 15 mL of 1 M ammonium hydroxide, homogenized and centrifuged, then washed 3x with MilliQ water and dried at 70°C overnight. The precipitated BaSO₄ from the liquid trap was collected in three or four 50 mL centrifuge tubes [dependent on accumulated volume] and centrifuged at 5,000 rpm for 10 min at 4°C. The pellets were combined, rinsed with MilliQ water three times, and homogenized. The resulting pellets were purified using the diethylenetriamine pentaacetate (DTPA) method of Bao (2006) then dried at 70°C overnight.

Chemostat Rate Estimations

In chemostats, csSRR was determined in a manner similar to batch experiments. OD₆₀₀ was converted to cell number (Leavitt et al., 2013), and moles of sulfate consumed was determined by the difference at sampling from initial individual media batches.

Dissolved Ions

Aliquots of media designated for analysis of dissolved ion concentrations were centrifuged at 10,000 rpm for 10 min at room temperature and the supernatant was transferred to a new microcentrifuge tube and frozen at −20°C until analysis. Samples were diluted in MilliQ water (1: 50) for analysis by ion chromatography (IC). Sulfate, lactate and acetate concentrations were determined using suppressed anion chromatography with conductivity detection (Metrohm 881 Compact IC Pro equipped with a Metrosep A Supp 7-250/4.0 column and a 2 mM Na₂CO₃ eluent or A Supp 5-100/4.0 column and mix of 1 mM Na₂CO₃, 3.2 mM NaHCO₃ with 25 mL HPLC grade acetone per L eluent). Sulfate, lactate, and acetate had detection limits better than 150, 150, and 800 μM, respectively. Sulfide concentrations were determined by diluting samples in MilliQ water (1: 65) and then performing spectrophotometric analysis following the methods of Cline (1969). The detection limits were 30 μM.

Isotope-Ratio Mass Spectrometry (IRMS)

Sulfur isotope ratios were measured in duplicate on each sample of precipitated BaSO₄ and Ag₂S from each experiment. Approximately 0.4 mg of material with 2 mg of V₂O₅ were loaded in tin capsules and analyzed on an Isoprime 100 IRMS interfaced with an Elementar vario ISOTOPE cube elemental analyzer (for the Rex mutant set) (Virginia Tech), or Thermo Scientific Finnigan Delta V Plus IRMS interface with a Costech 4010 elemental combustion system (Permease mutant set) (Washington University). All sulfur isotope values are reported as per mil variations relative to VCDT following the conventional delta notation:

$${\mathrm{\delta }}^{34}\text{S}=\left(\frac{{\left({}^{34}S{/}^{32}S\right)}_{\text{Sample}}}{{\left({}^{34}S{/}^{32}S\right)}_{\text{VCDT}}}-1\right).$$

Values of δ³⁴S were calibrated relative to international standards of BaSO₄ (IAEA-SO-5) and AgS₂ (IAEA-S-1 and IAEA-S-3). The external precision of δ³⁴S is ±0.25‰ (1σ) as estimated from repeated, long-term measurements of internal and international reference materials.

Oxygen isotope ratios were measured on duplicate samples of BaSO₄ from each experiment. Approximately 0.4 mg of material was loaded in silver capsules and analyzed using a Thermo Finnigan high temperature conversion elemental analyzer (TC/EA) coupled to a Thermo Delta Plus IRMS. All oxygen values are reported as per mil variations relative to VSMOW following conventional delta notation. Values of δ¹⁸O were calibrated relative to international standards of BaSO₄ (GSW-1, NBS-127, IAEA-SO-5, IAEA-SO-6). The external precision of δ¹⁸O is ≤0.2‰ (1σ) as estimated from repeated, long-term measurements of internal and international reference materials.

The sulfur and oxygen isotopic fractionation factors were determined following conventional methods. For the batch experiments [closed system], the apparent fractionation factors for a given set of experiments were calculated from linear regressions of δ values against the negative natural logarithm of the fraction of the reactant remaining (Hayes, 2001)

$${\mathrm{\delta }}_{measured}={\mathrm{\delta }}_{initial}-\text{ln}(f)*\epsilon$$

where f is the fraction of reactant remaining and ε is the fractionation factor. Uncertainty in the regressions is reported as the 95% confidence interval around a best-fit slope. Regressions were compared to each other using analysis of variance (ANOVA) to test for homogeneity of the regression slopes between pairs of regressions. For the chemostat experiments [open system], the isotopic fractionation factor was calculated from the difference between the initial and out flowing reactant divided the fraction of the product produced (Hayes, 1983, 2001)

$$\mathrm{\epsilon }=-(\frac{{\mathrm{\delta }}_{measured}-{\mathrm{\delta }}_{initial}}{f_{product}})$$

where f is the fraction of product produced (sulfide) and ε is the fractionation factor of sulfate. All ε are determined as reactant – product and the subscript refers to the chemical species for which the value is being reported.

Results

Growth Characteristics and Reaction Stoichiometry

Permease mutants were able to grow as sulfate reducers, suggesting that the annotated transport proteins are not the sole mechanism for sulfate import into DvH cells (Figure 3A). The Δrex mutant exhibited a longer lag phase and grew more slowly than the WT strain (Figure 3A). Strain IR1and2 showed growth characteristics similar to Δrex (Figure 3A). All isotopic results reported here derive from samples collected from exponential phase growth, with the exception of the final time point for the WT strain. The stationary phase timepoints are omitted from our analyses due to the differences in stress response, gene expression, translation, transcription, cell morphology and physiology induced during stationary phase (e.g., Kolter et al., 1993; Clark et al., 2006; Navarro Llorens et al., 2010). Growth rates and cell-specific sulfate-reduction rates (csSRRs) are shown in Table 2.

FIGURE 3

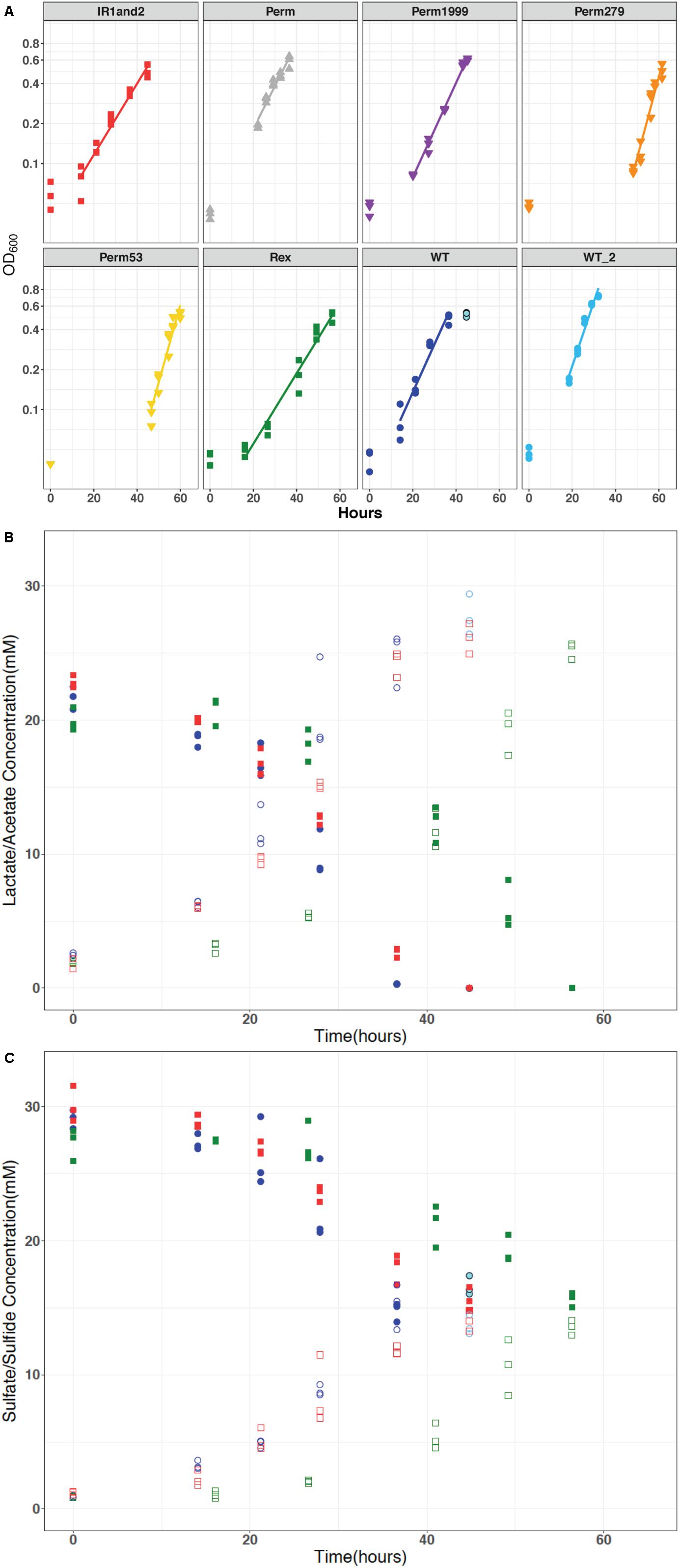
Figure 3. (A) Optical density measured at 600 nm (log scale) plotted against time for all DvH strains: wild type (WT and WT₂), triple permease knockout (ΔPerm), and the three individually expressed permeases: Perm53, Perm279, and Perm1999, Rex-promoter Sat mutant (IR1and2), and Rex mutant (Δrex), which show similar growth characteristics. (B) The representative concentrations of lactate and acetate versus time. These concentrations changed relative to sulfate as predicted by equation 1. (C) Representative concentrations of sulfate and sulfide for all strains were similar, varied inversely throughout the experiment as expected, and maintained mass-balance. The data for WT, IR1and2, Δrex are in dark blue, red, and green, respectively. In all panels, the stationary phase time points for the wild type are indicated in light blue.

All the strains showed similar reactant consumption rates and reaction stoichiometry. The governing stoichiometry for sulfate reduction via the oxidation of lactate (Rabus et al., 2013):

$2{\text{CH}}_3{\text{CHOHCOO}}^{-}+{\text{SO}}_4^{2-}\leftrightarrow 2{\text{CH}}_3{\text{COO}}^{-}+2{\text{HCO}}_3^{-}+{\text{HS}}^{-}+{\text{H}}^{+}$ held for all strains (Figures 3B,C). Differences in organic acid consumption and production were not observed across the strains. The similar dissimilatory consumption and production rates but differing growth rates likely implies an efficiency difference among the mutants.

Sulfur and Oxygen Isotope Fractionations Change With Batch Growth

For all batch experiments, sulfate δ³⁴S values increased as growth progressed, with an increase up to 8‰ (Figure 4A). The permease mutants, ΔPerm and Perm1999, exhibited ∼1‰ larger ³⁴ε fractionations than the WT strain (Table 2 and Figure 4A); however, this difference is small and approaches the uncertainties of the determinations. The Rex-related mutant strains Δrex and IR1and2 both showed larger ³⁴ε than the WT by ∼5‰ (Table 2 and Figure 4A) under comparable growth conditions. The sulfur isotope fractionations reported for all strains are comparable to values reported for DvH and other SRB (Mangalo et al., 2007; Turchyn et al., 2010; Sim et al., 2011a, b; Leavitt et al., 2013, 2016).

FIGURE 4

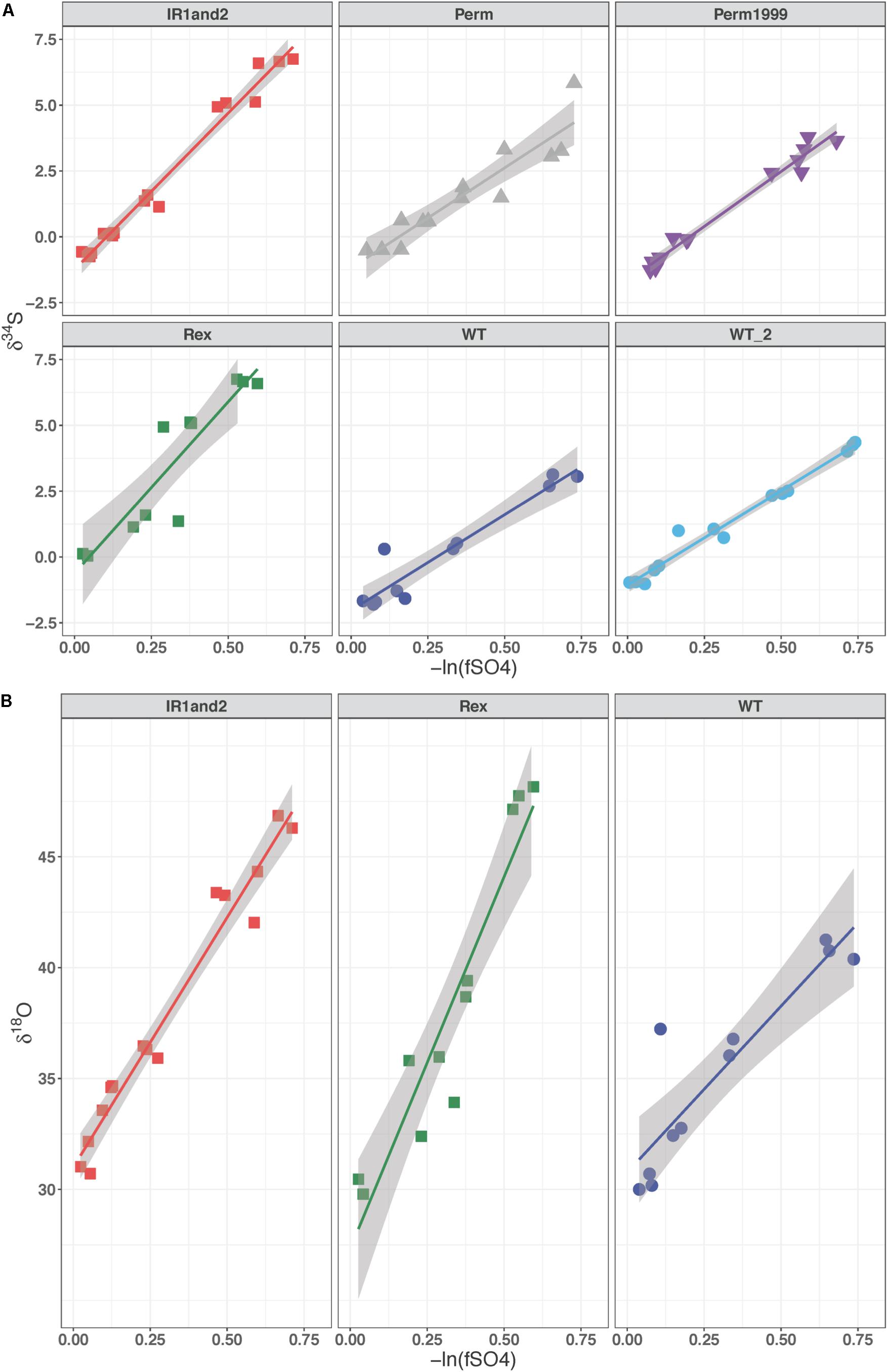
Figure 4. (A) δ³⁴S of residual sulfate plotted against the negative natural logarithm of the fraction of reactant sulfate remaining for the Permease and Rex mutant batch experiments. (B) δ¹⁸O of residual sulfate plotted against the negative natural logarithm of the fraction of reactant sulfate remaining in the Rex mutant experiments. The slope of these lines represents the fractionation factor (ε) and is plotted with the 95% confidence interval for the regression.

The media water of the Rex experimental set was enriched in ¹⁸O to a δ¹⁸O_H2O value of +130‰. As growth progressed in the Rex experimental set, residual sulfate became enriched in ¹⁸O, with δ¹⁸O_SO4 increasing from +29‰ to between +40‰ and +50‰ by the end of growth. The increase in the value of δ¹⁸O_SO4 with reaction progress in each sample is shown in Figure 4B. The values of ¹⁸ε were larger in both the Δrex and IR1and2 compared to the WT (Table 2). In these experiments, δ³⁴S_SO4 and δ¹⁸O_SO4 were linearly correlated (Figure 5).

FIGURE 5

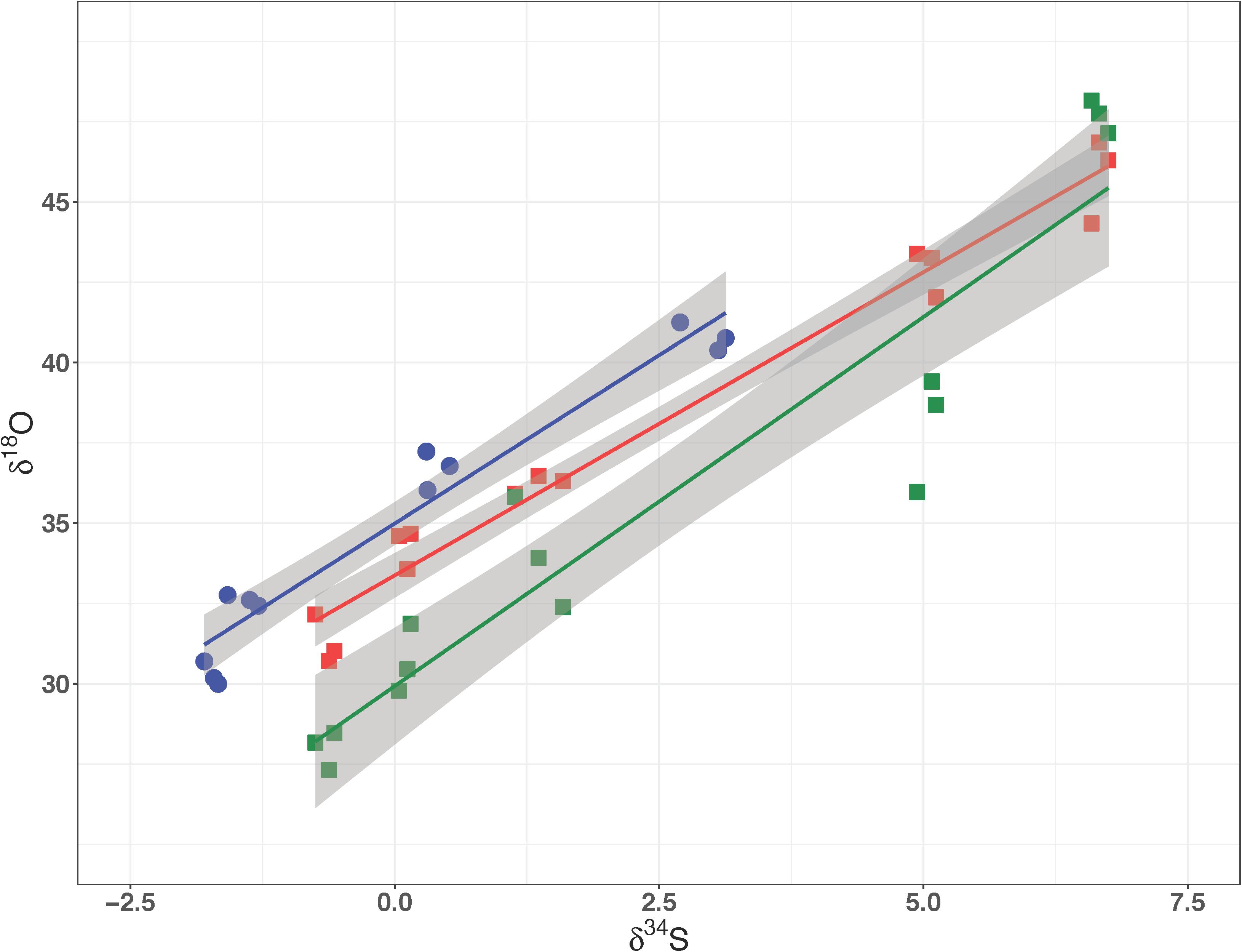
Figure 5. δ¹⁸O of residual sulfate plotted against its δ³⁴S from the Rex batch culture mutant experiment. In all three strains these relationships are linear, suggestive of a dominant kinetic isotope effect. The data for WT, IR1and2, Δrex are in dark blue, red, and green, respectively.

Sat Expression Affects Isotopic Fractionation

The role of Sat expression in isotope fractionation was investigated. To isolate the isotope effects of this enzyme, alterations in sulfate reduction rate were examined. Previous studies have observed that ³⁴ε varies strongly as a function of csSRR (Rees, 1973; Brunner and Bernasconi, 2005; Johnston et al., 2005, 2007; Bradley et al., 2011, 2016; Sim et al., 2011a; Leavitt et al., 2013; Wing and Halevy, 2011). We calculated csSRR in our Rex batch cultures (Figure 6) and compared both csSRR and growth rate to observed fractionations (Figure 7) to determine whether this relationship could account for the observed patterns.

FIGURE 6

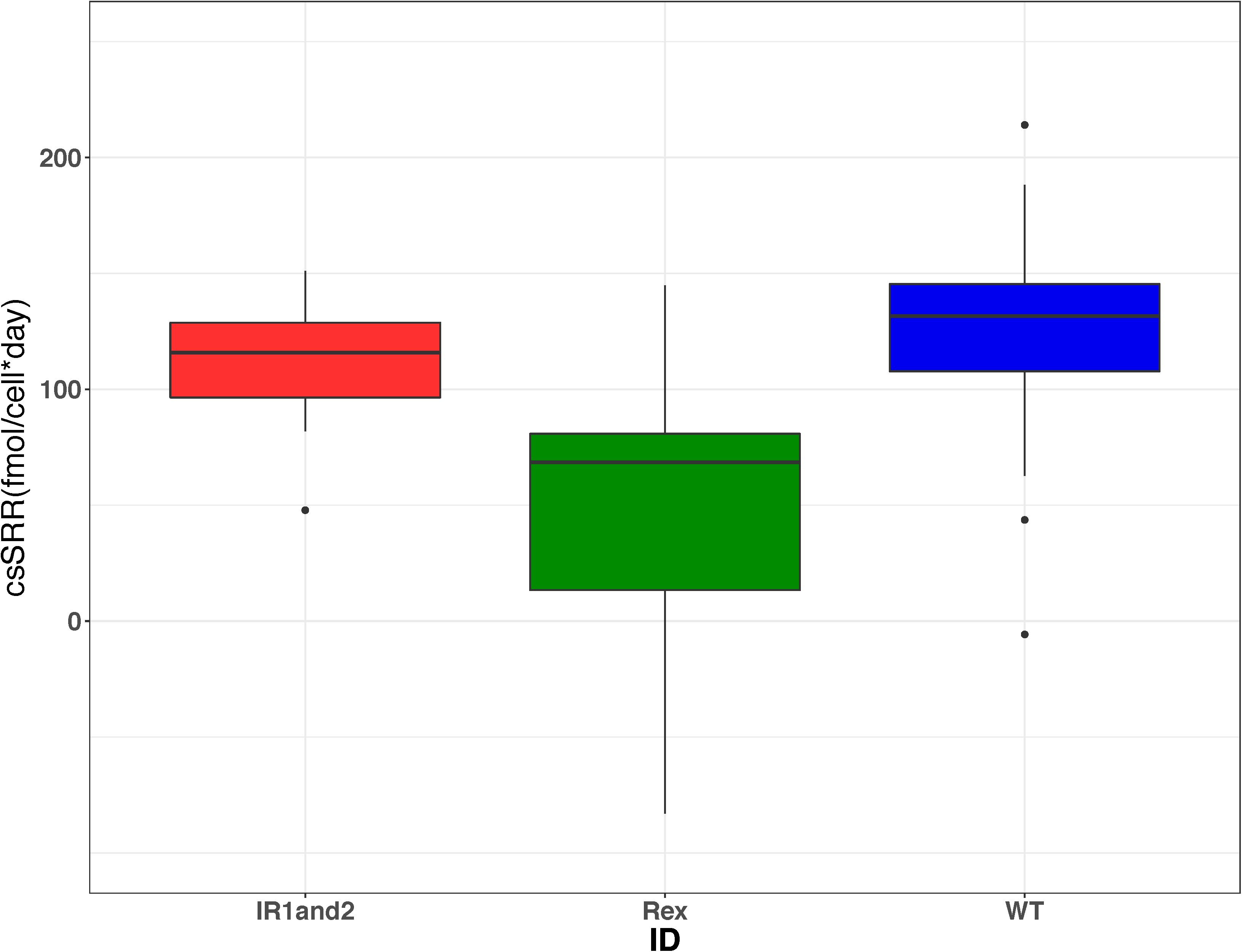
Figure 6. Boxplots showing the range of cell-specific sulfate reduction rates (csSRR) calculated from each harvested bottle in each of the three strains from the Rex batch culture experiments. These results show that the csSRR for the wild type is greater than that in the Δrex strain, but indistinguishable from the IR1and2 strain. The data for WT, IR1and2, Δrex are in dark blue, red, and green, respectively.

FIGURE 7

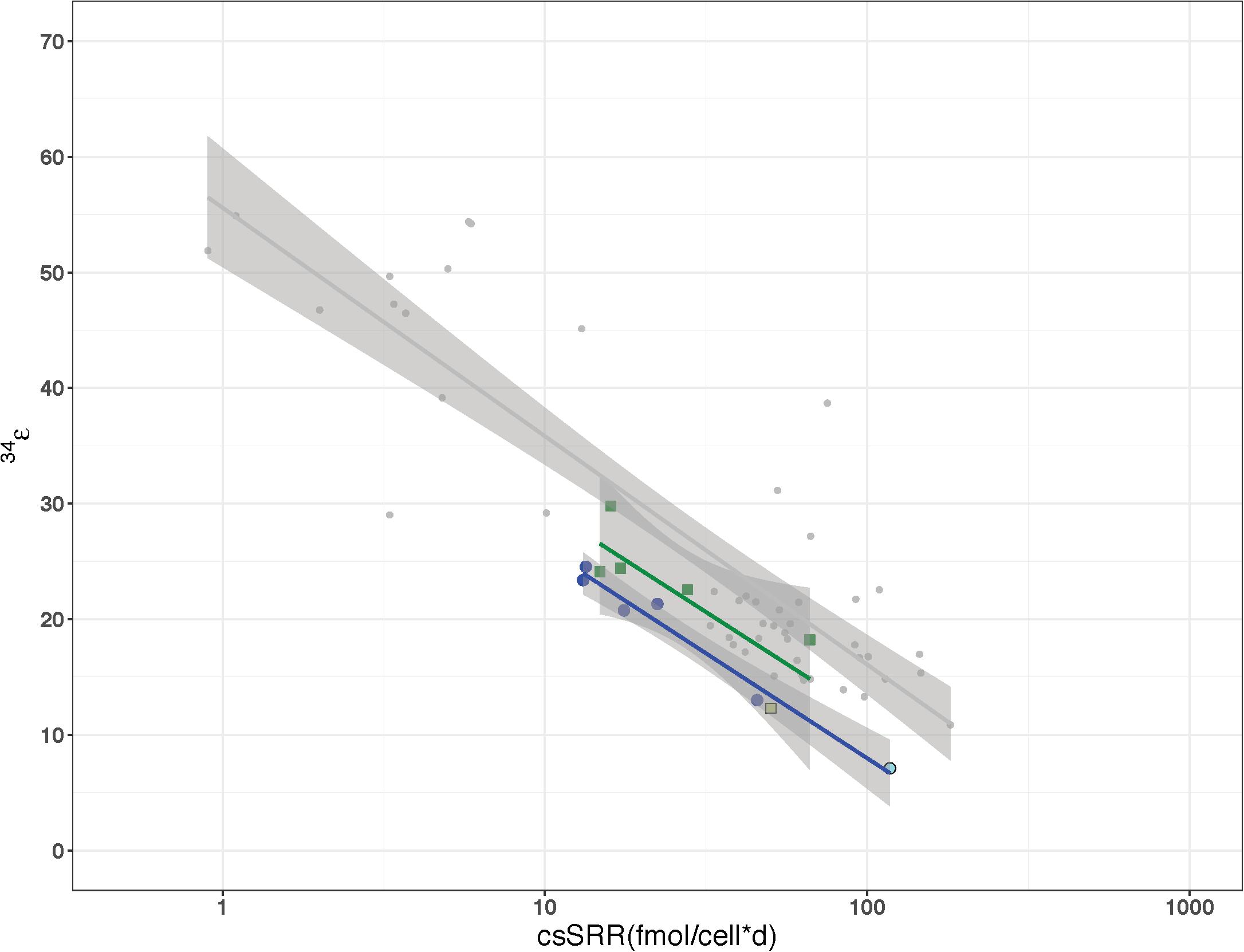
Figure 7. Relationship of cell-specific sulfate reduction rates (csSRR) to sulfur fractionation factor (³⁴ε) for D. vulgaris as previously reported by Leavitt et al. (2013) in comparison to the wild type strain (dark blue) and Δrex (green) grown in continuous and batch culture. The light blue and green colored symbols represent the batch fractionation factors for WT and Δrex, respectively.

The perturbations of Sat expression in Rex-related mutant strains impacted the observed sulfate oxygen and sulfur isotope fractionations. Although the WT and IR1and2 strains have csSRR that are statistically indistinguishable, the ¹⁸ε values decrease with increasing csSRR (Table 2). However, in the WT, IR1and2, and Δrex strains neither the relationship of ¹⁸ε with csSRR (p = 0.35) nor the relationship of ¹⁸ε with growth rate (p = 0.24) shows a discernable correlation. The magnitude of ³⁴ε for all three strains showed an inverse relationship with growth rate (p = 0.045), but no relationship with csSRR (p = 0.54) (Table 2).

Isolation of Growth Rate Effects in Chemostats

Previous work has shown that csSRR is correlated with ³⁴ε (Detmers et al., 2001; Sim et al., 2011b; Leavitt et al., 2013). The increased fractionation factors in the Δrex strain over the WT strain in batch could be explained via the decreased csSRR of Δrex. However, the csSRR for the WT and IR1and2 strains were indistinguishable so it is also possible to conclude that perturbed Sat activity was responsible for the differences in fractionations.

In order to clarify the issues of growth rate and csSRR effects on the sulfur isotope fractionation differences between WT and Δrex, these two strains were grown in parallel chemostats where the same steady state growth rate was maintained in each vessel (e.g., two chemostats run simultaneously using the same pump to maintain the same dilution rates). We examined five steady-state rates ranging from 0.008 to 0.051 hr^–1, which corresponds to a range of 0.096–0.614 of μ_max for the WT and a range of 0.129–0.823 of μ_max for Δrex. The effluent δ³⁴S_SO4 values of Δrex (16.4–9.4‰) partially overlapped with the more enriched values of the WT (12.8–5.9‰) (p = 0.02), relative to the media sulfate that has a δ³⁴S of −2.3‰. The evolved δ³⁴S_H2S values of Δrex (−13.2 to −8.5‰) were more depleted than the values of WT (−10.4 to −6.7‰). The ³⁴ε of Δrex was slightly larger than that of the WT (p = 0.063) (Table 2). If the ³⁴ε and csSRR values for both batch and continuous are considered, the slope of the regressions for the Δrex and WT strains are nearly equal to one another (−7.65 and −7.42, respectively) and to the slope (−8.59) that Leavitt et al. (2013) showed previously in the same strain (Figure 7). The only difference between the Δrex and WT regressions, when batch and continuous data were plotted together, were the y-intercepts of 47.0 and 42.1‰, respectively. In both the batch and chemostat cultures, strains with increased Sat transcription differed in ³⁴ε by ∼5‰ relative to the wild type.

Discussion

Fractionation in Permease Mutants

The two permease mutants, ΔPerm and Perm1999, showed an increase in ³⁴ε of ∼1‰ relative to the wild type strain (WT₂) (Table 2). Interpretation of these results must consider both the sulfate import mechanism and the change in csSRR, as well as the potential overlaps in uncertainties. The csSRR for ΔPerm is lower than the wild type (p = 0.013), and not clearly distinguishable from Perm1999 (p = 0.21). The hypothesis tested in this set of experiments was that perturbations in permease expression would change sulfate import rates and lead to altered fractionation. While little change in fractionation was observed, the results are confounded by changes in csSRR.

Desulfovibrio vulgaris str. Hildenborough (DvH) is still able to carry out sulfate reduction following the deletion of DVU0053, DVU0279, and DVU1999, which is consistent with the presence of additional mechanisms for sulfate transport (Marietou et al., 2018). The observed difference in ³⁴ε may suggest that the remaining transporters have a different fractionation, or that their expression changed in response to the deleted genes. However, given these results, there is little evidence that these particular sulfate transporters have much contribution to the overall expression of ³⁴ε.

Increased ¹⁸ε and ³⁴ε Due to Sat Expression

A linear correlation of δ¹⁸O_SO4 vs. δ³⁴S_SO4 has been interpreted to imply that the fractionation of oxygen isotopes is controlled by kinetic processes, rather than inorganic equilibrium (Mandernack et al., 2003; Turchyn et al., 2010; Mills et al., 2016; Antler et al., 2017). In contrast, when equilibrium processes dominate, the plot of δ¹⁸O_SO4 vs. δ³⁴S_SO4 is curved, approaching an asymptote of the value of δ¹⁸O_SO4 that is in equilibrium with water.

The relationships of δ¹⁸O_SO4 vs. δ³⁴S_SO4 in residual sulfate produced by the wild type D. vulgaris is similar to that of Δrex and in IR1and2. All three plots show a linear relationship between oxygen and sulfur isotope ratios with similar slopes. The wild type strain has a higher δ¹⁸O_SO4 intercept than the mutants – i.e., at the point when residual sulfate δ¹⁸O_SO4 has evolved to a similar value in all three strains, the mutant strains have produced residual sulfate that is more enriched in ³⁴S. These patterns suggest that in all these experiments, enrichment of ¹⁸O in residual sulfate is predominantly due to kinetic fractionation. Table 2 suggests that both ¹⁸ε and ³⁴ε are higher in Δrex and in IR1and2 than in the wild type.

Given these results, the question becomes: why does increased transcription of Sat result in higher kinetic ¹⁸ε and ³⁴ε? We will exclude the Δrex result: this strain had a lower csSRR than the wild type, and there is no requirement to attribute the observed changes in fractionation to any mechanism other than the observed change in csSRR. In the chemostat, Δrex showed a slight increase in fractionation relative to the wild type, but it was not clearly distinguishable. However, the csSRR for IR1and2 was similar to the wild type. One hypothesis is that increased Sat transcription results in increased Sat expression, and that this increases the rate at which intracellular sulfate is converted to APS, yielding a higher intracellular APS pool. This affects the expressed fractionation of the downstream steps. For example, if APS reduction is rate-limiting, then two strains operating at the same csSRR will have approximately equal rates of APS reduction. APS will be less quantitatively reduced in the strain with a higher intracellular pool of APS – and such a strain would be predicted to express higher isotopic fractionations at this step, as we observe in this experiment. In contrast, if sulfite reduction was rate limiting, then we would predict a significant back-flux from sulfite toward sulfate. This back-flux would carry the ¹⁸O signature of equilibrium exchange between sulfite and water. If we exclude this interpretation based on the linear relationship between δ¹⁸O_SO4 vs. δ³⁴S_SO4, then we can draw two inferences. First, that APS reduction is likely the rate-limiting step under these growth conditions. This conclusion is in accord with modeled metabolism of this strain, for other experiments grown under similar conditions (Wing and Halevy, 2011). Second, while we have no direct evidence that the IR1and2 strain has increased Sat expression or APS concentrations, these conditions are likely, given the increased Sat transcription in this strain. The inference that follows is that it is possible to change the isotope fractionations expressed during APS reduction by at least 15‰ for ¹⁸ε and 5‰ ³⁴ε, by perturbing upstream fluxes.

Other explanations should also be considered. Cellular overproduction of APS in the IR1and2 mutant is likely to result in hydrolysis of some of that APS (Baddiley et al., 1957; Robbins and Lipmann, 1958) – this would form sulfate from APS but without the concomitant recovery of ATP. This condition would exist, and even be exacerbated in the Δrex mutant, where a wider loss of transcriptional regulation may perturb cellular homeostasis. The effects of this on isotopic fractionation are difficult to predict, but given the myriad interactions between the enzymes of DSR and the range of electron carriers in the cell, it is not surprising to observe differences from the wild type. Rex may not be the only mechanism regulating Sat expression. The presence of APS has been shown to inhibit the activity of Sat in both the dissimilatory and assimilatory versions of the enzyme across multiple domains of life (Seubert et al., 1983, 1985; Renosto et al., 1984, 1990, 1991; Wang et al., 1995; MacRae et al., 2001; Hanna et al., 2002; Yu et al., 2007; Gay et al., 2009; Parey et al., 2013; Ravilious et al., 2013; Herrmann et al., 2014). Increased Sat transcription therefore may not translate linearly to increased Sat activity, particularly if it results in increased APS accumulation.

Conclusion

Mutant strains of the sulfate reducing bacterium D. vulgaris str. Hildenborough with mutations deleting sulfate transporters showed only small changes in overall sulfur isotope fractionation. The mutations targeted all the sulfate transporters known at the time they were constructed, but the continued ability of these strains to reduce sulfate, along with more recent genomic work, suggests that these strains have other sulfate transporters. More detailed analysis of the full range of sulfate transporters would be required to determine whether the sulfate affinity of individual transporters affects the overall expressed fractionation of the strains under various conditions.

Mutant strains targeting the expression of Sat showed differences in ¹⁸ε and ³⁴ε relative to wild type. In the case of the Δrex strain, we cannot conclude that there were any differences in fractionation apart from those imposed by a growth defect, or that differences were solely attributable to differential Sat expression. In the IR1and2 strain, however, increased ¹⁸ε and ³⁴ε probably results from increased Sat expression. The linearity of the relationship between residual sulfate δ¹⁸O_SO4 vs. δ³⁴S_SO4 suggests that these strains showed increased kinetic fractionation. These patterns are consistent with APS reduction as a rate-limiting step for sulfate reduction in this strain under these conditions. This demonstrates that variation in expressed fractionation can be imposed by perturbing fluxes in the portion of the metabolic network upstream from APS reduction, and places a minimum magnitude on the variation in fractionations that can be imposed at this step.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Author Contributions

DS, DJ, and AB designed the project and experiments. DS conducted the experiments. DS, DF, and DJ conducted isotope analyses. DS, DF, DJ, and AB analyzed the isotope data. DS and AB analyzed the geochemical and growth data. All authors contributed to the manuscript writing.

Funding

This research was funded by grants from the National Science Foundation (OCE-1536559 to AB and DJ) and NASA (13-EXO13-0082 to AB and DJ).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank J. D. Wall and G. M. Zane for the bacterial strains and their insightful comments, E. Beirne, S. Moore, and M. Suess for technical expertise, B. C. Gill for sample analysis, and W. D. Leavitt for helpful discussions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmicb.2020.529317/full#supplementary-material

References

Antler, G., Turchyn, A. V., Ono, S., Sivan, O., and Bosak, T. (2017).. Combined 34S, 33S and 18O isotope fractionation record different intracellular steps of microbial sulfate reduction. Geochim. Cosmochim. Acta. 203, 364–380 doi: 10.1016/j.gca.2017.01.015

CrossRef Full Text | Google Scholar

Antler, G., Turchyn, A. V., Rennie, V., Herut, B., and Sivan, O. (2013). Coupled sulfur and oxygen isotope insight into bacterial sulfate reduction in the natural environment. Geochim. Cosmochim. Acta. 118, 98–117. doi: 10.1016/j.gca.2013.05.005

CrossRef Full Text | Google Scholar

Baddiley, J., Buchanan, J. G., and Letters, R. (1957). Synthesis of Adenosine-5’ Sulphatophosphate. A degradation product of an intermediate enzymatic synthesis of sulphuric esters. J. Chem. Soc. 1957, 1067–1071. doi: 10.1039/jr9570001067

CrossRef Full Text | Google Scholar

Bao, H. (2006). Purifying barite for oxygen isotope measurement by dissolution and reprecipitation in a chelating solution. Anal. Chem. 78, 304–309. doi: 10.1021/ac051568z

PubMed Abstract | CrossRef Full Text | Google Scholar

Betts, R. H., and Voss, R. H. (1970). The kinetics of oxygen exchange between the sulfite ion and water. Can. J. Chem. 48, 2035–2041. doi: 10.1139/v70-339

CrossRef Full Text | Google Scholar

Bradley, A. S., Leavitt, W. D., and Johnston, D. T. (2011). Revisiting the dissimilatory sulfate reduction pathway. Geobiology 9, 446–457. doi: 10.1111/j.1472-4669.2011.00292.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bradley, A. S., Leavitt, W. D., Schmidt, M., Knoll, A. H., Girguis, P. R., and Johnston, D. T. (2016). Patterns of sulfur isotope fractionation during microbial sulfate reduction. Geobiology 14, 91–101. doi: 10.1111/gbi.12149

PubMed Abstract | CrossRef Full Text | Google Scholar

Brunner, B., and Bernasconi, S. M. (2005). A revised isotope fractionation model for dissimilatory sulfate reduction in sulfate reducing bacteria. Geochimi. Cosmochim. Acta 69, 4759–4771. doi: 10.1016/j.gca.2005.04.015

CrossRef Full Text | Google Scholar

Brunner, B., Bernasconi, S. M., Kleikemper, J., and Schroth, M. H. (2005). A model for oxygen and sulfur isotope fractionation in sulfate during bacterial sulfate reduction processes. Geochimi. Cosmochim. Acta 69, 4773–4785. doi: 10.1016/j.gca.2005.04.017

CrossRef Full Text | Google Scholar

Canfield, D. E. (2001). Isotope fractionation by natural populations of sulfate-reducing bacteria. Geochimi. Cosmochim. Acta 65, 1117–1124. doi: 10.1016/s0016-7037(00)00584-6

CrossRef Full Text | Google Scholar

Canfield, D. E. (2004). The evolution of the earth surface sulfur reservoir. Am. J. Sci. 304, 839–861. doi: 10.2475/ajs.304.10.839

PubMed Abstract | CrossRef Full Text | Google Scholar

Canfield, D. E., Farquhar, J., and Zerkle, A. L. (2010). High isotope fractionations during sulfate reduction in a low-sulfate euxinic ocean analog. Geology 38, 415–418. doi: 10.1130/g30723.1

CrossRef Full Text | Google Scholar

Chiba, H., and Sakai, H. (1985). Oxygen isotope exchange rate between dissolved sulfate and water at hydrothermal temperatures. Geochim. Cosmochim. Acta 49, 993–1000. doi: 10.1016/0016-7037(85)90314-x

CrossRef Full Text | Google Scholar

Christensen, G. A., Zane, G. M., Kazakov, A. E., Li, X., Rodlonov, D. A., Novichkov, P. S., et al. (2015). Rex (Encoded by DVU_0916) in Desulfovibrio vulgaris Hildenborough is a repressor of sulfate adenylyl transferase and is regulated by NADH. J. Bacteriol. 197, 29–39. doi: 10.1128/jb.02083-14

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, M. E., He, Q., Huang, K. H., Alm, E. J., Wan, X. F., Hazen, T. C., et al. (2006). Temporal transcriptomic analysis of Desulfovibrio vulgaris Hildenborough transitions into stationary phase during electron donor depletion. Appl. Environ. Microbiol. 72, 5578–5588. doi: 10.1128/aem.00284-06

PubMed Abstract | CrossRef Full Text | Google Scholar

Cline, J. D. (1969). Spectrophotometric determination of hydrogen sulfide in natural water. Limnol. Ocean 14, 454–458. doi: 10.4319/lo.1969.14.3.0454

CrossRef Full Text | Google Scholar

Detmers, J., Brüchert, V., Habicht, K. S., and Kuever, J. (2001). Diversity of sulfur isotope fractionations by sulfate-reducing prokaryotes. Appl. Environ. Microbiol. 67, 888–894. doi: 10.1128/aem.67.2.888-894.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Farquhar, J., Canfield, D. E., Masterson, A., Bao, H., and Johnston, D. T. (2008). Sulfur and oxygen isotope study of sulfate reduction in experiments with natural populations from Fællestrand, Denmark. Geochim. Cosmochim. Acta 72, 2805–2821. doi: 10.1016/j.gca.2008.03.013

CrossRef Full Text | Google Scholar

Farquhar, J., Johnston, D. T., Wing, B. A., Habicht, K. S., Canfield, D. E., Airieau, S., et al. (2003). Multiple sulphur isotopic interpretations of biosynthetic pathways: implications for biological signatures in the sulphur isotope record. Geobiology. 1, 27–36. doi: 10.1046/j.1472-4669.2003.00007.x

CrossRef Full Text | Google Scholar

Fike, D. A., Bradley, A. S., and Rose, C. V. (2015). Rethinking the ancient sulfur cycle. Annu. Rev. Earth Planet. Sci. 43, 593–622. doi: 10.1146/annurev-earth-060313-054802

CrossRef Full Text | Google Scholar

Fritz, P., Basharmal, G. M., Drimmie, R. J., Ibsen, J., and Qureshi, R. M. (1989). Oxygen isotope exchange between sulphate and water during bacterial reduction of sulphate. Chem. Geol. 79, 99–105. doi: 10.1016/0168-9622(89)90012-2

CrossRef Full Text | Google Scholar

Gay, S. C., Fribourgh, J. L., Donohue, P. D., Segel, I. H., and Fisher, A. J. (2009). Kinetic properties of ATP Sulfurylase and APS kinase from Thiobacillus denitrificans. Arch. Biochem. Biophys. 489, 110–117. doi: 10.1016/j.abb.2009.07.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Gyan, S., Shiohira, Y., Sato, I., Takeuchi, M., and Sato, T. (2006). Regulatory loop between redox sensing of the NADH/NAD+ ratio by Rex (YdiH) and oxidation of NADH by NADH dehydrogenase Ndh in Bacillus subtilis. J. Bacteriol. 188, 7062–7071. doi: 10.1128/jb.00601-06

PubMed Abstract | CrossRef Full Text | Google Scholar

Habicht, K. S., and Canfield, D. E. (1997). Sulfur isotope fractionation during bacterial sulfate reduction in organic-rich sediments. Geochim. Cosmochim. Acta 61, 5351–5361. doi: 10.1016/s0016-7037(97)00311-6

CrossRef Full Text | Google Scholar

Hanna, E., MacRae, I. J., Medina, D. C., Fisher, A. J., and Segel, I. H. (2002). ATP sulfurylase from the hyperthermophilic chemolithotroph Aquifex aeolicus. Arch. Biochem. Biophys. 406, 275–288. doi: 10.1016/s0003-9861(02)00428-9

CrossRef Full Text | Google Scholar

Hayes, J. M. (1983).). “Practice and principles of isotopic measurements in organic geochemistry,” in Organic Geochemistry of Contemporaneous and Ancient Sediments, ed. W. G. Meinschein (Bloomington, IN: Society of Economic Paleontologists and Mineralogists), 5.1–5.31.

Google Scholar

Hayes, J. M. (2001). Fractionation of carbon and hydrogen isotopes in biosynthetic processes. Rev. Mineral. Geochem. 43, 225–277. doi: 10.1515/9781501508745-006

CrossRef Full Text | Google Scholar

Herrmann, J., Ravilious, G. E., McKinney, S. E., Westfall, C. S., Lee, S. G., Baraniecka, P., et al. (2014). Structure and mechanism of soybean ATP Sulfurylase and the committed step in plant sulfur assimilation. J. Biol. Chem. 289, 10919–10929. doi: 10.1074/jbc.m113.540401

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnston, D. T., Farquhar, J., and Canfield, D. E. (2007). Sulfur isotope insights into microbial sulfate reduction: when microbes meet models. Geochim. Cosmochim. Acta 71, 3929–3947. doi: 10.1016/j.gca.2007.05.008

CrossRef Full Text | Google Scholar

Johnston, D. T., Farquhar, J., Wing, B. A., Kaufman, A. J., Canfield, D. E., and Habicht, K. S. (2005). Multiple sulfur isotope fractionations in biological systems: a case study with sulfate reducers and sulfur disproportionators. Am. J. Sci. 305, 645–660. doi: 10.2475/ajs.305.6-8.645

PubMed Abstract | CrossRef Full Text | Google Scholar

Jørgensen, B. B. (1982). Mineralization of organic-matter in the sea bed - the role of sulfate reduction. Nature. 296, 643–645. doi: 10.1038/296643a0

CrossRef Full Text | Google Scholar

Keller, K. L., Bender, K. S., and Wall, J. D. (2009). Development of a markerless genetic exchange system for Desulfovibrio vulgaris Hildenborough and its use in generating a strain with increased transformation efficiency. Appl. Environ. Microbiol. 75, 7682–7691. doi: 10.1128/aem.01839-09

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolter, R., Siegele, D. A., and Tormo, A. (1993). The stationary phase of the bacterial life cycle. Annu. Rev. Microbiol 47, 855–874. doi: 10.1146/annurev.mi.47.100193.004231

PubMed Abstract | CrossRef Full Text | Google Scholar

Korte, H. L., Fels, S. R., Christensen, G. A., Price, M. N., Kuehl, J. V., Zane, G. M., et al. (2014). Genetic basis for nitrate resistance in Desulfovibrio strains. Front. Microbiol. 5:153. doi: 10.3389/fmicb.2014.00153

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuehl, J. V., Price, M. N., Ray, J., Wetmore, K. M., Esquivel, Z., Kazakov, A. E., et al. (2014). Functional genomics with a comprehensive library of transposon mutants for the sulfate-reducing bacterium Desulfovibrio alaskensis G20. mBio 5, 1–13.

Google Scholar

Leavitt, W. D., Bradley, A. S., Santos, I. A. C., and Johnston, D. T. (2015). Sulfur isotope effects of dissimilatory sulfite reductase. Front. Microbiol. 6:1392. doi: 10.3389/fmicb.2015.01392

PubMed Abstract | CrossRef Full Text | Google Scholar

Leavitt, W. D., Halevy, I., Bradley, A. S., and Johnston, D. T. (2013). Influence of sulfate reduction rates on the Phanerozoic sulfur isotope record. PNAS 110, 11244–11249. doi: 10.1073/pnas.1218874110

PubMed Abstract | CrossRef Full Text | Google Scholar

Leavitt, W. D., Venceslau, S., Santos, I. A. C., Johnston, D. T., and Bradley, A. S. (2016). Fractionation of sulfur and hydrogen isotopes in Desulfovibrio vulgaris str. Hildenborough with perturbed DsrC expression. FEMS Microbiol. Lett. 363:fnw226. doi: 10.1093/femsle/fnw226

PubMed Abstract | CrossRef Full Text | Google Scholar

Lloyd, R. M. (1968). Oxygen isotope behavior in the sulfate-water system. J. Geophys. Res. 73, 6099–6110. doi: 10.1029/jb073i018p06099

CrossRef Full Text | Google Scholar

MacRae, I. J., Segel, I. H., and Fisher, A. J. (2001). Crystal structure of ATP Sulfurylase from Penicillium chrysogenum: insights into the allosteric regulation of sulfate assimilation. Biochem. 40, 6795–6804. doi: 10.1021/bi010367w

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandernack, K. W., Krouse, H. R., and Skei, J. M. (2003). A stable sulfur and oxygen isotopic investigation of sulfur cycling in an anoxic marine basin, Framvaren, Fjord, Norway. Chem. Geol. 195, 181–200. doi: 10.1016/s0009-2541(02)00394-7

CrossRef Full Text | Google Scholar

Mangalo, M., Meckenstock, R. U., Stichler, W., and Ensiedl, F. (2007). Stable isotope fractionation during bacterial sulfate reduction is controlled by reoxidation of intermediates. Geochim. Cosmochim. Acta 71, 4161–4171. doi: 10.1016/j.gca.2007.06.058

CrossRef Full Text | Google Scholar

Marietou, A., Røy, H., Jørgensen, B. B., and Kjeldsen, K. U. (2018). Sulfate transporters in dissimilatory sulfate reducing microorganisms: a comparative genomic analysis. Front. Microbiol. 9:309. doi: 10.3389/fmicb.2018.00309

PubMed Abstract | CrossRef Full Text | Google Scholar

Mills, J. V., Antler, G., and Turchyn, A. V. (2016). Geochemical evidence for cryptic sulfur cycling in salt marsh sediments. Earth Planet. Sci. Lett. 453, 23–32. doi: 10.1016/j.epsl.2016.08.001

CrossRef Full Text | Google Scholar

Navarro Llorens, J. M., Tormo, A., and Martínez-García, E. (2010). Stationary phase in gram-negative bacteria. FEMS Microbiol. Rev. 34, 476–495. doi: 10.1111/j.1574-6976.2010.00213.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Parey, K., Demmer, U., Warkentin, E., Wynen, A., ErmLer, U., and Dahl, C. (2013). Structural, biochemical, and genetic characterization of dissimilatory ATP sulfurylase from Allochromatium vinosum. PLoS One 8:e74707. doi: 10.1371/journal.pone.0074707

PubMed Abstract | CrossRef Full Text | Google Scholar

Price, M. N., Wetmore, K. M., Waters, R. J., Callaghan, M., Ray, J., Liu, H., et al. (2018). Mutant phenotypes for thousands of bacterial genes of unknown function. Nature 557, 503–509. doi: 10.1038/s41586-018-0124-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Rabus, R., Hansen, T. A., and Widdel, F. (2013). “Dissimilatory sulfate- and sulfur-reducing Prokaryotes,” in The Prokaryotes - Prokaryotic Physiology and Biochemistry, eds E. Rosenberg et al. Berlin, Germany: Springer-Verlag, 310–404.

Google Scholar

Ravcheev, D. A., Li, X., Latif, H., Zengler, K., Leyn, S. A., Korostelev, Y. D., et al. (2012). Transcriptional regulation of central carbon and energy metabolism in bacteria by redox-responsive repressor Rex. J. Bacteriol. 194, 1145–1157. doi: 10.1128/jb.06412-11

PubMed Abstract | CrossRef Full Text | Google Scholar

Ravilious, G. E., Herrmann, J., Lee, S. G., Westfall, C. S., and Jez, J. J. (2013). Kinetic mechanism of the dimeric ATP Sulfurylase from plants. Biosci. Rep. 33, 585–591.

Google Scholar

Rees, C. E. (1973). A steady-state model for sulphur isotope fractionation in bacterial reduction processes. Geochim. Cosmochim. Acta 37, 1141–1162. doi: 10.1016/0016-7037(73)90052-5

CrossRef Full Text | Google Scholar

Renosto, F., Martin, R. L., Borrell, J. L., Nelson, D. C., and Segel, I. H. (1991). ATP Sulfurylase from trophosome tissue of Riftia pachyptila (hydrothermal vent tube worm). Arch. Biochem. Biophys. 290, 66–78. doi: 10.1016/0003-9861(91)90592-7

CrossRef Full Text | Google Scholar

Renosto, F., Martin, R. L., Wailes, L. M., Daley, L. A., and Segel, I. H. (1990). Regulation of inorganic sulfate activation in filamentous fungi. J. Biol. Chem. 265, 10300–10308.

Google Scholar

Renosto, F., Seubert, P. A., and Segel, I. H. (1984). Adenosine 5’-phosphosulfate kinase from Penicillium chrysogenum. J. Biol. Chem. 259, 2113–2123.

Google Scholar

Robbins, P. W., and Lipmann, F. (1958). Separation of the two enzymatic phases in active sulfate synthesis. J. Biol. Chem. 233, 681–685.

Google Scholar

Rudnicki, M. D., Elderfield, H., and Spiro, B. (2001). Fractionation of sulfur isotopes during bacterial sulfate reduction in deep ocean sediments at elevated temperatures. Geochim. Cosmochim. Acta 65, 777–789. doi: 10.1016/s0016-7037(00)00579-2

CrossRef Full Text | Google Scholar

Santos, A. S., Venceslau, S. S., Grein, F., Leavitt, W. D., Dahl, C., Johnston, D. T., et al. (2015). A protein trisulfide couples dissimilatory sulfate reduction to energy conservation. Science 350, 1541–1545. doi: 10.1126/science.aad3558

PubMed Abstract | CrossRef Full Text | Google Scholar

Seubert, P. A., Hoang, L., Renosto, F., and Segel, I. H. (1983). ATP Sulfurylase from Penicillium chrysogenum: measurements of the true specific activity of an enzyme subject to the potent product inhibition and a reassessment of the kinetic mechanism. Arch. Biochem. Biophys. 225, 679–691. doi: 10.1016/0003-9861(83)90079-6

CrossRef Full Text | Google Scholar

Seubert, P. A., Renosto, F., Knudson, P., and Segel, I. H. (1985). Adenosinetriphosphate Sulfurylase from Penicillium chrysogenum: steady-state kinetics of the forward and reverse reactions, alternative substrate kinetics, and equilibrium binding studies. Arch. Biochem. Biophys. 240, 509–523. doi: 10.1016/0003-9861(85)90057-8

CrossRef Full Text | Google Scholar

Shen, Y., Buick, R., and Canfield, D. E. (2001). Isotopic evidence for microbial sulphate reduction in the early Archaean era. Nature. 410, 77–81. doi: 10.1038/35065071

PubMed Abstract | CrossRef Full Text | Google Scholar

Sim, M. S., Bosak, T., and Ono, S. (2011a). Large sulfur isotope fractionation does not require disproportionation. Science 1, 74–77. doi: 10.1126/science.1205103

PubMed Abstract | CrossRef Full Text | Google Scholar

Sim, M. S., Ogata, H., Lubitz, W., Adkins, J. F., Sessions, A. L., Orphan, V. J., et al. (2019). Role of APS reductase in biogeochemical sulfur isotope fractionation. Nat. Commun. 10:44.

Google Scholar

Sim, M. S., Ono, S., Donovan, K., Templer, S. P., and Bosak, T. (2011b). Effect of electron donors on the fractionation of sulfur isotopes by a marine Desulfovibrio sp. Geochim. Cosmochim. Acta 75, 4244–4259. doi: 10.1016/j.gca.2011.05.021

CrossRef Full Text | Google Scholar

Thode, G. E., Kleerekoper, H., and McElcheran, D. E. (1951). Isotope fractionation in the bacterial reduction of sulphate. Res. London. 4, 581–582.

Google Scholar

Turchyn, A. V., Brüchert, V., Lyons, T. W., Engel, G. S., Balci, N., Schrag, D. P., et al. (2010). Kinetic oxygen isotope effects during dissimilatory sulfate reduction: a combined theoretical and experimental approach. Geochim. Cosmochim. Acta 74, 2011–2024. doi: 10.1016/j.gca.2010.01.004

CrossRef Full Text | Google Scholar

Wang, R., Changxian, L., and Leyh, T. S. (1995). Allosteric regulation of the ATP Sulfurylase associated GTPase. Biochemistry 34, 490–495. doi: 10.1021/bi00002a013

PubMed Abstract | CrossRef Full Text | Google Scholar

Wankel, S. D., Bradley, A. S., Eldridge, D. L., and Johnston, D. T. (2014). Determination and application of the equilibrium oxygen isotope effect between water and sulfite. Geochim. Cosmochim. Acta 125, 694–711. doi: 10.1016/j.gca.2013.08.039

CrossRef Full Text | Google Scholar

Wing, B. A., and Halevy, I. (2011). Intracellular metabolite levels shape sulfur isotope fractionation during microbial sulfate respiration. PNAS 111, 18116–18125. doi: 10.1073/pnas.1407502111

PubMed Abstract | CrossRef Full Text | Google Scholar

Wortmann, U. G., Bernasconi, S. M., and Böttcher, M. E. (2001). Hypersulfidic deep biosphere indicates extreme sulfur isotope fractionation during single-step microbial sulfate reduction. Geology 29, 647–650. doi: 10.1130/0091-7613(2001)029<0647:hdbies>2.0.co;2

CrossRef Full Text | Google Scholar

Yu, Z., Landson, E. B., Segel, I. H., and Fisher, A. J. (2007). Crystal structure of the bifunctional ATP Sulfurylase - APS kinase from the chemolithotrophic thermophile Aquifex aeolicus. J. Mol. Biol. 365, 732–743. doi: 10.1016/j.jmb.2006.10.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Zane, G. M., Yen, H. B., and Wall, J. D. (2010). Effect of the deletion of qmoABC and the the promoter-distal gene encoding a hypothetical protein on sulfate reduction in Desulfovibrio vulgaris Hildenborough. Appl. Environ. Micro. 76, 5500–5509. doi: 10.1128/aem.00691-10

PubMed Abstract | CrossRef Full Text | Google Scholar