Contact Geometry Adaptation in Fretting Wear: A Constructive Review

Fretting is a special type of wear, which appears at the contact interface between two solids subjected to constant normal load and periodic tangential forces. Although most studies on fretting have been executed experimentally, some approaches for simulating fretting wear have also been introduced during the last decades. In particular, fretting wear analysis is concerned with the evolution of the surface profiles of the contacting bodies due to wear, and its modeling was executed using numerical, finite-element, semi-analytical, and analytical methods, including the method of dimensionality reduction. In the present review we discuss recent analytical results on fretting wear contact geometry adaptation.

1. Introduction

Contact of two machine parts established under external compressive loads and subjected to oscillating shear forces is often accompanied by friction and wear (Ciavarella and Demelio, 2001). In the case of oscillatory tangential motion of small amplitude, the particular type of wear which occurs at the sliding interface is called fretting (Vingsbo and Söderberg, 1988). Due to surface wear and damage, the shapes of the contacting bodies change and this process is called the contact geometry adaptation. Fretting phenomena, including fretting wear and accompanied variation of contact geometry, are encountered in many industrial applications, where contact parts experience oscillating small relative movements. For instance, the fretting wear characteristics of Inconel 690 U-tubes strongly influences the structural integrity of steam generators in nuclear power plants (Chai et al., 2005; Lee et al., 2009).

The problem of contact geometry adaptation in fretting wear can be formulated as a spatial-temporal contact problem with a variable contact geometry. In particular, fretting wear analysis is concerned with the evaluation of the surface profiles of the contacting bodies due to wear. Mathematical methods of solving elastic contact problems with wear were reviewed in a number of review papers by Aleksandrov and Kovalenko (1984) and Kovalenko (2001). Numerical simulation aspects of wear modeling were recently discussed in detail by Huajie and Hongzhao (2018), using the integration size as a principal characteristic (which is absent in analytical models). Recent studies on fretting wear damage in coated systems were reviewed by Ma et al. (2019). Fretting wear mechanisms and modeling were considered by Yue and Wahab (2019) and Meng et al. (2020) with a particular focus on models of debris and third-body fretting wear.

In the present review paper, we discuss different approaches to modeling fretting wear with the emphasis on analytical and semi-analytical methods, including the method of dimensionality reduction. It is to note here that though the present review is somewhat biased with the focus on the recent work of the authors, an up-to-date account of relevant studies is given as well. The aim of this review paper is to explore the theoretical ideas, analytical models and results relating to the concept of contact geometry adaptation in fretting wear to facilitate their further development (for instance, by extending the solutions of two-dimensional problems to the three-dimensional case). For this reason, the term “constructive review” is emphasized.

One of the things we shall concentrate on is the so-called wearing-in period in gross-slip fretting wear, when the initial contact state progresses into a kind of steady-state, in which the applied contact load is redistributed along the contact area in accordance with the wear equation. Under partial-slip fretting wear conditions, no such steady state exists, and, theoretically speaking, the initial contact state is expected to evolve into a kind of steady state (called limiting state), characterized by transferring the contact load primarily through the stick zone, where no wear occurs. In both cases our particular interest is focused on estimating the time needed to achieve the steady state or the limiting state.

1.1. Archard Wear Equation and Its Generalizations

The local wear is usually characterized by the linear wear rate, ẇ, where a dot denotes the derivative with respect to time. According to Archard's equation of wear (Archard, 1953), which is adopted in the majority of studies on fretting wear published to date, we have

$\begin{array}{ll}\stackrel{.}{w}=k_{w}pv,& (1)\end{array}$

where p is the contact pressure, v is the absolute value of the relative sliding velocity, and k_w is the coefficient of wear.

A mathematically straightforward generalization of Equation (1) leads to the Archard–Kragelsky wear equation

$\begin{array}{ll}\stackrel{.}{w}=K_w{p}^{\alpha }{v}^{\beta },& (2)\end{array}$

which was considered in a number of studies (Kragelsky, 1965; Meng and Ludema, 1995; Kragelsky et al., 2013). Recently, Argatov and Chai (2019a) put the Archard–Kragelsky equation into an ANN (artificial neural networks) framework, which allows to account for the dependence of the wear coefficient K_w on material parameters and operational conditions.

1.2. Reciprocal Sliding Wear

Let ΔT denote the period of tangential oscillations. Then, according to Equation (1), the linear wear resulting from one cycle will be

$\begin{array}{ll}\Delta w(x,t)=k_w{\displaystyle {\int }_t^{t+\Delta T}}p(x,\overline{t})v(x,\overline{t})d\overline{t}.& (3)\end{array}$

One simplification of the wear relation (3) is that, under certain conditions (e.g., under constant normal load and relatively small wear coefficient), the contact pressure may be assumed to not change appreciably during one cycle. In this way, Equation (3) simplifies as

$\begin{array}{ll}\Delta w(x,t)=k_{w}p(x,t){\displaystyle {\int }_t^{t+\Delta T}}v(x,\overline{t})d\overline{t}.& (4)\end{array}$

Another simplification is admissible in the gross slip regime, when the relative sliding velocity is supposed to become independent of the position of the point x on the contact interface, and thus, Equation (4) simplifies further $\Delta w(x,t)=k_{w}p(x,t)\overline{v}\Delta T$, where $\overline{v}$ is the average absolute value of sliding velocity, that is

$\begin{array}{ll}\overline{v}=\frac{1}{\Delta T}{\displaystyle {\int }_t^{t+\Delta T}}v(\overline{t})d\overline{t}.& (5)\end{array}$

Let now Δx denote the stroke of tangential oscillations. Then, Equation (5) can be rewritten as

$\begin{array}{ll}\overline{v}=\frac{2\Delta x}{\Delta T}.& (6)\end{array}$

In reciprocating sliding, it is convenient to operate both with the number of cycles, N, and the effective time variable, t, such that N = ⌊t/ΔT⌋, where ⌊x⌋ denotes the floor function (that is the largest integer less than or equal to x).

1.3. Energy Wear Equation

By introducing the sliding distance, s, such that ds = vdt, Equation (1) can be represented in the differential form as dw = k_wpds. Moreover, let μ denote the coefficient of friction. Then, introducing the frictional shear stress is q = μp, the wear increment can be further rewritten as

$\begin{array}{ll}dw={\alpha }_{V}qds,& (7)\end{array}$

where α_V is the energy wear coefficient, such that

$\begin{array}{ll}{k}_w=\mu {\alpha }_V.& (8)\end{array}$

In fretting wear, by combining Equations (3) and (7), (8), we arrive at the following wear equation (Mróz and Stupkiewicz, 1994; Fouvry et al., 1996, 2003):

$\begin{array}{ll}\Delta w(x,t)={\alpha }_V\Delta E_d(x,t).& (9)\end{array}$

Here, ΔE_d(x, t) is the frictional dissipated energy during one fretting cycle, that is

$\begin{array}{ll}\Delta E_d(x,t)={\displaystyle {\int }_s^{s+\Delta s}}q(x,t)ds.& (10)\end{array}$

While, in view of (8), the wear equations (3) and (10) are equivalent, the energy wear equation incorporates the friction mechanism and allows to account for variable coefficient of friction (Cheikh et al., 2007).

2. Fretting Wear in Gross Slip Regime

2.1. Formulation of the Model Wear Contact Problem

In the present review, we consider both two-dimensional and three-dimensional settings, highlighting their similarities and differences. The analysis of contact deformations is limited to the framework of linear elasticity and small strain analysis. While the Hertzian half-plane or half-space approximation can be employed in modeling the local stress-displacement field, in many cases, the developed analytical approach can be directly generalized to the case of layered elastic bodies with planar contact interface by utilizing the corresponding surface influence function. However, the effect of finite geometry on the wear scar profiles requires a special consideration. In what follows, the effect of local contact geometry is accounted for by means of the local gap function.

Let φ₀(x) denote the undeformed gap between the contacting surfaces as a function of Cartesian coordinate x. Then, according to Equation (1), the worn gap under plane-deformation conditions will be given by the time-continuous equation

$\begin{array}{ll}\phi (x,t)={\phi }_0(x)+k_w{\displaystyle {\int }_0^t}p(x,\overline{t})v(x,\overline{t})d\overline{t},& (11)\end{array}$

or by the time-increment equation Δφ(x, t_i+1) = k_wp(x, t_i)v(x, t_i)Δt, where Δt = t_i+1 − t₁ is the time increment. Note that, by the definition, the contact pressure p(x, t) is positive, and, therefore, the value of the integral in (11) monotonically increases with time, provided v(x, t) ≠ 0.

Another simplification which is implicitly or explicitly present in many studies on contact with wear, is to replace the problem for two contacting elastic bodies with the wear contact problem for one equivalent elastic body (whose surface influence function is composed from the surface influence functions of the given bodies) and a rigid punch, whose shape function is determined by the local gap function. Though, this is a usual approach in studying contact problems (e.g., for elastic bodies with rough surfaces), the formulation of the wear contact problem requires to consider the partition of the linear wear between the two wearing bodies, when the resulting wear scar profiles are determined.

A wear contact problem in gross slip fretting regime can be formulated as follows (Goryacheva, 1998):

$\begin{array}{ll}\frac{2}{\pi E^{*}}{\displaystyle {\int }_{-a(t)}^{a(t)}}K(x-\overline{x})p(\overline{x},t)d\overline{x}={\delta }_0(t)-\phi (x,t).& (12)\end{array}$

Here, K(x) is the normalized surface influence function, E^* is the reduced elastic modulus, δ₀(t) is the normal approach between the contacting bodies, and a(t) is the variable half-width of the contact interval.

Yet another simplifying assumption is incorporated into the governing integral equation (12), which implicitly states that the wear, while changing the contact geometry, does not significantly affect the surface influence function. In other words, small changes of the contact shape due to wear are assumed, and their influence on the contact pressure distribution is neglected. The geometry dependence of the Green functions was accounted for by Peigney (2004) using a first-order perturbation approach.

In light of (11) and (6), we have

$\begin{array}{ll}\phi (x,t)={\phi }_0(x)+\frac{2k\Delta x}{\Delta T}{\displaystyle {\int }_0^t}p(x,\overline{t})d\overline{t}.& (13)\end{array}$

Finally, in unilateral contact, the extent of the contact zone is determined by the condition of vanishing contact pressure at x = ±a(t).

It is to note here that the gross-slip regime assumes that the condition of sliding occurs at the entire contact interface. It is clear that the simple equation of wear (13) is violated at the turning points of the wear, since the sliding velocity goes through zero. This aspect, as well as the relative value of the displacement stroke, should be taken into account when considering the application of the analytical model to the analysis of experimental results.

The integral equation kernel K(x) depends on both the global shapes of the contacting bodies and the boundary conditions. Using the half-plane approximation, one obtains $K(x-\overline{x})=-ln\left[|x-\overline{x}|/H\right]-d_0$, where H is the characteristic length of the contact pair, and d₀ is the asymptotic constant (Aleksandrov et al., 1978; Argatov, 2001). It was Galin (1976) who first considered a two-dimensional wear contact problem with a constant area and applied the method of variables separation. Galin's method was further developed by Aleksandrov et al. (1978) and Komogortsev (1985) and extended to three-dimensional wear contact problems (Galin and Goriacheva, 1977; Kovalenko, 1985).

Numerical methods for solving the fretting wear contact problem of the type (12), (13) were developed in a number of studies, of which we refer especially to the papers by McColl et al. (2004), Chai et al. (2005), Mary and Fouvry (2007), and Bae et al. (2009) on finite-element simulations and (Serre et al., 2001; Sfantos and Aliabadi, 2006) on boundary-element simulations. Alternatives to finite and boundary element methods were proposed by Lee et al. (2009), using the influence function method, and (Nowell, 2010), using a quadratic programming technique. A general method for the analysis of plane contact problems for layered elastic structures in the presence of sliding wear was developed by Aleksandrov and Kovalenko (1980). Recent modeling results for coated systems, including functionally graded material (FGM) coatings, are discussed elsewhere (Ma et al., 2019).

2.2. Force-Controlled Steady-State Regime

In gross slip fretting wear, the following natural assumption makes sense (Galin, 1976; Komogortsev, 1985):

$\begin{array}{ll}p(x,t)=p_{\infty }+q(x,t),p_{\infty }=\frac{P}{2a},& (14)\end{array}$

where q(x, t) → 0 as t → ∞. In other words, the contact pressure is equalized during wear, i.e., p(x, t) → p_∞ as t → ∞. Of course, formula (14) holds true, provided the following assumption is fulfilled: both the contact force P and the contact half-width a are kept constant during the wear process.

While formula (14) has been proved to hold for a constant area of contact (Aleksandrov et al., 1978; Komogortsev, 1985), Argatov and Tato (2012) extended its applicability to the case of constant contact load P and variable contact half-width a(t), when

$\begin{array}{ll}P={\displaystyle {\int }_{-a(t)}^{a(t)}}p(\overline{x},t)d\overline{x},& (15)\end{array}$

by including into q(x, t) the boundary layers appearing near the ends of the contact interval. However, the problem of explicit constructing these boundary layers still remains open.

In the steady-state regime, the variation of contact zone depends on the contact geometry. For a paraboloidal gap ${\phi }_0(x)=x^2/(2R)$, the following differential equation holds (Argatov et al., 2011):

$\begin{array}{ll}{a}^2\frac{da}{dt}=\frac{1}{2}{k}_w\overline{v}RP.& (16)\end{array}$

Observe that Equation (16) states that in quasi steady state the contact zone evolves being governed by the wear coefficient k_w, the average sliding velocity $\overline{v}$, and the undeformed contact geometry, which is characterized by the curvature radius R. This fact was utilized by Lengiewicz and Stupkiewicz (2013) in their model of evolution of contact zone and wear accumulation, without referring to the underlying elasticity problem. The effect of elastic deformations on the wear scar profiles was accounted for by Argatov and Tato (2012). The model of fretting wear in quasi-steady-state gross-slip regime was generalized by Argatov et al. (2011) for the Archard–Kragelsky wear equation (2), which assumes a power law dependence of the wear rate on the contact pressure.

In contrast to the force-controlled loading, when the left-hand side of Equation (15) is suggested to be known, in the displacement-controlled loading, the variation of the contact approach will be specified. In such a case, due to the dissipative nature of wear accompanied by material removal, the total contact load should gradually vanish to the end of the fretting process. Such situation was analyzed by Peigney (2004), who determined the asymptotically stabilized state reached by an elastic body subjected to wear contact with a rigid indenter in the displacement-controlled cyclic loading.

2.3. Steady-State Contact Profile

Apparently, the problem of determining the worn shape in the operating state, that is the contact shape function φ_∞(x) that produces a uniform contact pressure under a constant load was first solved by Dundurs and Comninou (1980) in the case of an elastic half-space. In a more general case (12), the steady-state profile is given by

$\begin{array}{ll}{\phi }_{\infty }(x)=\frac{P}{\pi E^{*}a}\left\{{\displaystyle {\int }_{-a}^a}K(\overline{x})d\overline{x}-{\displaystyle {\int }_{-a}^a}K(x-\overline{x})d\overline{x}\right\}.& (17)\end{array}$

We note that φ_∞(0) = 0, and this explains the first term in the curly braces in (17). The steady-state solution in the case of Archard–Kragelsky model of wear (2) was obtained by Goryacheva (1998), who also studied its asymptotic stability.

Interestingly, the steady-state profile (17) is shown to be optimal, if the wear coefficient is assumed to be constant (Banichuk et al., 2010). The optimal shapes generated by wear process were evaluated by exploiting the dissipative nature of the wear process, which can be characterized, e.g., by minimization of friction dissipation power (Páczelt and Mróz, 2007). Based on the Hertzian half-space approximation, a three-dimensional computational method for determining the optimum contact geometry in fretting under the gross slip regime was developed by Gallego et al. (2006). Recently, Argatov and Chai (2019c) considered a practically important question of approximating the ideal profile (17) with a symmetric smooth profile composed of three parabolic arcs, which was introduced by Vázquez et al. (2010), exploiting the idea of compound curvature. The effect of friction is shown to result in the profile asymmetry, which depends on the direction of sliding (Argatov and Chai, 2020b).

2.4. Wearing-In Period

Any fretting wear test starts from the initial contact state, which is fully characterized by the initial contact geometry and loading conditions. The initial time interval, during which the contact pressure evolves from the initial one to the steady state pattern, is called the wearing-in period. Based on the Galin type analysis of the wear contact problem with a fixed contact zone, Argatov and Fadin (2011) have estimated the duration of the wearing-in period, T_in, as follows:

$\begin{array}{ll}{T}_{\text{in}}~\frac{a}{{\lambda }_{\text{min}}{k}_w\overline{v}{E}^{*}}.& (18)\end{array}$

Here, λ_min is the minimum characteristic value of the corresponding integral eigenvalue problem.

It is to note that the right-hand side of the relation (18) does not depend on the loading level. It is interesting that the wearing-in period in the displacement-controlled regime is about five times greater than that under the force-controlled loading (Argatov and Fadin, 2011). It is also shown (Argatov and Chai, 2020b) that the effect of friction extends the wearing-in period.

2.5. Wear of Functionally-Graded Wear-Resisting Materials

A range of wear contact profiles with variable wear resistance of a sliding punch was considered by Goryacheva (1998) in the case of the Archard–Kragelsky wear model (2) with a particular focus on the steady-state solutions. The transient wear contact problems for composite materials were considered recently using different approaches, including the method of dimensionality reduction with application to an axisymmetric heterogeneous annular cylindrical punch (Li et al., 2018) and a level-set based shape and topology optimization method with application to a Pasternak elastic foundation model (Feppon et al., 2017). By using an appropriate symmetrization of the integral equation kernel, Argatov and Chai (2019b) extended the Galin method for analyzing the transient contact pressure distribution and derived an upper estimate for the wearing-in period. Also, the effective wear coefficient was represented as

$\begin{array}{ll}{K}_{\text{eff}}(t)=K_{\text{eff}}^{\infty }+\frac{1}{P}{\displaystyle {\int }_{-a}^a}{k}_w(x)\left[p(x,t)-p_{\infty }(x)\right]dx,& (19)\end{array}$

where k_w(x) is a variable wear coefficient, p_∞(x) is the steady-state contact pressure distribution, and $K_{\text{eff}}^{\infty }$ is the steady-state value of the effective wear coefficient given by

$\begin{array}{ll}{K}_{\text{eff}}^{\infty }=2a{\left({\displaystyle {\int }_{-a}^a}\frac{dx}{k_w(x)}\right)}^{-1}.& (20)\end{array}$

Moreover, it was shown that the second term on the right-hand side of Equation (19) decreases exponentially with time during the wearing-in period, for which the following estimate was established (Argatov and Chai, 2019b):

$\begin{array}{ll}{T}_{\text{in}}\le \frac{2a}{\pi k_w^{\text{max}}\overline{v}{E}^{*}}\sqrt{{\displaystyle {\int }_{-1}^1}{\displaystyle {\int }_{-1}^1}|{{L}}_{\varkappa }(\xi ,\overline{\xi }){|}^{2}d\overline{\xi }d\xi }.& (21)\end{array}$

Here, $k_w^{\text{max}}$ is the maximum wear coefficient, and ${{L}}_{\varkappa }(\xi ,\overline{\xi })$ is the normalized integral kernel.

Interestingly, Equation (20) represents a generalization of the mixture rule of Khruschov (1974) for functionally graded wear-resisting composite materials (Friedrich, 1993; Yen and Dharan, 1996). Observe also (Argatov and Chai, 2019b) that while $K_{\text{eff}}^{\infty }$ is independent of the distribution of the wear resistance, that is independent of the distribution of the phases in a wearable multiphase material the duration of the wearing-in period T_in, in contrast, is sensitive to the phase fraction distribution.

2.6. Three-Dimensional Fretting Wear Contact Problems

The main difference between the 2D and 3D cases is a higher variability of the sliding velocity orientation that can occur in practice, so that the concept of anisotropic wear (Mróz and Stupkiewicz, 1994; Zmitrowicz, 2006) can be introduced in the spatial case. Otherwise, many features of the gross slip fretting wear are similar in the two cases. In particular, in the axisymmetric case with a constant contact radius a, Equation (14) still applies with $p_{\infty }=P/(\pi a^2)$. Also, formula (17) for the steady-state profile can be simply generalized by the appropriate choice of the integral equation kernel (which is determined by the corresponding surface influence function) and, of course, by extending the integration to the whole contact area. For the Hertzian type contact geometry with the initial gap ${\phi }_0(x)=(x_1^2+x_2^2)/(2R)$ and a variable contact area of radius a(t), the analog of Equation (16) reads as follows (Argatov, 2011):

$\begin{array}{ll}{a}^3\frac{da}{dt}=\frac{1}{\pi }{k}_w\overline{v}RP.& (22)\end{array}$

The axisymmetric model of fretting wear based on the Archard–Kragelsky wear model (2) was developed by Argatov et al. (2011), who have observed the phenomenon of the decrease of the wear coefficient due to the increase of the contact area followed by decrease of the contact pressure. Apparently, such an effect depends on the exponent α in Equation (2). In the mentioned study, it was evaluated to be greater than one.

The general Hertzian type contact with a variable elliptical contact area was considered by Argatov (2011) in application to local interwire contact under reciprocal sliding. A special consideration is required in the case of torsional fretting wear with an annular contact area, when the relative sliding velocity varies proportionally to the distance from the axis of symmetry. The analogous rotational contact problem with a sliding wear was analyzed by Galin and Goriacheva (1977), and Kovalenko (1985). The finite element method study of torsional fretting for a ball-on-flat configuration was conducted by Liu et al. (2014) under the assumption of variable coefficient of friction, whose variation due to the abrasive wear degradation is governed by the local contact history and the accumulated slip distance.

3. Fretting Wear in Partial Slip Regime

3.1. Stick Zone

Recall that the local contact of two elastically similar bodies during cyclic loading-unloading by a normal force only (i.e., at zero tangential force) is not accompanied by the relative tangential displacements at the contact interface, whereas some fretting can occur at the cyclic normal contact of dissimilar bodies. However, the tangential displacements mismatch appears for elastically similar bodies even in the case of cyclic tangential loading with constant normal load.

In a certain regime of fretting, called partial slip regime, the contact area, ω(t), which may vary in time, contains inside a stick zone, ω_*, where the contacting surfaces stick one to another, so that the contact geometry inside the stick zone remains untouched by wear, whereas wear occurs in a slip zone, where the contacting surfaces experience relative tangential movement. The theory of tangential contact with partial slip for the Hertzian geometry was developed by Cattaneo (1938) and Mindlin (1949). The 2D theory of tangential contact for elastically similar semi-infinite solids was developed by Jäger (1998) and Ciavarella (1998). The 3D Cattaneo–Mindlin model was extended by Jäger (1996) for the case of stepwise oblique loading. Further progress in its development is associated with devising the method of memory diagrams (Aleshin and Van Den Abeele, 2013; Aleshin et al., 2015). Recently, the 3D Cattaneo–Mindlin model was outlined for transversely isotropic materials by Argatov et al. (2018).

In the axisymmetric case, Jäger (1995) generalized the model of local tangential contact for two elastically similar bodies with arbitrary gap function. In the general non-axisymmetric three-dimensional case, Ciavarella (1998) introduced a simplified version of the Cattaneo–Mindlin theory (without Poisson's effect), which was recently extended for the case of transversely isotropic materials by Chai and Argatov (2018), who also applied the self-similarity solutions by Borodich (1983, 1989) to derive explicit tangential force-displacement relations in the case of self-similar gap between the contacting surfaces.

Further, Hills and Sosa (1999) reviewed analytical solutions for general elastic contact problems with partial slip, which can be used, for instance, in estimating frictional energy and the local wear rate in the initial stage of fretting. Analytical aspects of fretting fatigue damage were considered by Ciavarella and Demelio (2001) with application to dovetail joints. Numerical method for partial-slip frictional contact problems have been developed in a number of studies (Chen and Wang, 2008; Wang et al., 2013).

Let φ(x₁, x₂) be the gap between the surfaces of two elastically similar transversely isotropic semi-infinite bodies that do not exhibit the effect of coupling between the distributions of shearing contact tractions (in the case of identical materials this assumption implies the zero Poisson's ratio, see, e.g., Ciavarella, 1998). In many cases it may be assumed that the gap is described by a homogeneous function of degree d, such that

$\begin{array}{ll}\phi (c{x}_1,c{x}_2)=c^d\phi (x_1,x_2),& (23)\end{array}$

where c is an arbitrary positive constant.

Let also l and l^* be the characteristic sizes of the contact area ω and the stick zone ω_*, respectively. Then, the following relations hold between the relative size of the stick zone, the ratio of the tangential to the normal contact force, and the ratio of the tangential to the normal displacement (Chai and Argatov, 2018):

$\begin{array}{ll}\frac{l^{*}}{l}={\left(1-\frac{F_1}{\mu F_3}\right)}^{1/(d+1)},\frac{l^{*}}{l}={\left(1-\frac{M_1}{M_3}\frac{{\delta }_1}{\mu {\delta }_3}\right)}^{1/d}.& (24)\end{array}$

Here, M₁ and M₃ are effective elastic moduli. The Cattaneo–Mindlin model is recovered from Equation (24) for d = 2.

3.2. MDR-Based Approach

It is well-known (De Mul et al., 1986) that for a wide class of contact geometries, the Hertzian half-space analysis of local contact gives reliable results. The method of dimensionality reduction (MDR) developed by Popov and Heß (2015), and their collaborators, combines the axisymmetric Hertz theory of normal contact and the axisymmetric Cattaneo–Mindlin theory of tangential contact into a unified modeling framework by transforming a given 3D contact problem for two elastically similar solids into one-dimensional contact problem for an equivalent rigid punch and the Popov foundation, which is a linearly-elastic spring-like foundation that possesses both normal and tangential stiffnesses. The relation between the gap function φ(r, t) and the equivalent 1D profile g(x, t) represents the direct mapping rule from the original 3D contact problem into the 1D equivalent contact problem. Since the Popov foundation is spring-like, its normal reaction is given by $q_z(x,t)=E^{*}\left(\delta (t)-g(x,t)\right)$, where |x| ≤ a(t) and a(t) is a root of the equation g(a, t) = δ(t). The integration of the 1D normal contact reaction over the contact interval (−a(t), a(t)) yields the total normal force, F₃ (Note that in the displacement controlled mode, the contact approach δ(t) is assumed to be known).

The Popov foundation can be discretized by introducing a discretization step Δx, so that the normal and tangential stiffnesses of every individual spring element will be $\Delta k_z=E^{*}\Delta x$ and $\Delta k_x=G^{*}\Delta x$, respectively, where G^* is the effective shear modulus. Correspondingly, if an individual elastic spring element with a coordinate x receives normal, u_z(x, t), and tangential, u_x(x, t), displacements, the values of normal and tangential reaction forces, respectively, will be Δf_N(x, t) = u_z(x, t)Δk_z and Δf_T(x, t) = u_x(x, t)Δk_x (with compression-positive sign convention taken into account).

In a stick zone, the tangential displacement u_x(x, t) is determined by the punch's tangential displacement, $u_x^{(0)}(t)$, whereas in a slip zone Δf_T(x, t) = ±μΔf_N(x, t), as it is prescribed by Coulomb's law, where μ is the coefficient of friction. It is suggested (Dimaki et al., 2014, 2016) to consider the fretting wear as an incremental process, such that $\Delta u_x^{(0)}(t)=u_x^{(0)}(t+\Delta t)-u_x^{(0)}(t)$ is the tangential displacement increment of the 1D equivalent punch, which exactly corresponds to the increment of the relative tangential displacement of the contacting solids. According to the Archard wear equation (1), the linear change of the 3D profile is given as follows (Dimaki et al., 2016):

$\begin{array}{ll}\Delta \phi (r,t)=k_{w}p(r,t)\left(\Delta u_x^{(0)}(t)-\Delta u_x^{(3D)}(r,t)\right).& (25)\end{array}$

Here, $u_x^{(3D)}(r,t)$ and $\Delta u_x^{(3D)}(r,t)$ are the relative tangential displacement at the contact interface and its increment.

Thus, the numerical implementation of the MDR-based approach using Equation (25) will require the application of the inverse mapping (from the 1D contact problem to the 3D contact problem) for evaluating $u_x^{(3D)}(r,t)$ and the normal contact pressure p(r, t). The corresponding numerical procedures have been developed for both the gross-slip (Dimaki et al., 2016) and partial-slip (Dimaki et al., 2014) regimes.

3.3. Limiting Profile

Evidently, in the partial slip fretting wear, by the definition, there is a stick zone which remains untouched by wear for the entire periodic loading process. For instance, in the force-controlled mode with a constant normal contact load and a constant amplitude sinusoidal tangential force, the effect of wear on the contacting surfaces will exhibit itself in an increase of the contact approach as well as in an increase of the contact area. However, as it was observed by Ciavarella and Hills (1999), this process eventually leads to some limiting contact geometry that is characterized by the absence of wear outside the stick zone. In the case of the Archard wear model, the latter means that the contact pressure vanishes in the final slip zone.

In the axisymmetric case under displacement-controlled loading (when δ = const), the solution for the limiting profile can be easily obtained in terms of the limiting profile for the equivalent punch as follows (Popov, 2014):

$\begin{array}{ll}{g}_{\infty }(x)=\{\begin{array}{l}{g}_0(x),\left|x\right|\le c,\\ \delta ,c<\left|x\right|\le a_{\infty }.\end{array}& (26)\end{array}$

Here, g₀(x) is the initial equivalent profile, c is the radius of the stick zone, which depends on the tangential displacement amplitude $u_x^{(0)}$, δ is the contact approach, a_∞ is the limiting radius of the contact area, which is determined by the equation φ_∞(a) = φ₀(a). Finally, the function φ_∞(r) itself is determined by the inverse transform applied to g_∞(x).

Of course, formula (26) can be easily extended to the case of force-controlled loading by replacing δ with δ_∞, where δ_∞ is the limiting contact approach, and expressing c in terms of the normal and tangential contact loads F₃ and F₁, e.g., using Equation (24). However, it is instructive to distinguish the two cases, especially since it makes sense in the 3D case.

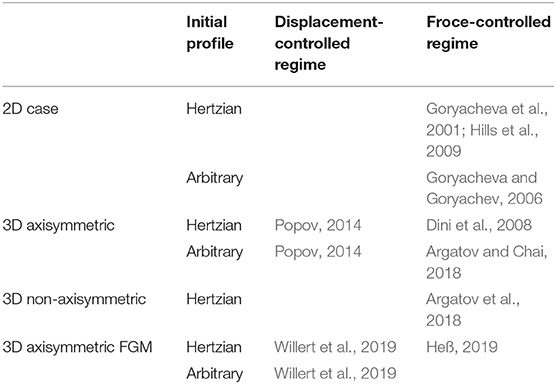
Table 1 shows the state of the art of the analysis of the final (limiting or asymptotic) contact geometry. We note that the solutions of Heß (2019) and Willert et al. (2019) were obtained for the case of power-law graded materials with Young's modulus varying with depth as $E(z)=E_0{(z/z_0)}^k$, where k ∈ (−1, 1).

TABLE 1

Table 1. Limiting shapes of profiles in fretting wear.

The MDR-based approach (Popov, 2014) was generalized by Chai and Popov (2016) for fretting wear in an adhesive contact in the Dugdale approximation when the adhesive (attractive) stress outside the contact area is assumed to be constant up to some critical distance and vanishing beyond this range. Recently, the analytical approach developed by Popov (2014) was extended by Dmitriev et al. (2016) and Mao et al. (2016) (see also Li, 2016) to a dual-mode fretting under the influence of superimposed normal oscillations (with amplitude $\Delta u_z^0$ and frequency ω_z) and tangential oscillations (with amplitude $\Delta u_x^0$ and frequency ω_x). It is interesting that Dmitriev et al. (2016) also provided experimental evidence for the correctness of the theoretically predicted limiting shape. We note also that recent experimental aspects of fretting wear were discussed in an extensive review by Meng et al. (2020).

3.4. Wear Accumulation

A number of numerical methods have been devised for simulating the contact geometry adaptation during fretting wear in the partial slip regime (Gallego and Nelias, 2007; Dimaki et al., 2014; Wang et al., 2015; Cardoso et al., 2019), when both the contact profiles (outside the stick zone) and the contact pressure distribution evolve in relation to each other.

Interestingly, a special focus on modeling of the evolution of the worn volume, V, was not shown until recently (Kasarekar et al., 2007). A simple mathematical model of wear accumulation in the case of initial Hertzian contact was developed by Chai and Argatov (2019) based on the dissipation energy model for the volume wear rate (Fouvry et al., 2003). The following one fitting parameter formula was suggested for the non-monotonic variation of the volume wear rate:

$\begin{array}{ll}\frac{dV}{dN}=w_0\left(1+{\beta }_1\frac{N}{N_1}\right)exp\left(-\frac{N}{N_1}\right).& (27)\end{array}$

Here, w₀ is the initial volume wear rate, which can be evaluated using the Cattaneo–Mindlin theory (Johnson, 1955), N is the number of cycles, N₁, is an auxiliary parameter, which is related to the total worn volume V_∞ = w₀(1 + β₁)N₁, and β₁ is the only fitting parameter.

The analytical model (27) implies that the wearing-in period is proportional to N₁, which, in turn, is estimated as

$\begin{array}{ll}{N}_1~\frac{G^{*}}{{(E^{*})}^{5/3}}\frac{R^{2/3}}{\mu k_w{P}^{1/3}}{n}_1(\chi ),& (28)\end{array}$

where χ = c/a₀ is the relative stick-zone radius, and a₀ is the initial (Hertzian) contact radius. In contrast to Equation (18), formula (28) shows that the duration of the wearing-in period (measured in number of cycles) in partial-slip fretting wear depends on the load level.

4. Discussion and Conclusions

The obtained results for wearing-in period (18), (21), and (28) merit comment. First, as we might intuitively expect, the larger the initial contact zone, the larger the wearing-in period. Second, as it could be foreseen from the physical dimension of the wear coefficient, the duration of the wearing-in period is inversely proportional to the characteristic value of the coefficient of wear. Third, in the gross-slip and partial-slip regimes, the wearing-in period is inversely proportional to E^* and (E^*)^2/3, respectively, so that the elasticity effect weakens in the second case.

4.1. Limitations of the Analytical Approach

It goes without saying that analytical methods are not so flexible as numerical ones, especially in applications to specific engineering problems. In contact mechanics, the success of analytical approach is critically dependent on the possibility to approximate the surface influence function, which, in turn, strongly depends on the contact geometry. The phenomenon of wear manifests itself in the variation of the latter, and, generally speaking, the main limitation of the current state-of-the-art analytical techniques is in their inability to effectively deal with varying geometry due to wear loss.

Perhaps, another reason for the slow progress in solving transient wear contact problems is the difficulty which may arise with the introduction of non-linear equations of wear. However, a further rapid advance can be achieved, for instance, in estimating the duration of wearing-in period, provided the problem formulation admits the existence a steady-state regime.

4.2. Open Problems

First, observe that Table 1 has a few empty cells, which indicate a number of still unsolved problems on limiting shapes of profiles in fretting wear. The limiting profile problem formulation assumes that in the limiting state the contact pressure vanishes outside of the stick zone. It makes sense to investigate whether a threshold model of wear, which assumes no wear below certain level of contact pressures, is suitable for describing the limiting state in practical fretting problems. Second, we point out that the analytical solutions (16) and (22) were obtained for the Hertzian local gap, though the method with which they were derived allows such generalizations. By the way, it is still interesting to analyze the boundary-layer problem in the wear contact problem with variable contact zone. Third, it is to note here that the effective wear coefficient (20) for functionally-graded wear-resisting materials was evaluated under the simplifying assumption of homogeneous elastic properties, which is implicitly or explicitly present in a majority of studies of wear contact problems for composite materials. Further, as it was already mentioned in section 1.3, the energy wear equation allows to account for variable coefficient of friction, which can be done in a straightforward manner in the gross slip regime.

It should be noted that the wearing-in period in gross-slip fretting wear is associated with the redistribution of the macroscopic contact pressure from the initial pattern, which is caused by the intact contact geometry (e.g., the Hertzian contact pattern in ball-on-plate contact), to an approximately uniform distribution, which reproduces the steady-state shape profile. In the case of non-conforming contact, there is still uncertainty regarding the experimental relation between the wearing-in period and the running-in period, which is primarily associated with the evolution of surface topography and shows the exponential evolution of the wear rate as well (Zhang et al., 2018). It is to note here that the recently developed artificial neural network modeling framework (Argatov and Chai, 2020a) can be utilized in analysis of experimental studies of wearing-in period and the so-called true wear coefficient. It is also apparently an open question as to whether the duration of the wearing-in period in periodic contact is longer than that in the wear contact problem for a single contact.

It was shown (Argatov and Chai, 2020b) that the eigenvalue problem associated with the wear contact problem with friction, generally speaking, may possess the complex-valued spectrum, and therefore, the contact pressure is predicted to approach the steady state exponentially decaying and oscillating. Such an oscillating behavior of the contact pressure during the wearing-in period, if exists, would be experimentally observed for large values of the friction coefficient.

4.3. Directions for Future Research

Based on the above review, one can suggest that further progress is expected in studying transient wear contact problems for functionally-graded wear-resisting materials. Also, further attention needs to be paid to the optimization problems in fretting wear, while combining different strategies for optimizing contacting parts, including geometrical (shape optimization) and material grading.

Observe that Archard's equation of wear or the work rate model are usually adopted in the majority of analytical studies to date. Further progress is needed in extending the results obtained for these linear wear models to other models, including non-linear, like the Archard–Kragelsky equation, or models which account for the effect of debris formation and third-body fretting wear.

Further, it is well-known and practically important that the Archard equation (1) as well as the Archard–Kragelsky equation (2) treat wear as a local process. In this respect, it would of interest to investigate what role the non-local nature of wear damage plays in the partial lip regime of fretting, especially near the boundary of the stick zone.

Lastly, caution is urged when the simple analytical models are applied for analyzing practical problems. For instance, one may argue that the analytical solutions for limiting profiles outlined in Table 1 do not predict the final state that is practically achieved in partial-slip fretting, since they assume complete removal of worn material. Nevertheless, the limiting shape profiles are useful, as they allow to upper estimate the differences in contact behavior that can be observed both in practice and experiment (Dini et al., 2008). An important asset of the developed analytical solutions is their explicit dependence on the model parameters, which can be effectively used for solving design and optimization problems.

Author Contributions

IA: methodology, formal analysis, and writing—original draft preparation. YC: conceptualization, methodology, and writing—reviewing and editing. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. NRF-2017M2B2A9072449).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aleksandrov, V. M., Galin, L. A., and Piriev, N. P. (1978). A plane contact problem for an elastic layer of considerable thickness in the presence of wear [in Russian]. Mech. Solids 4, 60–67.

Aleksandrov, V. M., and Kovalenko, E. V. (1980). Plane contact problems of the theory of elasticity for nonclassical regions in the presence of wear. J. Appl. Mech. Tech. Phys. 21, 421–427. doi: 10.1007/BF00920786

CrossRef Full Text | Google Scholar

Aleksandrov, V. M., and Kovalenko, E. V. (1984). “Mathematical methods in contact problems with wear,” in Nonlinear Models and Problems of Mechanics of Deformable Solids, ed K. V. Frolov (Moscow: Nauka), 77–89.

Aleshin, V., Matar, O. B., and Van Den Abeele, K. (2015). Method of memory diagrams for mechanical frictional contacts subject to arbitrary 2D loading. Int. J. Solids Struct. 60, 84–95. doi: 10.1016/j.ijsolstr.2015.02.016

CrossRef Full Text | Google Scholar

Aleshin, V., and Van Den Abeele, K. (2013). General solution to the Hertz-Mindlin problem via Preisach formalism. Int. J. Nonlinear Mech. 49, 15–30. doi: 10.1016/j.ijnonlinmec.2012.09.003

CrossRef Full Text | Google Scholar

Archard, J. F. (1953). Contact and rubbing of flat surfaces. J. Appl. Phys. 24, 981–988. doi: 10.1063/1.1721448

CrossRef Full Text | Google Scholar

Argatov, I., and Tato, W. (2012). Asymptotic modeling of reciprocating sliding wear-comparison with finite-element simulations. Eur. J. Mech. A Solids 34, 1–11. doi: 10.1016/j.euromechsol.2011.11.008

CrossRef Full Text | Google Scholar

Argatov, I. I. (2001). Solution of the plane Hertz problem. J. Appl. Mech. Tech. Phys. 42, 1064–1072. doi: 10.1023/A:1012534432055

CrossRef Full Text | Google Scholar

Argatov, I. I. (2011). Asymptotic modeling of reciprocating sliding wear with application to local interwire contact. Wear 271, 1147–1155. doi: 10.1016/j.wear.2011.05.028

CrossRef Full Text | Google Scholar

Argatov, I. I., Bae, J. W., and Chai, Y. S. (2018). The limiting shape of the transversely isotropic elastically similar solids in fretting. Int. J. Appl. Mech. 10:1850089. doi: 10.1142/S1758825118500898

CrossRef Full Text | Google Scholar

Argatov, I. I., and Chai, Y. S. (2018). Limiting shape of profiles in fretting wear. Tribol. Int. 125, 95–99. doi: 10.1016/j.triboint.2018.04.026

CrossRef Full Text | Google Scholar

Argatov, I. I., and Chai, Y. S. (2019a). An artificial neural network supported regression model for wear rate. Tribol. Int. 138, 211–214. doi: 10.1016/j.triboint.2019.05.040

CrossRef Full Text | Google Scholar

Argatov, I. I., and Chai, Y. S. (2019b). Effective wear coefficient and wearing-in period for a functionally graded wear-resisting punch. Acta Mech. 230, 2295–2307. doi: 10.1007/s00707-019-2366-9

CrossRef Full Text | Google Scholar

Argatov, I. I., and Chai, Y. S. (2019c). A note on optimal design of contact geometry in fretting wear. Int. J. Mech. Mater. Design 16, 415–422. doi: 10.1007/s10999-019-09467-9

CrossRef Full Text | Google Scholar

Argatov, I. I., and Chai, Y. S. (2020a). Artificial neural network modeling of sliding wear. J. Proc. Instit. Mech. Eng. J. doi: 10.1177/1350650120925582. [Epub ahead of print].

CrossRef Full Text | Google Scholar

Argatov, I. I., and Chai, Y. S. (2020b). Wear contact problem with friction: Steady-state regime and wearing-in period. Int. J. Solids Struct. 193–194:213–221. doi: 10.1016/j.ijsolstr.2020.02.019

CrossRef Full Text | Google Scholar

Argatov, I. I., and Fadin, Y. A. (2011). A macro-scale approximation for the running-in period. Tribol. Lett. 42, 311–317. doi: 10.1007/s11249-011-9775-9

CrossRef Full Text | Google Scholar

Argatov, I. I., Gómez, X., Tato, W., and Urchegui, M. A. (2011). Wear evolution in a stranded rope under cyclic bending: Implications to fatigue life estimation. Wear 271, 2857–2867. doi: 10.1016/j.wear.2011.05.045

CrossRef Full Text | Google Scholar

Bae, J. W., Lee, C. Y., and Chai, Y. S. (2009). Three dimensional fretting wear analysis by finite element substructure method. Int. J. Precis. Eng. Manufact. 10, 63–69. doi: 10.1007/s12541-009-0072-6

CrossRef Full Text | Google Scholar

Banichuk, N. V., Ragnedda, F., and Serra, M. (2010). Some optimization problems for bodies in quasi-steady state wear. Mech. Based Design Struct. Mach. 38, 430–439. doi: 10.1080/15397734.2010.483574

CrossRef Full Text | Google Scholar

Borodich, F. M. (1983). Similarity in the problem of contact between elastic bodies. J. Appl. Math. Mech. 47, 440–442. doi: 10.1016/0021-8928(83)90077-1

CrossRef Full Text | Google Scholar

Borodich, F. M. (1989). Hertz contact problems for an anisotropic physically nonlinear elastic medium. Strength Mater. 21, 1668–1676. doi: 10.1007/BF01533408

CrossRef Full Text | Google Scholar

Cardoso, R. A., Doca, T., Néron, D., Pommier, S., and Araújo, J. A. (2019). Wear numerical assessment for partial slip fretting fatigue conditions. Tribol. Int. 136, 508–523. doi: 10.1016/j.triboint.2019.03.074

CrossRef Full Text | Google Scholar

Cattaneo, C. (1938). Sul contatto di due corpi elastici: distribuzione locale degli sforzi. Rendiconti dell'Accademia nazionale dei Lincei 27, 342–348, 434-436, 474-478.

Chai, Y., Lee, C., Bae, J., Lee, S., and Hwang, J. (2005). Finite element analysis of fretting wear problems in consideration of frictional contact. Key Eng. Mater. 297–300:1406–1411. doi: 10.4028/www.scientific.net/KEM.297-300.1406

CrossRef Full Text | Google Scholar

Chai, Y. S., and Argatov, I. I. (2018). Local tangential contact of elastically similar, transversely isotropic elastic bodies. Meccanica 53, 3137–3143. doi: 10.1007/s11012-018-0870-y

CrossRef Full Text | Google Scholar

Chai, Y. S., and Argatov, I. I. (2019). Fretting wear accumulation in partial-slip circular Hertzian contact. Mech. Res. Commun. 96, 45–48. doi: 10.1016/j.mechrescom.2019.02.005

CrossRef Full Text | Google Scholar

Chai, Y. S., and Popov, V. L. (2016). Limiting shape due to fretting wear in an adhesive contact in Dugdale approximation. Phys. Mesomech. 19, 378–381. doi: 10.1134/S1029959916040044

CrossRef Full Text | Google Scholar

Cheikh, M., Quilici, S., and Cailletaud, G. (2007). Presentation of KI-COF, a phenomenological model of variable friction in fretting contact. Wear 262, 914–924. doi: 10.1016/j.wear.2006.10.001

CrossRef Full Text | Google Scholar

Chen, W. W., and Wang, Q. J. (2008). A numerical model for the point contact of dissimilar materials considering tangential tractions. Mech. Mater. 40, 936–948. doi: 10.1016/j.mechmat.2008.06.002

CrossRef Full Text | Google Scholar

Ciavarella, M. (1998). Tangential loading of general 3D contacts. ASME J. Appl. Mech. 65, 998–1003. doi: 10.1115/1.2791944

CrossRef Full Text | Google Scholar

Ciavarella, M., and Demelio, G. (2001). A review of analytical aspects of fretting fatigue, with extension to damage parameters, and application to dovetail joints. Int. J. Solids Struct. 38, 1791–1811. doi: 10.1016/S0020-7683(00)00136-0

CrossRef Full Text | Google Scholar

Ciavarella, M., and Hills, D. A. (1999). Brief note: Some observations on oscillating tangential forces and wear in general plane contacts. Eur. J. Mech. A Solids 18, 491–497. doi: 10.1016/S0997-7538(99)00117-5

CrossRef Full Text | Google Scholar

De Mul, J. M., Kalker, J. J., and Fredriksson, B. (1986). The contact between arbitrarily curved bodies of finite dimensions. J. Tribol. 108, 140–148. doi: 10.1115/1.3261134

CrossRef Full Text | Google Scholar

Dimaki, A. V., Dmitriev, A. I., Chai, Y. S., and Popov, V. L. (2014). Rapid simulation procedure for fretting wear on the basis of the method of dimensionality reduction. Int. J. Solids Struct. 51, 4215–4220. doi: 10.1016/j.ijsolstr.2014.08.003

CrossRef Full Text | Google Scholar

Dimaki, A. V., Dmitriev, A. I., Menga, N., Papangelo, A., Ciavarella, M., and Popov, V. L. (2016). Fast high-resolution simulation of the gross slip wear of axially symmetric contacts. Tribol. Trans. 59, 189–194. doi: 10.1080/10402004.2015.1065529

CrossRef Full Text | Google Scholar

Dini, D., Sackfield, A., and Hills, D. A. (2008). An axi-symmetric Hertzian contact subject to cyclic shear and severe wear. Wear 265, 1918–1922. doi: 10.1016/j.wear.2008.04.031

CrossRef Full Text | Google Scholar

Dmitriev, A. I., Voll, L. B., Psakhie, S. G., and Popov, V. L. (2016). Universal limiting shape of worn profile under multiple-mode fretting conditions: theory and experimental evidence. Sci. Rep. 6:23231. doi: 10.1038/srep23231

PubMed Abstract | CrossRef Full Text | Google Scholar

Dundurs, J., and Comninou, M. (1980). Shape of a worn slider. Wear 62, 419–424. doi: 10.1016/0043-1648(80)90183-0

CrossRef Full Text | Google Scholar

Feppon, F., Michailidis, G., Sidebottom, M. A., Allaire, G., Krick, B. A., and Vermaak, N. (2017). Introducing a level-set based shape and topology optimization method for the wear of composite materials with geometric constraints. Struct. Multidiscipl. Optimizat. 55, 547–568. doi: 10.1007/s00158-016-1512-4

CrossRef Full Text | Google Scholar

Fouvry, S., Kapsa, P., and Vincent, L. (1996). Quantification of fretting damage. Wear 200, 186–205. doi: 10.1016/S0043-1648(96)07306-1

CrossRef Full Text | Google Scholar

Fouvry, S., Liskiewicz, T., Kapsa, P., Hannel, S., and Sauger, E. (2003). An energy description of wear mechanisms and its applications to oscillating sliding contacts. Wear 255, 287–298. doi: 10.1016/S0043-1648(03)00117-0

CrossRef Full Text | Google Scholar

Friedrich, K. (1993). “Wear models for multiphase materials and synergistic effects in polymeric hybrid composites,” in in Advances in Composite Tribology, Vol. 8 of Composite Materials Series, ed K. Friedrich (Amsterdam: Elsevier), 209–273. doi: 10.1016/B978-0-444-89079-5.50010-6

CrossRef Full Text | Google Scholar

Galin, L. A. (1976). Contact problems of the theory of elasticity in the presence of wear. J. Appl. Math. Mech. 40, 931–936. doi: 10.1016/0021-8928(76)90132-5

CrossRef Full Text | Google Scholar

Galin, L. A., and Goriacheva, I. G. (1977). Axisymmetric contact problem of the theory of elasticity in the presence of wear. J. Appl. Math. Mech. 41, 826–831. doi: 10.1016/0021-8928(77)90164-2

CrossRef Full Text | Google Scholar

Gallego, L., and Nelias, D. (2007). Modeling of fretting wear under gross slip and partial slip conditions. J. Tribol. 129, 528–535. doi: 10.1115/1.2736436

CrossRef Full Text | Google Scholar

Gallego, L., Nélias, D., and Jacq, C. (2006). A comprehensive method to predict wear and to define the optimum geometry of fretting surfaces. J. Tribol. 128, 476–485. doi: 10.1115/1.2194917

CrossRef Full Text | Google Scholar

Goryacheva, I. G. (1998). Contact Mechanics in Tribology. Dordrecht: Kluwer. doi: 10.1007/978-94-015-9048-8

CrossRef Full Text | Google Scholar

Goryacheva, I. G., and Goryachev, A. P. (2006). The wear contact problem with partial slippage. J. Appl. Math. Mech. 70, 934–944. doi: 10.1016/j.jappmathmech.2007.01.010

CrossRef Full Text | Google Scholar

Goryacheva, I. G., Rajeev, R. T., and Farris, T. N. (2001). Wear in partial slip contact. J. Tribol. 123, 848–856. doi: 10.1115/1.1338476

CrossRef Full Text | Google Scholar

Heß, M. (2019). A study on gross slip and fretting wear of contacts involving a power-law graded elastic half-space. Fact. Univers. Ser. Mech. Eng. 17, 47–64. doi: 10.22190/FUME190121010H

CrossRef Full Text | Google Scholar

Hills, D. A., Sackfield, A., and Paynter, R. J. H. (2009). Simulation of fretting wear in halfplane geometries: part I-the solution for long term wear. J. Tribol. 131:031401. doi: 10.1115/1.3118785

CrossRef Full Text | Google Scholar

Hills, D. A., and Sosa, G. U. (1999). Origins of partial slip in fretting-a review of known and potential solutions. J. Strain Anal. Eng. Design 34, 175–181. doi: 10.1243/0309324991513731

CrossRef Full Text | Google Scholar

Huajie, L., and Hongzhao, L. (2018). “An overview of the numerical simulation wear models in mechanical systems,” in 2018 IEEE 9th International Conference on Mechanical and Intelligent Manufacturing Technologies (ICMIMT) (IEEE), 105–109. doi: 10.1109/ICMIMT.2018.8340430

CrossRef Full Text | Google Scholar

Jäger, J. (1995). Axi-symmetric bodies of equal material in contact under torsion or shift. Arch. Appl. Mech. 65, 478–487. doi: 10.1007/BF00835661

CrossRef Full Text | Google Scholar

Jäger, J. (1996). Stepwise loading of half-spaces in elliptical contact. ASME J. Appl. Mech. 63, 766–773. doi: 10.1115/1.2823361

CrossRef Full Text | Google Scholar

Jäger, J. (1998). A new principle in contact mechanics. J. Tribol. 120, 677–684. doi: 10.1115/1.2833765

CrossRef Full Text | Google Scholar

Johnson, K. (1955). Surface interaction between elastically loaded bodies under tangential forces. Proc. R. Soc. Lond. Ser. A 230, 531–548. doi: 10.1098/rspa.1955.0149

CrossRef Full Text | Google Scholar

Kasarekar, A. T., Bolander, N. W., Sadeghi, F., and Tseregounis, S. (2007). Modeling of fretting wear evolution in rough circular contacts in partial slip. Int. J. Mech. Sci. 49, 690–703. doi: 10.1016/j.ijmecsci.2006.08.021

CrossRef Full Text | Google Scholar

Khruschov, M. M. (1974). Principles of abrasive wear. Wear 28, 69–88. doi: 10.1016/0043-1648(74)90102-1

CrossRef Full Text | Google Scholar

Komogortsev, V. F. (1985). Contact between a moving stamp and an elastic half-plane when there is wear. J. Appl. Math. Mech. 49, 243–246. doi: 10.1016/0021-8928(85)90110-8

CrossRef Full Text | Google Scholar

Kovalenko, E. V. (1985). Study of the axisymmetric contact problem of the wear of a pair consisting of an annular stamp and a rough half-space. J. Appl. Math. Mech. 49, 641–647. doi: 10.1016/0021-8928(85)90085-1

CrossRef Full Text | Google Scholar

Kovalenko, E. V. (2001). “Contact problems for coated solids [in Russian],” in Mechanics of Contact Interactions, eds I. I. Vorovich and V. M. Aleksandrov (Moscow: Fizmatli), 459–475.

Kragelsky, I. V. (1965). Friction and Wear. London: Butterworths.

Google Scholar

Kragelsky, I. V., Dobychin, M. N., and Kombalov, V. S. (2013). Friction and Wear: Calculation Methods. Oxford: Pergamon Press.

Google Scholar

Lee, C. Y., Tian, L. S., Bae, J. W., and Chai, Y. S. (2009). Application of influence function method on the fretting wear of tube-to-plate contact. Tribol. Int. 42, 951–957. doi: 10.1016/j.triboint.2009.01.005

CrossRef Full Text | Google Scholar

Lengiewicz, J., and Stupkiewicz, S. (2013). Efficient model of evolution of wear in quasi-steady-state sliding contacts. Wear 303, 611–621. doi: 10.1016/j.wear.2013.03.051

CrossRef Full Text | Google Scholar

Li, Q. (2016). Limiting profile of axisymmetric indenter due to the initially displaced dual-motion fretting wear. Fact. Univers. Ser. Mech. Eng. 14, 55–61. doi: 10.22190/FUME1601055L

CrossRef Full Text | Google Scholar

Li, Q., Forsbach, F., Schuster, M., Pielsticker, D., and Popov, V. L. (2018). Wear analysis of a heterogeneous annular cylinder. Lubricants 6:28. doi: 10.3390/lubricants6010028

CrossRef Full Text | Google Scholar

Liu, J., Shen, H. M., and Yang, Y. R. (2014). Finite element implementation of a varied friction model applied to torsional fretting wear. Wear 314, 220–227. doi: 10.1016/j.wear.2014.01.006

CrossRef Full Text | Google Scholar

Ma, L., Eom, K., Geringer, J., Jun, T.-S., and Kim, K. (2019). Literature review on fretting wear and contact mechanics of tribological coatings. Coatings 9:501. doi: 10.3390/coatings9080501

CrossRef Full Text | Google Scholar

Mao, X., Liu, W., Ni, Y., and Popov, V. L. (2016). Limiting shape of profile due to dual-mode fretting wear in contact with an elastomer. Proc. Instit. Mech. Eng. C J. Mech. Eng. Sci. 230, 1417–1423. doi: 10.1177/0954406215619450

CrossRef Full Text | Google Scholar

Mary, C., and Fouvry, S. (2007). Numerical prediction of fretting contact durability using energy wear approach: optimisation of finite-element model. Wear 263, 444–450. doi: 10.1016/j.wear.2007.01.116

CrossRef Full Text | Google Scholar

McColl, I. R., Ding, J., and Leen, S. B. (2004). Finite element simulation and experimental validation of fretting wear. Wear 256, 1114–1127. doi: 10.1016/j.wear.2003.07.001

CrossRef Full Text | Google Scholar

Meng, H. C., and Ludema, K. C. (1995). Wear models and predictive equations: their form and content. Wear 181, 443–457. doi: 10.1016/0043-1648(95)90158-2

CrossRef Full Text | Google Scholar

Meng, Y., Xu, J., Jin, Z., Prakash, B., and Hu, Y. (2020). A review of recent advances in tribology. Friction 8, 221–300. doi: 10.1007/s40544-020-0367-2

CrossRef Full Text | Google Scholar

Mindlin, R. D. (1949). Compliance of elastic bodies in contact. ASME J. Appl. Mech. 16, 259–268.

Google Scholar

Mróz, Z., and Stupkiewicz, S. (1994). An anisotropic friction and wear model. Int. J. Solids Struct. 31, 1113–1131. doi: 10.1016/0020-7683(94)90167-8

CrossRef Full Text | Google Scholar

Nowell, D. (2010). Simulation of fretting wear in half-plane geometries-Part II: analysis of the transient wear problem using quadratic programming. J. Tribol. 132:021402. doi: 10.1115/1.4000733

CrossRef Full Text | Google Scholar

Páczelt, I., and Mróz, Z. (2007). Optimal shapes of contact interfaces due to sliding wear in the steady relative motion. Int. J. Solids Struct. 44, 895–925. doi: 10.1016/j.ijsolstr.2006.05.027

CrossRef Full Text | Google Scholar

Peigney, M. (2004). Simulating wear under cyclic loading by a minimization approach. Int. J. Solids Struct. 41, 6783–6799. doi: 10.1016/j.ijsolstr.2004.05.022

CrossRef Full Text | Google Scholar

Popov, V. L. (2014). Analytic solution for the limiting shape of profiles due to fretting wear. Sci. Rep. 4:3749. doi: 10.1038/srep03749

PubMed Abstract | CrossRef Full Text | Google Scholar

Popov, V. L., and Heß, M. (2015). Method of Dimensionality Reduction in Contact Mechanics and Friction. Heidelberg: Springer. doi: 10.1007/978-3-642-53876-6

CrossRef Full Text | Google Scholar

Serre, I., Bonnet, M., and Pradeilles-Duval, R.-M. (2001). Modelling an abrasive wear experiment by the boundary element method. Comptes Rendus de l'Académie des Sciences Series IIB Mechanics 329, 803–808. doi: 10.1016/S1620-7742(01)01402-7

CrossRef Full Text | Google Scholar

Sfantos, G. K., and Aliabadi, M. H. (2006). Application of BEM and optimization technique to wear problems. Int. J. Solids Struct. 43, 3626–3642. doi: 10.1016/j.ijsolstr.2005.09.004

CrossRef Full Text | Google Scholar

Vázquez, J., Sackfield, A., Hills, D., and Domínguez, J. (2010). The mechanical behaviour of a symmetrical punch with compound curvature. J. Strain Anal. Eng. Design 45, 209–222. doi: 10.1243/03093247JSA633

CrossRef Full Text | Google Scholar

Vingsbo, O., and Söderberg, S. (1988). On fretting maps. Wear 126, 131–147. doi: 10.1016/0043-1648(88)90134-2

CrossRef Full Text | Google Scholar

Wang, Z., Jin, X., Keer, L. M., and Wang, Q. (2013). Novel model for partial-slip contact involving a material with inhomogeneity. J. Tribol. 135:041401. doi: 10.1115/1.4024548

CrossRef Full Text | Google Scholar

Wang, Z., Yu, C., and Wang, Q. (2015). An efficient method for solving three-dimensional fretting contact problems involving multilayered or functionally graded materials. Int. J. Solids Struct. 66, 46–61. doi: 10.1016/j.ijsolstr.2015.04.010

CrossRef Full Text | Google Scholar

Willert, E., Dmitriev, A. I., Psakhie, S. G., and Popov, V. L. (2019). Effect of elastic grading on fretting wear. Sci. Rep. 9:7791. doi: 10.1038/s41598-019-44269-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Yen, B. K., and Dharan, C. K. H. (1996). A model for the abrasive wear of fiber-reinforced polymer composites. Wear 195, 123–127. doi: 10.1016/0043-1648(95)06804-X

CrossRef Full Text | Google Scholar

Yue, T., and Wahab, M. A. (2019). A review on fretting wear mechanisms, models and numerical analyses. Comput. Mater. Contin. 59, 405–432. doi: 10.32604/cmc.2019.04253

CrossRef Full Text | Google Scholar

Zhang, Y., Kovalev, A., and Meng, Y. (2018). Combined effect of boundary layer formation and surface smoothing on friction and wear rate of lubricated point contacts during normal running-in processes. Friction 6, 274–288. doi: 10.1007/s40544-018-0228-4

CrossRef Full Text | Google Scholar

Zmitrowicz, A. (2006). Wear patterns and laws of wear-a review. J. Theor. Appl. Mech. 44, 219–253.

Google Scholar