Reduced Gas-Phase Kinetic Models for Burning of Douglas Fir

New skeletal chemical kinetic models have been obtained by reducing a detailed model for the gas-phase combustion of Douglas Fir pyrolysis products. The skeletal models are intended to reduce the cost of high-resolution wildland fire simulations, without substantially affecting accuracy. The reduction begins from a 137 species, 4,533 reaction detailed model for combustion of gas-phase biomass pyrolysis products, and is performed using the directed relation graph with error propagation and sensitivity analysis method, followed by further reaction elimination. The reduction process tracks errors in the ignition delay time and peak temperature for combustion of gas-phase products resulting from the pyrolysis of Douglas Fir. Three skeletal models are produced as a result of this process, corresponding to a larger 71 species, 1,179 reaction model with 1% error in ignition delay time compared to the detailed model, an intermediate 54 species, 637 reaction model with 24% error, and a smaller 54 species, 204 reaction model with 80% error. Using the skeletal models, peak temperature, volumetric heat release rate, premixed laminar flame speed, and diffusion flame extinction temperatures are compared with the detailed model, revealing an average maximum error in these metrics across all conditions considered of less than 1% for the larger skeletal model, 10% for the intermediate model, and 24% for the smaller model. All three skeletal models are thus sufficiently accurate and computationally efficient for implementation in high-resolution wildland fire simulations, where other model errors and parametric uncertainties are likely to be greater than the errors introduced by the reduced kinetic models presented here.

1. Introduction

In order to reduce the computational cost of high-fidelity numerical simulations of wildland fire, computationally efficient—yet still physically accurate—reduced chemical kinetic models are required for the prediction of gas-phase combustion. In this paper, we present three such skeletal models for the combustion of gas-phase products resulting from the pyrolysis of Douglas Fir. The computational savings enabled by these models are substantial when compared to detailed models, making the skeletal models suitable for wildland fire simulations spanning large spatial and temporal scale ranges.

The need for such scale-resolving simulations arises from the considerable environmental and economic cost of wildland fires, as well as the difficulty in establishing future mitigation and avoidance strategies. It is anticipated that climate change will contribute to increased wildland fire activity, particularly in the Western U.S. (Barbero et al., 2015; Westerling, 2016), further increasing the importance of simulations in fire management efforts.

Predicting wildland fires using computational models remains, however, an inexact science. Such models can generally be divided into two categories: semi-empirical operational models used for nearly real-time incident response, and physics-based models used to understand the dynamics of fire spread (Coen et al., 2013). Although there is a growing trend in wildland fire research toward physics-based models (Linn et al., 2002, 2010; Sullivan, 2009; Mell et al., 2010; Morvan, 2011), these models remain limited by the daunting challenge of incorporating the physics of wildland fuel combustion in landscape-scale numerical simulations that are coupled to atmospheric dynamics and weather (Coen et al., 2013).

As a possible solution to this challenge, high-resolution numerical simulations at much smaller scales (e.g., 10 m and below) can, in principle, be used to develop improved subgrid-scale models for landscape-scale wildland fire simulations. As the scale of the simulations decreases, however, there is a greater need to more accurately model all relevant small-scale chemical and fluid processes. To adequately model fire spread, simulations must be able to resolve small-scale turbulent mixing, as well as capture the pyrolysis and subsequent gas-phase combustion of geometrically complex and spatially heterogeneous wildland fuels. The challenge of resolving turbulence can be addressed through advanced computational techniques such as adaptive mesh refinement (Wimer et al., 2019a,b), but the chemical models used for pyrolysis and combustion must be sufficiently detailed without significantly increasing the computational cost.

Although typical biomass pyrolysis models are not excessively large, gas-phase combustion models routinely involve hundreds or even thousands of different species and reactions. For example, Ranzi et al. (2008) have provided a gas-phase biomass combustion model—which is the basis for the present skeletal models—that contains 4,533 reactions and 137 species. Skeletal and other reduced models are typically an order of magnitude smaller. The widely-used multi-step DRM19 kinetic model, for instance, is a 19 species (plus N₂ and Ar), 84 reaction reduced model for methane combustion based on GRI-Mech 1.2 (Kazakov and Frenklach, 1995).

In the following, we outline the development of three new skeletal chemical kinetic models for gas-phase combustion of Douglas Fir pyrolysis products. The three models are targeted at large-scale simulations on high-performance computing resources, but are intended to provide three different levels of accuracy and computational cost. Users may thus choose the model best suited to their needs and available computational resources. All skeletal mechanisms include a similar number of species (i.e., 71 and 54 species), but have vastly different numbers of reactions (i.e., 1,179, 637, and 204 reactions).

The skeletal models are obtained by reducing the detailed chemical kinetic model for gas-phase biomass combustion from Ranzi et al. (2008). The reduction is performed using the directed relation graph with error propagation and sensitivity analysis method in a perfectly stirred reactor. We then show that all three skeletal models introduce relatively small errors, as compared to the detailed model, for various properties of premixed and diffusion flames.

The paper is organized as follows. In the next section, we outline the detailed model and reduction procedure, followed by a presentation of results from the three new skeletal models. Finally, we provide conclusions at the end.

2. Methodology

The overall reduction procedure tracks errors in ignition delay time and peak temperature in a constant-pressure, fixed volume perfectly stirred reactor (PSR) for the combustion of gases resulting from the pyrolysis of Douglas Fir. In the following, we describe the model and procedure used to obtain the Douglas Fir pyrolysis products, followed by descriptions of the detailed chemical kinetic model and the reduction process.

2.1. Pyrolysis Model

The pyrolysis kinetic model is that of Debiagi et al. (2015), which includes extractives and is a refined version of the model published by Corbetta et al. (2014). The model involves 28 reactions and 47 species (including volatile, non-volatile, and condensed phase species) and provides pathways for the thermal decomposition of the three main polymer components of wood: cellulose, hemicellulose, and lignin, in addition to two extractives. It predicts light fractions directly, while heavy fractions are described by lumped species. The advantage of using this model is that the gaseous lumped product species correspond to those in an associated gas-phase detailed kinetic model (Ranzi et al., 2008), which is the starting point for the model reduction performed here. Of the 47 species in the pyrolysis mechanism, 18 are gaseous or volatile.

The major components of wood are polymers, and the pyrolysis model reflects this by starting with de-polymerization reactions, although in a highly simplified manner. Cellulose is assumed to transform into active cellulose; i.e., a reactive form that leads to the monomeric form and other products like levoglucosan. Hemicellulose is assumed to decompose into intermediate species HCE1 and HCE2 that successively decompose with different activation energies, with different propensities to char. Lignin is assumed to be composed of LIG-C, LIG-O, and LIG-H (carbon, oxygen, and hydrogen rich derivatives of the β-O-4 molecule, respectively), that then decompose into intermediate components that lead to other products (Ranzi et al., 2008).

Extractives extend the applicable types of biomass that can be represented with this kinetic model. Previous versions of the pyrolysis mechanism (e.g., Corbetta et al., 2014) were only valid for specific types of biomass, depending on their carbon and hydrogen makeup. Extractives fall into two categories: hydrophilic and hydrophobic. Debiagi et al. (2015) chose to use a tannin (TANN) as the hydrophilic extractive and a triglyceride (TGL) as the hydrophobic extractive.

2.2. Douglas Fir Pyrolysis Products

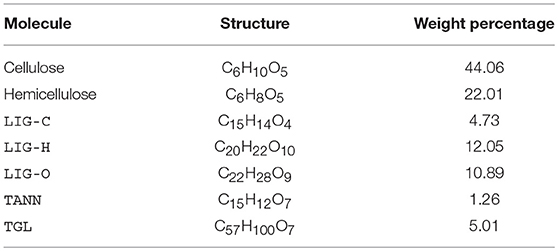
To carry out reduction of the gas-phase kinetic model, a realistic set of gas-phase pyrolysis products is required as input to the gas-phase calculations. Therefore, we have run simulations using the pyrolysis model described in the previous section over a range of times and temperatures. This requires selecting a target wood species to work with, since the initial concentrations of cellulose, hemicellulose, and lignin vary by species. We have selected Douglas Fir because of its widespread availability and native presence in the Rocky Mountain region. We obtained the initial mole fractions of cellulose, hemicellulose, LIG-C, LIG-H, LIG-O, TANN, and TGL for Douglas Fir from Debiagi et al. (2015), Faravelli et al. (2010), and Schwetz and Lipp (1985); Table 1 lists these in terms of weight percentages.

TABLE 1

Table 1. Weight percentages of the main components of Douglas Fir, including molecular structures.

The pyrolysis model is solved using an experimentally measured temperature time series (shown in Figure 1) as input. In the experiments, Douglas Fir samples were heated with a cone-calorimeter while simultaneously measuring surface temperature (via an infrared camera), gas temperature, and H₂O mole fraction. The latter two quantities were measured using dual-frequency comb laser diagnostics (Schroeder et al., 2017). Since the model describes pyrolysis (i.e., decomposition at high temperature in the absence of air), an approximately stoichiometric amount of air was assumed for comparison with the experimental dataset. The formation of pyrolysis gases is modeled using the surface temperature measured by the infrared camera, prior to any combustion occurring. More extensive details on the experiments are available in Makowiecki et al. (in preparation).

FIGURE 1

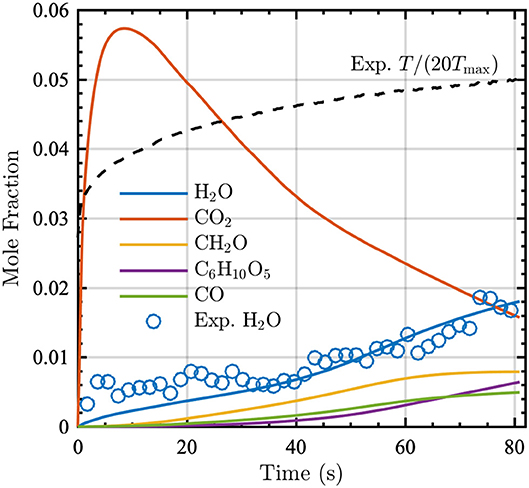
Figure 1. Mole fraction time series of the five most prevalent (by mole fraction at 80 s) gaseous pyrolysis products (indicated by lines) and the corresponding experimentally measured H₂O mole fraction (indicated by open circles). The normalized experimental temperature time series is also shown (black dashed line), where T_max = 639 K.

Figure 1 shows the evolution of the top five gaseous pyrolysis products as a function of time; at 80 s, these species account for approximately 74% of the total moles in the gas-phase. This figure indicates that the pyrolysis model accurately captures the production of H₂O vapor measured experimentally.

2.3. Detailed Combustion Model

The detailed gas-phase kinetic model bio1412 from the CRECK modeling group is used as the starting point for the reduced skeletal models. This model is publicly available at the website http://creckmodeling.chem.polimi.it, with verification data given by Ranzi et al. (2008). The model contains 4,533 reactions and 137 species and is built upon earlier work from the CRECK group (Ranzi et al., 2001). Although this model has been shown to give good agreement for the gas-phase combustion of solid fuel pyrolysis gases (Ranzi et al., 2008), it is generally too large for inclusion in already demanding simulations of wildland fire. Consequently, in the following we reduce this model to a size that is appropriate for high-fidelity numerical simulations.

2.4. Reduction Methodology

The CRECK detailed gas-phase combustion model is reduced using the Model Automatic Reduction Software (MARS) package (Niemeyer et al., 2010; Niemeyer and Sung, 2011, 2014, 2015). The reduction employs the directed relation graph with error propagation (DRGEP) and sensitivity analysis (SA) methods, followed by reaction elimination, which Niemeyer and colleagues have shown to be effective for reducing various surrogate fuel models.

Briefly, the process begins by applying DRGEP, which determines the importance of each species to the production or consumption of chosen target species (e.g., fuel, oxidizer, important pollutants). Next, a “greedy” SA removes individual species one-by-one and evaluates the error induced; it removes the species that least affect error and repeats the process on the remaining species until reaching the specified error limit. The error limit is determined by comparing predictions of the full, detailed kinetic model via autoignition and PSR simulations across expected conditions (e.g., pressure, temperature, equivalence ratio, and initial reactants) with those of the skeletal model. Ignition delay time and points along the upper PSR temperature response curve are chosen as metrics for the reduction, consistent with typical target parameters for premixed combustion mechanisms. Then, the contributions of each remaining reaction are examined, with the goal of eliminating reactions that are unimportant to the overall progression of the kinetic model, while remaining below the specified error tolerance. The final resulting model is considered the skeletal model.

This process is carried out for each targeted condition (e.g., pressure, temperature, equivalence ratio, initial reactants), resulting in a single skeletal model that consists of the union of species remaining over all conditions. This guarantees that the reduced model maintains error below the specified limit for autoignition and PSR results. Further, targeted species cannot be removed, regardless of their impact on the overall kinetics.

3. Results

3.1. Skeletal Combustion Models

Reduction calculations were performed using the fuel set composed of all 18 gas-phase pyrolysis products. The pressure was set to 1 atm, with temperatures ranging from 800 to 2,000 K and equivalence ratios from 0.5 to 1.5. The wide range of conditions included in the reduction reflects the similarly wide-ranges of temperatures and equivalence ratios found in real-world wildland fires.

To create a robust gas-phase combustion model, various sets of products from the pyrolysis model were used in the reduction, corresponding to the products at 20, 50, and 80 s (shown in Figure 1). However, the resulting reduced gas-phase models were all roughly the same size, with similar numbers of species and reactions. Therefore, only the reductions on the final pyrolysis products at 80 s will be discussed in the following sections.

Figure 2 shows the reduction process via DRGEPSA for the number of species remaining in the kinetic model as a function of error limit. Applying DRGEP with a maximum error of 30% (in ignition delay time and peak temperature in a PSR) to the detailed kinetic model removed 75 species and any reaction containing them, leaving 62 species. At this point in the reduction, the error in ignition delay time between the detailed model and the reduced model was approximately 21%. Applying sensitivity analysis removed 8 additional species and their associated reactions, resulting in a reduced model with 54 species and 637 reactions, giving approximately 24% error in ignition delay time, as compared to the detailed model. The reaction elimination step removed an additional 433 reactions, yielding a skeletal model with 204 reactions. For the ignition delay time in a PSR, this final skeletal model has 82.9% maximum error when compared to the detailed model. However, this most-reduced skeletal model retains only 54 species and 204 reactions, corresponding to 39.4% of the total number of species and 4.5% of the total number of reactions in the detailed model.

FIGURE 2

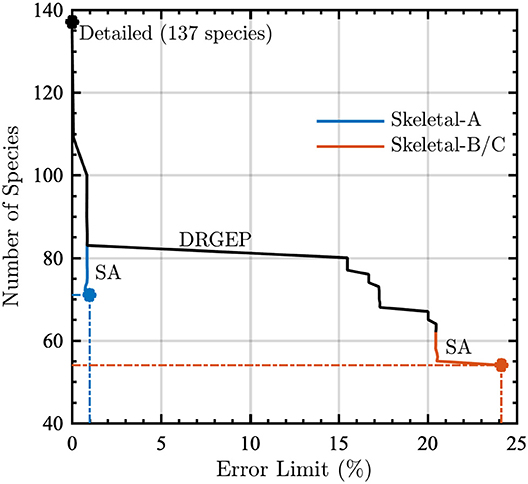
Figure 2. Number of species as a function of error limit during the reduction of the detailed model using the directed relation graph with error propagation (DRGEP) and sensitivity analysis (SA) method. Dash-dot lines indicate the number of species for the given error limit in skeletal models A (blue lines) and B (red lines) prior to the reaction elimination step (which produces Skeletal-C).

During the DRGEP process, Figure 2 indicates a significant increase in error at 81 species, corresponding to a jump from 1% to greater than 15% error. Consequently, we created another reduced model with 1% error for gas-phase combustion, hereby noted Skeletal-A. Following the same naming convention, Skeletal-B is the reduced model produced by DRGEPSA with 30% error, and Skeletal-C is the model obtained from Skeletal-B after the reaction elimination step. The numbers of species and reactions in these three models are summarized in Table 2, along with the detailed model. After the DRGEPSA process, the Skeletal-A model has only 1.00% error in ignition delay time compared to the detailed model, which increases to 24.1% error for Skeletal-B and 82.9% after the reaction elimination step in Skeletal-C. With the introduction of tabulated and dimensional reduction of chemistry, models on the order of one-thousand reactions and one-hundred species are suitable for computations (Hiremath et al., 2013), and thus all of the skeletal models developed here are sufficiently compact for implementation in high-resolution simulations. The final skeletal models and associated information on thermodynamic and transport properties are provided as text-based files in the Supplemental Material.

TABLE 2

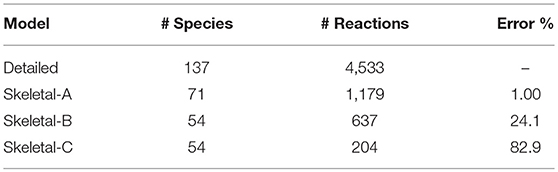
Table 2. Detailed and skeletal model details, indicating the final number of species and reactions, as well as the error in the ignition delay time with respect to the detailed model.

3.2. Validation of Skeletal Models

To validate the accuracy of the reduced skeletal models, which were obtained based solely on consideration of the ignition delay time and peak temperature in PSR calculations, here we compare PSR ignition delays, peak temperatures, and volumetric heat-release rates, premixed laminar flame speeds, and diffusion flame extinction points from the detailed and skeletal models.

Figure 3 shows that all three skeletal models match the ignition delay times of the detailed model for equivalence ratios from 0.5 to 1.5 over a wide range of temperatures. Although discrepancies do exist between the models at low temperatures, such temperatures are not of primary interest for wildland fire. In general, as expected, the larger Skeletal-A model is in better agreement with the detailed model, as compared to the Skeletal-B and Skeletal-C models.

FIGURE 3

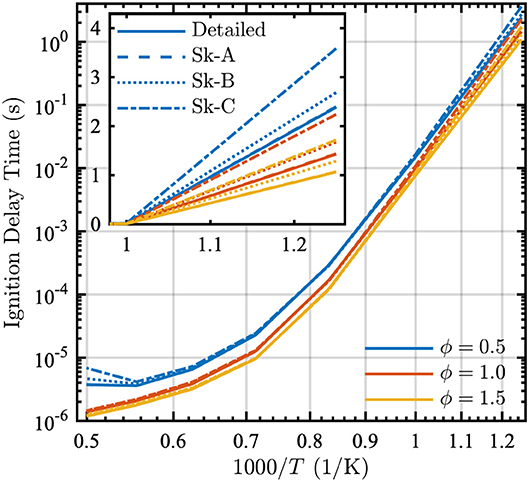
Figure 3. Ignition delay as a function of 1000/T in a PSR at equivalence ratios ϕ = [0.5, 1.0, 1.5] and P = 1 atm for the detailed (solid lines), Skeletal-A (dashed lines), Skeletal-B (dotted lines), and Skeletal-C (dash-dot lines) models. The inset shows ignition delay time vs. 1000/T for lower temperatures.

To assess the importance of the error in ignition delay, we compare the absolute error in the ignition delay time to an approximate characteristic turbulent mixing time τ_mix. This time is estimated as τ_mix ≈ 0.1 s based on a convective velocity of 1 cm/s and a characteristic length of 1 mm. For most practical conditions, the ignition delay will be dominated by mixing and therefore the error introduced by the reduction is reasonably small, as seen in Figure 4. The highest error occurs at low temperatures where the characteristic turbulent mixing time would be much longer than the approximate one used here, due to a lower convective velocity. While the deviations at T = 2,000 K look large, it must be kept in mind that the non-dimensional errors are on the order of 10⁻⁴ to 10⁻⁸, and therefore trivial for this application when compared to the mixing time.

FIGURE 4

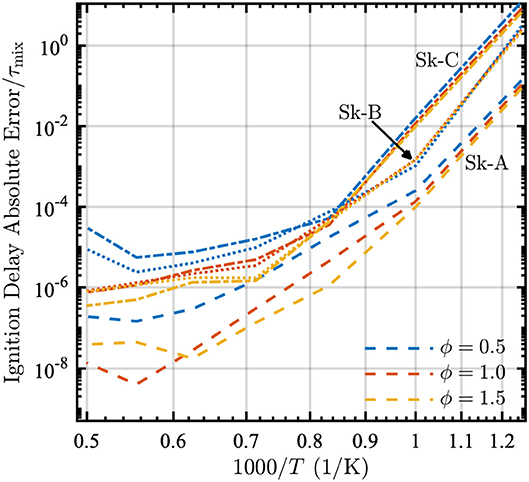
Figure 4. Absolute error relative to the mixing time τ_mix = 0.1 s as a function of 1000/T in a PSR at equivalence ratios ϕ = [0.5, 1.0, 1.5] and P = 1 atm for the Skeletal-A (dashed lines), Skeletal-B (dotted lines), and Skeletal-C (dash-dot lines) models.

The PSR calculations performed during the reduction process also provide the peak temperature and the volumetric heat-release rate as functions of residence time. These results are shown in Figures 5 and 6 for the detailed and skeletal models over equivalence ratios from 0.5 to 1.5.

FIGURE 5

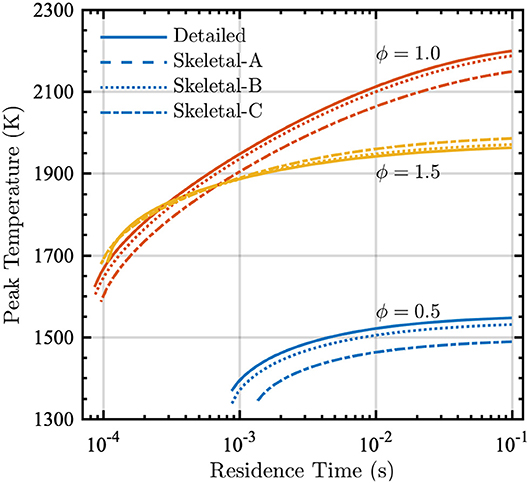
Figure 5. Peak temperature vs. residence time in a PSR at equivalence ratios ϕ = [0.5, 1.0, 1.5] and P = 1 atm for detailed (solid lines), Skeletal-A (dashed lines), Skeletal-B (dotted lines), and Skeletal-C (dash-dot lines) models.

FIGURE 6

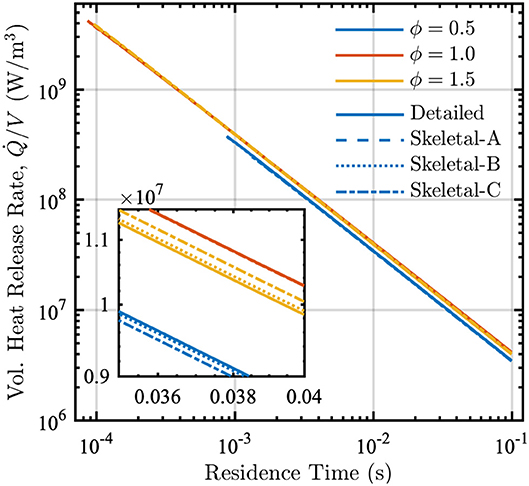
Figure 6. Volumetric heat release rate vs. residence time in a PSR at equivalence ratios ϕ = [0.5, 1.0, 1.5] and P = 1 atm for detailed (solid lines), Skeletal-A (dashed lines), Skeletal-B (dotted lines), and Skeletal-C (dash-dot lines) models.

For each of the models and at all equivalence ratios, the peak temperatures in Figure 5 decrease as the residence time decreases, consistent with the increased incidence of incomplete combustion for small residence times. The detailed and Skeletal-A models are in nearly perfect agreement, with small deviations in the Skeletal-B model for all conditions considered. Peak temperatures from the Skeletal-C model show a slight discrepancy with respect to the detailed and Skeletal-A and -B models, but the correct trends with varying residence time are nevertheless still captured.

The variation of the volumetric heat-release rate with residence time is nearly identical for the detailed and all three skeletal models, as shown in Figure 6. In particular, the volumetric heat release rate increases substantially as the residence time decreases. This occurs because more heat must be removed relative to the volume in order to maintain a constant-pressure reactor.

To validate the model reduction in non-homogeneous flame configurations, laminar flame speeds were computed for a one-dimensional premixed flame in Cantera (Goodwin et al., 2018) using both detailed and skeletal chemical kinetic models with mixture-averaged diffusion coefficients. The physical domain length was 50 cm, the reactants were at a temperature of 300 K and pressure of 1 atm, and flame speeds were computed over a range of equivalence ratios. Figure 7 shows that, once again, there is essentially no discrepancy between the detailed and Skeletal-A models. Although errors are larger for the Skeletal-B and -C models, these errors will generally be tolerable in simulations of real-world fires given the typically larger errors introduced by other physical models in the simulations (e.g., for turbulence, heat transfer, and fuel properties), as well as uncertainties in boundary and initial conditions.

FIGURE 7

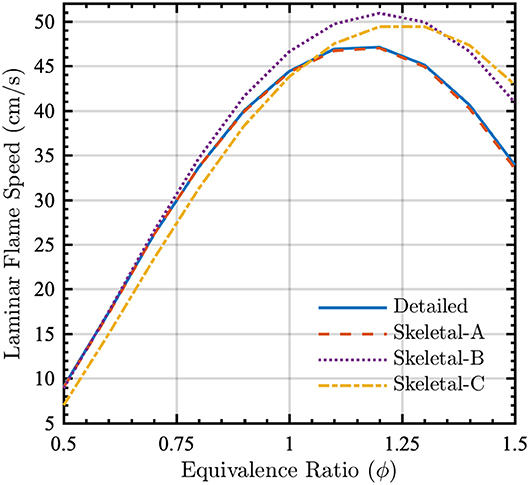
Figure 7. Laminar flame speed for a one-dimensional premixed flame as a function of equivalence ratio ϕ for detailed (solid lines), Skeletal-A (dashed lines), Skeletal-B (dotted lines), and Skeletal-C (dash-dot lines) models. The reactants were at 300 K and P = 1 atm.

Because wildland fires exhibit characteristics of both premixed and diffusion flames, the skeletal models were also used to compute the extinction temperature as a function of maximum strain rate for an opposed-jet diffusion flame. The simulations were performed using Cantera in an 18 mm domain with radiation. The fuel and air temperatures were T_fuel = 500 K and T_air = 300 K, respectively, and the pressure was P = 1 atm.

The results shown in Figure 8 indicate that the reduction process generally has minimal effect on the relation between the maximum temperature and strain rate at the extinction point. As with other metrics for the PSR and the premixed flame, the Skeletal-A model is in nearly perfect agreement with the detailed model, and the Skeletal-B and -C models display relatively small discrepancies when compared to the detailed model.

FIGURE 8

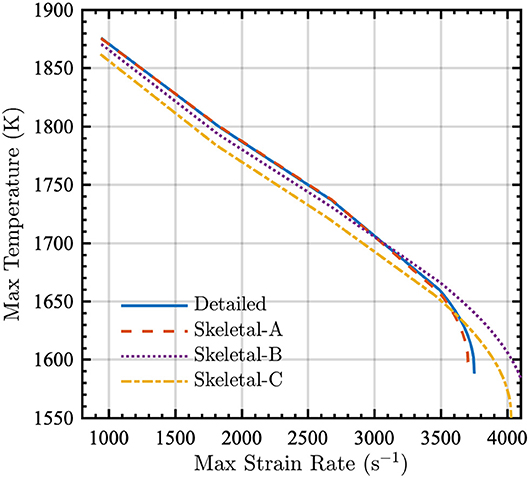
Figure 8. Maximum temperature in an opposed-jet diffusion flame as a function of maximum strain rate for detailed (solid lines), Skeletal-A (dashed lines), Skeletal-B (dotted lines), and Skeletal-C (dash-dot lines) models. The conditions of the opposed-jet configuration were T_fuel = 500 K, T_air = 300 K, and P = 1 atm.

As a quantitative summary of the errors in the skeletal models with respect to the detailed model, Table 3 shows the root-mean square (RMS) and maximum errors for various quantities of interest over all conditions (i.e., temperatures and equivalence ratios) considered in the present study. In general, the errors for the Skeletal-A model are extremely low and the maximum errors for the Skeletal-B model are below 25% for all metrics considered. As expected, the Skeletal-C model shows the greatest amount of error, although the RMS errors are maintained below 30%.

TABLE 3

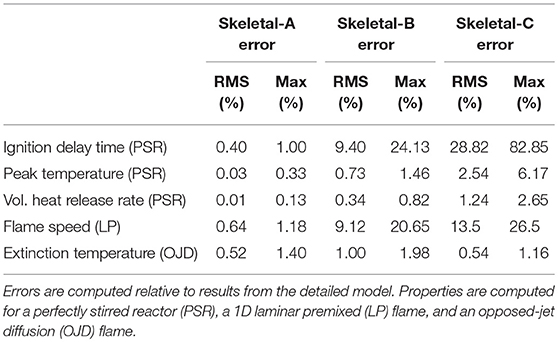
Table 3. Root mean square (RMS) and maximum error percentages from the Skeletal-A, Skeletal-B, and Skeletal-C reduced models for various properties of interest over the range of conditions considered in this study.

Table 3 shows that the maximum errors across all reduced models occur in the ignition delay time. As noted before, these errors are likely to be acceptable in most high-fidelity simulations of wildland fire given the significant increase in computational efficiency resulting from the reduction in number of species and reactions. Moreover, although the errors in ignition delay time are somewhat large in relative terms, they are small in absolute terms when compared to characteristic flow mixing times.

4. Conclusions

Three new skeletal chemical kinetic models (provided in the Supplemental Material) have been developed and validated for the combustion of gas-phase products resulting from the pyrolysis of Douglas Fir. The skeletal models were obtained by using the directed relation graph with error propagation method, “greedy” sensitivity analysis, and unimportant reaction elimination to reduce a detailed gas-phase model with 137 species and 4,533 reactions.

The three skeletal models had different sizes and resultant errors. The larger 71 species, 1,179 reaction skeletal model had a maximum error of 1% for combustion properties of interest over a wide range of conditions, while a more reduced model with 54 species and 637 reactions yielded maximum errors of roughly 21% and 24% in ignition delay time and laminar flame speed, respectively. The smallest 54 species, 204 reaction model had a maximum error of roughly 83% in ignition delay, with an average maximum error of 24%. These errors are reasonable given the complexity and uncertainty involved in modeling solid biomass combustion, although the larger skeletal model, with smaller error, is preferable if sufficient computational resources are available to allow its integration within high-fidelity simulations of wildland fire. It should also be noted that the largest errors were observed for all three skeletal models in the prediction of the ignition delay time, but these errors were small in absolute terms, particularly when compared to characteristic flow mixing times.

Ongoing work is focused on the use of additional performance measures in different flows, such as diffusion flames, as targets for MARS. A multi-dimensional finite volume model in OpenFOAM is currently under development to allow full coupling of pyrolysis and gas chemistry, thus permitting more direct comparisons with experimental data. An additional study will also be performed to quantify the maximum reduction allowable before the induced errors affect major simulation outcomes, as well as to expand to more general biomass flora.

Author Contributions

JG, KN, and JD were jointly responsible for the selection of the detailed model, the model reduction, and the validation of the skeletal model. AM and GR provided experimental data. Frequent discussions with NW, CL, and PH guided reduced model development, particularly with respect to computational constraints.

Funding

This research was supported by the Strategic Environmental Research and Development Program (SERDP) under grant W912HQ-16-C-0026 as project number RC-2642. Work by KN was supported by SERDP under project number RC-2651. CL is supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. NSF GRFP, DGE 1144083.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2019.00040/full#supplementary-material

The final skeletal models and associated information on thermodynamic and transport properties are provided as text-based files in the Supplemental Material.

References

Barbero, R., Abatzoglou, J., Larkin, N., Kolden, C., and Stocks, B. (2015). Climate change presents increased potential for very large fires in the contiguous united states. Int. J. Wildl. Fire 24, 892–899. doi: 10.1071/WF15083

PubMed Abstract | CrossRef Full Text | Google Scholar

Coen, J. L., Cameron, M., Michalakes, J., Patton, E. G., Riggan, P. J., and Yedinak, K. M. (2013). Wrf-fire: coupled weather–wildland fire modeling with the weather research and forecasting model. J. Appl. Meteorol. Climatol. 52, 16–38. doi: 10.1175/JAMC-D-12-023.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Corbetta, M., Frassoldati, A., Bennadji, H., Smith, K., Serapiglia, M. J., Gauthier, G., et al. (2014). Pyrolysis of centimeter-scale woody biomass particles: kinetic modeling and experimental validation. Energy Fuels 28, 3884–3898. doi: 10.1021/ef500525v

PubMed Abstract | CrossRef Full Text | Google Scholar

Debiagi, P. E. A., Pecchi, C., Gentile, G., Frassoldati, A., Cuoci, A., Faravelli, T., et al. (2015). Extractives extend the applicability of multistep kinetic scheme of biomass pyrolysis. Energy Fuels 29, 6544–6555. doi: 10.1021/acs.energyfuels.5b01753

PubMed Abstract | CrossRef Full Text | Google Scholar

Faravelli, T., Frassoldati, A., Migliavacca, G., and Ranzi, E. (2010). Detailed kinetic modeling of the thermal degradation of lignins. Biomass Bioenergy 34, 290–301. doi: 10.1016/j.biombioe.2009.10.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodwin, D. G., Speth, R. L., Moffat, H. K., and Weber, B. W. (2018). Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. Version 2.4.0. Available online at: https://www.cantera.org

PubMed Abstract

Hiremath, V., Lantz, S. R., Wang, H., and Pope, S. B. (2013). Large-scale parallel simulations of turbulent combustion using combined dimension reduction and tabulation of chemistry. Proc. Combust. Inst. 34, 205–215. doi: 10.1016/j.proci.2012.06.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Kazakov, A., and Frenklach, M. (1995). Reduced Reaction Sets Based on GRI-Mech 1.2. Available online at: http://combustion.berkeley.edu/drm/

PubMed Abstract

Linn, R., Reisner, J., Colman, J., and Winterkamp, J. (2002). Studying wildfire behavior using FIRETEC. Int. J. Wild. Fire 11, 233–246. doi: 10.1071/WF02007

PubMed Abstract | CrossRef Full Text | Google Scholar

Linn, R., Winterkamp, J., Weise, D., and Edminster, C. (2010). A numerical study of slope and fuel structure effects on coupled wildlfire behavior. Int. J. Wild. Fire 19, 179–201. doi: 10.1071/WF07120

PubMed Abstract | CrossRef Full Text | Google Scholar

Mell, W. E., McDermott, R. J., and Forney, G. P. (2010). “Wildland fire behavior modeling: perspectives, new approaches and applications,” in Proceedings of 3rd Fire Behavior and Fuels Conference, Spokane (Washington, DC), 45–62.

PubMed Abstract | Google Scholar

Morvan, D. (2011). Physical phenomena and length scales governing the behaviour of wildfires: a case for physical modelling. Fire Technol. 47, 437–460. doi: 10.1007/s10694-010-0160-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Niemeyer, K. E., and Sung, C.-J. (2011). On the importance of graph search algorithms for drgep-based mechanism reduction methods. Combust. Flame 158, 1439–1443. doi: 10.1016/j.combustflame.2010.12.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Niemeyer, K. E., and Sung, C.-J. (2014). Mechanism reduction for multicomponent surrogates: a case study using toluene reference fuels. Combust. Flame 161, 2752–2764. doi: 10.1016/j.combustflame.2014.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Niemeyer, K. E., and Sung, C.-J. (2015). Reduced chemistry for a gasoline surrogate valid at engine-relevant conditions. Energy Fuels 29, 1172–1185. doi: 10.1021/ef5022126

PubMed Abstract | CrossRef Full Text | Google Scholar

Niemeyer, K. E., Sung, C.-J., and Raju, M. P. (2010). Skeletal mechanism generation for surrogate fuels using directed relation graph with error propagation and sensitivity analysis. Combust. Flame 157, 1760–1770. doi: 10.1016/j.combustflame.2009.12.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranzi, E., Cuoci, A., Faravelli, T., Frassoldati, A., Migliavacca, G., Pierucci, S., et al. (2008). Chemical kinetics of biomass pyrolysis. Energy Fuels 22, 4292–4300. doi: 10.1021/ef800551t

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranzi, E., Dente, M., Goldaniga, A., Bozzano, G., and Faravelli, T. (2001). Lumping procedures in detailed kinetic modeling of gasification, pyrolysis, partial oxidation and combustion of hydrocarbon mixtures. Prog. Energy Combust. Sci. 27, 99–139. doi: 10.1016/S0360-1285(00)00013-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Schroeder, P., Wright, R., Coburn, S., Sodergren, B., Cossel, K., Droste, S., et al. (2017). Dual frequency comb laser absorption spectroscopy in a 16 MW gas turbine exhaust. Proc. Combust. Inst. 36, 4565–4573. doi: 10.1016/j.proci.2016.06.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwetz, K., and Lipp, A. (1985). Ullmann's encyclopedia of industrial chemistry. VCH: Deerfield Beach 28:315.

PubMed Abstract

Sullivan, A. L. (2009). Wildland surface fire spread modelling, 1990–2007. 1: physical and quasi-physical models. Int. J. Wildl. Fire 18, 349–368. doi: 10.1071/WF06143

PubMed Abstract | CrossRef Full Text | Google Scholar

Westerling, A. L. (2016). Increasing western us forest wildfire activity: sensitivity to changes in the timing of spring. Philos. Trans. R. Soc. B 371:20150178. doi: 10.1098/rstb.2015.0178

PubMed Abstract | CrossRef Full Text | Google Scholar

Wimer, N. T., Day, M. S., Lapointe, C., Makowiecki, A. S., Glusman, J. F., Daily, J. W., et al. (2019a). High-resolution numerical simulations of a large-scale helium plume using adaptive mesh refinement. arXiv 1901.10554. doi: 10.1103/APS.DFD.2018.GFM.V0083

PubMed Abstract | CrossRef Full Text | Google Scholar

Wimer, N. T., Lapointe, C., Christopher, J. D., Nigam, S. P., Hayden, T. R., Upadhye, A., et al. (2019b). Scaling of the puffing strouhal number for buoyant jets. arXiv[Preprint].arXiv:1901.01580.

PubMed Abstract | Google Scholar