The Role of Fuel Bed Geometry and Wind on the Burning Rate of Porous Fuels

The vast majority of wildland fires occur in windy conditions. However, most operational wildland fire models do not account for changes in burning rate or duration due to wind as no simple model exists. To gain some understanding of how wind and fuel bed properties interact to influence the burning rate and duration of wildland fuels, a relatively simple fuel bed, wood cribs, was first considered. The burning rate of 23 crib designs was measured in a wind tunnel under a range of windspeeds from 0 to 0.7 m/s. Fuel element thickness varied from 0.32 to 1.27 cm and fuel bed width from 12.7 to 60.96 cm. A range of crib porosities was tested as well covering the loosely-packed to densely-packed regime. A clear threshold behavior of the burning rate was seen depending on fuel bed geometry. For fuel beds with element length to thickness ratio (l/b) <30, the burning rate increased with wind. However, for fuel beds with element length to thickness ratio larger than 30, the burning rate actually decreased with wind. This change in burning rate was linked to a visual change in burning behavior. When the burning rate increased, the wind and flames were observed to penetrate the internal portions of the fuel bed and the crib would burn uniformly. When the burning rate decreased, the wind and flames did not penetrate the entire fuel bed and the burning front would most often propagate from the upwind edge to the downwind edge. It appeared that for these fuel bed geometries the wind was forced around the fuel, preventing any horizontal or, more importantly, vertical flow through the bed. These results are likely most applicable to isolated, small clumps of elevated fuel where the wind has the opportunity to divert around the fuel bed. Future work will include experiments that force the airflow through the fuel bed.

Introduction

Burning and heat release rate are important fire behavior metrics for both structure and wildland fires. Some general insights into burning rate behavior of porous fuel beds can be found from the literature on crib fires from the fire protection engineering field. The burning rate behavior of porous fuel beds has long been understood to be separated into two regimes (Gross, 1962; Block, 1971). In the loosely-packed regime, the burning rate is more closely approximated by the free burning rate of the individual sticks and is governed by heat and mass transfer processes near the surfaces. In this regime, the burning rate is more of a function of the stick dimensions, and is independent of the “porosity” of the fuel bed. In the densely-packed regime, the burning rate is limited by availability of oxidizer within the fuel bed. In this regime, the burning rate increases with the inter-stick spacing or the “porosity” of the fuel bed. There have been several proposed definitions for the porosity (φ) of the fuel bed, but perhaps the most widely used is that of Heskestad (1973):

$\begin{array}{l}\phi =s^{\frac{1}{2}}{b}^{\frac{1}{2}}\left(\frac{A_v}{A_s}\right)\end{array}$

where s is the spacing between sticks (cm), b is the stick thickness (cm), A_v is the area of the vertical shafts in the crib (cm²), and A_s is the exposed stick surface area (cm²), with the result that the porosity has units of cm. The transition between burning regimes occurs at a porosity of approximately 0.05 cm, with densely-packed and loosely packed cribs having porosities below and above this threshold, respectively. The fuel bed porosity and the identification of these two regimes not only gives an impression about the appearance of the fuel bed, but also describes the mechanisms that govern the burning behavior.

Unfortunately, the variation of the burning rate with forced ventilation is not well-understood, despite its obvious relevance and importance to wildland fires. In the only study dedicated to answering this question, Harmathy (1978) showed an increase in burning rate of cribs built with charring materials, but an insensitivity in non-charring materials, indicating that char oxidation is an important mechanism. Unfortunately, this was a relatively early paper, and consideration of the crib porosity [such as from Gross (1962), Block (1971), or Heskestad (1973)] was not carefully included so the full range of expected behavior was not elucidated. Other clues exist in the fire protection engineering literature as well. For example, for baskets of unordered wood cubes, Grumer and Strasser (1965) saw an increase in the burning rate of more than six times when air was blasted into the fuel bed. There have also been several studies of the effects of forced ventilation on burning rate for fuel beds in tunnel fires [for example, see (Carvel et al., 2001; Lönnermark and Ingason, 2008; Ingason and Li, 2010; Ingason and Lönnermark, 2010)] and compartment fires [for example, see (Alvares et al., 1984; Beyler, 1991; Chow and Chan, 1993; Peatross and Beyler, 1997)]. However, the interaction of the fire with the tunnel or enclosure adds significant complexity to the problem.

The understanding of the variables effecting the burning rate, and the related flame residence time, in the wildland fire literature is also poor. There are studies that suggest that no effect is seen and others that suggest an increase with wind. For example, Steward and Tennankore (1981) measured the burning rate of a single wooden dowel within a fuel bed consisting of vertical rods arranged in a uniform matrix. While the burning rate of the dowel was proportional to the diameter to the 3/2 power, no effect of wind speed was seen. On the contrary, Beaufait (1965) saw an increase in the residence time with wind speed for heading fires in beds of ponderosa pine needles. Beaufait (1965), however, noted that there was no effect of wind on the residence time for backing fires. Nelson (2003) argues in his model development that there is only a weak dependence of residence time with wind speed through the convective heat transfer coefficient. Many of these studies were performed for spreading fires which complicates the measurement and even the definition of these parameters (Nelson, 2003).

Our own previous work on the matter (McAllister and Finney, 2016a) was also inconclusive. Published as part of the proceedings of the Operation Tomodashi—-Fire Research workshop, the work was merely a preliminary investigation that raised more questions than it answered. In that work, seven crib designs were tested in a wind tunnel under a wind ranging from 0 to 0.7 m/s. It was seen that the burning rate of cribs with thicker (1.27 cm) sticks increased with wind speed, whereas the burning rate of cribs with thinner (0.64 cm) sticks decreased. Possible mechanisms were discussed, but it was clear that more experimentation was needed to fully understand the results. Our current work presents the results of significantly more testing and a clearer picture of the controlling mechanisms.

Experiment Description

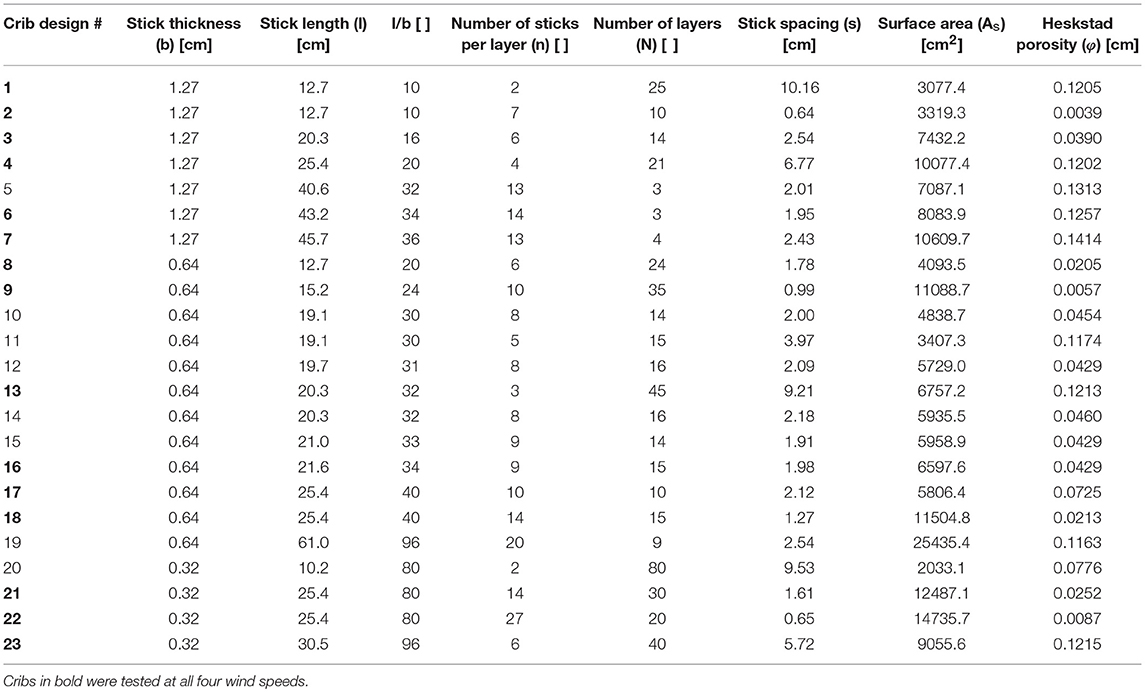
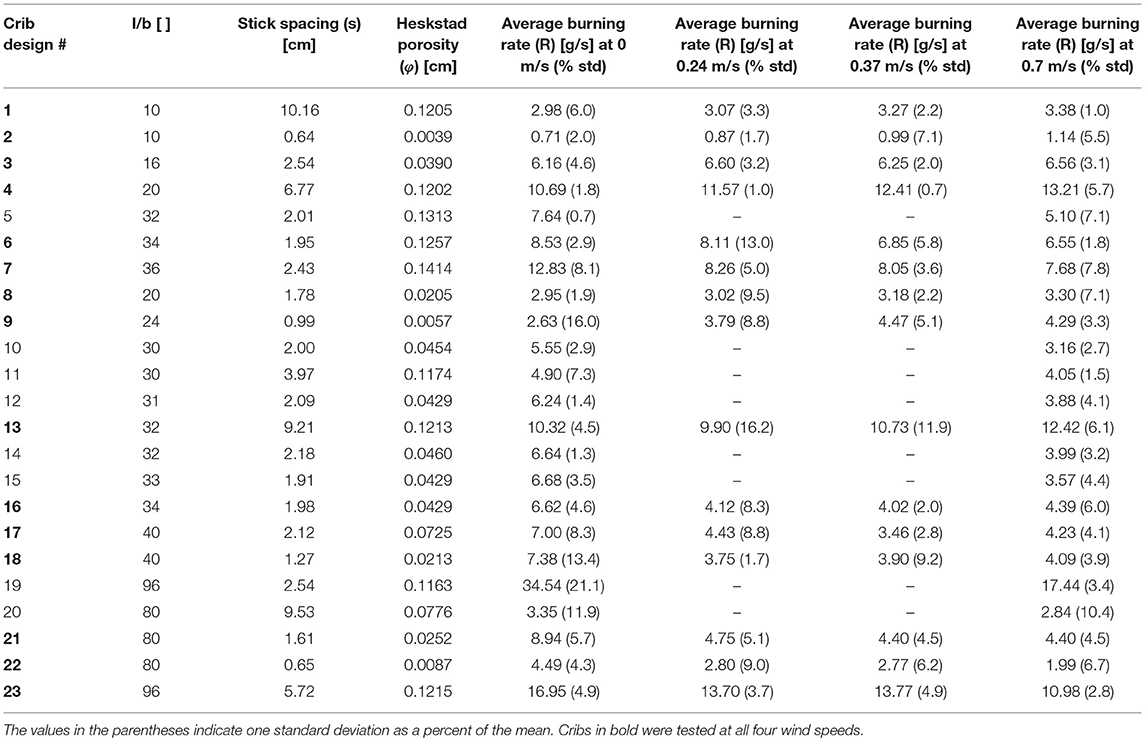
Twenty three crib designs were tested to examine the combined effect of forced ventilation and fuel bed properties. The full list of crib designs is shown in Table 1. The cribs were built out of square ponderosa pine sticks that were free of knots and other obvious defects. Three stick thicknesses were used (0.32, 0.64, and 1.27 cm). The length of the sticks, the number of sticks per layer, and the number of layers were varied to provide a wide variety of geometries and porosities (φ). Though no particular experiment design scheme was followed, the fuel bed parameters were varied in an exploratory manner, probing for any unexpected or non-linear behaviors.

TABLE 1

Table 1. Crib designs tested.

The moisture content of the cribs was controlled by conditioning them in a conditioning chamber set to 35°C and 3% relative humidity for at least 3 days before testing. The equilibrium moisture content was ~1%. Simultaneous ignition of the crib was achieved by quickly dunking the entire crib in 99% isopropyl alcohol and allowing it to drain. The total mass of alcohol used was 10% or less of the crib weight.

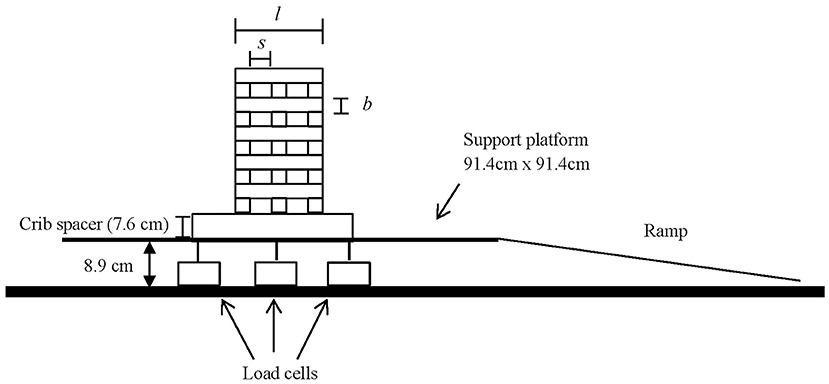
The weighing platform consisted of a 91.4 cm square, thin aluminum sheet that was supported by three 6-kg capacity load cells as in Figure 1. The load cells were calibrated to 0.1 g. Heat transfer to these load cells was minimized by covering the aluminum sheet with multiple layers of ceramic paper insulation, and by using 1.3 cm diameter ball bearings as contact points between the aluminum sheet and the load cells themselves. Because previous work indicated that the burning rate could be very sensitive to the spacing between the bottom of the crib and the weighing platform (McAllister and Finney, 2016b), two 7.62-cm-tall steel spacers were used to eliminate this effect. This weighing apparatus was placed inside of a 3 m by 3 m wind tunnel which was large enough for the flames to not interact with the walls. A gentle ramp was built ahead of the platform to compensate for the height of the load cells and platform so as to smooth out and guide the airflow. Wind speeds of 0, 0.24, 0.37, and 0.7 m/s were tested with the primary set of 15 crib designs, designated in Table 1. The remaining eight crib designs were only tested with 0 and 0.7 m/s, as these cribs were designed to help clarify the threshold behavior observed. The reported wind speeds are the free-stream value, measured at a height of 2.2 m above the wind tunnel floor. Boundary layer thickness at 0.7 m/s has been measured to be ~0.3 m at the location of the test section with freestream turbulence intensities of <2% (Rothermel, 1967). Because the height of the platform and load cells is about 0.2 m, the fuel beds sit just at the top of the boundary layer and are largely exposed to the freestream velocity.

FIGURE 1

Figure 1. Sketch of apparatus for a crib with 3 sticks per layer (n = 3) and 10 layers (N = 10).

The mass data from the load cells was recorded at 10 Hz. A sample of the raw mass and mass loss rate data are shown in Figure 2. The rate data was calculated here as the derivative of the mass data with time using a spline fit with ten degrees of freedom. In this particular example, ignition occurs at approximately 10 s, giving rise to considerable noise in the data. Because of this noise in the data, the spine fit to obtain the mass loss rate is unreliable for the short period around ignition. Even so, three phases of burning are seen in this data. The first phase, characterized by a short and steep drop in the mass, is the alcohol burning off which occurs relatively quickly. The second phase is the steady burning portion. The reported data is taken as the slope of the best fit line through this second phase of burning. The final phase is when the crib collapses and flaming ceases. All test combinations are repeated at least three times (for a total of 228 tests) and the results averaged.

FIGURE 2

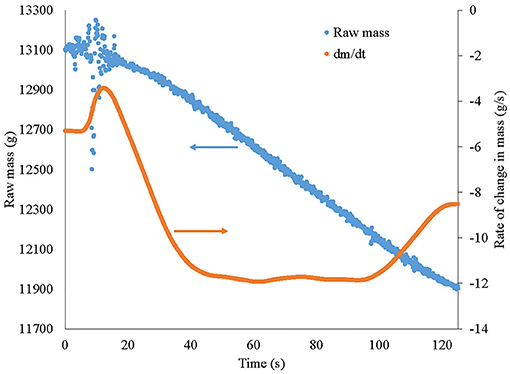
Figure 2. Raw mass and rate of change data for crib design #4 in 0.24 m/s wind. Ignition occurs at about 10 s, alcohol burnoff and stick ignition is complete by around 40 s, and steady burning occurs between about 40 and 100 s.

Results and Discussion

Before discussing the results in detail, some mention of the scaling of these experiments should be made. Several non-dimensional parameters can be used to provide some context. One such parameter is the non-dimensional heat release rate, or Q* defined as (for example see Quintiere, 2017 or Zukoski, 1995):

$\begin{array}{l}{Q}^{*}=\frac{\stackrel{.}{Q}}{{\rho }_{\infty }{c}_p{T}_{\infty }{g}^{\frac{1}{2}}{D}^{\frac{5}{2}}}=\frac{ṁ\Delta h_c}{{\rho }_{\infty }{c}_p{T}_{\infty }{g}^{\frac{1}{2}}{D}^{\frac{5}{2}}}\end{array}$

where $\stackrel{.}{Q}$ is the heat release rate (kW), ρ_∞ is the density of the ambient air (kg/m³), c_p is the specific heat of the ambient air (kJ/kg-K), T_∞ is the ambient air temperature (K), g is the acceleration due to gravity (m/s²), D is the characteristic length (m), ṁ is the burning rate (g/s), and Δh_c is the heat of combustion (kJ/g). For our purposes, we assumed that the heat of combustion was 14.1 kJ/g (Heskestad, 2006) and the properties of air were evaluated at 300 K. Using the average burning rate values from Table 2, Q* values ranged from 0.60 (crib design #5 at 0.7 m/s) to 12.72 (crib design #20 at 0 m/s). Q* for outdoor fires typically ranges from 0.5 up to 100 (Quintiere, 2017). Most fires will have Q* < 10 and, because Q* is related to the ratio of the flame height to the fire diameter, larger area fires have Q* < 2 (Zukoski, 1995). Given this range, the fires in these experiments are representative of the flame and plume regime expected for wildland fires.

TABLE 2

Table 2. Burning rate results averaged over three replicates.

Another scaling consideration to keep in mind is the relation of the wind speed to the amount of heat that is released. This can be done a number of ways. In some flame tilt literature (see for example Thomas, 1965 and Beyler, 2008), the ratio of the wind velocity (u_w) to the buoyant velocity (u_b) can be useful. This non-dimensional velocity is defined as,

$\begin{array}{c}{u}^{*}=\frac{u_w}{u_b}=\frac{u_w}{\left(\frac{g{ṁ}^{″}D}{{\rho }_{\infty }}\right)}\end{array}$

where ṁ″ is the burning rate per unit area. If u* < 1, the buoyant velocity dominates and the flames remain upright. If greater than one, the inertia of the wind becomes important and the flames tilt. Using the burning rates from Table 2, u* for the experiments here ranged from 0.33 (crib design #4 at 0.24 m/s) up to 1.75 (crib design #22 at 0.7 m/s), covering a wide range of behaviors. In the engineering literature, the Froude number is regularly used to quantify this balance between inertia and buoyancy forces. Using the flame length given by Quintiere (2006), the Froude number is defined here as (for example Pagni and Peterson, 1973):

$\begin{array}{c}Fr=\frac{u^2}{gL}=\frac{u^2}{g{\left(\frac{\stackrel{.}{Q}}{{\rho }_{\infty }{c}_p{T}_{\infty }\sqrt{g}}\right)}^{\frac{2}{5}}}=\frac{u^2}{g{\left(\frac{ṁ\Delta h_c}{{\rho }_{\infty }{c}_p{T}_{\infty }\sqrt{g}}\right)}^{\frac{2}{5}}}\end{array}$

Using data from Table 2, the Froude number ranged from 0.013 (crib design #4 at 0.24 m/s) to 0.2191 (crib design #22 at 0.7 m/s) using the wind speeds at the fuel level. In wildfire situations, wind speeds are often reported at a particular height above the ground (10 m or 20 ft), so the reported wind conditions are not necessarily the conditions experienced by the flames. In calculating wind speeds in operational fire spread models, often a logarithmic wind profile is assumed and the wind speed is reduced to the mid-flame height (Albini and Baughman, 1979). For comparison purposes, the range of Froude numbers tested here would correspond to 1.5 m tall shrubs with 3 to 8.5 m flames in 0.7 to 4.5 m/s mid-flame winds (see for example Scott and Burgan, 2005, shrub fuel model SH9).

As discussed in earlier work, distinct changes in the burning pattern were observed. In still air, loosely-packed cribs burned very uniformly with equal consumption rates throughout the entire fuel bed (see Figure 3). Densely-packed cribs in still air burned symmetrically from the outside edges inward, with the center core as the last portion to be consumed (see Figure 4). In wind, however, the burnout patterns were asymmetric. With only a couple of exceptions, most of the cribs burned faster on the windward side as the wind speed was increased. One of the most exaggerated cases is shown in Figure 5, where the burning resembled a propagating flame front from the front, windward side of the crib down wind. Additionally, some of the densely-packed cribs, when exposed to wind, seemed to burn out a bit faster on the bottoms, such that the crib appeared to decrease in height over the course of the test.

FIGURE 3

Figure 3. Loosely-packed crib (crib design #11) burning in a quiescent environment showing the entire fuel bed burning uniformly throughout.

FIGURE 4

Figure 4. Densely-packed crib (crib design #22) from the side (A) and from above (B) burning in a quiescent environment. The crib burns primarily from the outside inward, with lots of unburnt, white gases being emitted from the top of the fuel bed.

FIGURE 5

Figure 5. Crib design #22 in 0.7 m/s wind at various times after ignition: (A) approximately 30 s, (B) approximately 70 s, (C) approximately 195 s, (D) approximately 360 s.

Table 2 shows the average burning rate for all tests conducted. Also included in Table 2 is the standard deviation as a percent of the mean value to give an indication of the repeatability. The average standard deviation over all tests was 5.4% of the mean value, with a maximum value of 21.1%, demonstrating good consistency between tests.

Figures 6–8 plot the normalized burning rate results as a function of wind speed for the 1.27, 0.64, and 0.32 cm thick sticks, respectively. All data are scaled by the exposed surface area (A_s) and the inverse square root of the stick thickness (b^−0.5) as in Block (1971) and Heskestad (1973). Each point represents the average of three tests, and though it may not be visible in all cases, the error bars show one standard deviation for each condition. Also shown in the figures is the ideal burning rate for each stick thickness according to Tewarson and Pion (1976). The ideal burning rate is defined as the burning rate where the additional heat flux (such as from nearby burning surfaces) is just balanced by the heat losses. Some difference in the ideal rate may be expected due to differing wood species. The values from Tewarson and Pion (1976) are for Douglas-fir while ponderosa pine was tested here.

FIGURE 6

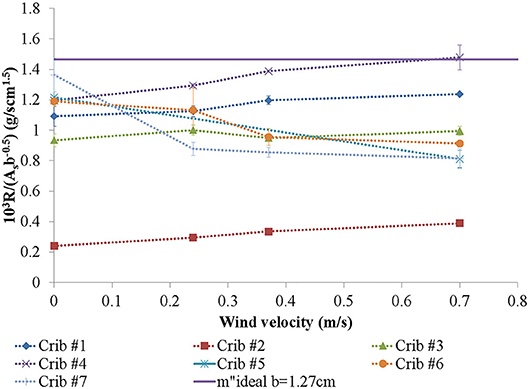
Figure 6. Scaled burning rate as a function of wind speed for cribs with 1.27 cm thick sticks. Ideal burning rate is from Tewarson and Pion (1976). See Table 1 for details on fuel bed parameters.

As shown in Figure 6 through Figure 8, the burning rate either increases or decreases with wind speed. Contrary to what was observed in previous work (McAllister and Finney, 2016a), this trend is not dependent upon stick thickness, but seems to depend on other factors that will be discussed further below. The maximum increase in burning rate was 69.9% percent from crib design #9, one of the most densely-packed cribs tested (φ = 0.0057 cm). In general, the largest increases in burning rate were seen for the densely-packed cribs. These cribs are generally considered to be ventilation limited, so logically, forcing air through these densely-packed cribs will lean out the gaseous air and fuel mixture internally, allowing for greater reaction rates and thus heat release rates. Interestingly, even some loosely-packed cribs (#s 1, 4, and 13) also showed modest increases in the burning rates of 13 to 23%. As pointed out by Harmathy (1978), char oxidation can be an important contributor to the overall burning rate. With forced ventilation, the char oxidation rate is increased, resulting in increased burning rate even in fuel beds that aren't ventilation limited.

In the case of crib designs #4 and 13, the addition of wind allowed the burning rate of the fuel bed to approach or exceed the estimated ideal of Tewarson and Pion (1976) (see Figures 6, 7). In general, for loosely-packed and transition-regime cribs, such as crib designs #4–7 (Figure 6), 10–17, 19 (Figure 7), 20, and 23 (Figure 8), the burning rate in no wind was already within about 20% of this ideal (or exceeded it). However, the burning rate of many of these crib designs dropped considerably as wind was added, indicating a shift in the balance between heat generated and heat lost. In general, this balance is what governs whether the burning rate will increase or decrease, but how this balance is achieved in all cases here is not obvious.

FIGURE 7

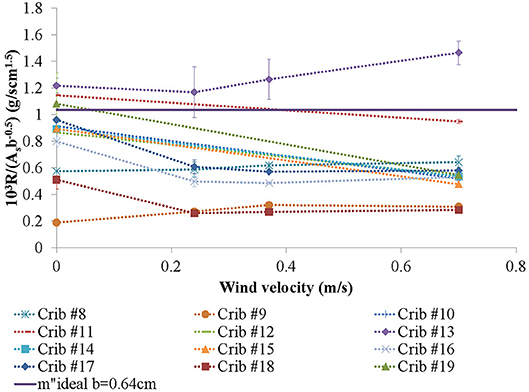
Figure 7. Scaled burning rate for cribs with 0.64 cm thick sticks. Ideal burning rate is from Tewarson and Pion (1976). See Table 1 for details on fuel bed parameters.

FIGURE 8

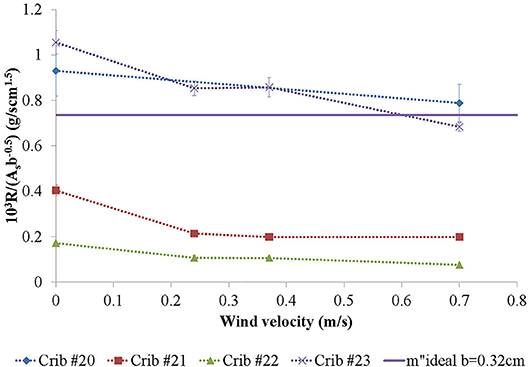
Figure 8. Scaled burning rate for cribs with 0.32 cm thick sticks. Ideal burning rate is from Tewarson and Pion (1976). See Table 1 for details on fuel bed parameters.

Though all cribs burned with some level of asymmetry in the wind, the cases with decreased burning rate had increasingly asymmetric burning patterns. In some cases, the downwind half of the crib chars but is nearly completely unconsumed before the upwind half burns out and collapses (see Figure 5). Visually, it appears as if the crib geometry is preventing the airflow through the crib. As the flow resistance through the crib increases, the path of least resistance for the flow is around, not through, starving portions of the internal area of the fuel bed of air. This, however, does not seem to be related to the porosity of the fuel bed, at least as defined by Heskestad (1973) or as bulk density (volume of fuel per fuel bed volume), as even loosely-packed cribs exhibit this behavior as well (for example, crib designs #5, 6, 7, 11, 19, 20, and 23). Interestingly, this transition from flow through to flow around occurred for cribs with large aspect ratios (long sticks relative to the stick thickness, or l/b). Figure 9 shows the burning rates at the highest wind speed tested (0.7 m/s) normalized by the quiescent case as a function of the aspect ratio (l/b). Despite one exception (crib design #13), there is a rather sharp threshold at an l/b ratio between about 25 and 30. Some exploratory statistical analysis was conducted to find an alternate explanation, but no other fuel bed property was found that explained this behavior in any meaningful way.

FIGURE 9

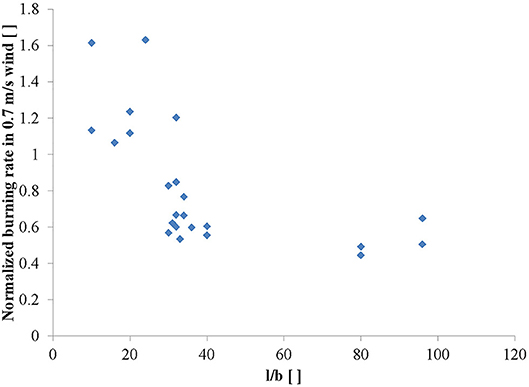
Figure 9. Burning rate under 0.7 m/s normalized by quiescent case as a function of the aspect ratio of the crib (l/b).

Though a surprisingly simple criteria, this ratio has physical meaning. In a quiescent environment, cribs with small aspect ratios are able to entrain air into the fuel bed from the sides efficiently enough so that the burning rate does not change significantly when flow from the bottom is completely blocked, for example by placing the crib directly on the ground (McAllister and Finney, 2016b). Because the sticks are relatively short, the horizontal distance to the center of the crib is relatively small. As cribs are built by stacking the sticks, the gap the air must pass through is a function of the stick thickness, so the thicker the stick, the less flow resistance encountered. In contrast, cribs with large aspect ratios rely heavily on airflow from underneath the crib. In these cases, the burning rate can decrease dramatically if the flow from underneath is blocked or restricted at all (McAllister and Finney, 2016b). When the sticks are long and thin, the air must travel further horizontally to the center and encounters a larger flow resistance. Additionally, though the fuel elements here are in arrays, Hoerner (1965) shows that the drag coefficient for a rectangular plate in cross flow doubles as the aspect ratio increases from 10 to ∞ as the flow transitions from three dimensional flow to two dimensional flow. Note that the drag coefficient for aspect ratios less than this is nearly constant at the minimum value. It is unsurprising then, that the air flow in from the sides of the cribs is much reduced as the aspect ratio increases.

However, the large aspect ratio cribs never relied on flow from the sides, so this horizontal flow diversion around the fuel bed shouldn't have a large effect on the burning rate. Thus, a second factor limiting the airflow in the crib may be at play here as well. In the wind, the flames are blown over so that they hug both the top and bottom of the crib as demonstrated in Figure 10A. The flames act to block air from diffusing into the fuel bed, but also are a great visible flow tracer indicating that there is very little flow entering the bottom of the crib. This perhaps could be because the flow going underneath is forced through a relatively small gap, generating an increased horizontal momentum that is difficult to redirect vertically. Additionally, by tipping the plume over, the driving force pulling air up through the bottom of the crib is significantly reduced. Because the plume is tilted in even the lowest wind speed tested here (see Figure 10B), this absence of flow from underneath could not only explain the decreasing burning rate but also why it is nearly constant with wind speed for several of these diminished cases (crib design #s 7, 16, 17, 18, 21, and 23).

FIGURE 10

Figure 10. Crib design #22 in 0.7 m/s (A) and 0.24 m/s (B) wind from behind demonstrating flames hugging the top and bottom sides of the fuel bed, blocking airflow from below.

Summary

The burning rate and residence time of porous fuel beds are important fire behavior metrics relevant to both structure and wildland fires. Unfortunately, the effect of wind is largely unknown. This work set out to understand how the fuel bed properties interact with the wind to dictate the burning rate. Twenty three crib designs were tested in a range of wind speeds and it was seen that the effect of wind was dependent on the fuel bed structure. For cribs with a small aspect ratio, defined as the ratio of the stick length to the thickness (l/b), the burning rate increased with wind speed. This increase was more pronounced for densely-packed fuel beds that are, by definition, ventilation limited. Loosely-packed fuel beds also had a modest increase in the burning rate due to increased char oxidation. For cribs with a large aspect ratio (l/b > 30), the burning rate decreased with wind. This decrease was likely due to flow patterns that limited flow through the sides, but primarily up through the bottom of the crib.

These results are likely most applicable to isolated, small clumps of elevated fuel (trees and shrubs) where the wind has the opportunity to divert around the fuel bed and would ordinarily flow vertically up into the fuel. Future work will include experiments that will force the airflow to actually pass through the fuel bed. To understand the effect of wind in surface fires, these experiments will include tests that block the flow from below.

Data Availability

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

The work was funded by the National Fire Decision Support Center.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank Sophia Vernholm for her tireless and careful construction of the fuel beds; Cyle Wold for setting up the data acquisition system; Mark Finney, Jason Forthofer, and Torben Grumstrup for many discussions; and Isaac Grenfell for help with data analysis.

References

Albini, F. A., and Baughman, R. G. (1979). U.S. Forest Service Research Note INT-221. Intermountain Forest and Range Experiment Station. Ogden, Utah.

Google Scholar

Alvares, N. J., Foote, K. L., and Pagni, P. J. (1984). Forced ventilation enclosure fires. Combust. Sci. Technol. 39, 55–81. doi: 10.1080/00102208408923783

CrossRef Full Text | Google Scholar

Beaufait, W. R. (1965). Characteristics of Backfires and Headfires in a Pine Needle Fuel Bed. U.S. Forest Service Research Note INT-39, Intermountain Forest and Range Experiment Station. Ogden, Utah.

Google Scholar

Beyler, C. L. (1991). “Analysis of compartment fires with overhead forced ventilation,” in Fire Safety Science–Proceedings of the Third International Symposium, 291–300. doi: 10.3801/IAFSS.FSS.3-291

CrossRef Full Text | Google Scholar

Beyler, C. L. (2008). “Fire hazard calculations for large, open hydrocarbon fires,” in SFPE Handbook of Fire Protection Engineering, 4th Edn, eds P. J. DiNenno, D. Drysdale, C. L. Beyler, W. D. Walton, R. L. P. Custer, J. R. Hall Jr., and J. M. Watts (Quincy, MA: National Fire Protection Association), 2591–3493.

Google Scholar

Block, J. A. (1971). A theoretical and experimental study of non-propagating free-burning fires. Symp. Combust. 13, 971–978. doi: 10.1016/S0082-0784(71)80097-8

CrossRef Full Text | Google Scholar

Carvel, R. O., Beard, A. N., Jowitt, P. W., and Drysdale, D. D. (2001). Variation in the heat release rate with forced longitudinal ventilation for vehicle fires in tunnels. Fire Saf. J. 36, 569–596. doi: 10.1016/S0379-7112(01)00010-8

CrossRef Full Text | Google Scholar

Chow, W. K., and Chan, W. L. (1993). Experimental studies on forced-ventilated fires. Fire Sci. Technol. 13, 71–87. doi: 10.3210/fst.13.1_71

CrossRef Full Text | Google Scholar

Gross, D. (1962). Experiments on the burning of cross piles of wood. J. Res. Nat. Bureau Stand. C Eng. Instrument. 66c, 99–105. doi: 10.6028/jres.066C.010

CrossRef Full Text | Google Scholar

Grumer, J., and Strasser, A. (1965). Uncontrolled fires–specific burning rates and induced air velocities. Fire Technol. 1, 256–268. doi: 10.1007/BF02588468

CrossRef Full Text | Google Scholar

Harmathy, T. Z. (1978). Experimental study on the effect of ventilation on the burning of piles of solid fuels. Combust. Flame 31, 259–264. doi: 10.1016/0010-2180(78)90138-4

CrossRef Full Text | Google Scholar

Heskestad, G. (1973). Modeling of enclosure fires. Symp. Combust. 14, 1021–1030. doi: 10.1016/S0082-0784(73)80092-X

CrossRef Full Text | Google Scholar

Heskestad, G. (2006). Heat of combustion in spreading wood crib fires with application to ceiling jets. Fire Saf. J. 41, 343–348. doi: 10.1016/j.firesaf.2006.01.008

CrossRef Full Text | Google Scholar

Hoerner, S. F. (1965). Fluid-Dynamic Drag, 2nd Edn. Midland Park, NJ, 3-15, 3-16.

Google Scholar

Ingason, H., and Li, Y. Z. (2010). Model scale tunnel fire tests with longitudinal ventilation. Fire Saf. J. 45, 371–384. doi: 10.1016/j.firesaf.2010.07.004

CrossRef Full Text | Google Scholar

Ingason, H., and Lönnermark, A. (2010). “Effects of longitudinal ventilation on fire growth and maximum heat release rate,” in Fourth International Symposium on Tunnel Safety and Security (Frankfurt), 17–19.

Google Scholar

Lönnermark, A., and Ingason, H. (2008). “The effect of air velocity on heat release rate and fire development during fires in tunnels,” in Fire Safety Science –Proceedings of the Ninth International Symposium, 701–712. doi: 10.3801/IAFSS.FSS.9-701

CrossRef Full Text | Google Scholar

McAllister, S., and Finney, M. (2016a). The effect of wind on burning rate of wood cribs. Fire Technol. 52, 1035–1050. doi: 10.1007/s10694-015-0536-4

CrossRef Full Text | Google Scholar

McAllister, S., and Finney, M. (2016b). Burning rates of wood cribs with implications for wildland fire. Fire Technol. 52, 1755–1777. doi: 10.1007/s10694-015-0543-5

CrossRef Full Text | Google Scholar

Nelson, R. M. (2003). Reaction times and burning rates for wind tunnel headfires. Int. J. Wildl. Fire 12, 195–211. doi: 10.1071/WF02041

CrossRef Full Text | Google Scholar

Pagni, P. J., and Peterson, T. G. (1973). Flame spread through porous fuels. Symp. Combust. 14, 1099–1107. doi: 10.1016/S0082-0784(73)80099-2

CrossRef Full Text | Google Scholar

Peatross, M. J., and Beyler, C. L. (1997). “Ventilation effects on compartment fire characterization,” in Fire Safety Science–Proceedings of the Fifth International Symposium, 403–414. doi: 10.3801/IAFSS.FSS.5-403

CrossRef Full Text | Google Scholar

Quintiere, J. G. (2006). Fundamentals of Fire Phenomena. West Sussex: John Wiley and Sons. doi: 10.1002/0470091150

CrossRef Full Text | Google Scholar

Quintiere, J. G. (2017). Principles of Fire Behavior, 2nd ed. New York, NY: CRC Press.

Google Scholar

Rothermel, R. C. (1967). Airflow Characteristics–Wind Tunnels and Combustion Facilities Northern Forest Fire Laboratory. Laboratory Report, Northern Forest Fire Laboratory, Intermountain Forest & Range Experiment Station, Forest Service, U.S. Department of Agriculture, Missoula, Montana.

Google Scholar

Scott, J. H., and Burgan, R. E. (2005). Standard Fire Behavior Fuel Models: A Comprehensive Set for Use With Rothermel's Surface Fire Spread Model. General Technical Report RMRS-GTR-153. U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station, Fort Collins, CO.

Google Scholar

Steward, F. R., and Tennankore, K. N. (1981). The measurement of the burning rate of an individual dowel in a uniform fuel matrix. Symp. Combust. 18, 641–646. doi: 10.1016/S0082-0784(81)80069-0

CrossRef Full Text | Google Scholar

Tewarson, A., and Pion, R. F. (1976). Flammability of plastics- I. Burning intensity. Combust. Flame 26, 85–103. doi: 10.1016/0010-2180(76)90059-6

CrossRef Full Text | Google Scholar

Thomas, P. H. (1965). Fire Spread in Wooden Cribs: Part III the Effect of Wind. Fire Research Note No. 600, Fire Research Station, Ministry of Technology and Fire Offices' Committee Joint Fire Research Organization.

Google Scholar

Zukoski, E. E. (1995). “Properties of fire plumes,” in Combustion Fundamentals of Fire, ed G. Cox (London: Academic Press), 101–219.

Google Scholar