Determination of the Corrosion Rate of Steel Bars in Concrete Based on the Porosity of Interfacial Zone

In the present paper, a simple model to predict the corrosion rate of steel bars in concrete is developed, considering the influence of the porosity of steel-concrete interfacial zone. Firstly, a model for the porosity of the interfacial zone is developed basing on the water-cement ratio gradient in the interfacial zone. Then the relationship between the porosity of the interfacial zone and the corrosion parameters of the steel bar in concrete is discussed, the anode-cathode ratio for the electrochemical corrosion process, the chloride threshold value and the resistivity of concrete are determined by the porosity of steel-concrete interfacial zone. The corrosion rate of steel bars, which is taken as the corrosion current density, is calculated by considering the cathodic concentration polarization of oxygen diffusion and resistance polarization of concrete, basing on the determined parameters above. Finally, the applicability and efficiency of the corrosion rate prediction model is verified by experiments.

Introduction

Reinforced concrete is the most widely used construction materials in the world. In the service life of reinforced concrete structure, the steel bars embedded in concrete face corrosion problems due to carbonization and chloride ions ingression of concrete, which causes cracking/spalling of concrete cover and strength degradation of the steel bar (Yu et al., 2017). Therefore, corrosion of steel bars is one of the major deterioration mechanism that threatens the durability of reinforced concrete structures.

The corrosion process of steel bar in concrete can be divided into two stages: corrosion initiation stage and corrosion propagation stage. The corrosion rate of steel bar in the propagation stage is defined as the speed of corrosion reaction. The corrosion rate not only describes the reduction rate of effective cross-section of the steel bar, which significantly influences the load bearing capacity of the structure, but also describes the formation and accumulation rate of corrosion products, which is closely related to the expansion cracking of concrete cover. Thus, the corrosion rate of steel bars has a significant influence on the durability of reinforced concrete structures.

In recent years, the corrosion rate of steel bars in concrete has been extensively studied, and various prediction models based on the electrochemical principle have been put forward (Otieno et al., 2011), in which, the corrosion rate is often represented by corrosion current density (Isgor and Razaqpur, 2006). Numerical models are developed to describe the electrochemical corrosion process, in which the distribution of the corrosion potential within the concrete cover is calculated by second order partial differential equation. Kranc and Sagüés (2001) proposed a numerical model with nonlinear boundary conditions determined by the electrochemical polarization process and mass transport process. Kim and Kim (2008) proposed a numerical model for localized corrosion rate in concrete, considering the influence of chloride ions around the steel bars. Bo et al. (2016) proposed an improved numerical model, considering the influences of temperature and relative humidity on the corrosion reaction control process. However, numerical model is too complicated for engineering, due to the time-consuming solution of partial differential equations. Some researchers developed simplified models to predict the steel bar corrosion rate, basing on the electrochemical corrosion control process. Song (1999) developed a simple model based on the cathodic polarization of corrosion. Jiang and Yuan (2012) established a model based on the activation polarization of corrosion. Arpit et al. (2019) proposed a model for steel bars by using the Butler Volmer equation, basing on the electrochemical reaction kinetics. However, for the simplified models, as well as the numerical models, the electrochemical corrosion parameters are difficult to be determined, and usually empirical values are adopted for the corrosion rate prediction, affecting the accuracy of the predicted results.

Electrochemical corrosion parameters are the key to predict the corrosion rate of steel bars. The chloride threshold value of concrete controls the depassivation of the steel bars and determines the initiation of the corrosion process. Kenny and Katz (2020) found that the threshold value is affected by the surface voids on the steel bar, and it increases with the decrease of the steel-concrete distance, which is determined by the pore size of the steel-concrete interfacial zone. Besides, the anode-cathode ratio a/c is also an essential parameter in the electrochemical process, when a/c = 0.2, the corrosion rate of the steel can be about 100 times higher than that of a/c = 10 (Chi, 2009). However, the anode-cathode ratio a/c is difficult to be quantified, due to the uncertainty of cathode area and anode area of the steel bar. Research (Angst et al., 2019) shows that the corrosion of steel bars occurs at the surface contacting with concrete pores, which is mainly because pores at the interfacial zone provide a primary pathway for chloride ingression, which can induce corrosion of steel bars. In addition, the chloride diffusion coefficient in the interfacial zone is 6–12 times greater than that in the bulk paste (Wu et al., 2015; Zhu et al., 2017), which decreases the resistivity of the concrete and accelerate the corrosion process due to the high porosity (Soylev and François, 2003). Thus, it can be summarized that the corrosion of steel bars in concrete is closely related to the pores in the steel-concrete interfacial zone. Therefore, in order to accurately determine the electrochemical parameters, it is necessary to consider the effect of the porosity of steel-concrete interfacial zone.

In this paper, the porosity of steel-concrete interfacial zone is considered to predict the corrosion rate of steel bars in concrete. Firstly, a model for the porosity of the interfacial zone is developed. Then the relationship between the porosity of the interfacial zone and electrochemical corrosion parameters is discussed, the anode-cathode ratio for the electrochemical corrosion process, the chloride threshold value and the resistivity of concrete are determined by the porosity of interfacial zone. The corrosion rate is calculated by a simple model that considers the cathodic concentration polarization of oxygen diffusion and resistance polarization of concrete pore solution, basing on the determined parameters. Finally, the applicability and efficiency of the corrosion rate prediction model is verified by experiments.

Determination of Porosity of Interfacial Zone

Over the past decades, much information has become available about the pore structure of steel-concrete interfacial zone. The quantification of the porosity in the interfacial zone can be performed by means of two techniques: Backscattered Electron (BSE) imaging technique, which gives local data, and mercury intrusion porosimetry technique, which gives bulk data. In this study, in order to investigate the porosity distribution in the interfacial zone, test data based on BSE imaging technique in literature (Belaid et al., 2001; Horne et al., 2007; Fangjie et al., 2018; Fangjie et al., 2019) is considered. In Horne’s study (Horne et al., 2007), the sections of specimens were observed in the scanning electron microscope, and the porosity of the interfacial zone were obtained based on the average atomic number contrast and displayed as a percentage of the total area in the BSE image. The measured porosity distribution in the steel-concrete interfacial zone is illustrated in Figure 1. It can be seen that, the porosity is high at the contact with steel bar and gradually decreases with distance from the surface of the steel bars, finally converges to the levels of porosity observed in the bulk paste.

FIGURE 1

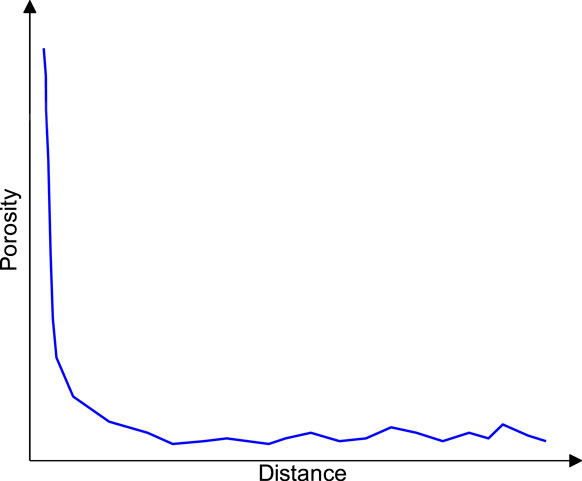
FIGURE 1. Porosity distribution in steel-concrete interfacial zone (Horne et al., 2007).

The porosity distribution in the interfacial zone be explained by the “wall effect” of cement grains (Lin et al., 2019). Olliver et al. (1995) found that the cement particles in interfacial zone are constrained by a “packing” effect imposed by the steel bar surface, which is called the “wall effect,” leading to a gradient of cement grain volume fraction α_c in the interfacial zone. The “wall effect” has been extensively studied in previous researches, some studies are mainly focused on the numerical explanation of the “wall effect,” among which, random packing models of particles have been developed and proved to be effective (Xu and Chen, 2012a; Xu and Chen, 2012b; Xu and Chen, 2013; Xu et al., 2013a; Xu et al., 2013b; Xu et al., 2019). These models can describe the mesostructure of concrete by randomly packing the 2D or 3D particles, considering that concrete is composed of randomly packed aggregate particles and cement particles. While some research focused on the laboratory experiments and obtained a distribution of the volume fraction of the solid particles (Yang and Yan, 2009). In this study, in order to simplify the calculation process, the gradient of the cement grain volume fraction in interfacial zone is described as follows (Nadeau, 2002), which is a regression equation from the test data:

${\alpha }_c\left(x\right)=\{\begin{array}{l}{\stackrel{\prime }{\alpha }}_c[1+a_c{\left(\frac{x-\delta }{\delta }\right)}^2],0\le x\le \delta \hfill \\ {\stackrel{\prime }{\alpha }}_c,x>\delta \hfill \end{array}(1)$

where x is the distance from the surface of the steel bar, δ is the thickness of the interfacial zone, and ${\stackrel{\prime }{\alpha }}_c$ is the volume fraction of cement in the bulk paste; a_c is a fitting parameter. With the limited information of the cement grain distribution in steel-concrete interfacial zone, it is often assumed that the steel-concrete interfacial zone is similar as the aggregate-paste zone (Liu and Weyers, 1998). In Horne’s study (Horne et al., 2007), the measured porosity of steel-cement paste interfacial zone and aggregate-cement paste interfacial zone is shown in Figure 2. It can be seen that, there is little difference between them, thus the value of parameter a_c can be equal to that of aggregate-cement paste interfacial zone −0.4959, which has been determined in literature (Nadeau, 2002).

FIGURE 2

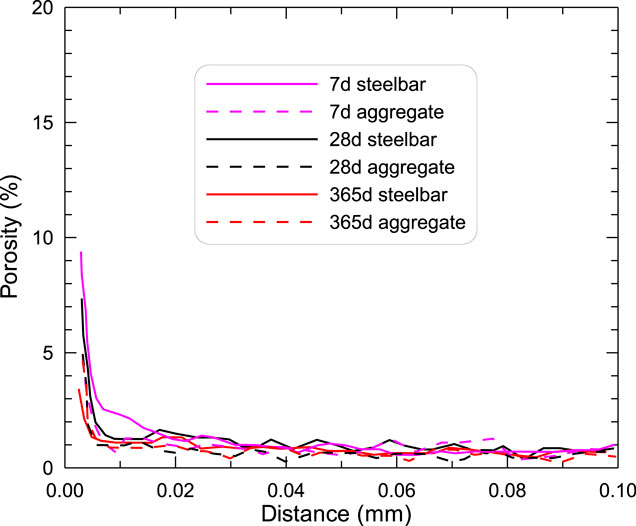
FIGURE 2. Porosity distribution in steel-concrete interfacial zone and aggregate-paste interfacial zone (Horne et al., 2007).

Since corrosion of steel bar is influenced greatly by the pores on the surface of steel bar, this paper focuses on the pores directly contacting with the steel bar, the porosity on the surface of steel bar φ_sur is calculated as follows.

According to Eq. 1, the volume fraction of cement particles at contact with the steel surface α_c (x = 0) can be expressed as:

${\alpha }_c={\stackrel{\prime }{\alpha }}_c\left(1+a_c\right)(2)$

As the cement grain volume fraction is known, the local water-cement ratio at the contact with the steel surface w/c_i can be calculated as:

$w/c_i=\frac{1-{\alpha }_c}{G_c{\alpha }_c}(3)$

where G_c is the specific gravity of cement. Combining Eq. 2 with Eq. 3, the local water-cement ratio w/c_i in contact with steel bar surface can be expressed as:

$w/c_i=\frac{1-{\stackrel{\prime }{\alpha }}_{c}1+a_c}{G_c{\stackrel{\prime }{\alpha }}_c\left(1+a_c\right)}=\frac{1}{G_c{\stackrel{\prime }{\alpha }}_c\left(1+a_c\right)}-\frac{1}{G_c}(4)$

According to Eq. 3, the volume fraction of cement in the bulk paste ${\stackrel{\prime }{\alpha }}_c$ can be calculated by the water-cement ratio in the bulk paste:

${\stackrel{\prime }{\alpha }}_c=\frac{1}{1+G_{c}w/c}(5)$

Combining Eq. 4 with Eq. 5, the local water-cement ratio w/c_i in contact with the steel bar surface can be expressed as a function of the water-cement ratio in the bulk paste:

$w/c_i=\frac{1+G_{c}w/c}{G_c\left(1+a_c\right)}-\frac{1}{G_c}(6)$

In order to calculate the porosity of the interfacial zone, the hydration degree of the cement should be determined, as the porosity of concrete changes with the hydration process of cement (Zhu et al., 2020). Bentz (2006) proposed a hydration degree model, by relating the instantaneous hydration rate to local probabilities for the dissolution and precipitation of the cement phases, in which the hydration degree of cement can be expressed as:

$\alpha \left(t\right)=\frac{p\left[e^{R\left(1-p\right)t}-1\right]}{e^{R\left(1-p\right)t}-p}(7)$

where $p={\rho }_{\mathrm{c}\mathrm{e}\mathrm{m}}\left(w/c\right)/\left(f_{exp}+{\rho }_{\mathrm{c}\mathrm{e}\mathrm{m}}CS\right)$ and $R=q\left(f_{\mathit{exp}}+{\rho }_{\mathrm{c}\mathrm{e}\mathrm{m}}CS\right)/{\left[1+{\rho }_{\mathrm{c}\mathrm{e}\mathrm{m}}\left(w/c\right)\right]}_2$, ρ_cem is the density of cement, f_exp is the volumetric expansion coefficient, CS is the chemical shrinkage of cement and q is a constant.

As the water-cement ratio and the hydration degree of cement are both known, the porosity can be calculated by Power’s model (Powers and Brownyard, 1946), which can be expressed as:

$\phi =\frac{w/c-0.36\alpha }{w/c+0.32}(8)$

where w/c is the water-cement ratio of the paste, in this study, w/c can be taken as the local water-cement ratio w/c_i in contact with the steel bar surface; α is the hydration degree of cement in contact with the steel bar surface.

It should be noted that, the porosity of steel-concrete interfacial zone is also related to the direction of steel bar. For the horizontally cast steel bar, the porosity of the topside and the underside is quite different due to the water bleeding effect. In order to eliminate the influence of water bleeding, only vertically cast steel bar is considered for the porosity prediction in this study.

Corrosion Rate Prediction

Anode-cathode Ratio

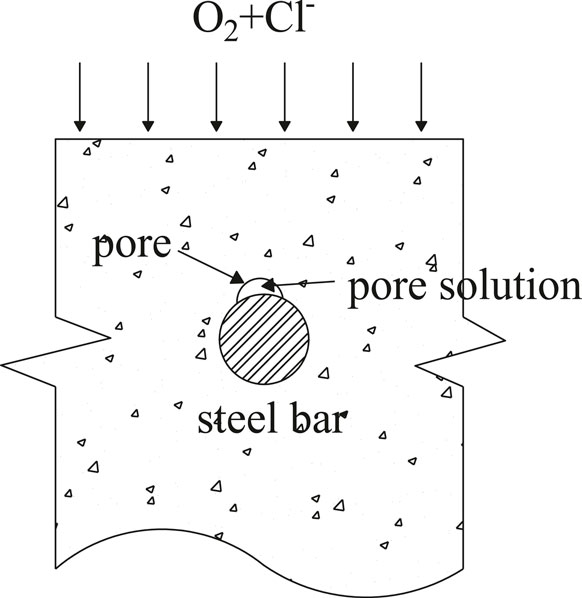
Corrosion of steel bars in concrete is an essentially complex process. Chloride ions diffuses through the concrete pore solution to the surface of steel bar, if the concentration of chloride ions reaches a critical value (threshold), the steel becomes active. The anode forms at the activated region where the steel bar contacting with the pore solution containing chloride, and the cathode forms at the passive region, as shown in Figure 3.

FIGURE 3

FIGURE 3. Corrosion mechanism of steel bar in concrete.

Therefore, the anode-cathode ratio is closely related to the pore in contact with the steel bar surface. In this study, anode-cathode ratio is determined by the porosity of the steel-concrete interfacial zone in contact with the steel bar. Therefore, the anode-cathode ratio a/c, which is defined as the ratio of anodic area to cathodic area, can be expressed as:

$a/c=A_{anode}/A_{cathode}=\frac{{\phi }_{sur}\cdot A_{steel}}{\left(1-\phi \right)A_{steel}}=\frac{{\phi }_{sur}}{1-{\phi }_{sur}}(9)$

where A_anode is the area of anodic region; A_cathode is the area of cathodic region; A_steel is the surface area of reinforcing bar; φ_sur is the porosity of concrete at the contact with steel bar.

Chloride Threshold Value

When the concrete chloride content at the steel bar surface exceeds a certain value, which is defined as the chloride threshold, depassivation of the steel bar occurs and the corrosion process initiates. A change of the chloride threshold can have a significant effect on the corrosion process of the steel bars. Observation of the corroded concrete structures shows that corrosion of steel bar initiates at the surface voids and steel-concrete interface with lower porosity can delay the initiation of corrosion (Angst et al., 2019), indicating that lower porosity of the interfacial zone can increase the chloride threshold. Kenny and Katz (2020) conducted a statistical analysis of the relationship between the chloride threshold and steel-concrete interfacial zone properties. Sixteen different concrete mixes were produced with water-cement ratios between 0.40 and 0.65, water-powder ratios ranging from 0.91 to 1.36. The specimens were subjected to cycles consisting of 2 weeks immersion in a 6% (mass%) NaCl solution followed by two weeks of air-drying. Corrosion initiation was monitored by measuring the potential difference between steel bars in each concrete specimen. The concentration of chloride was measured by drilling in each specimen, along a line parallel to the steel rebar. And the porosity of the steel-concrete interfacial zone was achieved by the BSE imaging analysis. The measured chloride threshold and porosity of interfacial zone for the different mixes are shown in Figure 4.

FIGURE 4

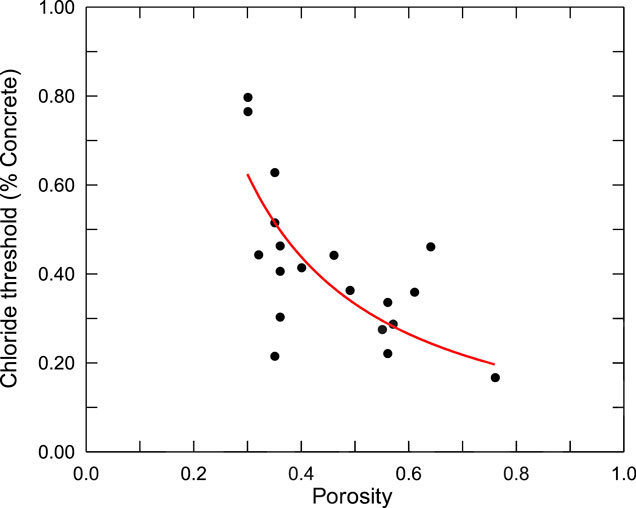
FIGURE 4. Measured chloride threshold and porosity (Kenny and Katz, 2020).

It can be seen that, with the increase of porosity of the steel-concrete interfacial zone, the chloride threshold decreases gradually, which can be expressed by the following regression equation, denoted as the red line in Figure 4:

$C_t=\frac{0.15}{{\phi }^{1.2}}-0.012(10)$

where C_t is the chloride threshold (mass% of concrete); φ is the porosity of steel-concrete interfacial zone.

Resistivity of Interfacial Zone

When the corrosion of steel bar occurs, electrons flow from anode to cathode through concrete, thus the resistivity of concrete has a close relationship with the corrosion rate of steel bar. In fact, ions can only migrate in the pore solution of concrete, thus the resistivity of concrete is mainly related to the characteristics of the concrete porosity. According to the modified Archie’s law (Andrade et al., 2012), the resistivity of concrete can be expressed by:

${\rho }_e={\rho }_0{\phi }^{-\tau }(11)$

where ρ₀ is the electrical resistivity of the pore aqueous phase (approximately 0.5 Ωm) and τ is a parameter which can be determined by experiments.

In Bediwy’s study (Bediwy and Bassuoni, 2018), 43 mixtures of concrete samples, including different water-cement ratios (0.3, 0.35, 0.4, 0.5, 0.6, 0.7) and different amount of cementitious materials, were prepared to investigate the porosity and the electrical resistivity of concrete. A two-pin bulk resistance meter was used to determine the bulk resistivity of the concrete samples and the porosity of concrete samples was measured by Mercury Intrusion Porosimetry. The measured results are shown in Figure 5.

FIGURE 5

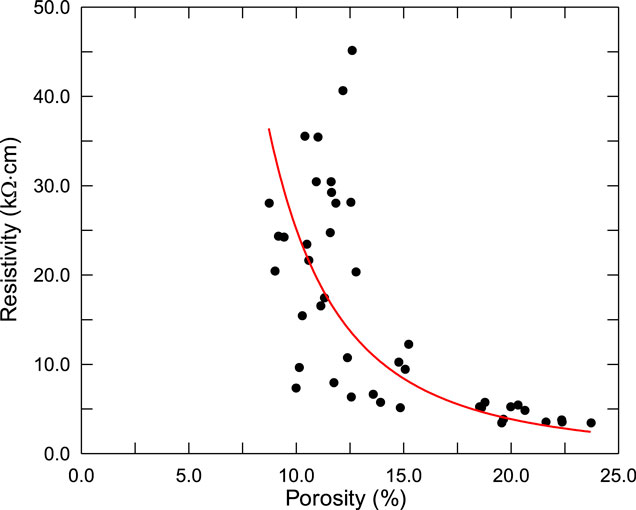
FIGURE 5. Measured resistivity and porosity (Bediwy and Bassuoni, 2018).

It can be seen that, with the increase of concrete porosity, the resistivity of concrete decreases gradually, and when the porosity exceeds 20%, the resistivity gradually converges to a constant value. Thus, the resistivity of concrete ρ can be expressed as follows, denoted as the red line in Figure 5:

$\rho =\{\begin{array}{l}{\rho }_0{\phi }^{-2.7},\phi \le 20\%\hfill \\ {0.2}^{-2.7}{\rho }_0,20\%<\phi \le 100\%\hfill \end{array}(12)$

In fact, the electrical resistivity ρ is also influenced by chloride ion concentration and the relative humidity in concrete, which can be expressed as:

$\rho =\{\begin{array}{l}{\rho }_0{\phi }^{-2.7}{K}_{Cl}{K}_h,\phi \le 20\%\\ {0.2}^{-2.7}{\rho }_0{K}_{Cl}{K}_h,20\%<\phi \le 100\%\end{array}(13)$

where K_Cl considers the influence of chloride concentration $C_{cl},K_{cl}=1–4C_{cl}$ when C_Cl < 2%, and K_Cl = 0.72 when C_Cl > 2% (Feng et al., 2018); K_h considers the influence of relative humidity h, K_h can be calculated as (Bo et al., 2016):

$K_h=\frac{1}{-1.3059h^2+3.6050h-1.3270}\left(R^2=0.99\right)(14)$

Corrosion Rate of Steel bar

The corrosion of steel bar in concrete is controlled by two polarization processes: cathodic concentration polarization of oxygen diffusion process and resistance polarization of concrete pore solution. Oxygen in concrete mainly diffuses through the pores not occupied by liquid water, while OH⁻ produced by the cathodic reaction mainly diffuses through the pore solution. When the relative humidity in concrete is high, the oxygen diffusion coefficient is small, the steel bar corrosion process is controlled by oxygen diffusion. When the relative humidity in concrete is low, the diffusion of OH⁻ in pore solution is very difficult, and the corrosion process is controlled by resistance polarization, due to the electric resistance of pore solution in concrete.

When the corrosion process of steel bar is completely controlled by oxygen concentration polarization, the corrosion rate can be calculated by the following equation, which is also the limitation of the current density (Song, 1999):

$i_{corr}=S{n}_{c}F{D}_{O_2}\frac{C_{O_2}}{C\left(1+a/c\right)}(15)$

where S is the solubility of oxygen, S = 0.028; n_c is the number of exchanged electrons in the cathodic reaction, n_c = 4; F is the Faraday constant, F = 96,494 C/mol; $C_{o_2}$ is the concentration of oxygen at the surface of concrete; C is the thickness of concrete cover; a/c is the anode-cathode ratio; $D_{o_2}$ is the oxygen diffusion coefficient, which can be calculated as (Xiao, 1995):

$D_{O_2}=1.92\times {10}^{-6}\times {\phi }^{1.8}\times {\left(1-h\right)}^{2.2}(16)$

where φ is the porosity of concrete, can be taken as the porosity in bulk paste, because the thickness of the steel-concrete interfacial zone is very small relative to the steel bar cover thickness; h is the relative humidity in concrete.

When the corrosion process of the steel bar is completely controlled by resistance polarization, the corrosion rate can be calculated by the following equation established by Alonso et al. (1988):

$i_{corr}=\frac{k_{corr}}{\rho }(17)$

where ρ is the concrete resistivity; k_corr is a fitting factor, k_corr = 1.0 V/m.

Considering that the corrosion of steel bars is controlled by the two processes mentioned above, the corrosion rate of steel bars in concrete can be expressed as:

$i_{corr}=\min \left[S{n}_{c}F{D}_{O_2}\frac{C_{O_2}}{C\left(1+a/c\right)},\frac{k_{corr}}{\rho }\right](18)$

It should be noted that, the calculated corrosion rate of steel bar in concrete is only for the corrosion propagation stage that the chloride ion concentration at the steel bar surface exceeds the chloride threshold. If the chloride concentration is lower than the threshold, the corrosion process will not occur and the corrosion rate of steel bar is equal to 0 A/m².

Verification of the Model

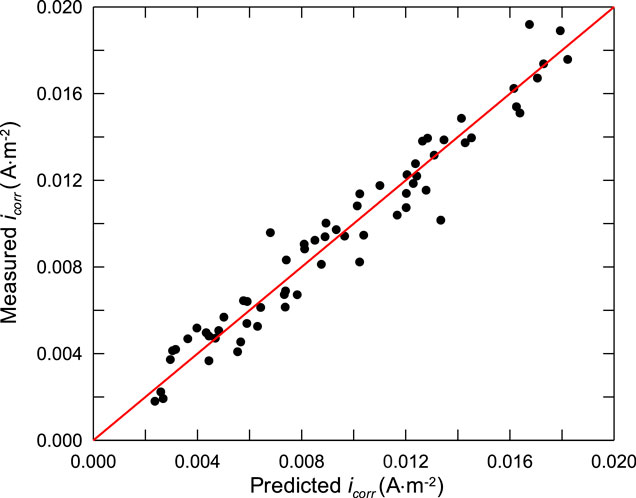
In order to verify the accuracy of the developed corrosion rate model of steel bar, accelerated corrosion test of steel bars in different concrete mixes was carried out. To eliminate the uncertainty caused by the calculation of chloride concentration when verifying the prediction model, NaCl was directly added into concrete during mixing, instead of soaking the specimens into NaCl solutions for chloride ingression. This is credible and feasible, because there is little evident difference of the chloride threshold between the condition of chloride addition and chloride penetration (Alonso and Sanchez, 2015), although the formation of passive films of steel in alkaline concrete pore solutions is affected by admixed chloride ions. Furthermore, the corrosion rate of steel is well related to concrete resistivity and the porosity of steel-concrete interfacial zone, no matter the corrosion is initiated by admixed chloride ions or penetrated chloride ions, this is because the corrosion rate of steel bars in concrete is mainly controlled by two polarization processes: cathodic concentration polarization of oxygen diffusion process and resistance polarization of concrete pore solution, which is mainly determined by the relative humidity of concrete, rather than the chloride penetration process. And the resistance of concrete is determined by the characteristics of concrete pore solution, which is affected by the porosity of steel-concrete interfacial zone and the chloride concentration, rather than the chloride penetration process.

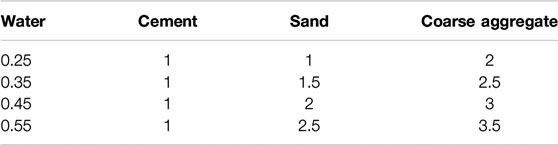
In the corrosion test, ordinary Portland cement with grade of 42.5, coarse aggregate with maximum size of 15 mm and natural river sand (fine aggregate) were used for the concrete preparation. Test specimens were cast with four water-cement ratios (0.25, 0.35, 0.45, 0.55), the mix proportion is shown in Table 1. For each concrete mix proportion, different amount of NaCl (1%, 2%, 3%, 4%, weight% of concrete) was added.

TABLE 1

TABLE 1. Mix proportion.

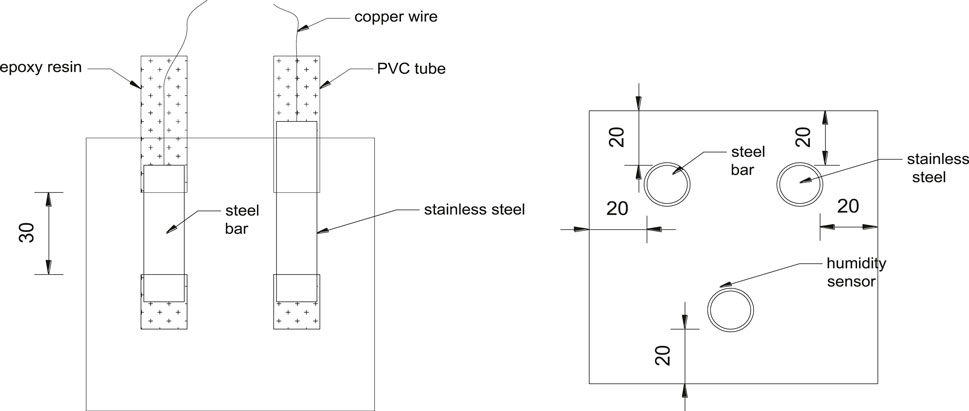
Concrete specimens were cast into 100 mm × 100 mm × 100 mm, HPB330 steel bar with diameter of 14 mm was embedded in concrete with cover thickness of 20 mm for corrosion test. Before casting, the steel bar was polished with sandpaper, a copper wire was welded on the end part of one side, and both end sides of the steel bar were wrapped with polyvinyl chloride plastic pipe. The length of the exposed part in concrete is 3 cm, so that the exposed area is 9.42 cm², the test specimen is shown in Figure 6. The specimens were demoulded after 2 days of casting, and then moved to the curing room with a constant temperature of (20 ± 2)°C and relative humidity of (60 ± 2)%. Considering that the relative humidity of concrete is an important factor in corrosion rate prediction, in order to eliminate the uncertainty caused by the calculation process of concrete relative humidity, the relative humidity at the same depth with the steel bar in concrete was directly monitored by embedded sensors. The corrosion rate of the steel bars was measured at curing age of 7, 14, 28, and 60 days by electrochemical technique. The corrosion current density of the steel bar in concrete, which is used to characterize the corrosion rate, were measured by linear polarization method with electrochemical workstation Parstat2263. During the test, the exposed area of the embedded steel bar was taken as the working electrode, the embedded stainless steel bar was taken as the auxiliary electrode, and the Cu-CuSO₄ electrode was taken as the reference electrode. The scanning range of the test was ±20 mV and the scanning rate was 0.167 mV/s. The corrosion rate of the steel bars was calculated by Stern and Geary (1957) equation, basing on the polarization resistance R_p values obtained by linear polarization measurements, and can be expressed as:

$i_{corr}=\frac{B}{R_P}(19)$

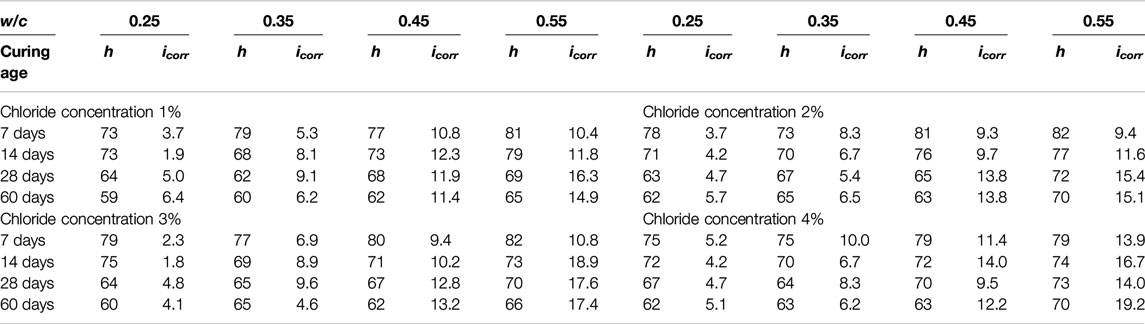
where B is a constant, and can be equal to 26 mV for the corrosion process of steel bars. The measured corrosion current density of steel bars and corresponding relative humidity in concrete are listed in Table 2.

FIGURE 6

FIGURE 6. Electrochemical test specimen.

TABLE 2

TABLE 2. Measured relative humidity (%) and corrosion current density (10⁻³ A/m²).

It can be seen from the test results that the corrosion rate of steel bars decreases with the decrease of the water-cement ratio of concrete. This is mainly due to the decrease of the porosity of concrete. Apart from this, the corrosion rate of steel bars does not show any other evident trend, which is mainly due to the coupling effect of many factors, this is also the main reason for the prediction of corrosion rate in this paper.

The density of ordinary Portland cement used in the experiment is 3.15 g/cm³, the volumetric expansion coefficient f_exp = 1.15, the chemical shrinkage of cement CS = 0.07 ml/g and the fitted parameter q = 0.05 h⁻¹. Since the specimens are directly exposed to atmosphere, the oxygen concentration on the surface of concrete $C_{o_2}$ is taken as 8.67 mol/m³. The parameters used in the prediction model are listed in Table 3, and the comparison between the predicted corrosion current density and measured current density is shown in Figure 7. It can be seen that, the predicted corrosion rate of the steel bars has a good agreement with the measured results, indicating that the proposed model for the corrosion rate of steel bars is accurate and effective.

TABLE 3

TABLE 3. Parameters in the model.

FIGURE 7

FIGURE 7. The predicted and measured corrosion current density.

It should be noted that the prediction model proposed in this paper does not consider the effect of temperature on the corrosion rate of steel bars. The verification experiments and the relevant parameters in the model are all under the condition of room temperature (20°C). Therefore, when the influence of temperature on the corrosion process is considered, the model proposed in this paper needs to be further improved.

Summary and Conclusions

A simple model to predict the corrosion rate of steel bars in concrete is developed considering the effect of steel-concrete interfacial zone porosity, the applicability and efficiency of the corrosion rate prediction model is verified by experiments. The main conclusions can be summarized as follows:

(1) A model for the porosity of the interfacial zone is developed basing on the water-cement ratio gradient in the interfacial zone.

(2) Equations to describe the relationship between chloride threshold, concrete resistivity and porosity of steel-concrete interface are obtained by regression of test data in literatures.

(3) A prediction model for the corrosion rate of steel bars in concrete is obtained by considering the influence of steel-concrete interfacial zone porosity on the anode-cathode ratio, chloride threshold and concrete resistivity.

(4) The proposed model for the corrosion rate of steel bars is verified to be accurate and effective by experiments.

Data Availability Statement

All datasets presented in this study are included in the article.

Author Contributions

ZX did the analysis of the model establishment, YS compared the model results and the data in literatures, and SS did the experiments. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Support from Science and Technology Project of Hebei Transportation Department No. TH‐201925 and No. TH‐201918 is gratefully acknowledged. Contribution of Li Qian, Duan Shichao and Li Pengfei is also gratefully acknowledged.

References

Alonso, M. C., and Sanchez, M. (2015). Analysis of the variability of chloride threshold values in the literature. Mater. Corros. 60 (8), 631–637. doi:10.1002/maco.200905296

CrossRef Full Text | Google Scholar

Alonso, C., Andrade, C., and González, J. A. (1988). Relation between resistivity and corrosion rate of reinforcements in carbonated mortar made with several cement types. Cement Concr. Res. 18 (5), 687–698. doi:10.1016/0008-8846(88)90091-9

CrossRef Full Text | Google Scholar

Andrade, C., Andrea, R. D., and Rebolledo, N. (2012). “Calculation of tortuosity factor for the model based in concrete resistivity,” in Second international conference on microstructural-related durability of cementitious composites, Amsterdam, The Netherlands, April 11–13, 2012.

Google Scholar

Angst, U. M., Geiker, M. R., Alonso, M. C., Polder, R., Isgor, O. B., Elsener, B., et al. (2019). The effect of the steel–concrete interface on chloride-induced corrosion initiation in concrete: a critical review by RILEM TC 262-SCI. Mater. Struct. Constr. 52 (4), 88. doi:10.1617/s11527-019-1387-0

CrossRef Full Text | Google Scholar

Arpit, G., Homayoon, S., Eshmaiel, G., Olubanwo, A. O., and Khorami, M. (2019). Predicting the corrosion rate of steel in cathodically protected concrete using potential shift. Construct. Build. Mater. 194, 344–349. doi:10.1016/j.conbuildmat.2018.10.153

CrossRef Full Text | Google Scholar

Bediwy, A., and Bassuoni, M. T. (2018). Resistivity, penetrability and porosity of concrete: a tripartite relationship. J. Test. Eval. 46 (2), 20160374. doi:10.1520/JTE20160374

CrossRef Full Text | Google Scholar

Belaid, F., Arliguie, G., and Francois, R. (2001). Porous structure of the ITZ around galvanized and ordinary steel reinforcements. Cement Concr. Res. 31 (11), 1561–1566. doi:10.1016/S0008-8846(01)00597-X

CrossRef Full Text | Google Scholar

Bentz, D. P. (2006). Influence of water-to-cement ratio on hydration kinetics: simple models based on spatial considerations. Cement Concr. Res. 36 (2), 238–244. doi:10.1016/j.cemconres.2005.04.014

CrossRef Full Text | Google Scholar

Bo, Y. U., Zhan, L., Liu, J., et al. (2016). Influences of temperature and humidity on control mode and rate of reinforcing steel corrosion. J. Build. Mater. 19 (05), 844–849. doi:1007-9629(2016)05-0844-06

Google Scholar

Chi, C. G. (2009). Research on electrochemical corrosion behavior of 70/30Cu-Ni alloy in seawater. Nanjing, China: Nanjing University of Aeronautics and Astronautics.

Google Scholar

Fangjie, C., Chun-Qing, L., Hassan, B., and Ma, B. (2018). Quantification of steel-concrete interface in reinforced concrete using Backscattered Electron imaging technique. Construct. Build. Mater. 179, 420–429. doi:10.1016/j.conbuildmat.2018.05.246

CrossRef Full Text | Google Scholar

Fangjie, C., Li, C. Q., Hassan, B., and Ma, B. (2019). Effect of design parameters on microstructure of steel-concrete interface in reinforced concrete. Cement Concr. Res. 119, 1–10. doi:10.1016/j.cemconres.2019.01.005

CrossRef Full Text | Google Scholar

Feng, X., Yifei, X., Shuguang, W., Li, W., Liu, W., and Du, D. (2018). Numerical model for corrosion rate of steel reinforcement in cracked reinforced concrete structure. Construct. Build. Mater. 180, 55–67. doi:10.1016/j.conbuildmat.2018.05.215

CrossRef Full Text | Google Scholar

Horne, A. T., Richardson, I. G., and Brydson, R. M. D. (2007). Quantitative analysis of the microstructure of interfaces in steel reinforced concrete. Cement Concr. Res. 37 (12), 1613–1623. doi:10.1016/j.cemconres.2007.08.026

CrossRef Full Text | Google Scholar

Isgor, O. B., and Razaqpur, A. G. (2006). Modelling steel corrosion in concrete structures. Mater. Struct. 39 (3), 291–302. doi:10.1007/s11527-005-9022-7

CrossRef Full Text | Google Scholar

Jiang, J., and Yuan, Y. (2012). Prediction model for the time-varying corrosion rate of rebar based on micro-environment in concrete. Construct. Build. Mater. 35, 625–632. doi:10.1016/j.conbuildmat.2012.04.077

CrossRef Full Text | Google Scholar

Kenny, A., and Katz, A. (2020). Steel-concrete interface influence on chloride threshold for corrosion - empirical reinforcement to theory. Construct. Build. Mater. 244, 118376. doi:10.1016/j.conbuildmat.2020.118376

CrossRef Full Text | Google Scholar

Kim, C.-Y., and Kim, J.-K. (2008). Numerical analysis of localized steel corrosion in concrete. Construct. Build. Mater. 22 (6), 1129–1136. doi:10.1016/j.conbuildmat.2007.02.007

CrossRef Full Text | Google Scholar

Kranc, S. C., and Sagüés, A. A. (2001). Detailed modeling of corrosion macrocells on steel reinforcing in concrete. Corrosion Sci. 43 (7), 1355–1372. doi:10.1016/s0010-938x(00)00158-x

CrossRef Full Text | Google Scholar

Lin, J., Chen, H., Zhang, R., and Liu, L. (2019). Characterization of the wall effect of concrete via random packing of polydispersed superball-shaped aggregates. Mater. Char. 154, 335–343. doi:10.1016/j.matchar.2019.06.024

CrossRef Full Text | Google Scholar

Liu, Y., and Weyers, R. E. (1998). Modeling the time-to-corrosion cracking in chloride contaminated reinforced concrete structures. ACI Mater. J. 95 (6), 675–681.

Google Scholar

Nadeau, J. C. (2002). Water-cement ratio gradients in mortars and corresponding effective elastic properties. Cement Concr. Res. 32 (3), 481–490. doi:10.1016/s0008-8846(01)00710-4

CrossRef Full Text | Google Scholar

Olliver, J. P., Maso, J. C., and Bourdette, B. (1995). Interfacial transition zone in concrete. Adv. Cement Base Mater. 2 (1), 30–38. doi:10.1016/1065-7355(95)90037-3

CrossRef Full Text | Google Scholar

Otieno, M. B., Beushausen, H. D., and Alexander, M. G. (2011). Modelling corrosion propagation in reinforced concrete structures - a critical review. Cement Concr. Compos. 33 (2), 240–245. doi:10.1016/j.cemconcomp.2010.11.002

CrossRef Full Text | Google Scholar

Powers, T. C., and Brownyard, T. L. (1946). Studies of the physical properties of hardened Portland cement paste. J. Proc. 43 (9), 249–336.

Google Scholar

Song, X. B. (1999). Corrosion of reinforcement in reinforced concrete structures. Beijing, China: Tsinghua University.

Google Scholar

Soylev, T. A., and François, R. (2003). Quality of steel-concrete interface and corrosion of reinforcing steel. Cement Concr. Res. 33 (9), 1407–1415. doi:10.1016/s0008-8846(03)00087-5

CrossRef Full Text | Google Scholar

Stern, M., and Geaby, A. L. (1957). Electrochemical polarization. J. Electrochem. Soc. 104 (1), 56–63. doi:10.1149/1.2428496

CrossRef Full Text | Google Scholar

Wu, K., Shi, H., Xu, L., Ye, G., and De Schutter, G. (2015). Microstructural characterization of ITZ in blended cement concretes and its relation to transport properties. Cement Concr. Res. 79, 243–256. doi:10.1016/j.cemconres.2015.09.018

CrossRef Full Text | Google Scholar

Xiao, C. Z. (1995). Corrosion of reinforcement in concrete and analysis of its durability. Tsinghua University.

Google Scholar

Xu, W. X., and Chen, H. S. (2012a). Quantitative characterization of the microstructure of fresh cement paste via random packing of polydispersed Platonic cement particles. Model. Simulat. Mater. Sci. Eng. 20 (7), 075003. doi:10.1088/0965-0393/20/7/075003

CrossRef Full Text | Google Scholar

Xu, W. X., and Chen, H. S. (2012b). Microstructural characterization of fresh cement paste via random packing of ellipsoidal cement particles. Mater. Char. 66, 16–23. doi:10.1016/j.matchar.2012.01.012

CrossRef Full Text | Google Scholar

Xu, W. X., and Chen, H. S. (2013). Numerical investigation of effect of particle shape and particle size distribution on fresh cement paste microstructure via random sequential packing of dodecahedral cement particles. Comput. Struct. 114–115, 35–45. doi:10.1016/j.compstruc.2012.10.009

CrossRef Full Text | Google Scholar

Xu, W., Chen, H., and Liu, L. (2013a). Evaluation of mesostructure of particulate composites by quantitative stereology and random sequential packing model of mono-/polydisperse convex polyhedral particles. Ind. Eng. Chem. Res. 52 (20), 6678–6693. doi:10.1021/ie3025449

CrossRef Full Text | Google Scholar

Xu, W. X., Lv, Z., and Chen, H. S. (2013b). Effects of particle size distribution, shape and volume fraction of aggregates on the wall effect of concrete via random sequential packing of polydispersed ellipsoidal particles. Phys. Stat. Mech. Appl. 392 (3), 416–426. doi:10.1016/j.physa.2012.09.014

CrossRef Full Text | Google Scholar

Xu, W., Wu, Y., and Gou, X. (2019). Effective elastic moduli of nonspherical particle-reinforced composites with inhomogeneous interphase considering graded evolutions of elastic modulus and porosity. Comput. Methods Appl. Mech. Eng. 350, 535–553. doi:10.1016/j.cma.2019.03.021

CrossRef Full Text | Google Scholar

Yang, J., and Yan, P. Y. (2009). Distribution characteristics of coarse aggregate in wall-affecting layer of concrete. J. Build. Mater. 12 (5), 580–583+620. doi:1007-9629(2009)05-0580-05

Google Scholar

Yu, B., Liu, Z. J., and Chen, Z. (2017). Probabilistic evaluation method for corrosion risk of steel reinforcement based on concrete resistivity. Construct. Build. Mater. 138, 101–113. doi:10.1016/j.conbuildmat.2017.01.100

CrossRef Full Text | Google Scholar

Zhu, Z., Chen, H., Liu, L., and Li, X. (2017). Multi-scale modelling for diffusivity based on practical estimation of interfacial properties in cementitious materials. Powder Technol. 307, 109–118. doi:10.1016/j.powtec.2016.11.036

CrossRef Full Text | Google Scholar

Zhu, Z., Xu, Z., Chen, Z., and Tan, Z. (2020). Evolution of microstructures of cement paste via continuous-based hydration model of non-spherical cement particles. Compos. B Eng. 185, 107795. doi:10.1016/j.compositesb.2020.107795

CrossRef Full Text | Google Scholar