Probing on the Stable Structure of Silicon-Doped Charged Magnesium Nanomaterial Sensor: SiMgn±1 (N = 2−12) Clusters DFT Study

The stable structures of silicon-doped charged magnesium nanomaterial sensor, SiMg_n^±1 (n = 2−12) clusters, were systematically investigated using the CALYPSO approach coupled with the density functional theory (DFT). The growth mechanism of SiMg_n^±1 (n = 2−12) nanosensors shows that the tetrahedral and tower-like structures are two basic structures, and almost all other clusters’ geometries are based on their variants. Most importantly, the fascinating SiMg₈^–1 and SiMg₈⁺¹ clusters are obtained through stability calculations of all the lowest energy state of clusters. These two clusters show the strongest local stability and thus can be served as reliable candidates for experimentally fabricated silicon-doped magnesium nanosensor. Electronic structural properties and chemical bonding analysis are also adopted to further study the stability of SiMg₈^–1 and SiMg₈⁺¹ nanosensors. The theoretical calculations of infrared (IR) and Raman spectra of SiMg−1 8and SiMg+1 8clusters show that their strongest spectral frequencies are distributed in the range of 80−240 cm^–1. We believe that our studies will stimulate future synthesis of silicon-doped magnesium in IoT nanosensors.

Introduction

Magnesium and silicon, as important optoelectronics and semiconductor sensor materials, have been the frontier of material science (Delgado et al., 2004; Capitán-Vallvey et al., 2006; Wang et al., 2015; Pradeep et al., 2017). With the widespread application of IoT sensors, the development and research of magnesium or silicon sensor at nanoscale with small size and good performance are increasingly sought after by researchers (Shukla et al., 2004; Pham et al., 2014). New nanosensor is one of the types of nanomaterials which can be studied through theoretical or experimental research (Zeng et al., 2012; Guo et al., 2014; Wang et al., 2020). Generally, experimental nanomaterials research often provides some new preparation methods, and experimental measurement of the physical and chemical quantities of materials. While theoretical studies of nanomaterials always tend to report on some new potential materials and calculate their physical and chemical properties. Notably, one of the most significant theoretical studies on the nanomaterials is that these predicating nanostructures must be stable and experimentally feasible. Fortunately, the atomic clusters is such an interesting and effective approach in theoretically constructing stable nanomaterials. Cluster systems are of extreme interest due to their physical and chemical properties which often vary with the number of atoms they contain, this makes different-sized nanomaterials have different properties.

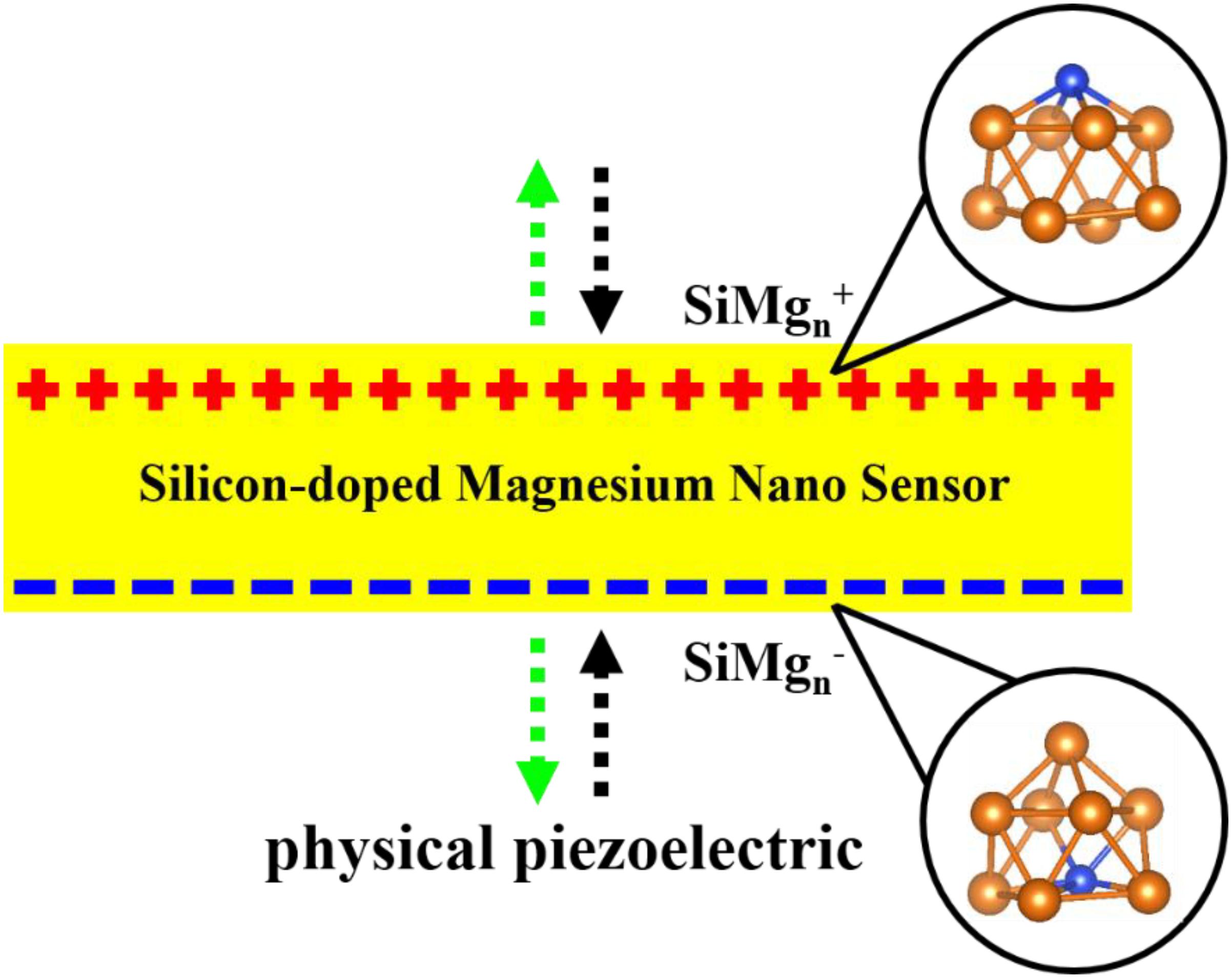
In recent years, there has been an increasing amount of reports on using atomic clusters together with the first-principle to predict new stable nanomaterials as potential sensors (Ding et al., 2015; Jin et al., 2015, 2016; Xia et al., 2016; Li et al., 2017; Chen et al., 2018; Shao et al., 2019; Zhao et al., 2019; Zhang et al., 2020) such as nanomaterials of Zr-B, Ta-B and Fe-O systems, etc. Nanomaterials of silicon and magnesium are inevitable and are studied through their clusters structures. Specifically, taking silicon-containing nanomaterials as an example, Han and Hagelberg (2001), Han et al. (2002, 2007) used density functional theory (DFT) at B3LYP/LanL2DZ level to study MoSi_n (n = 1–6), Mo₂Si_n (9−16), and WSi_n (n = 1–6, 12) clusters. Their investigations show that 9MoSi₃, Mo₂Si₁₀, and WSi₁₆ clusters have relatively higher stability than others and thus can be served as candidates for their experimental stable nanostructures. In addition, a considerable amount of studies have been reported on magnesium clusters (Köhn et al., 2001; Jellinek and Acioli, 2002; Heidari et al., 2011; Xia et al., 2016). These studies theoretically predicted that Mg₄, Mg₁₀ and Mg₂₀ clusters have relatively stable structures. It is exciting that these stable structures can be obtained through cluster spray experiments and can be used as preparations of their corresponding nanomaterials. It is well known that silicon and magnesium are important and widely used materials, such as semiconductors, building materials, sensors and so on, and magnesium silicide thin film sensor is a very interesting research object. When the research interest in magnesium silicide sensors is transferred to the nanometer size, it becomes very necessary to use cluster methods to study silicon-doped magnesium clusters. Surprisingly, to our best knowledge, except for our previous work on silicon doped neutral magnesium clusters (Zhu et al., 2020), few studies have been made on silicon-doped charged magnesium alloy nanomaterials. In addition, the physical and chemical properties of the clusters will vary with their size and charge. Therefore, studying magnesium clusters doped with silicon-doped cations and anions cannot only help enrich our understanding of silicon-doped magnesium at nanoscale, but can also provide some guidance for future applications. Interestingly, as shown in Figure 1, the silicon-doped small-sized anionic and cationic magnesium clusters are also physically equivalent to piezoelectric silicon-doped magnesium clusters. In other words, the piezoelectric state of the SiMg_n cluster can be equivalent to the silicon-doped magnesium nano-piezoelectric sensor to some extent. In short, this paper is to research the silicon-doped magnesium nano piezoelectric sensor and explore their stable structures through density functional theory (DFT) theoretical calculations. The paper is organized as following: Section “Computational Methods” describes the computational methods, the calculation results are reported and completely discussed in Section “Results and Discussions,” and the final conclusions can be found in Section “Conclusion.”

FIGURE 1

Figure 1. Silicon-doped magnesium nano-ceramic cluster under physical piezoelectric condition.

Computational Methods

CALYPSO structure searching code (Wang et al., 2010, 2012; Lv et al., 2012) was adopted to find the structures of low-lying isomers of piezoelectric silicon-doped small-sized magnesium clusters. Several useful structure search techniques, such as symmetry constraints, bond characterization matrix, atom-centered symmetrical function, and structure randomness generation, are included in CALYPSO code. It has been reported that the structures for various systems ranging from clusters to crystal structures have been successfully predicted using CALYPSO (Zhao et al., 2017; Sun et al., 2019; Lin et al., 2020; Lu and Chen, 2020a,b). Here, structure searching is performed for piezoelectric silicon-doped small-sized magnesium clusters up to 13 atoms. Each generation contains 50 structures, 60% of which are generated by CALYPSO’s special techniques, and 40% are generated randomly. In order to achieve the convergence of potential energy surface sampling, we followed each cluster for 20 generations. Based on the above search, 1000 structures can be obtained for each SiMg_n^±1 (n = 2−12) cluster. Among these structures, those with low energy and different structures are selected as candidates for subsequent structural optimization calculations. The calculations are performed using density functional theory (DFT) with the hybrid functional B3LYP (Becke, 1988; Lee et al., 1988). The all-electron 6-311G (d) basis set is used to confirmation of the lowest-energy structures of SiMg_n^±1 (n = 2−12) clusters. Taking different spin multiplicities may effect on structures into account, structural optimizations of each isomer of spin multiplicities of 2, 4, 6, and 8 are all implemented. In order to make sure that there is no imaginary frequency affecting the stationary character of state, the harmonic vibration frequency computation is carried out after each structural optimization. All above calculations are performed with the GAUSSIAN 09 program package (Frisch et al., 2009). Natural charge population (NCP), natural electronic configuration (NEC), molecular orbitals (MOs) and chemical bonding composition are analyzed by natural bond orbital (NBO). Total density of states (TDOS) and partial density of states (PDOS) are calculated and plotted by Multiwfn 3.7 (Lu and Chen, 2012a,b).

The choice of the B3LYP/6-311G(d) lev9el can be explained by Table 1, which presents the theoretical calculations results of the bound length (r), vibrational frequency (ω) of Si₂, Mg₂ and SiMg dimers by different functional and basis sets. Compared with experiments (Huber and Herzberg, 1979; Ruette et al., 2005), it can be safely concluded that B3LYP/6-311G(d) combination is an effective choice.

TABLE 1

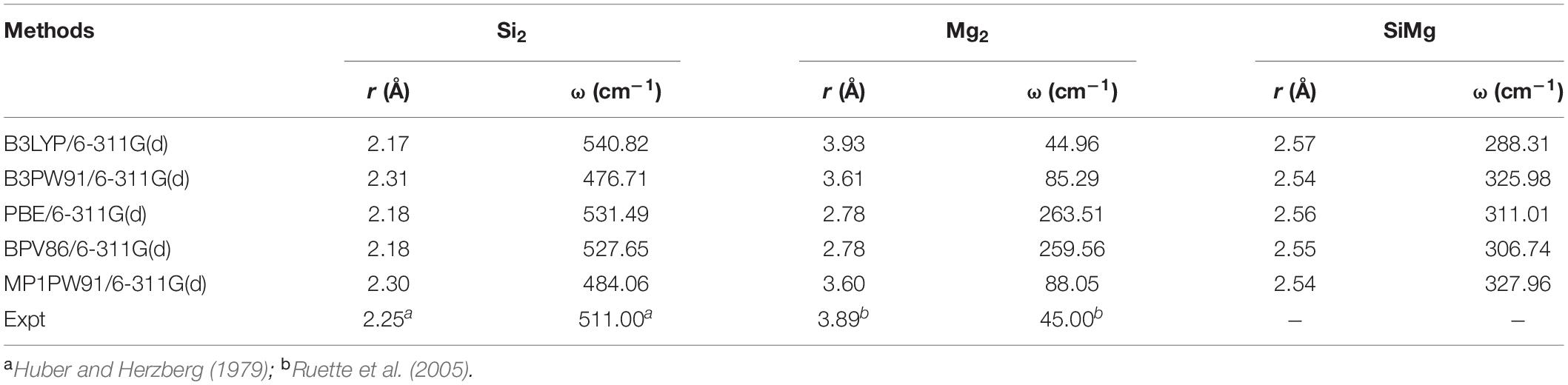
Table 1. Calculated values of bond length r (Å), frequency ω (cm^–1) for Si₂, Mg₂, and SiMg isomers using different methods.

Results and Discussion

Geometrical Structures of SiMg_n^±1 Nanosensors

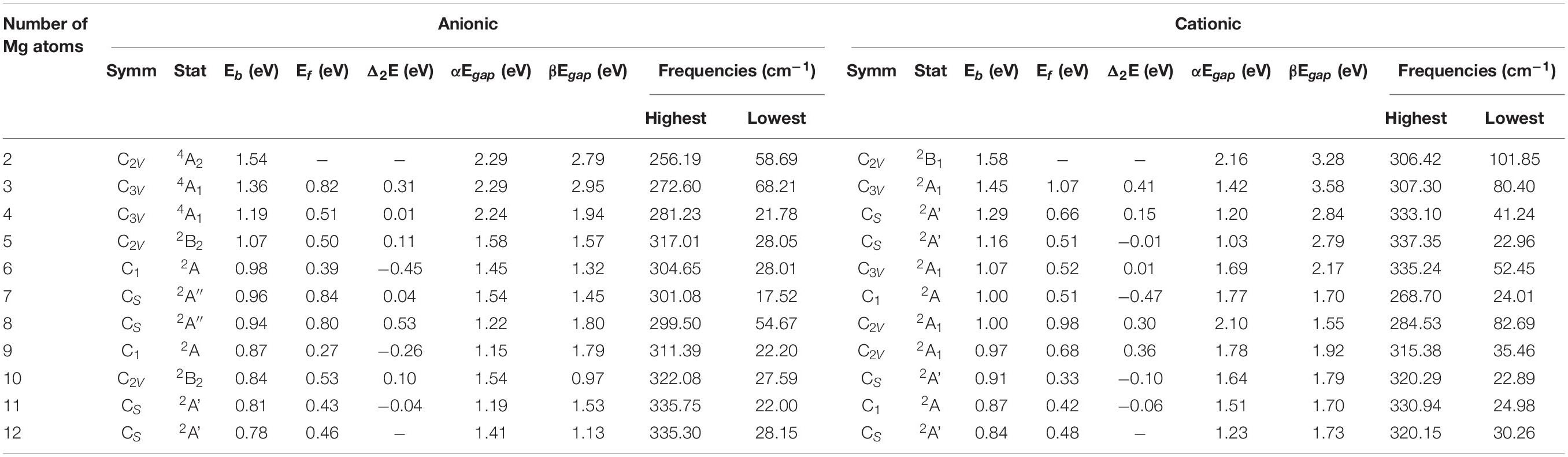
The global minima structures of SiMg_n^±1 (n = 2−12) clusters together with the corresponding symmetry, electronic state were obtained using the methods mentioned in Section “Computational Methods,” and displayed in Figure 2 and Table 2. The harmonic vibration frequency results of each structure are presented in Table 2, which can confirm that there is no imaginary frequency in these structures. Physically, the optimized structures can be regarded as the lowest-energy state structures of piezoelectric silicon-doped magnesium nanomaterials. The geometric analysis of the growth mechanism of these structures will be presented shortly below.

FIGURE 2

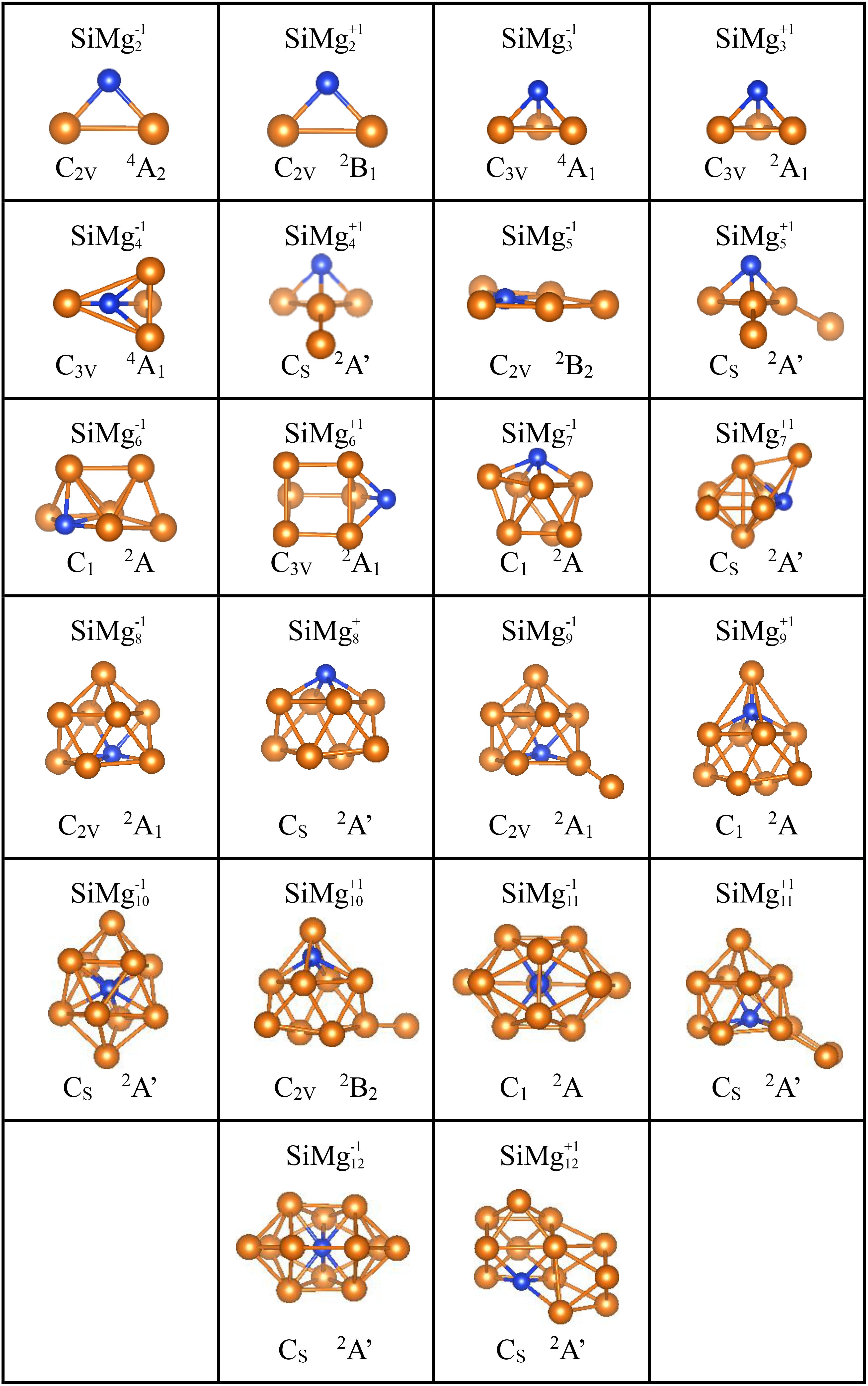
Figure 2. Optimized geometrical structures of ground state of SiMg${}_{\text{n}}^{\pm 1}$ (n = 2–12) clusters at B3LYP/6-311+G(d) level. The yellow and blue balls are magnesium and silicon atoms, respectively.

TABLE 2

Table 2. NCP of the ground state of SiMg${}_{\text{n}}^{-1}$ (n = 2–12) clusters.

As shown in Figure 2, SiMg₂^–1 and SiMg_n⁺¹ clusters have the same isosceles triangle structure. While both SiMg₃^–1 and SiMg₃⁺¹ clusters have the similar tetrahedral structure. For n = 4−12, the lowest energy structures of SiMg_n^±1 clusters differ from each other, which suggests that cationization and anionization have different effects on the structure of silicon-doped magnesium clusters. Moreover, except for the SiMg₅^–1cluster, which is a plane structure, all other clusters structures are three-dimensional (3D). Interestingly, it can be seen that some relative large-sized SiMg_n^±1 clusters can be directly formed by small-sized SiMg_n–1^±1 clusters attracting one magnesium atom in different orientation, such as SiMg₄^–1 and SiMg₃^–1, SiMg₉^–1 and SiMg₈^–1, SiMg₁₂^–1 and SiMg₁₁^–1, SiMg₄⁺¹ and SiMg₃⁺¹, SiMg₅⁺¹ and SiMg₄⁺¹, SiMg₉⁺¹and SiMg₈⁺¹, SiMg₁₀⁺¹and SiMg₉⁺¹. SiMg₆⁺¹ and SiMg₇⁺¹ displays relative irregular geometries and they cannot be formed by SiMg₅⁺¹and SiMg₆⁺¹ attracting one Mg atom. The similar situation also happens in SiMg₁₀^–1, SiMg₁₁⁺¹ and SiMg₁₂⁺¹, which show a little more complicated, and cannot be directly obtained by smaller size clusters of SiMg₉^–1, SiMg₁₀⁺¹ and SiMg₁₁⁺¹. However, these clusters can be considered to be based on the deformation of the tetrahedron (SiMg₃^±1) and a kind of tower (such as SiMg₈^–1, but not the atoms fixed in this position). It is necessary to point out that this type of structure growth mechanism is not discovered for the first time, and has been confirmed to exist in the previous reports of metal alloy cluster studies (Xia et al., 2016; Li et al., 2017; Chen et al., 2018; Zhao et al., 2019). However, it is worth noting that SiMg₈^–1 and SiMg₈⁺¹ clusters are special ones due to their tower-like structures. For n = 9−12, all SiMg_n^±1 clusters structures are tower-like-based structures originated from the transformation of SiMg₈^±1 structures. The following studies will show that the specificity of SiMg₈^–1 and SiMg₈⁺¹ clusters is not only exist in geometric structure, but also physical and chemical properties.

Electronic Properties of the Ground State of SiMg_n^±1 Nanosensors

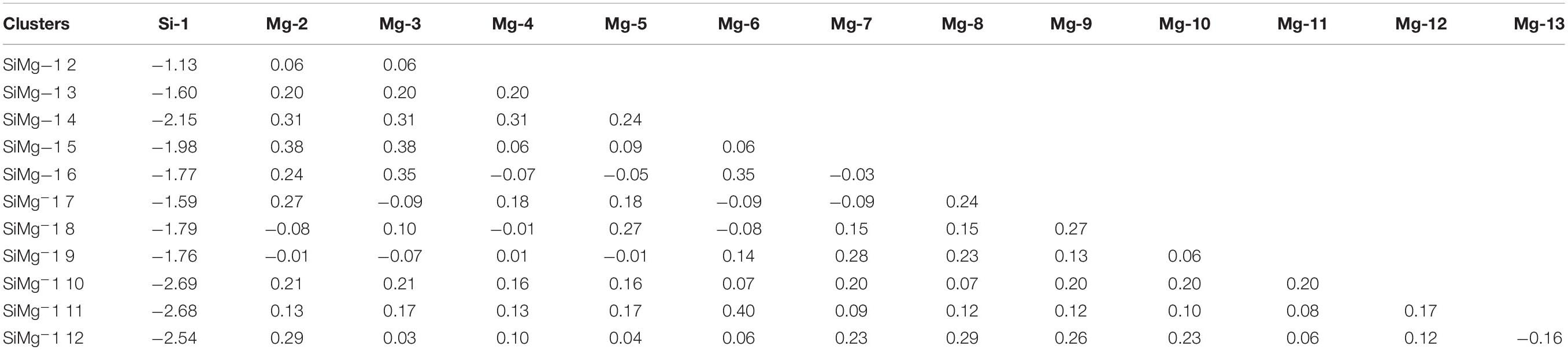
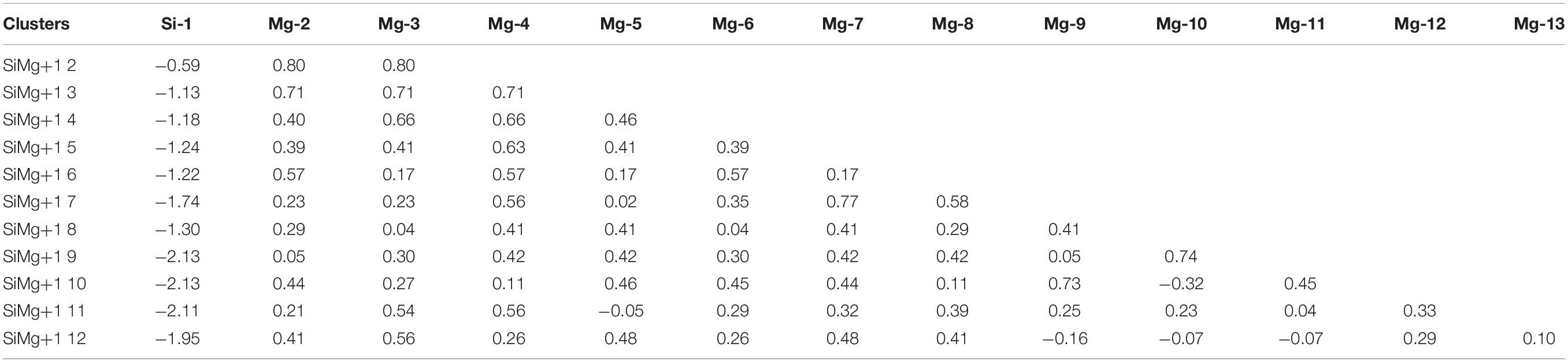
The studies of electronic properties of clusters, such as the natural charge population (NCP), natural electronic configuration (NEC), help us further understand the structures formation. The NCP and NEC of the ground state of SiMg_n^±1 (n = 2−12) clusters were analyzed by the natural bond orbital (NBO) (Reed et al., 1988a,b), and displayed in Tables 3–6. It can be seen from Tables 3, 4 that Si atoms are all negatively charged in all of SiMg_n^±1 (n = 2−12) clusters, while most Mg atoms are positively charged. To better understand the effect of silicon doping on the charge transfer of magnesium clusters, the total charges on silicon atoms in the ground state of SiMg_n^±1 (n = 2−12) clusters were presented in Figure 3. As shown in Figure 3, the Si atom charge overall decreases in both SiMg_n^±1 clusters as n increases and the maximal values can be found at SiMg₇^–1 and SiMg₈⁺¹, respectively. The local strong peaks of SiMg₇^–1 and SiMg₈⁺¹ indicate that the beryllium atoms are relatively difficult to get electrons in their structure, so when beryllium is doped into magnesium clusters, it is easy to be adsorbed on the surface of the structure, and the geometric structures of SiMg₇^–1 and SiMg₈⁺¹ in Figure 2 confirms this conclusion. NCP shows that the charges are transferred from Mg atoms to Si atoms in SiMg_n^±1 (n = 2−12) clusters. Si atom acts as charge receiver while the Mg atoms are charge donors is probably originated from the fact that electronegativity value of Si (1.90) is greater than that of Mg atom (1.31).

TABLE 3

Table 3. NCP of the ground state of SiMgn${}_{\text{n}}^{+1}$ (n = 2–12) clusters.

TABLE 4

Table 4. NEC of the ground state of SiMg${}_{\text{n}}^{-1}$ (n = 2–12) clusters.

TABLE 5

Table 5. NEC of the ground state of SiMg${}_{\text{n}}^{+1}$ (n = 2–12) clusters.

TABLE 6

Table 6. State, symmetry, E_b, E_f, Δ₂E, E_gap, and vibrational frequencies of the ground state of SiMg${}_{\text{n}}^{\pm 1}$ (n = 2−12) clusters.

FIGURE 3

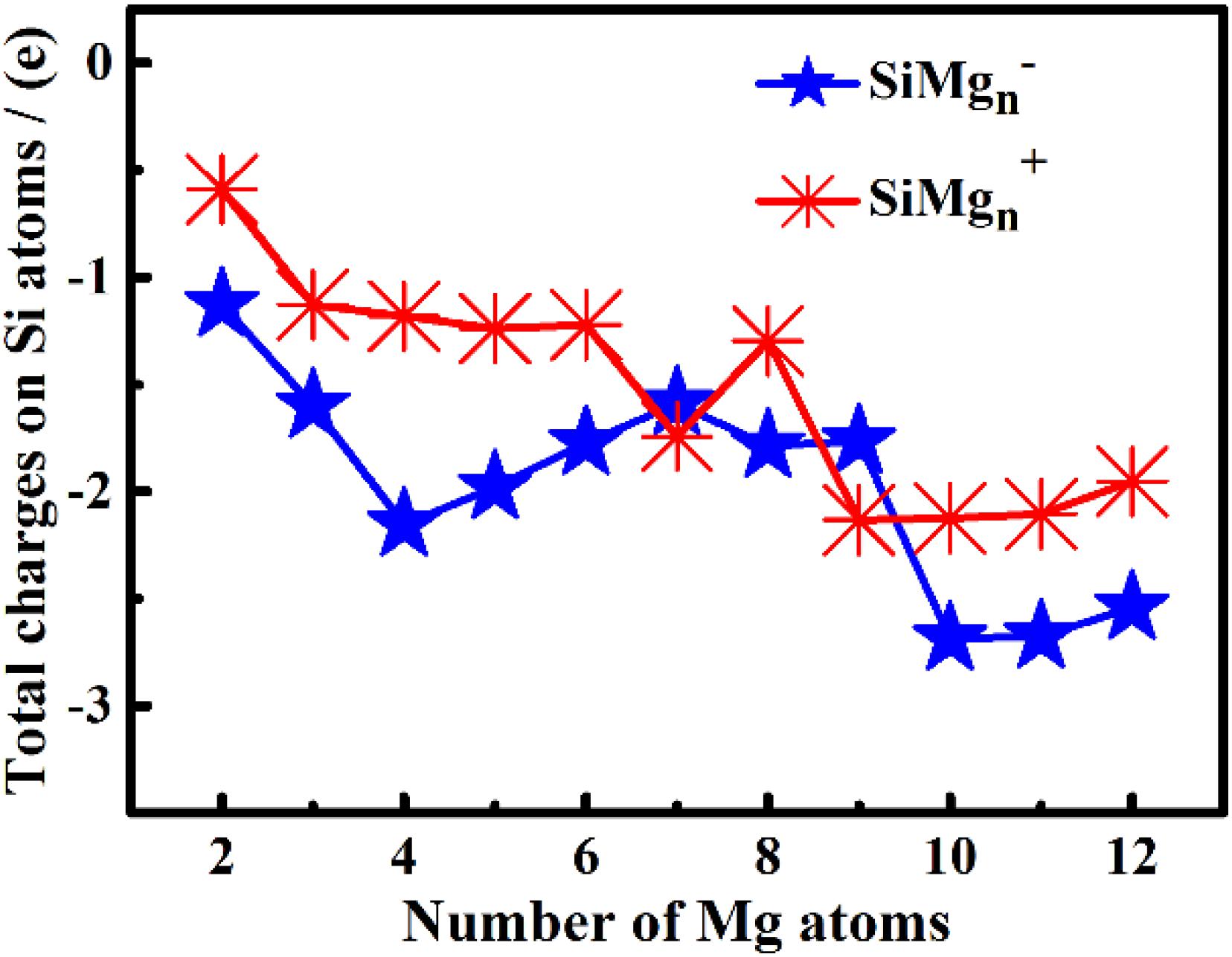
Figure 3. The total charges on silicon atoms in the lowest-energy states of SiMg${}_{\text{n}}^{\pm 1}$ (n = 2–12) clusters.

Tables 5, 6 present the NEC in the lowest-energy states of SiMg_n^±1 (n = 2−12) clusters. Compared with the NEC of the isolated Si (3s²3p²) and Mg (3s²) atoms, one can find that Si and Mg atoms lose electrons in 3s-orbital and gain electrons in 3p-orbitals in SiMg_n^±1 (n = 2−12) clusters. Quantitatively, as can be seen from Tables 5, 6, the Si 3s-orbital of SiMg_n^–1 clusters lost electrons is in the range of 0.13 to 0.44 electrons, while that of SiMg_n⁺¹ clusters ranges from 0.09 to 0.38 electrons. Correspondingly, the Si 3p-orbitals of SiMg_n^–1 clusters gained electrons ranges from 1.25 to 3.07 electrons, and that of SiMg_n⁺¹ clusters is in the range of 0.67 to 2.46 electrons. A significant conclusion is that Si atom in SiMg_n^–1 clusters gain and lose electrons is easier than the Si atom in SiMg_n⁺¹ clusters. Based on the analysis above, the lowest-energy states of SiMg_n^±1 (n = 2−12) clusters structures are mainly governed by the s- and p-orbitals interactions of Si and Mg atoms.

The Relative Stability of SiMg_n^±1 Nanosensors

The study of the relative stability of different sized clusters can reveal which clusters are most stable locally, which can further guide experiments to synthesize these stable clusters. The average binding energy E_b, fragmentation energy E_f and the second-order energy difference Δ₂E and HOMO-LUMO gap of the lowest energy states were calculated to research the relative stability of SiMg_n^±1 (n = 2−12) clusters. The results are summarized in Table 2 and are plotted in Figures 4, 5. Their equations are as follows:

FIGURE 4

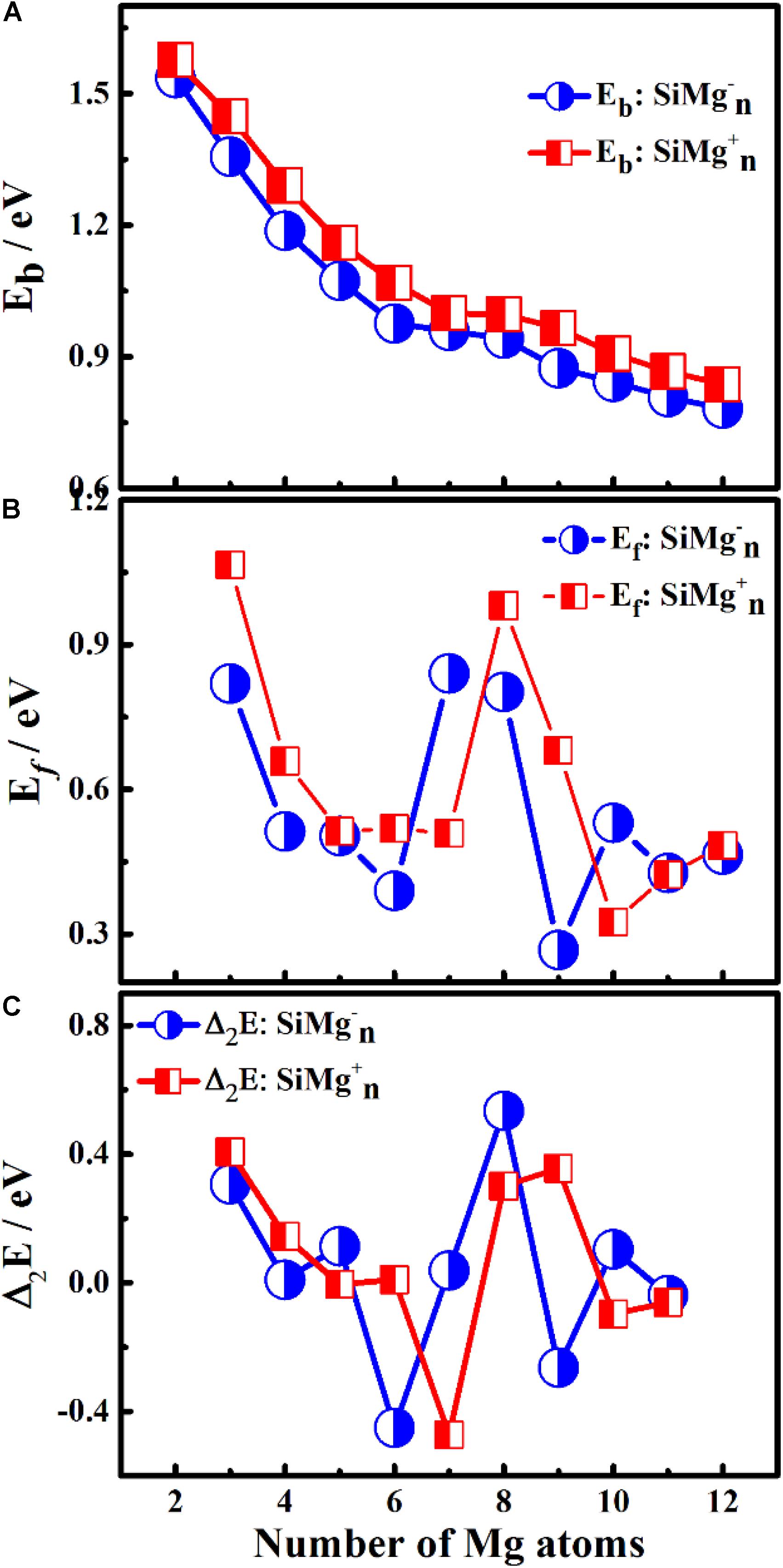
Figure 4. Size-dependent properties of panels (A) E_b, (B) E_f, and (C) Δ₂E for the ground state of SiMg${}_{\text{n}}^{\pm 1}$ (n = 2–12) clusters.

FIGURE 5

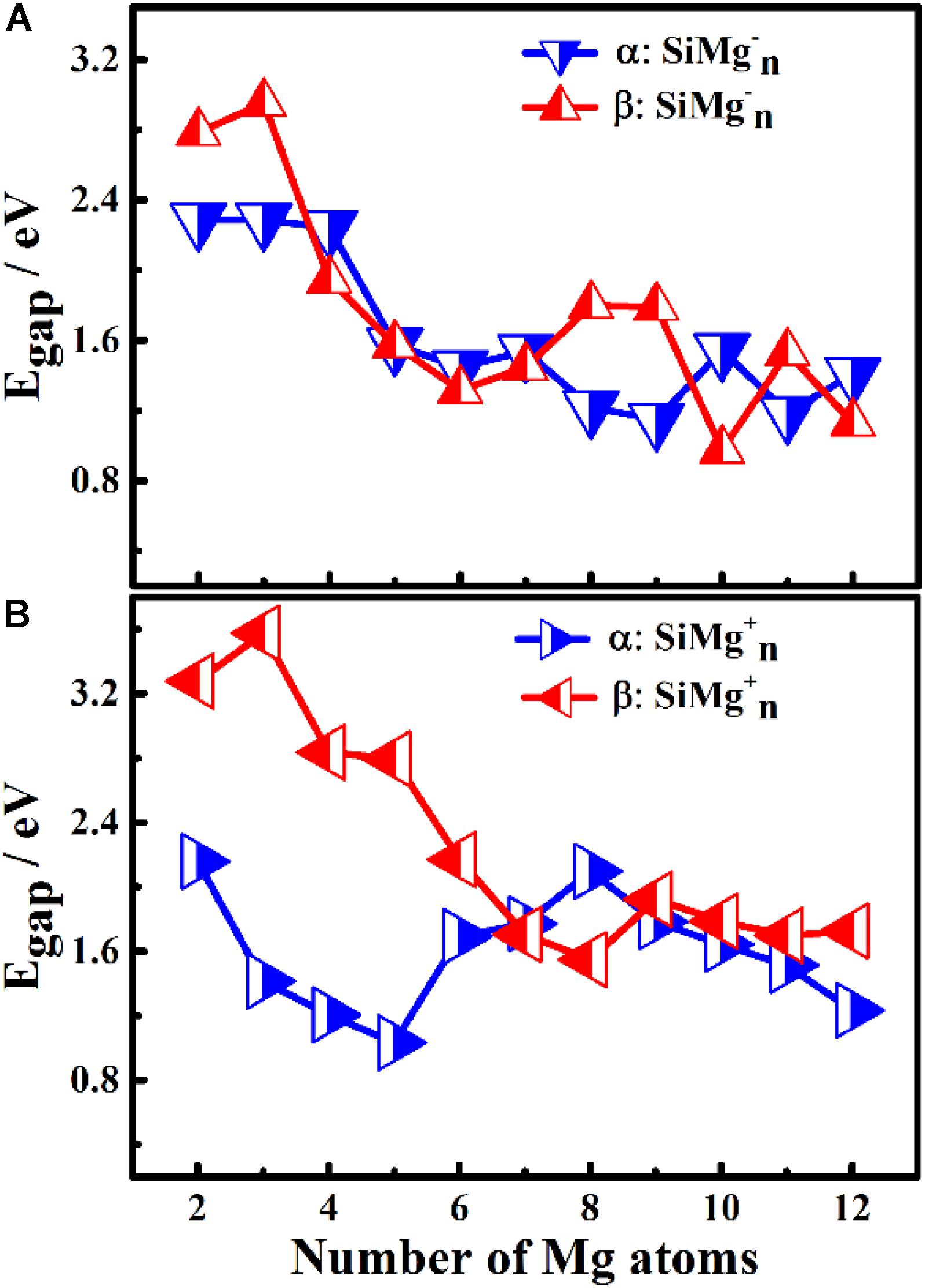
Figure 5. HOMO-LUMO energy gap of α and β electrons in ground state of panels (A) E_gap for SiMg${}_{\text{n}}^{-1}$, (B) E_gap for SiMg${}_{\text{n}}^{+1}$ (n = 2–12) clusters.

$$E_b(SiM{g}_n^{-1/+1})=[(n-1)E_k(M{g}^{-1/+1})+$$

$$E_k(Si)-E_k(SiM{g}_{n-1}^{-1/+1})]/(n+1)(1)$$

$$E_f(SiM{g}_n^{-1/+1})=E_k(SiM{g}_{n-1}^{-1/+1})+$$

$$E_k(Mg)-E_k(SiM{g}_n^{-1/+1})(2)$$

$${\mathrm{\Delta }}_{2}E(SiM{g}_n^{-1/+1})=E_k(SiM{g}_{n+1}^{-1/+1})+E_k(SiM{g}_{n-1}^{-1/+1})-$$

$$2E_k(SiM{g}_n^{-1/+1})(3)$$

E_k in Eq. (1) − Eq. (3) are the total energy of the corresponding atom and clusters.

As can be seen from Figure 4A, the E_b of SiMg_n^±1 (n = 2−12) clusters have the same size dependence, which decrease with the cluster size. Only two local weak peaks at SiMg₈^–1 and SiMg₈⁺¹ are found, which indicates that these clusters are more stable than their adjacent clusters. Moreover, the E_b values of SiMg_n⁺¹ clusters are always higher than that of the corresponding SiMg_n^–1, which reveals that SiMg_n⁺¹ clusters are more stable than the corresponding SiMg_n^–1. The fragmentation energy E_f can measure the energy of a small-sized cluster adsorbs a related atom to become a larger-sized cluster, which changes with the size and electronic structure of the cluster. A larger local E_f value indicates that the energy required to break the bond between the atoms of the cluster is greater, and correspondingly indicates that the cluster is more stable than its neighboring clusters. Figure 4B shows the E_f of SiMg_n^±1 (n = 2−12) clusters, and two E_f curves display similar oscillation behavior, except for n = 7 and 10. The local most stable structures are SiMg₇^–1, SiMg₈^–1, SiMg₁₀^–1, SiMg₈⁺¹. It is worth pointing out that the E_f value of SiMg₈^–1 (0.80 eV) is only slightly lower than that of SiMg₇^–1 (0.84 eV), and thus the stability of these two clusters is approximately equivalent.

The results of Δ₂E of SiMg_n^±1 clusters are shown in Figure 4C. One can find that the local strongest peaks are found at n = 5, 8, and 10 in SiMg_n^–1 clusters, while n = 8 and 9 in the SiMg_n⁺¹ clusters. Naturally, these five clusters are relative more stable than their neighbors. As one knows that HOMO-LUMO gap (E_gap) value is always responsible for cluster’s thermodynamic stability (Aihara, 1999). Notably, there are two kinds of HOMO-LUMO energy gaps, α and β electrons, due to the open-shell structures of SiMg_n^±1 clusters. As is shown in Figure 5A of SiMg_n^–1 clusters, the local maximum peaks of β-electrons E_gap are located at n = 3, 8, 9, and 11, while that of α-electrons are at n = 7 and 10. Figure 5B shows that α-electron of SiMg₈⁺¹, β-electrons of SiMg₃⁺¹and SiMg₉⁺¹clusters have local maximum E_gap values.

Combing the results of Eb, Ef, Δ₂E with E_gap, the hint toward stability of magic number clusters of SiMg_n^±1 (n = 2−12) is SiMg₈^–1 and SiMg₈⁺¹, or in other words these two clusters are most stable locally. Interestingly, we have concluded that SiMg₈^–1 and SiMg₈⁺¹ clusters are special ones with tower-like structures in Section “Geometrical Structures of SiMg_n^±1 Nanosensors.” This section’s research shows that their structural character probably has strong relationship with their local stability property.

The Chemical Bonding Analysis of SiMg_n^±1 Nanosensors

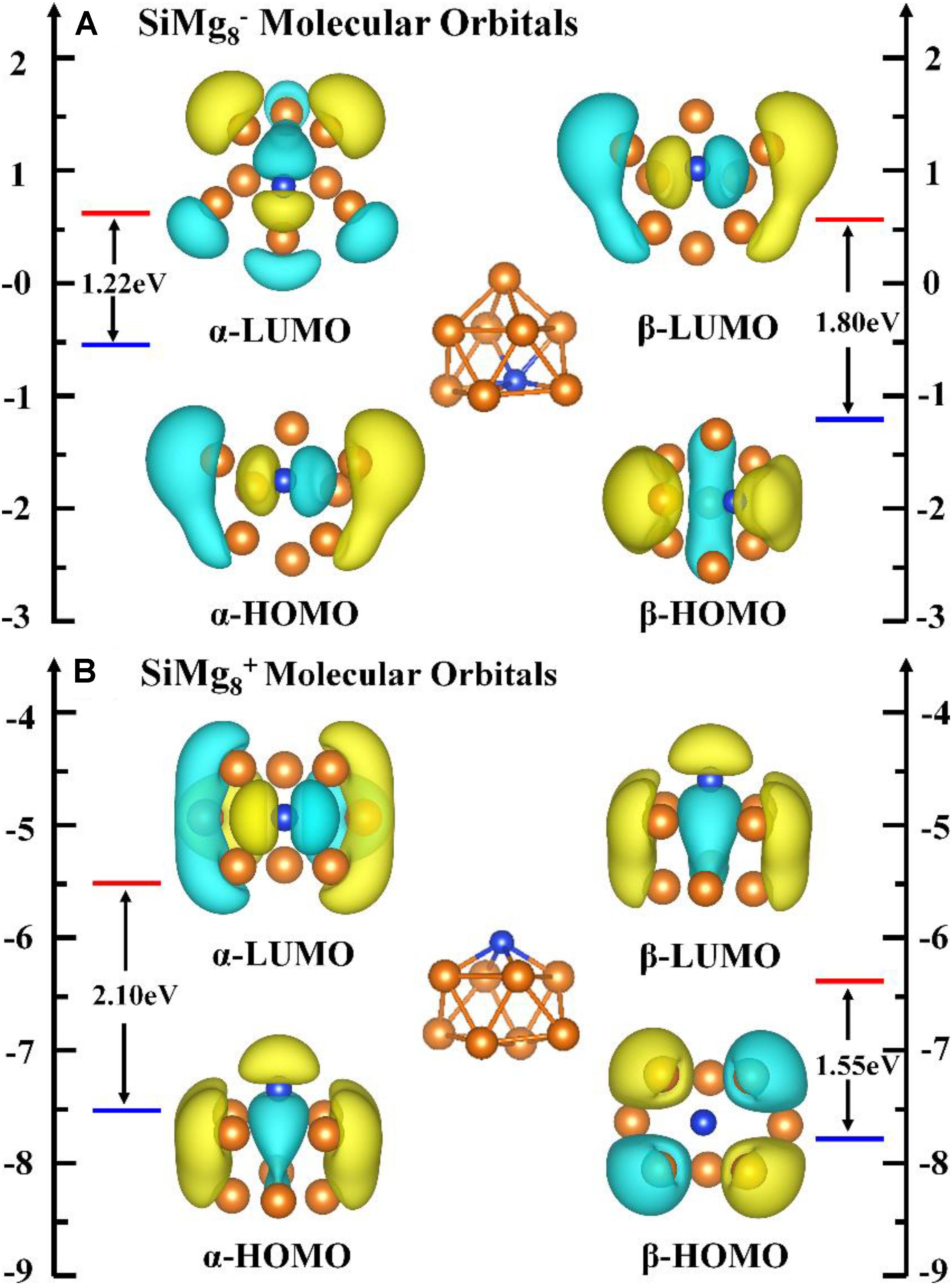
Since the most stable locally SiMg₈^–1 and SiMg₈⁺¹ clusters are found, it is interesting to study the relationship between their stability and chemical bonding. According to the NBO calculations in Section “Geometrical Structures of SiMg_n^±1 Nanosensors,” we can find that SiMg₈⁺¹cluster has C_S symmetry, one SiMg₂ unite and six central Mg atoms. While SiMg₈^–1 cluster has C_2V symmetry, one SiMg₆ unite and two central Mg atoms. In order to gain insight into their bonding properties, the (α-, β- electron) HOMO, (α-, β- electron) LUMO and top valence molecular orbitals (MOs) are analyzed and are plotted in Figure 6. Quantitative composition calculations for chemical bonding show that for SiMg₈^–1 cluster, α-electron HOMO has a contribution of 15.85% from Si 3p-orbitals, while β-electron HOMO has 30.05% contribution from Si 3p-orbitals. The α-electron HOMO of SiMg₈⁺¹ has 24.85% contribution from Si 3p-orbitals, but β-electron HOMO of SiMg₈⁺¹ is mainly composed of Mg 3p-orbitals, or in other words there is nearly no contribution from Si.

FIGURE 6

Figure 6. Molecular orbitals (MOs) of the most stable clusters of panels (A) SiMg${}_8^{-}$ and (B) SiMg${}_8^{+}$.

To qualitatively study the contribution from silicon atom to chemical bonding in other lower-energy HOMOs of SiMg₈^±1 clusters, total density of states (TDOS) and partial density of states (PDOS) calculations were performed and were displayed in Figure 7. TDOS and PDOS are read (Lu and Chen, 2012a,b):

FIGURE 7

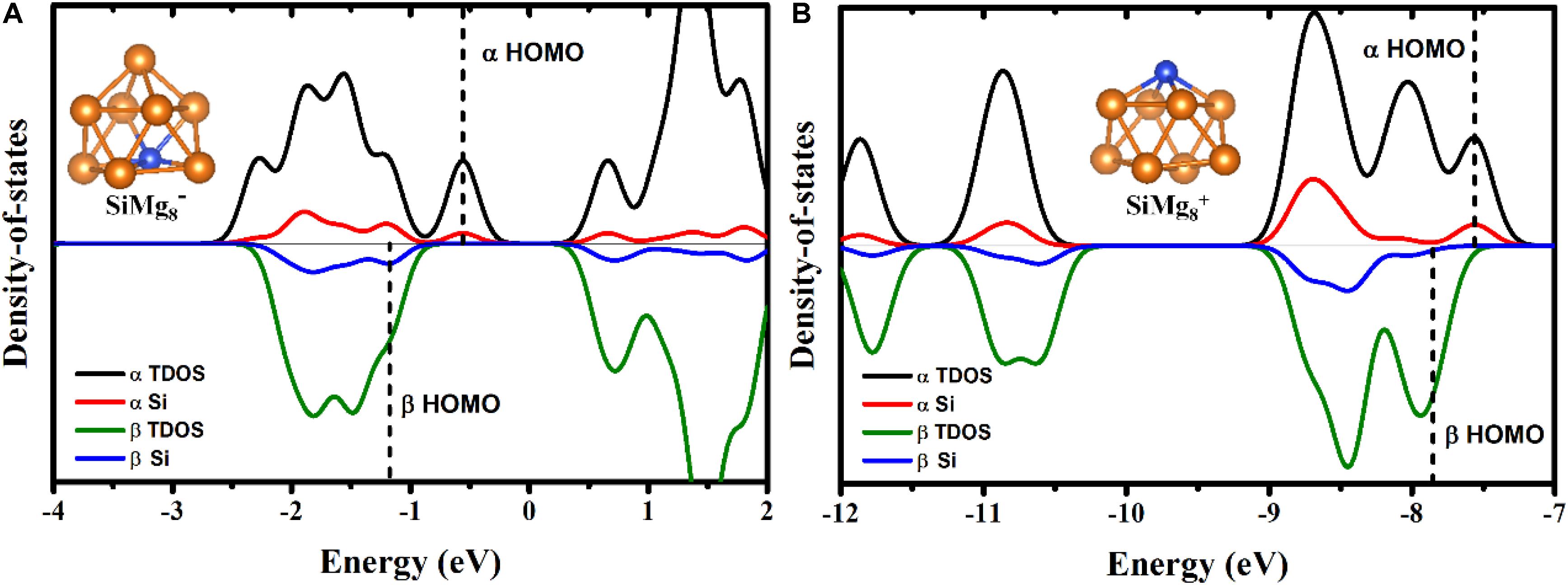
Figure 7. α - and β- elections TDOS and PDOS of the most stable clusters of panels (A) SiMg${}_8^{-}$ and (B) SiMg${}_8^{+}$.

$$TDOS(E)=\sum _i\mathrm{\delta }(E-{\mathrm{\epsilon }}_i)(4)$$

$$PDO{S}_A(E)=\sum _i{\mathrm{\Theta }}_{A,i}F(E-{\mathrm{\epsilon }}_i)(5)$$

ε_i is the energy of molecular orbital i (MOi), Θ_A,i is the contribution from part A to MOi. Here, part A is Si due to our interesting is how much contribution from Si to the lower-energy HOMOs. As shown in Figures 7A,B, the contribution from silicon atoms is always small in the most lower-energy HOMOs (the area to the left of the dotted line). Interestingly, Figure 7B shows that there is nearly no contribution from Si to β-electron HOMO of SiMg₈⁺¹, which works well with the MOs composition calculations above.

Compared with the research results of the local most stable neutral silicon-doped magnesium clusters (Zhu et al., 2020), we can find some interesting conclusions. First of all, whether silicon-doped magnesium clusters are neutral or charged, their local most stable clusters are composed of one silicon and eight magnesium atoms. Secondly, it is interesting to note that according to our research, SiMg₈^0,–1 clusters have very similar geometric structures, but the structure of SiMg₈⁺¹ has changed a lot. This shows that for neutral silicon-doped magnesium cluster nanosensors, anionization has little effect on its structure, but cationization is not. As we all know that anionic nanoclusters can be used for photoelectron spectra experiments, this conclusion obviously provides a very good guide for future experimental verification.

The Infrared (IR) and Raman Spectra of SiMg_n^±1 Nanosensors

In order to be able to experimentally distinguish SiMg₈^–1 and SiMg₈⁺¹ clusters, it is useful to calculate the infrared (IR) and Raman spectra. The Infrared and Raman spectra of SiMg₈^±1 together with atomic label are shown in Figure 8. As shown in Figure 8A, the highest intense IR frequency of SiMg₈^–1 cluster is located at 183 cm⁻¹with Mg7-Si1-Mg8 bonds in-plane tensile vibration. The second and third strongest peaks of SiMg−1 8cluster can be found at 125cm⁻¹and 270cm⁻¹. The vibration mode is Si1-Mg4 and Mg7-Mg8 in-bonds tensile vibration, Mg7-Si1-Mg8 bonds in-plane tensile vibration, respectively. Figure 8C shows the SiMg₈⁺¹ cluster’s IR spectra, and two relative strong peaks can be found. The strongest peak is located at 118cm⁻¹with Mg5-Mg4-Mg9-Mg7 out-of-plane wagging vibration of Si1 atom. The second strongest peak at 284cm⁻¹ corresponds to Mg9-Si1-Mg5 and Mg7-Si1-Mg4 bond tensile vibration. Three strong vibration peaks can be found in Figure 8B, which are the Raman spectra of SiMg₈^–1 cluster. The strongest peak at 227cm⁻¹with total breathing vibration. The second and third strongest Raman frequency at 214cm⁻¹and 116 cm⁻¹correspond to the Si1-Mg4, Mg7-Mg8, Mg9-Mg3-Mg5 in-bonds tensile vibration, Mg9-Si1-Mg5, Mg7-Mg8 bonds out-plane wagging vibration, respectively. Figure 8D shows that SiMg₈⁺¹cluster has three strong Raman peaks. The most active Raman frequency at 211cm⁻¹with Mg4–Mg6–Mg5 and Mg7-Mg3-Mg9 bonds in-plane stretching vibration. The other two strong peaks at 161cm⁻¹and 202cm⁻¹ resulted from Mg3–Mg5 bond in-plane stretching vibration, Mg4–Mg8–Mg7 and Mg5-Mg2-Mg9 bonds out-of-plane wagging vibration of Si1 atom, respectively.

FIGURE 8

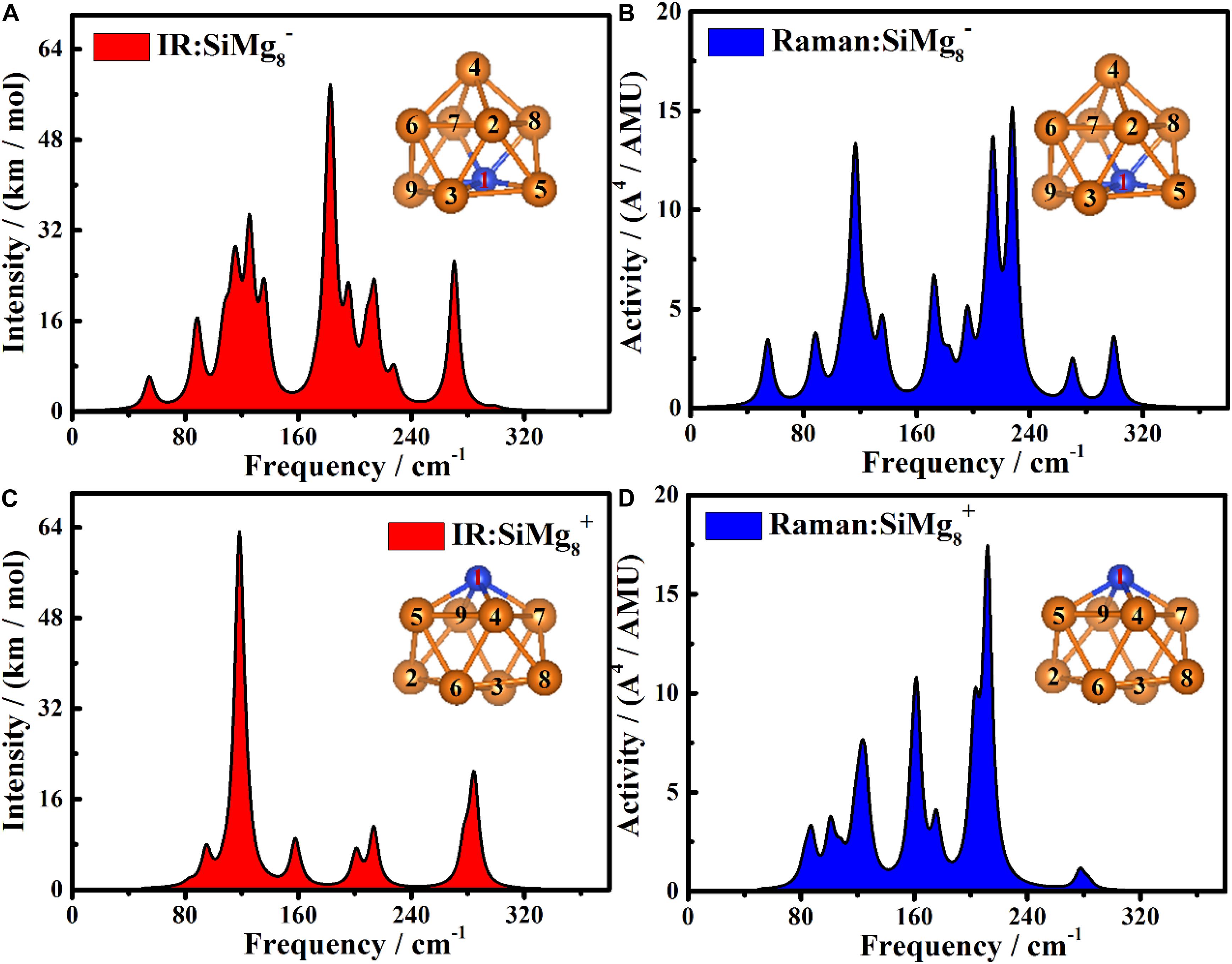
Figure 8. The Infrared and Raman spectra of the most stable clusters of panels (A) IR for SiMg${}_8^{-}$, (B) Raman for SiMg${}_8^{-}$, (C) IR for SiMg${}_8^{+}$, and (D) Raman for SiMg${}_8^{+}$.

Overall, the theoretical calculations of infrared (IR) and Raman spectra of SiMg₈^–1 and SiMg₈⁺¹ clusters show that their strongest spectral frequencies are distributed in the range of 80–240 cm^–1. In addition, the strongest infrared spectra difference between SiMg₈^–1 and SiMg₈⁺¹ is close to 65cm⁻¹, thus they can be distinguished experimentally. However, for SiMg₈^–1 and SiMg₈⁺¹, the strongest Raman spectra are relatively close and not easy to distinguish each other.

Conclusion

The stable structures of silicon-doped magnesium nano piezoelectric sensors SiMg_n^±1 (n = 2−12), were systematically investigated using the CALYPSO approach coupled with density functional theory. The geometrical growth mechanism of the ground state of SiMg_n^±1 (n = 2−12) nanosensors shows that tetrahedral structure (SiMg₃^±1) and tower-like structure (SiMg₈^±1) are two basic structures. Analysis of electronic structural properties reveals the effects of electron transfer and electron configuration on cluster structure formation. Most importantly, clusters relative stability calculations show that SiMg₈^±1 nanosensors have the strongest local stability, and thus can be regarded as candidates for their experimental stable nanostructures. Finally, further studies, such as chemical bonding analysis, infrared and Raman spectra calculations, were performed on these two clusters to in-depth study their stability and experimental identification of operability. We believe that these calculations can play theoretical guiding role in the development of silicon-doped magnesium nano piezoelectric sensors in future experiments and applications.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

LZ, JZ, and B-CZ wrote a major part of the manuscript. LZ and B-CZ summarized the literature, performed deep review, editing, and supervision. X-FW and M-KL wrote a small part of the manuscript, drawing, and editing. All authors have read and approved the article for publication.

Funding

This work was partly supported by the project of Fundamental Research Funds for the Central Universities (No. 2019CDYGYB011) and partly by the Cultivating Project for Young Scholar at Hubei University of Medicine (No. 2018QDJZR14).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aihara, J. I. (1999). Reduced HOMO- LUMO gap as an index of kinetic stability for polycyclic aromatic hydrocarbons. J. Phys. Chem. A 103, 7487–7495. doi: 10.1021/jp990092i

CrossRef Full Text | Google Scholar

Becke, A. D. (1988). Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098–3100. doi: 10.1103/PhysRevA.38.3098

PubMed Abstract | CrossRef Full Text | Google Scholar

Capitán-Vallvey, L. F., Fernández-Ramos, M. D., Lapresta-Fernández, A., Brunet, E., Rodríguez-Ubis, J. C., and Juanes, O. (2006). Magnesium optical one-shot sensor based on a coumarin chromoionophore. TALANTA 68, 1663–1670. doi: 10.1016/j.talanta.2005.08.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, B. L., Sun, W. G., Kuang, X. Y., Lu, C., Xia, X. X., Shi, H. X., et al. (2018). Structural stability and evolution of medium-sized tantalum-doped boron clusters: a half-sandwich-structured TaB₁₂^– cluster. Inorganic Chem. 57, 343–350. doi: 10.1021/acs.inorgchem.7b02585

PubMed Abstract | CrossRef Full Text | Google Scholar

Delgado, Y. S., Amy, V. M., and Xu, X. J. (2004). “Porous silicon chemical sensors,” in Frontiers of Multifunctional Integrated Nanosystems, Vol. 152, eds E. Buzaneva and P. Scharff (Dordrecht: Springer), 399–408. doi: 10.1007/1-4020-2173-9_33

CrossRef Full Text | Google Scholar

Ding, L. P., Zhang, F. H., Zhu, Y. S., Lu, C., Kuang, X. Y., Lv, J., et al. (2015). Understanding the structural transformation, stability of medium-sized neutral and charged silicon clusters. Sci. Rep. 5:15951. doi: 10.1038/srep15951

PubMed Abstract | CrossRef Full Text | Google Scholar

Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., et al. (2009). Gaussian 09, Revision A.02. Wallingford CT: Gaussian, Inc.

Google Scholar

Guo, W., Fu, M., Zhai, C., and Wang, Z. (2014). Hydrothermal synthesis and gassensing properties of ultrathin hexagonal ZnO nanosheets. Ceramics Int. 40, 2295–2298. doi: 10.1016/j.ceramint.2013.07.150

CrossRef Full Text | Google Scholar

Han, J. G., and Hagelberg, F. A. (2001). Density functional investigation of MoSi_n (n= 1–6) clusters. J. Mol. Struct. THEOCHEM 549, 165–180. doi: 10.1016/s0166-1280(01)00493-6

CrossRef Full Text | Google Scholar

Han, J. G., Xiao, C., and Hagelberg, F. (2002). Geometric and electronic structure of WSi_n (n= 1–6, 12) clusters. Struct. Chem. 13, 173–191. doi: 10.1023/a:1015712717153

CrossRef Full Text | Google Scholar

Han, J. G., Zhao, R. N., and Duan, Y. (2007). Geometries, stabilities, and growth patterns of the bimetal Mo₂-doped Si_n (n= 9-16) clusters: a density functional investigation. J. Phys. Chem. A 111, 2148–2155. doi: 10.1021/jp0661903

PubMed Abstract | CrossRef Full Text | Google Scholar

Heidari, I., De, S., Ghazi, S. M., Goedecker, S., and Kanhere, D. G. (2011). Growth and structural properties of Mg_n (n = 10-56) clusters: density functional theory study. J. Phys. Chem. 115, 12307–12314. doi: 10.1021/jp204442e

PubMed Abstract | CrossRef Full Text | Google Scholar

Huber, K. P., and Herzberg, G. (1979). “Constants of diatomic molecules,” in Molecular Spectra and Molecular Structure, eds K. P. Huber and G. Herzberg (Boston, MA: Springer), doi: 10.1007/978-1-4757-0961-2_2

CrossRef Full Text | Google Scholar

Jellinek, J., and Acioli, P. H. (2002). Magnesium clusters: structural and electronic properties and the size-induced nonmetal-to-metal transition. J. Phys. Chem. A 106, 10919–10925. doi: 10.1021/jp020887g

CrossRef Full Text | Google Scholar

Jin, Y., Lu, S., Hermann, A., Kuang, X., Zhang, C., Lu, C., et al. (2016). Probing the structural evolution of ruthenium doped germanium clusters: photoelectron spectroscopy and density functional theory calculations. Sci. Rep. 6:30116. doi: 10.1038/srep30116

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Y., Tian, Y., Kuang, X. Y., Zhang, C., Lu, C., Wang, J., et al. (2015). Ab initio search for global minimum structures of pure and boron doped silver clusters. J. Phys. Chem. A 119, 6738–6745. doi: 10.1021/acs.jpca.5b03542

PubMed Abstract | CrossRef Full Text | Google Scholar

Köhn, A., Weigend, F., and Ahlrichs, R. (2001). Theoretical study on clusters of magnesium. Phys. Chem. Chem. Phys. 3, 711–719. doi: 10.1039/b007869g

CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37, 785–789. doi: 10.1103/PhysRevB.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, P. F., Mei, T. T., Lv, L. X., Lu, C., Wang, W. H., Bao, G., et al. (2017). Structure and electronic properties of neutral and negatively charged RhB_n clusters (n = 3-10). J. Phys. Chem. A 121, 6510–6516. doi: 10.1021/acs.jpca.7b06123

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, J., Yu, T., Han, F., and Yang, G. (2020). Computational predictions of two−dimensional anode materials of metal−ion batteries. WIREs Comput. Mol. Sci. 10:e1473. doi: 10.1002/wcms.1473

CrossRef Full Text | Google Scholar

Lu, C., and Chen, C. (2020a). Indentation-strain stiffening in tungsten nitrides: mechanisms and implications. Phys. Rev. Mater. 4:043402. doi: 10.1103/PhysRevMaterials.4.043402

CrossRef Full Text | Google Scholar

Lu, C., and Chen, C. (2020b). Structure-strength relations of distinct MoN phases from first-principles calculations. Phys. Rev. Mater. 2020:044002. doi: 10.1103/PhysRevMaterials.4.044002

CrossRef Full Text | Google Scholar

Lu, T., and Chen, F. (2012a). Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 33, 580–592. doi: 10.1002/jcc.22885

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, T., and Chen, F. (2012b). Quantitative analysis of molecular surface based on improved marching tetrahedra algorithm. J. Mol. Graph. Model. 38, 314–323. doi: 10.1016/j.jmgm.2012.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Lv, J., Wang, Y., Zhu, L., and Ma, Y. (2012). Particle-swarm structure prediction on clusters. J. Chem. Phys. 137:084104. doi: 10.1063/1.4746757

CrossRef Full Text | Google Scholar

Pham, V. H., Nguyen, T. V., Nguyen, T. A., Pham, V. D., and Bui, H. (2014). Nano porous silicon microcavity sensor for determination organic solvents and pesticide in water. Adv. Nat. Sci. Nanosci. Nanotechnol. 5:045003. doi: 10.1088/2043-6262/5/4/045003

CrossRef Full Text | Google Scholar

Pradeep, N., Chaitra, V., Uma, V., and Grace, A. N. (2017). Simultaneous growth of magnesium oxide nanowire and nanocubes for gas sensor application. Sens. Lett. 15, 413–418. doi: 10.1166/sl.2017.3791

CrossRef Full Text | Google Scholar

Reed, A. E., Curtiss, L. A., and Weinhold, F. (1988a). Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 88, 899–926. doi: 10.1021/cr00088a005

CrossRef Full Text | Google Scholar

Reed, A. E., Weinstock, R. B., and Weinhold, F. (1988b). Natural population analysis. J. Chem. Phys. 83, 735–746. doi: 10.1063/1.449486

CrossRef Full Text | Google Scholar

Ruette, F., Saìnchez, M., Anez, R., Bermúdez, A., and Sierraalta, A. (2005). Diatomic molecule data for parametric methods. J. Mol. Struct. THEOCHEM 729, 19–37. doi: 10.1016/j.theochem.2005.04.024

CrossRef Full Text | Google Scholar

Shao, X., Qu, X., Liu, S., Yang, L., Yang, J., Liu, X., et al. (2019). Structure evolution of chromium-doped boron clusters: toward the formation of endohedral boron cages. RSC Adv. 9, 2870–2876. doi: 10.1039/C8RA09143A

CrossRef Full Text | Google Scholar

Shukla, S. K., Parashar, G. K., Mishra, A. P., Misra, P., Yadav, B. C., Shukla, R. K., et al. (2004). Nano-like magnesium oxide films and its significance in optical fiber humidity sensor. Sens. Actuat. B Chem. 98, 5–11. doi: 10.1016/j.snb.2003.05.001

CrossRef Full Text | Google Scholar

Sun, Y., Lv, J., Xie, Y., Liu, H., and Ma, Y. (2019). Route to a superconducting phase above room temperature in electron-doped hydride compounds under high pressure. Phys. Rev. Lett. 123:097001. doi: 10.1103/physrevlett.123.097001

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Li, X., Wei, B., Sun, R., Yu, W., Hoh, H. Y., et al. (2020). Activating basal planes of NiPS₃ for hydrogen evolution by nonmetal heteroatom doping. Adv. Funct. Mater. 30:1908708. doi: 10.1002/adfm.201908708

CrossRef Full Text | Google Scholar

Wang, J. W., Yao, Z. S., and Poon, A. W. (2015). Silicon-nitride-based integrated optofluidic biochemical sensors using a coupled-resonator optical waveguide. Front. Mater. 2:34. doi: 10.3389/fmats.2015.00034

CrossRef Full Text | Google Scholar

Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2010). Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82:094116. doi: 10.1103/physrevb.82.094116

CrossRef Full Text | Google Scholar

Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2012). CALYPSO: a method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070. doi: 10.1016/j.cpc.2012.05.008

CrossRef Full Text | Google Scholar

Xia, X., Kuang, X., Lu, C., Jin, Y., Xing, X. D., Merino, G., et al. (2016). Deciphering the structural evolution and electronic properties of magnesium clusters: an aromatic homonuclear metal. J. Phys. Chem. A 120, 7947–7954. doi: 10.1021/acs.jpca.6b07322

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, W., Liu, T., and Wang, Z. (2012). Impact of Nb doping on gas-sensing performance of TiO₂ thick-film sensors. Sens. Actuat. B Chem. 166–167, 141–149. doi: 10.1016/j.snb.2012.02.016

CrossRef Full Text | Google Scholar

Zhang, F. G., Zhang, H. R., Xin, W., Chen, P., Hu, Y. F., Zhang, X. Y., et al. (2020). Probing the structural evolution and electronic properties of divalent metal Be2Mgn clusters from small to medium-size. Sci. Rep. 10:6052. doi: 10.1038/s41598-020-63237-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L., Qu, X., Wang, Y., Lv, J., and Ma, Y. (2017). Effects of manganese doping on the structure evolution of small-sized boron clusters. J. Phys. Condens. Matter 29:265401. doi: 10.1088/1361-648X/aa7190

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y. R., Bai, T. T., Jia, L. N., Xin, W., Hu, Y. F., Zheng, X. S., et al. (2019). Probing the structural and electronic properties of neutral and anionic lanthanum-doped silicon clusters. J. Phys. Chem. C 123, 28561–28568. doi: 10.1021/acs.jpcc.9b07184

CrossRef Full Text | Google Scholar

Zhu, B., Zhang, S., and Zeng, L. (2020). The effect of silicon doping on the geometrical structures, stability, and electronic and spectral properties of magnesium clusters: DFT study of SiMg_n (n = 1−12) clusters. Int. J. Quant. Chem. 120:e26143. doi: 10.1002/qua.26143

CrossRef Full Text | Google Scholar