
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater., 23 July 2020
Sec. Biomaterials
Volume 7 - 2020 | https://doi.org/10.3389/fmats.2020.00212
This article is part of the Research TopicCell Mechanoresponse at Cell-Material InterfaceView all 26 articles
 Ramesh Subramani1†
Ramesh Subramani1† Alicia Izquierdo-Alvarez2
Alicia Izquierdo-Alvarez2 Pinaki Bhattacharya2,3
Pinaki Bhattacharya2,3 Mathieu Meerts4
Mathieu Meerts4 Paula Moldenaers4
Paula Moldenaers4 Herman Ramon1
Herman Ramon1 Hans Van Oosterwyck2,5*
Hans Van Oosterwyck2,5*Polyacrylamide (PAM) hydrogels are commonly used as substrates for cell mechanical and mechanobiological studies because of their tunable stiffness and ease of handling. The dependence of bulk rheological and local elastic properties (assessed by Atomic Force Microscopy, or AFM) of PAM hydrogels on its composition and polymerization temperature has been extensively studied. PAM hydrogels swell when immersed in media, but the influence of swelling on local elastic properties is poorly characterized. Direct measurements of the effect of swelling on PAM elastic properties are scarce. We report here, for the first time, the direct measurements of volumetric swelling and local elastic properties of PAM gels throughout the post-polymerization swelling process until equilibrium. First, local and global elastic properties (measured by rheology), were obtained during polymerization in the absence of swelling, and showed good agreement with each other. Four PAM hydrogel compositions were characterized thus, with corresponding storage shear moduli (as measured immediately after polymerization) of 4,530 Pa (termed stiffest), 2,900 Pa (stiff), 538 Pa (soft), and 260 Pa (softest). Next, all compositions were subjected to swelling in phosphate buffered saline. Swelling ratios and local elastic moduli were measured at 0, 3, 6, 9, 12, and 24 h post-polymerization for the soft and softest compositions, and once daily till 6 days post-polymerization for all four compositions. For the stiffest and stiff gels, swelling ratio, and local elastic modulus changed negligibly with time, while for the soft and softest gels, substantial changes between Day 0 and Day 1 were found for both swelling ratio (increased by 21.6 and 133%, respectively), and local elastic modulus decreased (by 33.7 and 33.3%, respectively), substantially. Experimental data were analyzed by a model that combined ideal elastomer mechanics and poroelastic swelling kinetics model. Model predictions confirmed the validity of present measurements with respect to past studies where swelling and elastic properties were not measured simultaneously. The present study underlines the important effect swelling can have on PAM elastic properties and provides detailed quantitative data to guide the duration taken to reach equilibrium—a useful information for cell mechanics experiments. In addition, the simultaneous measurements of swelling and local elastic moduli provide novel data for the validation of theoretical models.
Hydrogels are soft, hydrated materials that can mimic the properties of native tissues. They have gained considerable interest for cell culturing and cell delivery, in particular for the engineering of physiologically more relevant cellular microenvironments, e.g., for regenerative medicine applications. They have been used as deformable substrates in cell mechanical and mechanobiological studies to evaluate the role of extracellular matrix mechanical properties on cell fate. They are an essential ingredient of Traction Force Microscopy (TFM) procedures that aim at quantifying cellular forces from measuring cell-induced deformations of hydrogel substrates (Burton, 1998; Butler et al., 2002; Du Roure et al., 2005; Lin et al., 2013; Schwarz and Soiné, 2015; Steinwachs et al., 2016). These procedures, among others, require accurate data on the mechanical (elastic) properties of the hydrogels. In this context, polyacrylamide (PAM) hydrogels have been among the most popular materials for 2D TFM studies and cell mechanical studies in general. Their stiffness can be easily tuned by changing the concentrations of the monomer acrylamide and cross-linker, their transparent nature enables high-resolution live cell imaging, and their surface can be easily functionalized by covalently attaching a variety of adhesion ligands (Tse and Engler, 2010; Caliari and Burdick, 2016). At the same time care must be taken to control the mechanical behavior of PAM substrates in order to improve the reproducibility of cell culture experiments and accuracy of traction calculations.
A number of studies have focused on the effect of PAM composition and polymerization temperature on the mechanical properties of PAM hydrogels. Tse and Engler measured the elastic (Young's) modulus of PAM substrates by means of atomic force microscopy (AFM) for a large range of acrylamide (3–10% w/v) and N′N′ methylene bis acrylamide (MBA) (0.03–0.3% w/v) concentrations and reported values between 0.2 and 40 kPa that increase with increasing monomer and cross-linker concentration (Tse and Engler, 2010). Calvet et al. (2004) demonstrated by means of bulk shear rheology that for a given composition, an optimal temperature of polymerization exists for which the highest storage modulus is achieved. The pore sizes of the PAM hydrogels have been reported to be of the order of 20–200 nm and tend to decrease with increasing monomer and cross-linker concentration (Stellwagen, 1998). While composition and polymerization temperature affect the mechanical and structural properties immediately after gelation, they may change over time as a result of hydrogel swelling. Therefore, in order to avoid confounding the interpretation of results, protocols require that cell mechanics experiments are performed after equilibrium has been attained.
A limited number of studies have measured the change in elastic properties for PAM hydrogels attached to a rigid surface and immersed in phosphate buffered saline (PBS). Denisin and Pruitt (2016) measured elastic moduli by means of AFM for various PAM hydrogel compositions (total polymer content between 10 and 20% w/v) over a period of 10 days and reported that stiffness fluctuates over time, with an increase up to 55% after 10 days for the lowest polymer content (10%). While stiffness was measured every 2 days, swelling was only determined at the end of the 10 day periods (Denisin and Pruitt, 2016). Damljanović et al. (2005) performed indentation measurements over a 20 h time period and reported PAM softening of about 25% for a 4.5% acrylamide, 0.07% MBA hydrogel, however without performing any swelling measurements. These studies provide estimates of how long a duration needs to be waited out before equilibrium is attained. Yet, due to the lack of transient swelling data in both studies and the different time periods investigated, it remains unclear how the elastic properties of PAM hydrogels depend on the transient swelling ratio.
Theoretical models based on equilibrium thermodynamics have been developed to predict equilibrium swelling of polymer networks from free energy minimization, taking into account free energy contributions from the mixing of the solvent with the polymer network, from the elastic deformation of the polymer network and (if present) from the mixing of ions with the solvent (Brannon-Peppas and Peppas, 1991; Aalaie and Vasheghani-Farahani, 2012; Li et al., 2012). Such models have been applied to describe the relation between swelling ratio and osmotic pressure for electrically neutral PAM hydrogel networks swollen in water (Li et al., 2012) and to predict equilibrium swelling ratios of electrically charged PAM hydrogels in electrolyte solutions (Aalaie and Vasheghani-Farahani, 2012).
Swelling has been shown to increase the spatial heterogeneity of polymer networks such as PAM, as shown by light scattering (Johnson et al., 2004) and neutron scattering measurements (Mendes et al., 1991). In addition, when soft PAM hydrogels are attached to a rigid surface (as for cell culture applications) they may exhibit non-uniform swelling which might lead to surface creasing or buckling. This can lead to heterogeneity in surface structural and elastic properties and also influence cell behavior (Guvendiren and Burdick, 2010; Saha et al., 2010).
The main aim of the present study is to simultaneously characterize PAM hydrogel swelling and changes in local elastic properties during the transient swelling process post-polymerization. This fills a knowledge gap in the literature on PAM mechanical behavior that is potentially of interest to researchers working at the interface of cell mechanics, mechanobiology, and biomaterials. Thereby, the choice of length scale of local elastic properties, of durations investigated and of global elastic properties of the PAM hydrogels are driven by considerations of TFM experiments. Specifically, local elastic properties are measured using AFM at the surface of hydrogels attached to a rigid glass surface. Swelling ratios and local elastic moduli are obtained over relatively long (6 days, with 1 day interval) as well as short (24 h, with 3 h interval) periods, covering TFM culture periods that can span from a few hours to days (Plotnikov et al., 2014; Tang et al., 2014; Schwarz and Soiné, 2015). PAM compositions investigated possess post-polymerization bulk shear moduli under non-swelling conditions between 260 and 4,530 Pa. These global elastic properties are also in line with PAM hydrogels employed in cell mechanics experiments (Tse and Engler, 2010; Caliari and Burdick, 2016; Denisin and Pruitt, 2016). A theoretical analysis is performed in order to qualitatively interpret the above novel data and to compare these with past studies where swelling and elastic properties were investigated (but not simultaneously). This analysis combines previously established models of ideal elastomeric gels under free swelling conditions (Damljanović et al., 2005) and poroelastic models of swelling kinetics (Yoon et al., 2010). Lastly, although for studying the effect of swelling on the elastic properties, the use of bulk rheology (compared to AFM) is much less straightforward (because of technical and practical challenges to perform accurate bulk rheological measurements on hydrogels that are swelling within the rheometer for extensive periods of time), it is nevertheless an established technique for PAM hydrogel mechanical characterization and is often performed on PAM hydrogels. Moreover, AFM response is potentially heterogeneous; hence to address this, bulk shear rheological measurements were performed to characterize global elastic properties, which were used to verify local elastic properties during and after polymerization.
All chemicals were purchased from Sigma-Aldrich or BioRad company.
PAM hydrogels were prepared (Tse and Engler, 2010) by mixing acrylamide (A) and N′N′ methylene bis acrylamide (MBA) at different concentrations (reported throughout as grams of solute per 100 mL of mixture, %w/v) leading to four different stiffness values (termed stiffest, stiff, soft, and softest; see Table 1) (Tse and Engler, 2010). Polymerization was initiated by adding 12 μL of N,N,N,N-tetramethylethylene-diamine (TEMED) and ammonium persulfate at 0.1% final concentration.
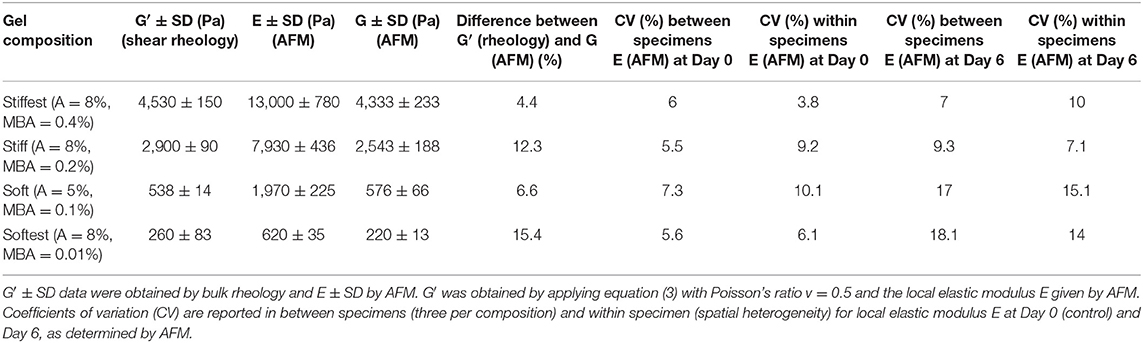
Table 1. Summary of global (in situ bulk shear rheology) and local (AFM) elastic properties obtained for four different gel compositions (A, acrylamide; MBA, N′N′ methylene bis acrylamide; concentrations are expressed as grams of solute per 100 mL of mixture, %w/v).
In situ bulk shear rheological measurements were performed for the four PAM compositions prior to swelling (Day 0). Storage (G′) and loss (G″) shear moduli were determined as functions of polymerization time (time sweep), loading frequency (frequency sweep) and shear strain amplitude (strain sweep). A Physica MCR 501 parallel plate shear rheometer with temperature control (Anton Paar GmbH, Graz, Austria) was used and all hydrogel specimens were prepared in situ. Initially the set-up was maintained at room temperature. Immediately after dispensing a 350 μL drop of polymerized solution on the bottom plate, a 20 mm diameter top plate was lowered from an initial gap of 20 mm to a final gap of 1 mm. After the top-plate reached the final gap, heavy mineral oil was poured over the exposed surface of the gel, and a solvent trap was placed over the entire set-up to prevent evaporation. For time sweep measurements, oscillatory loading was started immediately afterwards and continued for 1 h at room temperature and for a (engineering) shear strain amplitude of 1% and an angular frequency of 1 rad s−1. For strain sweep and frequency sweep measurements, the solution was left undisturbed at room temperature for 1 h, after which the temperature was increased to 37°C over a 50 s interval, and then held constant at 37°C until the end of the measurement. Strain-sweep measurements were performed at an angular frequency of 1 rad s−1, while the strain amplitude was increased from 0.01 to 100%. These tests demonstrated that the storage shear modulus of all gels varied by <5% over the entire strain range for all PAM compositions, thereby confirming linear elastic behavior. Frequency sweep measurements were performed for a strain amplitude of 1% and angular frequency was increased from 0.1 to 100 rad s−1. For each measurement (time sweep, strain sweep, frequency sweep), three specimens per composition were tested.
AFM was employed to assess the effect of swelling on the local elastic properties for the four PAM compositions at different points of time during polymerization, and during post-polymerization swelling. A JPK Nanowizard® III Bioscope-AFM (JPK Instruments AG, Berlin, Germany) was employed for all measurements, and for each time-point 3 specimens per composition were measured.
AFM measurements were performed on Day 0 at different polymerization times to enable comparison between local and bulk rheological (time sweep) properties. Measurements were performed at room temperature similar to time sweep bulk rheological measurements. Specimens were prepared by adhering a 100 μL drop of the acrylamide mixture to a pretreated (3-aminopropyltrimethoxysilane + glutaraldehyde) glass surface. This avoided any gel movement while measuring. The gel was flattened with a 12 mm diameter circular coverslip pretreated with Sigmacote® (to avoid sticking; Sigma-Aldrich), leading to a gel thickness of about 1 mm. At selected polymerization times (3, 6, 10, 15, and 30 min) gels were washed with deionized water (thereby removing unpolymerized material and arresting any further polymerization) and coverslips were removed prior to measurement.
AFM measurements were performed as a function of swelling time. Gels were prepared by adhering a 100 μL drop of the acrylamide mixture to a glass surface pretreated with 3-aminopropyltrimethoxysilane and glutaraldehyde to avoid any gel movement while measuring. Prepared gels were immersed in PBS buffer at 37°C. Measurements were performed at Day 0 (control), Day 1, Day 2, Day 3, Day 4, Day 5, and Day 6. Measurements were also performed at 3, 6, 9, 12, 15, and 24 h to assess the influence of swelling at shorter intervals for those two compositions that exhibited substantial swelling for the 6 day experiment (soft and softest gels).
Local elastic (Young's) moduli were determined by acquiring force–distance curves and analyzing them by means of a Hertz contact model. All curves were recorded for an approach and retract speed of 5 μm s−1 and a sampling frequency of 2–4 kHz. For each AFM measurement, the spring constant of the cantilever was calibrated using thermal tuning method and it was found to be in the range of 0.035–0.045 N/m. Probe tips with a 6.1 μm diameter polystyrene sphere (sQube® colloidal probe, CP-PNPL-PS-C-5, nominal spring constant = 0.08 N/m) or pyramid geometry (budget sensors, SiNi-30, nominal spring constant = 0.06 N/m) (half face angle = 35°) were used. The obtained data were fitted by means of the JPK-SPM data processing software that employs a Hertz contact model. For a spherical geometry the relation between force F and indentation δ is given by:
with E = elastic modulus, R = tip radius, v = Poisson's ratio. For a pyramidal tip the following relation was used:
where α = half face angle. A Poisson's ratio of 0.5 was assumed for the calculation of E. The obtained elastic modulus values were found to be independent of the choice of AFM probe tip geometry [as was also previously found by Engler et al. (2004)]. In order to assess spatial heterogeneity of the local elastic modulus, several spatial elasticity maps were acquired for a given specimen, with each map consisting of either 8 × 8 or 16 × 16 pixels and with map size varying from 10 to 50 μm wide. We assume the gels to be perfectly incompressible and linear elastic and possessing negligible viscous behavior. Hence, G is taken to be interchangeable with G′. Applying the relationship between G and elastic modulus E for linear elastic material:
implies that for Poisson's ratio v = 0.5 (perfect incompressibility), we have G′ = G = E/3.
In order to measure hydrogel volumetric swelling, PAM hydrogel specimens were prepared in exactly the same way as for AFM measurements as a function of swelling time. Specimens were attached to a glass surface in order to mimic the conditions during TFM (and AFM) experiments and substrate-attached gels were allowed to swell in PBS at 37°C. Swelling ratios were measured for long (up to 6 days; all gel compositions) and short (up to 24 h; soft and softest gels only) periods at the same time points as AFM measurements to enable direct comparison between elastic modulus and swelling ratio. The wet weights were measured for substrate-attached gels (i.e., including the weight of the glass slide) as a function of time. At the end of the swelling experiment substrate-attached specimens were dried in an oven at 65°C until they were completely desiccated, and the dry weight was measured (again, including the weight of the glass slide). Finally, the desiccated gels were rehydrated and removed from the glass slide. The weight of the glass slide was measured and subtracted from the weights that included the glass slide, in order to obtain the specimen wet (Mwet) and dry (Mdry) weights. The volumetric swelling ratio J(c) (with superscript (c) referring to constrained, i.e., substrate-attached, swelling) was calculated as J(c) = Vwet/Vdry = 1 + (ρPAM/ρPBS) (Mwet – Mdry)/Mdry where ρPAM = 1.443 g/cm3 and ρPBS = 1.010 g/cm3 were taken to be the mass densities of the polymer and the solvent, respectively. For each time point, three specimens per composition were measured.
In addition to the above swelling experiments, gels with identical concentration as above were prepared, except that the total volume of the pre-polymerization constituents was modified to yield polymerized gels of typical height 150 μm and diameter 12 mm. Polymerization occurred at room temperature, following which gels were allowed to swell unconstrained (also called free swelling) in PBS at 37°C. Gel swelling ratios J(u)–the superscript (u) refers to unconstrained—were measured at different time points as described above. Once swelling equilibrium was established, the equilibrium swelling ratios were noted and average and SD values were computed for each composition (3 gel specimens per composition). Note that depends on the attachment condition (constrained or unconstrained) but not on the gel dimensions. Free swelling (equilibrium) data was used to validate the predictions from the theoretical analysis (see next).
Swelling causes a gel to soften (Rubinstein and Colby, 2003). Under substrate-attached conditions, predicting the loss of mechanical resistance to indentation (as measured by AFM) requires sophisticated model development that is out of the scope of this study. Here we combine a well-established theoretical model of an ideal elastomeric gel (Flory and Rehner, 1943; Rubinstein and Colby, 2003; Damljanović et al., 2005; Cai and Suo, 2012) valid for unconstrained swelling with a previously reported poroelastic analysis of swelling kinetics (Yoon et al., 2010) in order to qualitatively assess our experimental results.
In the present experiments, distilled water was used as the solvent at the time of gel preparation, and the swelling experiments were carried out in PBS. The ionic strength of PBS (~2.3 mmol/L) is negligible and its mass density is nearly the same as distilled water. Hence no distinction is made between the two solvents in the theoretical model below.
The stress–stretch behavior of PAM hydrogels can be captured by means of a network of Gaussian chains (Flory and Rehner, 1943; Cai and Suo, 2012). When the PAM hydrogel is swollen in the PBS solvent, it is assumed that the mean-squared end-to-end distance of the chains continues to be distributed in a Gaussian fashion (also known as θ-solvent condition). The elastic behavior of the gel is characterized by the shear modulus G, which is equated with G′ as mentioned before. The shear modulus G(u) of a network of Gaussian chains is proportional to the number density of network chains N and the free energy of each chain Ψ (Rubinstein and Colby, 2003; Damljanović et al., 2005). As the amount of polymer remains unchanged during swelling, N is inversely proportional to the unconstrained volumetric swelling ratio J(u). The free energy Ψ is proportional to λ2/R, where R is the mean-squared end-to-end distance of each chain and λ is the linear stretch in each chain. Thus, we can take R to be independent of J(u) (Rubinstein and Colby, 2003). Assuming affine deformations within the network and isotropic macroscopic deformation, a swelling ratio of J(u) at the scale of the gel is equivalent to λ = (J(u))1/3 at the scale of each chain. For swelling in a θ-solvent, Ψ is proportional to (J(u))2/3 and finally G(u) is proportional to (J(u))−1/3. This dependence captures the result of two counteracting effects: decreasing number density of network chains and increasing free energy of each chain during swelling. Denoting the variables at preparation by the subscript “0,” the modulus at any instant of swelling is given by Rubinstein and Colby (2003):
At the instant of gel preparation, there are no differences between constrained and unconstrained gels, hence the superscript is omitted from G0 and J0 above. Let and denote the increases in gel height at any instant of swelling after preparation, respectively, in substrate-attached gels (as in our AFM experiments) and unconstrained gels. The poroelastic analysis of swelling kinetics by Yoon et al. showed that 1 ≤ Δ(c)/Δ(u) ≤ (1 + v)/(1 – v) (Yoon et al., 2010), where the lower limit is valid close to swelling initiation and the upper limit is reached at swelling equilibrium. For a Poisson's ratio of v = 0.5, this implies 1 ≤ Δ(c)/Δ(u) ≤ 3. For a thin gel [as in the present experiments, but also in Yoon et al. (2010)] it can be assumed that the cross-sectional area remains fixed during swelling if the gel is attached to the substrate, and only the height of the gel increases. Thus (Δ(c) + H0)/H0 = J(c)/J0 at any instant during swelling, where H0 is the height of the gel at preparation. When a gel of identical geometry (at preparation) is swollen under unconstrained conditions, the resulting deformation is isotropic, which implies (Δ(u) + H0)/H0 = (J(u)/J0)1/3. It follows from the above relations that Δ(c)/Δ(u) = (J(c)/J0 – 1)/((J(u)/J0)1/3 – 1). Using the result in Yoon et al. (2010) above, we obtain the limits for (J0/J(u))1/3 as:
Substituting this in Equation (4), the shear modulus of an unconstrained swollen gel is found to be bounded by:
Here too, the lower limit is valid close to swelling initiation and the upper limit is reached at swelling equilibrium (for v assumed to be 0.5).
We measured J0 and J(c) from the swelling experiments and G0 from AFM at the point of preparation. Thus (the right hand side of), Equations (5) and (6) will be used to predict equilibrium swelling ratios and shear moduli under free swelling conditions. As further validation, we will compare these predictions with equilibrium swelling ratios directly measured under free swelling conditions and with equilibrium shear moduli derived from these direct measurements and application of Equation (4). The inequalities in Equation (6) allow us to predict the bounds of shear modulus during swelling under unconstrained conditions. We will compare this prediction with the shear moduli from constrained gels G(c) that is measured here using AFM.
Li et al. (2012) introduced a formalism to express the balance between externally applied stress, the elastic stress in the polymer network, the osmotic pressure of mixing and the chemical potential of the solvent at any instant of swelling (Damljanović et al., 2005). For a gel under free swelling conditions, the applied stresses are zero and stretches are isotropic. Also, by definition, the chemical potential must vanish when the freely swelling gel reaches swelling equilibrium (henceforth denoted by subscript “eq”). Therefore, at equilibrium, the elastic stress in the network fully balances the osmotic pressure. For a network of Gaussian chains, an isotropic stretch λ = in the principal directions leads to an elastic stress (1 – ), as obtained by differentiating the free energy of stretching of the network (different from Ψ, the free energy of each chain) (Damljanović et al., 2005). Using Equation (4) to obtain the shear modulus at unconstrained swelling equilibrium, the following expression for the osmotic pressure due to mixing at swelling equilibrium can be written:
The predicted dependence of on across various gel compositions is compared with that in literature (Damljanović et al., 2005), where is either the value derived from the right hand side of Equation (5) and using measured J0 and J(c), or the value measured directly under free swelling conditions.
Finally, the poroelastic analysis of Yoon et al. (2010) of hydrogel swelling kinetics can be used to estimate the fluid diffusivity D inside the gel. Yoon et al. have among others derived a transient solution for the swelling kinetics of an ideal poroelastic, surface-attached thin hydrogel layer and showed that the specimen height as a function of time can be described by an infinite sum of exponential decay functions. The basic relaxation time (characteristic swelling time) τ is given by:
with H0 the initial gel height. We will estimate τ for the soft and softest gel compositions from the short-term swelling experiments and use Equation (8) to calculate D.
In situ bulk shear rheology measurements of G′ and G″ during time sweep experiments are shown in Figure 1A, and after polymerization (frequency sweep experiments) are shown in Figures 1B–D, for the four hydrogel compositions. The storage modulus is found to increase monotonically with time and to reach a stable plateau after about 30 min, at which point the polymerization process is considered to be complete. Figures 1B–D show the post-polymerization storage and loss shear moduli, and phase angle (tan δ = G″/G′) for the same hydrogel compositions as functions of angular frequency for samples that were left undisturbed during in situ polymerization. The storage modulus is found to be weakly dependent (softest gel) to almost independent (other compositions) of angular frequency. The storage shear modulus is found to decrease from 4,530 ± 150 Pa (stiffest), 2,900 ± 90 Pa (stiff), 538 ± 14 Pa (soft) to 260 ± 83 Pa (softest) with decreasing concentrations of cross-linker (MBA), acrylamide or both (see Table 1, G′ values reported are averaged from 1 rad/s). Tan δ values are always <0.012 for all gels except the softest gel. For the softest gel tan δ averages 0.104 at 1 rad/s and is always <0.27. These small values confirm that PAM stresses are governed by elastic instead of viscous effects for the tested frequency range (Calvet et al., 2004; Li et al., 2012; Abidine et al., 2015) and support the comparison of bulk rheology and AFM measurements, and the estimates obtained from the theoretical analysis.
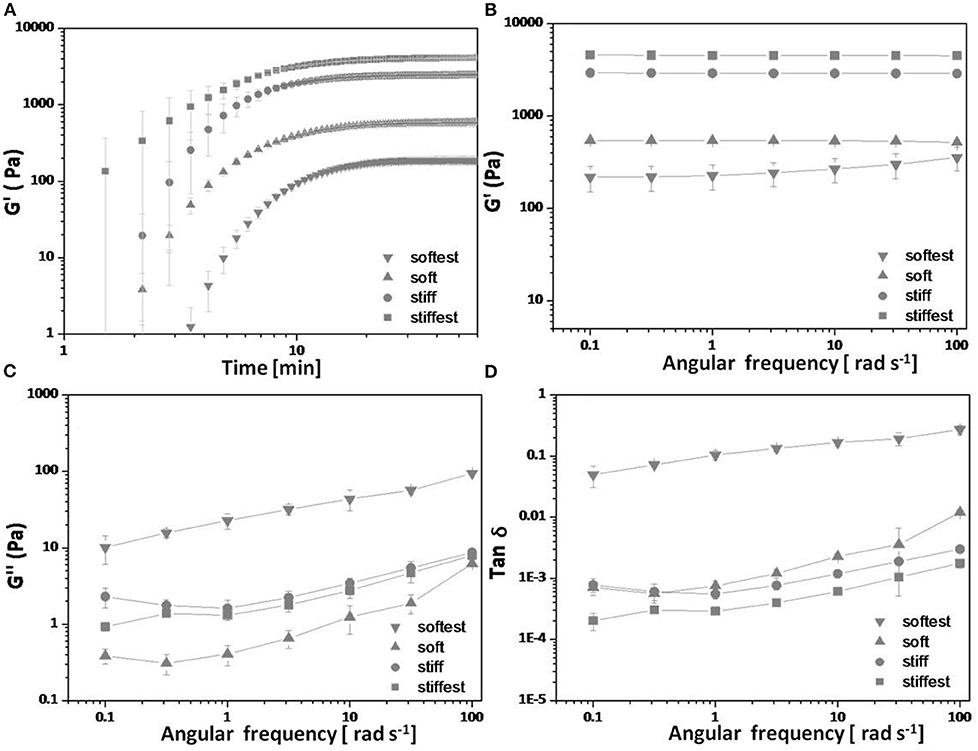
Figure 1. In situ bulk shear rheological measurements on four PAM hydrogel compositions (see Table 1): (A) Storage shear modulus G′ vs. polymerization time, (B) storage shear modulus G′ vs. angular frequency post-polymerization, (C) loss modulus G″ vs. angular frequency post-polymerization, and (D) Tan δ (=G″/G′) vs. angular frequency post-polymerization. All data points are averages (±SD) over three samples measured per composition.
Prior to evaluating the effect of swelling on the local elastic properties, AFM measurements were performed and compared to bulk shear rheological measurements in order to verify to what extent local and global elastic properties correspond. For the stiff hydrogel composition AFM measurements were also performed during polymerization and the local elastic moduli as a function of polymerization time were compared with the global elastic moduli as derived from time-sweep rheology (Figure 2A). Similar to the bulk rheological measurements, the local elastic moduli are found to monotonically increase with time and to reach a stable plateau after 30 min, while at all times being in agreement with the global elastic moduli. Post-polymerization force–distance curves were then acquired for all four hydrogel compositions and typical examples are shown in Figure 2B (an example of reference F–D curve of glass substrate was included in Figure 2B). The measured average local elastic modulus E is 13,000 ± 780 Pa for stiffest, 7,930 ± 437 Pa for stiff, 1,970 ± 225 Pa for soft and 620 ± 35 Pa for softest gels (values are averaged over three samples per composition). After converting these values into local G′ values using Equation (3), it was found that they are in good agreement with the global G′ values obtained by bulk rheology, with differences between AFM and shear rheology ranging from ~4 to 15% (see Table 1).
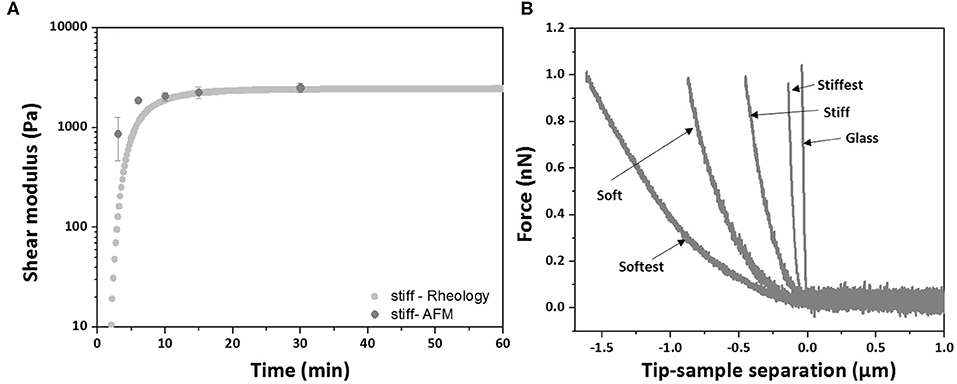
Figure 2. (A) Comparison of elastic modulus during polymerization between in situ bulk shear rheology (dotted curve) and AFM measurements (data points are averaged over three samples, whiskers indicate SD) for stiff hydrogel. (B) Typical AFM force-distance curves obtained for each hydrogel composition after polymerization at Day 0 (control).
In order to assess to what extent swelling affects the gel local elastic properties, AFM and swelling measurements were first performed at four different time points (Day 0 to Day 6) for all four compositions. Figures 3A,B show that the stiffest and stiff gels did not exhibit any measurable change in the elastic properties with time. The soft and softest gels (Figures 3C,D) exhibited a substantial decrease of the measured local elastic moduli of 33.7 and 33.3%, respectively, between Day 0 and Day 1, after which the values tended to reach a plateau. Additional measurements were then performed from 0 to 24 h for the soft and softest gels to assess the swelling kinetics in more detail (Figures 3E,F). These short term measurements demonstrated that after 6 (soft gels) to 9 h (softest gels) the elastic modulus did not change further.
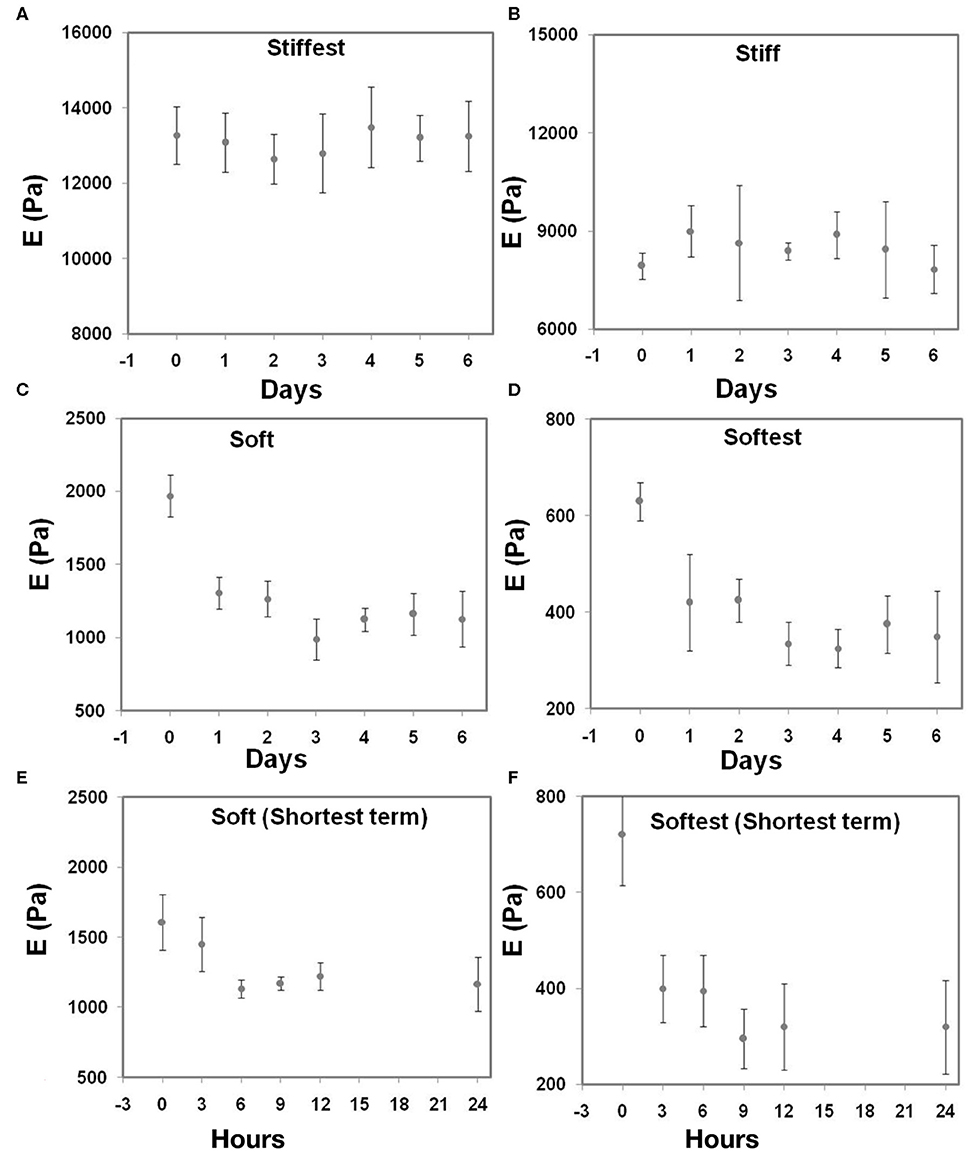
Figure 3. Local elastic modulus (as determined by AFM) of substrate-attached gels as a function of swelling time for four different hydrogel compositions during long term swelling up to 6 days (A,B) stiffest and stiff; (C,D) soft and softest; (E,F) are the short term swelling times from 0 to 24 h. All measurements were done in triplicate (whiskers indicate SD).
Volumetric swelling ratios (J(c)) as a function of time for gels attached to a glass surface are reported in Figure 4A for long term experiments (up to 6 days). For all time points swelling ratios were found to be lowest for the stiffest gel, and highest for the softest gel (apart from Day 0 of the short term experiments). While swelling ratios for the stiffest and stiff gels did not change with time, the soft and softest gels exhibited an increase in swelling ratio between Day 0 and Day 1 with 21.6 and 133%, respectively, after which no further changes could be noticed. Similar to AFM, swelling measurements were also performed for soft and softest gels from 0 to 24 h. These short term swelling experiments displayed similar trends as the AFM measurements: soft gels seemed to reach a plateau value earlier than softest gels, although for both gel compositions this occurred at earlier time points than for AFM (3 and 6 h for soft and softest gels, respectively). Taking the equilibrium times of the AFM measurements as upper bounds (6 and 9 h for soft and softest gels, respectively), we can estimate the relaxation time for the swelling kinetics of soft and softest gels. If we approximate the transient solution of specimen height [as derived by Yoon et al. (2010)] by a single exponential decay function with relaxation timeτ and take the equilibrium time equal to 3 times the relaxation time (i.e., define equilibrium if further change is <5% of the equilibrium solution), relaxation times of soft and softest gels are estimated to be 2 and 3 h, respectively. Using Equation (8) leads to fluid diffusivities of 5.6 × 10−11 and 3.8 × 10−11 m2/s for soft and softest gels, respectively.
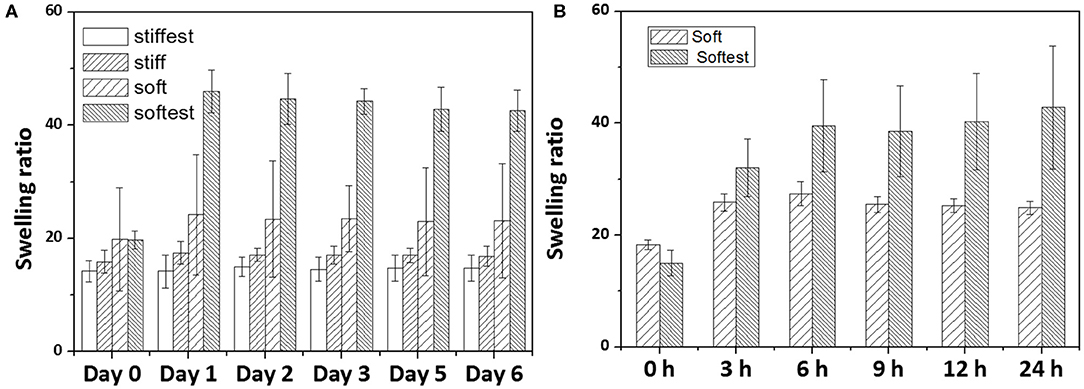
Figure 4. Measured swelling ratio of substrate-attached gels as a function of swelling time: (A) long term swelling experiments (up to 6 days) for four different hydrogel compositions (whiskers indicate SD); (B) short term swelling experiments (up to 24 h) for soft and softest hydrogels (whiskers indicate SD).
We also evaluated the effect of swelling on the spatial heterogeneity of the local elastic modulus, by calculating the average coefficient of variation (CV) of all AFM measurements within each specimen (i.e., for each specimen we first calculate a CV based on all local elasticity measurements for that specimen; then we average the CV values over the three specimens per composition). This measure of spatial heterogeneity was then compared to the coefficient of variation between specimens (i.e., by first calculating an average local modulus per specimen and then calculating the CV between average moduli, as obtained for 3 specimens per composition). As can be seen in Table 1, variability between specimens is of the same order of magnitude as variability within specimens (i.e., spatial heterogeneity) for both Day 0 and Day 6 measurements. Moreover, neither variability between specimens nor variability within specimens seem to be strongly affected by swelling, as CV values are comparable at Day 0 and Day 6.
Equilibrium swelling conditions were reached by Day 1 as swelling ratio of the samples did not change by more than 5% compared to values at Day 6 (Figure 4). In the following, values at Day 0 and Day 1 are denoted by subscripts “0” and “eq,” respectively, and shear modulus G is calculated using Equation (3). Figure 5 compares the predicted and observed values at free swelling equilibrium for swelling ratio and equilibrium shear modulus for the stiffest, stiff and softest gel samples. The predicted values of and are obtained using the right-hand side of Equations (5) and (6), respectively, whereas the observed values of are directly measured and those of obtained from Equation (4). The dependence of the predicted equilibrium osmotic pressure due to mixing Πmix,eq (Equation 7) on measured/predicted equilibrium swelling ratio under free swelling conditions shows a negative power-law relationship, with pressure values close to zero for very large equilibrium swelling ratios (Figure 5C). Measured (G(c)) and predicted (G(u)) shear moduli (normalized by the modulus at preparation, G0) as a function of swelling time were compared for short term experiments (up to 24 h) of soft and softest gels (Figure 6). The transient values of G(c), as measured by AFM, were found to be located within the bounds, predicted by Equation (6).
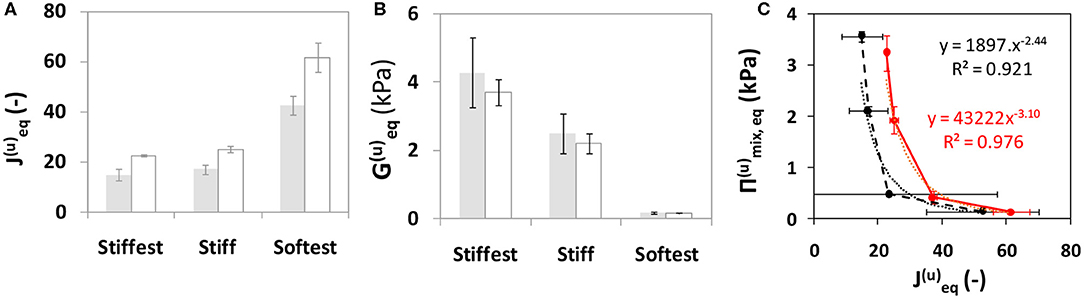
Figure 5. Gel swelling and elastic properties at equilibrium swelling (Day 1) conditions predicted (gray bar) and measured (white bar) under unconstrained swelling conditions. Dependence of (A) swelling ratio and (B) shear modulus on gels with varying cross-linker concentration (see Table 1) but identical monomer concentration (8% w/v); and (C) dependence of predicted osmotic pressure due to mixing on predicted/measured swelling ratio for all four gel compositions. Whiskers indicate SD.
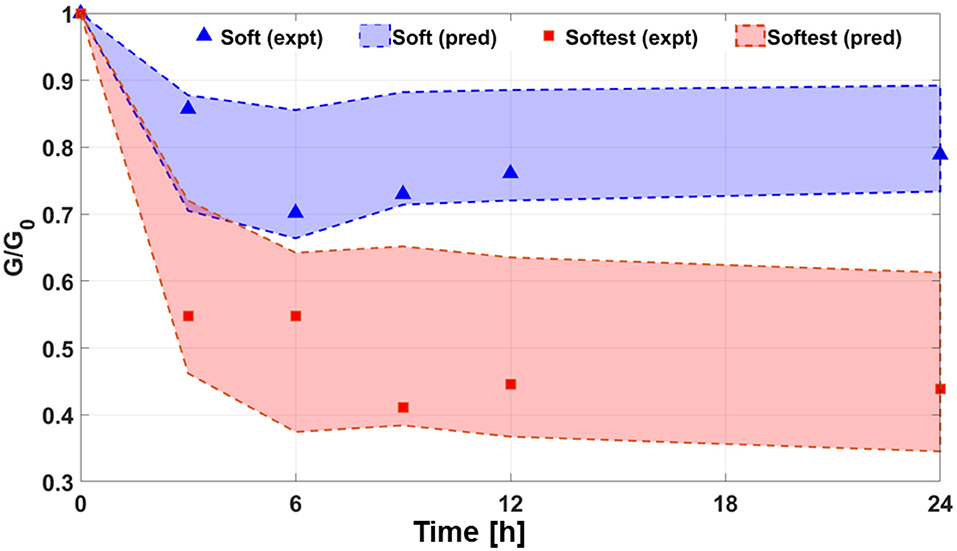
Figure 6. Changes in relative shear modulus as a function of swelling time for soft and softest gels for short-term swelling experiments (up to 24 h). Filled symbols are obtained from AFM measurements of G(c) and G0. Dashed lines bounding the shaded regions correspond to the bounds of G(u) predicted by Equation 5, and normalized by the AFM measurements of G0.
Previous studies on the mechanical characterization of PAM hydrogels have either used bulk rheological techniques (Calvet et al., 2004; Kizilay and Okay, 2004; Neamtu et al., 2006; Wang and Ugaz, 2006) or micro- to nanoscale techniques (AFM) (Engler et al., 2004), with only very few studies comparing global to local properties (Abidine et al., 2015). In this study we have combined in situ bulk shear rheology and AFM in order to obtain data on global and local elastic modulus during and after polymerization for a wide range of stiffness, and evaluated the effect of swelling on the elastic modulus. Bulk rheological data on storage moduli (Table 1 and Figure 1) display good reproducibility (CV < 5% for all compositions except for softest compositions) and agree well with previously reported rheological data on PAM gels for similar concentrations, including the fact that rheological behavior is governed by the elastic, instead of viscous component for the applied frequency range (tan δ of the order of 10−4-10−2 for stiffest, stiff and soft gels; order of 10−1 for softest gel) (Calvet et al., 2004; Wang and Ugaz, 2006).
Storage moduli from rheology measurements were compared with local AFM-derived moduli at different polymerization times for the stiff hydrogel composition (Figure 2A). At early time points (3, 6 min) AFM measurements slightly deviated from rheology measurements, which could be due to a lack of control in the polymerization time and which is expected to play a more important role at these early time points. Indeed, at later time points (10, 15, 30 min) moduli derived from rheology and AFM agree very well (differences <3.3%). Similarly, post-polymerization (30 min) moduli based on rheology and AFM were found to be in good agreement for all four PAM compositions, with differences that were <15%, which is of the same order as the CV of AFM-derived moduli (Table 1). For the conversion of local Young's modulus to shear modulus the Poisson's ratio was taken equal to 0.5. Instead of assuming a Poisson's ratio of 0.5, one can also combine bulk rheological (G′ values; Table 1) and AFM measurements in order to estimate the value of the Poisson's ratio. By combining Equations (1) or (2) with Equation (3), we obtained an average Poisson's ratio of 0.46, which suggests close to incompressible behavior of PAM hydrogels during AFM measurements and which is in agreement with the findings of a previous study on PAM that also combined AFM with bulk rheology (Abidine et al., 2015).
In order to evaluate the variability of the AFM measurements between specimens of the same composition as well as the variability between measurements on the same specimen (spatial heterogeneity), corresponding CV values of local elastic moduli were calculated (Table 1). Both types of variability led to CV values of the same order (6–8% for inter-specimen variability, 4–10% for intra-specimen variability) and are comparable to the variability previously reported in AFM studies on PAM hydrogels (Damljanović et al., 2005; Tse and Engler, 2010; Denisin and Pruitt, 2016). The intra-specimen variability could be because of local concentration fluctuations of monomer and cross-linker, which might lead to spatial heterogeneity of hydrogel network formation, which in turn could affect local stiffness (Kizilay and Okay, 2004; Saha et al., 2010). Swelling affected the spatial heterogeneity in the case of the soft and softest hydrogels, as can be derived from the fact that the CV value of AFM measurements within the same specimen increased between Day 0 and 6 from 10 to 15% for soft gels and from 6 to 14% for softest gels, respectively. This is in line with the findings of Kizilayet al. based on light scattering measurements (Kizilay and Okay, 2004).
Earlier work on PAM hydrogels has either reported swelling ratios as a function of PAM composition and solute concentration (Aalaie and Vasheghani-Farahani, 2012; Li et al., 2012), or elastic moduli as a function of storage time (Damljanović et al., 2005; Denisin and Pruitt, 2016). As the latter two studies did not (Damljanović et al., 2005) or only partially (single time point, Denisin and Pruitt, 2016) measure any swelling ratios, it has not been possible so far to correlate swelling ratios to changes in elastic properties in time. This is particularly true for substrate-attached PAM hydrogels, which is the configuration that is most relevant for cell mechanical and mechanobiological studies that e.g., make use of TFM. In the present study, we have measured the change in local elastic properties (based on AFM) and swelling ratios over relatively long (up to 6 days) time periods for four different PAM hydrogel compositions. The stiff and stiffest gel compositions did not show any change in elastic properties with time (Figure 3A), which correlated with the fact that swelling ratios did not change with time either (Figure 4). The soft and softest gel compositions exhibited a decrease in elastic modulus between Day 0 and Day 1 (Figures 3C,D), which was accompanied by an increase in swelling ratio between the same time points (Figure 4A). Additional short term experiments (up to 24 h) were done for the soft and softest gel compositions in order to assess their swelling kinetics in more detail. These experiments demonstrated that soft gels reached equilibrium faster than softest gels for both AFM and swelling measurements, although equilibrium times were found to be different between AFM (6 and 9 h for soft and softest gels, respectively), and swelling experiments (3 and 6 h for soft and softest gels, respectively). Possibly, these differences have to do with the temporal resolution of these measurements (3 h in between consecutive measurements) and inter-specimen variability (as different specimens were used for AFM and swelling experiments). The short term experiments enabled us to estimate fluid diffusivity values to be 5.6 × 10−11 and 3.8 × 10−11 m2/s for soft and softest gels, respectively. These values are in line with the values previously reported in Lin and Hu (2006) and Yoon et al. (2010) for polyacrylamide and poly(N-isopropylacrylamide) (PNIPAM) hydrogel systems, which were of the order of 1–5 × 10−11 m2/s.
The theoretical analysis based on models of equilibrium free swelling (Li et al., 2012) and swelling kinetics (Yoon et al., 2010) enables us to predict free swelling behavior for gels of the same dimensions as the ones used for our constrained-swelling experiments and compare predicted trends to literature data on PAM swelling. The predictions made by the model based on a network of Gaussian chains were found to agree excellently with observations regarding unconstrained equilibrium swelling ratio (Figure 5A) and shear modulus (Figure 5B). Interestingly, it was also found that the decrease in when going from the softest to stiff gel was much higher than the decrease when going from the stiff to stiffest gels. On the other hand, the unconstrained equilibrium shear modulus increased steadily going from the softest to stiff to stiffest gels. Note that going from softest to stiff to stiffest gels corresponds to an increase in cross-linker concentrations while acrylamide concentration remains fixed (Table 1). These changes in equilibrium properties with cross-linker concentration found in the present study are qualitatively similar to those reported by Li et al. (2012) for PAM gels of 1–4 wt% of cross-linker-to-monomer ratio [see Figures 4D, 5A, respectively in Li et al. (2012)]. Although the previously stated match between predictions and observations was highly satisfactory at each cross-linker concentration, this match should not be construed to indicate that the model explains the functional dependence of swelling and elastic properties with cross-linker concentration as well. Modeling such a functional dependence is outside the scope of the present study. For any gel composition, the differences in equilibrium shear moduli using predicted or measured equilibrium swelling ratio values were of the same order as the variation between gel samples. Finally, short-term (up to 24 h) constrained-swelling experimental data of soft and softest gels were compared to predicted free swelling data (Figure 6). The measured values of transient shear modulus values in constrained gels fall within the predicted bounds of shear moduli in freely swollen gels for both compositions. The lower bound of prediction characterizes the elasticity at the start of swelling, while the upper bound is reached at swelling equilibrium. Thus, our measurements and model predictions suggest that, when swelling equilibrium is reached, unconstrained gels of the soft and softest compositions will be, respectively, 13.1 and 39.8% stiffer than substrate-attached gels of the corresponding compositions.
Protocols for cell mechanics experiments (including TFM) require that equilibrium is attained prior to commencing experiments. The experimental results presented here underline the importance of this requirement, noting that the soft and softest gel in particular exhibited a decrease in the elastic modulus of 33.7 and 33.3%, respectively between Day 0 and Day 1. Attainment of equilibrium can be ensured by waiting for a sufficiently long period such that the elastic modulus is within the required level of tolerance of its equilibrium value. Such a period may be inferred from Figure 3, although for gels that possess composition, polymerization temperature, gel attachment and solute concentrations conditions that are similar to those considered in the present study.
In this study we reported, for the first time, simultaneous measurements of elastic properties at both global (based on shear rheology) and local (based on AFM) scales in PAM hydrogels. Four different compositions, together spanning a wide range of stiffness (storage shear modulus between 260 and 4,530 Pa), were assessed. Global and local elastic moduli, measured during and after gel polymerization, were found to be in good agreement for all compositions, with differences between global and local post-polymerization moduli being of the same order of magnitude as inter-specimen and intra-specimen variability of AFM measurements. Over the course of the swelling experiments the stiffest (G′ = 4,530 Pa) and stiff (G′ = 2,900 Pa) gels exhibited negligible changes in elastic modulus over time, whereas the soft (G′ = 538 Pa) and softest (G′ = 260 Pa) gels exhibited decreasesing elastic moduli of 33.7 and 33.3%, respectively, between Day 0 and Day 1 of swelling. These results demonstrate that swelling can have an important effect on PAM elastic properties and must be taken into account when using PAM as a substrate for cell culturing, particularly for PAM gels with low monomer and cross-linker concentrations. In addition to filling a gap in the literature of PAM hydrogel mechanics, this study provides data with much higher temporal resolution than before, which can be useful for validating combined elasticity and swelling kinetics models (Table S1).
All datasets generated for this study are included in the article/Supplementary Material.
Experiments were designed and conducted by RS, AI-A, and PB. Theoretical analysis was performed by PB and HV. The manuscript was written through contributions of all authors. HV approved the final manuscript. All authors contributed to the article and approved the submitted version.
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013/ERC Grant Agreement No. 308223) and from the KU Leuven Special Research Fund (BOF, IDO/13/016 and C14/17/111).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.00212/full#supplementary-material
Aalaie, J., and Vasheghani-Farahani, E. (2012). Swelling behavior of sulfonated polyacrylamide nanocomposite hydrogels in electrolyte solutions: comparison of theoretical and experimental results. Iran. Polymer J. 21, 175–183. doi: 10.1007/s13726-012-0016-3
Abidine, Y., Laurent, V. M., Michel, R., Duperray, A., Palade, L. I., and Verdier, C. (2015). Physical properties of polyacrylamide gels probed by AFM and rheology. Euro Phys. Lett. 109:38003. doi: 10.1209/0295-5075/109/38003
Brannon-Peppas, L., and Peppas, N. A. (1991). Equilibrium swelling behavior of pH-sensitive hydrogels. Chem. Eng. Sci. 46, 715–722. doi: 10.1016/0009-2509(91)80177-Z
Burton, K. (1998). Traction forces and subcellular structure imaged in contracting and locomoting cells. Proc. SPIE Int. Soc. Opt. Eng. 63–70. doi: 10.1117/12.307107
Butler, J. P., Toli-Nørrelykke, I. M., Fabry, B., and Fredberg, J. J. (2002). Traction fields, moments, and strain energy that cells exert on their surroundings. Am. J. Physiol. Cell Physiol. 282, C595–C605. doi: 10.1152/ajpcell.00270.2001
Cai, S., and Suo, Z. (2012). Equations of state for ideal elastomeric gels. Europhys. Lett. 97:34009. doi: 10.1209/0295-5075/97/34009
Caliari, S. R., and Burdick, J. A. (2016). A practical guide to hydrogels for cell culture. Nat. Methods 13, 405–414. doi: 10.1038/nmeth.3839
Calvet, D., Wong, J. Y., and Giasson, S. (2004). Rheological monitoring of polyacrylamide gelation: importance of cross-link density and temperature. Macromolecules 37, 7762–7771. doi: 10.1021/ma049072r
Damljanović, V., Lagerholm, B. C., and Jacobson, K. (2005). Bulk and micropatterned conjugation of extracellular matrix proteins to characterized polyacrylamide substrates for cell mechanotransduction assays. BioTechniques 39, 847–851. doi: 10.2144/000112026
Denisin, A. K., and Pruitt, B. L. (2016). Tuning the range of polyacrylamide gel stiffness for mechanobiology applications. ACS Appl. Mater. Interfaces 8, 21893–21902. doi: 10.1021/acsami.5b09344
Du Roure, O., Saez, A., Buguin, A., Austin, R. H., Chavrier, P., Siberzan, P., et al. (2005). Force mapping in epithelial cell migration. Proc. Natl. Acad. Sci. U.S.A. 102, 2390–2395. doi: 10.1073/pnas.0408482102
Engler, A. J., Richert, L., Wong, J. Y., Picart, C., and Discher, D. E. (2004). Surface probe measurements of the elasticity of sectioned tissue, thin gels and polyelectrolyte multilayer films: correlations between substrate stiffness and cell adhesion. Surf. Sci. 570, 142–154. doi: 10.1016/j.susc.2004.06.179
Flory, P. J., and Rehner, J. (1943). Statistical mechanics of cross-linked polymer networks II. Swelling. J. Chem. Phys. 11, 521–526. doi: 10.1063/1.1723792
Guvendiren, M., and Burdick, J. A. (2010). The control of stem cell morphology and differentiation by hydrogel surface wrinkles. Biomaterials 31, 6511–6518. doi: 10.1016/j.biomaterials.2010.05.037
Johnson, B. D., Beebe, D. J., and Crone, W. C. (2004). Effects of swelling on the mechanical properties of a pH-sensitive hydrogel for use in microfluidic devices. Mater. Sci. Eng. C 24, 575–581. doi: 10.1016/j.msec.2003.11.002
Kizilay, M. Y., and Okay, O. (2004). Effect of swelling on spatial inhomogeneity in poly(acrylamide) gels formed at various monomer concentrations. Polymer 45, 2567–2576. doi: 10.1016/j.polymer.2004.01.074
Li, J., Hu, Y., Vlassak, J. J., and Suo, Z. (2012). Experimental determination of equations of state for ideal elastomeric gels. Soft Matter 8, 8121–8128. doi: 10.1039/c2sm25437a
Lin, G. L., Cohen, D. M., Desai, R. A., Breckenridge, M. T., Gao, L., Humphries, M. J., et al. (2013). Activation of beta 1 but not beta 3 integrin increases cell traction forces. FEBS Lett. 587, 763–769. doi: 10.1016/j.febslet.2013.01.068
Lin, Y. Y., and Hu, B. W. (2006). Load relaxation of a flat rigid circular indenter on a gel half space. J. Non Cryst. Solids 352, 4034–4040. doi: 10.1016/j.jnoncrysol.2006.07.007
Mendes, E. Jr., Lindner, P., Buzier, M., Boué, F., and Bastide, J. (1991). Experimental evidence for inhomogeneous swelling and deformation in statistical gels. Phys. Rev. Lett. 66, 1595–1598. doi: 10.1103/PhysRevLett.66.1595
Neamtu, I., Nita, L. E., Chiriac, A. P., and Bercea, M. (2006). Rheological monitoring of in situ poly(acrylamide) gel preparation. J. Optoelectron. Adv. Mater. 8, 201–204. Available online at: https://old.joam.inoe.ro/arhiva/pdf8_1/Neamtu.pdf
Plotnikov, S. V., Sabass, B., Schwarz, U. S., and Waterman, C. M. (2014). High-resolution traction force microscopy. Methods Cell Biol. 123, 367–394. doi: 10.1016/B978-0-12-420138-5.00020-3
Saha, K., Kim, J., Irwin, E., Yoon, J., Momin, F., Trujillo, V., et al. (2010). Surface creasing instability of soft polyacrylamide cell culture substrates. Biophys. J. 99, L94–L96. doi: 10.1016/j.bpj.2010.09.045
Schwarz, U. S., and Soiné, J. R. D. (2015). Traction force microscopy on soft elastic substrates: a guide to recent computational advances. Biochim. Biophys. Acta 1853, 3095–3104. doi: 10.1016/j.bbamcr.2015.05.028
Steinwachs, J., Metzner, C., Skodzek, K., Lang, N., Thievessen, I., Mark, C., et al. (2016). Three-dimensional force microscopy of cells in biopolymer networks. Nat. Methods 13, 171–176. doi: 10.1038/nmeth.3685
Stellwagen, N. C. (1998). Apparent pore size of polyacrylamide gels: comparison of gels cast and run in Tris-acetate-EDTA and Tris-borate-EDTA buffers. Electrophoresis 19, 1542–1547. doi: 10.1002/elps.1150191004
Tang, X., Tofangchi, A., Anand, S. V., and Saif, T. A. (2014). A novel cell traction force microscopy to study multi-cellular system. PLoS Comput. Biol. 10:e1003631. doi: 10.1371/journal.pcbi.1003631
Tse, J. R., and Engler, A. J. (2010). Preparation of hydrogel substrates with tunable mechanical properties. Curr. Protoc. Cell Biol. 47 (Suppl. 47), 10–16. doi: 10.1002/0471143030.cb1016s47
Wang, J., and Ugaz, V. M. (2006). Using in situ rheology to characterize the microstructure in photopolymerized polyacrylamide gels for DNA electrophoresis. Electrophoresis 27, 3349–3358. doi: 10.1002/elps.200500910
Keywords: PAM hydrogel, swelling, AFM, bulk rheology, elastic modulus
Citation: Subramani R, Izquierdo-Alvarez A, Bhattacharya P, Meerts M, Moldenaers P, Ramon H and Van Oosterwyck H (2020) The Influence of Swelling on Elastic Properties of Polyacrylamide Hydrogels. Front. Mater. 7:212. doi: 10.3389/fmats.2020.00212
Received: 06 March 2020; Accepted: 10 June 2020;
Published: 23 July 2020.
Edited by:
Qiang Wei, Sichuan University, ChinaCopyright © 2020 Subramani, Izquierdo-Alvarez, Bhattacharya, Meerts, Moldenaers, Ramon and Van Oosterwyck. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hans Van Oosterwyck, aGFucy52YW5vb3N0ZXJ3eWNrQGt1bGV1dmVuLmJl
†Present address: Ramesh Subramani, Department of Food Processing Technology and Management, PSGR Krishnammal College for Women, Coimbatore, India
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.