Expanding the Build Plate: Functional Morphing 3D Printed Structures Through Anisotropy

Certain types of patterned metamaterials—gridshells and honeycombs—are capable of bistable behavior through a tailored combination of local and global geometric parameters. This is an alternative to prestressed or composite materials, which are typically used to induce multistability in thin structures. Globally bistable structures, contrary to arrays of bistable elements, allow large deformations in a single step. Furthermore, this category of structures offers greater manufacturability and scalability compared to laminate, prestressed, or multimaterial shells, since only geometry has to be considered. The simplicity of the material and geometrical requirements afford the designer easy and direct embedding in larger functional structures. In this study, the local and global response of bistable gridshells is interrogated through a manageable strain energy model, as well as through numerical and experimental methods. In addition, construction of bistable gridshells by employing various additive methods is examined and prototypes are presented for a series of functional devices. Finally, the availability of printed parts much larger than the build plate using commercial 3D printers is demonstrated, effectively “expanding” the dimensions of the build plate.

1. Introduction

Architectured materials with prescribed mechanical properties are increasingly being explored for their potential to influence diverse applications in actuation, acoustics and sensing to name a few. One category of such tunable metamaterials, namely multistable structures, offers new capabilities in energy harvesting (Harne and Wang, 2013), impact absorption (Whitman and La Saponara, 2007), and medical implants (Bobbert et al., 2018). Due to their tailored geometries, these materials enjoy strong synergies with Additive Manufacturing (AM) methods. In this work, we explore the universal availability of one such multistable structure in an array of AM processes and materials and suggest potential applications with accompanying demonstrators.

The popularity of multistable shells can be tied to the development of composite laminates as suitable materials for this category of structures. In particular, seminal work by Hyer (1981) and Hyer (1982) has contributed to this popularity. Laminates have been an attractive material for multistable shells since they allow bespoke mechanical properties and are capable of significant loads. The literature provides a plethora of examples that examine both the necessary layup, but also the influence of the curing process on the resulting stable geometries (Dano and Hyer, 1998; Giddings et al., 2010). However, composites present a number of obstacles, including limited scalability, need for expert labor and cost. Multistability can also be induced by material prestressing (Chillara and Dapino, 2017; Jiang et al., 2018), including residual stresses naturally occuring in AM methods (Loukaides et al., 2019), but accurately prescribing inelastic stresses is not yet straightforward in most manufacturing processes.

Similar behavior can be achieved instead by patterning homogeneous material to achieve the required mechanical properties. In turn, the simpler construction makes small and large scale structures feasible and facilitates MEMS, aerospace and architectural applications for multistable shells. The patterning of material to induce multistability takes many forms. Some examples include corrugations (Norman et al., 2009) and dimples (Norman et al., 2008). Nevertheless, the corresponding manufacturing methods involve plastic deformation and hence likely built-in stresses in the structure. Anisotropy encourages additional features, such as tristability (Vidoli and Maurini, 2008; Giomi and Mahadevan, 2012; Loukaides, 2014). Most recently, a curved square gridshell was shown to be bistable (Loukaides and Seffen, 2015). That study provides context for the present work, but focused on the theoretical treatment of the behavior. The physical demonstrator there was produced by removing material from a solid plate with a water-jet cutter. Here, through the use of commercially available 3D-printing devices, improved manufacturability and expanded applications are shown.

Fused Filament Fabrication/Fused Deposition Modeling (FFF/FDM), stereo-lithography (SLA) and Selective Laser Sintering (SLS) are now common technologies. In FDM, a filament of material is heated at one end and deposited layer-by-layer to create a 3D structure. In the SLS, a powder bed is heated locally, binding the melted powder locally and again creating 3D structures, layer by layer. SLA relies on the photopolymerization of a liquid resin, typically with a laser aimed at the bottom of a translucent tank. Although 3D printing was initially mostly used for prototyping and niche projects due to low production times and high cost, industrial uses are now a reality, including in the aerospace industry. The lower production speeds and increased cost are often offset by increased in-service performance of parts due to optimized geometries and functions not achievable through other manufacturing methods. In addition, costs for preparation, dedicated tools and operators are typically lowered or eliminated.

Many examples of 3D-printed, multistable structures are available in the literature (Shan et al., 2015; Che et al., 2017; Chen and Shea, 2018). However, these tend to fall into one of the following categories: structures based on bistable unit cells, most commonly a snap-through beam mechanism; structures employing exotic materials, such as shape memory polymers; and, multimaterial systems, which remain prohibitively expensive for the majority of users. All the aforementioned come with a plethora of envisioned uses and advantages, but their particular architectures complicate their construction and the potential for engineering applications.

This paper presents a route toward designing and additively manufacturing globally bistable architectures using a single material. The approach begins with an inextensional formulation of the strain energy, which is exploited to derive closed-form geometrical conditions for bistability of the structure. At the same time, feasible local and global geometries of gridshells are tested in a Finite Element (FE) model to establish their bistability. A fine mesh with improved resolution is used to examine local behavior. Furthermore, a range of demonstrators are manufactured in commercial FDM, SLS, and SLA 3D printers, while laboratory experiments allow a comparison with the analytical and numerical models. Finally, a collection of demonstrators of functional components is presented and explained.

2. Theoretical Background

Analytical models of thin structures quickly become intractable for arbitrary geometries, particularly in instances where they involve both bending and stretching deformation. Various simplifications have been employed in the past to allow for manageable models to emerge. Amongst those, the Uniform Curvature (UC) assumption has perhaps proved the most useful and is frequently encountered in the literature (Mansfield, 1962; Seffen, 2007; Fernandes et al., 2010; Seffen and Maurini, 2013). More recently, and based on this approach, an excellent design guide for multistable shells has been outlined (as detailed in Hamouche et al., 2016), even if it is limited to initially spherical shells.

The availability of bistability for honeycombs and gridshells was first established in Loukaides and Seffen (2015). In that work, an analytical investigation began by considering the homogenized properties of a square lattice of beams. The stretching, A, and bending stiffness, D, matrices were constructed, following the ABD matrix convention from Classical Laminate Theory (CLT). The homogenized properties were then used with a strain energy model and the UC assumption mentioned above to identify stable equilibria in the energy landscape. Here, we forgo the stretching contribution to the energy and revert to a simpler energy model by Guest and Pellegrino (2006). A basic description of that formulation is included below for convenience. Evidence of the absence of stretching in the structure is given in section 3, where a fine mesh Finite Element model was used to examine the local behavior of the lattice.

We begin by defining the relevant local and global geometrical parameters. Figure 1 shows a typical initial configuration for an orthotropic cylindrical square gridshell of radius ρ and central angle θ. Note that to achieve the desirable properties, the square pattern is at 45°, as detailed in Loukaides and Seffen (2015). The same figure shows the dimensions that define the local geometry and in particular the height, h, width, w, and length, d, of the ligaments. The length and arc length of the global structure are taken to be the same and equal to a (unless otherwise stated) such that a = ρθ.

FIGURE 1

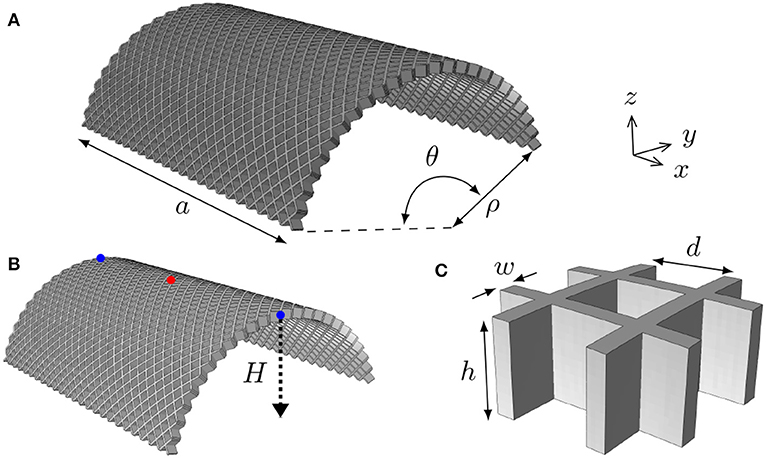
Figure 1. The relevant global (A) and local (C) dimensions are shown. Unless otherwise indicated, we are only concerned with square shells i.e., the arclength along the curved direction is equal to a. In (B), a diagram of the initial shell geometry is shown, indicating how the model is actuated. Throughout the simulation, the center nodes (red) are fixed, while the nodes shown in blue are moved in the negative Z direction.

In the absence of stretching, the strain energy formulation only requires the bending stiffness matrix, which takes the form:

$\begin{array}{ll}{\text{D}}^p=\left(\begin{array}{ccc}{D}_{11}& 0& 0\\ 0& D_{22}& 0\\ 0& 0& D_{66}\end{array}\right),& (1)\end{array}$

when the beams on a square lattice are aligned with directions 1, 2 and direction 3 is out of plane. Due to inherent symmetry in the geometry, D₁₁ = D₂₂. Hence, for simplicity, we use D₁₁ = D₂₂ = D₁ and D₆₆ = D₆. For arbitrary ligament sections, these are given by Lebée and Sab (2013) as

$\begin{array}{ll}{D}_1=\frac{EI}{d}\text{\hspace{1em} and\hspace{1em} }{D}_6=\frac{GJ}{d}& (2)\end{array}$

where E and G are the Young's and Shear Modulus of the constituent material, respectively; I and J are the moment of inertia and the torsion constant, respectively, which depend on the geometry of the cross-section of the ligaments.

As in Loukaides and Seffen (2015), we are interested in the stiffness when the lattice is rotated by π/4 rad. Applying a rotational transformation, T_π/4, consistent with CLT, we produce:

$\begin{array}{l}\text{D}={\text{T}}_{\pi /4}^{-1}{\text{D}}^p{({\text{T}}_{\pi /4}^{-1})}^{⊺}=\left(\begin{array}{ccc}\frac{D_1}{2}+D_6& \frac{D_1}{2}-D_6& 0\\ \\ \frac{D_1}{2}-D_6& \frac{D_1}{2}+D_6& 0\\ 0& 0& \frac{D_1}{2}\end{array}\right)\\ =\left(\begin{array}{ccc}\overline{D_1}& \overline{D_2}& 0\\ \overline{D_2}& \overline{D_1}& 0\\ 0& 0& \overline{D_6}\end{array}\right),& (3)\end{array}$

The barred symbols are defined above to simplify the subsequent algebra.

For the bending energy of the structure, we rely on a formulation by Guest and Pellegrino (2006), where the configuration of the shell was described in only two parameters, the shell curvature, C, and the orientation of the shell with respect to the principal curvatures, ϕ. Thus, the original configuation of the shell is always C = 1/ρ, where ρ is the initial radius of curvature and ϕ = 0. For a more detailed illustration we refer the reader to Guest and Pellegrino (2006). For inextensional deformation, the strain energy can be expressed as:

$\begin{array}{ll}U=\frac{1}{2}{\text{k}}^T\text{D}\text{k}& (4)\end{array}$

where, k is a vector describing the change in mid-surface curvatures. This can be expressed in terms of C and θ by making use of the Mohr's circle of curvature, which produces:

$\begin{array}{ll}\text{k}=\frac{C}{2}\left(\begin{array}{c}1-cos2\varphi \\ cos2\varphi +1\\ 2sin2\varphi \end{array}\right)-\left(\begin{array}{c}0\\ \frac{1}{\rho }\\ 0\end{array}\right)& (5)\end{array}$

The energy expression can be made dimensionless using convenient coefficients such that

$\begin{array}{ll}Û=\frac{U{\rho }^2}{\overline{D_1}},\widehat{\text{D}}=\frac{\text{D}}{\overline{D_1}},\widehat{\text{k}}=\rho \text{k},Ĉ=C\rho & (6)\end{array}$

and

$\begin{array}{ll}Û=\frac{1}{2}{\widehat{\text{k}}}^T\widehat{\text{D}}\widehat{\text{k}}& (7)\end{array}$

Due to the simplicity of the bending stiffness matrix, the resulting expression is manageable:

$\begin{array}{l}Û=\frac{1}{2}\\ -\frac{Ĉ(2D_1+4D_{6}cos(2\varphi ))-{Ĉ}^2(2D_1-D_1{cos}^2(2\varphi )+2D_6{cos}^2(2\varphi ))}{2(D_1+2D_6)}& (8)\end{array}$

Equilibria can be found by setting the partial derivatives of the energy expression with respect to Ĉ and ϕ to zero. In addition to the initial state, the resulting system always produces a second admissable solution, such that

$\begin{array}{ll}Ĉ=\frac{D_1-2D_6}{D_1+2D_6}\text{\hspace{1em} and\hspace{1em} }\varphi =\frac{\pi }{2}& (9)\end{array}$

Stability of this solution can be established by examining the Hessian of Û, H. Namely, H has to be positive definite, which is equivalent to its determinant being greater than zero. For the solution above, the determinant of H is

$\begin{array}{ll}\text{det}(\text{H})=\frac{4D_1(D_1^2-8D_1{D}_6+12D_6^2)}{{(D_1+2D_6)}^3}& (10)\end{array}$

Both D₁ and D₆ are positive for the structure presented here, hence the stability condition can be reduced to

$\begin{array}{ll}{D}_1^2-8D_1{D}_6+12D_6^2=(D_1-2D_6)(D_1-6D_6)>0& (11)\end{array}$

This inequality is satisfied when either D₁ < 2D₆ or D₁ > 6D₆. For the latter, substituting in the second solution results in a negative Ĉ, which is not admissable under the geometric interpretation of C by Guest and Pellegrino (2006). Hence, we can limit bistable solutions to the region D₁ > 6D₆. In terms of the moduli, this becomes

$\begin{array}{ll}\frac{EI}{d}>6\frac{GJ}{d}& (12)\end{array}$

which for isotropic materials, can be simplified further using the relationship between shear and Young's modulus, G = E/(2(1 + ν)). Thus,

$\begin{array}{ll}I>3\frac{J}{1+\nu }& (13)\end{array}$

Note that the formulation above does not consider the planform of the structure, nor does the initial central angle θ appear in the energy expression. In addition, assumptions necessary for the homogenization imply that when d is very small or very large compared to the ligament width, w, and to the planform size, a, respectively, the model breaks down. In the former case, the ligaments can no longer be treated as slender beams and in the latter, the interaction with the global curvature and the boundary effect preclude the homogenization. The formulation does however provide a clear boundary for facilitating the behavior with respect to the local geometry. This can be useful for designers and indeed provides a starting point for our numerical parametric study in section 3.

2.1. Bistability Criterion for Various Ligament Cross-Sections

We can then proceed to relate this result to various beam cross-sections. For example, for a circular section with radius r, $I_{\mathrm{\text{c}}}=\pi r^4/4$ and $J_{\mathrm{\text{c}}}=\pi r^4/2$. For isotropic materials, ν ≤ 0.5, hence

$\begin{array}{ll}3\frac{J_{\text{c}}}{1+\nu }=\frac{3}{2(1+\nu )}\pi r^4>\pi r^4>I_c& (14)\end{array}$

and bistability is not available.

The constant of torsion is not available in closed-form for arbitrary sections, hence we rely on approximations from Young and Budynas (2002) for the cases below. For the more general case of an elliptical section, $I_{\mathrm{\text{e}}}=\frac{\pi }{4}{\alpha }^3\beta$ and $J_{\mathrm{\text{e}}}\approx \frac{\pi {\alpha }^3{\beta }^3}{{\alpha }^2+{\beta }^2}$, where α and β are the semi-major and semi-minor axes, respectively, and the semi-major axis is assumed to be parallel to the shell through-thickness direction. Thus for the condition in Equation (13) to hold,

$\begin{array}{ll}\alpha >\beta \sqrt{\frac{12}{1+\nu }-1}& (15)\end{array}$

Although the Poisson's ratio is present in this expression, for typical materials its influence is very small. Again, we can set a general limit to the behavior by considering the most favorable value of the Poisson's ratio, ν = 0.5, which gives $\alpha >\beta \sqrt{7}$.

Finally, we perform the same calculation for a rectangular section using

$\begin{array}{ll}{I}_{\text{r}}=\frac{w{h}^3}{12}\text{\hspace{1em} and\hspace{1em} }{J}_{\text{r}}\approx h{w}^3\left[\frac{1}{3}-0.21\frac{w}{h}\left(1-\frac{w^4}{12h^4}\right)\right]& (16)\end{array}$

The condition in Equation (13) becomes

$\begin{array}{ll}\frac{w{h}^3}{12}>\frac{3}{1+\nu }h{w}^3\left[\frac{1}{3}-0.21\frac{w}{h}\left(1-\frac{w^4}{12h^4}\right)\right]& (17)\end{array}$

which simplifies to

$\begin{array}{ll}\frac{1}{12}>\frac{w^2}{h^2(1+\nu )}\left[1-0.63\frac{w}{h}\left(1-\frac{w^4}{12h^4}\right)\right]& (18)\end{array}$

If we set q = w/h, the required cross-sectional dimensions can be found by solving the equation

$\begin{array}{ll}\frac{q^2}{(1+\nu )}\left[1-0.63q\left(1-\frac{q^4}{12}\right)\right]-\frac{1}{12}=0& (19)\end{array}$

There are no closed-form solutions available for this 7th degree equation, but it can be solved numerically in a plethora of software packages (for example, here we use the vpasolve function in MATLAB). For example, setting ν = 0.5 gives q ≈ 0.4104, i.e., h > 2.44w for bistability to emerge. The remaining six solutions are either complex or negative. The variation of the h/w criterion with ν is shown in Figure 2.

FIGURE 2

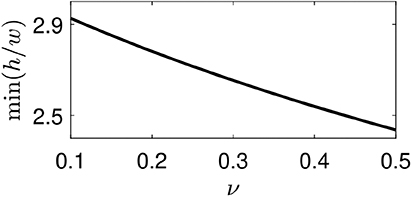
Figure 2. The Poisson's ratio, ν, of the constitutive material has a small effect on the local geometry bistability criterion, h/w.

The dimensionless strain energy, Û, based on the present formulation can be plotted on polar axes, again following from the examples in Guest and Pellegrino (2006). For the rectangular section gridshell and for three different ratios of h/w, this is shown in Figure 3. As the ratio decreases, the second equilibrium (red dot) ceises to be a local minimum in accordance with the h/w > 2.44 criterion.

FIGURE 3

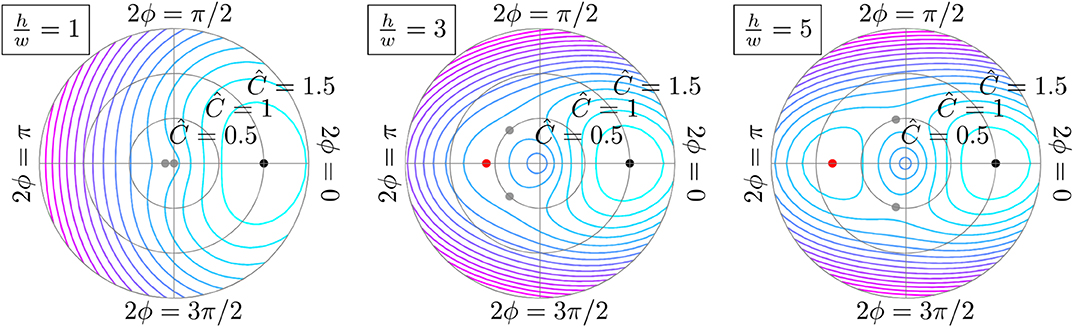
Figure 3. The dimensionless energy, Û, can be calculated for all possible configurations of curvature and rotation, when specific local geometries are chosen. The three polar plots were made by fixing w(= 1) and varying h for a rectangular ligament section. The initial geometry is shown in black, a second stable geometry in red, and unstable equilibria in gray.

In physical terms, since stretching is absent from the model, the bistability emerges as a consequence of global bending being energetically cheaper in the ϕ = π/2 orientation than intermediate configurations as ϕ is increased from zero. This in turn can be attributed to the increased influence that in-plane ligament bending has in those two orientations. When the direction of curvature aligns with the direction of the ligaments, all bending has to be expressed in the through-thickness direction of the ligaments.

3. Numerical Examination

In previous work, the numerical modeling of the gridshells was simplified by considering only slender local elements (Loukaides and Seffen, 2015). In FEA terms, the ligaments representing the local geometry were either composed of beam or shell elements. The analytical approach to the homogenization of the mechanical proporties made similar assumptions. In practice, slender local structural elements are less manufacturable and, for a range of applications, less functional since they are susceptible to buckling prior to the global geometry reaching alternative available stable states. In this work, we consider short and thick beams as representative of the ligaments. This allows for the more reliable examination of a greater variety of practical geometries. Hence, FE models using solid elements are employed here to capture the elastic response to actuation. At the same time, the analytical energy approach despite the homogenization, provides two useful directions to explore: the effect of the ligament height to the bistable behavior and the stretching of the midplane during bending.

An FEA model is pursued because it easily offers insights that would be difficult or impossible to measure in physical trials, such as the midplane strains of the structure. At the same time, it allows for optimization of design parameters that are not represented in the analytical model. For example, the central angle does not appear in the stability analysis in the previous section. This is because our homogenization model does not account for curvature, but we know empirically that it has an influence. Therefore, the numerical approach allows for investigations of deeper shells and shells of non-uniform curvature, for which few analytical models are currently available.

The commercial package Abaqus was used to develop and solve the FE problem. The mesh was constructed algorthmically so that its local refinement could be controlled exactly, rather than relying on Abaqus' meshing function. It is worth noting that the large number of geometrical features in the gridshell geometry can be challenging for CAD software, especially when the ligaments are modeled using solid elements. A MATLAB script was developed to parameterize the mesh, but also allowed the geometry, material and other simulation parameters to be easily manipulated. In other words, the Abaqus graphical interface was only used for post-processing and the models were defined in input files (.inp) that a custom MATLAB script produced. The C3D8R element is used, which is suited to large strain problems (Dassault Systèmes Simulia Corp., 2010).

A mesh sensitivity study was performed on a structure with parameters: θ = 5π/6, h = 5, d = 5, w = 1, and a = 85. The density of the mesh was determined by the number of elements along the width and height of ligaments. Results are shown in Figure 4, where force-displacement diagrams are plotted for four different meshes. For the “fine mesh” model in section 3.2, the 4 × 12 mesh was chosen. It is known that sharp corners, such as the ones present between ligaments in this structure, can result in stress singularities in numerical models. Given the convergence with respect to global behavior and the qualitative nature of this study, the present meshes were admitted to avoid significant computational cost.

FIGURE 4

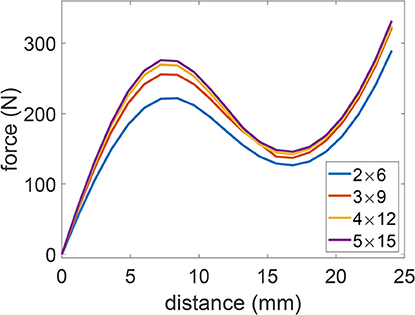
Figure 4. Force-displacement diagrams for different number of elements along the ligament width and height, showing converging results.

The analysis is carried out in two separate Dynamic Implicit steps with a duration of 10s each, which ensures quasi-static application; the typical ratio of strain energy to kinetic energy in the simulations is 10⁵. All degrees of freedom of the central region of the gridshell structure are fixed, whereas the rest of the structure is unconstrained. In the first step of the analysis, displacement control is applied near the mid-points of the initial-straight edges of the shell, actuating the structure toward a second stable state. Only one degree of freedom on these nodes is controlled, corresponding to the direction orthogonal to the initial directions of principal curvatures. The nodes are moved a distance equal to the initial height of the shell, H = ρ(1 − cos(θ/2)). The actuation path is shown for one node in Figure 1. In the second step, the displacement control is removed and the gridshell is allowed, load free, to return to an equilibrium state. If, after the second step, the structure returns to the original geometry, this is deemed a monostable configuration. Otherwise if, after relaxation, a second equilibrium state is observed, the configuration is deemed bistable. Similar actuation strategies are used in the literature to demonstrate or examine bistability physically or in simulations (Loukaides and Seffen, 2015; Hamouche et al., 2017). It is possible, in principle, that the second stable state is “missed” using this method, but both the quasi-static application and the actuation path should minimize that risk.

The material mechanical properties used in the simulations are representative of polyactic acid (PLA) and taken from Jamshidian et al. (2010). They are given in Table 1. In the same table, properties for a range of materials are given, all currently available for commercial 3D printers. These materials include polyamide (nylon). However, it is worth noting that the moduli are of little consequence to the multistable behavior for isotropic materials, since this is governed by the geometry of the metamaterial, rather than by the isotropic, homogeneous material used. Of course, for materials that cannot tolarate large strains, the morphing nature of the structure means that the yield point is easily reached, which renders them unsuitable for this application. In the simulations, the material is defined only in the elastic region, hence those limits are not examined. The perfectly elastic material used in the simulations means that known viscoelastic effects are also not captured. At the same time, the Poisson's ratio does have a minor effect, as indicated in the previous section.

TABLE 1

Table 1. Mechanical properties of typical thermoplastic materials, and some proprietary materials used in commercial printers.

3.1. Influence of Local and Global Parameters

Using the model above, a series of simulations captured the influence of the parameters for a range of geometrical parameters, as defined in Figure 1. The practical intention of the study was to identify a suitable design to be printed in a commercial 3D printer. The initial search used the capabilities of the Ultimaker 2 Extended FDM printer to guide the design (Ultimaker BV, 2017). We focus on a square planform with side a = 170 mm, which is close to the size of the build platform on the particular printer. A larger planform trivially allows for a greater number of unit elements to be included in the structure, and those slender features can then be manufactured more easily since the local dimensions approach the resolution of the printer head. A total of 75 simulations were performed: the central angle, θ, of the initial cylindrical configuration; the height, h, of the ligaments; and, the length, d of the ligaments were varied. The width of the ligaments was kept constant at w = 1 mm, to conform with printing capabilities. The mesh was composed of approximately 90,000 elements.

The results are summarized in Figure 5, where colormaps indicate regions of monostability (gray) and bistability (red). Shallow shells cannot be bistable. There is meanwhile a minimum value of the h/w for bistability that conforms to the minimum found in section 2. For low values of d, bistability is lost. In effect, a lower d means the material is almost isotropic. As long as the minimum values for θ and h/w are satisfied, bistability seems to be easily obtained, but practical consideration would still preclude large values of h (since surface strains would be prohibitive) and low values of w (since manufacturability would be challenging). From these results, a feasible design was chosen with parameters a = 170 mm, θ = 5π/6, h = 5 mm, d = 5 mm, and w = 1 mm. This design was printed as a flat structure in the Ultimaker printer and then formed against a cylindrical tool, with both the tool and the structure preheated to 150°C. This is shown in Figure 6 along with the same geometry printed with SLS of nylon and formed with the same method.

FIGURE 5

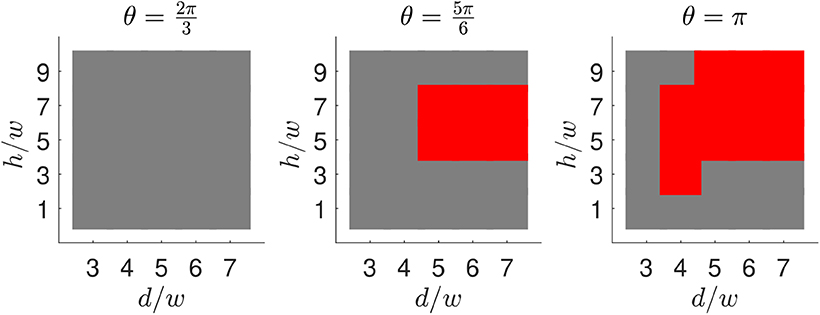
Figure 5. A total of 75 FE simulations were used to plot the colormaps. Red indicates bistability and gray monostability. The dimensions not appearing above were a = 170 mm and w = 1 mm.

FIGURE 6

Figure 6. Bistable gridshells made by FDM (top) and SLS of nylon powder (bottom) with the same local and global dimensions. Initial geometries are (A,C), respectively, with parameters a = 170 mm, θ = 5π/6, h = 5 mm, d = 5 mm, and w = 1 mm. Second stable geometries for the two structures are shown in (B,D).

3.2. Fine Mesh Model

In this section, we focus on a single geometry (the one used for the demonstrators in the previous section) for a handheld demonstrator and investigate the local mechanics. For an examination of deformation mechanics during forming and the strain conditions in the second state, a suitably fine mesh is needed. We define 12 elements along the thickness, t, four elements along the ligament width, w, and 20 elements along the ligament length, d, as can be seen in Figure 7. The particular design with this meshing produced approximately 1.9mil elements. The computational requirements of such a model can quickly escalate. Here, we employ Abaqus parallelization capabilities to facilitate the calculation. On 16 CPUs, the simulation took approximately 122 h.

FIGURE 7

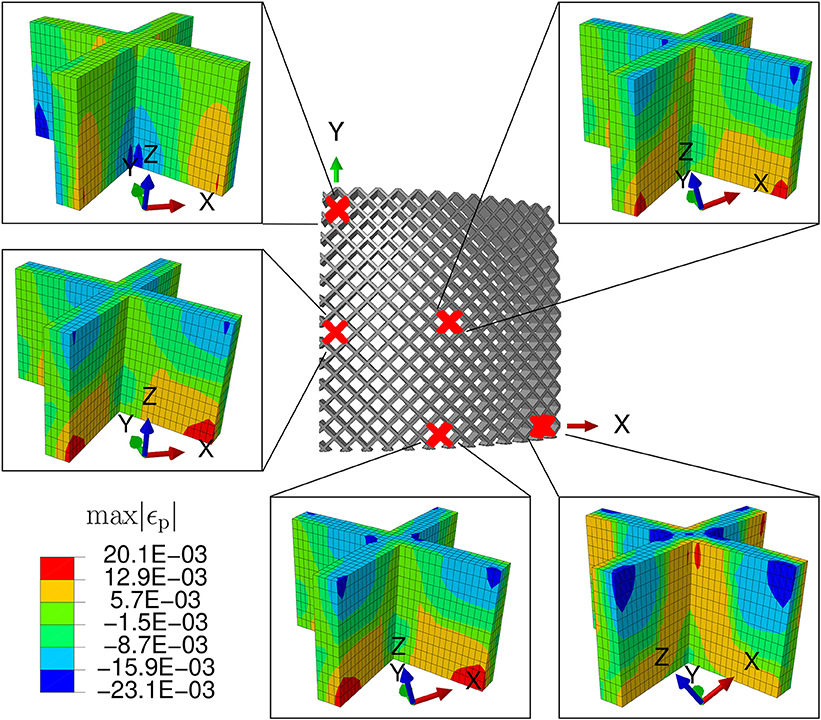
Figure 7. The local deformation of the structure at five locations on a quarter of the shell at the end of the simulation, i.e., while in the second stable geometry. The contours show the maximum (absolute value) principle strain.

Figure 7 shows only a quarter of the shell at the second configuration, since the initial and final geometries are symmetric along both the X and the Y-axes. In that view, we select five distinct locations and present the local deformation of unit cells. Despite the close-to-cylindrical final shape, different regions experience noticeably different strain conditions. The highest tensile strains are at the bottom surface and within the central region of the structure, while high compressive strains are prominent at the boundary region along the X-axis.

In Figure 8, the second stable state is interrogated further. In Figure 8A, we plot the von Mises stress at different element layers through the thickness, highlighting the dimished stresses in the mid-plane. The same observation is made more clear in Figure 8B, where the average strains across the structure at different locations are plotted. This provides evidence and justification for our assumption in the analytical description of the behavior. Finally, we isolate the middle surface by extracting the corresponding nodes from the mesh and measure the Gaussian Curvature across the resulting surface in Figure 8C.

FIGURE 8

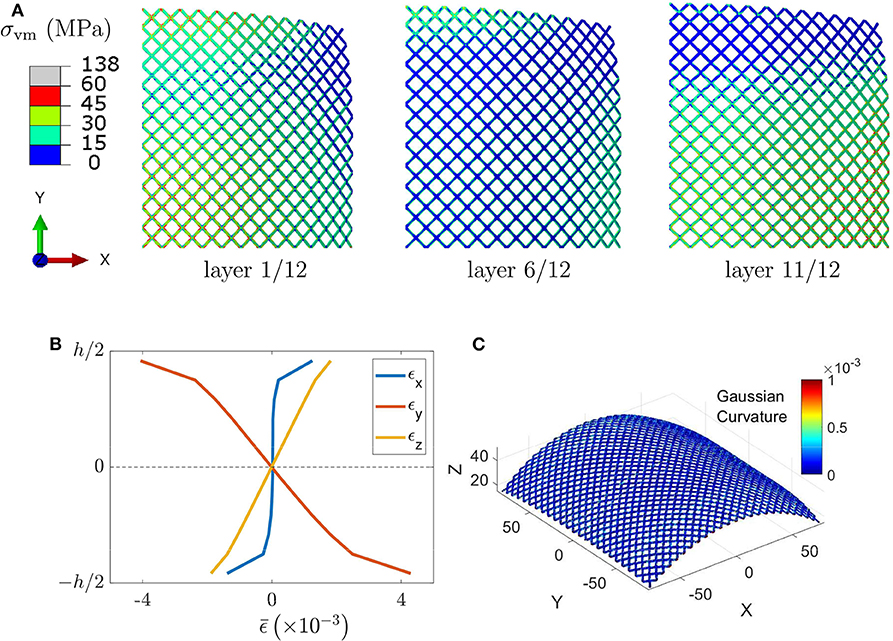
Figure 8. (A) The von Mises stress is shown for a quarter of the planform at different locations through the thickness. (B) The average strains through the thickness of the shell are symmetric about the midplane, indicating the inextentional nature of the deformation. (C) The Gaussian curvature across the midplane is displayed to demonstrate it is close to zero throughout.

4. Physical Testing and Concept Demonstrators

Following initial demonstrators manufactured with FDM and SLS machines and shown in section 3, further demonstrators were constructed on a Formlabs Form 2 SLA machine (Formlabs, 2018). Although this process is disadvantaged by a smaller build plate (measuring 140 × 140 mm), it provides better resolution and less pronounced inherent anisotropy in the underlying material. All the structures in this section were constructed with the Formlabs Durable resin—properties shown in Table 1. The physical behavior of the structures is briefly investigated here and contrasted with numerical results.

In order to examine the the influence of ligament height, the chosen design from section 3 was scaled by a factor of 0.5, to fit onto the smaller build platform. In addition to the scaled ligament height h = 2.5 mm, four additional gridshells were printed for h = 1.5, 2.0, 3.0, 3.5 mm. In Figure 9, we show force-displacement diagrams for FE simulations and physical tests during the first step as defined in section 3, i.e., the loading step. On the right, the experimental set-up is shown. This resembles a three-point bending test, with two cylinders pushing the edges of the shell, which is supported at the centre by a pin-like attachment. Since the set-up did not allow for negative forces to be measured, the test was repeated starting at the second geometry. Combining force-displacement diagrams from the two experiments, we obtain the plot shown on the right in Figure 9A. In the physical tests, bistability is lost for h < 2 mm or a ratio of h/w = 4. For the numerical tests, the limit is lower at h/w < 3. The h = 1.5 mm case seems to be bordeline given the barely distinquishible minimum in the energy plot, and seems to be facilitated by the idealized conditions of the numerical model. Reproducing the exact boundary conditions in FEA would significantly complicate the model. In addition, uncertainty about mechanical properties of the constitutive material might further explain the discrepancy. In both cases however, the theoretical minimum from section 2 holds.

FIGURE 9

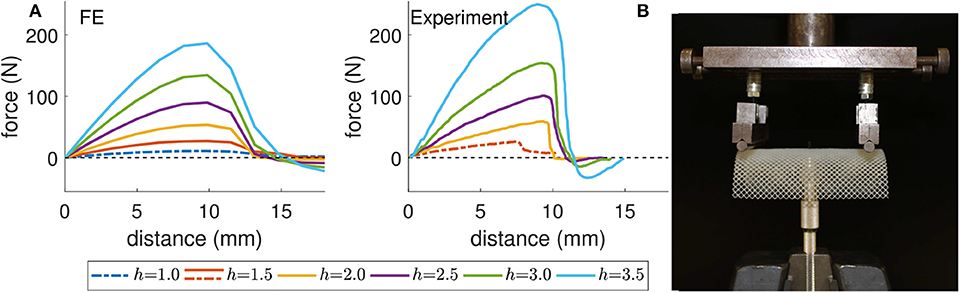
Figure 9. The influence of ligament thickness, h (in mm), was examined in FE and in physical tests (A). Bistable samples are shown with solid lines, monostable with dashed lines. The test set-up is shown on the right (B).

The SLA process allowed the production of the entire geometry without any secondary processes other than the removal of support structures and postcuring, hence gave us the greatest flexibility in examining a range of concepts. We describe these below and present images of prototypes.

4.1. Printing Parts Larger Than the Build Plate

A limitation of most commercial 3D printers is the size of the build plate. Typically its dimensions set an upper limit on the dimensions of the possible parts. However, by exploiting the bistability of this category of structures, we can print components that exceed the dimensions of the plate, at least in one direction, thus effectively “expanding” build plate. This is demonstrated here by printing a “spool” of material, in a spiral pattern, which has a second stable state that is much longer (see Figure 10). The local geometry for the demonstrator was the same as for the five samples in the beginning of this section and h = 2.5 mm. The same concept was demonstrated in Loukaides et al. (2019) for metal SLS, but by employing residual stresses, rather than a purely geometrical approach. This further highlights the synergy between metamaterials and AM, which benefits not only the products, but also the capabilities of the manufacturing processes themselves.

FIGURE 10

Figure 10. (A) Using this architecture, compact printed structures can be deployed to much larger configurations than the initial geometry shown on the top right—build plate shown for comparison. Demonstrator of a monolithic 3D-printed capsule with (B) closed and (C) open states.

This concept could become more powerful with multiple such geometries connected within one print, which lead to a complex functional component when deployed to their respective second state. The same design can be employed for deployable space structures, namely coilable booms, where bistability reduces the forces on the coil casing. This concept has been examined with CFRPs in the past (Fernandez et al., 2014), but AM offers a promising alternative route.

4.2. Encapsulation/Entrapment Applications

A second concept application is also shown in Figure 10. The basic design of the bistable gridshell is combined with two spherical caps and printed in a single manufacturing operation. The resulting structure has two stable geometries that correspond to closed and open configurations of the capsule. Given the scalability of the design, it is reasonable to envision applications in medicine (for example in localized drug delivery), MEMS and robotics. We can also envision remote actuation of such a mechanism, including using heat and magnetism (Loukaides et al., 2014).

4.3. Variable Curvature Multistable Gridshells

In order to expand the range of possible applications for these structures, variable curvature is essential. For example, if the gridshell is to be joined with another structure, one end might need to conform to a neighboring component, while the other end is optimized for a specific morphing function. This is the motivation behind work in recent literature that again employs composites (Brunetti et al., 2016). The designs produced include a conical shell i.e., linearly varying curvature, as well as designs that are initially flat at one end and cylindrical at the other, see Figure 11.

FIGURE 11

Figure 11. A bistable conical gridshell; initial (A) and second (B) stable geometries. In (C), a variable curvature gridshell is shown, which was printed flat one end and transitions to a cylinder over 1/3 of its length, with the remaining 2/3 maintaining a uniform cross-section. After actuation, the structure appears to have a second stable geometry, (D), which subsequently snaps dynamically after some delay, i.e., it demonstrates pseudobistability. This is shown in timestamped frames from a recording (E–G) of the transition.

This category of structures can demonstrate the phenomenon of pseudobistability (Brinkmeyer et al., 2012; Gomez et al., 2019). Such structures can be placed in a second geometry for a finite amount of time but then dynamically return to their initial geometry. For the demonstration in Figure 11 the shell with initial geometry shown in Figure 11C is manually actuated to the second geometry shown in Figure 11D by bending the structure along its length. The second geometry is maintained for 3.63 s with minor “springback” from the actuated position. It then dynamically transitions to the initial geometry as shown in Figure 11G.

4.4. A Bidirectional Bistable Valve

In Figure 12, two gridshells are joined at their four corners with ball-and-socket joints. When combined with compliant tubing the structure can allow or inhibit flow in one of two directions as shown in Figures 12A,B. The printed version is shown in its two geometries in Figures 12C,D. Taking advantage of AM capabilities, the joints are also printed in the same operation as an extension of the gridshell design used throughout this section.

FIGURE 12

Figure 12. A bidirectional bistable valve concept, made by attaching two shells with ball-and-socket joints. A diagrammatic explanation is shown in (A,B), with the two states of a physical demonstrator shown in (C,D).

For all of the aforementioned concepts, we can envision combining these structures with other emerging technologies. For example, multimaterial printing is now common in commercial printers and can provide the means for passive actuation of these structures through environental factors. Similarly, active materials can be used directly for this category of structures, so that the functional structure and the active material are one and the same.

5. Concluding Remarks

Two distinct areas of inquiry, namely architectured materials and additive manufacturing, are maturing in parallel and their combined capabilities open up new opportunities for designers and manufacturers alike. Here, these opportunities were examined for one category of morphing structures, known as multistable gridshells, thus accelerating the convergence of the underlying technologies. In summary, in this work:

• An analytical inextentional strain energy model, along with a suitable homogenization approach predicted the limits of the behavior with respect to the local geometry, thus providing accessible design criteria for designers.

• A parametric FE study facilitated a comparison with physical experiments and confirmed the analytical results with respect to local geometry. It also showed the strong influence of initial curvature and ligament length.

• A series of demonstrators were printed using diverse commercial printers to communicate the large and diverse range of new applications made possible through these technologies.

• The strong synergy of multistable gridshells and honeycombs with AM technologies was demonstrated.

Some work remains to translate this to industrial engineering applications, to a great extent because of material considerations. Polymers cannot suffer great stresses and are susceptible to creep, which particularly precludes them from applications involving morphing structures. More robust materials are needed for many applications proposed, but, conveniently, metal and composite AM technologies are also widely available now. Furthermore, variable curvature gridshells, diverse boundary conditions and interaction of the proposed structures with fluids are all under-investigated but intriguing and promising areas for future work.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author thanks Alexandros Ntrekos and Ben Earl for assistance in the construction of the demonstrators and testing. The author is also grateful to the two reviewers for their constructive feedback.

References

Bobbert, F., Janbaz, S., and Zadpoor, A. (2018). Towards deployable meta-implants. J. Mater. Chem. B 6, 3449–3455. doi: 10.1039/C8TB00576A

PubMed Abstract | CrossRef Full Text | Google Scholar

Brinkmeyer, A., Santer, M., Pirrera, A., and Weaver, P. (2012). Pseudo-bistable self-actuated domes for morphing applications. Int. J. Solids Struct. 49, 1077–1087. doi: 10.1016/j.ijsolstr.2012.01.007

CrossRef Full Text | Google Scholar

Brunetti, M., Vincenti, A., and Vidoli, S. (2016). A class of morphing shell structures satisfying clamped boundary conditions. Int. J. Solids Struct. 82, 47–55. doi: 10.1016/j.ijsolstr.2015.12.017

CrossRef Full Text | Google Scholar

Che, K., Yuan, C., Wu, J., Jerry Qi, H., and Meaud, J. (2017). Three-dimensional-printed multistable mechanical metamaterials with a deterministic deformation sequence. J. Appl. Mech. 84:011004. doi: 10.1115/1.4034706

CrossRef Full Text | Google Scholar

Chen, T., and Shea, K. (2018). An autonomous programmable actuator and shape reconfigurable structures using bistability and shape memory polymers. 3D Print. Addit. Manufact. 5, 91–101. doi: 10.1089/3dp.2017.0118

CrossRef Full Text | Google Scholar

Chillara, V., and Dapino, M. (2017). Mechanically-prestressed bistable composite laminates with weakly coupled equilibrium shapes. Composit. B Eng. 111, 251–260. doi: 10.1016/j.compositesb.2016.12.011

CrossRef Full Text | Google Scholar

Dano, M.-L., and Hyer, M. W. (1998). Thermally-induced deformation behavior of unsymmetric laminates. Int. J. Solids Struct. 35, 2101–2120. doi: 10.1016/S0020-7683(97)00167-4

CrossRef Full Text | Google Scholar

Dassault Systèmes Simulia Corp. (2010). Abaqus Analysis User's Manual.

EOS (2008). Material Data Sheet PA 2200. Available online at: http://eos.materialdatacenter.com/eo/standard/main/ds

Google Scholar

Fernandes, A., Maurini, C., and Vidoli, S. (2010). Multiparameter actuation for shape control of bistable composite plates. Int. J. Solids Struct. 47, 1449–1458. doi: 10.1016/j.ijsolstr.2010.02.007

CrossRef Full Text | Google Scholar

Fernandez, J. M., Viquerat, A., Lappas, V. J., and Daton-Lovett, A. J. (2014). “Bistable over the whole length (BOWL) CFRP booms for solar sails,” in Advances in Solar Sailing (Berlin; Heidelberg: Springer), 609–628. doi: 10.1007/978-3-642-34907-2_38

CrossRef Full Text | Google Scholar

Formlabs (2018). Form 2 Installation and Usage Instructions. Available online at: https://support.formlabs.com/s/article/Manuals-and-documentation

Formlabs (2018). Material Data Sheet for Durable Resin. Available online at: https://formlabs.com/3d-printers/form-3/tech-specs/#data-sheets

Giddings, P. F., Bowen, C. R., Salo, A. I., Kim, H. A., and Ive, A. (2010). Bistable composite laminates: effects of laminate composition on cured shape and response to thermal load. Composite Struct. 92, 2220–2225. doi: 10.1016/j.compstruct.2009.08.043

CrossRef Full Text | Google Scholar

Giomi, L., and Mahadevan, L. (2012). Multi-stability of free spontaneously curved anisotropic strips. Proc. R. Soc. A Math. Phys. Eng. Sci. 468, 511–530. doi: 10.1098/rspa.2011.0247

CrossRef Full Text | Google Scholar

Gomez, M., Moulton, D. E., and Vella, D. (2019). Dynamics of viscoelastic snap-through. J. Mech. Phys. Solids 124, 781–813. doi: 10.1016/j.jmps.2018.11.020

CrossRef Full Text | Google Scholar

Guest, S. D., and Pellegrino, S. (2006). Analytical models for bistable cylindrical shells. Proc. R. Soc. A Math. Phys. Eng. Sci. 462:839. doi: 10.1098/rspa.2005.1598

CrossRef Full Text | Google Scholar

Hamouche, W., Maurini, C., Vidoli, S., and Vincenti, A. (2017). Multi-parameter actuation of a neutrally stable shell: a flexible gear-less motor. Proc. R. Soc. A 473:20170364. doi: 10.1098/rspa.2017.0364

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamouche, W., Maurini, C., Vincenti, A., and Vidoli, S. (2016). Basic criteria to design and produce multistable shells. Meccanica 51, 2305–2320. doi: 10.1007/s11012-016-0375-5

CrossRef Full Text | Google Scholar

Harne, R. L., and Wang, K. (2013). A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 22:023001. doi: 10.1088/0964-1726/22/2/023001

CrossRef Full Text | Google Scholar

Hyer, M. W. (1981). Calculations of the room-temperature shapes of unsymmetric laminates. J. Composite Mater. 15, 296–310. doi: 10.1177/002199838101500401

CrossRef Full Text | Google Scholar

Hyer, M. W. (1982). The room-temperature shapes of four-layer unsymmetric cross-ply laminates. J. Composite Mater. 16, 318–340. doi: 10.1177/002199838201600406

CrossRef Full Text | Google Scholar

Jamshidian, M., Tehrany, E. A., Imran, M., Jacquot, M., and Desobry, S. (2010). Poly-lactic acid: production, applications, nanocomposites, and release studies. Comprehens. Rev. Food Sci. Food Saf. 9, 552–571. doi: 10.1111/j.1541-4337.2010.00126.x

CrossRef Full Text | Google Scholar

Jiang, X., Pezzulla, M., Shao, H., Ghosh, T. K., and Holmes, D. P. (2018). Snapping of bistable, prestressed cylindrical shells. Europhys. Lett. 122:64003. doi: 10.1209/0295-5075/122/64003

CrossRef Full Text | Google Scholar

Lebée, A., and Sab, K. (2013). Homogenization of a space frame as a thick plate: application of the bending-gradient theory to a beam lattice. Comput. Struct. 127, 88–101. doi: 10.1016/j.compstruc.2013.01.011

CrossRef Full Text | Google Scholar

Loukaides, E. G. (2014). Elementary morphing shells (Ph.D. thesis). Department of Engineering, University of Cambridge, Cambridge, United States.

Google Scholar

Loukaides, E. G., Lewis, R. W. C., and Bowen, C. R. (2019). Additive manufacture of multistable structures. Smart Mater. Struct. 28:02LT02. doi: 10.1088/1361-665X/aae4f6

CrossRef Full Text | Google Scholar

Loukaides, E. G., and Seffen, K. A. (2015). Multistable grid and honeycomb shells. Int. J. Solids Struct. 59, 46–57. doi: 10.1016/j.ijsolstr.2015.01.002

CrossRef Full Text | Google Scholar

Loukaides, E. G., Smoukov, S. K., and Seffen, K. A. (2014). Magnetic actuation and transition shapes of a bistable spherical cap. Int. J. Smart Nano Mater. 5, 270–282. doi: 10.1080/19475411.2014.997322

CrossRef Full Text | Google Scholar

Mansfield, E. H. (1962). Bending, buckling and curling of a heated thin plate. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 268, 316–327. doi: 10.1098/rspa.1962.0143

CrossRef Full Text | Google Scholar

Norman, A. D., Golabchi, M. R., Seffen, K. A., and Guest, S. D. (2008). Multistable textured shell structures. Adv. Sci. Technol. 54, 168–173. doi: 10.4028/www.scientific.net/AST.54.168

CrossRef Full Text | Google Scholar

Norman, A. D., Seffen, K. A., and Guest, S. D. (2009). Morphing of curved corrugated shells. Int. J. Solids Struct. 46, 1624–1633. doi: 10.1016/j.ijsolstr.2008.12.009

CrossRef Full Text | Google Scholar

Seffen, K. A. (2007). Morphing bistable orthotropic elliptical shallow shells. Proc. R. Soc. A Math. Phys. Eng. Sci. 463:67. doi: 10.1098/rspa.2006.1750

PubMed Abstract | CrossRef Full Text | Google Scholar

Seffen, K. A., and Maurini, C. (2013). Growth and shape control of disks by bending and extension. J. Mech. Phys. Solids 61, 190–204. doi: 10.1016/j.jmps.2012.08.003

CrossRef Full Text | Google Scholar

Shan, S., Kang, S. H., Raney, J. R., Wang, P., Fang, L., Candido, F., et al. (2015). Multistable architected materials for trapping elastic strain energy. Adv. Mater. 27, 4296–4301. doi: 10.1002/adma.201501708

PubMed Abstract | CrossRef Full Text | Google Scholar

Ultimaker (2016). Technical Data Sheet PLA. Available online at: https://ultimaker.com/en/products/materials

Google Scholar

Ultimaker BV (2016). Technical Data Sheet Nylon. Available online at: https://ultimaker.com/en/products/materials

Google Scholar

Ultimaker BV (2017). Ultimaker 2 Extended Manual. Available online at: https://ultimaker.com/en/resources/manuals

Vidoli, S., and Maurini, C. (2008). Tristability of thin orthotropic shells with uniform initial curvature. Proc. R. Soc. A Math. Phys. Eng. Sci. 464:2949. doi: 10.1098/rspa.2008.0094

CrossRef Full Text | Google Scholar

Whitman, Z., and La Saponara, V. (2007). Bistable structures for energy absorption, II: Composite structures under tension. J. Mech. Mater. Struct. 2, 359–375. doi: 10.2140/jomms.2007.2.359

CrossRef Full Text | Google Scholar

Young, W. C., and Budynas, R. G. (2002). Roark's Formulas for Stress and Strain, Vol. 6. New York, NY: McGraw-Hill.