Strain-Induced Modulation of Spin Configuration in LaCoO3

For oxides with octahedron ligand field, such as perovskite, spinel, and mullite, unit occupancy of e_g orbital plays a key role in governing the catalytic performance of oxygen redox in the application of renewable energy storage and conversion. The magnetic configurations greatly influence the e_g occupancy of these oxides. In this work, using the perovskite LaCoO₃ as an example, we use density functional theory (DFT) calculations to achieve an intermediate spin configuration corresponding to unit-like e_g occupancy via strain schemes. We determined that the introduction of strain by changing lattice constants effectively tailors electronic configurations. The low-spin ($t_{2\mathrm{g}}^6{e}_{\text{g}}^0$), intermediate-spin ($t_{2\mathrm{g}}^5{e}_{\text{g}}^1$), and high-spin ($t_{2\mathrm{g}}^4{e}_{\text{g}}^2$) configurations are obtained with the strain γ < 1.0%, 1.0% ≤ γ < 4.0%, and γ ≥ 4.0%, respectively. To obtain the e_g unit occupancy practically, Ba with a larger ionic radius relative to La is inserted into A site to replace La elements, introducing tensile strain to the pristine LaCoO₃. The Ba substitution of La leads to the desirable spin configuration with the unit-like e_g occupancy. These findings provide a scenario on how to precisely control the unit occupancy of e_g via defect induced strain.

Introduction

The development of oxygen catalysts plays a significant role in accelerating the oxygen redox reaction in energy storage and conversion devices. In relation to the discovery of highly efficient non-precious catalysts like oxide, one needs to perform in-depth access with regard to the relation between the crystal structure and the catalytic property. Electronic structures are the fundamental origin of excellent catalytic performances of materials (Suntivich et al., 2011a; Maitra et al., 2013; Li et al., 2016; Gani and Kulik, 2018; Wang et al., 2019a; Zhang et al., 2019; Xu et al., 2020). For perovskites, e_g orbital occupancy is one of the effective descriptors in illustrating catalytic behavior. In the 1970s, Matsumoto et al. (1977b) first proposed that e_g orbital features in bulk transition metal oxides could reflect the catalytic trend of oxygen reduction reaction (ORR). They pointed out that the formation and filling of a σ^∗ band due to the interaction between e_g orbital of transition metal ion and oxygen molecular orbital greatly affects the ORR activity (Matsumoto et al., 1977a, b). To date, this bulk descriptor has been widely used to understand and predict the catalytic performance of oxides. For instance, Wei et al. (2017) demonstrated that e_g occupancy of the active cation in octahedral sites is an efficient descriptor for the ORR/OER activities of spinel. They proposed that a moderate e_g filling (e_g ≈ 1) at the octahedral site can optimize ORR/OER activity. A similar conclusion in terms of e_g filling was further drawn in double perovskites (Jiang et al., 2018).

In 2010, Shao-Horn and colleagues presented research that confirmed that the e_g filling of transition metal ions in surface accounts for the ORR/OER activity of perovskites (Suntivich et al., 2011a, b). They found that maximum activity can be achieved when e_g orbital is occupied by a single electron for OE(R)R reaction. In contrast to traditional band theory, they assumed that a localized e_g electron in an orbital directed toward an O₂ molecule from the surface B cations is essential for ORR/OER. The use of the surface e_g filling promotes the accurate prediction of catalytic activities for ORR/OER over oxides. The probe of surface e_g filling is very challenging even to date. Compared with hard X-ray absorption spectroscopy (XAS), the soft XAS in principle enables one to access the surface properties depending on the incident energy and the corresponding modes. Shao-Horn and colleagues (Hong et al., 2015) claimed that the e_g occupancy in their previous studies (Suntivich et al., 2011a, b) was estimated on the basis of the oxidation state and spin state derived from bulk-sensitive measurements, i.e., hard X-ray absorption and magnetometry. In 2018, in their other review (Kuznetsov et al., 2018), they also mentioned that the values of e_g fillings were estimated from ex situ measurements or obtained from computed binding energies of oxygenated species on the surface. Therefore, the surface e_g descriptor in current reports fails to be solid. It could be more reasonable to be a bulk descriptor. In any case, the importance of Shao-Horn’s work reveals the relation between the e_g unit filling of bulk materials and the catalytic properties, even if the relation between bulk and surface remains inaccessible so far. Therefore, the e_g unit filling of bulk, rather than the surface, is the key to ensure high catalytic efficiency.

Perovskite oxides contain different spin configurations in a given system. For instance, LaCoO₃ exhibits three spin configurations of low ($t_{2\mathrm{g}}^6{e}_{\text{g}}^0$), intermediate ($t_{2\mathrm{g}}^5{e}_{\text{g}}^1$), and high spin ($t_{2\mathrm{g}}^4{e}_{\text{g}}^2$). For $e_{\text{g}}^1$, the unit occupancy contributes to a moderate hybridization between d_z^2 and oxygen 2p orbital to achieve an optimized catalytic activity. To date, much effort has been paid to improve the catalytic activity of LaCoO₃ by tuning its electronic structures. For example, the spin state of Co was adjusted by changing particle sizes of LaCoO₃ or doping Fe atom at Co sites to boost the catalytic performance (Zhou et al., 2016; Duan et al., 2017). However, the precise control of the specific intermediate spin configuration is still challenging. In principle, strain technology, defects, and interfacing are alternative schemes (Zhao et al., 2018, 2019, 2020a), among which the strain technology is one of the widely adopted schemes to tune electronic properties and thereby tailor the reactivity of materials. Mavrikakis et al. (1998) proposed that the strain changes the reactivity of transition metal surface by shifting the d-band center; this model is general and suitable for a number of metal surfaces to successfully explain chemical behaviors of materials under strain (Hammer et al., 1996, 1997; Holmblad et al., 1996; Kratzer et al., 1996; Hammer and Norskov, 2000; Liu et al., 2011). In addition, for the widely used platinum catalyst, a compressive strain of 1% can induce activity enhancement of more than 300% for ORR (Strasser et al., 2010; Escudero-Escribano et al., 2012; Asano et al., 2016; Escudero-Escribano et al., 2016). Wang et al. (2019b) found that the control of the thickness of two-dimensional transition metal at atomic level can achieve fine-tuning intrinsic strain. Moreover, the activity of oxygen reduction and hydrogen evolution reactions can be improved by more than an order of magnitude relative to corresponding nanoparticle counterparts. For oxides, strain primarily impacts the orbital characteristics, like energy level arrangement of the d subset and its occupancy, and consequently, the catalytic properties. The different strain along in-plane and out-of-plain direction can remove degenerate of e_g orbital, and alter the occupancy of d_z^2 (Freeland et al., 2011; Pesquera et al., 2012).

Although strain technology has been proven to be effective, the physics behind it remains inaccessible, and the modulation of e_g occupancy is not explored yet. Here, we use cubic LaCoO₃ as a model catalyst to systematically investigate the effect of strain on electronic configurations closely relevant for catalytic performance, such as d-band center and electron spin arrangements. We focus on the strain induced by modifying lattice in the absence of octahedral distortions. When the uniform strains were applied, the magnetic moment of Co atom showed step-like behavior versus strain (γ < 1.0%, Mag_Co: 0.0 μ_B; 1.0% ≤ γ < 4.0%, Mag_Co: 1.406 μ_B; γ ≥ 4.0%, Mag_Co: 2.561 μ_B). The substitution of La by large-radius Ba introduces strain leading to the e_g unit-like occupancy. Significantly, the lower oxidation state of Ba compared with La leads to a magnetic moment localized at the Co atom in Ba substitution-modified LaCoO₃ larger than that of the equivalent strained defect-free LaCoO₃. This work provides insights into the precise control of e_g unit occupancy via defect induced strain.

Computational Models and Setups

All calculations are performed in the framework of spin-polarized density functional theory (DFT), using the projector-augmented wave (PAW) method (Kresse and Joubert, 1999), as implemented in VASP code (Kresse and Furthmüller, 1996). The exchange–correlation interaction is treated in the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) (Perdew et al., 1996). To describe the electronic correlation effect of 3d electrons of Co element, the DFT+U method (Anisimov et al., 1991) with a U_eff of 2.8 eV was employed. The energy cutoff for the plane–wave basis is set to be 550 eV. The calculated lattice parameters of LaCoO₃ are a = b = c = 3.811 Å, which agree well with previous theoretical and experimental results (Ganguly and Vasanthacharya, 1986; Kushima et al., 2010; Rivadulla et al., 2013). A Monkhorst-Pack Γ-centered 11 × 11 × 11 k-point mesh was used for Brillouin zone sampling. Accordingly, for the 2 × 2 × 2 supercell, the 7 × 7 × 7 k-point mesh was adopted. The magnitude of the force acting on each atom to be allowed to relax is less than 0.01 eV/Å.

The substitutional energy per Ba atom in La_1–xBa_xCoO₃ with different composition x is defined as

$$E_{substitutional}^{Ba}=\frac{1}{x}(E_{L{a}_{1-x}B{a}_{x}Co{O}_3}-E_{LaCo{O}_3}+\frac{x}{2}{E}_{bulk}^{L{a}_2{O}_3}-x{E}_{bulk}^{BaO}-\frac{x}{4}{E}_{O_2}),$$

where E_{La_1–x Ba_x CoO_3}and E_{LaCoO_3} are the total energy of Ba substitution-modified LaCoO₃ and pristine LaCoO₃. $E_{\text{bulk}}^{{\mathrm{La}}_2{\mathrm{O}}_3}$, $E_{\text{bulk}}^{\text{BaO}}$, and E_{O_2} are the energy of bulk La₂O₃, bulk BaO, and oxygen gas, respectively.

Results and Discussion

Electronic and Elastic Properties of LaCoO₃

Prior to exploring the effect of strain on the electronic properties of bulk LaCoO₃, it is necessary to first calculate the electronic structures with effective on-site coulomb-exchange interaction parameter U_eff varying from 1.0 to 4.6 eV. Figure 1 presents the calculated bandgap of bulk LaCoO₃ (see Figure 2A) under different U_eff. It is found that the bulk LaCoO₃ exhibits metallic properties for U_eff < 1.8 eV. And, with the U_eff increasing beyond 1.8 eV, the bandgap occurs. When U_eff value of 2.8 eV was employed, a bandgap of 0.441 eV was observed which is in good consonance with experimental results (Chainani et al., 1992; Abbate et al., 1993; Arima et al., 1993). Therefore, we adopted the U_eff of 2.8 eV in the following discussions. As shown in Figure 2B, the degenerate 3d orbitals of the free Co atom are split into t_2g and e_g bands under the restriction of cubic symmetry of LaCoO₃. The valence bands and the conduction bands are attributed to t_2g and e_g, respectively. This indicates that six d electrons of trivalent Co ion fully occupied t_2g orbitals, agreeing well with non-magnetic ground states of LaCoO₃ (Abbate et al., 1993). Besides, there is significant hybridization O-2p and Co-3d, suggesting a strong covalent bond between Co and O. The empty states at the energy of 4.0 eV above Fermi level are the La 4f states. The Bader charge analysis suggests that the calculated charge transfer of La is +2.071e, close to its formal charges of +3e. The charge transfer of Co and O atom is +1.355e and −1.142e, respectively. This deviation of the charge transfer from the corresponding formal charges +3e and −2e further confirms the covalent feature of Co–O bond. In our DFT analysis for the effect of strain on the spin arrangement of LaCoO₃, the strain is achieved by equally changing lattice parameters along with a, b, and c directions. The strain is evaluated by γ = (a_s−a)/a×100%, where a_s and a are the lattice constants of strained and strain-free structure, respectively. The corresponding strain energy of LaCoO₃ is defined as ΔE = E_s−E, where E_s and E denote the total energy of strained and strain-free structure, respectively. Figure 2C shows the curve of the strain energy ΔE of LaCoO₃ versus γ. The minimum ΔE occurs at γ = 0, corresponding to the unstrained system.

FIGURE 1

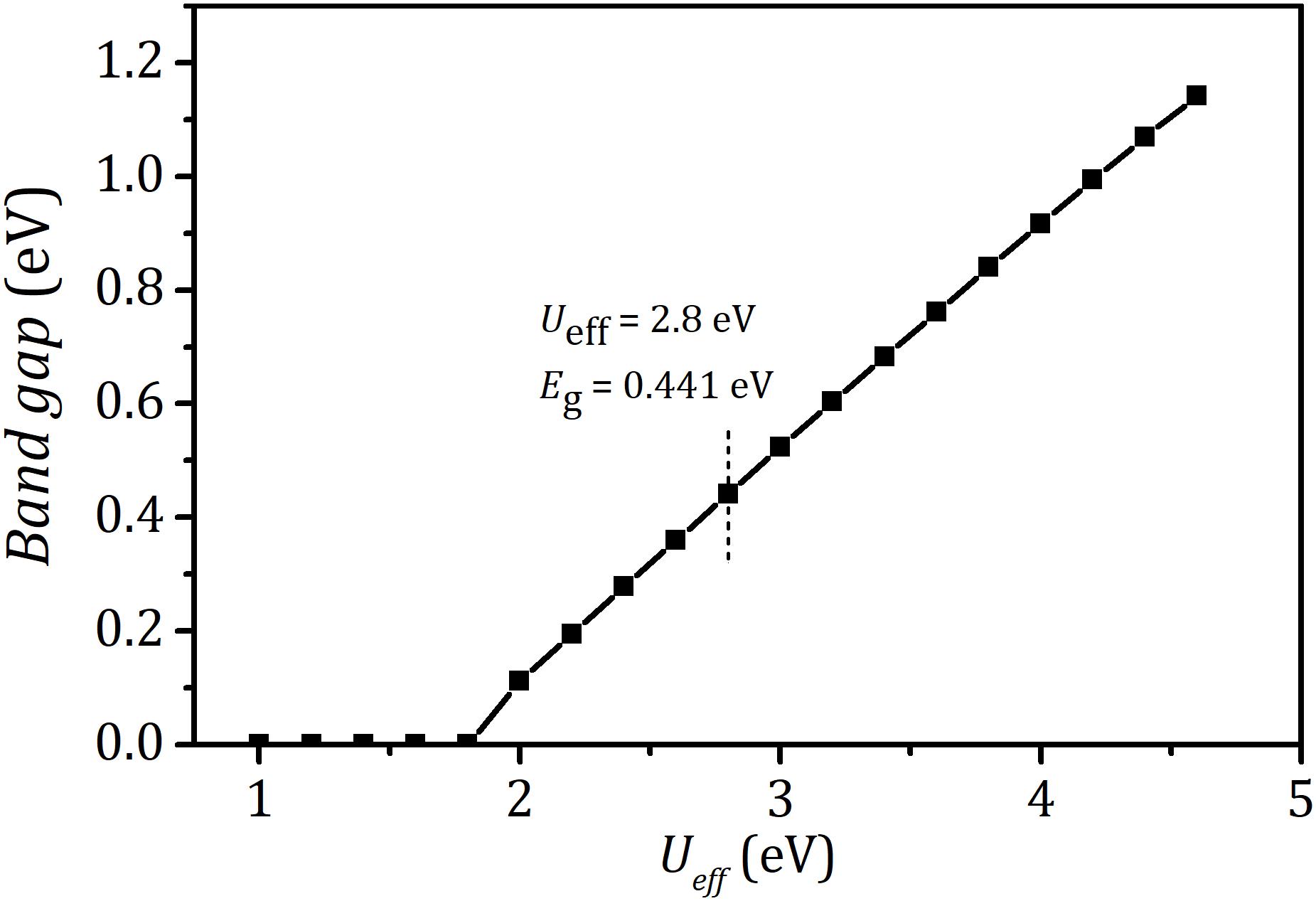
Figure 1. Bandgap of bulk LaCoO₃ as a function of effective coulomb-exchange interaction parameter U_eff (1.0–4.6 eV).

FIGURE 2

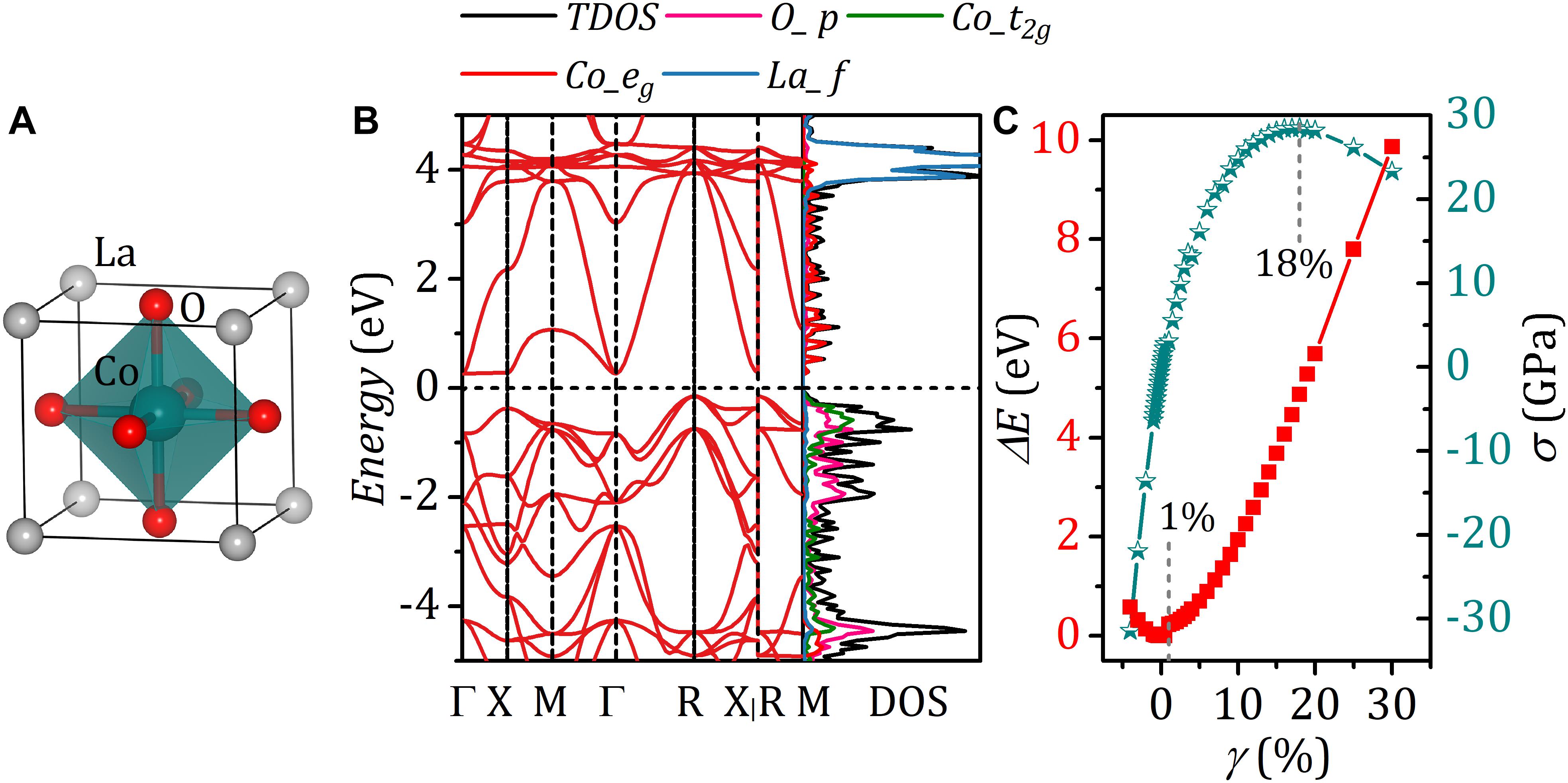
Figure 2. (A) Crystal structure of LaCoO₃ and (B) corresponding band structure. (C) Strain energy of LaCoO₃ versus strain γ and strain–stress curve.

To assess the strain effect on electronic configurations within a reasonable strain range, we first determined the ultimate strain of LaCoO₃ by calculating the strain–stress curve. It is evident that stress increases with strain and reaches a peak at 18%, as shown in Figure 2C. The ultimate strain of 18% suggests a good resistance to stress for LaCoO₃, which makes it possible to synthesize multicomponent perovskites by partially substituting La or Co, reflecting the diversity of perovskite-type oxides (Peña and Fierro, 2001; Smit et al., 2006). When the strain becomes larger than ultimate strain, the system is subject to attack by vacancy defects or high-temperature effects, etc., and the consequent collapse of crystal structures (Topsakal et al., 2010; Akhoundi et al., 2019).

Strain-Driven Spin-Arrangement Transition in LaCoO₃

Magnetic behaviors of materials arise from its spin arrangement. The results for the magnetic moment localized at Co atom (Mag_Co) under various strain (γ) are shown in Figure 3A and Supplementary Tables S1, S2. The main feature of the curve is that Mag_Co exhibits step-like change with strain in the calculated range from γ = −4.0 to 30%, reflecting low, intermediate, and high spin configurations. For strained LaCoO₃ with intermediate- and high-spin configurations, the magnetic moment of Co increases with strain. This positive correlation between magnetic moment and strain is a general behavior, which was observed in various materials (Kushima et al., 2010; Hsu et al., 2018; Zhao et al., 2020b). Given the slight variation in the magnetic moment over each terrace, we take the average values over the corresponding strain range as the DFT calculated Mag_Co, listed in Table 1. From Figure 3A, for γ < 1.0%, system manifests non-magnetic behavior. As strain increases (γ ≥ 1.0%), LaCoO₃ becomes ferromagnetic. Within γ = 1.0–4.0%, the values of Mag_Co maintain at around 1.406 μ_B. When γ ≥ 4.0%, the average Mag_Co is 2.561 μ_B. Owing to the dependence of magnetic moment on the U_eff parameter of the DFT+U method (Anisimov et al., 1991; Knížek et al., 2005), the calculated magnetic moments and actual magnetization values differ. Although a large U_eff value can be used to obtain the magnetic moment consistent with the experimental value, this would lead to the wrong estimation of the ground state energy (Tolba et al., 2018). To ensure the accuracy of results, we calculated the magnetic moments localized at Co atoms with U_eff = 3.0, 3.3, 3.5, 3.8, and 4.0 eV, for γ = 0.0, 2.0, and 8.0% (Supplementary Table S1). It is found that there is only a slight variation in the magnetic moment localized Co atom within the reasonable range of U_eff values (more information, see Supplementary Table S1), indicating the accuracy of our conclusion on the spin configuration transition. Furthermore, the previous theoretical investigation has shown that the strained LaCoO₃ has an intermediate-spin and high-spin configuration at a strain of 3 and 11%, respectively, which is consistent with the results in this work (Kushima et al., 2010).

TABLE 1

Table 1. Bond length, d_Co–O in Å and magnetic moment localized at Co atom, Mag_Co in μ_B of LaCoO₃.

FIGURE 3

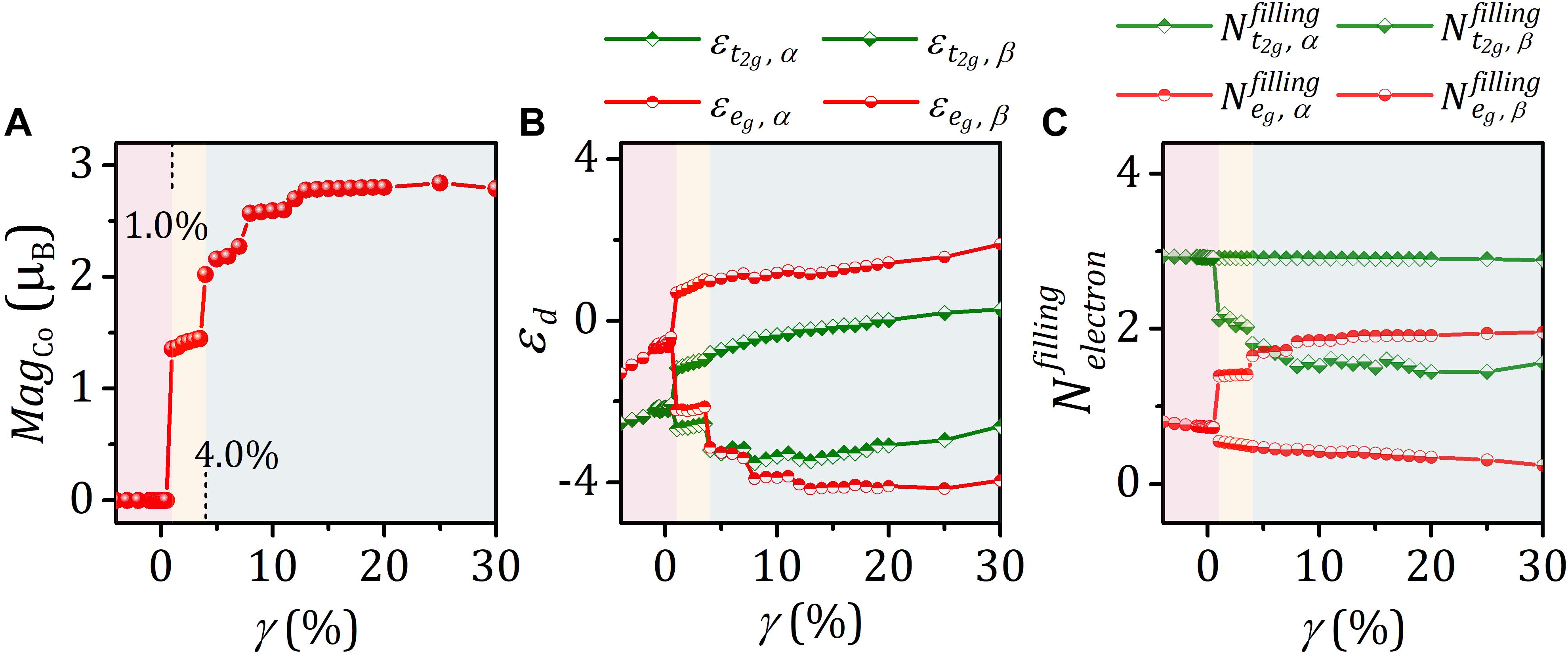
Figure 3. (A–C) Magnetic moment localized at Co atom (Mag_Co), d-band center (ε_d), and d-band filling ($N_{\text{electron}}^{\text{filling}}$) versus strain γ.

To seek the physical origin of the step-like dependence of Mag_Co on the strain, we analyze the electronic structures by calculating the d-band center and corresponding orbital occupancy (Figures 3B,C; for detailed data, see Supplementary Tables S2, S3). It is observed that t_2g and e_g bands are spin-degenerate for γ < 1.0% (Figure 3B). However, in the case of γ ≥ 1.0%, the spin degeneracy is lifted, and the degenerate d bands split into two bands. The corresponding spin splitting is estimated by the gap of d-band center between the majority α-spin and minority β-spin, presented in Figure 3B. The spin splitting increases with γ. As compared with the t_2g band, the degree of spin splitting is significantly larger in e_g, which is accompanied by the change of the octahedral field splitting. The octahedral field splitting is assessed by the gap of d-band center between the t_2g and e_g with same spin states. It is noted that the predominant change of the octahedral field split concentrates in majority α–spin d orbitals. The majority α–spin t_2g and e_g band centers show step-like descent as γ increases. Especially, the majority α–spin e_g-band center becomes lower than the t_2g-band center when γ ≥ 4.0%. This indicates the smallest octahedral field splitting occurs within γ ≥ 4.0% compared with that in γ < 1.0% and 1.0% ≤ γ < 4.0%. These changes of crystal field splitting and spin splitting would affect orbital occupancy and accordingly magnetic moment. The fundamental origin of the change of octahedral field splitting is the change of the electrostatic interaction between Co and O with different Co–O bond length (d_Co–O). The low-spin, intermediate-spin, and high-spin configurations are in the range d_Co–O < 1.925 Å, 1.925 Å ≤ d_Co–O < 1.982 Å, and d_Co–O ≥ 1.982 Å, respectively (Table 1).

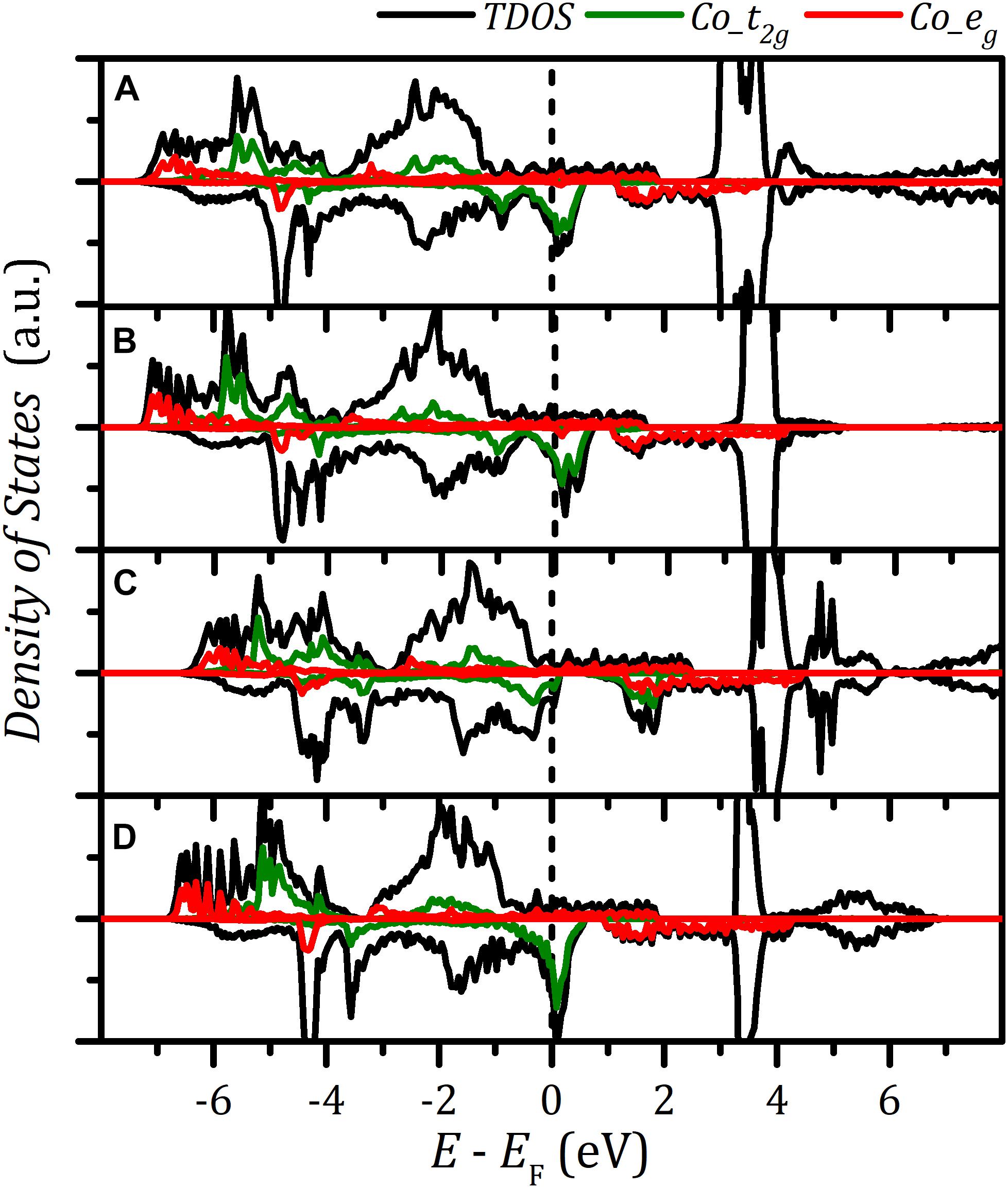
We further quantify the d band-filling numbers by integrating the projected densities of states with respect to energy up to the Fermi level. $N_{{\mathrm{e}}_{\text{g}},\mathrm{\alpha }}^{\text{filling}}$, $N_{{\mathrm{e}}_{\text{g}},\mathrm{\beta }}^{\text{filling}}$, $N_{{\mathrm{t}}_{2\mathrm{g}},\mathrm{\alpha }}^{\text{filling}}$, and $N_{{\mathrm{t}}_{2\mathrm{g}},\mathrm{\beta }}^{\text{filling}}$ were used to denote t_2g and e_g filling in different spin states. The corresponding data are listed in Supplementary Table S3. Figure 3C reveals that $N_{{\mathrm{e}}_{\text{g}},\mathrm{\alpha }}^{\text{filling}}$ increases with strain. In contrast, the minority β-spin t_2g bands exhibit a reverse filling trend. The rise of majority α–spin e_g band-filling number results in the enhancement of magnetic moment and the transition of spin configuration. $N_{{\mathrm{t}}_{2\mathrm{g}},\mathrm{\alpha }}^{\text{filling}}$and $N_{{\mathrm{e}}_{\text{g}},\mathrm{\beta }}^{\text{filling}}$ under strain were observed to be roughly constant. This follows from 3d⁶ electron configuration of trivalent Co ion and the d-orbital splitting under the octahedral field. The projected density of states of Co atoms (Figures 4a–e) indicates that with strain increasing the minority β–spin t_2g states shift upward with relative to Fermi level, whereas electrons gradually fill majority α–spin e_g states. Based on the analysis of the octahedral field, spin splitting, and d-orbital filling, we obtained low-spin, intermediate-spin, and high-spin arrangements in the corresponding octahedral field, illustrated in Figures 4f–h.

FIGURE 4

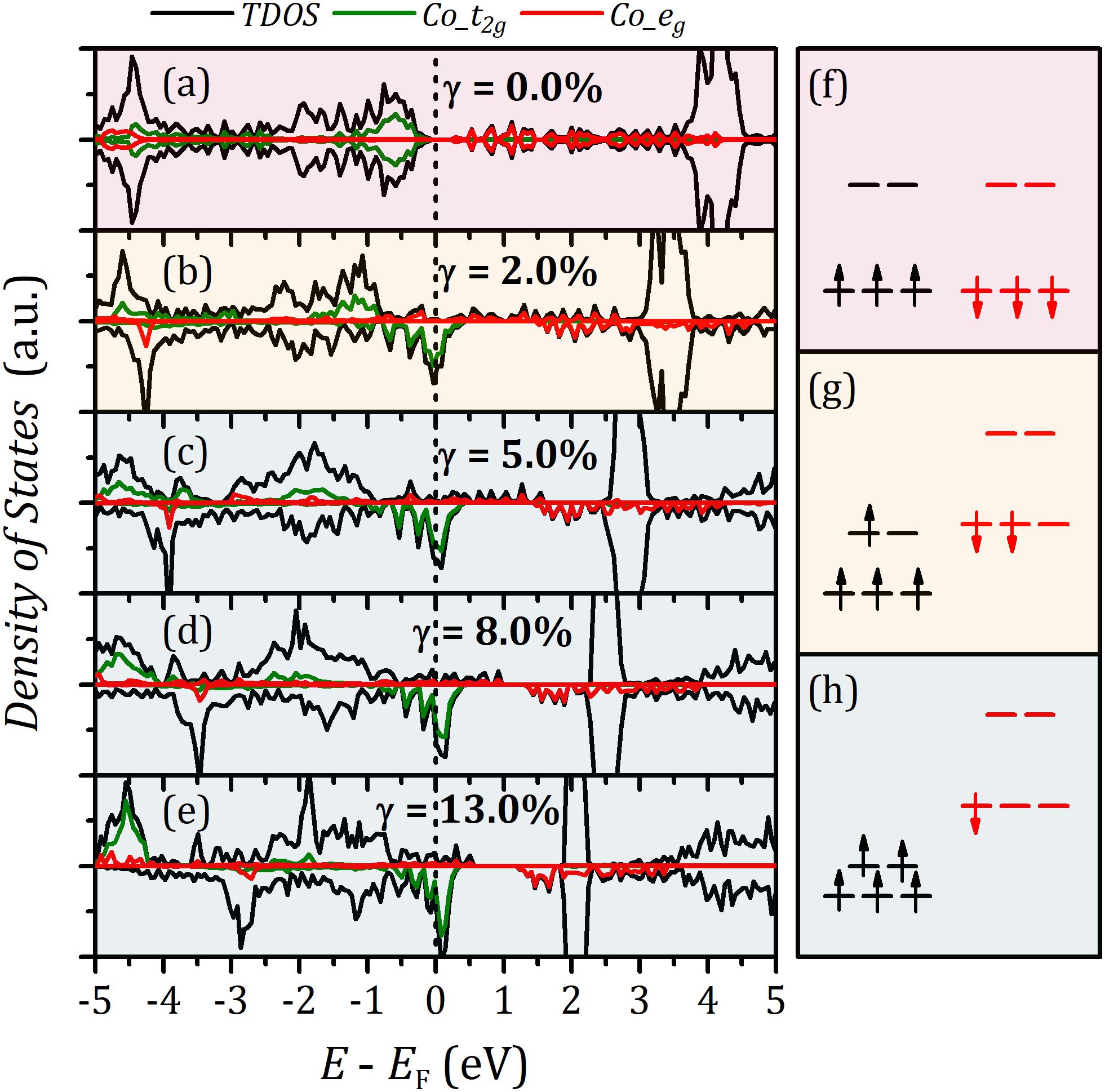
Figure 4. Density of states of LaCoO₃ under various strain: (a–e) γ = 0.0, 2.0, 5.0, 8.0, and 13.0%. The schematic diagram of crystal field and corresponding spin arrangements: (f) low spin, (g) intermediate spin, and (h) high spin.

Effect of Ba Substitution in LaCoO₃ on Magnetic Properties

Strain could be achieved through introduction of defect or epitaxial substrate, etc. To apply tensile strain in LaCoO₃, we used Ba with a larger radius than La to partially replace La atom of LaCoO₃ (Ba²⁺: 1.61 Å, La³⁺: 1.36 Å) (Shannon, 1976). Nine possible configurations were considered based on the Ba content and the locations of Ba atoms: La_0.875Ba_0.125CoO₃ (Ba_c), La_0.75Ba_0.25CoO₃ (Ba_c+b), La_0.75Ba_0.25CoO₃ (Ba_c+f1, Ba_c+f2, Ba_c+e1, Ba_c+e2), La_0.625Ba_0.375CoO₃ (Ba_c+f1+f3, Ba_{c+b +f1}), and La_0.5Ba_0.5CoO₃(Ba_c+f1+f2+f3) (see Figure 5). Here, c, b, f, and e denote corner, body center, face center, and edge center sites, respectively. Ba_c, Ba_c+b, and Ba_c+f1+f2+f3 denote Ba occupying the dispersive La sites to form Ba uniform-distributed structures (Figure 5). Other Ba substitutional defects distributed unevenly instead. The Ba substitutions can be formed due to the small substitutional energies of −0.356, −1.076, −1.083, −1.418, −1.415, −0.766, −1.076, 0.402, and 0.071 eV. The overall substitutional energies manifest the stability of the structure, reflecting the possibility of substituted perovskite compounds with the formula of A_1–xA′_xB₁–_xB′xO₃ (Peña and Fierro, 2001). In experiments, various R_1–xA_xCoO₃ (R = La, Pr, and Nd; A = Ba, Sr, and Ca), with x ranging from 0 to 0.5, have been successfully synthesized (Muta et al., 2002; Khalil, 2003; Masuda et al., 2003; Kun et al., 2013). For our investigated Ba substitution-modified LaCoO₃, the charge transfer of Ba is +1.552 to +1.577e, close to its formal charges of +2e (Table 2). The charge transfer of La approaches to its formal charge (+3e) with a value of about +2.0 e.

FIGURE 5

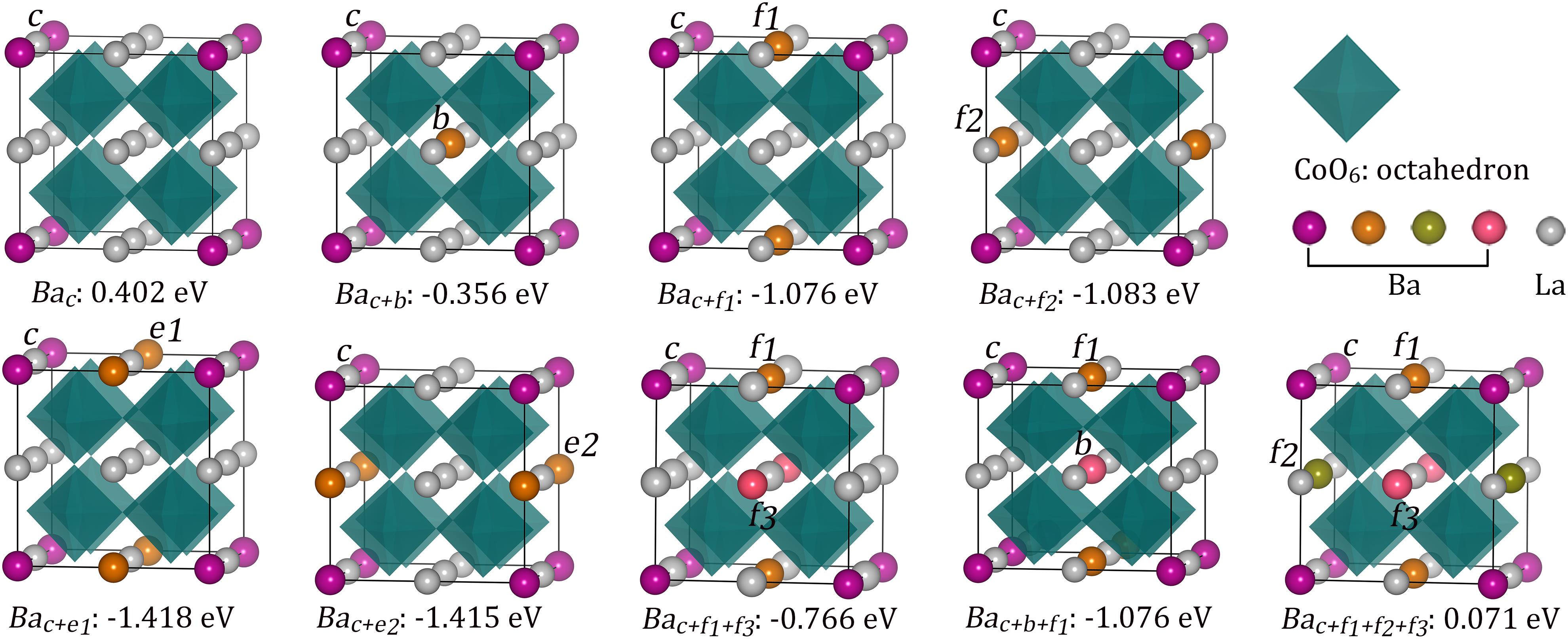
Figure 5. Optimized structures of Ba-substituted LaCoO₃ and corresponding stabilization energies of Ba substitutional defects.

TABLE 2

Table 2. The magnetic moment localized at Co atom, Mag_Co in μ_B, charge transfer of Co atom, ΔQ^Co, $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ in e, and the charge transfer of La and Ba atom, ΔQ^La, ΔQ^Ba in e, for Ba_c, Ba_c+b, Ba_c+f1, Ba_c+f2, Ba_c+e1, Ba_c+e2, Ba_c+f1+f3, and Ba_c+f1+f2+f3 defective systems ($\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ is the charge transfer of Co atom in defective LaCoO₃ due to the difference of electronic configuration between Ba and La).

The consequence of the introduction of Ba substitution at La site causes the lattice expansions. In this work, the uniform distribution of Ba atoms promotes homogeneous elongation of lattice constants along with a, b, and c directions (Ba_c: a_s = b_s = c_s = 0.96%; Ba_c+b: a_s = b_s = c_s = 1.31%; Ba_c+f1+f3: a_s = b_s = c_s = 1.74%; Ba_c+f1+f2+f3: a_s = b_s = c_s = 2.05%) (Figure 6A). For the systems with uneven distributions of Ba atoms (Ba_c+f1, Ba_c+f2, Ba_c+e1, Ba_c+e2, and Ba_c+b+f1), especially Ba_c+b+f1, the structures derivate away from cubic symmetry (see Figure 6A), resulting in anisotropic physical properties of Co atoms. The lattice expansion-induced strain corresponds to the intermediate-spin strain range of defect-free LaCoO₃ (1.0–4.0%) (Figure 6A). The corresponding magnetic moments of each Co atoms are listed in Table 2 and Supplementary Table S4. For Ba_c+b+f1 substitutional defect modified LaCoO₃, the magnetic moments of Co atom are largely different, with an average value of 2.157 μ_b ranging from 1.606 to 2.761 μ_b (Supplementary Table S4 and Figure 6B). In the case of slight deviation from cubic structures (Ba_{c+f1/f2/e1/e2}), Co atoms have the same magnetic moments (Ba_c+f1: 1.834 μ_b; Ba_c+f2: 1.836 μ_b; Ba_c+e1: 1.834 μ_b; Ba_c+e2: 1.833 μ_b) (Figure 6B and Table 2). For the systems with uniform Ba distribution, Ba_c, Ba_c+b, Ba_c+f1+f3, and Ba_c+f1+f2+f3, eight Co atoms in each structure are equivalent and possess the same magnetic moment (Ba_c: 2.111 μ_b; Ba_c+b: 2.377 μ_b; Ba_c+f1+f3: 1.936 μ_b; Ba_c+f1+f2+f3: 2.197 μ_b). Although the strain induced by Ba introduction is within the strain range of intermediate spin of defect-free LaCoO₃, the magnetic moments localized at Co atoms deviate from ∼1.5 μ_b of the intermediate spin structures.

FIGURE 6

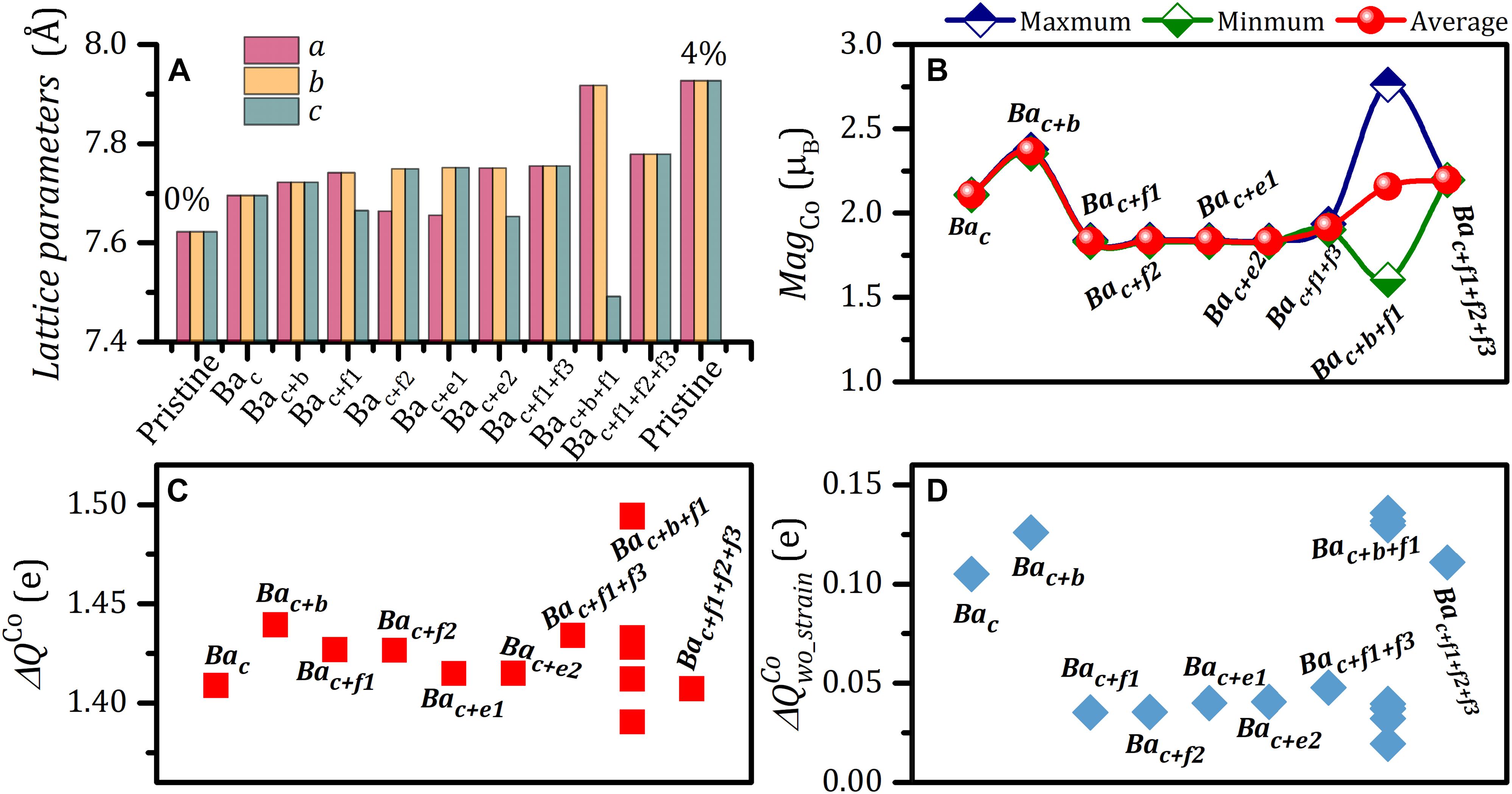
Figure 6. (A) Lattice parameters along a, b, and c directions, (B) magnetic moment localized at Co atom (Mag_Co), (C) charge transfer of Co atom, and (D) charge transfer of Co atom excluding effect of variation in lattice in Ba-substituted LaCoO₃.

To uncover the fundamental origin of the difference of magnetic moments between Ba-substituted LaCoO₃ and defect-free intermediate-spin LaCoO₃, we further analyze the charge states of Co atoms in Ba substitution modified LaCoO₃. Figures 6C,D outline the total charge transfer of Co to adjacent O atoms, ΔQ^Co and the charge transfer of Co owing to the valence electronic configuration difference between Ba²⁺ and La³⁺, $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$, excluding the charge change resulting from lattice relaxation. The total charge transfer of Co atoms varies from +1.40 to +1.45e, differing from the value in strain-free LaCoO₃ (+1.335 e) (Figure 6C]. The Ba valence states indeed induced the variation in charge transfer of Co (Figure 6D). Specifically, for Ba_c, Ba_c+b, and Ba_c+f1+f2+f3 substitution modified LaCoO₃, $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ is 0.105, 0.126, and 0.111 e, respectively. As a comparison to these structures with uniform distribution of Ba atom, in the defective systems with Ba_c+f1, Ba_c+f2, Ba_c+e1, and Ba_c+e2 substitutions, $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ dramatically decreases by 67–75% with values of 0.035–0.041e. It is a clear indication that the $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ is proportional to Mag_Co (e.g., Ba_c+b: $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ = 0.126e, Mag_Co = 2.365 μ_b; Ba_c+f1: $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ = 0.035e, Mag_Co = 1.835 μ_b) (Figures 6B,D and Supplementary Figure S1). Correspondingly, for Ba_c+f1+f3 substitution modified LaCoO₃, the small Mag_Co of 1.916 μ_b is accompanied by a small $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ of 0.048 e. For Ba_{c,f1/f2/e1/e2} and Ba_c+f1+f3, the extremely small $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ of about 0.04e results in Mag_Co of ∼1.8 μ_b, which is well consistent with 1.5-μ_b magnetic moment of the pristine intermediate-spin configuration.

This effect of $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ on Mag_Co is further verified by the results of Ba_c+b+f1 substitutional defect-modified LaCoO₃. For example, the large $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ on Co², Co⁵, and Co⁸ in Ba_c+b+f1 substitution-modified LaCoO₃ (upper case digits on Co represent the different Co sites; see Supplementary Figure S2 for details), are accompanied by large Mag_Co of 2.059, 2.757, and 2.758 μ_b (Supplementary Table S4). Meanwhile, the small Mag_Co of 1.781, 1.783, 1.606, and 1.752 μ_b are observed on Co¹, Co⁴, Co⁶, and Co⁷ atoms associating with the corresponding small $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ of 0.037, 0.040, 0.037, and 0.020e. However, Co³ atom in Ba_c+b+f1-modified LaCoO₃ is an abnormal case. The magnetic moment localized at Co³ site is 2.761 μ_b despite the small $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$ of 0.032e. Further analysis suggests that the charge transfer of Co³ site, using the charge state of Co atom of pristine strain-free LaCoO₃ as benchmark, is 0.036e, which is almost the same as $\mathrm{\Delta }{Q}_{\mathrm{wo}\mathrm{\_}\mathrm{strain}}^{\text{Co}}$. Therefore, the valence state of Ba dominates the charge transfer in Co³ site, eventually leads to large magnetic moment localized at Co³ site. Overall, the Ba substitutional defect-modified LaCoO₃ possesses intermediate-spin configurations. The values of magnetic moments localized at Co atoms deviating from the 1.5 μ_b of pristine strained intermediate spin LaCoO₃ results from the different electronic configurations between Ba and La. And, the degree of deviation depends on the magnitude of the charge transfer of Co atoms following from the different valence states between Ba and La.

The projected density of states of Co atom reveals that the systems with Ba_c, Ba_c+b, and Ba_c+f1+f2+f3 substitutional defect hold similar orbital occupations, which differs from Ba_c+f1+f3 substitution modified LaCoO₃ (Figures 7A–D). The d-orbital filling exhibit that, for Ba_c+f1+f3, the minority β-spin t_2g filling increases accompanied by reducing majority α–spin e_g filling, compared with the defective LaCoO₃ including Ba_c, Ba_c+b, and Ba_c+f1+f2+f3 substituents (Supplementary Figure S3), which contributes to the small magnetic moment. The defective systems with a small magnetic moment, Ba_c+f1, Ba_c+f2, Ba_c+e1, and Ba_c+e2, have similar d-orbital occupation as Ba_c+f1+f3 (Supplementary Figure S4). All these features of d-orbital occupation are found in different Co atoms of Ba_c+f1+f3 substitution modified LaCoO₃ (Supplementary Figure S5). Ba substitutional defects induce a unit-like e_g occupancy resulting in a moderate interaction between Co active center and oxygen-related adsorbates, which contributes to the reduction of the OER/ORR thermodynamic overpotential. Therefore, Ba substitution defect modified LaCoO₃ is promising for oxygen redox catalytic reactions.

FIGURE 7

Figure 7. Density of states: (A) Ba_c, (B) Ba_c+b, (C) Ba_c+f1+f3, and (D) Ba_c+f1+f2+f3.

Conclusion

In summary, we explored the dependence of spin configurations on strain in LaCoO₃ via DFT calculations. We found that strain by manipulation lattice constants can tune crystal field splitting and spin splitting, resulting in the transition of spin arrangement. The important e_g unit occupancy was achieved via applying tri-axial uniform strain ranging from 1.0 to 4.0%. To achieve the strain effects practically, the substitution of La by Ba with larger ionic radius effectively introduces strain, leading to the unit-like occupancy of e_g. Notably, there is larger magnetic moment localized at Co atom in Ba substitution modified LaCoO₃ relative to the equivalent strained defect-free LaCoO₃, due to the lower oxidation state of Ba than La. The response of spin configuration on strain induced by defect enables precise control of the unit occupancy of e_g during the catalyst design process.

Data Availability Statement

The datasets generated for this study are available via the corresponding author or other researchers following publication.

Author Contributions

LW performed the DFT calculations. LW, JL, and WW wrote this manuscript. WW administrated the project. MW provided the computational resources. HW, KL, YS, and ZL advised the research work.

Funding

This work was supported by the National Key Research and Development Program (Grant No. 2016YFB0901600), Tianjin City Distinguish Young Scholar Fund, National Natural Science Foundation of China (21573117 and 21975136), Tianjin Key Research and Development Program (Grant No. 18ZXSZSF00060), pen funds from National Engineering Lab for Mobile Source Emission Control Technology (NELMS2018A01), and the Fundamental Research Funds for the Central Universities (63185015).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2020.00060/full#supplementary-material

References

Abbate, M., Fuggle, J. C., Fujimori, A., Tjeng, L. H., Chen, C. T., Potze, R., et al. (1993). Electronic structure and spin-state transition of LaCoO3. Phys. Rev. B-Condens Matter 47, 16124–16130. doi: 10.1103/PhysRevB.47.16124

PubMed Abstract | CrossRef Full Text | Google Scholar

Akhoundi, E., Faghihnasiri, M., Memarzadeh, S., and Firouzian, A. H. (2019). Mechanical and strain-tunable electronic properties of the SnS monolayer. J. Phys. Chem. Solids 126, 43–54. doi: 10.1016/j.jpcs.2018.10.019

CrossRef Full Text | Google Scholar

Anisimov, V. I., Zaanen, J., and Andersen, O. K. (1991). Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 44, 943–954. doi: 10.1103/PhysRevB.44.943

PubMed Abstract | CrossRef Full Text | Google Scholar

Arima, T., Tokura, Y., and Torrance, J. B. (1993). Variation of optical gaps in perovskite-type 3d transition-metal oxides. Phys. Rev. B 48, 17006–17009. doi: 10.1103/PhysRevB.48.17006

PubMed Abstract | CrossRef Full Text | Google Scholar

Asano, M., Kawamura, R., Sasakawa, R., Todoroki, N., and Wadayama, T. (2016). Oxygen reduction reaction activity for strain-controlled pt-based model alloy catalysts: surface strains and direct electronic effects induced by alloying elements. ACS Catal. 6, 5285–5289. doi: 10.1021/acscatal.6b01466

CrossRef Full Text | Google Scholar

Chainani, A., Mathew, M., and Sarma, D. D. (1992). Electron-spectroscopy study of the semiconductor-metal transition in La1-xSrxCoO3. Phys. Rev. B 46, 9976–9983. doi: 10.1103/PhysRevB.46.9976

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, Y., Sun, S., Xi, S., Ren, X., Zhou, Y., Zhang, G., et al. (2017). Tailoring the Co 3d-O 2p covalency in LaCoO3 by Fe substitution to promote oxygen evolution reaction. Chem. Mater. 29, 10534–10541. doi: 10.1021/acs.chemmater.7b04534

CrossRef Full Text | Google Scholar

Escudero-Escribano, M., Malacrida, P., Hansen, M. H., Vej-Hansen, U. G., Velázquez-Palenzuela, A., Tripkovic, V., et al. (2016). Tuning the activity of Pt alloy electrocatalysts by means of the lanthanide contraction. Science 352, 73–76. doi: 10.1126/science.aad8892

PubMed Abstract | CrossRef Full Text | Google Scholar

Escudero-Escribano, M., Verdaguer-Casadevall, A., Malacrida, P., Grønbjerg, U., Knudsen, B. P., Jepsen, A. K., et al. (2012). Pt5Gd as a highly active and stable catalyst for oxygen electroreduction. J. Am. Chem. Soc. 134, 16476–16479. doi: 10.1021/ja306348d

PubMed Abstract | CrossRef Full Text | Google Scholar

Freeland, J. W., Liu, J., Kareev, M., Gray, B., Kim, J. W., Ryan, P., et al. (2011). Orbital control in strained ultra-thin LaNiO3/LaAlO3 superlattices. Europhys. Lett. 96:57004. doi: 10.1209/0295-5075/96/57004

CrossRef Full Text | Google Scholar

Ganguly, P., and Vasanthacharya, N. Y. (1986). Infrared and Mössbauer spectroscopic study of the metal-insulator transition in some oxides of perovskite structure. J. Solid State Chem. 61, 164–170. doi: 10.1016/0022-4596(86)90018-6

CrossRef Full Text | Google Scholar

Gani, T. Z. H., and Kulik, H. J. (2018). Understanding and breaking scaling relations in single-site catalysis: methane to methanol conversion by FeIV=O. ACS Catal. 8, 975–986. doi: 10.1021/acscatal.7b03597

CrossRef Full Text | Google Scholar

Hammer, B., Morikawa, Y., and Nørskov, J. K. (1996). CO chemisorption at metal surfaces and overlayers. Phys. Rev. Lett. 76, 2141–2144. doi: 10.1103/PhysRevLett.76.2141

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammer, B., Nielsen, O. H., and Nrskov, J. K. (1997). Structure sensitivity in adsorption: CO interaction with stepped and reconstructed Pt surfaces. Catal. Lett. 46, 31–35. doi: 10.1023/A:1019073208575

CrossRef Full Text | Google Scholar

Hammer, B., and Norskov, J. K. (2000). Theoretical surface science and catalysis - calculations and concepts. Adv. Catal. 45, 71–129. doi: 10.1021/acs.accounts.8b00399

PubMed Abstract | CrossRef Full Text | Google Scholar

Holmblad, P. M., Larsen, J. H., Chorkendorff, I., Nielsen, L. P., Besenbacher, F., Stensgaard, I., et al. (1996). Designing surface alloys with specific active sites. Catal. Lett. 40, 131–135. doi: 10.1007/BF00815272

CrossRef Full Text | Google Scholar

Hong, W. T., Risch, M., Stoerzinger, K. A., Grimaud, A., Suntivich, J., and Shao-Horn, Y. (2015). Toward the rational design of non-precious transition metal oxides for oxygen electrocatalysis. Energy Environ. Sci. 8, 1404–1427. doi: 10.1039/C4EE03869J

CrossRef Full Text | Google Scholar

Hsu, S.-H., Hung, S.-F., Wang, H.-Y., Xiao, F.-X., Zhang, L., Yang, H., et al. (2018). Tuning the electronic spin state of catalysts by strain control for highly efficient water electrolysis. Small Methods 2:1800001. doi: 10.1002/smtd.201800001

CrossRef Full Text | Google Scholar

Jiang, M., Li, J., Zhao, Y., Pan, L., Cao, Q., Wang, D., et al. (2018). Double perovskites as model bifunctional catalysts toward rational design: the correlation between electrocatalytic activity and complex spin configuration. ACS Appl. Mater. Interfaces 10, 19746–19754. doi: 10.1021/acsami.8b05353

PubMed Abstract | CrossRef Full Text | Google Scholar

Khalil, M. S. (2003). Synthesis, X-ray, infrared spectra and electrical conductivity of La/Ba–CoO3 systems. Mater. Sci. Eng. A 352, 64–70. doi: 10.1016/s0921-5093(02)00557-9

CrossRef Full Text | Google Scholar

Knížek, K., Novák, P., and Jirák, Z. (2005). Spin state of LaCoO3: dependence on CoO6 octahedra geometry. Phys. Rev. B 71:054420. doi: 10.1103/PhysRevB.71.054420

CrossRef Full Text | Google Scholar

Kratzer, P., Hammer, B., and Nørskov, J. K. (1996). Geometric and electronic factors determining the differences in reactivity of H2 on Cu(100) and Cu(111). Surf. Sci. 359, 45–53. doi: 10.1016/0039-6028(96)00309-3

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi: 10.1103/PhysRevB.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775. doi: 10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Kun, R., Populoh, S., Karvonen, L., Gumbert, J., Weidenkaff, A., and Busse, M. (2013). Structural and thermoelectric characterization of Ba substituted LaCoO3 perovskite-type materials obtained by polymerized gel combustion method. J. Alloys Compd. 579, 147–155. doi: 10.1016/j.jallcom.2013.05.019

CrossRef Full Text | Google Scholar

Kushima, A., Yip, S., and Yildiz, B. (2010). Competing strain effects in reactivity of LaCoO3 with oxygen. Phys. Rev. B 82:115435. doi: 10.1103/PhysRevB.82.115435

CrossRef Full Text | Google Scholar

Kuznetsov, D. A., Han, B., Yu, Y., Rao, R. R., Hwang, J., Román-Leshkov, Y., et al. (2018). Tuning redox transitions via inductive effect in metal oxides and complexes, and implications in oxygen electrocatalysis. Joule 2, 225–244. doi: 10.1016/j.joule.2017.11.014

CrossRef Full Text | Google Scholar

Li, H.-B., Yang, Z., Liu, J., Yao, X., Xiong, K., Liu, H., et al. (2016). Electronic properties and native point defects of high efficient NO oxidation catalysts SmMn2O5. Appl. Phys. Lett. 109:211903. doi: 10.1063/1.4968786

CrossRef Full Text | Google Scholar

Liu, H. Y., Yan, R. X., Zhang, R. G., Wang, B. J., and Xie, K. C. (2011). A DFT theoretical study of CH4 dissociation on gold-alloyed Ni(111) surface. J. Nat. Gas Chem. 20, 611–617. doi: 10.1016/s1003-9953(10)60252-6

CrossRef Full Text | Google Scholar

Maitra, U., Naidu, B. S., Govindaraj, A., and Rao, C. N. R. (2013). Importance of trivalency and the eg1 configuration in the photocatalytic oxidation of water by Mn and Co oxides. Proc. Natl. Acad. Sci. U. S. A. 110, 11704–11707. doi: 10.1073/pnas.1310703110

PubMed Abstract | CrossRef Full Text | Google Scholar

Masuda, H., Fujita, T., Miyashita, T., Soda, M., Yasui, Y., Kobayashi, Y., et al. (2003). Transport and magnetic properties of R1-xAxCoO3 (R = La, Pr and Nd; A = Ba, Sr and Ca). J. Phys. Soc. Jpn. 72, 873–878. doi: 10.1143/JPSJ.72.873

CrossRef Full Text | Google Scholar

Matsumoto, Y., Yoneyama, H., and Tamura, H. (1977a). Catalytic activity for electrochemical reduction of oxygen of lanthanum nickel oxide and related oxides. J. Electroanal. Chem. Interfacial Electrochem. 79, 319–326. doi: 10.1016/s0022-0728(77)80453-1

CrossRef Full Text | Google Scholar

Matsumoto, Y., Yoneyama, H., and Tamura, H. (1977b). Influence of the nature of the conduction band of transition metal oxides on catalytic activity for oxygen reduction. J. Electroanal. Chem. Interfacial Electrochem. 83, 237–243. doi: 10.1016/s0022-0728(77)80169-1

CrossRef Full Text | Google Scholar

Mavrikakis, M., Hammer, B., and Norskov, J. K. (1998). Effect of strain on the reactivity of metal surfaces. Phys. Rev. Lett. 81, 2819–2822. doi: 10.1103/PhysRevLett.81.2819

CrossRef Full Text | Google Scholar

Muta, K., Kobayashi, Y., and Asai, K. (2002). Magnetic, electronic transport, and calorimetric investigations of La1-xCaxCoO3 in comparison with La1-xSrxCoO3. J. Phys. Soc. Jpn. 71, 2784–2791. doi: 10.1143/JPSJ.71.2784

CrossRef Full Text | Google Scholar

Peña, M. A., and Fierro, J. L. G. (2001). Chemical structures and performance of perovskite oxides. Chem. Rev. 101, 1981–2018. doi: 10.1021/cr980129f

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi: 10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Pesquera, D., Herranz, G., Barla, A., Pellegrin, E., Bondino, F., Magnano, E., et al. (2012). Surface symmetry-breaking and strain effects on orbital occupancy in transition metal perovskite epitaxial films. Nat. Commun. 3:1189. doi: 10.1038/ncomms2189

PubMed Abstract | CrossRef Full Text | Google Scholar

Rivadulla, F., Bi, Z., Bauer, E., Rivas-Murias, B., Vila-Fungueiriño, J. M., and Jia, Q. (2013). Strain-induced ferromagnetism and magnetoresistance in epitaxial thin films of LaCoO3 prepared by polymer-assisted deposition. Chem. Mater. 25, 55–58. doi: 10.1021/cm3031472

CrossRef Full Text | Google Scholar

Shannon, R. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 32, 751–767. doi: 10.1107/S0567739476001551

CrossRef Full Text | Google Scholar

Smit, J. P., Stair, P. C., and Poeppelmeier, K. R. (2006). The adaptable lyonsite structure. Chem.-Eur. J. 12, 5944–5953. doi: 10.1002/chem.200600294

PubMed Abstract | CrossRef Full Text | Google Scholar

Strasser, P., Koh, S., Anniyev, T., Greeley, J., More, K., Yu, C., et al. (2010). Lattice-strain control of the activity in dealloyed core–shell fuel cell catalysts. Nat. Chem. 2, 454–460. doi: 10.1038/nchem.623

PubMed Abstract | CrossRef Full Text | Google Scholar

Suntivich, J., Gasteiger, H. A., Yabuuchi, N., Nakanishi, H., Goodenough, J. B., and Shao-Horn, Y. (2011a). Design principles for oxygen-reduction activity on perovskite oxide catalysts for fuel cells and metal–air batteries. Nat. Chem. 3, 546–550. doi: 10.1038/nchem.1069

PubMed Abstract | CrossRef Full Text | Google Scholar

Suntivich, J., May, K. J., Gasteiger, H. A., Goodenough, J. B., and Shao-Horn, Y. (2011b). A perovskite oxide optimized for oxygen evolution catalysis from molecular orbital principles. Science 334, 1383–1385. doi: 10.1126/science.1212858

PubMed Abstract | CrossRef Full Text | Google Scholar

Tolba, S. A., Gameel, K. M., Ali, B. A., Almossalami, H. A., and Allam, N. K. (2018). “The DFT+U: approaches, accuracy, and applications,” in Density Functional Calculations - Recent Progresses of Theory and Application, ed. G. Yang, (London: IntechOpen).

Google Scholar

Topsakal, M., Cahangirov, S., and Ciraci, S. (2010). The response of mechanical and electronic properties of graphane to the elastic strain. Appl. Phys. Lett. 96:091912. doi: 10.1063/1.3353968

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Chen, H., and Wang, W. (2019a). N–H bond activation in ammonia by TM-SSZ-13 (Fe, Co, Ni and Cu) zeolites: a first-principles calculation. Phys. Chem. Chem. Phys. 21, 1506–1513. doi: 10.1039/C8CP06263C

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Zeng, Z., Gao, W., Maxson, T., Raciti, D., Giroux, M., et al. (2019b). Tunable intrinsic strain in two-dimensional transition metal electrocatalysts. Science 363, 870–874. doi: 10.1126/science.aat8051

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, C., Feng, Z., Scherer, G. G., Barber, J., Shao-Horn, Y., and Xu, Z. J. (2017). Cations in octahedral sites: a descriptor for oxygen electrocatalysis on transition-metal spinels. Adv. Mater. 29:1606800. doi: 10.1002/adma.201606800

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, Y., Jiang, S.-X., Yin, W.-J., Sheng, W., Wu, L.-X., Nie, G.-Z., et al. (2020). Adsorption behaviors of HCN, SO2, H2S and NO molecules on graphitic carbon nitride with Mo atom decoration. Appl. Surf. Sci. 501:144199. doi: 10.1016/j.apsusc.2019.144199

CrossRef Full Text | Google Scholar

Zhang, T., Li, H., Yang, Z., Cao, F., Li, L., Chen, H., et al. (2019). Electrospun YMn2O5 nanofibers: a highly catalytic activity for NO oxidation. Appl. Catal. B: Environ. 247, 133–141. doi: 10.1016/j.apcatb.2019.02.005

CrossRef Full Text | Google Scholar

Zhao, G., Cheng, Y., Sun, P., Ma, W., Hao, S., Wang, X., et al. (2020a). Biocarbon based template synthesis of uniform lamellar MoS2 nanoflowers with excellent energy storage performance in lithium-ion battery and supercapacitors. Electrochim. Acta 331:135262. doi: 10.1016/j.electacta.2019.135262

CrossRef Full Text | Google Scholar

Zhao, Y., Li, Y., Liu, M., Xu, K., and Ma, F. (2020b). Strain-controllable phase and magnetism transitions in Re-Doped MoTe2 monolayer. J. Phys. Chem. C. 124, 4299–4307. doi: 10.1021/acs.jpcc.9b11036

CrossRef Full Text | Google Scholar

Zhao, G., Cheng, Y., Wu, Y., Xu, X., and Hao, X. (2018). New 2D carbon nitride organic materials synthesis with huge-application prospects in CN photocatalyst. Small 14:e1704138. doi: 10.1002/smll.201704138

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, G., Wang, A., He, W., Xing, Y., and Xu, X. (2019). 2D new nonmetal photocatalyst of sulfur-doped h-BN nanosheeets with high photocatalytic activity. Adv. Mater. Interfaces 6:1900062. doi: 10.1002/admi.201900062

CrossRef Full Text | Google Scholar

Zhou, S., Miao, X., Zhao, X., Ma, C., Qiu, Y., Hu, Z., et al. (2016). Engineering electrocatalytic activity in nanosized perovskite cobaltite through surface spin-state transition. Nat. Commun. 7:11510. doi: 10.1038/ncomms11510

PubMed Abstract | CrossRef Full Text | Google Scholar