Durability Prediction of GFRP Rebar Based on Elastic Modulus Degradation

A conventional method to study the durability of Glass Fiber Reinforced Polymer (GFRP) rebars is to carry out tensile tests on the corroded GFRP bars. The degree of corrosion of the GFRP bars could be quantified based on the measured ultimate tensile strength and the calculated strength reduction. However, it is difficult to directly monitor the reduction in tensile strength of the GFRP rebars that are embedded in concrete; therefore, this method cannot be implemented in real engineering practices. This study presents the reduction in elastic modulus of the GFPR rebars by real-time monitoring of the strain of the GFRP rebars, and then establishes the degradation model of the elastic modulus for the GFRP rebars in an alkaline corrosion environment. Therefore, the relationship between tensile strength and elastic modulus of GFRP rebars is proposed and verified by the experimental data obtained from the literature. The results show that it is feasible to use the Arrhenius equation to simulate the degradation model of the elastic modulus of the GFRP rebars. Thus, the tensile strength of the GFPR rebars can be related to its elastic modulus. Using the proposed relationship, the durability of GFRP rebars can be predicted by real-time monitoring of the elastic modulus of the GFRP rebars.

Introduction

Under severe service environment, typically represented by marine environment, the built-in steel bars of the conventional reinforced concrete structure are subjected to accelerated corrosion resulted from the continuous contact with chloride ions contained in sea water and sea fog, leading to poor durability of the structure. Some of the expensive remedies (e.g., epoxy coated or galvanized steel bars, and stainless-steel bars) have been proven ineffective in improving the durability of reinforced concrete structures (Clear et al., 1995). In recent years, Fiber Reinforced Polymer (FRP) has arisen as a prospective substitute for steel to resolve the corrosion issue of reinforced concrete structures, due to its advantages such as high strength, light weight, and strong corrosion resistance. Glass Fiber Reinforced Polymer (GFRP) bar is more widely applied compared to other FRP bars [e.g., Aramid fiber reinforced polymer (AFRP), carbon fiber reinforced polymer (CFRP)] owing to the low cost. However, glass fiber and common thermosetting resin matrix are prone to erosion by moisture, high temperature and alkali, which may result in polymer degradation, fiber–matrix debonding, fiber corrosion, and thereby, significantly decreased tensile strength (Gonenc, 2003; Chen et al., 2007). At present, the only durability test of GFRP bars was carried out by Canadian scholars Mufti et al. (2007) for five GFRP-Reinforced Concrete (RC) bridges that have been in service for 5–8 years employing scanning electron microscopy (SEM), Fourier transform infrared spectroscopy (FTIR), and glass transition temperature (Tg). The results did not show obvious strength degradation of the GFRP bars. Besides, there is still a lack of long-term durability data of GFRP bars in practical service environment. Therefore, it is important to strengthen monitoring of the durability of GFRP bars in practical service for promoting the practical application of GFRP-RC structures.

At present, accelerated aging test is normally applied to investigate the durability of GFRP bars. Generally, there are two types of accelerated aging test: (1) GFRP bars are placed in corrosion solution directly and the temperature of the solution is elevated to accelerate the strength degradation of GFRP bars (Phani and Bose, 1987; Wu et al., 2015; Wang et al., 2017, 2018); (2) GFRP bars are embedded in concrete before placed in corrosion solution, and similarly, the environment temperature is raised to accelerate the strength degradation of GFRP bars (Nelson, 1990; Davalos et al., 2011; Robert and Benmokrane, 2013). The retention rate of tensile strength is then used to evaluate the long-term durability of GFRP bars. Although the two accelerated aging tests demonstrated above can effectively predict the durability of GFRP bars, they are difficult to be implemented for GFRP bars in practical service. Furthermore, while corroded steel bars display visible warning signals such as expanded volume which leads to crack of concrete (Al-Salloum et al., 2013), degraded GFRP bars do not show any signals, which impose great challenges for engineers to determine the degradation degree of GFRP bars inside GFRP-RC structures. Some effective non-destructive evaluation developed techniques (Li et al., 2016, 2017; Jiang et al., 2017; Xu et al., 2018) for monitoring the initial bonding quality and long-term efficiency of the interfacial bonding between GFRP bars and concrete. However, so far, there has not been any relevant technology or method to monitor the tensile strength degradation of GFRP bars in practical service. Therefore, exploring such an effective method to provide large amount of durability data of GFRP bars is beneficial for optimizing the manufacture process of GFRP bars and the design of GFRP-RC structures.

Since GFRP rebars cannot be taken directly from the actual structure, it is difficult to monitor strength degradation of GFRP rebars during service. Therefore, finding data which are easy to monitor is vital to reflect the actual strength degradation law of GFRP rebars. Generally, the stress of GFRP bars is constant during service (Mukherjee and Arwikar, 2006), thus, the elastic modulus degradation degree of GFRP rebars can be monitored by real-time monitoring of the strain. If the relationship between the degradation law of GFRP rebars tensile strength and that of elastic modulus, then the tensile strength degradation can be predicted by real monitoring of GFRP rebars elastic modulus. As a consequence, this paper establishes the degradation model of elastic modulus and tensile strength of GFRP rebars with Arrhenius equation to deduce the conversion formula between the degradation rate of tensile strength and that of elastic modulus, so that the tensile strength degradation law of GFRP rebars can be obtained by real monitoring of their elastic modulus degradation for the purpose of predicting GFRP rebars durability.

Theoretical Study

Arrhenius Equation

For a laboratory scale, it is necessary to increase the temperature in order to accelerate the corrosion reaction between the GFRP rebars and the alkaline solution. The Arrhenius equation is defined as a relationship between the temperature and the degradation rate. Among the previous studies of the durability of FRP rebars, many scholars have used this equation to establish the strength degradation model for the FRP rebars (Davalos et al., 2011; Wang et al., 2017, 2018). The Arrhenius equation is expressed as below:

$\begin{array}{ll}k=A{e}^{-\frac{Ea}{RT}}& (1)\end{array}$

where k = degradation rate (1/time); A = constant of the material and degradation process; E_a = activation energy; R = universal gas constant; and T = Kelvin temperature. The primary assumption of this model is that the single dominant degradation mechanism of the material will not change with time and temperature during the exposure, but the rate of degradation will be accelerated with the increase in temperature. Equation (1) can be transformed into

$\begin{array}{ll}\frac{1}{k}=\frac{1}{A}exp(\frac{E_a}{RT})& (2)\end{array}$

$\begin{array}{ll}ln\frac{1}{k}=\frac{E\text{a}}{RT}-ln(A)& (3)\end{array}$

From Equation (2), the degradation rate k can be expressed as the inverse of time needed for a material property to reach a given value. From Equation (3), one can further observe that the logarithm of time needed for a material property to reach a given value is a linear function of 1/T with the slope of E_a/R.

According to Arrhenius theory, the relationship between tensile strength retention of GFRP rebars and exposure time for accelerated aging test was defined as

$\begin{array}{ll}SR=exp(-\frac{t}{\tau })& (4)\end{array}$

where SR = tensile strength retention value (%); t = exposure time; and τ = 1/k, as expressed in Equation (2) The form of this formula was modified by Chen et al. (2006) based on a study of Phani and Bose (1987), assuming that GFRP rebars degraded completely at infinite exposure time. The validity of this formula for describing the tensile strength degradation law of GFRP tendons has also been proved by many scholars by experiments (Davalos et al., 2011; Wu et al., 2015; Wang et al., 2017, 2018).

Thus Equation (4) can be transformed into:

$\begin{array}{ll}SR=exp(-kt)& (5)\end{array}$

$\begin{array}{ll}ln(SR)=-t·k& (6)\end{array}$

It can be known from Equation (6) that the logarithm of strength retention (SR) is a linear function of t with the slope of –k. Therefore, degradation rate can be obtained by measuring the strength retention (SR).

Substituting Equation (6) into Equation (3), the relationship between the exposure time and the temperature can be obtained:

$\begin{array}{ll}lnt=\frac{E\text{a}}{RT}+B& (7)\end{array}$

where $B=-ln\frac{A}{-ln(SR)}$.

Derivation

It is assumed that the GFRP rebars has a tensile strength retention SR after a exposure time t₁ (corresponding to a degradation rate k₁) and the same elastic modulus retention SR after a exposure time t₂ (corresponding to a degradation rate k₂):

$\begin{array}{ll}ln(SR)=-t_1.k_1& (8)\end{array}$

$\begin{array}{ll}ln(SR)=-t_2.k_2& (9)\end{array}$

$\begin{array}{ll}\frac{k_1}{k_2}=\frac{t_2}{t_1}& (10)\end{array}$

Substituting the Equation (8) and Equation (9) into Equation (10), the following relationship can be obtained:

$\begin{array}{ll}ln{t}_1=\frac{E{\text{a}}_1}{RT}+B_1& (11)\end{array}$

$\begin{array}{ll}ln{t}_2=\frac{E{\text{a}}_2}{RT}+B_2& (12)\end{array}$

where

$\begin{array}{ll}{B}_1=-ln\frac{A_1}{-ln(SR)},B_2=-ln\frac{A_2}{-ln(SR)}& (13)\end{array}$

E_a1 is the activation energy of tensile strength, E_a2 is the activation energy of elastic modulus, A₁ is constant of the material and degradation process related to tensile strength, and A₂ constant of the material and degradation process related to elastic modulus.

Substituting Equation (11) and Equation (12) into Equation (10) respectively, the relationship between the degradation rate of tensile strength(k₁₎ and the degradation rate of the elastic modulus (k₂) can be obtained.

$\begin{array}{ll}\frac{k_1}{k_2}=exp\left[\frac{E{a}_1}{RT}+B_2-(\frac{E{a}_2}{RT}+B_1)\right]& (14)\end{array}$

$\begin{array}{ll}{k}_1=a·e^{-\frac{b}{T}}·k_2,a=e^{B_2-B_1},b=\frac{E{a}_1}{R}-\frac{E{a}_2}{R}& (15)\end{array}$

where B₁, B₂, Ea₁/R, Ea₂/R can be obtained by fitting the test data.

With Equation (15), the relationship between degradation rate of GFRP rebars elastic modulus and that of tensile strength is obtained, so that the tensile strength degradation law can be reflected by monitoring the degradation law of GFRP rebars elastic modulus for the purpose of predicting their durability during the service.

Solving and Verifying the Conversion Formula

Five steps are to verify this theory:

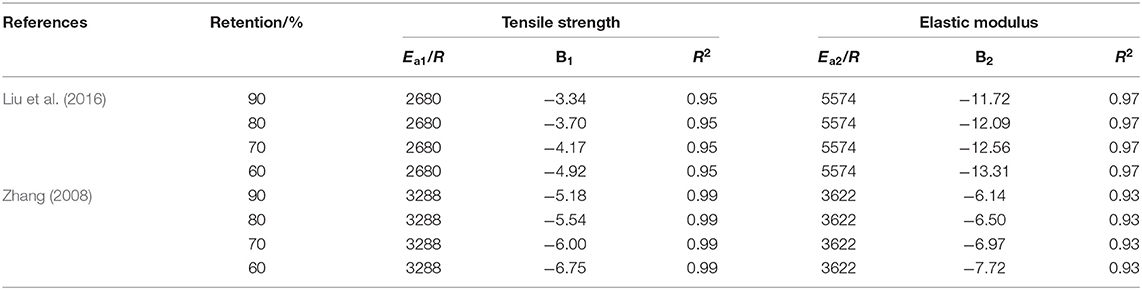
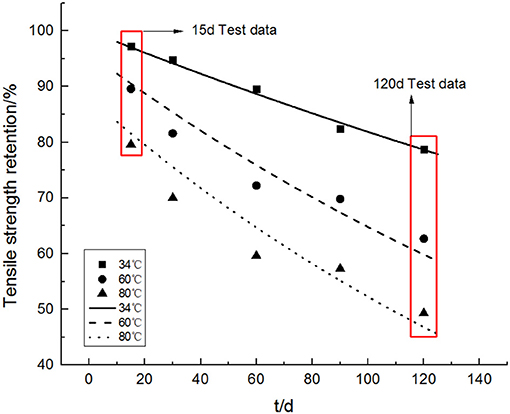
Firstly, appropriate data are chosen. To improve the reliability of the theory, this paper has chosen 2 groups of tests data. One group is the accelerated aging test of GFRP rebars performed by our research team in 2016, which mainly aims to study GFRP rebars durability in the alkaline environment. The GFRP rebars in the test are made of E44 epoxy resin and the corresponding fibers through pultrusion process, whose outside diameter is 9.2 ± 0.11 mm, shown in Figure 1. To create an alkaline environment for GFRP rebars, a plastic pipe with diameter of 63 mm and length of 250 mm is inserted into the prepared tensile test specimen of GFRP rebars, and PVC tubes are inserted the gap between the two ends of the plastic pipe and GFRP rebars. The three pieces are cemented together with epoxy resin AB glue. Then plastic pipe is injected with alkaline solution and sealed. The glass fiber heater band is used to enwind the plastic pipe to heat the solution in it. The test specimens are shown in Figure 2, the heating measures in Figure 3, and other information in Liu et al. (2016). The other group is the accelerated aging test of GFRP rebars performed by Professor Zichun Zhang from Harbin Institute of Technology (China) (Zhang, 2008). They are similar in the accurate measurement of elastic modulus retention of GFRP rebars in different exposure time, which is the key to verifying the theory. Data of the age of 30, 60, and 90 days are used to fit the data in Zhang (2008), and data of the age of 15 and 120 days are used to verify the validity of the conversion formula. The test data of the two tests are shown in Table 1.

FIGURE 1

Figure 1. GFRP rebar.

FIGURE 2

Figure 2. Test specimens.

FIGURE 3

Figure 3. Heating measures for specimens.

TABLE 1

Table 1. Test data of GFRP rebars exposed to alkaline solution.

Secondly, the test data in Table 1 are fitted by Equation (5), obtaining the relationship among tensile strength retention (Figure 4), elastic modulus retention (Figure 5), and the exposure time. Corresponding k values and correlation coefficients R² are summarized in Table 2. Figures 4, 5 indicate that the test data coincide well with the fitting curves, and Table 2 shows the correlation coefficients are >0.9. Thus, the time to reach a given tensile strength and elastic modulus retention at different temperatures can be approximately calculated through Equation (5).

FIGURE 4

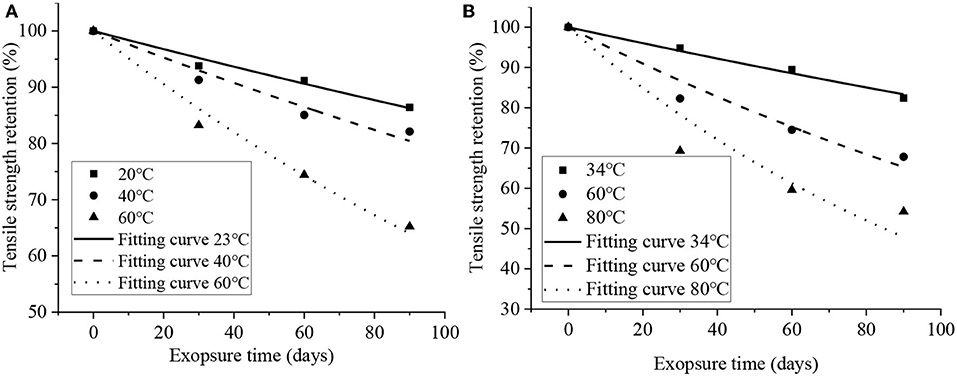
Figure 4. Fitted curves for tensile strength retention vs. time: (A) Liu et al. (2016) and (B) Zhang (2008).

FIGURE 5

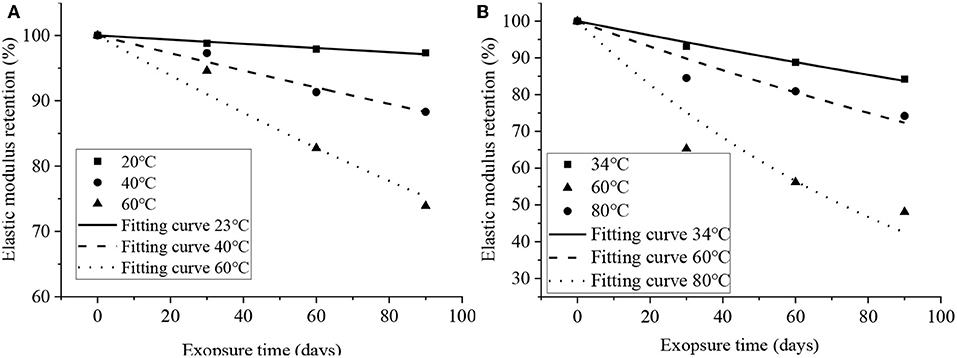
Figure 5. Fitted curves for elastic modulus retention vs. time: (A) Liu et al. (2016) and (B) Zhang (2008).

TABLE 2

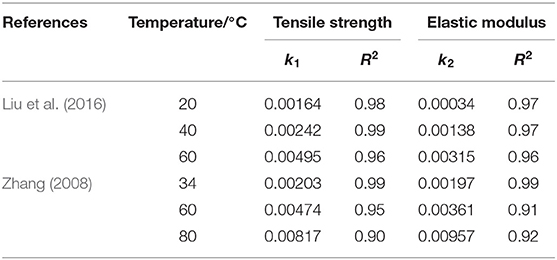
Table 2. Coefficients of regression equations for GFRP tensile strength and elastic modulus retention.

Thirdly, the Arrhenius relationships were obtained by plotting the natural log of time to reach 60, 70, 80, and 90% tensile strength and elastic modulus of GFRP rebars vs. 1/T the inverse of exposure temperature in Figures 6, 7. Straight lines were fitted to the data with the assumption that the degradation rate was a function of temperature as expressed in Equation (3). From the analysis, the regression coefficients E_a/R and correlation coefficients R² are listed in Table 3. The correlation coefficients for all regression lines were close to 1, and straight lines in Arrhenius plots for different tensile strength and elastic modulus retentions were nearly parallel to each other (the slopes of straight lines are E_a/R). This implies that the Arrhenius relation can be used to describe the tensile strength and elastic modulus degradation rate of GFRP bars. Moreover, Equation (5) can be used to define the time and temperature dependence of tensile strength and elastic modulus for GFRP bars exposed to alkaline solutions.

FIGURE 6

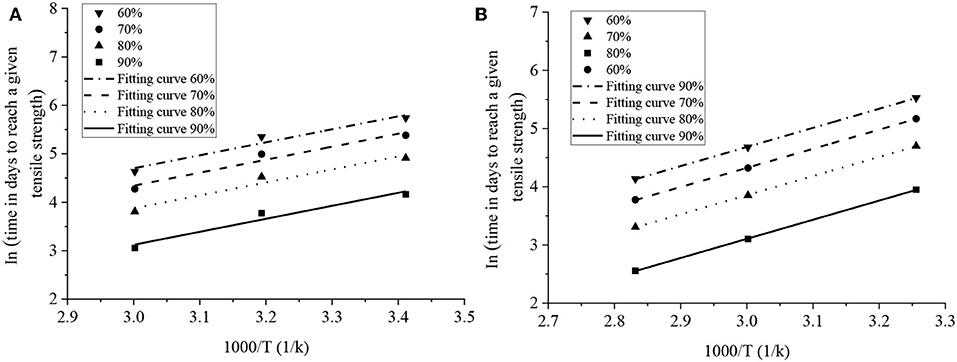
Figure 6. Arrhenius plots of tensile strength degradation: (A) Liu et al. (2016) and (B) Zhang (2008).

FIGURE 7

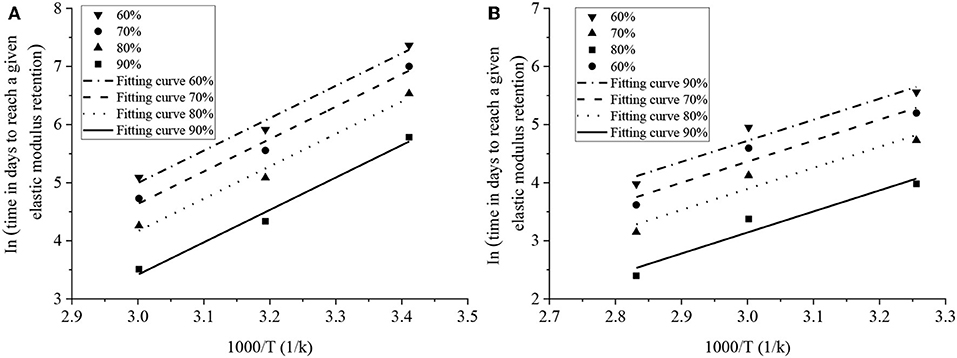
Figure 7. Arrhenius plots of elastic modulus degradation: (A) Liu et al. (2016) and (B) Zhang (2008).

TABLE 3

Table 3. Coefficients of regression equations for Arrhenius plots.

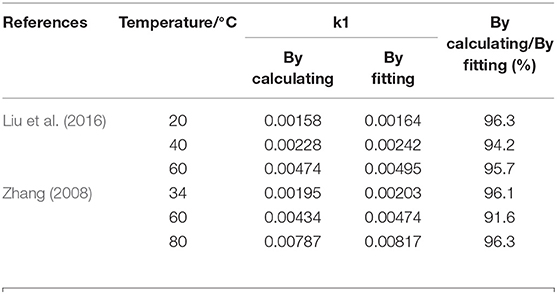
Fourth, the parameters shown in Table 3 are substituted in Equation (15) to obtain the tensile strength degradation rate of GFRP rebars (k₁) calculated by elastic modulus degradation rate of GFRP rebars (k₂). The test data results by Liu et al. (2016) are shown in Equation (16), and those by Zhang (2008) in Equation (17).

$\begin{array}{ll}{k}_1=0.00022·e^{\frac{2894}{T}}·k_2& (16)\end{array}$

$\begin{array}{ll}{k}_1=0.38·e^{\frac{334}{T}}·k_2& (17)\end{array}$

Finally, the tensile strength degradation rate of GFRP rebars (k₁) calculated through Equations (16) and (17) is compared with k₁ obtained by data fitting through Equation (5), shown in Table 4. It indicates that that the values of k₁ calculated by Equation (15) is basically the same as that fitted by Equation (5), which also proves the deduced conversion formula between tensile strength degradation rate and elastic modulus degradation rate of GFRP rebars is correct. Based on the test results in Zhang (2008), the test data and calculated curves are compared in Figure 8. Although the degradation model curve is obtained by fitting with experimental data of age of 30, 60, and 90 days, the degradation model can also well-simulate the experimental data of age of 15 and 120 days, which further explains that the congruent relationship exists between the degradation rate of GFRP rebars elastic modulus and that of their tensile strength during service.

TABLE 4

Table 4. The tensile strength degradation rate (k₁).

FIGURE 8

Figure 8. Comparisons between test data and calculated curves.

Conclusions

To solve the problem of monitoring the tensile strength degradation of GFRP rebars during their service, this paper has proposed a computing method for the tensile strength degradation rate of GFRP rebars during service and verified the method with test results. It is concluded that:

(1) GFRP rebars during service are under constant load. The change of GFRP rebars elastic modulus can be observed by monitoring the strain of GFRP rebars to obtain the degradation rate of their elastic modulus. Thus, the priority is to find the conversion relationship between the degradation rate of GFRP rebars elasticity modulus and that of their strength.

(2) When data fitting is conducted by using Arrhenius model (Equation 2) and strength degradation model (Equation 5), it is found that the test result is highly relevant to the fitting curve (R² ≥ 0.92), indicating that the strength degradation law based on Arrhenius theory also applies to elastic modulus. This is the key to the interconversion between the degradation rate of GFRP rebars strength and that of their elastic modulus.

(3) With the test data, the tensile strength degradation rate of GFRP rebars obtained by the formula is basically identical to the degradation rate by data fitting, which also proves the validity of the formula deduced in this paper.

(4) Due to the diversity of GFRP rebar type, the conversion relation expressions between the degradation rate of their elastic modulus and that of their tensile strength are not the same (e.g., Equations 16 and 17). Hence, it is vital for real durability monitoring of GFRP-RC structures to perform a specific accelerated aging test for GFRP rebars according to the actual engineering needs.

(5) The conversion relation between the degradation rate of GFRP rebars elastic modulus and that of their tensile strength in this paper provides possibility for analyzing and predicting the durability of GFRP rebars during service. However, no actual verification has been conducted for the theoretical formula. The further research has to focus on: (a) performing the accelerated aging test for GFRP rebars embedded in concrete and the real-time measurement for the degradation rate of tensile strength and that of elasticity modulus; (b) enhancing the monitoring of GFRP rebars during the real service. The data in those two tasks can be used to verify and modify the theoretical formula, so as to obtain more accurate conversion relation between the degradation rate of elastic modulus and that of tensile strength and improve the durability prediction precision of GFRP rebars during the actual service, to provide theoretical foundation for the durability design of GFRP–RC structures.

Data Availability Statement

All datasets generated for this study are included in the manuscript/supplementary files.

Author Contributions

JT incepted the research. HX and KG made theoretical analysis. JZ and ZL analyzed the data. KG and JT wrote the paper.

Funding

This work was supported by The Project of Ministry of Science and Technology (grant number 2018YFC0705601); National Natural Science Foundation of China (grant number 51978550); Fundamental Research Funds for the Central Universities (grant number 2019-YB 024); Natural Science Foundation of Hubei Province (grant number 2016CFA020).

Conflict of Interest

HX was employed by company China Construction Third Engineering Bureau Co., Ltd., Wuhan, China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Al-Salloum, Y. A., El-Gamal, S., Almusallam, T. H., Alsayed, S. H., and Aqel, M. (2013). Effect of harsh environmental conditions on the tensile properties of GFRP bars. Compos. Part B Eng. 45, 835–844. doi: 10.1016/j.compositesb.2012.05.004

CrossRef Full Text | Google Scholar

Chen, Y., Davalos, J. F., and Ray, I. (2006). Durability prediction for GFRP reinforcing bars using short-Term data of accelerated aging tests. J. Compos. Constr. 10, 279–286. doi: 10.1061/(ASCE)1090-0268(2006)10:4(279)

CrossRef Full Text | Google Scholar

Chen, Y., Davalos, J. F., Ray, I., and Kim, H. Y. (2007). Accelerated aging tests for evaluations of durability performance of frp reinforcing bars for concrete structures. Compos. Struct. 78, 101–111. doi: 10.1016/j.compstruct.2005.08.015

CrossRef Full Text | Google Scholar

Clear, K. C., Hartt, W. H., Mcintyre, J., and Lee, S. K. (1995). Performance of epoxy-coated reinforcing steel in highway bridges. NCHRP Report 370. Washington, DC: Transportation Research Board.

Google Scholar

Davalos, J. F., Chen, Y., and Ray, I. (2011). Long-term durability prediction models for GFRP bars in concrete environment. J. Compos. Mater. 46, 1899–1914. doi: 10.1177/0021998311427777

CrossRef Full Text | Google Scholar

Gonenc, O. (2003). Durability and service life prediction of concrete reinforcing materials (MS thesis). University of Wisconsin-Madison, Madison, WI, United States.

Google Scholar

Jiang, T., Kong, Q., Patil, D., Luo, Z., Huo, L., and Song, G. (2017). Detection of debonding between fiber reinforced polymer bar and concrete structure using piezoceramic transducers and wavelet packet analysis. IEEE Sens. J. 17, 1992–1998. doi: 10.1109/JSEN.2017.2660301

CrossRef Full Text | Google Scholar

Li, W., Fan, S., Ho, S. C. M., Wu, J., and Song, G. (2017). Interfacial debonding detection in fiber-reinforced polymer rebar–reinforced concrete using electro-mechanical impedance technique. Struct. Health Monitor. 17, 461–471. doi: 10.1177/1475921717703053

CrossRef Full Text | Google Scholar

Li, W., Ho, S. C. M., Patil, D., and Song, G. (2016). Acoustic emission monitoring and finite element analysis of debonding in fiber-reinforced polymer rebar reinforced concrete. Struct Health Monit. 16, 674–681. doi: 10.1177/1475921716678922

CrossRef Full Text | Google Scholar

Liu, J., Tu, J. W., and Guo, D. L. (2016). Study on the durability of GFRP reinforcement under the bearing strength condition. J. Wuhan Univ. Technol. 305, 59–63. doi: 10.3963/j.issn.1671-4431.2016.05.012

CrossRef Full Text | Google Scholar

Mufti, A., Bantha, N., Benmokrane, B., Boulfiza, M., and Newhook, J. (2007). Durability of gfrp composite rods. Concrete Int. 29, 37–42.

Google Scholar

Mukherjee, A., and Arwikar, S. J. (2006). Performance of glass fiber-reinforced polymer reinforcing bars on tropical environments – part 1: structural scale tests. ACI Struct. J. 102, 16–22.

Google Scholar

Nelson, W. (1990). Accelerated Testing—Statistical Models, Test Plans, and Data Analyses. New York, NY: Wiley.

Google Scholar

Phani, K. K., and Bose, N. R. (1987). Temperature dependence of hydrothermal ageing of csm-laminate during water immersion. Compos. Sci. Technol. 29, 79–87. doi: 10.1016/0266-3538(87)90050-9

CrossRef Full Text | Google Scholar

Robert, M., and Benmokrane, B. (2013). Combined effects of saline solution and moist concrete on long-term durability of GFRP reinforcing bars. Constr. Build. Mater. 38, 274–284. doi: 10.1016/j.conbuildmat.2012.08.021

CrossRef Full Text | Google Scholar

Wang, Z., Zhao, X. L., Xian, G., Wu, G., Raman, R. K. S., and Al-Saadi, S. (2018). Effect of sustained load and seawater and sea sand concrete environment on durability of basalt- and glass-fibre reinforced polymer (b/gfrp) bars. Corrosion Sci. 138, 200–218. doi: 10.1016/j.corsci.2018.04.002

CrossRef Full Text | Google Scholar

Wang, Z., Zhao, X. L., Xian, G., Wu, G., Singh Raman, R. K., Al-Saadi, S., et al. (2017). Long-term durability of basalt- and glass-fibre reinforced polymer (BFRP/GFRP) bars in seawater and sea sand concrete environment. Constr. Build. Mater. 139, 467–489. doi: 10.1016/j.conbuildmat.2017.02.038

CrossRef Full Text | Google Scholar

Wu, G., Dong, Z. Q., Wang, X., Zhu, Y., and Wu, Z. S. (2015). Prediction of long-term performance and durability of bfrp bars under the combined effect of sustained load and corrosive solutions. J. Compos. Constr. 19:04014058. doi: 10.1061/(ASCE)CC.1943-5614.0000517

CrossRef Full Text | Google Scholar

Xu, K., Ren, C., Deng, Q., Jin, Q., and Chen, X. (2018). Real-time monitoring of bond slip between GFRP bar and concrete structure using piezoceramic transducer-enabled active sensing. Sensors18:2653. doi: 10.3390/s18082653

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z. C. (2008). Thermosetting FRP Composited Rebars and Their Performance for Civil Infrastructures. Harbin: Harbin Institute of Technology.

Google Scholar