- Department of Physics and Chemistry, La Trobe Institute for Molecular Science, La Trobe University, Melbourne, VIC, Australia
In studies of the transfer, distribution and biochemical activity of metal ions it is typically assumed that the phospholipid bilayer acts as an inert barrier. Yet, there is mounting evidence that metal ions can influence the physical properties of membranes. Little is known of the basis of this effect. In this work the location and distribution of common metal ions: Na+, Mg2+, and Ca2+ in phospholipid membranes were studied. Computer simulations of lipid membrane segments in aqueous environment showed that the ions penetrate the membrane headgroup zone and co-localize with the phosphate and the ester moieties. Analysis of the chemical environment of the ions in the simulations suggested that the co-localization is facilitated by coordination to the polar oxygen atoms of the phosphate and ester groups in typical coordination geometries of each ionic species, where the coordination shells are completed by water molecules. In contrast, the counterions do not penetrate the headgroup zone but form a layer over the membrane instead; this layer is also an effective metal exclusion zone. Importantly, the choline groups appear to be distributed almost exactly in the same plane as the phosphate, suggesting that the zwitterion dipole is preferentially horizontally aligned: this suggests that the distribution of the Cl− over the membrane surface is not a direct result of interaction with the choline groups, but rather an effect of the field emanating from the metal ion content of the membrane. Such a well defined ion distribution is expected to have a strong influence on membrane properties, in particular phase transition temperatures via increased in-plane cohesion; this was proven by calorimetry measurements using differential scanning calorimetry of suspended liposomes and quartz crystal microbalance-based measurements on supported single bilayer membranes. These findings shed a new light on the role metal ions play in stabilizing biological membranes.
Introduction
Biological membranes exist in an aqueous environment that is rich in small ionic species (Alberts, 2015). There is abundant information about the role of these ions in biochemical processes, their transport across membranes and their role in gating ion channels and maintaining the membrane potential (Cooper, 1997). It is generally assumed that in these processes the phospholipid bilayer itself acts as an inert barrier, not affected by the ions that interact specifically with membrane proteins.
Yet, in model membrane studies ions were found to affect membrane structure and stability. Ca2+ and Mg2+ were shown to promote membrane fusion and permeability (Papahadjopoulos et al., 1977; Newton, 1978; Duzgunes et al., 1981; Brasnett et al., 2017). Alkaline and alkaline earth cations can cause a shift in phase transition temperatures (Garidel and Blume, 1999) and cause transient poration at the phase transition temperature of anionic lipids (Garidel and Blume, 2005; Riske et al., 2009). Sodium halogenide salts have a concentration-dependent effect on the equilibrium size of small unilamellar liposomes of both anionic and zwitterionic lipids (Claessens et al., 2004). Na+ and Ca2+ were shown to increase order, reduce lateral diffusion, and induce stiffening in charged as well as zwitterionic membranes (Garcia-Celma et al., 2007; Pabst et al., 2007; Pokorna et al., 2013). LiCl and KCl cause phase separation in multilamellar vesicles of zwitterionic lipids (Rappolt et al., 2001). Metal ions also affect interlamellar spacing and lamellar thickness in bilayer stacks (Loosley-Millman et al., 1982; Cunningham and Lis, 1989; Sanderson et al., 1991) and this effect is independent of membrane curvature (Kucerka et al., 2017). Vibration spectroscopy results suggest metal interaction with the headgroups alters membrane packing (Binder and Zschornig, 2002); these effects were explained with electrostatic interactions (Binder and Zschornig, 2002; Kucerka et al., 2017), yet, ESR studies with a hydrophobic spin label concluded the absence of any charge interactions between alkali metal cations and the phosphate (or the choline) moiety of the zwitterionic phosphatidylcholine lipid headgroup (Bartucci and Sportelli, 1993). From these reports it is clear that salts affect lipid-lipid interactions that manifest in changes in the measured physical properties, in particular phase transition temperatures, bending rigidity and lipid mobility. However, it is unclear how small ionic species affect lipid-lipid interactions.
The energetic theory of lipid self-assembly rests on the Tanford opposing force model (Tanford, 1974; Israelachvili and Mitchell, 1975). This model was intended to be semi-empirical-the lipid-lipid interaction that holds the membrane intact is estimated via the free energy of the oil-water interface, opposed by chain- and headgroup repulsion (the physical origins of which are not further specified). These two “forces” yield an equilibrium membrane density. Naturally, the model can be easily extended with attractive and repulsive terms derived from actual physical interactions, such as van der Waals attraction between the lipid alkane chains, charge repulsion between the headgroups etc. Hence, an electrostatic curvature free energy extension was developed for the self-assembly theory for charged surfactants based on the Poisson-Boltzmann equation (Evans et al., 1984). This theory also attempted to bridge the two, seemingly contradictory theories of ion adhesion, namely the ion binding model that described ion adhesion in terms of ionic dissociation equilibria and the double layer model that describes ion association with the Stern equations, showing that the first one is essentially an asymptotic case of the second for the case of strong binding (Ninham et al., 2017). This approach raises three important issues. First, the incompatibility of the models: in the double layer case, the ions respond to the overall membrane charge, that is, they are not penetrating the membrane but stay on the surface; while in the ion binding model, they attach to the charged moieties within the headgroup zone. Second, the ionic effects manifest as attractive force only in a curvature tension term, that is, in micelles and curved membranes. If applied to a lamellar membrane, the net effect may become repulsive, as the ions can be closer to each other than any of the charged headgroup moieties, at least in case of DDAB bilayers where this effect was studied (Dubois et al., 1998). Third, these models were developed for charged surfactants, and hence not applicable to neutral membranes. Yet, the adsorption of ions to zwitterionic membranes was also studied in the 1970s where NMR headgroup perturbation and zeta potential measurements have provided ample evidence of the presence of ionic double layers that can be described with the Stern equations (Mclaughlin et al., 1978). Furthermore, the predicted weak effect on lamellar membranes is inconsistent with reports of changes in lipid order, mobility and phase transition temperatures.
Previous computational studies attempting to locate the ions in the membrane yielded results seemingly in contradiction to the theories outlined above (Bockmann et al., 2003; Gurtovenko and Vattulainen, 2008; Vacha et al., 2009; Vernier et al., 2009). Depending on the type of force field used, sodium ions were found to penetrate the membrane, co-localizing with either the carbonyl (Bockmann et al., 2003; Gurtovenko and Vattulainen, 2008) or the phosphate (Vacha et al., 2009) moieties. While sodium ions were found to penetrate the membrane, potassium and cesium ions did not; chloride ions remained in the aqueous phase while iodide ions penetrated the membrane (Vacha et al., 2009). Earlier studies interpreted the distribution as a double layer (Bockmann et al., 2003; Gurtovenko and Vattulainen, 2008), whereas Vacha et al. noted that neither CsCl nor KCl formed a double layer (Vacha et al., 2009). While arguing for a dominant role for electrostatics, these results were ambiguous regarding the role of charge interactions, suggesting instead a diffusion driven, size limited process. Yang et al. suggested coordination as the mechanism of lipid-metal interaction based on free energy calculations (Yang et al., 2015). Overall, these studies could not provide a decisive explanation for the role of small ionic species in the membrane. Given that computational methods, resources and force fields have undergone a dramatic improvement in the past decade, there is an impetus to perform simulations of membrane-ion interactions based on these improved understanding.
In this work the distribution of Na+, Mg2+, Ca2+, and Cl− ions in DMPC model membranes was studied by computer modeling and calorimetric experiments. Evidence is provided that the cations penetrate the membrane and coordinate to the lipid head groups, whereas the counterions stay on the surface of the membrane. Experimental results show that the salts affect the phase transition temperature and viscosity of DMPC membranes.
Materials and Methods
Membrane Preparation
1,2-Dimyristoyl-sn-glycero-3-phosphocholine (DMPC) was purchased from Avanti Polar Lipids (Alabaster, AL, USA) and chloroform (ACS reagent, 99.8%) was from Sigma Aldrich (Castle Hill, NSW, Australia). Calcium chloride dihydrate (CaCl2.2H2O), magnesium chloride hexahydrate (MgCl2.6H2O) were purchased from Sigma-Aldrich and sodium chloride (NaCl) was obtained from Chem Supply Pty Ltd (Australia). Lyophilized lipids were dissolved in chloroform. To prepare membranes, 10 μmol of DMPC was measured into round bottom test tubes and the chloroform was evaporated using N2 gas and dried overnight. Liposomes were formed by hydrating the lipid layers in salt solutions (NaCl, MgCl2, CaCl2) of different concentrations.
Differential Scanning Calorimetry and Quartz Crystal Microbalance Measurements of Phase Transitions
SETARAM μDSC Evo3 instrument was used to perform Differential Scanning Calorimetry (DSC) experiments with hastelloy pressure cells loaded with 650 μl lipid suspension; pure buffer was used as reference. Three zones were recorded for each measurement. Heating-cooling temperature profiles were set up for the 10°-30°C range at a rate of 0.3 K min−1.
QSense E4 Quartz Crystal Microbalance (QCM) system (Q-Sense, Sweden; now owned by Biolin Scientific) was used to monitor the deposition of lipids in buffer solution. Gold coated AT-cut 5 MHz quartz sensor chips were used in all experiments. The quartz chips were cleaned in base piranha solution: H2O2 (30% solution): H2O: NH4OH (28% solution) in a ratio 1:3:1 at 70°C. The chips were then washed with ultrapure water and propane-2-ol and dried with nitrogen gas. For functionalization suitable for membrane deposition, the chips were immersed into a 2% solution of 3-mercaptopropionic acid (MPA) in propan-2-ol for 2 h. The chips were then immersed in propan-2-ol for approximately 6 min and dried with nitrogen gas. During the QCM experiments water was first introduced into the chamber to hydrate the MPA layer and then assay solutions were introduced. Single bilayer membranes were formed using the liposome deposition method from the respective salt solution following a protocol established before (Mechler et al., 2009; Hasan and Mechler, 2015). The method for determining phase transition temperatures from QCM data was described previously (Hasan and Mechler, 2016) and is briefly summarized in the Supplementary Information. An example is shown in Supplementary Figure 1.
Computer Simulations
The initial coordinates of solvated lipid containing 128 DMPC and 4038 (TIP3) water molecules was downloaded from the Automated Topology Builder (ATB) Repository version 1.2 website (Poger and Mark, 2010; Malde et al., 2011); this system had been equilibrated for 235.0 ns at 303.0 K, and had a nicely formed bilayer structure. The number of water and lipids lies in a range where the bilayer structure is independent of the ratio between water and lipid (Janiak et al., 1979). Ions were added to deliver a final ionic strength of either 0.10 or 1.0 M; for example, the simulation of 1 M CaCl2 included 128 DMPC, 3819 water molecules, 73 Ca2+ cations and 146 Cl− anions.
All simulations used the Gromos53a6 force field. In this force field, the DMPC molecule is represented using a “united atom” description; therefore, hydrogen atoms attached to carbon atoms are treated implicity (Oostenbrink et al., 2004); thus, the DMPC molecule consists 46 atoms, as illustrated in Figure 1. All simulations used the Gromacs (vers. 4.6.1) package (Hess et al., 2008). Lipid and solvent (including ions) were coupled separately to a thermal bath employing velocity rescaling (Bussi et al., 2007) with coupling time 1.0 ps. Simulations were conducted for 3 different temperatures, 273, 293, and 303 K. Pressure was maintained at 1 bar using a semi-isotropic Berendsen barostat (Berendsen et al., 1984) with coupling constant 5.0 ps; in the plane of the lipid the compressibility was set to 9.0 × 10−5 bar, representative of the alkane chain of the lipid tail (Blinowska and Brostow, 1975), while perpendicular to the lipid plane the compressibility was set to 4.5 × 10−5 bar, representative of the water environment. The time step was 2 fs. Simulations were performed with a single non-bonded cutoff of 10 Å and neighbor-list update frequency of 10 steps (20 fs). The PME method modeled long-range electrostatics (Essmann et al., 1995); the grid width was 1.2 Å with fourth-order spline interpolation. Bond lengths were constrained using LINCS (Hess, 2008). The MD protocol consisted of an initial minimization of water molecules, followed by 100 ps of MD with the lipid restrained to permit equilibration of the solvent. Calculations were continued for 650 ns from the geometries obtained after initial positionally restrained MD.
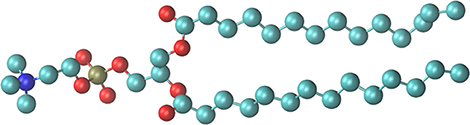
Figure 1. The DMPC model used for the simulations. Oxygen atoms are colored red, the phosphorous gold and nitrogen of the choline group blue.
Statistical Analysis of the Computational Results
Statistical analysis of the chemical environment of the cations was performed in each case following equilibration of the system. The final 100 frames of the simulation, totalling 5 ns, were analyzed. Each cation was located in the frames and the nearest Lewis base (oxygen atoms of the water molecules, ester and phosphate moieties of the lipids) atoms within a 0.3 nm cutoff were identified. The number of oxygen atoms within the cutoff provided the coordination number. This analysis was performed for Na+, Ca2+, and Mg2+ ions at three different temperatures: 273, 293, and 303 K, representing Lc, Pβ, and Lα phases of the membrane, respectively.
Results
Modeling Results
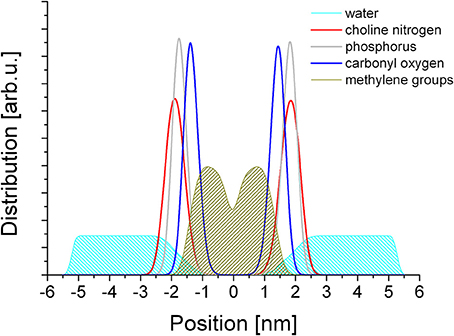
The simulations yielded a well equilibrated system in each case, where the statistical distribution of the metal ions and the geometry of the lipid molecules did not show any further change over time. Representative snapshots of the final frames of simulations for each metal ion are shown in Supplementary Figure 1. The distribution of the chemically distinct moieties of the lipid molecules, the water molecules and the metal ions were determined in reference to the inter-leaflet gap of the membrane that forms a smooth, well defined plane in each case. The distributions are shown in Figure 2.
From Figure 2 it is apparent that the headgroup zone as measured between the peak maxima of the choline (navy blue) and the ester (red) moieties spans a distance of ~5 Å. However, the distributions of the choline and phosphate groups effectively overlap, with a very small difference that is much less than the distance between the two in a linear molecule. This suggests that the headgroup is typically not linear but bent, with the two charged moieties situated in nearly the same plane, consistent with literature data on headgroup dipole orientation (Vernier et al., 2009). If the zwitterion dipole is horizontal, the dominant interaction with any chemical species in the aqueous phase is that of a rotating dipole, a net attractive interaction. The lipid conformation is disordered, as reflected in the distribution of the methylene groups that make up the alkane chains (Figure 2, olive). The distribution away from the center of the bilayer reaches well into the distribution of the ester groups, suggesting that the spatial orientation of the glycerol backbone is not well defined and that the alkane chains themselves have considerable freedom to have multiple trans/gauche conformations between the methylene groups. The distribution has a dip at the geometrical center of the bilayer that suggests very limited, if any, intercalation between the opposing leaflets, raising the possibility of leaflet slippage. Water penetration into the membrane is relatively deep: water molecules reach slightly below the ester moieties; however no water molecules enter the hydrophobic core.
The distribution of the ions follows a similar trend for the three salts studied here (Figure 3). In each case, the cations are found within the headgroup zone, co-localizing with either of the ester or the phosphate moieties, the former characteristic of Ca2+ (Figure 3A) and Na+ (Figure 3C) while the latter of Mg2+ (Figure 3B) species. Considering the fractioning of the cations between the bulk aqueous phase and the membrane, Ca2+ and Mg2+ are almost exclusively found in the membrane, suggesting permanent binding, whereas Na+ ions are also present in the aqueous phase in an equilibrium distribution. In contrast, the anions do not penetrate the membrane. In each case the Cl− ions form a layer over the membrane surface, corresponding to the cation concentration in the membrane, i.e., in case of Ca2+ most of the Cl− ions are found in this layer whereas in case of Na+ the layer is much less defined and the bulk concentration of the two ions is equal as expected.
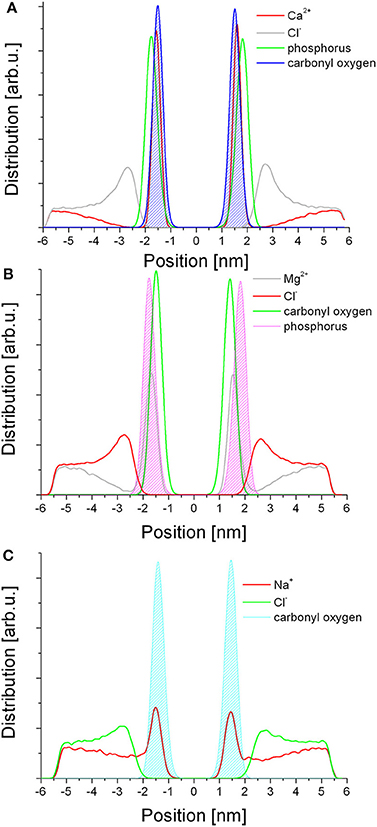
Figure 3. Distribution of the ionic species in relation to selected lipid moieties in each respective simulation. (A) Ca2+; (B) Mg2+; (C) Na+.
The Chemical Environment of the Metal Cations
Statistical analysis of the chemical environment of the cations was performed by locating each ion and identifying all chemical species within a 0.3 nm radius. When identifying molecules that contribute to the coordination shell, the ability to form dative bonds was also considered; of the chemical species present, the oxygen atoms of the water molecules and the ester and phosphate moieties of the lipid molecules are able to donate electron pairs. Consistently the nearest atoms in the coordination shells are the oxygen atoms of said moieties. The results are summarized in Table 1. The simulations have accurately reproduced the coordination shells formed around the cations, including known coordination numbers and geometries of each metal. The focus of the analysis was the membrane bound state where the metals coordinate to at least one of the lipid moieties. For Na+ the dominant coordination number is 6 at all temperatures. At 273 K (Lc phase membrane) the coordination shell of the membrane bound ions includes three carbonyl oxygen atoms of the ester moiety, which is reduced to two at 303 K (Lα phase). Hence Na+ appears to crosslink the lipid molecules, however, the general distribution as shown in Figure 3 suggests that the membrane bound state is in dynamic equilibrium with the bulk ionic concentration, i.e., the coordination bonds are weak and reversible. For Ca2+ 7 and 8 coordinate ions are found at all temperatures. The dominant coordination number is 8 at 273 K, 7 at 293 K, and 303 K, with the population of 8-coordinate ions increasing slightly in the latter. At all temperatures the coordination shell of the membrane bound ions includes 3–4 carbonyl oxygen atoms of the ester moiety of adjacent lipid molecules. Mg2+ ions are dominantly 5-coordinate with a fraction of coordination number 6 that is more substantial at 273 K but much reduced at 293 K and 303 K. Mg2+ appears to only coordinate to one lipid molecule at a time, to the phosphate moiety. There are populations of each metal with lesser coordination numbers that are likely transition states.
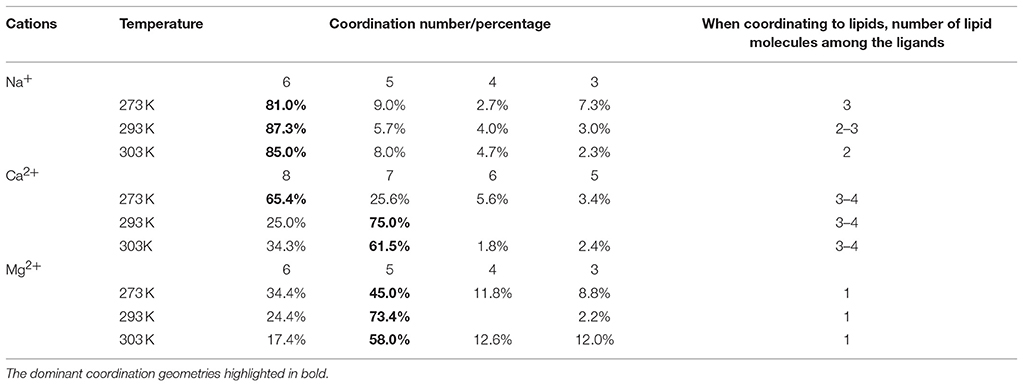
Table 1. Quantitative analysis of the chemical environments of the metal ions in the computational results.
Figure 4 shows examples of the coordination shells of each metal. An important feature of these snapshots is that water molecules of the coordination shell appear to be hydrogen bonding to oxygen atoms of the phosphate and the ester moieties of adjacent lipid molecules; this is most prominent in case of Mg2+. These observations imply that the bond energies of the metals crosslinking the lipid molecules would contribute to the overall internal energy of the membrane and thus the addition of metal ions has to increase the phase transition temperatures of the membranes. This allows for indirect experimental confirmation of the results.
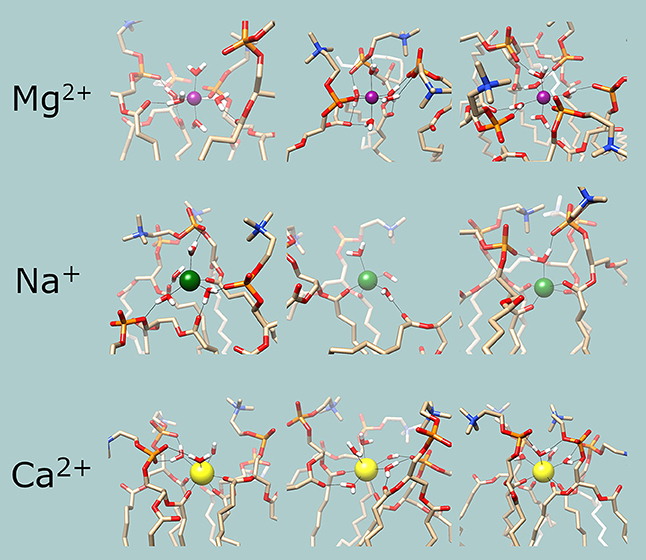
Figure 4. Examples of the chemical environments of the cations. Magenta: Mg2+; green: Na+; yellow: Ca2+. In the lipid and water molecules, oxygen is red, nitrogen is blue, phosphorous is orange and hydrogen is white. Hydrogen and coordination bonds are identified from distance and are indicated with thin black lines.
Phase Transition Measurements
Phase transition measurements were performed with DSC as well as QCM. The latter method is based on measuring changes in viscosity and has been demonstrated to be highly precise in determining phase transitions in single bilayer membranes. Comparison of the two methods allows the separation of curvature effects from the metal crosslinking effects on the phase transition. Examples of individual measurements are shown in Supplementary Figure 2 (QCM) and Supplementary Figure 3 (DSC). The results are summarized in Figure 5. It is clear that both divalent cations have a strong, concentration dependent effect on the main transition temperature of DMPC membranes. Ca2+ increased phase transition the most, consistent with the coordination to 3–4 lipid molecules. Mg2+, while it only coordinates to a single lipid directly, also had a strong effect due to the hydrogen bonds formed by the water molecules in the coordination shell to oxygens of the phosphate moieties of adjacent lipid molecules. The concentration dependence of the phase transition temperature reflects a dynamic equilibrium between the membrane bound and solvated metal ions. The increasing bulk cation concentration leads to increased metal content in the membrane; hence the binding energy contribution of the metal coordination to the membrane stability is increasing proportionally. This in turn increases the phase transition temperature. Consistently, the effect of Na+ was the weakest, as expected from the distribution between the aqueous and membrane bound state in the simulations. It is notable that in DSC measurements sodium had a largely concentration independent effect; in contrast QCM revealed a weak concentration dependent effect in the low concentration regime, consistent with increased lateral interaction with increasing Na+ presence within the membrane. The difference can be traced back to geometry factors; in DSC measurement using liposomes, curvature tension also affects the phase transition temperature (Hasan and Mechler, 2017), while in the “tensionless” lamellar membrane, as in the QCM measurements, the lateral interactions dominate. A difference, not in trend but in quantitative terms, is also present in the case of the two divalent cations, manifesting as an offset between the values measured with DSC and QCM.
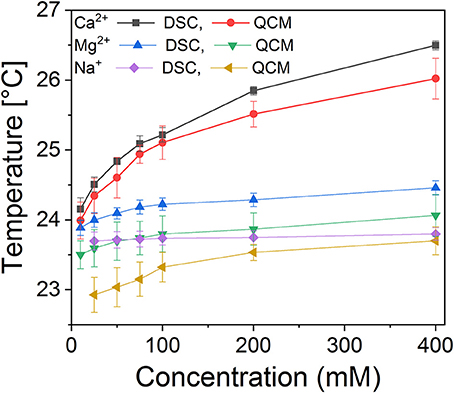
Figure 5. Calorimetric measurements of the main transition temperatures of DMPC membranes as a function of salt concentration, measured using DSC (suspended liposomes) and QCM surface calorimetry (supported single bilayer membrane).
Discussion
One of the key observations from the simulations is that no water molecules enter the hydrophobic core. Early theories of surfactant self-assembly postulated that the membrane has to be freely transferable to water molecules to allow for a pathway of liposome size relaxation (Finkelstein, 1976; Haran and Shporer, 1976; Tanford, 1979). Experimental observations of osmotic swelling of liposomes support this view (Chabanon et al., 2017). Yet, it was estimated that the energy cost of transporting a water molecule across an intact membrane is prohibitively high at room temperature (Porada et al., 2018), and hence the likely mechanism of water transfer is via transient pores as suggested earlier (Volkov et al., 1997). The results of our simulations are consistent with this latter view.
The presence of the metal cations in the headgroup zone of the membrane, as predicted by the simulations, is consistent with former computational studies (Bockmann et al., 2003; Gurtovenko and Vattulainen, 2008; Vacha et al., 2009), however not generally accepted in the field: it is believed that the metal cations cannot enter the membrane due to the size of their hydration shells (Claessens et al., 2007). Our results also clearly identify metal coordination, and not electrostatic interactions, as the mechanism of cation retention in the membrane, as suggested recently (Yang et al., 2015). Metal coordination is consistent with the concentration-dependent increase in the phase transition temperature as measured with DSC and QCM. It was shown before that the chain melting temperature is defined by the van der Waals interactions between the alkane chains of the lipid molecules (Hasan and Mechler, 2017), while the contribution of the headgroups is believed to be repulsive as per the Tanford model. The double layer forces introduced by Evans et al. (1984) act against the curvature of the membrane, but diminish in the plane. Hence, the observed increase in the phase transition temperature in the supported single bilayers is a conclusive evidence of a strong lateral interaction between the headgroups in the presence of the ions, consistent with the predicted coordination. This also explains the reported effect of the ionic environment on the size of PC liposomes, where charged and zwitterionic liposomes exhibited very similar size trend as a function of salt concentration, albeit the trendline started at somewhat higher salt concentrations for PC vesicles (Claessens et al., 2004), as well as the reported changes in lipid order and mobility in the presence of cations (Garcia-Celma et al., 2007; Pabst et al., 2007; Pokorna et al., 2013).
It is important to note that in case of magnesium the small size of the ion prohibits direct headgroup-to-headgroup coordination, and thus Mg2+ retains most of its hydration shell, replacing only one water molecule with a phosphate oxygen. However, the water-mediated crosslinking that is observed in the simulations is clearly observed in the increased phase transition temperatures in this case as well. Sodium is a weak Lewis acid, and hence it forms the least stable coordination shell, maintaining a dynamic equilibrium between the membrane bound and the aqueous phase; consistently the presence of sodium has very weak effect on the phase transition temperature. The coordination numbers of the cations in the simulations are consistent with the known coordination properties of these metals (Cordomi et al., 2009). The preference of Ca2+ and Na+ to bind to the ester moiety, while Mg2+ to the phosphate group, is consistent with the HSAB model where Ca2+ is the softest Lewis acid and Mg2+ is the weakest of the three, whereas carbonyl oxygens are softer Lewis bases than the oxygens of the phosphate group. Metal-specific coordination effects also offer a simple explanation to the radically different effect of different cations on surfactant packing as observed empirically (Kachar et al., 1984; Evans et al., 1985; Karaman et al., 1994).
In contrast to the cations, Cl− ions do not enter the membrane, and do not show any association to the cationic choline moieties, as the Coulombic interactions are much attenuated in the aqueous environment; however they might respond to the field emanating from the net positive charge of the membrane due to metal binding, forming a pseudo double layer with the coordinated ions. The sequestration of Cl− ions to the membrane surface could also result from the depletion of the counterions in the bulk of the solution.
These results potentially bridge and broaden the two models explaining the role of ions on surfactant self-assembly (Ninham et al., 2017). In the double layer model the presence of the ions contribute to the attractive forces, compressing the membrane together, opposed by headgroup hydration and chain repulsion (Fragata et al., 1997). Considering the distribution of the cations and the anions, a double layer does indeed exist in the zwitterionic membrane; however it is not formed in response to a charged surface, rather by the immobilization of the cations through coordination effect. On the other hand, the ion binding model assumes equilibrium between the charged surfactant molecules and their counterions; this model can be extended to zwitterionic membranes if the equilibrium is formed, as particularly clear in case of Na+, between coordinated and solution phase metal ions. Hence, as in case of the expression derived for charged membranes (Evans et al., 1984), the two models have a continuous transition in the coordination strength: the more permanent is the metal binding, the more dominant double layer effects become.
Conclusions
Computer simulation and experimental data was used to describe the role of simple salts in membrane stability. It was found that the cations penetrate the headgroup zone, coordinating to Lewis bases in accordance to their hardness, and not via Coulombic interactions. The binding energy contribution to lipid-lipid interaction manifests in increased phase transition temperature as confirmed with classical calorimetry methods in liposome suspensions as well as by using viscosity-based surface calorimetry on single bilayer membranes. The results suggest that the extended Tanford/IMN (opposing force) model of charged membrane stability in an ionic environment can be applied to neutral membranes where coordination effects replace charge interactions.
Data Availability Statement
The raw experimental data supporting the conclusions of this manuscript will be made available by the authors, without undue reservation, to any qualified researcher. The computational datasets are not publicly available because they are subjected to further data mining that may form the basis of further publications. Requests to access the datasets should be directed to the corresponding author.
Author Contributions
CL has conducted the computer simulations under guidance from BS. NB performed analysis of the dataset to identify coordination numbers and performed some of the preliminary experimental work. AH has performed experiments with DSC and QCM and contributed to manuscript writing. AM has devised and supervised the project, analyzed the data and written the manuscript in consultation with BS.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
AH acknowledges his Ph.D. scholarship from The Higher Committee for Education Development in Iraq (HCED).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2018.00080/full#supplementary-material
References
Alberts, B. (2015). Molecular Biology of the Cell. New York, NY: Garland Science, Taylor and Francis Group.
Bartucci, R., and Sportelli, L. (1993). ESR investigation on the phase-transitions of DPPC vesicles in presence of high-concentrations of Li+, Na+, K+ and Cs+. Colloid Polym. Sci. 271, 262–267. doi: 10.1007/BF00652366
Berendsen, H. J. C., Postma, J. P. M., Vangunsteren, W. F., Dinola, A., and Haak, J. R. (1984). Molecular-dynamics with coupling to an external bath. J. Chem. Phys. 81, 3684–3690. doi: 10.1063/1.448118
Binder, H., and Zschornig, O. (2002). The effect of metal cations on the phase behavior and hydration characteristics of phospholipid membranes. Chem. Phys. Lipids 115, 39–61. doi: 10.1016/S0009-3084(02)00005-1
Blinowska, A., and Brostow, W. (1975). Experimental volumetric properties of liquid n-alkanes and their binary mixtures. J. Chem. Thermodyn. 7, 787–794. doi: 10.1016/0021-9614(75)90255-4
Bockmann, R. A., Hac, A., Heimburg, T., and Grubmuller, H. (2003). Effect of sodium chloride on a lipid bilayer. Biophys. J. 85, 1647–1655. doi: 10.1016/S0006-3495(03)74594-9
Brasnett, C., Longstaff, G., Compton, L., and Seddon, A. (2017). Effects of cations on the behaviour of lipid cubic phases. Sci. Rep. 7, 8229. doi: 10.1038/s41598-017-08438-4
Bussi, G., Donadio, D., and Parrinello, M. (2007). Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101. doi: 10.1063/1.2408420
Chabanon, M., Ho, J. C. S., Liedberg, B., Parikh, A. N., and Rangamani, P. (2017). Pulsatile lipid vesicles under osmotic stress. Biophys. J. 112, 1682–1691. doi: 10.1016/j.bpj.2017.03.018
Claessens, M., Leermakers, F. A. M., Hoekstra, F. A., and Stuart, M. A. C. (2007). Opposing effects of cation binding and hydration on the bending rigidity of anionic lipid bilayers. J. Phys. Chem. B 111, 7127–7132. doi: 10.1021/jp070066h
Claessens, M., Van Oort, B. F., Leermakers, F. A. M., Hoekstra, F. A., and Stuart, M. A. C. (2004). Charged lipid vesicles: effects of salts on bending rigidity, stability, and size. Biophys. J. 87, 3882–3893. doi: 10.1529/biophysj.103.036772
Cooper, G. M. (1997). The Cell : A Molecular Approach. Washington, DC; Sunderland, MA.: ASM Press; Sinauer Associates.
Cordomi, A., Edholm, O., and Perez, J. J. (2009). Effect of force field parameters on sodium and potassium ion binding to dipalmitoyl phosphatidylcholine bilayers. J. Chem. Theory Comput. 5, 2125–2134. doi: 10.1021/ct9000763
Cunningham, B. A., and Lis, L. J. (1989). Interactive forces between phosphatidylcholine bilayers in mono-valent salt-solutions. J. Colloid Interface Sci. 128, 15–25. doi: 10.1016/0021-9797(89)90380-9
Dubois, M., Zemb, T., Fuller, N., Rand, R. P., and Parsegian, V. A. (1998). Equation of state of a charged bilayer system: measure of the entropy of the lamellar-lamellar transition in DDABr (vol 108, pg 7855, 1998). J. Chem. Phys. 109, 8731–8731. doi: 10.1063/1.477540
Duzgunes, N., Wilschut, J., Fraley, R., and Papahadjopoulos, D. (1981). Studies on the mechanism of membrane-fusion-role of headgrop composition in calcium-induced and magnesium-induced and magnesium-induced fusion of mixed phospholipd-vesicles. Biochim. Biophys. Acta 642, 182–195. doi: 10.1016/0005-2736(81)90148-6
Essmann, U., Perera, L., Berkowitz, M. L., Darden, T., Lee, H., and Pedersen, L. G. (1995). A smooth particle mesh ewald method. J. Chem. Phys. 103, 8577–8593. doi: 10.1063/1.470117
Evans, D. F., Brady, J., Kachar, B., and Ninham, B. W. (1985). Video enthanced differntial interference contrast microscopy-charactterizing colloidal materials. J. Solut. Chem. 14, 141–152. doi: 10.1007/BF00647060
Evans, D. F., Mitchell, D. J., and Ninham, B. W. (1984). Ion binding and dressed micelles. J. Phys. Chem. 88, 6344–6348. doi: 10.1021/j150669a057
Finkelstein, A. (1976). Water and nonelectrolyte of lipid bilayer membarnes. J. Gen. Physiol. 68, 127–135. doi: 10.1085/jgp.68.2.127
Fragata, M., Bellemare, F., and Nenonene, E. K. (1997). Mg(II) adsorption to a phosphatidylglycerol model membrane studied by atomic absorption and FT-IR spectroscopy. J. Phys. Chem. B 101, 1916–1921. doi: 10.1021/jp962426z
Garcia-Celma, J. J., Hatahet, L., Kunz, W., and Fendler, K. (2007). Specific anion and cation binding to lipid membranes investigated on a solid supported membrane. Langmuir 23, 10074–10080. doi: 10.1021/la701188f
Garidel, P., and Blume, A. (1999). Interaction of alkaline earth cations with the negatively charged phospholipid 1,2-dimyristoyl-sn-glycero-3-phosphoglycerol: a differential scanning and isothermal titration calorimetric study. Langmuir 15, 5526–5534. doi: 10.1021/la990217a
Garidel, P., and Blume, A. (2005). 1,2-Dimyristoyl-sn-glycero-3-phosphoglycerol (DMPG) monolayers: influence of temperature, pH, ionic strength and binding of alkaline earth cations. Chem. Phys. Lipids 138, 50–59. doi: 10.1016/j.chemphyslip.2005.08.001
Gurtovenko, A. A., and Vattulainen, I. (2008). Effect of NaCl and KCl on phosphatidylcholine and phosphatidylethanolamine lipid membranes: insight from atomic-scale simulations for understanding salt-induced effects in the plasma membrane. J. Phys. Chem. B 112, 1953–1962. doi: 10.1021/jp0750708
Haran, N., and Shporer, M. (1976). Study of water permeability through phospholipid vesicle membranes by 17O NMR. Biochim. Et Biophys. Acta 426, 638–646, doi: 10.1016/0005-2736(76)90128-0.
Hasan, I. Y., and Mechler, A. (2015). Viscoelastic changes measured in partially suspended single bilayer membranes. Soft Matter 11, 5571–5579. doi: 10.1039/C5SM00278H
Hasan, I. Y., and Mechler, A. (2016). Cholesterol rich domains identified in unilamellar supported biomimetic membranes via nano-viscosity measurements. Anal. Chem. 88, 5037–5041. doi: 10.1021/acs.analchem.6b01045
Hasan, I. Y., and Mechler, A. (2017). Nanoviscosity measurements revealing domain formation in biomimetic membranes. Anal. Chem. 89, 1855–1862. doi: 10.1021/acs.analchem.6b04256
Hess, B. (2008). P-LINCS: a parallel linear constraint solver for molecular simulation. J. Chem. Theory Comput. 4, 116–122. doi: 10.1021/ct700200b
Hess, B., Kutzner, C., Van Der Spoel, D., and Lindahl, E. (2008). GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 4, 435–447. doi: 10.1021/ct700301q
Israelachvili, J. N., and Mitchell, D. J. (1975). A model for the packing of lipids in bilayer membranes. Biochim. Biophys. Acta 389, 13–19. doi: 10.1016/0005-2736(75)90381-8
Janiak, M. J., Small, D. M., and Shipley, G. G. (1979). Temperature and compositional dependence of the structure of hydrated dimyristoyl lecithin. J. Biol. Chem. 254, 6068–6078.
Kachar, B., Evans, D. F., and Ninham, B. W. (1984). Video enhanced differential interference contrast miscroscopy-a new tool for the study of association of colloids and prebiotic assemblies. J. Colloid Interface Sci. 100, 287–301. doi: 10.1016/0021-9797(84)90436-3
Karaman, M. E., Ninham, B. W., and Pashley, R. M. (1994). Some aqueous solution and surface properties of dialkyl sulfosuccinate surfactants. J. Phys. Chem. 98, 11512–11518. doi: 10.1021/j100095a036
Kucerka, N., Dushanov, E., Kholmurodov, K. T., Katsaras, J., and Uhrikova, D. (2017). Calcium and zinc differentially affect the structure of lipid membranes. Langmuir 33, 3134–3141. doi: 10.1021/acs.langmuir.6b03228
Loosley-Millman, M. E., Rand, R. P., and Parsegian, V. A. (1982). Effects of mono-valent ion binding and screening on measured electrostatic forces between charged phospholipid-bilayers. Biophys. J. 40, 221–232. doi: 10.1016/S0006-3495(82)84477-9
Malde, A. K., Zuo, L., Breeze, M., Stroet, M., Poger, D., Nair, P. C., et al. (2011). An automated force field topology builder (ATB) and repository: version 1.0. J. Chem. Theory Comput. 7, 4026–4037. doi: 10.1021/ct200196m
Mclaughlin, A., Grathwohl, C., and Mclaughlin, S. (1978). Adsorption of divalent cations to phosphatidylcholine bilayer membranes. Biochim. Biophys. Acta 513, 338–357. doi: 10.1016/0005-2736(78)90203-1
Mechler, A., Praporski, S., Piantavigna, S., Heaton, S. M., Hall, K. N., Aguilar, M. I., et al. (2009). Structure and homogeneity of pseudo-physiological phospholipid bilayers and their deposition characteristics on carboxylic acid terminated self-assembled monolayers. Biomaterials 30, 682–689. doi: 10.1016/j.biomaterials.2008.10.016
Newton, C. (1978). Specificity of Ca2+ and Mg2+ binding to phosphatidylserine vesicles and resultant phase changes of bilayer membrane structure. Biochim. Biophys. Acta 506, 281–287. doi: 10.1016/0005-2736(78)90398-X
Ninham, B. W., Larsson, K., and Lo Nostro, P. (2017). Two sides of the coin. Part 1. Lipid and surfactant self-assembly revisited. Colloids Surf. B Biointerfaces 152, 326–338. doi: 10.1016/j.colsurfb.2017.01.022
Oostenbrink, C., Villa, A., Mark, A. E., and Van Gunsteren, W. F. (2004). A biomolecular force field based on the free enthalpy of hydration and solvation: the GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 25, 1656–1676. doi: 10.1002/jcc.20090
Pabst, G., Hodzic, A., Strancar, J., Danner, S., Rappolt, M., and Laggner, P. (2007). Rigidification of neutral lipid bilayers in the presence of salts. Biophys. J. 93, 2688–2696. doi: 10.1529/biophysj.107.112615
Papahadjopoulos, D., Vail, W. J., Newton, C., Nir, S., Jacobson, K., Poste, G., et al. (1977). Studies On membrane-fusion. 3. role of calcium-induced phase-changes. Biochim. Et Biophys. Acta 465, 579–598. doi: 10.1016/0005-2736(77)90275-9
Poger, D., and Mark, A. E. (2010). On the validation of molecular dynamics simulations of saturated and cis-monounsaturated phosphatidylcholine lipid bilayers: a comparison with experiment. J. Chem. Theory Comput. 6, 325–336. doi: 10.1021/ct900487a
Pokorna, S., Jurkiewicz, P., Cwiklik, L., Vazdar, M., and Hof, M. (2013). Interactions of monovalent salts with cationic lipid bilayers. Faraday Discuss. 160, 341–358. doi: 10.1039/C2FD20098H
Porada, S., Van Egmond, W. J., Post, J. W., Saakes, M., and Hamelers, H. V. M. (2018). Tailoring ion exchange membranes to enable low osmotic water transport and energy efficient electrodialysis. J. Memb. Sci. 552, 22–30. doi: 10.1016/j.memsci.2018.01.050
Rappolt, M., Pabst, G., Amenitsch, H., and Laggner, P. (2001). Salt-induced phase separation in the liquid crystalline phase of phosphatidylcholines. Colloids Surf. Physicochem. Eng. Aspects 183, 171–181. doi: 10.1016/S0927-7757(01)00568-4
Riske, K. A., Amaral, L. Q., and Lamy, M. T. (2009). Extensive bilayer perforation coupled with the phase transition region of an anionic phospholipid. Langmuir 25, 10083–10091. doi: 10.1021/la9012137
Sanderson, P. W., Lis, L. J., Quinn, P. J., and Williams, W. P. (1991). The hofmeister effect in relation to membrane lipid phase-stability. Biochim. Biophys. Acta 1067, 43–50. doi: 10.1016/0005-2736(91)90024-3
Tanford, C. (1974). Thermodynamics of micelle formation-prediction of micelle size and size distribution. Proc. Natl. Acad. Sci. U.S.A. 71, 1811–1815. doi: 10.1073/pnas.71.5.1811
Tanford, C. (1979). Hydrostatic pressure in small phospholipid vesicles. Proc. Natl. Acad. Sci. U.S.A. 76, 3318–3319. doi: 10.1073/pnas.76.7.3318
Vacha, R., Siu, S. W. I., Petrov, M., Boeckmann, R. A., Barucha-Kraszewska, J., Jurkiewicz, P., et al. (2009). Effects of alkali cations and halide anions on the DOPC lipid membrane. J. Phys. Chem. A 113, 7235–7243. doi: 10.1021/jp809974e
Vernier, P. T., Ziegler, M. J., and Dimova, R. (2009). Calcium binding and head group dipole angle in phosphatidylserine-phosphatidylcholine bilayers. Langmuir 25, 1020–1027. doi: 10.1021/la8025057
Volkov, A. G., Paula, S., and Deamer, D. W. (1997). Two mechanisms of permeation of small neutral molecules and hydrated ions across phospholipid bilayers. Bioelectrochem. Bioenerget. 42, 153–160. doi: 10.1016/S0302-4598(96)05097-0
Keywords: phospholipid, bilayer membrane, ionic environment, metal coordination, phase transition, computer simulations, calorimetry
Citation: Le CTM, Houri A, Balage N, Smith BJ and Mechler A (2019) Interaction of Small Ionic Species With Phospholipid Membranes: The Role of Metal Coordination. Front. Mater. 5:80. doi: 10.3389/fmats.2018.00080
Received: 29 May 2018; Accepted: 14 December 2018;
Published: 07 January 2019.
Edited by:
Nam-Joon Cho, Nanyang Technological University, SingaporeReviewed by:
Christian Douglas Lorenz, King's College London, United KingdomHock Jin Quah, University of Science, Malaysia
Copyright © 2019 Le, Houri, Balage, Smith and Mechler. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adam Mechler, YS5tZWNobGVyQGxhdHJvYmUuZWR1LmF1
 Chanh Thi Minh Le
Chanh Thi Minh Le Aamd Houri
Aamd Houri Nimalka Balage
Nimalka Balage Brian J. Smith
Brian J. Smith Adam Mechler
Adam Mechler