Prima Anugerahanti
Shovonlal Roy
Keith Haines- 1Department of Geography and Environmental Science, University of Reading, Reading, United Kingdom
- 2Department of Meteorology and National Centre for Earth Observation, University of Reading, Reading, United Kingdom
Sources of uncertainty in a marine biogeochemical model include input from physical processes and the choice of functional forms representing the strength and dependencies of biogeochemical processes. This study explores characteristic signatures from these uncertainties by generating ensembles from perturbing the biogeochemistry equations and perturbing physical input using a 1-D intermediately-complex model run at five oceanographic stations. Perturbed biogeochemistry ensemble (PBE) produces larger spreads than perturbed physics ensemble (PPE), and distinctly different ensemble variations. Fractions of nitrogen in phytoplankton pool from observations show a larger variability than in any single model-ensemble member, but the PBE spread generally captures this variability, whereas the PPE spread does not. The results show that the PBE method gives a more realistic representation of uncertainty than PPE in our 1D-model setup. Our method needs to be tested in more complex models in order to understand its significance on larger scales.
1. Introduction
Ocean biogeochemical (OBGC) models have been developed to understand how the ocean ecosystem responds to the changes in both the physics and the biogeochemistry (Doney et al., 2012; Yool et al., 2013; Butenschon et al., 2016). Key uncertainties that affect OBGC models include physical processes, with vertical mixing and upwelling of nutrients often poorly known (Doney, 1999; Friedrichs et al., 2006; Sinha et al., 2010), and the various choices for formulating the biological processes such as nutrient uptake, zooplankton grazing, and plankton mortality (Gentleman et al., 2003; Anderson et al., 2010; Adamson and Morozov, 2013). These biological processes are described by functional forms relating them to concentrations of plankton and nutrients, as well as ambient temperature and light availability. Different physical environments can strongly affect simulations of chlorophyll distribution through the water column (Friedrichs et al., 2006), as well as regional distributions of phytoplankton functional types at the surface ocean (Sinha et al., 2010). Spurious vertical velocities that can occur when assimilating physical ocean data into models can also raise nutrient concentrations in the upper water column (Subramanian and Palmer, 2017). Furthermore, when using different physical models, anthropogenic CO2 uptake can vary between 25 and 30% (Doney et al., 2004). The structure of an OBGC model, especially the choice of the functional representation of biogeochemical processes, strongly determine the model dynamics (Edwards and Yool, 2000; Fussmann and Blasius, 2005). For example, when the grazing function alone is altered from hyperbolic to sigmoidal (both of which are common in the literature) three times higher phytoplankton concentrations can been produced (Anderson et al., 2010). Impacts of altering mortality are shown in both uncoupled Nutrient-Phytoplankton-Zooplankton (NPZ) models (Steele and Henderson, 1992; Edwards and Yool, 2000) and coupled OBGC models (Yool et al., 2011). Choosing a linear mortality, can double the diatom biomass at high latitudes, compared to using other functions (Yool et al., 2011). So the uncertainties arising from both physical and biogeochemical formulations may contribute to discrepancies between the models and observations (Allen et al., 2010; Anderson, 2010).
One way of accounting for these multiple sources of uncertainty is to move away from deterministic simulations toward ensemble results which can be designed to deliver a probability distribution of outcomes. Perturbed physics ensembles have, for example been used to estimate the uncertainties of climate projections (Tinker et al., 2015; Subramanian and Palmer, 2017) or to forecast the climate probabilistically (Murphy et al., 2007; Tebaldi and Knutti, 2007). Ensembles are also regularly used to quantify uncertainties in data assimilation applications (Anderson, 2001; Moradkhani and Meskele, 2010; Roy et al., 2012) to allow weighting of model results compared with new observations.
Recently, Anugerahanti et al. (2018) has introduced an approach for generating an ensemble of an OBGC model by perturbing its core biogeochemistry processes. Here we extend the study of Anugerahanti et al. (2018), to decouple and compare the variability that may arise in an intermediately complex 1-D OBGC model from both biology and physics uncertainties, by generating three sets of ensembles perturbing: (i) the biogeochemistry, by altering the choice of functional forms (perturbed biogeochemistry ensemble, PBE), (ii) the physics, by adding noise to the vertical velocity, mixed layer depth (MLD) and therefore the vertical diffusivity coefficient, supplying nutrients to the surface layers (perturbed physics ensemble, PPE), and (iii) both the biogeochemistry and physics together (perturbed biogeochemistry and physics ensemble, PBPE). Since the OBGC model behavior varies across different biogeographical provinces (Kriest et al., 2012), the ensemble is run at five monitored ocean sites ranging from coastal to oligotrophic regions. We quantify the variability generated by the perturbed ensembles, identifying and distinguishing the characteristics from the different biological and physical perturbations based on several biogeochemical property metrics. From these characteristics we can explore how the different perturbations may affect the model dynamics.
This paper is organized as follows: Brief description of the 1-D OBGC model, generating the ensembles, and the description of metrics are explained in section 2. The basic diagnostics of the ensembles which relate to the bulk properties of the model states, followed by the effect of perturbations in vertical distribution of chlorophyll are discussed in section 3.1. The different characteristic signatures of the PBE and PPE are described and discussed in section 3.2. Finally the conclusions of the study are in section 4.
2. Methods
We use the Model of Ecosystem Dynamics, nutrient Utilization, Sequestration, and Acidification (MEDUSA 1.0) (Yool et al., 2011). MEDUSA is an intermediately complex biogeochemical model that has two phytoplankton types (diatoms and non-diatoms), two zooplankton types (mesozooplankton and microzooplankton), and three nutrients (dissolved inorganic nitrogen, silica, and iron), and uses nitrogen as the model currency. The 1-D version of this model is run in the Marine Model Optimization Testbed (MarMOT-1.1) (Hemmings et al., 2015). The physical forcings, such as vertical velocity and solar radiation, are taken from the NEMO-FOAM output (Storkey et al., 2010), with output frequency every 5-days for all of the stations. NEMO-FOAM is a data assimilation product and therefore biases in well observed quantities are small, however for temperature and mixed layer depth (MLD) we introduce an additional bias correction to match the mean seasonal physical conditions observed at the stations. The vertical diffusivity coefficient is matched to the bias corrected MLD. Bias correction is done for all of the stations apart from station PAP where observational data are insufficient, so at PAP we use unadjusted NEMO-FOAM output. The MEDUSA ensembles are run from 1 January 1998 to 31 December 2007, with output produced everyday, at five different oceanographic stations; oligotrophic [represented by stations BATS (32°50'N, 64°10'W) and ALOHA (22°45'N, 158°00'W)], coastal [represented by stations Cariaco (10°30'N, 64°40'W) and L4 (50°15'N, 4°12.3'W)], and abyssal plain [represented by station PAP (49°N, 16.5°W)]. Further information about running MEDUSA and a map of the station locations can be found in the Supplementary Section 1.
2.1. Generating the Ensembles
We generate the PBE by altering the equivalent functional forms for key biogeochemical processes. In the previous study (Anugerahanti et al., 2018) we used all possible functional form combinations, generally used in literature to describe four key processes; nutrient uptake, phytoplankton, and zooplankton mortalities, and zooplankton grazing. The functional forms for phytoplankton nutrient uptake are Monod (Uh), which is the default function, exponential (Ue), sigmoidal (Us), and trigonometric (Ut). For plankton mortalities, the default function is hyperbolic (denoted ζh for zooplankton and ρh for phytoplankton). Other functions available in MEDUSA are: linear (ζl,ρl), quadratic (ζq,ρq), and sigmoidal (ζs,ρs). Finally, for zooplankton grazing, we use Holling type III (G1), which is the default function, and Holling type II (G2). The shape defining parameters for these functional forms are tuned to each other so that over a wide range of conditions the key processes remains similar (see Anugerahanti et al., 2018). Rate maxima are also similar to the original MEDUSA-1.0 run, apart from linear and quadratic mortalities, as these functions have no shape defining parameters. These process formulations with respective alternative functions made 128 combinations, which was the size of the original ensemble reported in Anugerahanti et al. (2018). But to reduce the computational cost while keeping the ensemble properties mostly unchanged, here we limit the biogeochemical ensemble to 12 members chosen using principal component analysis (PCA) and k-means cluster, to span a similar range of variability for measurable metrics of chlorophyll and nutrients as the larger ensemble (see Supplementary Section 2, for further details).
At each of the stations the PPE is generated by adding “noise” to the vertical velocity, temperature, MLD, and vertical diffusivity, in a regionally dependent and covarying way (as these fields are related) in order to increase variability (see Supplementary Section 3 for details). The vertical diffusivity profile is then matched to the perturbed MLD. The perturbations for vertical velocity at all stations are done by first subtracting the monthly average vertical velocity. The anomalies are multiplied by a random number between −2 and 2 and added to each 5 day average field. These anomalies are generated randomly for each ensemble member. For station PAP, the perturbations to MLD are similar to perturbing the vertical velocity, and the vertical diffusivity profile is matched with the perturbed MLD. Further explanation of the PPE generation is in the Supplementary Section 3, Figures S4, S5. We use a PPE ensemble size of 12 members to match the PBE ensembles discussed above. Finally the combination of perturbing physics and biogeochemistry together is generated by running the PBE using the physical inputs from the PPE, to produce a PBPE.
2.2. Ensemble Metrics
We are interested in key properties of the model ensembles which we use to compare with observations at the five oceanographic stations. The spread of the annual means of dissolved inorganic nitrogen (DIN mmol m−3), chlorophyll (mg m−3), and zooplankton (mmol m −3) concentrations are the basic diagnostics throughout the water column. At the oligotrophic stations a deep chlorophyll maximum (DCM) is a common feature that occurs below the mixed layer when surface chlorophyll concentration is low (Fennel and Boss, 2003; Letelier et al., 2004). The DCM evolution is explored phenologically by its maximum depth and concentration over the winter (December–January–February), spring (March–April–May), summer (June–July–August), and fall (September–October–November). The range of DCM depth, timing of maximum depth, and concentration are examined for both the PPE, PBE, and the observational data.
We also examine the fractions of total nitrogen in the phytoplankton pool to reveal a signature of the processes which have been varied within the ensembles, in particular this distinguishes PPE from PBE induced variations. This fraction is calculated by using the chlorophyll to nitrogen ratios, taken from Yool et al. (2011), for both the in situ and model ensemble. This metric can give an indication of the processes involved in the temporal changes seen from the in situ observations, suggesting it may be possible to infer which processes (physical, biological, or both) may be responsible for model-observational discrepancies at different times.
3. Results
3.1. Chlorophyll Range and Distributions
Perturbations to the vertical velocity and MLD used for the PPE, produce relatively little spread in the bulk properties, especially for phytoplankton and zooplankton Figure 2. The PPE DIN concentrations vary little in the top 75 m (in all stations except PAP), however the DIN range increases below, suggesting that the physical variations impact more below the euphotic layers. These deeper variations however do not have much impact on bulk properties near the surface such as the total DIN, chlorophyll (phytoplankton), or zooplankton concentrations (as seen in Figure 2). At the oligotrophic stations, the PPE range is clearly insufficient to cover the in situ concentrations. However, at all five stations, from surface to deep water, the observed chlorophyll values mostly lie within the much larger PBE range (Figures 2A–D), suggesting that the full range of biological production through a strong nutrient gradient can be obtained by perturbing the biological processes. Only at the oligotrophic stations, below ~100 m, are in situ chlorophyll concentrations still outside the PBE range. The combined PBPE ensemble has a slightly wider range than PBE but is otherwise similar.
The PBE and PPE members also differ in DCM generation at the oligotrophic stations. Figure 3 shows chlorophyll distributions from four different members at BATS and ALOHA, (see monthly profiles of PPE in Supplementary Section 5, Figures S8–S11). The DCM is always present for part of each year but with considerable variability in maximum chlorophyll concentration and depth. In observations the deepest DCM always occurs in the summer and the shallowest in winter (Mignot et al., 2014). The range of DCM depths from the PBE is larger than that from the PPE, with observed deepest DCM depths generally within the PBE range [e.g., the deepest DCM depths at ALOHA, are 51–115 m (PBE), 82–95 m (PPE), and depth = 114 m from observations]. Similarly, for the minimum DCM depth, the PBE produces a larger range, although this still underestimates that in the observations (PPE DCM range = 21–37 m, PBE = 3–51 m, observation = 92 m). Additionally all PPE members have the deepest DCM later in the autumn, instead of in summer, but not all PBE members show this discrepancy. There are some differences in chlorophyll distributions between PPE members and the default run, especially the thickness of the chlorophyll layer during winter/spring at BATS, although differences are not as distinct as for the PBE, as seen in Figure 3. The PBPE follows the pattern and timings of PBE, although the DCM depth range is slightly wider (e.g., at ALOHA, PBPE range 69–118 m for maximum DCM depth).
These results suggest that perturbing the biogeochemistry can result in considerably greater variability in the evolution of the DCM, compared to perturbing the physics alone. Furthermore, when perturbing both physics and biogeochemistry, the effect of perturbing the latter predominantly determines the ensemble spread and chlorophyll distribution.
3.2. Characteristics of the Different Ensembles
The phytoplankton nitrogen fraction shows how much nitrogen resides in the phytoplankton pool, relative to the total DIN and phytoplankton nitrogen. The size of the phytoplankton nitrogen fraction can also indicate the concentration of nutrients (DIN) in the water column. For example, at ALOHA and BATS, the observed phytoplankton nitrogen fractions are always close to 1, indicating that most of the time, this region is nutrient limited. At stations such as L4, the phytoplankton nitrogen fraction can change drastically over the course of a season in both the observations and the model (Figures 4C,G).
From Figures 4A,B, the proportion of nitrogen in phytoplankton is seen to vary strongly across the PBE members. In contrast the PPE shows very little spread in nitrogen fractions across the whole ensemble (Figures 4E,F). However, at the coastal stations L4 and Cariaco, there is more variability between PPE ensemble members (Figures 4G,H), and the timing of maximum phytoplankton nitrogen fraction varies across the ensemble.
The contrast between PBE and PPE is more distinct in the phytoplankton nitrogen fractions than in the spread differences in chlorophyll, for example seen in Figure 2, where the PPE chlorophyll range is seen to show more spread than the phytoplankton nitrogen fraction, especially in the oligotrophic regions. The small changes in the functional representation of uptake, grazing, and mortality curves in the PBE, represented by the exchange arrows in the upper part of Figure 1, can strongly alter the mean nitrogen distributions because they directly alter the cycling between biological pools. In contrast the PPE variability really only alters the supply of nutrients from deeper layers, represented by the lower part of Figure 1, and not the fluxes between the biological compartments and biological fractional distributions, hence the smaller PPE spreads in Figures 4E–H. The larger PBE spreads mostly capture the observed seasonal variations in nitrogen fractions e.g., at L4, where the PPE ensemble cannot, and thus PBE provides a better representation of uncertainty.
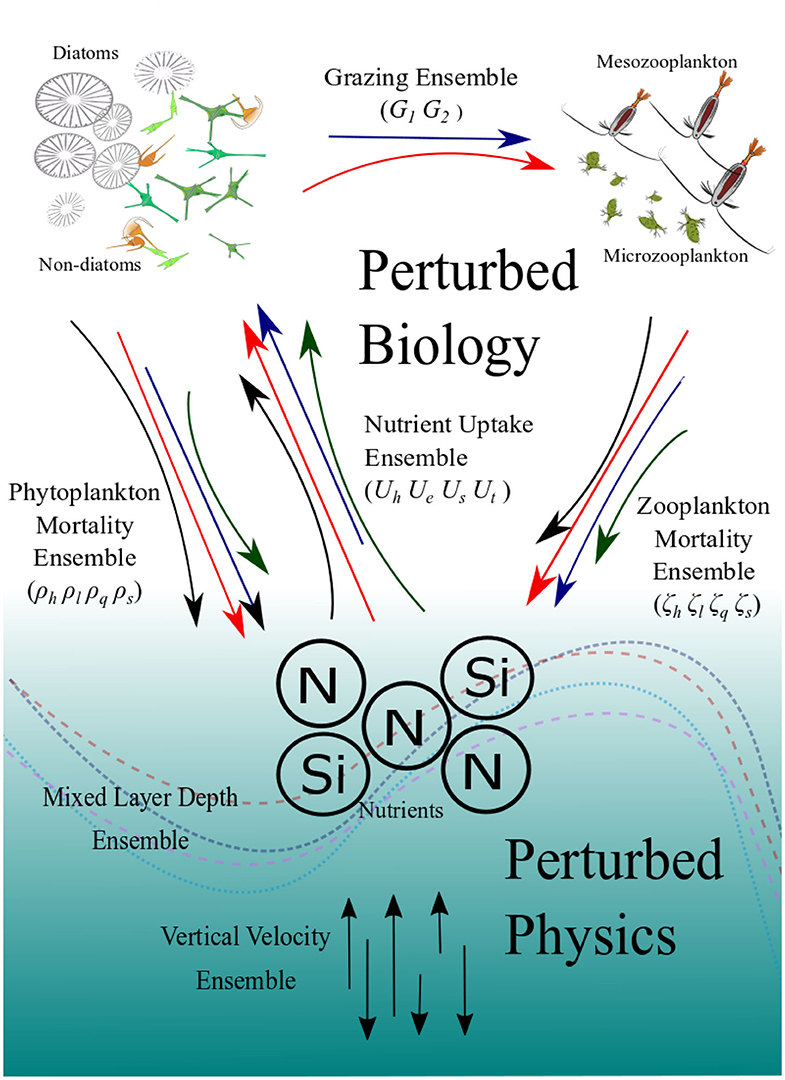
Figure 1. Schematic diagram showing how the ensembles are generated. The colored and curved arrows in the top part represent the different functional forms which describe the key biogeochemical processes which generate the PBE. The straight vertical arrows at the bottom represent varying vertical velocities and the curved lines represent climatology of mixed-layer depths which generate the PPE. The PBPE is the combination of the two.
4. Discussion
Previous studies such as Najjar et al. (2007), show that a simple biogeochemical model forced by different GCMs can produce large variability in dissolved organic matter both in the surface and at depth. Another study by Séférian et al. (2013) shows that atmosphere-ocean models differing in ocean subgrid physics and resolution can also produce varying biogeochemical tracers, such as nutrients and chlorophyll. In this study, we found that the uncertainty arising from biogeochemistry processes gives a larger range, especially in chlorophyll and zooplankton, as shown in Figures 2, 4. In terms of bulk properties, the fact that a PPE generates a small range, is consistent with studies where different ocean general circulation models are coupled with the same OBGC model (e.g., Sinha et al., 2010). However, below the depths of ~75 m the PPE DIN shows a larger range, due to the absence of activities between nutrient phytoplankton and zooplankton, and physics perturbations therefore have more effect on DIN. At PAP the larger PPE DIN range, at depths of active phytoplankton growth may occur due to the restricted sampling to winter months, when biological activity is low even at the surface, and the physical perturbations are the only control on DIN.
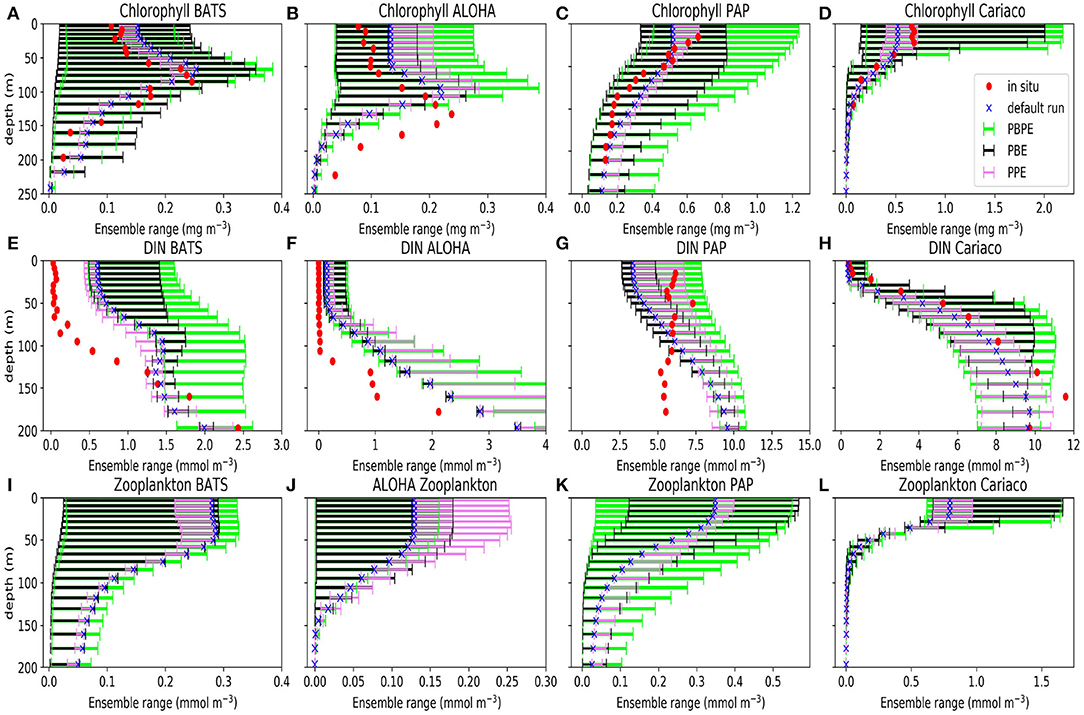
Figure 2. Ensemble range of mean chlorophyll (A–D), DIN (E–H), and zooplankton (I–L) profiles calculated from 1 January 1998 to 31 December 2007 at BATS (A,E,I), ALOHA (B,F,J), PAP (C,G,K), and Cariaco (D,H,L). Blue crosses show the mean concentrations from the default run, red dots show the mean concentration from in situ, the violet bars denote the mean concentration from PPE, the green bars show the mean concentrations from the PBPE, and the black bars show the mean concentrations from the PBE. For station PAP the annual mean is taken between 2002 and 2004 for DIN and between 2003 and 2005 for chlorophyll (see Supplementary Section 4, Figures S6, S7, for the in situ monthly averages for DIN and chlorophyll at PAP). The model calculations for the annual means matched with the timing of observational sampling. Station L4 profiles are not shown because in situ data are only available at the surface.
Physically perturbing the vertical velocity, MLD, vertical diffusivity, and temperature in the PPE can alter the chlorophyll distributions in the water column and the depth of DCMs because these physical variables control the nutrients (vertical velocity and MLD) and light (MLD) availability (Siegel et al., 2002). The variations in nutrient and light availability then alter the timing of peak phytoplankton concentrations (Henson et al., 2013). Perturbing the MLD using the described method in Supplementary Section 3, changes the magnitude of vertical diffusivity leading to an increase/decrease in nutrient concentrations at euphotic depths (Huisman et al., 2006). From Figure 4 the PPE range depends on the model temperature bias; at stations where the model bias is small, such as BATS and ALOHA (mean temperature bias are −0.24 and −0.44, respectively), the range of phytoplankton nitrogen fraction is low, and the seasonality is similar across members. However, at stations where model temperature bias is high, such as L4 and Cariaco (mean temperature bias are 0.90 and −1.58, respectively), the PPE range is larger, with more variable seasonality.
Perturbing the biogeochemistry produces a larger range of DCM depths, as the DCM depends on nutrient uptake, zooplankton grazing, and plankton mortality from surface to deep water. This makes the depth of the DCM vary across all ensemble members when the grazing or mortality functions are altered (e.g., Figures 3B,G). The DCMs occur at depths where the phytoplankton growth rate is in balance with the loss rate (Fennel and Boss, 2003; Cullen, 2014). Variations in DCM depths, pattern, and continuity across the PBE are therefore due to different loss and growth rates throughout euphotic depths. In oligotrophic regions, the nutrient concentration is low in the top ~150 m (see Figures 2E,F). Some PBE members produce higher phytoplankton loss rates compared to growth rate in the top 75 m due to the nutrient scarcity (e.g., members which use G2, ρh, and ρl). At deeper depths, nutrient is plentiful allowing phytoplankton growth to exceed the loss rate, giving a deeper DCM for these PBE members. When the mixed layer becomes deeper, a balance cannot be achieved as light becomes a limiting factor and chlorophyll concentrations reduce (see Figures 3B,G). The slightly larger maximum DCM depth range in PBPE may be caused by the additional net upwelling and the change in mixed layer depth from perturbing the physics, which gives the maximum depth for members with more downwelling and deeper MLD, and therefore a deeper DCM.
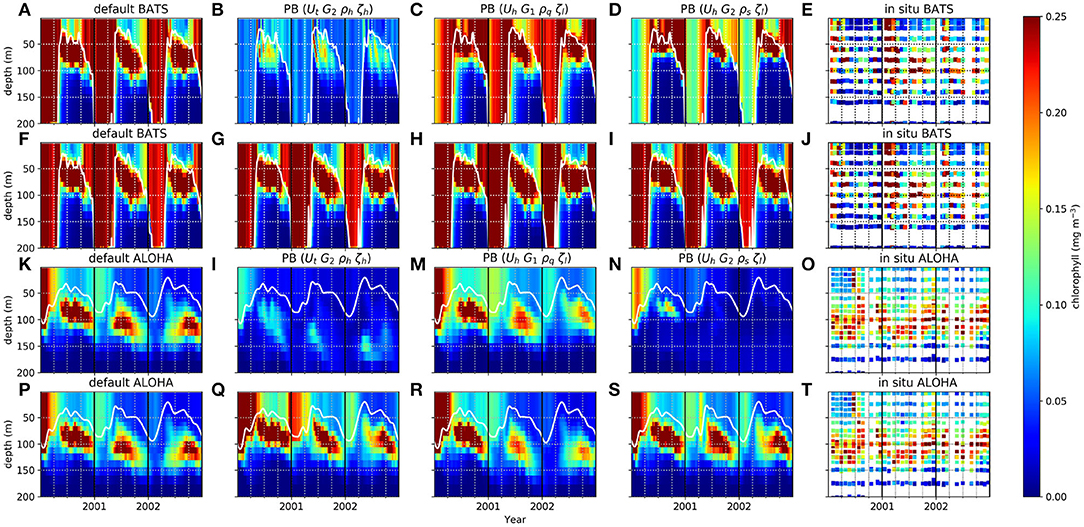
Figure 3. Chlorophyll distribution in the water column from 1st January 2000 to 31st December 2002 at station BATS (A–J) and ALOHA (K–T). White solid lines are the MLDs. Selected ensemble members, that are the most distinct from default run from PBE, with their functional form combinations are shown in (B–D), for BATS, and (K–N) for ALOHA, and for PPE are shown in (G–I) for BATS and (Q–S) for ALOHA.
PBE and PPE ranges are also shown and compared for nitrogen fractions in Figure 4, because nitrogen is the model currency and we can examine its distribution to phytoplankton across different ensemble members, and these variables are available from observations. Variations in phytoplankton nitrogen proportions, both temporal and between the PPE members, may result from perturbing the MLD, as this can also controls the timing of maximum phytoplankton concentrations, by controlling the light and nutrient availability, as well as distribution of phytoplankton in the water column (Behrenfeld et al., 2013; Henson et al., 2013).
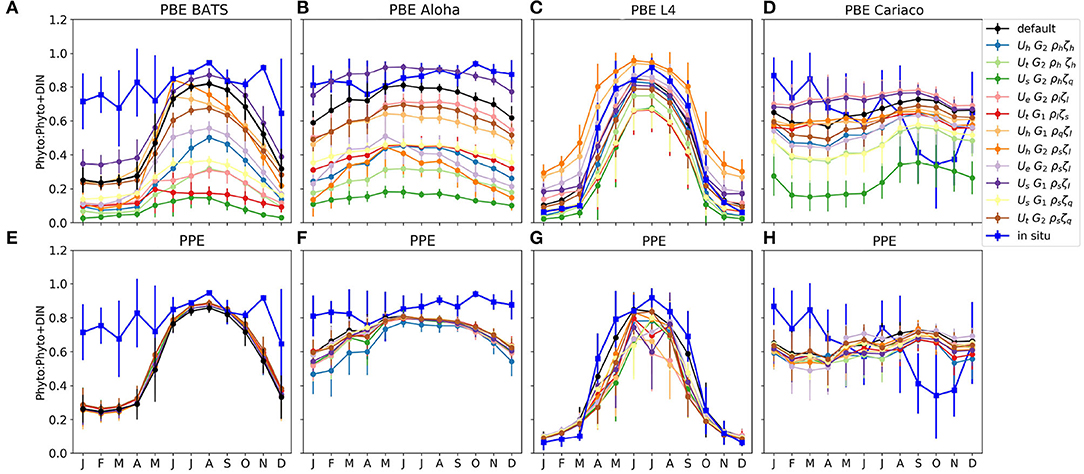
Figure 4. Monthly averaged phytoplankton fraction P/(P+D) in nitrogen units at the surface for four oceanographic stations. (A–D) and (E–H) show the phytoplankton fraction from PBE and PPE, respectively, with different lines representing ensemble members. The observations are shown in blue. The bars are the standard deviations of the monthly P/(P+D). The nitrogen within phytoplankton is calculated using the chlorophyll to nitrogen ratio which is calculated using the C:N conversion fraction, and the calculation is described in Yool et al. (2011). These are calculated from 1 January 1998 to 31 December 2007, apart from station L4, which are calculated from January 2000, to match the in situ data.
At station BATS, only three PBE members produce a nitrogen fraction comparable to that seen in the observations; the default function, UhG2ρsζl, and UsG1ρsζl. This is because the hyperbolic uptake function has higher nutrient uptake at low nutrient concentrations, compared to other functional forms, and both sigmoidal phytoplankton mortalities and linear zooplankton mortality produce lower phytoplankton loss. Note that the uptake functions in the default MEDUSA and the ensemble do not permit acclimatization in nutrient uptake, such as described in Smith et al. (2009). The underestimation at the oligotrophic stations may also be caused by the bias introduced when reducing the ensemble members from 128 to 12 (see details in Supplementary Section 2), which considers observations and model outputs at all stations across different oceanographic regions, in which there are 10 other PBE members that produce higher phytoplankton nitrogen fractions than the default run.
Apart from the possibility of inefficient uptake in the MEDUSA 1-D model, some physical parameters, such as horizontal advection and eddies, are not represented at all. In the subtropical gyre 3-D advection is thought to be essential in controlling primary productivity (Palter et al., 2005; Dave and Lozier, 2010), which may explain the discrepancies between the in situ and ensemble phytoplankton nitrogen fractions shown in Figure 4. In order to fully address the physical model bias, the impact of 3-D advection should be represented, and any errors in that circulation would need to be accounted for through ensemble spread, possibly by using multi-model ensembles, although even these may contain shared biases (Abramowitz et al., 2019).
Both PBE and PPE spreads are better at capturing the nitrogen fraction at light limited stations such as L4. The ensembles generally follow the observations, even when nutrients become limiting in the summer, because light also controls the nutrient uptake rate. The observed phytoplankton nitrogen fraction generally falls within the PBE range throughout the year, for example from October-March, the in situ phytoplankton fraction generally matches ensemble members with lower phytoplankton growth rates at low concentrations (such as UtG2ρlζs and UhG2ρhζh), and from April to September it matches members with higher phytoplankton growth rates and high zooplankton mortality (such as UhG1ρsζl and UhG2ρqζl). This is consistent with North Atlantic bloom studies, where the phytoplankton nitrogen proportions and growth rates change over the year (Roy et al., 2012; Behrenfeld et al., 2013; Behrenfeld and Boss, 2014), being controlled by nutrients, light, and mixed layer conditions. For example in the summer, the growth rate of phytoplankton is in equilibrium with loss rate as nutrient is depleted and grazing rates are high (Behrenfeld et al., 2013; Behrenfeld and Boss, 2014).
These results suggest that in a 1-D biogeochemical model the PBE generates enough spread to encompass the uncertainty within the observed phytoplankton fraction even if the region is seasonally varying, and can explain the variations of growth and loss rate in phytoplankton. We can also see that none of the single PBE or PPE members fully capture the observations throughout the year, therefore using a single set of functional forms is not sufficient to capture the observed behavior and its uncertainty. The PBE ensemble members that best match the in situ fractions vary through the year as the ensemble members behave differently depending on the concentrations of nutrient, phytoplankton, and zooplankton, especially in strongly seasonally varying regions.
We have further attempted to compare our PBE model with different biogeochemical model types used previously in model intercomparison studies (e.g., Kwiatkowski et al., 2014). Acknowledging that the PBE model presented here was a 1D model, running only at 5 stations, a rigorous comparison with 3D models would be difficult. However, when compared to all surface observations at five stations, the mean of PBE surface chlorophyll produces a correlation of 0.55, with correlation range of [0.491, 0.583] produced by model ensemble members. In the inter-comparison study, Kwiatkowski et al. (2014) reported the range of [0.15, 0.50] across all models. Similarly, considering all observed surface DIN at five stations, the mean of PBE produces a correlation of 0.41, with the ensemble correlation range of [0.333, 0.595], which are lower than for the models reported by Kwiatkowski et al. (2014) which has surface DIN within the range [0.94, 0.79]. However, generality of the results needs to be tested beyond the five stations, and through comparison of other models with observations beyond annual average of surface fields.
When assessing the risks of climate change a structural ensemble may also be useful for representing model uncertainty. It has been shown in earlier studies, e.g., by Hawkins and Sutton (2012) using a CMIP3 multimodel ensemble, that the uncertainty in climate change predictions may be strongly dominated by model uncertainty in the near term, and the detection time for anthropogenic impacts is conditioned by these uncertainties. The PBE ensemble method clearly demonstrates the importance of structural uncertainties, which should then be relevant in assessing climate change impacts on ecological indicators such as phytoplankton phenology.
5. Summary and Conclusion
We have run three different ensembles using 1-D MEDUSA, generated by perturbing the biology (PBE), the physics (PPE), and both together (PBPE). The ensemble spreads, chlorophyll distributions, and characteristics of these ensembles are explored. The PBE and PBPE generally produce larger spread of the chlorophyll annual means compared to PPE, and are able to encompass the in situ concentrations seen at five different oceanographic stations. Below the active phytoplankton growth region, the PPE produces larger DIN (nutrient) spread than PBE, as below this depth there is less biological activity and nutrient supply is dependent on the PPE. For the chlorophyll distributions we used the time evolution of the DCM as an ensemble metric at oligotrophic stations and this shows that across different ensemble members the PBE and PBPE produce larger spreads of DCM depth compared to PPE, with different chlorophyll patterns. This is because the PBE produces more variable loss and growth rates of phytoplankton with different nutrient supply rates. This means that perturbing the biogeochemistry produces a stronger effect than perturbing physics.
To see how nitrogen, the model currency, is distributed to the phytoplankton compartments, we used phytoplankton nitrogen fraction as a metric. This metric shows that the PBE produces a much larger spread than PPE in terms of the monthly variability, and nearly covers the in situ standard deviations, especially at the strongly seasonally varying stations. The large spread from the PBE show that altering the steepness of the uptake, mortality, and grazing curves changes the way nitrogen is distributed to the phytoplankton compartments, while in PPE the perturbations only alter the nutrient supply, both in terms of distribution in the water column and concentrations.
Our 1D-model experiments suggest that the PBE or PBPE better represent model uncertainties arising from the model structural errors, as shown by their ensemble ranges, and how the model currency is distributed between the different compartments. A 1D model does however contain many simplifications when it comes to ocean physics. To understand the implications of model structural errors on larger scales, this method should also be tested in 3D coupled physical-biogeochemical models.
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material. The model output for this paper is being made available in the University of Reading Research Data Archive, and will be accessible at: http://dx.doi.org/10.17864/1947.214; http://dx.doi.org/10.17864/1947.257.
Author Contributions
SR and KH conceived the study, and led the development of the methodology with PA. PA run the model, performed the analysis, created visualization, and wrote the first draft of the manuscript. All authors contributed significantly to writing the subsequent drafts and prepared the final version for publication.
Funding
This study was funded by the Bakrie Center Foundation (grant no. 1307/BCF-SK/RSCH/VII/2015) and Yayasan Batavia Prosperindo Peduli (grant no. 005), Indonesia.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The observation data for the oceanographic stations can be obtained from the following websites; http://hahana.soest.hawaii.edu/hot/hot-dogs/bextraction.html for Station ALOHA, http://bats.bios.edu/bats-data/ for Station BATS, http://imars.marine.usf.edu/cariaco/biochemistry-microbiology-cruise-results for Station Cariaco, https://www.westernchannelobservatory.org.uk/data.php for Station L4, and http://projects.noc.ac.uk/pap/data for Station PAP. The matlab code to derive the mixed layer depth can be accessed in https://uk.mathworks.com/matlabcentral/fileexchange/53370-to-compute-mixed-layer-depth-based-on-subjective-method?focused=5514769&tab=function. The authors would like to thank Kevin White, for his advice on this study, and John Hemmings, for providing the most recent version of the MarMOT code.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2020.00549/full#supplementary-material
References
Abramowitz, G., Herger, N., Gutmann, E., Hammerling, D., Knutti, R., Leduc, M., et al. (2019). ESD Reviews: model dependence in multi-model climate ensembles: weighting, sub-selection and out-of-sample testing 10, 91–105. doi: 10.5194/esd-10-91-2019
Adamson, M. W., and Morozov, A. Y. (2013). When can we trust our model predictions? Unearthing structural sensitivity in biological systems. Proc. R. Soc. Lond. A 469:20120500. doi: 10.1098/rspa.2012.0500
Allen, J. I., Aiken, J., Anderson, T. R., Buitenhuis, E., Cornell, S., Geider, R. J., et al. (2010). Marine ecosystem models for earth systems applications: the MarQUEST experience. J. Mar. Syst. 81, 19–33. doi: 10.1016/j.jmarsys.2009.12.017
Anderson, J. L. (2001). An ensemble adjustment Kalman filter for data assimilation. Month. Weath. Rev. 129, 2884–2903. doi: 10.1175/1520-0493(2001)129<2884:AEAKFF>2.0.CO;2
Anderson, T. R. (2010). Progress in marine ecosystem modelling and the “unreasonable effectiveness of mathematics”. J. Mar. Syst. 81, 4–11. doi: 10.1016/j.jmarsys.2009.12.015
Anderson, T. R., Gentleman, W. C., and Sinha, B. (2010). Influence of grazing formulations on the emergent properties of a complex ecosystem model in a global ocean general circulation model. Prog. Oceanogr. 87, 201–213. doi: 10.1016/j.pocean.2010.06.003
Anugerahanti, P., Roy, S., and Haines, K. (2018). A perturbed biogeochemistry model ensemble evaluated against in situ and satellite observations. Biogeosciences 15, 6685–6711. doi: 10.5194/bg-15-6685-2018
Behrenfeld, M. J., and Boss, E. S. (2014). Resurrecting the ecological underpinnings of ocean plankton blooms. Annu. Rev. Mar. Sci. 6, 167–194. doi: 10.1146/annurev-marine-052913-021325
Behrenfeld, M. J., Doney, S. C., Lima, I., Boss, E. S., and Siegel, D. A. (2013). Annual cycles of ecological disturbance and recovery underlying the subarctic Atlantic spring plankton bloom. Glob. Biogeochem. Cycles 27, 1291–1293. doi: 10.1002/2013GB004681
Butenschon, M., Clark, J., Aldridge, J. N., Icarus Allen, J., Artioli, Y., Blackford, J., et al. (2016). ERSEM 15.06: A generic model for marine biogeochemistry and the ecosystem dynamics of the lower trophic levels. Geosci. Model Dev. 9, 1293–1339. doi: 10.5194/gmd-9-1293-2016
Cullen, J. J. (2014). Subsurface chlorophyll maximum layers: enduring enigma or mystery solved? Annu. Rev. Mar. Sci. 7, 207–239. doi: 10.1146/annurev-marine-010213-135111
Dave, A. C., and Lozier, M. S. (2010). Local stratification control of marine productivity in the subtropical North Pacific. J. Geophys. Res. 115, 1–16. doi: 10.1029/2010JC006507
Doney, S. C. (1999). Major challenges confronting marine biogeochemical modeling. Glob. Biogeochem. Cycles 13, 705–714.
Doney, S. C., Lindsay, K., Caldeira, K., Campin, J., Drange, H., Dutay, J., et al. (2004). Evaluating global ocean carbon models : the importance of realistic physics. Glob. Biogeochem. Cycles 18:GB3017. doi: 10.1029/2003GB002150
Doney, S. C., Ruckelshaus, M., Emmett Duffy, J., Barry, J. P., Chan, F., English, C. A., et al. (2012). Climate change impacts on marine ecosystems. Annu. Rev. Mar. Sci. 4, 11–37. doi: 10.1146/annurev-marine-041911-111611
Edwards, A., and Yool, A. (2000). The role of higher predation in plankton population models. J. Plankton Res. 22, 1085–1112. doi: 10.1093/plankt/22.6.1085
Fennel, K., and Boss, E. (2003). Subsurface maxima of phytoplankton and chlorophyll: steady-state solutions from a simple model. Limnol. Oceanogr. 48, 1521–1534. doi: 10.4319/lo.2003.48.4.1521
Friedrichs, M. A. M., Hood, R. R., and Wiggert, J. D. (2006). Ecosystem model complexity versus physical forcing: quantification of their relative impact with assimilated Arabian Sea data. Deep Sea Res. Part II Top. Stud. Oceanogr. 53, 576–600. doi: 10.1016/j.dsr2.2006.01.026
Fussmann, G. F., and Blasius, B. (2005). Community response to enrichment is highly sensitive to model structure. Biol. Lett. 1, 9–12. doi: 10.1098/rsbl.2004.0246
Gentleman, W., Leising, A., Frost, B., Strom, S., and Murray, J. (2003). Functional responses for zooplankton feeding on multiple resources: a review of assumptions and biological dynamics. Deep Sea Res. Part II Top. Stud. Oceanogr. 50, 2847–2875. doi: 10.1016/j.dsr2.2003.07.001
Hawkins, E., and Sutton, R. (2012). Time of emergence of climate signals. Geophys. Res. Lett. 38, 1–6. doi: 10.1029/2011GL050087
Hemmings, J. C. P., Challenor, P. G., and Yool, A. (2015). Mechanistic site-based emulation of a global ocean biogeochemical model (MEDUSA 1.0) for parametric analysis and calibration: an application of the Marine Model Optimization Testbed (MarMOT 1.1). Geosci. Model Dev. 8, 697–731. doi: 10.5194/gmd-8-697-2015
Henson, S., Cole, H., Beaulieu, C., and Yool, A. (2013). The impact of global warming on seasonality of ocean primary production. Biogeosciences 10, 4357–4369. doi: 10.5194/bg-10-4357-2013
Huisman, J., Pham Thi, N. N., Karl, D. M., and Sommeijer, B. (2006). Reduced mixing generates oscillations and chaos in the oceanic deep chlorophyll maximum. Nature 439, 322–325. doi: 10.1038/nature04245
Kriest, I., Oschlies, A., and Khatiwala, S. (2012). Sensitivity analysis of simple global marine biogeochemical models. Glob. Biogeochem. Cycles 26, 1–15. doi: 10.1029/2011GB004072
Kwiatkowski, L., Yool, A., Allen, J. I., Anderson, T. R., Barciela, R., Buitenhuis, E. T., et al. (2014). IMarNet: An ocean biogeochemistry model intercomparison project within a common physical ocean modelling framework. Biogeosciences 11, 7291–7304. doi: 10.5194/bg-11-7291-2014
Letelier, R. M., Karl, D. M., Abbott, M. R., and Bidigare, R. R. (2004). Light driven seasonal patterns of chlorophyll and nitrate in the lower euphotic zone of the North Pacific Subtropical Gyre. Limnol. Oceanogr. 49, 508–519. doi: 10.4319/lo.2004.49.2.0508
Mignot, A., Claustre, H., Uitz, J., Poteau, A., Ortenzio, F. D., and Xing, X. (2014). Understanding the seasonal dynamics and the deep chlorophyll maximum in oligotrophic. Glob. Biogeochem. Cycles 28, 856–876. doi: 10.1002/2013GB004781.Received
Moradkhani, H., and Meskele, T. T. (2010). “Chapter II: Probabilistic assessment of the satellite retrieval error translation to hydrologic response,” in Satellite Rainfall Applications for Surface Hydrology, eds M. Gebremichael and F. Hossain (Netherlands: Springer), 235–241.
Murphy, J. M., Booth, B. B. B., Collins, M., Harris, G. R., Sexton, D. M. H., and Webb, M. J. (2007). A methodology for probabilistic predictions of regional climate change from perturbed physics ensembles. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 365, 1993–2028. doi: 10.1098/rsta.2007.2077
Najjar, R. G., Jin, X., Louanchi, F., Aumont, O., Caldeira, K., Doney, S. C., et al. (2007). Impact of circulation on export production, dissolved organic matter, and dissolved oxygen in the ocean: results from Phase II of the Ocean Carbon-cycle Model Intercomparison Project (OCMIP-2). Glob. Biogeochem. Cycles 21:GB3007. doi: 10.1029/2006GB002857
Palter, J. B., Lozier, M. S., and Barber, R. T. (2005). The effect of advection on the nutrient reservoir in the North Atlantic subtropical gyre. Nature 437, 687–692. doi: 10.1038/nature03969
Roy, S., Broomhead, D. S., Platt, T., Sathyendranath, S., and Ciavatta, S. (2012). Sequential variations of phytoplankton growth and mortality in an NPZ model: a remote-sensing-based assessment. J. Mar. Syst. 92, 16–29. doi: 10.1016/j.jmarsys.2011.10.001
Séférian, R., Bopp, L., Gehlen, M., Orr, J. C., Ethé, C., Cadule, P., et al. (2013). Skill assessment of three earth system models with common marine biogeochemistry. Clim. Dyn. 40, 2549–2573. doi: 10.1007/s00382-012-1362-8
Siegel, D. A., Doney, S. C., and Yoder, J. A. (2002). The North Atlantic spring phytoplankton bloom and Sverdrup's critical depth hypothesis. Science 296, 730–733. doi: 10.1126/science.1069174
Sinha, B., Buitenhuis, E. T., Le Quere, C., and Anderson, T. R. (2010). Progress in Oceanography Comparison of the emergent behavior of a complex ecosystem model in two ocean general circulation models. Prog. Oceanogr. 84, 204–224. doi: 10.1016/j.pocean.2009.10.003
Smith, S., Yamanaka, Y., Pahlow, M., and Oschlies, A. (2009). Optimal uptake kinetics: physiological acclimation explains the pattern of nitrate uptake by phytoplankton in the ocean. Mar. Ecol. Prog. Ser. 384, 1–12. doi: 10.3354/meps08022
Steele, J. H., and Henderson, E. W. (1992). The role of predation in planckton models. J. Plankton Res. 14, 157–172. doi: 10.1093/plankt/14.1.157
Storkey, D., Blockley, E., Furner, R., Guiavarc'h, C., Lea, D., Martin, M., et al. (2010). Forecasting the ocean state using NEMO:the new FOAM system. J. Oper. Oceanogr. 3, 3–15. doi: 10.1080/1755876X.2010.11020109
Subramanian, A. C., and Palmer, T. N. (2017). Ensemble superparameterization versus stochastic parameterization: a comparison of model uncertainty representation in tropical weather prediction. J. Adv. Model. Earth Syst. 9, 1231–1250. doi: 10.1002/2016MS000857
Tebaldi, C., and Knutti, R. (2007). The use of the multi-model ensemble in probabilistic climate projections. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 365, 2053–2075. doi: 10.1098/rsta.2007.2076
Tinker, J., Lowe, J., Holt, J., Pardaens, A., and Wiltshire, A. (2015). Validation of an ensemble modelling system for climate projections for the northwest European shelf seas. Prog. Oceanogr. 138, 211–237. doi: 10.1016/j.pocean.2015.07.002
Yool, A., Popova, E. E., and Anderson, T. R. (2011). MEDUSA-1.0: a new intermediate complexity plankton ecosystem model for the global domain. Geosci. Model Dev. 4, 381–417. doi: 10.5194/gmd-4-381-2011
Keywords: perturbed biogeochemistry ensemble, ocean biogeochemical model, ensemble modeling, structural uncertainty, perturbed physics ensemble
Citation: Anugerahanti P, Roy S and Haines K (2020) Perturbed Biology and Physics Signatures in a 1-D Ocean Biogeochemical Model Ensemble. Front. Mar. Sci. 7:549. doi: 10.3389/fmars.2020.00549
Received: 17 June 2019; Accepted: 16 June 2020;
Published: 28 July 2020.
Edited by:
Wolfgang Koeve, GEOMAR Helmholtz Center for Ocean Research Kiel, GermanyReviewed by:
Filippa Fransner, University of Bergen, NorwayIris Kriest, GEOMAR Helmholtz Center for Ocean Research Kiel, Germany
Copyright © 2020 Anugerahanti, Roy and Haines. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Prima Anugerahanti, panu09@jamstec.go.jp; Shovonlal Roy, shovonlal.roy@reading.ac.uk