- 1Institute of Immunobiology, Kantonsspital St. Gallen, St. Gallen, Switzerland
- 2Marchuk Institute of Numerical Mathematics, Russian Academy of Sciences, Moscow, Russia
Adaptive immune responses develop in secondary lymphoid organs such as lymph nodes (LNs) in a well-coordinated series of interactions between migrating immune cells and resident stromal cells. Although many processes that occur in LNs are well understood from an immunological point of view, our understanding of the fundamental organization and mechanisms that drive these processes is still incomplete. The aim of systems biology approaches is to unravel the complexity of biological systems and describe emergent properties that arise from interactions between individual constituents of the system. The immune system is greater than the sum of its parts, as is the case with any sufficiently complex system. Here, we review recent work and developments of computational LN models with focus on the structure and organization of the stromal cells. We explore various mathematical studies of intranodal T cell motility and migration, their interactions with the LN-resident stromal cells, and computational models of functional chemokine gradient fields and lymph flow dynamics. Lastly, we discuss briefly the importance of hybrid and multi-scale modeling approaches in immunology and the technical challenges involved.
Introduction
The lymphatic vascular system extends throughout the body, collecting interstitial tissue fluid through a network of initial lymphatic vessels (1). The lymph is then carried to the collecting lymphatics and distributed through lymphoid organs before returning to the venous circulation. Secondary lymphoid organs such as lymph nodes (LNs) form at bifurcation points along the lymphatic vasculature and serve as checkpoints for immune cells (2, 3). Adaptive immune responses are initiated and maintained in LNs via coordinated interactions between T cells, B cells, dendritic cells (DCs) and the LN-resident stromal cells (4–6) (Figure 1A). Traditionally, stromal cells have been described as connective tissue cells which organize the underlying LN infrastructure and cellular compartmentalization, however in recent decades their critical roles in regulation and coordination of immune responses have been established (7–9).
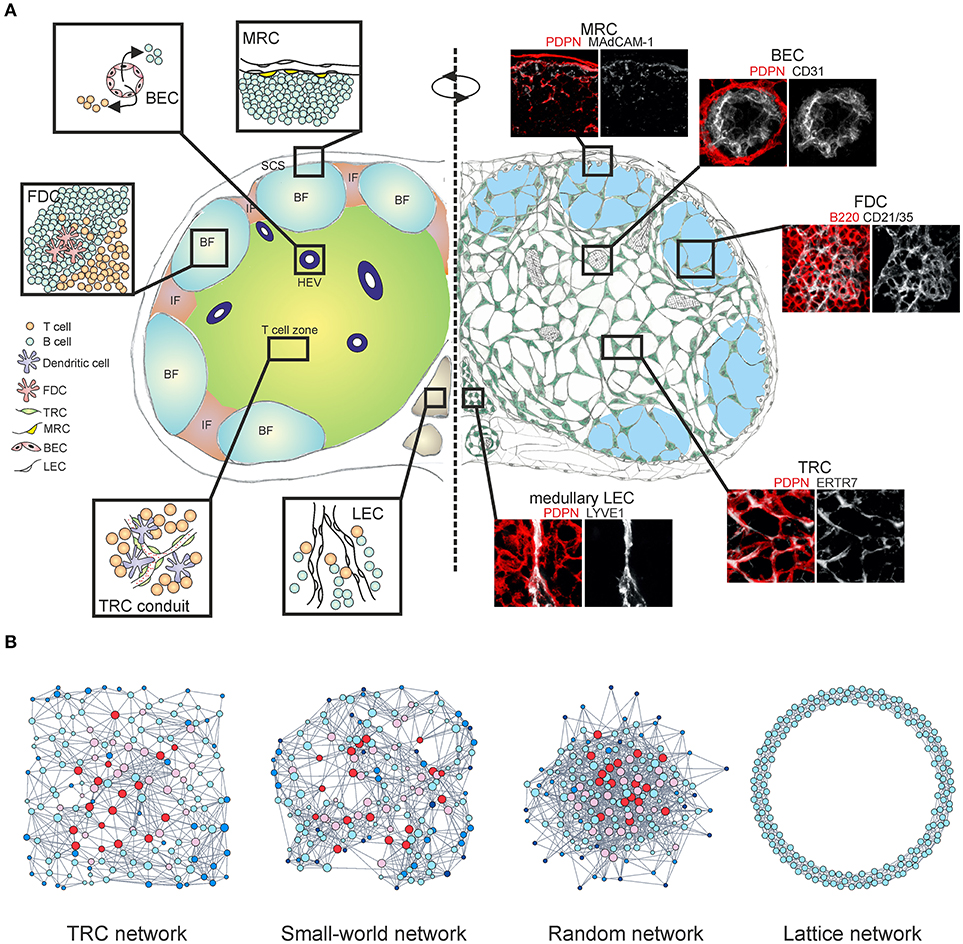
Figure 1. Multi-layered microarchitecture of the LN. (A) Schematic overview of the LN architecture and cellular organization. Zoom-in panels represent confocal microscopy images stained for indicated markers. BF, B cell follicle; IF, inter-follicular; SCS, subcapsular sinus; HEV, high endothelial venule; FDC, follicular dendritic cell; TRC, T cell zone fibroblastic reticular cell; MRC, marginal reticular cell; BEC, blood endothelial cell; LEC, lymphatic endothelial cell. (B) Network graphs of the TRC network and equivalent network models; Watts-Strogatz small-world network, Erdos-Renyi random network and 1D ring lattice network. Colors indicate nodes with low (blue) or high (red) betweenness centrality.
Lymph Node Stromal Cell Framework
CD45− non-hematopoietic stromal cells in LNs originate from mesenchymal and endothelial precursors and can be divided into four major subsets based on the expression of podoplanin (PDPN) and CD31; PDPN−CD31+ blood endothelial cells (BECs), PDPN+CD31+ lymphatic endothelial cells (LECs), PDPN+CD31− fibroblastic reticular cells (FRCs) and PDPN−CD31− double-negative cell fraction (10, 11). Stromal cell subsets form site-dependent niches customized for efficient interactions with immune cells, separating the LN into distinct regions (Figure 1A).
The lymph drains to the LN subcapsular sinus (SCS) through several afferent lymphatic vessels, carrying antigen, signaling molecules and immune cells. The SCS is lined with two types of LECs, the floor and ceiling LECs. It has been demonstrated that ceiling LECs express the atypical chemokine receptor CCRL1 (ACKR4) which binds CCR7 ligands CCL19 and CCL21, whilst floor LECs are devoid of its expression (12). Differential expression of CCRL1 creates chemokine gradients for DCs to migrate from the SCS to the LN parenchyma. The outer cortex of the LN under the SCS contains B cell follicles which are populated by several stromal cell subsets critical for B cell-dependent responses. B cells sense the CXCL13 gradient and migrate to the follicles in a CXCR5-dependent manner (13), where they interact with a dense network of CD21+CD35+ follicular dendritic cells (FDCs) in order to sample antigens (14, 15). A monolayer of MadCAM1+ marginal reticular cells (MRCs) also contributes to B cell homing by expression of CXCL13 (16) and they have also been shown to express RANKL (TNFSF11) in LNs (17). The specific expression of RANKL by MRCs was subsequently confirmed by single-cell RNA sequencing, although MadCAM1 expression could not be readily detected (18). It was previously shown that MRCs are able to proliferate and differentiate into FDCs during inflammation-induced remodeling of the B cell follicles (19), however the phenotype and function of MRCs still remain poorly understood.
Furthermore, the B cell zone-resident reticular cells alongside the expanding FDC network orchestrate germinal center formation during inflammation (20). Additional stromal cell subsets have been reported in the B cell follicle, such as the CXCL13-producing stromal cells surrounding inflamed B cell follicles (21) and a CXCL12+ reticular stromal subset in the dark zone of the germinal center following infection (22). Clearly, the heterogeneity of B follicle stromal cells requires further dissection in order to identify the key players in the development of humoral immunity.
The LN is a highly vascularized organ as the blood vasculature needs to deliver oxygen and nutrients to cells in the LN parenchyma. Advances in microscopy technologies have enabled 3D imaging and quantification of the topology of the entire microvascular network in LNs (23). Importantly, during inflammation the vasculature must expand in order to accommodate the increasing metabolical demand of the LN, which is achieved through proliferation of BECs and subsequent return to homeostasis by stochastic deletion of both pre-existing and newly generated blood vessels (24). The majority of lymphocytes enter the LN paracortex through specialized blood vessels called high endothelial venules (HEVs) which mediate transendothelial extravasation (25, 26). The specific roles of HEVs in lymphocyte motility and chemotaxis as opposed to capillary endothelial cells have been recently elucidated by transcriptional profiling (27).
Upon entering the LN parenchyma, T cells crawl along the FRC network searching for cognate antigen loaded on DCs (28–30). FRCs in the T cell zone (TRC) produce homeostatic chemokines CCL19 and CCL21, guiding T cells and DCs into the relevant compartments and facilitating T-DC interactions necessary for developing adaptive immunity and antiviral responses (31–33) (Figure 1A). The interaction between PDPN+ perivascular FRCs and the platelet-derived C-type lectin-like receptor 2 (CLEC-2) has been shown to promote VE-cadherin expression by HEVs through local sphingosine-1-phosphate (S1P) release by platelets, effectively maintaining the vascular integrity of HEVs (34). While DCs crawl on the FRC network, the interaction between PDPN+ FRCs and CLEC-2 on DCs induces actin cytoskeleton remodeling and promotes DC motility (35). Furthermore, the same axis permits stretching of the FRC network in order to accommodate rapid LN expansion during an immune response, whilst DC-derived lymphotoxin beta receptor (LTβR) ligands promote FRC survival by modulating PDPN expression (36–38). A recent study employing single-cell RNA sequencing has suggested the existence of nine non-endothelial stromal cell clusters within LNs, however the expression of the canonical stromal cell marker PDPN was not sufficient to distinguish the clusters on a single cell level (18).
In addition to the emerging roles of FRCs in regulation of immune responses (39), the FRC network serves a fundamental role in the formation of the LN conduit system (40, 41). The conduit system emerges as a complex branched mesh of micro-vessels from the floor of the SCS, comprising of a collagen-rich core surrounded by a microfibrillar zone and a basement membrane. A sparse network of conduits enwrapped by FDCs pervades the B cell follicles and drains the lymph through the T cell zone where it forms a dense re-entrant loop network ensheathed by the TRCs (42). The conduits rapidly transport small signaling molecules, chemokines and soluble antigens with the lymph and deliver them to the relevant stromal cells and lymphocytes (43, 44). The conduits size exclusion criterion of <70 kDa for entry of lymph-borne antigens has been recently shown to be dependent on plasmalemma vesicle associated protein (PLVAP) expression by SCS and medullary LECs (45). Ultimately the lymph is carried through the conduit system to the medullary lymphatics where it drains out of the LN through an efferent lymphatic vessel. Egress of lymphocytes occurs at the cortical and medullary sinuses through sensing of sphingosine-1-phosphate (S1P) produced by LECs (46–48).
In conclusion, stromal cells exhibit niche-specific functions and heterogeneity, indicating the complexity of their specialized interactions with immune cells. Many questions still remain open regarding their development and plasticity in homeostasis and during ongoing immune responses.
Stromal-Immune Cell Interaction Models
T cell motility and migration patterns arise from cell-intrinsic cues such as actin polymerization and cell-extrinsic cues which include integrin-dependent adhesion, physical guidance of the microenvironment, and chemotactic gradients (49). Based on these observations it has been proposed that T cells switch between two modes of intranodal migration (50); anchorage-dependent motility mediated by engagement of LFA-1 with ICAM-1 on DCs and FRCs (31, 51), and anchorage-independent motility driven by FRC-derived chemokines and lysophosphatidic acid (LPA) (52). Moreover, a recent study demonstrated that LFA-1 and CCR7 contribute complementary and not sequentially to intranodal T cell migration. Interestingly, the authors also show that T cells migrate in a continuous sliding locomotion rather than in a caterpillar-like manner (53, 54).
Intranodal T cell motility is closely linked to search strategies employed in order to efficiently find cognate antigen loaded on DCs (55). Additionally, migration patterns are heterogeneous between T cell subsets such as CD4 and CD8, and whether they are naive, activated or memory T cells (56–59). Thus, T cells can exhibit a spectrum of search patterns, ranging from diffusive random walks analogous to Brownian motion, superdiffusive Lévy walks and subdiffusive random motion (49, 60). It has been shown in a recent report using Agent-Based Models (ABM) that naive T cells in LNs exhibit a type of superdiffusive walk which fits best as a lognormal modulated correlated random walk among the idealized computational models studied (61) (Table 1). Similarly, another ABM study demonstrated that T cell migration in inflamed LNs best fits an inverse heterogeneous correlated random walk (78).
Numerous computational T cell migration studies in LNs did not readily include the underlying reticular network structure. Furthermore, these analyses were performed using rule-derived modeling methodologies that are phenomenological in nature, rather than a biophysics-based approach (85). However, several modeling studies have simulated the TRC network with randomized connectivity and addressed its involvement in guiding T cell motion. In one study a 3D ABM approach was used to simulate infection responses in order to observe T-DC encounters and T cell differentiation in LNs under different antigen conditions (77). 3D Cellular Potts Models (CPM) offer a complementary modeling framework to simulate dynamics of T cell and DC migration alongside the TRC network. It was shown that the complex cell movement is determined by the densely packed LN environment, even though similar migratory behavior of T cells was observed whether they preferentially adhered to the TRC network or not (73). Interestingly, the study demonstrated the existence of small dynamic T cell streams within LNs, which the authors speculate occur alongside the TRC network fibers. Another study simulated migration of T cells and DCs on the TRC network and found that constraining cell movement on the TRC network does not increase the frequency of T-DC encounters compared to Brownian motion in free 3D space (75). A subsequent theoretical study confirmed in simulations that the TRC network has only a minor effect on the contact probability between T cells and DCs (76).
A question then naturally arises; do lymphocytes require the TRC network as a guiding structure for cellular movement? The answer seems evident from plethora of experimental work, corroborated by a recent reports demonstrating that deficiency in CCR7-mediated chemokine sensing and integrin LFA-1-dependent adhesion in T cells does not abrogate intranodal migration and firm attachment to the TRC network (53, 72). However, the existing theoretical models were characterized by poorly resolved sets of multi-scale control processes regulating various cell migration modes and antigen-driven functional states of immune cells. Ultimately, the theoretical framework of many modeling studies lacked the necessary quantitative data to faithfully recapitulate the stromal-immune cell interactions. In order to extend the analogy, the simulations would represent a “car with no fuel and no wheels, moving along a random road map.”
An alternative approach to examine the TRC network at a fundamental level would be to employ the theory of complex networks, also called graph theory (86, 87). Within this mathematical framework the TRC network is denoted as a series of nodes (cells) connected with edges (cell protrusions). A recent study demonstrated that the TRCs organize as a non-stochastic small-world network with highly robust topological properties, ensuring that network failure does not occur even when up to half of the network is destroyed (66, 88). Specific genetic ablation of CCL19-producing TRCs led to highly reduced numbers of hematopoietic cells in LNs and impaired intranodal migration of T cells with marked reduction in average cell speed and motility. The few T cells that did enter the LNs exhibited undirected movement around the HEVs and were not able to migrate deeper into the paracortex, despite the conduit system still being present (20, 66). The loss of FRCs and HEVs is also associated with graft-vs.-host disease after allogeneic hematopoietic stem cell transplantation and it has been recently shown that FRCs can prime alloreactive T cells through Delta-like Notch ligands (89, 90). Moreover, the TRC network is capable of fully regenerating after complete ablation and this observation is indicative of a formation of a cost-effective, optimally robust network structure that simply could not have a random configuration (91, 92) (Figure 1B). The heterogeneous topological properties of real world networks could not be explained by the random network model, thus it is likely that these networks evolved by optimizing two competitive selection criteria: high connectivity which confers efficiency of information transfer and low connection cost during formation of the network (93). Likewise, spatial embedding in many real world networks has significant confining effects on the overall topological structure by restricting the formation of long-distance connections (94, 95) (Figure 1B).
The intricate structure of LNs determines organ functionality, however the reverse also holds true; the diverse cellular interactions require a particular underlying structure to be present (96). Although it is widely accepted the TRC network serves as a “road system” for T cell and DC migration (29, 97), it remains unclear whether and to which extent dynamic cell movements are spatially constrained by the intricate network fibers (92, 98). Hence, incorporating quantitative data into integrative models may provide answers to these fundamental questions.
Integrative Lymph Node Models
Maintenance of chemokine gradients by stromal cells is crucial for lymphoid organ development and spatiotemporal segregation of specialized immune cell compartments (99, 100). Chemotaxis in LNs has been modeled using ABMs in order to simulate large numbers of T cells in a computationally efficient manner. By modeling T cell motion as a persistent random walk and allowing for cell crowding on a 3D lattice, a basic T cell ingress-egress model in LNs could be constructed (74). Lymphocytes must navigate efficiently within spatially heterogeneous chemokine fields that also vary over the time course of an immune response. It was shown that temporal sensing of rising chemokine concentrations is required for directional persistence of DC and neutrophil migration (101). Moreover, chemotactic-driven directional movement of DCs is steered by soluble forms of CCL19 and CCL21, whilst immobilized form of CCL21 on FRCs induces both DC motility and integrin-dependent adhesion (102).
Functional chemokine gradients of CCL19 and CCL21 have been simulated in various LN regions using a fluid flow model where the intranodal chemokine dynamics are described by ordinary (ODE) and partial differential equations (PDE) (68). Similarly, using a reaction-diffusion PDE model, highly heterogeneous distribution of IFN-α has been found, where certain LN subdomains are highly protected, whilst others are characterized by much lower levels of the cytokine (62). In a recent theoretical study, it has been demonstrated by reaction-diffusion-advection modeling that hypersensitivity in antigen recognition by immune cells can occur when chemotactic strength is higher than a predicted threshold, leading to immune system instability (69). In the case of cytokine concentration fields, it has been demonstrated that the size of cytokine niches on a single-cell level are governed by a simple mechanism dependent on cytokine diffusion and the density of consumer cells present in the niche (103).
It is important to consider another relevant aspect of LN functionality, namely lymph flow dynamics which contribute greatly to antigen, cytokine and chemokine transport. In order to gain insights into the quantitative flow parameters regulating lymph transport, a computational lymph flow model of the LN was constructed (63, 65). Interestingly, the model predicted that 90% of lymph traveled the peripheral path through the SCS and medullary sinuses. In a subsequent study the authors expanded their computational model to include intranodal CCL19 and CCL21 chemokine gradients (68). An integrative LN model with realistic 3D geometry has been recently developed in order to study lymph transport phenomena (82). The relationship between the structural LN geometry and fluid pathways has been investigated using image-based modeling of fluid flow in order to study the permeability of the LN tissue (64, 71). Furthermore, fluid flow dynamics of the blood microvasculature and the conduit system have been successfully integrated in the existing LN model (67, 70). The model predicted high robustness of the conduit system, with 60–90% elimination of conduits required to halt the lymph flux. Moreover, computational simulations of lymph flow can be expanded on larger spatial scales by modeling the entire human lymphatic system interconnected between hundreds of LNs (84).
In order to model complex biological phenomena with continuous and discrete variables, and across several spatial scales, hybrid and multi-scale modeling approaches are necessary (104–108). In recent years these models have been used to describe spatial dynamics of immune responses in LNs (79–81, 83). A summary of the integrative modeling frameworks described here and their implementation in elaborating LN processes and functions is available in Table 1. These multi-scale modeling approaches will prove invaluable in unraveling complex mechanisms of immune system control in future studies.
Concluding Remarks
Systems biology approaches have made tremendous advances in the past decade due to a high demand for bioinformatics-based computational methods necessary to describe biological systems on a global level (109). Likewise, quantitative and computational in silico models in immunology have become critical for understanding the emergent properties of both single cells and whole tissues (110, 111). However, the development of mathematical LN models is still confronted with technical challenges. Understanding the multi-layered compartmentalization of the LN is an important prerequisite so that the initial assumptions of the model reflect the functionality observed experimentally. To date, our knowledge of the heterogeneity of stromal cells that construct the underlying foundations of a LN is still incomplete. The directional cues und critical immunoregulatory functions of stromal cells enable the formation of specialized micro-environmental niches for immune cells within the LN, effectively facilitating immune responses (11). The described computational models largely do not take into account an additional layer of complexity, which is introduced by the fact that chemoattractant fields significantly change during inflammation and ongoing immune responses, influencing the migration and composition of immune cells. Moreover, the LN stromal compartment undergoes extensive remodeling in order to accommodate the increased LN size and proliferative demands of developing adaptive immune responses (9). Therefore, mathematical models must take into account how the spatial constraints of the LN and heterogeneous chemoattractant gradient fields affect the non-uniform distribution of immune cells, the spatiotemporal dynamics of cellular interactions and the anisotropy of non-Brownian immune cell movement patterns. To this end, quantitative data on immune cell motility metrics in homeostasis and disease/inflammatory states are critically needed for the development and calibration of biophysics-based models.
One major difficulty lies in delineating the complexity of the fundamental LN architecture and simplifying the components to a degree necessary to obtain biologically meaningful conclusions. Morphometric studies have been instrumental in describing the structural framework of distinct LN regions. However, quantitative data is still lacking for the organization of lymphatic endothelium in the medullary region, a comprehensive description of the B follicular stromal cells has not been fully elaborated and the structure of the fine-grained conduit system has not been extensively studied. Absence of detailed structural parameters represents a major caveat in data-driven systems biology approaches (112). Nevertheless, novel high-resolution imaging technologies coupled with multi-scale computational models will give us valuable insights into the inner “clockwork” of the LN.
Author Contributions
All authors contributed to writing the manuscript. Figure and data were generated by H-WC, LO, and MN, table was generated by GB.
Funding
This study received financial support from the Swiss National Science Foundation (grants 166500 and 159188 to BL) and the Russian Science Foundation (grant 18-11-00171 to GB).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Moore JE Jr, Bertram CD. Lymphatic system flows. Annu Rev Fluid Mech. (2018) 50:459–82. doi: 10.1146/annurev-fluid-122316-045259
2. Mebius RE. Organogenesis of lymphoid tissues. Nat Rev Immunol. (2003) 3:292–303. doi: 10.1038/nri1054
3. Onder L, Morbe U, Pikor N, Novkovic M, Cheng HW, Hehlgans T, et al. lymphatic endothelial cells control initiation of lymph node organogenesis. Immunity (2017) 47:80–92.e84. doi: 10.1016/j.immuni.2017.05.008
4. Mueller SN, Germain RN. Stromal cell contributions to the homeostasis and functionality of the immune system. Nat Rev Immunol. (2009) 9:618–29. doi: 10.1038/nri2588
5. Turley SJ, Fletcher AL, Elpek KG. The stromal and haematopoietic antigen-presenting cells that reside in secondary lymphoid organs. Nat Rev Immunol. (2010) 10:813–25. doi: 10.1038/nri2886
6. Malhotra D, Fletcher AL, Turley SJ. Stromal and hematopoietic cells in secondary lymphoid organs: partners in immunity. Immunol Rev. (2013) 251:160–76. doi: 10.1111/imr.12023
7. Mueller SN, Ahmed R. Lymphoid stroma in the initiation and control of immune responses. Immunol Rev. (2008) 224:284–94. doi: 10.1111/j.1600-065X.2008.00657.x
8. Chang JE, Turley SJ. Stromal infrastructure of the lymph node and coordination of immunity. Trends Immunol. (2015) 36:30–9. doi: 10.1016/j.it.2014.11.003
9. Alexandre YO, Mueller SN. Stromal cell networks coordinate immune response generation and maintenance. Immunol Rev. (2018) 283:77–85. doi: 10.1111/imr.12641
10. Fletcher AL, Malhotra D, Acton SE, Lukacs-Kornek V, Bellemare-Pelletier A, Curry M, et al. Reproducible isolation of lymph node stromal cells reveals site-dependent differences in fibroblastic reticular cells. Front Immunol. (2011) 2:35. doi: 10.3389/fimmu.2011.00035
11. Malhotra D, Fletcher AL, Astarita J, Lukacs-Kornek V, Tayalia P, Gonzalez SF, et al. Transcriptional profiling of stroma from inflamed and resting lymph nodes defines immunological hallmarks. Nat Immunol. (2012) 13:499–510. doi: 10.1038/ni.2262
12. Ulvmar MH, Werth K, Braun A, Kelay P, Hub E, Eller K, et al. The atypical chemokine receptor CCRL1 shapes functional CCL21 gradients in lymph nodes. Nat Immunol. (2014) 15:623–30. doi: 10.1038/ni.2889
13. Ansel KM, Harris RB, Cyster JG. CXCL13 is required for B1 cell homing, natural antibody production, and body cavity immunity. Immunity (2002) 16:67–76. doi: 10.1016/s1074-7613(01)00257-6
14. Allen CD, Cyster JG. Follicular dendritic cell networks of primary follicles and germinal centers: phenotype and function. Semin Immunol. (2008) 20:14–25. doi: 10.1016/j.smim.2007.12.001
15. Wang X, Cho B, Suzuki K, Xu Y, Green JA, An J, et al. Follicular dendritic cells help establish follicle identity and promote B cell retention in germinal centers. J Exp Med. (2011) 208:2497–510. doi: 10.1084/jem.20111449
16. Katakai T. Marginal reticular cells: a stromal subset directly descended from the lymphoid tissue organizer. Front Immunol. (2012) 3:200. doi: 10.3389/fimmu.2012.00200
17. Katakai T, Suto H, Sugai M, Gonda H, Togawa A, Suematsu S, et al. Organizer-like reticular stromal cell layer common to adult secondary lymphoid organs. J Immunol. (2008) 181:6189–200. doi: 10.4049/jimmunol.181.9.6189
18. Rodda LB, Lu E, Bennett ML, Sokol CL, Wang X, Luther SA, et al. Single-cell RNA sequencing of lymph node stromal cells reveals niche-associated heterogeneity. Immunity (2018) 48:1014–28.e6. doi: 10.1016/j.immuni.2018.04.006
19. Jarjour M, Jorquera A, Mondor I, Wienert S, Narang P, Coles MC, et al. Fate mapping reveals origin and dynamics of lymph node follicular dendritic cells. J Exp Med. (2014) 211:1109–22. doi: 10.1084/jem.20132409
20. Cremasco V, Woodruff MC, Onder L, Cupovic J, Nieves-Bonilla JM, Schildberg FA, et al. B cell homeostasis and follicle confines are governed by fibroblastic reticular cells. Nat Immunol. (2014) 15:973–81. doi: 10.1038/ni.2965
21. Mionnet C, Mondor I, Jorquera A, Loosveld M, Maurizio J, Arcangeli ML, et al. Identification of a new stromal cell type involved in the regulation of inflamed B cell follicles. PLoS Biol. (2013) 11:e1001672. doi: 10.1371/journal.pbio.1001672
22. Rodda LB, Bannard O, Ludewig B, Nagasawa T, Cyster JG. Phenotypic and morphological properties of germinal center dark zone Cxcl12-expressing reticular cells. J Immunol. (2015) 195:4781–91. doi: 10.4049/jimmunol.1501191
23. Kelch ID, Bogle G, Sands GB, Phillips AR, LeGrice IJ, Dunbar PR. Organ-wide 3D-imaging and topological analysis of the continuous microvascular network in a murine lymph node. Sci Rep. (2015) 5:16534. doi: 10.1038/srep16534
24. Mondor I, Jorquera A, Sene C, Adriouch S, Adams RH, Zhou B, et al. Clonal proliferation and stochastic pruning orchestrate lymph node vasculature remodeling. Immunity (2016) 45:877–88. doi: 10.1016/j.immuni.2016.09.017
25. Forster R, Braun A, Worbs T. Lymph node homing of T cells and dendritic cells via afferent lymphatics. Trends Immunol. (2012) 33:271–80. doi: 10.1016/j.it.2012.02.007
26. Girard JP, Moussion C, Forster R. HEVs, lymphatics and homeostatic immune cell trafficking in lymph nodes. Nat Rev Immunol. (2012) 12:762–73. doi: 10.1038/nri3298
27. Lee M, Kiefel H, LaJevic MD, Macauley MS, Kawashima H, O'Hara E, et al. Transcriptional programs of lymphoid tissue capillary and high endothelium reveal control mechanisms for lymphocyte homing. Nat Immunol. (2014) 15:982–95. doi: 10.1038/ni.2983
28. Katakai T, Hara T, Sugai M, Gonda H, Shimizu A. Lymph node fibroblastic reticular cells construct the stromal reticulum via contact with lymphocytes. J Exp Med. (2004) 200:783–95. doi: 10.1084/jem.20040254
29. Bajenoff M, Egen JG, Koo LY, Laugier JP, Brau F, Glaichenhaus N, et al. Stromal cell networks regulate lymphocyte entry, migration, and territoriality in lymph nodes. Immunity (2006) 25:989–1001. doi: 10.1016/j.immuni.2006.10.011
30. Link A, Vogt TK, Favre S, Britschgi MR, Acha-Orbea H, Hinz B, et al. Fibroblastic reticular cells in lymph nodes regulate the homeostasis of naive T cells. Nat Immunol. (2007) 8:1255–65. doi: 10.1038/ni1513
31. Chai Q, Onder L, Scandella E, Gil-Cruz C, Perez-Shibayama C, Cupovic J, et al. Maturation of lymph node fibroblastic reticular cells from myofibroblastic precursors is critical for antiviral immunity. Immunity (2013) 38:1013–24. doi: 10.1016/j.immuni.2013.03.012
32. Yang CY, Vogt TK, Favre S, Scarpellino L, Huang HY, Tacchini-Cottier F, et al. Trapping of naive lymphocytes triggers rapid growth and remodeling of the fibroblast network in reactive murine lymph nodes. Proc Natl Acad Sci USA. (2014) 111:E109–18. doi: 10.1073/pnas.1312585111
33. Fletcher AL, Acton SE, Knoblich K. Lymph node fibroblastic reticular cells in health and disease. Nat Rev Immunol. (2015) 15:350–61. doi: 10.1038/nri3846
34. Herzog BH, Fu J, Wilson SJ, Hess PR, Sen A, McDaniel JM, et al. Podoplanin maintains high endothelial venule integrity by interacting with platelet CLEC-2. Nature (2013) 502:105–9. doi: 10.1038/nature12501
35. Acton SE, Astarita JL, Malhotra D, Lukacs-Kornek V, Franz B, Hess PR, et al. Podoplanin-rich stromal networks induce dendritic cell motility via activation of the C-type lectin receptor CLEC-2. Immunity (2012) 37:276–89. doi: 10.1016/j.immuni.2012.05.022
36. Acton SE, Farrugia AJ, Astarita JL, Mourao-Sa D, Jenkins RP, Nye E, et al. Dendritic cells control fibroblastic reticular network tension and lymph node expansion. Nature (2014) 514:498–502. doi: 10.1038/nature13814
37. Astarita JL, Cremasco V, Fu J, Darnell MC, Peck JR, Nieves-Bonilla JM, et al. The CLEC-2-podoplanin axis controls the contractility of fibroblastic reticular cells and lymph node microarchitecture. Nat Immunol. (2015) 16:75–84. doi: 10.1038/ni.3035
38. Kumar V, Dasoveanu DC, Chyou S, Tzeng TC, Rozo C, Liang Y, et al. A dendritic-cell-stromal axis maintains immune responses in lymph nodes. Immunity (2015) 42:719–30. doi: 10.1016/j.immuni.2015.03.015
39. Buechler MB, Turley SJ. A short field guide to fibroblast function in immunity. Semin Immunol. (2018) 35:48–58. doi: 10.1016/j.smim.2017.11.001
40. Gretz JE, Anderson AO, Shaw S. Cords, channels, corridors and conduits: critical architectural elements facilitating cell interactions in the lymph node cortex. Immunol Rev. (1997) 156:11–24. doi: 10.1111/j.1600-065X.1997.tb00955.x
41. Gretz JE, Norbury CC, Anderson AO, Proudfoot AE, Shaw S. Lymph-borne chemokines and other low molecular weight molecules reach high endothelial venules via specialized conduits while a functional barrier limits access to the lymphocyte microenvironments in lymph node cortex. J Exp Med. (2000) 192:1425–40. doi: 10.1084/jem.192.10.1425
42. Bajenoff M, Germain RN. B-cell follicle development remodels the conduit system and allows soluble antigen delivery to follicular dendritic cells. Blood (2009) 114:4989–97. doi: 10.1182/blood-2009-06-229567
43. Sixt M, Kanazawa N, Selg M, Samson T, Roos G, Reinhardt DP, et al. The conduit system transports soluble antigens from the afferent lymph to resident dendritic cells in the T cell area of the lymph node. Immunity (2005) 22:19–29. doi: 10.1016/j.immuni.2004.11.013
44. Roozendaal R, Mempel TR, Pitcher LA, Gonzalez SF, Verschoor A, Mebius RE, et al. Conduits mediate transport of low-molecular-weight antigen to lymph node follicles. Immunity (2009) 30:264–76. doi: 10.1016/j.immuni.2008.12.014
45. Rantakari P, Auvinen K, Jappinen N, Kapraali M, Valtonen J, Karikoski M, et al. The endothelial protein PLVAP in lymphatics controls the entry of lymphocytes and antigens into lymph nodes. Nat Immunol. (2015) 16:386–96. doi: 10.1038/ni.3101
46. Grigorova IL, Schwab SR, Phan TG, Pham TH, Okada T, Cyster JG. Cortical sinus probing, S1P1-dependent entry and flow-based capture of egressing T cells. Nat Immunol. (2009) 10:58–65. doi: 10.1038/ni.1682
47. Grigorova IL, Panteleev M, Cyster JG. Lymph node cortical sinus organization and relationship to lymphocyte egress dynamics and antigen exposure. Proc Natl Acad Sci USA. (2010) 107:20447–52. doi: 10.1073/pnas.1009968107
48. Pham TH, Baluk P, Xu Y, Grigorova I, Bankovich AJ, Pappu R, et al. Lymphatic endothelial cell sphingosine kinase activity is required for lymphocyte egress and lymphatic patterning. J Exp Med. (2010) 207:17–27. doi: 10.1084/jem.20091619
49. Krummel MF, Bartumeus F, Gerard A. T cell migration, search strategies and mechanisms. Nat Rev Immunol. (2016) 16:193–201. doi: 10.1038/nri.2015.16
50. Katakai T, Kinashi T. Microenvironmental control of high-speed interstitial T cell migration in the lymph node. Front Immunol. (2016) 7:194. doi: 10.3389/fimmu.2016.00194
51. Katakai T, Habiro K, Kinashi T. Dendritic cells regulate high-speed interstitial T cell migration in the lymph node via LFA-1/ICAM-1. J Immunol. (2013) 191:1188–99. doi: 10.4049/jimmunol.1300739
52. Takeda A, Kobayashi D, Aoi K, Sasaki N, Sugiura Y, Igarashi H, et al. Fibroblastic reticular cell-derived lysophosphatidic acid regulates confined intranodal T-cell motility. Elife (2016) 5:e10561. doi: 10.7554/eLife.10561
53. Hons M, Kopf A, Hauschild R, Leithner A, Gaertner F, Abe J, et al. Chemokines and integrins independently tune actin flow and substrate friction during intranodal migration of T cells. Nat Immunol. (2018) 19:606–16. doi: 10.1038/s41590-018-0109-z
54. Oakes PW, Fowell DJ. CCR7 fuels and LFA-1 grips. Nat Immunol. (2018) 19:516–8. doi: 10.1038/s41590-018-0118-y
55. Textor J, Henrickson SE, Mandl JN, von Andrian UH, Westermann J, de Boer RJ, et al. Random migration and signal integration promote rapid and robust T cell recruitment. PLoS Comput Biol. (2014) 10:e1003752. doi: 10.1371/journal.pcbi.1003752
56. Hugues S, Scholer A, Boissonnas A, Nussbaum A, Combadiere C, Amigorena S, et al. Dynamic imaging of chemokine-dependent CD8+ T cell help for CD8+ T cell responses. Nat Immunol. (2007) 8:921–30. doi: 10.1038/ni1495
57. Mandl JN, Liou R, Klauschen F, Vrisekoop N, Monteiro JP, Yates AJ, et al. Quantification of lymph node transit times reveals differences in antigen surveillance strategies of naive CD4+ and CD8+ T cells. Proc Natl Acad Sci USA. (2012) 109:18036–41. doi: 10.1073/pnas.1211717109
58. Kastenmuller W, Brandes M, Wang Z, Herz J, Egen JG, Germain RN. Peripheral prepositioning and local CXCL9 chemokine-mediated guidance orchestrate rapid memory CD8+ T cell responses in the lymph node. Immunity (2013) 38:502–13. doi: 10.1016/j.immuni.2012.11.012
59. Banigan EJ, Harris TH, Christian DA, Hunter CA, Liu AJ. Heterogeneous CD8+ T cell migration in the lymph node in the absence of inflammation revealed by quantitative migration analysis. PLoS Comput Biol. (2015) 11:e1004058. doi: 10.1371/journal.pcbi.1004058
60. Harris TH, Banigan EJ, Christian DA, Konradt C, Tait Wojno ED, Norose K, et al. Generalized Levy walks and the role of chemokines in migration of effector CD8+ T cells. Nature (2012) 486:545–8. doi: 10.1038/nature11098
61. Fricke GM, Letendre KA, Moses ME, Cannon JL. Persistence and adaptation in immunity: T cells balance the extent and thoroughness of search. PLoS Comput Biol. (2016) 12:e1004818. doi: 10.1371/journal.pcbi.1004818
62. Bocharov G, Danilov A, Vassilevski Y, Marchuk G, Chereshnev V, Ludewig B. Reaction-diffusion modeling of interferon distribution in secondary lymphoid organs. Math Model Nat Phenom. (2011) 6:13–26. doi: 10.1051/mmnp/20116702
63. Jafarnejad M, Woodruff MC, Zawieja DC, Carroll MC, Moore JE Jr. Modeling lymph flow and fluid exchange with blood vessels in lymph nodes. Lymphat Res Biol. (2015) 13:234–47. doi: 10.1089/lrb.2015.0028
64. Cooper LJ, Heppell JP, Clough GF, Ganapathisubramani B, Roose T. An image-based model of fluid flow through lymph nodes. Bull Math Biol. (2016) 78:52–71. doi: 10.1007/s11538-015-0128-y
65. Jamalian S, Davis MJ, Zawieja DC, Moore JE Jr. Network scale modeling of lymph transport and its effective pumping parameters. PLoS ONE (2016) 11:e0148384. doi: 10.1371/journal.pone.0148384
66. Novkovic M, Onder L, Cupovic J, Abe J, Bomze D, Cremasco V, et al. Topological small-world organization of the fibroblastic reticular cell network determines lymph node functionality. PLoS Biol. (2016) 14:e1002515. doi: 10.1371/journal.pbio.1002515
67. Grebennikov D, van Loon R, Novkovic M, Onder L, Savinkov R, Sazonov I, et al. Critical issues in modeling lymph node physiology. Computation (2017) 5:3. doi: 10.3390/computation5010003
68. Jafarnejad M, Zawieja DC, Brook BS, Nibbs RJB, Moore JE Jr. A novel computational model predicts key regulators of chemokine gradient formation in lymph nodes and site-specific roles for CCL19 and ACKR4. J Immunol. (2017) 199:2291–304. doi: 10.4049/jimmunol.1700377
69. Lee S, Kim SW, Oh Y, Hwang HJ. Mathematical modeling and its analysis for instability of the immune system induced by chemotaxis. J Math Biol. (2017) 75:1101–31. doi: 10.1007/s00285-017-1108-7
70. Savinkov R, Kislitsyn A, Watson DJ, Loon RV, Sazonov I, Novkovic M, et al. Data-driven modeling of the FRC network for studying the fluid flow in the conduit system. Eng Appl Artificial Intelligence (2017) 62:341–9. doi: 10.1016/j.engappai.2016.10.007
71. Cooper L, Zeller-Plumhoff B, Clough G, Ganapathisubramani B, Roose T. Using high resolution X-ray computed tomography to create an image based model of a lymph node. J Theor Biol. (2018) 449:73–82. doi: 10.1016/j.jtbi.2018.04.021
72. Tasnim H, Fricke GM, Byrum JR, Sotiris JO, Cannon JL, Moses ME. Quantitative measurement of naive T cell association with dendritic cells, FRCs, and blood vessels in lymph nodes. Front Immunol. (2018) 9:1571. doi: 10.3389/fimmu.2018.01571
73. Beltman JB, Maree AF, Lynch JN, Miller MJ, de Boer RJ. Lymph node topology dictates T cell migration behavior. J Exp Med. (2007) 204:771–80. doi: 10.1084/jem.20061278
74. Bogle G, Dunbar PR. On-lattice simulation of T cell motility, chemotaxis, and trafficking in the lymph node paracortex. PLoS ONE (2012) 7:e45258. doi: 10.1371/journal.pone.0045258
75. Donovan GM, Lythe G. T-cell movement on the reticular network. J Theor Biol. (2012) 295:59–67. doi: 10.1016/j.jtbi.2011.11.001
76. Graw F, Regoes RR. Influence of the fibroblastic reticular network on cell-cell interactions in lymphoid organs. PLoS Comput Biol. (2012) 8:e1002436. doi: 10.1371/journal.pcbi.1002436
77. Gong C, Mattila JT, Miller M, Flynn JL, Linderman JJ, Kirschner D. Predicting lymph node output efficiency using systems biology. J Theor Biol. (2013) 335:169–84. doi: 10.1016/j.jtbi.2013.06.016
78. Read MN, Bailey J, Timmis J, Chtanova T. Leukocyte motility models assessed through simulation and multi-objective optimization-based model selection. PLoS Comput Biol. (2016) 12:e1005082. doi: 10.1371/journal.pcbi.1005082
79. Baldazzi V, Paci P, Bernaschi M, Castiglione F. Modeling lymphocyte homing and encounters in lymph nodes. BMC Bioinformatics (2009) 10:387. doi: 10.1186/1471-2105-10-387
80. Palsson S, Hickling TP, Bradshaw-Pierce EL, Zager M, Jooss K, O'Brien PJ, et al. The development of a fully-integrated immune response model (FIRM) simulator of the immune response through integration of multiple subset models. BMC Syst Biol. (2013) 7:95. doi: 10.1186/1752-0509-7-95
81. Prokopiou S, Barbarroux L, Bernard S, Mafille J, Leverrier Y, Arpin C, et al. Multiscale modeling of the early CD8 T-cell immune response in lymph nodes: an integrative study. Computation (2014) 2:159. doi: 10.3390/computation2040159
82. Kislitsyn A, Savinkov R, Novkovic M, Onder L, Bocharov G. Computational approach to 3D modeling of the lymph node geometry. Computation (2015) 3:222. doi: 10.3390/computation3020222
83. Bouchnita A, Bocharov G, Meyerhans A, Volpert V. Hybrid approach to model the spatial regulation of T cell responses. BMC Immunol. (2017) 18:29. doi: 10.1186/s12865-017-0205-0
84. Tretyakova R, Savinkov R, Lobov G, Bocharov G. Developing computational geometry and network graph models of human lymphatic system. Computation (2018) 6:1. doi: 10.3390/computation6010001
85. Camley BA, Rappel WJ. Physical models of collective cell motility: from cell to tissue. J Phys D Appl Phys. (2017) 50:113002. doi: 10.1088/1361-6463/aa56fe
86. Newman ME. The structure and function of complex networks. SIAM Rev. (2003) 45:167–256. doi: 10.1137/S003614450342480
87. Subramanian N, Torabi-Parizi P, Gottschalk RA, Germain RN, Dutta B. Network representations of immune system complexity. Wiley Interdiscip Rev Syst Biol Med. (2015) 7:13–38. doi: 10.1002/wsbm.1288
88. Novkovic M, Onder L, Bocharov G, Ludewig B. Graph theory-based analysis of the lymph node fibroblastic reticular cell network. Methods Mol Biol. (2017) 1591:43–57. doi: 10.1007/978-1-4939-6931-9_4
89. Suenaga F, Ueha S, Abe J, Kosugi-Kanaya M, Wang Y, Yokoyama A, et al. Loss of lymph node fibroblastic reticular cells and high endothelial cells is associated with humoral immunodeficiency in mouse graft-versus-host disease. J Immunol. (2015) 194:398–406. doi: 10.4049/jimmunol.1401022
90. Chung J, Ebens CL, Perkey E, Radojcic V, Koch U, Scarpellino L, et al. Fibroblastic niches prime T cell alloimmunity through Delta-like Notch ligands. J Clin Invest. (2017) 127:1574–88. doi: 10.1172/JCI89535
91. Barabasi AL, Oltvai ZN. Network biology: understanding the cell's functional organization. Nat Rev Genet. (2004) 5:101–13. doi: 10.1038/nrg1272
92. Wong HS, Germain RN. Robust control of the adaptive immune system. Semin Immunol. (2018) 36:17–27. doi: 10.1016/j.smim.2017.12.009
93. Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. (2009) 10:186–98. doi: 10.1038/nrn2575
94. Barrat A, Barthélemy M, Vespignani A. The effects of spatial constraints on the evolution of weighted complex networks. J Stat Mech. (2005) 2005:P05003. doi: 10.1088/1742-5468/2005/05/p05003
96. Junt T, Scandella E, Ludewig B. Form follows function: lymphoid tissue microarchitecture in antimicrobial immune defence. Nat Rev Immunol. (2008) 8:764–75. doi: 10.1038/nri2414
97. Mempel TR, Junt T, von Andrian UH. Rulers over randomness: stroma cells guide lymphocyte migration in lymph nodes. Immunity (2006) 25:867–9. doi: 10.1016/j.immuni.2006.11.002
98. Textor J, Mandl JN, de Boer RJ. The reticular cell network: a robust backbone for immune responses. PLoS Biol. (2016) 14:e2000827. doi: 10.1371/journal.pbio.2000827
99. Mueller SN, Hosiawa-Meagher KA, Konieczny BT, Sullivan BM, Bachmann MF, Locksley RM, et al. Regulation of homeostatic chemokine expression and cell trafficking during immune responses. Science (2007) 317:670–4. doi: 10.1126/science.1144830
100. Moore JE, Brook BS, Nibbs RJB. Chemokine transport dynamics and emerging recognition of their role in immune function. Curr Opin Biomed Eng. (2018) 5:90–5. doi: 10.1016/j.cobme.2018.03.001
101. Petrie Aronin CE, Zhao YM, Yoon JS, Morgan NY, Prustel T, Germain RN, et al. Migrating myeloid cells sense temporal dynamics of chemoattractant concentrations. Immunity (2017) 47:862–74.e863. doi: 10.1016/j.immuni.2017.10.020
102. Schumann K, Lammermann T, Bruckner M, Legler DF, Polleux J, Spatz JP, et al. Immobilized chemokine fields and soluble chemokine gradients cooperatively shape migration patterns of dendritic cells. Immunity (2010) 32:703–13. doi: 10.1016/j.immuni.2010.04.017
103. Oyler-Yaniv A, Oyler-Yaniv J, Whitlock BM, Liu Z, Germain RN, Huse M, et al. A tunable diffusion-consumption mechanism of cytokine propagation enables plasticity in cell-to-cell communication in the immune system. Immunity (2017) 46:609–20. doi: 10.1016/j.immuni.2017.03.011
104. Southern J, Pitt-Francis J, Whiteley J, Stokeley D, Kobashi H, Nobes R, et al. Multi-scale computational modeling in biology and physiology. Prog Biophys Mol Biol. (2008) 96:60–89. doi: 10.1016/j.pbiomolbio.2007.07.019
105. Dada JO, Mendes P. Multi-scale modeling and simulation in systems biology. Integr Biol. (2011) 3:86–96. doi: 10.1039/c0ib00075b
106. Cappuccio A, Tieri P, Castiglione F. Multiscale modeling in immunology: a review. Brief Bioinform. (2016) 17:408–18. doi: 10.1093/bib/bbv012
107. Stéphanou A, Volpert V. Hybrid modeling in biology: a classification review. Math Model Nat Phenom. (2016) 11:37–48. doi: 10.1051/mmnp/201611103
108. Bocharov G, Volpert V, Ludewig B, Meyerhans A, editors. Multi-scale and integrative modeling approaches. In: Mathematical Immunology of Virus Infections. Cham: Springer International Publishing (2018). p. 221–42.
109. Germain RN, Meier-Schellersheim M, Nita-Lazar A, Fraser ID. Systems biology in immunology: a computational modeling perspective. Annu Rev Immunol. (2011) 29:527–85. doi: 10.1146/annurev-immunol-030409-101317
110. Mirsky HP, Miller MJ, Linderman JJ, Kirschner DE. Systems biology approaches for understanding cellular mechanisms of immunity in lymph nodes during infection. J Theor Biol. (2011) 287:160–70. doi: 10.1016/j.jtbi.2011.06.037
111. Narang V, Decraene J, Wong SY, Aiswarya BS, Wasem AR, Leong SR, et al. Systems immunology: a survey of modeling formalisms, applications and simulation tools. Immunol Res. (2012) 53:251–65. doi: 10.1007/s12026-012-8305-7
Keywords: lymph node, stromal cells, systems biology, network topology, morphology, lymph flow, fibroblastic reticular cells, computational models
Citation: Novkovic M, Onder L, Cheng H-W, Bocharov G and Ludewig B (2018) Integrative Computational Modeling of the Lymph Node Stromal Cell Landscape. Front. Immunol. 9:2428. doi: 10.3389/fimmu.2018.02428
Received: 20 August 2018; Accepted: 02 October 2018;
Published: 23 October 2018.
Edited by:
Matteo Iannacone, San Raffaele Hospital (IRCCS), ItalyReviewed by:
Scott N. Mueller, The University of Melbourne, AustraliaSophie Acton, University College London, United Kingdom
Copyright © 2018 Novkovic, Onder, Cheng, Bocharov and Ludewig. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mario Novkovic, bWFyaW8ubm92a292aWNAa3NzZy5jaA==
 Mario Novkovic
Mario Novkovic Lucas Onder
Lucas Onder Hung-Wei Cheng
Hung-Wei Cheng Gennady Bocharov
Gennady Bocharov Burkhard Ludewig
Burkhard Ludewig