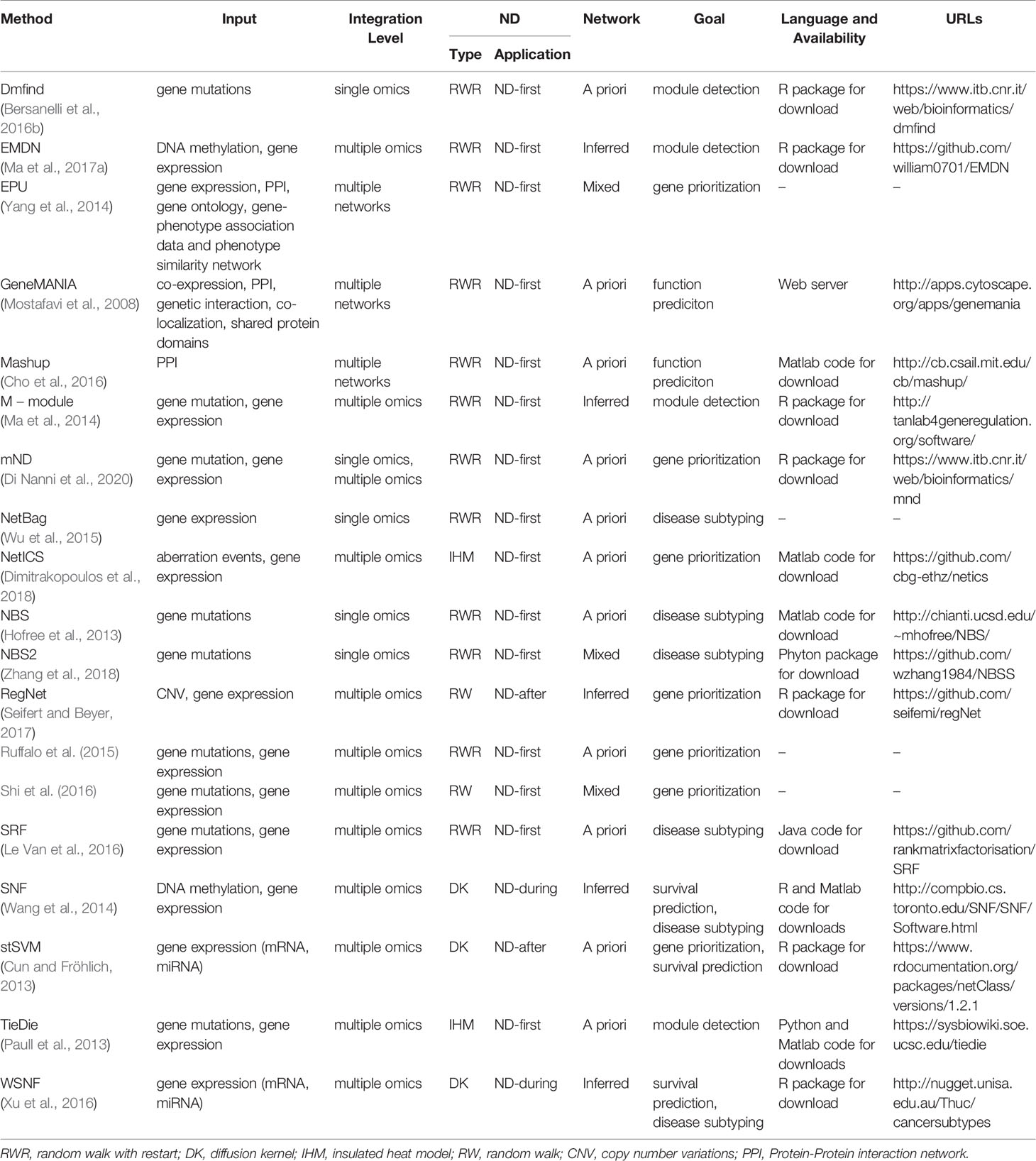
- 1Institute of Biomedical Technologies, National Research Council, Milan, Italy
- 2Department of Industrial and Information Engineering, University of Pavia, Pavia, Italy
- 3Department of Physics and Astronomy, University of Bologna, Bologna, Italy
- 4National Institute of Nuclear Physics (INFN), Bologna, Italy
The development of integrative methods is one of the main challenges in bioinformatics. Network-based methods for the analysis of multiple gene-centered datasets take into account known and/or inferred relations between genes. In the last decades, the mathematical machinery of network diffusion—also referred to as network propagation—has been exploited in several network-based pipelines, thanks to its ability of amplifying association between genes that lie in network proximity. Indeed, network diffusion provides a quantitative estimation of network proximity between genes associated with one or more different data types, from simple binary vectors to real vectors. Therefore, this powerful data transformation method has also been increasingly used in integrative analyses of multiple collections of biological scores and/or one or more interaction networks. We present an overview of the state of the art of bioinformatics pipelines that use network diffusion processes for the integrative analysis of omics data. We discuss the fundamental ways in which network diffusion is exploited, open issues and potential developments in the field. Current trends suggest that network diffusion is a tool of broad utility in omics data analysis. It is reasonable to think that it will continue to be used and further refined as new data types arise (e.g. single cell datasets) and the identification of system-level patterns will be considered more and more important in omics data analysis.
Introduction
“Omics” technologies provide data related to different types of molecular entities (e.g. DNAs, RNAs, proteins) at increasing sensitivity, down to single-cell level (Hu et al., 2018). This offers the opportunity for integrative analyses that lead to a more comprehensive view of a biological system (Higdon et al., 2015; Karczewski and Snyder, 2018). However, integrative analyses involve several issues due to types of biological information considered, coverage of the pool of molecular entities under investigation, data distribution types, noise and research questions that need to be addressed (Ritchie et al., 2015; Ahmad and Fröhlich, 2016; Huang et al., 2017), just to mention a few. Therefore, the development of integrative methods is one of the main challenges in bioinformatics.
Integrative methods can be classified in three groups by objective (Figure 1A): understanding of the molecular mechanisms (e.g. genes prioritization, function prediction, module detection), clustering of samples (e.g. identification of disease subtypes) or prediction of samples' outcome/phenotype (e.g. survival) (Kristensen et al., 2014). These three objectives can be achieved using a single type or multiple types of omics, possibly combined with data about molecular networks (Figure 1B), in a supervised or unsupervised settings.
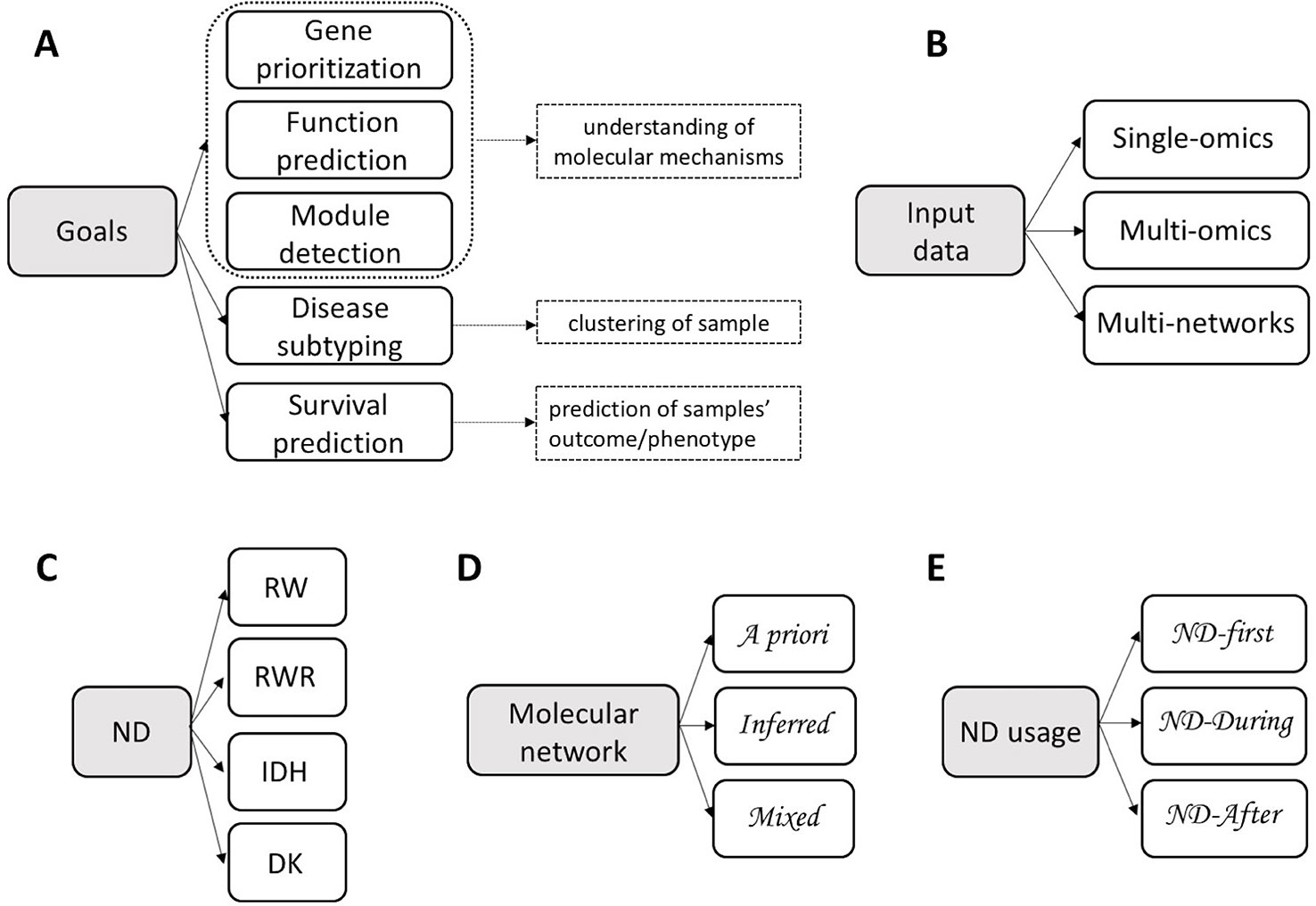
Figure 1 Classification of integrative methods. Criteria: (A) Goals; (B) Input data; (C) Network Diffusion (ND) model: Random Walk (RW), Random Walk with Restart (RWR), Insulated Heat Diffusion (IHD), Diffusion Kernel (DK); (D) Molecular network; (E) ND usage.
From a methodological point of view, the arising importance of interaction networks and the type of statistical approach pave the way for a first broad classification of integrative methods. In particular, these can be divided into four broad classes depending on whether they use molecular networks and Bayesian theory: network-free non-Bayesian, network-free Bayesian, network-based non-Bayesian and network-based Bayesian (Bersanelli et al., 2016a).
Molecular networks represent a powerful framework to integrate and explain omics datasets (Bersanelli et al., 2016a; Yan et al., 2017; Su et al., 2018). Indeed, the interactome, a term that designates the whole set of macromolecular interactions within a cell, could underlie most genotype to phenotype relationships (Vidal et al., 2011) and can be used to guide our understanding of how alterations detected by omics technologies perturb the system as a whole (Caldera et al., 2017). A known system-level pattern is, for instance, the presence of gene networks that are “hot” spots of mutations in cancer and reflect the several possible combinations of mutations that are likely to lead to the similar pathological phenotype, because affect the same pathways (Barabási et al., 2011; Boyle et al., 2017). More generally, network-based approaches enable the study of the relation between the topological and dynamical properties of a network and the biological system modelled by means of the network. For example, the distance between genes in a gene network is related to the functional similarity of the genes (Sharan et al., 2007) and their involvement in the same disease (Barabási et al., 2011). It is important to underline that network-based and network-free approaches to multi-omics data analysis can be combined within the same pipeline. For instance, a multivariate analysis for disease stratification can be performed using a (network free) classic multivariate regression and, then, the results can be further refined considering a network-based method.
In the last decades, the mathematical machinery of network diffusion (ND)—also referred to as network propagation—has been exploited in many network-based pipelines with different aims, like gene prioritization, gene module identification, drug target prediction and disease subtyping, thanks to its ability of amplifying association between variables (e.g. genes) that lie in network proximity (Cowen et al., 2017). Another important class of network-based approaches is the one inspired by percolation theory (Aleta and Moreno, 2019). One of the main applications of this theory is the study of robustness of biological systems, but also in finance and social networks (Reis et al., 2014; Brummitt and Kobayashi, 2015; Baggio et al., 2016; Gao et al., 2016).
ND has been incorporated in many pipelines that jointly analyse biological networks and multiple collections of scores (“layers”) derived from omics assays. These ND-based methods for multi-omics data analysis will be the main focus of this review.
The success of ND can be brought back to a series of benefits. Considering gene-centric datasets as a practical example, first of all, ND is a powerful way to embed the information about molecular interactions among genes into a gene-wise dataset. ND quantifies the proximity between genes in a global way, that is considering all possible paths among the genes, capturing the complexity of biological networks beyond the limits of local approaches (e.g. shortest path length) (Wang and Marcotte, 2010). ND highlights genes in network proximity and with high input scores. By so doing, it amplifies genetic associations according to the architecture of the molecular network, a result that offers insights in agreement with the so-called local hypothesis; that is, the hypothesis that genes that lie in network proximity within molecular networks co-work in the development of cellular functions and are therefore co-responsible for pathological phenotypes (Barabási et al., 2011). Moreover, by a data analysis perspective, ND transforms sparse input vectors into dense vectors. This operation eliminates missing values and ties, two situations that are often difficult to handle. This imputation step facilitates the joint analysis of different data types and is particularly important in the integration of multiple omics that vary in scope and coverage. For instance, mutations may affect just a few tens of genes of a tumor cell, while gene expression changes are observed for a much higher number of genes. More generally, in a multi-omic analysis of a biological process, only a subset of the genes is associated with the various types of measured alterations. In this context, ND can be used to highlight common network regions where different types of omics signals converge. ND can be performed not only at early stages of the integration pipeline (e.g. data imputation), but also at later stages, for instance to refine the results on the basis of molecular network data. Lastly, ND is suitable to analyse patient-level molecular profiles, promoting studies within the scope of precision medicine.
Recently, Cowen et al. (2017) provided a general overview of the unifying mathematical machinery of ND, showing its broad utility in several problems of genetic research, while, previously, Wang and Marcotte (2010) described the application of ND to the problem of predicting gene function and phenotype. Here, we focus on the use of ND in multi-omics data analysis. We extend previous studies by adding recent developments in the field. We will give hints on molecular networks, the scaffolding on which ND takes place. Then, we will summarize the mathematical machinery of ND. Lastly, we will review the integrative methods that use ND by aim, input data type, molecular network, way in which ND is exploited during the integrative analysis and application. The trends of recent works suggest that ND will continue to be used and further developed to meet the requirements of novel research questions that arise as novel data types will be more and more available, like single cell datasets.
MoleculaR Networks: The Scaffolding for Diffusion
Network-based methods require, by definition, a molecular network that enters the analysis pipeline at some point. The complex web of molecular interactions that occur within human cells is often referred to as “interactome” (Barabási et al., 2011). Such interactions can be of rather different types and are usually distinguished in two classes: biophysical and functional (Caldera et al., 2017). Biophysical interactions indicate actual molecular contact between two molecular entities, such as protein–DNA biding or protein–protein binding in a protein complex. Functional interactions indicate any kind of biologically relevant interaction (at the molecular scale), like co-expression or synthetic lethality.
There is still no unique reference for the human interactome (Luck et al., 2017), but several efforts are underway. Four proteome-scale PPI interaction maps have been recently generated using different high-throughput approaches based on binary interaction or complex mapping (Luck et al., 2017). The Genotype-Tissue Expression (GTEx) project aims at the construction of a specific network for each major human tissue (GTEx Consortium, 2015). Projects like ENCODE97 and the Roadmap Epigenomics provide data about gene regulatory networks (Kellis et al., 2014; Kundaje et al., 2015). The IMEx Consortium is an international collaboration of major public interaction data providers aimed at establishing a non-redundant set of biophysical molecular interactions (Orchard et al., 2012). In addition to primary databases, which collect curated experimental data from small and/or large scale studies, there are several meta-databases, which integrate data from several primary databases, and prediction-databases, which also provide predicted (biophysical and/or functional) interactions obtained from the analysis of biological datasets (De Las Rivas and Fontanillo, 2010).
Multiple collections of scores can be mapped on molecular networks in rather different ways, depending on data types and data analysis purposes. We can classify the resulting networks in three broad categories: multi-weighted networks, multiplex networks and networks of networks.
In a multi-weighted network, a series of weights are associated with nodes and/or links. For instance, the same biological network can be characterized by different omics weights on different layers (e.g. gene expression, methylation, somatic mutations). A multi-weighted network therefore consists of a single-layer network with multiple attributes associated with the same nodes and links, but sometimes can be referred to as a multi-layer network.
Two categories of structural multi-layer networks are multiplex networks and networks of networks. A multiplex is a collection of networks with the same set of nodes and varying intra-layer topologies and inter-layer relationships are trivially given (Menichetti et al., 2014).
A network of networks (sometimes also referred to as heterogeneous networks) is a collection of networks with different nodes (in principle also representing entities of different nature) with multiple types of connections (specific intra-layer links and specific inter-layer connections) (Kivelä et al., 2014). The classification of multi-layer networks is indeed non-trivial; for instance, the categories described can have significant overlaps. It is possible to build hybrid networks where on a core multiplex some layer-specific nodes and links are introduced and consequently different types of inter-layer links are established; for more details about multilayer networks and their classification see the work of Kivelä et al. (2014).
Mathematics of the Network Diffusion Process
ND processes can be summarized as the spreading of biological information throughout the network along network edges, initially retained in the so-called “seed nodes”. Each node will therefore gain or lose biological information according to the network proximity to the seeds and to its topological features. ND is realized by means of different methods that can be brought back to random walks, random walks with restarts and diffusion kernels.
From a mathematical perspective, considering a network G of n nodes, the biological information is encoded in an n-dimensional array x0 where the i-th entry accounts for the amount of biological signal initially present in node i. We can therefore define x0 as the initial state of the network. Then, starting from t=0 up to a fixed time (finite or infinite) the state of the network xt evolves according to the network topology until it reaches a final state xT, where, as previously mentioned, T can either a finite or an infinite time. Under the appropriate settings, when T=∞, the final state of the diffusive algorithm may correspond to a steady state or steady-flow state of an associated physical model, allowing a clear interpretation of the results (Bersanelli et al., 2016b).
In general, the final state of a diffusion process consists of a graph-based transformation fG of the initial biological information x0, which is linear in most cases so that fG reduces to a matrix MG and
We classify the diffusion processes used by integrative methods, similarly to Cowen et al. (2017), on the basis of the specific transformation MG in four categories (Table 1 and Figure 1C):
1. Random Walk (RW): ;
2. Random Walk with Restart (RWR): ;
3. Insulated Heat Diffusion (IHD): ;
4. Diffusion Kernel (DK): MG = eα(D−A).
Here above, A is the adjacency matrix of the network, D is a diagonal matrix of nodes degree (number of interactions), k is the number of time-steps and α∈(0,1) is a tuning parameter. Differently from Cowen et al. (2017) we choose to differentiate between RWR and IHD. In fact, the different normalization of the adjacency matrix A (symmetric for the RWR, column normalization for the IHD) implies different behaviours in the relative diffusion processes. Indeed, the RWR implies a symmetric diffusion where information flows through each link with the same intensity in each direction (Vanunu et al., 2010). Conversely, IHD implies an asymmetric diffusion where information (or heat) tends to flow out from highly connected nodes much easier than from poorly connected ones (Leiserson et al., 2015). Such differences in the diffusion matrix therefore imply dissimilar behaviours of information flow, mainly in relation to network hubs: at infinite time in the RWR hubs tend to naturally gather relatively more information than in the IHD, since IHD is characterized by an intrinsic hub penalization. Therefore, despite RWR and IHD are conceptually similar, they may present sensibly different results, especially when applied to complex biological networks with thousands of vertices and tens to hundreds thousands links.
Independently from the specific kind of diffusion model, the matrix MG is usually hard to recover analytically because it implies inverting or power-expanding a high-dimensional graph-based transition matrix: alternative numerical approaches would be needed and the direct inversion of the matrix MG is possibly replaced with converging iterative procedures (Zhou et al., 2004).
The choice of the most appropriate diffusion process depends on the goal of the analysis. For instance, if one is interested only in considering a local neighborhood of the seeds may choose RW with a finite number of steps (Cun and Fröhlich, 2013), while RWR and IHD quantify network proximity to seeds considering simultaneously all the possible network paths among network nodes (Hofree et al., 2013; Leiserson et al., 2015).
Network Diffusion in Integrative Data Analysis
ND requires data about the variables (x0) and about their relations (A). An important difference between integrative methods that use ND concerns the type of network in use, that is the way in which the adjacency matrix is defined. Three broad categories can be recognized (Table 1 and Figure 1D): the topology of the network in use can be defined by means of a priori knowledge, e.g. collected from molecular interactions databases; alternatively, a network can be inferred from the analysis of one or more biological datasets; lastly, a mixed approach that combines a priori and novel knowledge is possible.
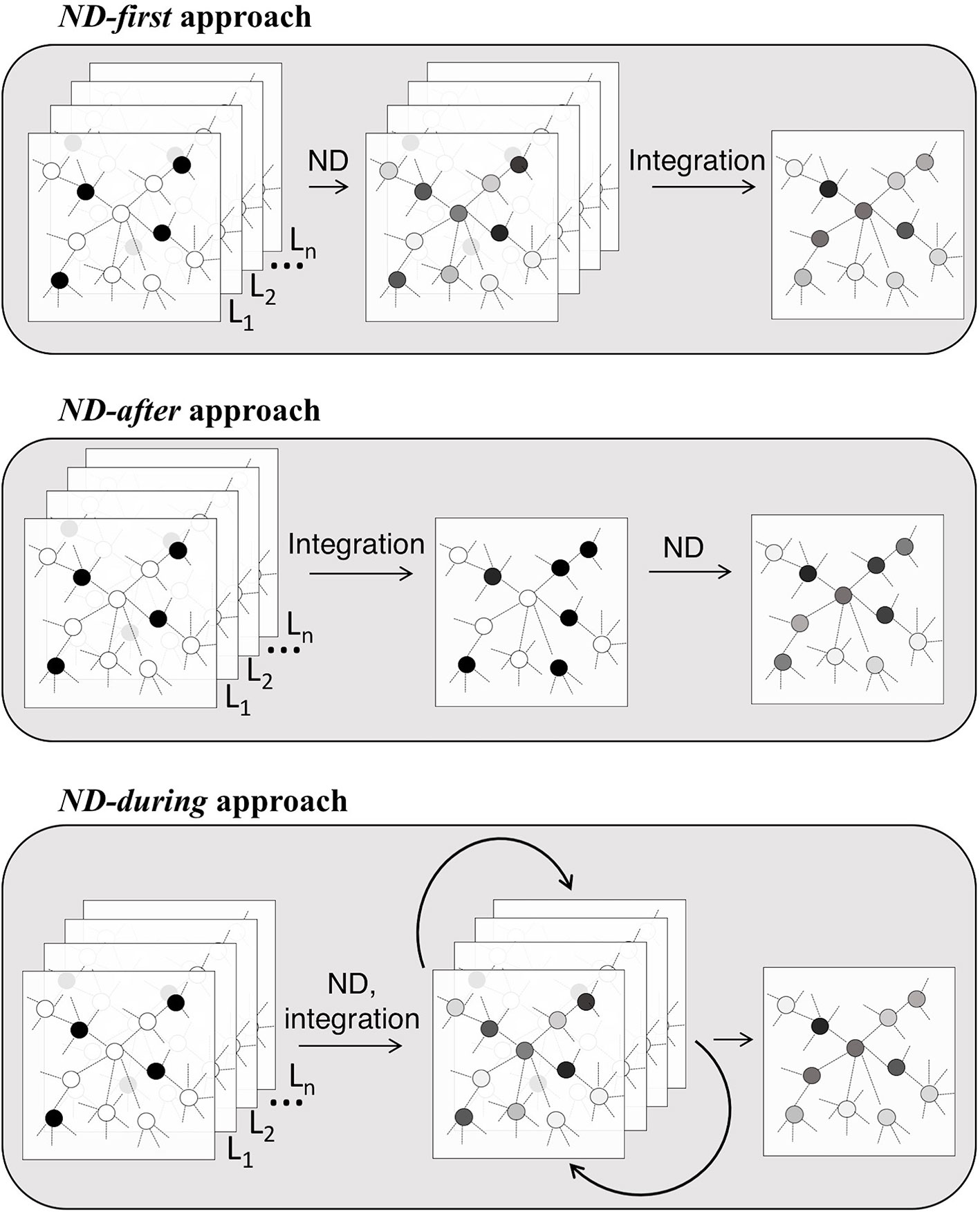
ND can be applied before, after or during the “integration step” of the analysis pipeline (Table 1 and Figures 1E, 2). In the ND-first approach, ND is applied to a series of collections of initial scores, each of which summarizes data of a single sample or multiple samples; the resulting collections of ND scores are subsequently integrated. An example of this approach is TieDIE (Paull et al., 2013), where ND is applied to two collections of scores, one representing mutated genes while the other differentially expressed genes, on the same network; the two resulting ND score vectors are then jointly analysed and the minimum of the two ND scores of a gene is considered as the one chosen for the gene.
The ND-after approach consists in the application of ND after a first process of integration of different data types into a unique structure. For instance, stSVM (Cun and Fröhlich, 2013) first integrates omics data and subsequently applies ND to define a global ranking of miRNA and mRNA using statistics about their differential expression integrated in a heterogeneous network.
The ND-during refers to the application of a type of ND in which each layer communicate information one another. This is the case of SNF (Wang et al., 2014), in which patient similarity networks, obtained from each of their data types separately, exchange information during the ND process, leading to a unique “fused” patient network.
On the basis of data types, we can distinguish integrative methods that use ND to analyse a single type of omics, multiple omics or multiple networks (Table 1 and Figures 1B, 3).
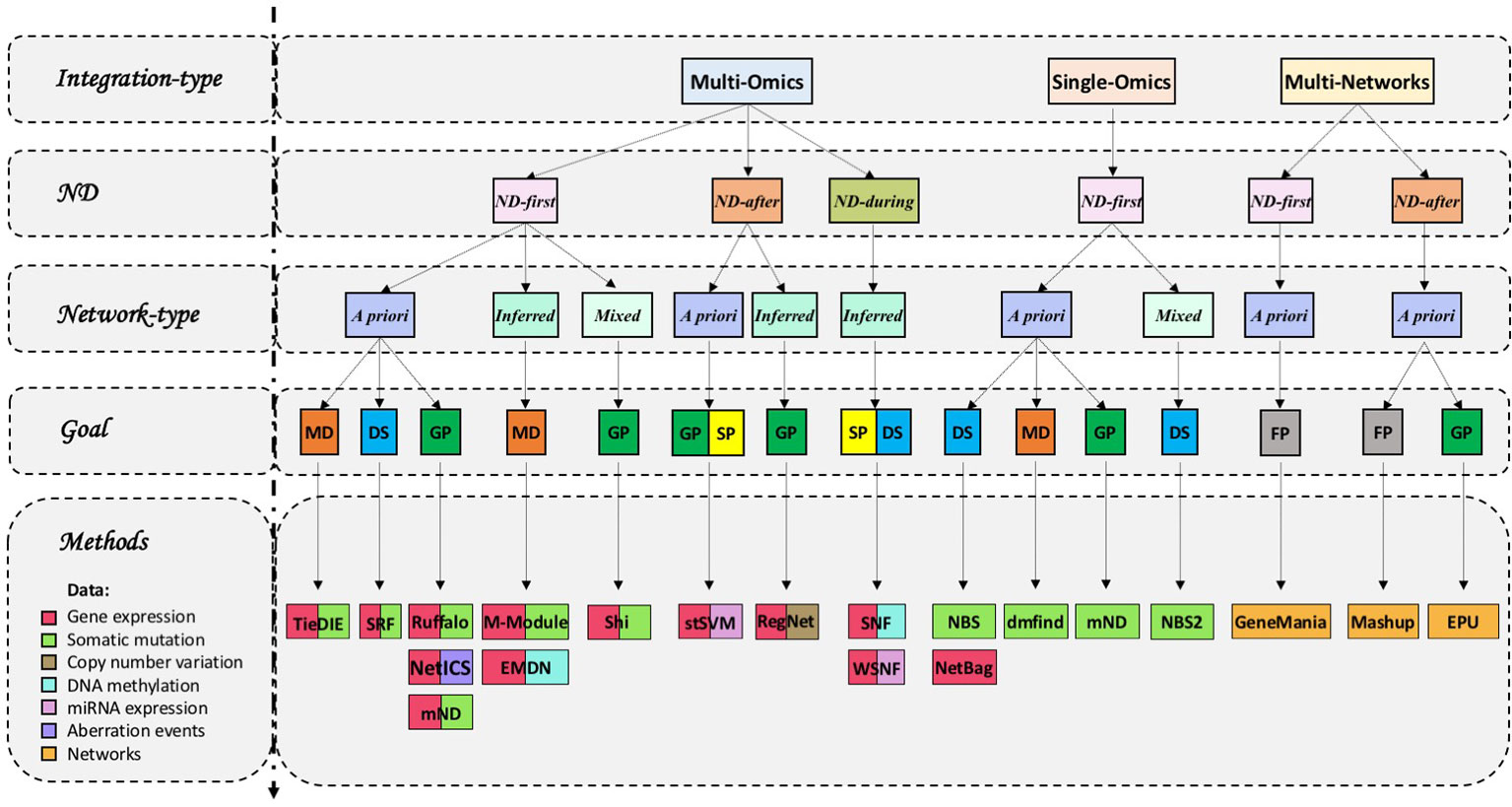
Figure 3 Network diffusion methods for the integrative analyses of multiple biological layers. GP, gene prioritization; MD, module detection; FP, function prediction; DS, disease subtyping; SP, survival prediction. We classified methods according to their main use described by the respective authors.
Single Omics
Integrative methods for the analysis of a single type of omics consider a series of molecular profiles, such as patient-wise mutation profiles.
The method called “dmfind” (Bersanelli et al., 2016b) compares ND scores obtained from a series of descriptive statistics, such as gene mutation frequencies. Subsequently, the network smoothing index (NSI) is obtained by comparison of ND scores with initial molecular profiles (Bersanelli et al., 2016b). When applied to gene networks, NSI highlights genes in network proximity enriched by initial information according to a tuning parameter ϵ (Barabási et al., 2011). The integration is therefore realised by subtracting NSIs belonging to two patient groups (ND-first), an operation that prioritizes genes that participate in differentially enriched modules (Bersanelli et al., 2016b).
tlsb 0.1ptNBS (Network-Based Stratification) (Hofree et al., 2013) is a method that stratifies tumor mutations finding clusters of similar patients. It applies ND to a binary somatic mutation matrix (genes-by-samples). Then, the resulting collections of ND scores are jointly analysed (ND-first) using a network-constrained non-negative matrix factorization to find k patient groups. It has been applied to study 13 cancer types with exome-level mutation data (Zhong et al., 2015), liver cancer (Fujimoto et al., 2016) and in a pan-cancer genomic analysis (Liu and Zhang, 2015).
NetBags (NETwork Based clustering Approach with Gene signatures) (Wu et al., 2015) essentially applies the strategy of NBS to a binary genes-by-samples matrix that represents the significantly expressed genes.
NBS2 (Network-Based Supervised Stratification) (Zhang et al., 2018) was proposed as a development of NBS (Hofree et al., 2013). NBS2 uses cancer-specific a priori knowledge of molecular interaction networks. Unlike previous approaches, the weights of each molecular interaction are adjusted by a supervised strategy so that the stratification of propagated mutation profiles after random walk is close to the pre-defined tumor subtypes.
Lastly, mND (Di Nanni et al., 2020) has been developed to yield gene prioritizations and it is applicable to both datasets originating from a single type or multiple types of omics, which can be distributed over multiple layers with the same underlying network structure. We will further describe this method in the next section.
Multi-Omics Integration
In multi-omics data integration each layer typically contains scores obtained from a distinct omic assay. Most methods deal with two types of layers (Figure 3).
Genomics and Transcriptomics
Many methods tackled the problem of analysing the relation between genomic aberrations and gene expression changes.
Ruffalo et al. (2015) presents a ND-based method to predict “silent” players in cancer by integration of somatic mutations and gene expression data, where a silent player is a gene neither mutated nor differentially expressed but which plays a role in cancer development and progression. Inputs are represented as two binary matrices of somatic mutation and gene expression (genes-by-samples).
The authors explored several ways (e.g. the minimum, the maximum, the product, the average) of combining diffusion scores (ND-first) to obtain the features of a logistic regression model that predicts a gene's association with cancer.
Also Shi et al. (2016) use patient-wise gene mutation and gene expression data to prioritize genes. The approach constructs a bipartite graph of outlying genes and mutated genes considering an influence graph (that captures a priori biological pathway information), mutational and expression data. A two-step diffusion is performed to calculate diffusion scores for each patient and these scores are subsequently combined (ND-first) by robust rank aggregation.
mND (Di Nanni et al., 2020) prioritizes genes taking into account the network proximity of the genes and their first neighbours to other altered genes considering multiple types of biological evidence. It works without constraints for the type and number of input, applying ND to a general gene-by-samples matrix, where each column represents a vector of scores (e.g. gene mutation frequencies, p-values from differentially expressed genes). Then, the resulting collections of ND scores are integrated (ND-first) by calculating for each gene the product between the sum of its network constrained scores and the sum of the contributions of its top k first neighbours. Beyond prioritizing genes, mND provides the opportunity to classify genes in each layer suggesting genes role in relation to the context of the alterations detected.
Differently from the methods described above that yield gene prioritizations, TieDIE (Tied Diffusion Through Interacting Events) (Paull et al., 2013) has been developed to identify a subnetwork that links a source gene set (S) carrying genomic alterations to a target set (T) of differentially expressed genes on the same a priori network. TieDIE transforms the two collections of input scores in the corresponding ND scores and then (ND-first) the minimum of the two scores of a gene is used as the final score for that gene. TieDIE has been used to study several cancers, such as, Papillary Thyroid Carcinoma (Agrawal et al., 2014), Prostate Cancer (Drake et al., 2016), Leukemia (Huang et al., 2018) and in an extensive immugenomic analysis of 33 diverse cancer types (Thorsson et al., 2018).
Another method that seeks to identify gene modules is M-Module (Ma et al., 2014). It infers co-expression networks from multiple data that represent disease stage transitions. Then genes are ranked in each networks via ND, incorporating also gene mutations as priors. In each network, ND scores are transformed in gene ranks, gene ranks into z-scores and the average z-score across all is used to obtain a final gene rank (ND-first). Gene modules are therefore identified using a graph entropy-based measure that quantifies connectivity of a module in multiple networks. Authors of M-Module proposed different variants of the algorithms: NMF-DM, in which modules of each network are discovered using a non-negative matrix factorization algorithm (Ma et al., 2016), SMMN, which uses modularity measure to discovery modules (Ma et al., 2017b) and S2-jNMF a novel semisupervised joint nonnegative matrix factorization algorithm (Ma et al., 2018). M-Module has been applied to several studies [e.g. Chen et al. (2016); Han et al. (2017); Zhou et al. (2017)].
SRF (Le Van et al., 2016) aims at discovering cancer subtypes by combining mutation and expression data across samples. ND is applied only to the binary matrix of gene mutations. The identification of subtypes is performed by rank matrix factorization of the ranked diffusion matrix and ranked expression matrix (ND-first).
Copy number variations (CNVs) are another type of genomics aberration that has been jointly analysed with transcriptomics. The main goal of RegNet (Seifert and Beyer, 2017) is the quantification of the impact of gene expression changes on user-defined target genes in a network inferred from gene expression and CNVs. The approach learns a regulatory network by modelling the expression level of each gene as a linear combination of the expression levels of all other potential regulator genes and the gene-specific copy number, lasso regression is used in combination with a significance test for lasso (Lockhart et al., 2014) to find the relevant predictors for each gene. Next, ND is applied using the learned network to quantify impacts of sample-specific gene expression changes on other clinically relevant target genes using network-diffusion. RegNet was able to predicts novel cancer gene candidates in oligodendrogliomas (Gladitz et al., 2018).
Epigenomics and Transcriptomics
The algorithm of M-Module is employed in EMDN framework (Epigenetic Module based on Differential Networks) (Ma et al., 2017a) to characterize epigenetic modules by using differential co-methylation and co-expression networks, without incorporating genes mutations information as prior information. In this way EMDN applies ND as RW without restart, but with a symmetric normalization of the adjacency matrix.
An interesting method that aims to find disease subtypes and predict phenotypes is SNF (Similarity Network Fusion) (Wang et al., 2014). It works without constraints for the type of input but requires that samples are matched across omics. First, networks of samples for the various types of omics are built, then, networks are fused into one network by using the non-linear method of message passing theory (KNN and graph diffusion) that iteratively updates each of the network making it more similar to other networks in each step.
Several studies in cancer have exploited SNF method to integrate GE and DM data, like: Kidney Renal Cell Carcinoma (Deng et al., 2016), medulloblastoma (Cavalli et al., 2017); further, thanks to its versatility, SNF has been used to integrate other types of omics: miRNA and GE in Colorectal liver metastasis (Pitroda et al., 2018) and in Ovarian cancer (Zhang et al., 2016); miRNA, mRNA, lncRNA, and DNA methylation in Pancreatic Ductal Adenocarcinoma (Raphael et al., 2017); GE, miRNA and CNV in triple-negative breast cancer (Chiu et al., 2018).
Transcriptomics: mRNA and miRNA
Xu et al. (2016) have proposed a modification of SNF method called WSNF (Weighted Similarity Network Fusion) that takes into consideration the level of importance of genes to identify disease subtypes. WSNF constructs a miRNA-TF-mRNA regulatory network from different interaction databases, then assesses the weight of each features (miRNA, TF, mRNA), calculated as a linear combination of two terms: ranking of features obtained using ND and expression variation across all patients in expression datasets. Weights are introduced into the formula of Euclidean distance to calculate the distance between two patients then SNF method is applied.
stSVM (smoothed t-statistic support vector machine) (Cun and Fröhlich, 2013) combines a priori network information and omics data (miRNA and GE) to discover biomarker signature and predict disease prognosis. It smoothens gene-wise statistics from experimental data (both miRNA and gene expression) over the biological network, constructed by integration of PPI with miRNA-target gene network, using a P-step random walk kernels. A permutation test is conducted to select significant genes that will be used to train a support vector machine (SVM) classifier. It has been used in an integrative study of miRNA and GE to predict response to a monoclonal antibody in Head and Neck Squamous Cell Cancer (De Cecco et al., 2017).
Genomics, Epigenomics and Transcriptomics
NetICS (Network-based Integration of Multi-omics Data) (Dimitrakopoulos et al., 2018) prioritizes cancer genes by their mediator effect, defined as the proximity of the gene to aberration events (SM, CNV, DM, a differentially expressed miRNA), differentially expressed genes and proteins in a molecular network given a priori. The method uses a per-sample bidirectional IHD process and initial heat vectors (h1, h2) are defined, respectively, as the number of the aberrant and differentially expressed genes of the sample. Final scores for all genes are obtained by means of the Hadamard product of the exchanged heat matrices (E1, E2) (ND-first): E = E1 ◦ E2.
Lastly, diffusion scores of all samples are combined to obtain global gene ranking via a robust aggregation, in which a gene's rank is calculated as the sum of its per-sample ranks.
Integration of Multiple Networks
In the integration of multiple networks each layer represents a biological network. The two main applications are gene function prediction and gene prioritization.
Mashup (Cho et al., 2016) uses ND on several protein–protein interaction networks to predict gene function and genetic interactions. It applies RWR algorithm separately on each network and then a matrix factorization based technique is used to reduce dimension of the diffusion results (ND-first). The feature learning step allows to obtain a low-dimensional feature vectors of proteins that best approximates the RWR matrix and results more robust to noise; feature vectors are used to train SVM classifiers to predict genetic interactions.
Mostafavi et al. (2008) developed GeneMANIA (Multiple Association Network Integration Algorithm), a tool for predicting gene function by integration of multiple networks (e.g. co-expression, PPI, genetic interaction, co-localization, shared protein domains). Given d networks encoded as matrices W1,…,Wd, they are integrated into a “composite network” (Wcomb), obtained by weighted average of individual networks:
where the vector [α = α1, …, αd] corresponds to network weights and is computed by solving a ridge regression problem. Then given the Wcomb matrix, a variation of the Gaussian field label propagation algorithm (a RWR where functions of unlabeled data are predicted starting from differently labeled data and network structure) is applied to predict the gene function. GeneMANIA has been applied in several studies (e.g. O'Roak et al. (2012); Tkach et al. (2012); Giudice et al. (2014); Karki et al. (2018); Sepulcre et al. (2018)).
Differently from above methods, EPU (Ensemble Positive Unlabeled learning) (Yang et al., 2014) uses a supervised learning method, that falls in the class of Positive-Unlabeled learning method, for disease gene identification by integrating multiple biological data sources (PPI, gene expression data, Gene Ontology, Phenotype-gene association data and Phenotype similarity network). ND is applied on three biological networks (Gene Expression network, PPI network, Gene ontology similarity network) to obtain weights for unlabelled genes (not associated with disease). The resulting three collections of ND scores are combined into a set of integrated scores using, for each gene, the mean of its three ND scores (ND-first). These integrated scores are used to train three machine-learned prediction models (Weighted-KNN, Weighted-Naïve Bayes, Weighted-SVM) and their results are integrated by an ensemble learning algorithm.
Discussion
ND based approaches have been proposed to solve several problems in biological data analysis, including data integration. These methods analyse multiple collections of scores derived from different omics assays in combination with molecular networks or similarity networks, and apply ND on such networks. The main applications include: gene function prediction; gene prioritization; identification of gene modules and molecular pathways; disease subtyping; and prediction of an outcome. In all these applications, ND is a tool to transform one or more initial vectors of scores into vectors that reflect the network proximity between network nodes on which the scores are mapped. This data transformation is exploited for different purposes, such as: embedding a molecular interaction data into omics datasets; amplifying associations between the studied variables; missing value imputation; enabling comparisons among different data types; highlighting network regions enriched in multiple types of scores; and studying molecular profiles at patient-level scale.
ND processes, which can be brought back to four classes, require the tuning of a parameter (k or α) that controls the diffusion process reach or the relative importance of topology and input scores. In many cases, the issue about tuning of such parameter has been solved showing that the performance of the proposed integrative method is robust to small variations of the parameter. A dependency between the optimal value and the network in use has been suggested (Hofree et al., 2013).
Most methods apply ND to transform a series of input score collections to get as many collections of ND scores—in which the network topology is embedded—and, subsequently, combine the ND scores: we referred to these methods as ND-first. The combination of a series of ND scores for the same variable (e.g. a gene) is performed with simple mathematical operators, such as the mean or the minimum, or with more elaborated techniques, such as non-negative matrix factorization and support vector machines. ND scores may require a step of transformation, such as normalization, to enable the direct comparison between scores at different scale [e.g. Hofree et al. (2013)], or ranking, to work on the relative importance rather than absolute values [(e.g. Ma et al. (2014); Shi et al. (2016))]. Other integrative methods, firstly integrate multiple data types, then use ND: we referred to these methods as ND-after. In these methods, ND is one of the last steps that lead to the final output. A third class of methods perform ND simultaneously with the integrative step (ND-during). The class of simultaneous diffusion approaches is very promising as it encodes the diffusion processes on multi-layer networks (Aleta and Moreno, 2019). In principle, simultaneous diffusion allows to extend the classical analysis of multi-omics data on complex networks. For instance, in the case of heterogeneous networks, layer-specific nodes bring an indirect contribution to the ND scores on each other layer. Such an output is not possible neither in ND-first nor in ND-after approaches. ND-after integrative approaches build an aggregate network encoding weighted or unweighted aggregate links; such an aggregate network is therefore algebraically put together, independently from the diffusion process. The same considerations hold for ND-first approaches, but such integration issues are addressed once the ND is performed on each layer separately. Therefore, ND-after and ND-first approaches could be very informative about a specific biological analysis but they present an intrinsic lack of scalability, as the way in which properly combine and weigh networks (before or after ND) strongly depends on the biological context. Conversely, an ND-during (simultaneous) approach maintains the available biological information and avoids additional data manipulations before and after the application of the diffusive algorithm. However, simultaneous approaches may introduce computational issues as omics data size and number of layers increase.
Most of the approaches do not assess the statistical significance of ND scores. In several works it was proposed to use empirical p values (Bersanelli et al., 2016b), which provide also the benefit of mitigating the over-estimation of hub importance. In a recent work, the calculation of empirical p values using degree-normalized random seeds was shown to be more accurate, but computationally more demanding, than random seeds (Biran et al., 2019).
A specific combination of omics (e.g. gene mutations and gene expression changes) and a quite specific formulation of the problem is often required. While this specificity offers advantages within the domain of the original problem, it also poses constraints to applicability and further extension. Furthermore, efforts are still required to develop methods that combine more than two omics.
A relevant issue is the reliability of interactomes. The problem of defining a reference human interactome is open in molecular biology as well as the problem of quantifying the reliability of such cell-scale reconstructions, because experimental technologies currently used to detect interactions involves a series of issues (Luck et al., 2017). Therefore, a careful network selection must be made by users based on the research questions they wish to address. Further, some methods take into account the directions of interactions in their algorithms, but cell-scale reconstructions do not provide information about “the direction” of the interaction, which requires a deeper understanding of the mechanistic relation between the two interacting partners. Modelling this information is not trivial and usually comes at the cost of a relevant reduction of coverage in terms of genes that can be analysed.
ND has become a popular tool in integrative analyses. The trends of recent works suggest that it will continue to be used and further refined as demands relative to new data types arise. For example, recent works apply ND to single cell data analysis, mainly to impute missing expression data (Van Dijk et al., 2018; Ye et al., 2019).
Author Contributions
ND and EM conceived the study. ND, EM, and MB performed literature search and wrote the manuscript. ND drafted figures and tables. EM and LM critically reviewed the manuscript. All authors approved the final manuscript.
Funding
This research was funded by: European Union's Horizon 2020 research and innovation programme, grant GEMMA 825033; Italian Ministry of Education, University and Research, project INTEROMICS PB05 and project BBMRI-it n. K75; Fondazione Regionale per la Ricerca Biomedica (Regione Lombardia), project LYRA 2015-0010 and project FindingMS ERAPERMED2018-233 GA 779282.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Agrawal, N., Akbani, R., Aksoy, B. A., Ally, A., Arachchi, H., Asa, S. L., et al. (2014). Integrated genomic characterization of papillary thyroid carcinoma. Cell 159 (3), 676–690. doi: 10.1016/j.cell.2014.09.050
Ahmad, A., Fröhlich, H. (2016). Integrating heterogeneous omics data via statistical inference and learning techniques. Genomics Comput. Biol. 2, 32. doi: 10.18547/gcb.2016.vol2.iss1.e32
Aleta, A., Moreno, Y. (2019). Multilayer networks in a nutshell. Annu. Rev. Condensed Matter Phys. 10, 45–62. doi: 10.1146/annurev-conmatphys-031218-013259
Baggio, J. A., BurnSilver, S. B., Arenas, A., Magdanz, J. S., Kofinas, G. P., De Domenico, M. (2016). Multiplex social ecological network analysis reveals how social changes affect community robustness more than resource depletion. Proc. Natl. Acad. Sci. 113 (48), 13708–13713. doi: 10.1073/pnas.1604401113
Barabási, A. L., Gulbahce, N., Loscalzo, J. (2011). Network medicine: a network-based approach to human disease. Nat. Rev. Genet. 12 (1), 56. doi: 10.1038/nrg2918
Bersanelli, M., Mosca, E., Remondini, D., Giampieri, E., Sala, C., Castellani, G., et al. (2016a). Methods for the integration of multi-omics data: mathematical aspects. BMC Bioinf. 17 (2), S15. doi: 10.1186/s12859-015-0857-9
Bersanelli, M., Mosca, E., Remondini, D., Castellani, G., Milanesi, L. (2016b). Network diffusion-based analysis of high-throughput data for the detection of differentially enriched modules. Sci. Rep. 6, 34841. doi: 10.1038/srep34841
Biran, H., Kupiec, M., Sharan, R. (2019). Comparative analysis of normalization methods for network propagation. Front. Genet. 10, 4. doi: 10.3389/fgene.2019.00004
Boyle, E. A., Li, Y. I., Pritchard, J. K. (2017). An expanded view of complex traits: from polygenic to omnigenic. Cell 169 (7), 1177–1186. doi: 10.1016/j.cell.2017.05.038
Brummitt, C. D., Kobayashi, T. (2015). Cascades in multiplex financial networks with debts of different seniority. Phys. Rev. E 91 (6), 062813. doi: 10.1103/PhysRevE.91.062813
Caldera, M., Buphamalai, P., Müller, F., Menche, J. (2017). Interactome-based approaches to human disease. Curr. Opin. Syst. Biol. 3, 88–94. doi: 10.1016/j.coisb.2017.04.015
Cavalli, F. M., Remke, M., Rampasek, L., Peacock, J., Shih, D. J., Luu, B., et al. (2017). Intertumoral heterogeneity within medulloblastoma subgroups. Cancer Cell 31 (6), 737–754. doi: 10.1016/j.ccell.2017.05.005
Chen, C., Ma, F. W., Du, C. Y., Wang, P. (2016). Multiple differential networks strategy reveals carboplatin and melphalan-induced dynamic module changes in retinoblastoma. Med. Sci. Monitor: Int. Med. J. Exp. Clin. Res. 22, 1508. doi: 10.12659/MSM.897877
Chiu, A. M., Mitra, M., Boymoushakian, L., Coller, H. A. (2018). Integrative analysis of the inter-tumoral heterogeneity of triple-negative breast cancer. Sci. Rep. 8 (1), 11807. doi: 10.1038/s41598-018-29992-5
Cho, H., Berger, B., Peng, J. (2016). Compact integration of multi-network topology for functional analysis of genes. Cell Syst. 3 (6), 540–548. doi: 10.1016/j.cels.2016.10.017
Cowen, L., Ideker, T., Raphael, B. J., Sharan, R. (2017). Network propagation: a universal amplifier of genetic associations. Nat. Rev. Genet. 18 (9), 551. doi: 10.1038/nrg.2017.38
Cun, Y., Fröhlich, H. (2013). Network and data integration for biomarker signature discovery via network smoothed t-statistics. PloS One 8 (9), e73074. doi: 10.1371/journal.pone.0073074
De Cecco, L., Giannoccaro, M., Marchesi, E., Bossi, P., Favales, F., Locati, L., et al. (2017). Integrative miRNA-gene expression analysis enables refinement of associated biology and prediction of response to cetuximab in head and neck squamous cell cancer. Genes 8 (1), 35. doi: 10.3390/genes8010035
De Las Rivas, J., Fontanillo, C. (2010). Protein–protein interactions essentials: key concepts to building and analyzing interactome networks. PloS Comput. Biol. 6 (6), e1000807. doi: 10.1371/journal.pcbi.1000807
Deng, S. P., Cao, S., Huang, D. S., Wang, Y. P. (2016). Identifying stages of kidney renal cell carcinoma by combining gene expression and dna methylation data. IEEE/ACM Trans. Comput. Biol. Bioinf. 14 (5), 1147–1153. doi: 10.1109/TCBB.2016.2607717
Di Nanni, N., Gnocchi, M., Moscatelli, M., Milanesi, L., Mosca, E. (2020). Gene relevance based on multiple evidences in complex networks. Bioinf. btz652 36 (3), 865–871. doi: 10.1093/bioinformatics/btz652
Dimitrakopoulos, C., Hindupur, S. K., Häfliger, L., Behr, J., Montazeri, H., Hall, M. N., et al. (2018). Network-based integration of multi-omics data for prioritizing cancer genes. Bioinformatics 34 (14), 2441–2448. doi: 10.1093/bioinformatics/bty148
Drake, J. M., Paull, E. O., Graham, N. A., Lee, J. K., Smith, B. A., Titz, B., et al. (2016). Phosphoproteome integration reveals patient-specific networks in prostate cancer. Cell 166 (4), 1041–1054. doi: 10.1016/j.cell.2016.07.007
Fujimoto, A., Furuta, M., Totoki, Y., Tsunoda, T., Kato, M., Shiraishi, Y., et al. (2016). Whole-genome mutational landscape and characterization of noncoding and structural mutations in liver cancer. Nat. Genet. 48 (5), 500. doi: 10.1038/ng.3547
Gao, J., Barzel, B., Barabási, A. L. (2016). Universal resilience patterns in complex networks. Nature 530 (7590), 307. doi: 10.1038/nature16948
Giudice, J., Xia, Z., Wang, E. T., Scavuzzo, M. A., Ward, A. J., Kalsotra, A., et al. (2014). Alternative splicing regulates vesicular trafficking genes in cardiomyocytes during postnatal heart development. Nat. Commun. 5, 3603. doi: 10.1038/ncomms4603
Gladitz, J., Klink, B., Seifert, M. (2018). Network-based analysis of oligodendrogliomas predicts novel cancer gene candidates within the region of the 1p/19q co-deletion. Acta Neuropathologica Commun. 6 (1), 49. doi: 10.1186/s40478-018-0544-y
GTEx Consortium (2015). The Genotype-Tissue Expression (GTEx) pilot analysis: multitissue gene regulation in humans. Science 348 (6235), 648–660. doi: 10.1126/science.1262110
Han, L., Chen, C., Liu, C. H., Zhang, M., Liang, L. (2017). Revealing differential modules in uveal melanoma by analyzing differential networks. Mol. Med. Rep. 15 (4), 2261–2266. doi: 10.3892/mmr.2017.6232
Higdon, R., Earl, R. K., Stanberry, L., Hudac, C. M., Montague, E., Stewart, E., et al. (2015). The promise of multi-omics and clinical data integration to identify and target personalized healthcare approaches in autism spectrum disorders. Omics 19 4, 197–208. doi: 10.1089/omi.2015.0020
Hofree, M., Shen, J. P., Carter, H., Gross, A., Ideker, T. (2013). Network-based stratification of tumor mutations. Nat. Methods 10 (11), 11. doi: 10.1038/nmeth.2651
Hu, Y., An, Q., Sheu, K., Trejo, B., Fan, S., Guo, Y. (2018). Single cell multi-omics technology: methodology and application. Front. In Cell Dev. Biol. 6, 28. doi: 10.3389/fcell.2018.00028
Huang, S., Chaudhary, K., Garmire, L. X. (2017). More is better: recent progress in multi-omics data integration methods. Front. Genet. 8, 84. doi: 10.3389/fgene.2017.00084
Huang, L., Liu, D., Wang, N., Ling, S., Tang, Y., Wu, J., et al. (2018). Integrated genomic analysis identifies deregulated JAK/STAT-MYC-biosynthesis axis in aggressive NK-cell leukemia. Cell Res. 28 (2), 172. doi: 10.1038/cr.2017.146
Karczewski, K. J., Snyder, M. P. (2018). Integrative omics for health and disease. Nat. Rev. Genet. 19 (5), 299. doi: 10.1038/nrg.2018.4
Karki, R., Place, D., Samir, P., Mavuluri, J., Sharma, B. R., Balakrishnan, A., et al. (2018). IRF8 regulates transcription of Naips for NLRC4 inflammasome activation. Cell 173 (4), 920–933. doi: 10.1073/pnas.1318948111
Kellis, M., Wold, B., Snyder, M. P., Bernstein, B. E., Kundaje, A., Marinov, G. K., et al. (2014). Defining functional DNA elements in the human genome. Proceedings of the National Academy of Sciences 111 (17), 6131–6138. doi: 10.1073/pnas.1318948111
Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., Porter, M. A. (2014). Multilayer networks. J. Complex Networks 2 (3), 203–271. doi: 10.1093/comnet/cnu016
Kristensen, V. N., Lingjærde, O. C., Russnes, H. G., Vollan, H. K. M., Frigessi, A., Børresen-Dale, A. L. (2014). Principles and methods of integrative genomic analyses in cancer. Nat. Rev. Cancer 14 (5), 299–313. doi: 10.1038/nrc3721
Kundaje, A., Meuleman, W., Ernst, J., Bilenky, M., Yen, A., Heravi-Moussavi, A., et al. (2015). Integrative analysis of 111 reference human epigenomes. Nature 518 (7539), 317. doi: 10.1038/nature14248
Le Van, T., Van Leeuwen, M., Carolina Fierro, A., De Maeyer, D., Van den Eynden, J., Verbeke, L., et al. (2016). Simultaneous discovery of cancer subtypes and subtype features by molecular data integration. Bioinformatics 32 (17), i445–i454. doi: 10.1093/bioinformatics/btw434
Leiserson, M. D., Vandin, F., Wu, H. T., Dobson, J. R., Eldridge, J. V., Thomas, J. L., et al. (2015). Pan-cancer network analysis identifies combinations of rare somatic mutations across pathways and protein complexes. Nat. Genet. 47 (2), 106. doi: 10.1038/ng.3168
Liu, Z., Zhang, S. (2015). Tumor characterization and stratification by integrated molecular profiles reveals essential pan-cancer features. BMC Genomics 16 (1), 503. doi: 10.1186/s12864-015-1687-x
Lockhart, R., Taylor, J., Tibshirani, R. J., Tibshirani, R. (2014). A significance test for the lasso. Ann. Stat 42 (2), 413. doi: 10.1214/13-AOS1175
Luck, K., Sheynkman, G. M., Zhang, I., Vidal, M. (2017). Proteome-scale human interactomics. Trends In Biochem. Sci. 42 (5), 342–354. doi: 10.1016/j.tibs.2017.02.006
Ma, X., Gao, L., Tan, K. (2014). Modeling disease progression using dynamics of pathway connectivity. Bioinformatics 30 (16), 2343–2350. doi: 10.1093/bioinformatics/btu298
Ma, X., Tang, W., Wang, P., Guo, X., Gao, L. (2016). Extracting stage-specific and dynamic modules through analyzing multiple networks associated with cancer progression. IEEE/ACM Trans. Comput. Biol. Bioinf. 15 (2), 647–658. doi: 10.1109/TCBB.2016.2625791
Ma, X., Liu, Z., Zhang, Z., Huang, X., Tang, W. (2017a). Multiple network algorithm for epigenetic modules via the integration of genome-wide DNA methylation and gene expression data. BMC Bioinf. 18 (1), 72. doi: 10.1186/s12859-017-1490-6
Ma, X., Sun, P., Qin, G. (2017b). Identifying condition-specific modules by clustering multiple networks. IEEE/ACM Trans. Comput. Biol. Bioinf. 15 (5), 1636–1648. doi: 10.1109/TCBB.2017.2761339
Ma, X., Dong, D., Wang, Q. (2018). Community detection in multi-layer networks using joint nonnegative matrix factorization. IEEE Trans. Knowledge Data Eng. 31 (2), 273–286. doi: 10.1109/TKDE.2018.2832205
Menichetti, G., Remondini, D., Panzarasa, P., Mondragón, R. J., Bianconi, G. (2014). Weighted Multiplex Networks. PloS One 9 (6), e97857. doi: 10.1371/journal.pone.0097857
Mostafavi, S., Ray, D., Warde-Farley, D., Grouios, C., Morris, Q. (2008). GeneMANIA: a real-time multiple association network integration algorithm for predicting gene function. Genome Biol. 9 (1), S4. doi: 10.1186/gb-2008-9-s1-s4
O'Roak, B. J., Vives, L., Girirajan, S., Karakoc, E., Krumm, N., Coe, B. P., et al. (2012). Sporadic autism exomes reveal a highly interconnected protein network of de novo mutations. Nature 485 (7397), 246. doi: 10.1038/nature10989
Orchard, S., Kerrien, S., Abbani, S., Aranda, B., Bhate, J., Bidwell, S., et al. (2012). Protein interaction data curation: the International Molecular Exchange (IMEx) consortium. Nat. Methods 9 (4), 345. doi: 10.1038/nmeth.1931
Paull, E. O., Carlin, D. E., Niepel, M., Sorger, P. K., Haussler, D., Stuart, J. M. (2013). Discovering causal pathways linking genomic events to transcriptional states using Tied Diffusion Through Interacting Events (TieDIE). Bioinformatics 29 (21), 2757–2764. doi: 10.1093/bioinformatics/btt471
Pitroda, S. P., Khodarev, N. N., Huang, L., Uppal, A., Wightman, S. C., Ganai, S., et al. (2018). Integrated molecular subtyping defines a curable oligometastatic state in colorectal liver metastasis. Nat. Commun. 9 (1), 1793. doi: 10.1038/s41467-018-04278-6
Raphael, B. J., Hruban, R. H., Aguirre, A. J., Moffitt, R. A., Yeh, J. J., Stewart, C., et al. (2017). Integrated genomic characterization of pancreatic ductal adenocarcinoma. Cancer Cell 32 (2), 185–203. doi: 10.1016/j.ccell.2017.07.007
Reis, S. D., Hu, Y., Babino, A., Andrade, J. S., Jr., Canals, S., Sigman, M., et al. (2014). Avoiding catastrophic failure in correlated networks of networks. Nat. Phys. 10 (10), 762. doi: 10.1038/nphys3081
Ritchie, M. D., Holzinger, E. R., Li, R., Pendergrass, S. A., Kim, D. (2015). Methods of integrating data to uncover genotype–phenotype interactions. Nat. Rev. Genet. 16, 85–97. doi: 10.1038/nrg3868
Ruffalo, M., Koyutürk, M., Sharan, R. (2015). Network-based integration of disparate omic data to identify” silent players” in cancer. PloS Comput. Biol. 11 (12), e1004595. doi: 10.1371/journal.pcbi.1004595
Seifert, M., Beyer, A. (2017). regNet: An R package for network-based propagation of gene expression alterations. Bioinformatics 34 (2), 308–311. doi: 10.1093/bioinformatics/btx544
Sepulcre, J., Grothe, M. J., Uquillas, F. D. O., Ortiz-Terán, L., Diez, I., Yang, H. S., et al. (2018). Neurogenetic contributions to amyloid beta and tau spreading in the human cortex. Nat. Med. 24 (12), 1910. doi: 10.1038/s41591-018-0206-4
Sharan, R., Ulitsky, I., Shamir, R. (2007). Network-based prediction of protein function. Mol. Syst. Biol. 3, 88. doi: 10.1038/msb4100129
Shi, K., Gao, L., Wang, B. (2016). Discovering potential cancer driver genes by an integrated network-based approach. Mol. Biosyst. 12 (9), 2921–2931. doi: 10.1039/C6MB00274A
Su, C., Tong, J., Zhu, Y., Cui, P., Wang, F. (2018). Network embedding in biomedical data science. Briefings In Bioinf. 21 (1), 182–197. doi: 10.1093/bib/bby117
Thorsson, V., Gibbs, D. L., Brown, S. D., Wolf, D., Bortone, D. S., Yang, T. H. O., et al. (2018). The immune landscape of cancer. Immunity 48 (4), 812–830. doi: 10.1016/j.immuni.2018.03.023
Tkach, J. M., Yimit, A., Lee, A. Y., Riffle, M., Costanzo, M., Jaschob, D., et al. (2012). Dissecting DNA damage response pathways by analysing protein localization and abundance changes during DNA replication stress. Nat. Cell Biol. 14 (9), 966. doi: 10.1038/ncb2549
Van Dijk, D., Sharma, R., Nainys, J., Yim, K., Kathail, P., Carr, A. J., et al. (2018). Recovering gene interactions from single-cell data using data diffusion. Cell 174 (3), 716–729. doi: 10.1016/j.cell.2018.05.061
Vanunu, O., Magger, O., Ruppin, E., Shlomi, T., Sharan, R. (2010). Associating genes and protein complexes with disease via network propagation. PloS Comput. Biol. 6 (1), e1000641. doi: 10.1371/journal.pcbi.1000641
Vidal, M., Cusick, M. E., Barabási, A. L. (2011). Interactome networks and human disease. Cell 144 (6), 986–998. doi: 10.1016/j.cell.2011.02.016
Wang, P. I., Marcotte, E. M. (2010). It's the machine that matters: predicting gene function and phenotype from protein networks. J. Proteomics 73 (11), 2277–2289. doi: 10.1016/j.jprot.2010.07.005
Wang, B., Mezlini, A. M., Demir, F., Fiume, M., Tu, Z., Brudno, M., et al. (2014). Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 11 (3), 333. doi: 10.1038/nmeth.2810
Wu, L., Liu, Z., Xu, J., Chen, M., Fang, H., Tong, W., et al. (2015). NETBAGs: a network-based clustering approach with gene signatures for cancer subtyping analysis. Biomarkers In Med. 9 (11), 1053–1065. doi: 10.2217/bmm.15.96
Xu, T., Le, T. D., Liu, L., Wang, R., Sun, B., Li, J. (2016). Identifying cancer subtypes from mirna-tf-mrna regulatory networks and expression data. PloS One 11 (4), e0152792. doi: 10.1371/journal.pone.0152792
Yan, J., Risacher, S. L., Shen, L., Saykin, A. J. (2017). Network approaches to systems biology analysis of complex disease: integrative methods for multi-omics data. Briefings In Bioinf. 19 (6), 1370–1381. doi: 10.1093/bib/bbx066
Yang, P., Li, X., Chua, H.-N., Kwoh, C.-K., Ng, S.-K. (2014). Ensemble positive unlabeled learning for disease gene identification. PloS One 9 (5), e97079. doi: 10.1371/journal.pone.0097079
Ye, W., Ji, G., Ye, P., Long, Y., Xiao, X., Li, S., et al. (2019). scNPF: an integrative framework assisted by network propagation and network fusion for preprocessing of single-cell RNA-seq data. BMC Genomics 20 (1), 347. doi: 10.1186/s12864-019-5747-5
Zhang, D., Chen, P., Zheng, C. H., Xia, J. (2016). Identification of ovarian cancer subtype-specific network modules and candidate drivers through an integrative genomics approach. Oncotarget 7 (4), 4298. doi: 10.18632/oncotarget.6774
Zhang, W., Ma, J., Ideker, T. (2018). Classifying tumors by supervised network propagation. Bioinformatics 34 (13), i484–i493. doi: 10.1093/bioinformatics/bty247
Zhong, X., Yang, H., Zhao, S., Shyr, Y., Li, B. (2015). Network-based stratification analysis of 13 major cancer types using mutations in panels of cancer genes. BMC Genomics 16 (7), S7. doi: 10.1186/1471-2164-16-S7-S7
Zhou, D., Bousquet, O., Lal, T. N., Weston, J., Schölkopf, B. (2004). “Learning with local and global consistency,” in Advances in neural information processing systems, 321–328.
Keywords: integrative analysis, omics data, biological networks, precision medicine, network-diffusion
Citation: Di Nanni N, Bersanelli M, Milanesi L and Mosca E (2020) Network Diffusion Promotes the Integrative Analysis of Multiple Omics. Front. Genet. 11:106. doi: 10.3389/fgene.2020.00106
Received: 31 July 2019; Accepted: 29 January 2020;
Published: 27 February 2020.
Edited by:
Rosalba Giugno, University of Verona, ItalyReviewed by:
Giosue' Lo Bosco, University of Palermo, ItalyLuciano Cascione, Istituto Oncologico della Svizzera Italiana, Switzerland
Copyright © 2020 Di Nanni, Bersanelli, Milanesi and Mosca. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ettore Mosca, ZXR0b3JlLm1vc2NhQGl0Yi5jbnIuaXQ=
 Noemi Di Nanni
Noemi Di Nanni Matteo Bersanelli
Matteo Bersanelli Luciano Milanesi
Luciano Milanesi Ettore Mosca
Ettore Mosca