- 1Landscape Ecology and Ecosystem Dynamics Working Group, Institute of Botany and Landscape Ecology, University of Greifswald, Greifswald, Germany
- 2Chair of Forest Growth and Woody Biomass Production, Institute of Forest Growth and Forest Computer Sciences, TU Dresden, Dresden, Germany
Changes in the environment will alter the growth rate of trees and forests. Different disciplines assess such growth rates differently, for example, with tree-ring width data, forest inventories or with carbon-flux data from eddy covariance towers. Such data is used to quantify forests biomass increment, forest’s carbon sequestration or to reconstruct environmental variables before instrumental records. However, raw measurement data is typically not considered to be representative for the average growth rate of trees or forests. Depending on the research question, the effects of certain environmental variables or effects of tree and forest structure have to be removed first. It can be challenging to define and quantify a growth trend that can answer a specific research question because trees and forests grow and respond to environmental change in multiple ways simultaneously, for example, with altered radial increment, height growth, and stand density. Further challenges pose time-lagged feedback loops, for example, between height and radial increment or between stand density and radial increment. Generally, different environments will lead to different tree and forest structures, but because of tree’s longevity this adaptation to the new environment will take decades or even centuries. Consequently, there can be an offset between the present forest structure and what we term the potential natural forest (PNF): Similar to the potential natural vegetation (PNV), the PNF represents that forest that would develop under the current environmental conditions in the absence of human intervention. Because growth rates are affected by the tree and forest structure, growth-trend estimates will differ between the present and the potential forest. Consequently, if the legacy effects of the past are not of interest, the PNF is the theoretical baseline to correct and estimate growth trends.
Introduction to Growth Trends
Understanding growth trends of trees and forest ecosystems is important because of their role in the global carbon and water cycles, because these growth trends determine the sustainable wood production in forestry, and because they are related to past growing conditions and thus climate reconstructions.
Tree growth depends on environmental variables like climate, soil, and atmospheric composition. Thus, different environments correspond to different growth rates of trees and forests. Each change in an environmental variable can potentially alter growth rates, for example, changes in temperature, precipitation, competition, or atmospheric CO2. Generally, estimating growth trends can become quite complicated because trees and forests are complex adaptive systems – CAS (Levin et al., 2013; Filotas et al., 2014; Puettmann et al., 2016). Environmental change has different effects on radial increment, height growth, and stand density, while all of these variables also affect each other in feedback loops.
Most people have an intuitive understanding of the term “growth trend,” but due to potential misunderstandings some clarification is provided here: First, the terms “trend” and “rate” have to be distinguished. “Rates” generally describe the change of a variable over a fixed time period. For example, speed is the change in location over time and can be measured in meters per second. Similarly, growth rates are a change in size or weight over time, for example, the wood volume increment of a tree in one year. In contrast, a “growth trend” is the rate of a rate: Just like a car can accelerate/break (measured in m/s2), a growth rate can speed up or slow down. In case of wood volume, it could be measured in m3/a2 (cubic meters per squared year). Squared time is not intuitively understood by many, thus when reporting growth trends typically growth-rate time-series are plotted, where the slope represents the growth trend. Figure 1 shows various types of growth rates and trends that are frequently used in various disciplines that study tree and forest growth.
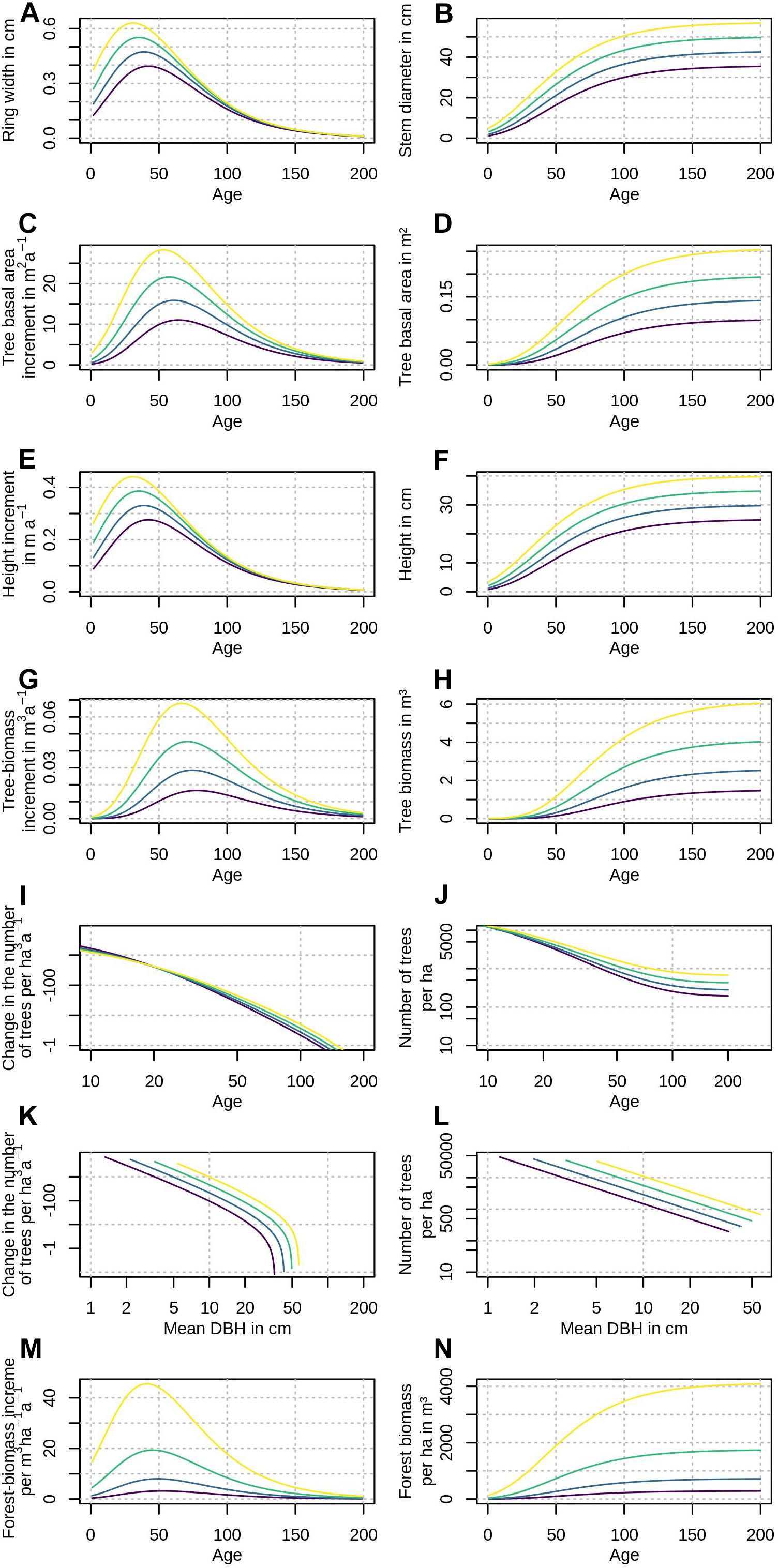
Figure 1. Various types of idealized growth rates show how different tree and forests parameters change with age and stem diameter. Different colors represent better (yellow) or worse (purple) growth conditions. Different disciplines use different growth-rate types to explore trends, for example, changes in stem diameter or basal area (A–D), changes in tree height at a given age (yield tables in forestry: E,F), self-thinning lines (I–L), and tree-biomass or wood volume increment (G,H,M,N).
Second, the time scale at which growth trends are analyzed matters. Mostly, growth trends in forests refer to decadal or longer periods while growth-rate differences between two successive years (high-frequency variability) are typically not referred to as trend. Though, technically, even this difference is a trend. Importantly, a growth trend does not say anything about the magnitude of the growth rate.
Third, it has to be clarified which growth-rate variable is changing, i.e., shows a trend. Different disciplines use different variables or dimensions of tree and forest growth, for example, average annual tree-ring width, annual wood-volume increment per hectare or annual carbon exchange per hectare (Randerson et al., 2002). It is sometimes assumed that there is a fixed functional relationship between these different variables, but as outlined later, such relationships can change.
Finally, raw growth-rate measurements like tree-ring width or forest inventory measurements typically have to be processed in some way. This is because many variables affect tree growth but the cumulative effect of all variables combined does not necessary answer each research question. For example, one has to remove the effects of tree size/age to quantify the effects of environmental change on tree growth. In dendrochronology, this raw data processing is particularly prominent and known as detrending (Cook and Kairiukstis, 1990; Melvin, 2004; Melvin and Briffa, 2008). Detrending methods, which are related to tree and forest-growth models, frequently spark controversies and discussions.
In this article, we summarize studies that showed how tree’s and forests respond to environmental change in multiple ways simultaneously, for example, with altered radial increment, height-diameter ratio, stand density, and wood density. Based on these findings from past studies, we argue that growth trend estimates could be biased when only looking at one dimension of tree and forest growth (e.g., radial increment, but not stand density) and when trees and forests had no time to adapt to the new environmental conditions. To avoid or at least discuss potential biases in growth-trend estimates in future studies we propose the concept of the potential natural forest (PNF), which is that forest that would develop without human intervention under the respective environmental conditions. We argue that the growth rates of this PNF can differ from the growth rates of the present forest, which is not (yet) adapted to the new environment.
Controversies Around Growth Trends
Past studies on growth trends frequently sprouted controversies. Typically, the processing of the raw data is criticized and it is argued that the effect of one variable or another has not been accounted for sufficiently and the reported growth trend is thus biased.
For example, van der Sleen et al. (2015) report no growth stimulation by rising CO2-levels in the atmosphere, while Brienen et al. (2016) assume this result to be biased by recruitment waves and changing age/size distributions. In another case, Scharnweber et al. (2019) show that reconstructions of past climate in northern central Europe, based on tree rings, are likely biased due to a fertilizing effect of atmospheric nitrogen deposition. Nitrogen deposition essentially result in higher growth rates under similar climatic conditions. Comparable nitrogen fertilization effects were reported for North America (Ibáñez et al., 2018). Further, for white spruce in Alaska, various studies have reported an increase in drought sensitivity (Barber et al., 2000; Beck et al., 2011). This was derived from simple correlation analyses of radial growth with precipitation or drought indices, which often show higher values over the last decades (D’Arrigo et al., 2008). Because of that, it was typically assumed that white spruce would show reduced growth under a drier climate. In contrast to the studies assuming reduced white spruce growth under warmer and drier climate, Sullivan et al. (2017) reported only limited evidence for such a negative growth trend. While they applied state of the art data “detrending” [“signal-free methodology,” (Melvin and Briffa, 2008, 2014)], uncertainties still remain because of potentially huge sample biases (Duchesne et al., 2019), which even the best data processing cannot yet quantify: Even when selecting a representative sample of trees in a population at one point in time (Nehrbass-Ahles et al., 2014; Xu et al., 2019), growth trends could still be biased. This is because fast growing trees typically die at a younger age. In the earliest years of a tree-ring chronology, only slow growing trees are thus left, which is known as the “slow-grower survivorship bias” (Brienen et al., 2012, 2016; Bowman et al., 2013; Alexander et al., 2018).
These examples show the effects of the tree-size distribution, atmospheric nitrogen deposition or sample biases on growth-trend estimates. Besides these three examples, there are many more factors which drive forest growth, illustrating how difficult it can be to quantify growth trends. Generally, (conceptual) tree or forest growth models are deployed to disentangle which and how each variable affects tree and forest growth.
Defining Growth Trends Based on Growth Models
Definitions of growth trends are always based on a growth-rate model, even when not stated explicitly. As the controversies in the last section showed, biases and errors are typically caused by the effect of variables that were not considered in these models adequately. Thus, definitions of growth trends must center around the question how environmental variables, tree dimensions and forest structure affect different kinds of growth rates. The importance of various growth drivers can vary in space and time, while models ideally describe growth based in all possible environments, but see Wilmking et al. (2017) for a detailed discussion on this topic and the Uniformitarian Principle.
Tree-Ring Model (Radial Growth)
One simplified model is the “Conceptual Linear Aggregate Model for Tree Rings” (Fritts and Swetnam, 1989; Cook and Kairiukstis, 1990), which describes the growth rate (R = tree-ring width) as a function of the input variables tree size (A), climate (C), endogenous and exogenous disturbances (δD1, δD2), anthropogenic pollutants (P), as well as an error term (E). It was modified by King et al. (2013) to include genetic effects (g).
Raw growth-rate measurements thus represent the cumulative effect of many variables. Quantifying a specific type of growth rate means to select a subset of variables and to remove the effect of all other variables from the raw measurements. For example, if only the effect of climate on tree-ring width (Rclimate) is of interest, the effects caused by all other variables, like tree size, must be accounted for.
In some cases, the effects of certain variables do not need to be quantified or removed. This is because in contrast to growth rates, growth trends typically only concern decadal or longer time scales. Thus, as long as a variable is normally distributed and shows no trend in time (Figures 2A,B) it only adds noise to a growth-rate estimate, but it should not bias the growth trend (Figure 2C). Of course, higher noise will make small growth trends harder to detect and it is thus preferable to quantify each effect if possible.
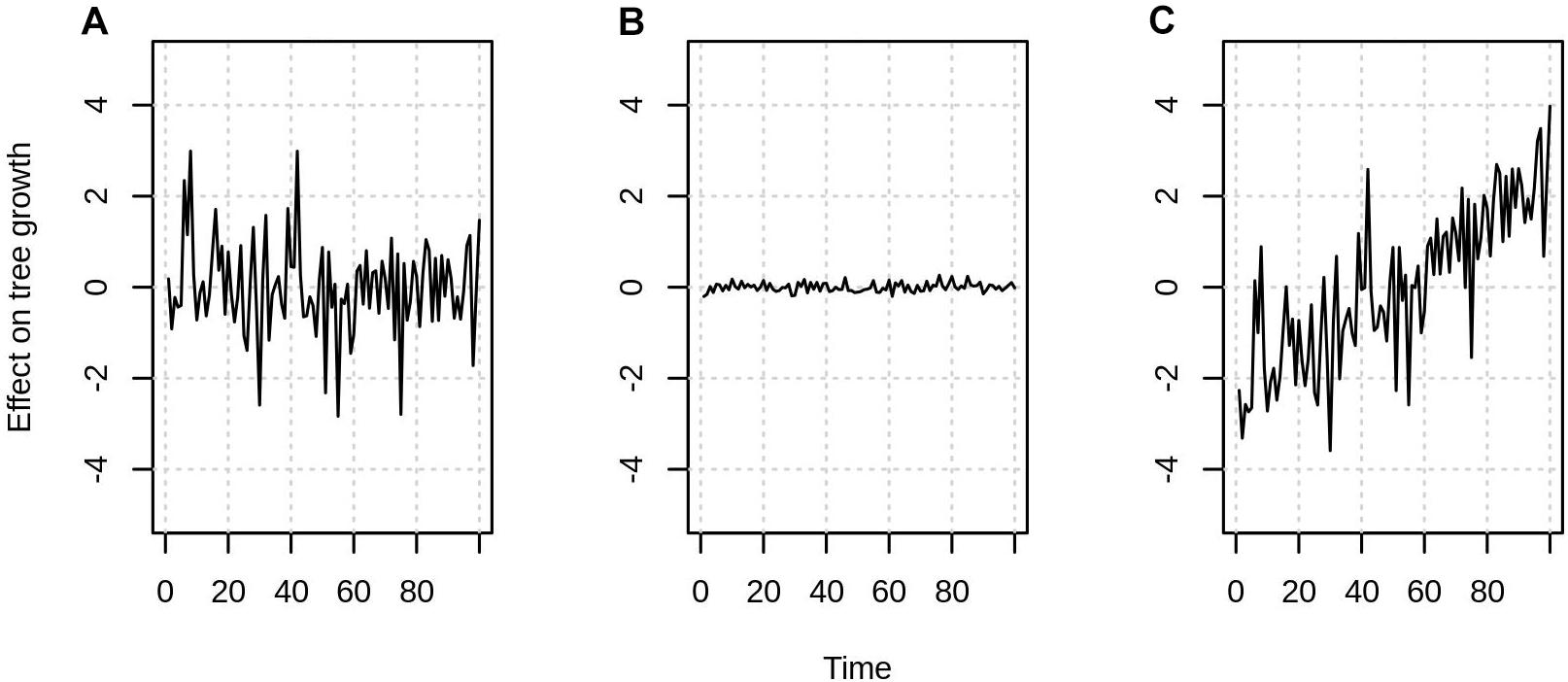
Figure 2. Variable’s effect on tree growth can either be (A) significant with no trend in time, (B) insignificant, (C) significant with a trend in time. Effects like in (C) always have to be accounted for when estimating growth trends. While effects like (A,B) might be ignored.
Tree Growth Model (Radial and Height Growth)
While the Eq. 1 aims to estimate radial tree growth, other models aim to predict wood volume, wood biomass increment, or the amount of carbon sequestered. For example, the annual increment in woody aboveground tree-biomass (ΔBMtree) can be calculated from the respective biomass difference in two successive years. Tree aboveground biomass in one year (BMtree) can be calculated as a function of tree diameter (or basal area, both via tree-ring width), tree height, a form factor (F), that accounts for the (idealized) conical shape of a stem, and wood density (ρ):
Assuming that carbon makes up ∼50% of the woody biomass, the respective amount of carbon can be calculated my multiplying ΔBMtree with 0.5.
Forest Growth Model
The forest’s above ground standing biomass per area (ΔBMforest) can be calculated as the product of the average biomass of a tree () and the stand density (N, number of trees per area). The change in forest biomass between (ΔBMforest) two points in time describes the respective growth rate.
Challenges to Scale Up From One to the Next Model
As outlined above, models can estimate different types of growth rates, like (annual) tree-ring width, average annual tree-biomass increment, or annual forest-biomass increment. Theoretically, it could be argued that different types of growth rates like tree-ring width and forest biomass are strongly related to each other and that one growth rate can be calculated from another. However, this might be a too simplistic assumption that does not consider that trees and forests are complex adaptive systems (Levin et al., 2013; Puettmann et al., 2016).
In particular, the key consequence from Eqs 3 and 4 is that multiple variables are required to calculate one growth rate from another. Therefore, it is not possible to calculate the forest biomass per hectare from the average tree biomass alone; in this case, the number of trees is needed as well. This becomes a problem when environmental change also influences the number of trees, i.e., stand density, which in turn affects individual tree biomass increment (i.e., a feedback loop via competition). This points toward a key challenge: Trees and forests respond to environmental change in multiple ways simultaneously. The same ring width (after accounting for tree-size effects) can correspond to different tree- and forest-biomass increments. The challenge in creating a good growth-rate model is thus not only to identify all the relevant parameters, but also to identify all “pathways” how these variables affect different dimensions of tree and forest growth.
Thus, the definition of a growth trend at any scale first requires a complex growth model. This model must include all relevant variables for tree and forest growth with all their functional relationships, including indirect effects and (time-lagged) feedback loops. The model then determines which growth-rate types are suitable to answer a specific research question. For example, if there is evidence that environmental change affects stand density, which in turn affects radial tree growth via competition, then tree-ring width alone is an insufficient measure of trees reaction to the environmental change. Figure 3 shows a schematic growth model that includes various direct effects and feedback loops and the next sections highlight the importance of the (time-lagged) feedback loops.
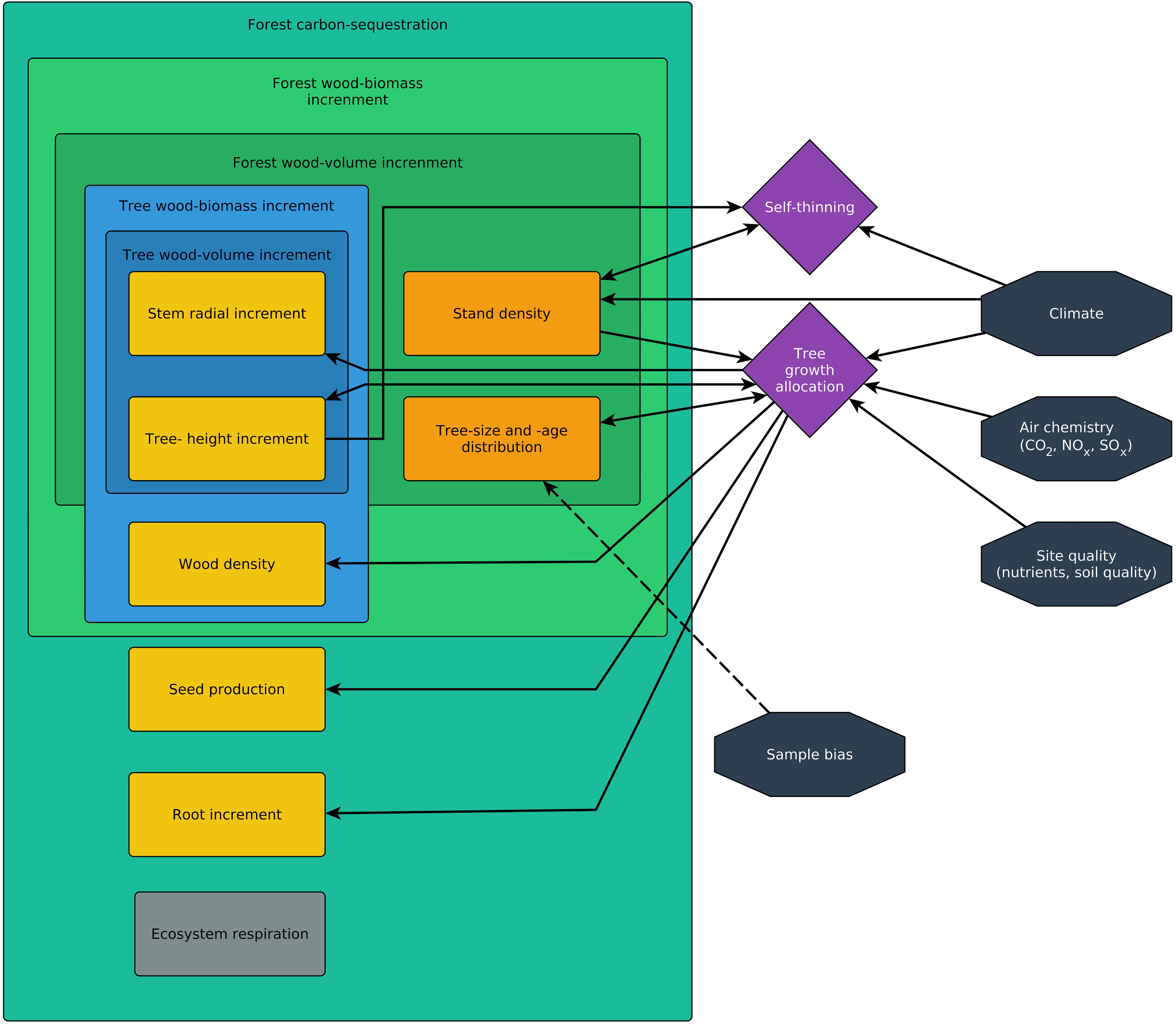
Figure 3. This simplified schematic model shows how different types of growth rates are connected. Arrows indicate the effect of one variable or process on another and highlight the direct and indirect effects that connect growth rates, environmental conditions, and sample biases (black), processes (purple), as well as forest and tree parameters (orange).
The Forest-Structure Feedback Loop
Jump et al. (2017) describe “structural overshoot” effects, i.e., how more favorable environmental conditions in the past can lead to a higher above-ground biomass, but when the environmental conditions deteriorate (e.g., get drier), this biomass cannot be sustained anymore. Dieback of branches, canopies, and whole trees might be the consequence. Similarly, Sperry et al. (2019) use the ecohydrological equilibrium to model stand-level acclimation to changing CO2-concentrations and rising temperatures via changes in leaf area index (LAI) and tree biomass. Both articles are related to the concept of the carrying capacity, where a limited resource controls the maximum viable number and size of the individuals. In forestry, the carrying capacity is often studied via self-thinning lines (Reineke, 1933; Yoda et al., 1963; Bi, 2001; Pretzsch, 2009a) as shown in Figure 1L. Self-thinning lines describe the highest number of individuals that can survive at a given tree size (in an even-aged forest). Importantly, self-thinning lines depend on the environmental conditions.
The structural overshoot effect can lead to different growth rates under the same environmental conditions, and is caused by more beneficial environmental conditions in the past. It could thus be argued, that a forest structure can be called “non-representative” for the current environmental conditions, whenever the environmental conditions change faster than the forest structure is able to adapt. Forest structural changes might be an altered stand density and the tree-size distribution, along with altered generation times (Pretzsch et al., 2014; Forrester, 2019). Various studies focused on such effects: For example, stand density has been shown to decline with decreasing moisture (Eamus et al., 2001; Wang et al., 2006), higher tree densities increase drought stress (Finley and Zhang, 2019; Andrews et al., 2020), and stand density was found to be negatively correlated to resilience/resistance (Bottero et al., 2017). Furthermore, López-Serrano et al. (2005) found that drought appears to induce self-thinning in young stands, and Ruiz-Benito et al. (2013) report that denser forests are more vulnerable to increased mortality rates. On a global level, Crowther et al. (2015) found that stand density is positively correlated with temperature and moisture, although local determinants of stand density can be more complex. In forestry, thinning procedures were repeatedly proposed or already applied to reduce drought susceptibility to adapt forests to expected future climate change (D’Amato et al., 2013; Grant et al., 2013; Rais et al., 2014; Thomas and Waring, 2015; Sohn et al., 2016; Mausolf et al., 2018; Manrique-Alba et al., 2020). Though, not all studies found that environmental change and growth trends alter self-thinning lines (Pretzsch et al., 2014).
Generally, the feedback loop between tree and forest structure and growth rates is linked to the costs and gains of trees and forests “infrastructure”: higher trees with larger crowns could theoretically photosynthesize more, but they also require larger vessels/tracheids (Sanio, 1872; Mencuccini et al., 2007) which makes them more susceptible to embolisms during droughts, while more leaves lead to higher respiration costs, which is only worth these expenses given sufficient resources (water, light) and benign environmental conditions. Similarly, more trees per area could result in a larger forest biomass increment, but only if sufficient resources are available to support that many trees (carrying capacity).
Changes in forest structure do of course mostly not occur abruptly but gradually over decades or even centuries. Just as treelines are known to lag behind climate change by at least 50 years (Körner, 2012), stand density will often only change slowly. Of course, decreases in stand density due to die-back are likely much faster than increases. The frequently reported drought-related increases in mortality (Allen et al., 2010, 2015; Wang et al., 2012) are indicators of such quick reductions in stand density. Such drought related die-offs are often seen as a bad thing, but on an ecosystem level it could be argued that some die-backs are actually adaptive. Generally, trees and forests have to balance the counteracting forces of resilience and adaptation (Parrott and Lange, 2013; Filotas et al., 2014).
Growth-Allocation Feedback Loops
Trees grow in more than just one dimension. Because of that, Hember et al. (2015) argued that the use of radial growth time-series can bias the assessment of growth trends and that it would be better to calculate biomass increments from stem diameter, tree height, a form factor and wood density (Eq. 3). The issue is not just a non-linear relationship between radial growth and tree-biomass increment, which would still allow to calculate one measure from the other. The issue is rather that the resource allocation varies between years and trees depending on the environment and the general tree state. Next to radial and height growth, resource allocation also varies for seed production (Hacket-Pain et al., 2015; Vacchiano et al., 2017; Gavinet et al., 2019), wood density (Pretzsch et al., 2018) and root growth (Ledo et al., 2018).
Several studies have shown changes in the allocation of resources depending on the climatic conditions (Martínez and López-Portillo, 2003; López-Serrano et al., 2005; Lines et al., 2012; Poorter et al., 2012; Hulshof et al., 2015; Gavinet et al., 2019). In particular, under dry conditions trees invest more resources in radial and root growth and less resources in height growth (Way and Oren, 2010; Lines et al., 2012). Though, Franceschini et al. (2016) found no effects of precipitation on growth allocation, while they did find temperature effects. Reduced height growth under dry conditions is at least partially caused by wood anatomical restrictions: In tall trees, larger lumen diameters of tracheids and vessels at the stem base are needed to sustain sufficient hydraulic conductivity (Sanio, 1872; Mencuccini et al., 2007; Carrer et al., 2015). But while larger lumen diameters are required by higher trees, they also make trees more susceptible to drought induced embolisms. Thus, a typical response of trees to drought is to reduce the lumen diameter within the range of their phenotypic plasticity. Drier climate is thus linked to smaller trees and globally, canopy height is positively related to water availability (Klein et al., 2015; Grote et al., 2016). This suggests that in an anticipated drier future shorter trees will likely dominate (Fajardo et al., 2018, 2019; Olson et al., 2018). Reduced height growth, relative to diameter growth, can generally be seen as an adaptation to dry conditions.
It is important to consider that height growth has a cumulative effect, i.e., that past height growth can pose a burden on future growth. Namely, it can be distinguished between short-term and long-term effects of resource allocation (López-Serrano et al., 2005; Maseda and Fernandez, 2006): While the annual (short-term) difference in resource allocation to height and radial growth might be small, past height growth can significantly reduce future growth (and generation time). A tree that is already tall needs wider vessels/tracheids at the stem base to ensure sufficient water transport, which increases trees’ drought susceptibility. This would imply that under similar climatic conditions a tree that is taller might show reduced growth compared to a tree with the same diameter but a lower height.
Furthermore, stem density and canopy closure are also well-known to affect growth allocation due to competition for light (Pretzsch, 2009a; Franceschini et al., 2016). Under low light conditions, competition for light makes trees allocate more resources to height growth. Even-aged forests, or natural recruitment waves will thus result in a different growth allocation than undisturbed uneven-aged forests because of different light regimes during the ontogeny. Lastly, high concentrations of atmospheric ozone were also reported to shift allocation toward increased height growth at the expanse of radial growth (Pretzsch et al., 2010).
How Representative is the Sample?
Estimating growth trends critically depends on measurements that are representative for the whole (tree-ring, tree, forest), otherwise, the results can be biased. Next to representative site conditions, the selection of individual trees is crucial for growth-rate estimates. During forestry inventories, either all, or a random selection of trees are measured. Such data is representative, but long time-series are often not available. Extracting cores from the stem and using tree rings as archives of past growth has thus frequently been used to obtain long time-series of radial tree growth. In dendrochronology, the effect of biases caused by the tree-selection method within a site have been explored by Nehrbass-Ahles et al. (2014), who argued that either all trees or a random selection of trees should be sampled. Xu et al. (2019) explored in more detail how many trees of which size class have to be selected to minimize sampling effort and still derive a representative sample set. However, even when coring all trees in a forest stand, the sample will not necessarily be representative in the decades prior to sampling the cores. This is because in a forest individual trees continuously die and decompose. Such trees will then be missing from the sample. This becomes a problem because trees do not die randomly or evenly distributed in time. Instead, slow growing trees often live longer, probably because ultimately tree height (not age) kills a tree due to hydraulic limitations (Sanio, 1872; Thomas, 2002; Bond et al., 2007; Mencuccini et al., 2007; Trouillier et al., 2018). As a result, further back in time the faster growing trees are missing, which will look like a positive growth trend and is known as the “slow-grower survivorship bias” (Melvin, 2004; Bowman et al., 2013; Brienen et al., 2016; Duchesne et al., 2019). Thus, to derive any growth trends, the frequency of slow and fast growers in the retrospective sample must match exactly the frequency of such slow and fast growers in the forest in the respective year, otherwise the growth rate is over- or underestimated. We agree with Duchesne et al. (2019), that there is no statistical method (yet) that can disentangle such sample biases from real growth trends. Missing information on the frequency of fast and slow growing trees in a forest is thus a key challenge when estimating growth trends from tree-ring data, while data from forest inventories or eddy covariance towers is unavailable for long-time series.
The Potential Natural Forest
The previous sections outlined that trees and forests react and adapt in multiple ways to environmental change. We thus argue that each environment will lead to a typical forest and tree structure, which includes a characteristic stand density, size frequency-distribution, generation time as well as growth allocation. Based on the concept of the potential natural vegetation – PNV (Tüxen and Preising, 1956), we call this emerging forest type the “potential natural forest” – PNF. This forest can be defined as the hypothetical forest that would develop under the current environmental conditions and without disturbances and human intervention. The PNF thus describes the offset between the current forest, caused by the environmental conditions in the past, and the forest that would emerge at a given site, if the reaction of tree’s and forests would not lag behind the environmental change, and if the forest would not be disturbed. For simplicity, we here neglect successional cycles, natural disturbances, changing species compositions, and permanent anthropogenic site changes like the depositions of nutrients or pollutants (Chiarucci et al., 2010), though, the PNF concept could be extended to include such effects.
To illustrate the PNF concept and how it is related to growth-trend estimates, we created a virtual dataset of two forests PNF-E1 and PNF-E2, which developed under the environmental conditions E1 and E2, respectively (Supplementary Table 1). Both forests differ in (a) their tree size-frequency distribution (Supplementary Figure 1), (b) height-age relationships (Supplementary Figure 2), (c) age-diameter relationship (Supplementary Figure 3), and (d) wood density. Given these variables, we then calculated other tree and forest variables like tree and forest basal area, wood volume, and wood biomass (Eqs 3 and 4). The relative differences between both forests is shown in Figure 4A. When PNF-E1 is exposed to environment E2, the tree and forest parameters will slowly change and the PNF-E1 will turn into PNF-E2. But this adaptation process might take many decades. Consequently, for some time the PNF-E1 will experience an environment to which it is not (yet adapted). In our example we thus compare three growth rates: The growth rates of both forests PNF-E1 and PNF-E2 in their native environments E1 and E2, as well as the growth rate of PNF-E1 when exposed to E2 without time for adaptation. This example thus illustrates how growth trends can differ if a forest does or does not have time to adapt to environmental change.
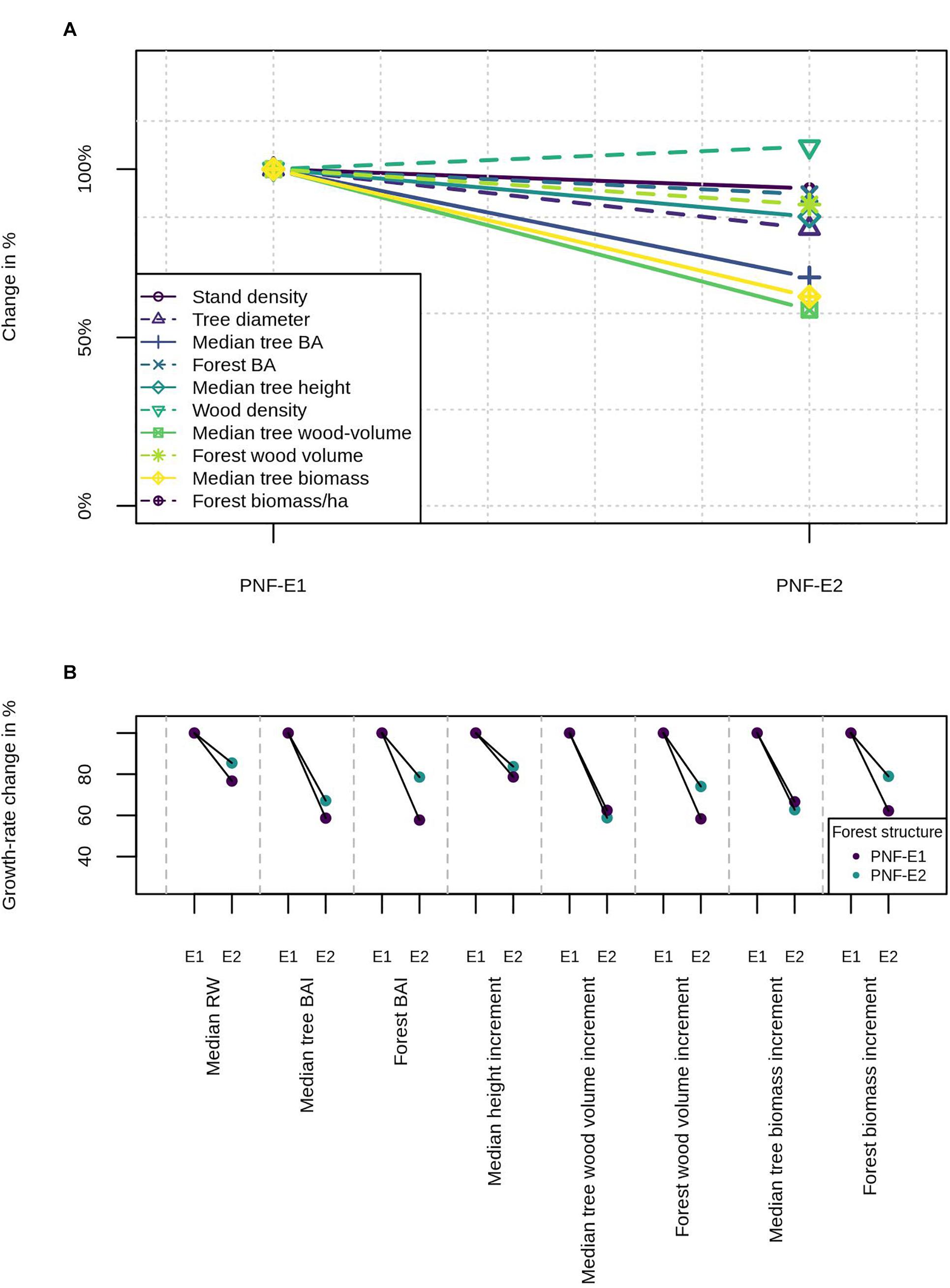
Figure 4. Example of two forests PNF-E1 and PNF-E2 that developed under their respective environments E1 and E2. Both forests differ in their structural parameters (A). When PNF-E1 is exposed to E2, it will slowly adapt and turn into PNF-E2. However, without time for adaptation the growth rates will differ (B). Structural overshoot and a stand density above the carrying capacity result in lower growth rates of a forest that is not adapted to E2.
Annual growth rates were calculated from the age-size relationships (e.g., ring width ∼ diameter). To calculate the growth rate of PNF-E1 under the new environment E2, we applied the respective age-size relationships from PNF-E2 to the forest structure of PNF-E1, multiplied by a reduction factor to simulate structural overshoot effects and stand densities above the carrying capacity. Figure 4B illustrates the results and shows, that the growth trends (growth rate change in percent) differ between the different types of growth rates. Most importantly with respect to the PNF, it also shows that growth rates drop more when the forest had no time to adapt. Effect sizes should of course be taken with a grain of salt since this is a hypothetical example created to demonstrate the PNF.
Application of the PNF
It depends on the research question if it matters that the present forest under study and the PNF have potentially different growth rates. The PNF should be used to remove the legacy effect of the past and only assess how much trees or forests would grow after the ecosystem is in the stable state defined by the environmental conditions. The PNF should not be used if these legacy effects are in fact of interest. How exactly to apply the PNF concept will depend on the dataset, research question and methodology. One simple empirical way could be to fit a smoothing spline to the data. This (multidimensional) spline would essentially return the typical growth rate at a given tree and forest structure, just as the regional curve standardization (RCS) is already used to return the expected tree-ring width at a given age. Though, other methods like physiologically meaningful equations or agent-based models would be possible too. Generally, the PNF can be useful for different disciplines:
For example, given the data from successive forest inventories over several decades, one might ask how the annual forest biomass increment per hectare has changed due to climate change. For each inventory, the individual tree and forest biomass could be calculated from the measured values (DBH, tree height, stand density, wood density). The differences in biomass between two inventories would then be the tree and forest growth-rates. Though, the trees and forest structure may currently adapt to the new climatic conditions and have not yet reached the new stable state (the PNF) yet. If this matters for the research question, it must also be investigated how tree growth will change the forest structure and how much the new forest structure in return affects individual tree and forest growth (feedback loop). As outlined above, this includes assessing the effects of stand density, the tree-size distribution and the growth allocation within trees.
Dendrochronologists often use tree-ring data to reconstruct temperature or precipitation before instrumental records: At a given site, summer temperature might have a strong effect on tree growth, and thus correlate with tree-ring width. Growth trends would indicate gradual changes in the summer temperature. Because raw data is unsuitable to reconstruct climatic variables (age trends), dendrochronologists have developed various detrending methods, which are generally closely related to growth models. For example, the RCS method attempts to quantify the effects of tree age/size on tree-ring width. On the other hand, information on stand density, tree size distribution or height growth is typically not available for dendrochronological datasets. But as outlined above, those variables are affected by environmental change and they affect tree-ring width (feedback loop). To avoid biases, reconstructions of climate variables would ideally also be based on the growth rate of the PNF to quantify how much the climatic variable changed each tree and forest variable.
Lastly, eddy covariance towers measure the CO2 uptake and emission of ecosystems. It can be challenging to attribute a changing rate of CO2 sequestration to one cause or another. In forests, CO2 uptake is mostly caused by tree’s photosynthesis. Increasing rates of carbon sequestration could thus indicate more photosynthesis, which typically also indicates a positive trend in the forest’s biomass increment. However, without additional information on the forest, the cause of this trend cannot be explored further. For example, in a relatively young afforestation forest, a positive growth trend would mostly be caused by trees approaching the size/age of their highest productivity. Eddy covariance data alone cannot be used to explore the causes of the observed trend in more detail because it cannot distinguish between diameter-, height-, root growth, and the soil’s carbon balance. Given additional data, the PNF concept could be applied to eddy covariance data to understand where in a forest more or less carbon is sequestered and how certain environmental changes shift CO2 accumulation rate by altering stand density, tree size distribution or carbon allocation within the trees.
An alternative to the PNF, to account for the legacy effects of the past, would be a fixed baseline forest which could be simulated with agent-based models (Pretzsch, 2009b; Grimm and Railsback, 2013; Mäkelä and Valentine, 2020). For example, a planted, even-aged pure forest with a precisely defined forest structure could be such a fixed baseline. It could be used to assess how much biomass this exact forest would produce in each environment. However, calculating growth trends of such a baseline forest is probably not any easier than estimating the growth rate of the PNF, it just transposes the mathematical equations of the growth rate model and it limits the interpretation to certain forestry practices. In most cases the PNF is thus preferable.
Conclusion
In this article, we describe the challenges that surround the definition and quantification of tree and forest growth-trends and put special emphasis on time-lagged feedback loops. In particular, we describe how trees and forests respond in multiple ways to environmental change and thus argue that characteristic tree and forest structures will emerge under different environmental conditions. However, because of tree’s long generation times and growth rates, their adaptation to the new environmental conditions can lag behind decades to centuries, causing an offset between the present forest and what we termed the PNF. Those two forests may show different growth rates under the same environmental conditions. This difference can be important when quantifying and reporting growth trends. For example, two forests that developed under dry and moist conditions, respectively, will show different h/d ratios of trees, different stand densities and different size-frequency distributions. When exposed to exactly the same climatic conditions today, they will likely also show different growth rates and trends. After being exposed to the same climate over long time periods, both forests will develop into the potential natural forest that is characteristic for this environment.
The PNF is in line with a framework that was recently proposed by Forrester (2019) that describes how to estimate stand biomass growth-rates based on stand density, size probability density-function and size-growth relationship. Essentially, this refers to the same feedback loops described in this article. Similarly, and in agreement with our description of temporal changes in the forest structure, Evans et al. (2017) proposed to use tree-ring data in combination with forest inventory data or to combine them with individual based models, that account for changes in the stand basal area and thus the competition within a stand.
Currently few, if any, long time-series datasets are detailed enough to apply the PNF concept to estimate growth trends. Nonetheless, we believe that the PNF is already a useful concept because it enables researchers to consider the full complexity of tree and forest growth and discuss uncertainties when reporting growth trends. In the future, more detailed time-series data that cover longer time-periods will become available, which will then allow to turn the theoretical concept into a mathematical model or detrending procedure.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Author Contributions
MT conceived the idea of this manuscript and wrote the first draft. All authors discussed and refined the manuscript together.
Funding
MT was funded by the German Research Foundation (DFG) within the Research Training Group RESPONSE (DFG RTG 2010). We acknowledge support for the Article Processing Charge from the DFG (German Research Foundation, 393148499) and the Open Access Publication Fund of the University of Greifswald.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffgc.2020.581334/full#supplementary-material
References
Alexander, M. R., Rollinson, C. R., Babst, F., Trouet, V., and Moore, D. J. P. (2018). Relative influences of multiple sources of uncertainty on cumulative and incremental tree-ring-derived aboveground biomass estimates. Trees 32, 265–276. doi: 10.1007/s00468-017-1629-0
Allen, C. D., Breshears, D. D., and McDowell, N. G. (2015). On underestimation of global vulnerability to tree mortality and forest die-off from hotter drought in the Anthropocene. Ecosphere 6, 1-55. doi: 10.1890/ES15-00203.1
Allen, C. D., Macalady, A. K., Chenchouni, H., Bachelet, D., McDowell, N., Vennetier, M., et al. (2010). A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 259, 660–684. doi: 10.1016/j.foreco.2009.09.001
Andrews, C. M., D’Amato, A. W., Fraver, S., Palik, B., Battaglia, M. A., and Bradford, J. B. (2020). Low stand density moderates growth declines during hot droughts in semi−arid forests. J. Appl. Ecol. 57, 1089–1102. doi: 10.1111/1365-2664.13615
Barber, V. A., Juday, G. P., and Finney, B. P. (2000). Reduced growth of Alaskan white spruce in the twentieth century from temperature-induced drought stress. Nature 405, 668–673. doi: 10.1038/35015049
Beck, P. S. A., Juday, G. P., Alix, C., Barber, V. A., Winslow, S. E., Sousa, E. E., et al. (2011). Changes in forest productivity across Alaska consistent with biome shift. Ecol. Lett. 14, 373–379. doi: 10.1111/j.1461-0248.2011.01598.x
Bond, B. J., Czarnomski, N. M., Cooper, C., Day, M. E., and Greenwood, M. S. (2007). Developmental decline in height growth in Douglas-fir. Tree Physiol. 27, 441–453. doi: 10.1093/treephys/27.3.441
Bottero, A., D’Amato, A. W., Palik, B. J., Bradford, J. B., Fraver, S., Battaglia, M. A., et al. (2017). Density-dependent vulnerability of forest ecosystems to drought. J. Appl. Ecol. 54, 1605-1614. doi: 10.1111/1365-2664.12847
Bowman, D. M. J. S., Brienen, R. J. W., Gloor, E., Phillips, O. L., and Prior, L. D. (2013). Detecting trends in tree growth: not so simple. Trends Plant Sci. 18, 11–17. doi: 10.1016/j.tplants.2012.08.005
Brienen, R. J. W., Gloor, E., and Zuidema, P. A. (2012). Detecting evidence for CO2 fertilization from tree ring studies: the potential role of sampling biases. Glob. Biogeochem. Cycles 26:GB1025. doi: 10.1029/2011GB004143
Brienen, R. J. W., Gloor, M., and Ziv, G. (2016). Tree demography dominates long-term growth trends inferred from tree rings. Glob. Change Biol. 23, 474–484. doi: 10.1111/gcb.13410
Carrer, M., von Arx, G., Castagneri, D., and Petit, G. (2015). Distilling allometric and environmental information from time series of conduit size: the standardization issue and its relationship to tree hydraulic architecture. Tree Physiol. 35, 27-33.
Chiarucci, A., Araújo, M. B., Decocq, G., Beierkuhnlein, C., and Fernández-Palacios, J. M. (2010). The concept of potential natural vegetation: an epitaph? J. Veg. Sci. 21, 1172–1178. doi: 10.1111/j.1654-1103.2010.01218.x
Cook, E. R., and Kairiukstis, L. A. (1990). Methods of Dendrochronology: Applications in the Environmental Sciences. Berlin: Springer Science & Business Media.
Crowther, T. W., Glick, H. B., Covey, K. R., Bettigole, C., Maynard, D. S., Thomas, S. M., et al. (2015). Mapping tree density at a global scale. Nature 525, 201–205. doi: 10.1038/nature14967
D’Amato, A. W., Bradford, J. B., Fraver, S., and Palik, B. J. (2013). Effects of thinning on drought vulnerability and climate response in north temperate forest ecosystems. Ecol. Appl. 23, 1735–1742. doi: 10.1890/13-0677.1
D’Arrigo, R., Wilson, R., Liepert, B., and Cherubini, P. (2008). On the ‘Divergence Problem’ in Northern forests: a review of the tree-ring evidence and possible causes. Glob. Planet. Change 60, 289–305. doi: 10.1016/j.gloplacha.2007.03.004
Duchesne, L., Houle, D., Ouimet, R., Caldwell, L., Gloor, M., and Brienen, R. (2019). Large apparent growth increases in boreal forests inferred from tree-rings are an artefact of sampling biases. Sci. Rep. 9:6832. doi: 10.1038/s41598-019-43243-1
Eamus, D., Hutley, L. B., and O’Grady, A. P. (2001). Daily and seasonal patterns of carbon and water fluxes above a north Australian savanna. Tree Physiol. 21, 977–988. doi: 10.1093/treephys/21.12-13.977
Evans, M. E. K., Falk, D. A., Arizpe, A., Swetnam, T. L., Babst, F., and Holsinger, K. E. (2017). Fusing tree-ring and forest inventory data to infer influences on tree growth. Ecosphere 8:e01889. doi: 10.1002/ecs2.1889
Fajardo, A., Martínez−Pérez, C., Cervantes−Alcayde, M. A., and Olson, M. E. (2019). Stem length, not climate, controls vessel diameter in two trees species across a sharp precipitation gradient. New Phytol. 225, 2347-2355. doi: 10.1111/nph.16287
Fajardo, A., McIntire, E. J. B., and Olson, M. E. (2018). When short stature is an asset in trees. Trends Ecol. Evol. 34, 193-199. doi: 10.1016/j.tree.2018.10.011
Filotas, E., Parrott, L., Burton, P. J., Chazdon, R. L., Coates, K. D., Coll, L., et al. (2014). Viewing forests through the lens of complex systems science. Ecosphere 5, 1-23. doi: 10.1890/ES13-00182.1
Finley, K., and Zhang, J. (2019). Climate effect on ponderosa pine radial growth varies with tree density and shrub removal. Forests 10:477. doi: 10.3390/f10060477
Forrester, D. I. (2019). Linking forest growth with stand structure: tree size inequality, tree growth or resource partitioning and the asymmetry of competition. For. Ecol. Manag. 447, 139–157. doi: 10.1016/j.foreco.2019.05.053
Franceschini, T., Martin-Ducup, O., and Schneider, R. (2016). Allometric exponents as a tool to study the influence of climate on the trade-off between primary and secondary growth in major north-eastern American tree species. Ann. Bot. 117, 551–563. doi: 10.1093/aob/mcw003
Fritts, H. C., and Swetnam, T. W. (1989). Dendroecology: a tool for evaluating variations in past and present forest environments. Adv. Eco. Res. 19, 111–188. doi: 10.1016/S0065-2504(08)60158-0
Gavinet, J., Ourcival, J., and Limousin, J. (2019). Rainfall exclusion and thinning can alter the relationships between forest functioning and drought. New Phytol. 223, 1267–1279. doi: 10.1111/nph.15860
Grant, G. E., Tague, C. L., and Allen, C. D. (2013). Watering the forest for the trees: an emerging priority for managing water in forest landscapes. Front. Ecol. Environ. 11:314–321. doi: 10.1890/120209
Grimm, V., and Railsback, S. F. (2013). Individual-Based Modeling and Ecology. Princeton, NJ: Princeton University Press.
Grote, R., Gessler, A., Hommel, R., Poschenrieder, W., and Priesack, E. (2016). Importance of tree height and social position for drought-related stress on tree growth and mortality. Trees 30, 1467–1482. doi: 10.1007/s00468-016-1446-x
Hacket-Pain, A. J., Friend, A. D., Lageard, J. G. A., and Thomas, P. A. (2015). The influence of masting phenomenon on growth-climate relationships in trees: explaining the influence of previous summers’ climate on ring width. Tree Physiol. 35, 319–330. doi: 10.1093/treephys/tpv007
Hember, R. A., Kurz, W. A., and Metsaranta, J. M. (2015). Ideas and perspectives: use of tree-ring width as an indicator of tree growth. Biogeosci. Discuss. 12, 8341–8352. doi: 10.5194/bgd-12-8341-2015
Hulshof, C. M., Swenson, N. G., and Weiser, M. D. (2015). Tree height-diameter allometry across the United States. Ecol. Evol. 5, 1193–1204. doi: 10.1002/ece3.1328
Ibáñez, I., Zak, D. R., Burton, A. J., and Pregitzer, K. S. (2018). Anthropogenic nitrogen deposition ameliorates the decline in tree growth caused by a drier climate. Ecology 99, 411–420. doi: 10.1002/ecy.2095
Jump, A. S., Ruiz−Benito, P., Greenwood, S., Allen, C. D., Kitzberger, T., Fensham, R., et al. (2017). Structural overshoot of tree growth with climate variability and the global spectrum of drought−induced forest dieback. Glob. Change Biol. 23, 3742–3757. doi: 10.1111/gcb.13636
King, G. M., Gugerli, F., Fonti, P., and Frank, D. C. (2013). Tree growth response along an elevational gradient: climate or genetics? Oecologia 173, 1587–1600. doi: 10.1007/s00442-013-2696-6
Klein, T., Randin, C., and Körner, C. (2015). Water availability predicts forest canopy height at the global scale. Ecol. Lett. 18, 1311–1320. doi: 10.1111/ele.12525
Körner, C. (2012). Alpine Treelines: Functional Ecology of the Global High Elevation Tree Limits. Berlin: Springer Science & Business Media.
Ledo, A., Paul, K. I., Burslem, D. F. R. P., Ewel, J. J., Barton, C., Battaglia, M., et al. (2018). Tree size and climatic water deficit control root to shoot ratio in individual trees globally. New Phytol. 217, 8–11. doi: 10.1111/nph.14863
Levin, S., Xepapadeas, T., Crépin, A.-S., Norberg, J., de Zeeuw, A., Folke, C., et al. (2013). Social-ecological systems as complex adaptive systems: modeling and policy implications. Environ. Dev. Econ. 18, 111–132. doi: 10.1017/S1355770X12000460
Lines, E. R., Zavala, M. A., Purves, D. W., and Coomes, D. A. (2012). Predictable changes in aboveground allometry of trees along gradients of temperature, aridity and competition: predictable variation in tree aboveground allometry. Glob. Ecol. Biogeogr. 21, 1017–1028. doi: 10.1111/j.1466-8238.2011.00746.x
López-Serrano, F. R., García-Morote, A., Andrés-Abellán, M., Tendero, A., and del Cerro, A. (2005). Site and weather effects in allometries: a simple approach to climate change effect on pines. For. Ecol. Manag. 215, 251–270. doi: 10.1016/j.foreco.2005.05.014
Mäkelä, A., and Valentine, H. T. (2020). Models of Tree and Stand Dynamics: Theory, Formulation and Application, 1st Edn. Berlin: Springer.
Manrique-Alba, À, Beguería, S., Molina, A. J., González-Sanchis, M., Tomàs-Burguera, M., Campo, A. D., et al. (2020). Long-term thinning effects on tree growth, drought response and water use efficiency at two Aleppo pine plantations in Spain. Sci. Total Environ. 728:138536. doi: 10.1016/j.scitotenv.2020.138536
Martínez, A. J., and López-Portillo, J. (2003). Allometry of Prosopis glandulosa var. Torreyana along a topographic gradient in the Chihuahuan desert. J. Veg. Sci. 14, 111–120. doi: 10.1111/j.1654-1103.2003.tb02133.x
Maseda, P. H., and Fernandez, R. J. (2006). Stay wet or else: three ways in which plants can adjust hydraulically to their environment. J. Exp. Bot. 57, 3963–3977. doi: 10.1093/jxb/erl127
Mausolf, K., Wilm, P., Härdtle, W., Jansen, K., Schuldt, B., Sturm, K., et al. (2018). Higher drought sensitivity of radial growth of European beech in managed than in unmanaged forests. Sci. Total Environ. 642, 1201–1208. doi: 10.1016/j.scitotenv.2018.06.065
Melvin, T. M. (2004). Historical Growth Rates and Changing Climatic Sensitivity of Boreal Conifers. Ph.D. thesis, University of East Anglia, Norwich.
Melvin, T. M., and Briffa, K. R. (2008). A “signal-free” approach to dendroclimatic standardisation. Dendrochronologia 26, 71–86. doi: 10.1016/j.dendro.2007.12.001
Melvin, T. M., and Briffa, K. R. (2014). CRUST: software for the implementation of Regional Chronology Standardisation: Part 1. Signal-Free RCS. Dendrochronologia 32, 7–20. doi: 10.1016/j.dendro.2013.06.002
Mencuccini, M., Hölttä, T., Petit, G., and Magnani, F. (2007). Sanio’s laws revisited. Size-dependent changes in the xylem architecture of trees. Ecol. Lett. 10, 1084–1093. doi: 10.1111/j.1461-0248.2007.01104.x
Nehrbass-Ahles, C., Babst, F., Klesse, S., Nötzli, M., Bouriaud, O., Neukom, R., et al. (2014). The influence of sampling design on tree-ring-based quantification of forest growth. Glob. Change Biol. 20, 2867–2885. doi: 10.1111/gcb.12599
Olson, M. E., Soriano, D., Rosell, J. A., Anfodillo, T., Donoghue, M. J., Edwards, E. J., et al. (2018). Plant height and hydraulic vulnerability to drought and cold. Proc. Natl. Acad. Sci. U.S.A. 115, 7551–7556. doi: 10.1073/pnas.1721728115
Parrott, L., and Lange, H. (2013). “An introduction to complexity science,” in Managing Forests as Complex Adaptive Systems: Building Resilience to the Challenge of Global Change, eds C. Messier, K. J. Puettmann, and K. D. Coates (Abingdon: Routledge), 31–46.
Poorter, H., Niklas, K. J., Reich, P. B., Oleksyn, J., Poot, P., and Mommer, L. (2012). Biomass allocation to leaves, stems and roots: meta-analyses of interspecific variation and environmental control: Tansley review. New Phytol. 193, 30–50. doi: 10.1111/j.1469-8137.2011.03952.x
Pretzsch, H. (2009b). Forest Dynamics, Growth and Yield: From Measurement to Model. 2010th Edn. Berlin: Springer.
Pretzsch, H., Biber, P., Schütze, G., Kemmerer, J., and Uhl, E. (2018). Wood density reduced while wood volume growth accelerated in Central European forests since 1870. For. Ecol. Manag. 429, 589–616. doi: 10.1016/j.foreco.2018.07.045
Pretzsch, H., Biber, P., Schütze, G., Uhl, E., and Rötzer, T. (2014). Forest stand growth dynamics in Central Europe have accelerated since 1870. Nat. Commun. 5:4967. doi: 10.1038/ncomms5967
Pretzsch, H., Dieler, J., Matyssek, R., and Wipfler, P. (2010). Tree and stand growth of mature Norway spruce and European beech under long-term ozone fumigation. Environ. Pollut. 158, 1061–1070. doi: 10.1016/j.envpol.2009.07.035
Pretzsch H. (ed.) (2009a). “Forest dynamics, growth, and yield,” in Forest Dynamics, Growth and Yield (Berlin: Springer Berlin Heidelberg), 1–39. doi: 10.1007/978-3-540-88307-4_1
Puettmann, K. J., Parrott, L., and Messier, C. (2016). Teaching complex adaptive systems science in natural resource management: examples from forestry. Nat. Sci. Educ. 45, 1-7. doi: 10.4195/nse2016.04.0009
Rais, A., van de Kuilen, J.-W. G., and Pretzsch, H. (2014). Growth reaction patterns of tree height, diameter, and volume of Douglas-fir (Pseudotsuga menziesii [Mirb.] Franco) under acute drought stress in Southern Germany. Eur. J. For. Res. 133, 1043–1056. doi: 10.1007/s10342-014-0821-7
Randerson, J. T., Chapin, F. S., Harden, J. W., Neff, J. C., and Harmon, M. E. (2002). Net ecosystem production: a comprehensive measure of net carbon accumulation by ecosystems. Ecol. Appl. 12:11.
Reineke, L. H. (1933). Perfection a stand-density index for even-aged forest. J. Agric. Res. 46, 627–638.
Ruiz-Benito, P., Lines, E. R., Gómez-Aparicio, L., Zavala, M. A., and Coomes, D. A. (2013). Patterns and drivers of tree mortality in Iberian forests: climatic effects are modified by competition. PLoS One 8:e56843. doi: 10.1371/journal.pone.0056843
Sanio, K. (1872). Über die Grosse der Holzzellen bei der gemeinen Kiefer (Pinus silvestris). Jb. Wiss. Bot. 8, 401–420.
Scharnweber, T., Heußner, K.-U., Smiljanic, M., Heinrich, I., van der Maaten-Theunissen, M., van der Maaten, E., et al. (2019). Removing the no-analogue bias in modern accelerated tree growth leads to stronger medieval drought. Sci. Rep. 9:2509. doi: 10.1038/s41598-019-39040-5
Sohn, J. A., Hartig, F., Kohler, M., Huss, J., and Bauhus, J. (2016). Heavy and frequent thinning promotes drought adaptation in Pinus sylvestris forests. Ecol. Appl. 26, 2190–2205. doi: 10.1002/eap.1373
Sperry, J. S., Venturas, M. D., Todd, H. N., Trugman, A. T., Anderegg, W. R. L., Wang, Y., et al. (2019). The impact of rising CO2 and acclimation on the response of United States forests to global warming. Proc. Natl. Acad. Sci. U.S.A. 116:201913072. doi: 10.1073/pnas.1913072116
Sullivan, P. F., Pattison, R. R., Brownlee, A. H., Cahoon, S. M. P., and Hollingsworth, T. N. (2017). Limited evidence of declining growth among moisture-limited black and white spruce in interior Alaska. Sci. Rep. 7:15344. doi: 10.1038/s41598-017-15644-7
Thomas, H. (2002). Ageing in plants. Mech. Ageing Dev. 123, 747–753. doi: 10.1016/S0047-6374(01)00420-1
Thomas, Z., and Waring, K. M. (2015). Enhancing resiliency and restoring ecological attributes in second-growth ponderosa pine stands in Northern New Mexico, USA. For. Sci. 61, 93–104. doi: 10.5849/forsci.13-085
Trouillier, M., van der Maaten-Theunissen, M., Scharnweber, T., Würth, D., Burger, A., Schnittler, M., et al. (2018). Size matters—a comparison of three methods to assess age- and size-dependent climate sensitivity of trees. Trees 33, 183-192. doi: 10.1007/s00468-018-1767-z
Tüxen, R., and Preising, E. (1956). Die heutige potentielle natürliche Vegetation als Gegenstand der Vegetationskartierung: mit 10 Tabellen. Stolzenau: Selbstverl. d. Bundesanst. für Vegetationskartierung.
Vacchiano, G., Hacket-Pain, A., Turco, M., Motta, R., Maringer, J., Conedera, M., et al. (2017). Spatial patterns and broad-scale weather cues of beech mast seeding in Europe. New Phytol. 215, 595–608. doi: 10.1111/nph.14600
van der Sleen, P., Groenendijk, P., Vlam, M., Anten, N. P. R., Boom, A., Bongers, F., et al. (2015). No growth stimulation of tropical trees by 150 years of CO2 fertilization but water-use efficiency increased. Nat. Geosci. 8, 24–28. doi: 10.1038/ngeo2313
Wang, W., Peng, C., Kneeshaw, D. D., Larocque, G. R., and Luo, Z. (2012). Drought-induced tree mortality: ecological consequences, causes, and modeling. Environ. Rev. 20, 109–121. doi: 10.1139/a2012-004
Wang, X., Fang, J., Tang, Z., and Zhu, B. (2006). Climatic control of primary forest structure and DBH–height allometry in Northeast China. For. Ecol. Manag. 234, 264–274. doi: 10.1016/j.foreco.2006.07.007
Way, D. A., and Oren, R. (2010). Differential responses to changes in growth temperature between trees from different functional groups and biomes: a review and synthesis of data. Tree Physiol. 30, 669–688. doi: 10.1093/treephys/tpq015
Wilmking, M., Scharnweber, T., van der Maaten-Theunissen, M., and van der Maaten, E. (2017). Reconciling the community with a concept—The uniformitarian principle in the dendro-sciences. Dendrochronologia 44, 211–214. doi: 10.1016/j.dendro.2017.06.005
Xu, K., Wang, X., Liang, P., Wu, Y., An, H., Sun, H., et al. (2019). A new tree-ring sampling method to estimate forest productivity and its temporal variation accurately in natural forests. For. Ecol. Manag. 433, 217–227. doi: 10.1016/j.foreco.2018.10.066
Keywords: forest growth-trends, potential natural vegetation, tree-rings, forest inventory, eddy covariance, stand density, carbon allocation, sample bias
Citation: Trouillier M, van der Maaten-Theunissen M, Scharnweber T and Wilmking M (2020) A Unifying Concept for Growth Trends of Trees and Forests – The “Potential Natural Forest”. Front. For. Glob. Change 3:581334. doi: 10.3389/ffgc.2020.581334
Received: 08 July 2020; Accepted: 09 September 2020;
Published: 25 September 2020.
Edited by:
Aaron Weiskittel, University of Maine, United StatesReviewed by:
Aaron Teets, Northern Arizona University, United StatesFen Zhang, Lanzhou University, China
Copyright © 2020 Trouillier, van der Maaten-Theunissen, Scharnweber and Wilmking. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mario Trouillier, bWFyaW8udHJvdWlsbGllckB1bmktZ3JlaWZzd2FsZC5kZQ==; dHJvdWlsbGllckBwb3N0ZW8uZGU=
 Mario Trouillier
Mario Trouillier Marieke van der Maaten-Theunissen
Marieke van der Maaten-Theunissen Tobias Scharnweber
Tobias Scharnweber Martin Wilmking
Martin Wilmking