- 1Institute of Physics, University of Rostock, Rostock, Germany
- 2Department of Life, Light, and Matter (LLM), University of Rostock, Rostock, Germany
The fate of phosphorus (P) in the eco-system is strongly affected by the interaction of phosphates with soil components and especially reactive soil mineral surfaces. As a consequence, P immobilization occurs which eventually leads to P inefficiency and thus unavailability to plants with strong implications on the global food system. A molecular level understanding of the mechanisms of the P binding to soil mineral surfaces could be a key for the development of novel strategies for more efficient P application. Much experimental work has been done to understand P binding to several reactive and abundant minerals especially goethite (α-FeOOH). Complementary, atomistic modeling of the P-mineral molecular systems using molecular dynamics (MD) simulations is emerging as a new tool in environmental science, which provides more detailed information regarding the mechanisms, nature, and strength of these binding processes. The present study characterizes the binding of the most abundant organic phosphates in forest soils, inositol hexaphosphate (IHP), and glycerolphosphate (GP), to the 100 diaspore (α-AlOOH) surface plane. Here, different molecular models have been introduced to simulate typical situations for the P-binding at the diaspore/water interface. For all models, quantum mechanics/molecular mechanics (QM/MM) based MD simulations have been performed to explore the diaspore–IHP/GP–water interactions. The results provide evidence for the formation of monodentate (M) and bidentate (B) motifs for GP and M and as well as two monodentate (2M) motifs for IHP with the surface. The calculated interaction energies suggest that GP and IHP prefer to form the B and 2M motif, respectively. Moreover, IHP exhibited stronger binding than GP with diaspore and water. Further, the role of water in controlling binding strengths via promoting of specific binding motifs, formation of H-bonds, adsorption and dissociation at the surface, as well as proton transfer processes is demonstrated. Finally, the P-binding at the 100 diaspore surface plane is weaker than that at the 010 plane, studied previously (Ganta et al., 2019), highlighting the influential role of the coordination number of Al atoms at the top surface of diaspore.
1. Introduction
Phosphorus (P) is essential for plant growth and plays an important role in photosynthesis, energy storage, cell growth, and many other plant processes. It has been pointed out that P scarcity could arise in near future (Cordell and Neset, 2014) and to cope with this situation there is a need to understand the P cycle in forest and agro-ecosystems (Bol et al., 2016, 2018; Missong et al., 2018). In general, phosphates bind to soil components like soil organic matter (Gros et al., 2017, 2019; Ahmed et al., 2018a) and to soil minerals like Fe/Al(oxyhydr)oxides (Hens and Merckx, 2001; Jiang et al., 2015; Kruse et al., 2015; Ahmed et al., 2019) and amorphous Fe/Al hydroxide mixtures (Gypser et al., 2018). The P bound to soil minerals forms colloidal P complexes and consequently becomes unavailable to plants causing P inefficiency (Holzmann et al., 2015; Bol et al., 2016). These colloidal P complexes disperse during heavy rains and accumulate in specific regions resulting in P leaching which further reduces P availability to plants (Boy et al., 2008). Molecular level understanding of P adsorption onto these soil minerals could support efforts to improve P availability to plants (Bol et al., 2016).
Goethite (α-FeOOH) is one of the most common and abundant soil minerals that interacts strongly with phosphates (Parfitt and Atkinson, 1976; Torrent et al., 1992; Chitrakar et al., 2006; Kubicki et al., 2012; Ahmed et al., 2019). It is a highly reactive soil mineral containing ferric ions (Fe+3) with common surface planes as 010, 100, 110, 021 (according to Pnma space group) (Cornell and Schwertmann, 2003). The surface iron atoms are coordinated by 3, 4, 5, or more atoms depending on the surface plane as well as the pH of the environment. Consequently, goethite exhibits different levels of saturation according to the interaction with its environment. The same holds true for most minerals, i.e., minerals exhibit a net positive or negative surface charge based on surface (un)saturation and pH (Cornell and Schwertmann, 2003). Hence, the type of surface plane, its termination and saturation are important factors that influence the adsorption of phosphates onto soil minerals. For instance, Ahmed et al. (2018b) studied glyphosate adsorption at goethite surface with three different degrees of (un)saturation (Fe surface atoms coordinated by 3, 4, and 5 O−2/OH− groups) and showed the effect of the surface's (un)saturation on phosphate binding stability.
In addition to surface saturation and pH, the Fe and Al ratio in amorphous Fe/Al hydroxides is also vital for understanding the phosphates' interaction with soil minerals. Gypser et al. (2018) showed the influence of the Fe:Al ratio in amorphous Fe/Al hydroxide mixtures on phosphate adsorption/desorption rates. The omnipresent Al in weathering environment results in most of Fe oxides in soils being substituted by Al and goethite is no exception (Cornell and Schwertmann, 2003). Diaspore (α-AlOOH) is isomorphous with goethite with Al+3 oxidation state exhibiting a higher surface energy compared to goethite (Guo and Barnard, 2011). Since amorphous Fe/Al hydroxide mixtures exist in soils, analyzing phosphate binding to diaspore provides additional insight into the P interaction with these amorphous mixtures.
Orthophosphates (Newman and Tate, 1980), inositolhexaphosphate (IHP) (Turner et al., 2002; Doolette et al., 2009; Gerke, 2015), and glycerolphosphate (GP) (Pant et al., 1999; Vincent et al., 2013; Missong et al., 2016) are the most abundant phosphates in soils. Orthophosphate interaction with goethite has been studied extensively (Parfitt and Atkinson, 1976; Torrent et al., 1992; Chitrakar et al., 2006; Ahmed et al., 2019). Yan et al. (2014) studied sorption of different phosphates involving GP and IHP on aluminum (oxyhydr)oxides. They found that the maximum adsorbed phosphate normalized to the mass of adsorbent increases with decreasing crystallinity of the minerals: α−Al2O3 < boehmite < amorphous Al(OH)3. Moreover, they concluded that the phosphate adsorption, interfacial reactions, and phosphate fate in the environment are strongly affected by molecular structure and size of phosphates, and degree of crystallinity and crystal structure of mineral surfaces. Li et al. (2017) suggested that GP adsorbs onto the goethite surface through its phosphate group forming inner-sphere complexes. IHP has six phosphate groups, and in general it exhibits strong binding with P-fixing minerals compared to other phosphates with fewer phosphate groups. Anderson and Arlidge (1962) suggested that the total number of phosphate groups in a compound determines the stability of its interaction with minerals. Ognalaga et al. (1994) showed that IHP forms inner-sphere complexes with goethite through its phosphate groups and suggested that up to four phosphate groups could be involved in binding with the mineral surface; the remaining non-interacting phosphate groups could alter the electrochemical properties of the surroundings. However, Guan et al. (2006) revealed that only three phosphate groups were bound to aluminum hydroxide while the other three groups remained free. This was based on adsorption experiments of IHP on amorphous aluminum hydroxide, FTIR characterization, and quantum chemical calculations.
Quantum chemical calculations become increasingly important when it comes to develop a mechanistic understanding of chemical processes in general. Although not yet widely used, computational chemistry approaches to environmentally relevant questions are recognized as tools to complement experimental investigations. Interestingly, as early as 1973 Tossell et al. (1973) studied electronic structure and bonding in iron oxide minerals with molecular simulations and validated this approach with experimental studies. Kwon and Kubicki (2004) used molecular simulations to resolve controversies in experimental studies related to phosphate surface complexes on iron hydroxides. In another study, Kubicki et al. (2012) demonstrated that phosphate interaction with goethite involves a variety of surface complexes in multiple configurations, which explained the difficulties one faces when interpreting, e.g., IR spectra. Moreover, Ahmed et al. (2018b) explored the possible binding mechanisms for glyphosate (GLP) with three goethite surface planes (010, 001, and 100) in the presence of water via ab initio molecular dynamics simulations. The results showed the prominence of water in controlling the GLP–goethite–water interactions. Further (Ahmed et al., 2019) investigated the molecular level mechanism of phosphate binding at the goethite–water interface referring to the possible phosphate binding motifs formed at the modeled goethite surface planes. Moreover, the theoretical assignment of IR spectra in the latter study introduced a benchmark for characterizing experimental IR data for a distribution of adsorbed phosphate species. This incomplete list already indicates the huge potential of computational chemistry as an emerging powerful tool for detailed investigations of complex geochemical reactions and especially reaction mechanisms of P-species in soil (for a more complete overview, see also Kubicki, 2016).
Which computational methods are available today? Thinking of it in terms of a hierarchy (Kubicki, 2016; Ozboyaci et al., 2016), quantum mechanics (QM) methods are at the top because they provide, at least in principle, an unbiased ab initio description in terms of the molecular Schrödinger equation. In practice, such a treatment is not feasible except for the simplest cases. Density Functional Theory (DFT) has emerged as a low-cost alternative, which despite of the involved approximations often provides reliable results even for systems with hundreds of atoms (Kubicki, 2016). At the bottom of the hierarchy there are molecular mechanics (MM) methods, which are based on parameterized empirical functions (force fields) describing bonded and non-bonded interactions. This allows to treat millions of atoms, but unless special purpose force fields are used chemical reactions, i.e., bond making and breaking, cannot be simulated (González, M.A., 2011). Here, the hybrid QM/MM approach comes into play, combining the accuracy of QM methods with the efficiency of MM methods. In this approach, the reactive region of the molecular system is treated at the QM level while the remaining part of the system enters at the MM level (Senn and Thiel, 2009). By this, the bond changes, proton transfer events and hydrogen bonds (HBs), e.g., at water-mineral interfaces can be properly described. Besides providing energies in dependence on nuclear positions, forces on the nuclei can be calculated as well. This is prerequisite for molecular dynamics simulations which gives statistical information including thermally accessible configurations (Marx and Hutter, 2009).
In an earlier hybrid QM/MM study of IHP and GP binding to the 010 diaspore surface plane we have demonstrated a strong interaction of IHP/GP with the diaspore surface (Ganta et al., 2019). Here, IHP forms multiple intramolecular HBs with three of its phosphate groups bound to the surface, while GP is bound through its single phosphate group only. Overall, it has been found that proton transfers from phosphate to water or surface have a stabilizing effect, most likely due to the interaction of the HBs dipole with surface charges. Moreover, in case of IHP intramolecular HBs can be formed, which lead to a steric constraint that could weaken the binding to the surface. Since the interaction of IHP and GP with diaspore is not yet fully explored, in the present work we extend our previous study in two directions, i.e., we consider a chemically different surface plane and incorporate the effect of saturation of the diaspore surface on phosphates adsorption. In our previous work (Ganta et al., 2019), IHP/GP and water showed strong and spontaneous interactions with an unsaturated diaspore surface (010 in pnma) where the surface Al atoms are coordinated by four oxygens (O−2/OH− groups). Here, a more saturated diaspore surface (100 in pnma) is selected where the surface Al atoms are coordinated by five oxygens i.e., O−2/OH− groups. The main objective of current work is to characterize the binding mechanism of IHP and GP at this diaspore–water interface and also to understand the effect of (un)saturation of the diaspore surface on this binding mechanism.
2. Molecular Modeling Approach
In general, the surface charge of a certain mineral can be determined as a function of pH via its point of zero charge (PZC) (Tan, 2011). For pH > PZC, the mineral surface is saturated with negative surface charges which attract cations. In contrast, for pH < PZC, the mineral surface is unsaturated with positive surface charges which attract anions. The phosphates in general exhibit overall negative charge and hence can be adsorbed at the partially unsaturated 100 diaspore surface (according to the Pnma space group) (Tan, 2011). The diaspore unit cell has four AlO(OH) units i.e., total of 16 atoms with lattice constants a = 9.4253, b = 2.8452, c = 4.4007 Å (see Figure 1C). The 100 surface plane model is generated by repetition of the diaspore unit cell as 1a × 8b × 5c along x, y, z axes, respectively (see Figure 1D). In total, the used diaspore slab consists of 640 atoms (160 Al, 160 H, and 320 O atoms). Observe that the surface Al atoms are coordinated by five oxygen atoms (see Figure S3B). The phosphates IHP and GP (see Figures 1A,B) are modeled to have their phosphate group(s) interacting via inner-sphere complexes with surface Al atoms of diaspore (see Figures 1F–H, Figures S2A–C). The diaspore-IHP/GP complexes are then solvated using the solvate plugin from the VMD package (Humphrey et al., 1996) with a water layer of about 18 Å perpendicular to the surface along the x axis and with a density of ≈ 1g cm-3 ( see Figure 1E). Since we are interested in IHP/GP interaction at diaspore–water interface, the QM part of the system (see dashed box in Figure 1E) includes the top layer of diaspore (160 atoms), IHP (54 atoms)/GP (19 atoms), and a few water molecules (≈ 53 molecules depending on the setup) surrounding IHP/GP within layer of ≈ 10 Å perpendicular to the diaspore surface. The enclosing QM box has a size of 22 × 8b × 5c Å i.e., 22 × 22.7616 × 22.0035 Å, where b, c are diaspore lattice constants (see Figure 1E). The remaining part of the system is treated at the MM level.
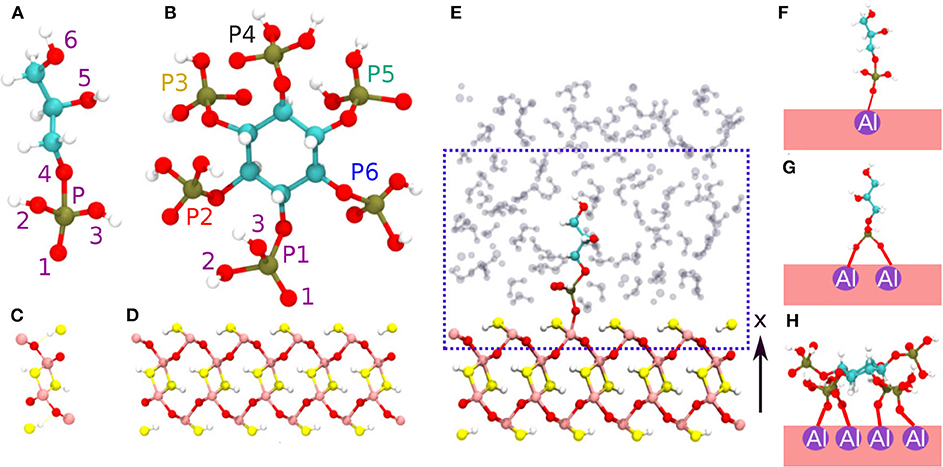
Figure 1. Phosphates GP (A) and IHP (B). The oxygen and phosphorus atoms are labeled here to ease the discussion of diaspore–IHP/GP–water interactions. Diaspore unit cell (C), side view of the modeled diaspore surface (D), diaspore–GP–water complex and the blue box including atoms described at quantum mechanical level of theory (QM part) and remaining atoms at molecular mechanics level (MM part) (E), M motif (F), B motif (G), 4M motif (H). Pink, red, yellow, white, lime, and cyan colors correspond to Al, bridging oxygen, hydroxyl oxygen, hydrogen, phosphorus, and carbon, respectively.
The initial motifs of diaspore–GP complexes include the monodentate motif M (1Al + 1O) (see Figure 1F) and bidentate motif B (2Al + 2O, here both oxygens are from same phosphate group) (see Figure 1G). Note that in contrast to this setup, in the 010 case the two oxygens bind to the same Al atom. In addition to these two, the diaspore–IHP complexes include the four monodentate motif 4M (4Al + 4O) as experimental studies suggest that IHP forms multiple bonds with the goethite surface (Ognalaga et al., 1994; Guan et al., 2006) (see Figure 1H, Figure S2C). Note that in principle even more initial conditions/motifs could be sampled. But considering the size of the modeled systems here and the used computationally expensive QM/MM level of theory the initial configurations for the MD simulations are limited to the most common and experimentally observed binding motifs. More technical details about QM and MM methods and their mutual interaction adopted here is given in Supplementary Material. The QM/MM based MD simulations are performed for 25 ps with 0.5 fs time step and with an average temperature of 300 K maintained using canonical sampling through the velocity rescaling thermostat (CSVR) (Bussi et al., 2007). Here, for each molecular model the first 10 ps of the MD trajectory is assigned for equilibration. The last 15 ps of the trajectory is considered as the production trajectory which is used for analysis of interactions at diaspore–water interface with IHP/GP.
To analyze the interaction energies of the complexes, snapshots are taken at every 100 fs of the production trajectory and interaction energies between diaspore and IHP/GP (Ediaspore−IHP/GP), IHP/GP and water (EIHP/GP−water), and diaspore and water (Ediaspore−water) are calculated. For example, the interaction energy Eint between diaspore and GP for a certain diaspore–GP–water snapshot is calculated as follows:
where Ediaspore−GP, EGP, and Ediaspore denote electronic energies of the diaspore–GP complex, GP and diaspore surface, respectively. Likewise, the interaction energies for each pair of diaspore, IHP/GP and water are calculated at every 100 fs during the corresponding production trajectory. The interaction energies with water are divided by the total number of water molecules involved in the simulation box for better comparison. More details regarding the calculation of interaction energies are given in Ganta et al. (2019).
The HBs strength between IHP/GP and water as well as for the intramolecular HBs of one IHP motif are analyzed using geometrical correlations of distances between atoms in HB as discussed in Strassner (2006), Limbach et al. (2009), Yan and Kühn (2010), and Zentel and Kühn (2017). The quantities q1 and q2 in Figures 4, 6 below are defined as the deviation of the hydrogen from HB center assuming a linear HB (q1) and the total HB length (q2) (see Figure 2A). Geometrically q1 and q2 are defined as Å and q2 = (r1+r2) Å where r1, r2 denote the distance between donor oxygen and hydrogen (OD—H) and distance between hydrogen and acceptor oxygen (H⋯OA), respectively (see Figure 2A). The same holds true for intramolecular HBs between phosphate groups for the IHP case (see Figure 2B).
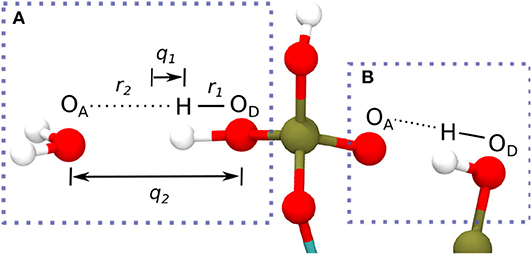
Figure 2. Definition of coordinates q1 and q2 in a HB between water's oxygen (OA) and IHP's oxygen (OD) from a phosphate group (A) (Limbach et al., 2009), intramolecular HB in IHP (B).
A HB will be called strong if q1≈0 and q2 is in the range 2.2-2.5 Å. Similarly, moderate and weak HBs have q2 distances ranging from 2.5 to 3.2 and 3.2 to 4 Å, respectively. Also if q1 < 0 the hydrogen atom stays with the donor oxygen and if q1 > 0 the hydrogen atom (proton) transferred to the acceptor oxygen. In the following a HB analysis is performed for the QM part of the system only as the emphasis of this study is on the interface region where the binding/adsorption process takes place.
3. Results and Discussion
3.1. Diaspore–GP–Water Interactions
3.1.1. GP M Motif
For the GP-M initial condition a stable monodentate (1Al+1O) motif is observed between GP and the diaspore surface over the course of the production trajectory with the Al-O1 average bond length of 2.3 Å (see Figures 3A–D). The average geometry of the PO4 moiety here has root mean square deviation (RMSD) value of 0.17 Å with respect to free tetrahedral (see Figure S2D).
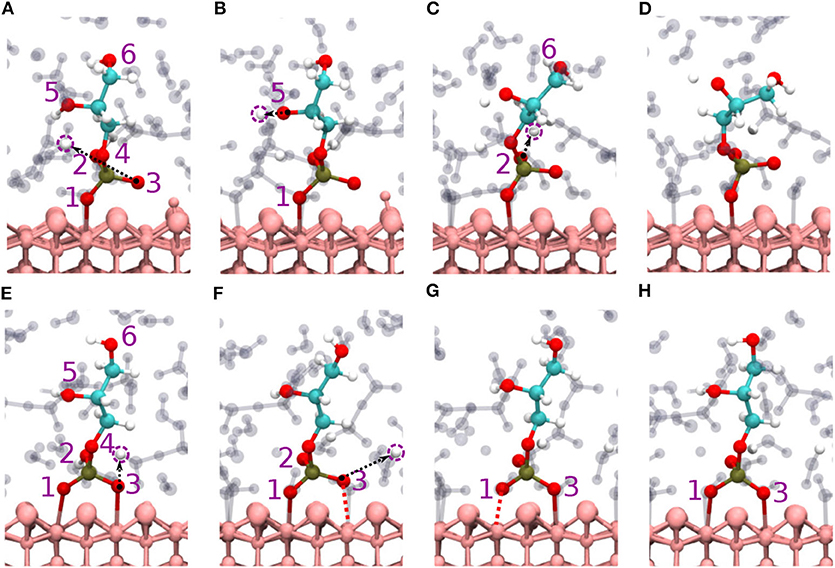
Figure 3. Diaspore–GP–water snapshots displaying proton transfer events and GP dynamics along trajectories. Proton transfers observed during production trajectory of M motif from O3 to water (A) from O5 to water (B), and from O2 to water (C), GP M motif at 25 ps (D). Proton transfer events in B (2Al+2O) motif from O3 to water (E), from O2 to water and momentary dissociation of Al1-O1 bond (F), momentary dissociation of Al2-O3 bond (G), GP B motif at 25 ps (H).
Proton transfer events from GP to the diaspore surface are not observed, instead three proton transfer events are found from O3, O5, and O2 oxygens of GP to water (see Figures 3A–C), respectively. On average, eight HBs are observed between GP and water in the production trajectory. Here, the GPs oxygen atoms act as HB donors (OxD) as well as acceptors (OxA). Exemplary analysis of six of the above eight HBs shows that four (O2A, O3A, O5A, O5D) are strong to moderately strong HBs and two (O1A, O6A) moderately strong to weak HBs (see Figures 4A–C).
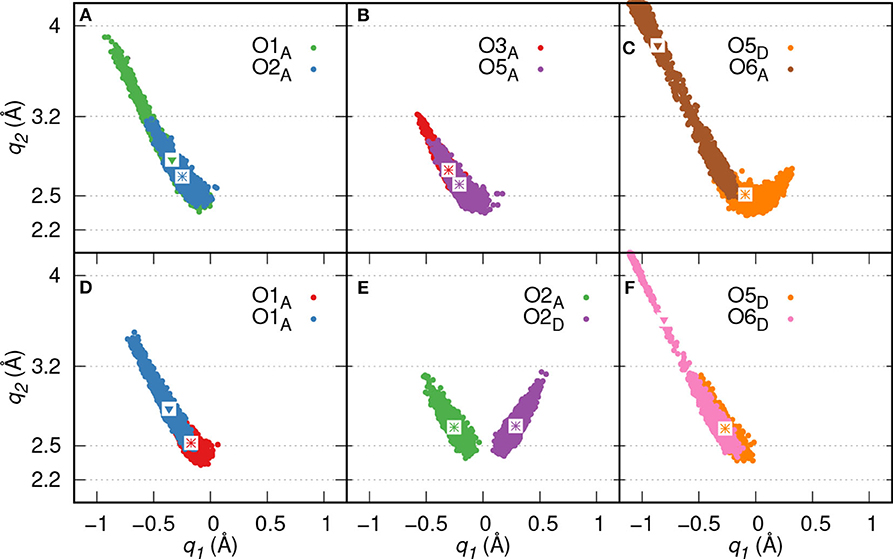
Figure 4. HB correlation q2 vs. q1 of HBs formed between GP and water in GP's M motif (A–C) and B motif (D–F), respectively. The average q1 and q2 coordinate pairs are shown as points in white square boxes. A strong to moderately strong HB is denoted as * while a moderately strong HB and a moderately strong to weak HB are denoted as ∙ and ▾, respectively.
Regarding the diaspore–water interaction, an average of 17 water molecules (out of 40 surface Al atoms) formed M binding motifs (Al-OH2O) with the diaspore surface and have average bond length of 1.9-2.3 Å. Also moderately strong HBs are observed between water and diaspore (see Figure S1A). This scheme of diaspore–water interactions is also observed for the other diaspore–IHP/GP–water models studied below. For the average diaspore–water interaction energy per water molecule one obtains about −3 kcal/mol for all considered models.
The time averaged interaction energy per surface bond between diaspore and GP is around −23 kcal/mol (see Table 1). The average GP–water interaction energy per water molecule is −2.6 kcal/mol.
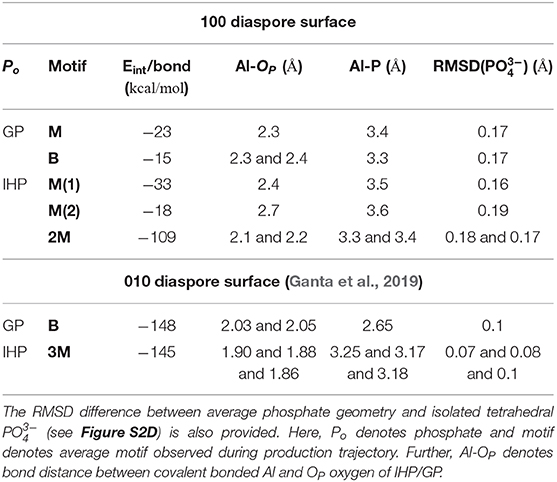
Table 1. The per bond time averaged interaction energies (calculated with Equation 1) of diaspore–IHP/GP complexes and some selected bond lengths and distances.
3.1.2. GP B Motif
The B motif (2Al+2O i.e., Al1-O1 and Al2-O3) is observed over the course of the production trajectory with Al1-O1 and Al2-O3 covalent bond length ranging from 2-2.7 and 1.9-2.7 Å with an average value of 2.4 and 2.3 Å, respectively (see Figures 3E–H). Most notably the Al2-O3 and Al1-O1 bonds are elongated and compressed in an alternating see-saw fashion as seen in Figures 3F,G. The B motif's average geometry of the PO4 moiety has a RMSD value of 0.17 Å with respect to the free tetrahedral .
Proton transfer events are observed from O3 and O2 oxygens to water (see Figures 3E,F), respectively. The B motif features on average a total of seven HBs between GP and water. According to Figures 4D–F, four (O1A, O2A, O2D, O5D) strong to moderately strong HBs and two (O1A, O6D) moderately strong to weak HBs are formed between GP and water.
The average interaction energy per surface bond between diaspore and GP for the B motif is around −15 kcal/mol. The per surface bond interaction energy here is smaller than for the M motif due to GP's see-saw type of motion over the surface. Nevertheless, the total interaction energy observed here is larger than for the M motif and hence the B motif is more likely to form.
Note that due to the formation of a strong to moderately strong HB with water, the O3 oxygen in M cannot easily transform into the B motif, i.e., the barrier is too high to be sampled in the present trajectory (see Figure 4B). The average GP–water interaction energy per water molecule is around −2.3 kcal/mol. The smaller value as compared with M could be due to the additional proton transfer event observed in that case.
3.2. Diaspore–IHP–Water Interactions
3.2.1. IHP M Motifs
Here, two initial configurations (M, B motifs) of the diaspore–IHP–water model resulted in two different M final motifs. In the first case, M(1), the initial configuration was an M motif, wherein O11 oxygen is aligned to form a M motif with a surface Al atom (see Figure S2A). A stable M motif is observed throughout the production trajectory with average Al-O11 bond length of 2.4 Å (see Figures 5A–D). The series of events that are observed during the formation of the M(1) motif are: a proton transfer from O12 to water (see Figure 5A), followed by intramolecular proton transfer from O62 to O12 and formation of O13-H-O61 intramolecular HB (see Figure 5B). After a few femtoseconds, the O12-H-O62 HB is formed and a proton transfer is observed from O32 to water (see Figure 5C) to reach the final M motif in Figure 5D. The events in Figures 5A–C occurred within 2 ps of the simulation trajectory. Overall, a total of three protons transfer events are observed from IHP to water from O12, O53, and O32 (see Figures 5A–C), respectively. On average IHP has formed 19 HBs with water over the course of the production trajectory. Analyzing for illustration 12 out of these 19 HBs, IHP has formed nine (O12A, O21A, O22A, O23A, O31A, O43A, O51A, O53A, O63D) strong to moderately strong HBs, two (O33D, O41A) moderately strong HBs and one (O31A) moderately strong to weak HB with water (see Figures 6A–E). Interestingly, IHP also forms multiple intramolecular HBs, for instance, O13-H-O61, O41-H-O52, and O12-H-O62 (see Figures 5A–C). Analyzing the strength of the intramolecular HBs between P1 and P6 phosphate groups, one finds two (O13-H-O61, O12-H-O62) moderately strong HBs (see Figure 6F). The average geometry of PO4 moiety has a RMSD value of 0.16 Å with respect to the free tetrahedral .
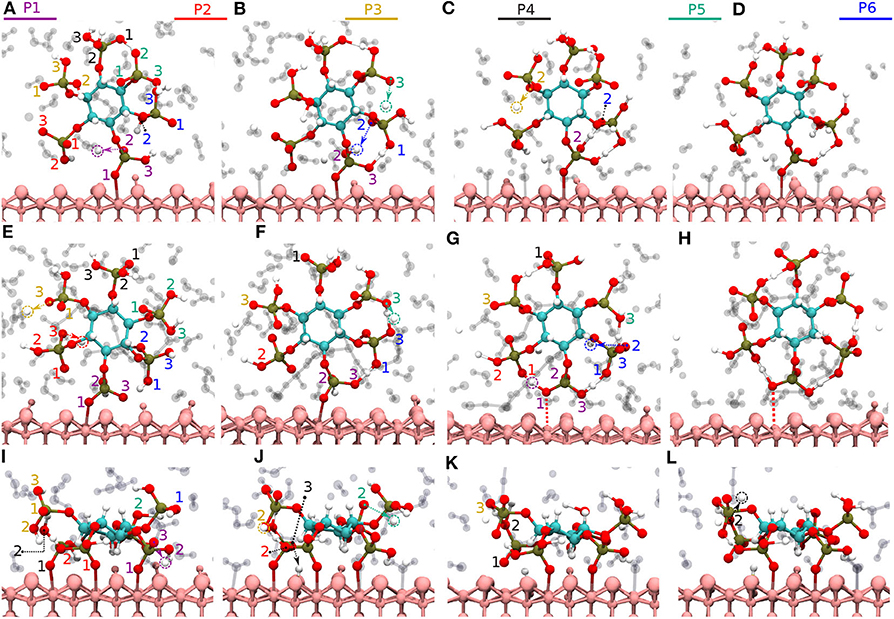
Figure 5. Diaspore–IHP–water snapshots displaying proton transfer events and IHP dynamics along trajectories. The phosphate groups are color-coded and the oxygen atom label color denotes to the phosphate group it belongs. In M(1) motif, proton transfer from O12 to water (A), proton transfer from O53 to water and intramolecular proton transfer from O62 to O12 (B), moderately strong O12-H-O62 HB and proton sharing between O12 to O62 oxygens and proton transfer from O32 to water (C), M(1) motif at 25 ps (D). In M(2) motif, dissociation of Al2-O13 covalent bond due to O13-H-O61 HB and proton transfers from O23 and O33 to water (E), proton transfer from O53 to water and formation of O53-H-O63 HB (F), dissociation of Al1-O11 bond due to formation of O11-H-O21 HB (G), M(2) motif at 25ps (H). In 2M motif, dissociation of Al4-O51 bond and proton transfer from O13 to water (I), proton transfer from O43 to diaspore and from O32 to water, also proton sharing and HB between O22 and O32 (J), and between O33 and O42 followed by dissociation of Al3-O41 bond (K), proton transfer from O42 to water and 2M motif at 25 ps (L).
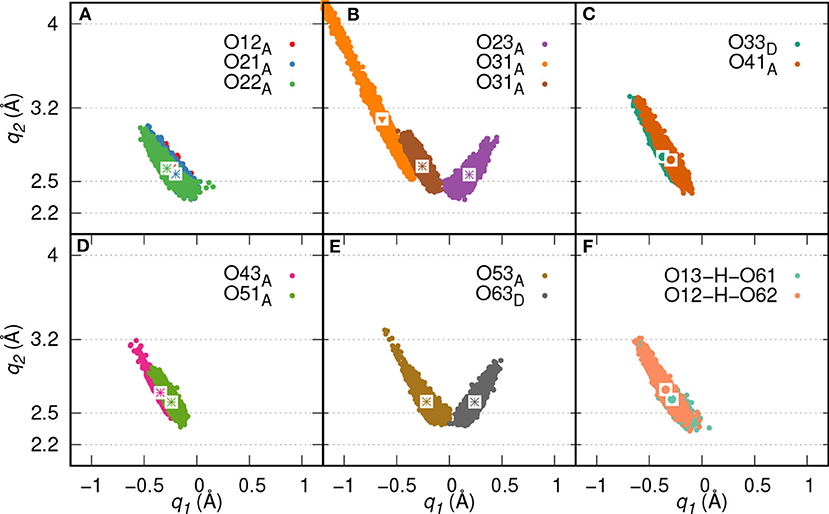
Figure 6. HB correlation q2 vs. q1 of HBs formed between IHP and water (A–E) and between P1 and P6 phosphate groups (F) along trajectory of IHP's M(1) motif. The average q1 and q2 coordinate pairs are shown as points in white square boxes. A strong to moderately strong HB is denoted as * while a moderately strong HB and a moderately strong to weak HB are denoted as • and ▾, respectively.
The time averaged interaction energy per surface bond between diaspore and IHP is around −33 kcal/mol (see Table 1) and between IHP and water is around −5.5 kcal/mol per water molecule. Notice that IHP exhibits a larger interaction energy with water as well with the diaspore surface compared to GP.
For the M(2) motif, the initial configuration had the O11 and O13 oxygens aligned such as to form a B motif with adjacent surface Al atoms (see Figure S2B). The Al2-O13 covalent bond is dissociated during the trajectory and the B motif is transformed into the M(2) motif (see Figures 5E,F). Over the course of the production trajectory the Al1-O11 bond length ranges from 2.4 to 3.2 Å with an average of 2.7 Å. In more detail, the series of events that unfold in this case are as follows: From the O23 and O33 oxygens, two protons are transferred to water and the Al2-O13 covalent bond is dissociated (see Figure 5E). After a few femtoseconds, a proton transfer is observed from O53 to water followed by formation of an intramolecular HB between O53 and O63 oxygens (see Figure 5F). Also formation of the intramolecular O13-H-O61 HB is observed. With progressing simulation time an intramolecular proton transfer event is observed from O12 to O21, followed by formation of O11-H-O21 HB. Afterwards, the Al1-O11 covalent bond weakens at around 6 ps and its bond length ranges from 2.4 to 3.2 Å further on (see Figure 5G, Figure S1B). In addition, a proton transfer is observed from O62 to water (see Figure 5G). The snapshot at 25 ps shows that multiple inter- and intramolecular HBs are observed for IHP (see Figure 5H). Their characterization in terms of HB geometries leads to a similar distribution of HB strengths as for M(1). Overall the average geometry of PO4 moiety has RMSD value of 0.19 Å with respect to the free tetrahedral .
The average interaction energy per surface bond between the diaspore surface and IHP in this case is around −18 kcal/mol. The interaction energy observed here is smaller than for the M(1) case as the Al1-O11 bond length is longer due to formation of O13-H-O61 and O12-H-O21 intramolecular HBs. The observed interaction energy between IHP and water here is −5.7 kcal/mol per water molecule which is slightly higher than for the M(1) case, probably due to additional proton transfer from IHP to water.
3.2.2. IHP 2M Motif
Here, IHP is initially aligned parallel to surface with the non-protonated oxygens of the four phosphate groups forming a 4M motif, i.e., Al1-O11, Al2-O21, Al3-O41, Al4-O51 covalent bonds with the surface (see Figure S2C). However, only a stable 2M motif is observed along the production trajectory with average bond lengths of Al1-O11, Al2-O21 as 2.13 and 2.22 Å, respectively. The events observed during simulation that led to the formation of 2M motif are as follows: within a few picoseconds, the Al-O51 bond is dissociated transforming 4M into a 3M motif. A proton transfer is observed from O13 oxygen to water and from O43 oxygen to diaspore (see Figures 5I,J). Further, an intramolecular HB is observed between O22 and O32 oxygens and two proton transfer events from O32 and O52 to water (see Figure 5J). The Al3-O41 covalent bond is disassociated due to intramolecular HB formed between O33 and O42 oxygens (see Figure 5K), followed by a proton transfer event from O42 to water (see Figure 5L). Totally four proton transfer events are observed from IHP to water and an average of 19 HBs are formed between IHP and water. The inter- and intra-molecular HBs have a similar distribution of strengths as for M(1) and M(2). The average geometry of the PO4 moieties deviate from that of free tetrahedral with RMSD values of 0.18 and 0.17 Å.
The interaction energy between IHP and diaspore in the 2M motif is −109 kcal/mol per bond (see Table 1). The interaction energy is larger here compared to M(1) and M(2) motifs due to the additional covalent bond and a proton transfer from IHP to the diaspore surface. Hence, the 2M motif is more likely to form compared to both the M(1) and M(2) motifs. The average interaction energy per water molecule with IHP is −5.9 kcal/mol which is slightly larger than the IHP–water interaction energy observed in M(1) motif case due to additional proton transfer from IHP to water here.
3.3. Effect of Surface Saturation
In the following we will compare the present results with those of our previous work for the 010 surface plane (Ganta et al., 2019). The 010 diaspore surface plane is relatively unsaturated, i.e. the surface Al atoms are coordinated by only four oxygen atoms (see Figure S3A). In contrast, for the present more saturated 100 plane, surface Al atoms are coordinated by five oxygens (see Figure S3B). Also the 010 diaspore surface plane exhibits higher electrostatic potential compared to the 100 surface plane as shown in Figure S6.
For the 010 plane the largest total interaction energy was observed for the B and 3M motif in case of GP and IHP, respectively (see Table 1). In case of 100 plane, the B and 2M motifs dominate the total interaction energies. Comparing the two B motifs for GP one finds that the binding to 010 being 10 times stronger than to 100 surface plane. The reason for the weaker interaction energy in case of 100 is due to see-saw type of motion of GP yielding a weakening/strengthening of Al1-O1 and Al2-O3 bonds which is not observed for the 010 plane. This can be attributed to the fact that in case of 010 plane the two oxygens are coordinated to the same Al, whereas for 100 plane the coordination is with two neighboring Al atoms, whose distances is such as to require unfavorably large OP-P-OP angles for strong binding. Further stabilization of the GPs B motif in the 010 plane case comes from two additional proton transfers observed from GP to the diaspore surface.
Regarding the total interaction energies, the dominant binding motifs for the diaspore–IHP complexes are also different for 010 (3M) and 100 (2M). In case of 100 the total interaction energy is about two times smaller than for 010. Comparing the two motifs we note in particular that the interaction with the two surfaces is different. This is nicely illustrated by the fact that no stable 4M motif could be observed for the 100 case. One reason for the transformation of the 4M motif to 2M motif is that the Al-OP bonds (regions R1 and R2, see Figures S5A–C) at the 100 diaspore surface are inclined due to OP and surface hydroxyl oxygen repulsion. Hence the movement of oxygens in the Al-OP bonds (regions R1 and R2) is restricted to the space between consecutive surface hydroxyl oxygens or to move away from surface (see Figures S5A–C). Consequently, upon equilibration the oxygens in the Al-OP bonds could dissociate from diaspore as they are confined between consecutive surface hydroxyl oxygens (see Figures S5A–C). In contrast for the 010 diaspore–IHP case, the oxygens in the Al-OP bonds (regions R3 and R4, Figures S5E–G) are not restricted and they are free to move. Hence a stable 3M motif is observed over the course of production trajectory (see Figures S5E–G). Looking at it from a geometric point of view, Al-Al distances on the 010 surface are about 4.4–5.4 Å which is much larger than the 2.4 Å for the 100 surface where the 2M motif forms (see Figures S5D,H). Given the typical distances between the phosphate groups in IHP, bonding to the 100 surface plane yields a higher strain and thus it becomes weaker as compared with the 010 surface plane.
In case of the 100 surface the diaspore–water interaction energy is 3.4 times smaller compared to the 010 case. In fact less than half of surface Al atoms formed M motifs with water compared to the 010 diaspore surface. Also the radial distribution function of diaspore surface oxygens with water hydrogens in Figure S4 shows higher water accumulation near the 010 diaspore surface compared to the 100 diaspore surface which suggests stronger interaction for the 010 diaspore surface with water.
4. Summary and Conclusions
In our previous study (Ganta et al., 2019), a strong and spontaneous binding of IHP and GP with the 010 diaspore surface has been described, which provided the motivation for studying the effect of surface saturation on these interactions. Therefore, the more saturated 100 diaspore surface has been investigated here using periodic boundary QM/MM based MD simulations. The analysis of the MD trajectories showed the importance of inter- and intramolecular HBs in the formation of final motifs and also shed light on effects that lead to disassociation and association of P-O-Al bonds in the diaspore–IHP/GP–water complexes.
In case of the diaspore–GP–water complexes, the B motif's interaction energy per bond is 1.5 times smaller than the M motif. But considering the total average interaction energy, GP is more likely to form a B motif with the 100 diaspore surface.
Regarding the diaspore–IHP–water complexes, the interaction energy per bond follows the order 2M > M(1) > M(2). Here, the M(2) motif's interaction energy is 1.8 times smaller than the M(1) motif due to longer Al-Op bond length, i.e., due to movement of IHP away from the diaspore surface. Thus the 2M motif will be also dominating considering the total interaction energy. This is due to the additional covalent bond and a proton transfer to the diaspore surface. Hence IHP is likely to form a 2M motif with the 100 diaspore surface.
Regarding the water interaction with 100 diaspore and IHP/GP, it can be concluded that the average IHP-water interaction energy is about 2.3 times larger than the GP-water one due to IHP's higher water accessible surface area. Both IHP and GP show proton transfer events to water and formation of strong to moderately strong HBs with water. The diaspore–water interaction energy is only 1.1 times that of the GP-water case, but 2.8 times smaller than IHP-water one. Thus, water has a stronger interaction with IHP than with the 100 diaspore surface.
Of course, studying a particular perfect surface plane can at best give qualitative trends if compared to real surfaces of mineral particles in soil. Studying two abundant surface planes, however, it is possible to pinpoint important factors which influence the behavior of P-compounds at the mineral/water interface. The present investigation focused on the effects of surface saturation and thus electrostatic potential on IHP/GP adsorption. The soil minerals exhibit a positive charge with an unsaturated surface and active sites for pH < PZC. For a pH far below PZC a higher positive charge, i.e, more unsaturated surface is observed (Cornell and Schwertmann, 2003; Tan, 2011). The IHP and GP adsorption onto goethite (with PZC around 9–10) is decreased with increasing pH and reached near zero values for pH around 10 (Celi et al., 1999; Li et al., 2017). This shows that the mineral surface saturation varies with pH and thus the ability of a mineral to adsorb phosphates. Higher surface saturation leads to more negative charges on the 100 surface as compared to the 010 case. Phosphates in water are partially deprotonated and thus have an effective negative charge. Thus the phosphate groups will be attracted stronger to the 010 diaspore surface plane. The denser distribution of water around the 010 surface compared to the 100 surface and transformation of IHP's M and B motifs to 2M motif highlight the stronger electrostatic potential of 010 surface than 100.
Comparing our previous study (Ganta et al., 2019) with the present one, it can be concluded that the diaspore surfaces with different degrees of saturation exhibit different interaction energies with phosphates. Moreover, both surface planes form multiple bonds with IHP while the B binding motif dominates for GP. The overall interaction energies show that IHP is bound to diaspore stronger than GP and this confirms the prevailing view that the number of phosphate groups is a decisive parameter determining the adsorption strength (Anderson and Arlidge, 1962). This could also explain why higher percentages of IHP is found in the forest soil colloid samples than GP as revealed by liquid-state NMR measurements (Missong et al., 2016). However, not all available phosphate groups will contribute to the binding, with details depending on the surface saturation. The present study also stresses the importance of inter- and intra-molecular HBs and the observation that IHP is less protonated than solution counterparts when pH < PZC as shown by Johnson et al. (2012). For both modeled diaspore surfaces, there is no observed dissociation for the bonds involved in C-O, C-H, and C-O-P as suggested by Celi et al. (1999) and Li et al. (2017). In the present case of IHP we cannot confirm the suggestion of a 4M motif made by Ognalaga et al. (1994).
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Author Contributions
PG has performed the present work and analyzed the results. AA and OK have suggested, designed, and supervised the scientific approach for the present study. All authors have discussed and interpreted the present results and contributed to writing the submitted manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
All authors gratefully acknowledge the financial support by the German Research Foundation (DFG) as a part of the SPP 1685 Priority program Ecosystem Nutrition: Forest strategies for limited phosphorus resources. AA would like to thank the financial support by the InnoSoilPhos-project, funded by the German Federal Ministry of Education and Research (BMBF) in the frame of the BonaRes-program (No. 031A558). This research was performed within the scope of the Leibniz Science Campus Phosphorus Research Rostock. The authors thank the North German Supercomputing Alliance for providing HPC resources (project mvp00016).
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffgc.2020.00071/full#supplementary-material
References
Ahmed, A. A., Gros, P., Kühn, O., and Leinweber, P. (2018a). Molecular level investigation of the role of peptide interactions in the glyphosate analytics. Chemosphere 196, 129–134. doi: 10.1016/j.chemosphere.2017.12.162
Ahmed, A. A., Gypser, S., Leinweber, P., Freese, D., and Kühn, O. (2019). Infrared spectroscopic characterization of phosphate binding at the goethite-water interface. Phys. Chem. Chem. Phys. 21, 4421–4434. doi: 10.1039/C8CP07168C
Ahmed, A. A., Leinweber, P., and Kühn, O. (2018b). Unravelling the nature of glyphosate binding to goethite surfaces by ab initio molecular dynamics simulations. Phys. Chem. Chem. Phys. 20, 1531–1539. doi: 10.1039/C7CP06245A
Anderson, G., and Arlidge, E. Z. (1962). The adsorption of inositol phosphates and glycerophosphate by soil clays, clay minerals, and hydrated sesquioxides in acid media. J. Soil Sci. 13, 216–224. doi: 10.1111/j.1365-2389.1962.tb00699.x
Bol, R., Gruau, G., Mellander, P.-E., Dupas, R., Bechmann, M., Skarbøvik, E., et al. (2018). Challenges of reducing phosphorus based water eutrophication in the agricultural landscapes of Northwest Europe. Front. Mar. Sci. 5:276. doi: 10.3389/fmars.2018.00276
Bol, R., Julich, D., Brödlin, D., Siemens, J., Kaiser, K., Dippold, M. A., et al. (2016). Dissolved and colloidal phosphorus fluxes in forest ecosystems–an almost blind spot in ecosystem research. J. Soil Sci. Plant Nutr. 179, 425–438. doi: 10.1002/jpln.201600079
Boy, J., Valarezo, C., and Wilcke, W. (2008). Water flow paths in soil control element exports in an andean tropical montane forest. Eur. J. Soil Sci. 59, 1209–1227. doi: 10.1111/j.1365-2389.2008.01063.x
Bussi, G., Donadio, D., and Parrinello, M. (2007). Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101:1–014101:6. doi: 10.1063/1.2408420
Celi, L., Lamacchia, S., Marsan, F. A., and Barberis, E. (1999). Interaction of inositol hexaphosphate on clays: adsorption and charging phenomena. Soil Sci. 164, 574–585. doi: 10.1097/00010694-199908000-00005
Chitrakar, R., Tezuka, S., Sonoda, A., Sakane, K., Ooi, K., and Hirotsu, T. (2006). Phosphate adsorption on synthetic goethite and akaganeite. J. Colloid Interface Sci. 298, 602–608. doi: 10.1016/j.jcis.2005.12.054
Cordell, D., and Neset, T.-S. (2014). Phosphorus vulnerability: a qualitative framework for assessing the vulnerability of national and regional food systems to the multi-dimensional stressors of phosphorus scarcity. Glob. Environ. Chang. 24, 108–122. doi: 10.1016/j.gloenvcha.2013.11.005
Cornell, R. M., and Schwertmann, U. (2003). The Iron Oxides: Structure, Properties Reactions Occurrence and Uses. Weinheim: Wiley-VCH Verlag GmbH and Co. KGaA.
Doolette, A., Smernik, R., and Dougherty, W. (2009). Spiking improved solution phosphorus31 nuclear magnetic resonance identification of soil phosphorus compounds. Soil Sci. Soc. Am. J. 73, 919–927. doi: 10.2136/sssaj2008.0192
Ganta, P. B., Kühn, O., and Ahmed, A. A. (2019). QM/MM simulations of organic phosphorus adsorption at the diaspore–water interface. Phys. Chem. Chem. Phys. 21, 24316–24325. doi: 10.1039/C9CP04032C
Gerke, J. (2015). Phytate (inositol hexakisphosphate) in soil and phosphate acquisition from inositol phosphates by higher plants: a review. Plants 4, 253–266. doi: 10.3390/plants4020253
González, M.A. (2011). Force fields and molecular dynamics simulations. Collect. SFN 2011 12, 169–200. doi: 10.1051/sfn/201112009
Gros, P., Ahmed, A., Kühn, O., and Leinweber, P. (2017). Glyphosate binding in soil as revealed by sorption experiments and quantum-chemical modeling. Sci. Tot. Environ. 586, 527–535. doi: 10.1016/j.scitotenv.2017.02.007
Gros, P., Ahmed, A. A., Kühn, O., and Leinweber, P. (2019). Influence of metal ions on glyphosate detection by FMOC-Cl. Environ. Model. Assess. 191:244. doi: 10.1007/s10661-019-7387-2
Guan, X.-H., Shang, C., Zhu, J., and Chen, G.-H. (2006). ATR-FTIR investigation on the complexation of myo-inositol hexaphosphate with aluminum hydroxide. J. Colloid Interface Sci. 293, 296–302. doi: 10.1016/j.jcis.2005.06.070
Guo, H., and Barnard, A. S. (2011). Thermodynamic modelling of nanomorphologies of hematite and goethite. J. Mater. Chem. 21, 11566–11577. doi: 10.1039/c1jm10381d
Gypser, S., Hirsch, F., Schleicher, A. M., and Freese, D. (2018). Impact of crystalline and amorphous iron- and aluminum hydroxides on mechanisms of phosphate adsorption and desorption. J. Environ. Sci. 70, 175–189. doi: 10.1016/j.jes.2017.12.001
Hens, M., and Merckx, R. (2001). Functional characterization of colloidal phosphorus species in the soil solution of sandy soils. Environ. Sci. Technol. 35, 493–500. doi: 10.1021/es0013576
Holzmann, S., Missong, A., Puhlmann, H., Siemens, J., Bol, R., Klumpp, E., et al. (2015). Impact of anthropogenic induced nitrogen input and liming on phosphorus leaching in forest soils. J. Soil Sci. Plant Nutr. 179, 443–453. doi: 10.1002/jpln.201500552
Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD – visual molecular dynamics. J. Mol. Graph. 14, 33–38. doi: 10.1016/0263-7855(96)00018-5
Jiang, X., Bol, R., Nischwitz, V., Siebers, N., Willbold, S., Vereecken, H., et al. (2015). Phosphorus containing water dispersible nanoparticles in arable soil. J. Environ. Qual. 44, 1772–1781. doi: 10.2134/jeq2015.02.0085
Johnson, B. B., Quill, E., and Angove, M. J. (2012). An investigation of the mode of sorption of inositol hexaphosphate to goethite. J. Colloid Interface Sci. 367, 436–442. doi: 10.1016/j.jcis.2011.09.066
Kruse, J., Abraham, M., Amelung, W., Baum, C., Bol, R., Kühn, O., et al. (2015). Innovative methods in soil phosphorus research: a review. J. Soil Sci. Plant Nutr. 178, 43–88. doi: 10.1002/jpln.201400327
Kubicki, J. D., (ed.). (2016). Molecular Modeling of Geochemical Reactions. Chichester: Wiley and Sons.
Kubicki, J. D., Paul, K. W., Kabalan, L., Zhu, Q., Mrozik, M. K., Aryanpour, M., et al. (2012). ATR–FTIR and Density Functional Theory study of the structures, energetics, and vibrational spectra of phosphate adsorbed onto goethite. Langmuir 28, 14573–14587. doi: 10.1021/la303111a
Kwon, K. D., and Kubicki, J. D. (2004). Molecular orbital theory study on surface complex structures of phosphates to iron hydroxides-calculation of vibrational frequencies and adsorption energies. Langmuir 20, 9249–9254. doi: 10.1021/la0487444
Li, H., Wan, B., Yan, Y., Zhang, Y., Cheng, W., and Feng, X. (2017). Adsorption of glycerophosphate on goethite: a macroscopic and infrared spectroscopic study. J. Soil Sci. Plant Nutr. 181, 557–565. doi: 10.1002/jpln.201700517
Limbach, H.-H., Tolstoy, P. M., Pérez-Hernández, N., Guo, J., Shenderovich, I. G., and Denisov, G. S. (2009). Oho hydrogen bond geometries and NMR chemical shifts: from equilibrium structures to geometric H/D isotope effects, with applications for water, protonated water, and compressed ice. Isr. J. Chem. 49, 199–216. doi: 10.1560/IJC.49.2.199
Marx, D., and Hutter, J. (2009). Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods. Cambridge, UK: Cambridge University Press.
Missong, A., Bol, R., Willbold, S., Siemens, J., and Klumpp, E. (2016). Phosphorous forms in forest soil colloids as revealed by liquid-state P-NMR. J. Soil Sci. Plant Nutr. 179, 159–167. doi: 10.1002/jpln.201500119
Missong, A., Holzmann, S., Bol, R., Nischwitz, V., Puhlmann, H., Wilpert, K., et al. (2018). Leaching of natural colloids from forest topsoils and their relevance for phosphorus mobility. Sci. Tot. Environ. 634, 305–315. doi: 10.1016/j.scitotenv.2018.03.265
Newman, R. H., and Tate, K. R. (1980). Soil phosphorus characterisation by 31 P Nuclear Magnetic Resonance. Commun. Soil Sci. Plant Anal. 11, 835–842. doi: 10.1080/00103628009367083
Ognalaga, M., Frossard, E., and Thomas, F. (1994). Glucose-1-phosphate and myo-inositol hexaphosphate adsorption mechanisms on goethite. Soil Sci. Soc. Am. J. 332–337. doi: 10.2136/sssaj1994.03615995005800020011x
Ozboyaci, M., Kokh, D. B., Corni, S., and Wade, R. C. (2016). Modeling and simulation of protein-surface interactions: achievements and challenges. Q. Rev. Biophys. 49:e4. doi: 10.1017/S0033583515000256
Pant, H. K., Warman, P. R., and Nowak, J. (1999). Identification of soil organic phosphorus by 31 P Nuclear Magnetic Resonance spectroscopy. Commun. Soil. Sci. Plant Anal. 30, 757–772. doi: 10.1080/00103629909370244
Parfitt, R. L., and Atkinson, R. J. (1976). Phosphate adsorption on goethite (α-FeOOOH). Nature 264, 740–742. doi: 10.1038/264740a0
Senn, H. M., and Thiel, W. (2009). QM/MM methods for biomolecular systems. Angew. Chem. 48, 1198–1229. doi: 10.1002/anie.200802019
Strassner, T. (2006). Isotope effects in chemistry and biology. Edited by amnon kohen and hans-heinrich limbach. Angew. Chem. 45, 6420–6421. doi: 10.1002/anie.200585384
Tan, K. (2011). Principles of Soil Chemistry, Fourth Edition. Books in Soils, Plants, and the Environment. New York, NY: Taylor & Francis.
Torrent, J., Schwertmann, U., and Barron, V. (1992). Fast and slow phosphate sorption by goethite-rich natural materials. Clays Clay Miner. 40, 14–21. doi: 10.1346/CCMN.1992.0400103
Tossell, J. A., Vaughan, D. J., and Johnson, K. H. (1973). Electronic structure of ferric iron octahedrally coordinated to oxygen. Nat. Phys. Sci. 244, 42–45. doi: 10.1038/physci244042a0
Turner, B. L., Papházy, M. J., Haygarth, P. M., and Mckelvie, I. D. (2002). Inositol phosphates in the environment. Philos. Trans. R. Soc. B 357, 449–469. doi: 10.1098/rstb.2001.0837
Vincent, A. G., Vestergren, J., Gröbner, G., Persson, P., Schleucher, J., and Giesler, R. (2013). Soil organic phosphorus transformations in a boreal forest chronosequence. Plant Soil 367, 149–162. doi: 10.1007/s11104-013-1731-z
Yan, Y., and Kühn, O. (2010). Geometric correlations and infrared spectrum of adenine-uracil hydrogen bonds in CDCl3 solution. Phys. Chem. Chem. Phys. 12, 15695–15703. doi: 10.1039/c0cp00009d
Yan, Y. P., Liu, F., Li, W., Liu, F., Feng, X. H., and Sparks, D. L. (2014). Sorption and desorption characteristics of organic phosphates of different structures on aluminium (oxyhydr)oxides. Eur. J. Soil Sci. 65, 308–317. doi: 10.1111/ejss.12119
Keywords: P-efficiency, P-adsorption, inositolhexaphosphate (IHP), glycerolphosphate (GP), diaspore (AlOOH), QM/MM simulations
Citation: Ganta PB, Kühn O and Ahmed AA (2020) QM/MM Molecular Dynamics Investigation of the Binding of Organic Phosphates to the 100 Diaspore Surface. Front. For. Glob. Change 3:71. doi: 10.3389/ffgc.2020.00071
Received: 12 December 2019; Accepted: 20 May 2020;
Published: 17 June 2020.
Edited by:
Friederike Lang, University of Freiburg, GermanyReviewed by:
Zachary E. Kayler, University of Idaho, United StatesDaniel Tunega, University of Natural Resources and Life Sciences Vienna, Austria
Copyright © 2020 Ganta, Kühn and Ahmed. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ashour A. Ahmed, YXNob3VyLmFobWVkQHVuaS1yb3N0b2NrLmRl
 Prasanth B. Ganta
Prasanth B. Ganta Oliver Kühn
Oliver Kühn Ashour A. Ahmed
Ashour A. Ahmed