An Analysis of Current Sustainability of Mexican Cities and Their Exposure to Climate Change

Estrada, Francisco; Velasco, Julián A.; Martinez-Arroyo, Amparo; Calderón-Bustamante, Oscar

doi:10.3389/fenvs.2020.00025

ORIGINAL RESEARCH article

Front. Environ. Sci., 12 March 2020

Sec. Interdisciplinary Climate Studies

Volume 8 - 2020 | https://doi.org/10.3389/fenvs.2020.00025

This article is part of the Research Topic Sustainability Challenges for our Urban Futures View all 10 articles

$\nFrancisco Estrada,$ Francisco Estrada^1,2^*

Julián A. Velasco¹

Amparo Martinez-Arroyo¹

Oscar Calderón-Bustamante¹

¹Centro de Ciencias de la Atmósfera, Universidad Nacional Autónoma de México, Ciudad Universitaria, Mexico City, Mexico
²Institute for Environmental Studies (IVM), VU Amsterdam, Amsterdam, Netherlands

The increasing demand for goods and services in cities around the world due to a rapidly growing urban population is pushing the socioecological systems that support them to their limits. The complexity of urban socioeconomic and environmental systems and their interactions generate a challenging multidimensional decision problem. In response, governments around the world are currently generating a variety of measurements that aim to portrait the main factors that are related to the level of sustainability that a city shows. While the objective of these efforts is to help in the process of urban policy making, these measures are often hard to interpret and do not lend to discover underlying characteristics that may be common among a group of cities. Moreover, these measures are typically focused on describing the current state and omit future challenges such as climate change, which may significantly affect any evaluation of urban sustainability. Recently, the Institute of Ecology and Climate Change (INECC) of Mexico produced a dataset of 36 sustainability related variables for over 100 cities that has the objective of helping federal and state level governments defining sustainable urban strategies. Here we use multivariate statistical techniques to (1) decrease the dimensionality of the dataset and find indices that could be more useful to decision makers; (2) find commonalities among cities include in the dataset in order to help in designing urban strategies for cities with similar characteristics; (3) cities are ranked in terms of their sustainability and characteristics and; (4) the sustainability ranking is compared to estimates of how much the current climate in each of these cities is expected to change during this century, which would add further challenges to maintain or improve urban sustainability.

Introduction

Urbanization is one of the most significant trends of this century. Cities occupy about one percent of the Earth's land but account 60–80 percent of energy consumption and over 70 percent of carbon emissions; more than half of humanity lives in urban settlements (Munich Re Group, 2004; Akbari et al., 2009; Dobbs et al., 2011). Climate change impacts would be particularly large in cities due to their enormous levels of exposure and the convergence of socioeconomic and environmental problems and risks: cities account for ~80% of GDP generated worldwide and, by 2050, 70% of the world population (Stern, 2008; Estrada et al., 2017). At the same time, cities have a crucial role in facing climate change. This implies the need of a better understanding of urbanization processes, interactions, and feedbacks with other systems under different timeframes and scales.

By 2030, 60 percent of the world's population is expected to live in cities and around 90 percent of this urban expansion will take place in the developing countries (UN Habitat, 2015). Therefore, leading urban expansion in optimal directions by sustainability goals could foster reducing inequalities within cities and between regions (Sobrino et al., 2015).

Since its popularization in 1972, sustainability remains a broadly defined concept that has been applied to mean everything from environmental protection and social cohesion to economic growth and neighborhood design (Kropp and Lein, 2013). Interpretation of this concept has always caused debate, including the extent to which sustainability could be both a goal and a process, and how the economic, social, and environmental dimensions could be reconciled (Simon, 1989).

More holistic interpretations of sustainability are emerging that focus on urbanization and cities as key components of this process (Simon et al., 2018). There is a need to place this concept into a more functional decision-making context where changes in development plans can be evaluated in a more consistent way with present and future societal needs.

The dataset used in this paper, comes from the Platform of Knowledge about Sustainable Cities (PKSC) of the National Institute of Ecology and Climate Change (INECC) of Mexico. This institutional effort constitutes a self-evaluation tool for local authorities. The PKSC dataset was conceived as a assembly of urban data from a growing number of Mexican cities (135 at present) that is planned to be regularly updated to offer a dynamic description of sustainability for selected cities. It considers ten main dimensions that are related the goal of attaining urban sustainability. This dataset has the objective of facilitating the formulation of urban development policies, which would be prioritized and evaluated, taking into consideration the needs of society.

Urban data analysis must consider that cities are not closed systems; they exert environmental, social, and economic pressure on larger geographic areas. New metrics are needed to identify desirable and undesirable development patterns, synergies, as well as underserved urban aspects. These metrics could help designing better urbanization policies at local, national, and international level. The use of multivariate techniques to analyze to the broad dataset provided by the platform, with the addition of climate change scenarios for each location, is a step toward transforming the PKSC into a useful tool for policy-making.

This paper is structured as follows. Section Data and methods describes the datasets and methods used, and briefly discusses the benefits of multivariate analysis to analyze multidimensional datasets such as those commonly used to evaluate urban sustainability. Multivariate sustainability indices are proposed, and their interpretation is discussed in section Multivariate sustainability indices, cities similarities, and rankings. Cities are analyzed using biplots of indices and cities are ranked according to multidimensional scores. Cluster analysis is used to find groups of cities that are most similar according to the proposed sustainability indices. Section Climate change and urban sustainability challenges discusses the expected changes in climate for the different cities using distance measures based on 19 bioclimatic indices between current climate and expected changes in climate during this century. Cities are grouped according to their current sustainability scores and the level of challenges that changes in climate will impose them. Section Summary of main findings and conclusions summarizes the main findings, proposes future extensions to the present analysis and concludes.

Data and Methods

Datasets Description and Sources

The dataset of variables related to sustainability in Mexican cities was obtained from the PKSC platform of INECC¹ The PKSC has the main objective of providing multidimensional information to stakeholders, decision-makers, and society at large about urban challenges, green growth, mitigation, and adaptation instruments to climate change. For this study, we consider the variables that are described in Table 1. Form a total of 36 variables that are available from PKSC (Table A1), 22 were selected for this study. The selection of these variables was done in collaboration with INECC and it responds mainly to data quality and availability as well as to the represent ability of multiple dimensions of urban sustainability as conceptualized in PKSC, and avoiding excessive overlap of variables measuring very similar characteristics. These variables cover key socio-environmental aspects such as: water, energy, atmospheric pollution, motorization, urban greenspaces, population, GDP, waste generation, land use and management. Table A2 in the Appendix lists all the cities included in the analyses and their ID number.

TABLE 1

Table 1. List of variables selected from PKSC for this study and their description.

To evaluate the potential changes in climate that the cities could face during this century, we use the projections from four General Circulation Models (CCSM4, HadGEM2-AO, IPSL-CM5A-LR, MIROC-ESM-CHEM) included in the Coupled Model Intercomparison Project phase 5 (CMIP5). We followed commonly used general guidelines for climate change scenarios for impact assessment, which include selecting at least two climate models and contrasting emissions scenarios (IPCC-TGICA, 2007; Conde et al., 2011; Estrada, 2018). The climate variables used are monthly mean, maximum, minimum temperatures, and accumulated precipitation. To explore the uncertainty caused by different development pathways, we include the RCP2.6, RCP4.5, RCP6.0, and RCP8.5 emissions scenarios. However, most of results are presented mainly for the RCP8.5 and RCP2.6 scenarios as they depict the most dissimilar trajectories and cover the full emissions uncertainty considered by the IPCC. The RCP8.5 represents a high-warming scenario with no international mitigation and the RCP2.6 an stringent climate policy scenario consistent with the Paris Climate Agreement goals. All scenarios were obtained from the WorldClim 1.4 downscaled database (Hijmans et al., 2005). Two future temporal horizons are considered: mid-term and long-term scenarios, referred to as 2050 (the average of 2041–2060) and 2070 (the average of 2061–2080), respectively. We concentrate in the mid-term scenario results since the consistency between the PKSC data and the climate projections decreases with time as large socioeconomic and ecological changes are expected to occur during the century which are not reflected by the current PKSC dataset. However, the combination of the PKSC analysis and the long-term climate scenarios provides some insights that may be valuable for decision-makers. Thus, the 2070 results are included in the Appendix and are only briefly discussed in the text.

The statistical techniques used to analyze the information contained in the PKSC dataset are described briefly in the remainder of this section and Figure A1 provides a flowchart describing how these techniques were applied. Principal Component Analysis (PCA) is commonly used to reduce the dimensionality in a set of interrelated variables, while retaining most of the variability present in the original dataset (Jolliffe, 2002). Moreover, this technique has the potential to provide insights about the interrelations of variables and their spatial and temporal patterns, as well as to suggest new interpretations of the original data (Jolliffe, 2002; Wilks, 2011). Note that the interpretability of the results of PCA does not come from the mathematical procedure, but from the experience and ingenuity of the analyst and thus have a subjective component (Jolliffe, 2002). PCA makes use of the variance-covariance structure of the data to produce linear combinations $Y_{i} = \sum_{j = 1}^{n} a_{i j} x_{j}$ that are orthogonal to the original dataset X. The first principal component (PC1) is the linear combination $Y_{i} = \sum_{j = 1}^{n} a_{i j} x_{j}$ that maximizes $v a r (a_{1}' X) = a_{1}' Σ a_{1}$ subject to the constraint $a_{1}' a_{1} = 1$ and where Σ is the variance-covariance matrix of the dataset X. The maximization of quadratic forms on the unit sphere is achieved when a₁ is equal to the eigenvector associated to the largest eigen value (called by convention the first eigenvector) of the variance-covariance matrix of X. The remaining principal components (PC) are the linear combinations of $a_{1}' X$ that maximize $v a r (a_{j}' X)$ subject to the constraints $a_{j}' a_{j} = 1$ and $c o v (a_{j}' X, a_{k}' X) = 0$ for all j ≠ k. The factor loadings L are the product of the eigenvector entries and the squared root of the eigenvalue that corresponds to that particular eigenvector. Loadings represent the correlations between the PC and the original variables and help determining which variables are more closely associated to a particular PC. Scores $Y_{i} = \sum_{j = 1}^{n} a_{i j} x_{j}$ are the projection of the original variables in the new principal component coordinate system. Principal component rotation can help further separating the main variability modes in the dataset and to simplify the interpretation of the PC. For the analysis presented in this paper, varimax rotation normalized is applied, although several other rotation methods are possible, including orthogonal, and oblique (Jolliffe, 2002). In the case of rotated PCA, the scores are calculated as F = BZ where F is the matrix of scores, Z is the matrix of standardized values of X and B = L(L′L)⁻¹ is the matrix of loadings (Harman, 1976; Jolliffe, 2002). An important step is to select the number of eigenvectors to be rotated, as selecting too few (underrotation) could distort or lead to mixed modes and selecting too many (overrotation) could contaminate the analysis leading to excessive separation of modes (O'Lenic and Livezey, 1988). As suggested by O'Lenic and Livezey (1988), here we analyze the existence of “shelves” which would suggest the mixing of signals and, depending on the amount of explained variance, they could indicate that the remaining PC may represent noise. In the case of no clear “shelves,” we combine this truncation criteria with the Kaiser rule which suggests that the PCs with associated eigenvalues smaller than 1 should be discarded (Johnson and Wichern, 2007). The total amount of explained variance of the set of selected PCs is the same before and after rotation. However, after rotation, the explained variance is redistributed among the PCs, and their relative contribution will likely be different.

Cluster analysis is a multivariate exploratory data technique to classify similar cases or variables into meaningful structures based on the values of a data matrix X. The aim of this unsupervised learning technique is to find the “natural” grouping of variables or cases contained in a dataset (Johnson and Wichern, 2007). The agglomeration method used for the analysis in this paper is hierarchical clustering, which starts by considering that every observation in the dataset is an individual cluster. This technique requires selecting some similarity (or distance) measure and an amalgamation rule. Several distance measures have been proposed (e.g., Euclidean, Manhattan, Chebychev) as well as amalgamation (linkage) rules (e.g., single linkage, complete linkage, Ward's method) and different selections of linkage and distance can lead to different groupings (Johnson and Wichern, 2007; Hartigan, 2015). The results presented here are based on Ward's method and Euclidean distances.

Bioclimatic Indices

We derived 19 bioclimatic variables (Hijmans et al., 2005) from monthly values of temperature and precipitation for current climate (1960–1990) and each of the future climate change scenarios (four GCM and two RCPs). These variables have been used extensively to predict potential impacts of climate change on ecosystems and species at worldwide (Anderson et al., 2011; Guisan et al., 2017). These indices are listed and described in Table A3. The data were interpolated to a pixel resolution of ~5 × 5 km pixel size for Mexico.

Euclidean Distances as A Description of Climatic Departure

To establish the degree of exposure of urban cities to climate change scenarios is the first step to a comprehensive evaluation of city vulnerability. This provides decision-makes information to help design adequate public policies to adaptation and mitigation in the mid and long-term. The current climate space (i.e., combinations of temperature and precipitation) are usually used to define land use and regulation plans for each city. Here we represent climatic departure by means of Euclidean distances which provide a measure of dissimilarity between current and future climatic conditions for a given of geographical location. The Euclidean distance for n-dimensions is calculated as $d (p, q) = \sqrt{\sum_{i = 1}^{n} {(p_{i} - q_{i})}^{2}}$ . This metric also helps to assess how much climatic exposure is projected for each location and temporal horizon, across different models, and emission scenarios. Figure A2 shows that most Mexican cities are projected to exhibit very different climate spaces since the mid-term and that exposure is expected to vary considerably across space.

Multivariate Sustainability Indices, Cities Similarities, and Rankings

As a first step, PCA analysis was conducted on the PKSC dataset to extract indices that retain a significant portion of the information of the original dataset and to could help identifying the main factors related to sustainability in Mexican cities. The scree plot of the eigenvalues (Figure A3) shows that the explained variance decreases smoothly for each additional PC and no shelves are present before the magnitude of the eigenvalues drops below 1, which occurs after PC9. For this reason, the first 9 PC were retained, and the remaining PC were discarded. The set of 9 PC account for about 76% of the variance in the original dataset.

Varimax normalized rotation was applied to the retained PCs and the resulting factor loadings are shown in Table A4 and a list of names and interpretations of the rotated PCs is provided in Table A5. PC1 accounts for about 14% of the total variance of the PKSC dataset and the loading coefficients indicate that the variables that are more strongly correlated with it are POP, GMP, and AG01. Given that these coefficients are all positive, PC1 can be interpreted as an index of city size and development in which high score values correspond to cities with large population, higher economic development and higher per capita water consumption. The association between city size and development, and higher per capita water consumption has been discussed previously in the literature. Economic development and urbanization tend to lead to higher per capita water consumption due to the increase in use showers, washing machines and other residential appliances (McDonald et al., 2014; Paterson et al., 2015). There are some evidence that this association may not hold for cities in highly developed countries (Mahjabin et al., 2018), but the present analysis suggests that for Mexico, city size and development are still associated with higher levels of water consumption. In itself, PC1 suggests that the current scheme of urban development in Mexico can have strong implications for local and regional water resources that are prone to lead to hotspots of high water consumption and scarcity (World Bank, 2018).

The values of the elements of the loading vector indicate that the most important variables in PC2 are the rate of motorization (MO04), the per capita greenhouse gas emissions from transport (MO10) and, to a lesser extent, urban solid waste generation (RE02). PC2 explains about 12% of the total variance of the original dataset and can be interpreted as an index of the relative size of the motor vehicle fleet and its emission efficiency. High PC2 score values are associated to cities in which the motor vehicle fleet and its greenhouse gas emissions are large. This suggests that in such cities transport is dominantly private, urban density is likely low and the use of non-motorized transport is limited, which would lead to higher levels of energy consumption per person/kilometer and higher per capita sector emissions (Gwilliam, 2013; World Bank, 2014).

PC4 is the third most important component in terms of explained variance (about 10%), and the variables that are more closely related to it are the percentage of green areas with respect to the total area of the city (BS06), the proportion of companies with ISO14001 certification (IN11) and the amount of green areas per capita (BS01). PC4 can be interpreted as an index of conservation of green spaces and improved environmental standards. High score values in PC4 are associated with cities with greener and more environmentally committed cities. PC5 and PC6 explain a similar amount of variance (8%) and are related to household characteristics within cities. PC5 is related to the type of energy households have access to. Positive values in this index correspond to access to electrical and solar power, while negative values to more traditional sources of energy such as charcoal and wood for cooking. Access to improved water and sanitation is represented by PC6 which is strongly correlated to the percentage of households with piped water (AG04) and the percentage of households with access to the city's sewage system or to a septic tank (AG06).

The entries of the third loading vector show that PC3 is strongly related to the ratio of the growth rates of urban built-up area and population (BS03) and the amount of reforested area (US06), respectively. The factor loading coefficients for these variables have opposite signs, implying that positive score values in PC3 correspond to cities with high rates of increase in built-up area per capita and small reforestation efforts. PC3 can be interpreted as an urban sprawl index, in which high values indicate expansion of the urban spot while low values denote deliberate efforts to recover green spaces. The remaining three components (PC7, PC8, and PC9) account individually for about 6% of the explained variance and each of them is highly correlated to only one variable. These three PCs are related to different aspects of city management: PC7 is related to air quality represented by the annual per capita emissions of criteria pollutants (negative values in this index denote cities with poorer air quality); PC8 to the city's level of urban and territorial planning (higher values, more regulations); PC9 to the installed capacity to treat residual water (low values correspond to better capacity). Below we present some examples of the usefulness of developing indices by means of rotated principal component analysis to explore the performance of cities in a bidimensional and multidimensional context.

Figure 1 shows a scatter plot of PC1 and PC2 which summarizes about 25% of the explained variance of the original data. The distribution of cities within the four quadrants of the figure depict different development paths in city growth and transport that have implications about the future sustainability of cities. Quadrant I includes cities with high levels of population and GMP and a transport sector with a large vehicle fleet (dominantly private) and high GHG emissions. The largest cities in México, namely Valle de México (Mexico City metropolitan area), Monterrey and Guadalajara, show a relatively smaller per capita vehicle fleet size and more efficient in comparison to less developed cities in the same quadrant. According to a study from the Mexican Institute for Competitivity (IMCO)², Valle de México and Monterrey have much lower CO₂ emissions per vehicle than the average of Mexican cities; Valle de México and Guadalajara and Monterrey rank 1st, 3rd, and 10th, respectively, as the cities with the best public transport system in the country. Large cities that want to improve their sustainability in terms of transport and emissions reduction would have to implement policies to move toward quadrant IV, in which is also characterized by high levels of development but with smaller motorization rates and GHG emissions per capita. It is important to keep in mind that cities in both quadrants I and IV are still characterized by high levels of water consumption per capita that may lead to water scarcity and compromise their sustainability goals. Quadrant III represents the case of smaller, less developed cities and with smaller, less GHG-intensive transport sector. This quadrant suggests a much larger use of public and non-motorized options of transport. Cities in quadrant II represent a more concerning case of urban development path in which the levels of emissions and vehicle fleet are much larger than those that would correspond to city size and development. This is the case of cities such as Guanajuato, Cabo San Lucas, Cárdenas, Zitácuaro and Uruapan. This type of development would be characterized by a less developed public transport system and a less efficient, probably older, private fleet. Outlying values in this figure could constitute useful case studies to provide lessons about how to improve urban transport for the urbanization planning. A relatively rapid transition toward the adoption of clean energy and improving the public transportation systems will be useful to mitigate greenhouse emissions in the short and medium term as the urban expansion continues to increase.

FIGURE 1

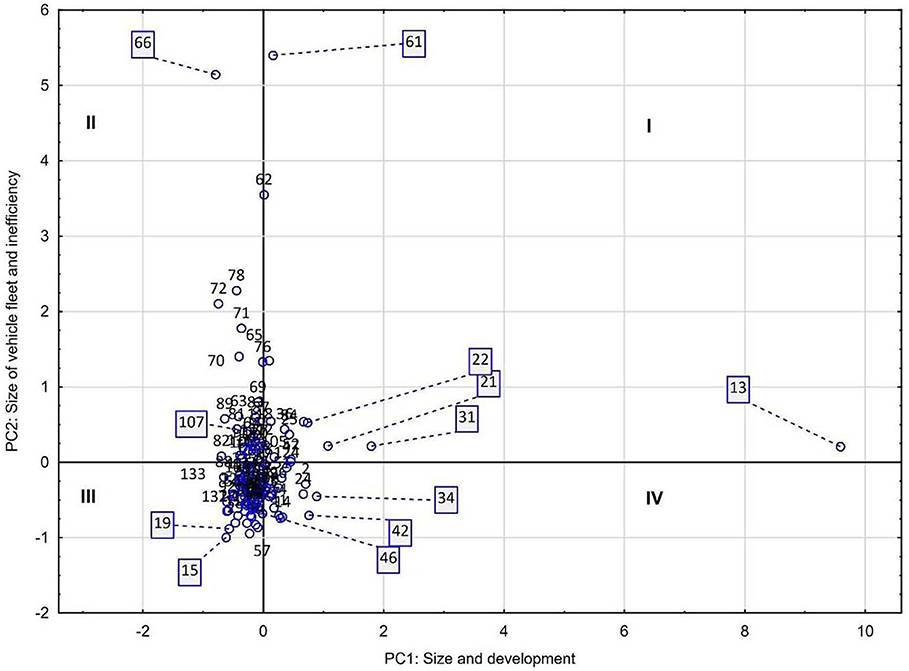
Figure 1. Scatter plot city size and development index (PC1) and size of vehicle fleet and inefficiency index (PC2). A list of names and ID numbers of Mexican cities is provided in Table A2.

City growth can lead to different urbanization intensities and ecological restoration decisions. The cities included in this analysis illustrate how cities with similar sizes and development can show very different rates of urbanization and recovery of greenspaces. Both quadrants I and IV in Figure 2 correspond to large, developed cities but that have smaller rates of urban sprawl and larger reforested areas (quadrant IV) or where the urbanized area has grown faster than population (quadrant I). Monterrey and Guadalajara provide contrasting examples when comparing these two indices: while they show similar size and development scores, Monterrey has a much smaller urban footprint. Other cities in quadrant IV, such as Tampico and Playa del Carmen, are moderately large and developed cities but where the rate of urbanization is smaller than population growth, exerting less pressure over greenspaces. Quadrant II is characterized by smaller, less developed cities but that show high rates of urban sprawl, and low efforts of ecological restoration. The most extreme case is San Cristobal de las Casas, which shows the highest score value in PC3 (i.e., the combination of the high urbanization rate with respect to population growth and low levels of reforestation) of all the cities in the dataset. In contrast, San Miguel de Allende is the city with the lowest urban footprint. The adoption of conservation and reforestation actions would have an impact on human well-being and help to avoid more habitat fragmentation as these cities continue growing.

FIGURE 2

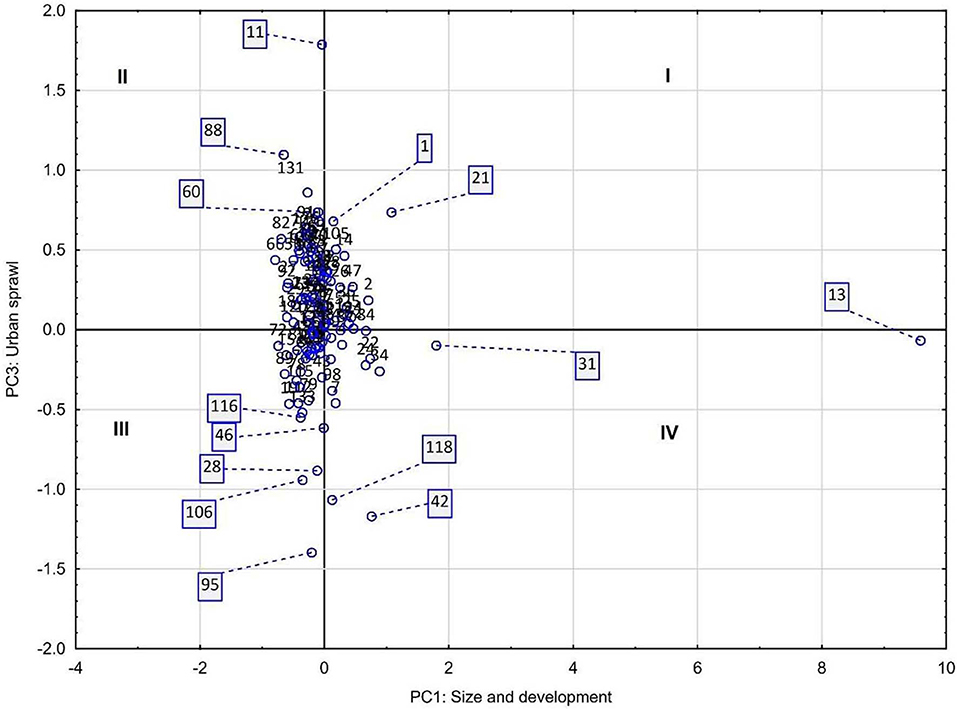
Figure 2. Scatter plot of city size and development index (PC1) and urban sprawl index (PC3). Cozumel is an outlying value in PC3 and it was excluded from the figure to improve clarity. A list of names and ID numbers of Mexican cities is provided in Table A2.

The relationship between the level of urban sprawl (PC3) in cities in Mexico and their level of urban and territorial planning (PC8) is explored in Figure 3. In contrast to the previous figures, there is a highly statistically significant relationship between PC3 and PC8, but with the opposite sign that could be expected. For these cities, a higher level of urban and territorial planning implies a higher level of urban sprawl. This result is interesting because it may suggest that normative urban or territorial planning actions are enacted as remedial (i.e., after urban sprawling is a problem) and not as preventive measures.

FIGURE 3

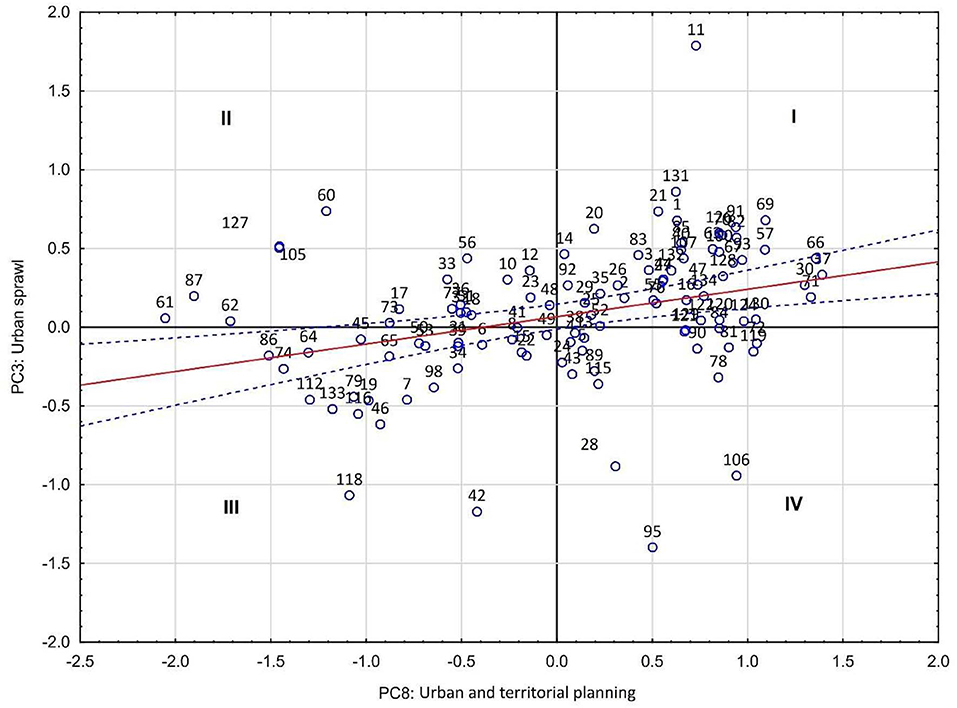
Figure 3. Scatter plot of urban sprawl index (PC3) and urban and territorial planning index (PC8). The regression line is: PC3 = 0.07 + 0.33PC8; the slope coefficient is significant at the 5% level. Cozumel and San Cristobal de las Casas are outlying values in PC3 and PC8, respectively, and were excluded from this analysis and figure. A list of names and ID numbers of Mexican cities is provided in Table A2.

Our analysis also suggests that charcoal and wood for cooking is still a common practice of a large proportion of households in many Mexican cities (PC5). Moreover, for the data at hand, city size, and development show a positive but not statistically significant relationship with transitioning to electricity and cleaner energies. The environmental impacts of charcoal production such as deforestation, forest degradation, and greenhouse gas emission are well-established (Chidumayo and Gumbo, 2013). Air quality (PC7) is also a negative factor affecting several cities in Mexico and our analysis suggests that it is not directly related to city size or degree of economic development. However, a regression analysis (excluding Cozumel) does indicate a statistically significant positive relationship between air pollution (PC7) and urban sprawl (PC3). The regression equation is PC7 = −0.04 + 0.18PC3, where the slope coefficient is significant at the 10% level. The implementation of strategies to recover and/or expand greenspace areas, for example by means of urban protected areas, can help to simultaneously improve air quality, reduce greenhouse gas emissions through carbon sequestration, reduce impacts of heat island effects, and protect local biodiversity (Armson et al., 2012; Trzyna, 2014; Abhijith et al., 2017).

Cluster analysis can be used to classify similar cities and to get insights into what makes them similar. Figure 4 shows the cluster groups obtained for larger, more developed cities, based on the PC2–PC9 indices. At a linkage distance of 10, three groups of cities are formed which can be broadly described as (from left to right): (1) coastal/oil cities which includes cities with ports and tourism (e.g., Veracruz, Acapulco, Puerto Vallarta, Playa del Carmen), and oil industry (e.g., Poza Rica, Minatitlán, Coatzacoalcos); (2) El Bajío region which correspond to metropolitan areas in Jalisco, Aguascalientes, Guanajuato, Michoacán, Querétaro, San Luis Potosí y Zacatecas which have high economic growth and living standards, as well as very high levels of industrialization. Some of the cities included in this group are Guadalajara, Aguascalientes and Zamora; (3) Cities with large manufacturing and services industries such as Valle de México, Monterrey, Tampico, Toluca and Tijuana. These groups suggest that economic activity and some geographical features are two of the main determinants of the environmental and sustainability characteristics of Mexican cities.

FIGURE 4

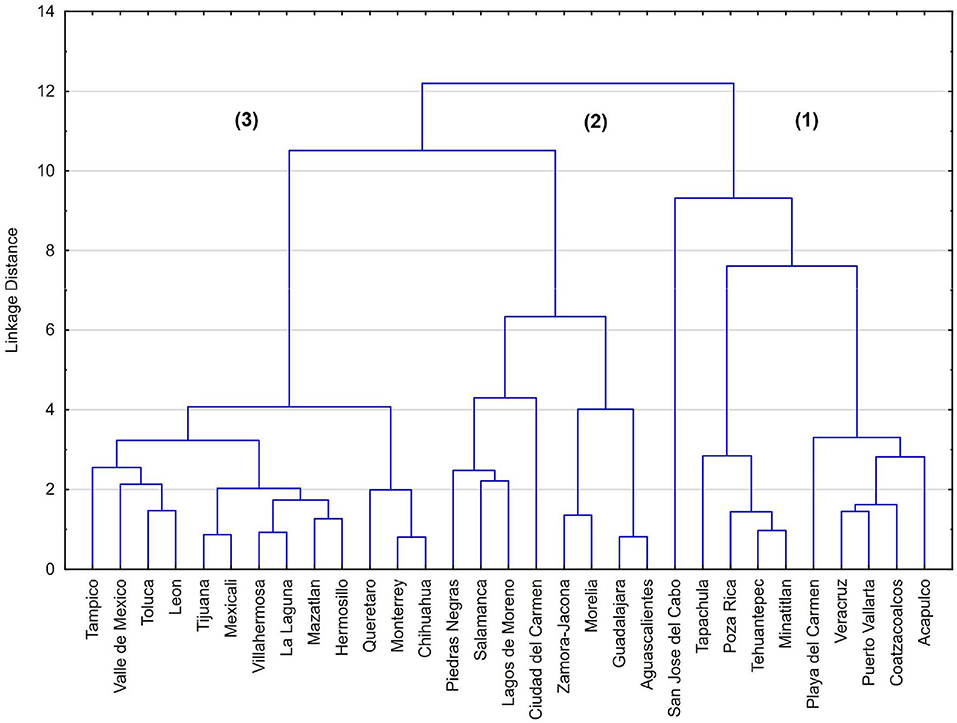
Figure 4. Cluster analysis for the largest, more developed cities (PC1>0), based on the PC2–PC9 indices. Ward's amalgamation method and Euclidean distances were used.

A simple composite index is proposed to summarize the information contained in all of the indices presented in this section, and to help rank cities according to their performance in the different dimensions. As discussed in the previous paragraphs, the nine rotated principal components that were selected represent particular sets of characteristics of cities, and positive/negative values in these indices can be associated to challenges or advantages certain cities have in terms of potential sustainability. For example, negative (positive) values in PC7 are associated to higher (lower) levels of criteria pollutants, which pose a challenge to sustainability; positive (negative) values in PC6 are associated more (less) widespread access to improved water and sanitation, which improves quality of life and contributes to urban sustainability. Table A6 provides a list of all PCs and their assumed effects on sustainability depending on their sign in the corresponding score values. Based on these rules, each PC was transformed into a dichotomous variable that takes the value of 1 if for a particular city its score contributes to urban sustainability and zero otherwise. The composite sustainability index is the average value of the transformed PCs. For the calculations presented here, PC1 was used to separate large and most developed cities from those that are smaller and less developed. To illustrate the calculation procedure, consider the case of a particular city for which only one the conditions expressed in Table A6 is satisfied. Then the score of the city in the composite sustainability index would be 1 divided by the total number of PCs included in the composite index.

Toluca, Monterrey and Ciudad del Carmen share the highest position in the composite index, while cities such as Valle de México, San Luis Potosí-Soledad and Piedras Negras follow in the second position (Table 2; Table A7). Cities that are commonly considered as sustainable such as Guadalajara and Aguascalientes are ranked as medium in this composite index. It is important to underline that this type of analysis is empirical and highly dependent on the sustainability proxy variables that are used. At the bottom part of this table oil-cities such as Minantitlán, Poza Rica and Coatzacoalcos are found, and the less sustainable city in this ranking is Acapulco. These results are consistent with other studies based on different measures of urban sustainability. Table 3 presents the rankings based on the composite index for the group of smaller, less developed cities (see Table A8 for score values). The cities with the highest ranking are Cuauhtemoc and Tepatitlán de Morelos, followed by cities such as La Paz, Uruapan and Cozumel, which rank second place in this list. Oaxaca, Pachuca and Cuautla have the lowest ranking.

TABLE 2

Table 2. Ranking of larger, more developed cities according to their score in the composite index.

TABLE 3

Table 3. Ranking of smaller, less developed cities according to their score in the composite index.

Climate Change and Urban Sustainability Challenges

Climatic Departures and Sustainability Ranking of Cities

We explore the relationship between degree of climate change exposure for 2050 of Mexican cities (i.e., Euclidean distances) and our derived sustainability ranking from PC scores. Also, we explore individually how PC scores vary across climate departures for each emission scenario. We did not find a general spatial or geographical pattern across cities (Figure 5). However, as mentioned in the previous section, cities form clusters according to the sustainability scores in a way that is related to their dominant economic activities and some geographical features such as proximity to the coast.

FIGURE 5

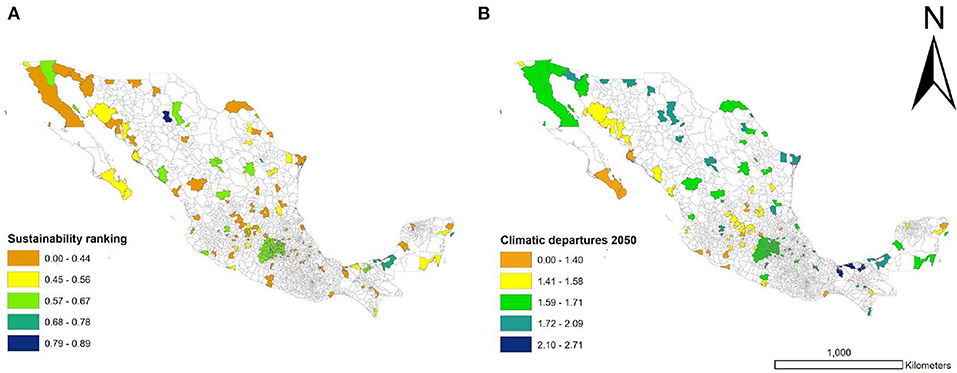
Figure 5. Geographical distribution of sustainability ranking values (A) and climatic departures using Euclidean distances averaged for all climate change scenarios (GCM and RCPs) for 2050 (B).

We ranked Mexican cities according to their projected climate change exposure for 2050. Quartiles were used to classify those cities with high exposure from those with low exposure (Table 4). However, we noted that all Mexican cities are projected to be exposed to substantial novelty in climate conditions across all GCM and RCPs (Figure 6). This is particularly true under the RCP8.5 that can be interpreted as an inaction scenario (see Tables A9, A10 for 2050 and 2070). For instance, Coatzacoalcos and Minatitlán exhibit relatively low sustainable ranking values and likely will be exposed to non-analog climates in the near future (Figure 6). Oaxaca and Cuauhtémoc are cities with low and high ranking in sustainability, respectively, but both cities are projected to be exposed to moderate climate departures in comparison with other cities (Figure 6).

TABLE 4

Table 4. Ranking of Mexican cities according to its projected exposure to climate change in 2050.

FIGURE 6

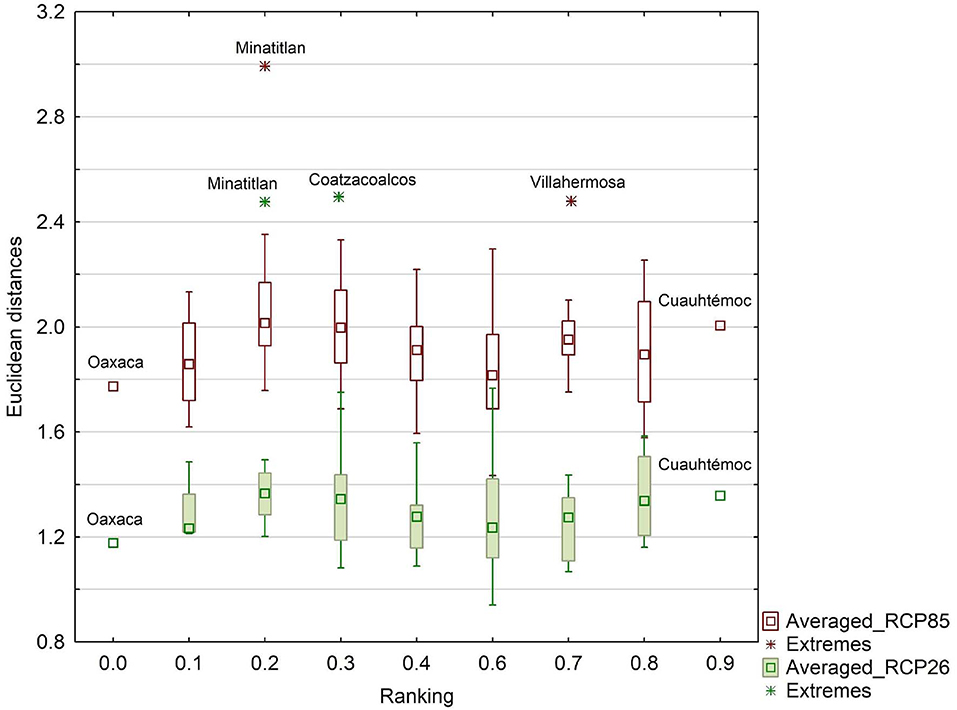
Figure 6. Boxplots of the average Euclidean distances from four Global Circulation Models for RCP 2.6 and RCP 8.5. The Euclidean distances capture the exposure of each city to novel climates.

Cluster analysis allows to further explore how cities can be classified based on their future climate exposure and current scores in the composite sustainability index. Figure 7 shows that at a linkage distance of 2, five groups of cities are formed. By characterizing these groups by their average values in the projected climate exposure and the composite sustainability index, cluster analysis suggests which groups of cities may be more at risk. While all groups are expected to face challenges under climate change conditions (RCP8.5), they do differ in levels of climatic exposure and presumably in their capability to absorb the impacts and manage them. Considering the mid-term climate scenario (2050), the group with the highest average score in the composite sustainability index (0.68), labeled (d) in Figure 7, is expected to experience the second largest change in climate (2.02). Cities such as Valle de Mexico, Monterrey and Toluca are included in this group (see Table A11). Groups (e) and (c) that include Guadalajara, Aguascalientes, Querétaro and León, would face moderate changes in climate and have relatively high scores on the composite sustainability index. Climate change is expected to be a particularly important challenge for two groups of cities, labeled in Figure 7 as (b) and (a). Cluster (b) has the highest average climatic departure (2.29) and the second lowest sustainability score (0.36), while cluster (a) has the third largest climatic departure (1.92) and the lowest sustainability score (0.24). Cities in these groups include Acapulco, Oaxaca and Poza Rica are likely to become risk hotspots under climate change conditions. The long-term horizon (2070) under the RCP8.5 implies much larger exposure for most Mexican cities (Table A10). Keeping all other things constant, climatic departures in 2070 by themselves would produces considerable changes in how cities cluster (Table A12), and under such conditions four cities (Cárdenas, Coatzacoalcos, Minatitlán, and Villahermosa) would face disproportionate climate exposure. However, the realism and usefulness of the analysis of such long-term horizons would greatly improve if projections for variables such as those included in the PKSC were available. The absence of socioeconomic and ecological scenarios with adequate spatial resolution for the assessment of the consequences of climate change at local scales constitutes a common limitation, and appropriate downscaling/projection methods are still lacking (IPCC, 2014; Samir and Lutz, 2014).

FIGURE 7

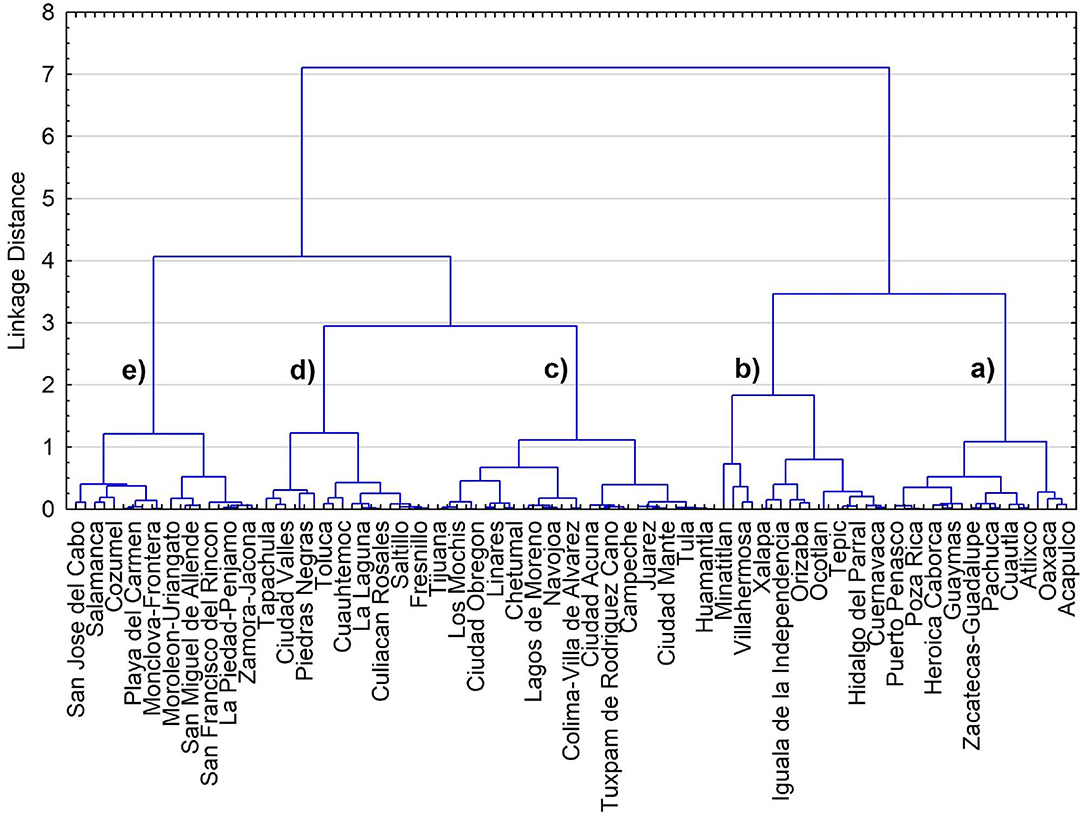
Figure 7. Cluster analysis of cities based on their score in the composite sustainability index and in their climatic departures in 2050 under the RCP8.5 scenario. Ward's amalgamation method and Euclidean distances were used.

Note that even if strong international mitigation actions like the Paris Climate Accord (RCP2.6; Figure 6) can significantly reduce the departures from current climate, the residual risks are still large. Moreover, cities may experience particularly large impacts from climate change due to the convergence of environmental and socioeconomic factors. A recent global study showed that local climate change due to the urban heat island (UHI) effect could significantly amplify the economic losses from global climate change (Estrada et al., 2017). City-level actions to improve local environmental conditions, such as reducing the UHI, constitute an important risk reduction instrument for city governments, and have been shown to have net economic benefits, even if co-benefits are ignored (EPA US, 2008; Estrada et al., 2017). Accordingly, an explicit incorporation of climate change in the urban planning and development agenda should be a priority for local authorities in these Mexican cities.

Climate Change and Sustainability Challenges

Investigating the associations between some of the individual PC scores and climatic departures for 2050 using the Euclidean distances reveals some interesting patterns. Socio-environmental problems tend to scale with city size, as more population and income per capita usually imply more demand for goods and services which translates to more pressure and depletion of natural resources and ecosystems (Grimm et al., 2008). Water is a prime example of climate change challenges in urban areas (World Bank, 2018) and, as it was discussed in the previous section, urban development in Mexico seems to be intrinsically related to higher per capita water consumption. Climate change will pose additional challenges to satisfy the ever-growing consumption requirements of urban population (e.g., food, water, energy, infrastructure) and this is expected to result in environmental impacts extending beyond current urban areas (Jiang et al., 2013). Figure 8A shows a scatter plot of PC1, which scores cities according their size, development degree and level of per capita water consumption, and the climatic departures from current normals. The most urbanized cities in Mexico, namely Valle de México, Monterrey and Guadalajara, are projected to experience significant changes in climate. Impacts from global climate change in such urbanized cities can expected to be considerably amplified by the local changes in climate due to the UHI effect (Estrada et al., 2017). The creation of more greenspaces and implementation of white, green roofs and cool pavement could help to reduce the joint impacts of local and global climate change (EPA US, 2008; Estrada et al., 2017; Imran et al., 2018). Cities such as Minatitlán, and Coatzacoalcos which have a very low score in the composite vulnerability are expected to experience the largest changes in climate. Moreover, the areas where these cities are located already face significant challenges due environmental pollution form the oil industry which have affected ecosystems' health (Mendoza-Carranza et al., 2016; Ruiz-Fernández et al., 2016).

FIGURE 8

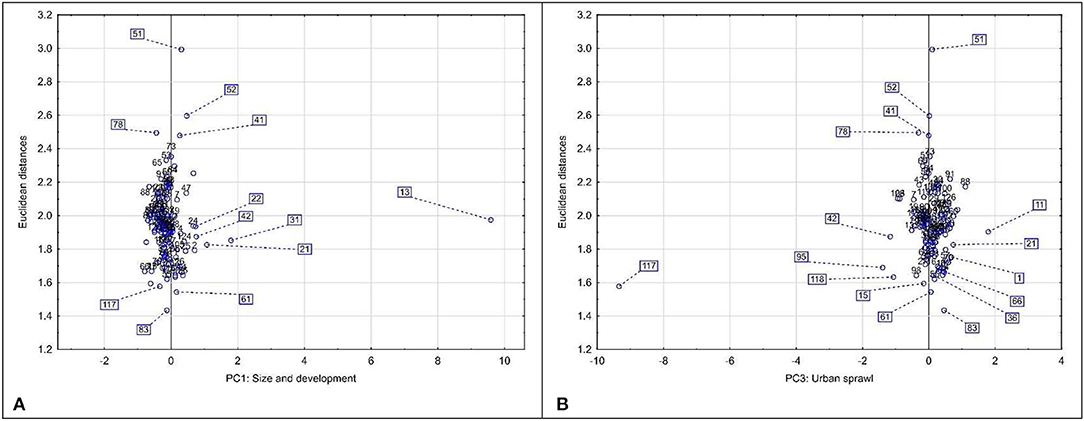
Figure 8. Scatter plots of urban sustainability indices and climatic departures. (A,B) show scatter plots of climatic departures from current normals and the city size and development index (PC1), and the urban sprawl index, respectively. A list of names and ID numbers of Mexican cities is provided in Table A2.

A scatter plot of between the urban sprawl index (PC3) and climatic departures under the RCP8.5 (Figure 8B) complements this discussion. Guadalajara and some cities such as Querétaro, Aguascalientes and Guanajuato, which have become increasingly important in terms of their population count and their contribution to the national product, have rates of urbanization larger than population growth. Although for these cities the projected changes in climate are moderate, such fast urbanization processes can lead to rapid and large changes in local climate (Estrada et al., 2009; Li and Bou-Zeid, 2013) and widespread impacts ranging from loss of productive farmland, changes in energy demand, alterations of the hydrologic cycle, biodiversity loss, and habitat fragmentation (Foley et al., 2005; Grimm et al., 2008; Seto et al., 2011). On the opposite side, some cities like San Miguel de Allende, Playa del Carmen, Tampico and markedly Cozumel show large efforts for ecological restoration and climatic departures for these cities are expected to be moderate. These examples illustrate the wide variety of current conditions and future changes that characterize urban areas in Mexico, and point to the need of coupling platforms such as PKSC with multivariate exploratory techniques to find commonalities among cities to help decision-makers in designing urban strategies.

Summary of Main Findings and Conclusions

We analyzed a multidimensional dataset related to urban sustainability that was produced by the Mexican government to help federal, state, and local level governments defining sustainable pathways for urban development. By means of rotated principal component analysis, 9 indices were defined which in total account for about 76% of the explained variance of the original dataset. These indices are related to city size and level of economic development, size and GHG-efficiency of the vehicle fleet, urban sprawl, conservation of greenspaces and good environmental practices, access to improved water, type of energy households have access to, air quality, urban and territorial planning, and the installed capacity to treat residual water.

The analysis reveals features that are relevant for understanding some patterns of growth of cities in Mexico which can be useful for helping urban policy design. The strong association between city size and development and higher per capita water consumption suggests that the current scheme of urban development in Mexico is likely to have strong implications for present and, in particular, future urban sustainability. This index explains the largest share of variance in the PKSC dataset (about 14%) and suggests that important efforts in Mexican cities should be devoted to breaking the linkage between city growth and water consumption, as has been done in other cities around the world (McDonald et al., 2014; Paterson et al., 2015). The structure and GHG-efficiency of the transport sector are diverse among cities and constitute the second most important index for describing urban areas in Mexico. Large, more developed cities in Mexico tend to rely more on privately own motor-vehicles than on public transport, which generally leads to higher levels of energy consumption per person/kilometer and higher per capita sector emissions. Valle de México, Monterrey and Guadalajara, show a relatively smaller per capita vehicle fleet size and more efficient in comparison to less developed cities as well as much lower CO₂ emissions per vehicle than the average of Mexican cities. The formation of conglomerations of urban centers and of megacities is increasingly common, and it poses important urban policy challenges as local social and environmental problems —such as emissions, pollution and transport— become more regionally intertwined and decision-making more complex as it requires better coordination to be effective. Results suggest that improving public transport would contribute to reducing motor-vehicle fleet size and emissions. More efficient ways of transport have been shown to provide important health co-benefits due to improvements in air quality (Kelly and Fussell, 2015; Kwan and Hashim, 2016).

City growth can lead to different urbanization intensities and ecological restoration decisions. The cities with similar sizes and development can show very different rates of urbanization and recovery of greenspaces. Interestingly, results show that in the case of Mexican cities, urban sprawl and urban and territorial planning are negatively related, suggesting that normative actions are remedial and not preventive measures. A statistically significant relationship (10% significance level) was found between urban sprawl and atmospheric pollution, but not with city size, and development. This finding strongly suggests that promoting legislation for effective urban and territorial planning should be a clear policy goal for improving sustainability in Mexican cities.

Using cluster analysis, cities were classified according to their scores in the rotated principal components (PC2-PC9). PC1 was used to separate the sample of cities in two subsamples: (1) large, more developed cities and; (2) small, less developed cities. Three main groups were identified that can be broadly described as: (1) coastal/oil cities; (2) metropolitan areas in El Bajío region; (3) large manufacturing and services industries. These groups suggest that economic activity and some geographical features are two of the main determinants of the environmental and sustainability characteristics of Mexican cities. Moreover, further analysis of the common features of these groups of cities can help designing policies to tackle shared socioeconomic and environmental challenges to improve urban sustainability.

A simple composite index was proposed to help rank cities according to their performance in the different dimensions included in PKSC. Comparing all cities, Toluca, Monterrey and Ciudad del Carmen share the highest position in the composite index, while Oaxaca, Pachuca and Cuautla have the lowest ranking.

The exposure of Mexican cities to future climate change scenarios will be relatively severe according to metric based on Euclidean distances. This metric allows to combine temperature and precipitation variables in a single index. The exposure is projected to be more severe in business-as-usual emission scenarios (RCP 8.5). We find high variability between GCMs which suggests that a more comprehensive evaluation incorporating more models will be necessary to have a more complete picture of climate change exposure across Mexican cities. By means of cluster analysis we define five groups of cities according to their climatic exposure and their scores in the composite sustainability index. Cities such as Acapulco, Oaxaca and Poza Rica are likely to become risk hotspots under climate change conditions. Moreover, ambitious international mitigation actions such as those proposed in the Paris Climate Accord can significantly reduce future changes in climate, but the residual risks are still large and call for strong local adaptation strategies. Our analysis based on the composite sustainability index and climatic departures can help policy makers to identify cities that would be most affected by climate change and that are currently less prepared for them. This information can help guiding risk and vulnerability reduction actions based on improving current socioecological indicators and on designing adaptation strategies, as well as for prioritizing most vulnerable cities. Moreover, our analysis points out that urban sustainability assessments and effective urban policy making cannot ignore climate change anymore as it is an increasingly important factor that can limit urban viability, particularly if its interactions with other socio-ecological risks that converge in cities are considered.

The PKSC data shows that there is already a significant deficit of green spaces and ecological policies for the business sector across many Mexican cities. How urban policies will shape the development of Mexican cities in the next decade will have a predominant and persistent influence on their viability. Degradation of the environment due to urbanization will be likely amplified in the next few decades due to climate change. As we show, climatic departures are projected to be rather severe and residual risks are likely large even the most stringent international mitigation scenarios if no local adaptation strategies are adopted. It is well-established that urban green surfaces and water bodies are effective strategies to mitigate impacts of the urban heat island effects, to promote climate change adaptation (Martínez-Arroyo and Jáuregui, 2000; Wong and Yu, 2005; Sun and Chen, 2012) as well as to help to people relate to nature (Fuller and Gaston, 2009), which has been recently suggested to improve substantially health well-being (White et al., 2019). To avoid the potential socioeconomic and environmental negative impacts of the joint effects of the UHI and global warming, municipal authorities should prioritize implementing ecological restoration strategies across urban areas.

Future work should focus on two aspects that would help advancing the evaluation of urban sustainability under climate change conditions. First, further research and transdisciplinary discussion needs to continue about how to define urban sustainability, what set of dimensions and variables provide meaningful proxy measures for it, and about how to produce consistent measures across geography (Kropp and Lein, 2013). Vulnerability is sometimes considered an emergent property of socio-ecological systems with vulnerability patterns emerging from the interaction of the biophysical, social, and political domains at multiple scales (De Sherbinin et al., 2007; Oppenheimer et al., 2014; Weber et al., 2015). Future extensions of this work will focus on developing local socioeconomic and environmental scenarios for Mexican cities and integrating into the analysis how the evolution of social relations, political discourses, and demographic trends can affect the proposed sustainability indices and modify the relationships between cities. Research about the potential impacts of local and global warming on urban areas would benefit from adopting a risk management perspective. Introducing dynamic metrics such as those that aim to establish the timing and velocity of exceeding risk thresholds across cities would constitute a useful tool for decision-makers and would enrich government efforts such as the PKSC (Loarie et al., 2009; Hawkins and Sutton, 2012; Mora et al., 2013). For instance, time of emergence (Hawkins and Sutton, 2012) is a metric used to estimate the year at which a novel climate combination (i.e., non-analog climates) would occur for the first time at each site (Williams and Jackson, 2007). Similarly, estimating the velocity of climate change (Loarie et al., 2009) would be useful to establish the speed of changing conditions across geography. These metrics have been used in assessments of climate change exposure on biodiversity (La Sorte et al., 2019) and to apply them for urban policy and planning would be a sensible extension.

Data Availability Statement

The datasets analyzed in this article are not publicly available. Requests to access the datasets should be directed to contacto@inecc.gob.mx; feporrua@atmosfera.unam.mx.

Author Contributions

FE, JV, and OC-B processed and analized the data. FE, JV, and AM-A developed the idea and wrote the paper.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer YM declared a shared affiliation, with no collaboration, with the authors to the handling editor at time of review.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2020.00025/full#supplementary-material

Footnotes

1. ^https://www.gob.mx/inecc/acciones-y-programas/crecimiento-verde.

2. ^https://imco.org.mx/banner_es/indice-movilidad-urbana-2018-barrios-mejor-conectados-ciudades-mas-equitativas/

References

Abhijith, K. V., Kumar, P., Gallagher, J., McNabola, A., Baldauf, R., Pilla, F., et al. (2017). Air pollution abatement performances of green infrastructure in open road and built-up street canyon environments – a review. Atmos. Environ. 162, 71–86. doi: 10.1016/j.atmosenv.2017.05.014