pH as a Primary Control in Environmental Microbiology: 2. Kinetic Perspective

In a companion paper, we examined the thermodynamic responses of microbial redox reactions to pH changes. Here we explore how these thermodynamic responses may affect the composition and function of microbial communities. We simulate butyrate syntrophic oxidation, sulfate reduction, and methanogenesis by microbial consortia at pH ranging from 7 to 5. The simulation accounts for the thermodynamics of microbial metabolisms and the interactions among microbes. The results show that thermodynamic responses to variation in pH can be strong enough to speed up or slow down microbial metabolisms. These kinetic changes then shape the outcome of microbial interactions, including the membership and activity of microbial consortia. Moreover, the kinetic changes modulate carbon fluxes and the efficiency of methane production. The simulation results support the hypothesis that environmental pH can shape the composition and metabolic function of microbial communities by changing the energy yields of redox reactions. They also add to the current theories of microbial ecology. Specifically, due to pH-induced thermodynamic responses, the principle of competitive exclusion fails for microbial processes with significant thermodynamic limitations, which allows the co-occurrence of competing respiration reactions in natural environments. Taken together, these results confirm that pH is a primary control in environmental microbiology. They also highlight the feasibility and potential of biogeochemical kinetic modeling in uncovering and illuminating mechanistic relationships between environmental parameters and microbial communities.

Introduction

Environmental pH is one of the most informative parameters for studying microbes in natural environments. pH represents the chemical activities of protons—a reactant that participates in biological energy conservation, interacts with cellular surface components and structures, and involves in metabolism-related chemical reactions, including redox reactions, mineral dissolution and precipitation, and reactions of natural organic matter (Kinniburgh et al., 1999; Konings et al., 2002; Paul et al., 2006). Reflecting these relationships, pH correlates with community composition across a wide range of biogeochemical conditions (Thompson et al., 2017), and pH variation induces significant changes in the metabolic functions of microbial communities (Kotsyurbenko et al., 2004; Ye et al., 2012).

In a companion paper (Jin and Kirk, 2018), we hypothesize that the correlation between pH and microbial communities may also reflect the thermodynamic and kinetic responses of microbial metabolisms to pH variation. This hypothesis is based on the dependence of chemotrophic microbes on chemical energy in the environment (Thauer et al., 1977; Jin, 2012). Chemotrophs liberate chemical energy in the environment by catalyzing redox reactions and save a part of the liberated energy by making adenosine triphosphate (ATP) molecules. They then spend the ATPs to maintain biomass and make new cells. Any factors that influence the energy available in the environment, therefore, have the potential to affect the metabolisms of individual microbial groups and the composition and metabolic activity of microbial communities.

To test this hypothesis, we examined the effect of pH variation on the energy yields of microbial redox reactions (Jin and Kirk, 2018). We focused on redox reactions involved in organic matter degradation, including syntrophic oxidation, iron reduction, sulfate reduction, and methanogenesis, and computed their energy yields at pH ranging from 1 to 14. The results show that energy yields vary significantly in response to both direct and indirect impacts of pH variation. The direct impact is due to the changes in proton chemical activities and applies to the reactions that consume or produce protons; the indirect impact comes from the control of pH on chemical speciation–pH variation affects the distribution of solute mass among possible chemical species and thus the activities of chemical species involved in microbial reactions.

These results demonstrate that pH variations can alter the energy yields of microbial redox reactions. However, thermodynamics alone is limited in its ability to predict the metabolic rates and population sizes of microbes or to account for the correlation between pH and microbial communities (Bethke et al., 2011; Amenabar et al., 2017). These limitations arise in part from the complexity of microbial metabolisms in natural settings. In addition to thermodynamics, microbial metabolisms are subject to control by a wide range of biogeochemical factors, including substrate availability, geochemical reactions, and microbial interactions (Panikov, 1995; Jin et al., 2013). But most thermodynamic calculations are reaction specific, and do not explicitly consider concurrent geochemical reactions or microbial metabolisms.

Here we apply kinetic modeling to explore how pH may influence the composition and metabolic activity of simple microbial consortia. According to microbial kinetic theory, the rates of microbial metabolisms depend on the thermodynamic drives of microbial respiration, the differences between the energy available in the environment and the energy conserved by ATP synthesis (Jin and Bethke, 2003, 2007). A change in pH could raise or lower the thermodynamic drives and speed up or slow down individual microbial metabolisms, which in turn shape microbial interactions and the membership of microbial consortia.

We simulate microbial metabolisms using biogeochemical reaction modeling (Bethke, 2008; Jin et al., 2013). In addition to changing the energy yields of redox reactions, pH also directly affects the kinetic parameters of microbes. In our simulation, we assume that pH only impacts the energy yields. This assumption is of course an oversimplification but it allows us to concentrate on the outcome of pH-induced changes of energy yields. We can include the changes of microbial kinetic parameters, but the results would bear the combined effects of microbial kinetic and thermodynamic responses. Thus, they would not be straightforward in illustrating the significance of the thermodynamic effect—the focus of the current study.

We focus on syntrophic butyrate oxidation, sulfate reduction, and methanogenesis. Butyrate is a common intermediate in the degradation of natural organic matter whereas sulfate reduction and methanogenesis are common microbial processes in anoxic environments (Monokova, 1975; Molongoski and Klug, 1980; Lovley and Klug, 1982). Our simulation considers microbial interactions, including competition and syntrophy, and computes rates of respiration and growth by accounting for the chemical energy in the environment. We seek to demonstrate how pH can influence the outcome of microbial interactions—the membership and activity of microbial consortia—by changing the energy yields of redox reactions.

Methods

We simulate the progress of microbial metabolisms using the rates of microbial respiration, biosynthesis, and maintenance. Microbial respiration couples redox reactions to the synthesis of ATP. The redox reactions can be represented as

$\begin{array}{rc}{\displaystyle \sum _{\text{D}}}{\nu }_{\text{D}}\text{D}+{\displaystyle \sum _{\text{A}}}{\nu }_{\text{A}}\text{A}\vec{\leftarrow }{\displaystyle \sum _{{\text{D}}^{+}}}{\nu }_{{\text{D}}^{+}}{\text{D}}^{+}+{\displaystyle \sum _{{\text{A}}^{-}}}{\nu }_{{\text{A}}^{-}}{\text{A}}^{-},& (1)\end{array}$

where D and D⁺ are electron donors and their oxidized forms, respectively, A and A⁻ are electron acceptors and their reduced forms, respectively, and ν_D and others are stoichiometric coefficients. The energies ΔG_A available from the reactions are the negative of the Gibbs free energy changes [J·(mol reaction)⁻¹, or J·mol⁻¹], and are calculated according to

$\begin{array}{cc}\Delta G_A=-\Delta G^o-RT\ln \left(\frac{{\displaystyle \prod _{{\text{D}}^{\text{+}}}{\text{a}}_{{\text{D}}^{\text{+}}}^{{\nu }_{{\text{D}}^{\text{+}}}}}·{\displaystyle \prod _{{\text{A}}^{\text{-}}}{\text{a}}_{{\text{A}}^{\text{-}}}^{{\nu }_{{\text{A}}^{\text{-}}}}}}{{\displaystyle \prod _{\text{D}}{\text{a}}_{\text{D}}^{{\nu }_{\text{D}}}}·{\displaystyle \prod _{\text{A}}{\text{a}}_{\text{A}}^{{\nu }_{\text{A}}}}}\right),& (2)\end{array}$

where ΔG° is the standard Gibbs free energy change, a is the chemical activity, R is the gas constant (J·mol⁻¹·K⁻¹), and T is the temperature in kelvin (K). Chemical activity is calculated as the product of activity coefficients (M⁻¹) and molal concentrations of chemical species. Activity coefficients are calculated according to an extended form of the Debye-Hückel equation (Helgeson, 1969).

Respiration rate r (mol·kg⁻¹·s⁻¹, mol per kg water per s) can be calculated according to the thermodynamically consistent rate law (Jin and Bethke, 2005, 2007):

$\begin{array}{rc}r=k·\left[X\right]·{\displaystyle \prod _i}{F}_i,& (3)\end{array}$

where k is the rate constant [mol·(g dry weight)⁻¹·s⁻¹, or mol·g⁻¹·s⁻¹], [X] is the biomass concentration [g dry weight·(kg water)⁻¹, or g·kg⁻¹], and F_i represents different controlling factors, including the kinetic factors of electron donor (F_D) and acceptor (F_A), and the thermodynamic potential factor (F_T). The kinetic factors are calculated according to

$\begin{array}{rc}{F}_{\text{D}}=\frac{m_{\text{D}}}{K_{\text{D}}+m_{\text{D}}}& (4)\end{array}$

and

$\begin{array}{rc}{F}_{\text{A}}=\frac{m_{\text{A}}}{K_{\text{A}}+m_{\text{A}}},& (5)\end{array}$

where m_D and m_A are the molal concentrations of electron donor and acceptor, respectively, and K_D and K_A are the half-saturation constants (M) for electron donor and acceptor, respectively. The thermodynamic potential factor is calculated according to

$\begin{array}{rc}{F}_{\text{T}}=1-exp(-\frac{f}{\chi ·RT}),& (6)\end{array}$

where f is the thermodynamic drive (J·mol⁻¹), and χ is the average stoichiometric number. The thermodynamic drive,

$\begin{array}{rc}f=\Delta G_{\text{A}}-\Delta G_{\text{C}},& (7)\end{array}$

is the difference between the energy ΔG_A (J·mol⁻¹) available in the environment and the energy ΔG_C (J·mol⁻¹) conserved by respiration.

According to Jin (2007), the energy ΔG_C (J·mol⁻¹) conserved by syntrophic butyrate oxidizers is a function of hydrogen partial pressure P_H2 (atm),

$\begin{array}{cc}\Delta G_C=\{\begin{array}{cc}3.5\times {10}^4,& P_{{\text{H}}_2}<{10}^{-9}\text{atm}\\ -1.78\times {10}^4-2.5\times {10}^3·\ln \left(P_{{\text{H}}_2}\right),& {10}^{-9}\text{atm}<P_{{\text{H}}_2}<{10}^{-3}\text{atm}\\ 0,& P_{{\text{H}}_2}>{10}^{-3}\text{atm}\end{array}.& (8)\end{array}$

According to this model, the conserved energy reaches its largest value at H₂ partial pressure less than 10⁻⁹ atm, and declines with increasing H₂ partial pressure. At the partial pressure of 10⁻³ atm or more, the conserved energy declines to 0.

For sulfate reducers and methanogens, the conserved energy ΔG_C is calculated as

$\begin{array}{rc}\Delta G_{\text{C}}={\nu }_{\text{P}}·\Delta G_{\text{P}},& (9)\end{array}$

the product of the ATP yield ν_P of respiration and the phosphorylation energy ΔG_P (Jin and Bethke, 2002, 2003). The phosphorylation energy is the energy required to synthesize ATP from ADP and phosphate in the cytoplasm, and its value is taken as 45 kJ·(mol ATP)⁻¹ (Jin, 2012).

Microbes utilize the conserved energy ΔG_C to synthesize biomass. The rate at which the biomass concentration [X] changes with time, or the net growth rate, is

$\begin{array}{rc}\frac{d\left[\text{X}\right]}{dt}=Y·r-D·\left[\text{X}\right],& (10)\end{array}$

where Y is the biomass yield, the grams of biomass dry weight synthesized per mol reaction (g·mol⁻¹), and D is the specific rate of maintenance and death (s⁻¹) (van Bodegom, 2007). The product of the growth yield and respiration rate, Y·r, gives the biosynthesis rate. Equation (10) neglects that many microbes can persist through adverse environmental conditions via dormancy and other survival mechanisms. Instead, it assumes that microbial population sizes depend solely on biosynthesis rate relative to the rate of maintenance.

We simulate the metabolisms of neutrophilic syntrophic butyrate oxidizers, sulfate reducers, and methanogens using the React program of the software package Geochemist's Workbench version 9.0 (Bethke, 2008). The simulation assumes that aqueous chemical speciation is at thermodynamic equilibrium, and describes these reactions on the basis of the updated LLNL Thermodynamic Database (Delany and Lundeen, 1990). Evaluating microbial rate laws (Equations 3 and 10) requires a series of microbial parameters; their values are listed in Table 1.

TABLE 1

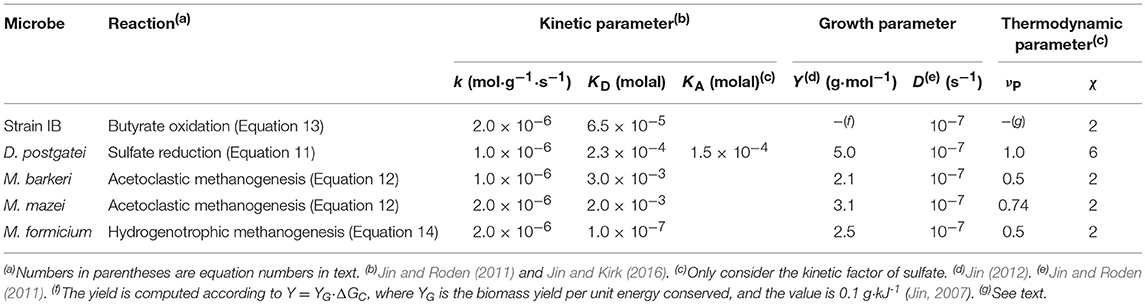
Table 1. Kinetic parameters (rate constant k, and half-saturation constant K_D and K_A), growth parameters (growth yield Y and specific maintenance rate D), and thermodynamic parameters (ATP yield ν_P and average stoichiometric number χ) of microbial metabolism.

We carry out the simulation by varying pH from 7 to 5. Most neutrophilic microbes live over 4 pH units (Rosso et al., 1995). Taking pH 7 as the optimal growth pH, a decrease of 2 pH units would decrease microbial growth rates to 0. Hence we simulate the metabolisms at pH ranging from 7 to 5. We assume that microbial parameters, such as rate constant k and half-saturation constants K_D and K_A, remain constant at different pHs. This assumption is necessary for testing the hypothesis that microbial thermodynamic responses to pH are strong enough to modulate the kinetics of microbial metabolisms and the outcome of microbial interactions. The input scripts are available in Supplementary Material.

Results

In the companion paper (Jin and Kirk, 2018), we analyzed the thermodynamic responses of individual redox reactions to pH changes. Microbes rarely, if ever, live in isolation in nature. Instead, they often join each other in communities to carry out a network of biogeochemical reactions and perform a wide range of ecological functions (Nielsen et al., 2011; Xavier, 2011). By working together, microbes build different working relationships, such as competition and syntrophy. Here we apply biogeochemical reaction modeling to predict how the thermodynamic responses to pH may influence the outcome of microbial competition and syntrophy.

Competition

A classic example of microbial competition is the competition for acetate between sulfate reducers and methanogens (Lovley and Philips, 1987). Sulfate reducers oxidize acetate to inorganic carbon by reducing sulfate to sulfide,

$\begin{array}{rc}\text{Acetate}+{\text{SO}}_4^{2-}+{\text{H}}^{+}\vec{\leftarrow }2{\text{HCO}}_3^{-}+{\text{H}}_2\text{S}.& (11)\end{array}$

Methanogens convert acetate to CO₂ and methane,

$\begin{array}{rc}\text{Acetate}+{\text{H}}_2\text{O}\vec{\leftarrow }{\text{HCO}}_3^{-}+\text{C}{\text{H}}_4.& (12)\end{array}$

In the companion paper (Jin and Kirk, 2018), we show that a pH decrease from 7 to 5 raises the energy yields of both reactions and thus has the potential to speed up the metabolisms of both microbial groups. Nevertheless, according to the principle of competitive exclusion, sulfate reducers win the competition against methanogens because sulfate reducers can hold acetate concentrations either below the thresholds required by running methanogenesis (Lovley et al., 1982) or below the levels required for sustaining methanogen populations (Bethke et al., 2008).

Closed Environment

We first simulate the competition between a sulfate reducer and a methanogen in a closed environment. Schönheit et al. (1982) monitored acetate oxidation in laboratory batch reactors by a representative sulfate reducer—Desulfobacter postgatei—and by a model methanogen—Methanosarcina barkeri. In their experiments, the two microbes grew together at 30°C in growth media with pH 6.9, 10 mmolal acetate, and 20 mmolal sulfate. We simulated the experiments by taking the initial biomass concentrations at 1.5 g·(kg H₂O)⁻¹ for D. postgatei and 2.0 g·(kg H₂O)⁻¹ for M. barkeri. These initial biomass concentrations are estimated by fitting the simulation results to the concentrations of acetate, methane, and sulfide during the first hour of the experiments (Figure 1). Also, to best fit the experimental observations, we set a lag time of 10 min before the two microbes start to consume acetate.

FIGURE 1

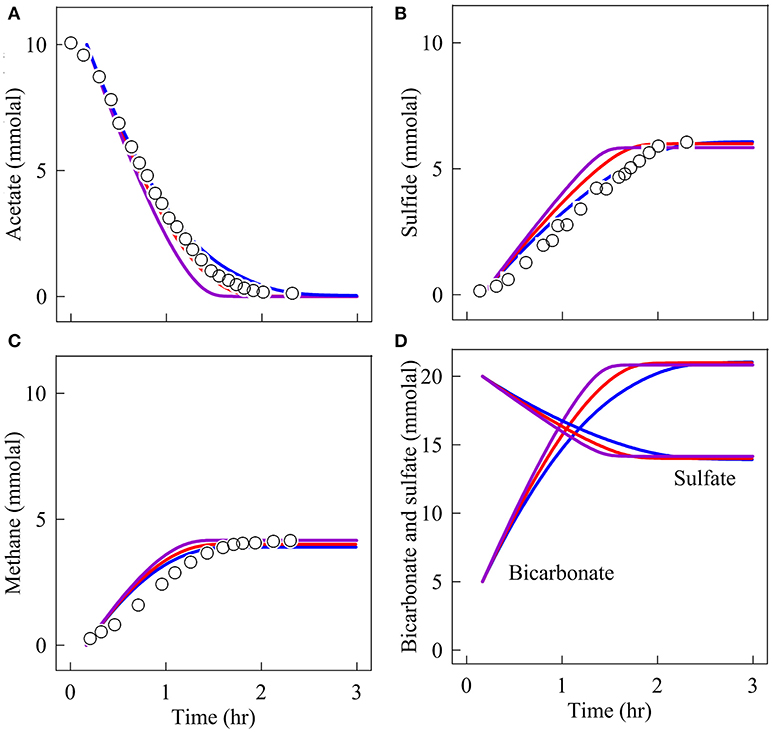
Figure 1. Variation with time in the concentrations of acetate (A), sulfide (B), methane (C), bicarbonate, and sulfate (D) in a batch reactor inoculated with Desulfobacter postgatei and Methanosarcina barkeri. Data points are the experimental results of Schönheit et al. (1982, their figure 3) at pH 7; the lines are the simulation results at pH 7 (blue), 6 (red), and 5 (purple) using microbial rate laws (Equations 3 and 10) and the parameters in Table 1.

Figure 1 shows how chemical concentrations change with time according to the experimental observations and the simulation results. Acetate concentration decreases with time while sulfide and methane concentrations increase. After 1.5 h, methane concentration reaches a constant value. An hour later, sulfide also stabilizes. The simulation results predict that neither microbe grows much—during the experiments, their biomass concentrations increase by less than 2% of the initial concentrations (results not shown). But the rates of sulfate reduction and methanogenesis vary significantly over time (Figure 2). Both rates are about 1.5 × 10⁻⁶ molal·s⁻¹ at the beginning of the experiments and decrease almost linearly with time. The rates of methanogenesis and sulfate reduction fall near 0 around hour 1.7 and 3, respectively. In other words, methanogenesis stops earlier than sulfate reduction. The modeling results also show that D. postgatei and M. barkeri differ from each other in the contribution to acetate consumption. Overall, 59% of the acetate is consumed by D. postgatei while M. barkeri uses the remaining 41%.

FIGURE 2

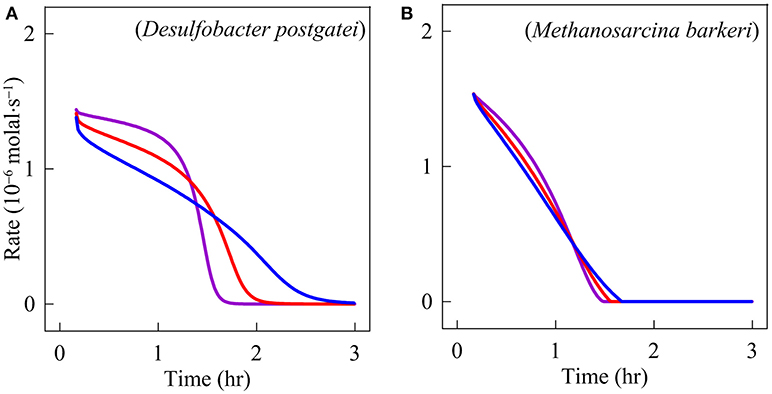
Figure 2. Variation with time in respiration rates of Desulfobacter postgatei (A) and Methanosarcina barkeri (B). The lines are the simulation results at pH 7 (blue), 6 (red), and 5 (purple).

The simulation results demonstrate that the energy availability limits the progress of both sulfate reduction and methanogenesis (Figure 3). At the beginning of the experiments, the energy available to D. postgatei is 75 kJ·mol⁻¹, much larger than that to M. barkeri, 40 kJ·mol⁻¹. As the experiments progress, the acetate consumption and the accumulation of sulfide, bicarbonate, and methane decrease the available energy (Figures 1, 3A,B). About 1.5 h into the experiments, energy available to M. barkeri decreases to 25 kJmol⁻¹ and the thermodynamic drive disappears. As such, the thermodynamic potential factor decreases to zero and methanogenesis ceases (Equation 3). At this time, energy available to D. postgatei is 55 kJmol⁻¹, still larger than the energy it conserves, allowing sulfate reduction to continue. After 2 h into the experiment, however, energy available to D. postgatei approaches 45 kJmol⁻¹, the energy conserved by the organism, and the reaction slows. This result supports the hypothesis that sulfate reducers can win the competition by lowering acetate below the threshold level required for running methanogenesis (Lovley et al., 1982).

FIGURE 3

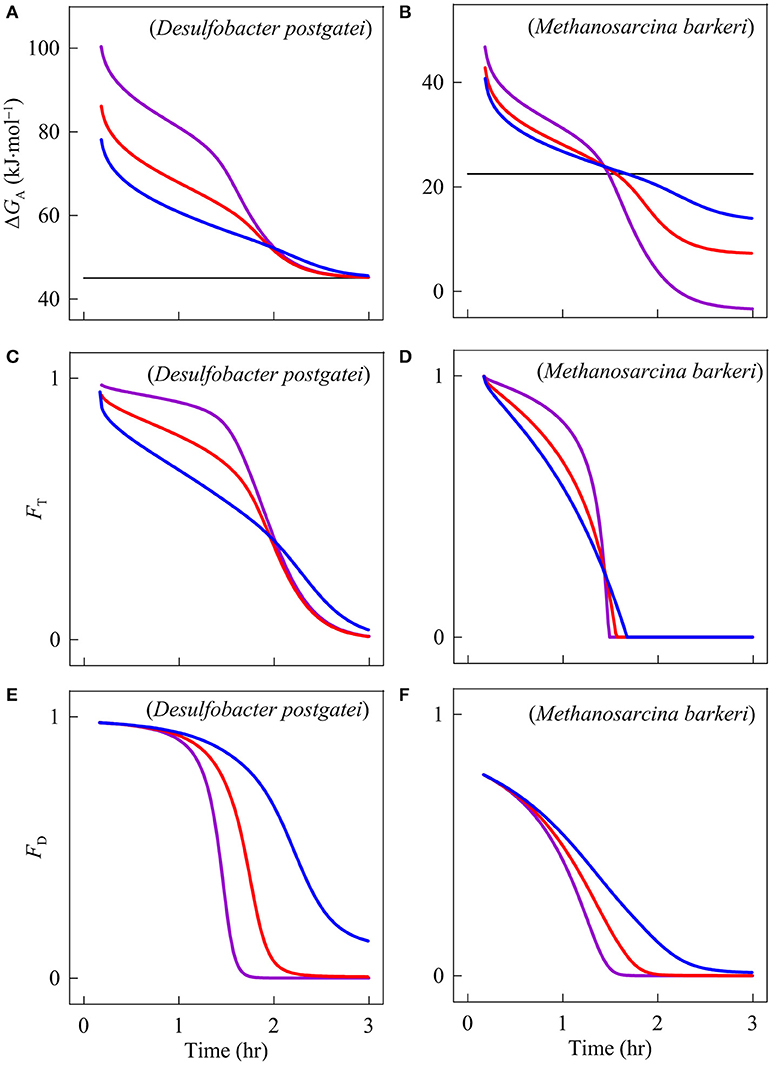
Figure 3. Variation with time in the available energy ΔG_A (A,B), the thermodynamic potential factor F_T (C,D), and the kinetic factor F_D of Desulfobacter postgatei and Methanosarcina barkeri (E,F). The lines are the simulation results at pH 7 (blue), 6 (red), and 5 (purple).

Figures 1, 2 also show the simulation results at pH 6 and 5. According to these results, sulfide production is faster at lower pH. For example, at the beginning of the experiments, sulfide is produced at 1.08 × 10⁻⁶, 1.22 × 10⁻⁶, and 1.35 × 10⁻⁶ molal·s⁻¹ at pH 7, 6, and 5, respectively. Accordingly, sulfide reaches its maximum concentration after 2.5, 2, and 1.7 h, respectively. In comparison, the pH changes have little impact on methane production. Methane is produced 1.38 ± 0.05 × 10⁻⁶ molal·s⁻¹ in each simulation.

Figure 3A shows that the energy yield of D. postgatei responds significantly to pH changes. The pH decreases from 7 to 6 and from 6 to 5 raise the energy yield by about 7.1 kJ·mol⁻¹ and 13.6 kJ·mol⁻¹, respectively. As a result, the thermodynamic potential factor increases, speeding up sulfate reduction (Figures 2A, 3C).

Figure 3B shows that the energy yield of methanogenesis also responds to the pH changes. The pH decreases from 7 to 6 and from 6 to 5 raise the energy yield by about 1.4 kJ·mol⁻¹ and 3.6 kJ·mol⁻¹, respectively. These increases raise the thermodynamic potential factor (Figure 3D). However, the rate does not respond notably to the pH changes because, in addition to the thermodynamic control, methanogenesis rate is also limited by the concentration of acetate (Equation 3, Figures 2B, 3F). Compared to D. postgatei, M. barkeri is more sensitive to the decrease in acetate concentrations because it has a relatively large half-saturation constant (Table 1). At pH 6 and 5, acetate concentration decreases faster than at pH 7, decreasing further the kinetic factor F_D of acetate (Figures 1A, 3F). This change offsets the gain in energy provided by the decreasing pH and thus, the simulation predicts that the methanogenesis rate remains roughly unchanged at the different pHs.

Semi-open Environment

We then simulate the competition between D. postgatei and M. barkeri in a hypothetical semi-open system. We assume that fluid containing 5 mM acetate, 5 mM sulfate, and 1 mM bicarbonate has a temperature of 25°C and flows continuously through the system with a residence time of 3.7 day (or a turnover rate of 0.27 per day). We carry out the simulation at different pHs, from 5 to 7, for 10 years, well pass the time (0.5 year) when the system reaches steady state.

Figure 4 shows the simulation results. At pH 7, D. postgatei dominates the system but fails to drive out M. barkeri. At steady state, the hypothetical system contains 4.56 mM sulfide, 0.46 sulfide, 0.25 mM methane, and 0.21 mM acetate. D. postgatei grows to a concentration of 0.54 g·kg⁻¹, and consumes 94.8% of the acetate flowing into the system. In contrast, M. barkeri has a concentration of 0.02 g·kg⁻¹ and consumes the remaining 5.2% of the acetate.

FIGURE 4

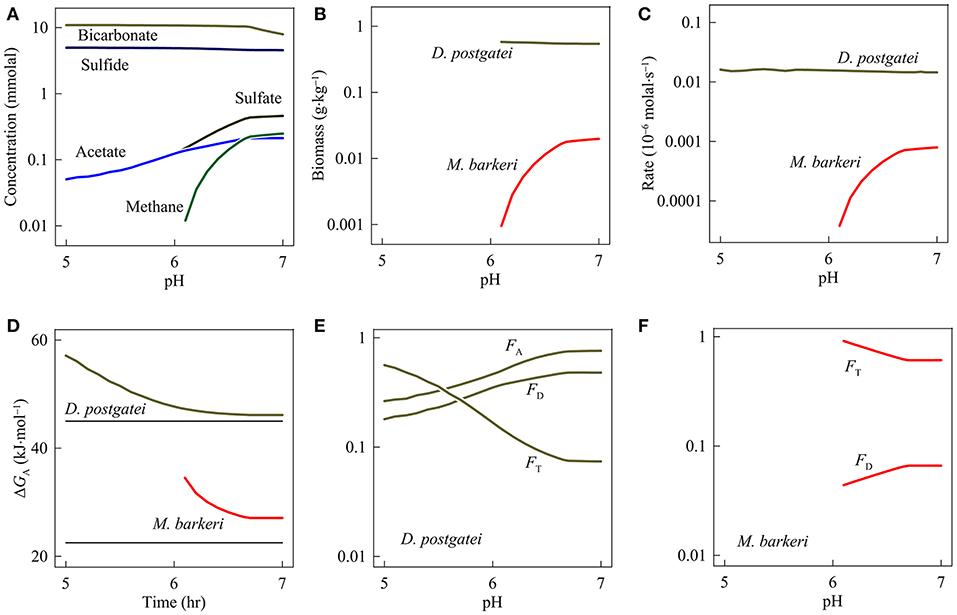
Figure 4. Variation with pH in the concentrations of bicarbonate, sulfide, sulfate, acetate, and methane (A), and the biomass concentrations (B), the respiration rates (C), the available energies ΔG_A (D), the thermodynamic potential factors F_T, and the kinetic factors F_D and F_A of Desulfobacter postgatei (E) and Methanosarcina barkeri (F).

As pH decreases from 7 to 6.1, M. barkeri persists but decreases in abundance relative to D. postgatei. Sulfate, acetate, and methane concentrations fall to 0.15, 0.14, and 0.01 mM, respectively, at pH 6.1 while sulfide concentration rises to 4.87 mM. Coupled with these changes, D. postgatei biomass rises slightly to 0.58 g·kg⁻¹ as pH decreases to 6.1 while M. barkeri biomass decreases to 0.95 mg·kg⁻¹. At this point, methanogenesis only accounts for about 0.2% of the acetate consumption.

Only at pH equal to or less than 6, can D. postgatei drive M. barkeri out of the system. At pH 5, sulfate and acetate concentrations both decrease to 0.05 mM. The concentrations of sulfide and D. postgatei biomass rise to 4.97 mM and 0.59 g·kg⁻¹, respectively.

Above pH 6, the failure of D. postgatei to exclude M. barkeri is due to the significant thermodynamic limitation on sulfate reduction (Figure 4D). This control reflects the combined effects of neutral to near-neutral pH, acetate consumption, and bicarbonate and sulfide accumulation. As a consequence, the thermodynamic potential factor remains relatively small, lowering the rates of sulfate reduction and biosynthesis (Equations 3 and 10). To maintain biosynthesis rates above the rate of maintenance and cell death and thereby to avoid a decline in the biomass concentration, D. postgatei must balance the small thermodynamic potential factor by maintaining a modest kinetic factor of acetate. Specifically, it must maintain acetate concentrations above 0.13 mM, obtaining a kinetic factor above 0.4 (Figure 4F). In turn, these acetate concentrations are large enough for M. barkeri to achieve biosynthesis rates above the rate of maintenance and cell death (Table 1) and to survive in the system.

On the other hand, between pH 5 and 6, the energy available to D. postgatei rises well above the conserved energy (Figure 4D), raising the thermodynamic potential factor above 0.2. Under this condition, D. postgatei can lower acetate concentrations below the levels required for the survival of M. barkeri. These results are consistent with the hypothesis that sulfate reducers can drive methanogens out of the system by holding acetate concentrations below the levels needed for sustaining methanogen populations (Bethke et al., 2008). The results also support our hypothesis that pH can control the membership and metabolic activity of microbial consortia, and influence the outcome of microbial competition.

Syntrophy

A classic example of syntrophy is the interspecies hydrogen transfer, which takes place between H₂-producing and H₂-consuming microbes (Schink and Stams, 2013). Previous studies have emphasized H₂ levels as a determining factor of H₂-based syntrophic interactions. For example, butyrate-oxidizing microbes, such as Syntrophomonas wolfei, can oxidize butyrate to acetate by reducing protons to H₂. For butyrate oxidation to remain thermodynamically favorable, butyrate oxidizers can partner with microbes that consume H₂ and thereby maintain H₂ levels low. In the companion paper (Jin and Kirk, 2018), we show that pH can play a similar role as H₂–pH affects the thermodynamics of both butyrate oxidation and hydrogentrophic redox reactions. Therefore, we expect that pH can also affect the kinetics of individual redox reactions in the syntrophic interaction and the dynamics of syntrophic consortia.

Laboratory Experiments

Wu et al. (1994) studied butyrate degradation using a consortium of three microbes, butyrate-oxidizing strain IB, Methanobacterium formicium, and Methanosarcina mazei. In their experiments, strain IB oxidizes butyrate and produces acetate and H₂,

$\begin{array}{rc}\text{Butyrate}+2{\text{H}}_2\text{O}\vec{\leftarrow }2\text{Acetate}+2{\text{H}}_2+{\text{H}}^{+}& (13)\end{array}$

M. formicium catalyzes hydrogenotrophic methanogenesis,

$\begin{array}{rc}4{\text{H}}_2+{\text{H}}^{+}+{\text{HCO}}_3^{-}\vec{\leftarrow }{\text{CH}}_4+3{\text{H}}_2\text{O}& (14)\end{array}$

M. mazei drives acetoclastic methanogenesis (reaction 12). The three microbes grew at 37°C in batch reactors of 108 mL headspace and 50 mL growth medium. The medium had a pH of 7 and contained 4.3 mM butyrate, 4.1 mM isobutyate, 6.3 mM acetate, and 48.0 mM bicarbonate.

Jin (2007) developed a kinetic model for the three microbes. This model computes microbial reaction rates according to (Equations 3 and 10), and simulates butyrate degradation by accounting for the response of syntrophic energy conservation to H₂ partial pressure (Equation 8). Here we update the microbial parameters of the model to reflect recent developments of biogeochemical reaction modeling (see Table 1), and repeat the simulation.

According to the experimental observations and the simulation results at pH 7 (Figure 5), butyrate and isobutyrate concentrations decrease with time and are nearly depleted after day 25. Acetate concentration remains relatively stable during the first 10 days of the experiments and then accumulates to 10 mM after day 20. H₂ partial pressure peaks during the first couple of days and then decreases to 10⁻⁴ atm and remains at this level till day 20. Afterwards, H₂ partial pressure decreases to about 4.0 × 10⁻⁵ atm at day 27. The simulation also predicts the accumulations of dissolved inorganic carbon (DIC) and methane. At day 27, DIC reaches 57 mM and methane has a partial pressure of 0.17 atm.

FIGURE 5

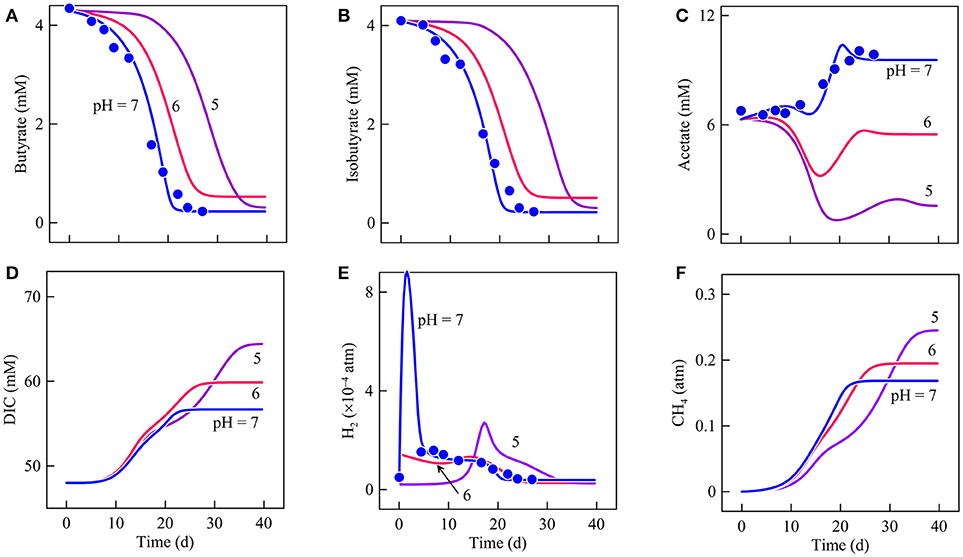
Figure 5. Variation with time in the concentrations of butyrate (A), isobutyrate (B), acetate (C), dissolved inorganic carbon (DIC, D), and the partial pressures of H₂ (E) and methane (F) in batch reactors of differ pHs. Data points are the results of Wu et al. (1994); lines are the results of biogeochemical reaction modeling, accounting for the impact of pH on the energy available from microbial reactions.

Figure 6 shows the variations with time in the biomass concentrations and respiration rates of strain IB, M. mazei, and M. formicium according to the simulation results. The biomass concentrations of the three microbes vary similarly over time. They first increase to maximum values over about 20 days and then start to decrease slowly. Around day 20, the consortium is dominated by M. mazeri, whose maximum biomass concentration is 38.1 mg·kg⁻¹. The biomass concentrations of strain IB and M. formicium are only 5.2 and 9.5 mg·kg⁻¹, respectively. The rates of butyrate oxidation and hydrogenotrophic methanogenesis also vary similarly. The rates increase during the first 19 days, and then drop to 0. In comparison, the rate of M. mazei peaks twice during the experiments. The first peak appears around day 12 and the second comes on day 19, the same time when strain IB and M. formicium reach their maximum rates of butyrate oxidation and hydrogenotrophic methanogenesis, respectively.

FIGURE 6

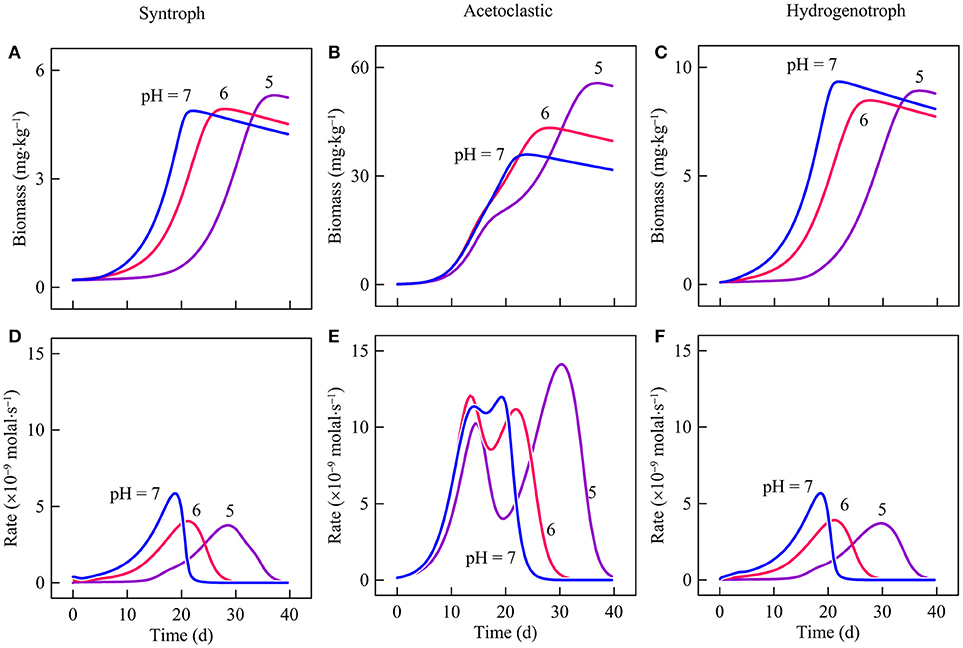
Figure 6. Variation with time in the biomass concentrations and respiration rates of strain IB (A,D), Methanosarcina mazei (B,E), and Methanobacterium formicium (C,F) in batch reactors of differ pHs. Lines are the results of biogeochemical reaction modeling, accounting for the impact of pH on the energy available from microbial reactions.

Similar patterns of rates and biomass concentrations of strain IB and M. formicium confirm that the metabolisms of the two microbes depend on each other and thus interact syntrophically. On the other hand, the rate variation of M. mazei suggests that its metabolism is not closely coupled to butyrate oxidation, likely because acetate was provided at the beginning of the experiments.

pH Impact

To explore how pH may potentially affect butyrate degradation by the microbial consortium, we re-ran the updated model with medium at pH 6 and at pH 5. The results suggest that lowering pH can influence microbial metabolisms and interactions in at least three ways.

First, a decrease in pH affects butyrate degradation rates and hence the carbon fluxes from butyrate to CO₂ and methane. The simulation results indicate that, relative to pH 7, butyrate consumption slows by 4 and 15 days, respectively, at pH 6 and 5 (Figure 5A). Accordingly, lowering pH also delays variations in the biomass concentration and the respiration rate of strain IB (Figures 6A,D). For example, at pH 7, the biomass concentration reaches its maximum value at day 20. At pH 6 and 5, the maximum values appear on day 26 and 39, respectively. This delay in the metabolism explains the absence of an initial H₂ peak at pH 6 and 5 (Figure 5E).

The delay in butyrate degradation can be accounted for by the thermodynamic response of syntrophic butyrate oxidation. For strain IB, both the available energy and conserved energy depend on the partial pressures of H₂. At pH 7, the available energy first decreases briefly because of the H₂ peak and then increases to more than 10 kJ·mol⁻¹ after day 5 (Figure 7A). Conserved energy also drops at the beginning of the experiments and then recovers, exceeding 5 kJ·mol⁻¹ after day 5 (Figure 7B). As a result, the thermodynamic drive declines initially and then rises to about 7 kJ·mol⁻¹ after day 5 (Figure 7C). The drive remains at this level until day 15 and then starts to decrease because of acetate accumulation. After day 20, the drive decreases to nearly 0.

FIGURE 7

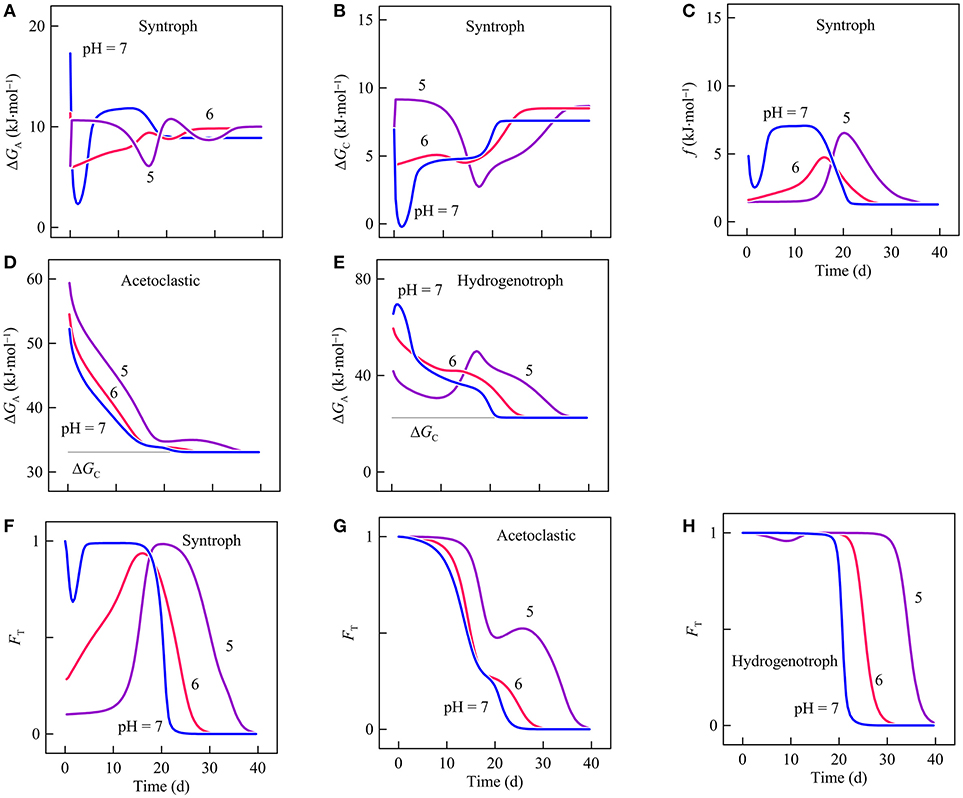
Figure 7. Variation with time in the energy available (A), the conserved energy (B), and the thermodynamic drive (C) of strain IB, the energy available to Methanosarcina mazei (D) and to Methanobacterium formicium (E), and the thermodynamic factor of syntrophic butyrate oxidation (F), acetoclastic methanogenesis (G), and hydrogenotrophic methanogenesis (H) in batch reactors of differ pHs. Lines are the results of biogeochemical reaction modeling, accounting for the impact of pH on the energy available from microbial reactions.

Available energy also depends on pH. Specifically, available energy decreases with decreasing pH (Jin and Kirk, 2018). Thus, the thermodynamic drive is smaller at pH 6 than pH 7. At pH 5, during the first 10 days, the available energy is relatively large because of the small H₂ partial pressure. But the small partial pressure also allows strain IB to save more energy. As a result, the thermodynamic drive remains smaller than the value at pH 6. Smaller thermodynamic drives at pH 6 and 5 slow down the metabolism of strain IB (Figure 7F).

The delay in butyrate oxidation affects the metabolisms of M. formicium and M. mazei. M. formicium depends on strain IB for the supply of H₂. As a result, the delayed butyrate oxidation also delays the metabolism of M. formicium. The acetate for M. mazei comes from two sources, the acetate provided at the beginning of the experiments and the acetate produced by strain IB. The two different sources give rise to the two peak rates (Figure 6E). The first peak is made possible by the consumption of the initial acetate supply and the second is due to the acetate produced by butyrate oxidation. Delayed butyrate oxidation, therefore, delays the arrival of the second peak.

Second, a decrease in pH may also modulate the interactions between hydrogenotrophic and acetoclastic methanogenesis. In the reactors, methanogenesis by M. mazei is inhibited by the accumulation of methane. Methane accumulation decreases the thermodynamic drives and hence rates of both M. formicium and M. mazei (Figures 7D,E,G,H). But M. mazei is affected more because the energy available from acetoclastic methanogenesis (reaction 12) tends to be smaller than that of hydrogenotrophic methanogenesis (reaction 14), and because M. mazei conserves more energy than M. formicium per methane (Equations 6 and 7, Table 1). These thermodynamic differences allow M. formicium to make a proportionally larger contribution to methane production than M. mazei.

This effect can be evaluated in terms of the contribution of M. mazei to methane production. In the reactors, 4.3 mM butyrate, 4.1 mM isobutyrate and 6.3 mM acetate are provided. If the metabolisms of M. mazei and M. formicium are independent of each other and are not inhibited by methane accumulation, M. formicium would produce 4.2 mol methane, and M. mazei would produce 23.1 mol per liter of medium. In other words, M. mazei would account for 84.6% of methane production. According to the simulation results, at pH 7, M. mazei accounts for 76.1% of methane production. Thus, methane accumulation decreases the contribution of M. mazei by 8.5%.

At lower pH, this effect is lessened because methane production by M. formicium is delayed. The delay gives M. mazei an opportunity to consume more acetate and to make a bigger contribution to methane production (Figures 5C,F, 6B,E). At pH 6 and 5, M. mazei accounts for 80.9 and 83.9% of methane production, respectively. Corresponding to the increasing methane production, the biomass concentration of M. mazeri also increases (Figures 6B,C). At pH 6, M. mazeri reaches a maximum biomass concentration of 45.8 mg·kg⁻¹ at day 28. At pH 5, the maximum biomass concentration of 57.4 mg·kg⁻¹ is achieved on day 58.

Lastly, the pH decreases may regulate the efficiency of methane production. Microbial communities degrade organic carbon to CO₂ and methane. The efficiency of methane production is quantified as the ratio of methane production to the sum of CO₂ and methane productions (Ye et al., 2012),

$\begin{array}{rc}\eta =\frac{C_{\text{C}{\text{H}}_4}}{C_{\text{C}{\text{O}}_2}+C_{\text{C}{\text{H}}_4}},& (15)\end{array}$

where C_CO2 and C_CH4 are the total CO₂ and methane produced in the reactors. In the experiments, methane is produced by both acetoclastic and hydrogenotrophic methanogenesis but CO₂ is produced only by acetoclastic methanogenesis. The hydrogenotrophic pathway instead consumes CO₂. As such, the efficiency of methane generation increases with the increasing contribution of hydrogenotrophic methanogenesis. According to the simulation results, the proportion of acetoclastic to hydrogenotrophic methanogenesis changes with pH. Therefore, the methane production efficiency η also varies with pH. Specifically, a decrease in pH lowers the efficiency of methane production. According to the simulation results, at pH 7, the efficiency of methane production is 65.7%. At pH 6 and 5, the efficiency decreases to 61.8 and 59.6%, respectively.

Discussion

We explored the relationship between pH and microbial communities using biogeochemical kinetic modeling. We simulated how pH variation speeds up or slows down microbial respiration and growth and in turn influences microbial interactions, including the competition between sulfate reducers and methanogens and the syntrophy among butyrate oxidizers and methanogens.

Kinetic Response

In the companion paper (Jin and Kirk, 2018), we show that the variations in environmental pH change significantly the energy yields of syntrophic oxidation, sulfate reduction, and methanogenesis. In this paper, we simulate the kinetics of these processes using the thermodynamically consistent Monod equation (Equation 6)—this equation accounts for the energy yields of microbial redox reactions as well as the energy conserved by respiration. The simulation results show that a decrease in pH speeds up the metabolism of acetotrophic sulfate reducers. Specifically, decreases of one pH unit speed up the progress by 12%. The decrease in pH also slows down the metabolism of butyrate syntrophic oxidizers. A decrease of one pH unit decreases the rate by >10%. These results are consistent with the predictions from the thermodynamics of the redox reactions (reactions 11 and 13), and support that the thermodynamic responses of redox reactions can be strong enough to affect the kinetics of microbial metabolisms.

The pH decreases also raise the energy yields of acetoclastic and hydrogenotrophic methanogenesis (reactions 12 and 14) and hence have the potential of raising the metabolic activities of methanogens (Jin and Kirk, 2018). But our kinetic simulations fail to support these predictions. The inconsistencies between the thermodynamic and kinetic predictions highlight the complexity of microbial kinetics and the importance of microbial interactions.

For example, the rate of acetoclastic methanogenesis depends on the kinetic factor of acetate concentration as well as the thermodynamic factor of the energy yield. The modeling results show that in the batch reactor experiments of Schönheit et al. (1982), the pH decreases do raise the energy yields of acetoclastic methanogenesis, but this increasing effect is counteracted by the decreasing acetate concentrations. As a result, the rate doesn't respond much to the pH changes (Figures 1–3).

In the experiments of Wu et al. (1994), the pH decreases do not raise the energy yield of hydrogenotrophic methanogenesis. In the experiments, H₂-consuming M. formicium relies on H₂-producing strain IB for the supply of H₂. The energy yield of hydrogenotrophic methanogenesis depends not only on pH but also on the concentrations of H₂. At lower pH, H₂ production from butyrate oxidation slows down and H₂ concentration decreases, thereby lowering the energy yield at the beginning of the experiments and slowing down hydrogenotrophic methanogenesis.

The discrepancies between the thermodynamic predictions and kinetic modeling reiterate the difference between thermodynamic and kinetic modeling: the predictions made from reaction thermodynamics should be treated as the potential responses of microbial metabolisms. Whether the predictions are relevant or not requires biogeochemical modeling that considers not only the kinetics of microbial metabolisms of interest, but also the impact from concurrent biogeochemical processes.

Competitive Exclusion vs. Co-occurrence

In addition to the observation-based modeling, we also simulated the competition between D. postgatei and M. barkeri in a hypothetical semi-open environment (Figure 4). The results show that, despite its kinetic and thermodynamic advantages, D. postgatei is not always capable of excluding M. barkeri from the system, and that environmental pH can play a role in the outcome of microbial competition. The simulation demonstrates that pH can determine whether competitors coexist or are excluded from the environment. These results might help resolve the disagreement between the principle of competitive exclusion and metabolic diversities in natural environments.

According to the principle of competitive exclusion (Hardin, 1960), where different microbes reduce various electron acceptors by competing for a limiting electron donor, they cannot coexist, and only the one with competitive advantage can survive. In natural sediments and aquifers, common electron acceptors include O₂, nitrate, ferric minerals, sulfate, and CO₂, and the apparent pattern in electron acceptor usage appears to conform to this principle (Kuivila et al., 1989; Chapelle et al., 1995; Bethke et al., 2011). Among these electron acceptors, O₂ is the most thermodynamically favorable one, followed by nitrate, ferric mineral, sulfate, and CO₂, respectively. Accordingly, O₂ is typically the first electron acceptor to be depleted from the environment, whereas CO₂ is the last.

But different anaerobic respiration reactions can take place simultaneously. The co-occurrence of iron reduction, sulfate reduction, and methanogenesis have been discovered in various settings, from biofilms to surface sediments and aquifers (Raskin et al., 1996; Metje and Frenzel, 2007; Flynn et al., 2013). Different mechanisms have been proposed to account for these co-occurrences, including spatial heterogeneity, dynamic biogeochemical conditions, and complex microbial interactions (Roy and Chattopadhyay, 2007; Bethke et al., 2011).

In our modeling example (Figure 4), D. postgatei can consume acetate and grow faster than M. barkeri (Table 1). But under the assumed flow and chemical conditions, the competitive exclusion principle only applies at pH ≤ 6.0. At pH above 6.0, the two microbes co-exist, due to the relatively significant thermodynamic limitation on the rates of sulfate reduction and biosynthesis. To balance the thermodynamic limitation, D. postgatei must maintain acetate at relatively large concentrations in order to achieve a relatively large kinetic factor F_D of acetate. These acetate concentrations exceed thresholds required for sustaining M. barkeri population.

Between pH 5 and 6, the relatively low pH raises the energy yield of sulfate reduction, which loosens the thermodynamic control and raises the rates of sulfate reduction and biosynthesis. Such favorable thermodynamic response allows D. postgatei to exclude M. barkeri by lowering acetate concentrations.

These results suggest that the competitive exclusion principle may not always be applicable, especially where microbes of competitive advantage are subject to significant thermodynamic limitations. They also illustrate a decisive role of pH in the outcome of microbial competition, and support our hypothesis that environmental pH is capable of shaping microbial community composition by affecting the thermodynamics and kinetics of individual microbial metabolisms.

Microbial Kinetic Model

This study focuses on how microbial thermodynamic responses to pH may affect the kinetics of individual microbial metabolism and the outcome of microbial interactions. In addition, pH also directly affects the catalytic capacity of microbes, therefore the kinetic parameters of microbial respiration and growth (Equation 3). This impact arises from the dependence of enzyme activities on cytoplasmic pH. Cytoplasmic pH modifies enzyme conformations and is critical for the formation and maintenance of the catalytically-competent active sites within enzymes (Leprince and Quiquampoix, 1996; Nielsen and McCammon, 2003). In addition, many enzymes are regulated allosterically by effector molecules. The presence of effector molecules and their interactions with enzymes depend on cytoplasmic pH (Makhlynets et al., 2015). Although cytoplasmic pH is tightly regulated by microbes, it does vary in accordance with the changes in environmental pH, albeit to lesser extents (Booth, 1985; Kobayashi et al., 2000; Padan et al., 2005).

Current models consider the direct pH impact on the forward rates by including a pH factor (Ng and Schaffner, 1997; Tienungoon et al., 2000). Enzyme activities respond to pH variations by following bell- or triangular-shaped curve. For example, the pH impact can be described using a triangular function,

$\begin{array}{cc}{F}_{\text{pH}}=\{\begin{array}{c}\frac{{\text{pH}}_{\text{opt}}-\text{pH}}{{\text{pH}}_{\text{opt}}-{\text{pH}}_{\text{min}}},{\text{pH}}_{\text{min}}\le \text{pH}\le {\text{pH}}_{\text{opt}};\\ \frac{{\text{pH}}_{\text{max}}-\text{pH}}{{\text{pH}}_{\text{max}}-{\text{pH}}_{\text{opt}}},{\text{pH}}_{\text{opt}}<\text{pH}\le {\text{pH}}_{\text{max}}.\end{array}& (16)\end{array}$

Here pH_opt, pH_min, and pH_max are the optimal, minimum, and maximum pHs for growth. We propose to determine the values of pH_opt, pH_min, and pH_max based on the pH response of rate-limiting enzymes of microbial respiration. For example, methyl-coenzyme reductase is likely a rate-limiting step of methanogenesis (Bonacker et al., 1992). Based on previous laboratory observations of methyl-coenzyme M reductase of Methanosarcina thermophila (Jablonski and Ferry, 1991), we set pH_opt at 6.9, pH_min at 4.9, and pH_max at 8.9.

By combining the pH factor and the thermodynamic factor, we consider not only the direct impact of pH on respiration enzymes, but also the indirect impact by changing the thermodynamics of microbial respiration. These dual effects may explain a common pattern in the response of microbial metabolism to pH—the metabolic response is asymmetric about optimal pH. Specifically, between the minimum and optimal pHs, the slope of the increase in microbial rates differs from the slope of decrease between optimal and maximum pHs. The asymmetric responses have been widely reported for laboratory cultures, including syntrophs (Zhang et al., 2005; Hatamoto et al., 2007), iron reducers (Xu et al., 2005; Sun et al., 2014), sulfate reducers (Baena et al., 1998; O'Flaherty et al., 1998), and methanogens (Zehnder and Wuhrmann, 1977; Huser et al., 1982).

Taking acetoclastic methanogenesis as an example, according to the pH factor (Equation 16), a deviation from optimal pH always leads to the inhibition of microbial metabolism. Likewise, moving pH toward optimal pHs would promote microbial metabolism. However, for neutrophilic methanogens whose optimal pH is 7, increases in pH above the optimal pH raise their thermodynamic drives and hence rates, counteracting decreases by the direct pH effect on the forward rates of methanogenesis.

Combining the pH factor and the thermodynamic factor, the modified Monod equation predicts that rates of acetoclastic methanogenesis respond to pH asymmetrically. As shown in Figure 8, the slope predicted for the rate increase between pH_min and pH_opt is almost twice as large as the slope predicted for the decrease between pH_opt and pH_max. This prediction agrees with previous laboratory observations, such as those of Methanosarcina mazei (Maestrojuan and Boone, 1991).

FIGURE 8

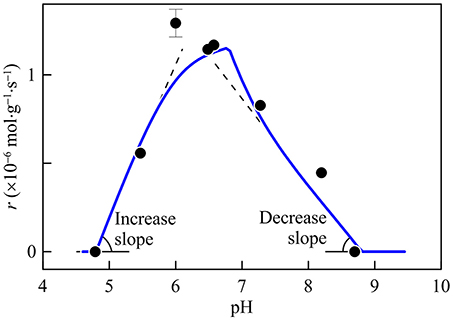
Figure 8. Variation with time in the rate of acetoclastic methanogenesis. Solid line is the prediction by the pH factor and the thermodynamic factor, assuming that acetate is abundant and the kinetic factor F_D takes a value of one; data points are computed from the experimental results of Methanosarcina mazei, using a growth yield of 2 g·(mol acetate)⁻¹ (Maestrojuan and Boone, 1991). The slopes of increase and decrease are 0.86 and 0.49 mol·g⁻¹·s⁻¹ per pH unit, respectively.

In simulating microbial metabolisms, we purposely set the pH factor to one (Equation 16). In other words, we assumed that pH only impacts the thermodynamics of microbial redox reactions. This assumption allows us to focus on microbial thermodynamic responses. Despite this simplification, the simulation may still be relevant to natural environments, especially those that host diverse microbial communities. For example, environments with neutral pH may host a seed bank of microbes whose optimal pHs are at pH 6 or 5. Thus, lowering pH to 6 lowers the respiration rate for microbes with optimal pH of 7, but would raise the rate for those with optimal pH of 6 (or their pH factors become one). As a result, microbes with an optimal pH of 6 would take over and drive out those whose optimal pHs are not 6, providing that other microbial properties, such as growth yields and maintenance rates, do not change.

Consistent with this interpretation, results of Petrie et al. (2003) and Kirk et al. (2013) suggest that the contribution of Anaeromyxobacter species to iron reduction increased as pH decreased in their field and bioreactor studies, respectively. As shown in the companion paper, iron reduction becomes more thermodynamically favorable as pH decreases. Thus, the shift in iron reducer identity was not likely a response to a thermodynamic limitation but possibly a reflection of differences in pH optima. These observations suggest that our results are best applied to environments that host diverse communities of microorganisms with different optimal pHs. We further propose that thermodynamics may provide insight into the kinetic response of microbial metabolisms to pH variations, whereas pH optima may dictate the identity of species that catalyze the reactions at a given pH.

Concluding Comments

We applied biogeochemical kinetic modeling to simulate the responses of syntrophic butyrate oxidation, sulfate reduction, and methanogenesis to pH changes. Our modeling is biased by two assumptions. We assume that pH does not affect the amount of energy conserved by microbes. We also assume that microbial kinetic parameters, including rate constants, half-saturation constants, and maintenance rates, do not change with pH. These assumptions overlook the complexity of microbial metabolisms and may have underestimated the extent to which pH impacts cell metabolisms. But these assumptions allow us to focus on microbial thermodynamic responses and to test whether the pH-induced thermodynamic responses alone are strong enough for significant changes in the composition and activity of microbial communities.

The simulation results show that, by accounting for the thermodynamics and kinetics of microbial reactions and the interactions among microbes, biogeochemical kinetic modeling can be applied to gauge and tune the predictions made from thermodynamics. For example, a pH decrease from 7 to 6 or to 5 raises the energy yield of acetotrophic sulfate reduction, but lowers the energy yield of syntrophic butyrate oxidation. Based on the thermodynamic responses, we predict that acetotrophic sulfate reduction would speed up, but syntrophic butyrate oxidation would slow down by the pH decrease. The kinetic modeling results confirm the predictions—a one-unit decrease in pH can raise the rate of acetotrophic sulfate reduction and lower the rate of syntrophic butyrate oxidation by >10%.

Our results also show that thermodynamic predictions are not always relevant. A pH decrease from 7 to 6 or to 5 raises the energy yield of acetoclastic and hydrogenotrophic methanogenesis, and hence can speed up the two reactions. But the kinetic modeling results suggest that, in closed environments, such as in laboratory batch reactors, the thermodynamic influence of pH on acetoclastic methanogenesis can be canceled by the impact of decreasing acetate concentrations. Also, where hydrogenotrophic methanogens live syntrophically with H₂-producing butyrate oxidizers, both the energy yield and rate of methanogenesis may depend primarily on the H₂ production by butyrate oxidizers, instead of environmental pH.

The simulation of the semi-open system supports the hypothesis that by changing the energy yields of microbial redox reactions, environmental pH is capable of changing the composition of microbial communities. According to the simulation results, environmental pH dictates the outcome of the competition between D. postgatei and M. barkeri. Between pH 6 and 7, despite the competitive advantage of D. postgatei over M. barkeri, the two microbes live together in the system. Between pH 5 and 6, only D. postgatei stays, and M. barkeri disappears. The different outcomes come from the influence of pH on the energy yield of sulfate reduction. Between pH 6 and 7, D. postgatei is subject to a significant thermodynamic limitation, and must balance that limitation by keeping acetate concentrations relatively large—large enough for sustaining the cells of M. barkeri. Decreasing pH to or below 6 alleviates the thermodynamic limitation and enables D. postgatei to expel M. barkeri by lowering acetate concentrations below the minimum levels required for sustaining M. barkeri.

By raising or lowering the energy yields of microbial redox reactions, environmental pH is also capable of shaping the ecological functions of microbial communities. The modeling results of butyrate syntrophic degradation show that pH variation is capable of changing microbially-driven carbon fluxes in three ways. First, environmental pH affects the magnitudes of carbon fluxes. Lowering pH from 7 to 5 decrease the rates of butyrate oxidation and hence the fluxes of C from butyrate to CO₂ and methane. This decrease is mainly due to the decreases in the energy available from the syntrophic oxidation of butyrate.

Second, environmental pH regulates the contributions of hydrogenotrophic and acetoclastic methanogenesis to methane production. Compared to the hydrogenotrophic pathway, acetoclastic methanogenesis is more sensitive to the accumulation of methane in the environment because of its limited available energy. The simulation results show that lowering pH from 7 to 5 decreases the thermodynamic drive of the hydrogenotrophic pathway and subsequently its production of methane. In turn, this effect alleviates the methane inhibition of the acetoclastic pathway, allowing it to produce more methane.

Last, variation in pH changes the efficiency of methane production. By working together, syntrophic butyrate oxidation, and hydrogenotrophic and acetoclastic methanogenesis convert butyrate to CO₂ and methane. Environmental pH can influence the efficiency of methane production by changing the relative significances of the two methanogenesis pathways. Specifically, decreases in pH decrease the efficiency of methane production from butyrate, a result that is consistent with previous observations in wetlands (Ye et al., 2012). Taken together, these results provide a mechanistic view of how environmental pH modulate the fluxes and composition of C in the environment. Although we focused on butyrate degradation, we expect that pH also influence the C fluxes from other organic compounds and hence the biogeochemical cycling of C—a topic to be further investigated.

In addition, the modeling results add to the current theories of environmental microbiology. For example, current theories attribute microbial competitive advantages to two different mechanisms—by lowering substrate levels below the thresholds required for driving the catabolisms of competitors (Lovley et al., 1982) or below the thresholds for sustaining the populations of competitors (Bethke et al., 2008). Our simulation results suggest that the two mechanisms are applicable to two different environmental settings—the first is applicable to batch reactors and other closed environments, whereas the second applies to flow-through reactors or other semi-open environments.

The modeling results also suggest that the principle of competitive exclusion may not always be applicable. This principle predicts that where electron donors are limiting, microbial respiration reactions segregated into spatially-distinct zones. According to the simulation results, this principle may not be applicable to respiration reactions of significant thermodynamic limitations, where the energy yields of redox reactions are close to the energy conserved by respiration. Under this condition, respiration reactions of competitive advantage may take place simultaneously with reactions of competitive disadvantage. Only where the thermodynamic control becomes relatively insignificant, can the respiration reactions of competitive advantage exclude competing reactions from the environment by lowering electron donor concentrations. Thus, by modifying the energy yields of microbial redox reactions, environmental pH can determine whether the competitive exclusion principle is applicable, or whether different microbial redox reactions take place simultaneously or segregated into different zones.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This research was funded by the National Science Foundation under Award EAR-1636815 and by National Aeronautics and Space Administration under Grant NNX16AJ59G.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2018.00101/full#supplementary-material

References

Amenabar, M. J., Shock, E. L., Roden, E. E., Peters, J. W., and Boyd, E. S. (2017). Microbial substrate preference dictated by energy demand rather than supply: Nat. Geosci. 10, 577–581. doi: 10.1038/ngeo2978

CrossRef Full Text | Google Scholar

Baena, S., Fardeau, M. L., Labat, M., Ollivier, B., Garcia, J. L., and Patel, B. K. C. (1998). Desulfovibrio aminophilus sp. nov., a novel amino acid degrading and sulfate reducing bacterium from an anaerobic dairy wastewater lagoon. Syst. Appl. Microbiol. 21, 498–504. doi: 10.1016/S0723-2020(98)80061-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bethke, C. M. (2008). Geochemical and Biogeochemical Reaction Modeling. Cambridge:Cambridge University Press.

Google Scholar

Bethke, C. M., Ding, D., Jin, Q., and Sanford, R. A. (2008). Origin of microbiological zoning in groundwater flows. Geology 36, 739–742. doi: 10.1130/G24859A.1

CrossRef Full Text | Google Scholar

Bethke, C. M., Sanford, R. A., Kirk, M. F., Jin, Q., and Flynn, T. M. (2011). The thermodynamic ladder in geomicrobiology. Am. J. Sci. 311, 183–210. doi: 10.2475/03.2011.01

CrossRef Full Text | Google Scholar

Bonacker, L. G., Baudner, S., and Thauer, R. K. (1992). Differential expression of the two methyl-coenzyme M reductases in Methanobacterium thermoautotrophicum as determined immunochemically via isoenzyme-specific antisera. Eur. J. Biochem. 206, 87–92. doi: 10.1111/j.1432-1033.1992.tb16904.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Booth, I. R. (1985). Regulation of cytoplasmic pH in bacteria. Microbiol. Rev. 49, 359–378.

PubMed Abstract | Google Scholar

Chapelle, F. H., McMahon, P. B., Dubrovsky, N. M., Fujii, R. F., Oaksford, E. T., and Vroblesky, D. A. (1995). Deducing the distribution of terminal electron-accepting processes in hydrologically diverse groundwater systems. Water Resour. Res. 31, 359–371. doi: 10.1029/94WR02525

CrossRef Full Text | Google Scholar

Delany, J. M., and Lundeen, S. R. (1990). The LLNL Thermodynamical Database. Lawrence Livermore National Laboratory Report UCRL-21658.

Flynn, T. M., Sanford, R. A., Ryu, H., Bethke, C. M., Levine, A. D., Ashbolt, N. J., et al. (2013). Functional microbial diversity explains groundwater chemistry in a pristine aquifer. BMC Microbiol. 13:146. doi: 10.1186/1471-2180-13-146

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardin, G. (1960). The competitive exclusion principle. Science 131, 1292–1297. doi: 10.1126/science.131.3409.1292

PubMed Abstract | CrossRef Full Text | Google Scholar

Hatamoto, M., Imachi, H., Fukayo, S., Ohashi, A., and Harada, H. (2007). Syntrophomonas palmitatica sp. nov., an anaerobic, syntrophic, long-chain fatty-acid-oxidizing bacterium isolated from methanogenic sludge. Int. J. Syst. Evolu. Microbiol. 57, 2137–2142. doi: 10.1099/ijs.0.64981-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Helgeson, H. C. (1969). Thermodynamics of hydrothermal systems at elevated temperatures and pressures. Am. J. Sci. 267, 729–804. doi: 10.2475/ajs.267.7.729

CrossRef Full Text | Google Scholar

Huser, B. A., Wuhrmann, K., and Zehnder, A. J. B. (1982). Methanothrix soehngenii gen. nov. sp. nov., a new acetotrophic non-hydrogen-oxidizing methane bacterium. Arch. Microbiol. 132, 1–9.

Google Scholar

Jablonski, P. E., and Ferry, J. G. (1991). Purification and properties of methyl coenzyme M methylreductase from acetate-grown Methanosarcina thermophila. J. Bacteriol. 173, 2481–2487. doi: 10.1128/jb.173.8.2481-2487.1991

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Q. (2007). Control of hydrogen partial pressures on the rates of syntrophic microbial metabolisms: a kinetic model for butyrate fermentation. Geobiology 5, 35–48. doi: 10.1111/j.1472-4669.2006.00090.x

CrossRef Full Text | Google Scholar

Jin, Q. (2012). Energy conservation of anaerobic respiration. Am. J. Sci. 312, 573–628. doi: 10.2475/06.2012.01

CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2002). Kinetics of electron transfer through the respiratory chain. Biophys. J. 83, 1797–1808. doi: 10.1016/S0006-3495(02)73945-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2003). A new rate law describing microbial respiration. Appl. Environ. Microbiol. 69, 2340–2348. doi: 10.1128/AEM.69.4.2340-2348.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2005). Predicting the rate of microbial respiration in geochemical environments. Geochim. Cosmochim. Acta 69, 1133–1143. doi: 10.1016/j.gca.2004.08.010

CrossRef Full Text | Google Scholar

Jin, Q., and Bethke, C. M. (2007). The thermodynamics and kinetics of microbial metabolism. Am. J. Sci. 307, 643–677. doi: 10.2475/04.2007.01

CrossRef Full Text | Google Scholar

Jin, Q., and Kirk, M. F. (2016). Thermodynamic and kinetic response of microbial reactions to high CO2. Front. Microbiol. 7:1696. doi: 10.3389/fmicb.2016.01696

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Q., and Kirk, M. F. (2018). pH as a primary control in environmental microbiology: 1. Thermodynamic perspective. Front. Environ. Sci. 6:21. doi: 10.3389/fenvs.2018.00021

CrossRef Full Text | Google Scholar

Jin, Q., and Roden, E. E. (2011). Microbial physiology-based model of ethanol metabolism in subsurface sediments. J. Contam. Hydrol. 125, 1–12. doi: 10.1016/j.jconhyd.2011.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Jin, Q., Roden, E. E., and Giska, J. R. (2013). Geomicrobial kinetics: extrapolating laboratory studies to natural environments. Geomicrobiol. J. 30, 173–185. doi: 10.1080/01490451.2011.653084

CrossRef Full Text | Google Scholar

Kinniburgh, D. G., van Riemsdijk, W. H., Koopal, L. K., Borkovec, M., Benedetti, M. F., and Avena, M. J. (1999). Ion binding to natural organic matter: competition, heterogeneity, stoichiometry and thermodynamic consistency. Colloids Surf. A Physicochem. Eng. Aspects 151, 147–166. doi: 10.1016/S0927-7757(98)00637-2

CrossRef Full Text | Google Scholar

Kirk, M. F., Santillan, E. F. U., Sanford, R. A., and Altman, S. J. (2013). CO2-induced shift in microbial activity affects carbon trapping and water quality in anoxic bioreactors. Geochim. Cosmochim. Acta 122, 198–208. doi: 10.1016/j.gca.2013.08.018

CrossRef Full Text | Google Scholar

Kobayashi, H., Saito, H., and Kakegawa, T. (2000). Bacterial strategies to inhabit acidic environments. J. Gen. Appl. Microbiol. 46, 235–243. doi: 10.2323/jgam.46.235

PubMed Abstract | CrossRef Full Text | Google Scholar

Konings, W. N., Albers, S.-V., Koning, S., and Driessen, A. J. M. (2002). The cell membrane plays a crucial role in survival of bacteria and archaea in extreme environments. Antonie van Leeuwenhoek 81, 61–72. doi: 10.1023/A:1020573408652

PubMed Abstract | CrossRef Full Text | Google Scholar

Kotsyurbenko, O. R., Chin, K.-J., Glagolev, M. V., Stubner, S., Simankova, M. V., Nozhevnikova, A. N., et al. (2004). Acetoclastic and hydrogenotrophic methane production and methanogenic populations in an acidic West-Siberian peat bog. Environ. Microbiol. 6, 1159–1173. doi: 10.1111/j.1462-2920.2004.00634.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuivila, K. M., Murray, J. W., Devol, A. H., and Novelli, P. C. (1989). Methane production, sulfate reduction and competition for substrates in the sediments of Lake Washington. Geochim. Cosmochim. Acta 53, 409–416. doi: 10.1016/0016-7037(89)90392-X

CrossRef Full Text | Google Scholar

Leprince, F., and Quiquampoix, H. (1996). Extracellular enzyme activity in soil: effect of pH and ionic strength on the interaction with montmorillonite of two acid phosphatases secreted by the ectomycorrhizal fungus Hebeloma cylindrosporum. Eur. J. Soil Sc. 47, 511–522. doi: 10.1111/j.1365-2389.1996.tb01851.x

CrossRef Full Text | Google Scholar

Lovley, D. R., Dwyer, D. F., and Klug, M. J. (1982). Kinetic analysis of competition between sulfate reducers and methanogens for hydrogen in sediments. Appl. Environ. Microbiol. 43, 1373–1379.

PubMed Abstract | Google Scholar

Lovley, D. R., and Klug, M.J. (1982). Intermediary metabolism of organic matter in the sediments of a eutrophic lake. Appl. Environ. Microbiol. 43, 552–560.

PubMed Abstract | Google Scholar

Lovley, D. R., and Philips, E. J. (1987). Competitive mechanisms of sulfate reduction and methane production in the zone of ferric iron reduction in sediments. Appl. Environ. Microbiol. 53, 2636–2641.

PubMed Abstract | Google Scholar

Maestrojuan, G. M., and Boone, D. R. (1991). Characterization of Methanosarcina barkeri MST and 227, Methanosarcina mazei S-6T, and Methanosarcina vacuolata Z-761T. Int. J. Syst. Evolu. Microbiol. 41, 267–274. doi: 10.1099/00207713-41-2-267

CrossRef Full Text | Google Scholar

Makhlynets, O. V., Raymond, E. A., and Korendovych, I. V. (2015). Design of allosterically regulated protein catalysts. Biochemistry 54, 1444–1456. doi: 10.1021/bi5015248

PubMed Abstract | CrossRef Full Text | Google Scholar

Metje, M., and Frenzel, P. (2007). Methanogenesis and methanogenic pathways in a peat from subarctic permafrost. Environ. Microbiol. 9, 954–964. doi: 10.1111/j.1462-2920.2006.01217.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Molongoski, J. J., and Klug, M. J. (1980). Anaerobic metabolism of particulate organic matter in the sediments of hypereutrophic lake. Freshw. Biol. 10, 507–518. doi: 10.1111/j.1365-2427.1980.tb01225.x

CrossRef Full Text | Google Scholar

Monokova, S.V. (1975). Volatile fatty acids in bottom sediments of the Rybinsk reservoir. Hydrobiol. J. 11, 45–48.

Google Scholar

Ng, T. M., and Schaffner, D. W. (1997). Mathematical models for the effects of pH, temperature, and sodium chloride on the growth of Bacillus stearothermophilus in salty carrots. Appl. Environ. Microbiol. 63, 1237–1243.

PubMed Abstract | Google Scholar

Nielsen, J. E., and McCammon, J. A. (2003). Calculating pKa values in enzyme active sites. Protein Sci. 12, 1894–1901. doi: 10.1110/ps.03114903

PubMed Abstract | CrossRef Full Text | Google Scholar

Nielsen, U. N., Ayres, E., Wall, D. H., and Bardgett, R. D. (2011). Soil biodiversity and carbon cycling: a review and synthesis of studies examining diversity–function relationships. Eur. J. Soil Sci. 62, 105–116. doi: 10.1111/j.1365-2389.2010.01314.x

CrossRef Full Text | Google Scholar

O'Flaherty, V., Mahony, T., O'Kennedy, R., and Colleran, E. (1998). Effect of pH on growth kinetics and sulphide toxicity thresholds of a range of methanogenic, syntrophic and sulphate-reducing bacteria. Process Biochem. 33, 555–569. doi: 10.1016/S0032-9592(98)00018-1

CrossRef Full Text | Google Scholar

Padan, E., Bibi, E., Ito, M., and Krulwich, T. A. (2005). Alkaline pH homeostasis in bacteria: new insights. Biochim. Biophys. Acta Biomembranes 1717, 67–88. doi: 10.1016/j.bbamem.2005.09.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Panikov, N. S. (1995). Microbial Growth Kinetics. London: Chapman and Hall.

Google Scholar

Paul, A., Stösser, R., Zehl, A., Zwirnmann, E., Vogt, R. D., and Steinberg, C. E. W. (2006). Nature and abundance of organic radicals in natural organic matter: effect of pH and irradiation. Environ. Sci. Technol. 40, 5897–5903. doi: 10.1021/es060742d

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrie, L., North, N. N., Dollhopf, S. L., Balkwill, D. L., and Kostka, J. E. (2003). Enumeration and characterization of iron(III)-reducing microbial communities from acidic subsurface sediments contaminated with uranium(VI). Appl. Environ. Microbiol. 69, 7467–7479. doi: 10.1128/AEM.69.12.7467-7479.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Raskin, L., Rittmann, B. E., and Stahl, D. A. (1996). Competition and coexistence of sulfate-reducing and methanogenic populations in anaerobic biofilms: Appl. Environ. Microbiol. 62, 3847–57.

PubMed Abstract | Google Scholar

Rosso, L., Lobry, J. R., Bajard, S., and Flandrois, J. P. (1995). Convenient model to describe the combined effects of temperature and pH on microbial growth. Appl. Environ. Microbiol. 61, 610–616.

PubMed Abstract | Google Scholar

Roy, S., and Chattopadhyay, J. (2007). Towards a resolution of ‘the paradox of the plankton': a brief overview of the proposed mechanisms. Ecol. Complex 4, 26–33. doi: 10.1016/j.ecocom.2007.02.016

CrossRef Full Text | Google Scholar

Schink, B., and Stams, A. J. M. (2013). “Syntrophism among prokaryotes,” in The Prokaryotes: Prokaryotic Communities and Ecophysiology, eds E. Rosenberg, E. F. DeLong, S. Lory, E. Stackebrandt, and F. Thompson (Berlin; Heidelberg: Springer), 471–493.

Google Scholar

Schönheit, P., Kristjansson, J. K., and Thauer, R. K. (1982). Kinetic mechanism for the ability of sulfate reducers to out-compete methanogens for acetate. Arch. Microbiol. 132, 285–288.

Google Scholar

Sun, D., Wang, A., Cheng, S., Yates, M., and Logan, B. E. (2014). Geobacter anodireducens sp. nov., an exoelectrogenic microbe in bioelectrochemical systems. Int. J. Syst. Evolu. Microbiol. 64, 3485–3491. doi: 10.1099/ijs.0.061598-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Thauer, R. K., Jungermann, K., and Decker, K. (1977). Energy conservation in chemotrophic anaerobic bacteria. Bacteriolog. Rev. 41, 100–180.

PubMed Abstract | Google Scholar

Thompson, L. R., Sanders, J. G., McDonald, D., Amir, A., Ladau, J., Locey, K. J., et al. (2017). A communal catalogue reveals Earth's multiscale microbial diversity. Nature 551, 457–463. doi: 10.1038/nature24621

PubMed Abstract | CrossRef Full Text | Google Scholar

Tienungoon, S., Ratkowsky, D. A., McMeekin, T. A., and Ross, T. (2000). Growth limits of Listeria monocytogenesas a function of temperature, pH, NaCl, and lactic acid. Appl. Environ. Microbiol. 66, 4979–4987. doi: 10.1128/AEM.66.11.4979-4987.2000

PubMed Abstract | CrossRef Full Text | Google Scholar

van Bodegom, P. (2007). Microbial maintenance: a critical review on its quantification. Microbiol Ecol. 53, 513–523. doi: 10.1007/s00248-006-9049-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, W.-M., Jain, M. K., and Zeikus, J. G. (1994). Anaerobic degradation of normal- and branched-chain fatty acids with four or more carbons to methane by a syntrophic methanogenic triculture. Appl. Environ. Microbiol. 60, 2220–2226.

PubMed Abstract | Google Scholar

Xavier, J. B. (2011). Social interaction in synthetic and natural microbial communities. Mol. Syst. Biol. 7:483. doi: 10.1038/msb.2011.16

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, M., Guo, J., Cen, Y., Zhong, X., Cao, W., and Sun, G. (2005). Shewanella decolorationis sp. nov., a dye-decolorizing bacterium isolated from activated sludge of a waste-water treatment plant. Int. J. Syst. Evolu. Microbiol. 55, 363–368. doi: 10.1099/ijs.0.63157-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Ye, R., Jin, Q., Bohannan, B., Keller, J. K., McAllister, S. A., and Bridgham, S. D. (2012). pH controls over anaerobic carbon mineralization, the efficiency of methane production, and methanogenic pathways in peatlands across an ombrotrophic–minerotrophic gradient. Soil Biol. Biochem. 54, 36–47. doi: 10.1016/j.soilbio.2012.05.015

CrossRef Full Text | Google Scholar

Zehnder, A. J. B., and Wuhrmann, K. (1977). Physiology of a Methanobacterium strain AZ. Arch. Microbiol. 111, 199–205. doi: 10.1007/BF00549357

CrossRef Full Text | Google Scholar

Zhang, C., Liu, X., and Dong, X. (2005). Syntrophomonas erecta sp. nov., a novel anaerobe that syntrophically degrades short-chain fatty acids. Int. J. Syst. Evol. Microbiol. 55, 799–803. doi: 10.1099/ijs.0.63372-0

PubMed Abstract | CrossRef Full Text | Google Scholar