Finite Heterogeneous Rate Constants for the Electrochemical Oxidation of VO2+ at Glassy Carbon Electrodes

The electrochemical oxidation of VO²⁺ at planar glassy carbon electrodes is investigated via stationary and rotating linear sweep voltammetry as well as via chronoamperometry. It is demonstrated that introducing finite kinetic rate constants into the Butler-Volmer equation captures the experimentally observed concentration dependence of the ordinate intercept in Koutecký-Levich plots that cannot be explained by using the classical model. This new concept leads to a three-term Koutecký-Levich equation considering mass transport limitations, Butler-Volmer kinetics, as well as finite heterogeneous kinetics simultaneously. Based on these findings it is pointed out that stationary linear sweep voltammetry followed by an irreversible Randles-Ševčík analysis is not sufficient for deducing the electrode kinetics of the VO²⁺-oxidation. In contrast, it is verified experimentally and theoretically that a Tafel analysis will still provide reasonable values of k⁰ = 1.35 · 10⁻⁵ cm/s and α = 0.38, respectively. Finally, it is shown that introducing the concept of finite heterogeneous kinetics into the theory of stationary linear sweep voltammetry also explains the failure of the irreversible Randles-Ševčík relation leading to an extension of the classical model and providing insight into the electrochemical oxidation reaction of VO²⁺.

1. Introduction

In vanadium redox flow battery (VRFB) research, stationary¹ linear sweep voltammetry (S-LSV) and stationary cyclic voltammetry (S-CV) are the most prevalent techniques used for the fast assessment of the kinetic performance of surface-modified carbon felt electrodes, and numerous studies have been published on that topic (Flox et al., 2013a,b; Gao et al., 2013; Hammer et al., 2014; Suárez et al., 2014; Liu et al., 2015; Park and Kim, 2015; He et al., 2016, 2018; Kim et al., 2016; Park et al., 2016; Ryu et al., 2016; Zhang et al., 2016; Zhou et al., 2016; González et al., 2017; Jiang et al., 2017; Ghimire et al., 2018; Xiang and Daoud, 2019; Yang et al., 2019). However, regarding the complex diffusion domain inside a felt electrode, the common approach of relating the peak-to-peak separation of an S-CV curve to the electrodes' kinetics (valid for a planar electrode in semi-infinite diffusion space only; Matsuda and Ayabe, 1954; Nicholson and Shain, 1964; Nicholson, 1965) does not seem to be appropriate. Applying the irreversible Randles-Ševčík relation for deducing the intrinsic kinetics of a felt electrode is also not possible since (a) the electrochemically active electrode area of the fiber network is unknown or at least uncertain and (b) the variation of the peak height with respect to the potential sweep rate becomes ambiguous when non-planar electrodes are involved (Aoki et al., 1983, 1984, 1985; Aoki, 1988). Since the majority of publications are dedicated to felt electrodes and respective diffusion domain effects rarely receive sufficient attention (Menshykau and Compton, 2008; Smith et al., 2015; Peinetti et al., 2016; Tichter et al., 2019a), literature values of the intrinsic vanadium redox kinetics might spread over orders of magnitude, as discussed recently in the paper by Friedl and Stimming (2017). Unfortunately, studies involving planar electrodes providing a well-defined, semi-infinite diffusion domain are unpopular in case of the VRFB system and a quantification of the intrinsic kinetics of novel electrode materials usually remains untested (Oriji et al., 2004; Han et al., 2011; Li et al., 2011, 2012, 2013, 2014; Jin et al., 2013; Dai et al., 2017). Compared to S-CV/LSV measurements at planar electrodes, studies using a rotating disc electrode (RDE) are even more unpopular (Zhong and Skyllas-Kazacos, 1992; Oriji et al., 2004). This is somewhat astonishing since they are well established in other fields of energy conversion (e.g., the fuel cell community) and can provide valuable information on the proceeding electrode reactions. With this paper we present a recent and comprehensive study on the oxidation reaction of VO²⁺ at electrochemically activated glassy carbon electrodes involving stationary and rotating linear sweep voltammetry as well as chronoamperometry. It is demonstrated that a Koutecký-Levich analysis of the RDE limiting currents yields a theoretically unexpected non-zero ordinate intercept proportional to the inverse VO²⁺ concentrations. Furthermore, it is shown that interpreting S-LSV data in terms of the irreversible Randles-Ševčík relation leads to values in the electron transfer coefficient α that contradict the findings from Tafel analysis of RDE data. We account for these two unexpected features simultaneously by introducing finite heterogeneous kinetic rate constants into the Butler-Volmer equation. Based on this idea, a three-term Koutecký-Levich equation is derived, allowing for unraveling mass transport, Butler-Volmer electrode kinetics and finite heterogeneous electron transfer kinetics. In this manner, the maximum heterogeneous rate constant for the oxidation reaction of VO²⁺ is found to be k_max = 2.6 · 10^-2 cm/s. By including the estimated maximum rate constant into the theory of stationary linear sweep voltammetry, we also propose a model that captures the deviations of the experimental S-LSV data from the ideal irreversible Randles-Ševčík behavior. Finally, it is shown mathematically that the classical Tafel analysis of RDE data is unaffected by the limited electron transfer kinetics and should therefore be preferred for kinetic characterization.

2. Experimental Section

2.1. Electrochemical Measurements

The oxidation of VO²⁺ was investigated at electrochemically activated glassy carbon surfaces. The electrochemical activation was performed according to the conditioning given in Table 1. As an electrolyte solution, 2 M H₂SO₄ (ROTIPURANⓇ Ultra 95%, Carl Roth) with different concentrations of VO²⁺ [0.00, 0.02, 0.04, 0.06, and 0.08 M, Vanadium(IV) sulfate oxide hydrate, 99.9% (metals basis), Alfa Aesar] was used. All measurements were performed in a three electrode setup consisting of a Ag/AgCl reference (saturated, 198 mV vs. SHE), a Pt-mesh counter electrode, and a glassy carbon disc (7 mm diameter, embedded into a PEEK cylinder) working electrode. Data was acquired using a PalmSens Em-Stat potentiostat (PalmSens). The working electrode was connected to a control panel (MetrohmAutolabⓇ RDE-2) to adjust the rotation speed during the measurements.

TABLE 1

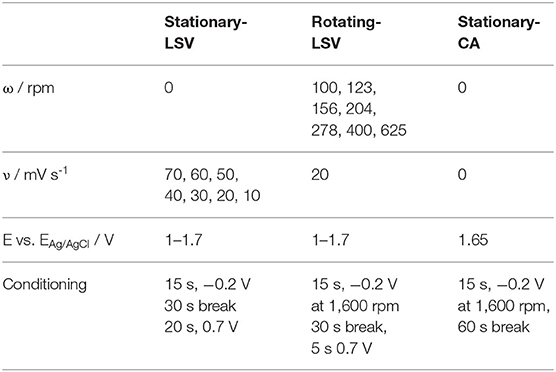
Table 1. Overview of all linear sweep (LSV) and chronoamperometry (CA) measurements with corresponding pretreatments.

2.2. Pretreatment of the Electrode

Prior to each measurement, the glassy carbon electrode was polished in two successive steps (step 1: 1.0 micron, BUEHLER 40-10081 and step 2: 0.05 micron, BUEHLER 40-10083). Electrochemical activation was performed under rotation in a chronoamperometric three-step sequence (step 1: 2 V vs. E_Ref for 15 s, step 2: −1 V vs. E_Ref for 5 s, step 3: 2 V vs. E_Ref for 5 s, each step at ω = 1,600 rpm). Subsequently, S-LSV, R-LSV, and S-CA measurements were performed as given in Table 1.

3. Results and Discussion

3.1. RDE Measurements

The desired reaction of this study, the electrochemical oxidation of VO²⁺, can be formulated as

$\begin{array}{ll}V{O}^{2+}+H_{2}O\stackrel{-e^{-}}{\to }V{O}_2^{+}+2H^{+}& (1)\end{array}$

and has a standard electrode potential of $E^0-E_{SHE}=$ 0.995 V. To eliminate errors resulting from parasitic reactions such as the carbon corrosion or the oxygen evolution reaction, the datasets obtained for vanadium containing electrolytes were corrected by the corresponding vanadium-free baselines in pure 2 M sulfuric acid. This entirely subtractive correction is based on the assumption that any parasitic reactions proceed in parallel and do not impair the desired oxidation of VO²⁺. Furthermore, it holds only under the presumption that the electrode area is independent of the applied electrode potential. These assumptions are considered reasonable as long as the upper potential limit does not allow for the formation of gaseous oxygen, which was ensured throughout the entire study. This correction is illustrated for the electrolyte containing 0.02 M vanadyl sulfate in Figure 1A: stationary and Figure 1B: rotating linear sweep as well as the Figure 1C: chronoamperometric measurements. Gray lines represent the baseline in pure 2 M sulfuric acid solution and black lines the measurements in 2 M sulfuric acid containing 0.02 M vanadyl sulfate. The corresponding baseline corrected curves are shown in Figures 1A1–C1. Baseline corrected data at the different vanadyl sulfate concentrations are depicted in Figures 1A2–C2. In the S-LSV measurements (Figure 1A2) a potential sweep rate of ν = 10 mV/s was used. The rotation rate in the R-LSV experiments in Figure 1B2 was set to ω = 100 rpm.

FIGURE 1

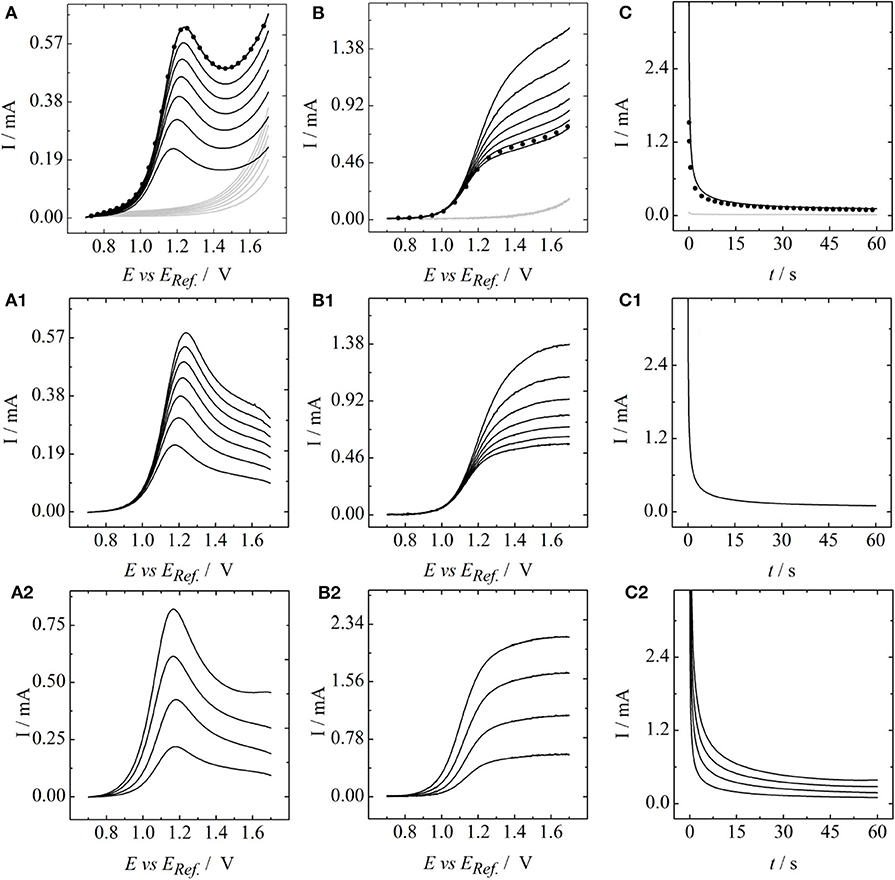
Figure 1. (A) Stationary and (B) rotating linear sweep as well as (C) chronoamperometric measurements at a glassy carbon surface. Gray lines: 2 M sulfuric acid as a baseline, black lines: vanadyl sulfate containing 2 M sulfuric acid, black dots: repetition of initial measurements to check experimental reproducibility. (A1–C1) Represent baseline corrected data at a VO²⁺ concentration of 0.02 M for (A1) varying scanrates and (B1) varying rotation rates. (A2–C2) Represent baseline corrected data for varying concentrations of VO²⁺ at (A2): a fixed scanrate of 10 mV/s and (B2): a fixed rotation rate of 100 rpm. Potentials were referred to a saturated Ag/AgCl reference.

It can be seen that increasing the scan rate (Figure 1A1) or the rotation rate (Figure 1B1) at fixed VO₂⁺-concentration results in a set of curves starting at the same kinetic origin. In contrast, an increase in the concentrations, as shown in Figures 1A2,B2, results in a negative shift of the entire LSV curves. This is expected, as the exchange current is proportional to the analyte concentration. In case of the S-LSVs a peak current with constant peak position is obtained for the different concentrations, whereas in case of the R-LSVs the limiting current scales linearly with respect to the concentrations. The chronoamperometric measurements of Figure 1C2 also show a linear scaling of the current with the concentrations. Based on the datasets of Figures 1, 2A shows a Randles-Ševčík plot, Figure 2B a Koutecký-Levich plot and Figure 2C a Cottrell plot for the different concentrations of VO²⁺. In all cases straight lines are obtained. At this point we want to draw the reader's attention to the experimentally observed ordinate intercepts in the Koutecký-Levich plots in particular. These are not expected from a theoretical point of view and will be discussed in detail in section 3.2. Based on the data of Figures 2A–C,A1,C1 depict the slopes obtained from the analysis in Figures 2A,C, plotted versus the corresponding concentrations of VO²⁺. A plot of the inverse slope of Figure 2B versus the analyte concentration leads to Figure 2B1. In all cases a linear concentration dependence is obtained, providing a slope that corresponds to the second partial derivatives of the Koutecký-Levich eq. 3, the irreversible Randles-Ševcík eq. 2 and the Cottrell equation eq. 4, respectively.

$\begin{array}{ll}{I}_R^{″}=\frac{{\partial }^2{I}_R}{\partial c\partial {\nu }^{1/2}}& (2)\end{array}$

$\begin{array}{ll}{I}_K^{″}=\frac{{\partial }^2{I}_K}{\partial c\partial {\omega }^{1/2}}& (3)\end{array}$

$\begin{array}{ll}{I}_C^{″}=\frac{{\partial }^2{I}_C}{\partial c\partial t^{-1/2}}& (4)\end{array}$

These second partial derivatives are used in the following section for further analysis.

FIGURE 2

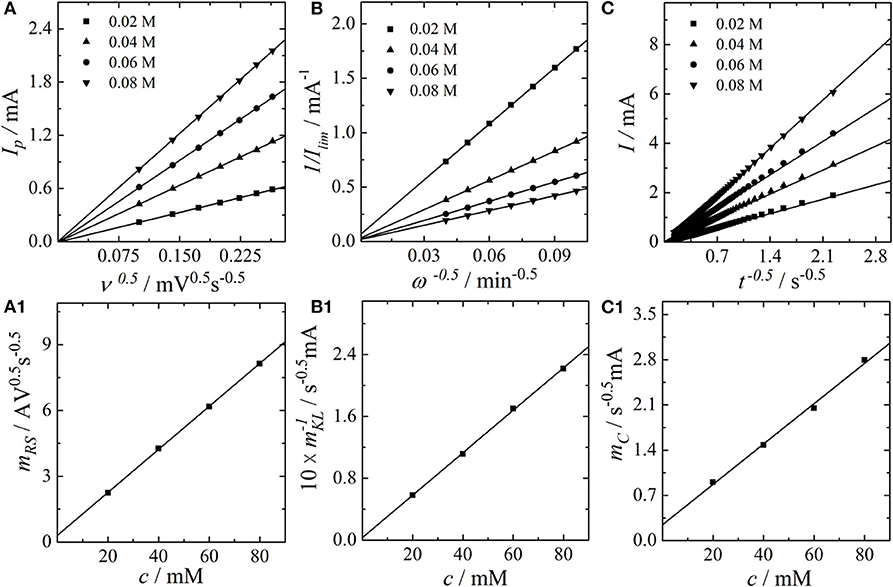
Figure 2. (A) Randles-Ševčík-Plot of the peak currents vs. the square root of the scan rate, (B) Koutecký-Levich plot of the inverse limiting currents vs. the inverse square root of the electrode rotation rate, and (C) Cottrell plot of the current vs. the inverse square root of the experiment duration. (A1) plot of the Randles-Ševčík slopes vs. the concentrations, (B1) plot of the inverse Koutecký-Levich slopes vs. the concentrations, and (C1) plot of the Cottrell slopes vs. the concentrations.

By combining the second partial derivative of the Cottrell equation with the second partial derivative of the Koutecký-Levich equation, we obtain the diffusion coefficient of the VO²⁺-ion via

$\begin{array}{ll}D=489\eta {\left(\frac{I_K^{″}}{I_C^{″}}\right)}^6.& (5)\end{array}$

Compared to the classical Koutecký-Levich or Cottrell analysis, this expression appears to be superior in estimating diffusion coefficients since (a) it does not depend on the active electrode area (which might differ from the geometric area) and (b) it accounts for different analyte concentrations as well. Furthermore, it is not necessary to know the value of n a priori. Following this strategy, we determine the diffusion coefficient of the VO²⁺-cation in 2 M H₂SO₄ to a value of 2.26 · 10^-6 cm²/s, in good agreement with the average value given in Zhong and Skyllas-Kazacos (1992) and slightly smaller than the value reported in our recent study (Tichter et al., 2019b), which was obtained from S-CV fitting of a felt electrode. A similar combination of the second partial derivative of the irreversible Randles-Ševčík equation obtained from Figure 2A1 with the second partial derivative of the Cottrell equation allows for a determination of the electron transfer coefficient as

$\begin{array}{ll}\alpha =1.294\frac{RT}{nF}{\left(\frac{I_P^{″}}{I_C^{″}}\right)}^2.& (6)\end{array}$

Nevertheless, it has to be noted that this expression requires the values of n to be known (in the present case it is assumed that n = 1). Via Equation (6), we estimate the electron transfer coefficient for the electrochemical oxidation of VO²⁺ at the glassy carbon electrode to α = 0.32. At this stage we highlight the importance of the baseline correction as shown in Figure 1, which was necessary in order to remove additively scaling parasitic currents. However, we refer to an alternative way for estimating α, which is independent of the current magnitude and is outlined in the early findings of Matsuda and Ayabe (1954). There, the authors propose that it is possible to obtain the electron transfer coefficient for an electrochemically irreversible reaction (taking place at a planar electrode in semi-infinite diffusion space) by analyzing the peak shape and the peak position of a S-LSV curve via Equations (7) and (8) only. Also in this context, however, the value of n has to be known.

$\begin{array}{ll}\alpha =\frac{1.85RT}{nF(E_p-E_{p/2})}& (7)\end{array}$

$\begin{array}{ll}\alpha =\frac{RT}{2nF}{\left(\frac{\partial I_P}{\partial ln(\nu )}\right)}^{-1}& (8)\end{array}$

Another, and probably the most straightforward way for obtaining the electron transfer coefficient is given in terms of a Tafel-analysis of RDE data (Equation 9).

$\begin{array}{ll}\alpha =\frac{RT}{nF}\left(\frac{\partial ln(\frac{I{I}_L}{I_L-I})}{\partial (E-E^{eq})}\right)& (9)\end{array}$

In order to deduce α, Figure 3A: a Tafel plot, Figure 3B: a plot of the peak position versus the logarithm of the scan rate and Figure 3C: the peak shape analysis for the oxidation of vanadyl sulfate at a glassy carbon electrode. The values of the electron transfer coefficient are listed in Table 2.

FIGURE 3

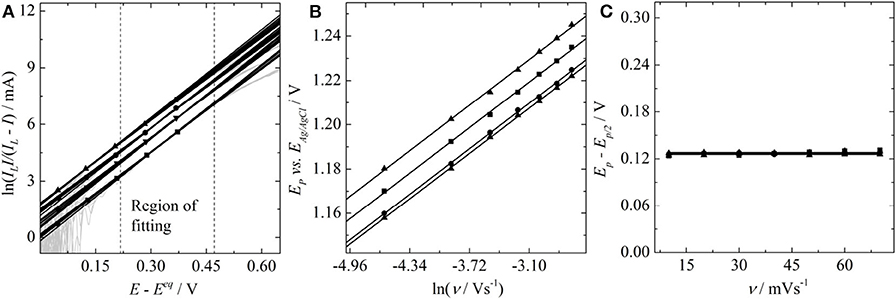
Figure 3. (A) Tafel plots (dashed lines are the limits of the fitting region), (B) plot of the peak position vs. the logarithm of the scan rate, and (C) peak-shape analysis for the oxidation of vanadyl sulfate in concentrations of 0.02 M (square), 0.04 M (down-triangle), 0.06 M (circle), and 0.08 M (up-triangle) at a glassy carbon electrode in 2 M H₂SO₄.

TABLE 2

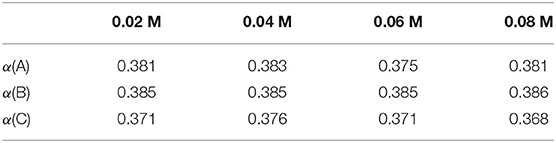
Table 2. Values of the electron transfer coefficient α, estimated from Tafel-, Randles-Ševčík-, and Matsuda-Ayabe analysis.

All the values of α given in Table 2 are close to α = 0.38 and therefore diverge significantly from the value of α = 0.32 determined by Equation (6). No dependence of α on the concentrations is observed. Consequently, the average of the α value is taken for all individual concentrations. Thus, analyzing the dependence of the peak-potential on the logarithm of the scan rate according to Equation (7) yields α = 0.385, the shape analysis according to Equation (8) leads to α = 0.372, and a Tafel analysis provides α = 0.38. Furthermore, a Tafel analysis provides the standard heterogeneous rate constant to k⁰ = 1.35 · 10⁻⁵ cm/s. The significant deviation in the α values given in Table 2 from the findings involving Equation (6) as well as the unexpected non-zero ordinate intercepts in Koutecký-Levich analysis will be discussed in the following subsections.

3.2. Concept of Finite Heterogeneous Kinetics

The experimentally observed non-zero ordinate intercepts obtained in Koutecký-Levich plots are the main motivation for the following considerations. Such a behavior cannot be explained with the classical Koutecký-Levich model (Equation 10), since a limiting current, or better, a hydrodynamic limiting current caused by mass transfer limitations—corresponds to infinitely fast reaction kinetics forcing $I_{kin}^{-1}\to$ 0. Consequently, the extrapolation to infinite rotation rate will actually give a zero-ordinate intercept.

$\begin{array}{ll}\frac{1}{I_K}=\frac{1}{I_{kin}}+\frac{1}{0.201nFAc{D}^{2/3}{\eta }^{-1/6}\sqrt{\omega }}& (10)\end{array}$

However, we propose that a current plateau, usually associated with the hydrodynamic limiting current, can also be reached by a limitation of the heterogeneous reaction kinetics itself. Thus, the term $I_{kin}^{-1}$ will become small and constant, but it will not approach zero. The current plateau achieved under these circumstances will always be lower than the hydrodynamic limiting current, which is indeed what is observed experimentally. By calculating the hydrodynamic limiting current with the classical Koutecký-Levich equation using the previously obtained value of D, the estimated hydrodynamic limiting current values are always larger than their experimentally measured analogs. Thus, we suggest that for implementing the concept of a maximum kinetic current into the Koutecký-Levich equation, a third and additively scaling inverse current term that does neither depend on the overpotential, nor on the rotation rates is required. Subsequently, it needs to be clarified whether or not this extra quantity will depend on the analyte concentrations. By thoroughly examining the Koutecký-Levich plots for the different concentrations of VO²⁺ we found a linear relation between the ordinate intercepts and the inverse analyte concentration, which is depicted in Figure 4. Consequently, we propose that the maximum kinetic current has to be considered as a linear function of the concentration. Assuming that the slope of the line in Figure 4 can be expressed in terms of the maximum kinetic current, which we define by I_max = nFAck_max, we obtain a maximum heterogeneous rate constant of k_max = 0.026 cm/s. This hypothetic limit is the starting point for further considerations, where the idea of finite kinetics will be introduced into the Butler-Volmer equation.

FIGURE 4

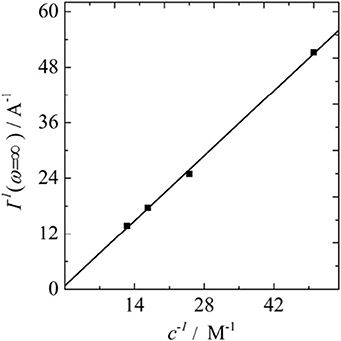
Figure 4. Plot of the ordinate intercepts of the Koutecký-Levich plots at different concentrations of vanadyl sulfate vs. the inverse concentrations.

3.3. Theoretical Discussion

First, we recall the classical Butler-Volmer equation as

$\begin{array}{ll}I=nFA{k}^0\left(c_{red,s}{e}^{\alpha \xi }-c_{ox,s}{e}^{-(1-\alpha )\xi }\right),& (11)\end{array}$

where ξ = nF(E − E⁰)/RT denotes the dimensionless electrode potential and c_red,s and c_ox,s denote the surface concentrations of the electrochemically active species. Other variables have their usual meaning. An introduction of a maximum achievable rate constant k_max yields

$\begin{array}{ll}I=nFA{k}^0\left(c_{red,s}\frac{k_{max}{e}^{\alpha \xi }}{k_{max}+k^0{e}^{\alpha \xi }}-c_{ox,s}\frac{k_{max}{e}^{-(1-\alpha )\xi }}{k_{max}+k^0{e}^{-(1-\alpha )\xi }}\right).& (12)\end{array}$

It is readily seen that Equation (12) reduces to Equation (11) when k_max becomes very large which corresponds to the case of no kinetic limitations. In contrast, if k_max is comparably small, the effect of kinetic limitations can be expected to be more prominent. Equation (12) is the starting point for all further considerations.

3.3.1. Rotating Electrode Polarography With Finite Kinetics

Introducing the above definition of the maximum kinetic current as

$\begin{array}{ll}{I}_{max}=nFA{c}_b{k}_{max},& (13)\end{array}$

where the index b represents the bulk concentration, as well as the exchange current as

$\begin{array}{ll}{I}^{eq}=nFA{k}^0{c}_{red,b}{e}^{\alpha a}=nFA{c}_{ox,b}{k}^0{e}^{-(1-\alpha )a},& (14)\end{array}$

where a = nF(E^eq − E⁰)/RT is the dimension-less equilibrium potential, we get

$\begin{array}{ll}I=I^{eq}\left(\frac{c_{red,s}}{c_{red,b}}\frac{I_{max,an}{e}^{\alpha (a-\xi )}}{I_{max,an}+I^{eq}{e}^{\alpha (a-\xi )}}-\frac{c_{ox,s}}{c_{ox,b}}\frac{I_{max,ca}{e}^{-(1-\alpha )(a-\xi )}}{I_{max,ca}+I^{eq}{e}^{-(1-\alpha )(a-\xi )}}\right).& (15)\end{array}$

For a rotating electrode we substitute the steady state formalism c_red,s/c_red,b = 1 − I/I_L,an and c_ox,s/c_ox,b = 1 − I/I_L,ca with I_l,an and I_l,c being the anodic and cathodic limiting currents expressed by the Levich equation. Since the backward reaction can be neglected at absolute overpotentials larger than 118/n mV, Equation (15) can be simplified for an exemplary anodic reaction to

$\begin{array}{ll}I=I^{eq}\left(\left(1-\frac{I}{I_{L,an}}\right)\frac{I_{max,an}{e}^{\alpha (a-\xi )}}{I_{max,an}+I^{eq}{e}^{\alpha (a-\xi )}}\right)& (16)\end{array}$

This expression can be rearranged to give the following desired three-term Koutecký-Levich equation

$\begin{array}{ll}\frac{1}{I}=\frac{1}{I_{kin}}+\frac{1}{I_{L,an}}+\frac{1}{I_{max}}.& (17)\end{array}$

The first two terms in Equation (17) form the classical Koutecký-Levich equation, whereas the third term 1/I_max contains the maximum rate constant and is therefore responsible for the non-zero ordinate intercept in Koutecký-Levich plots. As k_max tends to infinity, the third term vanishes, and Equation (17) reduces to the classical expression. Unifying the term of the hydrodynamic limiting current with the maximum kinetic current, the latter two terms in Equation (17) provide the measured limiting current I_lim,me as

$\begin{array}{ll}{I}_{lim,me}=\frac{I_{lim,an}{I}_{max,an}}{I_{lim,an}+I_{max,an}}.& (18)\end{array}$

Consequently, the unlimited kinetic current can be obtained from measured data as

$\begin{array}{ll}ln(I_{kin})=ln\left(\frac{I_{lim,me}I}{I_{lim,me}-I}\right)=ln(I^{eq})+\frac{\alpha nF(E-E^{eq})}{RT},& (19)\end{array}$

which is in principle just a rearranged version of Equation (18) as well as an alternative form of the conventional “mass transfer correction” described by Equation (9). This underlines that even if the heterogeneous kinetics are finite, the value of α and I^eq (and thus k⁰) can still be determined by using Tafels law if the current gets normalized properly to its limiting value.

3.3.2. Stationary Electrode Polarography With Finite Kinetics

If the model of finite kinetic rate constants is valid for a rotating electrode, it has to apply also to stationary measurements. In analogy to the limiting currents of an RDE experiment it can be assumed that the finite electrode kinetics will reduce the peak height in a S-LSV curve, which would in turn explain the misleading results of α obtained from the classical Randles-Ševčík analysis. To support this assumption, the theory of stationary electrode polarography, accounting for finite heterogeneous kinetics, will be re-derived in this paragraph. Starting again with Equation (12) and replacing the surface activities by their known expressions of the convoluted current for semi-infinite planar diffusion as

$\begin{array}{ll}{c}_{red,s}=c_{red,b}-\frac{1}{nFA\sqrt{\pi D}}{\displaystyle {\int }_0^t}\frac{I(\tau )}{\sqrt{t-\tau }}d\tau & (20)\end{array}$

$\begin{array}{ll}{c}_{ox,s}=c_{ox,b}+\frac{1}{nFA\sqrt{\pi D}}{\displaystyle {\int }_0^t}\frac{I(\tau )}{\sqrt{t-\tau }}d\tau & (21)\end{array}$

we obtain

$\begin{array}{r}\frac{I(t)}{nFA{k}^0{k}_{max}}=\frac{c_{red,b}{e}^{\alpha \xi (t)}}{k_{max}+k^0{e}^{\alpha \xi (t)}}-\frac{c_{ox,b}{e}^{-(1-\alpha )\xi (t)}}{k_{max}+k^0{e}^{-(1-\alpha )\xi (t)}}\\ -\frac{1}{nFA\sqrt{\pi D}}\left[\frac{e^{\alpha \xi (t)}}{k_{max}+k^0{e}^{\alpha \xi (t)}}+\frac{e^{-(1-\alpha )\xi (t)}}{k_{max}+k^0{e}^{-(1-\alpha )\xi (t)}}\right]\\ {\displaystyle {\int }_0^t}\frac{I(\tau )}{\sqrt{t-\tau }}d\tau .& (22)\end{array}$

Defining a new constant $k_{fin}=k^0/k_{max}$ and taking the definition of the dimensionless rate constant and the dimensionless current as

$\begin{array}{ll}\Lambda =\frac{k^0\sqrt{RT}}{\sqrt{nF\nu D}}& (23)\end{array}$

$\begin{array}{ll}\chi (\xi )=\frac{I(\xi )}{nFA{c}_{red,b}\sqrt{\frac{nF\nu D}{RT}}}& (24)\end{array}$

we obtain the following integral equation (Equation 25).

$\begin{array}{ll}\begin{array}{c}\frac{\chi (\xi )}{\Lambda }\frac{1+k_{fin}(e^{\alpha \xi }+e^{-(1-\alpha )\xi })+k_{fin}^2{e}^{\xi (2\alpha -1)}}{e^{\alpha \xi }+e^{-(1-\alpha )\xi }+2k_{fin}{e}^{\xi (2\alpha -1)}}=\\ \frac{(1-e^{a-\xi })+k_{fin}(1+e^a)e^{-(1-\alpha )\xi }}{1+e^{-\xi }+2k_{fin}{e}^{-(1-\alpha )\xi }}-\frac{1}{\sqrt{\pi }}{\displaystyle {\int }_0^{\xi }}\frac{\chi (\xi )}{\sqrt{\xi -\zeta }}d\zeta \end{array}& (25)\end{array}$

The desired dimension-less current function χ(ξ) can be evaluated accurately as Riemann-Stieltjes integral after eliminating the singularity in the denominator similar to Nicholson and Shain (1964). In case of no kinetic limitations it is obvious that k_max → ∞ and thus k_fin → 0. Therefore, Equation (25) condenses to the expression (Equation 26) of (Matsuda and Ayabe, 1954):

$\begin{array}{ll}\frac{\chi (\xi )}{\Lambda }\frac{1}{e^{\alpha \xi }+e^{-(1-\alpha )\xi }}=\frac{(1-e^{a-\xi })}{1+e^{-\xi }}-\frac{1}{\sqrt{\pi }}{\displaystyle {\int }_0^{\xi }}\frac{\chi (\xi )}{\sqrt{\xi -\zeta }}d\zeta .& (26)\end{array}$

3.3.3. Simulation of Data

In this section, Equation (25) is used for simulating stationary LSV responses that are subsequently evaluated using the irreversible Randles-Ševčík relation as well as Equations (7) and (8) in order to reproduce the experimentally observed error. For the simulation we took α = 0.38 and k⁰ = 1.35 · 10^-5 cm/s as extracted from the Tafel plots of Figure 3A and k_max = 0.026 cm/s as extracted from Figure 4 as well as the estimated value of D = 2.26 · 10^-6cm²/s. Simulations were performed using our in-house developed software Polarographica (Tichter and Schneider, 2019). The calculated voltammogramms as well as the corresponding Randles-Ševčík plot, conducted peak-shape analysis, and plotted the dimensionless peak potential vs. the scan rate, as shown in Figure 5.

FIGURE 5

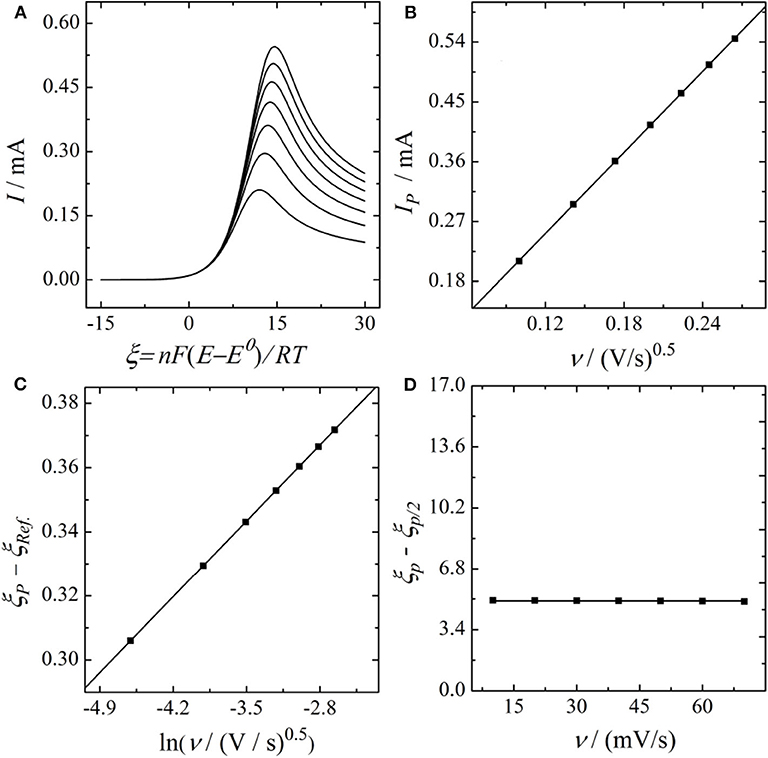
Figure 5. (A) S-LSV curves, (B) Randles-Ševčík Plot, (C) Matsuda-Ayabe analysis, and (D) peak shape analysis of an electrochemical reaction (the oxidation of VO²⁺ with finite kinetics simulated for the set of parameters obtained previously via Tafel analysis and Kouteck-Levich analysis).

Analyzing the simulated dataset of Figure 5 gives α = 0.343 for the Randles-Ševčík analysis, α = 0.371 for the peak shape analysis and α = 0.378 for the plot of the peak potential vs. the logarithm of the scan rate. This confirms our expectation, that significant deviations from the original α value are obtained as soon as finite kinetics are present. Furthermore, it shows that the largest error in α is obtained by the classical Randles-Ševčík analysis which captures the experimentally observed trend. Consequently, we conclude that, in stationary potential sweep experiments, the finite heterogeneous kinetics predominantly affect the current magnitude. Nevertheless, it has to be noted that also the accuracy of the shape analysis and the plot of the peak potential vs. the scan rate are affected by the kinetic limitations, even if these deviations are minor. Based on these findings we finally conclude that S-LSV measurements are not well-suited for estimating the electrode kinetics in a straightforward way, even if planar electrodes are involved. In contrast, since Tafel analysis of RDE data is independent of the finite electrode kinetics, we refer it as a more reliable way for investigating electrode kinetics.

3.3.4. Practical Relevance of Finite Kinetics

In the previous sub-paragraphs, the experimental verification and theoretical treatment of finite heterogeneous electrode kinetics were introduced. However, so far, we have not yet discussed the practical relevance and the possible origin of such a limitation. When regarding an electrode reaction like the electrochemical oxidation of VO²⁺, the classical analysis usually accounts for Butler-Volmer electron transfer kinetics coupled to mass transfer only. Consequently, no intermediate reaction steps are considered. Such additional reaction steps might be, however, responsible for the finiteness of the electrode reaction kinetics. In this context one might think of (a) an adsorption/desorption of the electrochemically active vanadium species preceding or following the electron transfer or (b) of rearrangements in the solvate shell of the vanadium ions which have to occur before an electrochemical reaction can proceed. However, since we do not have any experimental evidence for either scenario (a) or (b), we do no attempt to speculate about possible reaction mechanisms at this stage. In contrast, we want to underline that analyzing the kinetic limit of an electrochemical reaction with the strategy outlined in this paper can offer valuable insights in the intrinsic activity of novel catalyst materials, since an overpotential independent performance indicator is obtained. In this manner, our strategy might also lead to a better understanding of intermediate reaction steps. Therefore, it can be extraordinarily important for the experimentalists community when screening alternative catalyst materials for possible applications in a VRFB.

4. Summary and Conclusions

The kinetics of the VO²⁺/VO₂²⁺ redox couple was investigated at planar glassy carbon electrodes via rotating and stationary linear sweep voltammetry as well as stationary chronoamperometry. A combination of the Koutecký-Levich equation with the Cottrell equation allowed for a precise determination of the diffusion coefficient of the vanadyl cation, leading to D = 2.26 · 10^-6 cm²/s. A similar combination of the irreversible Randles-Ševčík equation with the Cottrell equation provided an electron transfer coefficient of α = 0.32. Contrary, calculating the electron transfer coefficient via Tafel analysis of RDE data provided α = 0.38. This deviation in the electron transfer coefficient as well as the experimentally observed non-zero ordinate intercepts in Koutecký-Levich plots, which cannot be explained by the classical model are explained simultaneously by introducing the concept of finite heterogeneous electron transfer kinetics into the Butler-Volmer equation. In this manner, a three term Koutecký-Levich type equation was derived, which allows for the determination of the maximum kinetic rate constant to k_max= 0.026 cm/s. By considering the modified Butler-Volmer equation as the boundary condition for stationary electrode polarography, the experimentally observed deviation in the electron transfer coefficients could be simulated as well. Based on the modified version of the Butler-Volmer equation it was shown that Tafel analysis of RDE data will not be affected by the finite heterogeneous kinetics. Therefore, we concluded that the Tafel analysis in a rotating disc electrode setup is the most accurate method to determine the kinetic parameters of a reaction.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

TT carried out the data acquisition and conception, developed the theory, and wrote the manuscript. JS carried out the conception and scientific discussion and wrote the manuscript. CR carried out the scientific supervision and wrote the manuscript. All authors contributed to the article and approved the submitted version.

Funding

We acknowledge support from the Open Access Publication Initiative of Freie Universität Berlin.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnote

1. ^Stationary refers to an electroanalytical experiment without any forced convection of the electrolyte.

References

Aoki, K. (1988). Theory of irreversible cyclic voltammetry at microcylinder electrodes. J. Electroanalyt. Chem. 247, 17–27. doi: 10.1016/0022-0728(88)80127-X

CrossRef Full Text | Google Scholar

Aoki, K., Honda, K., Tokuda, K., and Matsuda, H. (1985). Voltammetry at microcylinder electrodes Part I. Linear sweep voltammetry. J. Electroanalyt. Chem. 182, 267–279. doi: 10.1016/0368-1874(85)87005-2

CrossRef Full Text | Google Scholar

Aoki, K., Tokuda, K., and Matsuda, H. (1983). Theory of linear sweep voltammetry with finite diffusion space part I. J. Electroanalyt. Chem. 146, 417–424. doi: 10.1016/S0022-0728(83)29080601-9

CrossRef Full Text | Google Scholar

Aoki, K., Tokuda, K., and Matsuda, H. (1984). Theory of linear sweep voltammetry with finite diffusion space part II. J. Electroanalyt. Chem. 160, 33–45. doi: 10.1016/S0022-0728(84)80113-8

CrossRef Full Text | Google Scholar

Dai, L., Jiang, Y., Meng, W., Zhou, H., Wang, L., and Zhangxing, H. (2017). Improving the electrocatalytic performance of carbon nanotubes for VO²⁺/VO²⁺ redox reaction by KOH activation. Appl. Surface Sci. 401, 106–113. doi: 10.1016/j.apsusc.2017.01.002

CrossRef Full Text | Google Scholar

Flox, C., Rubio-Garcíia, J., Skoumal, M., Andreu, T., and Morante, J. R. (2013a). Thermo-chemical treatments based on NH₃/O₂ for improved graphite-based fiber electrodes in vanadium redox flow batteries. Carbon 60, 280–288. doi: 10.1016/j.carbon.2013.04.038

CrossRef Full Text | Google Scholar

Flox, C., Skoumal, M., Rubio-Garcia, J., Andreu, T., and Ramón Morante, J. (2013b). Strategies for enhancing electrochemical activity of carbon-based electrodes for all-vanadium redox flow batteries. Appl. Energy 109, 344–351. doi: 10.1016/j.apenergy.2013.02.001

CrossRef Full Text | Google Scholar

Friedl, J., and Stimming, U. (2017). Determining electron transfer kinetics at porous electrodes. Electrochim. Acta 227, 235–245. doi: 10.1016/j.electacta.2017.01.010

CrossRef Full Text | Google Scholar

Gao, C., Wang, N., Peng, S., Liu, S., Lei, Y., Liang, X., et al. (2013). Influence of Fenton's reagent treatment on electrochemical properties of graphite felt for all vanadium redox flow battery. Electrochim. Acta 88, 193–202. doi: 10.1016/j.electacta.2012.10.021

CrossRef Full Text | Google Scholar

Ghimire, P. C., Schweiss, R., Scherer, G. G., Wai, N., Lim, T. M., Bhattarai, A., et al. (2018). Titanium carbide-decorated graphite felt as high performance negative electrode in vanadium redox flow atteries. J. Mater. Chem. A 6, 6625–6632. doi: 10.1039/c8ta00464a

CrossRef Full Text | Google Scholar

González, Z., Flox, C., Blanco, C., Granda, M., Morante, J. R., Menéndez, R., et al. (2017). Outstanding electrochemical performance of a graphene-modified graphite felt for vanadium redox flow battery application. J. Power Sources 338, 155–162. doi: 10.1016/j.jpowsour.2016.10.069

CrossRef Full Text | Google Scholar

Hammer, E.-M., Berger, B., and Komsiyska, L. (2014). Improvement of the performance of graphite felt electrodes for vanadium-redox-flow-batteries by plasma treatment. Int. J. Renew. Energy Dev. 3, 7–12. doi: 10.14710/ijred.3.1.7-12

CrossRef Full Text | Google Scholar

Han, P., Wang, H., Liu, Z., Chen, X., Ma, W., Yao, J., et al. (2011). Graphene oxide nanoplatelets as excellent electrochemical active materials for VO²⁺/VO²⁺ and V²⁺/V³⁺ redox couples for a vanadium redox flow battery. Carbon 49, 693–700. doi: 10.1016/j.carbon.2010.10.022

CrossRef Full Text | Google Scholar

He, Z., Jiang, Y., Zhou, H., Cheng, G., Meng, W., Wang, L., et al. (2016). Graphite felt electrode modified by square wave potential pulse for vanadium redox flow battery. Int. J. Energy Res. 41, 439–447. doi: 10.1002/er.3626

CrossRef Full Text | Google Scholar

He, Z., Li, M., Li, Y., Zhu, J., Jian, Y., Meng, W., et al. (2018). Flexible electrospun carbon nanofiber embedded with TiO₂ as excellent negative electrode for vanadium redox flow battery. Electrochim. Acta 281, 601–610. doi: 10.1016/j.electacta.2018.06.011

CrossRef Full Text | Google Scholar

Jiang, Y., He, Z., Li, Y., Zhu, J., Zhou, H., Meng, W., et al. (2017). Carbon layer-exfoliated, wettability enhanced, SO₃H-functionalized carbon paper: a superior positive electrode for vanadium redox flow battery. Carbon 127, 297–304. doi: 10.1016/j.carbon.2017.11.006

CrossRef Full Text | Google Scholar

Jin, J., Fu, X., Liu, Q., Liu, Y., Wei, Z., Niu, K., et al. (2013). Identifying the active site in nitrogen-doped graphene for the VO²⁺/VO²⁺ redox reaction. ACS Nano 7, 4764–4773. doi: 10.1021/nn3046709

CrossRef Full Text | Google Scholar

Kim, K. J., Lee, H. S., Kim, J., Park, M.-S., Kim, J. H., Kim, Y.-J., et al. (2016). Superior electrocatalytic activity of a robust carbon-felt electrode with oxygen-rich phosphate groups for all-vanadium redox flow batteries. ChemSusChem 9, 1329–1338. doi: 10.1002/cssc.201600106

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, B., Gu, M., Nie, Z., Wei, X., Wang, C., Sprenkle, V., et al. (2014). Nanorod niobium oxide and powerful catalysts for an all vanadium redox flow battery. Nano Lett. 14, 158–165. doi: 10.1021/nl403674a

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W., Liu, J., and Yan, C. (2011). Multi-walled carbon nanotubes used as an electrode reaction catalyst for VO²⁺/VO²⁺ for a vanadium redox flow battery. Carbon 49, 3463–3470. doi: 10.1016/j.carbon.2011.04.045

CrossRef Full Text | Google Scholar

Li, W., Liu, J., and Yan, C. (2012). The electrochemical catalytic activity of single-walled carbon nanotubes towards VO²⁺/VO²⁺ and V²⁺/V³⁺ redox pairs for an all vanadium redox flow battery. Electrochim. Acta 79, 102–108. doi: 10.1016/j.electacta.2012.06.109

CrossRef Full Text | Google Scholar

Li, W., Liu, J., and Yan, C. (2013). Reduced graphene oxide with tunable C/O ratio and its activity towards vanadium redox pairs for an all vanadium redox flow battery. Carbon 55, 313–320. doi: 10.1016/j.carbon.2012.12.069

CrossRef Full Text | Google Scholar

Liu, T., Li, X., Nie, H., Xu, C., and Zhang, H. (2015). Investigation on the effect of catalyst on the electrochemical performance of carbon felt and graphite felt for vanadium flow batteries. J. Power Sources 286, 73–81. doi: 10.1016/j.jpowsour.2015.03.148

CrossRef Full Text | Google Scholar

Matsuda, H., and Ayabe, Y. (1954). Zur Theorie der Randles-Ševčík'schen Kathodenstrahl-Polarographie. Z. Elektrochem. 59, 494–503. doi: 10.1002/bbpc.19550590605

CrossRef Full Text | Google Scholar

Menshykau, D., and Compton, R. G. (2008). The influence of electrode porosity on diffusional cyclic voltammetry. Electroanalysis 22, 2387–2394. doi: 10.1002/elan.200804334

CrossRef Full Text | Google Scholar

Nicholson, R. S. (1965). Theory and application of cyclic voltammetry for measurement of electrode reaction kinetics. Anal. Chem. 37, 1351–1355. doi: 10.1021/ac60230a016

CrossRef Full Text | Google Scholar

Nicholson, R. S., and Shain, I. (1964). Theory of stationary electrode polarography single scan and cyclic methods applied to reversible, irreversible, and kinetic systems. Anal. Chem 36, 706–723. doi: 10.1021/ac60210a007

CrossRef Full Text | Google Scholar

Oriji, G., Katayama, Y., and Miura, T. (2004). Investigation on V(IV)/V(V) species in a vanadium redox flow battery. Electrochim. Acta 49, 3091–3095. doi: 10.1016/j.electacta.2004.02.020

CrossRef Full Text | Google Scholar

Park, J. J., Park, J. H., Park, O. O., and Yang, J. H. (2016). Highly porous graphenated graphite felt electrodes with catalytic defects for high performance vanadium redox flow batteries produced via FNiO/Ni redox reactions. Carbon 110, 17–26. doi: 10.1016/j.carbon.2016.08.094

CrossRef Full Text | Google Scholar

Park, S., and Kim, H. (2015). Fabrication of nitrogen-doped graphite felts as positive electrodes using polypyrrole as a coating agent in vanadium redox flow batteries. J. Mater. Chem. A 3, 12276–12283. doi: 10.1039/C5TA02674A

CrossRef Full Text | Google Scholar

Peinetti, A., Gilardoni, R., Mizrahi, M., Requejo, F., Gonzalez, G., and Battaglini, F. (2016). Numerical simulation of the diffusion processes in nanoelectrode arrays using an axial neighbor symmetry approximation. Analyt. Chem. 88, 5752–5759. doi: 10.1021/acs.analchem.6b00039

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryu, J., Park, M., and Cho, J. (2016). Catalytic effects of B/N-co-doped porous carbon incorporated with Ketjenblack nanoparticles for all-vanadium redox flow batteries. J. Electrochem. Soc. 163, 5144–5149. doi: 10.1149/2.0191601jes

CrossRef Full Text | Google Scholar

Smith, R. E., Davies, T. J., Baynes, N. d. B., and Nichols, R. J. (2015). The electrochemical characterization of graphite felts. J. Electroanalyt. Chem. 747, 29–38. doi: 10.1016/j.jelechem.2015.03.029

CrossRef Full Text | Google Scholar

Suárez, D. J., González, Z., Blanco, C., Granda, M., Menéndez, R., and Santamaría, R. (2014). Graphite felt modified with bismuth nanoparticles as negative electrode in a vanadium redox flow battery. ChemSusChem 7, 914–918. doi: 10.1002/cssc.201301045

CrossRef Full Text | Google Scholar

Tichter, T., Andrae, D., Mayer, J., Schneider, J., Gebhard, M., and Roth, C. (2019a). Theory of cyclic voltammetry in random arrays of cylindrical microelectrodes applied to carbon felt electrodes for vanadium redox flow batteries. Phys. Chem. Chem. Phys. 21, 9061–9068. doi: 10.1039/C9CP00548J

PubMed Abstract | CrossRef Full Text | Google Scholar

Tichter, T., and Schneider, J. (2019). Polarographica program. Available online at: https://github.com/Polarographica/Polarographica_program.

Tichter, T., Schneider, J., Andrae, D., Gebhard, M., and Roth, C. (2019b). Universal algorithm for simulating and evaluating cyclic voltammetry at macroporous electrodes by considering random arrays of microelectrodes. Chem. Phys. Chem. 21, 428–441. doi: 10.1002/cphc.201901113

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiang, Y., and Daoud, W. A. (2019). Investigation of an advanced catalytic effect of cobalt oxide modification on graphite felt as the positive electrode of the vanadium redox flow battery. J. Power Sources 416, 175–183. doi: 10.1016/j.jpowsour.2019.01.079

CrossRef Full Text | Google Scholar

Yang, D.-S., Han, J. H., Jeon, J. W., Lee, J. Y., Kim, D.-G., Seo, D. H., et al. (2019). Multimodal porous and nitrogen-functionalized electrode based on graphite felt modified with carbonized porous polymer skin layer for all-vanadium redox flow battery. Mater. Today Energy 11, 159–165. doi: 10.1016/j.mtener.2018.11.003

CrossRef Full Text | Google Scholar

Zhang, Z., Xi, J., Zhou, H., and Qiu, X. (2016). KOH etched graphite felt with improved wettability and activity for vanadium flow batteries. Electrochim. Acta 218, 15–23. doi: 10.1016/j.electacta.2016.09.099

CrossRef Full Text | Google Scholar

Zhong, S., and Skyllas-Kazacos, M. (1992). Electrochemical behaviour of vanadium(V)/vanadium(IV) redox couple at graphite electrodes. J. Power Sources 39, 1–9. doi: 10.1016/0378-7753(92)85001-Q

CrossRef Full Text | Google Scholar

Zhou, H., Shen, Y., Xi, J., Qiu, X., and Chen, L. (2016). ZrO₂-nanoparticle-modified graphite felt: bifunctional effects on vanadium flow batteries. Appl. Mater. Interfaces 8, 15369–15378. doi: 10.1021/acsami.6b03761

PubMed Abstract | CrossRef Full Text | Google Scholar