- 1College of Nuclear Science and Technology, Harbin Engineering University, Harbin, China
- 2China Nuclear Power Engineering Co., Ltd., Beijing, China
During the refueling of PWR, the spent fuel assemblies are transferred from the reactor building to the fuel building through an underwater tube. The heat transfer characteristics of the spent fuel assembly in the top-corner area of the carrier with poor heat transfer conditions is important for the safety design. Experiments were carried out and single phase natural convection and pool boiling heat transfer coefficients of the three fuel rods in the top-corner area of the carrier under different heat flux was measured and obtained. The new correlations were presented. The results can provide a reference for evaluating the thermal safety state and the maximum surface temperature of the fuel assembly during the transportation process in future engineering applications.
Introduction
During a refueling of the light water reactor, the spent fuel assemblies are transferred from the reactor building to the fuel building through an underwater tube, as shown in Figure 1A. When the fuel assembly is transferred horizontally through the transfer tube, it is carried and protected by the perforated carrier and the transport trolley (Guo and Wang, 2013), as shown in Figure 1B. It is important for the design of a fuel transfer device to consider the hypothetical accidents such as the mechanical failure and loss of power supply. In this situation, the spent fuel assembly may be trapped in the transfer tube. Therefore, to avoid the overheating of the assembly, it is necessary to study the heat transfer of the fuel assembly in the transfer tube to find out that whether the decay heat of the fuel assembly can be removed only rely on natural convection cooling.
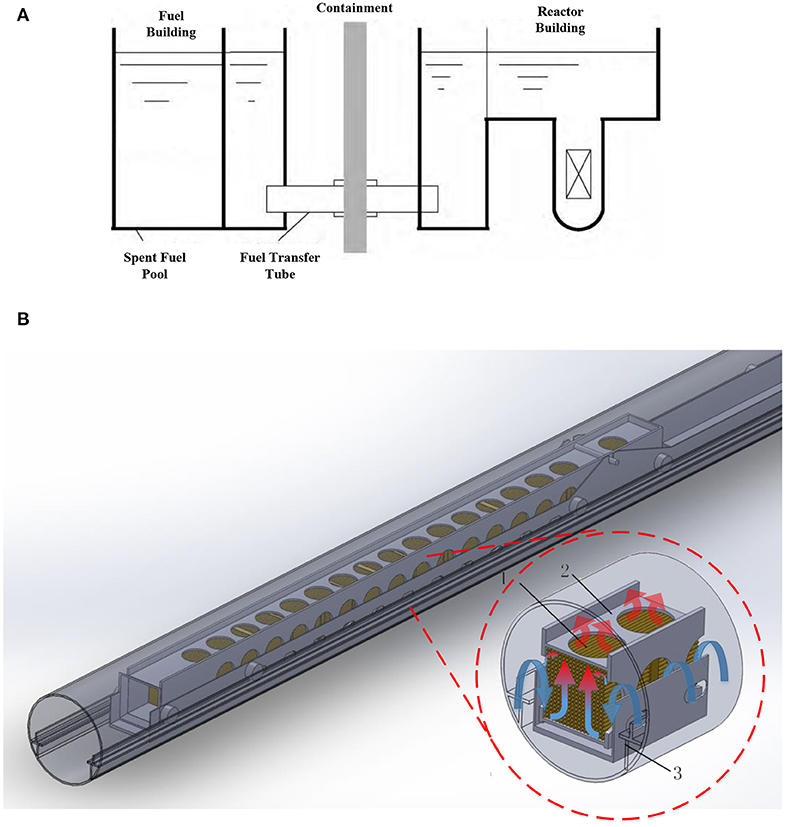
Figure 1. Schematic of fuel transfer system. (A) Schematic of fuel transfer system. (B) Schematic of carrier and transport trolley in the transfer tube. The symbol “1” refers to fuel assembly; the symbol “2” refers to carrier; the symbol “3” refers to transport trolley.
The driving force of natural circulation in the transfer tube comes from the density difference of hot and cold fluids. The cold water from the pool flows from the lower part of the tube to the fuel assembly. The water flows into the fuel assembly through the circular holes on both sides of the carrier. The cooling water is heated in the fuel assembly and then flows out of the assembly through the top holes of the carrier due to the buoyancy. The water flows back to the pool through the upper part of the tube.
In the previous analysis, the flow field in the transfer tube can be decomposed into two directions: longitudinal flow along the transfer tube and crosswise flow in the cross section of the transfer tube, respectively (Xi-dao et al., 2018). The flow of cooling water in the cross section of the fuel assembly in the transfer tube is shown in Figure 1B. The natural convection in the cross section is more complicated compared with the longitudinal flow along the transfer tube. It is a key factor affecting the cladding temperature of the fuel assembly.
The fuel assembly usually employs an arrangement of 17 × 17. The core of the cooling problem of the fuel assembly in the transfer channel is the natural convection heat transfer of the horizontal rod bundle. However, the fuel assembly is located in the carrier in the transfer tube, which is a semi-closed rectangular cavity. This would result to a weakened heat exchange. Therefore, the natural convection heat transfer of the fuel assembly in the carrier is different from the natural convection in an infinite space or in enclosure.
When the temperature of cooling water is low, the flow in the tube bundles is single-phase natural convection. The disturbance and the pre-heating effects of the lower tube will enhance and weaken the heat transfer ability of the upper tube bundles, respectively. The natural convective heat transfer characteristics of the tube bundles are very different from a single rod. There are some researches focused on the heat transfer of the tube bundle and the single tube under different conditions, respectively.
Studies of the steady state free convection heat transfer from horizontal isothermal cylinders with low Rayleigh numbers were presented, such as Sadeghipour and Asheghi (1994) and Tokanai et al. (1997). The correlations were presented to calculate the Nusselt numbers in terms of Rayleigh numbers in these studies, which are in the condition of infinite space. The pitch-to-diameter ratio has a significant influence on the heat transfer behavior.
There are some results of the natural convection of the tube bundles in enclosure too. Keyhani and Dalton (1996) studied the natural convection heat transfer in enclosed horizontal 3 × 3, 5 × 5, and 7 × 7 rods with a pitch-to-diameter ratio of 1.35. Each array was positioned in an isothermal square enclosure with a width-to-diameter ratio of 20.6. The experimental results show that the heat transfer behavior is related to the relative size of the closed boundary and the position of the tube bundles. A two-dimensional solution for natural convection in an enclosure with 2 × 2 tube bundles was obtained by Park et al. (2015). The numerical results show the similar conclusions with Keyhani that locations of the cylinders affect the heat transfer in the enclosure.
Ashjaee et al. (2008) studied the steady two-dimensional free convection heat transfer from a horizontal, isothermal cylinder located underneath an adiabatic ceiling using a Mach–Zehnder interferometer. When the Rayleigh number is 14,500 to 40,000, and the ratio of the height of the rod top and the plate to the diameter (L/D) of the rod ranges from 0.5 to 1.5, the local Nusselt number at the rod top is the minimum value of the entire rod surface. Sebastian (Sebastian and Shine, 2015) developed a two-dimensional model for natural convection heat transfer of a single rod with a horizontal confinement at the top. The calculation results are in good agreement with the experimental results. The results show that the local Nusselt number at the top of the rod is the minimum value of the entire rod surface within a certain L/D range. However, the boundary conditions studied by Ashjaee and Sebastian are oversimplified compared to the boundary conditions of the fuel assembly in the carrier. The difference in heat transfer characteristics between single rods and rod bundles is also very big, and it is difficult to directly use their results to evaluate safety of fuel assembly.
On the other side, when the temperature reaches the saturation temperature, the single-phase convection in the fuel assembly will turn into the pool boiling. There are many results present to study the different factors affecting boiling, such as wall materials, surface characteristics, and physical properties of working fluids. The Rohsenow pool boiling model is widely used for heat transfer calculation of the flat plate and the single tube. However, the model error of Rohsenow is as much as ±50% in some conditions due to the complexity of the boiling (Pioro et al., 2004a,b). Therefore, different specialized experiments are developed to get better estimates for different conditions.
The pool boiling of the horizontal bundle is more complicated than the condition of a single tube. The heat transfer of the upper parts of the bundles can be enhanced or weaken under different conditions. Kang studied the 2 × 1 tube bundle to reveal the buddle effect (Kang, 2015, 2016). Zhang studied the multiple tube bundles to reveal the nucleate pool boiling (Zhang et al., 2018). These studies have similar results that the heat transfer of the upper part is enhanced when the bubbles generated from the lower parts of the bundles scour the upper parts and thin the liquid film as well as the bubbles gathered and fallen. Under the condition of high heat flux, experimental results show that the upper tube will be coated by the bubbles generated in the lower part of the tube bundle, which can weaken the heat transfer of the upper tube (Swain and Das, 2018).
The pool boiling of the fuel bundle in the transfer tube is different with the bundle in the reboiler or the steam generator. The carrier influences the inflow and outflow of the fluid. Some of the fuel elements on the top-corner of the fuel assembly are in a semi-closed state, and bubbles are likely to accumulate at this position and affect heat transfer.
The heat transfer of the fuel assembly in the transfer tube under natural convection is different with the regular horizontal tube bundle, including the single-phase condition and the two-phase condition. The natural convection heat transfer of fuel assembly in the transfer tube is a key factor to effect the temperature of the spent fuel and the cladding integrity. However, the heat transfer of the fuel assembly in the carrier of the fuel transfer tube is not specially studied yet. This paper present an experiment to study the natural convection heat transfer on the cross-section which is affected by the carrier. New correlations are also presented both for single-phase and the two-phase conditions.
Experimental Setup
The experiment of full-scale ratio is not realistic due to the expensiveness and long-period. Therefore, a simplified test facility is developed based on the similar rules and the theoretical analysis (Xi-dao et al., 2018).
A set of electrical heating rods is used to simulate the fuel assembly. The heat flux of the heating rod is uniform. Considering the heating uniformity of the real fuel element, 1.65 or 2.62 multiply the power density in the test with the mean heat flux of the fuel element conservatively.
The test facility is shown in Figure 2A. The symbol A in this figure refers to an electric heating rod with a length of 750mm, which is used to simulate the fuel assembly near the central symmetry plane. The symbol B refers to the carrier. The symbol C refers to the transfer trolley. The symbol D refers to the cooler, which is used to simulate the heat exchange of at the inlet of the transfer tube. A mesh resistance element was added between the heating rod and the cooler to simulate the pressure loss caused by the transshipment tube and the transfer device out of the experimental section. The main geometric parameters of the test facility is listed in Table 1.
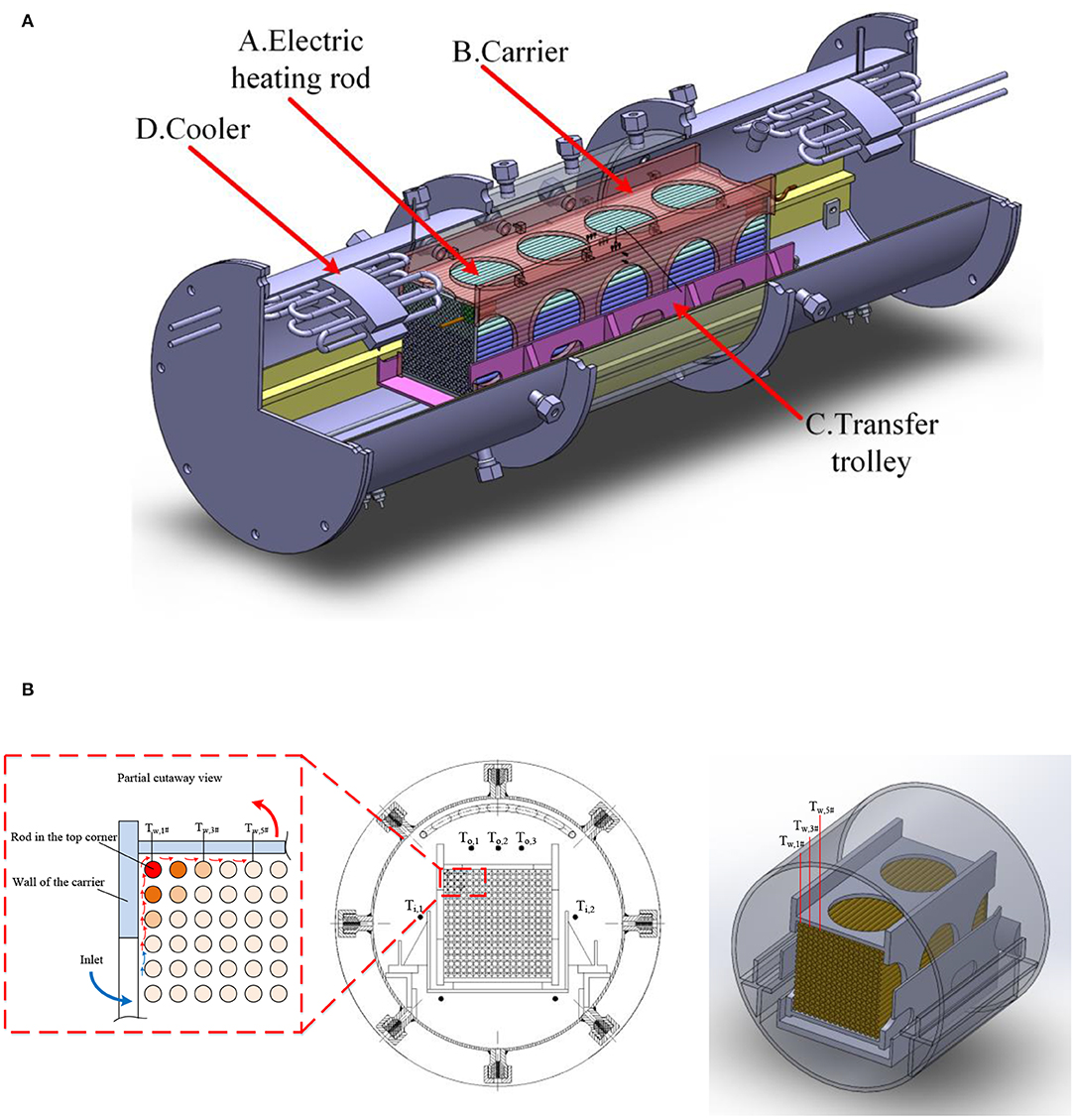
Figure 2. 3D model and tube wall temperature measurement of the test facility. (A) 3D model of the Test facility. (B) Schematic diagram of wall temperature measurement in upper corner of the fuel carrier.
According to the previous research results (Guo and Wang, 2013), the maximum temperature of the cladding of the fuel assembly is located on the top of the fuel rod at the top corner of the carrier. In order to reduce the interference to the flow field of the top-corner area of the carrier, thermocouples are only fixed on the top of 1#, 3#, and 5# heating rod at intervals, as shown in Figure 2B.
Experimental Parameters for Single-Phase Natural Convection
The temperature of inlet of the fuel assembly is controlled as 60, 70, and 80°C, respectively. The heat flux of the heating rod is controlled as 3900, 4300, 6200, and 6800 W/m2. T-Type thermocouples and pressure gauges with high precision were employed. The instruments were calibrated. The overall error of the temperature measurement is about ±1.5°C, and the over error of the pressure measurement is about ±0.14%. The data acquisition system was Solartron IMP 35951C.
In the test, the power of the heating rod is set to a fixed value, and then the temperatures of the both sides of the fuel assembly simulated are adjusted by controlling the cooler. The data are acquired when the system and all the measurement are stable.
Parameters for Pool Boiling Test
During the pool boiling experiment, the pressure is controlled at 0.1MPa. The inlet subcooled temperatures of the assembly are controlled under 0.5°C. The range of heat flux on the surface of the heating rod is 2,400–20,000 W/m2. The heating rod is made of polished 316L stainless steel with a surface roughness Ra≈0.8 μm. Thermocouples were fixed on top of 1#, 3#, and 5# heating rods as before.
In order to exclude the influence of the unstable vaporized core on the wall surface of the heating pipe on the test results, the surface aging of the heating pipe was carried out before the formal test. The tests were performed from low heat flux to high heat flux. The power of the heating rod and the temperature of each thermocouple were recorded when the condition is stable.
Experimental Results and Discussion
Single Phase Experimental Results
In the data processing, the local Nusselt number Nutop on the top corner of the fuel rod in the natural convection is calculated from the following:
The temperature used to define the physical property parameters is defined as tm = (tw + tin)/2, where the tw is the top wall temperature of the rod in the top-corner of the carrier, and the tin is the temperature of cooling water at the inlet of the carrier. λf is the thermal conductivity of water evaluated at the temperature tm. The characteristic length D employs the hydraulic diameter of the fuel rod.
A series of experiments were conducted on the test facility to get the local heat transfer data on the top of the rod at the top-corner of the carrier. Figure 3A shows a comparison of the heat transfer coefficient for the different rod location. For the same Rayleigh Number (Ra number), the Nutop at the top of the 1 # rod is the smallest, and the Nu number at the top of the 5 # rod is the largest.
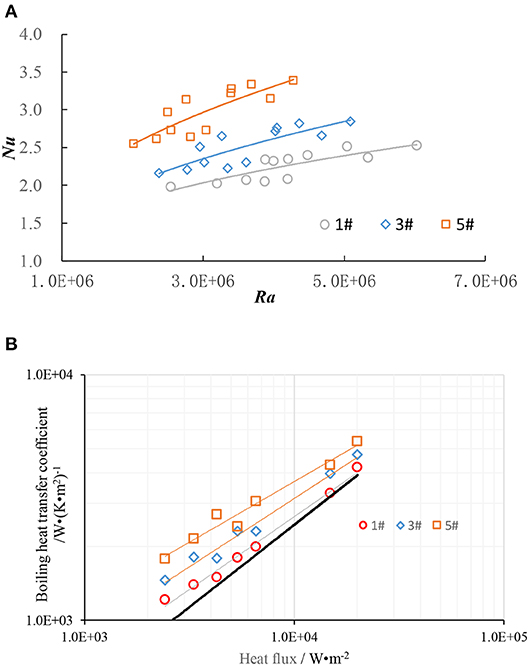
Figure 3. Heat transfer characteristics of fuel assemblies in transfer tube. (A) The Nusselt number of single-phase natural convection. (B) The pool boiling heat transfer coefficient.
From the experiment data, it is found that the heat transfer coefficient is relative with heating power and distance from the top-corner of the carrier. When the heat flux of fuel rod and water temperature at the inlet of the carrier are the same, the closer the rod to the top-corner of the carrier, the smaller the natural convective heat transfer coefficient.
Pooling Boiling Experimental Results
In the test, the system pressure is atmospheric pressure. The characteristic temperature is the saturation temperature of the water at the test pressure. The characteristic length of the pool boiling is defined as: l* = σ/[g(ρl − ρg)]. where σ is the surface tension, with the unit of N · m−1, ρg is the density in gaseous phase, ρl is the density in liquid phase. The unit of the density is kg · m−3.
Figure 3B shows the pool boiling heat transfer coefficients at the top of 1 #, 3 #, and 5 # rods. The solid black line in the figure is the single-rod pool boiling heat transfer coefficient calculated by the Rohsenow correlation (Rohsenow, 1952), which is used to compare with the fuel assembly test results. Although the bubble movement is hindered by the carrier, it can be seen that the boiling heat transfer coefficient at the top of the fuel assembly 1 #, 3 #, and 5 # heating rods is still higher than that of a single rod.
With the increase of heat flux density, the rod bundle effect of boiling heat transfer coefficient of 1 #, 3 #, and 5 # rods gradually weakened. Under the condition of heat flux about 2 × 104W/m2, the boiling heat transfer coefficient of 1 # rod closest to the top corner of the carrier is almost equal to that of a single rod.
New Correlations for Local Heat Transfer Coefficients
The published correlations were developed using the data for plates, wires, and outside surfaces of tubes (Pioro et al., 2004b; Shah, 2017). Since the correlations do not contain the effects of the semi-closed rectangular cavity and the lower tube heat flux, the calculated heat transfer coefficients does not agree with the present experimental data. Therefore, it is not reasonable to use the correlation equations available on the literature to predict the present experimental data.
Single-Phase Heat Transfer Correlations
The Nusselt Number of the top corner of the fuel element in the natural convection can be expressed with a function of Rayleigh Number Ra. Through the regression analysis of the experimental data with the help of a computer program (which uses the least square method as a regression technique) three correlations were determined as follows:
A comparison between the measured Nusselt and the calculated values by Equation (2) to (4) is shown in Figure 4A. The newly developed correlation predicts the present experimental data within ±10%.
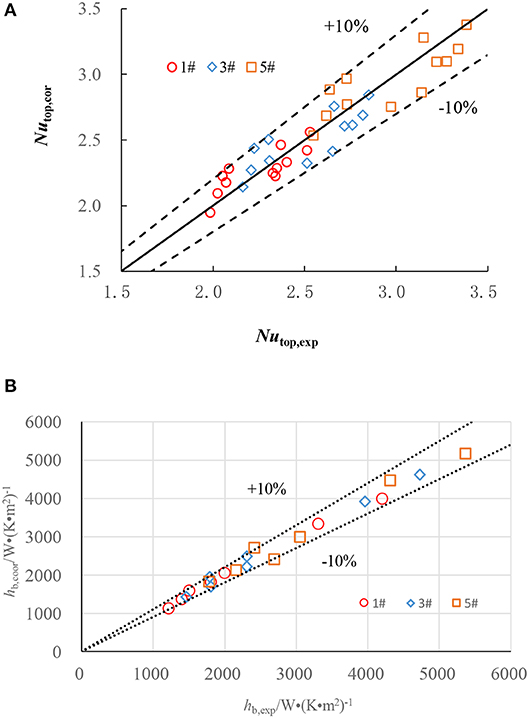
Figure 4. Comparison of calculated data with experimental data. (A) Comparison of calculated heat transfer coefficients with single phase experimental data. (B) Comparison of calculated heat transfer coefficients with pool boiling experimental data.
Pooling Boiling Heat Transfer Correlations
A Pioro -type (Pioro et al., 2004b) correlation is introduced here to predict local pool boiling heat transfer coefficients.
where htop is the boiling heat transfer coefficient of the top corner of the fuel elements with unit of W · m−2 · K−1; q is the heat flux of the heating rod surface with the unit of W · m−2; k is liquid heat transfer coefficient with the unit of W · m−1 · K−1; hfg is the latent heat of vaporization with the unit of J · kg−1;Pr is the Prandtl Number;l* is the characteristic length. C, n and m are to be solved.
htop, q, Pr and the physical property parameters can be calculated based on the experiment data, and then the coefficient C, n and m can be solved by multiple regression. The coefficient C, n and mare solved, and the boiling heat transfer coefficient can be expressed by the equation of (6)–(8) for the position of 1#, 3#, and 5#, respectively:
Figure 4B plots the error range of the fitted equations of (6) to (8). As shown in the figure, the errors of the predicted quantities from these equations are <10%, which means that the precision of the fitting process of these equations was good.
Conclusions
An experimental heat transfer investigation for the horizontal rod-bundle in a semi-closed rectangular cavity submerged in the cooling water tube was conducted to find the characteristics of the fuel transfer device under natural circulation conditions. The major conclusions of the present study are as follows:
In the single-phase natural convection test and the pool-boiling test, the heat transfer coefficient of the 1# heating rod closest to the top corner of the carrier was the smallest.
Within the parameters of the pool-boiling test, the heating rod in the upper row of the heating rod is affected by the steam generated from the lower heating tube, and the boiling heat transfer coefficient is higher than that of the single tube pool boiling heat transfer coefficient. As the heating power increases, the boiling heat transfer coefficient of the 1 # heating rod is closer to that of a single rod.
Through the regression analysis of the experimental data, new empirical correlations suitable for single-phase and pool boiling heat transfer were developed, which can provide a reference for evaluating the thermal safety status and maximum surface temperature of fuel assembly during transfer.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
HX is graduate advisor of XM.
Funding
This work was supported by China Nuclear Power Engineering Co Ltd.
Conflict of Interest
XM was employed by the company China Nuclear Power Engineering Co., Ltd.
The authors declare that this study received funding from China Nuclear Power Engineering Co., Ltd. The funder had the following involvement with the study: Experimental study of thermo-hydraulic characteristics in the transfer channel of double pressure containment (No. KY514).
References
Ashjaee, M., Eshtiaghi, A.H, Yaghoubi, M., and Yousefi, T. (2008). Experimental investigation on free convection from a horizontal cylinder beneath an adiabatic ceiling. Exp. Therm. Fluid Sci. 32, 614–623. doi: 10.1016/j.expthermflusci.2007.07.004
Guo, Q., and Wang, H. (2013). “Numerical simulation on 3D flow in the fuel transfer canal and local flow field analysis,” in ASME Proceedings of the 21th International Conference on Nuclear Engineering (Chengdu: ASME).
Kang, M. G. (2015). Effects of elevation angle on pool boiling heat transfer of tandem tubes. Int. J. Heat Mass Transf. 85, 918–923. doi: 10.1016/j.ijheatmasstransfer.2015.02.041
Kang, M. G. (2016). Pool boiling heat transfer from an inclined tube bundle. Int. J. Heat Mass Transf. 101, 445–451. doi: 10.1016/j.ijheatmasstransfer.2016.05.099
Keyhani, M., and Dalton, T. (1996). Natural convection heat transfer in horizontal rod-bundle enclosures. J. Heat Transfer 118, 598–605. doi: 10.1115/1.2822674
Park, Y. G., Ha, M. Y., and Park, J. (2015). Natural convection in a square enclosure with four circular cylinders positioned at different rectangular locations. Int. J. Heat Mass Transf. 81, 490–511. doi: 10.1016/j.ijheatmasstransfer.2014.10.065
Pioro, I. L., Rohsenow, W., and Doerffer, S. S. (2004a). Nucleate pool-boiling heat transfer, I: Review of parametric effects of boiling surface. Int. J. Heat Mass Transf. 47, 5033–5044. doi: 10.1016/j.ijheatmasstransfer.2004.06.019
Pioro, I. l., Rohsenow, W., and Doerffer, S. S. (2004b). Nucleate pool-boiling heat transfer, II: Assessment of prediction methods. Int. J. Heat Mass Transf. 47, 5045–5057. doi: 10.1016/j.ijheatmasstransfer.2004.06.020
Rohsenow, W. M. (1952). A method of correlating heat transfer data for surface boiling of liquids. Transac. ASME. 74, 969–976.
Sadeghipour, M. S., and Asheghi, M. (1994). Free convection heat transfer from arrays of vertically separated horizontal cylinders at low Rayleigh numbers. Int. J. Heat Mass Transf. 37, 103–109. doi: 10.1016/0017-9310(94)90165-1
Sebastian, G., and Shine, S. R. (2015). Natural convection from horizontal heated cylinder with and without horizontal confinement. Int. J. Heat Mass Transf. 82, 325–334. doi: 10.1016/j.ijheatmasstransfer.2014.11.063
Shah, M. M. (2017). A correlation for heat transfer during boiling on bundles of horizontal plain and enhanced tubes. Int. J. Refrigerat. 78, 47–59. doi: 10.1016/j.ijrefrig.2017.03.010
Swain, A., and Das, M. K. (2018). Performance of porous coated 5 × 3 staggered horizontal tube bundle under flow boiling. Appl. Therm. Eng. 128, 444–452. doi: 10.1016/j.applthermaleng.2017.09.038
Tokanai, H., Kuriyama, M., Harada, E., and Konno, H. (1997). Natural convection heat transfer from vertical and inclined arrays of horizontal cylinders to air. J. Chem. Eng. Japan 30, 728–734. doi: 10.1252/jcej.30.728
Xi-dao, M., Yang, L., Hai-jun, J., and Qiang, G. (2018). “Design and distortion analysis of thermal-hydraulics test facility for the fuel transfer tube,” in ASME Proceedings of the 26th International Conference on Nuclear Engineering (London: ASME).
Zhang, K., Hou, Y. D., Tian, W. X., Zhang, Y. P., Su, G. H., and Qiu, S. Z. (2018). Experimental investigation on steam-water two-phase flow boiling heat transfer in a staggered horizontal rod bundle under cross-flow condition. Exp. Therm. Fluid Sci. 96, 192–204. doi: 10.1016/j.expthermflusci.2018.03.009
Keywords: fuel transfer tube, fuel assembly, natural convection, pool boiling heat transfer, horizontal bundle
Citation: Mao X and Xia H (2020) Natural Convection Heat Transfer of the Horizontal Rod-Bundle in a Semi-closed Rectangular Cavity. Front. Energy Res. 8:74. doi: 10.3389/fenrg.2020.00074
Received: 25 February 2020; Accepted: 14 April 2020;
Published: 05 May 2020.
Edited by:
Jun Wang, University of Wisconsin-Madison, United StatesReviewed by:
Mingjun Wang, Xi'an Jiaotong University, ChinaClaudio Tenreiro, University of Talca, Chile
Copyright © 2020 Mao and Xia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xi-dao Mao, bWFveGlkYW8mI3gwMDA0MDsxMjYuY29t
 Xi-dao Mao
Xi-dao Mao Hong Xia1
Hong Xia1