Numerical Study on Laminar-Turbulent Transition Flow in Rectangular Channels of a Nuclear Reactor

Laminar-turbulent transition flow can be observed in thermal engineering applications, but the flow resistance and heat transfer characteristics are not fully understood. In this work, flow and heat transfer for the laminar-turbulent transition in a rectangular channel were predicted by a four-equation transition turbulent model. A set of correlations for the heat transfer coefficient in a rectangular channel were developed and implemented in the RELAP5/MOD3.1 code to make it capable of analyzing a plate-type fuel assembly with rectangular coolant channels. The improved RELAP5/MOD3.1 code was employed to analyze the SBLOCA along with the SBO scenario for an integrated pressurized reactor, illustrating the effects of model modification on the evolution of the accident.

1. Introduction

Rectangular channels have been widely used in thermal engineering applications, such as nuclear reactors with a plate-type fuel element (Tian et al., 2018) and high-efficiency heat exchangers (Xu et al., 2018), due to their characteristics of high heat transfer capacity and easy manufacture. The height of the channel is generally smaller than 3 mm, which can increase the heat transfer capacity. Furthermore, the wetted area concentrations for heat transfer in heat exchange facilities with rectangular channels are greater than for those with circular channels, resulting in a high volumetric energy density, which will benefit the miniaturization of heat-exchanger equipment.

Most heat exchangers operate in the regime of turbulent flow to reach a high heat transfer coefficient; however, there are still many heat exchangers that operate in the laminar-turbulent transition regime. In the startup period or accident scenario of a nuclear power plant, the coolant experiences flow regimes from laminar to turbulent flow with the transition regime between them (Shi et al., 2016). Besides, a power plant may experience the transition flow regime when updating it from the laminar regime (Silin et al., 2010a). For the internal flow in circular tubes, the transition regime refers to the state with a Reynolds number between 2,300 and 4,000. Experimental investigations have been carried out to evaluate the heat transfer coefficient and pressure drop for internal and external transition flow (Whan and Rothfus, 1959). Cioncolini and Santini (2006) obtained the heat transfer coefficient for transition flow in helically coiled pipes. Draad et al. (1998) compared the heat transfer characteristics of the laminar-turbulent transition for Newtonian and non-Newtonian fluids by experiment. Bertsche et al. (2016) investigated the heat transfer coefficients for liquid in a circular tube with Prandtl numbers varying from 7 to 41, finding that the Gnielinski correlation was of high accuracy for a Reynolds number between 1,000 and 4,000. Silin et al. (2010a,b) carried out experimental work to study the heat transfer characteristics in the laminar to turbulent transition regime for water flowing in a rectangular channel.

Based on these experimental and theoretical investigations, the heat transfer and flow resistance correlations can be developed. Gnielinski (1976) proposed a correlation with satisfactory accuracy in the Reynolds number range between 3,000 and 10⁶. Interpolation functions were proposed to satisfy the requirement of continuity in code development (Churchill, 1977). In the safety analysis codes for nuclear power plants, such as RELAP5 and TRACE, the heat transfer and resistance coefficients were obtained by data interpolation from the laminar and fully turbulent regimes. In general, the mechanisms for the laminar-turbulent transition were not well-resolved from the experimental work, and the current system analysis codes cannot predict the heat transfer and flow resistance characteristics for laminar-turbulent transition flow, although they are significant for the design and safety analysis of nuclear power plants.

Recently, with the development of CFD technology and of knowledge on the mechanisms of transition intermittency, which is defined as the ratio of the mean duration of turbulent flow to the total duration, Abraham et al. (2011) investigated the characteristics of laminar-turbulent transition flow by using CFD technology. In these works, mechanical models for the intermittency and the transition onset criteria were proposed to model the transition intermittency along with the traditional two-equation SST k-ω model.

In our previous paper, the concept for an integrated modular reactor was proposed for the application of a submarine, where there were strong demands for miniaturization and volumetric energy density (Jiang et al., 2018). To obtain a high rate of volumetric heat release, plate-type fuels were employed in the fuel assembly. During the design and safety analysis, it was found that the current system codes, RELAP5, just employed a linear interpolation to tackle the flow resistance and heat transfer coefficient in the transition regime, which is oversimplified. Furthermore, there is no model to consider the effects of a rectangular channel geometry on the flow and heat transfer characteristics in RELAP5, which would also introduce high deviations and uncertainties in the safety analysis procedure. In the current work, the transition SST model was employed to predict the heat transfer and flow resistance of transition flow in rectangular channels. An empirical formula was developed based on the CFD results and was used to improve the reactor system code, RELAP5. A typical scenario, an accident involving a small break loss of coolant with station blockout, for an integrated small modular reactor was simulated by using the improved RELAP5 code to show the improvement offered by and necessity of model improvement.

2. Method

2.1. Numerical Models for a Transition SST Model

The most commonly used turbulent model is the Reynolds Averaged Navier-Stokes (RANS) model, due to its high robustness and economy. However, it cannot predict the laminar-turbulent transition since it does not consider transition intermittency. Abraham et al. (2011) carried out a series of studies on the development and validation of a transition SST turbulent model for transition flow in a circular channel. In the transition SST model, the intermittency and the momentum-thickness Reynolds number were modeled by two additional partial differential equations along with the modified SST k-ω equations. In the current work, this model was employed to predict the flow and heat transfer characteristics in rectangular channels. Here we introduce this model briefly. The governing equations for the transition SST turbulent model are given as (ANSYS Inc., 2017):

$\begin{array}{ll}\frac{\partial }{\partial t}(\rho \gamma )+\frac{\partial }{\partial x_i}(\rho u_i\gamma )=\frac{\partial }{\partial x_j}((\mu +\frac{{\mu }_t}{{\sigma }_{\gamma }})\frac{\partial \gamma }{\partial x_j})+P_{\gamma }& (1)\end{array}$

$\begin{array}{ll}\frac{\partial }{\partial t}(\rho {\text{Re}}_{\theta t})+\frac{\partial }{\partial x_i}(\rho u_i{\text{Re}}_{\theta t})=\frac{\partial }{\partial x_j}({\sigma }_{\theta t}(\mu +{\mu }_t)\frac{\partial {\text{Re}}_{\theta t}}{\partial x_j})+P_{\theta t}& (2)\end{array}$

$\begin{array}{l}\frac{\partial }{\partial t}(\rho k)+\frac{\partial }{\partial x_i}(\rho k{u}_i)=\frac{\partial }{\partial x_j}({\Gamma }_k\frac{\partial k}{\partial x_j})+S_k+\gamma G_k\\ -min(max(\gamma ,0.1),1.0)Y_k& (3)\end{array}$

$\begin{array}{ll}\frac{\partial }{\partial t}(\rho \omega )+\frac{\partial }{\partial x_i}(\rho \omega u_i)=\frac{\partial }{\partial x_j}({\Gamma }_{\omega }\frac{\partial \omega }{\partial x_j})+S_{\omega }+G_{\omega }-Y_{\omega }& (4)\end{array}$

The definitions of the parameters used in these equations can be found in the nomenclature.

To ensure the numerical stability of the iteration process, the transition SST models were solved alternately along with the governing equations for mass, momentum, and energy by using the coupled strategy (ANSYS Inc., 2017). The grid thickness of the first layer in the wall direction is about 0.006 mm, and the grid expansion ratio in the wall-normal direction is carefully controlled to be <1.05. The grid size along the flow direction is kept at 0.06 mm. The selected mesh is carefully checked to make sure that the calculated result is mesh-independent. In this condition, the y⁺ values for the near-wall cells were <1.0 for all Reynolds numbers, which met the calculation standard. All these equations were solved using the commercial CFD code ANSYS Fluent 18.1.

2.2. Model Validation

The capacity of the transition SST model for predicting the flow and heat transfer characteristics in the transition intermittency regime was validated by the experimental data of Cioncolini and Santini (2006) and Silin et al. (2010a,b). In Cioncolini and Santini's experiment, the friction factors for fully developed flow from laminar to turbulent regimes in a circular tube with an inner diameter of 6.06 mm were measured. In Silin et al.'s work, the local heat transfer coefficients for transition flow in a rectangular channel of 60 mm width and 2.7 mm thickness were measured. The boundary condition is set as the experiment. The inlet is set as the velocity inlet with the corresponding Reynold number ranging from 1,564 to 3,010. The outlet is set as the pressure outlet. A uniform heat flux is given at the wall. A comparison between the results calculated by the transition SST model and the experimental data are shown in Figure 1.

FIGURE 1

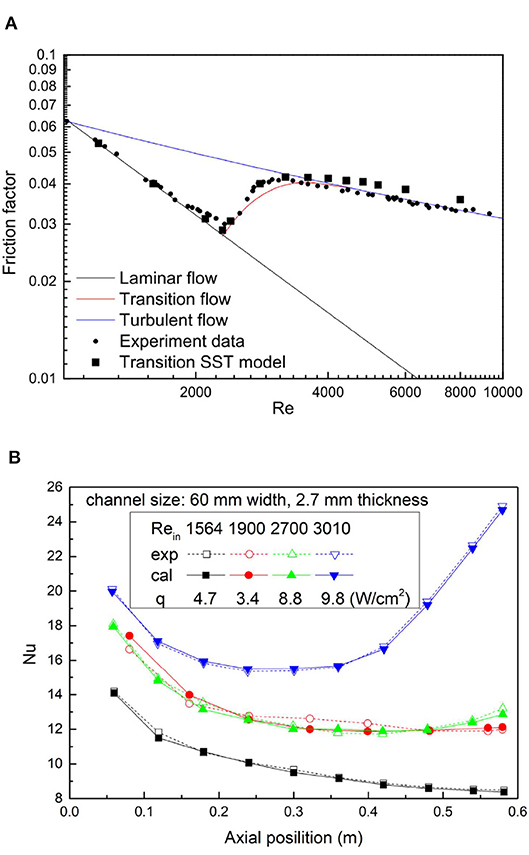
Figure 1. Model validation. (A) Validation of the friction factor. (B) Validation of the heat transfer coefficient.

2.3. Development of Correlations for Transition Flow in a Rectangular Channel

In RELAP5 code, three flow regimes are considered in the estimation of single-phase flow resistance and the heat transfer coefficient, including the laminar, laminar-turbulent transition, and turbulent flow regimes. The Darcy-Weisbach friction factor is used to compute the flow resistance in tubes (Colebrook, 1939).

$f=\{\begin{array}{l}\begin{array}{l}\frac{64}{\mathrm{Re}}\\ \begin{array}{l}{\left\{-2{\log }_{10}\left[\frac{ϵ}{3.7d_h}+\frac{2.51}{\text{Re}}\left(1.14-2{\log }_{10}\left(\frac{ϵ}{d_h}-\frac{21.25}{{\text{Re}}^{0.9}}\right)\right)\right]\right\}}^{-2}\hfill \end{array}\\ 0\le \text{Re}\le 2200\\ \text{Re}\ge 3000\end{array}\hfill \end{array}$

For the transition regime with Reynolds number between 2,200 and 3,000, an interpolation strategy is used, that is,

$\begin{array}{ll}f=\left(3.75-\frac{8250}{\text{Re}}\right)(f_{T,3000}-f_{L,2200})+f_{L,2200}& (6)\end{array}$

where f_{T, 3000} and f_{L, 2200} are the friction factor at Reynolds numbers of 3,000 and 2,200, calculated by turbulent and laminar models, respectively. As for the heat transfer coefficient, RELAP5 employs the Dittus-Boelter equation when Re >3,000 (Dittus and Boelter, 1985) and a constant laminar heat transfer coefficient at Re <2,100. In the transition regime with 2, 100 ≤ Re ≤ 3, 000, linear interpolation is employed to obtain the heat transfer coefficient.

The accuracy of the correlations used in RELAP5 for the friction factor and heat transfer coefficient should be estimated before being utilized to the conditions of a rectangular channel. The friction factor and Nusselt number obtained from CFD simulations are compared with the RELAP5 correlations, as shown in Figures 2A,B. Other than the RELAP5 correlations, the Gnielinski equation and the Blasius equation (Trinh, 2010) for the heat transfer coefficient and friction factor in the turbulent regime, respectively, are also employed as references. The deviations between the reference data from CFD and the data from the RELAP5 equations are significant, which means that the original empirical correlations for flow resistance and heat transfer in RELAP5 are not applicable for a rectangular channel under the transition condition. The set of Blasius equations (using the Blasius equation for Re ≥ 3,000, the laminar model for Re ≤ 2,200, and linear interpolation otherwise) can give good accuracy with a largest deviation of <8 %, which means that the set of Blasius equations are qualified to predict the friction factor in rectangular channels with acceptable accuracy. Dittus-Boelter and Gnielinski correlations predict similar results when the Nusselt number is larger than 30; however, they both fail in the transition regime. Thus, a new set of heat transfer correlations should be developed.

FIGURE 2

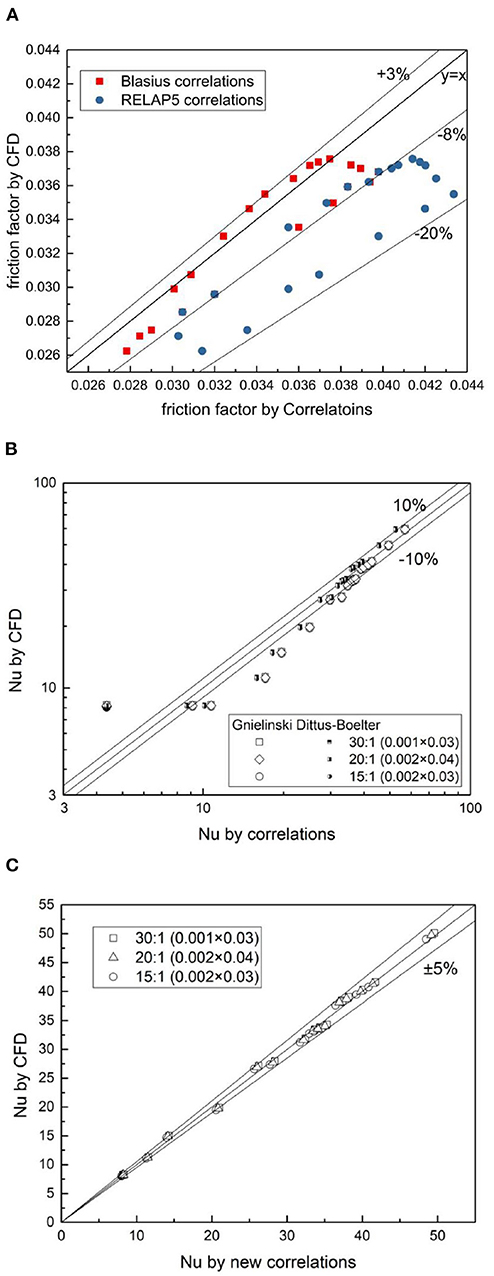
Figure 2. Assessments of friction factor and heat transfer correlations. (A) Assess the RELAPS5 and Blasius correlation for friction transfer. (B) Assess the RELAPS5 and Gnielinski correlation for heat transfer. (C) Assess the new developed correlation for heat transfer.

It can be obtained from the analytical solution for laminar flow heat transfer in the rectangular channel that the Nusselt number equals 4.32 for a rectangular channel with a unit aspect ratio and equals 8.23 for a channel with an infinite aspect ratio (infinite plate). Besides, the Nusselt number in the laminar regime is independent of the Reynolds number and Prandtl number; thus, from data fitting, the correlation for the laminar Nusselt number can be obtained, which is

$\begin{array}{ll}\text{Nu}=8.23{\left(1+10^3{\alpha }^{-2.97}\right)}^{-0.0933}& (7)\end{array}$

For the fully turbulent regime, the heat transfer correlation is

$\begin{array}{ll}\text{Nu}=0.007{\text{Re}}^{0.95}{\text{Pr}}^{0.4}{\left(1+10^3{\alpha }^{-2.97}\right)}^{-0.0933}& \left(8\right)\end{array}$

For the transition regime, it is

$\begin{array}{l}\text{Nu}=[-0.04255{\left(\frac{\text{Re}}{100}\right)}^3+3.433{\left(\frac{\text{Re}}{100}\right)}^2-90.47\left(\frac{\text{Re}}{100}\right)\\ +786.2]{\text{Pr}}^{0.4}{\left(1+10^3{\alpha }^{-2.97}\right)}^{-0.0933}& \left(9\right)\end{array}$

The demarcation point between the transition and laminar regimes is determined by the largest intersection point of Equations (7) and (9); while the discreteness point between the transition and turbulent regimes is determined by the smallest intersection point of Equations (8) and (9). The applicable range of the proposed correlations covers an aspect ratio from 15:1 to 30:1 and a channel height from 1 to 2 mm. The newly developed heat transfer correlations were also assessed against the CFD data and showed a maximum deviation of <5% (Figure 2C).

3. Results

3.1. Structure of the RELAP5/MOD3.1 Code and Model Modification

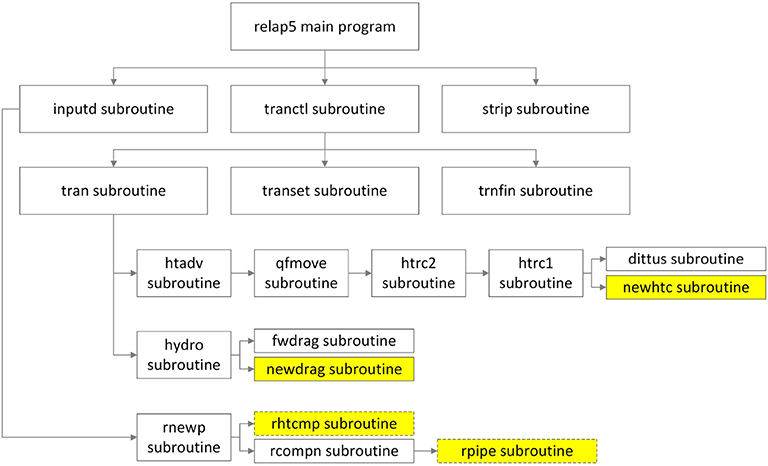
The RELAP5/MOD3.1 code is written in the FORTRAN language with more than 600 subroutines with a top-down structure, as illustrated in Figure 3. The main program, “relap5,” calls the “inputd” and “tranctl” subroutines to read the input cards and to perform the transient calculation, respectively. Among the subroutines called by the “tran” subroutine, the “dittus” subroutine is used to calculate the single-phase heat transfer coefficients for the regimes from laminar to turbulent. The “fwdrag” subroutine is called to compute the wall drag force. By default, the correlations for a circular tube are used in these subroutines. As is already known, these correlations for a circular tube are not applicable for the rectangular channel. However, these subroutines should not be replaced since they will still be used in other circular components, such as heat exchangers and pipes. Thus, two new subroutines for heat transfer and flow resistance in the rectangular channel are added to the RELAP5 code and are named “dittusrectangular” and “fwdragrectangular.”

FIGURE 3

Figure 3. Structure of the RELAP5/MOD3.1 code.

The rectangular channel is modeled by the pipe component in RELAP5 even though the cross-section is not circular. One more word is added to the pipe card to identify the shape of the pipe cross-section. Besides, a word describing the geometry information is also added to the boundary condition card for the heat structure to help to select the correlations for heat transfer; that is, the thermal boundary of the heat structure is circular or rectangular. The “inputd” subroutine is called by the main program to read the input cards of the problem. Among the subroutines called by “inputd,” the “rhtcmp” and “rpipe” subroutines are used to read the information for the heat structure and pipe components, respectively. Thus, these two subroutines were modified to make them applicable to the new cards of the heat structure and pipe with one additional word for geometry information. After the above modification to the source code and the input card, the RELAP5/MOD3.1 code can be used to analyze a reactor with rectangular channels.

3.2. Application of RELAP5/MOD3.1 Code to an SBLOCA With SBO Scenario for an Integrated Modular Reactor

IP200 is an integrated pressurized water reactor with its main facilities in the reactor pressure vessel (RPV) to minimize the length of connecting pipes and to enhance the inherent safety. Plate-type fuel assemblies are placed at the bottom of the RPV, and once-through steam generators are installed in the upper part of the RPV around the core, symmetrically. The rising section above the active zone and the downcomer below the steam generators are used as the hot leg and cold leg, respectively. A plenum is built by the steam at the top of the RPV, working as the pressurizer. Compared with other traditional reactors used on land, such as AP1000 and EPR1000, IP200 has the advantages of small size and high volumetric rate of heat release. The schematic diagram and main design parameters of IP200 can be found in Jiang et al. (2018). The passive safety system (PSS) is critical for the safety of IP200 since the volumetric heat release is significantly high, especially under accident conditions. However, in the safety analysis related to the PSS of IP200, RELAP5 code with correlations for a circular tube and rod bundle were employed in the simulations (Jiang et al., 2018). In this work, the improved RELAP5/MOD3.1 code was used to assess the PSS of IP200. The typical accident scenario, a small break loss of coolant accident (SBLOCA) along with Station Blockout (SBO), was applied to evaluate the performance of the PSS.

The RELAP5 nodalization model for the IP200 PSS can be found in our previous paper on the safety analysis of the IP200 reactor (Jiang et al., 2018). In the current work, the SBLOCA with SBO accident was analyzed with the improved RELAP5/MOD3.1 code to evaluate the effectiveness and performance of the PSS. In the first 1000.0 s, the reactor operates in the full-power steady state. At the 1000.0 s, the valve on the vent pipe of the pressurizer is opened by accident, and the station blockout occurs. Meanwhile, the reactor scrams, and both the coolant pumps and feedwater pumps shut down. During the accident, there are three different flow regimes in a rectangular channel in the core: the turbulent, transition, and laminar flow regimes. The core cooling and the residual heat removal fully depend on the PSS. The accident sequences of the SBLOCA plus SBO scenario were modeled by the original RELAP5/MOD3.1 code and by the improved code with new heat transfer and flow resistance models for rectangular channels. The results are compared in Figure 4. The comparison shows that the modifications on the heat transfer and flow resistance models make significant differences to the accident evolution after SBLOCA and SBO.

FIGURE 4

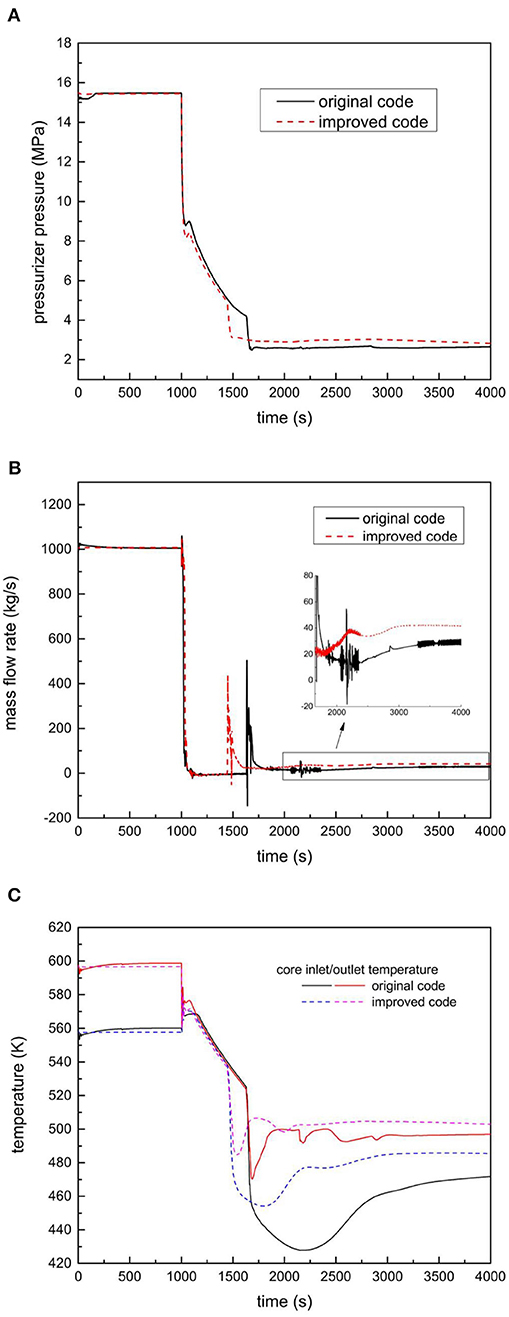
Figure 4. Comparisons between the original and improved RELAP5/MOD3.1 codes. (A) Pressure in pressurizer. (B) Mass flow rate in the core. (C) Coolant temperature at core inlet and outlet.

After the initiation of SBLOCA, the pressure in the RPV plunges sharply due to the leakage of vapor from the break. The rate of depressurization then decreases when the two-phase blowdown begins. Meanwhile, the pressure in the containment increases. The valves on the vent pipe and on the sump pipe open when the pressure difference between the RPV and the containment reaches 0.2 and 0.02 MPa, respectively. After that, the natural circulation for the fluid in the RPV and containment can be built. The pressure in the RPV decreases with the injection of cold water from the containment, while the coolant temperature at the inlet of the core plummets since the cold water injection will flow past the primary side of the steam generator to the inlet of the core. The discharged vapor and two-phase mixture from the RPV to the containment will be cooled by the ultimate heat exchanger, by which long-term cooling can be established.

It can be seen that there are significant differences between the results from the original RELAP5/MOD3.1 code and the improved code; these are caused by the changes in the models for flow resistance and heat transfer. In general, as can be observed from Figures 2A,B, the models in the original RELAP5 code over-estimated the friction factor for all flow regimes and over-estimated the heat transfer coefficient in the transition flow regime. The over-prediction of heat transfer would affect the temperature in the fuel but has negligible effects on the total energy released to the coolant, especially in the quasi-steady long-term cooling stage. However, the over-estimation of the friction factor would increase the flow resistance in a core with rectangular channels, which would reduce the coolant flow rate, especially under the natural circulation period. This conclusion can be obtained from Figure 4B; the mass flow rate in the core predicted by the improved code is larger than that by the original code, which leads to a decline in the temperature increase in the core, as shown in Figure 4C. From the above application of the improved RELAP5/MOD3.1 code, we find that the improved code can predict the accident evolution more reasonably. Quantitative assessment of this improved code is not presented in this paper since there are no experimental data for IP200 or other types of reactors with a plate-type fuel assembly available.

4. Discussion

In this work, the flow and heat transfer characteristics for the laminar-turbulent transition were predicted by a CFD methodology with a four-equation transition turbulent model. A set of heat transfer coefficient correlations were developed. The models for the friction factor and heat transfer coefficient in RELAP5/MOD3.1 code were modified to make it applicable for the safety analysis of a reactor with a plate-type fuel assembly. After the modification to the code, it was applied to analyze the SBLOCA with SBO scenario in an integrated pressurized reactor. The following conclusions can be drawn.

1. A combination of the Blasius equation and the laminar friction factor model can predict the flow resistance in rectangular channels with satisfactory accuracy.

2. A set of heat transfer correlations for coolant flow in a rectangular channel under all flow regimes was proposed and compiled into the RELAP5/MOD3.1 code to extend the applicability and accuracy of this code for safety analysis for a reactor with a plate-type fuel assembly.

3. The SBLOCA with SBO accident for an integrated pressurized reactor was analyzed by the improved RELAP5/MOD3.1 code to demonstrate the impacts of model modification on accident evolution.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

ZW and RZ carried out the CFD simulation. TY, ZL, and YH developed the correlations. JW and TC improved the RELAP5 code and wrote the manuscript.

Funding

The authors greatly appreciate support from the National Natural Science Foundation of China (No. 11705035), the Natural Science Foundation of Heilongjiang Province, China (No. LH2019A009), and the Open Fund Program of the State Key Laboratory of Nuclear Power Safety Monitoring Technology and Equipment (No. K-A2019.414).

Conflict of Interest

ZW, ZL, and YH were employed by company China Nuclear Power Engineering Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abraham, J. P., Sparrow, E. M., and Minkowycz, W. J. (2011). Internal-flow Nusselt numbers for the low-Reynolds-number end of the laminar-to-turbulent transition regime. Int. J. Heat Mass Transfer 54, 584–588. doi: 10.1016/j.ijheatmasstransfer.2010.09.012

CrossRef Full Text | Google Scholar

ANSYS Inc. (2017). ANSYS Fluent Theory Guide v18.1. ANSYS Inc.

Bertsche, D., Knipper, P., and Wetzel, T. (2016). Experimental investigation on heat transfer in laminar, transitional and turbulent circular pipe flow. Int. J. Heat Mass Transfer 95, 1008–1018. doi: 10.1016/j.ijheatmasstransfer.2016.01.009

CrossRef Full Text | Google Scholar

Churchill, S. W. (1977). Comprehensive correlating equations for heat, mass and momentum transfer in fully developed flow in smooth tubes. Indus. Eng. Chem. Fundament. 16, 109–116. doi: 10.1021/i160061a021

CrossRef Full Text | Google Scholar

Cioncolini, A., and Santini, L. (2006). An experimental investigation regarding the laminar to turbulent flow transition in helically coiled pipes. Exp. Thermal Fluid Sci. 30, 367–380. doi: 10.1016/j.expthermflusci.2005.08.005

CrossRef Full Text | Google Scholar

Colebrook, C. F. (1939). Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. J. Instit. Civil Eng. 11, 133–156. doi: 10.1680/ijoti.1939.13150

CrossRef Full Text | Google Scholar

Dittus, F. W., and Boelter, L. M. K. (1985). Heat transfer in automobile radiators of the tubular type. Int. Commun. Heat Mass Transfer 12, 3–22. doi: 10.1016/0735-1933(85)90003-X

CrossRef Full Text | Google Scholar

Draad, A. A., Kuiken, G. D. C., and Nieuwstadt, F. T. M. (1998). Laminar-turbulent transition in pipe flow for Newtonian and non-Newtonian fluids. J. Fluid Mech. 377, 267–312. doi: 10.1017/S0022112098003139

CrossRef Full Text | Google Scholar

Gnielinski, V. (1976). New equations for heat and mass transfer in turbulent pipe and channel flow. Int. Chem. Eng. 16, 359–368.

Google Scholar

Jiang, N., Peng, M., and Cong, T. (2018). Simulation analysis of an open natural circulation for the passive residual heat removal in IPWR. Ann. Nuclear Energ. 117, 223–233. doi: 10.1016/j.anucene.2018.03.037

CrossRef Full Text | Google Scholar

Shi, S., Hibiki, T., and Ishii, M. (2016). Startup instability in natural circulation driven nuclear reactors. Prog. Nuclear Energ. 90, 140–150. doi: 10.1016/j.pnucene.2016.03.016

CrossRef Full Text | Google Scholar

Silin, N., Masson, V., Osorio, D., and Converti, J. (2010a). Hydrodynamic transition delay in rectangular channels under high heat flux. Ann. Nuclear Energ. 37, 615–620. doi: 10.1016/j.anucene.2009.12.013

CrossRef Full Text | Google Scholar

Silin, N., Masson, V. P., and Garcia, J. C. (2010b). Convection in a rectangular channel with a flow of water in laminar-turbulent transition with high heat fluxes. Latin Am. Appl. Res. 40, 125–130.

Google Scholar

Tian, C., Wang, J., Cao, X., Yan, C., and Ala, A. A. (2018). Experimental study on mixed convection in an asymmetrically heated, inclined, narrow, rectangular channel. Int. J. Heat Mass Transfer 116, 1074–1084. doi: 10.1016/j.ijheatmasstransfer.2017.09.099

CrossRef Full Text | Google Scholar

Trinh, K. T. (2010). On the blasius correlation for friction factors. arXiv preprint arXiv:1007.2466.

Google Scholar

Whan, G. A., and Rothfus, R. R. (1959). Characteristics of transition flow between parallel plates. AIChE J. 5, 204–208. doi: 10.1002/aic.690050215

CrossRef Full Text | Google Scholar

Xu, Z., Han, Z., Wang, J., and Liu, Z. (2018). The characteristics of heat transfer and flow resistance in a rectangular channel with vortex generators. Int. J. Heat Mass Transfer 116, 61–72. doi: 10.1016/j.ijheatmasstransfer.2017.08.083

CrossRef Full Text | Google Scholar

Nomenclature

.