Theoretical Investigation on the Fully Developed Turbulent Heat Transfer Characteristics of Liquid Sodium

Liquid sodium has been used as the working medium for the high-temperature heat pipe and the generation IV sodium cooled fast reactor due to its extremely high conductivity. The heat transfer characteristics of sodium in a circular pipe is one of the most essential focuses in engineering applications. In this paper, a model to predict the heat transfer coeffcient of fully developed sodium flowing in tube was developed based on universal velocity, turbulent eddy diffusivity, and the linear law inside the thermal boundary layer. The Kays correlation for turbulent Prandtl number was used to predict the turbulent Prandtl in the bulk flow with y + larger than 60. This model was validated by experiment data of Hg, NaK, and sodium, showing superior accuracy than existing models. Besides, the dependence of the accuracy on the model parameters was also analyzed, demonstrating the universal applicability of the current model.

Introduction

Liquid metals, especially liquid sodium, have been widely used in high-temperature heat transfer process in industry and power applications, such as sodium cooled fast reactors in France, China, and Russia, and the high temperature heat pipe used in space facilities. To ensure the safety of the facilities, the heat transfer coefficient should be accurately estimated in the thermal design process of industrial applications. However, the heat transfer characteristics of liquid metal are quite different from traditional fluids. The molecular Prandtl numbers of traditional fluids vary from 1 to 10, while the Prandtl numbers of liquid metals are always <0.1, even 0.01. Furthermore, as for liquid sodium, the Prandtl number is in the range of 0.01–0.001 due to extremely large thermal conductivities. The difference in Prandtl number changes the heat transfer characteristics in the near wall and bulk regions. The thermal boundary layers of liquid metal are much thicker than the momentum boundary layer, resulting in the failure of correlations for heat transfer of traditional fluids in the applications of liquid metals. Besides, the discrepancy in the thermal and momentum boundary layers leads to the failure of Reynolds analogy. Thus, the traditional computational fluids dynamics treatment on the energy equation based on Reynolds analogy and the unit turbulent Prandtl number is not validated in liquid metals.

In the past few decades, researchers have devoted themselves to theoretical and experimental investigations. Lyon (1951) proposed the first empirical correlation for turbulent heat transfer of liquid sodium. Then Lubarsky and Kaufman (1955) corrected the Lyon correlation based on experiment data and published a new correlation for channels with specified geometry. Schleisiek (1970) carried out a series of experiments on liquid sodium heat transfer in a 9-mm inner diameter pipe and derived a formula for Nusselt number based on 24 sets of data. Shi et al. (1981) also gave correlations for liquid sodium, but these correlations have limited applicable range of Peclet number <3,000. Except for the correlations aiming at liquid sodium heat transfer, several correlations were also proposed based on data from other liquid metals, such as mercury (Hg) (Chang and Akins, 1972), sodium–potassium (NaK) eutectic (Sleicher et al., 1973), and lead–bismuth eutectic (LBE) (Ibragimov et al., 1961). In addition, Dwyer (1966) proposed a heat transfer correlation for the universal applications of liquid metal. However, these correlations predict the Nusselt number with large differences. Furthermore, the results show a noticeable divergence even for the same working fluid, especially for sodium and NaK eutectic, which means the investigation on the heat transfer characteristics of sodium has still not matured.

In this work, a theoretical model was proposed to predict the turbulent heat transfer coefficient of liquid sodium. This model employed the correlations for universal velocity and eddy diffusivity to predict the distributions of velocity and turbulence. The linear law was used to predict the non-dimensional temperature in the near wall linear sublayer inside the thermal boundary layer. Beyond this sublayer, the turbulent Prandtl number was predicted using the Kays correlation (Kays, 1994), which is only related to the local turbulent parameters. The governing equations for non-dimensional temperature and heat flux can be solved after being discretized on the radial direction. The model was validated by experiment data, showing superior accuracy compared with other available models. The uncertainty from the model parameters was also investigated based on the parametric analysis.

Method

Governing Equations for Heat Transfer

The governing equation for energy conservation in a fully developed pipe can be simplified into the following format:

$\begin{array}{ll}\rho c_p{u}_x\frac{\partial T}{\partial x}=\frac{1}{r}\frac{\partial }{\partial r}(rq)& (1)\end{array}$

Due to the wall heat flux, the temperature in the pipe cannot be described by a fully developed field with zero gradient in the flow direction since the temperature rises along the pipe. However, the temperature increases linearly with the flow direction in a pipe when the flow and thermal parameters are fully developed. Thus, the temperature T(x, r) in the pipe can be divided into two parts plus a fixed wall temperature at the inlet, that is,

$\begin{array}{ll}T(x,r)=T_{w,x=0}+\frac{\partial T}{\partial x}x-\theta (r)& (2)\end{array}$

where T_{w,x = 0} is the wall temperature at the channel inlet; θ(r) is the temperature along the radial direction, which is independent from the axial location, that is, fully developed just as the velocity field. $\frac{\partial T}{\partial x}x$ is the temperature increase in the pipe, which is linear with the flow distance or heated length, and can be calculated based on the energy balance, i.e.,

$\begin{array}{ll}\frac{\partial T}{\partial x}=\frac{2q_w}{r_w\rho c_p{u}_m}& (3)\end{array}$

After substituting Equations (2) and (3) into Equation 1, we can obtain:

$\begin{array}{ll}\frac{2q_w{u}_x}{r_w{u}_m}=\frac{1}{r}\frac{\partial }{\partial r}(rq)& (4)\end{array}$

Let $R=\frac{r}{r_w}$ and $q^{+}=\frac{q}{q_w}$. Then Equation 4 can be transformed into:

$\begin{array}{ll}\frac{1}{R}\frac{d}{dR}(R{q}^{+})=\frac{2u_x}{u_m}& (5)\end{array}$

According to Fourier's law on heat transfer, the radial heat flux at any radial location can be written as

$\begin{array}{ll}q=k_{eff}\frac{\partial T}{\partial r}=k_{eff}\frac{d\theta }{dr}& (6)\end{array}$

where

$\begin{array}{ll}{k}_{eff}=k_l+k_t=k_l+\rho c_p{\epsilon }_q& (7)\end{array}$

Given $\mathrm{\text{Pr}}=\frac{c_p\mu }{k_l}$ and $\mathrm{\text{P}}{\mathrm{\text{r}}}_t=\frac{{\epsilon }_m}{{\epsilon }_q}$, Equation 6 can be changed into:

$\begin{array}{ll}\frac{d\theta }{dR}=\frac{q{r}_w}{k_l(1+\frac{\text{Pr}}{\text{P}{\text{r}}_t}\frac{{\epsilon }_m}{\nu })}& (8)\end{array}$

Define the following non-dimensional parameters:

$\begin{array}{ll}\{\begin{array}{c}{u}^{+}=\frac{u_x}{u_{\tau }}\hfill \\ u_m^{+}=\frac{u_m}{u_{\tau }}\hfill \\ {\theta }^{+}=\frac{{\theta }_w-\theta }{{\theta }_{\tau }}=-\frac{\theta }{{\theta }_{\tau }}\hfill \\ r_w^{+}=\frac{r_w{u}_{\tau }}{\nu }\hfill \end{array}\hfill & (9)\end{array}$

where $u_{\tau }=\sqrt{{\tau }_w/\rho }$ and θ_τ = q_w/ρc_pu_τ.

Then, Equations (5) and (8) can be written as:

$\begin{array}{ll}\frac{1}{R}\frac{d}{dR}(R{q}^{+})=\frac{2u^{+}}{u_m^{+}}& (10)\end{array}$

$\begin{array}{ll}\frac{d{\theta }^{+}}{dR}=-\frac{q^{+}{r}_w^{+}\text{Pr}}{(1+\frac{\text{Pr}}{\text{P}{\text{r}}_t}\frac{{\epsilon }_m}{\nu })}& (11)\end{array}$

The boundary conditions for Equations (10) and (11) are listed as follows:

$\begin{array}{ll}{q}^{+}{|}_{R=1}=1& (12)\end{array}$

$\begin{array}{ll}{q}^{+}{|}_{R=0}=0& (13)\end{array}$

$\begin{array}{ll}{\theta }^{+}{|}_{R=1}=0& (14)\end{array}$

$\begin{array}{ll}\frac{d{\theta }^{+}}{dR}{|}_{R=0}=0& (15)\end{array}$

Until now, we obtained the governing equations and boundary conditions for the dimensionless temperature and heat flux along the radial direction. These equations can be solved numerically by the finite difference method with limited discrete grid along the radius of the pipe. The total length of the radius can be divided into n − 1 identical intervals with n points, including the points at the pipe center (i = 0) and on the wall (i = n). Thus, the interval is:

$\begin{array}{ll}\Delta R=1/(n-1)& (16)\end{array}$

and the radial location referred from the center of the tube is:

$\begin{array}{ll}{R}_i=(i-1)\Delta R,i=1-n& (17)\end{array}$

The discrete format for Equations (10) and (11) on the n grid in the radial direction of the pipe can be written as:

$\begin{array}{ll}{q}_i^{+}=\left(\frac{u_i^{+}}{u_m^{+}}{R}_i+\frac{u_{i-1}^{+}}{u_m^{+}}{R}_{i-1}\right)\frac{\Delta R}{R_i}+\frac{R_{i-1}}{R_i}{q}_{i-1}^{+}& (18)\end{array}$

and

$\begin{array}{ll}{\theta }_{i-1}^{+}={\theta }_i^{+}+\frac{\Delta R\text{Pr}{r}_w^{+}}{2}\left[\frac{q_i^{+}}{1+\frac{\text{Pr}}{\text{P}{\text{r}}_{t,i}}{\left(\frac{{\epsilon }_m}{\nu }\right)}_i}+\frac{q_{i-1}^{+}}{1+\frac{\text{Pr}}{\text{P}{\text{r}}_{t,i-1}}{\left(\frac{{\epsilon }_m}{\nu }\right)}_{i-1}}\right]& (19)\end{array}$

where the mean universal velocity $u_m^{+}$ is calculated by:

$\begin{array}{l}{u}_m^{+}=\frac{{\displaystyle {\int }_0^{R_w}}2\pi u^{+}RdR}{\pi R_w^2}\\ ={\displaystyle {\int }_0^1}2u^{+}RdR\\ =\Delta R{\displaystyle \sum _{i=1}^n}(R_{i-1}{u}_{i-1}^{+}+R_i{u}_i^{+})& (20)\end{array}$

Theoretically, Equations (18) and (19) can be solved iteratively under the following conditions:

$\begin{array}{ll}{q}_1^{+}=0& (21)\end{array}$

$\begin{array}{ll}{\theta }_n^{+}=0& (22)\end{array}$

Auxiliary Models and Strategy to Solve the Governing Equations

As mentioned earlier, the numerical solutions for governing equations (Equations 10, 11) for energy balance in the radial direction could be obtained by solving Equations (18) and (19) with the boundary conditions of Equations (21) and (22). However, the radial profiles for the velocity, turbulent eddy diffusivity, and turbulent Prandtl number are still unknown and should be given to solve the above governing equations.

Universal Velocity and Eddy Diffusivity

As for the fully developed turbulent flow in the circular tube, various non-dimensional universal velocity profiles have been proposed in the last century, such as Prandtl's linear law for the sublayer (Johnson, 2016) and Taylor's logarithmic law for the logarithmic regime beyond the buffer layer (Taylor, 1916). Most of these correlations were only validated for the boundary layer, except the universal velocity correlation proposed by Reichardt (1957), that is,

$\begin{array}{l}{u}^{+}=\frac{1}{\kappa }ln\left[\left(1+0.4y^{+}\right)\frac{1.5\left(1+R\right)}{1+2R^2}\right]+\\ \left(5.5-\frac{ln\kappa }{\kappa }\right)\left[1-exp\left(-\frac{y^{+}}{11}\right)-\frac{y^{+}}{11}exp\left(-\frac{y^{+}}{3}\right)\right]& (23)\end{array}$

where the non-dimensional radial R locates in the range 0 ≤ R ≤ 1. The non-dimensional distance to the wall is calculated by

$\begin{array}{ll}{y}^{+}=y{u}_{\tau }/\nu =(1-R)r_w^{+}& (24)\end{array}$

Reichardt (1957) also proposed an empirical correlation for the eddy diffusivity for the momentum transfer caused by the stochastic movement of fluid from the wall to the center of the duct, which can be expressed in terms of the fraction of eddy diffusivity and kinematic viscosity, that is,

$\begin{array}{ll}\frac{{\epsilon }_{\tau }}{\nu }=\{\begin{array}{ll}\kappa \left[y^{+}-11tanh\left(\frac{y^{+}}{11}\right)\right]& \text{for}\${\text{y}}^{\text{+}}\le \text{50}\$\\ \frac{\kappa }{3}{y}^{+}\left(1+R\right)\left(0.5+R^2\right)& \text{for}\$\text{50}<{\text{y}}^{\text{+}}\le {\text{r}}_{\text{w}}^{\text{+}}\$\end{array}& (25)\end{array}$

where κ = 0.4.

Turbulent Prandtl Number

As for the liquid metal with the molecular Prandtl number much <1, the velocity boundary layer is much thinner than the thermal boundary layer, which means the Reynolds analogy with the turbulent Prandtl number near to unit is not validated under these conditions. Researchers proposed several correlations for the turbulent Prandtl number (Pr_t) with a different molecular Prandtl number for the prediction of heat transfer characteristics. These correlations are only related to the Reynolds number, the molecular Prandtl number, the Peclet number, or the maximum eddy diffusivity in the tube, which means the calculated turbulent Prandtl number is kept as a constant along the radial direction. However, the essential laminar law for the non-dimensional temperature (θ⁺ = Pr · y⁺) in the laminar regime inside the thermal boundary layer cannot be satisfied if Equation 19 is directly solved with a constant turbulent Prandtl number. This discrepancy is caused by the improper assumption of a uniform turbulent Prandtl number in the radial direction. As a matter of fact, the turbulent Prandtl number is highly associated to y⁺, especially in the near wall region with y⁺ less than about 100 (Kawamura et al., 1999; Duponcheel et al., 2014). Thus, the turbulent Prandtl number relevant to the local y⁺ should be specified for an exact prediction of the temperature profile in the radial direction. However, as can be noted from the limited DNS and LES simulations (Kawamura et al., 1998, 1999; Tiselj and Cizelj, 2012; Duponcheel et al., 2014), the turbulent Prandtl number in the near wall region is highly related to the local turbulent Peclet number non-linearly (Kawamura et al., 1999; Tiselj and Cizelj, 2012; Duponcheel et al., 2014), and there is no universal correlation for the localized turbulent Prandtl number in the near wall region so far (Grötzbach, 2013; Roelofs et al., 2015).

As for the bulk flow region, Bricteux et al. (2012) assessed the DNS and LES data and pointed out that the turbulent Prandtl number should be about 2 for the bulk regime with y⁺ larger than 200. Duponcheel et al. (2014) assessed the available models with results from large eddy simulation (LES) and found that the Kays correlation (Kays, 1994) is capable of predicting the turbulent Prandtl number in the bulk region, that is,

$\begin{array}{ll}\text{P}{\text{r}}_t=0.85+\frac{0.7}{\text{P}{\text{e}}_t}& (26)\end{array}$

where Pe_t is the turbulent Peclet number defined as

$\begin{array}{l}\text{P}{\text{e}}_t=\frac{{\nu }_t}{\nu }\text{Pr}\end{array}$

In Duponcheel et al. (2014), it is claimed that the Kays correlation (Kays, 1994) is validated for y+ < 100; nevertheless, it can be noted from the comparison between the Kays correlation and the LES data that the Kays correlation agrees well with the LES data for y+ < 65, which fortunately gives the opportunity to model the heat transfer of the low Prandtl number liquid metal by using the approach introduced in the next section.

Treatment on the Near Wall Heat Transfer Without Turbulent Prandtl Number in the Thermal Boundary Layer

As noted in the investigations on the universal velocity profile vs. the non-dimensional wall distance y⁺, linear, and logarithmic laws are universal for all kinds of flow conditions in the turbulent flow regime, independent from the Reynolds number of the flow. The non-dimensional temperature, θ⁺, which is defined in Equation 9, also satisfies the linear law and the logarithmic law in the boundary layer. Thus, we can use the conception of the wall function to calculate θ⁺ in the thermal boundary layer. The near wall profile of θ⁺ could be solved by the wall function based on y⁺, instead of the governing equation in the thermal boundary layer if the wall function for temperature is known priorly. However, due to the failure of the Reynolds analogy in the temperature distribution and the velocity distribution, the universal wall function for temperature in liquid metal with a low molecular Prandtl number is unknown. Besides, the thickness of the thermal boundary layer is much larger than that of the momentum boundary layer. The node in the velocity logarithmic regime may still be in the linear regime for energy transfer. Thus, the approach to set the first node in both the thermal and momentum logarithmic regimes, which is commonly used when dealing with water flow and heat transfer, is not validated.

Fortunately, from the DNS and LES studies on the heat transfer of liquid metal with a low Prandtl number, it can be observed that the thickness of the linear regime in the thermal boundary layer increases with decreasing the molecular Prandtl number (Kader, 1981; Kawamura lab, 2008; Duponcheel et al., 2014). Besides, the thermal linear regime is beyond y⁺ of 60 when the molecular Prandtl number is <0.01, as noted by Bricteux et al. (2012). As for the liquid sodium, the molecular Prandtl number is <0.01 for most of the conditions. That means, the thickness of the thermal linear regime should be larger than about 60. The non-dimensional temperature θ⁺ could be predicted by the linear law in the thermal linear regime. Thus, the radial non-dimensional temperature distribution θ⁺ could be calculated by:

$\begin{array}{ll}{\theta }^{+}=\text{Pr}·y^{+}& (27)\end{array}$

if y⁺ is <$y_c^{+}$, and by Equation 19 if y⁺ is larger than $y_c^{+}$, where $y_c^{+}$is the critical non-dimensional wall distance set to be 60 in this work.

Results and Discussion

Analysis on the Non-dimensional Parameters Along the Radial Direction

After solving the governing equations for non-dimensional heat flux and temperature (Equations 18, 19, 30), the non-dimensional heat transfer coefficient can be obtained by:

$\begin{array}{ll}\text{Nu}=\frac{hd}{k_l}=\frac{2\text{Pr}·r_w^{+}}{{\theta }_m^{+}}& (28)\end{array}$

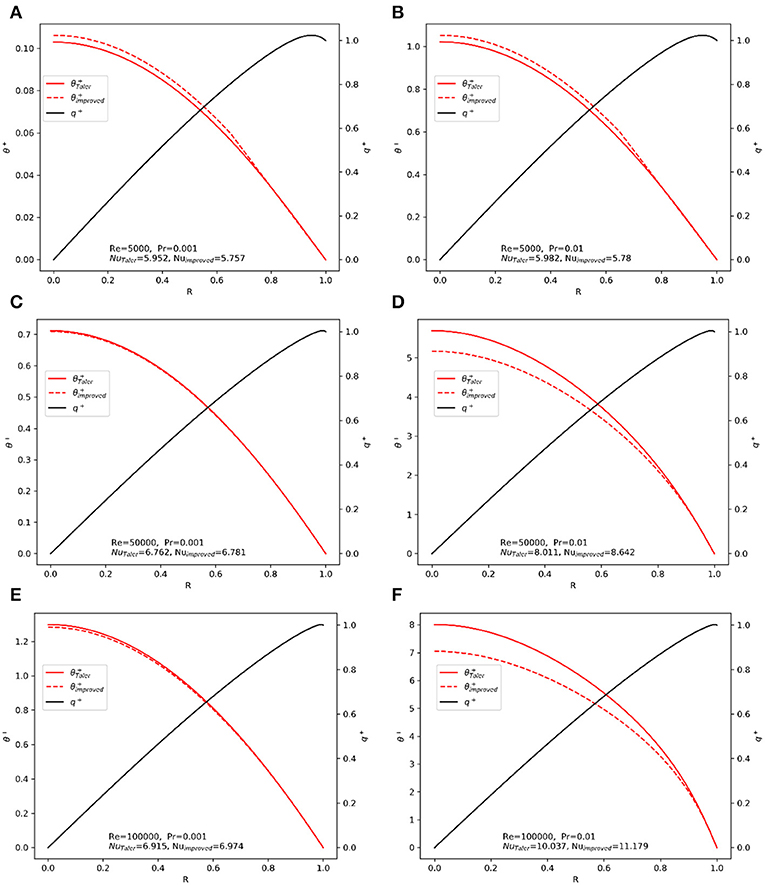
The non-dimensional temperature and heat flux distributions for liquid metal with a different molecular Prandtl number under various flow conditions can be obtained. First, the dimensionless heat flux is obtained by solving Equation 18 with the boundary condition from heated surface, i.e., Equation 13. Then, the non-dimensional temperature can be solved by Equations (30) or (19) based on y⁺ of the corresponding node. Results for six typical conditions are presented in Figure 1, including Reynolds numbers of 5,000, 50,000, and 100,000 and molecular Prandtl numbers of 0.001 and 0.01 for sodium under different thermal conditions. The results from the model proposed by Taler (2016) are presented as references. For low Reynolds number conditions, the effects of the molecular Prandtl number are quite small, and our model predicts higher non-dimensional temperature than Taler's model, which means a lower heat transfer coefficient. Under the conditions with a moderate to high Reynolds number, our model will present a higher Nusselt number than Taler's model, and the difference between these two models increases with the molecular Prandtl number. It should be mentioned that the linear approach on the near wall temperature distribution affects the temperature distribution not only in the linear regime but also in the bulk regime, since our model will degenerate into Taler's model if the critical y⁺ for the upper limit of the linear regime is set to be zero.

FIGURE 1

Figure 1. (A–F) Non-dimensional heat flux and temperature along the radial direction.

Model Validation With Experiment Data

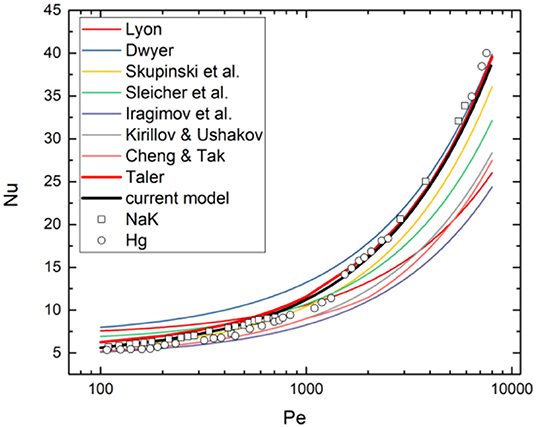
In this section, the Nusselt number predicted by Equations (18) and (19) based on the turbulent Prandtl number given by Kays (1994) is compared with the experiment data to validate the accuracy of the models. First, the heat transfer data from Hg and NaK (Skupinski et al., 1965) were used as the benchmark database. Besides, the results predicted by correlations for liquid metal heat transfer are also given as references. As can be noted from the comparisons in Figure 2, the Nusselt number predicted by Taler correlation (Taler, 2016) and the current model with Pr_t obtained from Kays correlation (Kays, 1994) shows superior agreement with the experiment data. The heat transfer coefficient data for liquid sodium (Fuchs, 1974) are also used to validate the model. As can be noted from Figure 3, the accuracy of the current model is much better than any other models when predicting the liquid metal with an extremely low molecular Prandtl number.

FIGURE 2

Figure 2. Comparison of the Nusselt number with a different Peclet number.

FIGURE 3

Figure 3. Comparison of the Nusselt number for liquid sodium.

Parameter Sensitivity Analysis on the Critical y⁺ for Linear Sublayer

As mentioned above, the upper limit y⁺ of the linear regime in the thermal boundary layer is set to be 60 in the current model. However, the validation region of the Kays correlation (Kays, 1994) is beyond y⁺of about 65. Besides, the upper limit of the linear regime may vary with the molecular Prandtl number. Thus, it is necessary to analyze the effects of critical y⁺ (denoted as $y_{crit}^{+}$) on the model accuracy. In this section, $y_{crit}^{+}$ varies from 50 to 70, and the results are analyzed to measure the potential uncertainties introduced by the selection of $y_{crit}^{+}$. The results are shown in Figure 4, which demonstrates negligible effects of $y_{crit}^{+}$ on the predicted Nusselt number, especially for flow with a high Reynolds number.

FIGURE 4

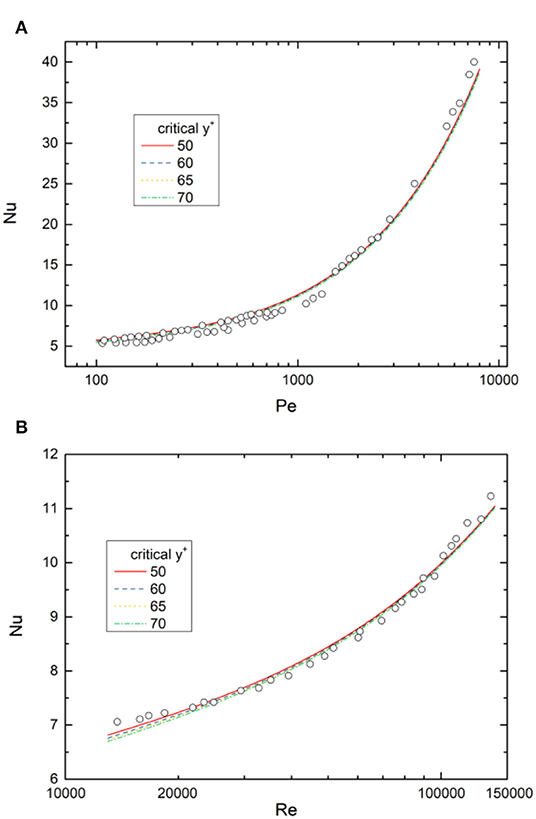
Figure 4. Effects of $y_{crit}^{+}$ on prediction of Nusselt number. (A) Nusselt vs. Peclet number. (B) Nusselt vs. Reynolds number.

Conclusions

In this paper, a new model for turbulent heat transfer of liquid sodium in a circular pipe was proposed. This model was developed based on the universal profiles for velocity and eddy diffusivity, generally applicable for turbulent flow in pipes. The Kays correlation was employed to predict the turbulent Prandtl number in the bulk flow region with non-dimensional wall distance y⁺ larger than 60. In the near wall region with y⁺ <60, the linear law was used instead of the turbulent Prandtl number to predict the temperature distribution. The profiles of non-dimensional temperature and heat flux can be obtained by solving the governing equations for temperature and heat flux. The selection of y⁺ equaling to 60 as the upper limit of the linear regime has little effects on the heat transfer characteristics, which is proved by a sensitivity study related to the influences of critical y⁺ on the predicted Nusselt number. The new model developed in this paper has superior accuracy when compared with other available correlations by the validation with the experiment data.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary files.

Author Contributions

RZ contributed significantly to the analysis and manuscript preparation. ZhenyW performed the data analysis and wrote the manuscript. ZhenhW checked the English writing thoroughly. TR and JS approved the final version.

Funding

The authors greatly appreciate support from the Natural Science Foundation of Heilongjiang Province, China (Grant No. LH2019A009) and the Open Fund Program of the State Key Laboratory of Nuclear Power Safety Monitoring Technology and Equipment (K-A2019.414).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are thankful for the support from the Fundamental Science on Nuclear Safety and Simulation Technology Laboratory, Harbin Engineering University, China.

References

Bricteux, L., Duponcheel, M., Winckelmans, G., Tiselj, I., and Bartosiewicz, Y. (2012). Direct and large eddy simulation of turbulent heat transfer at very low 22Prandtl number: application to lead–bismuth flows. Nucl. Eng. Des. 246, 91–97. doi: 10.1016/j.nucengdes.2011.07.010

CrossRef Full Text | Google Scholar

Chang, B. H., and Akins, R. (1972). An experimental investigation of natural convection in mercury at low grashof numbers. Int. J. Heat Mass Transf. 15, 513–525. doi: 10.1016/0017-9310(72)90214-1

CrossRef Full Text | Google Scholar

Duponcheel, M., Bricteux, L., Manconi, M., Winckelmans, G., and Bar tosiewicz, Y. (2014). Assessment of RANS and improved near-wall modeling for forced convection at low Prandtl numbers based on LES up to Re τ =2,000. Int. J. Heat Mass Transf. 75, 470–482. doi: 10.1016/j.ijheatmasstransfer.2014.03.080

CrossRef Full Text | Google Scholar

Dwyer, O. (1966). Recent developments in liquid-metal heat transfer. Atom. Energy Rev. 4, 84–95.

Google Scholar

Fuchs, H. (1974). Heat transfer to liquid sodium: theoretical and experimental in vestigations on temperature profiles and turbulent temperature fluctuations in a circular tube (Ph.D. thesis). ETH Zurich, Zurich, Switzerland.

Google Scholar

Grötzbach, G. (2013). Challenges in low-prandtl number heat transfer simulation and modelling. Nucl. Eng. Des. 264, 41–55. doi: 10.1016/j.nucengdes.2012.09.039

CrossRef Full Text | Google Scholar

Ibragimov, M. K., Subbotin, V., and Ushakov, P. (1961). Investigation of heat transfer in the turbulent flow of liquid metals in tubes. Sov. J. At. Energy 8, 48–50. doi: 10.1007/BF01491235

CrossRef Full Text | Google Scholar

Johnson, R. W. (2016). Handbook of Fluid Dynamics. Florida City, FL: CRC Press. doi: 10.1201/b19031

CrossRef Full Text | Google Scholar

Kader, B. (1981). Temperature and concentration profiles in fully turbulent bound ary layers. Int. J. Heat Mass Transf. 24, 1541–1544. doi: 10.1016/0017-9310(81)90220-9

CrossRef Full Text | Google Scholar

Kawamura lab (2008). DNS Database of Wall Turbulence and Heat Transfer. Available online at: https://www.rs.tus.ac.jp/t2lab/db/ (accessed September 27, 2018).

Kawamura, H., Abe, H., and Matsuo, Y. (1999). DNS of turbulent heat transfer in channel flow with respect to reynolds and prandtl number effects. Int. J. Heat Fluid Fl. 20, 196–207. doi: 10.1016/S0142-727X(99)00014-4

CrossRef Full Text | Google Scholar

Kawamura, H., Ohsaka, K., Abe, H., and Yamamoto, K. (1998). DNS of turbulent heat transfer in channel flow with low to medium-high Prandtl number fluids. Int. J. Heat Fluid Fl. 19, 482–491. doi: 10.1016/S0142-727X(98)10026-7

CrossRef Full Text | Google Scholar

Kays, W. M. (1994). Turbulent Prandtl number—where are we J. Heat Transf. 116, 284–295. doi: 10.1115/1.2911398

CrossRef Full Text | Google Scholar

Lubarsky, B., and Kaufman, S. J. (1955). Review of Experimental Investigations of Liquid-Metal Heat Transfer. Technical Report, Lewis Flight Propulsion Lab.

Google Scholar

Lyon, R. N. (1951). Liquid metal heat transfer coefficients. Chem. Eng. Prog. 47, 75–79.

Google Scholar

Reichardt, H. (1957). The Principles of Turbulent Heat Transfer. NACA-TM-1408, Technical Report, NASA.

Roelofs, F., Shams, A., Otic, I. M., Bottcher, Duponcheel, M. Y., Bartosiewicz, Y., et al. (2015). Status and perspective of turbulence heat transfer modelling for the industrial appli cation of liquid metal flows. Nucl. Eng. Des. 290, 99–106. doi: 10.1016/j.nucengdes.2014.11.006

CrossRef Full Text | Google Scholar

Schleisiek, K. (1970). Heat transfer and boiling during forced convection of sodium in an induction-heated tube. Nucl. Eng. Des. 14, 60–68. doi: 10.1016/0029-5493(70)90084-1

CrossRef Full Text | Google Scholar

Shi, S., Zhang, Z., Zhang, J., and Li, J. (1981). Experimental study on the heat tranfer to liquid metal sodium flowing in circular tube and annuli (in chinese). J. Eng. Thermopys. 2, 173–180.

Skupinski, E., Tortel, J., and Vautrey, L. (1965). Determination des coefficients de con vection d'un alliage sodium-potassium dans un tube circulaire. Int. J. Heat Mass Transf. 8, 937–951. doi: 10.1016/0017-9310(65)90077-3

CrossRef Full Text | Google Scholar

Sleicher, C., Awad, A., and Notter, R. (1973). Temperature and eddy diffusivity profiles in nak. Int. J. Heat Mass Transf. 16, 1565–1575. doi: 10.1016/0017-9310(73)90184-1

CrossRef Full Text | Google Scholar

Taler, D. (2016). Heat transfer in turbulent tube flow of liquid metals. Procedia Eng. 157, 148–157. doi: 10.1016/j.proeng.2016.08.350

CrossRef Full Text | Google Scholar

Taylor, G. (1916). Conditions at the surface of a hot body exposed to the wind. Brit. Adv. Com. Aero. Rep. Memor. 272, 423–429.

Tiselj, I., and Cizelj, L. (2012). DNS of turbulent channel flow with conjugate heat transfer at prandtl number 0.01. Nucl. Eng. Des. 253, 153–160. doi: 10.1016/j.nucengdes.2012.08.008

CrossRef Full Text | Google Scholar

Nomenclature