Simulation of Critical Heat Flux Phenomenon Using a Non-heating Hydrogen Evolving System

Pool boiling critical heat flux (CHF) at saturated condition was simulated using the hydrogen at the copper cathode in the aqueous solution of sulfuric-acid. The critical current density (CCD) was observed at the cell potential-current density curve, which is analogous to the CHF at the boiling curve. The CHF values calculated by the gas generation rate at the CCD condition showed large discrepancies with the existing CHF values of water boiling system. Meanwhile, the superficial mechanism triggering the CHF and the CCD showed similar characteristics except the size of bubbles. The variation of bubble departure volume with respect to the current density was similar to that of the water vapor but the bubble volume of the present system was 440 times smaller at CCD condition. The critical heat flux value using the present non-heating experiment was corrected accounting for the bubble volumes and the discrepancy with the water CHF was <10%. It is concluded that the water CHF condition can be simulated by the non-heating hydrogen evolving system.

Introduction

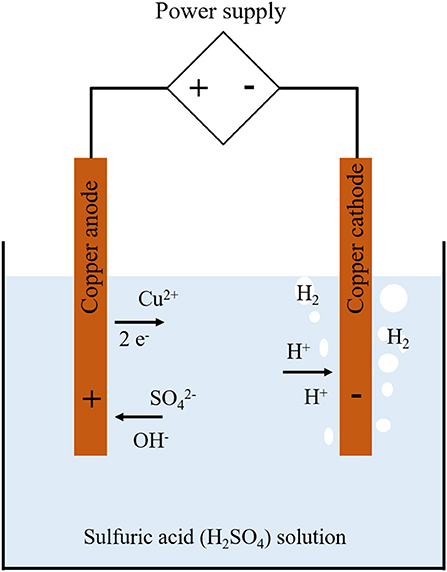
The nucleate boiling allows larger heat transfer coefficients than the single phase convection. Thus, smaller heat exchangers and cooling devices are expected using the boiling heat transfer. There exists the maximum manageable heat flux resulting in the burnout of the system, critical heat flux (CHF). The surface temperature increased rapidly after the CHF point with heat flux controlled system compared with the temperature controlled system, since the transition boiling regime is not encountered due to the boiling hysteresis (Carey, 2008). Therefore, numerous studies have been devoted to the measurement and modeling of the CHF over half a century (Kutateladze, 1950; Zuber, 1959; Gaertner, 1965; Katto and Yokoya, 1968; Van Ouwerkerk, 1972; Lienhard and Dhir, 1973; Lienhard et al., 1973; Haramura and Katto, 1983; Saylor and Simon, 1989; Sadasivan et al., 1992; Unal et al., 1992; Sturgis and Mudawar, 1999; Kandlikar, 2001; Jeong et al., 2002; Bang et al., 2005; Zhang et al., 2006; Roday and Jensen, 2009; Sakashita and Ono, 2009; Ahn and Kim, 2012; Lloveras et al., 2012; O'Hanley et al., 2013). Particularly, many of CHF researches have been performed for the water-cooled nuclear power plant systems, which are basically heat flux controlled systems, while the conventional fossil-fuelled boilers are temperature controlled system (Groeneveld et al., 2018). Hence, the CHF phenomenon is often regarded as one of the important research issue at the nuclear industry. However, the difficulties in the CHF experiments involve in the phenomenological extreme conditions such as high heat flux over 1,000 kW/m², the large thermal inertia and thermal expansion which endangers the controlling thermal condition and integrity of the test facility. The present study motivated by these difficulties and attempted to simulate the water pool boiling CHF at saturated condition using the hydrogen gas evolving system which can be realized using aqueous solution of sulfuric acid with copper anode and cathode as shown in Figure 1 and the hydrogen reduction process adopted in this study is shown in Equation (1).

$\begin{array}{ll}{\text{Cathode}:2\text{H}}^{+}+{2\text{e}}^{-}\to {\text{H}}_2\uparrow & (1)\end{array}$

$\begin{array}{ll}\text{Anode}:\text{Cu}\to {\text{Cu}}^{2+}+{2\text{e}}^{-}& (2)\end{array}$

This system enables to avoid experimental difficulties with the boiling systems by replacing the vaporization with the electrochemical reaction. The basic idea comes from the fact that the existing models for the CHF condition were based on the hydrodynamics, which means that if the existing models reflect the nature of the phenomena, any gas bubbles can simulate the CHF condition. Comparisons of bubble behaviors on the both systems were performed to establish the similarities and differences between water pool boiling CHF and the hydrogen evolving system. The aqueous solution of sulfuric-acid (H₂SO₄) of 1.5 M was used as working fluid, which evolves hydrogen gas on the cathode surface. Horizontal disk and thin cylindrical ribbon made of copper were employed as the cathodes to simulate heating surface.

FIGURE 1

Figure 1. Scheme of a sulfuric acid electrolysis system.

Backgrounds

Existing CHF Models

Kutateladze (1950) developed the CHF correlation, Equation (3) based on a dimensional analysis. He insisted that the latent heat, gravity, surface tension and densities of the fluids are the important parameters on the CHF value. For water-vapor system, the value of 0.16 for coefficient K was suggested.

$\begin{array}{ll}{q}_{CHF}^{″}=K{h}_{lg}{\rho }_g{\left[\frac{\sigma g({\rho }_l-{\rho }_g)}{{{\rho }_g}^2}\right]}^{1/4},& (3)\end{array}$

or,

$\begin{array}{ll}{q}_{CHF}^{″}=K{h}_{lg}{{\rho }_g}^{1/2}{[\sigma g({\rho }_l-{\rho }_g)]}^{1/4}.& (4)\end{array}$

Zuber (1959) established the “Hydrodynamic instability model” developing the Kutateladze's theory. He applied instability theories to the CHF phenomena: The Rayleigh-Taylor instability for the diameters and intervals of the vapor columns which were half the size of and a unit size of critical wavelength, λ_T,c, respectively. He also applied the critical Kelvin-Helmholtz wavelength, λ_H,c, which causes the vapor columns to collapse. Then the CHF triggers as the escaping vapor has become limited. Zuber used K value of 0.131 in Equation (4). Kutateladze and Zuber assumed the infinite upward facing horizontal plain surface heater, at the atmospheric pressure and saturated condition.

Katto and Yokoya (1968) investigated the influence of the fluid layer between vapor mushroom and the heated surface on the heat transfer. They reported that the heat transfer is strongly affected by the critical interference height which is similar to the height of the vapor stem investigated by Gaertner (1965). They observed that the formation and the detachment of the vapor mushroom have constant periods near the CHF. When the vapor mushroom leaves the surface, the fresh bulk fluid permeates the partially dried surface and momentary fills macrolayer. Then, the following vapor mushroom grows and thus the liquid layer is evaporated again. As the heat flux increases, this periodical phenomenon repeated, and the thickness of the macrolayer becomes thinner. And then at a certain high heat flux, the liquid in the macrolayer is fully evaporated triggering the CHF.

Haramura and Katto (1983) established the “Macrolayer dryout model.” They improved Katto and Yokoya's study (1968) and developed their CHF correlation, Equation (5) with parameters reflecting macrolayer thickness and hovering time. They postulated the thickness of macrolayer as a fourth of the λ_H. According to them, the CHF occurs when the liquid in macrolayer is completely vaporized during the hovering time, which is defined as the period from the vapor mushroom generation to departure. Thus, the correlation was derived from the heat balance equation as expressed in the Equation (6).

$\begin{array}{ll}{q}_{CHF}^{″}=h_{lg}{{\rho }_g}^{1/2}{[\sigma g({\rho }_l-{\rho }_g)]}^{1/4}{(1+k)}^{5/16}{(\frac{{\pi }^4}{2^{11}·3^2})}^{1/16}{(\frac{A_v}{A_h})}^{5/8}{(1-\frac{A_v}{A_h})}^{5/16}{[(\frac{{\rho }_l}{{\rho }_g}+1)/{(\frac{11}{16}\frac{{\rho }_l}{{\rho }_g}+1)}^{3/5}].}^{5/16}& (5)\end{array}$

$\begin{array}{ll}{\tau }_d{q}_{CHF}^{″}={\delta }_l{h}_{lg}{\rho }_l(A_h-A_v).& (6)\end{array}$

τ_d, δ_l, A_h, and A_v are hovering period, thickness of imacrolayer, heated area, and area of vapor stem, respectively. However, several researchers (Williamson and El-Genk, 1991; Sadasivan et al., 1992; Unal et al., 1992) opposed the approach of defining the thickness of the macrolayer based on the Kelvin-Helmholtz instability by Haramura and Katto (1983).

Van Ouwerkerk (1972) observed irreversible growth of dry areas at the pool boiling CHF condition using glass disk and n-heptane. The dry areas underneath the vapor mushroom were observed at 80% of CHF value regardless of the pressure. However, as pressure increased vapor shrank and thus dry areas were reduced. Hence, the CHF condition was delayed as pressure increased.

Ha and No (1998) proposed dry spot model and insisted that the critical number of bubbles surrounding an isolated bubble is five. The successive study of Ha and No (1998, 2000) hypothesized that rewetting of the microlayer under the bubble is impeded when the number of bubbles surrounding single bubble exceeds a critical number and then this disturbance of rewetting can trigger the CHF. Chung and No (2007) established nucleate boiling limitation model which predicts CHF condition based on dry area fraction studied by Ha and No (1998). As a result, they proposed the heat flux prediction equation from nucleate boiling to a CHF expressed as following relation.

$\begin{array}{ll}{q}^{″}=q_{nb}^{″}(n_{ib}/n_a)& (7)\end{array}$

where q”_nb, n_ib, and n_a denote nucleate boiling heat flux, number of isolated bubbles without coalescence and expected number of isolated bubbles, respectively.

Existing Interpretation for the CCD

A gas evolving electrode system has upper operational limits so called critical current density (CCD) (Vogt et al., 2004). This limit of the gas generation rate can be roughly elucidated that the vigorous generation of bubble forms the film on the active surface and this gaseous film impedes the convection of the bulk liquid, which is quite similar to the film formation after departure from nucleate boiling (DNB). Therefore, the critical point can also be found in the gas evolving system. Some researchers (Mazza et al., 1978; Sillen et al., 1982) refereed that the boiling and gas evolving system have strong analogy analogy on the evidence of similarity between boiling curve and cell potential-current density curve, where the cell potential (potential difference between two electrodes) and current density correspond to the superheat and heat flux, respectively.

The electrochemical industry often regards the CCD phenomenon as the “anode(or cathode) effect” (Kellogg, 1950; Mazza et al., 1978; Zhuxian and Mingjie, 1987; Vogt, 2000). The anode effect was generally explained in two types: The anode effect is initiated by (1) the formation of intermediate compounds affecting surface wettability such as CF_x and COF_x and (2) the accumulation of gas on the surface, which reduces active surface area without formation of intermediate compounds (Zhuxian and Mingjie, 1987; Vogt, 2000). Despite of the achievements of the existing analogy studies (Vogt et al., 2004; Vogt, 2013) for a nucleate bubble regime, the detailed analogy analysis between the CHF and CCD (anode effect) has not been performed sufficiently.

Previous Study

The authors' research group conducted the CCD experiments using the hydrogen evolution electrode varying the orientation of electrode and channel gap size, previously (Ohk et al., 2019). The tendency of the CCD was compared with the existing CHF results using various working fluids. The correlation reflecting hydrodynamic parameters was also derived and well-agreed with the existing CHF results which generally follow (sinθ)^0.5 as in the Figure 2. It was concluded that the hydrogen evolving system can simulate the CHF tendency qualitatively with respect to the surface orientation. However, the quantitative simulation of the CHF has still remained.

FIGURE 2

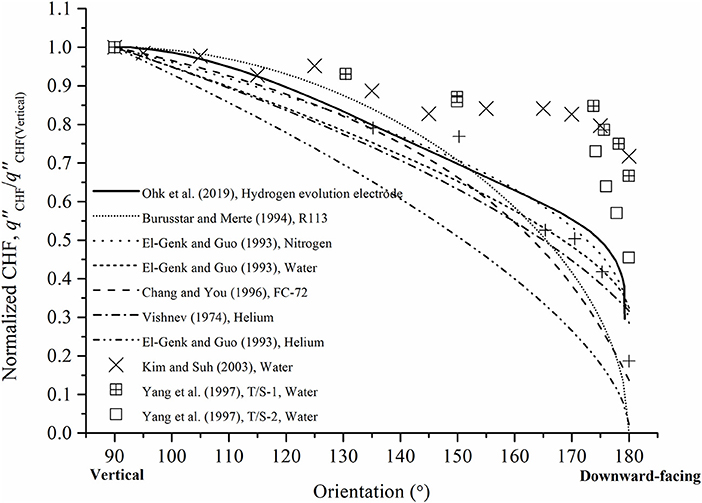
Figure 2. Comparison of normalized CHF of existing studies with hydrogen evolution system (Ohk et al., 2019).

Experimental Setup

Experimental Procedure and Test Apparatus

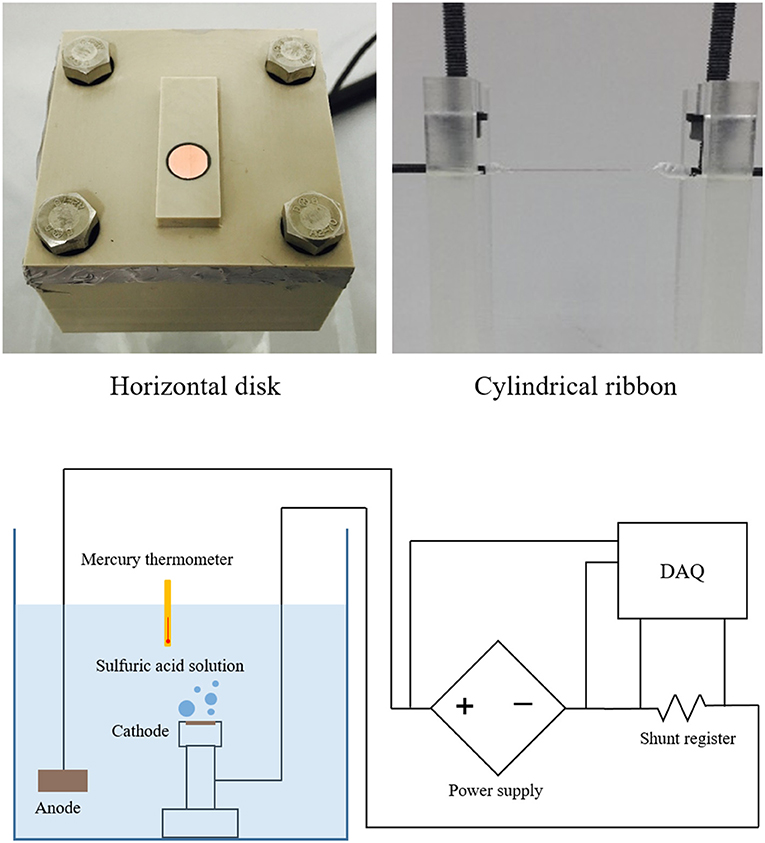
Two types of cathodes, disk of 0.01 m diameter and thin cylindrical ribbon of 2 × 10⁻⁴ m thickness were employed for two independent experiments. One of these cathodes and the anode of 0.40 m × 0.50 m × 0.60 m block were located in the top-opened glass container filled with the aqueous solution of sulfuric-acid (H₂SO₄) of 1.5 M at atmospheric pressure and room temperature of 294 K. The mercury thermometer was located away from the cathode to measure bulk fluid temperature and the K-type thermocouple was set near the cathode surface to monitor the physical properties of the working fluid. The high-speed camera (Phantom Lab 111 6GMono, Komi) recorded the hydrogen evolution at the cathode surface. The electric current was controlled using power supply (N8952A, Keysight) simulating the typical heat flux controlled CHF experiments. The cell potential value was monitored and recorded by data acquisition system (34972A, Keysight) while the electric current was varied. To establish steady state condition at each current stage, time duration of about 20 s was maintained to get stabilized cell potential value. The CCD criterion was determined when cell potential was abruptly increased, which is similar to the abrupt temperature increase at the CHF condition as the cell potential of the present system is analogous to the superheat of the boiling system. The visual image of the hydrogen behavior around the CCD point was recorded. Three repeated experiments were conducted to measure the CCD and the discrepancy between minimum and maximum value was within 1.65%. The experimental apparatus, two types of the cathode and electric circuit were depicted in Figure 3.

FIGURE 3

Figure 3. Experimental apparatus and electric circuit.

The CHF value using the present hydrogen evolving system was calculated based on the gas generation rate at the CCD condition. The gas generation rate can be calculated by Equation (8) suggested by Vogt et al. (2004). Equation (8) can be simplified at the CCD condition without any subreaction during the experiment as expressed in Equation (9) (Vogt, 1984), which is de facto the calculation of the number of moles of hydrogen reduced by the electric current together with the Boyle and Charles relations. Then the CHF at the saturated condition can be obtained by converting the gas generation rate with gas density and latent heat as in Equation (10).

$\begin{array}{l}{\stackrel{\bullet }{V}}_G=\stackrel{\bullet }{N}{f}_G\frac{R_{m}T}{p}{\left(1-\frac{p_{H2O}}{p}\right)}^{-1}\\ \begin{array}{c}=\frac{I\epsilon \nu }{nF}{f}_G\frac{R_{m}T}{p}{\left(1-\frac{p_{H2O}}{p}\right)}^{-1}.\end{array}& (8)\end{array}$

$\begin{array}{ll}{\stackrel{\bullet }{V}}_{G,CCD}=\frac{I\nu }{nF}{V}_m\left(\frac{T}{273.15}\right).& (9)\end{array}$

$\begin{array}{ll}{q}_{CHF}^{″}=\frac{{\stackrel{\bullet }{V}}_{G,CCD}{\rho }_g{h}_{lg}}{A}.& (10)\end{array}$

Uncertainty Analysis

Uncertainties in the proposed experimental methodology were analyzed using data reduction techniques (Coleman and Steele, 1999). As the final dependent variable was the CHF value using gas generation rate at the CCD, the uncertainty can be expressed as

$\begin{array}{l}{q}_{CHF}^{″}=\frac{{\dot{V}}_G{h}_{lg}{\rho }_g}{A},\\ U_{q_{CHF}^{″}}{}^2={\left(\frac{\partial q_{CHF}^{″}}{\partial {\dot{V}}_G}{U}_{{\dot{V}}_G}\right)}^2+{\left(\frac{\partial q_{CHF}^{″}}{\partial A}{U}_A\right)}^2.& (11)\end{array}$

The measurement error of the cathode area, A was assumed to be half of the resolution of the milling machine; 2.5 × 10⁻⁴ m. Thus, the U_A can be calculated as 3.93 × 10⁻⁶ m². And then, the uncertainty of the gas generation rate at the cathode surface can be expressed as

$\begin{array}{l}{\stackrel{\bullet }{V}}_G=V_m\left(\frac{I\nu }{nF}\right)\left(\frac{T}{273.15}\right),\\ \begin{array}{c}{U_{\stackrel{\bullet }{V}G}}^2={\left(\frac{\partial {\stackrel{\bullet }{V}}_G}{\partial T}{U}_T\right)}^2+{\left(\frac{\partial {\stackrel{\bullet }{V}}_G}{\partial I}{U}_I\right)}^2.\end{array}& (12)\end{array}$

The measurement error of the temperature, T was estimated as standard accuracy of the K-type thermocouple, 2.2 K. However, the uncertainty of the current, I was calculated using Ohm's law and thus

$\begin{array}{ll}{U_I}^2={\left(\frac{\partial I}{\partial R}{U}_R\right)}^2+{\left(\frac{\partial I}{\partial V}{U}_V\right)}^2,& (13)\end{array}$

where the uncertainties of R and V were stipulated in the manual of the product models, SCRD-R0001-5.0-H and Keysight 34972A, respectively. The calculated fractional maximum uncertainties were about 5.05%, showing the inherent accuracy of the experimental method. The largest uncertainties were caused by the tolerance of the shunt register, 5%.

Results and Discussion

Analogous Curve

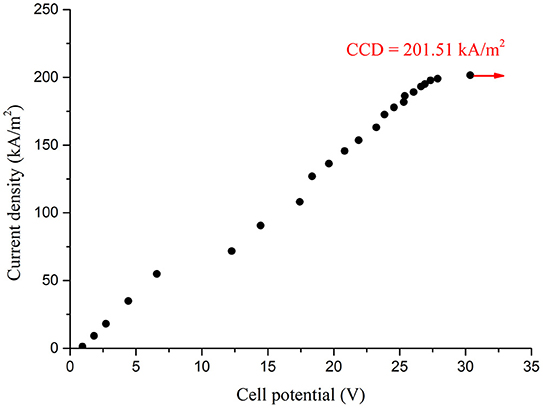
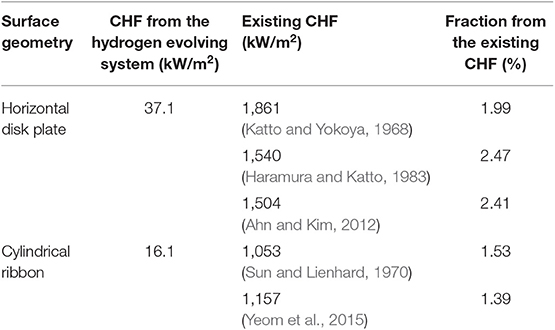
Figures 4, 5 compares the typical boiling curve by Nukiyama (1966) and the cell potential-current density curve measured using 10 mm copper disk. The cell potential increased as the applied current density increased up to the highest cell potential at the CCD, 201.51 kW/m², which shows resemblance to the nucleate boiling regime up to the CHF. In general, the CHF is detected by the rapid increase in the heater temperature. Similarly, the CCD was detected by the rapid increase in the cell potential in the present study. Therefore, this result has similarity with the CHF detection experiments in typical boiling system. The measured CCD was converted into the water CHF using Equations (9) and (10) as 37.1 kW/m². This value is much smaller than that of the existing CHF values, which used identical geometric condition with the present experiment (Katto and Yokoya, 1968; Haramura and Katto, 1983; Ahn and Kim, 2012). The similar curve with Figure 5 was also obtained using the thin cylindrical ribbon and the comparisons with the boiling CHF was presented in Table 1. Though the current experimental results show much smaller CHF values than the CHF values with water boiling system, the ratios of the CHF values lie within 1.39–2.47%.

FIGURE 4

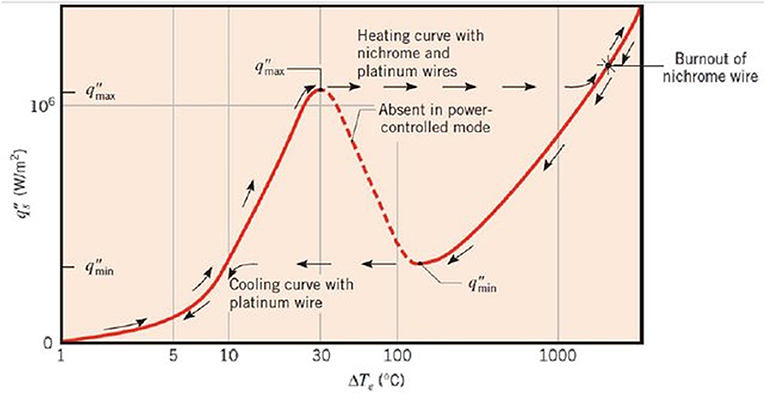
Figure 4. Typical boiling curve (Nukiyama, 1966).

FIGURE 5

Figure 5. Cell potential-current density curve.

TABLE 1

Table 1. Comparison of the water CHF value between the present work and existing value.

Bubble Behaviors at the CHF and the CCD

Figure 6 compares the bubble behaviors between the hydrogen evolving system and the water boiling system (Figures 6A–C) and (Figures 6D–F) (Ahn and Kim, 2012), respectively. The photographs were taken in series, from just before the CCD to after the CCD. Both systems had identical sizes of active surfaces and materials, 10 mm diameter of copper disks.

FIGURE 6

Figure 6. Comparison of bubble behaviors between hydrogen evolving and water boiling system. (A) Just before CCD, (B) at CCD triggers, (C) after CCD, (D) just before CHF, (E) at CHF triggers, and (F) after CHF.

Figures 6A,D were taken at the nucleate bubble regime, just before the CCD and the CHF. The nucleate bubble on the edge of the surface maintained surface rewetting and thus kept its own regime in the both cases. Figures 6B,E depict the CCD and the CHF regime, respectively. The bubbles at the edge of the surface started to coalescence. Hence, the surface rewetting impeded due to the liquid inflow and thus a certain critical point was reached in the both cases. After that, the gaseous film covered the entire surface as shown in Figures 6C,F. In this regime, the cell-potential and the surface temperature greatly increased in the hydrogen evolving system and boiling system, respectively.

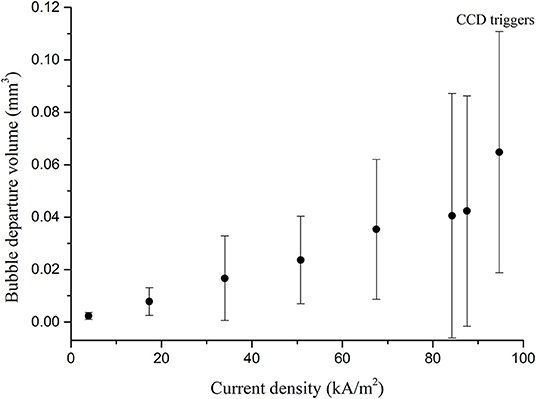
Based on the observation, it can be postulated that the macroscopic mechanism of the CCD and the CHF is similar except the bubble size. The relatively small hydrogen bubbles were observed compared with the vapor bubbles just before the CCD regime. In order to investigate more details of the bubble size, the hydrogen departure volumes were measured with respect to the current density using high speed camera. The thin cylindrical ribbon was used to capture the generalized bubble shapes. Fifty hydrogen bubbles were randomly selected and their diameters were measured to convert into volume assuming the bubbles had the perfect spherical shape due to its small size scale, as shown in Figure 7. Fifty data were averaged at each current density with standard deviations as shown in the Figure 8. The result was compared with those of water boiling experiment up to the CHF regime performed by Yeom et al. (2015) who also used the thin cylindrical ribbon as the heating surface as shown in the Figure 9. The hydrogen departure volume increased as the current density increased. Then the slope increased near the CCD point. It seems that the vigorous bubble coalescence on the surface impeded the liquid inflow and increased the cell-potential, the CCD. The trend of bubble volume with respect to the heat flux by Yeom et al. (2015) was similar to the present work. The vapor volume increased as heat flux increased and showed great increase in the CHF regime. However, the vapor volume at the CHF regime was about 440 times larger than that of the CCD regime. The size scale of hydrogen bubble was similar to the existing hydrogen evolving experiment (Vogt et al., 2004), and Vogt et al. (2004) referred that the increased cell potential affected the surface wettability. Based on these observations, the CCD of the hydrogen evolving system simulates the miniature scale of the water CHF.

FIGURE 7

Figure 7. Hydrogen bubble behaviors on thin cylindrical ribbon.

FIGURE 8

Figure 8. Hydrogen departure volume according to the current density.

FIGURE 9

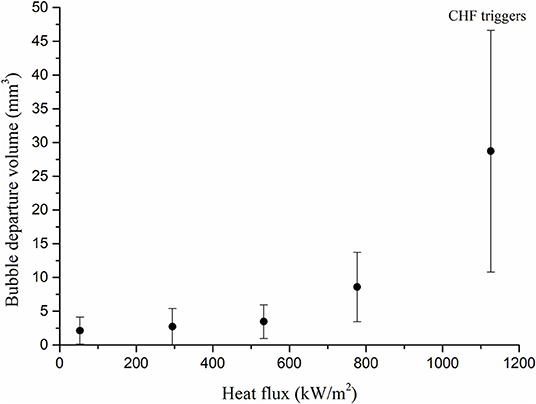
Figure 9. Bubble departure volume according to the heat flux (Yeom et al., 2015).

Water CHF Prediction

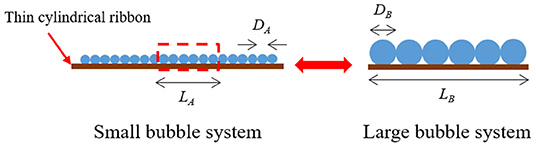
The water CHF was predicted by the measured CCD accounting for the differences in vapor/gas volume generation rates based on the miniature CHF assumption. For simplicity, the representative bubble concept at each CHF condition was postulated as shown in the Figure 10. As a result, the diameter and the lifetime of the bubbles in each system are same. Also, the bubble coalescence assumed to occur only for the 1-dimansional lateral direction because the cylindrical ribbon is thin enough to suppress the occurrence of 2-dimensional coalescence. Thus, heat flux (W/m²) relationship between the two different system can be simplified as linear heat generation rate (W/m) as expressed in Equation (14) with a certain magnification factor, C.

$\begin{array}{ll}C\frac{Q_A}{L_A}=\frac{Q_B}{L_B}& (14)\end{array}$

And the heat flow Q, can be substituted by the total bubble volume at saturated boiling condition since we assumed that the bubbles have the same lifetime, independent of the function of time.

$\begin{array}{ll}C\frac{n_b{V}_A}{L_A}=\frac{n_b{V}_B}{L_B}.& (15)\end{array}$

The unit heater length, L can be substituted by n_b× D, and thus the magnification factor C can be derived as

$\begin{array}{ll}C=\left(\frac{\pi /6{D_B}^3}{\pi /6{D_A}^3}\right)\left(\frac{n_b{D}_A}{n_b{D}_B}\right)={\left(\frac{D_B}{D_A}\right)}^2.& (16)\end{array}$

To apply the magnification factor for the present work, D_A and D_B in Equation (16) can be substituted to hydrogen departure diameter at the CCD triggers, 0.47 mm and bubble diameter measured by Yeom et al. (2015) at the CHF triggers, 3.79 mm, respectively. As a result, the magnification factor between two system was calculated as 65.03 and thus the CHF simulated by the present system can be corrected using relationship of Equation (14).

$\begin{array}{l}{\text{CHF}}_{HES,C}=C\times {\text{CHF}}_{HES}=65.03\times 16.1\\ \begin{array}{c}=1,046.98{\text{kW}/\text{m}}^2\end{array}& (17)\end{array}$

The measured CHF by the Yeom et al. (2015) was 1,157 kW/m². Finally, the discrepancy was largely reduced within 9.51%.

FIGURE 10

Figure 10. Ideal configuration of bubble arrangement at CHF regime.

However, the proposed analogy approach using the hydrogen evolving system will not achieve full analogy with the boiling process by nature. There are several sacrificed factors such as conduction phenomenon, contact angle, buoyancy difference due to the different bubble size, change of interfacial tension including surface tension due to the surface charge in the electrode system, etc. These factors are important in boiling processes but many of them are not considered in most CHF modeling, which means that the limited number of these factors contributes to the CHF.

Conclusion

Water pool boiling CHF at saturated condition was simulated using the hydrogen evolving system, which is essentially thermal free condition. The cell potential according to the current density curve, which is analogous to the typical boiling curve was obtained and the CCD was measured in analogous way to the boiling CHF, which by nature is much smaller than the water CHF values.

The superficial mechanism of the CHF and the CCD were compared using photographs. The CHF and the CCD triggered when the nucleate bubble on the edge of the surface started to coalescence. It is concluded that the similar bubble behaviors can be observed in both cases except the size of bubbles. The characteristics of hydrogen evolving system was tested using the thin ribbon electrode. The variation of bubble volume from nucleate bubble regime to the CHF and the CCD showed similar tendency in both systems. The hydrogen bubble volume was 440 times smaller than vapor volume measured in boiling heat transfer system near the CHF. Based on the observation, a miniature CHF model was postulated.

A magnification factor was derived by the miniature CHF model accounting for the differences in vapor/gas volume generation rates. The discrepancy between the existing CHF and the CHF from the hydrogen evolving system with magnification factor was <10%.

The possibility of simulating the CHF condition using a non-heating hydrogen evolving system was explored based on the fact that most CHF models were derived from the hydrodynamics. This work was partly successful in predicting the CHF value accounting for the volume generation rates. However, in order to achieve the full analogy between the hydrogen evolving system and the boiling heat transfer system, further works are needed regarding conduction, contact angle, surface tension and engineered surface such as roughness, porosity, and wettability.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This study was sponsored by Korean Ministry of Science and Information & Communication Technology and was supported by Nuclear Research & Development program grant funded by the National Research Foundation (NRF) (Grant code: 2017M2A8A4015283).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahn, H. S., and Kim, M. H. (2012). Visualization study of critical heat flux mechanism on a small and horizontal copper heater. Int. J. Multiph. Flow 41, 1–12. doi: 10.1016/j.ijmultiphaseflow.2011.12.006

CrossRef Full Text | Google Scholar

Bang, I. C., Chang, S. H., and Baek, W. P. (2005). Visualization of a principle mechanism of critical heat flux in pool boiling. Int. J. Heat Mass Transf. 48, 5371–5385. doi: 10.1016/j.ijheatmasstransfer.2005.07.006

CrossRef Full Text | Google Scholar

Carey, V. P. (2008). Liquid-Vapor Phase-Change Phenomena. Boca Raton, FL; London; New York, NY: CRC Press.

Google Scholar

Chung, H. J., and No, H. C. (2007). A nucleate boiling limitation model for the prediction of pool boiling CHF. Int. J. Heat Mass Transf. 50, 2944–2951. doi: 10.1016/j.ijheatmasstransfer.2006.12.023

CrossRef Full Text | Google Scholar

Coleman, H. W., and Steele, W. G. (1999). Experimental and Uncertainty Analysis for Engineers. New York, NY: John Wiley and Son.

Google Scholar

Gaertner, R. F. (1965). Photographic study of nucleate pool boiling on a horizontal surface. J. Heat Transf. 87, 17–27. doi: 10.1115/1.3689038

CrossRef Full Text | Google Scholar

Groeneveld, D. C., Ireland, A., Kaizer, J., and Vasic, A. (2018). An overview of measurements, data compilations and prediction methods for the critical heat flux in water-cooled tubes. Nucl. Eng. Des. 331, 211–221. doi: 10.1016/j.nucengdes.2018.02.031

CrossRef Full Text | Google Scholar

Ha, S. J., and No, H. C. (1998). A dry-spot model of critical heat flux in pool and forced convection boiling. Int. J. Heat Mass Transf. 41, 303–311. doi: 10.1016/S0017-9310(97)00140-3

CrossRef Full Text | Google Scholar

Ha, S. J., and No, H. C. (2000). A dry-spot model of critical heat flux applicable to both pool boiling and subcooled forced convection boiling. Int. J. Heat Mass Transf. 43, 241–250. doi: 10.1016/S0017-9310(99)00135-0

CrossRef Full Text | Google Scholar

Haramura, Y., and Katto, Y. (1983). A new hydrodynamic model of critical heat flux, applicable widely to both pool and forced convective boiling on submerged bodies in saturated liquids. Int. J. Heat Mass Transf. 26, 389–399. doi: 10.1016/0017-9310(83)90043-1

CrossRef Full Text | Google Scholar

Jeong, Y. H., Baek, W. P., and Chang, S. H. (2002). Non-heating simulation of pool-boiling critical heat flux. Int. J. Heat Mass Transf. 45, 3987–3996. doi: 10.1016/S0017-9310(02)00100-X

CrossRef Full Text | Google Scholar

Kandlikar, S. G. (2001). A theoretical model to predict pool boiling CHF incorporating effects of contact angle and orientation. J. Heat Transf. 123, 1071–1079. doi: 10.1115/1.1409265

CrossRef Full Text | Google Scholar

Katto, Y., and Yokoya, S. (1968). Principal mechanism of boiling crisis in pool boiling. Int. J. Heat Mass Transf. 11, 993–1002. doi: 10.1016/0017-9310(68)90005-7

CrossRef Full Text | Google Scholar

Kellogg, H. H. (1950). Anode effect in aqueous electrolysis. J. Electrochem. Soc. 97, 133–142. doi: 10.1149/1.2777980

CrossRef Full Text | Google Scholar

Kutateladze, S. S. (1950). A hydrodynamic model of the critical heat transfer in boiling liquids with free convection. Zhurn. Tekhc. Fiz. 20, 1389–1392.

Google Scholar

Lienhard, J. H., and Dhir, V. K. (1973). Hydrodynamic prediction of peak pool-boiling heat fluxes from finite bodies. J. Heat Transf. 95, 152–158. doi: 10.1115/1.3450013

CrossRef Full Text | Google Scholar

Lienhard, J. H., Dhir, V. K., and Riherd, D. M. (1973). Peak pool boiling heat-flux measurements on finite horizontal flat plates. J. Heat Transf. 95, 477–482. doi: 10.1115/1.3450092

CrossRef Full Text | Google Scholar

Lloveras, P., Salvat-Pujol, F., Truskinovsky, L., and Vives, E. (2012). Boiling crisis as a critical phenomenon. Phys. Rev. Lett. 108:215701. doi: 10.1103/PhysRevLett.108.215701

PubMed Abstract | CrossRef Full Text | Google Scholar

Mazza, B., Pedeferri, P., and Re, G. (1978). Hydrodynamic instabilities in electrolytic gas evolution. Electrochim. Acta 23, 87–93. doi: 10.1016/0013-4686(78)80102-9

CrossRef Full Text | Google Scholar

Nukiyama, S. (1966). The maximum and minimum values of the heat Q transmitted from metal to boiling water under atmospheric pressure. Int. J. Heat Mass Transf. 9, 1419–1433. doi: 10.1016/0017-9310(66)90138-4

CrossRef Full Text | Google Scholar

O'Hanley, H., Coyle, C., Buongiorno, J., McKrell, T., Hu, L. W., Rubner, M., et al. (2013). Separate effects of surface roughness, wettability and porosity on the boiling critical heat flux. Appl. Phys. Lett. 103:024102. doi: 10.1063/1.4813450

CrossRef Full Text | Google Scholar

Ohk, S. M., Park, H. K., and Chung, B. J. (2019). CHF experiments on the influence of inclination and gap size. Int. J. Heat Mass Transf. 132, 929–938. doi: 10.1016/j.ijheatmasstransfer.2018.12.076

CrossRef Full Text | Google Scholar

Roday, A. P., and Jensen, M. K. (2009). A review of the critical heat flux condition in mini-and microchannels. J. Mech. Sci. Technol. 23, 2529–2547. doi: 10.1007/s12206-009-0711-y

CrossRef Full Text | Google Scholar

Sadasivan, P., Chappidi, P. R., Unal, C., and Nelson, R. A. (1992). Possible mechanism of macrolayer formation. Int. Commun. Heat Mass Transf. 19, 801–815. doi: 10.1016/0735-1933(92)90016-B

CrossRef Full Text | Google Scholar

Sakashita, H., and Ono, A. (2009). Boiling behaviors and critical heat flux on a horizontal plate in saturated pool boiling of water at high pressures. Int. J. Heat Mass Transf. 52, 744–750. doi: 10.1016/j.ijheatmasstransfer.2008.06.040

CrossRef Full Text | Google Scholar

Saylor, J. R., and Simon, T. W. (1989). The effect of a dimensionless length scale on the critical heat flux in saturated, pool boiling. Am. Soc. Mech. Eng. Heat Transf. Div. 108, 71–80.

Google Scholar

Sillen, C. W. M. P., Barendrecht, E., Janssen, L. J. J., and Van Stralen, S. J. D. (1982). Gas bubble behaviour during water electrolysis. Int. J. Hydr. Energy 7, 577–587. doi: 10.1016/0360-3199(82)90038-6

CrossRef Full Text | Google Scholar

Sturgis, J. C., and Mudawar, I. (1999). Critical heat flux in a long, rectangular channel subjected to one-sided heating- I. flow visualization. Int. J. Heat Mass Transf. 42, 1835–1847. doi: 10.1016/S0017-9310(98)00274-9

CrossRef Full Text | Google Scholar

Sun, K. H., and Lienhard, J. H. (1970). The peak pool boiling heat flux on horizontal cylinders. Int. J. Heat Mass Transf. 13, 1425–1439. doi: 10.1016/0017-9310(70)90178-X

CrossRef Full Text | Google Scholar

Unal, C., Daw, V., and Nelson, R. A. (1992). Unifying the controlling mechanisms for the critical heat flux and quenching: the ability of liquid to contact the hot surface. J. Heat Transf. 117, 558–567. doi: 10.1115/1.2911909

CrossRef Full Text | Google Scholar

Van Ouwerkerk, H. J. (1972). Burnout in pool boiling: the stability of boiling mechanisms. Int. J. Heat Mass Transf. 15, 25–34. doi: 10.1016/0017-9310(72)90163-9

CrossRef Full Text | Google Scholar

Vogt, H. (1984). The rate of gas evolution at electrodes–I. an estimate of the efficiency of gas evolution from the supersaturation of electrolyte adjacent to a gas-evolving electrode. Electrochim. Acta 29, 167–173. doi: 10.1016/0013-4686(84)87043-7

CrossRef Full Text | Google Scholar

Vogt, H. (2000). On the mechanism of the anode effect in aluminum electrolysis. Metall. Mater. Trans. B-Proc. Metall. Mater. Proc. Sci. 31, 1225–1230. doi: 10.1007/s11663-000-0009-z

CrossRef Full Text | Google Scholar

Vogt, H. (2013). Heat transfer in boiling and mass transfer in gas evolution at electrodes – the analogy and its limits. Int. J. Heat Mass Transf. 59, 191–197. doi: 10.1016/j.ijheatmasstransfer.2012.12.018

CrossRef Full Text | Google Scholar

Vogt, H., Aras, Ö., and Balzer, R. J. (2004). The limits of the analogy between boiling and gas evolution at electrodes. Int. J. Heat Mass Transf. 47, 787–795. doi: 10.1016/j.ijheatmasstransfer.2003.07.023

CrossRef Full Text | Google Scholar

Williamson, C. R., and El-Genk, M. S. (1991). “High-speed photographic analysis of saturated nucleate pool boiling at low heat flux,” in ASME Winter Annual Meeting (Atlanta, GA).

Google Scholar

Yeom, H., Sridharan, K., and Corradini, M. L. (2015). Bubble dynamics in pool boiling on nanoparticle-coated surfaces. Heat Transf. Eng. 36, 1027–1027. doi: 10.1080/01457632.2015.979116

CrossRef Full Text | Google Scholar

Zhang, W., Hibiki, T., Mishima, K., and Mi, Y. (2006). Correlation of critical heat flux for flow boiling of water in mini-channels. Int. J. Heat Mass Transf. 49, 1058–1072. doi: 10.1016/j.ijheatmasstransfer.2005.09.004

CrossRef Full Text | Google Scholar

Zhuxian, Q., and Mingjie, Z. (1987). Studies on anode effect in molten salts electrolysis. Electrochim. Acta 32, 607–613. doi: 10.1016/0013-4686(87)87049-4

CrossRef Full Text | Google Scholar

Zuber, N. (1959). Hydrodynamic aspects of boiling heat transfer (Dissertation). University of California, Los Angeles, CA, United States.

Google Scholar

Nomenclature