The Effect of Hydration on the Structure and Transport Properties of Confined Carbon Dioxide and Methane in Calcite Nanopores

With increasing interest in using or displacing confined water for CH₄ recovery or CO₂ storage in nanoporous environments, understanding the organization and diffusion of gases is confined water environments is essential. In this study, the effect of hydration on the structure and diffusivity of confined carbon dioxide (CO₂) and methane (CH₄) in 2 nm slit-shaped calcite nanopore was studied using classical molecular dynamics simulations. The absence of confined water and the effect of different water concentrations including one layer of confined water composed of 150 water molecules, 500 water molecules, and 1,296 water molecules that correspond to the density of bulk water of 1 g/cm³ on the structural arrangement and diffusivity of confined CO₂ and CH₄ were investigated. Water molecules were found to influence the anisotropic distribution and mobility of confined CO₂ and CH₄ significantly by altering the structures of the adsorbed gas layers onto the calcite surfaces. The preferential adsorption of water on calcite surface over CO₂ and CH₄ resulted in the displacement of the adsorbed gas molecules toward the center of the pore. This water-induced displacement impacts the diffusivity of the confined gases by enabling transport through the center of the pore where there are fewer intermolecular collisions and less steric hindrance for transporting the molecules. Therefore, the diffusivity of CO₂ and CH₄ is higher in the presence of a single water layer as opposed to in pores without water. Energetic calculations showed that van der Waals and electrostatic interactions contributed to the affinity of CO₂ for calcite surfaces, while van der Waals interactions dominate CH₄ interactions with calcite and the surrounding water molecules. The anisotropic variations in the diffusivities of confined fluids emerge from changes in the organization of confined fluids and potential differences in the free energy distributions as a function of the orientation of the calcite surface. These findings suggest that any efforts to potentially engineer the nano-scale pore environment in calcite for enhanced gas recovery or storage will require us to consider the organization and anisotropic transport behaviors of confined fluids.

Introduction

With more than 80% of our energy needs being met by the subsurface environments (BP Global, 2015), there is a significant interest in environmentally benign approaches to recover and store fluids in complex materials characterized by chemical and morphological heterogeneity and nano-scale porosity. Various studies have shown that the properties and transport of confined fluids such as water (Bonnaud et al., 2010; Ho and Striolo, 2015; Hu et al., 2015; Chakraborty et al., 2017), gases such as CO₂ (Chialvo et al., 2012; Le T. et al., 2017; Striolo and Cole, 2017; Simoes Santos et al., 2018), and hydrocarbons (Cole et al., 2013; Le et al., 2015a,b; Wu et al., 2015; Le T. T. B. et al., 2017; Herdes et al., 2018; Obliger et al., 2018; Simoes Santos et al., 2018) in nanoporous environments differs from bulk behaviors due to changes in the structure and affinity of confined liquids (Wang H. et al., 2016; Johnston, 2017) and gases (Yuan et al., 2015; Sun et al., 2016a,b, 2017; Wang S. et al., 2016a,b) for the solid interfaces. With increasing interest in enhanced gas recovery coupled with subsurface CO₂ storage, a fundamental understanding of the changes in the structure of CO₂ and CH₄ and transport properties of these gases through water-bearing nanoporous environments provides a scientific basis for the observed fate and transport of these gases at the field scale (Glezakou and McGrail, 2013; Gadikota et al., 2017; Gadikota, 2018; Gadikota and Allen, 2018).

Confined geometries impose inhomogeneity and anisotropy on the structure and dynamics of confined fluids due to the interaction of fluid-solid interfaces (Granick, 1991; Relat-Goberna and Garcia-Manyes, 2015) which can be successfully probed using classical Molecular Dynamics (MD) simulations. Further, MD simulations explain the underlying subnano- and nano-scale mechanisms including adsorption and interfacial phenomena, and thermophysical properties such as viscosity and transport properties such as diffusion. In this study, the structure and transport properties of CH₄ and CO₂ in various water-bearing environments at calcite interfaces are probed using classical MD simulations. Calcite interfaces are chosen since calcite-bearing rocks are one of the major constituents of hydrocarbons reservoirs in the world (Addari and Satta, 2015) including shale reservoirs (Xu et al., 2005). Calcite is present in almost all geological systems and represents the main constituent of limestone which forms most of the world's hydrocarbons reservoirs (Meldrum and Cölfen, 2008; Geysermans and Noguera, 2009; Addari and Satta, 2015; Bovet et al., 2015; Côté et al., 2015). For this reason, several studies focused on understanding gas interactions in calcite nano-pores (Franco et al., 2016; Sun et al., 2016b, 2017; Wang S. et al., 2016a,b; Bui et al., 2017; Simoes Santos et al., 2018). Further, shale formations such as the Middle Bakken region in North America are characterized by a significant fraction of calcite which contribute to pore sizes that are 2 nm or greater (Liu et al., 2017). Therefore, a pore size of 2 nm was chosen as a reasonable approximation for a representative pore size of calcite.

This approach is intended to facilitate a calibrated understanding of the influence of confined water on the structure and diffusivity of CO₂ and CH₄ in calcite nanopores. Further, important scientific insights were developed by probing the interactions of confined mixed gases in calcite nanopores. CO₂ was found to displace adsorbed hydrocarbons in calcite nanopores and the adsorption of CO₂ was influenced by the quantity of surface adsorption sites (Simoes Santos et al., 2018). As an example, the preferential adsorption of CO₂ on the pore surface was found to weaken the adsorption of n-butane (Le et al., 2015a). An evaluation of the diffusivity of methane, nitrogen and CO₂ confined in calcite slit-shaped nanopore showed that the diffusivity of the simulated fluids close to the surface differs from the molecules away from the solid interface and toward the center of the pore (Franco et al., 2016). This anisotropic behavior was evident in the diffusivity of methane through hydrated calcite pores (Bui et al., 2017). In the absence of any dissolved gas solutes, the translational and rotational dynamics of confined water were found to be dependent on the local density variation and the local hydrogen bonds connectivity, respectively (Mutisya et al., 2017). Further, the self-diffusion coefficient of water in confined quartz (Ishikawa and Tsuchiya, 2017) and montmorillonite (Rao and Leng, 2016; Gadikota et al., 2017) was lower compared to bulk water.

The chemistry of the solid interface has a significant impact on the diffusion and adsorption of different fluids (Schaef et al., 2013, 2015; Lee et al., 2014, 2017; Kadoura et al., 2016; Sun et al., 2016b; Fazelabdolabadi and Alizadeh-Mojarad, 2017; Gadikota et al., 2017). In addition to the chemistry of the solid interface, the pore size had a strong influence on the diffusivity of fluids. For example, octane diffusion was found to increase rapidly with the size of the montmorillonite interlayer pore (Wang H. et al., 2016). The decrease in the density of octane as it migrates from the nanopore to mesopore enhances the diffusivity which aids hydrocarbon recovery from the subsurface (Wang H. et al., 2016). In this work, MD simulations were performed to investigate the structure and transport behavior of confined CO₂ and CH₄ in calcite slit shaped nanopore with varying levels of hydration to mimic water-bearing nanopores in the subsurface environments.

Models and Methods

Atomistic Models and Initial Configuration

The simulation system is composed of a periodic slit-shaped calcite nanopore with a width of 2 nm. The simulation box with dimensions of 48.57 × 39.92 × 68.58 Å consists of two calcite blocks with each block composed of 6 calcite layers (Figure 1). The calcite surfaces were obtained by cutting calcite along the (104) crystallographic surface based on calcite unit cell. The calcite surfaces were immobilized in the simulation. Table 1 below describes the interatomic parameters used in this study.

FIGURE 1

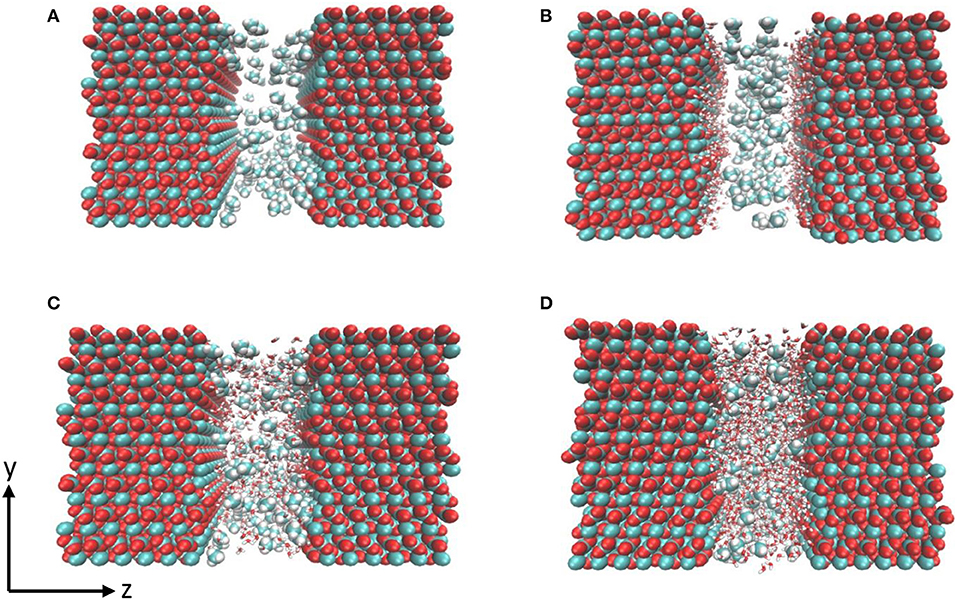
Figure 1. Snapshot of the initial configurations composed of calcite surface and methane (A) with no water, (B) single water layer, (C) 500 water molecules, and (D) 1 g/cm³ of confined water. Water molecules are shown as red and white sticks, carbon and hydrogen in methane are represented in cyan and white respectively.

TABLE 1

Table 1. Lennard–Jones 6–12 potential parameters.

Four systems were constructed to investigate the effect of hydration on the structure and diffusivity of CO₂ and CH₄. First, 100 molecules of pure CO₂ and CH₄ were randomly distributed in the pore space to investigate the structure and dynamics of gases in the absence of pore water as shown in Figure 1A. In the second case, a single layer of water composed of 150 water molecules was added at the calcite interface (Figure 1B). The thickness of water layer was chosen based on experimental observations reported by Fenter et al. (2000). In the third configuration, the nanopore was solvated with 500 number of water molecules (Figure 1C). The fourth scenario, the density of confined water was set to mimic that of bulk water i.e., density of 1 g/cm³ of water (1,296 molecules) for potential comparison with previous studies (Figure 1D) (Mutisya et al., 2017).

Simulation Details and Algorithm

Canonical ensemble (NVT) simulation was performed on the product of energy minimization for 10 ns using Nose-Hoover (Nosé, 1984; Hoover, 1985) thermostat with time constant of 1 ps to control the temperature of both surface and the fluids. The energy of the initial configurations was minimized using steepest descent method for 50,000 steps to ensure that the energy is <100 kJ mol⁻¹ nm⁻¹. The simulations were performed at standard temperature and the pressure was calculated based on Ping Robinson equation of state (EOS) (Peng and Robinson, 1976) by inserting specific number of gas molecules to satisfy the required density. One hundred molecules of CH₄ were inserted in the system free of water to match a pressure of about 125 bar which was studied experimentally to represent the shale pressure (Zhong et al., 2016; Xing et al., 2018). Number of CO₂ molecules was chosen as an equimolar of methane for comparison purposes. Since we are interested in the effect of water on the properties of confined gases, number of CH₄ and CO₂ molecules were kept constant in all four configurations and various amount of water were added into each system.

Statistics were evaluated by dividing each simulation into three 1.5 ns blocks. Each block was treated as an independent replicate. The SHAKE algorithm was used to keep the water molecules rigid (Ryckaert et al., 1977). Van der Waals (vdW) interactions were modeled by Lennard-Jones (LJ) 12-6 function, and electrostatic interactions, which modeled by Coulomb's function as shown in Equation 1.

$\begin{array}{ll}{U}_{ij}={\displaystyle \sum _{i<j}}\left[4{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]+\frac{q_i{q}_j}{r_{ij}}\right]& \left(1\right)\end{array}$

In Equation (1), q_iand q_j are the charges of i and j, r_ij is the distance between i and j. LJ parameters (i.e., ε_ij and σ_ij) for unlike molecular interactions were calculated based on Lorentz-Berthelot rule as following:

$\begin{array}{ll}{\sigma }_{ij}=\frac{{\sigma }_{ii}+{\sigma }_{jj}}{2}& \left(2\right)\end{array}$

$\begin{array}{ll}{\epsilon }_{ij}=\sqrt{{\epsilon }_{ii}{\epsilon }_{jj}}& \left(3\right)\end{array}$

The intramolecular interactions accounted for bond stretching, angle bending and dihedrals. Electrostatic and dispersion interactions were computed in real space up to a distance of 14 Å. Long range electrostatic interactions were evaluated using particle mesh Ewald (PME) (Darden et al., 1993). Simulations were carried out using the GROMACS program. Simulation results were analyzed to determine the structure and diffusivity in the calcite nanopores. The structural changes in the gas molecules in confinement were evaluated using radial distribution functions (RDFs) extracted from the trajectory using VMD (Humphrey et al., 1996).

The self-diffusion coefficients were calculated for each gas (i.e., CO₂ and CH₄) in the calcite nanopore. The diffusion coefficients were calculated based on the mean square displacement (MSD) for the directions and the plane parallel to the pore dimensions (D_X, D_Y, and D_XY) according to the following equation:

$\begin{array}{ll}D=\frac{1}{2d}{\displaystyle \underset{t\to \infty }{lim}}\frac{d}{dt}{\displaystyle \sum _{i=1}^N}{\left[r_i\left(t\right)-r_i\left(0\right)\right]}^2& \left(4\right)\end{array}$

Where d is the number of dimensions (1 for D_X and D_Y and 2 for D_XY). The diffusion coefficients in x and y directions (i.e., D_X and D_Y) were calculated to determine if diffusion is isotropic or anisotropic for the confined fluids. The diffusivity of the molecules is considered to be isotropic if the diffusion coefficients in X and Y directions are equal, otherwise the diffusion is anisotropic (Bui et al., 2017).

Evaluation of Forcefields

The calcite surface was modeled using forcefield developed by Xiao et al. (2011). CO₂, CH₄, and water were modeled using EPM2 (Harris and Yung, 1995), OPLS/AA (Jorgensen et al., 1996), and SPC/E (Berendsen et al., 1987) models respectively. Several forcefields were used in the literature to model confined gases. For example, OPLS-UA (Bui et al., 2017), OPLS-AA (Gadikota et al., 2017), CVFF (Yuan et al., 2015), COMPASS (Sun et al., 2016a,b), and TraPPE-UA (Simoes Santos et al., 2018) were used to represent CH₄ in confinement. To evaluate the appropriate forcefield, MD simulations were performed using several forcefields to reproduce the properties of the confined CH₄ in the calcite pore and compare the governed data from each forcefield with published data. The structure of the confined CH₄ in 4 nm calcite pore with density of 96 kg/m³ and 375 K was calculated and compared with the data reported by Simoes Santos et al. (2018). We employed both Trappe-UA and OPLS-AA forcefields to calculate CH₄ distribution. As shown in Figure 2, the distribution of CH₄ in calcite nanopores are in reasonable agreement. Both forcefields proved the ability to reproduce the required data, however, we used OPLS-AA since the interatomic potentials of C and H are specified independently (Gadikota et al., 2017). To validate the choice of OPLS-AA further, the density of methane was calculated at standard temperature and pressure by simulating 500 methane molecules using NPT ensemble for 10 ns. Nose-Hoover thermostat and Parrinello–Rahman barostat (Parrinello and Rahman, 1982) were used to control the temperature and pressure, respectively. The governed density is 0.648 ± 0.013 kg/m³ which is consistent with the experimental value which is about 0.656.

FIGURE 2

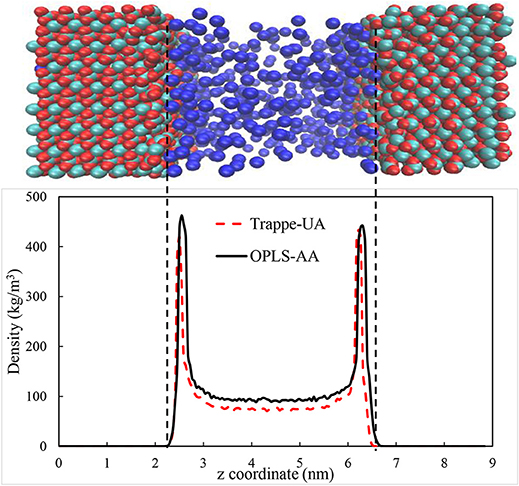
Figure 2. The distribution of methane in 4 nm calcite nanopore under 375 K and density of 96 Kg/m³. The calcium, carbonate and methane species are shown by cyan, red, and blue colors, respectively.

Similarly, various forcefields such as EPM2 (Headen and Boek, 2010; Liu L. et al., 2015; Fazelabdolabadi and Alizadeh-Mojarad, 2017; Mohammed and Mansoori, 2018a,b,c), TraPPE (Javanbakht et al., 2015; Simoes Santos et al., 2018), and COMPASS (Liu B. et al., 2015; Liu et al., 2016; Fang et al., 2017) were used to model CO₂ and its behavior under bulk and confinement conditions. Various studies validated simulated properties such as diffusivity (Moultos et al., 2014, 2016) and solubility (Vlcek et al., 2011) of CO₂ in water using the EMP2 forcefield. To validate the choice of EMP2 forcefield in this study, the diffusion coefficient of CO₂ in water was calculated by dissolving 5 CO₂ molecules in 2000 SPC/E water molecules in an initial cell of 4 × 4 × 4 nm³ to be consistent with previous studies (Moultos et al., 2014). The system was simulated for 5 ns under 1 bar and 323 K using NPT ensemble. The produced self-diffusion coefficient is in reasonable agreement with the experimental and simulated data (Versteeg and Van Swaaij, 1988; Moultos et al., 2014). The diffusion coefficient for CO₂ in water is 4.3 (±0.4) × 10⁻⁵ cm²/s compared with 4 × 10⁻⁵ cm²/s (Moultos et al., 2014) and 3.4 × 10⁻⁵ cm²/s (Versteeg and Van Swaaij, 1988) reported in previous studies.

Results and Discussion

The Structure of the Confined Fluids

Probing the structure of gases in varying confined water environments provides insights into changes in the affinity of gases for the solid interfaces. As shown in Figure 3, the density profiles of gases (CO₂, CH₄) differ when there is no water, one layer of interfacial water composed of 150 molecules, 500 molecules of confined water, and confined water mimicking the density of bulk water (with 1,296 water molecules) in the calcite nanopore. In the absence of water, both CO₂ and CH₄ show a layered structure on the calcite surface and the density profiles are symmetric with respect to the pore center (Figure 3A). These density profiles indicate that CO₂ and CH₄ are adsorbed to create a single layer on the calcite surface in the absence of water which is consistent with previous studies (Franco et al., 2016; Sun et al., 2017; Wang et al., 2017; Simoes Santos et al., 2018). The higher density of CO₂ at the interface compared to CH₄ is attributed to the higher energetic affinity of CO₂ on the calcite interface compared to CH₄ as reported by Wang S. et al. (2016b).

FIGURE 3

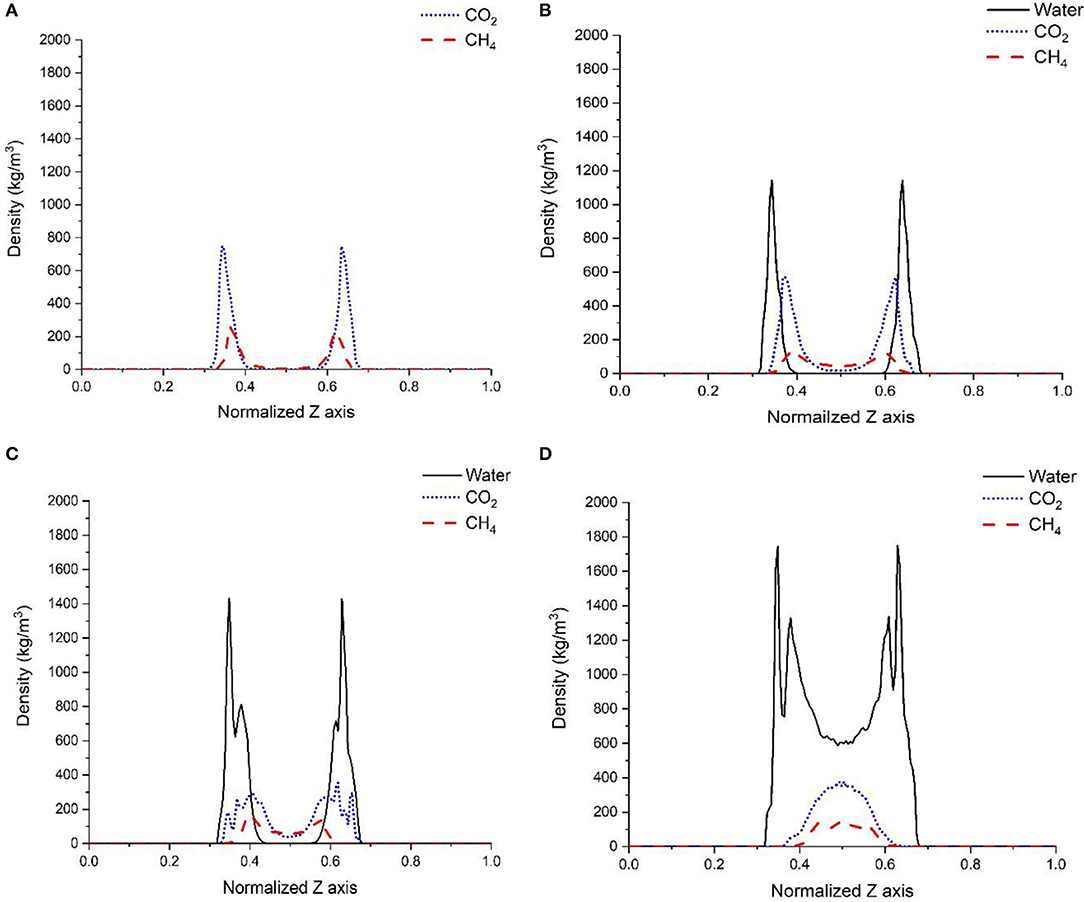
Figure 3. Density profiles of CO₂, and CH₄ in the absence of pore water (A), one layer of confined water composed of 150 water molecules (B), 500 water molecules (C), and 1,296 water molecules that correspond to a density of bulk water of 1 g/cm³ (D). The X-axis represents the normalized pore surface in the z-direction.

In the presence of a single layer of interfacial water, the peak density of CO₂ at the calcite interface decreases from 749 to 550 kg/m³. Similarly, the peak density of CH₄ decreases from 239 to 126 kg/m³. Further, a higher density of CO₂ and CH₄ is noted at the center of the pore in the presence of interfacial water. A reduction in the number of molecules in the adsorbed shells of CO₂ and CH₄ and the shift of these shells away from the calcite surface is noted. CO₂ and CH₄ adsorbed layers were shifted by ~1.5 Å compared to the case where there is no water (Figure 3B). The variation in the relative density of CO₂ and CH₄ due to the presence of water layer can be explained by two factors: the higher adsorption energy of water on the calcite surface compared to CO₂ and CH₄ (Wang S. et al., 2016b) and the difference in the interfacial tension of CO₂ and CH₄ with water. CO₂ has lower interfacial tension with water compared with CH₄ and is partially miscible with water (Bachu and Bennion, 2008; Sakamaki et al., 2011; Yasuda et al., 2016).

In the third scenario, 500 water molecules were randomly distributed in the pore space to represent the abundance of the confined water within the pore. The equilibrium density profiles are shown in Figure 3C. After equilibrating the cell for 5 ns, the water molecules were arranged into two layers on the calcite surface as noted by the peak positions at 0.35 and 0.38 nm in Figure 3C. This specific arrangement of water molecules at calcite interfaces was noted experimentally and computationally (Fenter and Sturchio, 2004; Geissbühler et al., 2004; Argyris et al., 2008; Heberling et al., 2011; Ou et al., 2014; Keller et al., 2015; Fazelabdolabadi and Alizadeh-Mojarad, 2017). A significant reduction in the relative densities of CO₂ and CH₄ at the calcite interface is noted and compared to the case where a single layer of interfacial water is present. A bi-layered arrangement of CO₂ molecules with one peak located near the water-CO₂ interface and another at the calcite-water interface was noted. The existence of the water film leads to a wider distribution of CO₂ molecules at the calcite interface.

In the presence of interfacial water mimicking the density of bulk water, the bi-layer arrangement of water molecules was noted (Figure 3D) which is consistent with the studies reported by Keller et al. (2015) and Mutisya et al. (2017). Higher concentrations of CO₂ and CH₄ were noted at the center of the calcite pore in the presence of this interfacial water. The density maps in Figures 4, 5 provide further insights into the distribution of gases in varying levels of confined water. In general, the presence of different amounts of water displaces more CH₄ molecules toward the pore center compared with CO₂. At a density of 1 g/cm³, a phase separation was noticed between water and CH₄ molecules which are concentrated at the pore center. In contrast, CO₂ molecules was displaced toward the center of the pore while being solvated in the water phase, as shown in Figures 4, 5d.

FIGURE 4

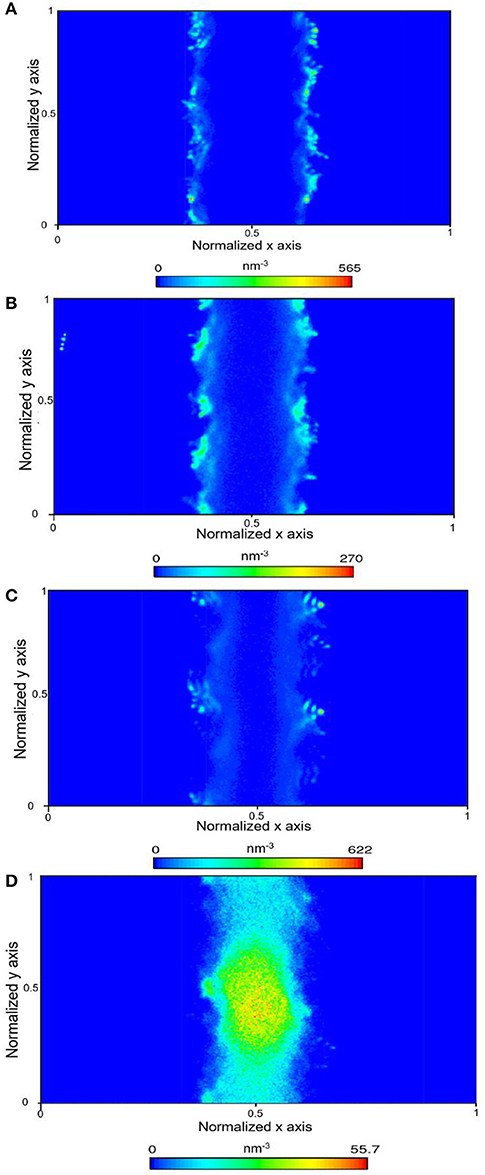
Figure 4. Density map density of CO₂ within the calcite nanopore in the absence of pore water (A), one layer of confined water composed of 150 water molecules (B), 500 water molecules (C), and 1296 water molecules that correspond to a density of bulk water of 1 g/cm³ (D).

FIGURE 5

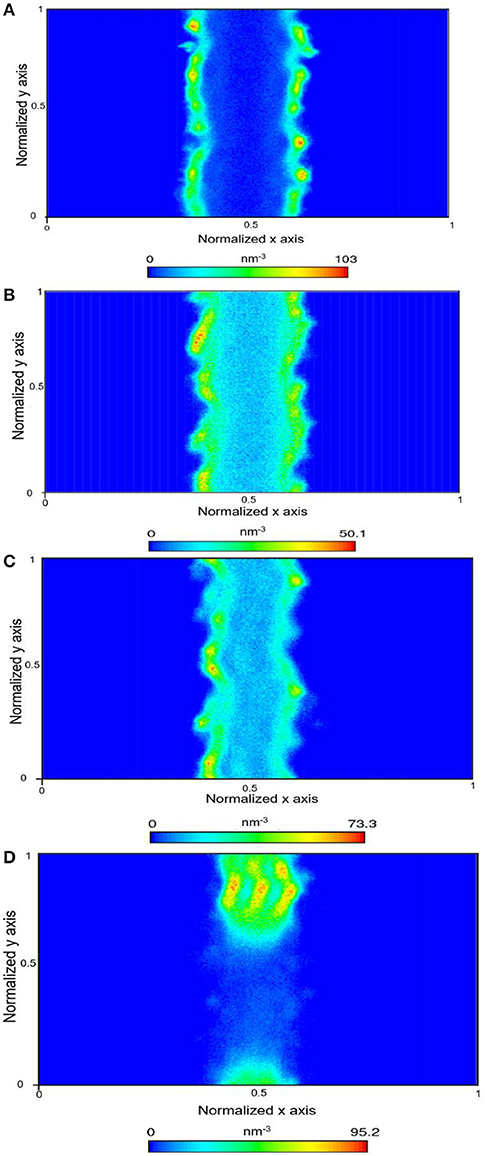
Figure 5. Density map density of CH₄ within the calcite nanopore in the absence of pore water (A), one layer of confined water composed of 150 water molecules (B), 500 water molecules (C), and 1,296 water molecules that correspond to a density of bulk water of 1 g/cm³ (D).

It was interesting to note that the structure of a single layer of interfacial water (Figure 1B) did not change in the presence of CO₂ or CH₄ (Figures 6A,B). In the presence of 500 and 1,296 water molecules with 100 molecules of CO₂ (Figure 6A), the Ca_calcite-O_water interface changed significantly unlike in the case with 100 molecules of CH₄ (Figure 6B). The water layer in the system bearing CO₂ is about 1.3 times wider than CH₄ and is shifted away from the calcite surface. One hypothesis is that the higher solubility of CO₂ in water compared to CH₄ influences the interfacial structure of water. For example, at 298 K, the solubility of CO₂ and CH₄ in water are 0.0286 and 0.0008 mol/kg_water, respectively (Wiesenburg and Guinasso, 1979; Duan and Sun, 2003). The hydration of CO₂ in water potentially results in less sharp water layer. In the presence of interfacial water with a density similar to bulk water, fewer number of oxygen atoms corresponding to the water molecules are present in the first shell of Ca²⁺ in calcite.

FIGURE 6

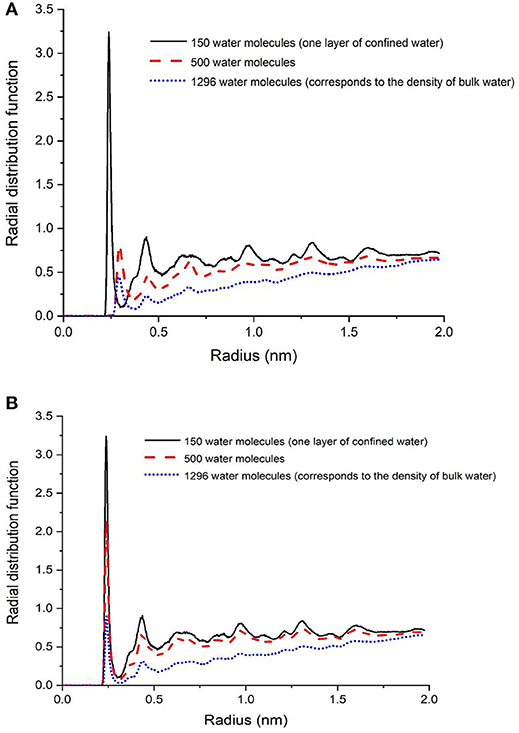
Figure 6. Radial distribution function of calcium in calcite with respect to oxygen in water in systems composed of a single water layer, 500 water molecules, and 1 g/cm³ of confined water in presence of CO₂ (A) and CH₄ (B).

Higher confined water concentrations reduced the number of oxygen atoms corresponding to calcite in the first coordination shell of C_CH4 and C_CO2. In the absence of water, about 11 and 9 oxygen atoms corresponding to calcite in the first coordination shell of C_CO2 and C_CH4 are noted. These data are consistent with the higher adsorption affinity of CO₂ for the calcite interface compared to CH₄. In the presence of 300, 500, and 1,296 water molecules, the number of oxygen atoms corresponding to calcite in the first coordination shell of C_CO2 are about 4, 3, and 1. Similarly, in the presence of CH₄, 300, 500, and 1,296 water molecules, the number of oxygen atoms corresponding to calcite in the first coordination shell of C_CH4 are about 3, 2, and <1, respectively. These data suggest that increasing the number of water molecules reduces the affinity of the gas molecules for the calcite interface.

The number of oxygen atoms corresponding to water in the first coordination shell of C_CH4 were in the range of 4–6 in varying confined water concentrations. The number of oxygen atoms corresponding to water in the first coordination shell of C_CO2 were about 10, 5, and 4 in the presence of 300, 500, and 1,296 water molecules. These data suggested that the number of water molecules in the confinement had a much stronger influence on the coordination behavior of water molecules with CO₂, unlike CH₄.

The orientation of the CO₂ molecules is determined by comparing the coordination behavior of oxygen and carbon in CO₂ with calcite and water interfaces. In all the simulated systems, the number of oxygen atoms in CO₂ are about twice the number of carbon atoms in CO₂ in the first shell. This observation suggests that the CO₂ molecules orientated parallel to the calcite surface, which is consistent with previous reports of CO₂ orientation with Na-montmorillonite surface (Botan et al., 2010; Myshakin et al., 2013; Yang et al., 2015; Kadoura et al., 2016). Also, the number of oxygen atoms of CO₂ in the first shell of the oxygen atoms of water is twice the number of carbon atoms in the case where a single layer of interfacial water is present. This observation is consistent with the orientation of CO₂ parallel to the water interface (Zhao et al., 2011).

Diffusivity of CO₂ and CH₄ Through Nanopores

The diffusivity of CO₂ and CH₄ through calcite nanopores without water, one layer of interfacial water composed of 150 water molecules, 500 water molecules, and 1,296 water molecules to mimic the density of bulk water yielded interesting insights. In general, the diffusion coefficients of CO₂ and CH₄ in the absence of water are in reasonable agreement with Sun et al. (2017) after accounting for the differences in temperature. The temperature used in this study is 298 K compared with 323 K studied by Sun et al. (2017). The diffusion coefficient for CO₂ in the absence of water is 0.4 x 10⁻⁵ cm²/s at 298 K compared with 2 × 10⁻⁵ cm²/s at 323 K. The diffusion coefficient for CH₄ is ~20 × 10⁻⁵ cm²/s at 298 K compared with 35 × 10⁻⁵ cm²/s at 323 K. CO₂ and CH₄ diffusivities in the presence of interfacial water with a density similar to bulk water are in the range reported by Mutisya et al. (2017) and Bui et al. (2017) (Table 2).

TABLE 2

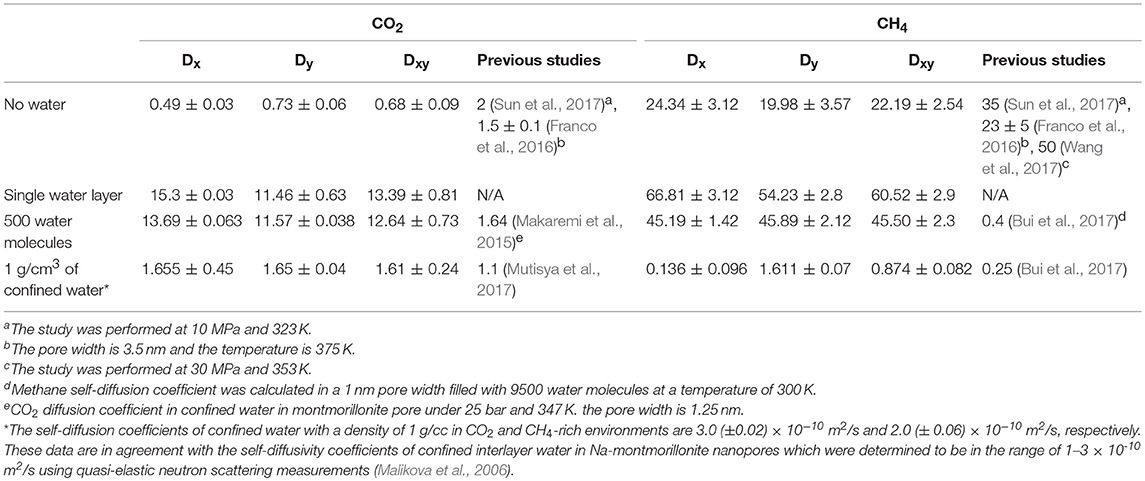
Table 2. The self-diffusion coefficients (10⁻⁹ m²/s) of CO₂ and CH₄ in the absence of pore water, one layer of confined water composed of 150 water molecules, 500 water molecules, and 1,296 water molecules that correspond to a density of bulk water of 1 g/cm³.

The diffusivities are calculated in X, Y directions and in XY plane. The anisotropic variations in the diffusivity of gases in the X and Y directions are noted and shown in Table 2, which is consistent with the data reported by Franco et al. (2016). The diffusion coefficients of CH₄ in X and Y directions are not equal in systems without water and in the presence of single water layer which is consistent with previous studies (Wang S. et al., 2016a; Bui et al., 2017). CH₄ diffusivity in the X direction is higher than that in Y direction by about 4.36 × 10⁻⁵ and 12.58 × 10⁻⁵ cm²/s in the absence of water and the presence of one layer of interfacial water, respectively. However, this difference is much smaller in systems containing more water molecules (Table 2).

Further, an increase in the diffusivity of CO₂ and CH₄ in the presence of one layer of interfacial water was noted. The diffusivity of CO₂ increased from ~ 0.4 × 10⁻⁵ to ~ 13 × 10⁻⁵ cm²/s on introducing a single layer of interfacial water in the simulation system. To date, studies have not reported the diffusivity of CO₂ in calcite nanopores in the presence of one layer of interfacial water. In the absence of pore water, CO₂ has a strong preference for the calcite interface as shown in Figure 3A. In the presence of interfacial water, the density of CO₂ at the interface is reduced which potentially allows for greater mobility within the pore space. Similar diffusivities of CO₂ are noted in the presence of a single layer of interfacial water and in the presence of 500 water molecules.

Similarly, the diffusivity of CH₄ in calcite nanopore composed of a single water layer is about three times higher than the diffusivity in calcite nanopores without water. The reduced affinity of CH₄ for the calcite surface in aqueous environments may be one of the factors enhancing the diffusivity of CH₄ at these conditions. CH₄ diffusivity in the system without water is much higher compared with CO₂ due to the reduced adsorption affinity to the calcite surface. Another contributing factor to the variation in the diffusivity is the molecular weight. The molecular weight of CO₂ is higher than CH₄. Enhanced diffusivity of CH₄ in the calcite nanopore in the presence of a single layer of interfacial water and 500 water molecules is noted.

The in-plane diffusivity (D_xy) of both CO₂ and CH₄ interestingly increased in the systems contain a single water layers compared to the systems free of water due to the reduction in the concentration of the gases adsorbed layers onto the pore surfaces in the presence of water molecule. In the systems free of water, the predominant movement of the molecules is the surface diffusion onto the calcite surface, however, when a preconstructed water layer added to the system, it prevents some of the gases molecules to be adsorbed which are consequently could move faster in the pore space. When additional water added to the system, the diffusivities of CO₂ and CH₄ decreased compared to the scenario of single water layer due the increase in the overall systems density which leads to more intermolecular collisions and higher steric hindrance.

Diffusivities of CO₂ and CH₄ in interfacial water with a density similar to bulk water are 1.6 × 10⁻⁵ and 0.87 × 10⁻⁵ cm²/s, respectively. The diffusivities of CO₂ and CH₄ in Na-montmorillonite nanopore bearing two layers of interlayer water at similar conditions are 1.04 × 10⁻⁵ and 0.85 × 10⁻⁵ cm²/s (Gadikota et al., 2017) which are in reasonable agreement with this study. It is interesting to note that despite the differences in the solid interface i.e., calcite vs. Na-montmorillonite, similar diffusivities of CO₂ and CH₄ in interfacial water are predicted. These data suggest that the diffusivities of fully solvated CO₂ and CH₄ are much lower compared to gases in the absence of confined water.

One of the important outcomes of this study is the observed differences in the diffusivities of confined CO₂ and CH₄ in the x and y directions. These data are the first systematic observations of the influence of varying levels of confined water on the diffusivities of confined CH₄ and CO₂. These differences are attributed to the organization of the water molecules in confinement and the interfacial interactions between the gases, water, and solid interfaces. In the absence of water, one of the key factors influencing the transport of gases is their interactions with calcium and carbonate species on the calcite surface. Previous studies by Bui et al. (2017) showed that the anisotropy in the diffusivity of gas molecules such as CH₄ in calcite pores is significantly greater compared to other solid substrates such as silica, MgO, alumina, and muscovite using Principal Component Analyses. The anisotropic variation in the diffusivities of the confined gas molecules is attributed to the difference in the energy barriers as the gas molecules are transported along a specific direction. It is important to note that the x- and y-orientations are interchanged in the data in this study with respect to the studies performed by Bui and co-workers. Regardless the scientific insights are similar.

In this study, diffusivity of methane in the x-direction is greater than that of the diffusivity in the y-direction in the absence of water suggesting that the free energy barrier for the movement of methane molecules in the x-direction is lower compared to the energy barrier associated with diffusivity in the y-direction. It was also interesting to note that as the water content in calcite pores is increased to 500 molecules and then 1,296 molecules, the diffusivity of methane molecules in the x and y directions are roughly equal, and then diffusivity in the y-direction exceeds that in the x-direction. These data suggest that the solvation free energy distributions of confined methane within the calcite pores vary with the water content. Our observations noted in Figure 5d suggest that in the presence of 1,296 water molecules, methane molecules undergo phase separation, which allows the molecules to move freely in the y-direction relative to the x-direction.

However, the observed diffusion behaviors of CO₂ in varying levels of confined water differ significantly from that of CH₄. Previous studies also showed that the solvation free energies of CO₂ in confined water are much lower compared to CH₄ (Gadikota et al., 2017). Unlike methane, the phase separation of CO₂ molecules in environments composed of 1,296 water molecules is not observed (Figure 4d). This observation is consistent with the similar diffusivities of CO₂ in the x and y directions in 1,296 water molecules. In the absence of confined water, the diffusivity of CO₂ in the y-direction is greater compared to that in the x-direction. However, the trends in the observed diffusivities are switched in the presence of a single layer of water and 500 water molecules. These data suggest that the energy barriers associated with the movement of CO₂ vary significantly in the x and y directions in the presence of fewer water molecules.

Intermolecular Interactions

The van der Waals and electrostatic energies associated with the interactions of CO₂ and CH₄ with calcite interfaces with varying levels of water hydration were determined. These calculations provide insights into the energetics driving the interactions of CO₂ and CH₄ in confined water environments. In the absence of confined pore water, the affinity of CH₄ for the calcite interface was driven by van der Waals interactions. In the case of CO₂, however, the electrostatic and van der Waals interactions enhance the affinity of the calcite surface (Table 3). The overall energetic affinity of CO₂ for the calcite interface is much higher compared to that of CH₄. These findings are consistent with previous studies that pointed to the higher adsorption affinity of CO₂ for the calcite surface compared to CH₄ at the same conditions (Sun et al., 2016b; Wang S. et al., 2016b; Simoes Santos et al., 2018). The quadruple moment of CO₂ gives rise to the enhanced electrostatic interactions leading to higher affinity of CO₂ for calcite interfaces compared to CH₄ (Lithoxoos et al., 2010; Saha et al., 2010; Skarmoutsos et al., 2013; Duan et al., 2016; Liu et al., 2016; Molyanyan et al., 2016).

TABLE 3

Table 3. Intermolecular interactions (kJ/mol) of calcite-fluids and fluids-fluids.

In the presence of a single layer of interfacial water, the van der Waals affinity of CO₂ and CH₄ for the calcite interface is lower than the systems free of water (Table 3). These data are consistent with the reduced number of first shell oxygen atoms corresponding to calcite with respect to the carbon atoms in CO₂ and CH₄. The number of oxygen atoms in calcite in the first shell of CO₂ decrease from 9 to about 3. Similarly, the number of oxygen atoms in calcite in the first shell of CO₂ decrease from 11 to about 4. The van der Waals and electrostatic affinity of CO₂ for the single layer of interfacial water compared to CH₄ is noted (Table 3).

When the number of water molecules in the calcite nanopore is increased to 500, the solvation of CO₂ and CH₄ in the confined water close to the calcite surface is noted from the overlap in the density distributions of gases with that of confined water (Figure 3C). The van der Waals affinity of gases corresponding to the solvation behavior increases with the increase in the number of water molecules (Table 3). The increase in the electrostatic energetic interactions of CO₂ with the calcite surface from −801 kJ/mol in the presence of a single layer of interfacial water to −1,412 kJ/mol in the presence of 500 water molecules is attributed to CO₂ solvation close to the calcite interface. The electrostatic interactions of methane with calcite in the presence of 500 water molecules are negligible.

The interaction of gases with the calcite surfaces are significantly reduced when the density of the interfacial water is similar to that of bulk water. The progressive reduction in the van der Waals affinity associated with CO₂ and CH₄ interactions with calcite with increasing water levels is noted (Table 3). This observation is consistent with the reduced number of oxygen atoms of calcite in the first coordination shell corresponding to C_gas-O_calcite. The number of oxygen atoms in calcite in the first shell of CO₂ or CH₄ are less than one when the density of interfacial water is similar to that of bulk water. Previous studies reported high van der Waals affinity of solvated gases for the solid interface (i.e., Na and Ca-montmorillonite) (see Schaef et al., 2013, 2015; Lee et al., 2014, 2015, 2017) with a pore size smaller than 1 nm. In this study, a pore size of 2 nm is simulated. With smaller pore sizes i.e., when the solid interfaces are closer, the overall energetic contributions arising from interactions with the solid interface may differ. In case of CO₂, the van der Waals and electrostatic interactions arising from interactions with water contribute to CO₂ solvation. However, the van der Waals interactions are the primary contributors to CH₄ solvation in confined water.

Conclusion

To provide a fundamental understating of the influence of hydration on CO₂ storage and CH₄ recovery from calcite nanopore, classical molecular dynamics simulations were performed. Introducing water molecules into the nanopores showed a significant impact on the dynamics and transport properties of CO₂ and CH₄. The preferential adsorption of water onto the calcite surface enabled the displacement of the adsorbed gases toward the center of the pore, which is an advantage for CH₄ recovery. Higher water concentrations facilitated the solvation of CO₂ molecules in the center of pore while CH₄ was found to phase separate at similar conditions. In the presence of water films at calcite interfaces, the density of CO₂ and CH₄ closer to the solid interface is higher compared to the center of the pore which is attributed to the van der Waals affinity in the case of CO₂ and CH₄ and, electrostatic affinity in the case of CO₂. Anisotropic diffusivities of CO₂ and CH₄ in specific water environments are attributed the differences in the directional free energy distributions, influence of solvation and the structure of confined water. While previous studies suggested that the diffusivities of gases vary in bulk and confined fluid environments, our results show that the extent of hydration has a strong influence on the adsorption and diffusivity of confined gases. With increasing interest in the recovery of gases such as CH₄ using water or storage of CO₂ by displacing pore fluids in the subsurface environments, understanding the changes in the organization, and transport of confined fluids is increasingly important as discussed in this study.

Author Contributions

SM performed the MD simulations and the analyses. GG developed the concept and assisted in writing the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer VG and handling editor declared their shared affiliation at the time of the review.

Acknowledgments

The authors gratefully acknowledge the Wisconsin Alumni Research Foundation and the College of Engineering at the University of Wisconsin, Madison for supporting this research effort.

References

Addari, D., and Satta, A. (2015). Influence of HCOO–on calcite growth from first principles. J. Phys. Chem. C 119, 19780–19788. doi: 10.1021/acs.jpcc.5b04161

CrossRef Full Text | Google Scholar

Argyris, D., Tummala, N. R., Striolo, A., and Cole, D. R. (2008). Molecular structure and dynamics in thin water films at the silica and graphite surfaces. J. Phys. Chem. C, 112, 13587–13599. doi: 10.1021/jp300679v

CrossRef Full Text | Google Scholar

Bachu, S., and Bennion, D. B. (2008). Interfacial tension between CO₂, freshwater, and brine in the range of pressure from (2 to 27) MPa, temperature from (20 to 125) C, and water salinity from (0 to 334 000) mg· L– 1. J. Chem. Eng. Data 54, 765–775. doi: 10.1021/je800529x

CrossRef Full Text | Google Scholar

Berendsen, H. J. C., Grigera, J. R., and Straatsma, T. P. (1987). The missing term in effective pair potentials. J. Phys. Chem. 91, 6269–6271. doi: 10.1021/j100308a038

CrossRef Full Text | Google Scholar

Bonnaud, P. A., Coasne, B., and Pellenq, R. J. (2010). Molecular simulation of water confined in nanoporous silica. J. Phys. Condens. Mat. 22:284110. doi: 10.1088/0953-8984/22/28/284110

PubMed Abstract | CrossRef Full Text | Google Scholar

Botan, A., Rotenberg, B., Marry, V., Turq, P., and Noetinger, B. (2010). Carbon dioxide in montmorillonite clay hydrates: thermodynamics, structure, and transport from molecular simulation. J. Phys. Chem. C 114, 14962–14969. doi: 10.1021/jp1043305

CrossRef Full Text | Google Scholar

Bovet, N., Yang, M., Javadi, M. S., and Stipp, S. L. S. (2015). Interaction of alcohols with the calcite surface. Phys. Chem. Chem. Phys. 17, 3490–3496. doi: 10.1039/C4CP05235H

PubMed Abstract | CrossRef Full Text | Google Scholar

BP Global (2015). BP Statistical Review of World Energy.

Bui, T., Phan, A., Cole, D. R., and Striolo, A. (2017). Transport mechanism of guest methane in water-filled nanopores. J. Phys. Chem. C 121, 15675–15686. doi: 10.1021/acs.jpcc.7b02713

CrossRef Full Text | Google Scholar

Côté, A. S., Darkins, R., and Duffy, D. M. (2015). Deformation twinning and the role of amino acids and magnesium in calcite hardness from molecular simulation. Phys. Chem. Chem. Phys. 17, 20178–20184. doi: 10.1039/C5CP03370E

PubMed Abstract | CrossRef Full Text | Google Scholar

Chakraborty, S., Kumar, H., Dasgupta, C., and Maiti, P. K. (2017). Confined water: structure, dynamics, and thermodynamics. Accounts Chem. Res. 50, 2139–2146. doi: 10.1021/acs.accounts.6b00617

PubMed Abstract | CrossRef Full Text | Google Scholar

Chialvo, A. A., Vlcek, L., and Cole, D. R. (2012). Aqueous CO₂ solutions at silica surfaces and within nanopore environments. Insights from isobaric–isothermal molecular dynamics. J. Phys. Chem. C 116, 13904–13916. doi: 10.1021/jp3001948

CrossRef Full Text | Google Scholar

Cole, D. R., Ok, S., Phan, A., Rother, G., Striolo, A., and Vlcek, L. (2013). Carbon-bearing fluids at nanoscale interfaces. Proc. Earth Plan. Sci. 7, 175–178. doi: 10.1016/j.proeps.2013.03.226

CrossRef Full Text | Google Scholar

Darden, T., York, D., and Pedersen, L. (1993). Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98, 10089–10092. doi: 10.1063/1.464397

CrossRef Full Text | Google Scholar

Duan, S., Gu, M., Du, X., and Xian, X. (2016). Adsorption equilibrium of CO₂ and CH₄ and their mixture on Sichuan basin shale. Energy Fuels 30, 2248–2256. doi: 10.1021/acs.energyfuels.5b02088

CrossRef Full Text | Google Scholar

Duan, Z., and Sun, R. (2003). An improved model calculating CO₂ solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 193, 257–271. doi: 10.1016/S0009-2541(02)00263-2

CrossRef Full Text | Google Scholar

Fang, T., Wang, M., Wang, C., Liu, B., Shen, Y., Dai, C., et al. (2017). Oil detachment mechanism in CO₂ flooding from silica surface: molecular dynamics simulation. Chem. Eng. Sci. 164, 17–22. doi: 10.1016/j.ces.2017.01.067

CrossRef Full Text | Google Scholar

Fazelabdolabadi, B., and Alizadeh-Mojarad, A. (2017). A molecular dynamics investigation into the adsorption behavior inside {001} kaolinite and {1014} calcite nano-scale channels: the case with confined hydrocarbon liquid, acid gases, and water. Appl. Nanosci. 7, 155–165. doi: 10.1007/s13204-017-0563-1

CrossRef Full Text | Google Scholar

Fenter, P., Geissbühler, P., DiMasi, E., Srajer, G., Sorensen, L. B., and Sturchio, N. C. (2000). Surface speciation of calcite observed in situ by high-resolution X-ray reflectivity. Geochim. Cosmochim. Acta 64, 1221–1228. doi: 10.1016/S0016-7037(99)00403-2

CrossRef Full Text | Google Scholar

Fenter, P., and Sturchio, N. C. (2004). Mineral–water interfacial structures revealed by synchrotron X-ray scattering. Prog. Surf. Sci. 77, 171–258. doi: 10.1016/j.progsurf.2004.12.001

CrossRef Full Text | Google Scholar

Franco, L. F., Castier, M., and Economou, I. G. (2016). Anisotropic parallel self-diffusion coefficients near the calcite surface: a molecular dynamics study. J. Chem. Phys. 145:084702. doi: 10.1063/1.4961408

PubMed Abstract | CrossRef Full Text | Google Scholar

Gadikota, G. (2018). “Multi-scale X-ray scattering for probing chemo-morphological coupling in pore-to-field and process scale energy and environmental applications,” in Small Angle Scattering and Diffraction, eds M. K. K. Dias Franco and F. Yokaichiya (London, UK: Intech Open), 71–83.

Gadikota, G., and Allen, A. (2018). “Microstructural and structural characterization of materials for CO₂ storage using multi-scale X-ray scattering methods,” in Materials and Processes for CO₂ Capture, Conversion, and Sequestration, eds L. Li and W. Wong-Ng (Hoboken, NJ: Wiley Books), 296–313.

Google Scholar

Gadikota, G., Dazas, B., Rother, G., Cheshire, M. C., and Bourg, I. C. (2017). Hydrophobic solvation of gases (CO₂, CH₄, H₂, noble gases) in clay interlayer nanopores. J. Phys. Chem. C 121, 26539–26550. doi: 10.1021/acs.jpcc.7b09768

CrossRef Full Text | Google Scholar

Geissbühler, P., Fenter, P., DiMasi, E., Srajer, G., Sorensen, L. B., and Sturchio, N. C. (2004). Three-dimensional structure of the calcite–water interface by surface X-ray scattering. Surf. Sci. 573, 191–203. doi: 10.1016/j.susc.2004.09.036

CrossRef Full Text | Google Scholar

Geysermans, P., and Noguera, C. (2009). Advances in atomistic simulations of mineral surfaces. J. Mater. Chem. 19, 7807–7821. doi: 10.1039/b903642c

CrossRef Full Text | Google Scholar

Glezakou, V.-A., and McGrail, B. P. (2013). “Density functional simulations as a tool to probe molecular interactions in wet supercritical CO₂,” in Applications of Molecular Modeling to Challenges in Clean Energy, Vol. 1133, eds G. Fitzgerald and N. Govind (Washington, DC: American Chemical Society), 31–49.

Google Scholar

Granick, S. (1991). Motions and relaxations of confined liquids. Science 253, 1374–1379. doi: 10.1126/science.253.5026.1374

PubMed Abstract | CrossRef Full Text | Google Scholar

Harris, J. G., and Yung, K. H. (1995). Carbon dioxide's liquid-vapor coexistence curve and critical properties as predicted by a simple molecular model. J. Phys. Chem. B 99, 12021–12024. doi: 10.1021/j100031a034

CrossRef Full Text | Google Scholar

Headen, T. F., and Boek, E. S. (2010). Molecular dynamics simulations of asphaltene aggregation in supercritical carbon dioxide with and without limonene. Energy Fuels 25, 503–508. doi: 10.1021/ef1010397

CrossRef Full Text | Google Scholar

Heberling, F., Trainor, T. P., Lützenkirchen, J., Eng, P., Denecke, M. A., and Bosbach, D. (2011). Structure and reactivity of the calcite–water interface. J. Colloid Interf. Sci. 354, 843–857. doi: 10.1016/j.jcis.2010.10.047

PubMed Abstract | CrossRef Full Text | Google Scholar

Herdes, C., Petit, C., Mejía, M. A., and Muller, E. A. (2018). Combined experimental, theoretical and molecular simulation approach for the description of the fluid phase behavior of hydrocarbon mixtures within shale rocks. Energy Fuels 32, 5750–5762. doi: 10.1021/acs.energyfuels.8b00200

CrossRef Full Text | Google Scholar

Ho, T. A., and Striolo, A. (2015). Water and methane in shale rocks: flow pattern effects on fluid transport and pore structure. AICHE J. 61, 2993–2999. doi: 10.1002/aic.14869

CrossRef Full Text | Google Scholar

Hoover, W. G. (1985). Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31:1695.

PubMed Abstract | Google Scholar

Hu, Y., Devegowda, D., Striolo, A., Phan, A., Ho, T. A., Civan, F., et al. (2015). The dynamics of hydraulic fracture water confined in nano-pores in shale reservoirs. J. Unconv. Oil Gas Resour. 9, 31–39. doi: 10.1016/j.juogr.2014.11.004

CrossRef Full Text | Google Scholar

Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: visual molecular dynamics. J. Mol. Graph. 14, 33–38. doi: 10.1016/0263-7855(96)00018-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishikawa, S., and Tsuchiya, N. (2017). Structure of interfacial water on quartz and its self-diffusion coefficient revealed by molecular dynamics simulations. Proc. Earth Plan. Sci. 17, 853–856. doi: 10.1016/j.proeps.2017.01.036

CrossRef Full Text | Google Scholar

Javanbakht, G., Sedghi, M., Welch, W., and Goual, L. (2015). Molecular dynamics simulations of CO₂/water/quartz interfacial properties: impact of CO₂ dissolution in water. Langmuir 31, 5812–5819. doi: 10.1021/acs.langmuir.5b00445

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnston, C. T. (2017). “Infrared studies of clay mineral-water interactions,” in Developments in Clay Science, Vol. 8, eds W. P. Gates, J. T. Kloprogge, J. Madejová, and F. Bergaya (Amsterdam: Elsevier), 288–309.

Google Scholar

Jorgensen, W. L., Maxwell, D. S., and Tirado-Rives, J. (1996). Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118, 11225–11236. doi: 10.1021/ja9621760

CrossRef Full Text | Google Scholar

Kadoura, A., Narayanan Nair, A. K., and Sun, S. (2016). Molecular dynamics simulations of carbon dioxide, methane, and their mixture in montmorillonite clay hydrates. J. Phys. Chem. C 120, 12517–12529. doi: 10.1021/acs.jpcc.6b02748

CrossRef Full Text | Google Scholar

Keller, K. S., Olsson, M. H. M., Yang, M., and Stipp, S. L. S. (2015). Adsorption of ethanol and water on calcite: dependence on surface geometry and effect on surface behavior. Langmuir 31, 3847–3853. doi: 10.1021/la504319z

PubMed Abstract | CrossRef Full Text | Google Scholar

Le, T., Striolo, A., and Cole, D. R. (2015a). CO₂-C₄H₁₀ mixtures simulated in silica slit pores: relation between structure and dynamics. J. Phys. Chem. C 119, 15274–15284. doi: 10.1021/acs.jpcc.5b03160

CrossRef Full Text | Google Scholar

Le, T., Striolo, A., and Cole, D. R. (2015b). Propane simulated in silica pores: adsorption isotherms, molecular structure, and mobility. Chem. Eng. Sci. 121, 292–299. doi: 10.1016/j.ces.2014.08.022

CrossRef Full Text | Google Scholar

Le, T., Striolo, A., Turner, C. H., and Cole, D. R. (2017). Confinement effects on carbon dioxide methanation: a novel mechanism for abiotic methane formation. Sci. Rep. 7:9021. doi: 10.1038/s41598-017-09445-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Le, T. T. B., Striolo, A., Gautam, S. S., and Cole, D. R. (2017). Propane–water mixtures confined within cylindrical silica nanopores: structural and dynamical properties probed by molecular dynamics. Langmuir 33, 11310–11320. doi: 10.1021/acs.langmuir.7b03093

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, M. S., McGrail, B. P., and Glezakou, V. A. (2014). Microstructural response of variably hydrated Ca-rich montmorillonite to supercritical CO₂. Environ. Sci. Technol. 48, 8612–8619. doi: 10.1021/es5005889

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, M. S., McGrail, B. P., Rousseau, R., and Glezakou, V. A. (2017). Molecular level investigation of CH₄ and CO₂ adsorption in hydrated calcium–montmorillonite. J. Phys. Chem. C 122, 1125–1134. doi: 10.1021/acs.jpcc.7b05364

CrossRef Full Text | Google Scholar

Lee, M. S., Peter McGrail, B., Rousseau, R., and Glezakou, V. A. (2015). Structure, dynamics and stability of water/scCO₂/mineral interfaces from ab initio molecular dynamics simulations. Sci. Rep. 5:14857. doi: 10.1038/srep14857

PubMed Abstract | CrossRef Full Text | Google Scholar

Lithoxoos, G. P., Labropoulos, A., Peristeras, L. D., Kanellopoulos, N., Samios, J., and Economou, I. G. (2010). Adsorption of N₂, CH₄, CO and CO₂ gases in single walled carbon nanotubes: a combined experimental and Monte Carlo molecular simulation study. J. Supercrit. Fluid 55, 510–523. doi: 10.1016/j.supflu.2010.09.017

CrossRef Full Text | Google Scholar

Liu, B., Shi, J., Sun, B., Shen, Y., Zhang, J., Chen, X., et al. (2015). Molecular dynamics simulation on volume swelling of CO₂-alkane system. Fuel 143, 194–201. doi: 10.1016/j.fuel.2014.11.046

CrossRef Full Text | Google Scholar

Liu, B., Shi, J., Wang, M., Zhang, J., Sun, B., Shen, Y., et al. (2016). Reduction in interfacial tension of water–oil interface by supercritical CO₂ in enhanced oil recovery processes studied with molecular dynamics simulation. J. Supercrit. Fluid 111, 171–178. doi: 10.1016/j.supflu.2015.11.001

CrossRef Full Text | Google Scholar

Liu, K., Ostadhassan, M., Zhou, J., Gentzis, T., and Rezaee, R. (2017). Nanoscale pore structure characterization of the Bakken shale in the USA. Fuel 209, 567–578. doi: 10.1016/j.fuel.2017.08.034

CrossRef Full Text | Google Scholar

Liu, L., Nicholson, D., and Bhatia, S. K. (2015). Adsorption of CH₄ and CH₄/CO₂ mixtures in carbon nanotubes and disordered carbons: a molecular simulation study. Chem. Eng. Sci. 121, 268–278. doi: 10.1016/j.ces.2014.07.041

CrossRef Full Text | Google Scholar

Makaremi, M., Jordan, K. D., Guthrie, G. D., and Myshakin, E. M. (2015). Multiphase Monte Carlo and molecular dynamics simulations of water and CO₂ intercalation in montmorillonite and beidellite. J. Phys. Chem. C 119, 15112–15124. doi: 10.1021/acs.jpcc.5b01754

CrossRef Full Text | Google Scholar

Malikova, N., Cadène, A., Marry, V., Dubois, E., and Turq, P. (2006). Diffusion of water in clays on the microscopic scale: modeling and experiment. J. Phys. Chem. B 110, 3206–3214. doi: 10.1021/jp056954z

PubMed Abstract | CrossRef Full Text | Google Scholar

Meldrum, F. C., and Cölfen, H. (2008). Controlling mineral morphologies and structures in biological and synthetic systems. Chem. Rev. 108, 4332–4432. doi: 10.1021/cr8002856

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammed, S., and Mansoori, G. A. (2018a). Effect of CO2 on the interfacial and transport properties of water/binary and asphaltenic oils: insights from molecular dynamics. Energy Fuels 32, 5409–5417. doi: 10.1021/acs.energyfuels.8b00488

CrossRef Full Text | Google Scholar

Mohammed, S., and Mansoori, G. A. (2018b). The role of supercritical/dense CO₂ Gas in altering aqueous/oil interfacial properties: a molecular dynamics study. Energy Fuels 32, 2095–2103. doi: 10.1021/acs.energyfuels.7b03863

CrossRef Full Text | Google Scholar

Mohammed, S., and Mansoori, G. A. (2018c). Molecular insights on the interfacial and transport properties of supercritical CO₂/brine/crude oil ternary system. J. Mol. Liq. 263, 268–273. doi: 10.1016/j.molliq.2018.05.009

CrossRef Full Text | Google Scholar

Molyanyan, E., Aghamiri, S., Talaie, M. R., and Iraji, N. (2016). Experimental study of pure and mixtures of CO₂ and CH₄ adsorption on modified carbon nanotubes. Int. J. Environ. Sci. Technol. 13, 2001–2010. doi: 10.1007/s13762-016-0989-0

CrossRef Full Text | Google Scholar

Moultos, O. A., Tsimpanogiannis, I. N., Panagiotopoulos, A. Z., and Economou, I. G. (2014). Atomistic molecular dynamics simulations of CO₂ diffusivity in H₂O for a wide range of temperatures and pressures. J. Phys. Chem. B 118, 5532–5541. doi: 10.1021/jp502380r

CrossRef Full Text | Google Scholar

Moultos, O. A., Tsimpanogiannis, I. N., Panagiotopoulos, A. Z., and Economou, I. G. (2016). Self-diffusion coefficients of the binary (H₂O+ CO₂) mixture at high temperatures and pressures. J. Chem. Thermodyn. 93, 424–429. doi: 10.1016/j.jct.2015.04.007

CrossRef Full Text | Google Scholar

Mutisya, S. M., Kirch, A., de Almeida, J. M., Sánchez, V. M., and Miranda, C. R. (2017). Molecular dynamics simulations of water confined in calcite slit pores: an NMR spin relaxation and hydrogen bond analysis. J. Phys. Chem. C 121, 6674–6684. doi: 10.1021/acs.jpcc.6b12412

CrossRef Full Text | Google Scholar

Myshakin, E. M., Saidi, W. A., Romanov, V. N., Cygan, R. T., and Jordan, K. D. (2013). Molecular dynamics simulations of carbon dioxide intercalation in hydrated Na-montmorillonite. J. Phys. Chem. C 117, 11028–11039. doi: 10.1021/jp312589s

CrossRef Full Text | Google Scholar

Nosé, S. (1984). A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 52, 255–268. doi: 10.1080/00268978400101201

CrossRef Full Text | Google Scholar

Obliger, A., Ulm, F. J., and Pellenq, R. J. M. (2018). Impact of nanoporosity on hydrocarbon transport in shales' organic matter. Nano Lett. 18, 832–837. doi: 10.1021/acs.nanolett.7b04079

PubMed Abstract | CrossRef Full Text | Google Scholar

Ou, X., Li, J., and Lin, Z. (2014). Dynamic behavior of interfacial water on Mg (OH)₂ (001) surface: a molecular dynamics simulation work. J. Phys. Chem. C 118, 29887–29895. doi: 10.1021/jp509373d

CrossRef Full Text | Google Scholar

Parrinello, M., and Rahman, A. (1982). Strain fluctuations and elastic constants. J. Chem. Phys. 76, 2662–2666. doi: 10.1063/1.443248

CrossRef Full Text | Google Scholar

Peng, D. Y., and Robinson, D. B. (1976). A new two-constant equation of state. Ind. Eng. Chem. Fund. 15, 59–64. doi: 10.1021/i160057a011

CrossRef Full Text | Google Scholar

Rao, Q., and Leng, Y. (2016). Molecular understanding of CO₂ and H₂O in a montmorillonite clay interlayer under CO₂ geological sequestration conditions. J. Phys. Chem. C, 120, 2642–2654. doi: 10.1021/acs.jpcc.5b09683

CrossRef Full Text | Google Scholar

Relat-Goberna, J., and Garcia-Manyes, S. (2015). Direct observation of the dynamics of self-assembly of individual solvation layers in molecularly confined liquids. Phys. Rev. Lett. 114:258303. doi: 10.1103/PhysRevLett.114.258303

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryckaert, J. P., Ciccotti, G., and Berendsen, H. J. (1977). Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23, 327–341. doi: 10.1016/0021-9991(77)90098-5

CrossRef Full Text | Google Scholar

Saha, D., Bao, Z., Jia, F., and Deng, S. (2010). Adsorption of CO₂, CH₄, N₂O, and N₂ on MOF-5, MOF-177, and zeolite 5A. Environ. Sci. Technol. 44, 1820–1826. doi: 10.1021/es9032309

CrossRef Full Text | Google Scholar

Sakamaki, R., Sum, A. K., Narumi, T., Ohmura, R., and Yasuoka, K. (2011). Thermodynamic properties of methane/water interface predicted by molecular dynamics simulations. J. Chem. Phys. 134:144702. doi: 10.1063/1.3579480

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaef, H. T., Glezakou, V. A., Owen, A. T., Ramprasad, S., Martin, P. F., and McGrail, B. P. (2013). Surface condensation of CO₂ onto kaolinite. Environ. Sci. Tech. Lett. 1, 142–145. doi: 10.1021/ez400169b

CrossRef Full Text | Google Scholar

Schaef, H. T., Loring, J. S., Glezakou, V. A., Miller, Q. R., Chen, J., Owen, A. T., et al. (2015). Competitive sorption of CO₂ and H₂O in 2: 1 layer phyllosilicates. Geochim. Cosmochim. Acta 161, 248–257. doi: 10.1016/j.gca.2015.03.027

CrossRef Full Text | Google Scholar

Simoes Santos, M., Franco, L., Castier, M., and Economou, I. G. (2018). Molecular dynamics simulation of n-alkanes and CO₂ confined by calcite nanopores. Energy Fuels 32, 1934–1941. doi: 10.1021/acs.energyfuels.7b02451

CrossRef Full Text | Google Scholar

Skarmoutsos, I., Tamiolakis, G., and Froudakis, G. E. (2013). Carbon-based nanoporous networks as media for the separation of CO₂/CH₄ mixtures: a molecular dynamics approach. J. Phys. Chem. C 117, 19373–19381. doi: 10.1021/jp401978m

CrossRef Full Text | Google Scholar

Striolo, A., and Cole, D. R. (2017). Understanding shale gas: recent progress and remaining challenges. Energy Fuels 31, 10300–10310. doi: 10.1021/acs.energyfuels.7b01023

CrossRef Full Text | Google Scholar

Sun, H., Sun, W., Zhao, H., Sun, Y., Zhang, D., Qi, X., et al. (2016a). Adsorption properties of CH₄ and CO₂ in quartz nanopores studied by molecular simulation. RSC Adv. 6, 32770–32778. doi: 10.1039/C6RA05083B

CrossRef Full Text | Google Scholar

Sun, H., Zhao, H., Qi, N., and Li, Y. (2017). Effects of surface composition on the microbehaviors of CH₄ and CO₂ in slit-nanopores: a simulation exploration. ACS Omega 2, 7600–7608. doi: 10.1021/acsomega.7b01185

CrossRef Full Text | Google Scholar

Sun, H., Zhao, H., Qi, N., Qi, X., Zhang, K., Sun, W., et al. (2016b). Mechanistic insight into the displacement of CH₄ by CO₂ in calcite slit nanopores: the effect of competitive adsorption. RSC Adv. 6, 104456–104462. doi: 10.1039/C6RA23456A

CrossRef Full Text | Google Scholar

Versteeg, G. F., and Van Swaaij, W. P. (1988). Solubility and diffusivity of acid gases (carbon dioxide, nitrous oxide) in aqueous alkanolamine solutions. J. Chem. Eng. Data 33, 29–34. doi: 10.1021/je00051a011

CrossRef Full Text | Google Scholar

Vlcek, L., Chialvo, A. A., and Cole, D. R. (2011). Optimized unlike-pair interactions for water–carbon dioxide mixtures described by the SPC/E and EPM2 models. J. Phys. Chem. B 115, 8775–8784. doi: 10.1021/jp203241q

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Wang, X., Jin, X., and Cao, D. (2016). Molecular dynamics simulation of diffusion of shale oils in montmorillonite. J. Phys. Chem. C 120, 8986–8991. doi: 10.1021/acs.jpcc.6b01660

CrossRef Full Text | Google Scholar

Wang, S., Feng, Q., Javadpour, F., and Yang, Y. B. (2016a). Breakdown of fast mass transport of methane through calcite nanopores. J. Phys. Chem. C 120, 14260–14269. doi: 10.1021/acs.jpcc.6b05511

CrossRef Full Text | Google Scholar

Wang, S., Feng, Q., Zha, M., Javadpour, F., and Hu, Q. (2017). Supercritical methane diffusion in shale nanopores: effects of pressure, mineral types, and moisture content. Energy Fuels 32, 169–180. doi: 10.1021/acs.energyfuels.7b02892

CrossRef Full Text | Google Scholar

Wang, S., Zhou, G., Ma, Y., Gao, L., Song, R., Jiang, G., et al. (2016b). Molecular dynamics investigation on the adsorption behaviors of H₂O, CO₂, CH₄ and N₂ gases on calcite (1 1⁻ 0) surface. Appl. Surf. Sci. 385, 616–621. doi: 10.1016/j.apsusc.2016.05.026

CrossRef Full Text | Google Scholar

Wiesenburg, D. A., and Guinasso, N. L. Jr. (1979). Equilibrium solubilities of methane, carbon monoxide, and hydrogen in water and sea water. J. Chem Eng. Data, 24, 356–360. doi: 10.1021/je60083a006

CrossRef Full Text | Google Scholar

Wu, H., Chen, J., and Liu, H. (2015). Molecular dynamics simulations about adsorption and displacement of methane in carbon nanochannels. J. Phys. Chem. C, 119, 13652–13657.

Google Scholar

Xiao, S. E., Edwards, S. A., and Grater, F. (2011). A new transferable forcefield for simulating the mechanics of CaCO₃ crystals. J. Phys. Chem. C 115, 20067–20075. doi: 10.1021/jp202743v

CrossRef Full Text | Google Scholar

Xing, J., Hu, S., Jiang, Z., Wang, X., Wang, J., Sun, L., et al. (2018). Classification of controlling factors and determination of a prediction model for shale gas adsorption capacity: a case study of Chang 7 shale in the Ordos Basin. J. Nat. Gas. Sci. Eng. 49, 260–274. doi: 10.1016/j.jngse.2017.11.015

CrossRef Full Text | Google Scholar

Xu, T., Apps, J. A., and Pruess, K. (2005). Mineral sequestration of carbon dioxide in a sandstone–shale system. Chem. Geol. 217, 295–318. doi: 10.1016/j.chemgeo.2004.12.015

CrossRef Full Text | Google Scholar

Yang, N., Liu, S., and Yang, X. (2015). Molecular simulation of preferential adsorption of CO₂ over CH₄ in Na-montmorillonite clay material. Appl. Surf. Sci. 356, 1262–1271. doi: 10.1016/j.apsusc.2015.08.101

CrossRef Full Text | Google Scholar

Yasuda, K., Mori, Y. H., and Ohmura, R. (2016). Interfacial tension measurements in water– methane system at temperatures from 278.15 K to 298.15 K and pressures up to 10 MPa. Fluid Phase Equilibr. 413, 170–175. doi: 10.1016/j.fluid.2015.10.006

CrossRef Full Text | Google Scholar

Yuan, Q., Zhu, X., Lin, K., and Zhao, Y. P. (2015). Molecular dynamics simulations of the enhanced recovery of confined methane with carbon dioxide. Phys. Chem. Chem. Phys. 17, 31887–31893. doi: 10.1039/C5CP06649B

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, L., Lin, S., Mendenhall, J. D., Yuet, P. K., and Blankschtein, D. (2011). Molecular dynamics investigation of the various atomic force contributions to the interfacial tension at the supercritical CO₂-water interface. J. Phys. Chem. B 115, 6076–6087. doi: 10.1021/jp201190g

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhong, J., Chen, G., Lv, C., Yang, W., Xu, Y., Yang, S., et al. (2016). Experimental study of the impact on methane adsorption capacity of continental shales with thermal evolution. J. Nat. Gas Geosci. 1, 165–172. doi: 10.1016/j.jnggs.2015.12.001

CrossRef Full Text | Google Scholar