“Bristle-State” Friction: Modeling Slip Initiation and Transient Frictional Evolution From High-Velocity Earthquake Rupture Experiments

Fracture mechanics theory and seismological observations suggest that slip-rate is constantly changing during earthquake rupture, including dramatic acceleration from static conditions to high velocity sliding followed by deceleration and arrest. This slip history is partly determined by a complex frictional evolution, including overcoming peak friction, rapid weakening, and re-strengthening (or healing). Recent experimental developments have allowed friction evolution measurements under realistic slip histories reaching high co-seismic slip-rates of meters per second. Theoretical work has focused on describing the observed steady-state weakening at these high-velocities, but the transient behavior has only been fit by direct parameterizations without state variable dependence, needed to simulate arbitrary slip-histories. Commonly used forms of rate-state friction (RSF) are based on low-velocity, step-change experiments and have been shown to not fit the entire frictional evolution using a single set of realistic parameters. Their logarithmic form precludes zero fault slip-rate, assuming it is never truly static, thus does not capture slip initiation phenomena that might contribute to nucleation behavior. Inverting high slip-rate and friction data from different types of experiments, we show that RSF can work by using parameter ranges far from typical low-velocity values. In comparison, we introduce “bristle-state” friction (BSF) models, developed by control-system engineers to predict the transient frictional evolution during arbitrary stressing, especially reversals through static conditions. Although BSF models were also designed for low-velocities, we show that their form provides advantages for fitting frictional evolution measurements under high slip-rate, long-displacement, non-trivial slip histories, especially during the initial strengthening stage.

Introduction: Frictional Evolution Stages and Sliding Regimes During Earthquake Rupture

Earthquake nucleation and rupture models implement constitutive relations to represent the frictional response to transient slip pulses. However, these frictional models have been tested almost exclusively on steady-state measurements and simple velocity-step experiments of the transition between them (Scholz, 2019). In contrast, kinematic inversions of seismic and geodetic data (Wald, 1996) or fracture mechanics theory (Tinti et al., 2005) estimate fault slip histories during earthquakes that never reach steady-state, as the slip-rate is continuously changing—first accelerating dramatically from static to high-velocity unstable sliding, followed by deceleration and arrest—all within a short event duration. Frictional resistance to these changes in slip-rate follow a common set of stages. First, to undergo unstable sliding, shear stress must reach and overcome peak friction (Pennestrı̀ et al., 2016), appearing as an initial strengthening. With accelerating slip, the fault then experiences significant weakening, potentially due to powder lubrication (Reches and Lockner, 2010), grain fragmentation to weaker phases (Hung et al., 2019; Rattez and Veveakis, 2019), acoustic fluidization (Van der Elst et al., 2012), flash-heating (Goldsby and Tullis, 2011; Kitajima et al., 2011), frictional melt (Niemeijer et al., 2011), and/or other chemical processes (Violay et al., 2013). As the slip deficit is used up, fault slip must decelerate and friction will re-strengthen or heal (Violay et al., 2019), allowing seismologically-inferred self-healing pulsed slip behavior (Heaton, 1990) and larger dynamic than static stress drops (Brune, 1970). Recent experimental developments (Di Toro et al., 2004; Hirose and Shimamoto, 2005; Reches and Lockner, 2010) have allowed measurement of friction evolution under these non-trivial slip histories, reaching co-seismic slip-rates of meters per second; Figure 1 shows an example.

FIGURE 1

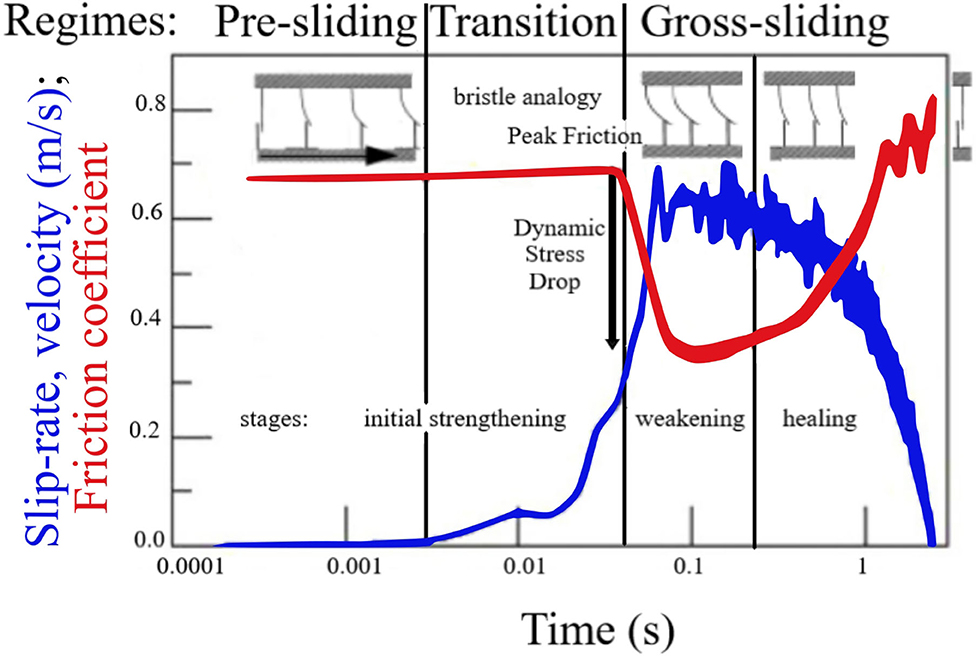
Figure 1. Conceptual cartoon describing the bristle analogy for internal state variable evolution and different sliding regimes as applied to a conception of earthquake rupture process. Fault frictional evolution stages (initial strengthening, weakening, and healing) are labeled within the figure, while the corresponding sliding regimes are organized on top. Motivated by Figure 2E of Liao and Reches (2019), frictional data from a spinning flywheel impact experiment on a Sierra White granite sample [run 733 from Chang et al. (2012)]. The logarithmic time scale (x axis) enhances the evolution at early times and the initial strengthening stage, it also makes the initial acceleration look less dramatic in comparison to the deceleration. Motivating data are plotted with a linear time scale with inversions in the Supplement.

Of these stages, transient frictional evolution in the initial strengthening stage, during nucleation, is particularly understudied, because it is short-lived (Liao and Reches, 2019). Consequently, many fault friction models leave it out entirely (Supplement 1). Although long observed, recent high-velocity experiments suggest initial strengthening could be larger than previously thought (Sone and Shimamoto, 2009). This is partly due to the special experimental attention needed to accurately measure static friction, where slip initiates, separate from the increase in applied shear stress during initial elastic loading. The initial increase in strength (friction) has been suggested to act as a barrier to rupture growth, playing a part in final earthquake magnitude and slip complexity (Lapusta, 2009). Recent geodetic observations suggest that stress increase due to slow, aseismic “preslip” occurring adjacent to the nucleation zone may be an important component of spontaneous earthquake generation (Roeloffs, 2006; Socquet et al., 2017). Further support for this “preslip” hypothesis comes from laboratory nucleation experiments (Latour et al., 2013; McLaskey et al., 2015; Passelègue et al., 2016; Svetlizky et al., 2018), where precursory slip has been observed proceeding “labquakes” of different scales, materials, and conditions. Understanding how friction evolves in the nucleation stage warrants revisiting friction models designed for slip initiation.

While the stages of frictional evolution summarize experimental rupture observations, they lack a framework for broader frictional phenomenon and parameterizations. In tribology, common behaviors from a wide-range of interfacial observations have been organized into different regimes: pre-sliding, gross-sliding, and the transition between them (Al-Bender et al., 2004). As shown in Figure 1, the regime organization focuses more on slip initiation, compared to fault models which commonly only address gross-sliding. During pre-sliding, slip fronts propagate along the interface, yet some elastically-coupled contacts remain stuck, holding back the entire fault segment from unstable sliding (Svetlizky et al., 2018). In gouge, force chains conceptually fit this role (Lyu et al., 2019). Also referred to as partial slip or incipient sliding, the friction force shows a nonlinear, hysteretic dependence on bulk displacement (Selvadurai et al., 2017). Hertz-Mindlin contacts (Mindlin, 1949) can capture this non-linearity and have been modeled in geomechanics and rock physics (Boitnott et al., 1992; Saltiel et al., 2017a), but not earthquake rupture. Although non-linear, the pre-sliding regime is still dominated by elastically stuck asperities; peak friction, or breakaway force, occurs after the interface starts to yield, failing though fracture (Chen et al., 2020) or other processes depending on conditions. Capturing this transition regime, also referred to as “stiction,” is critical to modeling velocity reversals (as static conditions are reached each time before re-accelerating in the opposite direction) (Saltiel et al., 2017b). Fault slip is not commonly thought to reverse, except potentially from overshoot (Brodsky et al., 2020), but “stiction” is also relevant during initiation from static. Friction increases over a finite slip to a peak above the steady-state curve, then evolves to gross-sliding conditions (Al-Bender et al., 2004). The main gross-sliding observations, well-established in velocity-steps, are steady-state rate-dependence and frictional lag, the transition toward a new steady-state. In this regime asperities are constantly broken and remade, friction depends on slip-rate and contact history, often tracked through the evolution of an internal state variable (Supplement 1.2).

To the authors' knowledge this sliding regime framework is new to earthquake source physics, and common fault friction models lack mechanics of slip initiation. There are very few models that attempt to quantitatively fit the transient behavior during all three evolution stages (Supplement 1.5). In order to address these issues, we introduce to the geophysics community the bristle analogy for frictional state (Dahl, 1976) as well as a group of models we term “bristle-state,” designed to capture all three sliding regimes. We then derive an analytical form for state evolution assuming no elastic coupling. Finally, we test the ability of these models to capture high-velocity measurements of frictional evolution during simulated earthquake rupture.

Methods: Friction Parameterizations and Analytical Solution

“Bristle-State” Friction Formulation Development and Components

Given the challenges of modeling all the sliding regimes with current fault friction laws (reviewed in Supplement 1), we explore alternative parameterizations, from the control-systems engineering community, designed to predict friction during arbitrary driving stresses. A group of models have been used to capture all the sliding regime behaviors using the analogy of bristles on a brush which must bend elastically before the brush can begin gross-sliding (Aström and De Wit, 2008). As their nomenclature can be confusing, we introduce the name “bristle-state” friction (BSF), to refer to state-variable models that employ this bristle analogy, where state is the average deflection of asperity bristles (Pennestrı̀ et al., 2016). It is not to be confused with other models based on this analogy, such as the Bristle Model (Haessig and Friedland, 1991) or the Compressed Bristle Model (Drincic and Bernstein, 2012), but use different mathematical forms to represent asperities as a population of elastic bristles with a range of stiffness. BSF models retain rate and state dependence, thus are straightforward to compare with standard rate-state friction (RSF) formulations (Supplement 1.2) for fault settings. Also like RSF, these models were proposed for purely empirical (i.e., curve fitting) reasons. We appreciate the need for physics-based models (Supplement 1.3), but argue for the importance of empirical parameterizations, especially given the complex and diverse relevant fault conditions and processes. BSF's conceptual attraction is its flexibility for attributing types of deformational processes (i.e., elastic, plastic) without trying to prescribe specific mechanisms (i.e., fracture, melt). In the following, we briefly discuss their historical and conceptual development, highlighting the origin of each term and what it was designed to capture.

Dahl Model

Observations of frictional lag first necessitated models of friction outside of steady-state. Dahl (1968) introduced the internal state variable dependence through a differential equation, which was later incorporated by Dieterich (1979) in what became the RSF model widely used to describe rock friction. While RSF was designed to describe experiments of step changes in velocity, Dahl's model was designed for transitioning through static conditions as a ball bearing rolls back and forth (Dahl, 1976). This simulates pre-sliding and the associated hysteresis, equivalently described by a lag in the friction force when there is a change in the direction of motion. The Dahl model also introduces the bristle deflection analogy for the internal state variable—the load initially deforms the asperities elastically, like bristles, until gross-sliding brings permanent displacement. This analogy directly addresses the ‘stiction' phase through the asperities' elastic range (Pennestrı̀ et al., 2016). This linear elasticity is clear through the proportionality between the current friction coefficient (μ) and bristle deflection, or state, (θ):

$\begin{array}{ll}\mu (\theta )={\alpha }_0\theta ,& (1)\end{array}$

where α₀ is bristle stiffness. The state variable evolves according to the following equation:

$\begin{array}{ll}\frac{d\theta }{dt}=v-\frac{{\alpha }_0|v|\theta }{{\mu }_k},& (2)\end{array}$

where v is the sliding velocity and μ_k is the constant kinetic friction coefficient. While the Dahl model introduces the internal state variable, its bristle analogy, and the differential equation form of state evolution, it is designed for the pre-sliding regime, so it has no steady-state velocity dependence. This can be easily seen by setting the state evolution equation to zero (as is the case for steady-state) and the velocity dependence drops out.

Stribeck Curve

The classic Stribeck curve is a steady-state velocity curve which includes the observation of increased static friction around zero velocity, then weakens with velocity before increasing again in velocity strengthening behavior at high velocity (Stribeck, 1902). This was observed in lubricated friction, where the weakening is attributed to building up hydrodynamic pressure (and thus lower effective normal stress), transitioning to strengthening as the lubricating film grows thicker and must be viscously sheared. Later observed in dry friction settings, the term “viscous friction” coefficient (α₃) has remained, for the proportionality between velocity (or strain-rate) and friction (Al-Bender et al., 2004). The Stribeck friction model gives steady-state friction (μ_ss):

$\begin{array}{ll}{\mu }_{ss}=\left[{\mu }_c+({\mu }_s-{\mu }_c)e^{-{(\frac{v}{v_s})}^2}\right]sgn(v)+{\alpha }_{3}v,& (3)\end{array}$

where μ_c is the Coulomb friction coefficient, μ_s is the static friction coefficient, and v_s is the Stribeck velocity. It can be seen that the peak friction coefficient is μ_s, while the local minimum is μ_c, and v_s defines the velocities over which the first term dominates, while α₃v takes over as velocity increases (Liu et al., 2015). A negative α₃ gives high-velocity rate-weakening behavior. The simple linear velocity dependence of steady-state friction at velocities v > >v_s is retained in the BSF model described below, and is responsible for its shortcomings in fitting steady-state friction data (Supplement 2).

Stribeck is a single variable (velocity) dependent friction model, which describes the steady-state velocity weakening and strengthening curves as well as the stiction phase. Since it lacks state variable dependence it cannot describe frictional lag or hysteresis.

“Bristle-State” Friction

By adding the Stribeck curve to the Dahl model, de Wit et al. (1993) created a model that could capture the common observations of all three sliding regimes, including steady-state, hysteresis and lag, stiction, as well as stick-slip motion. They called it the modified Dahl model, and it is an example of an integrated friction model, incorporating a variety of frictional phenomena into a single formulation (Al-Bender et al., 2004). The functional form clearly combines aspects of the previous formulations:

$\begin{array}{llll}\mu (v(t),\theta (t))& =& a_{3}v(t)+a_0\theta (t)& (4)\end{array}$

$\begin{array}{llll}\frac{d\theta (t)}{dt}& =& -\frac{\left|v(t)\right|\theta (t)}{L}+\frac{a_{1}v(t)}{L}+\frac{a_{2}v(t)}{L}{e}^{-{(\frac{v(t)}{v_s})}^2},& (5)\end{array}$

where μ is the current friction coefficient; a₃ is now the viscous friction parameter with units of s/m, related to α₃ above; a₀ is the bristle stiffness, related to α₀, which we set to unity, absorbing it into the state variable, and thus drop for the rest of this study; L is a constant with dimensions of length, related to D in RSF (Supplement 1.2); v_s is the characteristic (Stribeck) velocity, described above; a₁ is the Coulomb friction parameter; related to μ_c; and a₂ is the Stribeck friction parameter, related to μ_s – μ_c, and defines the weight of the stiction effect. In this study, we only use positive velocities so |v(t)| is replaced by v(t). Although the state variable has the interpretation of the average deflection of the bristles, by absorbing the stiffness, a₀, into the state variable it takes on the units of friction coefficient or unit-less, ensuring that a₁ and a₂ are also unit-less.

We refer to this model as an example “bristle-state” model in an effort to define a group of similar models that vary slightly in form but use the same analogy for internal state variable and the integrated approach. The more common, but more complex, example (LuGre) is given in the Supplement 1.4. Modified Dahl was previously implemented to fit measurements of shear stress oscillations on rock fractures in the pre-sliding regime (Saltiel et al., 2017b), but to the authors' knowledge these models have not otherwise been applied to geophysical problems.

Analytical Solution of State Evolution Equations for Direct Velocity Forcing

To test the hypothesis that the BSF model can better capture the initiation and transient friction evolution during realistic rupture experiments, we quantitatively invert a range of high-velocity datasets. Following the interpretations of the original experimental papers, and in an effort to simplify our analysis and focus purely on the frictional evolution, we assume that the measurements give the slip-rate history on the interface. This allows us to apply the constitutive relations to a single slider block without a driving spring, eliminating the coupling between sliding velocity and friction from a spring's finite compliance. We can thus also neglect inertia in the force balance.

Our approach assumes that the experiments give the fault zone's effective frictional response to a realistic slip history, providing the opportunity to test which models can produce the observed frictional evolution for that specific slip history. In a way, the elastic aspects of the BSF model design allow for an elastic response in the fault zone, which can be interpreted as the scale of the entire experimental apparatus, not the interface's asperity scale. We acknowledge that these assumptions and the friction laws do not explicitly represent the physical processes occurring during earthquake rupture, or even in the experiments. Our empirical approach is to represent the phenomenon mathematically, not explain them physically. By finding a constitutive relation that captures the frictional evolution, it can be applied to finite rupture models to explore the importance of frictional changes within the context of the entire elastodynamic problem.

These assumptions are useful because they simplify the inversion and minimize the number of free parameters, including stiffness and inertia would add under-constrained parameters. By applying the driving velocity directly to the interface as a sliding velocity, the differential equation for state evolution can be solved to give the state variable in the analytical function:

$\begin{array}{l}\theta (v(t))=e^{{\int }_0^t\text{}-\text{}\frac{v(\xi )}{L}d\xi }{\displaystyle {\int }_0^t\frac{v(\zeta )[a_1{e}^{{\int }_0^{\zeta }\frac{v(\xi )}{L}d\xi }+a_2{e}^{-\frac{v{(\zeta )}^2}{v_s^2}-{\int }_0^{\zeta }\frac{v(\xi )}{L}d\xi }{}_{]}}{L}}\\ d\zeta +c{e}^{{\int }_0^t-\frac{v(\xi )}{L}d\xi }, or\\ \mu (v(t))=a_{3}v(t)\\ +e^{G(v(t))}{\displaystyle {\int }_0^t\frac{v(\zeta )[a_1{e}^{-H(v(t))}+a_2{e}^{-\frac{v{(\zeta )}^2}{v_s^2}}{e}^{-H(v(t))}{}_{]}}{L}}d\zeta +c{e}^{G(v(t))},& (6)\end{array}$

where the functions $G(v(t))={\int }_0^t-\frac{v(\xi )}{L}d\xi$ and $H(v(t))={\int }_0^{\zeta }-\frac{v(\xi )}{L}d\xi$, give the effect of the specific slip-rate history, and c is an integration constant that gives the initial friction at zero sliding velocity. Although the integrals require numerical calculation, this analytical form allows direct calculation of the friction force given a slip-rate history. In comparison, when using the fully coupled differential equations, including spring stiffness, the slip-rate needs to be solved for as well as friction.

This same analysis undertaken with the RSF aging law ($\frac{d\theta }{dt}=1-\frac{\theta (t)v(t)}{D}$) is illuminating, because it is equivalent to the state evolution for the BSF model ($\frac{d\theta }{dt}=-\frac{v(t)\theta (t)}{L}+\frac{a_{1}v(t)}{L}+\frac{a_{2}v(t)}{L}{e}^{-{(\frac{v(t)}{v_s})}^2}$) when the final two terms are equal to 1. Equivalent analysis gives the following analytical solution for state in the RSF aging law:

$\begin{array}{l}\theta \left(v\left(t\right)\right)=e^{{\int }_0^t-\frac{v\left(\xi \right)}{D}d\xi }{\displaystyle {\int }_0^t{e}^{-{\int }_0^{\zeta }-\frac{v\left(\xi \right)}{D}d\xi }}d\zeta +c{e}^{{\int }_0^t-\frac{v\left(\xi \right)}{D}d\xi }, or\\ \mu (v(t))={\mu }_0+a\ln \left(\frac{v}{v_0}\right)+bln(\frac{v_0}{D}{e}^{G\left(v\left(t\right)\right)}{\displaystyle {\int }_0^t{e}^{-H\left(v\left(t\right)\right)}}d\zeta \\ +c{e}^{G\left(v\left(t\right)\right)})n& (7)\end{array}$

The mathematical steps taken to reach these forms, constant velocity solutions, further justification, and consequences of this assumption are discussed further in Appendix A.

Results: Fitting Non-Trivial, High-Velocity Experiments

In order to compare the ability of BSF and RSF for capturing the observed frictional response to realistic rupture, we performed a MCMC inversion (detailed in Appendix B) of the analytical equations above on two sets of high velocity experiments (a third is included in Supplement 3), each with its own benefits and issues representing earthquake rupture. For each study, we digitized the slip-rate and corresponding frictional evolution from published figures and found a best-fitting set of parameters for each model to minimize the misfit (χ²) to the data.

Steady Acceleration/Deceleration From Sone and Shimamoto (2009)

Sone and Shimamoto (2009) utilized a high-velocity rotary-shear apparatus (Hirose and Shimamoto, 2005), to deform samples of recovered Chelungpu fault gouge from the location of the 1999 Chi Chi earthquake. They measured the applied shear stress evolution under a constant normal stress of 0.56 MPa, consistent with the depth of the sample, at constant and varying shear rates. The constant velocity experiments and their model are described and compared with BSF results in Supplement 2. To simulate the slip-rate history of the Chi Chi earthquake, they manually accelerated and decelerated the slip velocity to reproduce a kinematic waveform inversion solution for the approximate sample locality, where the fault accelerated to ~1.9 m/s in 6 s, then decelerated back to stationary in 4 s (Ji et al., 2003). The experiments roughly follow this with constant acceleration/deceleration, except the acceleration increases for the final second to the deceleration rate (Figure 2). The experiment was run five times with slightly different velocity histories, Sone and Shimamoto (2009) provided a representative curve, which we digitized, along with one of the five equivalent measurements of friction evolution. The focus is on capturing the relative magnitude and evolution trends, so digitization errors are not a problem.

FIGURE 2

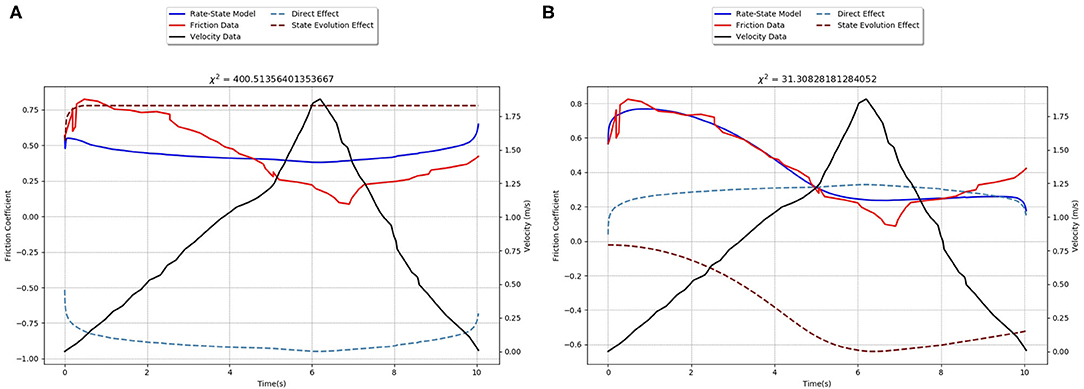
Figure 2. Best-fitting models, with χ²-values given on top of the plots, for the Sone and Shimamoto (2009) steady acceleration/deceleration experimental data. RSF with restricted parameter ranges: (A) a and b [−0.03 to 0.03], D [<1 mm], and v₀ [<10⁻⁴ m/s] are restricted to values consistent with low-velocity measurements, while in (B) only v₀ is restricted to this range. The solid red line is the frictional data; the solid blue line shows the inversion fit for each model; the solid black line is the driving velocity data which the interface is forced at; the dotted blue line is the direct effect term of each friction model; while the dotted brown line is the state evolution term. In order to best fit both terms on the plot with minimal overlap, they are offset. In RSF, μ₀ provides a natural offset, since the friction coefficient is the sum of the two terms and μ₀ (thus the friction coefficient curve is a summation of the two terms, as they are plotted, plus this additional offset). As expected, commonly used RSF parameters cannot capture the dynamic friction evolution at high-velocities, but with the parameters outside of these common ranges, the model is able to reproduce more of the observed frictional evolution stages.

While Sone and Shimamoto (2009) found that RSF with the aging law was not able to capture both the weakening and healing trends of their data with a single set of parameters (their Figure 4), they did not perform a full inversion, but explored the range of behaviors by finding the parameters needed for each trend individually. If parameter values are restricted to the ranges found in low-velocity experiments, the inversion shows that RSF is not able to capture the full amplitude of frictional changes in the data, staying within a narrow range of friction coefficients (Figure 2A). If all the parameters are given a wide range of values except for v₀, which was restricted to values below 10⁻⁴ m/s, then RSF can fit the weakening or healing, but not both (Figure 2B). Both the RSF and BSF models with full flexibility in free parameters are able to capture all three frictional evolution stages (Figure 3). Given BSF's conceptual attention to initial strengthening, as described in section “Bristle-State” Friction Formulation Development and Components, it is better able to match the sharpness of the friction peak, whereas the best-fit RSF model broadens the peak significantly. Yet over all, the two models follow the general trends and have similar goodness-of-fit χ²-values.

FIGURE 3

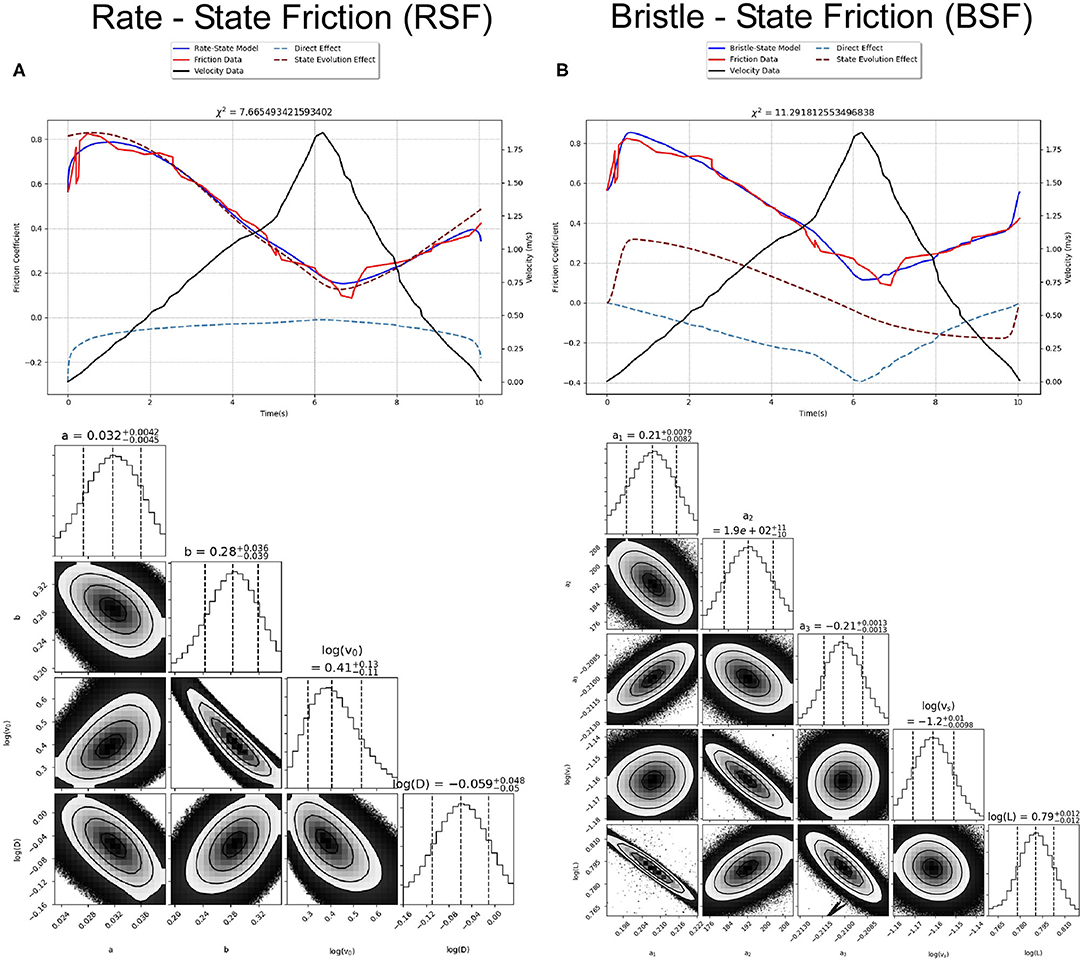
Figure 3. Best-fitting models (same details as Figure 2 above) and MCMC posterior probability distribution corner plots are shown for fully flexible inversions of (A) RSF and (B) BSF. In order to best fit both terms on the plot with minimal overlap, they are offset. RSF doesn't require an additional offset because μ₀ is part of the friction coefficient, but BSF the friction is only the sum of these two terms, so we use the initial friction coefficient (μ(t = 0)) such that the initial values for each term is zero (thus the friction coefficient curve is a summation of the two terms, as they are plotted, plus this additional offset). The triangle plot shows the 1D and 2D projections of the posterior probability distributions of our model parameters. In the 1D plots, the vertical lines show median and the 1-sigma values of the parameters while the 2D histograms show the contour intervals for the 0.5, 1, 1.5, and 2 sigma levels 11.7, 39.3, 67.5, and 86.4% confidence intervals. Although the fully flexible RSF model achieves a slightly lower χ², this includes digitization errors and visual inspection suggests BSF better fits the initial peak.

The parameter v₀ is interesting because it is a relative value, set to be lower than experimental velocities, that is often assumed not to affect the behavior. Commonly set to order ~10⁻⁶ m/s (the lowest experimental velocities), or even as low as background plate tectonic rates (~10⁻¹² m/s), v₀ is the constant velocity at which a steady-state friction is measured. The steady-state friction relation for RSF is ${\mu }_{ss}={\mu }_0+\left(a-b\right)ln\left(\frac{v}{v_0}\right)$, thus μ_ss= μ₀ when v = v₀. When v₀ is left as a free parameter (while the steady-state relationship defines μ₀), the inversion is able to fit the data (Figure 3A), but v₀ must be much higher, in this inversion ~2.5 m/s. This higher v₀ makes the direct effect negative and thus varies its effect more dramatically to capture the initial peak. In many of our best-fit models, v crosses v₀ during the initial strengthening stage, so the direct effect goes from negative to positive and varies greatly compared to a low v₀ where velocity must change orders of magnitude to change the direct effect significantly. These behaviors are outside of the original RSF interpretation.

Although the steady-state friction relation for this form of BSF friction is not ideal (as discussed in Stribeck Curve), Supplement 2 shows the same best-fit parameters were able to reproduce the peak friction of their constant velocity measurements, providing a relation between peak friction and velocity that fits their data much better than their relation. This further supports that the BSF inversion is capturing the underlying frictional behavior.

Spontaneously Developing Slip From Rubino et al. (2017)

Rubino et al. (2017) presents novel measurements of evolving local friction and velocity of dynamic ruptures at different normal stresses in an analog Homalite fault using ultrahigh speed full-field imaging techniques. Since their reported velocities are calculated by imaging the movement at the fault interface, our assumption of applying the actual slip velocity (not a driving velocity) to the model is accurate. The ruptures were induced by rapid expansion of an electrically charged wire filament, but the subsequent slip develops spontaneously. Since the sample has limited dimensions (~200 mm), the entire fault ruptures, not terminating in a healing stage. Still, this dataset offers an opportunity to test each friction models' ability to match the initial strengthening and weakening stages at high slip velocities (up to ~20 m/s), which are spontaneously developed, not prescribed experimentally. The paper shows that rupture propagates steadily along the fault (their Supplementary Figures 3.2a, 3.3a, 3.4a), so we use the data from a single location (showing no evidence of edge effects) at two different normal stress conditions (their Figures 4A,B). They also include data from an intermediate stress condition at a shallower fault angle, but the rupture has a very different slip-rate history, including a reflected super-shear crack, and the friction evolution is too complex, with friction peaking before velocity increase was measured, to model with our simple force balance.

FIGURE 4

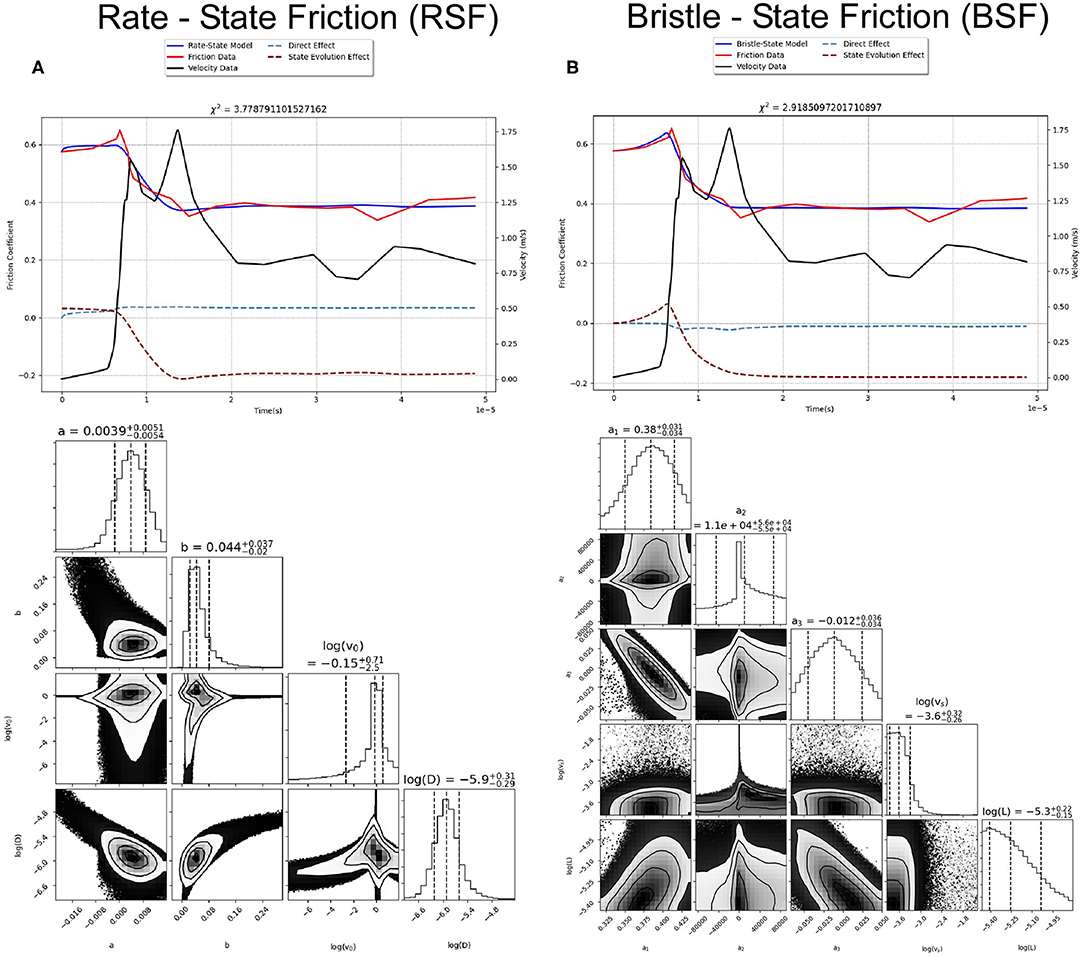
Figure 4. Best-fits of (A) RSF and (B) BSF models to spontaneously developing slip experiment at 5.66 MPa normal stress from Rubino et al. (2017), details are the same as for Figure 3 above.

Rubino et al. (2017) appeal to the combined model of RSF with flash-heating, Equation (1.5) in Supplementary Material, to explain the dramatic weakening at high velocities. They show that the final steady-state friction values for their three experiments fit the steady-state version of this friction law, providing best-fit parameter values (a-b, v₀, μ_w, v_w). They claim that the initial strengthening is quantitatively consistent with the RSF direct effect, but did not model their transient friction measurements. To test this hypothesis, we invert the frictional data for the experiments at normal stresses of 5.66 MPa (Figure 4) and 17.6 MPa (Supplement) using RSF combined with flash-heating (Supplement Figure 4.1b), as well as standard RSF (Figure 4A). We found that the combined model is not able to match the peak friction, given the provided parameter values for either normal stress experiment, offering no improvement to standard RSF. With all six free parameters left free, the inversion was able to find a set of parameters that could match the frictional peak for high normal stress data (Supplement), but not at the lower normal stress (Figure 4A). In comparison, the best-fit BSF model is able to fit the peak at both normal stresses (Figure 4B and Supplement).

Discussion and Conclusion: Model Comparison

The sliding regime framework and the bristle state variable analogy, from engineering and tribology literature, are conceptually useful for addressing slip initiation, as in earthquake nucleation, and transient frictional evolution, as co-seismic slip is never expected to reach steady-state. Although originally designed for low-velocity settings, we show that the BSF formulation is sufficiently flexible to describe the observed frictional evolution in high-velocity, realistic slip-history experiments, performing well relative to (various forms of) RSF. At the same time, we show that RSF can represent aspects of the experimental results, given parameter values outside of common use and interpretation. We do not endorse the use of these extreme parameter values, unrealistically high v₀ was found to be vital for fitting the data, but it should be noted that parameters from current RSF simulations are not consistent with these experiments. Although this inconsistency has been known for the magnitude of steady-state high-velocity weakening [motivating the development of new laws such as flash-heating (Rice, 1999)], we highlight that the transient evolution also requires modification. We acknowledge that since BSF is new to rock friction, there is little context to evaluate or interpret BSF parameter values; this will be undertaken in future work by exploring a wide range of rock friction experiments.

As expected, the BSF model shows clear benefits for fitting the initial strengthening stage, due to the attention to pre-sliding and transition processes. Although the overall χ²-values are not always significantly different, visual inspection shows that BSF fits the rate and magnitude of peak friction better than RSF. In Figure 3A RSF smooths out the frictional peak significantly compared to the data and (b) BSF fit. Figure 4A shows a low RSF peak friction, earlier than the data and (b) BSF initial evolution. The supplementary examples show similar behavior, and in those cases that RSF can fit the frictional peak relatively well, the overall χ² is much poorer. These results suggest that BSF might prove a useful parameterization for friction during the initiation of slip and thus inform models of earthquake nucleation.

In this study, we are only representing the temporal evolution of friction in a single location undergoing realistic slip-rate histories, but applying these parameterizations to finite fault dynamic rupture models could help address the interplay between temporal frictional evolution and spatial heterogeneities, such as fluid pressure. Observations of preslip nucleation often appeal to spatially varying conditions to explain how aseismic slip grows into seismic events, but models that capture the friction evolution to peak could explore the possible contribution of temporally evolving friction on this behavior.

Data Availability Statement

The digitized datasets, inversion code, and MCMC results used for the analysis are provided as Supplementary files at DOI: 10.6084/m9.figshare.11473530. The original authors should be contacted in order to obtain the non-digitized datasets.

Author Contributions

SS was responsible for the writing, analysis, and formulation of the study. TM was responsible for the inversion, as well as contribution to the writing and analysis. JGFC contributed to the formulation and literature background. JC provided resources. All authors contributed to the article and approved the submitted version.

Funding

SS acknowledges the support of the Lamont-Doherty Fellowship in Earth and Environmental Sciences. TM acknowledges graduate funding support from the NSF grant EAR/#1615203. JGFC acknowledges the sponsorship of the National Research Center for Integrated Natural Disaster Management ANID/FONDAP/15110017, as well as grant no. 15090013 (Andean Geothermal Center of Excellence, CEGA).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Many thanks to B. P. Bonner, B. Delbridge, P. Bhattacharya, A.M. Rubin, C. Marone, and R. Madariaga for fruitful discussions. Reviewer’s comments also improved the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.00373/full#supplementary-material

References

Al-Bender, F., Lampaert, V., and Swevers, J. (2004). Modeling of dry sliding friction dynamics: from heuristic models to physically motivated models and back. CHAOS 14, 446–460. doi: 10.1063/1.1741752

PubMed Abstract | CrossRef Full Text | Google Scholar

Aström, K. J., and De Wit, C. C. (2008). Revisting the LuGre friction model. IEEE Control Systems Magazine. 28, 101-114. doi: 10.1109/MCS.2008.929425

CrossRef Full Text | Google Scholar

Boitnott, G. N., Biegel, R. L., and Scholz, C. H. (1992). Micromechanics of rock friction 2: quantitative modeling initial friction with contact theory. J. Geophys. Res. 97, 8965–8978. doi: 10.1029/92JB00019

CrossRef Full Text | Google Scholar

Brodsky, E. E., Mori, J. J., Anderson, L., Chester, F. M., Conin, M., Dunham, E. M., et al. (2020). The state of stress before, during, and after a major earthquake. Annu. Rev. Earth Planet. Sci. 48, 2.1–2.26. doi: 10.1146/annurev-earth-053018-060507

CrossRef Full Text | Google Scholar

Brune, J. N. (1970). Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. 75, 4997–5009. doi: 10.1029/JB075i026p04997

CrossRef Full Text | Google Scholar

Chang, J. C., Lockner, D. A., and Reches, Z. (2012). Rapid acceleration leads to rapid weakening in earthquake-like laboratory experiments. Science 338, 101–105. doi: 10.1126/science.1221195

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Carpenter, B. M., and Reches, Z. (2020). Asperity failure control of stick–slip along brittle faults. Pure Appl. Geophys. 117, 3225–3242. doi: 10.1007/s00024-020-02434-y

CrossRef Full Text | Google Scholar

Dahl, P. R. (1968). A Solid Friction Model. No. TOR-0158 (3107-18)-1. El Segundo, CA: The Aerospace Corporation.

Google Scholar

Dahl, P. R. (1976). Solid friction damping in mechanical vibrations. AIAA J. 14, 1675–1682. doi: 10.2514/3.61511

CrossRef Full Text | Google Scholar

de Wit, C. C., Olsson, H., Astrom, K. J., and Lischinsky, P. (1993). “Dynamic friction models and control design,” in 1993 American Control Conference (San Francisco, CA: IEEE), 1920–1926.

Google Scholar

Di Toro, G., Goldsby, D. L., and Tullis, T. E. (2004). Friction falls towards zero in quartz rock as slip velocity approaches seismic rates. Nature 427, 436–439. doi: 10.1038/nature02249

PubMed Abstract | CrossRef Full Text | Google Scholar

Dieterich, J. H. (1979). Modeling of rock friction: 1. Experimental results and constitutive equations. J. Geophys. Res. 84, 2161–2168. doi: 10.1029/JB084iB05p02161

CrossRef Full Text | Google Scholar

Drincic, B., and Bernstein, D. S. (2012). A frictionless bristle-based friction model that exhibits hysteresis and stick-slip behavior. J. Sound Vibrat. doi: 10.1109/ACC.2011.5991180

CrossRef Full Text | Google Scholar

Goldsby, D. L., and Tullis, T. (2011). Flash heating leads to low frictional strength of crustal rocks at earthquake slip rates. Science 334, 216–218. doi: 10.1126/science.1207902

PubMed Abstract | CrossRef Full Text | Google Scholar

Haessig, D. A., and Friedland, B. (1991). On the modeling and simulation of friction. J. Dyn. Sys. Meas. Control. 113, 354–362. doi: 10.1115/1.2896418

CrossRef Full Text | Google Scholar

Heaton, T. H. (1990). Evidence for and implications of self-healing pulses of slip in earthquake rupture. Phys. Earth Planet. Inter. 64, 1–20. doi: 10.1016/0031-9201(90)90002-F

CrossRef Full Text | Google Scholar

Hirose, T., and Shimamoto, T. (2005). Growth of a molten zone as a mechanism of slip weakening of simulated faults in gabbro during frictional melting. J. Geophys. Res. 110:B05202. doi: 10.1029/2004JB003207

CrossRef Full Text | Google Scholar

Hung, C. C., Kuo, L. W., Spagnuolo, E., Wang, C. C., Di Toro, G., Wu, W. J., et al. (2019). Grain fragmentation and frictional melting during initial experimental deformation and implications for seismic slip at shallow depths. J. Geophys. Res. Solid Earth 124, 11150–11169. doi: 10.1029/2019JB017905

CrossRef Full Text | Google Scholar

Ji, C., Helmberger, D. V., Wald, D. J., and Ma, K. F. (2003). Slip history and dynamic implications of the 1999 Chi-Chi, Taiwan, earthquake. J. Geophys. Res. 108:2412. doi: 10.1029/2002JB001764

CrossRef Full Text | Google Scholar

Kitajima, H., Chester, F. M., and Chester, J. S. (2011). Dynamic weakening of gouge layers in high-speed shear experiments: Assessment of temperature-dependent friction, thermal pressurization, and flash heating. J. Geophys. Res. Solid Earth 116, 1–19. doi: 10.1029/2010JB007879

CrossRef Full Text | Google Scholar

Lapusta, N. (2009). Seismology: the roller coaster of fault friction. Nat. Geosci. 2:676. doi: 10.1038/ngeo645

CrossRef Full Text | Google Scholar

Latour, S., Schubnel, A., Nielsen, S., Madariaga, R., and Vinciguerra, S. (2013). Characterization of nucleation during laboratory earthquakes. Geophys. Res. Lett. 40, 5064–5069. doi: 10.1002/grl.50974

CrossRef Full Text | Google Scholar

Liao, Z., and Reches, Z. E. (2019). An experimentally-based friction law for high-velocity, long-displacement slip-pulse events during earthquakes. Earth Planet. Sci. Lett. 515, 209–220. doi: 10.1016/j.epsl.2019.03.032

CrossRef Full Text | Google Scholar

Liu, Y. F., Li, J., Zhang, Z. M., Hu, X. H., and Zhang, W. J. (2015). Experimental comparison of five friction models on the same test-bed of the micro stick-slip motion system. Mech. Sci. 6, 15–28. doi: 10.5194/ms-6-15-2015

CrossRef Full Text | Google Scholar

Lyu, Z., Riviere, J., Yang, Q., and Marone, C. (2019). On the mechanics of granular shear: the effect of normal stress and layer thickness on stick-slip properties. Tectonophysics 763, 86–99. doi: 10.1016/j.tecto.2019.04.010

CrossRef Full Text | Google Scholar

McLaskey, G. C., Kilgore, B. D., and Beeler, N. M. (2015). Slip-pulse rupture behavior on a 2 m granite fault. Geophys. Res. Lett. 42, 7039–7045. doi: 10.1002/2015GL065207

CrossRef Full Text | Google Scholar

Mindlin, R. D. (1949). Compliance of elastic bodies in contact. J. Appl. Mech. 6, 259–268.

Google Scholar

Niemeijer, A., Di Toro, G., Nielsen, S., and Di Felice, F. (2011). Frictional melting of gabbro under extreme experimental conditions of normal stress, acceleration, and sliding velocity. J. Geophys. Res. 116:B07404. doi: 10.1029/2010JB008181

CrossRef Full Text | Google Scholar

Passelègue, F. X., Schubnel, A., Nielsen, S., Bhat, H. S., Deldicque, D., and Madariaga, R. (2016). Dynamic rupture processes inferred from laboratory microearthquakes. J. Geophys. Res. Solid Earth 121, 4343–4365. doi: 10.1002/2015JB012694

CrossRef Full Text | Google Scholar

Pennestrì, E., Rossi, V., Salvini, P., and Valentini, P. P. (2016). Review and comparison of dry friction force models. Nonlinear Dynam. 83, 1785–1801. doi: 10.1007/s11071-015-2485-3

CrossRef Full Text | Google Scholar

Rattez, H., and Veveakis, E. (2019). Weak phases production and heat generation controls fault friction during seismic slip. Nat. Commun. 11:350. doi: 10.31223/osf.io/xupr8

PubMed Abstract | CrossRef Full Text | Google Scholar

Reches, Z., and Lockner, D. A. (2010). Fault weakening and earthquake instability by powder lubrication Nature 467, 452–455. doi: 10.1038/nature09348

CrossRef Full Text | Google Scholar

Rice, J. R. (1999). Flash heating at asperity contacts and rate-dependent friction. Eos Trans. AGU Fall Meet. Suppl. 80:F681.

Google Scholar

Roeloffs, E. A. (2006). Evidence for aseismic deformation rate changes prior to earthquakes. Annu. Rev. Earth Planet. Sci. 34, 591–627. doi: 10.1146/annurev.earth.34.031405.124947

CrossRef Full Text | Google Scholar

Rubino, V., Rosakis, A. J., and Lapusta, N. (2017). Understanding dynamic friction through spontaneously evolving laboratory earthquakes. Nat. Commun. 8:15991. doi: 10.1038/ncomms15991

PubMed Abstract | CrossRef Full Text | Google Scholar

Saltiel, S., Bonner, B. P., and Ajo-Franklin, J. B. (2017a). Strain-dependent partial slip on rock fractures under seismic-frequency torsion. Geophys. Res. Lett. 44, 4756–4764. doi: 10.1002/2017GL073108

CrossRef Full Text | Google Scholar

Saltiel, S., Bonner, B. P., Mittal, T., Delbridge, B., and Ajo-Franklin, J. (2017b). Experimental evidence for dynamic friction on rock fractures from frequency-dependent nonlinear hysteresis and harmonic generation. J. Geophys. Res. Solid Earth 122, 4982–4999. doi: 10.1002/2017JB014219

CrossRef Full Text | Google Scholar

Scholz, C. H. (2019). The Mechanics of Earthquakes and Faulting, 3rd Edn. Cambridge: Cambridge University Press.

Google Scholar

Selvadurai, P. A., Parker, J. M., and Glaser, S. D. (2017). Numerical modeling describing the effects of heterogeneous distributions of asperities on the quasi-static evolution of frictional slip. Rock Mech. Rock Eng. 50, 3323–3335. doi: 10.1007/s00603-017-1333-9

CrossRef Full Text | Google Scholar

Socquet, A., Valdes, J. P., Jara, J., Cotton, F., Walpersdorf, A., Cotte, N., et al. (2017). An 8 month slow slip event triggers progressive nucleation of the 2014 Chile megathrust. Geophys. Res. Lett. 44, 4046–4053. doi: 10.1002/2017GL073023

CrossRef Full Text | Google Scholar

Sone, H., and Shimamoto, T. (2009). Frictional resistance of faults during accelerating and decelerating earthquake slip. Nat. Geosci. 2:705. doi: 10.1038/ngeo637

CrossRef Full Text | Google Scholar

Stribeck, R. (1902). Die wesentlichen eigenschaften der gleit- und rollenlager – The key qualities of sliding and roller bearings. Z. Vereines Seutscher Ing. 48, 1342–1348, 1432–1437.

Google Scholar

Svetlizky, I., Bayart, E., and Fineberg, J. (2018). Brittle fracture theory describes the onset of frictional motion. Annu. Rev. Condens. Matter Phys. 10, 253–273. doi: 10.1146/annurev-conmatphys-031218-013327

CrossRef Full Text | Google Scholar

Tinti, E., Fukuyama, E., Piatanesi, A., and Cocco, M. (2005). A kinematic source-time function compatible with earthquake dynamics. Bull. Seismol. Soc. Am. 95, 1211–1223. doi: 10.1785/0120040177

CrossRef Full Text | Google Scholar

Van der Elst, N. J., Brodsky, E. E., Le Bas, P. Y., and Johnson, P. A. (2012). Auto-acoustic compaction in steady shear flows: experimental evidence for suppression of shear dilatancy by internal acoustic vibration. J. Geophys. Res. Solid Earth 117:04. doi: 10.1029/2011JB008897

CrossRef Full Text | Google Scholar

Violay, M., Nielsen, S., Spagnuolo, E., Cinti, D., Di Toro, G., and Di Stefano, G. (2013). Pore fluid in experimental calcite-bearing faults: abrupt weakening and geochemical signature of co-seismic processes. Earth Planet. Sci. Lett. 361, 74–84. doi: 10.1016/j.epsl.2012.11.021

CrossRef Full Text | Google Scholar

Violay, M., Passelegue, F., Spagnuolo, E., Di Toro, G., and Cornelio, C. (2019). Effect of water and rock composition on re-strengthening of cohesive faults during the deceleration phase of seismic slip pulses. Earth Planet. Sci. Lett. 522, 55–64. doi: 10.1016/j.epsl.2019.06.027

CrossRef Full Text | Google Scholar

Wald, D. J. (1996). Slip history of the 1995 Kobe, Japan, earthquake determined from strong motion, teleseismic, and geodetic data. J. Phys. Earth 44, 489–503. doi: 10.4294/jpe1952.44.489

CrossRef Full Text | Google Scholar